MetaTrader 5 / テスター
English Русский 中文 Español Português
preview
血液型遺伝最適化(BIO)

血液型遺伝最適化(BIO)

MetaTrader 5 — テスター |
18 0
Andrey Dik
Andrey Dik

内容

  1. はじめに
  2. アルゴリズムの実装
  3. テスト結果


はじめに

ある日、検査室で看護師が患者から採血している様子を見ていたとき、ふとした考えが頭に浮かびました。世代から世代へと厳密な遺伝法則に従って受け継がれてきた血液型という古くからの仕組みが、まったく新しい視点で目の前に現れたのです。この自然な遺伝の性質を最適化アルゴリズムの分野で活用できたらどうなるだろうかと考えたのです。

私たちはそれぞれ、親から受け継いだ固有の組み合わせを持っています。血液型が輸血時の適合性を決定するように、最適化においても、パラメータがどのように継承され、どのように突然変異するかを決定できるのではないかと考えました。このアイデアが気に入り、研究の時間が取れたときに改めて取り組むことにしました。そして実験を重ねた結果、血液型遺伝最適化(BIO)アルゴリズムが誕生しました。これは、血液型の遺伝という自然法則を、解の進化を制御するための比喩として用いた手法です。このアルゴリズムでは、4つの血液型が、パラメータ変異に対する4つの異なる戦略へと進化し、遺伝の法則が子孫がどのように親の特性を獲得し、修正するかを決定します。

自然界と同様に、子の血液型は親の血液型の単純な平均ではなく、遺伝法則に従って決まります。BIOにおいても、新しい解のパラメータは、継承と突然変異の仕組みを通じて形成されます。それぞれの血液型は、解空間を探索するための独自のアプローチをもたらします。これには、見つかった最良の値を保守的に維持するものから、新たな有望領域や探索方向を切り開く大胆な突然変異までが含まれます。

本記事では、生物学的な着想とアルゴリズムとしての厳密さを融合させたBIOアルゴリズムの原理を紹介し、すでにおなじみの関数を用いたテスト結果を示します。それでは、始めていきましょう。


アルゴリズムの実装

まず、親から子へ血液型がどのように遺伝するのかを示した表を見てみましょう。ご覧のとおり、血液型の遺伝は一様ではありません。世界人口における血液型分布には興味深い統計があります。最も多いのは血液型1（O型）で、世界人口の約40%が該当します。次に多いのが血液型2（A型）で、約30%の人が持っています。血液型3（B型）は約20%、そして血液型4（AB型）は最も少なく、全体の約10%しか存在しません。

遺伝の仕組みを調べる中で、血液型1は他のすべての血液型に対して劣性であることを知りました。つまり、血液型1の人は、子どもに血液型1しか伝えることができません。一方で、血液型2と血液型3は互いに共優性を示し、両者が組み合わさることで血液型4が生まれます。進化の観点から見ると、血液型4は最も新しい血液型だと言えます。

私は、血液型が持ついくつかの独特な性質にも強い関心を持ちました。たとえば、血液型1は「万能供血者」として知られており、どの血液型の人にも輸血することができます。これに対して血液型4は「万能受血者」であり、どの血液型の血液でも受け取ることができます。 

これら血液型システムの特徴すべてが、私のアルゴリズムに対応する仕組みを組み込む着想となりました。血液型1は基本であり、かつ最も一般的であるため、アルゴリズムにおいては「見つかった最良解を保持する戦略」に対応させています。親の血液型の組み合わせと、子が取り得る血液型を示す血液型遺伝表は、親解の「血液型」に基づいて新しい解の「血液型」を決定する基盤となり、それがBIOアルゴリズムにおけるパラメータ変異の方法へ直接影響します。

血液型

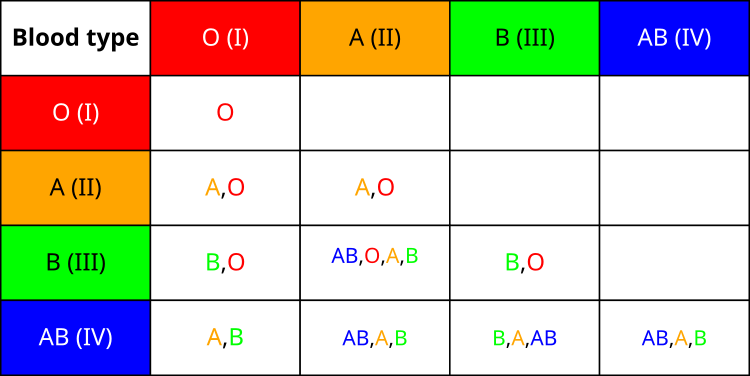
図1：血液型遺伝表 

BIOアルゴリズムは、非常にシンプルなアイデアに基づいています。集団内の各解（親個体）は、それぞれ1から4までの固有の「血液型」を持ち、これは集団内での順序番号によって決定されます。新しい世代の解を生成する際には、現在の集団から2つの「親」を選択します。その選択確率は線形ではなく二次的であり、優れた解ほど親として選ばれる確率が大幅に高くなります。

ここからが最も興味深い部分です。親の血液型に基づき、特別な遺伝行列（コード内ではInitメソッドに記述されている）を用いて、「子」である新しい解が取り得る血液型を決定します。その後、この新しい解の各パラメータについて処理をおこないます。もし血液型1が選ばれた場合、そのパラメータには現在見つかっている最良解の値を使用します。これは、血液型1が万能供血者であるという性質になぞらえたものです。血液型2が選択された場合は、親のどちらか一方から値を取得し、それに冪乗します。これにより、パラメータ範囲の端を探索しやすくなります。血液型3では、親の値を取得したうえで、それを最良解の方向へランダムな量だけ近づけます。そして血液型4では、親の値をパラメータ範囲の境界に対して反転させる、いわば反転操作をおこない、新たな探索領域を開拓します。

新しい世代を生成した後、現在の大域最良解よりも優れた解が現れていないかを確認し、次の反復のために最良の個体を保存します。このようにして、血液型遺伝のアナロジーを用いながら、異なるパラメータ変異戦略を組み合わせて解空間を探索するのがBIOアルゴリズムです。以下に、アルゴリズムの疑似コードを示します。

初期化

  1. popSize（デフォルト50）のエージェントからなる集団を生成します。
  2. 両親の血液型（1、2、3、4）に基づいて子の血液型候補を決定する血液型遺伝行列を作成します。
  3. パラメータの範囲（最小値、最大値、ステップ値）を初期化します。

メインループ

  1. 最初の反復の場合(revision=false)
    • すべてのエージェントの位置をパラメータ範囲内でランダムに初期化
    • revisionフラグをtrueに設定
  2. 集団内の各エージェントについて：
    • 二次的な確率分布を用いて親エージェント（父親と母親）を選択
    • bloodType = 1 + (population_position % 4)により両親の血液型を決定
    • 子解の各パラメータについて：
      • 両親の血液型に基づき、遺伝行列から子の血液型候補を取得
      • 子が血液型1の場合：
        • そのパラメータに最良既知解の値を使用
      • それ以外の場合：
        • 父親または母親のいずれかからパラメータ値をランダムに選択
        • 子の血液型に応じて変異を適用：
          • 血液型2：指数20のべき乗分布を適用
          • 血液型3：ランダム係数を用いて最良解の方向へ移動
          • 血液型4：パラメータ範囲全体に対して値を反転
      • パラメータが許容範囲およびステップ内に収まることを保証

改訂フェーズ

  1. いずれかのエージェントがより良い適応度を持つ場合、大域最良解を更新します。
  2. 現在の集団を拡張された集団配列の後半へコピーします。
  3. 適応度に基づいて拡張集団をソートします。
  4. 次世代のために最良のエージェントを保持します。

それでは、アルゴリズムコードの記述を始めましょう。C_AO_BIOクラスはC_AOから派生し、BIOアルゴリズムを実装します。このクラスは、個体（エージェント）を表現するデータ構造と、それらを制御する仕組みを前提としています。

    C_AO_BIO()：コンストラクタです。外部BIOパラメータを初期化し、集団サイズpopSizeを50に設定します。また、paramsパラメータ配列のサイズを、popSizeを表す1要素に設定します。
    SetParams()    ：クラスのパラメータを設定するメソッドで、この場合はパラメータ配列からpopSizeを設定します。
    Init ()    ：パラメータの最小値、最大値、変更ステップ、エポック数を受け取り、アルゴリズムを初期化するメソッドです。
    Moving ()およびRevision ()：集団内のエージェントの移動（進化）と、その評価および最良個体の選択を担当するメソッドです。
    S_PapaおよびS_Mama：
    • S_Papaは血液型配列(bTypes)を含む構造体です。
    • S_Mamaは4つのS_Papaオブジェクトの配列を持ち、遺伝的組み合わせのための「親」の存在を示します。

    このように構造体で表現することで、親の血液型を指定するだけで子の血液型候補を直接取得できます。たとえば「ma[1].pa[2].bTypes」のように指定し、1と2はそれぞれ母親と父親の血液型を表します。

    GetBloodType()メソッドは、指定されたエージェントの血液型を返し、GetBloodMutation ()メソッドは、血液型に応じた遺伝子変異の仕組みを実装します。

    //——————————————————————————————————————————————————————————————————————————————
class C_AO_BIO : public C_AO
{
  public: //--------------------------------------------------------------------
  C_AO_BIO ()
  {
    ao_name = "BIO";
    ao_desc = "Blood Inheritance Optimization";
    ao_link = "https://www.mql5.com/ja/articles/17246";

    popSize = 50; // population size

    ArrayResize (params, 1);
    params [0].name = "popSize"; params [0].val = popSize;
  }

  void SetParams ()
  {
    popSize = (int)params [0].val;
  }

  bool Init (const double &rangeMinP  [],  // minimum values
             const double &rangeMaxP  [],  // maximum values
             const double &rangeStepP [],  // step change
             const int     epochsP = 0);   // number of epochs

  void Moving   ();
  void Revision ();

  private: //-------------------------------------------------------------------
  struct S_Papa
  {
      int bTypes [];
  };
  struct S_Mama
  {
      S_Papa pa [4];
  };
  S_Mama ma [4];

  S_AO_Agent p [];

  int  GetBloodType     (int ind);
  void GetBloodMutation (double &gene, int indGene, int bloodType);
};
//——————————————————————————————————————————————————————————————————————————————

    Initメソッドは、C_AO_BIOクラスのインスタンスを初期化し、エージェント集団とその特性を設定することで、アルゴリズムを実行可能な状態に準備します。ここでは、このメソッドの実装内容を見ていきます。

    StandardInitメソッドの呼び出し：最初の行ではStandardInitメソッドを呼び出し、その戻り値をチェックします。このメソッドは、アルゴリズムが動作するために必要な基本パラメータが正しく設定されているかを確認し、必要に応じて初期化をおこないます。

    エージェント配列の初期化

    • まず、エージェント配列pのサイズを、指定された集団サイズ(popSize)の2倍に拡張します。
    • 次にforループ内で、各エージェントに対してInitメソッドを呼び出し、座標パラメータを用いてエージェントを初期化します。
    血液型の初期化
    • 続いて、S_MamaおよびS_Papa構造体に含まれる血液型配列(bTypes)のサイズを設定します。
    • ma[0].pa[0]やma[1].pa[2]など、親の血液型の組み合わせごとに、特別な遺伝行列に基づいて子の血液型候補が設定され、それぞれArrayResizeを用いて配列サイズが指定されます。

    このように、C_AO_BIOクラスのInitメソッドは、最適化アルゴリズムを実行するための重要な準備処理を担っています。具体的には、エージェント集団の生成、初期パラメータの設定、そして血液型の関連付け規則（遺伝規則）の定義をおこないます。これにより、子孫の取り得る血液型を即座に取得できるようになり、さらに「血液型」に基づくパラメータを用いたアルゴリズム内での進化処理を可能にしています。

    //——————————————————————————————————————————————————————————————————————————————
bool C_AO_BIO::Init (const double &rangeMinP  [],
                     const double &rangeMaxP  [],
                     const double &rangeStepP [],
                     const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (p, popSize * 2);
  for (int i = 0; i < popSize * 2; i++) p [i].Init (coords);

  //1-1
  ArrayResize (ma [0].pa [0].bTypes, 1);

  ma [0].pa [0].bTypes [0] = 1;

  //2-2
  ArrayResize (ma [1].pa [1].bTypes, 2);

  ma [1].pa [1].bTypes [0] = 1;
  ma [1].pa [1].bTypes [1] = 2;

  //3-3
  ArrayResize (ma [2].pa [2].bTypes, 2);

  ma [2].pa [2].bTypes [0] = 1;
  ma [2].pa [2].bTypes [1] = 3;

  //1-2; 2-1
  ArrayResize (ma [0].pa [1].bTypes, 2);
  ArrayResize (ma [1].pa [0].bTypes, 2);

  ma [0].pa [1].bTypes [0] = 1;
  ma [0].pa [1].bTypes [1] = 2;

  ma [1].pa [0].bTypes [0] = 1;
  ma [1].pa [0].bTypes [1] = 2;

  //1-3; 3-1
  ArrayResize (ma [0].pa [2].bTypes, 2);
  ArrayResize (ma [2].pa [0].bTypes, 2);

  ma [0].pa [2].bTypes [0] = 1;
  ma [0].pa [2].bTypes [1] = 3;

  ma [2].pa [0].bTypes [0] = 1;
  ma [2].pa [0].bTypes [1] = 3;

  //1-4; 4-1
  ArrayResize (ma [0].pa [3].bTypes, 2);
  ArrayResize (ma [3].pa [0].bTypes, 2);

  ma [0].pa [3].bTypes [0] = 2;
  ma [0].pa [3].bTypes [1] = 3;

  ma [3].pa [0].bTypes [0] = 2;
  ma [3].pa [0].bTypes [1] = 3;

  //2-3; 3-2
  ArrayResize (ma [1].pa [2].bTypes, 4);
  ArrayResize (ma [2].pa [1].bTypes, 4);

  ma [1].pa [2].bTypes [0] = 1;
  ma [1].pa [2].bTypes [1] = 2;
  ma [1].pa [2].bTypes [2] = 3;
  ma [1].pa [2].bTypes [3] = 4;

  ma [2].pa [1].bTypes [0] = 1;
  ma [2].pa [1].bTypes [1] = 2;
  ma [2].pa [1].bTypes [2] = 3;
  ma [2].pa [1].bTypes [3] = 4;

  //2-4; 4-2; 3-4; 4-3; 4-4
  ArrayResize (ma [1].pa [3].bTypes, 3);
  ArrayResize (ma [3].pa [1].bTypes, 3);
  ArrayResize (ma [2].pa [3].bTypes, 3);
  ArrayResize (ma [3].pa [2].bTypes, 3);
  ArrayResize (ma [3].pa [3].bTypes, 3);

  ma [1].pa [3].bTypes [0] = 2;
  ma [1].pa [3].bTypes [1] = 3;
  ma [1].pa [3].bTypes [2] = 4;

  ma [3].pa [1].bTypes [0] = 2;
  ma [3].pa [1].bTypes [1] = 3;
  ma [3].pa [1].bTypes [2] = 4;

  ma [2].pa [3].bTypes [0] = 2;
  ma [2].pa [3].bTypes [1] = 3;
  ma [2].pa [3].bTypes [2] = 4;

  ma [3].pa [2].bTypes [0] = 2;
  ma [3].pa [2].bTypes [1] = 3;
  ma [3].pa [2].bTypes [2] = 4;

  ma [3].pa [3].bTypes [0] = 2;
  ma [3].pa [3].bTypes [1] = 3;
  ma [3].pa [3].bTypes [2] = 4;

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

    Movingメソッドは、継承と突然変異の概念をエージェントの集団に適用して、最適化プロセスで進化的なステップを実行します。もう少し詳しく見てみましょう。

    修正の必要性の確認：メソッドの最初の部分では、エージェントを更新または「移動」する必要があるかどうかを確認し、revisionがfalseの場合、エージェントの座標（a [i] .c [j]）の初期化（または更新）がおこなわれます。

    • 各エージェントは、u.RNDfromCIメソッドを使用して範囲[rangeMin [j]、rangeMax [j]で生成されたランダムな値を受け取ります。
    • 次に、u.SeInDiSpを使用して値を必要な範囲に収め、rangeStepで指定されたステップを適用します。

    修正状態への切り替え：最初の反復の後、次のステージに切り替えられるようにrevisionパラメータがtrueに設定され、メソッドは実行を完了します（戻ります）。

    変数の初期化：メソッドの開始時に、ランダム値と両親の血液型を担当する変数が初期化されます (papIND、mamIND、pBloodType、mBloodType、cBloodType、bloodIND)。

    基本的な集団ループ(popSize)：このメソッドは、集団内の各エージェントに対してループを実行します。

    • 親のランダムなインデックス（papINDとmamIND）は、ランダム確率を生成するu.RNDprobab()メソッドを用いて決定されます。
    • GetBloodType関数によって、両親の血液型が取得されます。

    座標によるループ(coords)：各エージェント座標のメインループ内：

    • 選択された親のbTypes配列から、ランダムに血液型インデックスが選択されます（母親と父親の血液型に基づく）。
    • 選択された血液型が1の場合、エージェントはcB[c]の値を取得します。それ以外の場合は、混合がおこなわれます。
      • エージェントの座標値は、父親または母親のどちらかからランダムに選ばれます。
      • GetBloodMutation関数を用いて、血液型に基づき選ばれた値が変異されます。
      • u.SeInDiSpメソッドで値が調整され、許容範囲内に収まるようにします。

    Movingメソッドは、集団の進化を模倣するアルゴリズムの重要な部分で、ランダムな初期化と、血液型遺伝の原理に基づくエージェントパラメータの変異と組み合わせのメカニズムを含みます。このメソッドは、ランダム性と遺伝性の要素を組み合わせ、新しい子孫を作成し、異なる値を持つ個体を生成します。これにより、解空間におけるさらなる最適化や探索の準備が整います。

    //——————————————————————————————————————————————————————————————————————————————
void C_AO_BIO::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int j = 0; j < coords; j++)
      {
        a [i].c [j] = u.RNDfromCI (rangeMin [j], rangeMax [j]);
        a [i].c [j] = u.SeInDiSp (a [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]);
      }
    }
    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  double rnd        = 0.0;
  int    papIND     = 0;
  int    mamIND     = 0;
  int    pBloodType = 0;
  int    mBloodType = 0;
  int    cBloodType = 0;
  int    bloodIND   = 0;

  for (int i = 0; i < popSize; i++)
  {
    rnd = u.RNDprobab ();
    rnd *= rnd;
    papIND = (int)u.Scale (rnd, 0.0, 1.0, 0, popSize - 1);

    rnd = u.RNDprobab ();
    rnd *= rnd;
    mamIND = (int)u.Scale (rnd, 0.0, 1.0, 0, popSize - 1);

    pBloodType = GetBloodType (papIND);
    mBloodType = GetBloodType (mamIND);

    for (int c = 0; c < coords; c++)
    {
      bloodIND   = MathRand () % ArraySize (ma [mBloodType - 1].pa [pBloodType - 1].bTypes);
      cBloodType = ma [mBloodType - 1].pa [pBloodType - 1].bTypes [bloodIND];

      if (cBloodType == 1) a [i].c [c] = cB [c];
      else
      {
        if (u.RNDbool () < 0.5) a [i].c [c] = p [papIND].c [c];
        else                    a [i].c [c] = p [mamIND].c [c];

        GetBloodMutation (a [i].c [c], c, cBloodType);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

    GetBloodTypeメソッドは、渡されたindインデックス（現在の集団内の位置）に基づいて血液型を決定します。このメソッドは、単純な剰余演算を用いてインデックスと血液型を対応させます。これにより、利用可能なインデックス（0〜3）の間で血液型が循環的に分配される仕組みになっています。

    //——————————————————————————————————————————————————————————————————————————————
int C_AO_BIO::GetBloodType (int ind)
{
  if (ind % 4 == 0) return 1;
  if (ind % 4 == 1) return 2;
  if (ind % 4 == 2) return 3;
  if (ind % 4 == 3) return 4;

  return 1;
}
//——————————————————————————————————————————————————————————————————————————————

    GetBloodMutationメソッドは、血液型とインデックスに応じて遺伝パラメータ（遺伝子）の値を変更（突然変異）するために設計されています。

    パラメータは次のとおりです。

    • gene：変更される遺伝子値への参照
    • indGene：突然変異の範囲を取得するための遺伝子インデックス
    • bloodType：突然変異のロジックを決定する血液型

    血液型2：PowerDistributionが遺伝子値に適用されます。指定された範囲に基づき遺伝子が変化し、確率的に値が分布します。

    血液型3：遺伝子は、cB[indGene]集団内のその遺伝子の現在の最良値と現在値の差の一部だけ増加します。この割合（バイアス）は[0.0, 1.0]のランダム値によって決まります。

    その他の血液型（デフォルト）：遺伝子は、指定された範囲に対して対称（逆）になるように変更されます。新しい値はrangeMin[indGene]とrangeMax[indGene]の間に収まります。

    //——————————————————————————————————————————————————————————————————————————————
void  C_AO_BIO::GetBloodMutation (double &gene, int indGene, int bloodType)
{
  switch (bloodType)
  {
    case 2:
      gene = u.PowerDistribution (gene, rangeMin [indGene], rangeMax [indGene], 20);
      return;
    case 3:
      gene += (cB [indGene] - gene) * u.RNDprobab ();
      return;
    default:
    {
      gene = rangeMax [indGene] - (gene - rangeMin [indGene]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

    Revisionメソッドは、BIOアルゴリズムにおける集団の更新とソートを担当します。最初のforループ（0からpopSizeまで）では、メソッドはa[i]集団のすべてのメンバーを順に処理します。現在のa[i].f個体の適合度関数値fが、現在の最良値fBを上回る場合、fBは新しい値で更新され、現在の個体の座標cがcB配列にコピーされます。2番目のforループでは、a[i]集団の現在のメンバーがp配列の末尾（popSizeインデックスから）にコピーされます。次にpT配列が作成されます。これは現在の集団サイズの2倍(popSize * 2)です。最後にu.Sortingソートメソッドが呼び出され、統合されたp配列をソートし、その結果をpTに格納します。

    //——————————————————————————————————————————————————————————————————————————————
void C_AO_BIO::Revision ()
{
  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    // Update the best global solution
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ArrayCopy (cB, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    p [popSize + i] = a [i];
  }

  S_AO_Agent pT []; ArrayResize (pT, popSize * 2);
  u.Sorting (p, pT, popSize * 2);
}
//——————————————————————————————————————————————————————————————————————————————


    テスト結果

    このアルゴリズムは、3つの異なるテスト関数（Hilly、Forest、Megacity）と、異なる探索空間次元（5×2、25×2、500×2次元）で、合計10,000回の目的関数評価を用いてテストされました。全体結果の53.80%は、BIOが集団ベースの最適化アルゴリズムの中で平均的な位置にあることを示しており、新しい手法としては十分に良好な結果と言えます。 

    BIO|Blood Inheritance Optimization|50.0|
    =============================
    5 Hilly's; Func runs:10000; result:0.8156790458423091
    25 Hilly's; Func runs:10000; result:0.6533623929914842
    500 Hilly's; Func runs:10000; result:0.3087659267627686
    =============================
    5 Forest's; Func runs:10000; result:0.8993708810337727
    25 Forest's; Func runs:10000; result:0.6531872390668734
    500 Forest's; Func runs:10000; result:0.21759965952460583
    =============================
    5 Megacity's; Func runs:10000; result:0.6784615384615384
    25 Megacity's; Func runs:10000; result:0.4763076923076923
    500 Megacity's; Func runs:10000; result:0.13901538461538585
    =============================
    All score:4.84175 (53.80%)

    アルゴリズムの動作を可視化した際に見られる唯一の問題は、次元の小さい問題において局所最適解に陥りやすい傾向であり、これは集団アルゴリズムではよくある現象です。

    Hilly

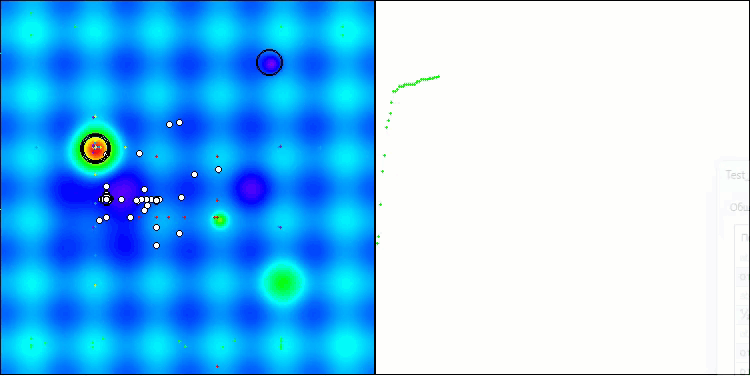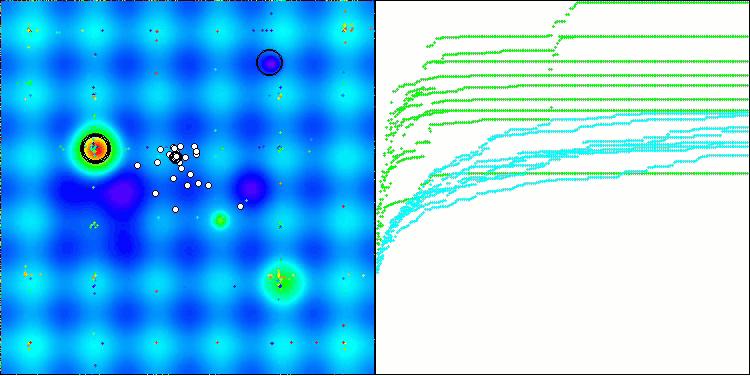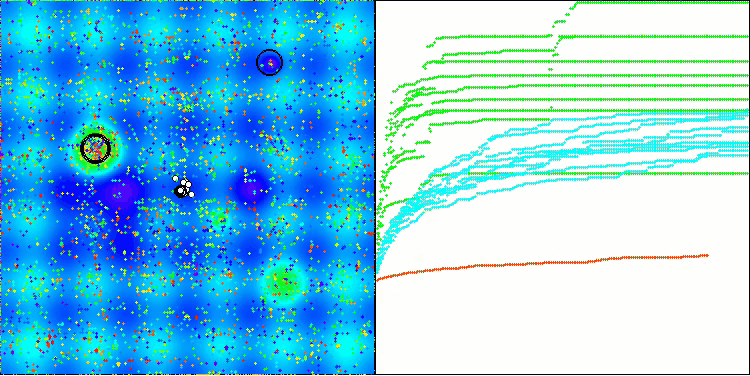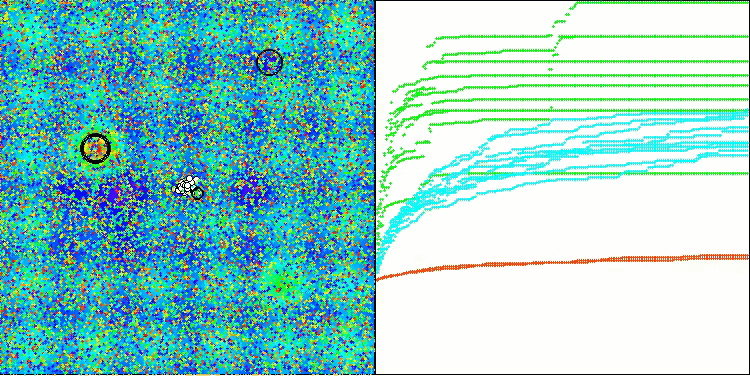
    Hillyテスト関数のBIO

    Forest

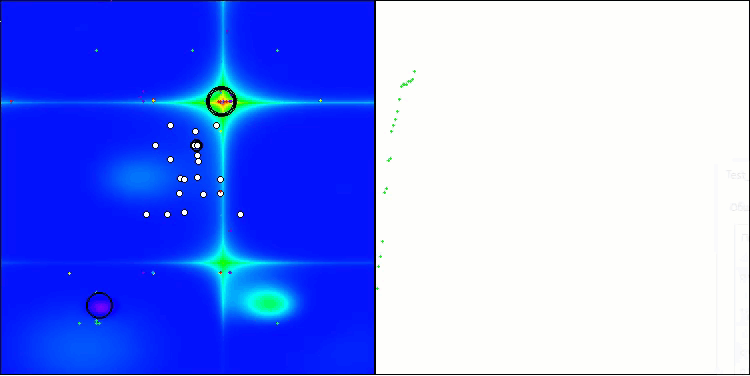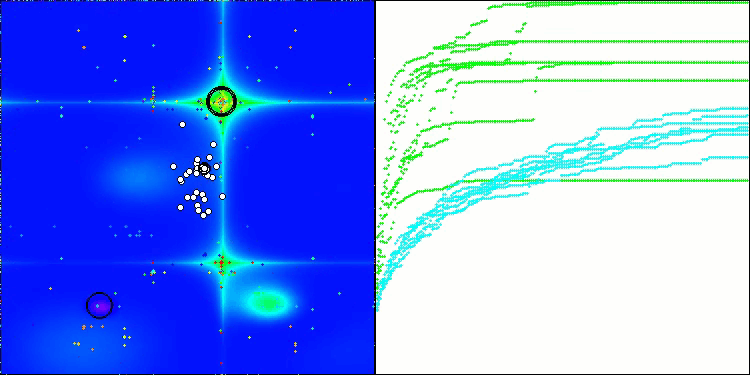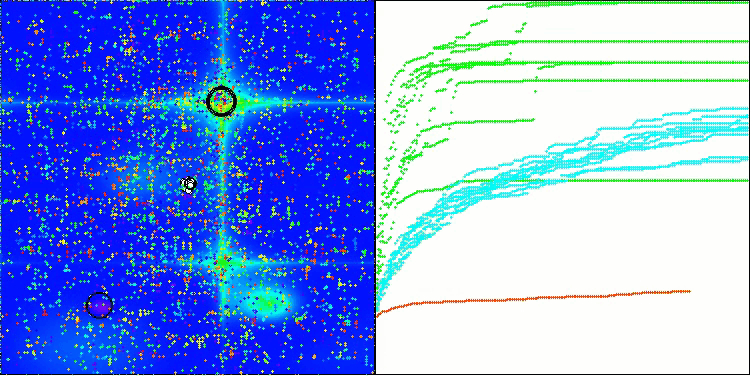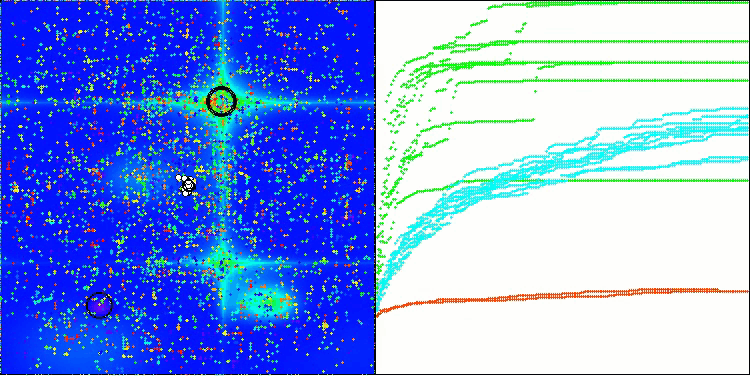
    Forestテスト関数のBIO

    Megacity

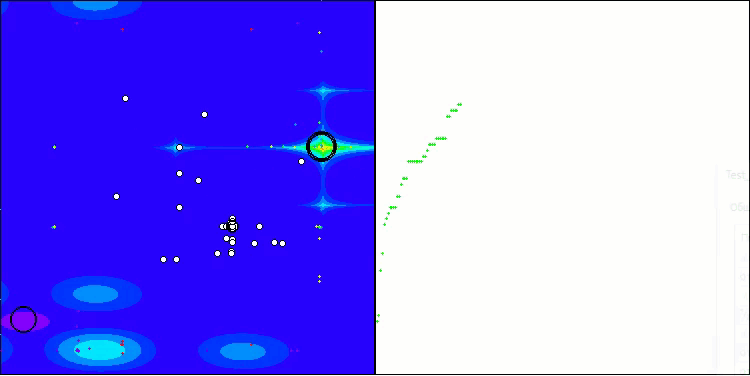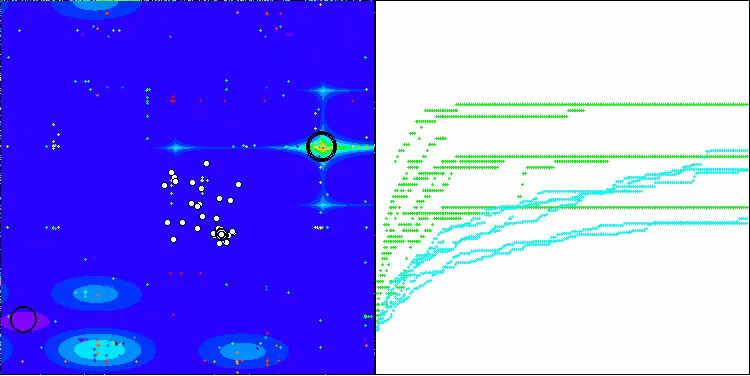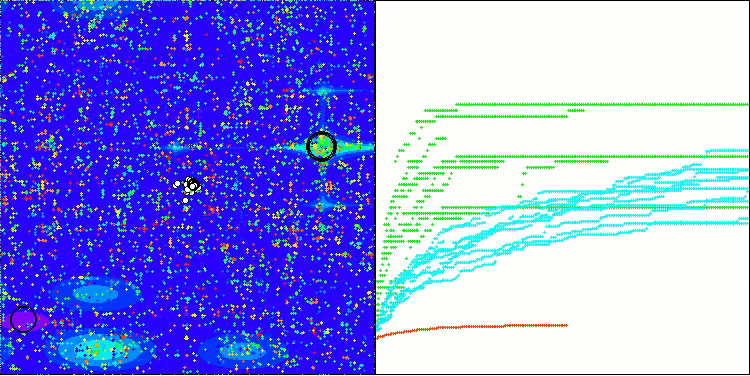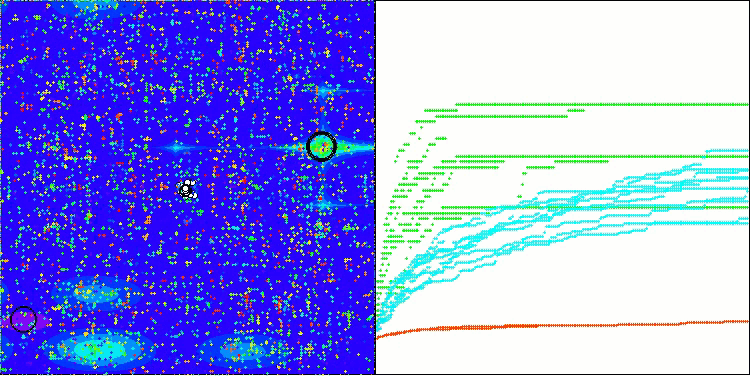
    Megacityテスト関数のBIO

    テスト結果に基づくと、BIOアルゴリズムは集団ベース最適化アルゴリズムのランキング表で第20位に位置しています。

    # AO 詳細 Hilly Hilly最終 Forest Forest最終 Megacity（離散） Megacity最終 最終結果 MAXの%
    10p(5F) 50p(25F) 1000p(500F) 10p(5F) 50p(25F) 1000p(500F) 10p(5F) 50p(25F) 1000p(500F)
    1 ANS across neighbourhood search 0.94948 0.84776 0.43857 2.23581 1.00000 0.92334 0.39988 2.32323 0.70923 0.63477 0.23091 1.57491 6.134 68.15
    2 CLA コードロックアルゴリズム(joo) 0.95345 0.87107 0.37590 2.20042 0.98942 0.91709 0.31642 2.22294 0.79692 0.69385 0.19303 1.68380 6.107 67.86
    3 AMOm 動物移動最適化m 0.90358 0.84317 0.46284 2.20959 0.99001 0.92436 0.46598 2.38034 0.56769 0.59132 0.23773 1.39675 5.987 66.52
    4 (P+O)ES (P+O)進化戦略 0.92256 0.88101 0.40021 2.20379 0.97750 0.87490 0.31945 2.17185 0.67385 0.62985 0.18634 1.49003 5.866 65.17
    5 CTA 彗星の尾アルゴリズム(joo) 0.95346 0.86319 0.27770 2.09435 0.99794 0.85740 0.33949 2.19484 0.88769 0.56431 0.10512 1.55712 5.846 64.96
    6 TETA 時間進化移動アルゴリズム（joo） 0.91362 0.82349 0.31990 2.05701 0.97096 0.89532 0.29324 2.15952 0.73462 0.68569 0.16021 1.58052 5.797 64.41
    7 SDSm 確率的拡散探索M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
    8 AAm アーチェリーアルゴリズムM 0.91744 0.70876 0.42160 2.04780 0.92527 0.75802 0.35328 2.03657 0.67385 0.55200 0.23738 1.46323 5.548 61.64
    9 ESG 社会集団の進化(joo) 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
    10 SIA 等方的焼きなまし(joo) 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
    11 ACS 人工協調探索 0.75547 0.74744 0.30407 1.80698 1.00000 0.88861 0.22413 2.11274 0.69077 0.48185 0.13322 1.30583 5.226 58.06
    12 DA 弁証法的アルゴリズム 0.86183 0.70033 0.33724 1.89940 0.98163 0.72772 0.28718 1.99653 0.70308 0.45292 0.16367 1.31967 5.216 57.95
    13 BHAm ブラックホールアルゴリズムM 0.75236 0.76675 0.34583 1.86493 0.93593 0.80152 0.27177 2.00923 0.65077 0.51646 0.15472 1.32195 5.196 57.73
    14 ASO 無政府社会最適化 0.84872 0.74646 0.31465 1.90983 0.96148 0.79150 0.23803 1.99101 0.57077 0.54062 0.16614 1.27752 5.178 57.54
    15 RFO ロイヤルフラッシュ最適化（joo） 0.83361 0.73742 0.34629 1.91733 0.89424 0.73824 0.24098 1.87346 0.63154 0.50292 0.16421 1.29867 5.089 56.55
    16 AOSm 原子軌道探索M 0.80232 0.70449 0.31021 1.81702 0.85660 0.69451 0.21996 1.77107 0.74615 0.52862 0.14358 1.41835 5.006 55.63
    17 TSEA 亀甲進化アルゴリズム(joo) 0.96798 0.64480 0.29672 1.90949 0.99449 0.61981 0.22708 1.84139 0.69077 0.42646 0.13598 1.25322 5.004 55.60
    18 DE 差分進化 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
    19 CRO 化学反応の最適化 0.94629 0.66112 0.29853 1.90593 0.87906 0.58422 0.21146 1.67473 0.75846 0.42646 0.12686 1.31178 4.892 54.36
    20 BIO 血液型遺伝最適化(joo) 0.81568 0.65336 0.30877 1.77781 0.89937 0.65319 0.21760 1.77016 0.67846 0.47631 0.13902 1.29378 4.842 53.80
    21 BSA 鳥群アルゴリズム 0.89306 0.64900 0.26250 1.80455 0.92420 0.71121 0.24939 1.88479 0.69385 0.32615 0.10012 1.12012 4.809 53.44
    22 HS ハーモニー検索 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
    23 SSG 苗木の播種と育成 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
    24 BCOm 細菌走化性最適化M 0.75953 0.62268 0.31483 1.69704 0.89378 0.61339 0.22542 1.73259 0.65385 0.42092 0.14435 1.21912 4.649 51.65
    25 ABO アフリカ水牛の最適化 0.83337 0.62247 0.29964 1.75548 0.92170 0.58618 0.19723 1.70511 0.61000 0.43154 0.13225 1.17378 4.634 51.49
    26 (PO)ES (PO)進化戦略 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
    27 TSm タブーサーチM 0.87795 0.61431 0.29104 1.78330 0.92885 0.51844 0.19054 1.63783 0.61077 0.38215 0.12157 1.11449 4.536 50.40
    28 BSO ブレインストーム最適化 0.93736 0.57616 0.29688 1.81041 0.93131 0.55866 0.23537 1.72534 0.55231 0.29077 0.11914 0.96222 4.498 49.98
    29 WOAm 鯨最適化アルゴリズムM 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
    30 AEFA 人工電界アルゴリズム 0.87700 0.61753 0.25235 1.74688 0.92729 0.72698 0.18064 1.83490 0.66615 0.11631 0.09508 0.87754 4.459 49.55
    31 AEO 人工生態系ベースの最適化アルゴリズム 0.91380 0.46713 0.26470 1.64563 0.90223 0.43705 0.21400 1.55327 0.66154 0.30800 0.28563 1.25517 4.454 49.49
    32 ACOm 蟻コロニー最適化M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
    33 BFO-GA 細菌採食の最適化：Ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
    34 SOA シンプル最適化アルゴリズム 0.91520 0.46976 0.27089 1.65585 0.89675 0.37401 0.16984 1.44060 0.69538 0.28031 0.10852 1.08422 4.181 46.45
    35 ABHA 人工蜂の巣アルゴリズム 0.84131 0.54227 0.26304 1.64663 0.87858 0.47779 0.17181 1.52818 0.50923 0.33877 0.10397 0.95197 4.127 45.85
    36 ACMO 大気雲モデルの最適化 0.90321 0.48546 0.30403 1.69270 0.80268 0.37857 0.19178 1.37303 0.62308 0.24400 0.10795 0.97503 4.041 44.90
    37 ADAMm 適応モーメント推定M 0.88635 0.44766 0.26613 1.60014 0.84497 0.38493 0.16889 1.39880 0.66154 0.27046 0.10594 1.03794 4.037 44.85
    38 ATAm 人工部族アルゴリズムM 0.71771 0.55304 0.25235 1.52310 0.82491 0.55904 0.20473 1.58867 0.44000 0.18615 0.09411 0.72026 3.832 42.58
    39 ASHA 人工シャワーアルゴリズム 0.89686 0.40433 0.25617 1.55737 0.80360 0.35526 0.19160 1.35046 0.47692 0.18123 0.09774 0.75589 3.664 40.71
    40 ASBO 適応型社会行動最適化(ASBO) 0.76331 0.49253 0.32619 1.58202 0.79546 0.40035 0.26097 1.45677 0.26462 0.17169 0.18200 0.61831 3.657 40.63
    41 MEC mind evolutionary computation 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
    42 CSA 円探索アルゴリズム 0.66560 0.45317 0.29126 1.41003 0.68797 0.41397 0.20525 1.30719 0.37538 0.23631 0.10646 0.71815 3.435 38.17
    43 IWO 侵入雑草最適化 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
    44 Micro-AIS 微小人工免疫系 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54
    45 COAm カッコウ最適化アルゴリズムM 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21

    		RW ランダムウォーク 0.48754 0.32159 0.25781 1.06694 0.37554 0.21944 0.15877 0.75375 0.27969 0.14917 0.09847 0.52734 2.348 26.09


    まとめ

    血液型遺伝最適化(BIO)アルゴリズムの開発およびテストを通じて、いくつかの重要な結論に至りました。まず第一に、血液型遺伝の関連性を用いるというアプローチは、集団最適化アルゴリズムにおける異なる突然変異戦略を整理・構成する方法として有効であることが確認されました。さまざまな関数および次元に対するテストにより、本アルゴリズムは汎用性が高く、単純な低次元問題から、より複雑な高次元問題まで効果的に適用できることが示されました。

    特に重要なのは、本記事で提示したBIOの実装が、あくまで概念実証を目的とした基本的なバージョンであるという点です。本アルゴリズムの本質的なアイデアは、特定の突然変異オペレータそのもの（これらは他のものに置き換えることが可能）ではなく、血液型になぞらえた「戦略継承構造」にあります。この構造により、アルゴリズムの改良や拡張に対して非常に広い可能性が開かれます。各「血液型」は、他の最適化アルゴリズムから借用した突然変異オペレータや、特定のタスク向けに新たに設計されたオペレータと自由に関連付けることができます。さらに、「血液型」の数自体を変更したり、新たな戦略を追加したり、既存の戦略を組み合わせたりすることも可能です。

    現在のテスト結果では、集団最適化アルゴリズムのランキングにおいて約54%という良好な位置を示しており、基本的な実装であっても本アプローチの有効性が確認されました。観測された局所最適解への停滞傾向についても、突然変異オペレータの改良や、探索空間をより広く探索する新たな戦略を導入することで克服可能であると考えられます。

    アルゴリズムの今後の発展において最も有望な方向性は、各「血液型」に対応する突然変異オペレータが最適化過程の中で動的に変化し、目的関数のランドスケープに適応する適応型アルゴリズムの構築であると考えています。また、古典的なABO血液型システムに限らず、他の生物学的遺伝様式を取り入れる可能性を検討することも興味深く、これにより異なる遺伝システムに基づくアルゴリズム群の創出が期待されます。

    以上より、BIOは単なる新しい最適化アルゴリズムではなく、血液型というメタファーを通じて探索戦略の継承という共通概念で結ばれたアルゴリズム群を構築するための柔軟な概念的基盤であり、さまざまな応用分野における性能向上を目指した今後の研究および改良に対して大きな可能性を有しています。

    Tab

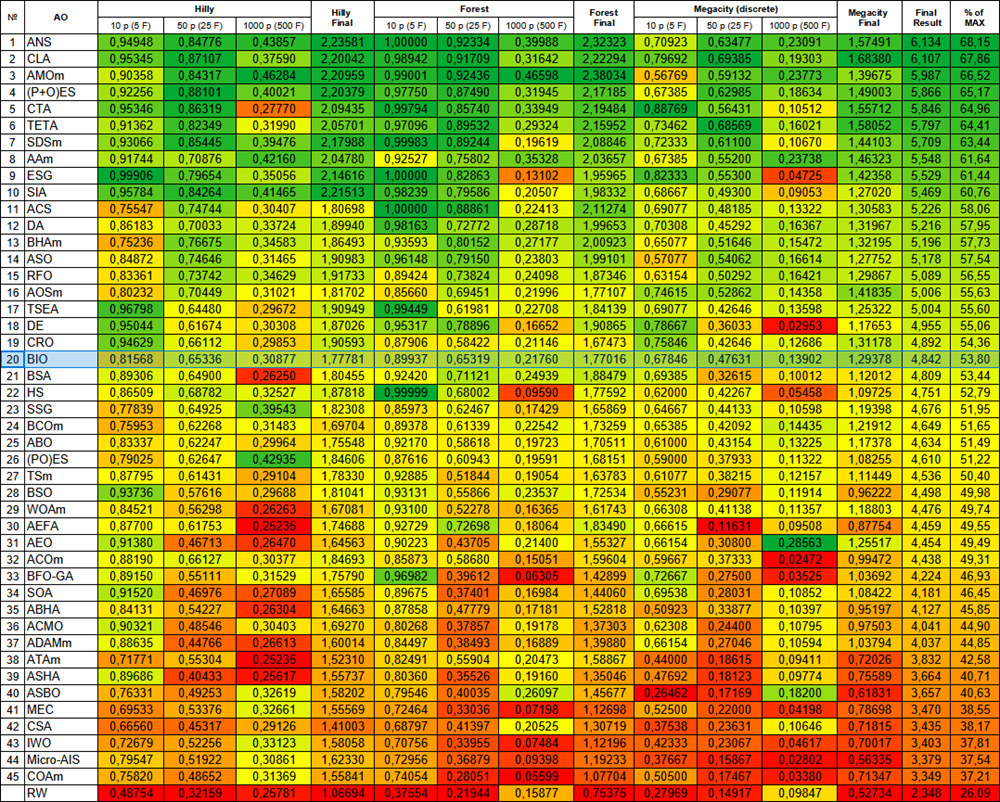
    図2：対応するテストに応じたアルゴリズムのカラーグラデーション

    チャート

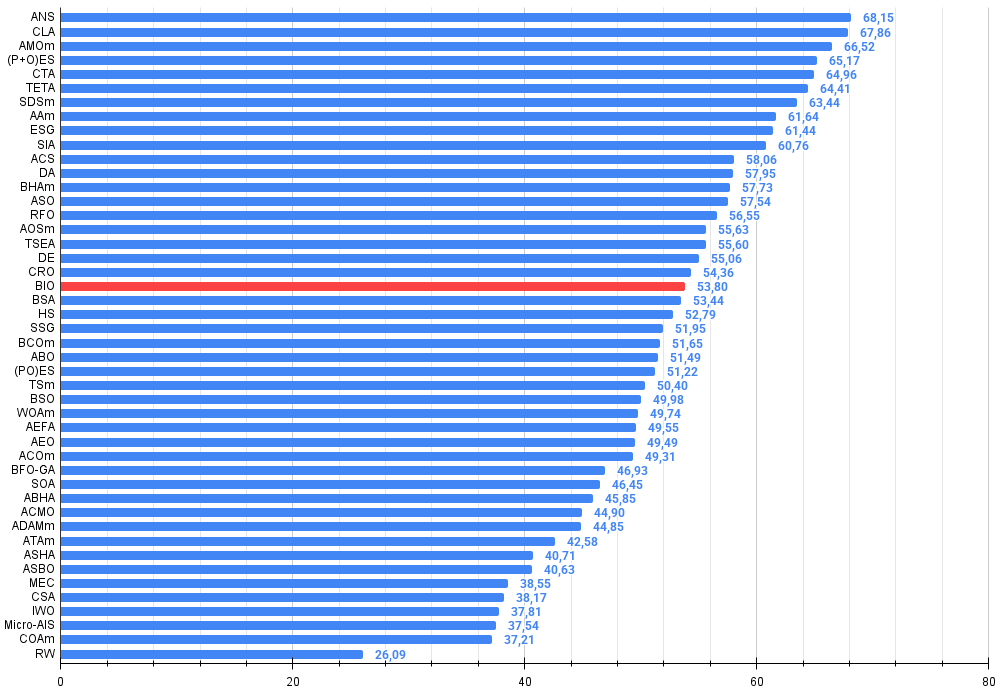
    図3：アルゴリズムテスト結果のヒストグラム（0から100のスケール、高いほど良い）100は理論上の最大値であり、アーカイブには評価表を計算するためのスクリプトがあります。

    BIOの長所と短所

    長所

    1. 外部パラメータなし
    2. 血液型による遺伝についての興味深い考え
    3. 高次元および中次元関数の良好な収束

    短所：

    1. 低次元の問題では、局所的な極値に行き詰まってしまう


    この記事には、最新版のアルゴリズムコードを含むアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。



    記事で使用されているプログラム

    # 名前 種類 説明
    1 #C_AO.mqh
    		 インクルード
    		 集団最適化の親クラス
    アルゴリズム
    2 #C_AO_enum.mqh
    		 インクルード
    		 集団最適化アルゴリズムの列挙
    3 TestFunctions.mqh
    		 インクルード
    		 テスト関数のライブラリ
    4
    		 TestStandFunctions.mqh
    		 インクルード
    		 テストスタンド関数ライブラリ
    5
    		 Utilities.mqh
    		 インクルード
    		 補助関数のライブラリ
    6
    		 CalculationTestResults.mqh
    		 インクルード
    		 比較表の結果を計算するスクリプト
    7
    		 Testing AOs.mq5
    		 スクリプト すべての集団最適化アルゴリズムの統一テストスタンド
    8
    		 Simple use of population optimization algorithms.mq5
    		 スクリプト
    		 可視化せずに集団最適化アルゴリズムを使用する簡単な例
    9
    		 Test_AO_BIO.mq5
    		 スクリプト BIOテストスタンド

    MetaQuotes Ltdによってロシア語から翻訳されました。
    元の記事: https://www.mql5.com/ru/articles/17246

    添付されたファイル |
    ZIPをダウンロード
    BIO.zip (166.57 KB)

    警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

    この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。

    この著者による他の記事

    ディスカッションに移動
    EAのサンプル EAのサンプル
    一般的なMACDを使ったEAを例として、MQL4開発の原則を紹介します。
    市場シミュレーション（第9回）：ソケット(III) 市場シミュレーション（第9回）：ソケット(III)
    本日の記事は前回の記事の続編です。今回はエキスパートアドバイザー(EA)の実装を取り上げ、特にサーバー側コードがどのように実行されるかに焦点を当てます。前回の記事で示したコードだけでは、すべてを期待どおりに動作させるには不十分であるため、もう少し深く掘り下げる必要があります。そのため、これから起こることをよりよく理解するには、両方の記事を読む必要があります。
    エラー 146 (「トレードコンテキスト ビジー」) と、その対処方法 エラー 146 (「トレードコンテキスト ビジー」) と、その対処方法
    この記事では、MT4において複数のEAの衝突をさける方法を扱います。ターミナルの操作、MQL4の基本的な使い方がわかる人にとって、役に立つでしょう。
    初級から中級まで：イベント(I) 初級から中級まで：イベント(I)
    ここまでに示された内容を踏まえると、いよいよチャート上で直接銘柄を操作するようなアプリケーションの実装を始めることができそうです。しかし、その前に、初心者にはやや混乱しやすい概念について触れておく必要があります。つまり、チャート上で表示することを目的として開発されるMQL5のアプリケーションは、これまで見てきた方法と同じようには作られないということです。本記事では、この点を少しずつ理解していきます。