MetaTrader 5 / 例
English Русский 中文 Español Deutsch Português
preview
コードロックアルゴリズム（CLA）

コードロックアルゴリズム（CLA）

MetaTrader 5 — 例 | 17 10月 2024, 09:34
139 0
Andrey Dik
Andrey Dik

内容

1. はじめに
2. アルゴリズムの実装
3.テスト結果


1. はじめに

「デジタルロック」や「コンビネーションロック」とも呼ばれるコードロックは、部屋、金庫、キャビネットなどへのアクセスを管理するためのセキュリティ機構です。一般的なロックとは異なり、鍵を使わず、特定の数字の組み合わせを入力することで解錠します。

通常、コードロックはキーパッドや回転機構を備え、ユーザーがコードシーケンスを入力できるようになっています。正しい組み合わせが入力されると、ロック解除のメカニズムが作動し、ユーザーはドアや金庫の中身にアクセスできます。ユーザーは自分でコードを設定するか、あらかじめ提供されたコードを使用することができます。

コードロックの利点：

  • 安全性：コードを定期的に変更すれば、高いレベルのセキュリティを提供します。
  • 利便性：鍵を持ち歩く必要がないため、便利です。
  • 複数コードの設定：モデルによっては、異なるユーザーや時間帯ごとに複数のコードを設定できます。

コードロックはホームセキュリティ、商業施設、ホテル、学校、オフィスなど、出入管理が求められるさまざまな分野で広く利用されています。これを最適化アルゴリズムの文脈で応用するアイデアは非常に興味深いものです。例えば、機械学習問題における最適パラメータの発見やその他の最適化課題の解決に、コードロックの原理を応用するシステムを構築することが可能です。

正しい数字の組み合わせを入力して解錠するコードロックの動作原理は、パラメータを繰り返し変更し、その効率を評価することで最適解を見つけようとする最適化アルゴリズムの仕組みに似ていると言えます。

たとえば、次のようにコードロックのアナロジーを使った最適化アルゴリズムを想像できます。

  1. パラメータとしての組み合わせ：最適化対象のパラメータは、入力される「組み合わせ」として表現されます。
  2. 組み合わせの妥当性チェック：アルゴリズムは、ユーザーが錠に異なる組み合わせを試すように、パラメータ値を調整し、その有効性を評価します。
  3. ロック解除としての最適解：アルゴリズムが最適なパラメータを見つけたとき、それは最適解の「ロック解除」として解釈できます。

このように、コードロックは機械学習や取引システム開発など、さまざまな分野で最適解を導き出す最適化アルゴリズムの着想を与える存在となっています。


2. アルゴリズムの実装

エージェントの母集団をロックの母集団と想像してみましょう。各ロックは問題の解を表します。これにより、コードロックアルゴリズムのおおよその擬似コードをスケッチすることができます。

1. 初期化
      サイズがpopSizeであるロックの配列を作成します。各ロックはcoordsセットのディスクを持ち、それぞれのセットはlockDiscs個のディスクを持ちます。
2. ロックの組み合わせを選択
      最初のステップでは、各ロックのセット内の各ディスクを0から9の間の乱数で初期化します。
      それ以外の場合、各ロックに対して次の操作をおこないます。
         - 乱数がcopyProbより小さい場合、ランダムに選択されたロックからディスクのセットをコピーします。
         - そうでない場合、各ディスクのセットごとに
            - 乱数がrotateProbより小さい場合、ディスクに0から9までの乱数を設定します。
            - それ以外の場合は、ランダムに選ばれたロックからディスクをコピーします。
3. ロックの組み合わせの品質を評価
      各ロックの組み合わせ品質を更新します。   
      最高の組み合わせ品質を持つロックを検索し、必要に応じて大域的最適解を更新します。
      すべてのロックを共通のロックバスケットにコピーし、
      そのバスケットを適応度に基づいて並べ替えます。
4.指定されたエポック数または停止基準に達するまで、ステップ2と3を繰り返します。

概念は非常に興味深いものですが、まだいくつかの疑問が残っています。特に、ロックの組み合わせコードがどのように問題の解を示すのかは、まったく明確ではありません。より深く理解するために、イラストがあると助かります。

そこで、1つ以上のパラメータを最適化する必要がある問題の解を、コードロックという形で表現してみましょう。この場合、各パラメータは数字の組み合わせとして表現でき、それぞれの数字は別々のディスクに配置されます。ディスクの枚数に制限はありません。この数値はアルゴリズムの外部パラメータとして指定されます。こうして、各パラメータはデジタルラベルが付けられたディスクのセットで表現されることになります。

例えば、タスクパラメータに9つのディスクのセットがあり、それぞれが0から9までの番号を持つ場合、その組み合わせは000000000から999999999までとなります。結果の数値を、対応するパラメータのminからmaxまでの範囲にスケーリングします。したがって、最適化するパラメータが3つあれば、コンビネーションロックは3×9＝27のデジタルディスクを持つことになります。図1は、1つのパラメータの符号化メカニズムを示しています。

コード

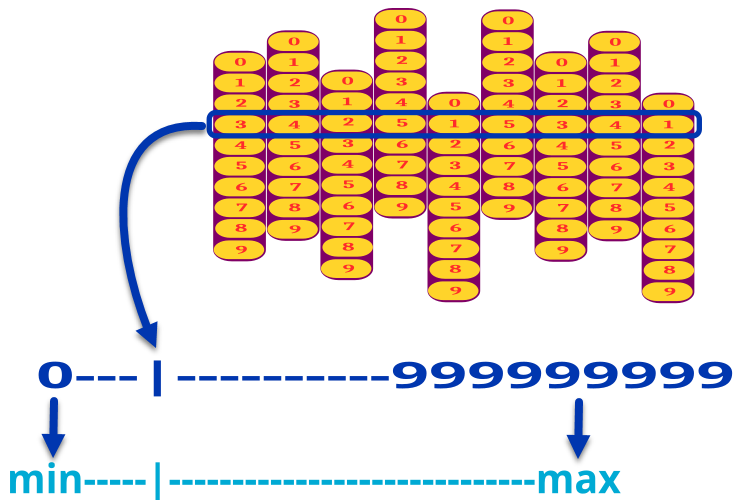
図1：タスクパラメータをデジタルコードから実数値にデコードする

交叉や突然変異といった最適化アルゴリズムの演算子は、コードロックの考え方を用いてCLA最適化アルゴリズムに統合されています。

1. 交叉：遺伝的アルゴリズムにおける交叉は、2つの親から遺伝情報を組み合わせて子孫を生成するものです。

  • コードロックの文脈では、交叉は異なるロックのディスク値を組み合わせ、エンコードされたタスクパラメータの新しい組み合わせを作成するプロセスと考えられます。
  • この操作により、アルゴリズムはパラメータの新たな組み合わせを探索するための組み合わせ的な可能性を得ることができます。これは、ユーザーがコードロックで複数の組み合わせを試み、成功した組み合わせを活用する仕組みに似ています。

2. 突然変異：遺伝的アルゴリズムにおける突然変異は、ランダムな変化を加えて集団に多様性をもたらす操作です。

  • コードロックの文脈では、突然変異はディスクを任意の位置にランダムに回転させてロックの組み合わせを変えることとして解釈できます。
  • これにより、アルゴリズムが解空間全体を探索し、局所最適解に陥るのを回避するのに役立ちます。

一般的に、交叉と突然変異を最適化アルゴリズムに統合することで、解の多様性が向上し、最適解への収束が速くなるだけでなく、早期収束を避けることができます。このアプローチは、探索空間が広く、目的関数が複雑な最適化問題に特に有効です。実際、遺伝子の演算子をアナロジーに用いることで、ディスクの回転操作が解空間での探索における選択肢となります。

問題の解決には、コードロックの正しい数字の組み合わせを見つけ出す必要があります。ディスクを回転させて正しいコードを発見し、鍵を開けるという手順です。遺伝的アルゴリズムがバイナリコードの値（0か1）を「回転」させて確率的に値を得るのに対し、コンビネーションロックアルゴリズムではディスクの回転に確率分布を用いることが可能です。いくつかの選択肢が考えられます。

1つ目の選択肢として、ガウス分布を使用してパラメータの変異をおこなうことができます。この場合、各パラメータは正規分布（ガウス分布）に従ったランダムな値に変化し、現在の値を大きく変えることなく、パラメータに少しずつランダムな変更を加えます。

ガウス分布を突然変異に用いると、パラメータ変化の度合いを調整できるため、非常に便利です。パラメータの変更は現在の値に近い小さな範囲でおこなわれるため、現行の解の有利な特性を保ちながら、突然変異によるランダムな要素で探索空間の新たな領域に挑戦することができます。

その結果、ガウス分布を利用することで、新しい解を探索しつつ、現在の解の良好な特性を維持するバランスが取れ、複雑なパラメータ空間での最適解探索を効率的に進めることが可能になります。

突然変異過程には、ベキ分布を使用することも可能です。ガウス分布とは異なり、ベキ分布布は裾が重いため、大きなパラメータ変化が発生する確率が高くなり、パラメータ空間をより根本的に探索したい場合に有効です。これにより、アルゴリズムが局所的なトラップから脱出し、広範囲に探索することが促進されます。

さらに、3番目のオプションとして、一様分布を使用することも考えられます。これにより、ロックディスク上の任意の数を均等な確率で選択できるようになります。

これで、理論的な部分から実際にコードを書いたり、実践的な研究に移行する準備が整いました。

問題解決を表すエージェントCLAアルゴリズムでは、S_CLA_Agent構造体を用いてロックを記述します。以下に、その主な構成要素を示します。

  • f：エージェントの適応度を表します。初期値は-DBL_MAXで、これはdouble型の最小値を意味します。
  • struct S_Lock：ロック配列を含む入れ子構造体。この配列は、最適化される1つのタスクパラメータのコードの組み合わせを格納します。
  • S_Lock code []：S_Lock構造体の配列。この配列全体が「ロック」に相当します。
  • void Init (int coords, int lockDiscs)：初期化関数で、coordsはパラメータセットの数を定義し、lockDiscsは各セットにおけるディスクの数を定義します。code配列はこの関数内で初期化されます。

この構造体全体はCLA最適化アルゴリズムにおけるエージェントを表し、それぞれのエージェントは独自の適応度とロックの組み合わせを持ち、アルゴリズムの実行中に最適化されていきます。

//——————————————————————————————————————————————————————————————————————————————
struct S_CLA_Agent
{
    double f;  //fitness

    struct S_Lock
    {
        int lock [];
    };

    S_Lock code [];


    void Init (int coords, int lockDiscs)
    {
      f = -DBL_MAX;

      ArrayResize (code, coords);

      for (int i = 0; i < coords; i++)
      {
        ArrayResize (code [i].lock, lockDiscs);
      }
    }
};
//——————————————————————————————————————————————————————————————————————————————

次に、C_AOクラスから派生したC_AO_CLAクラスについて説明します。以下の主要な構成要素があります。

  • C_AO_CLA ()：クラスのコンストラクタで、オブジェクトを初期化します。popSize、lockDiscs、copyProb、rotateProb 、paramsなどが、このコンストラクタ内で初期化されます。
  • SetParams()：params配列の値に基づいて、アルゴリズムのパラメータを設定します。
  • Init ()：初期化関数で、検索範囲とエポック数をパラメータとして受け取ります。
  • Moving ()とRevision()：アルゴリズムの主要なロジックを実行するために使用される関数です。
  • lockDiscs、copyProb、rotateProb：アルゴリズムのパラメータを格納するための変数です。
  • S_CLA_Agent agent []：エージェントの配列です。各エージェントはS_CLA_Agent構造体のオブジェクトです。
  • maxLockNumber、S_CLA_Agent parents []、S_CLA_Agent parTemp []：クラス内部で使用されるprivate変数と配列です。
  • ArrayToNumber ()とLockToDouble ()：それぞれ、コードの組み合わせ配列を数値に変換するため、およびロックを浮動小数点数に変換するために使用されるprivateメソッドです。
//——————————————————————————————————————————————————————————————————————————————
class C_AO_CLA : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_CLA () { }
  C_AO_CLA ()
  {
    ao_name = "CLA";
    ao_desc = "Code Lock Algorithm";
    ao_link = "https://www.mql5.com/ru/articles/14878";

    popSize     = 100;   //population size

    lockDiscs   = 8;     //lock discs
    copyProb    = 0.8;   //copying probability
    rotateProb  = 0.03;  //rotate disc probability

    ArrayResize (params, 4);

    params [0].name = "popSize";     params [0].val = popSize;

    params [1].name = "lockDiscs";   params [1].val = lockDiscs;
    params [2].name = "copyProb";    params [2].val = copyProb;
    params [3].name = "rotateProb";  params [3].val = rotateProb;
  }

  void SetParams ()
  {
    popSize    = (int)params [0].val;

    lockDiscs  = (int)params [1].val;
    copyProb   = params      [2].val;
    rotateProb = params      [3].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();
  void Injection (const int popPos, const int coordPos, const double value);

  //----------------------------------------------------------------------------
  int    lockDiscs;    //lock discs
  double copyProb;     //copying probability
  double rotateProb;   //rotate disc probability

  S_CLA_Agent agent [];

  private: //-------------------------------------------------------------------
  int maxLockNumber; //max lock number

  S_CLA_Agent parents [];
  S_CLA_Agent parTemp [];

  int    ArrayToNumber (int &arr []);
  double LockToDouble  (int lockNum, int coordPos);
};
//——————————————————————————————————————————————————————————————————————————————

C_AO_CLAクラスにInitメソッドを定義します。このメソッドは、与えられた探索範囲とエポック数でアルゴリズムを初期化します。各ステップの説明は、次の通りです。

1. if(!StandardInit (rangeMinP, rangeMaxP, rangeStepP))return false;：指定された検索範囲でStandardInit関数を呼び出します。初期化に失敗した場合、この関数はfalseを返します。

2. ArrayResize (agent, popSize);：agent配列のサイズをpopSizeの母集団のサイズに変更します。

3. for (int i = 0; i < popSize; i++) agent [i].Init (coords, lockDiscs);：このループは、指定された数のcoords座標とlockDiscsロックディスクで、集団内の各エージェントを初期化します。

4.ArrayResize (parents, popSize * 2);ArrayResize (parTemp, popSize * 2);：parent配列とparTemp配列のサイズを 2 つの母集団のサイズに変更します。

5. for (int i = 0; i < popSize * 2; i++) { parents [i].Init (coords, lockDiscs);parTemp [i].Init (coords, lockDiscs); }：このループは、parents配列とparTemp配列のそれぞれの親と一時的な親を初期化します。

6.maxLockNumber = 0; for (int i = 0; i < lockDiscs; i++) { maxLockNumber += 9 * (int)pow (10, i); }：ループは、ロックディスクの数(lockDiscs).を使用して、maxLockNumberロックの組み合わせの最大数を計算します。

7. return true;：これまでの操作がすべて成功した場合、この関数は「true」を返します。

この関数は，CLAコードロック最適化アルゴリズムのエージェントと親を初期化し，ロックディスクの数に基づいてロックの組み合わせの最大数を設定します。

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_CLA::Init (const double &rangeMinP  [], //minimum search range
                     const double &rangeMaxP  [], //maximum search range
                     const double &rangeStepP [], //step search
                     const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (agent, popSize);
  for (int i = 0; i < popSize; i++) agent [i].Init (coords, lockDiscs);

  ArrayResize (parents, popSize * 2);
  ArrayResize (parTemp, popSize * 2);

  for (int i = 0; i < popSize * 2; i++)
  {
    parents [i].Init (coords, lockDiscs);
    parTemp [i].Init (coords, lockDiscs);
  }

  maxLockNumber = 0;
  for (int i = 0; i < lockDiscs; i++)
  {
    maxLockNumber += 9 * (int)pow (10, i);
  }

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

ロックのデジタルコンビネーションの選択はC_AO_CLAクラスのMovingメソッドで説明されています。プロセスは以下の通りです。

  • val = 0.0;code = 0;pos = 0;：メソッドで使用する変数の初期化。
  • if (!revision) {...}.：revisionがfalseの場合、コードブロックが実行されます。このコードブロックの中で、エージェントと親はランダムな値で初期化されます。 
  • 次に、各エージェントと各親について、codeとvalの値が計算され、エージェント座標の更新に使用されます。その後、revisionがtrueに設定され、関数が完了します。
  • for (int i = 0; i < popSize; i++) {...}.：このコードブロックは、revisionがtrueの場合に実行されます。エージェントはコードブロック内で更新されます。乱数がcopyProb より小さい場合、親のロックコードがエージェントにコピーされます。そうでない場合、エージェントのロックコードは、ランダムな値か親のロックコードで更新されます。 
  • その後、各エージェントのcodeとvalの値が計算されます。これらの値は、エージェントの座標を更新するために使用されます。

この関数は、CLA最適化アルゴリズムにおけるエージェントの更新に使用されます。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_CLA::Moving ()
{
  double val  = 0.0;
  int    code = 0;
  int    pos  = 0;

  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        for (int l = 0; l < lockDiscs; l++)
        {
          agent [i].code [c].lock [l] = u.RNDminusOne (10);
        }

        code = ArrayToNumber (agent [i].code [c].lock);
        val  = LockToDouble  (code, c);
        a [i].c [c] = u.SeInDiSp  (val, rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    for (int i = 0; i < popSize * 2; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        for (int l = 0; l < lockDiscs; l++)
        {
          parents [i].code [c].lock [l] = u.RNDminusOne (10);
        }
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      if (u.RNDprobab () < copyProb)
      {
        int pos = u.RNDminusOne (popSize);
        ArrayCopy (agent [i].code [c].lock, parents [pos].code [c].lock, 0, 0, WHOLE_ARRAY);
      }
      else
      {
        for (int l = 0; l < lockDiscs; l++)
        {
          if (u.RNDprobab () < rotateProb)
          {
            //pos = u.RNDminusOne (popSize);
            //agent [i].code [c].lock [l] = (int)round (u.GaussDistribution (agent [i].codePrev [c].lock [l], 0, 9, 8));
            //agent [i].code [c].lock [l] = (int)round (u.PowerDistribution (agent [i].codePrev [c].lock [l], 0, 9, 20));
            agent [i].code [c].lock [l] = u.RNDminusOne (10);
          }
          else
          {
            pos = u.RNDminusOne (popSize);
            agent [i].code [c].lock [l] = parents [pos].code [c].lock [l];
          }
        }
      }

      code = ArrayToNumber (agent [i].code [c].lock);
      val  = LockToDouble  (code, c);
      a [i].c [c] = u.SeInDiSp  (val, rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————
一般的にC_AO_CLAクラスのRevisionメソッドは、大域解を更新するためのものです。このメソッドでは次がおこなわれます。
  • ind = -1;：最高の適応度を持つエージェントのインデックスを追跡するために使用されるind変数を初期化します。
  • for (int i = 0; i < popSize; i++) {...}：ループは母集団内の各エージェントを通過し、エージェントの適応度が現在のfB最良適応度値を超えているかどうかをチェックします。超えている場合、fBが更新され、indには現在のインデックスが設定されます。
  • if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);：最良適応度を持つエージェントが見つかった場合、その座標がcBにコピーされます。
  • for (int i = 0; i < popSize; i++) { agent [i].f = a [i].f; }： ループはa配列の現在の値に基づいて各エージェントの適応度を更新します。
  • for (int i = 0; i < popSize; i++) { parents [i + popSize] = agent [i]; }：このループは、各エージェントをpopSizeの位置からparent配列にコピーします。
  • u.Sorting (parents, parTemp, popSize * 2);：parTemp配列を一時ストレージとして使用して、parents配列を並び替えます。
一般的に、この関数はCLAアルゴリズムにおいてエージェントと「親」ロックの適応度を更新するために使用されます。これには、最良の適応度値を更新し、親集団を適応度順に並べ替えることが含まれます。
//——————————————————————————————————————————————————————————————————————————————
void C_AO_CLA::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    agent [i].f = a [i].f;
  }

  for (int i = 0; i < popSize; i++)
  {
    parents [i + popSize] = agent [i];
  }

  u.Sorting (parents, parTemp, popSize * 2);
}
//——————————————————————————————————————————————————————————————————————————————

ArrayToNumberメソッドは、コードの組み合わせの文字を数字に変換します。メソッドアクション：

  • result = 0;：結果を格納する変数を初期化します。
  • for (int i = 0; i < ArraySize (arr); i++) {...}：このループはarr配列の各要素を通過します。arr [i]の各要素に対して、現在のresult値を10倍し、arr [i]を足します。
  • return result;：最終的な結果値を返します。

一般に、このメソッドは、配列の各要素を10進数表現の桁として解釈することで、整数の配列を1つの整数に変換します。

例えば、arr入力配列の値（コードの組み合わせ）が |0|3|1|5|7|0|だとすると、組み合わせの左側にあるゼロをすべて捨て、3から数字を作り始める必要があります。その結果、得られる数字は31570となります。配列のすべてのセルに0が含まれている場合、最終的な数値は0になります。

//——————————————————————————————————————————————————————————————————————————————
int C_AO_CLA::ArrayToNumber (int &arr [])
{
  int result = 0;
  for (int i = 0; i < ArraySize (arr); i++)
  {
    result = result * 10 + arr [i];
  }
  return result;
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_CLAクラスのLockToDouble メソッドは、コードの組み合わせを最適化されたパラメータのスケールに変換します。この関数が何をするかは次の通りです。

  • LockToDouble (int lockNum, int coordPos)：このメソッドは 2 つのパラメータをとります：lockNumはcoordPosロックの番号で、座標配列内の座標位置です（最適化されたパラメータ）。
  • return u.Scale (lockNum, 0, maxLockNumber, rangeMin [coordPos], rangeMax [coordPos]); ：lockNumを [0,maxLockNumber]の範囲から[rangeMin [coordPos], rangeMax [coordPos]]にスケーリングした値を返します。

一般的に、このメソッドは、与えられた範囲に基づいてロックナンバーを浮動小数点数に変換するために使用されます。言い換えれば、ロックナンバーは最適化されたタスクパラメータの値に変換されます。

//——————————————————————————————————————————————————————————————————————————————
double C_AO_CLA::LockToDouble (int lockNum, int coordPos)
{
  return u.Scale (lockNum, 0, maxLockNumber, rangeMin [coordPos], rangeMax [coordPos]);
}
//——————————————————————————————————————————————————————————————————————————————


3. テスト結果

テスト関数に対するCLA最適化アルゴリズムの結果は素晴らしく、可能な最大値の67.86％に達したことは非常に良い成果です。これは、CLAアルゴリズムが複雑な関数の最適化において高い性能を示していることを意味します。

これらの結果は、CLAアルゴリズムが非常に効果的であり、多次元関数の最適化が求められるさまざまな問題に適切に適用できることを示しています。そのスケーラビリティと複雑な問題への対応能力により、幅広い最適化問題を解決するための有望なツールとなっています。

CLA|Code Lock Algorithm|100.0|8.0|0.8|0.03|
=============================
5 Hilly's; Func runs:10000; result:0.9534490932631814
25 Hilly's; Func runs:10000; result:0.8710742215971827
500 Hilly's; Func runs:10000; result:0.375900385878165
=============================
5 Forest's; Func runs:10000; result:0.9894215656296362
25 Forest's; Func runs:10000; result:0.917091907561472
500 Forest's; Func runs:10000; result:0.3164221021938828
=============================
5 Megacity's; Func runs:10000; result:0.7969230769230768
25 Megacity's; Func runs:10000; result:0.693846153846154
500 Megacity's; Func runs:10000; result:0.19303076923077062
=============================
All score:6.10716 (67.86%)

テスト関数のアルゴリズム演算の可視化では、次元の小さい関数では結果の広がりが目立ちますが、タスクパラメータの数が増えるにつれて結果の広がりは減少します。さらに、収束曲線（赤線）の形状からは、大規模な問題（1000パラメータ）に対するアルゴリズムの潜在能力が明らかです。この曲線は加速しながら伸びており、適応度関数の実行回数（私たちのテストルール）の制限を取り除けば、アルゴリズムは大域最適にますます近づくことが期待されます。

Hilly

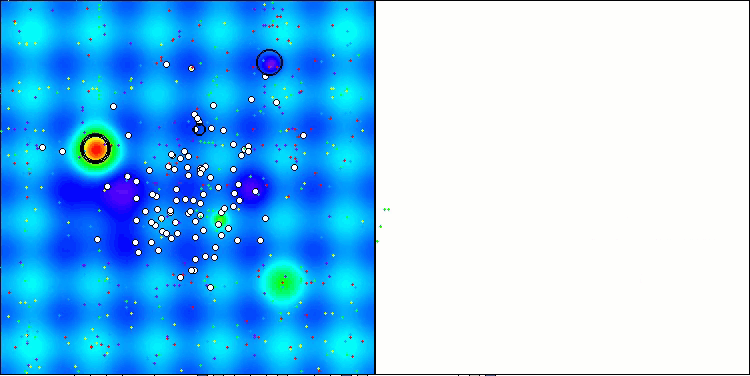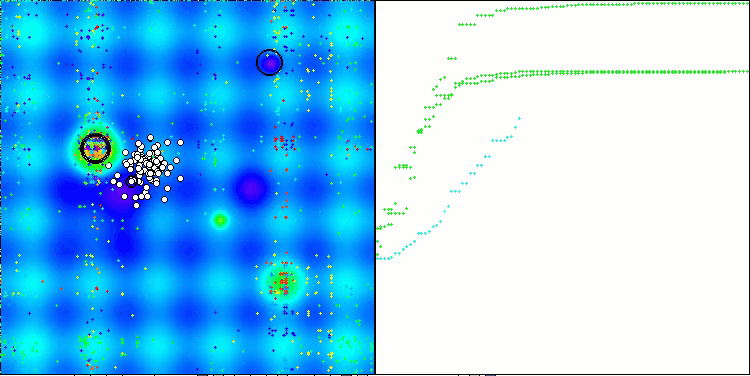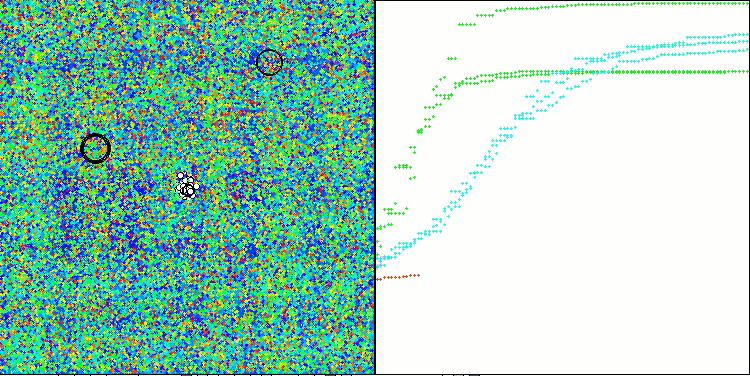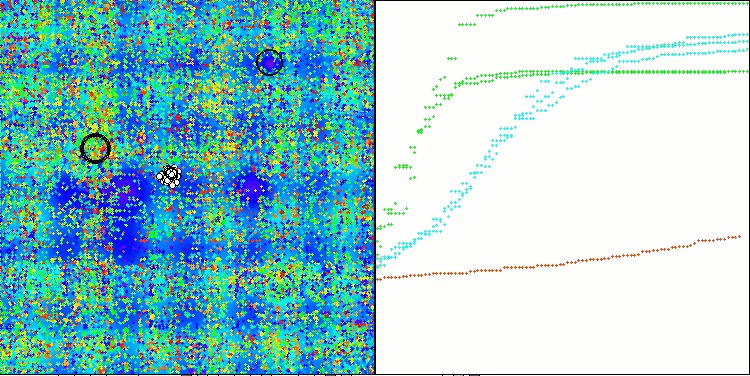
  Hillyテスト関数のCLA

Forest

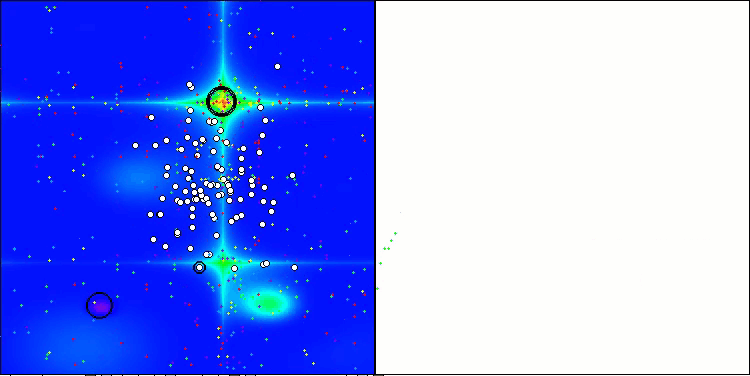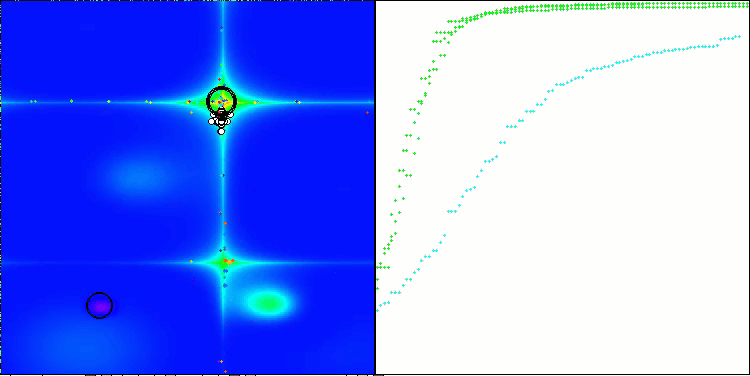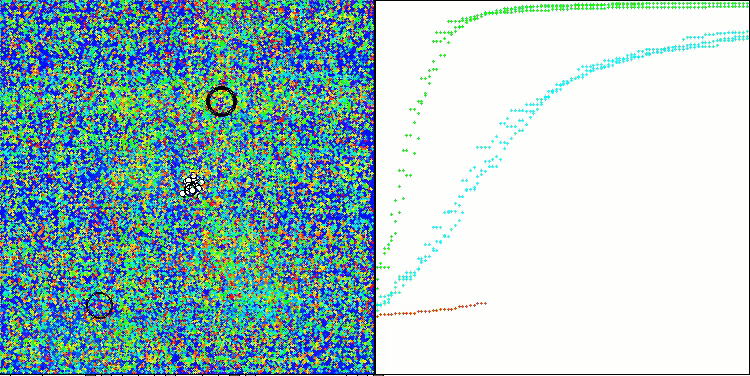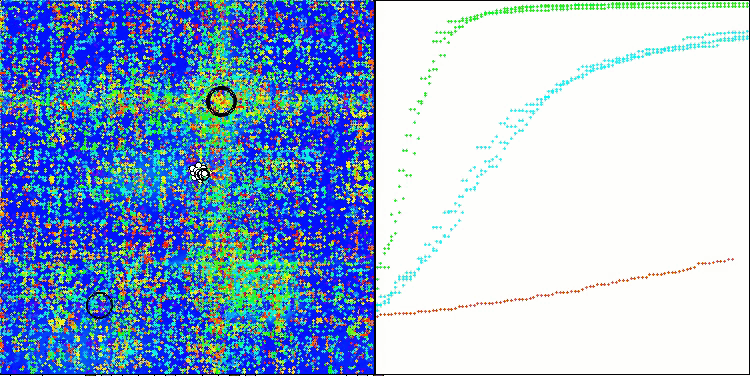
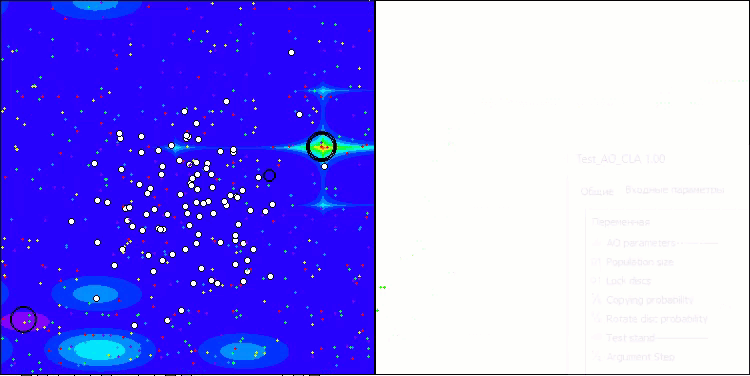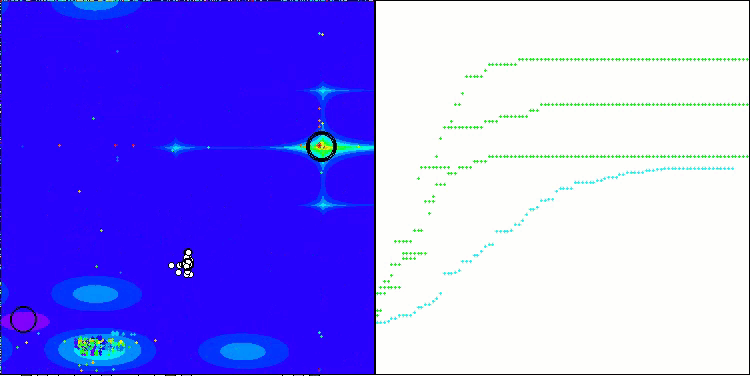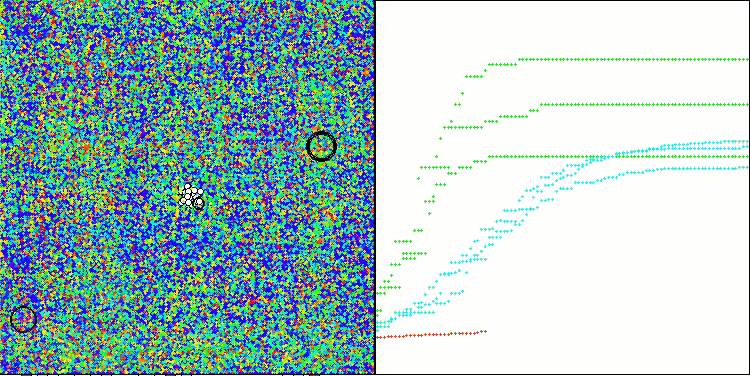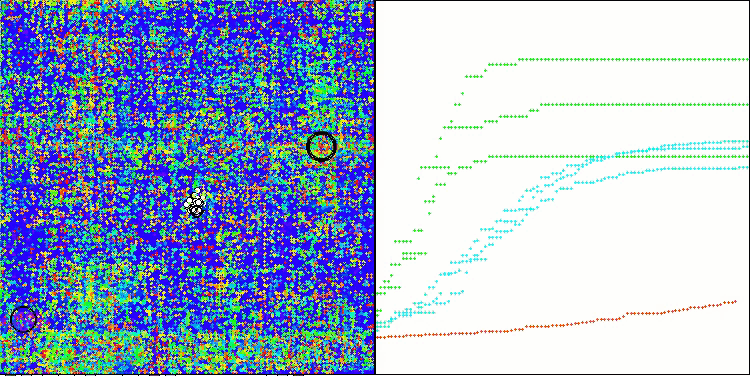
  Forestテスト関数のCLA

Megacity

  Megacityテスト関数のCLA


コードロックアルゴリズムはランキング表で2位となりました。10個のパラメータを持つシャープなForest関数では、CLAがテーブルのリーダーであるBGAを上回る結果を出しました。すべてのテスト関数の結果セルは緑色で表示されており（表にあるすべてのアルゴリズムとの比較）、これは異なるタイプのタスクに対して非常に均一な性能を示しています。個々のテストにおいても、目立った失敗は見られませんでした。 

# AO 詳細 Hilly Hilly最終 Forest Forest最終 Megacity（離散） Megacity最終 最終結果 MAXの%
10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F)
1 BGA バイナリ遺伝的アルゴリズム 0,99989 0,99518 0,42835 2,42341 0,96153 0,96181 0,32027 2,24360 0,91385 0,95908 0,24220 2,11512 6,782 75,36
2 CLA コードロックアルゴリズム 0.95345 0.87107 0.37590 2.20042 0.98942 0.91709 0.31642 2.22294 0.79692 0.69385 0.19303 1.68380 6.107 67.86
3 (P+O)ES (P+O）進化戦略 0.92256 0.88101 0.40021 2.20379 0.97750 0.87490 0.31945 2.17185 0.67385 0.62985 0.18634 1.49003 5.866 65.17
4 CTA 彗尾アルゴリズム 0.95346 0.86319 0.27770 2.09435 0.99794 0.85740 0.33949 2.19484 0.88769 0.56431 0.10512 1.55712 5.846 64.96
5 SDSm 確率的拡散探索M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
6 ESG 社会集団の進化 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
7 SIA 等方的焼きなまし 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
8 TSEA 亀甲進化アルゴリズム 0.96798 0.64480 0.29672 1.90949 0.99449 0.61981 0.22708 1.84139 0.69077 0.42646 0.13598 1.25322 5.004 55.60
9 DE 差分進化 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
10 BSA 鳥群アルゴリズム 0.89306 0.64900 0.26250 1.80455 0.92420 0.71121 0.24939 1.88479 0.69385 0.32615 0.10012 1.12012 4.809 53.44
11 HS ハーモニー検索 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
12 SSG 苗木の播種と育成 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
13 (PO)ES (PO）進化戦略 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
14 BSO ブレインストーム最適化 0.93736 0.57616 0.29688 1.81041 0.93131 0.55866 0.23537 1.72534 0.55231 0.29077 0.11914 0.96222 4.498 49.98
15 WOAm 鯨最適化アルゴリズムM 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
16 ACOm 蟻コロニー最適化M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
17 BFO-GA 細菌採食の最適化：Ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
18 MEC Mind Evolutionary Computation 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
19 IWO 侵入雑草最適化 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
20 Micro-AIS 微小人工免疫系 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54
21 COAm カッコウ最適化アルゴリズムM 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21
22 SDOm 螺旋ダイナミクス最適化M 0.74601 0.44623 0.29687 1.48912 0.70204 0.34678 0.10944 1.15826 0.42833 0.16767 0.03663 0.63263 3.280 36.44
23 NMm ネルダー=ミード法M 0.73807 0.50598 0.31342 1.55747 0.63674 0.28302 0.08221 1.00197 0.44667 0.18667 0.04028 0.67362 3.233 35.92
24 FAm ホタルアルゴリズムM 0.58634 0.47228 0.32276 1.38138 0.68467 0.37439 0.10908 1.16814 0.28667 0.16467 0.04722 0.49855 3.048 33.87
25 GSA 重力探索法 0.64757 0.49197 0.30062 1.44016 0.53962 0.36353 0.09945 1.00260 0.32667 0.12200 0.01917 0.46783 2.911 32.34
26 BFO 細菌採餌最適化 0.61171 0.43270 0.31318 1.35759 0.54410 0.21511 0.05676 0.81597 0.42167 0.13800 0.03195 0.59162 2.765 30.72
27 ABC 人工蜂コロニー 0.63377 0.42402 0.30892 1.36671 0.55103 0.21874 0.05623 0.82600 0.34000 0.14200 0.03102 0.51302 2.706 30.06
28 BA コウモリアルゴリズム 0.59761 0.45911 0.35242 1.40915 0.40321 0.19313 0.07175 0.66810 0.21000 0.10100 0.03517 0.34617 2.423 26.93
29 SA 焼きなまし 0.55787 0.42177 0.31549 1.29513 0.34998 0.15259 0.05023 0.55280 0.31167 0.10033 0.02883 0.44083 2.289 25.43
30 IWDm intelligent water drops M 0.54501 0.37897 0.30124 1.22522 0.46104 0.14704 0.04369 0.65177 0.25833 0.09700 0.02308 0.37842 2.255 25.06
31 PSO 粒子群最適化 0.59726 0.36923 0.29928 1.26577 0.37237 0.16324 0.07010 0.60572 0.25667 0.08000 0.02157 0.35823 2.230 24.77
32 ボイド ボイドアルゴリズム 0.43340 0.30581 0.25425 0.99346 0.35718 0.20160 0.15708 0.71586 0.27846 0.14277 0.09834 0.51957 2.229 24.77
33 MA モンキーアルゴリズム 0.59107 0.42681 0.31816 1.33604 0.31138 0.14069 0.06612 0.51819 0.22833 0.08567 0.02790 0.34190 2.196 24.40
34 SFL Shuffled Frog-Leaping 0.53925 0.35816 0.29809 1.19551 0.37141 0.11427 0.04051 0.52618 0.27167 0.08667 0.02402 0.38235 2.104 23.38
35 FSS 魚群検索 0.55669 0.39992 0.31172 1.26833 0.31009 0.11889 0.04569 0.47467 0.21167 0.07633 0.02488 0.31288 2.056 22.84
36 RND ランダム 0.52033 0.36068 0.30133 1.18234 0.31335 0.11787 0.04354 0.47476 0.25333 0.07933 0.02382 0.35648 2.014 22.37
37 GWO 灰色オオカミオプティマイザ 0.59169 0.36561 0.29595 1.25326 0.24499 0.09047 0.03612 0.37158 0.27667 0.08567 0.02170 0.38403 2.009 22.32
38 CSS 荷電系探索 0.44252 0.35454 0.35201 1.14907 0.24140 0.11345 0.06814 0.42299 0.18333 0.06300 0.02322 0.26955 1.842 20.46
39 EM 電磁気学的アルゴリズム 0.46250 0.34594 0.32285 1.13129 0.21245 0.09783 0.10057 0.41085 0.15667 0.06033 0.02712 0.24412 1.786 19.85


まとめ

バイナリ遺伝的アルゴリズム(BGA)は、CLAアルゴリズムを開発する上で重要な役割を果たしました。私の目標は、より高速なアルゴリズムを作成することでした。そのため、私は2進符号化を10進符号化に置き換えるというアイデアを思いつきました。コードロック機構は、このアルゴリズム作成のプロトタイプとなり、結果的に成功を収めました。CLAはBGAよりも高速に動作しますが、効率性に関してはBGAと競合します。さらに、10進エンコーディングでは数値の組み合わせを生成する際に異なる分布を使用することができ、これは特定のタスクに役立ちます（コード内では、ベキ乗分布と正規分布がコメントアウトされており、必要に応じて利用可能です）。実験によると、この場合、単純な一様分布を用いる方が効果的であることがわかりました。

以上をまとめると、CLAコンビネーションロックアルゴリズムは、すべてのテスト機能において優れた結果、安定性、効率性を示しました。これは、アルゴリズムの高いスケーラビリティと複雑な問題に対処する能力を示すだけでなく、さまざまな最適化シナリオにおけるCLAアルゴリズムの柔軟性と有望な特性を浮き彫りにしています。

タブ

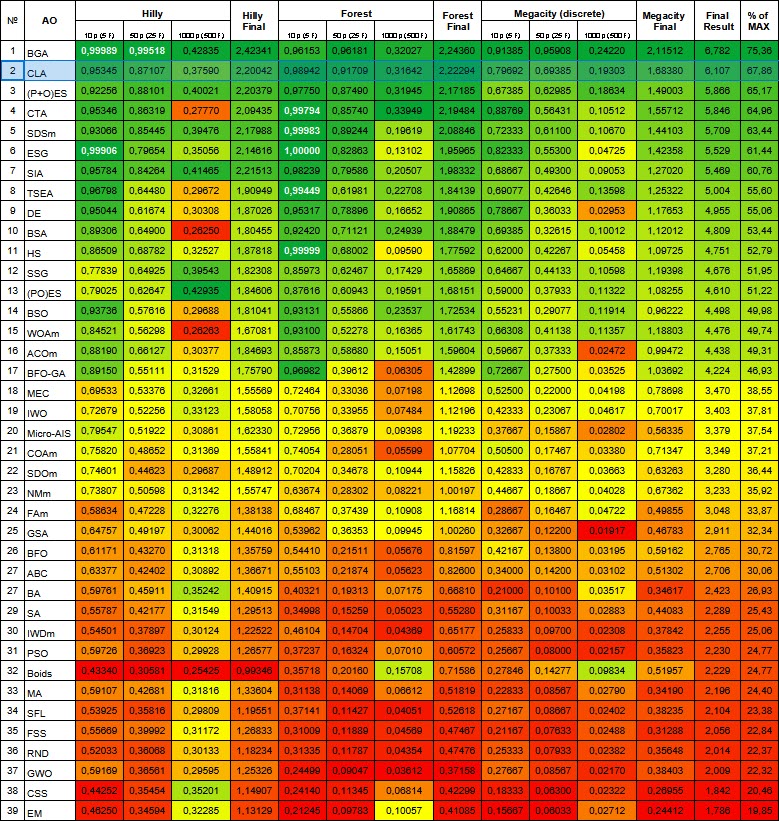
図2：関連テストによるアルゴリズムのカラーグラデーション 0.99以上の結果は白で強調表示される

チャート

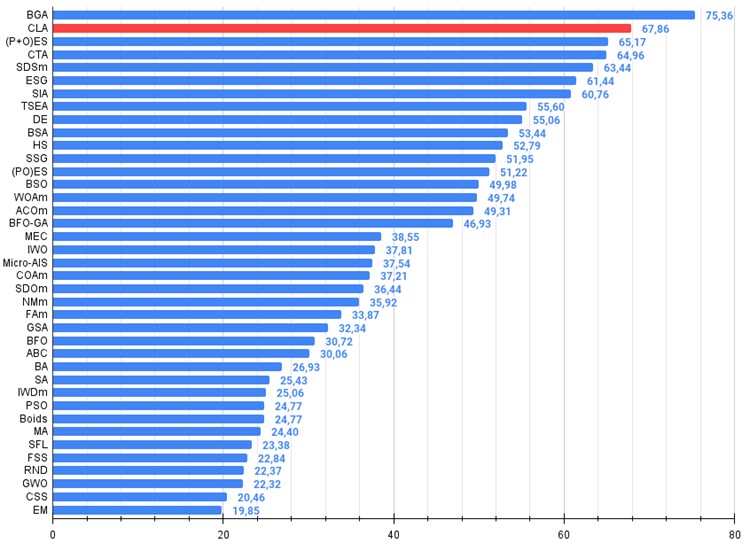
図3：アルゴリズムのテスト結果のヒストグラム（0から100までのスケールで、多ければ多いほど良い、

ここで、100は理論的に可能な最大の結果であり、アーカイブにはレーティング表を計算するスクリプトが含まれている）


CLAの長所と短所

長所：

  1. 様々な種類の関数に対して優れた収束性を発揮する
  2. 実装がシンプル

短所

  1. 低次元関数に関する結果が散らばる

この記事には、最新版のアルゴリズムコードを含むアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/14878

添付されたファイル |
ZIPをダウンロード
CLA.zip (25.42 KB)
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動
MQL5の統合：Python MQL5の統合：Python
Pythonは、特に金融、データサイエンス、人工知能、機械学習の分野で多くの特徴を持つ、よく知られた人気のプログラミング言語です。また、Pythonは取引にも有効な強力なツールです。MQL5では、この強力な言語を統合して使用することで、目的を効果的に達成することができます。本記事では、Pythonの基本的な情報を学んだ後、MQL5でPythonを統合して使用する方法を紹介します。
多通貨エキスパートアドバイザーの開発（第11回）：最適化の自動化（最初のステップ） 多通貨エキスパートアドバイザーの開発（第11回）：最適化の自動化（最初のステップ）
良いEAを得るためには、取引戦略の複数のインスタンスから優れたパラメータセットを選択する必要があります。これを実現するためには、さまざまな銘柄で最適化を行い、最良の結果を選ぶという手動のプロセスがあります。しかし、この作業をプログラムに任せ、より生産的な活動に専念したほうが効率的です。
Candlestick Trend Constraintモデルの構築（第8回）：エキスパートアドバイザーの開発 (I) Candlestick Trend Constraintモデルの構築（第8回）：エキスパートアドバイザーの開発 (I)
今回は、前回の記事で作成した指標を元に、MQL5で最初のエキスパートアドバイザー(EA)を作成します。リスク管理を含め、取引プロセスを自動化するために必要な全機能を紹介します。これにより、手動の取引執行から自動化されたシステムへとスムーズに移行できるメリットがあります。
あらゆるタイプのトレーリングストップを開発してEAに接続する方法 あらゆるタイプのトレーリングストップを開発してEAに接続する方法
この記事では、様々なトレーリングストップを簡単に作成するためのクラスと、トレーリングストップを任意のEAに接続する方法について説明します。