MetaTrader 5 / テスター
English Русский Español Português
preview
ニューロボイド最適化アルゴリズム2 (NOA2)

ニューロボイド最適化アルゴリズム2 (NOA2)

MetaTrader 5 — テスター |
24 0
Andrey Dik
Andrey Dik

内容

  1. はじめに
  2. アルゴリズムの実装
  3. テスト結果


はじめに

長年にわたり最適化アルゴリズムを研究する中で、私は常に2つの並行するインスピレーションに惹かれてきました。1つは生物群の自己組織化、もう1つはニューラルネットワークの適応学習能力です。この2つのパラダイムを統合することで、Craig Reynoldsが提案した、空間的知能を持つボイド（人工生命）と、ニューラルネットワークの適応学習能力を組み合わせたハイブリッド型アルゴリズムを開発するに至りました。

私の研究の出発点は、従来の群アルゴリズムが複雑な探索空間の探索には適している一方、探索履歴から学習する能力に欠けることにあります。一方で、ニューラルネットワークは複雑なパターンの学習には優れていますが、最適化問題に直接適用した場合、空間的パターンの効果的な探索には苦戦しがちです。私の研究を動機付けた問いは一見単純に思えます。群の各エージェントが専用のニューラルネットワークを使って、自らの移動戦略を改善できるとしたらどうなるかということです。

その結果生まれたアルゴリズムでは、各エージェントが従来のボイドルールである凝集、分離、整列に従うことで、自己組織化し、探索空間を効率的に探索できるようになっています。しかし、従来のボイド実装とは異なり、各エージェントは多層ニューラルネットワークを備えており、その経験に基づいて継続的に学習し、探索空間の特性に応じて移動戦略を適応させていきます。このニューラルネットワークによる制御のレベルは、ボイドの行動に徐々に影響を与え、初期段階では探索重視の戦略を支配していたものが、有望な領域が特定されるにつれて活用重視の移動へとシフトしていきます。

開発中に私が最も魅力的だと感じたのは、ニューラルネットワークが探索空間内での位置に応じて異なる戦略を進化させる様子を観察したことです。有望領域の近くにあるエージェントは局所的な活用を強化するニューラルパターンを発達させ、一方で希薄な領域にあるエージェントは探索行動をサポートしました。このような自発的な専門化は、個々の学習プロセスから自然に生じ、明示的な大域的調整がなくても、文脈依存的で多様な行動を持つ群を形成します。

本記事では、NOA2アルゴリズムのアーキテクチャ、実装の詳細、性能分析を紹介するとともに、各種ベンチマーク関数に対するその能力を実証します。 


アルゴリズムの実装

前述の通り、ニューロボイドアルゴリズムの主な考え方は、群アルゴリズムの集団知能とニューラルネットワークの適応学習の2つのパラダイムを組み合わせることにあります。

Craig Reynoldsによって提案された従来のボイドアルゴリズムでは、エージェントは、凝集（群れの中心に向かって移動する）、分離（衝突を避ける）、整列（近隣の方向と速度に合わせる）の3つの単純なルールに従います。これらのルールにより、鳥の群れのような現実的な集団行動が生まれます。ニューロボイドはこの概念を拡張し、各エージェントに探索空間での経験から学習する個別のニューラルネットワークを持たせています。このニューラルネットワークは2つの主要な機能を持ちます。

  1. 適応型運動制御：エージェントの現在の状態や移動履歴に基づいて速度を調整します。
  2. ボイドの標準ルールの修正：文脈に応じて、凝集、分離、整列ルールの影響を動的に調整します。

その結果、各エージェントは探索空間を効率的に探索するために必要な社会的行動を保持しつつ、学習を通じて適応度関数の特性に個別に適応するハイブリッドアルゴリズムが実現されます。これにより、探索と活用の間に自己調整されたバランスが生まれます。

このアプローチの主な利点は、各エージェントが最適な移動戦略を独立して学習できることです。その結果、アルゴリズムは異なるタイプの最適化ランドスケープに自動的に適応しつつ、集団行動によって探索は維持され、中央制御なしで空間探索を継続することができます。簡単な例えとして、空を飛ぶ鳥の群れを想像してください。彼らは協調して移動し、衝突せず、互いに離れず、同じ方向に飛びます。この行動は、近傍の個体の近くにいる（群れから離れない）、近傍の個体と衝突しない（距離を保つ）、同じ方向に飛ぶ（共通の進路を維持する）という、3つの単純なルールで表現できます。

これがいわゆるボイド（boid、「bird-oid」）アルゴリズムの基礎です。群れの中のそれぞれの鳥はこれらのルールに従うだけでなく、自己の経験からも学習します。どの行動が成功（たとえば、より多くの食物を見つけた）につながったか、どの行動が失敗だったかを記憶します。時間が経つにつれて、鳥はより賢くなり、どのように飛ぶかの意思決定が改善されます。これがニューロボイドアルゴリズムの本質です。つまり、集団移動の単純なルールと、各エージェントが自身の経験から学習する能力を組み合わせることです。名前の「ニューロ」は学習能力を意味します。このアプローチが特に興味深いのは、集団による探索の力（重要な領域を見逃さない）と個々の学習の利点（各自が自分の領域で最適化される）を同時に活用できる点にあります。

NOA2-illustration

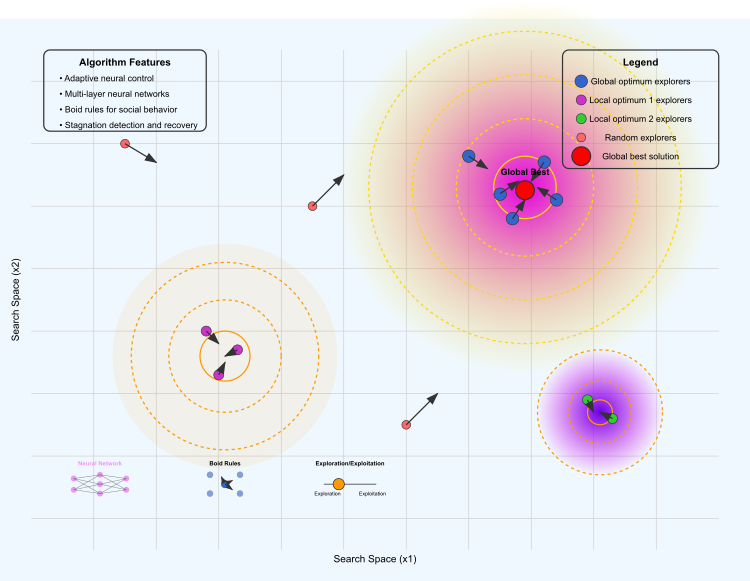
図1：NOA2アルゴリズムの動作 

図には、以下の主要な要素が示されています。最適化ランドスケープでは、黄色から紫の領域が大域最適解を表し、オレンジ色および紫色の領域は局所最適解を示しています。等高線は、適応度関数の「高さ」を表しています。 

エージェントの異なるグループとして、青色は大域最適解周辺を探索するエージェント、紫色は第一の局所最適解付近に集中するエージェント、緑色は第二の局所最適解を探索するエージェント、赤色は空間内をランダムに探索するエージェントです。矢印はボイドの移動方向を示しています。赤い点は、現在までに見つかった最良解を示しています。

NOA2-diagram

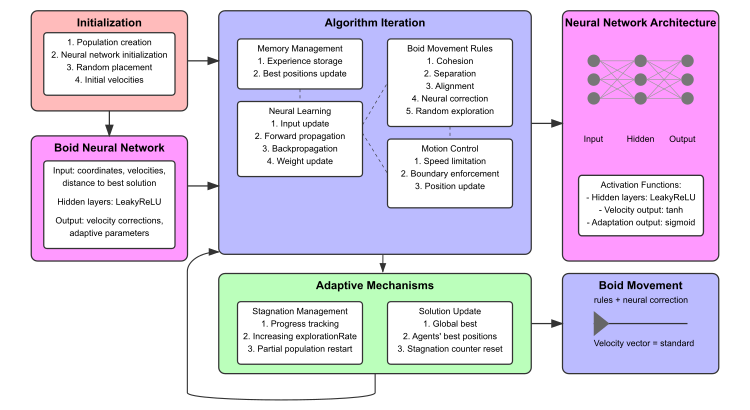
図2：NOA2アルゴリズムの動作 

図には、初期化ブロック（赤色）、ボイドニューラルネットワーク（ピンク色）、アルゴリズム反復処理のサブブロック（青色）、適応メカニズム（緑色）が含まれています。また、ニューラルネットワークの構造と接続例の可視化も示されています。下部には、ニューラルネットワーク構造のミニ図、ボイド移動ルールの可視化、および探索と活用のバランスを示す図が配置されています。

基本概念を理解したところで、次にアルゴリズムの擬似コードの説明に進むことができます。

初期化

  • 探索パラメータを設定し、エージェントの集団を生成します。
  • 各エージェントに対してランダムな位置、低速、ニューラルネットワーク（入力層 → 隠れ層 → 出力層）、および空の経験メモリを初期化します。
  • 大域最良適応度を負の無限大に設定し、停滞カウンタを0にリセットします。

メインループ

  • 各反復処理において、以下を実行します。

    適応度評価

    • 全エージェントの適応度を計算します。
    • 個体および大域の最良位置を更新します。
    • 経験をメモリバッファに保存します。

    停滞管理

    • 改善が見られない場合は探索を強化し、弱いエージェントを時々再初期化します。
    • 改善がある場合は探索レベルを徐々に低下させます。

    ニューラル処理

    • 各エージェントに対して
      • 入力（位置、速度、最良位置までの距離、適応度）から隠れ層を経て出力へのフォワードパスをおこないます。
      • 十分な経験が蓄積され、改善が検出された場合はニューラルネットワークの重みを更新します。

    移動更新

    • 各エージェントに対して
      • 標準的なボイド力（凝集、分離、整列）を計算します。
      • ニューラル修正力および直接的なニューラル補正項を適用します。
      • 確率的にランダム試行要素を追加します。
      • 速度制限と境界条件を適用します。
      • 最終速度に基づき位置を更新します。

補助計算

  • 適応度を正規化して質量を計算し、各エージェントに質量を割り当てます。
  • 凝集：近傍エージェントの重心に向かって移動します。
  • 分離：隣接エージェントとの混雑を回避します。
  • 整列：近傍エージェントと速度を調整します。
  • ニューラル更新：適応度の向上に基づいて簡易的なバックプロパゲーションをおこないます。

戻り値：大域最良位置および大域最良適応度

これでアルゴリズムコードを作成する準備が整いました。まず、ニューラルネットワーク構造に基づく最適化タスク用のニューロボイドエージェントを表すS_NeuroBoids_Agent構造体を定義します。実装では、エージェントは以下の主要なコンポーネントと機能を持ちます。

座標と速度

  • x []：現在のエージェントの座標
  • dx []：現在のエージェントの速度
ニューラルネットワーク
  • inputs []：ニューロンへの入力値（座標、速度、既知の最良位置までの距離など）
  • outputs []：ニューラルネットワークの出力値（速度補正や適応パラメータ）
  • weights []：ニューラルネットワーク内の接続の重み
  • biases []：各ニューロンのバイアス
メモリ
  • memory []：以前の座標とその適応度を保存する配列
  • memory_size：メモリの最大容量
  • memory_index：現在のメモリインデックス
適応度および重み
  • best_local_fitness：エージェントの局所最良適応度
  • m：エージェントの質量
  • cB[]：エージェントが見つけた最良位置の座標
  • fB：最良位置における適応度値

初期化(Init)：すべての配列や変数をゼロまたはランダム値で初期化します。配列サイズを設定し、影響値（重みやバイアス）は小さなランダム値で初期化されます。

活性化関数：Tanh、ReLU、Sigmoidなど、ニューラルネットワークで使用される各種活性化関数です。

入力データの更新(UpdateInputs)：入力配列を現在の座標、速度、既知の最良位置までの距離、および現在の適応度値で埋めます。

フォワードパス(ForwardPass)：入力、重み、バイアスを用い、活性化関数を適用してニューラルネットワークの出力を計算します。

経験学習(Learn)：現在の経験が過去よりも良好であれば、蓄積された経験に基づき重みとバイアスを更新します。

経験の記憶(MemorizeExperience)：現在の座標とエージェントの適応度をメモリに保存します。

最良位置の更新(UpdateBestPosition)：現在の適応度値が過去の最良値よりも良ければ、最良位置を更新します。

//——————————————————————————————————————————————————————————————————————————————
// Neuro-boid agent structure
//——————————————————————————————————————————————————————————————————————————————
struct S_NeuroBoids_Agent
{
    double x       [];            // current coordinates
    double dx      [];            // current speeds
    double inputs  [];            // neuron inputs
    double outputs [];            // neuron outputs
    double weights [];            // neuron weights
    double biases  [];            // neuron biases
    double memory  [];            // memory of previous positions and their fitnesses
    int    memory_size;           // memory size for accumulating experience
    int    memory_index;          // current index in memory
    double best_local_fitness;    // best local agent fitness
    double m;                     // boid mass
    double cB [];                 // best position coordinates
    double fB;                    // fitness function value

    // Agent initialization
    void Init (int coords, int neuron_size)
    {
      ArrayResize (x, coords);
      ArrayResize (dx, coords);
      ArrayInitialize (x, 0.0);
      ArrayInitialize (dx, 0.0);

      // Initialize the best position structure
      ArrayResize     (cB, coords);
      ArrayInitialize (cB, 0.0);
      fB = -DBL_MAX;

      // Inputs: coordinates, speeds, distance to best, etc.
      int input_size = coords * 2 + 2; // x, dx, dist_to_best, current_fitness
      ArrayResize (inputs, input_size);
      ArrayInitialize (inputs, 0.0);

      // Outputs: Speed correction and adaptive factors for flock rules
      int output_size = coords + 3; // dx_correction + 3 adaptive parameters
      ArrayResize (outputs, output_size);
      ArrayInitialize (outputs, 0.0);

      // Weights and biases for each output
      ArrayResize (weights, input_size * output_size);
      ArrayInitialize (weights, 0.0);
      ArrayResize (biases, output_size);
      ArrayInitialize (biases, 0.0);

      // Initialize weights and biases with small random values
      for (int i = 0; i < ArraySize (weights); i++)
      {
        weights [i] = 0.01 * (MathRand () / 32767.0 * 2.0 - 1.0);
      }

      for (int i = 0; i < ArraySize (biases); i++)
      {
        biases [i] = 0.01 * (MathRand () / 32767.0 * 2.0 - 1.0);
      }

      // Initialize memory for accumulating experience
      memory_size = 10;
      ArrayResize (memory, memory_size * (coords + 1)); // coordinates + fitness
      ArrayInitialize (memory, 0.0);
      memory_index = 0;
      best_local_fitness = -DBL_MAX;

      // Initialize mass
      m = 0.5;
    }

    // Activation function - hyperbolic tangent
    double Tanh (double input_val)
    {
      return MathTanh (input_val);
    }

    // ReLU activation function
    double ReLU (double input_val)
    {
      return (input_val > 0.0) ? input_val : 0.0;
    }

    // Sigmoid activation function
    double Sigmoid (double input_val)
    {
      return 1.0 / (1.0 + MathExp (-input_val));
    }

    // Updating neural network inputs - Corrected version
    void UpdateInputs (double &global_best [], double current_fitness, int coords_count)
    {
      int input_index = 0;

      // Coordinates
      for (int c = 0; c < coords_count; c++)
      {
        inputs [input_index++] = x [c];
      }

      // Speeds
      for (int c = 0; c < coords_count; c++)
      {
        inputs [input_index++] = dx [c];
      }

      // Distance to the best global solution
      double dist_to_best = 0;
      for (int c = 0; c < coords_count; c++)
      {
        dist_to_best += MathPow (x [c] - global_best [c], 2);
      }
      dist_to_best = MathSqrt (dist_to_best);
      inputs [input_index++] = dist_to_best;

      // Current fitness function
      inputs [input_index++] = current_fitness;
    }

    // Direct distribution over the network
    void ForwardPass (int coords_count)
    {
      int input_size = ArraySize (inputs);
      int output_size = ArraySize (outputs);

      // For each output, calculate the weighted sum of the inputs + bias
      for (int o = 0; o < output_size; o++)
      {
        double sum = biases [o];

        for (int i = 0; i < input_size; i++)
        {
          sum += inputs [i] * weights [o * input_size + i];
        }

        // Apply different activation functions depending on the output
        if (o < coords_count) // Use the hyperbolic tangent to correct the speed
        {
          outputs [o] = Tanh (sum);
        }
        else // Use sigmoid for adaptive parameters
        {
          outputs [o] = Sigmoid (sum);
        }
      }
    }

    // Learning from accumulated experience
    void Learn (double learning_rate, int coords_count)
    {
      if (memory_index < memory_size) return; // Insufficient experience

      // Find the best experience in memory
      int best_index = 0;
      double best_fitness = memory [coords_count]; // The first fitness function in memory

      for (int i = 1; i < memory_size; i++)
      {
        double fitness = memory [i * (coords_count + 1) + coords_count];
        if (fitness > best_fitness)
        {
          best_fitness = fitness;
          best_index = i;
        }
      }

      // If the current experience is not better than the previous one, do not update the weights
      if (best_fitness <= best_local_fitness) return;

      best_local_fitness = best_fitness;

      // Simple method for updating weights
      int input_size = ArraySize (inputs);
      int output_size = ArraySize (outputs);

      // Simple form of gradient update
      for (int o = 0; o < output_size; o++)
      {
        for (int i = 0; i < input_size; i++)
        {
          int weight_index = o * input_size + i;
          if (weight_index < ArraySize (weights))
          {
            weights [weight_index] += learning_rate * outputs [o] * inputs [i];
          }
        }

        // Update offsets
        biases [o] += learning_rate * outputs [o];
      }
    }

    // Save current experience (coordinates and fitness)
    void MemorizeExperience (double fitness, int coords_count)
    {
      int offset = memory_index * (coords_count + 1);

      // Save the coordinates
      for (int c = 0; c < coords_count; c++)
      {
        memory [offset + c] = x [c];
      }

      // Save the fitness function
      memory [offset + coords_count] = fitness;

      // Update the memory index
      memory_index = (memory_index + 1) % memory_size;
    }

    // Update the agent's best position
    void UpdateBestPosition (double current_fitness, int coords_count)
    {
      if (current_fitness > fB)
      {
        fB = current_fitness;
        ArrayCopy (cB, x, 0, 0, WHOLE_ARRAY);
      }
    }
};

C_AO_NOA2クラスはNOA2アルゴリズムの実装であり、C_AO基底クラスを継承しています。ここではクラスの構造と主要な要素について詳しく見ていきます。

主なパラメータ
  • popSize：エージェント（ボイド）の集団サイズ
  • cohesionWeight、cohesionDist：凝集ルールの重みと距離
  • separationWeight、separationDist：分離ルールの重みと距離
  • alignmentWeight、alignmentDist：整列ルールの重みと距離
  • maxSpeed、minSpeed：エージェントの最大速度と最小速度
  • learningRate：ニューラルネットワークの学習率
  • neuralInfluence：ニューラルネットワークがエージェントの動きに与える影響
  • exploreRate：解空間のランダム探索の確率
  • m_stagnationCounter、m_prevBestFitness：停滞カウンタと直前の最良適応度値
クラスメソッド
  • SetParams ()：「params」配列に保存された値に基づきアルゴリズムパラメータを設定します
  • Init ()：初期化。エージェントの値の範囲を定義するパラメータを受け取り、アルゴリズムの初期条件を設定します。
  • Moving ()：各種相互作用ルールに基づくエージェントの移動を担当します。
  • Revision ()：アルゴリズム実行中にエージェントの状態を修正するために使用されます。

エージェント：S_NeuroBoids_Agent agent []：集団内のボイドを表すエージェントの配列

privateメソッド（クラス内で使用）

  • CalculateMass ()：エージェントの質量
  • Cohesion ()：凝集ルール
  • Separation ()：分離ルール
  • Alignment ()：整列ルール
  • LimitSpeed ()：エージェントの速度を制限します
  • KeepWithinBounds ()：エージェントを指定された境界内に保持します。
  • Distance ()：2つのエージェント間の距離を計算します。
  • ApplyNeuralControl ()：エージェントにニューラルネットワークによる制御を適用します。
  • AdaptiveExploration()：適応型探索を実装します。
//——————————————————————————————————————————————————————————————————————————————
// Class of neuron-like optimization algorithm inherited from C_AO
//——————————————————————————————————————————————————————————————————————————————
class C_AO_NOA2 : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_NOA2 () { }
  C_AO_NOA2 ()
  {
    ao_name = "NOA2";
    ao_desc = "Neuroboids Optimization Algorithm 2 (joo)";
    ao_link = "https://www.mql5.com/ja/articles/17497";

    popSize          = 50;     // population size

    cohesionWeight   = 0.6;    // cohesion weight
    cohesionDist     = 0.001;  // cohesion distance

    separationWeight = 0.005;  // separation weight
    separationDist   = 0.03;   // separation distance

    alignmentWeight  = 0.1;    // alignment weight
    alignmentDist    = 0.1;    // alignment distance

    maxSpeed         = 0.001;  // maximum speed
    minSpeed         = 0.0001; // minimum speed 

    learningRate     = 0.01;   // neural network learning speed
    neuralInfluence  = 0.3;    // influence of the neural network on movement
    explorationRate  = 0.1;    // random exploration probability

    ArrayResize (params, 12);

    params [0].name  = "popSize";          params [0].val = popSize;

    params [1].name  = "cohesionWeight";   params [1].val  = cohesionWeight;
    params [2].name  = "cohesionDist";     params [2].val  = cohesionDist;

    params [3].name  = "separationWeight"; params [3].val  = separationWeight;
    params [4].name  = "separationDist";   params [4].val  = separationDist;

    params [5].name  = "alignmentWeight";  params [5].val  = alignmentWeight;
    params [6].name  = "alignmentDist";    params [6].val  = alignmentDist;

    params [7].name  = "maxSpeed";         params [7].val  = maxSpeed;
    params [8].name  = "minSpeed";         params [8].val  = minSpeed;

    params [9].name  = "learningRate";     params [9].val  = learningRate;
    params [10].name = "neuralInfluence";  params [10].val = neuralInfluence;
    params [11].name = "explorationRate";  params [11].val = explorationRate;

    // Initialize the stagnation counter and the previous best fitness value
    m_stagnationCounter = 0;
    m_prevBestFitness   = -DBL_MAX;
  }

  void SetParams ()
  {
    popSize          = (int)params [0].val;

    cohesionWeight   = params [1].val;
    cohesionDist     = params [2].val;

    separationWeight = params [3].val;
    separationDist   = params [4].val;

    alignmentWeight  = params [5].val;
    alignmentDist    = params [6].val;

    maxSpeed         = params [7].val;
    minSpeed         = params [8].val;

    learningRate     = params [9].val;
    neuralInfluence  = params [10].val;
    explorationRate  = params [11].val;
  }

  bool Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0);
  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  double cohesionWeight;     // cohesion weight
  double cohesionDist;       // cohesion distance

  double separationWeight;   // separation weight
  double separationDist;     // separation distance

  double alignmentWeight;    // alignment weight
  double alignmentDist;      // alignment distance

  double minSpeed;           // minimum speed
  double maxSpeed;           // maximum speed

  double learningRate;       // neural network learning speed
  double neuralInfluence;    // influence of the neural network on movement
  double explorationRate;    // random exploration probability

  int m_stagnationCounter;   // stagnation counter
  double m_prevBestFitness;  // previous best fitness value

  S_NeuroBoids_Agent agent []; // agents (boids)

  private: //-------------------------------------------------------------------
  double distanceMax;     // maximum distance
  double speedMax [];     // maximum speeds by measurements

  int neuron_size;        // neuron size (number of inputs)

  void   CalculateMass       ();                                  // calculation of agent masses 
  void   Cohesion            (S_NeuroBoids_Agent &boid, int pos); // cohesion rule
  void   Separation          (S_NeuroBoids_Agent &boid, int pos); // separation rule
  void   Alignment           (S_NeuroBoids_Agent &boid, int pos); // alignment rule
  void   LimitSpeed          (S_NeuroBoids_Agent &boid);          // speed limit
  void   KeepWithinBounds    (S_NeuroBoids_Agent &boid);          // keep within bounds
  double Distance            (S_NeuroBoids_Agent &boid1, S_NeuroBoids_Agent &boid2); // calculate distance
  void   ApplyNeuralControl  (S_NeuroBoids_Agent &boid, int pos); // apply neural control
  void   AdaptiveExploration ();                                  // adaptive research
};
//——————————————————————————————————————————————————————————————————————————————

Initメソッドは、アルゴリズムおよびエージェントのパラメータを初期化する役割を持ちます。処理はStandardInitを呼び出すことから始まり、範囲の最小値、最大値と探索ステップの配列を渡します。標準の初期化が失敗した場合、メソッドは直ちにfalseを返します。エージェントのニューラルネットワークで使用されるニューロン数もここで設定されます。

この場合、サイズは、座標数の2倍にdist_to_bestとcurrent_fitnessを加えた値として計算されます。エージェント配列のサイズは指定されたpopSizeに従って変更されます。その後、各エージェントに対してInitメソッドが呼ばれ、ニューラルネットワークを含む各種パラメータが初期化されます。

最大距離および速度の計算

  • distanceMax変数は0に初期化されます。
  • 各座標について、範囲の最大値と最小値の差に基づいて最大速度が計算されます。
  • 最大距離は各座標の最大速度の二乗和の平方根として計算されます。

停滞カウンタ(m_stagnationCounter)は0にリセットされ、前回の最良適応度値を保持する変数(m_prevBestFitness)は取り得る最小値に設定されます。メソッドは、凝集、分離、整列の重み、最大および最小速度、学習率、ニューラルネットワークの影響度、探索確率など、さまざまなグローバル変数を設定します。すべての手順が正常に完了した場合、メソッドはtrueを返し、初期化が成功したことを示します。

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_NOA2::Init (const double &rangeMinP  [],  // minimum search range
                      const double &rangeMaxP  [],  // maximum search range
                      const double &rangeStepP [],  // search step
                      const int    epochsP)         // number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  // Determine the size of a neuron
  neuron_size = coords * 2 + 2; // x, dx, dist_to_best, current_fitness

  // Initialize the agents
  ArrayResize (agent, popSize);
  for (int i = 0; i < popSize; i++)
  {
    agent [i].Init (coords, neuron_size);
  }

  distanceMax = 0;
  ArrayResize (speedMax, coords);

  for (int c = 0; c < coords; c++)
  {
    speedMax [c] = rangeMax [c] - rangeMin [c];
    distanceMax += MathPow (speedMax [c], 2);
  }

  distanceMax = MathSqrt (distanceMax);

  // Reset the stagnation counter and the previous best fitness value
  m_stagnationCounter = 0;
  m_prevBestFitness   = -DBL_MAX;

  GlobalVariableSet ("#reset", 1.0);

  GlobalVariableSet ("1cohesionWeight",   params [1].val);
  GlobalVariableSet ("2cohesionDist",     params [2].val);

  GlobalVariableSet ("3separationWeight", params [3].val);
  GlobalVariableSet ("4separationDist",   params [4].val);

  GlobalVariableSet ("5alignmentWeight",  params [5].val);
  GlobalVariableSet ("6alignmentDist",    params [6].val);

  GlobalVariableSet ("7maxSpeed",         params [7].val);
  GlobalVariableSet ("8minSpeed",         params [8].val);

  GlobalVariableSet ("9learningRate",     params [9].val);
  GlobalVariableSet ("10neuralInfluence", params [10].val);
  GlobalVariableSet ("11explorationRate", params [11].val);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Movingメソッドは、受け取ったデータとエージェント間の相互作用に基づき、環境内でのエージェントの移動を担当します。まず、#resetグローバル変数の値を確認します。値が1.0の場合はパラメータがリセットされ、revision変数がfalseに設定され、その後#resetは0.0に戻ります。凝集、分離、整列の重み、最小および最大速度、学習率、ニューラルネットワークの影響度、探索比率などの各種パラメータはグローバル変数から取得されます。これらのパラメータは、エージェントの挙動を変更するために設定可能です。

revision変数がfalseの場合、エージェントの座標xと速度dxが初期化されます。各座標には指定範囲内のランダム値が適用され、速度は小さなランダム値に設定されます。また、各座標には現在の位置に基づいたエージェントの状態が格納されます。その後、AdaptiveExploration()メソッドが呼び出され、停滞状態に応じてエージェントの探索行動を適応的に変更します。

エージェント移動のメインループ（エージェントごと）

  • エージェントの現在の経験を保存します。
  • エージェントが見つけた最良位置を更新します。
  • エージェントのニューラルネットワークの入力データを更新します。
  • ニューラルネットワークを通してデータを直接伝播させます。
  • 蓄積された経験に基づきエージェントを学習させます。
質量計算：CalculateMass()メソッドを呼び出し、各エージェントの質量に基づいて相互作用を評価します。

    ルール適用と移動：エージェントを順にループ処理し、ボイドアルゴリズムの標準ルールを各エージェントに適用します。

    • 凝集：エージェント同士が互いに近づこうとします。
    • 分離：衝突を避けるためにエージェント同士が近づきすぎないようにします
    • 整列：エージェントは近隣のエージェントと同じ方向に移動しようとします。
    さらに、ApplyNeuralControl()メソッドが呼び出され、ニューラルネットワークによる制御が適用されます。LimitSpeed()メソッドでエージェントの速度を制限し、KeepWithinBounds()メソッドでエージェントが指定領域内に留まるようにします。最後に、各座標ごとに現在の速度を加算してエージェントの位置と状態を更新します。

    //——————————————————————————————————————————————————————————————————————————————
void C_AO_NOA2::Moving ()
{
  double reset = GlobalVariableGet ("#reset");
  if (reset == 1.0)
  {
    revision = false;
    GlobalVariableSet ("#reset", 0.0);
  }

  // Get parameters from global variables for interactive configuration
  cohesionWeight   = GlobalVariableGet ("1cohesionWeight");
  cohesionDist     = GlobalVariableGet ("2cohesionDist");

  separationWeight = GlobalVariableGet ("3separationWeight");
  separationDist   = GlobalVariableGet ("4separationDist");

  alignmentWeight  = GlobalVariableGet ("5alignmentWeight");
  alignmentDist    = GlobalVariableGet ("6alignmentDist");

  maxSpeed         = GlobalVariableGet ("7maxSpeed");
  minSpeed         = GlobalVariableGet ("8minSpeed");

  learningRate     = GlobalVariableGet ("9learningRate");
  neuralInfluence  = GlobalVariableGet ("10neuralInfluence");
  explorationRate  = GlobalVariableGet ("11explorationRate");

  // Initialization of initial positions and speeds
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        agent [i].x [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        agent [i].dx [c] = (rangeMax [c] - rangeMin [c]) * u.RNDfromCI (-1.0, 1.0) * 0.001;

        a [i].c [c] = u.SeInDiSp (agent [i].x [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  // Adaptive research depending on stagnation
  AdaptiveExploration ();

  //----------------------------------------------------------------------------
  // Main loop of boid movement
  for (int i = 0; i < popSize; i++)
  {
    // Save the current experience
    agent [i].MemorizeExperience (a [i].f, coords);

    // Update the agent's best position
    agent [i].UpdateBestPosition (a [i].f, coords);

    // Update the neural network inputs
    agent [i].UpdateInputs (cB, a [i].f, coords);

    // Forward propagation through the neural network
    agent [i].ForwardPass (coords);

    // Learning from accumulated experience
    agent [i].Learn (learningRate, coords);
  }

  // Calculate masses
  CalculateMass ();

  // Application of rules and movement
  for (int i = 0; i < popSize; i++)
  {
    // Standard rules of the boid algorithm
    Cohesion (agent [i], i);
    Separation (agent [i], i);
    Alignment (agent [i], i);

    // Apply neural control
    ApplyNeuralControl (agent [i], i);

    // Speed limit and keeping within bounds
    LimitSpeed (agent [i]);
    KeepWithinBounds (agent [i]);

    // Update positions
    for (int c = 0; c < coords; c++)
    {
      agent [i].x [c] += agent [i].dx [c];
      a [i].c [c] = u.SeInDiSp (agent [i].x [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

    CalculateMassメソッドは、エージェントの適応度（生産性）に基づいて「質量」を計算し、これらの値を正規化します。maxMassとminMass変数はそれぞれ-DBL_MAXとDBL_MAXで初期化され、集団内のエージェントの中で最大および最小の適応度を見つけるために使用されます。メソッドはまず、少なくとも1つのエージェントが存在するかどうかを確認するため、popSize（集団サイズ）が0より大きいかをチェックします。エージェントが存在しない場合、メソッドは終了します。最初のループでは、すべてのエージェント（インデックス0からpopSizeまで）を順に処理し、それぞれの適応度（a[i].fの値）が現在のmaxMassより大きいか、またはminMassより小さいかを確認します。

    このループの結果、全エージェントの中で最大および最小の適応度値が決定されます。次のループでは、再びすべてのエージェントを順に処理し、それぞれの「質量」（m変数）をu.Scale関数を用いて計算します。この関数により、適応度値が正規化されます。 

    //——————————————————————————————————————————————————————————————————————————————
void C_AO_NOA2::CalculateMass ()
{
  double maxMass = -DBL_MAX;
  double minMass = DBL_MAX;

  // Check for data presence before calculations
  if (popSize <= 0) return;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > maxMass) maxMass = a [i].f;
    if (a [i].f < minMass) minMass = a [i].f;
  }

  for (int i = 0; i < popSize; i++)
  {
    agent [i].m = u.Scale (a [i].f, minMass, maxMass, 0.1, 1.0);
  }
}
//——————————————————————————————————————————————————————————————————————————————

    ApplyNeuralControlメソッドは、ニューラルネットワークの出力に基づいて「ボイド型」エージェントの制御を適用する役割を持ちます。メソッドは、エージェントのcoordsのすべての座標に対して順に処理をおこないます。各座標cについて、現在のインデックスがboid.outputs出力配列の範囲を超えていないかを確認します。インデックスが正しい場合、エージェントの速度dx[c]は、ニューラルネットワーク出力の対応する値にneuralInfluenceを掛けた値で補正されます。

    後続の処理を簡略化するため、boid.outputs配列のサイズが取得されます。凝集係数(cohesion_factor)、分離係数(separation_factor)、整列係数(alignment_factor)について、対応するインデックスが出力配列の範囲内かをチェックします。インデックスが範囲外の場合は、デフォルト値として0.5が割り当てられます。これらの比率は、ニューラルネットワークの影響を反映させるために基準重みをスケーリングする際に使用され、凝集、分離、整列のエージェントの挙動に影響を与えます。

    • local_cohesion：凝集重みを設定します。
    • local_separation：分離重みを設定します。
    • local_alignment：整列重みを設定します。

    さらに、与えられたexplorationRate確率に基づき、ランダム探索をおこなうかどうかを判定します。条件が満たされる場合、摂動を加える座標cがランダムに選ばれます。摂動量perturbation_sizeは、エージェントの質量（適応度の指標）とその座標の可能な値の範囲に基づいて計算されます。これにより、エージェントの質量に依存せずランダム変動の大きさを制御できます。perturbation_sizeからperturbation_sizeの範囲から選ばれたランダム摂動がdx[c]に加算されます。ApplyNeuralControlメソッドは、ニューラルネットワークの出力結果をエージェントの移動管理に統合し、速度を調整すると同時に、ランダム探索の必要性も考慮します。

    //——————————————————————————————————————————————————————————————————————————————
// Apply neural control to a boid
void C_AO_NOA2::ApplyNeuralControl (S_NeuroBoids_Agent &boid, int pos)
{
  // Use the neural network outputs to correct the speed
  for (int c = 0; c < coords; c++)
  {
    // Make sure the index is not outside the array bounds 
    if (c < ArraySize (boid.outputs))
    {
      // Apply neural speed correction with a given influence
      boid.dx [c] += boid.outputs [c] * neuralInfluence;
    }
  }

  // Use the neural network outputs to adapt the flock parameters
  // Check that the indices do not go beyond the array bounds
  int output_size = ArraySize (boid.outputs);

  double cohesion_factor   = (coords < output_size) ? boid.outputs [coords] : 0.5;
  double separation_factor = (coords + 1 < output_size) ? boid.outputs [coords + 1] : 0.5;
  double alignment_factor  = (coords + 2 < output_size) ? boid.outputs [coords + 2] : 0.5;

  // Scale the base weights considering neural adaptation
  // These variables are local and do not change global parameters
  double local_cohesion   = cohesionWeight * (0.5 + cohesion_factor);
  double local_separation = separationWeight * (0.5 + separation_factor);
  double local_alignment  = alignmentWeight * (0.5 + alignment_factor);

  // Random study with a given probability
  if (u.RNDprobab () < explorationRate)
  {
    // Select a random coordinate for perturbation
    int c = (int)u.RNDfromCI (0, coords - 1);

    // Adaptive perturbation size depending on mass (fitness)
    double perturbation_size = (1.0 - boid.m) * (rangeMax [c] - rangeMin [c]) * 0.01;

    // Add random perturbation
    boid.dx [c] += u.RNDfromCI (-perturbation_size, perturbation_size);
  }
}
//——————————————————————————————————————————————————————————————————————————————

    C_AO_NOA2クラスのAdaptiveExplorationメソッドは、最適化プロセスにおける停滞段階に応じて適応型探索を実装します。まず、fB目的関数値が、以前の最良値であるm_prevBestFitnessと比較して変化しているかを確認します。両者の差が0.000001未満であれば進展がないとみなし、m_stagnationCounterを増加させます。そうでない場合は停滞が終了したとみなし、カウンタをリセットし、現在のfBの値を新しい最良値として保存します。

    停滞の回数が20を超えた場合、ランダム探索の確率(explorationRate)が増加しますが、ランダム変化の確率が高くなりすぎないよう上限は0.5に制限されます。また、50回の停滞イテレーションごとに部分的な再初期化がおこなわれます。この際、集団の70%のエージェントは、指定されたrangeMinおよびrangeMaxの範囲内で新しいランダム値により再初期化されます。一方、残りの上位エージェントは現在の位置のまま保持されます。再初期化後、停滞カウンタはリセットされます。

    進展があった場合、かつparams配列のパラメータ数が11より多ければ、探索確率explorationRateはパラメータ配列から設定されます。パラメータ数が少ない場合は、デフォルト値として0.1が設定されます。

    //——————————————————————————————————————————————————————————————————————————————
// Adaptive research depending on stagnation
void C_AO_NOA2::AdaptiveExploration ()
{
  // Determine if there is progress in the search
  if (MathAbs (fB - m_prevBestFitness) < 0.000001)
  {
    m_stagnationCounter++;
  }
  else
  {
    m_stagnationCounter = 0;
    m_prevBestFitness = fB;
  }

  // Increase research during stagnation
  if (m_stagnationCounter > 20)
  {
    // Increase the probability of random exploration
    explorationRate = MathMin (0.5, explorationRate * 1.5);

    // Perform a partial restart every 50 stagnation iterations
    if (m_stagnationCounter % 50 == 0)
    {
      // Restart 70% of the population leaving the best agents
      int restart_count = (int)(popSize * 0.7);

      for (int i = popSize - restart_count; i < popSize; i++)
      {
        for (int c = 0; c < coords; c++)
        {
          agent [i].x [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
          agent [i].dx [c] = (rangeMax [c] - rangeMin [c]) * u.RNDfromCI (-1.0, 1.0) * 0.001;
        }
      }

      // Reset the stagnation counter
      m_stagnationCounter = 0;
    }
  }
  else
  {
    // If progress is good enough, use the normal research level 
    if (11 < ArraySize (params))
    {
      explorationRate = params [11].val;
    }
    else
    {
      explorationRate = 0.1; // default value
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

    C_AO_NOA2クラスのCohesionメソッドは、ボイドのエージェントベースモデルにおける「凝集」の挙動を実装する役割を持ちます。以下が変数の宣言です。

    • centerX：近傍エージェントの重心座標を格納する配列で、サイズはcoordsの数に対応します。
    • numNeighbors：近傍エージェントの数をカウントする変数で、指定距離内にあるエージェントを追跡します（質量を考慮）。
    • sumMass：近傍エージェントの質量の合計で、重心座標を正規化するために使用されます。

    最初のループ（0からpopSize）では、現在のボイド（posインデックスのエージェント）を除く集団内のすべてのエージェントの質量を合計します。次のループでは、すべてのエージェントを順に処理し、現在のボイドからの距離がcohesionDist係数を掛けた最大距離以内かどうかを確認します。エージェントまでの距離が指定距離より近い場合、そのエージェントの座標（質量を考慮）をcenterXに加算し、numNeighborsを増加させます。

    近傍エージェントの座標合計と質量が計算された後、近傍エージェントが存在するか(numNeighbors > 0)および質量の合計が正か(sumMass > 0.0)を確認します。条件を満たす場合、重心座標は質量の合計で割ることにより正規化されます。その後、現在のボイドの速度dxは、与えられたcohesionWeightに基づき重心の方向に加算されます。つまり、ボイドは近傍エージェントの重心に向かって移動するようになります。

    Cohesionメソッドは、重心を計算し、ボイドの速度を調整することで「凝集」する挙動を実現します。この挙動は群れや集団のシミュレーションにおいて重要な要素です。cohesionDistパラメータやcohesionWeightパラメータにより、この挙動が影響を与える距離や、重心がボイドの移動に与える影響の度合いを調整することが可能です。

    //——————————————————————————————————————————————————————————————————————————————
// Find the center of mass of other boids and adjust the speed towards the center of mass
void C_AO_NOA2::Cohesion (S_NeuroBoids_Agent &boid, int pos)
{
  double centerX [];
  ArrayResize (centerX, coords);
  ArrayInitialize (centerX, 0.0);

  int numNeighbors = 0;
  double sumMass = 0;

  for (int i = 0; i < popSize; i++)
  {
    if (pos != i) sumMass += agent [i].m;
  }

  for (int i = 0; i < popSize; i++)
  {
    if (pos != i)
    {
      if (Distance (boid, agent [i]) < distanceMax * cohesionDist)
      {
        for (int c = 0; c < coords; c++)
        {
          centerX [c] += agent [i].x [c] * agent [i].m;
        }

        numNeighbors++;
      }
    }
  }

  if (numNeighbors > 0 && sumMass > 0.0)
  {
    for (int c = 0; c < coords; c++)
    {
      centerX [c] /= sumMass;
      boid.dx [c] += (centerX [c] - boid.x [c]) * cohesionWeight;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

    C_AO_NOA2クラスのSeparationメソッドは、モデル内のエージェントに対して「分離」の挙動を実装します。この挙動は、ボイドと近傍エージェントとの衝突を防ぐことを目的としています。moveXパラメータ（cohesionDist配列と同様の構造）は、ボイドを他のエージェントから押し離すための変位ベクトルを格納するために使用されます。

    moveX配列のサイズはcoordsの数に対応し、ランダム値の累積を避けるため最初に0で初期化されます。その後、集団内のすべてのエージェント（インデックス0からpopSize）を順に処理します。各エージェントについて、現在のボイドに近いかどうかをDistance関数を用いて確認します。ボイドとエージェントの距離が指定された最大距離（separationDist係数を掛けた値）より小さい場合、各座標についてエージェントの座標を現在のボイドの座標から減算します。これにより、現在のボイドの方向に向かうベクトル、すなわちエージェントから押し返すベクトルが生成されます。

    すべてのエージェントに対するループが終了した後、ボイドの現在の速度dxは、計算されたmoveX変位ベクトルにseparationWeightを掛けて加算されます。これにより、反発力の強さを制御できます。separationWeightの値が大きいほど、ボイドは衝突をより強く回避します。

    Separationメソッドは、ボイドが最も近い隣接エージェントから反発する挙動を実現し、衝突を防ぎます。この挙動は群れのシミュレーションにおいて重要であり、各エージェントのパーソナルスペースを維持し、より自然な相互作用を促進します。separationDistやseparationWeightのパラメータにより、反発の半径や強さを柔軟に調整することが可能です。

    //——————————————————————————————————————————————————————————————————————————————
// Pushing away from other boids to avoid collisions
void C_AO_NOA2::Separation (S_NeuroBoids_Agent &boid, int pos)
{
  double moveX [];
  ArrayResize (moveX, coords);
  ArrayInitialize (moveX, 0.0);

  for (int i = 0; i < popSize; i++)
  {
    if (pos != i)
    {
      if (Distance (boid, agent [i]) < distanceMax * separationDist)
      {
        for (int c = 0; c < coords; c++)
        {
          moveX [c] += boid.x [c] - agent [i].x [c];
        }
      }
    }
  }

  for (int c = 0; c < coords; c++)
  {
    boid.dx [c] += moveX [c] * separationWeight;
  }
}
//——————————————————————————————————————————————————————————————————————————————

    C_AO_NOA2クラスのAlignmentメソッドは、モデル内のエージェントに対して「整列」の挙動を実装します。この挙動により、ボイドは近隣エージェントの速度と調和して動くことで、より統一された集団移動を実現します。avgDXは近隣エージェントの平均速度ベクトルを格納するための配列で、サイズはcoordsの数に対応します。numNeighborsは、指定距離内にいる近隣エージェントの数を追跡するカウンタです。

    ループでは、集団内のすべてのエージェントを順に処理します。各ループ内で、対象のエージェントが現在のボイド自身でないかを確認します。他のエージェントまでの距離が最大距離にalignmentDist係数を掛けた値より小さい場合、そのエージェントの現在の速度dxをavgDXに加算し、numNeighborsを1増加させます。ループ処理が完了した後、近隣エージェントが存在する場合(numNeighbors > 0)、合計された速度ベクトルを近隣エージェントの数で割り、平均速度avgDXを計算します。その後、ボイドの現在の速度dxは、alignmentWeightに基づき近隣エージェントの平均速度方向に調整されます。 

    Alignmentメソッドにより、ボイドは自身の速度を近隣エージェントの速度に適応させることができます。この挙動により、ボイドの集団はより結束して移動し、衝突や急激な方向変更の発生を抑えることが可能です。alignmentDistおよびalignmentWeightのパラメータは、整列効果の半径や、近隣エージェントの速度の平均値が現在のボイドの速度に与える影響度を設定するために使用されます。  
    //——————————————————————————————————————————————————————————————————————————————
// Align speed with other boids
void C_AO_NOA2::Alignment (S_NeuroBoids_Agent &boid, int pos)
{
  double avgDX [];
  ArrayResize (avgDX, coords);
  ArrayInitialize (avgDX, 0.0);

  int numNeighbors = 0;

  for (int i = 0; i < popSize; i++)
  {
    if (pos != i)
    {
      if (Distance (boid, agent [i]) < distanceMax * alignmentDist)
      {
        for (int c = 0; c < coords; c++)
        {
          avgDX [c] += agent [i].dx [c];
        }

        numNeighbors++;
      }
    }
  }

  if (numNeighbors > 0)
  {
    for (int c = 0; c < coords; c++)
    {
      avgDX [c] /= numNeighbors;
      boid.dx [c] += (avgDX [c] - boid.dx [c]) * alignmentWeight;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

    C_AO_NOA2クラスのLimitSpeedメソッドは、モデル内のエージェント（ボイド）の速度を制御し、速度が指定範囲内に収まるようにするために設計されています。speedはボイドの現在の速度を格納する変数であり、速度ベクトルの長さとして計算されます。座標ループ(coords)では、各座標に対して速度の二乗(boid.dx[c] * boid.dx[c])を計算し、それらを合計します。これにより、速度ベクトルの長さの二乗が得られます。その後、MathSqrt関数を用いて平方根を計算し、長さ（実速度）を求めます。速度が十分に大きい場合（1e-10より大きい場合）は処理を続行します。現在の速度が許容される最小速度(speedMax[0] * minSpeed)より小さい場合、速度ベクトルを正規化（現在の長さで割る）し、最小速度に調整します。

    逆に、現在の速度が最大許容値(speedMax[0] * maxSpeed)より大きい場合は、同様に速度ベクトルを正規化して最大の速度に設定します。もし速度がほぼゼロの場合（ゼロまたは非常に近い場合）、速度ベクトルの各座標はu.RNDfromCI(-1.0, 1.0)関数で生成された小さなランダム値に最大速度を掛けた値に置き換えられます。

    LimitSpeedメソッドにより、ボイドの速度は適切な範囲内に保たれ、移動が遅すぎたり速すぎたりすることを防ぎます。この挙動により、速度の大きな変動による不自然な動きを避けることができ、より現実的なエージェントシミュレーションが可能になります。minSpeedおよびmaxSpeedのパラメータを設定することで、シミュレーションの目的に応じてエージェントの速度や挙動を調整できます。

    //——————————————————————————————————————————————————————————————————————————————
// Speed limit
void C_AO_NOA2::LimitSpeed (S_NeuroBoids_Agent &boid)
{
  double speed = 0;

  for (int c = 0; c < coords; c++)
  {
    speed += boid.dx [c] * boid.dx [c];
  }

  speed = MathSqrt (speed);

  // If the speed is not zero (prevent division by zero)
  if (speed > 1e-10)
  {
    // If the speed is too low, increase it
    if (speed < speedMax [0] * minSpeed)
    {
      for (int c = 0; c < coords; c++)
      {
        boid.dx [c] = boid.dx [c] / speed * speedMax [c] * minSpeed;
      }
    }
    // If the speed is too high, reduce it
    else
      if (speed > speedMax [0] * maxSpeed)
      {
        for (int c = 0; c < coords; c++)
        {
          boid.dx [c] = boid.dx [c] / speed * speedMax [c] * maxSpeed;
        }
      }
  }
  else
  {
    // If the speed is almost zero, set a small random speed
    for (int c = 0; c < coords; c++)
    {
      boid.dx [c] = u.RNDfromCI (-1.0, 1.0) * speedMax [c] * minSpeed;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

    C_AO_NOA2クラスのKeepWithinBoundsメソッドは、エージェント（ボイド）を指定された境界内に保持するために設計されています。ボイドが領域の端に近づきすぎた場合、このメソッドは進行方向を変更し、境界内に押し戻す処理をおこないます。メソッドはまず、すべての座標に対してループをおこない、多次元空間に対応できるようにします。

    各座標について、ボイドの位置(boid.x[c])が最小境界(rangeMin[c])より小さいかどうかを確認します。小さい場合は、速度の方向(boid.dx[c])を反転させるために「boid.dx[c] *= -1.0」とします。これにより、ボイドは逆方向に移動します。その後、境界から少し押し戻す値として「(rangeMax[c] - rangeMin[c]) * 0.001」を加え、ボイドを領域内に戻す補正をおこないます。

    最大境界(rangeMax[c])についても同様のチェックをおこないます。ボイドの位置が最大値を超えた場合、速度を反転させ、前述と同様の値を減算して調整します。

    KeepWithinBoundsメソッドにより、ボイドの移動は指定された領域内に制限され、領域外に飛び出すことを防ぎ、常に境界内に留まるように制御されます。 

    //——————————————————————————————————————————————————————————————————————————————
// Keep the boid within the boundaries. If it gets too close to the edge,
// push it back and change direction.
void C_AO_NOA2::KeepWithinBounds (S_NeuroBoids_Agent &boid)
{
  for (int c = 0; c < coords; c++)
  {
    if (boid.x [c] < rangeMin [c])
    {
      boid.dx [c] *= -1.0;
      // Add a small push from the border
      boid.dx [c] += (rangeMax [c] - rangeMin [c]) * 0.001;
    }
    if (boid.x [c] > rangeMax [c])
    {
      boid.dx [c] *= -1.0;
      // Add a small push from the border
      boid.dx [c] -= (rangeMax [c] - rangeMin [c]) * 0.001;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

    C_AO_NOA2クラスのDistanceメソッドは、2つのエージェント（ボイド）間の距離を多次元空間で計算するために設計されています。ユークリッド距離を計算する式を用いており、distは2つのボイドの座標差の二乗和を格納する変数です。

    メソッドはすべての座標に対してループ処理をおこない、任意の次元空間で距離を計算できるようにしています。各座標cについて、対応するボイドの座標差(boid1.x[c]-boid2.x[c])の二乗を計算します。

    計算結果((boid1.x[c]-boid2.x[c])^2)はdist変数に加算されます。ループ処理が終了すると、distには座標差の二乗和が格納されます。実際の距離を求めるため、メソッドはMathSqrtを用いて平方根を計算し、ユークリッド距離を求めます。

    //——————————————————————————————————————————————————————————————————————————————
// Calculate the distance between two boids
double C_AO_NOA2::Distance (S_NeuroBoids_Agent &boid1, S_NeuroBoids_Agent &boid2)
{
  double dist = 0;

  for (int c = 0; c < coords; c++)
  {
    dist += MathPow (boid1.x [c] - boid2.x [c], 2);
  }

  return MathSqrt (dist);
}
//——————————————————————————————————————————————————————————————————————————————

    C_AO_NOA2クラスのRevisionメソッドは、最適化中に見つかった最良解に関する情報を更新する役割を持ちます。この処理では、適応度関数の値とその値に対応する座標の更新がおこなわれます。さらに、進捗を監視し、顕著な改善がある場合にはアルゴリズムパラメータを適応させます。メソッドはa配列で表される集団全体を処理し、popSize（エージェントの数）を対象とします。

    ループ内では、各エージェントの適応度値(a[i].f)が現在の最良値(fB)より大きいかどうかを確認します。現在のエージェントが最良の適応度を示す場合、適応度関数の大域最良値が更新され、fBにa[i].fの新しい値が割り当てられます。その後、最良解の座標も更新されます。各座標cについて、最良解の座標を格納するcB配列は、現在のエージェントの値で更新されます。解の改善が見つかったため、停滞カウンタ(m_stagnationCounter)は0にリセットされます。

    メソッドはhasProgress変数を用いて進捗の有無を判定します。これは、適応度関数の現在の最良値と前回の最良値の絶対差(MathAbs(fB-m_prevBestFitness))を計算し、この差が0.000001より大きい場合に進捗ありと見なすものです。進捗があった場合、m_prevBestFitnessは現在の最良値fBで更新されます。
    また、探索速度であるexplorationRateも適応されます。改善が見つかった場合は減少させ、params配列の値や現在のexplorationRateを考慮して調整されます。

    //——————————————————————————————————————————————————————————————————————————————
// Update the best solution found
void C_AO_NOA2::Revision ()
{
  // Update the best coordinates and fitness function value
  for (int i = 0; i < popSize; i++)
  {
    // Update the global best solution
    if (a [i].f > fB)
    {
      fB = a [i].f;
      for (int c = 0; c < coords; c++)
      {
        cB [c] = a [i].c [c];
      }

      // Reset the stagnation counter when a better solution is found
      m_stagnationCounter = 0;
    }
  }

  // Check for progress to adapt the algorithm parameters
  bool hasProgress = MathAbs (fB - m_prevBestFitness) > 0.000001;
  if (hasProgress)
  {
    m_prevBestFitness = fB;
    explorationRate = MathMax (params [11].val * 0.5, explorationRate * 0.9);
  }
}
//——————————————————————————————————————————————————————————————————————————————


    テスト結果

    テスト結果はかなり弱いです。

    NOA2|Neuroboids Optimization Algorithm 2 (joo)|50.0|0.6|0.001|0.005|0.03|0.1|0.1|0.1|0.01|0.01|0.3|0.1|
    =============================
    5 Hilly's; Func runs:10000; result:0.47680799582735267
    25 Hilly's; Func runs:10000; result:0.30763714006051013
    500 Hilly's; Func runs:10000; result:0.2544737238936433
    =============================
    5 Forest's; Func runs:10000; result:0.3238017030688524
    25 Forest's; Func runs:10000; result:0.20976876473929068
    500 Forest's; Func runs:10000; result:0.15740101965732595
    =============================
    5 Megacity's; Func runs:10000; result:0.27076923076923076
    25 Megacity's; Func runs:10000; result:0.14676923076923082
    500 Megacity's; Func runs:10000; result:0.09729230769230844
    =============================
    All score:2.24472 (24.94%)

    可視化では控えめな探索能力が示されています。グローバル変数を用いてアルゴリズムの外部パラメータを変更できるため、ボイドの挙動を実験的に観察でき、興味深い行動パターンを明らかにすることが可能です。以下に、数ある挙動パターンの一部の可視化例を示します。

    Hilly

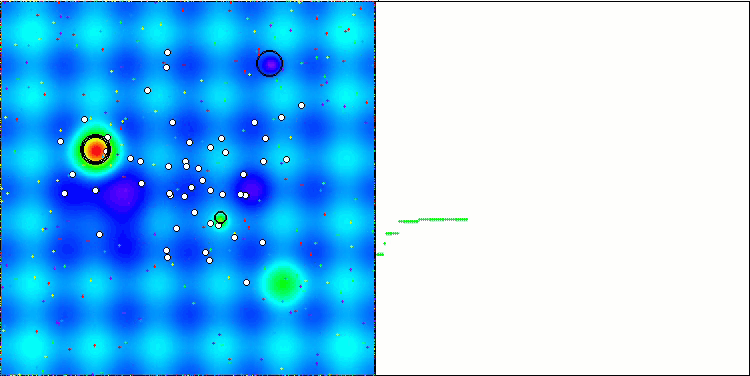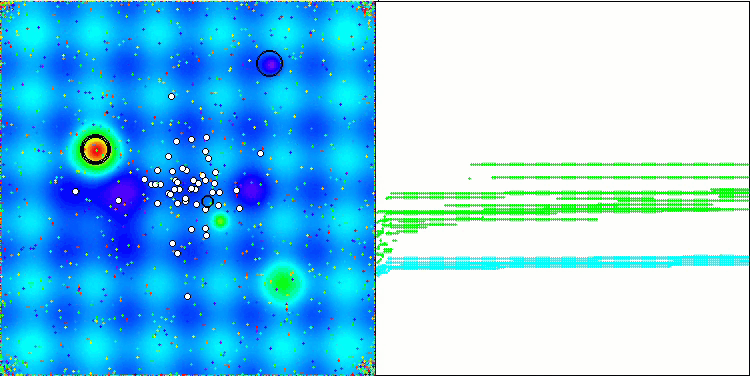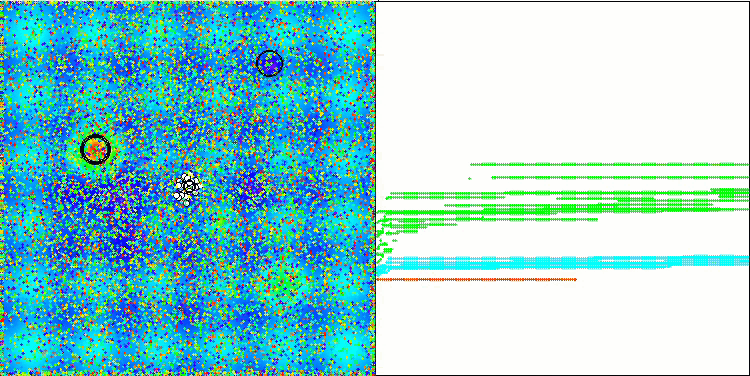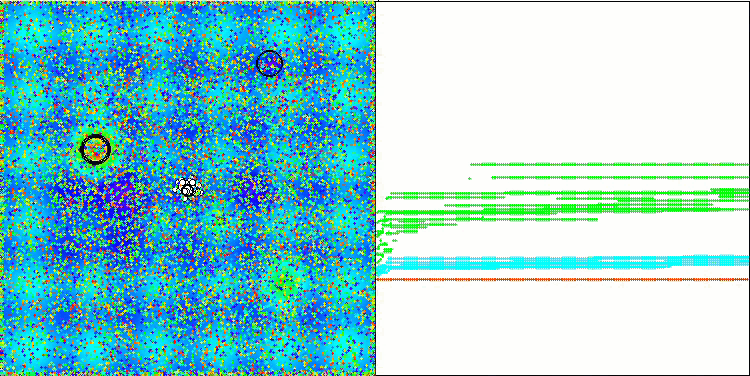
    Hillyテスト関数のNOA2

    Forest

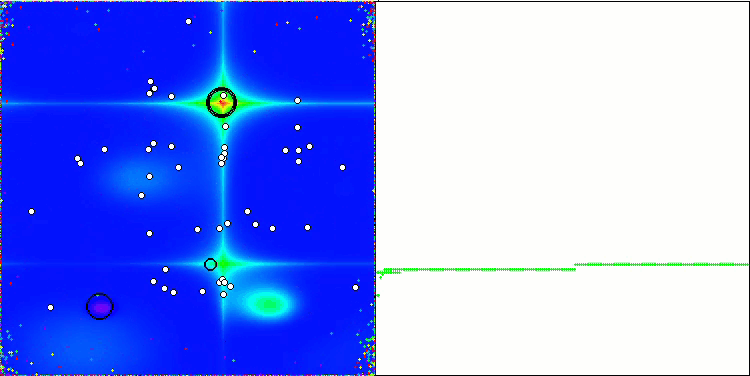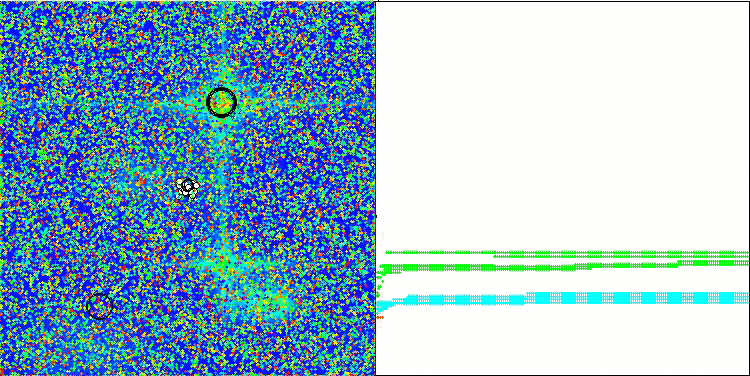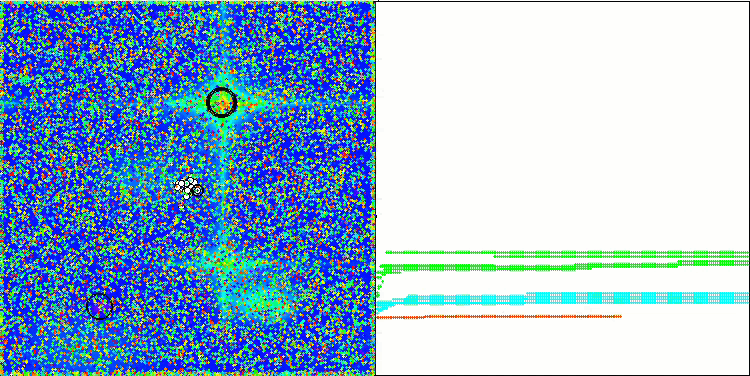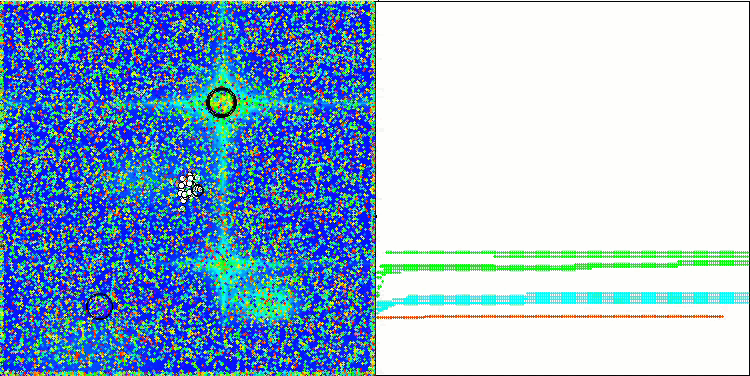
    Forestテスト関数のNOA2

    Megacity

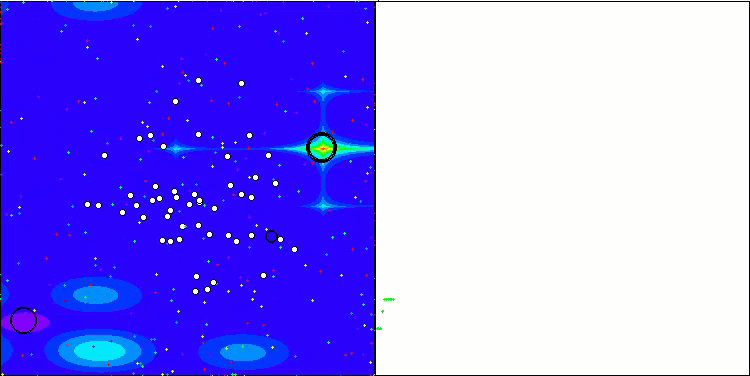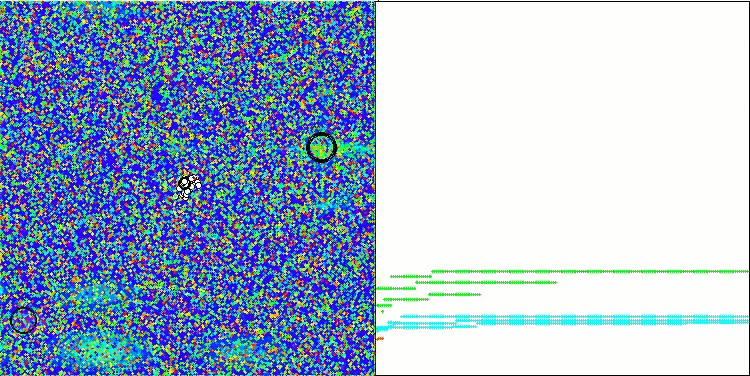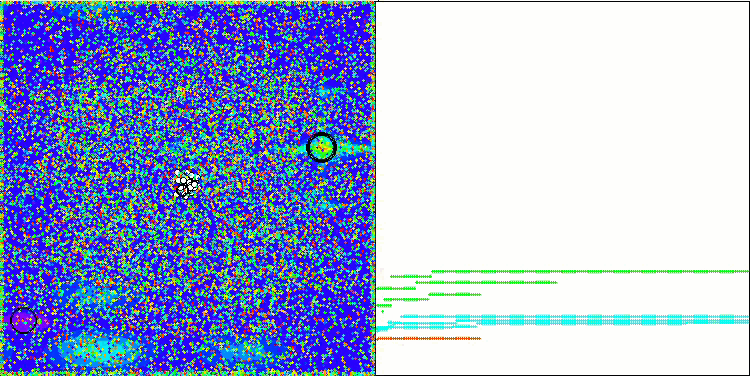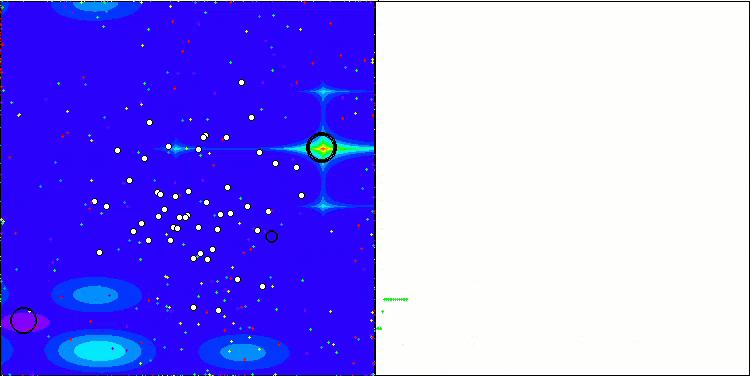
    Megacityテスト機能のNOA2

    テスト結果に基づき、基本バージョンのNOA2アルゴリズムは、参考情報として我々の集団最適化アルゴリズムのランキング表に含まれています。

    # AO 詳細 Hilly Hilly最終 Forest Forest最終 Megacity（離散） Megacity最終 最終結果 MAXの%
    10p(5F) 50p(25F) 1000p(500F) 10p(5F) 50p(25F) 1000p(500F) 10p(5F) 50p(25F) 1000p(500F)
    1 ANS across neighbourhood search 0.94948 0.84776 0.43857 2.23581 1.00000 0.92334 0.39988 2.32323 0.70923 0.63477 0.23091 1.57491 6.134 68.15
    2 CLA コードロックアルゴリズム(joo) 0.95345 0.87107 0.37590 2.20042 0.98942 0.91709 0.31642 2.22294 0.79692 0.69385 0.19303 1.68380 6.107 67.86
    3 AMOm 動物移動最適化m 0.90358 0.84317 0.46284 2.20959 0.99001 0.92436 0.46598 2.38034 0.56769 0.59132 0.23773 1.39675 5.987 66.52
    4 (P+O)ES (P+O)進化戦略 0.92256 0.88101 0.40021 2.20379 0.97750 0.87490 0.31945 2.17185 0.67385 0.62985 0.18634 1.49003 5.866 65.17
    5 CTA 彗星の尾アルゴリズム(joo) 0.95346 0.86319 0.27770 2.09435 0.99794 0.85740 0.33949 2.19484 0.88769 0.56431 0.10512 1.55712 5.846 64.96
    6 TETA 時間進化移動アルゴリズム(joo) 0.91362 0.82349 0.31990 2.05701 0.97096 0.89532 0.29324 2.15952 0.73462 0.68569 0.16021 1.58052 5.797 64.41
    7 SDSm 確率的拡散探索M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
    8 BOAm ビリヤード最適化アルゴリズムM 0.95757 0.82599 0.25235 2.03590 1.00000 0.90036 0.30502 2.20538 0.73538 0.52523 0.09563 1.35625 5.598 62.19
    9 AAm アーチェリーアルゴリズムM 0.91744 0.70876 0.42160 2.04780 0.92527 0.75802 0.35328 2.03657 0.67385 0.55200 0.23738 1.46323 5.548 61.64
    10 ESG 社会集団の進化(joo) 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
    11 SIA 等方的焼きなまし(joo) 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
    12 ACS 人工協調探索 0.75547 0.74744 0.30407 1.80698 1.00000 0.88861 0.22413 2.11274 0.69077 0.48185 0.13322 1.30583 5.226 58.06
    13 DA 弁証法的アルゴリズム 0.86183 0.70033 0.33724 1.89940 0.98163 0.72772 0.28718 1.99653 0.70308 0.45292 0.16367 1.31967 5.216 57.95
    14 BHAm ブラックホールアルゴリズムM 0.75236 0.76675 0.34583 1.86493 0.93593 0.80152 0.27177 2.00923 0.65077 0.51646 0.15472 1.32195 5.196 57.73
    15 ASO 無政府社会最適化 0.84872 0.74646 0.31465 1.90983 0.96148 0.79150 0.23803 1.99101 0.57077 0.54062 0.16614 1.27752 5.178 57.54
    16 RFO ロイヤルフラッシュ最適化(joo) 0.83361 0.73742 0.34629 1.91733 0.89424 0.73824 0.24098 1.87346 0.63154 0.50292 0.16421 1.29867 5.089 56.55
    17 AOSm 原子軌道探索M 0.80232 0.70449 0.31021 1.81702 0.85660 0.69451 0.21996 1.77107 0.74615 0.52862 0.14358 1.41835 5.006 55.63
    18 TSEA 亀甲進化アルゴリズム(joo) 0.96798 0.64480 0.29672 1.90949 0.99449 0.61981 0.22708 1.84139 0.69077 0.42646 0.13598 1.25322 5.004 55.60
    19 DE 差分進化 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
    20 SRA レストラン経営達人アルゴリズム(joo) 0.96883 0.63455 0.29217 1.89555 0.94637 0.55506 0.19124 1.69267 0.74923 0.44031 0.12526 1.31480 4.903 54.48
    21 CRO 化学反応の最適化 0.94629 0.66112 0.29853 1.90593 0.87906 0.58422 0.21146 1.67473 0.75846 0.42646 0.12686 1.31178 4.892 54.36
    22 BIO 血液型遺伝最適化(joo) 0.81568 0.65336 0.30877 1.77781 0.89937 0.65319 0.21760 1.77016 0.67846 0.47631 0.13902 1.29378 4.842 53.80
    23 BSA 鳥群アルゴリズム 0.89306 0.64900 0.26250 1.80455 0.92420 0.71121 0.24939 1.88479 0.69385 0.32615 0.10012 1.12012 4.809 53.44
    24 HS ハーモニー検索 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
    25 SSG 苗木の播種と育成 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
    26 BCOm 細菌走化性最適化M 0.75953 0.62268 0.31483 1.69704 0.89378 0.61339 0.22542 1.73259 0.65385 0.42092 0.14435 1.21912 4.649 51.65
    27 ABO アフリカ水牛の最適化 0.83337 0.62247 0.29964 1.75548 0.92170 0.58618 0.19723 1.70511 0.61000 0.43154 0.13225 1.17378 4.634 51.49
    28 (PO)ES (PO)進化戦略 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
    29 TSm タブーサーチM 0.87795 0.61431 0.29104 1.78330 0.92885 0.51844 0.19054 1.63783 0.61077 0.38215 0.12157 1.11449 4.536 50.40
    30 BSO ブレインストーム最適化 0.93736 0.57616 0.29688 1.81041 0.93131 0.55866 0.23537 1.72534 0.55231 0.29077 0.11914 0.96222 4.498 49.98
    31 WOAm 鯨最適化アルゴリズムM 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
    32 AEFA 人工電界アルゴリズム 0.87700 0.61753 0.25235 1.74688 0.92729 0.72698 0.18064 1.83490 0.66615 0.11631 0.09508 0.87754 4.459 49.55
    33 AEO 人工生態系ベースの最適化アルゴリズム 0.91380 0.46713 0.26470 1.64563 0.90223 0.43705 0.21400 1.55327 0.66154 0.30800 0.28563 1.25517 4.454 49.49
    34 ACOm 蟻コロニー最適化M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
    35 BFO-GA 細菌採食の最適化：Ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
    36 SOA シンプル最適化アルゴリズム 0.91520 0.46976 0.27089 1.65585 0.89675 0.37401 0.16984 1.44060 0.69538 0.28031 0.10852 1.08422 4.181 46.45
    37 ABHA 人工蜂の巣アルゴリズム 0.84131 0.54227 0.26304 1.64663 0.87858 0.47779 0.17181 1.52818 0.50923 0.33877 0.10397 0.95197 4.127 45.85
    38 ACMO 大気雲モデルの最適化 0.90321 0.48546 0.30403 1.69270 0.80268 0.37857 0.19178 1.37303 0.62308 0.24400 0.10795 0.97503 4.041 44.90
    39 ADAMm 適応モーメント推定M 0.88635 0.44766 0.26613 1.60014 0.84497 0.38493 0.16889 1.39880 0.66154 0.27046 0.10594 1.03794 4.037 44.85
    40 CGO カオスゲーム最適化 0.57256 0.37158 0.32018 1.26432 0.61176 0.61931 0.62161 1.85267 0.37538 0.21923 0.19028 0.78490 3.902 43.35
    41 ATAm 人工部族アルゴリズムM 0.71771 0.55304 0.25235 1.52310 0.82491 0.55904 0.20473 1.58867 0.44000 0.18615 0.09411 0.72026 3.832 42.58
    42 CFO 中心力最適化 0.60961 0.54958 0.27831 1.43750 0.63418 0.46833 0.22541 1.32792 0.57231 0.23477 0.09586 0.90294 3.668 40.76
    43 ASHA 人工シャワーアルゴリズム 0.89686 0.40433 0.25617 1.55737 0.80360 0.35526 0.19160 1.35046 0.47692 0.18123 0.09774 0.75589 3.664 40.71
    44 ASBO 適応型社会行動最適化(ASBO) 0.76331 0.49253 0.32619 1.58202 0.79546 0.40035 0.26097 1.45677 0.26462 0.17169 0.18200 0.61831 3.657 40.63
    45 MEC mind evolutionary computation 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
    NOA2 ニューロボイド最適化アルゴリズム2(joo ) 0.47681 0.30764 0.25447 1.03892 0.32380 0.20977 0.15740 0.69097 0.27077 0.14677 0.09729 0.51483 2.245 24.94


    まとめ

    私が開発したニューラルボイド最適化アルゴリズム(NOA2)は、群知能（ボイドアルゴリズム）の原理とニューラルネットワークによる制御を組み合わせたハイブリッドアプローチです。主なアイデアは、ニューラルネットワークを用いてボイドエージェントの行動パラメータを適応的に制御することにあります。現在の実装では、隠れ層を持たない単純な単層ニューラルネットワークを使用しています。入力層は、現在の座標、速度、最良解までの距離、適応度関数の値を受け取り、出力層はボイド群の行動ルールに対する速度補正および適応パラメータを定義します。

    このバージョンには中間層は存在せず、入力数は(coords*2 + 2)で定義されます。ここでcoordsは探索空間の次元数です。出力には各座標の補正値に加え、群れルールを適応させるための3つの追加パラメータが含まれます。アルゴリズムには設定可能なパラメータが非常に多いため、最適な組み合わせを見つけることは困難です。様々な組み合わせを試みましたが、テスト関数上で最良の結果を示す理想的な構成はまだ見つかっていません。

    現状の形では、このアルゴリズムは明確に概念実証としての位置付けであり、ハイブリッド最適化手法の実験として全体的に興味深いものです。しかし、十分な性能を示すには至っておらず、実施したテストでは最小限のスコアしか得られません。あくまでアルゴリズムのハイブリッド化アプローチの例として理解されるべきです。興味のある研究者や開発者にとって、NOA2のコードは異なる構成やパラメータを試す出発点となり得ます。また、集団ベース手法と機械学習手法の利点を活かした、より高度なハイブリッド最適化アルゴリズムの開発にも応用可能です。

    Tab

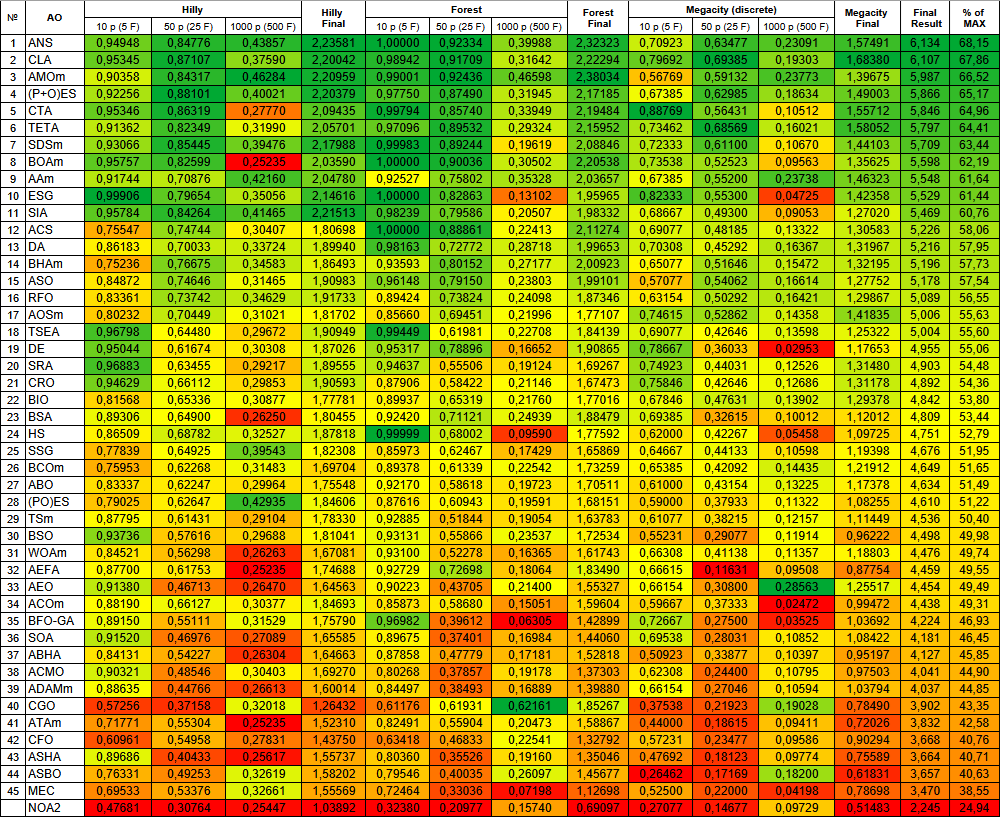
    図3：対応するテストに応じたアルゴリズムのカラーグラデーション

    チャート

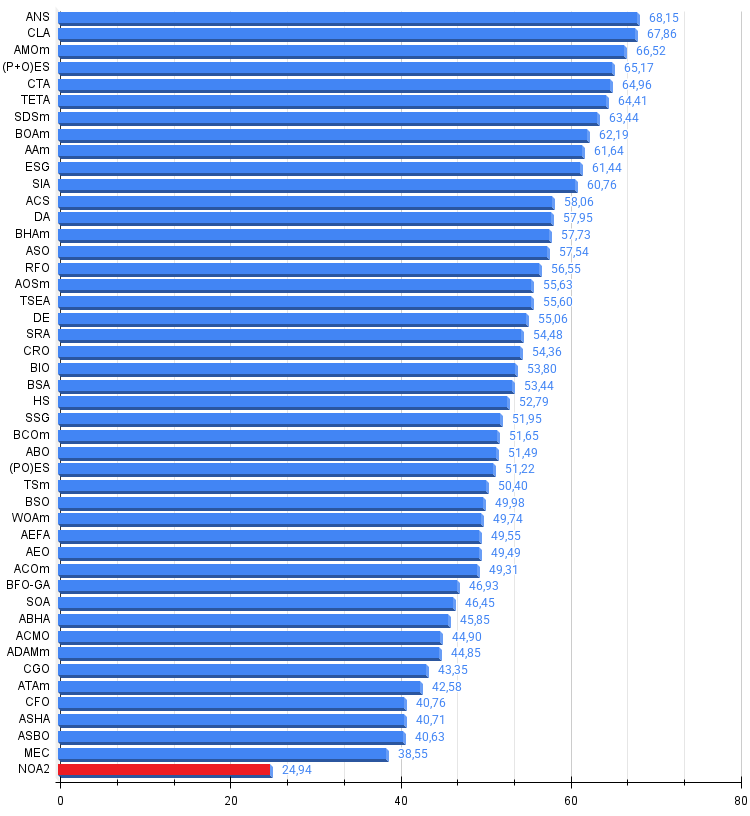
    図4：アルゴリズムテスト結果のヒストグラム（0から100のスケール、高いほど良い）100は理論上の最大値であり、アーカイブには評価表を計算するためのスクリプトがあります。

    NOA2の長所と短所

    長所

    1. 興味深いアイディア

    短所

    1. 結果は弱い

    この記事には、最新版のアルゴリズムコードを含むアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。


    記事で使用されているプログラム

    # 名前 種類 詳細
    1 #C_AO.mqh
    		 インクルード
    		 集団最適化アルゴリズムの親クラス
    2 #C_AO_enum.mqh
    		 インクルード
    		 集団最適化アルゴリズムの列挙
    3 TestFunctions.mqh
    		 インクルード
    		 テスト関数のライブラリ
    4 TestStandFunctions.mqh
    		 インクルード
    		 テストスタンド関数ライブラリ
    5 Utilities.mqh
    		 インクルード
    		 補助関数のライブラリ
    6 CalculationTestResults.mqh
    		 インクルード
    		 比較表の結果を計算するスクリプト
    7 Testing AOs.mq5
    		 スクリプト すべての集団最適化アルゴリズムの統一テストスタンド
    8 Simple use of population optimization algorithms.mq5
    		 スクリプト
    		 可視化せずに集団最適化アルゴリズムを使用する簡単な例
    9 Test_AO_NOA2.mq5
    		 スクリプト NOA2テストスタンド

    MetaQuotes Ltdによってロシア語から翻訳されました。
    元の記事: https://www.mql5.com/ru/articles/17497

    添付されたファイル |
    ZIPをダウンロード
    NOA2.zip (186.45 KB)

    警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

    この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。

    この著者による他の記事

    ディスカッションに移動
    初級から中級まで：インジケーター(III) 初級から中級まで：インジケーター(III)
    本記事では、DRAW_COLOR_LINEやDRAW_FILLINGなど、さまざまなグラフィック表示インジケーターの宣言方法について解説します。さらに、複数のインジケーターを用いてグラフを簡単かつ実践的に、そして高速に描画する方法も学びます。これにより、MetaTrader 5や市場全体の見方が大きく変わることでしょう。
    FXにおけるスワップ差裁定：合成ポートフォリオの構築と一貫したスワップフローの生成 FXにおけるスワップ差裁定：合成ポートフォリオの構築と一貫したスワップフローの生成
    金利差を活用して利益を得る方法をご存じでしょうか。本記事では、FXにおけるスワップ差裁定（スワップアービトラージ）を活用し、毎晩安定した利益を生み出し、市場の変動に強いポートフォリオを構築する方法について解説します。
    市場シミュレーション（第14回）：ソケット(VIII) 市場シミュレーション（第14回）：ソケット(VIII)
    多くのプログラマは、Excelの使用をやめて、Pythonに直接移行し、PythonでExcelファイルを生成して後から結果を分析できるパッケージを使うべきだと考えるかもしれません。しかし、前回の記事で述べたように、この方法は多くのプログラマにとって最も簡単な解決策ではありますが、すべてのユーザーに受け入れられるわけではありません。そして、このような場合、常に正しいのはユーザーです。私たちプログラマは、すべてをうまく機能させる方法を見つけなければなりません。
    MQL5 MVCパラダイムにおけるテーブルのビューおよびコントローラーコンポーネント：コンテナ MQL5 MVCパラダイムにおけるテーブルのビューおよびコントローラーコンポーネント：コンテナ
    この記事では、コンテンツのスクロールに対応したContainer（コンテナ）コントロールの作成について解説します。その過程で、既存のグラフィックライブラリのコントロールクラスを改良していきます。