MetaTrader 5 / 例
English Русский 中文 Español Deutsch Português 한국어 Français Italiano Türkçe
preview
母集団最適化アルゴリズム：蟻コロニー最適化(ACO)

母集団最適化アルゴリズム：蟻コロニー最適化(ACO)

MetaTrader 5 — 例 | 16 1月 2023, 12:47
454 0
Andrey Dik
Andrey Dik

あらゆる行動の大きな秘密は、社会的行動である...

F.バートレット

内容

1.はじめに
2.アルゴリズムの原則
3.修正版
4.テスト結果


1.はじめに

ベルギーの研究者マルコ・ドリゴは、蟻のコロニーにおける集団知のプロセスを科学的に記述した数理モデルを作成しました。1992年に博士論文として発表し、アルゴリズムとして実装しました。

蟻コロニー最適化（ACO）は、組合せ最適化問題を幅広く解決するための集団ベースの確率的探索手法です。ACOはスティグマジーの概念に基づいています。1959年、ピエール＝ポール・グラッセは、シロアリの巣作り行動を説明するためにスティグマギー理論を考案しました。スティグマギーは、ギリシャ語のスティグマ（記号）とエルゴン（作用）という2つの言葉から構成されています。

正統な定義は、環境との相互作用によって時間的に拡張された集団のメンバー間の間接的な相互作用のタイプです。つまり、あるエージェントが痕跡を残すか、何らかの方法でロケールを変更することで、他のエージェントがそのエリアに入る際に何らかの情報を受け取ることができるのです。蟻の場合、スティグマギーはフェロモンです。蟻はフェロモンの痕跡を地面に残し、それによって他の蟻の意思決定に影響を与えるなど、間接的にコミュニケーションをとっているのです。このような個体間の単純なコミュニケーションから、コロニー全体の複雑な行動や能力が生み出されています。

蟻は社会性昆虫で、コロニーを形成して生活しています。蟻の行動は、餌を探すという目的によってコントロールされています。探索中は、コロニーを歩き回ります。蟻は餌を求めて移動を繰り返し、その際にフェロモンと呼ばれる有機化合物を地表に沈着させます。このように、蟻はフェロモンの痕跡を利用して互いにコミュニケーションをとっています。

蟻は食べ物を見つけると、運べるだけ運びます。帰るときには、餌の量と質に応じて、途中でフェロモンを沈殿させます。その結果、他の蟻がこのルートをたどることができるのです。フェロモンレベルが高いほど、この特定の経路を選択する確率が高くなり、特定の経路を通過する蟻が多いほど、この経路にフェロモンが多く残されることになります。

次の例を見てみましょう。コロニーから食料を調達する方法が2つあるとします。初めには、地上にはフェロモンがありません。つまり、この2つの道を選ぶ確率は等しくなります(50%)。2匹の蟻が餌に向かうために2つの異なる道を選んだとしましょう。この2つのパスの距離は異なっています。近道を行く蟻は、もう1匹の蟻より先に餌にありつくことができます。餌を見つけると、それを少し取ってコロニーに戻ります。その帰り道、地面にフェロモンを付着させます。短い道を行く蟻は、早くコロニーに到着します。

3匹目の蟻が餌を探しに出かけようとすると、地上のフェロモンの量に応じて距離の短い道を通るようになります。短い道の方が長い道よりもフェロモンが多いので、3匹目の蟻はフェロモンが多い道を通ることになります。長い方の道を通った蟻がコロニーに戻る頃には、フェロモンの量が多い方の道をすでに多くの蟻が通っています。そして、別の蟻がコロニーから目的地（餌）へ行こうとすると、それぞれの経路のフェロモンレベルが同じであることがわかります。そこで、その中からランダムに1つを選びます。これを何度も繰り返すことで、しばらくすると短い道の方がフェロモンを多く獲得し、蟻がこの道を通る確率が高くなります。

ACOアルゴリズムは、群知能アルゴリズムの一種です。蟻コロニーの採餌過程をモデル化し、蟻コロニー内部のデータ転送機構を利用して、様々な環境下での最短経路を確立しています。経路上に残っているフェロモンの濃度が高いほど、蟻はこの経路を選択する可能性が高くなります。同時に、フェロモンの濃度は時間の経過とともに減少します。そのため、蟻のコロニーの行動により、蟻は常に学習し、フィードバック機構により最適化され、最短の採餌経路を決定しているのです。ACOアルゴリズムは、経路探索に広く用いられています。


2.アルゴリズムの原則

ACOでは、人工蟻と呼ばれるソフトウェアエージェントの集合が、与えられた最適化問題に対して良い解を探します。ACOを適用するには、最適化問題を、重み付きグラフ上の最適経路を求める問題に変換します。人工蟻（以下、蟻）は、グラフに沿って徐々に解を構築していきます。解を構成するプロセスは確率的で、フェロモンモデル（グラフの構成要素（ノードまたはエッジ）に関連するパラメータのセットで、実行中に蟻によって値が変更される）に依存します。

巡回セールスマン問題のアルゴリズムについて考えてみましょう。位置（都市）とその間の距離のセットがあります。問題は、各都市を一度だけ訪れる、長さが最小の閉じた経路を見つけることです。都市の集合とグラフの頂点の集合を関連付けて定義したグラフを構成グラフといいます。任意の都市から他の都市に移動することが可能であるため、構成グラフは完全連結となり、頂点の数は都市の数に等しくなります。頂点間の辺の長さをその頂点が表す都市間の距離に比例させ、フェロモン値とヒューリスティック値をグラフの辺に関連付けます。フェロモン値は実行時に変化し、蟻コロニーの経験の蓄積を表す。一方、ヒューリスティック値は問題に依存する値です。

蟻は次のような方法で解を構築します。各蟻はランダムに選ばれた都市（建設グラフの頂点）からスタートします。そして、各構築ステップでグラフの辺に沿って移動します。各蟻は自分の経路を記憶しておき、次のステップで、すでに訪れた頂点につながらない辺の中から選択します。蟻はグラフのすべての頂点を訪問した時点で解を構築したことになります。各構築ステップにおいて、蟻はまだ訪問していない頂点につながる辺の中から、辿るべき辺を確率的に選択します。フェロモン値とヒューリスティック情報に基づいて確率的なルールを設定し、あるエッジに関連するフェロモン値とヒューリスティック値が高いほど、蟻がその特定のエッジを選択する確率が高くなります。すべての蟻が旅を終えると、端のフェロモンが更新されます。それぞれのフェロモン値は、最初は一定の割合で減少しています。この手順は、終了基準が満たされるまで繰り返されます。

フェロモンによるコミュニケーションは、自然界に広く存在する最も効果的なコミュニケーション方法の1つです。フェロモンは、蜂、蟻、シロアリなどの社会性昆虫がエージェント間のコミュニケーションに使用しています。人工フェロモンはその実現性の高さから、マルチロボットや群ロボットシステムで採用されています。

蟻が本当に最短ルートを見つけたのか、どうすれば理解できるのでしょうか。そのための素晴らしいテストケースがあります。円形に並べられた点です。それらにとっては、最短経路は常に同じで、円です。  

最初のACOアルゴリズムは、蟻システムと呼ばれ、いくつかの都市を結ぶ最短の往復路を見つけることを目的とした巡回セールスマン問題の解決を目指したものでした。一般的なアルゴリズムは比較的単純で、蟻の一群がそれぞれ可能な都市のラウンドの1つを作るというものです。各ステージで、蟻はある都市から別の都市へ、いくつかのルールに従って道を選びます。

  1. 各都市を1回ずつ訪問する必要があります。
  2. 遠方の都市は選ばれにくくなります（視認性）。
  3. 2つの都市の境界に敷かれたフェロモン痕跡が濃ければ濃いほど、この境界が選ばれる可能性が高くなります。
  4. 蟻は経路を完了した後、経路が短ければ通過したすべての辺にフェロモンをより多く堆積させます。
  5. 各反復の後、フェロモンの軌跡は蒸発します。

都市

図1：5つの節点で可能なパスの一例

3.修正版

ACOアルゴリズムの代表的なバリエーションがいくつか知られています。考察してみましょう。

蟻システム(AS)
蟻システムは、最初のACOアルゴリズムです。

蟻コロニーシステム(ACS)
蟻コロニーシステムアルゴリズムでは、オリジナルの蟻システムを3つの側面から改良しています。
1.エッジの選択は搾取に偏ります（フェロモンが多い最短エッジを選ぶ確率に有利になる）。
2.解を構築する際、蟻は局所的なフェロモン更新規則を適用して、選択した辺のフェロモンレベルを変化させます。
3.各反復の終わりには、最適な蟻だけが修正されたグローバルフェロモン更新ルールを適用してトラックを更新することができます。

エリート蟻システム
このアルゴリズムでは、最適解は、各反復の後、他のすべての蟻と一緒に（たとえ経路が再訪されていなくても）その経路上にフェロモンを堆積させます。エリート戦略の目的は、すべての蟻の探索を、現在の最良のルートのリンクを含む解を構築することに向けさせることです。

Max-min ant system (MMAS).
このアルゴリズムでは、各軌跡上のフェロモンの最大数と最小数を制御します。最高のグローバルツアーや最高のリピートツアーだけが、その軌跡にフェロモンを加えることができるのです。探索アルゴリズムの停滞を避けるため、各トレースのフェロモン量の可能な範囲を区間[τ max, τ min]で制限しています。解の探索を高速化するため、すべてのエッジはτmaxで初期化されます。停滞に近づくとトレースはτmaxに再初期化されます。

ランクベースアントシステム(Asrank)
すべての解は、その長さによってランク付けされます。この繰り返しでは、一定数の優秀な蟻だけが自分の課題を更新することができます。フェロモンの付着量は溶液ごとに計量され、経路の短い溶液は経路の長い溶液よりもフェロモンを多く付着させます。

並列蟻コロニー最適化(PACO)
コミュニケーション戦略を持つ蟻コロニーシステム(ACS)です。
人工蟻はいくつかのグループに分けられます。巡回セールスマン問題で動作するACSにおいて、グループ間のフェロモンレベルを更新するために7つのコミュニケーション方法が提案されています。

Continuous orthogonal ant colony (COAC).
COACフェロモン堆積機構により、蟻は協調的かつ効率的に解決策を模索することができます。直交設計法を用いることで、許容範囲内の蟻は、グローバルな探索能力と精度を高め、選択したエリアを素早く効率的に探索することができます。また、直交設計法と適応的半径調整法は、他の最適化アルゴリズムに拡張することで、実用的な問題を解決する上でより広い利点を提供することができます。

蟻コロニーの再帰的最適化
これは、探索領域全体をいくつかの小領域に分割し、その小領域で問題を解決する蟻コロニーの再帰的な形態です。すべてのサブドメインの結果を比較し、最も優れた数個が次のレベルへ移動します。選択された結果に対応するサブドメインをさらに細分化し、所望の精度が得られるまでこのプロセスを繰り返す。この手法は、不正確な物理学的インバージョン問題でテストされ、その有効性が証明されています。

上記で検討した蟻コロニーアルゴリズムは、もともとグラフ上の最適化問題を解くために開発されたものです。このようなアルゴリズムに問題を組み込み、問題条件をアルゴリズムのパラメータであるグラフのノードの座標として与えています。そのため、ACOの原理に基づくアルゴリズムは、高度に専門化されています。ここでのタスクでは、固定座標を使用しないため、このようなアルゴリズムは適用できません。似たようなものを含め、どのようなコーディネートでも構いません。金融商品取引の分野で、ニューラルネットワークの学習も含めた幅広い最適化問題を解決するためには、私たちの特別なテストをクリアできるような普遍的なアルゴリズム、つまり全く新しいACOを開発する必要があるのです。

アルゴリズムの基本的な考え方について考えてみましょう。正統的なものと同じように、蟻のコロニーを作るのです。移動した道をフェロモンで印付けすることはできません。彼らは多次元空間のどこにでも行き、ルートを記憶し、保存することができます。連続的なステップの場合、同じルートを通る確率はゼロになる傾向があるため、適切とは言えないようです。また、繰り返しのない順次通過の問題がないため、ノードを記憶する必要は全くありません。問題をアルゴリズムの外に持ち出すことが必要です。何をすべきでしょうか。現段階では、どのような概念で開発を進めていけばいいのか、まったくわからない状態です。

さて、それではもう一度、私たちの新しいアルゴリズムと正統なアルゴリズムとを区別する主な点を記します。

1.空間には定点がない。

2.一定の順序で道を進む必要はない。

3.道がないので、フェロモンでマーキングするものがない。

では、蟻のコロニーをイメージして、どんなものがあるのか見てみましょう。フェロモンで目印をつけるのは、蟻が歩いた道ではなく、まさに歩いた地点です。適性関数の値を、現在の反復における蟻の位置のフェロモンの数とすることにしましょう。そうすると、蟻はフェロモンがたくさんある座標に向かって移動しなければならなくなりますが、フェロモンが最も多く出ている一点にすべての蟻が単純に集まってしまうと、問題が生じます。点が最適化された関数の変数であることを考えると、これは必ずしも最適な解とは言えません。古典的なACOでは、ノードまでの経路の長さも重要であることは覚えています。選んだ道は短ければ短いほどいいです。そこで、現在地から蟻が行くべき場所までの距離を計算する必要があります。つまり、蟻はある種のランダム性を持って互いに向かってくるという概念を受け入れます。

動きにどんなランダム性を持たせられるのでしょうか。

  • まず、次の位置を選択する際のランダム要素PheromoneEffect_Pを追加します。
  • 次に、次の位置PathLengthEffect_Pまでの距離を考慮したランダムファクターを追加します（距離が小さいほど良い選択となります）。

そこで、次の位置を選ぶ基準として、蟻がいる特定の各位置のフェロモンの量と、これらすべての点の間の距離をペアにした2つの基準を用意しました。しかし、この2つの選択基準だけで行っても、蟻は自分の位置をノードとする虚数図の辺に沿って空間を移動することになります。より良い場所を見つけることにはなりません。

この場合、蟻が感じることができるフェロモンの影響半径PheromoneRadius_P（点間距離の比率）を加えます。そうすると、蟻は移動した先のポイントをすり抜けてしまいます。これにより、蟻が多次元空間を移動する際の自由度が増します。

蟻が新しい場所を探索するためには、いずれかの座標に沿った方向ベクトルから外れることを許容する必要があります。特定の座標での増分からの偏差を与えるPathDeviation_P比を導入しましょう。多次元空間なので、変位ベクトルに続いて、ある座標は正の増分を持ち、他の座標は負の増分を持ち、増分は異なるモジュロ値を持つことができます。この比率によって、これらすべてを考慮することが可能となり、蟻が餌を探す際にある程度の自由度が与えられます（関数の極限）。

では、変位ベクトルとは何で、蟻の移動距離はどのように測ればよいのでしょうか。これらの問いに答えるには、3次元空間の2点間の距離を計算する方程式を使います。

ベクトル式

図2を見ると、変位ベクトルを視覚的に表現することができます。


ベクター

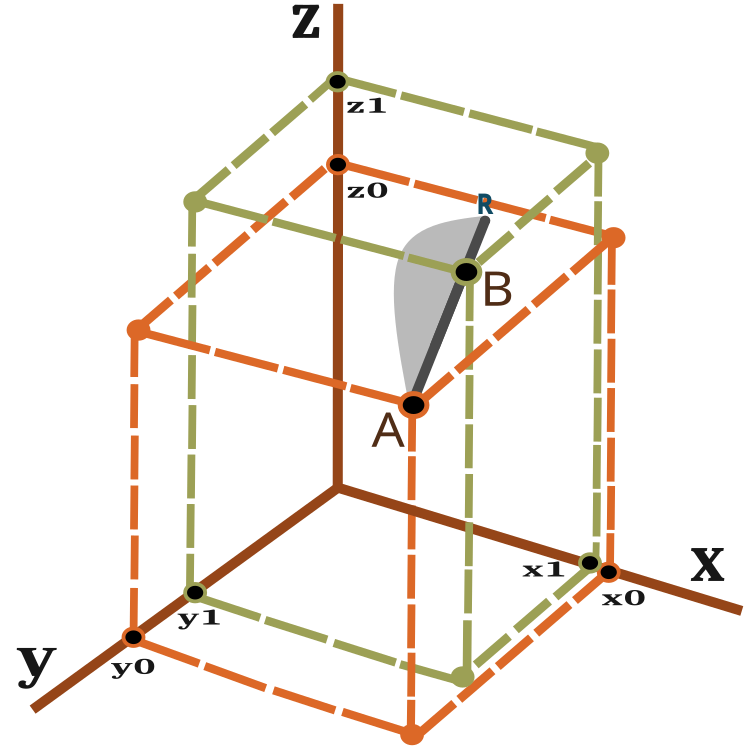
図2：蟻の移動ベクトル

n次元空間についても、同様の計算が可能です。

蟻は1回の反復（エポック）でA点からB点まで移動し、R点まで滑る可能性がある。B点からR点までの距離はPheromoneRadius_P比に依存し、BR=AB×PheromoneRadius_Pとして計算できます。

ARライン上に新たに位置する確率を、図2にグレーの領域で模式的に示しました（ノンスケール）。したがって、蟻の新しい居場所は点Bに傾く可能性が高い。確率移動の原理については、前回説明しました。

このアルゴリズムは、各反復において以下のステップを含みます。

1) 空間に蟻をランダムに配置する。
2）蟻のフェロモン量の値（適応度関数）を決定する。
3）蟻から蟻への距離を計算する。
4）蟻が移動する優先地点を選択する。
5) ARベクトル上の点の確率を計算する。
6) ARベクトル上で得られた点の座標を算出する。
7)停止条件が満たされるまで、手順2から繰り返す。

それでは、アルゴリズムコードの解説に進みます。まず、蟻の説明を含む構造体を書きましょう、ここで、

  • c [] - 蟻の座標 
  • cLast [] - 前の座標
  • cB [] - すべての反復処理における最適な座標
  • f - 現在のフェロモン値
  • fB - 全ての反復で到達したフェロモン値の最大値

蟻構造体のコンストラクタでは、fとfBの値をdouble型で表現できる最小の値で初期化します。

//——————————————————————————————————————————————————————————————————————————————
struct S_Ants
{
    double cLast  []; //last coordinates
    double c      []; //coordinates
    double cB     []; //best coordinates

    double f;     //pheromone of the current coordinates
    double fB;    //pheromone of the best coordinates

    S_Ants ()
    {
      f  = -DBL_MAX;
      fB = -DBL_MAX;
    }
};
//——————————————————————————————————————————————————————————————————————————————

すべての蟻の間のペアごとの距離を格納できる配列の構造体が必要です。

struct S_Paths
{
    double a [];
};

修正ACOアルゴリズムをクラスとして書いてみます。このクラスには、以前の記事で考察した、最適化アルゴリズムを構築するという開発概念の枠内で十分かつ必要な3つのpublicメソッド InitAnts ()、Preparation ()、Dwelling () がまだあるだけです。また、GenerateRNDants()やAntsMovement ()などのprivateメソッドもあり、すでにここでのアルゴリズムでは定番となっています。ants []構造体配列は蟻のコロニーです。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_ACO
{
  public:
  //----------------------------------------------------------------------------
  S_Ants ants      []; //ants
  double rangeMax  []; //maximum search range
  double rangeMin  []; //manimum search range
  double rangeStep []; //step search
  double cB        []; //best coordinates
  double fB;           //pheromone of the best coordinates

  void InitAnts (const int    coordinatesP,       //number of opt. parameters
                 const int    antHillSizeP,
                 double       pheromoneEffectP,
                 double       pathLengthEffectP,
                 double       pheromoneRadiusP,
                 double       pathDeviationP);

  void Preparation ();
  void Dwelling ();

  private:
  //----------------------------------------------------------------------------
  S_Paths paths [];
  int coordinates;        //number of coordinates
  int antHillSize;        //ant hill size

  double goals     [];

  double pheromoneEffect;
  double pathLengthEffect;
  double pheromoneRadius;
  double pathDeviation;
  bool   dwelling;

  void   GenerateRNDants ();
  void   AntsMovement    ();

  double SeInDiSp             (double in, double inMin, double inMax, double step);
  double RNDfromCI            (double min, double max);
  double Scale                (double In, double InMIN, double InMAX, double OutMIN, double OutMAX, bool revers);
};
//——————————————————————————————————————————————————————————————————————————————

初期化メソッドでは、変数と配列のサイズに初期値を割り当てます。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACO::InitAnts (const int    coordinatesP,       //number of opt. parameters
                         const int    antHillSizeP,
                         double       pheromoneEffectP,
                         double       pathLengthEffectP,
                         double       pheromoneRadiusP,
                         double       pathDeviationP)
{
  fB = -DBL_MAX;

  coordinates      = coordinatesP;
  antHillSize      = antHillSizeP;
  pheromoneEffect  = pheromoneEffectP;
  pathLengthEffect = pathLengthEffectP;
  pheromoneRadius  = pheromoneRadiusP;
  pathDeviation    = pathDeviationP;

  ArrayResize (rangeMax,  coordinates);
  ArrayResize (rangeMin,  coordinates);
  ArrayResize (rangeStep, coordinates);

  dwelling = false;

  ArrayResize (ants,  antHillSize);
  ArrayResize (paths, antHillSize);

  for (int i = 0; i < antHillSize; i++)
  {
    ArrayResize (ants  [i].c,      coordinates);
    ArrayResize (ants  [i].cLast,  coordinates);
    ArrayResize (ants  [i].cB,     coordinates);
    ArrayResize (paths [i].a,      antHillSize);
  }

  ArrayResize (cB,    coordinates);
  ArrayResize (goals, antHillSize);
}
//——————————————————————————————————————————————————————————————————————————————

Preparation ()メソッドは、各反復で最初に呼び出されます。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACO::Preparation ()
{
  if (!dwelling)
  {
    fB = -DBL_MAX;
    GenerateRNDants ();
    dwelling = true;
  }
  else AntsMovement ();
}
//——————————————————————————————————————————————————————————————————————————————

GenerateRNDants ()メソッドは、ランダムな蟻のコロニーを作成する役割を担っています。蟻の座標は、与えられた範囲内でランダムに割り当てられます。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACO::GenerateRNDants ()
{
  for (int s = 0; s < antHillSize; s++)
  {
    for (int k = 0; k < coordinates; k++)
    {
      ants [s].c     [k] = RNDfromCI (rangeMin [k], rangeMax [k]);
      ants [s].c     [k] = SeInDiSp (ants [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
      ants [s].cLast [k] = ants [s].c [k];
      ants [s].cB    [k] = ants [s].c [k];
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Dwelling ()メソッドで蟻の現在座標を記憶し、現在の反復時に得られたフェロモンの最大値を更新します。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACO::Dwelling ()
{
  for (int i = 0; i < antHillSize; i++)
  {
    ArrayCopy (ants [i].cLast, ants [i].c, 0, 0, WHOLE_ARRAY);

    //remember the best coordinates for the ant
    if (ants [i].f > ants [i].fB)
    {
      ants [i].fB = ants [i].f;
      ArrayCopy (ants [i].cB, ants [i].c, 0, 0, WHOLE_ARRAY);
    }

    //remember the best coordinates for the anthill
    if (ants [i].f > fB)
    {
      fB = ants [i].f;
      ArrayCopy (cB, ants [i].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

AntsMovement ()アルゴリズムのメインメソッドです。ある蟻から別の蟻までの距離の計算、蟻が移動する好ましい点の選択の計算、ARベクトル上の点の確率の計算などの動作をおこないます。ARベクトル上で得られた点の座標を算出します。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACO::AntsMovement ()
{
  double rndPh;
  double rndPt;
  double summCoordinates = 0.0;
  double scores [];
  ArrayResize (scores, antHillSize);

  double maxPh = -DBL_MAX;
  double minPh =  DBL_MAX;
  double maxPt = -DBL_MAX;
  double minPt =  DBL_MAX;
  double goal;
  double goalBest = -DBL_MAX;
  int    goalInd  = 0;

  //measure the distance between all the ants-----------------------------------
  for (int i = 0; i < antHillSize; i++)
  {
    for (int k = 0; k < antHillSize; k++)
    {
      if (i == k)
      {
        paths [i].a [k] = DBL_MAX;
        continue;
      }
         
      for (int c = 0; c < coordinates; c++) summCoordinates += pow (ants [i].cLast [c] - ants [k].cLast [c], 2.0);

      paths [i].a [k] = pow (summCoordinates, 0.5);

      if (maxPt < paths [i].a [k]) maxPt = paths [i].a [k];
      if (minPt > paths [i].a [k]) minPt = paths [i].a [k];
    }
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < antHillSize; i++)
  {
    maxPh = -DBL_MAX;
    minPh =  DBL_MAX;

    for (int k = 0; k < antHillSize; k++)
    {
      if (i != k)
      {
        if (maxPh < ants [k].f) maxPh = ants [k].f;
        if (minPh > ants [k].f) minPh = ants [k].f;
      }
    }

    goalBest = -DBL_MAX;
    goalInd  = 0;

    for (int k = 0; k < antHillSize; k++)
    {
      if (i != k)
      {
        rndPh = RNDfromCI (0.0, pheromoneEffect);
        rndPt = RNDfromCI (0.0, pathLengthEffect);

        goal = Scale (ants  [k].f,     minPh, maxPh, 0.0, 1.0, false) * rndPh *
               Scale (paths [i].a [k], minPt, maxPt, 0.0, 1.0, true)  * rndPt;

        if (goalBest < goal)
        {
          goalBest = goal;
          goalInd  = k;
        }
      }
    }
    
    double wayToGoal      = paths [i].a [goalInd];
    double radiusNearGoal = wayToGoal * pheromoneRadius;
    double endWay         = wayToGoal + radiusNearGoal;

    double x = RNDfromCI (-1.0, 1.0);
    double y = x * x;
    
    if (x > 0.0) y = Scale (y, 0.0, 1.0, wayToGoal, endWay,    false);
    else         y = Scale (y, 0.0, 1.0, 0.0,       wayToGoal, true);

    for (int j = 0; j < coordinates; j++)
    {
      double incrementFactor = y / wayToGoal;
      double coordDistance = ants [goalInd].cLast [j] - ants [i].cLast [j];
      
      ants [i].c [j] =  ants [i].cLast [j] + (coordDistance * incrementFactor);
      double w = coordDistance * RNDfromCI (-1.0, 1.0) * pathDeviation;
      ants [i].c [j] += w;
      
      ants [i].c [j] = SeInDiSp (ants [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

数値範囲間をスケーリングする関数に注目するとよいでしょう。これらについては、以前の記事ですでに検討しました。今回はその関数を拡張します。revers入力は、下図のようにスケーリング方向を変更するために使用します。

スケール

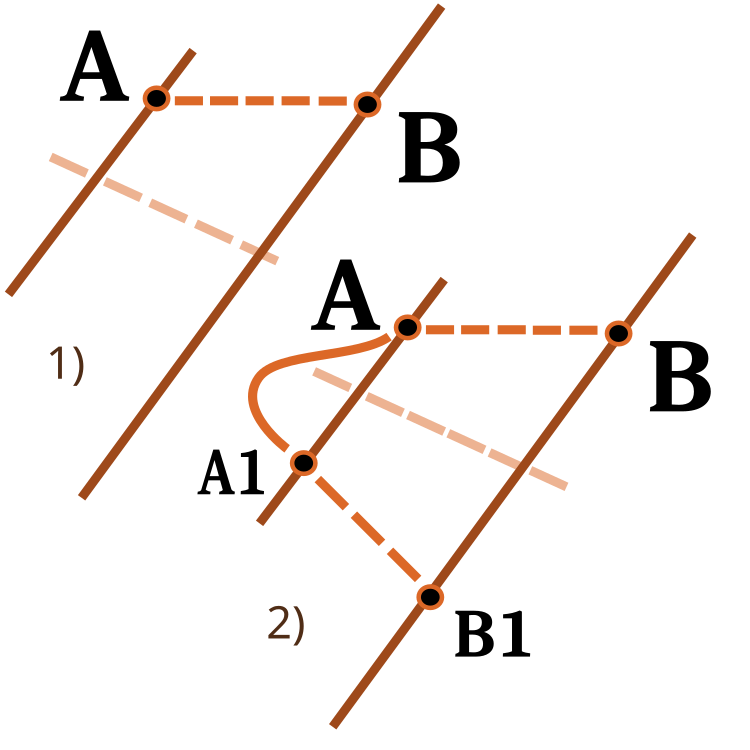
図3：数値範囲間での数値のスケーリング

1) ダイレクトスケーリング、2) リバーススケーリング

//——————————————————————————————————————————————————————————————————————————————
double C_AO_ACO::Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers)
{
  if (OutMIN == OutMAX) return (OutMIN);
  if (InMIN == InMAX) return (double((OutMIN + OutMAX) / 2.0));
  else
  {
    if (In < InMIN) return revers ? OutMAX : OutMIN;
    if (In > InMAX) return revers ? OutMIN : OutMAX;

    double res = (((In - InMIN) * (OutMAX - OutMIN) / (InMAX - InMIN)) + OutMIN);

    if (!revers) return res;
    else         return OutMAX - res;
  }
}
//——————————————————————————————————————————————————————————————————————————————

4.テスト結果

Func1

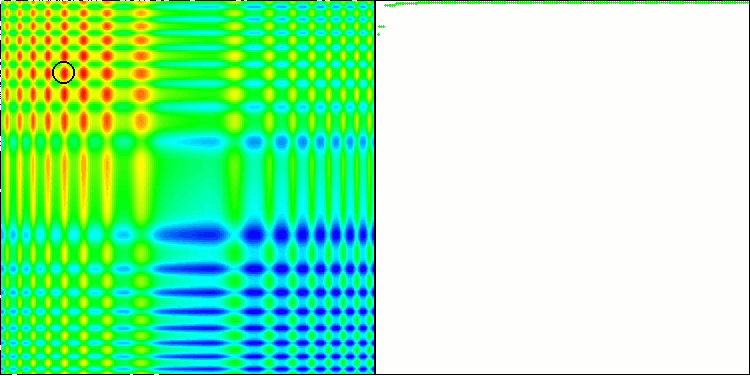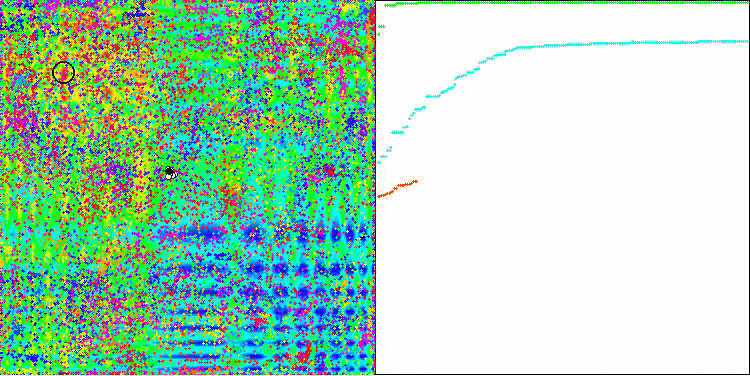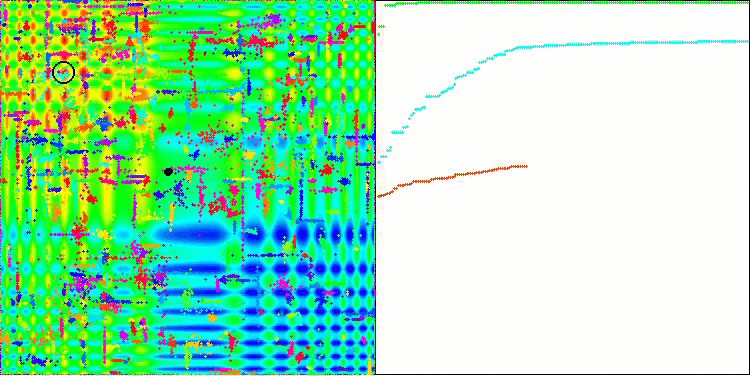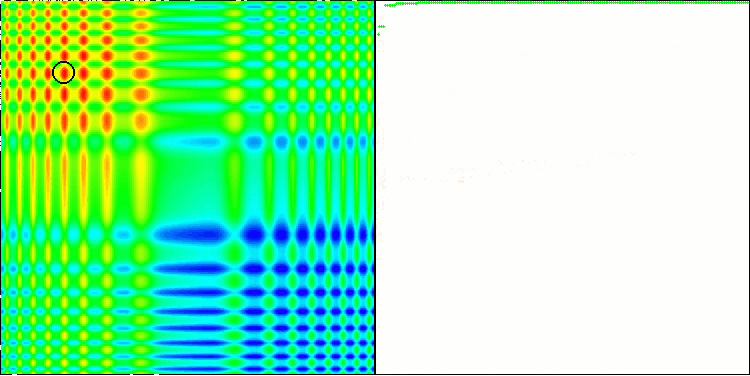
Skinテスト関数のACO

Func2

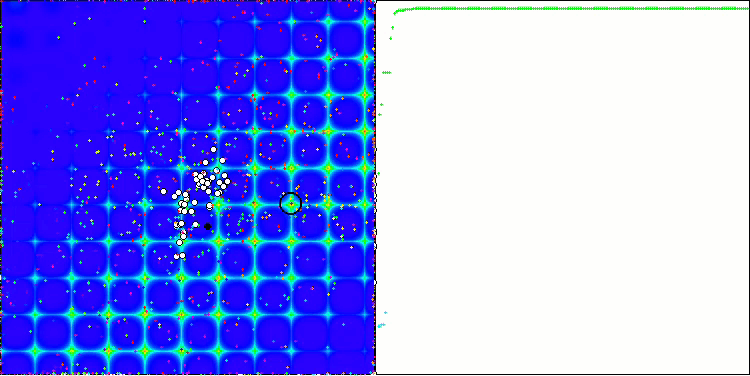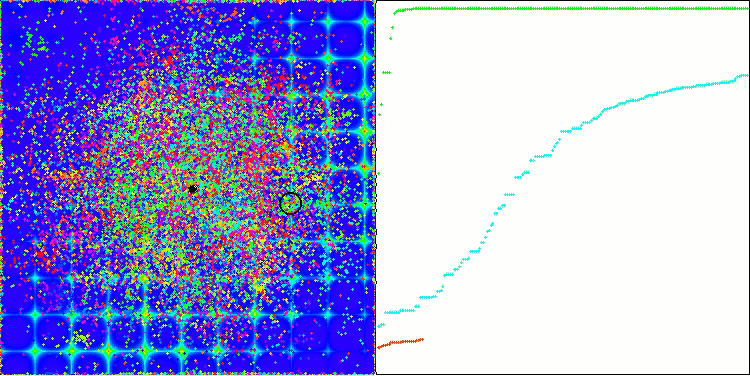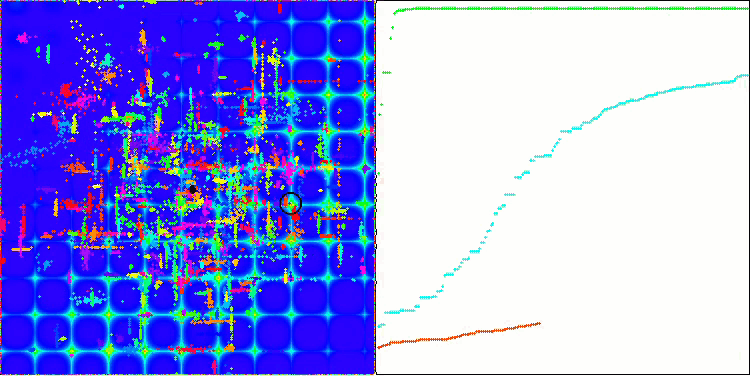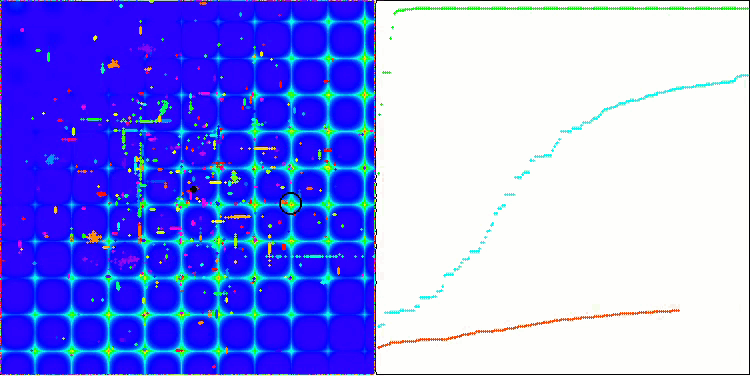
Forestテスト関数のACO

Func3

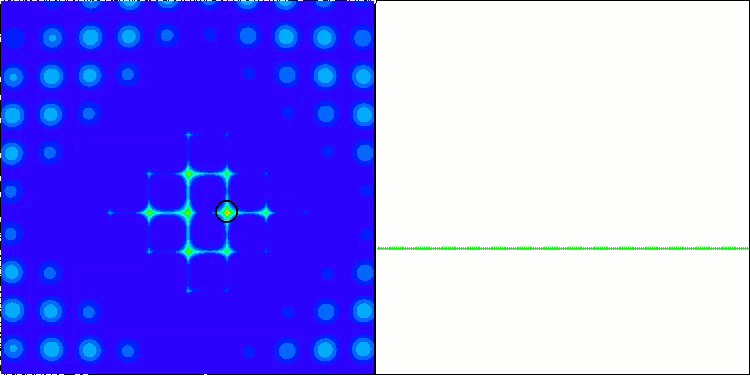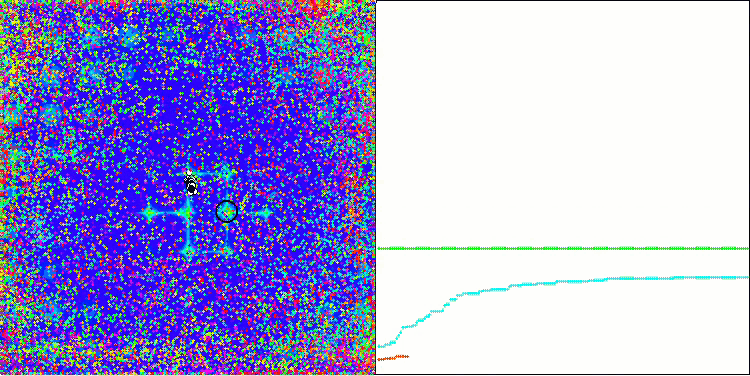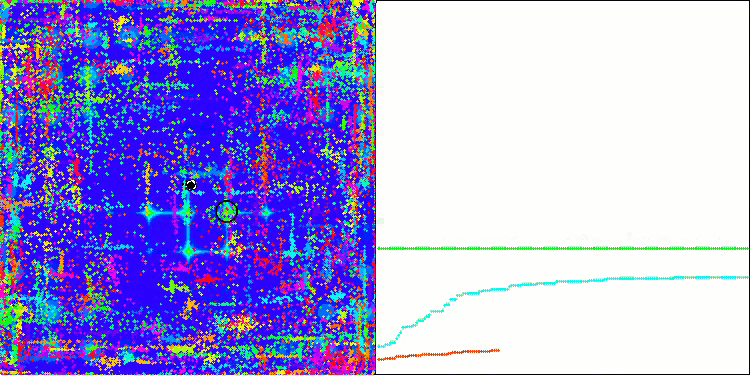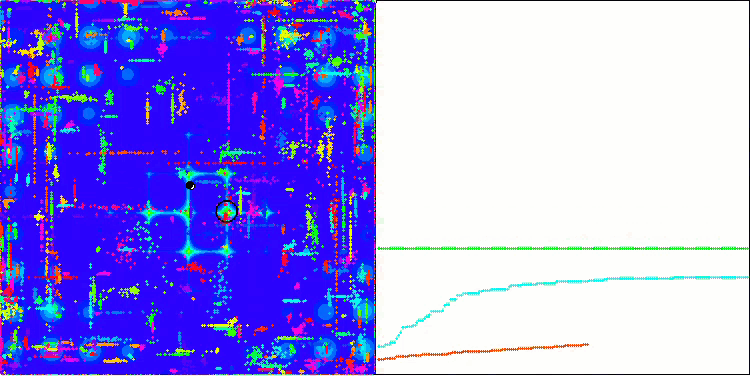
Megacityテスト関数のACO

そろそろ結論を出します。従来の蟻コロニーアルゴリズムは、金融商品の取引における最適化問題には適用できません。しかし、その限界を回避するために、蟻コロニーアルゴリズムという全く新しい概念が登場し、ACOのさらなる発展を可能にしているのです。このようなアルゴリズムは、すでに巡回セールスマン問題など、さまざまな問題に適用することができます。

さらに、レーティングテーブルの新しいリーダーも誕生しました。この結果について、もう少し詳しく考えてみましょう。まず、テストスタンドの結果に注目します。

2022.10.27 16:46:28.678    Test_AO_ACO (EURUSD,M1)    =============================
2022.10.27 16:46:50.599    Test_AO_ACO (EURUSD,M1)    1 Skin's; Func runs 1000 result: 13.969156176320473; Func runs 10000 result: 13.986949123110085
2022.10.27 16:46:50.599    Test_AO_ACO (EURUSD,M1)    Score1: 0.99502; Score2: 0.99599
2022.10.27 16:47:12.424    Test_AO_ACO (EURUSD,M1)    20 Skin's; Func runs 1000 result: 8.514904198298202; Func runs 10000 result: 11.56159524595023
2022.10.27 16:47:12.424    Test_AO_ACO (EURUSD,M1)    Score1: 0.69826; Score2: 0.86403
2022.10.27 16:48:04.200    Test_AO_ACO (EURUSD,M1)    500 Skin's; Func runs 1000 result: 4.962716036996786; Func runs 10000 result: 6.488619274853463
2022.10.27 16:48:04.200    Test_AO_ACO (EURUSD,M1)    Score1: 0.50498; Score2: 0.58800
2022.10.27 16:48:04.200    Test_AO_ACO (EURUSD,M1)    =============================
2022.10.27 16:48:25.999    Test_AO_ACO (EURUSD,M1)    1 Forest's; Func runs 1000 result: 15.805601165115196; Func runs 10000 result: 15.839944455892518
2022.10.27 16:48:25.999    Test_AO_ACO (EURUSD,M1)    Score1: 0.99087; Score2: 0.99302
2022.10.27 16:48:47.897    Test_AO_ACO (EURUSD,M1)    20 Forest's; Func runs 1000 result: 3.568897096569507; Func runs 10000 result: 10.45940001108266
2022.10.27 16:48:47.897    Test_AO_ACO (EURUSD,M1)    Score1: 0.22374; Score2: 0.65571
2022.10.27 16:49:41.855    Test_AO_ACO (EURUSD,M1)    500 Forest's; Func runs 1000 result: 1.3412234994286016; Func runs 10000 result: 2.7822130728041756
2022.10.27 16:49:41.855    Test_AO_ACO (EURUSD,M1)    Score1: 0.08408; Score2: 0.17442
2022.10.27 16:49:41.855    Test_AO_ACO (EURUSD,M1)    =============================
2022.10.27 16:50:03.740    Test_AO_ACO (EURUSD,M1)    1 Megacity's; Func runs 1000 result: 11.8; Func runs 10000 result: 11.8
2022.10.27 16:50:03.740    Test_AO_ACO (EURUSD,M1)    Score1: 0.78667; Score2: 0.78667
2022.10.27 16:50:26.002    Test_AO_ACO (EURUSD,M1)    20 Megacity's; Func runs 1000 result: 1.75; Func runs 10000 result: 3.9200000000000004
2022.10.27 16:50:26.002    Test_AO_ACO (EURUSD,M1)    Score1: 0.11667; Score2: 0.26133
2022.10.27 16:51:21.075    Test_AO_ACO (EURUSD,M1)    500 Megacit 's; Func runs 1000 result: 0.6335999999999999; Func runs 10000 result: 1.2312
2022.10.27 16:51:21.075    Test_AO_ACO (EURUSD,M1)    Score1: 0.04224; Score2: 0.08208

2022.10.27 16:49:41.075    Test_AO_ACO (EURUSD,M1)    =============================
2022.10.27 16:51:21.075    Test_AO_ACO (EURUSD,M1)    All score for C_AO_ACO: 0.5468768583006471

このアルゴリズムは、滑らかなSkin関数に対して優れた収束性とスケーリング能力を発揮し、特に20関数と500関数のテストにおいて優れた結果を示しました。シャープなブレイクを持つ滑らかなForest関数では、分離はさらに顕著になります。このアルゴリズムは、極限に達しても探索を継続します。離散Megacity関数では、500個の関数を持つ問題でのみ、ランダムRNDアルゴリズムに降伏しました。

AO

実行

Skin

Forest

Megacity（discrete）

最終結果

2パラメータ（1F）

40パラメータ（20F）

1000パラメータ（500F）

2パラメータ（1F）

40パラメータ（20F）

1000パラメータ（500F）

2パラメータ（1F）

40パラメータ（20F）

1000パラメータ（500F）

ACOm

1000

0.99502

0.69826

0.50498

0.99087

0.22374

0.08408

0.78667

0.11667

0.04224

0.54688

10,000

0.99599

0.86403

0.58800

0.99302

0.65571

0.17442

0.78667

0.26133

0.08208

RND

1000

0.98744

0.61852

0.49408

0.89582

0.19645

0.14042

0.77333

0.19000

0.14283

0.51254

10,000

0.99977

0.69448

0.50188

0.98181

0.24433

0.14042

0.88000

0.20133

0.14283

PSO

1000

0.98436

0.72243

0.65483

0.71122

0.15603

0.08727

0.53333

0.08000

0.04085

0.47695

10,000

0.99836

0.72329

0.65483

0.97615

0.19640

0.09219

0.82667

0.10600

0.04085

PSOm

1000

0.96678

0.64727

0.57654

0.80616

0.13388

0.06800

0.53333

0.08067

0.04211

0.45144

10,000

0.99505

0.64986

0.57654

0.90401

0.18194

0.07104

0.74667

0.10400

0.04211


終わりに

このアルゴリズムには多くの設定があるので、さらに良い結果を得ることが可能です。特定の種類のタスクに合わせたカスタマイズが可能です。最初のパラメータPheromoneEffect_Pは収束率に直接影響します。特に滑らかな単調関数、例えば放物線に対して有効です。収束率は100%になるが、これは同時に、大きく設定すると離散関数の極値で行き詰まる一因となります。

第2パラメータPathLengthEffect_Pは、蟻の怠惰の度合いを示しています。パラメータ値が高い場合は、より近いターゲットを選択して移動します。最良の結果を得るためには、このパラメータと最初のパラメータのバランスをとることが必要です。このパラメータは、より多くの餌がある地点に行こうとする蟻の欲求に対抗するために設計されており、代わりに、より小さな領域を詳細に調べるために最も近いターゲットを選択することがあります。これは、Forest関数の例のように、最適なポイントが非常に近くにあることが判明する場合に非常に有効です。

最も重要な成果は、正統的なACOの主な問題点である「離散的な組合せ問題しか解けない」という問題を取り除くことに成功したことです。これで、蟻コロニーアルゴリズムをニューラルネットワークの学習に利用できるようになりました。

テストスタンドでは、蟻が多次元関数の測定値に集中し、極値の特徴的なグループが強調されているため、視覚的に非常に興味深く観察することができます。もしかしたら、この効果を具体的な問題解決に利用できるかもしれませんが、これにはさらなる研究が必要です。

このアルゴリズムには興味深い性質があり、2変数の問題を解く場合、40変数の最適化よりも極値で行き詰まる確率がやや高くなります。アルゴリズムは、複数の変数を含む解を探索し続けます。これは、探索空間のすべての座標を結ぶ手段としてベクトルを用いたことによる効果だと推測されます。例えば、蟻が新しい良い場所に移動した場合、一部の座標が個別に変化するのではなく、すべての座標が空間的に良い方向に変化します。

作成したアルゴリズムは新しく、詳細が未解明なので、どなたか、テストスタンドが最終的に0.6以上の値を示すようなアルゴリズム設定を共有していただければ、表の結果を更新することができますので、ありがたいです。以前に検討したアルゴリズムについてもお願いします。

賛成：
1.アルゴリズムはかなり高速である。
2.汎用性がある。このアルゴリズムは、様々な最適化問題に利用することができます。
3.極値だけに注目しない能力。
4.滑らかな関数と離散的な関数の両方に対して、かなり良好な収束性を示す。
5.スケーラブルである。

反対：
1.おそらく、同じPSOでも滑らかな関数の場合よりも収束までに多くの反復を必要とするが、これはPSOがすでに停止している場所でも探索を継続できることで部分的に相殺されている。
2.アルゴリズムのパラメータが結果に強く影響する。

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/11602

添付されたファイル |
ZIPをダウンロード
q3_The_world_of_AO_7ACOg.zip (29.23 KB)
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動
DoEasy - コントロール（第25部）：Tooltip WinFormsオブジェクト DoEasy - コントロール（第25部）：Tooltip WinFormsオブジェクト
今回は、Tooltipコントロールの開発と、ライブラリの新しいグラフィカルプリミティブの開発を開始する予定です。当然ながら、すべての要素にツールチップがあるわけではないですが、すべてのグラフィックオブジェクトにはツールチップを設定する機能があります。
ニューラルネットワークが簡単に（第31部）：進化的アルゴリズム ニューラルネットワークが簡単に（第31部）：進化的アルゴリズム
前回の記事では、非勾配最適化手法の調査を開始しました。遺伝的アルゴリズムについて学びました。今日は、このトピックを継続し、進化的アルゴリズムの別のクラスを検討します。
データサイエンスと機械学習（第09回）:K近傍法(KNN) データサイエンスと機械学習（第09回）:K近傍法(KNN)
これは、訓練データセットから学習しない遅延アルゴリズムです。代わりにデータセットを保存し、新しいサンプルが与えられるとすぐに動作します。シンプルでありながら、実世界でさまざまなケースに応用されています。
フラクタルによる取引システムの設計方法を学ぶ フラクタルによる取引システムの設計方法を学ぶ
これは、最も人気のあるテクニカル指標に基づいて取引システムを設計する方法を学ぶための連載の新しい記事です。フラクタル指標という新しい指標を学び、それを基にした取引システムを設計し、MetaTrader 5ターミナルで実行する方法について学びます。