
集団型ADAM(適応モーメント推定法)
内容
はじめに
機械学習の世界では、データが急速に増加し、アルゴリズムがますます複雑になる中で、最適化は高い成果を得るための重要な役割を果たしています。数多くの手法がこの課題に取り組んでいますが、その中でもADAM (Adaptive Moment Estimation)アルゴリズムは、その洗練さと効率の高さで際立っています。
2014年にD. P. KingmaとJ. Baによって提案されたADAMアルゴリズムは、AdaGradやRMSPropなど先行する手法の長所を組み合わせたものです。このアルゴリズムは、ニューラルネットワークの重みをニューロンの活性化関数の勾配を用いて最適化することを目的として設計されました。適応的な一次および二次モーメント推定に基づいており、実装が容易で計算効率も高いのが特徴です。また、必要とするメモリ資源は最小限であり、勾配の対角スケーリングに依存しないため、大規模なデータや多数のパラメータを扱う問題に特に適しています。
ADAMは、非定常な目的関数や、勾配がノイズを含んだり疎であったりする状況でも良好に機能します。さらに、アルゴリズムのハイパーパラメータは解釈しやすく、複雑な調整を必要としない場合が多いです。
しかし、ニューラルネットワーク分野での高い効率にもかかわらず、ADAMは解析的勾配の利用に限定されているため、応用範囲は狭まっています。本稿では、ADAMアルゴリズムを数値的な勾配を扱える集団ベースの最適化アルゴリズムへと変換する革新的な手法を提案します。この修正により、ADAMの適用範囲をニューラルネットワークの枠を超えて広げるだけでなく、一般的な最適化問題の幅広い解決に新たな可能性を開きます。
私たちの研究の目的は、元のADAMの利点を保持しつつ、解析的勾配が利用できない状況でも効果的に動作する汎用的なオプティマイザーを構築することにあります。これにより、修正されたADAMは大域的最適化や多目的最適化といった分野にも応用可能となり、その潜在力と実用的価値を大きく高めることができます。
アルゴリズムの実装
ADAMアルゴリズムはしばしば確率的勾配に基づく最適化手法に分類されます。しかし重要なのは、ADAM自体の中核的なロジックには内部的な確率的要素が含まれていないという点です。ADAMに関連づけられる確率性は、実際にはデータの準備やアルゴリズムへの入力方法に由来するものであり、その内部的な仕組みに起因するものではありません。したがって、データ準備における確率性と、最適化アルゴリズム自体の決定論的な性質とを区別することが重要です。
ADAMアルゴリズム自体は完全に決定論的です。同じ入力データと初期条件が与えられれば、常に同一の結果を出力します。ADAMにおけるパラメータ更新は、乱数要素を含まない明確に定義された数式に基づいています。
この「ADAMアルゴリズムの決定論的な性質」と「データ準備における確率的な性質」との区別は、その動作や修正の可能性を正しく理解するために欠かせません。この事実を踏まえることで、確率的データ準備が適用できない、あるいは望ましくない問題に対しても、ADAMの強力な最適化特性を保持したまま適応させる道が開けます。
それでは数式を含む擬似コードを見ていきましょう。
1. 初期化
m₀ = 0(一次モーメントの初期化)
v₀ = 0(二次モーメントの初期化)
t = 0(ステップカウンタ)
2. 各ステップ t において:
t = t + 1
gₜ = ∇ₜf(θₜ₋₁) (勾配の計算)
3. 一次および二次モーメントの更新:
mₜ = β₁ · mₜ₋₁ + (1 - β₁) · gₜ
vₜ = β₂ · vₜ₋₁ + (1 - β₂) · gₜ²
m̂ₜ = mₜ / (1 - β₁ᵗ)
v̂ₜ = vₜ / (1 - β₂ᵗ)
4. パラメータの更新:
θₜ = θₜ₋₁ - α · m̂ₜ / (√v̂ₜ + ε)
ここで
θₜ:ステップtにおけるモデルパラメータ
f(θ):目的関数
α:学習率(通常α = 0.001)
β₁、β₂:モーメントの減衰比(通常β₁ = 0.9、β₂ = 0.999)
ε:ゼロ除算を防ぐための小さな定数(通常は10⁻⁸)
mₜ、vₜ:勾配の一次および二次モーメントの推定値
m̂ₜ、v̂ₜ:補正されたモーメント推定値
これらの式はADAMアルゴリズムの本質を示しており、勾配の一次・二次モーメントの推定に基づいて各パラメータの学習率を適応的に調整していることが分かります。ここで確認できるように、アルゴリズム自体には確率性は一切存在しません。通常、ADAMアルゴリズムは数多くのソフトウェア実装を通じてニューラルネットワークのアーキテクチャに組み込まれています。しかし本稿では少し魔法をかけ、ADAMを独立した自己完結的な存在にするだけでなく、集団的かつ真に確率的な手法へと変換します。
まずは、ADAMを集団形式で実装することから始めます。その際、元の数式は保持しつつ、最初の最適化パラメータの初期化段階にのみランダム性を導入します。ですが、これはほんの始まりにすぎません。次の段階では、この勾配法の動作ダイナミクスそのものに確率性を組み込み、その結果を検証していきます。
次に、勾配と二つのモーメントベクトル(一次と二次)を格納するためのS_Gradients構造体を定義します。Init (int coords)メソッドは配列のサイズを設定し、それらをゼロで初期化します。
//—————————————————————————————————————————————————————————————————————————————— // Structure for storing gradients and moments struct S_Gradients { double g []; // Gradients double m []; // Vectors of the first moment double v []; // Vectors of the second moment // Method for initializing gradients void Init (int coords) { ArrayResize (g, coords); ArrayResize (m, coords); ArrayResize (v, coords); ArrayInitialize (g, 0.0); // Initialize gradients to zeros ArrayInitialize (m, 0.0); // Initialize the first moment with zeros ArrayInitialize (v, 0.0); // Initialize the second moment with zeros } }; //——————————————————————————————————————————————————————————————————————————————
C_AO_ADAMクラスは、ADAM最適化アルゴリズムを実装したものです。クラスの主な機能は以下のとおりです。
- コンストラクタ:集団サイズ、学習率、減衰率といったアルゴリズムのパラメータを初期化します。
- SetParams:params配列からパラメータ値を設定し、初期化後に変更できるようにします。
- Init:パラメータ範囲やエポック数を受け取り、アルゴリズムを実行可能な状態に準備します。
- MovingとRevision:最適化ステップを実行し、モデルパラメータを更新するとともに、アルゴリズムの状態を確認します。
//—————————————————————————————————————————————————————————————————————————————— class C_AO_ADAM : public C_AO { public: //-------------------------------------------------------------------- // Class destructor ~C_AO_ADAM () { } // Class constructor C_AO_ADAM () { ao_name = "ADAM"; // Algorithm name ao_desc = "Adaptive Moment Estimation"; // Algorithm description ao_link = "https://www.mql5.com/ja/articles/16443"; // Link to the article popSize = 50; // Population size alpha = 0.001; // Learning ratio beta1 = 0.9; // Exponential decay ratio for the first moment beta2 = 0.999; // Exponential decay ratio for the second moment epsilon = 1e-8; // Small constant to prevent division by zero // Initialize the parameter array ArrayResize (params, 5); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "alpha"; params [1].val = alpha; params [2].name = "beta1"; params [2].val = beta1; params [3].name = "beta2"; params [3].val = beta2; params [4].name = "epsilon"; params [4].val = epsilon; } // Method for setting parameters void SetParams () { popSize = (int)params [0].val; // Set population size alpha = params [1].val; // Set the learning ratio beta1 = params [2].val; // Set beta1 beta2 = params [3].val; // Set beta2 epsilon = params [4].val; // Set epsilon } // Initialization method bool Init (const double &rangeMinP [], // minimum search range const double &rangeMaxP [], // maximum search range const double &rangeStepP [], // search step const int epochsP = 0); // number of epochs void Moving (); // Moving method void Revision (); // Revision method //---------------------------------------------------------------------------- double alpha; // Learning ratio double beta1; // Exponential decay ratio for the first moment double beta2; // Exponential decay ratio for the second moment double epsilon; // Small constant S_Gradients grad []; // Array of gradients private: //------------------------------------------------------------------- int step; // Iteration step int t; // Iteration counter }; //——————————————————————————————————————————————————————————————————————————————
C_AO_ADAMクラスのInitメソッドは、アルゴリズムの初期化をおこないます。
- StandardInitを呼び出して既定のパラメータを設定します。失敗した場合はfalseを返します。
- ステップおよび反復カウンタtをリセットします。
- popSize(集団サイズ)に応じてgrad勾配配列のサイズを再設定します。
- 集団内の各個体について、coords(座標)を用いて勾配を初期化します。
すべての操作が成功した場合、このメソッドはtrueを返します。
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_ADAM::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { // Standard initialization if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- step = 0; // Reset step counter t = 1; // Reset iteration counter ArrayResize (grad, popSize); // Resize the gradient array for (int i = 0; i < popSize; i++) grad [i].Init (coords); // Initialize gradients for each individual return true; } //——————————————————————————————————————————————————————————————————————————————
C_AO_ADAMクラスのMovingメソッドは、ADAMアルゴリズムにおける最適化ステップを実装します。
1. ステップ確認(step < 2の場合)
- 集団内の各個体について、目的関数値と座標の前回値を保存します。
- 指定された範囲内で新しいランダムな座標を生成し、許容範囲に収まるよう調整します。
- ステップカウンタをインクリメントし、メソッドを終了します。
2. 勾配の計算(step ≥ 2の場合):各個体について、目的関数値と座標の変化量を計算します。
- ゼロ除算を防ぐために小さなε値を加えます。この値はアルゴリズムの外部パラメータであり、探索特性にも影響を与えます。
- パラメータごとに勾配を計算します。
3. 各個体のパラメータ更新
- 目的関数値と座標の前回値を保存します。
- 勾配の一次モーメントおよび二次モーメントの推定値を更新します。
- 補正モーメント推定値を計算し、ADAMの更新式を用いて座標を更新します。
- 座標が許容範囲を超えないように調整します。
4. 反復カウンタtをインクレメント
このように、Movingメソッドは適応的な勾配モーメントを用いて最適化中の個体の位置を更新する役割を担います。アルゴリズムの最初の2ステップは、適合度関数値の変化に基づいて勾配を計算するために必要です。これは、勾配が解析的な式を知らずに数値的に計算されるためであり、少なくとも2点が必要となります。前の2ステップで得られた解は、後続のステップで利用されます。
ADAMアルゴリズムのロジック自体は、勾配をどのように計算するかを特定しているわけではありません。勾配は解析的にも数値的にも計算可能であり、その計算はアルゴリズム本体の外でおこなわれます。アルゴリズムを使用方法から切り離して抽象的に理解することは、機械学習プロジェクト全体における各構成要素の役割を把握するうえで非常に重要です。これにより、各要素が最終結果へ与える影響を適切に評価でき、アルゴリズムを異なる課題へ適応させやすくなります。
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ADAM::Moving () { //---------------------------------------------------------------------------- if (step < 2) // If step is less than 2 { for (int i = 0; i < popSize; i++) { a [i].fP = a [i].f; // Save the previous value of the function for (int c = 0; c < coords; c++) { a [i].cP [c] = a [i].c [c]; // Save the previous coordinate value // Generate new coordinates randomly a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); // Bringing new coordinates to acceptable values a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } step++; // Increase the step counter return; // Exit the method } //---------------------------------------------------------------------------- double ΔF, ΔX; // Changes in function and coordinates for (int i = 0; i < popSize; i++) { ΔF = a [i].f - a [i].fP; // Calculate the change of the function for (int c = 0; c < coords; c++) { ΔX = a [i].c [c] - a [i].cP [c]; // Calculate the change in coordinates if (ΔX == 0.0) ΔX = epsilon; // If change is zero, set it to epsilon grad [i].g [c] = ΔF / ΔX; // Calculate the gradient } } // Update parameters using ADAM algorithm for (int i = 0; i < popSize; i++) { // Save the previous value of the function a [i].fP = a [i].f; for (int c = 0; c < coords; c++) { // Save the previous coordinate value a [i].cP [c] = a [i].c [c]; // Update the biased first moment estimate grad [i].m [c] = beta1 * grad [i].m [c] + (1.0 - beta1) * grad [i].g [c]; // Update the biased second moment estimate grad [i].v [c] = beta2 * grad [i].v [c] + (1.0 - beta2) * grad [i].g [c] * grad [i].g [c]; // Calculate the adjusted first moment estimate double m_hat = grad [i].m [c] / (1.0 - MathPow (beta1, t)); // Calculate the adjusted estimate of the second moment double v_hat = grad [i].v [c] / (1.0 - MathPow (beta2, t)); // Update coordinates a [i].c [c] = a [i].c [c] + (alpha * m_hat / (MathSqrt (v_hat) + epsilon)); // Make sure the coordinates stay within the allowed range a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } t++; // Increase the iteration counter } //——————————————————————————————————————————————————————————————————————————————
C_AO_ADAMクラスのRevisionメソッドは、以下の処理をおこないます。
- 最良個体のインデックスindを-1に初期化します。
- 集団内のすべての個体を順に確認し、現在の個体の関数値がこれまでに見つかった最良の値fBより大きい場合、最良の大域解を更新し、最良個体のインデックスを記録します。
- 最良個体が見つかった場合、その座標をcB配列にコピーします。
このようにして、Revisionメソッドは適合度関数の値に基づき、最良個体の座標を特定して保持します。
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ADAM::Revision () { int ind = -1; // Best individual index for (int i = 0; i < popSize; i++) { if (a [i].f > fB) // If the current value of the function is greater than the best one { fB = a [i].f; // Update the best value of the function ind = i; // Store the index of the best individual } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); // Copy the coordinates of the best individual } //——————————————————————————————————————————————————————————————————————————————
ご覧の通り、ADAMアルゴリズムは現在、集団ベースの手法に拡張されており、外部パラメータで集団サイズを1に設定した場合は、通常の非集団型ADAMと全く同じ動作をします。これで、テスト関数を用いてアルゴリズムを評価する準備が整いました。次に、結果を見ていきましょう。
ADAM|Adaptive Moment Estimation|50.0|0.001|0.9|0.999|0.00000001|
=============================
5 Hilly's; Func runs:10000; result:0.3857584301959297
25 Hilly's; Func runs:10000; result:0.29733109680042824
500 Hilly's; Func runs:10000; result:0.25390478702062613
=============================
5 Forest's; Func runs:10000; result:0.30772687797850234
25 Forest's; Func runs:10000; result:0.1982664040653052
500 Forest's; Func runs:10000; result:0.15554626746207786
=============================
5 Megacity's; Func runs:10000; result:0.18153846153846154
25 Megacity's; Func runs:10000; result:0.12430769230769231
500 Megacity's; Func runs:10000; result:0.09503076923077
=============================
All score:1.99941 (22.22%)
残念ながら、現時点での結果は最良とは言えません。しかし、これは潜在的な成長の余地を示しており、アルゴリズムに改善を導入する余地を提供します。特に、アルゴリズムに真の確率的要素を導入することが考えられます。
前述の集団型ADAMアルゴリズムの実装では、各エージェントは著者の元のロジックの別々の「スレッド」を表しており、まるで探索空間の丘を這う蛇のように、初期ランダム初期化によって場全体に分布しています。これらの蛇は互いに干渉せず、最良解に関する情報も交換しません。アルゴリズムは勾配ベースであるため、できるだけ近接した点での表面の変化を考慮することが重要です。数値微分のステップを小さくすると収束が遅くなり、逆にステップを大きくすると探索空間で大きく飛び跳ねるため、点間の表面情報を得ることが困難になります。
これらの問題を解決するため、集団の一部をハイブリッド個体にします。ハイブリッド個体は他のエージェントの解の要素で構成されます。具体的には、個体の適合度で集団をソートし、リストの下位(最も弱い個体がいる位置)にハイブリッドを作成します。このような個体では、より適応度の高い個体の解の要素に基づいて、新しい空間上の点を生成することで解を形成します。適合度が高い個体ほど、その位置情報がハイブリッドに伝わる確率が高くなります。
このように、集団の一部は元のアルゴリズムロジックに従った解を表し、もう一部はハイブリッドとして、集団の解の要素を組み合わせたものとなります。生成されるハイブリッドは単に他の個体の一部をコピーしたものではなく、各要素はべき乗則に従った確率分布に従って変化します。このべき乗則の度合いを「ハイブリッド安定性」と呼びます。度合いが高いほどハイブリッドの変化は小さくなり、集団内の最良解の要素に近い状態を維持します。
次に、アルゴリズムの更新版に移ります。C_AO_ADAMmクラスはC_AO_ADAMクラスに対していくつかの変更を加えたもので、理論的には機能や挙動にプラスの影響を与える可能性があります。主な変更点は以下の通りです。
1. 新しいパラメータ
- hybridsPercentage:集団におけるハイブリッドの割合を決定します。
- hybridsResistance:ハイブリッドの変化への抵抗を調整します。
2. C_AO_ADAMmクラスのコンストラクタでは、新しいhybridsPercentageおよびhybridsResistanceパラメータを初期化します。これらの値はparams配列に追加されます。
3. SetParamsメソッドでは、新しいhybridsPercentageおよびhybridsResistanceパラメータを設定するための文字列をサポートし、動的に値を変更できるようにします。
hybridsPercentageを「1」に設定すると、事実上ADAMロジックが無効化されます。一方、この値を「0」に設定すると、アルゴリズムに組合せ的特性はなくなります。いくつかの試行の結果、最適値は「0.5」であることが分かり、最良の結果を得ました。
2番目のパラメータは、ハイブリッドの変化への抵抗を制御します。低い値を設定すると、ハイブリッドは親から特徴を継承した後に大きく変化し、最適化パラメータの許容範囲全体をカバーすることが可能です。一方、非常に高い値(たとえば「20」以上)を設定すると、ハイブリッドの変動はほぼゼロとなり、親個体の最良特性のみを伝える存在になります。このパラメータの最適値は試行の結果「10」と判明しました。
//—————————————————————————————————————————————————————————————————————————————— class C_AO_ADAMm : public C_AO { public: //-------------------------------------------------------------------- // Class destructor ~C_AO_ADAMm () { } // Class constructor C_AO_ADAMm () { ao_name = "ADAMm"; // Algorithm name ao_desc = "Adaptive Moment Estimation M"; // Algorithm description ao_link = "https://www.mql5.com/ja/articles/16443"; // Link to the article popSize = 100; // Population size hybridsPercentage = 0.5; // Percentage of hybrids in the population hybridsResistance = 10; // Resistance of hybrids to changes alpha = 0.001; // Learning ratio beta1 = 0.9; // Exponential decay ratio for the first moment beta2 = 0.999; // Exponential decay ratio for the second moment epsilon = 0.1; // Small constant to prevent division by zero // Initialize the parameter array ArrayResize (params, 7); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "hybridsPercentage"; params [1].val = hybridsPercentage; params [2].name = "hybridsResistance"; params [2].val = hybridsResistance; params [3].name = "alpha"; params [3].val = alpha; params [4].name = "beta1"; params [4].val = beta1; params [5].name = "beta2"; params [5].val = beta2; params [6].name = "epsilon"; params [6].val = epsilon; } // Method for setting parameters void SetParams () { popSize = (int)params [0].val; // Set population size hybridsPercentage = params [1].val; // Set the percentage of hybrids in the population hybridsResistance = params [2].val; // Set hybrids' resistance to change alpha = params [3].val; // Set the learning ratio beta1 = params [4].val; // Set beta1 beta2 = params [5].val; // Set beta2 epsilon = params [6].val; // Set epsilon } // Initialization method bool Init (const double &rangeMinP [], // minimum search range const double &rangeMaxP [], // maximum search range const double &rangeStepP [], // search step const int epochsP = 0); // number of epochs void Moving (); // Moving method void Revision (); // Revision method //---------------------------------------------------------------------------- double hybridsPercentage; // Percentage of hybrids in the population double hybridsResistance; // Resistance of hybrids to changes double alpha; // Learning ratio double beta1; // Exponential decay ratio for the first moment double beta2; // Exponential decay ratio for the second moment double epsilon; // Small constant S_Gradients grad []; // Array of gradients private: //------------------------------------------------------------------- int step; // Iteration step int t; // Iteration counter int hybridsNumber; // Number of hybrids in the population }; //——————————————————————————————————————————————————————————————————————————————
C_AO_ADAMmクラスのInitメソッドでは、前クラスの同名メソッドと比較して以下の変更が加えられています。
- 集団内のハイブリッド個体の数を、hybridsPercentageの割合に基づいて計算します。この新しい値hybridsNumberは、集団の構成を制御するために使用されます。
- ハイブリッドの数がpopSizeを超えないようにチェックを追加しました。これにより、配列の範囲外参照に関連するエラーを防ぎます。
これらの変更により、Initメソッドはアルゴリズムのハイブリッド関連機能に対してより適応的になり、集団内の個体の状態や初期化を正しく管理できるようになっています。
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_ADAMm::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { // Standard initialization if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- step = 0; // Reset step counter t = 1; // Reset iteration counter hybridsNumber = int(popSize * hybridsPercentage); // Calculation of the number of hybrids in the population if (hybridsNumber > popSize) hybridsNumber = popSize; // Correction ArrayResize (grad, popSize); // Resize the gradient array for (int i = 0; i < popSize; i++) grad [i].Init (coords); // Initialize gradients for each individual return true; } //——————————————————————————————————————————————————————————————————————————————
Movingメソッドには、前バージョンと比較していくつかの変更が加えられています。
パラメータの更新はADAMアルゴリズムに基づいておこなわれますが、このブロックにはハイブリッド個体を扱う条件が追加されました。個体インデックスiがpopSize - hybridsNumber以上の場合はハイブリッド個体と見なし、hybridsResistanceパラメータと乱数分布を用いて新しい座標を生成します。これにより、ハイブリッド個体は親個体から受け継いだ特徴に小さな変化、いわば特徴の突然変異を持たせることができます。一方、非ハイブリッド個体については、一次および二次モーメントのバイアス付き推定値を更新し、続いて補正モーメント推定値を計算して座標を更新します。
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ADAMm::Moving () { //---------------------------------------------------------------------------- if (step < 2) // If step is less than 2 { for (int i = 0; i < popSize; i++) { a [i].fP = a [i].f; // Save the previous value of the function for (int c = 0; c < coords; c++) { a [i].cP [c] = a [i].c [c]; // Save the previous coordinate value // Generate new coordinates randomly a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); // Bringing new coordinates to acceptable values a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } step++; // Increase the step counter return; // Exit the method } //---------------------------------------------------------------------------- double ΔF, ΔX; // Changes in function and coordinates double cNew; for (int i = 0; i < popSize; i++) { ΔF = a [i].f - a [i].fP; // Calculate the change of the function for (int c = 0; c < coords; c++) { ΔX = a [i].c [c] - a [i].cP [c]; // Calculate the change in coordinates if (ΔX == 0.0) ΔX = epsilon; // If change is zero, set it to epsilon grad [i].g [c] = ΔF / ΔX; // Calculate the gradient } } // Update parameters using ADAM algorithm for (int i = 0; i < popSize; i++) { // Save the previous value of the function a [i].fP = a [i].f; for (int c = 0; c < coords; c++) { // Save the previous coordinate value a [i].cP [c] = a [i].c [c]; if (i >= popSize - hybridsNumber) { double pr = u.RNDprobab (); pr *= pr; int ind = (int)u.Scale (pr, 0, 1, 0, popSize - 1); cNew = u.PowerDistribution (a [ind].c [c], rangeMin [c], rangeMax [c], hybridsResistance); } else { // Update the biased first moment estimate grad [i].m [c] = beta1 * grad [i].m [c] + (1.0 - beta1) * grad [i].g [c]; // Update the biased second moment estimate grad [i].v [c] = beta2 * grad [i].v [c] + (1.0 - beta2) * grad [i].g [c] * grad [i].g [c]; // Calculate the adjusted first moment estimate double m_hat = grad [i].m [c] / (1.0 - MathPow (beta1, t)); // Calculate the adjusted estimate of the second moment double v_hat = grad [i].v [c] / (1.0 - MathPow (beta2, t)); // Update coordinates //a [i].c [c] = a [i].c [c] + (alpha * m_hat / (MathSqrt (v_hat) + epsilon)); cNew = a [i].c [c] + (alpha * m_hat / (MathSqrt (v_hat) + epsilon)); } // Make sure the coordinates stay within the allowed range a [i].c [c] = u.SeInDiSp (cNew, rangeMin [c], rangeMax [c], rangeStep [c]); } } t++; // Increase the iteration counter } //——————————————————————————————————————————————————————————————————————————————
Revisionメソッドには、前バージョンと比較していくつかの変更が加えられています。
まず、ソート用の配列を準備します。集団のサイズに合わせて一時的な配列aTを作成し、続いてu.Sorting ()メソッドを呼び出して並べ替えをおこないます。ソートされた集団配列により、ハイブリッドはより適応度の高い個体から特徴を受け継ぐ確率が高くなります。一時的な集団配列はクラスフィールドとして保持することも可能でしたが、今回はより明確にするためにこのように実装されています。
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ADAMm::Revision () { int ind = -1; // Best individual index for (int i = 0; i < popSize; i++) { if (a [i].f > fB) // If the current value of the function is greater than the best one { fB = a [i].f; // Update the best value of the function ind = i; // Store the index of the best individual } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); // Copy the coordinates of the best individual //---------------------------------------------------------------------------- S_AO_Agent aT []; ArrayResize (aT, popSize); u.Sorting (a, aT, popSize); } //——————————————————————————————————————————————————————————————————————————————
テスト結果
それでは、改良された真に確率的な集団型ADAMmの結果を見てみましょう。
ADAMm|Adaptive Moment Estimation M|100.0|0.5|10.0|0.001|0.9|0.999|0.1|
=============================
5 Hilly's; Func runs:10000; result:0.8863499654810468
25 Hilly's; Func runs:10000; result:0.4476644542595641
500 Hilly's; Func runs:10000; result:0.2661291031673467
=============================
5 Forest's; Func runs:10000; result:0.8449728914068644
25 Forest's; Func runs:10000; result:0.3849320103361983
500 Forest's; Func runs:10000; result:0.16889385703816007
=============================
5 Megacity's; Func runs:10000; result:0.6615384615384616
25 Megacity's; Func runs:10000; result:0.2704615384615384
500 Megacity's; Func runs:10000; result:0.10593846153846247
=============================
All score:4.03688 (44.85%)
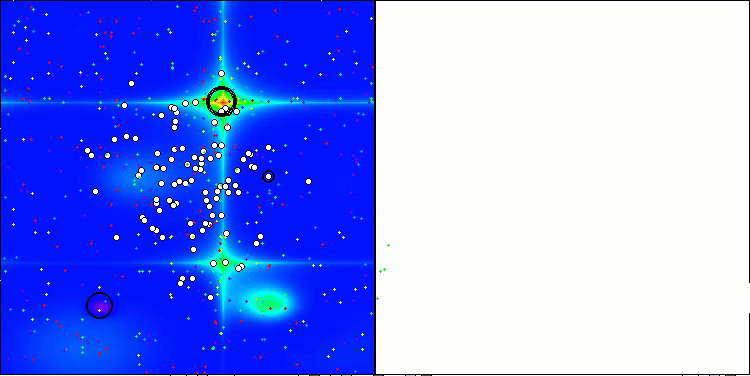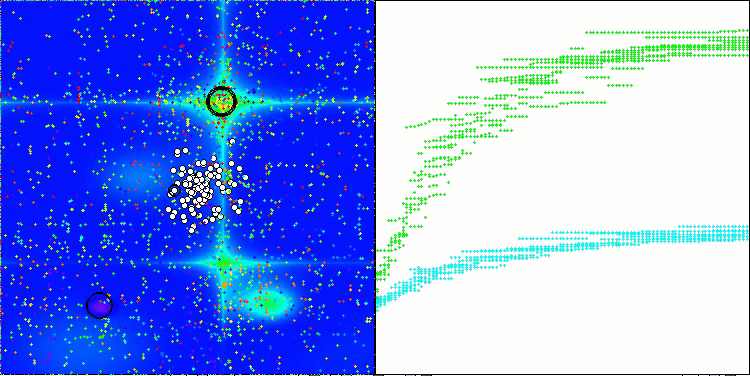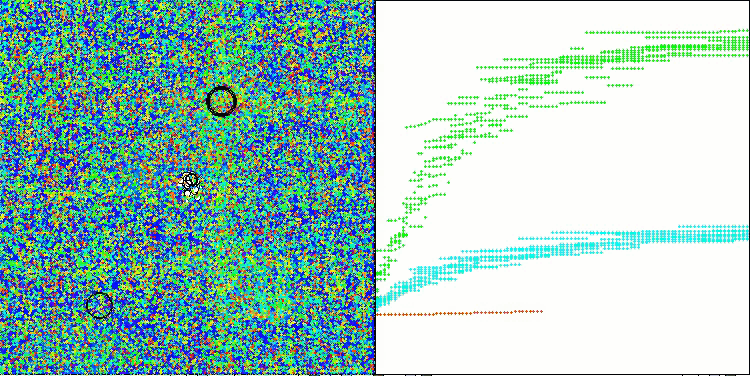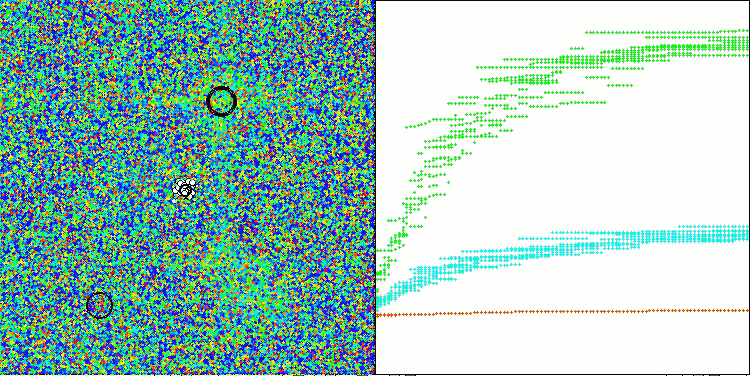
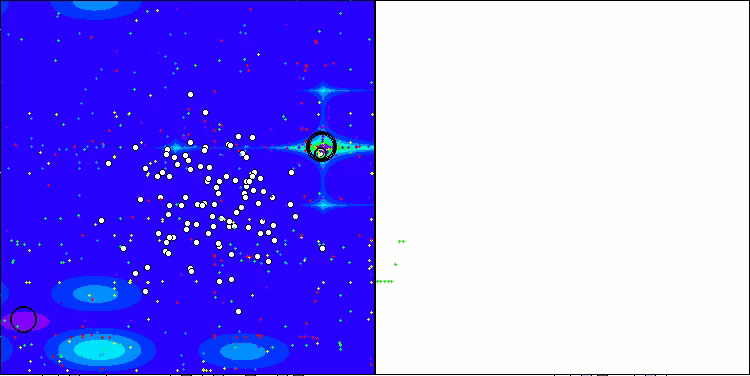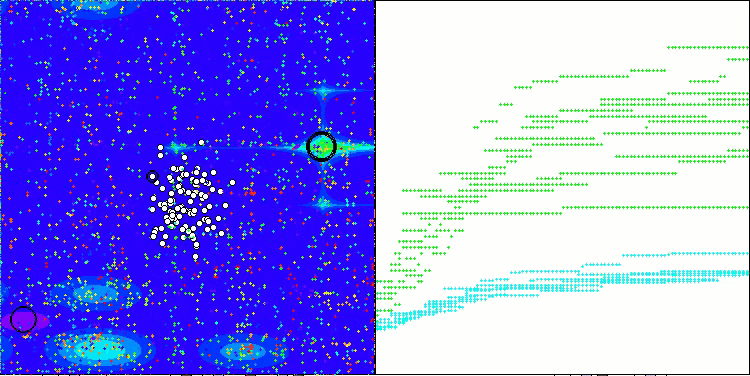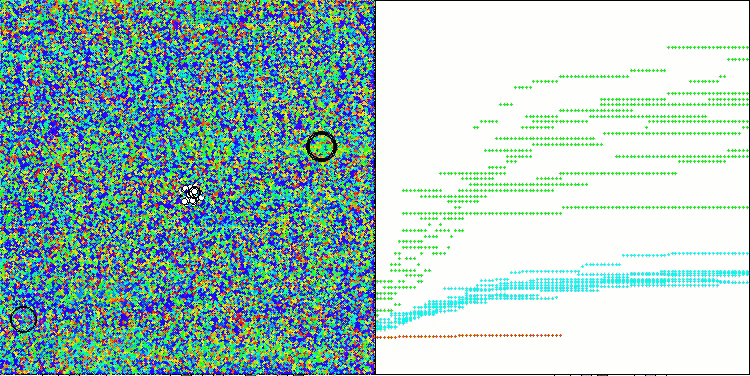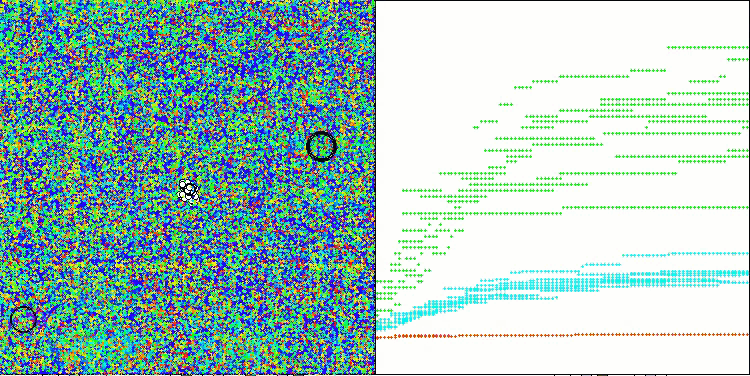
得られた結果は大幅に改善されました。以下は、単純なADAM集団アルゴリズムの可視化であり、探索空間を移動する個体の蛇のような特異な動きが四方に広がっている様子を示しています。また、確率的集団型ADAMmの可視化も示されており、探索エージェントが大域最適解に向かってより活発に移動している様子が確認できます。ただし、この場合は特徴的な蛇の形状は失われています。
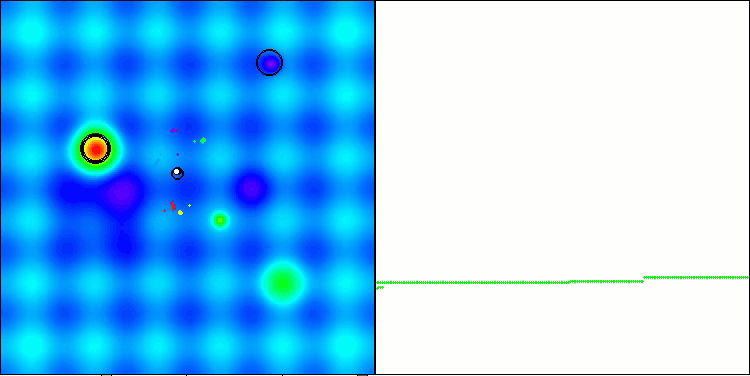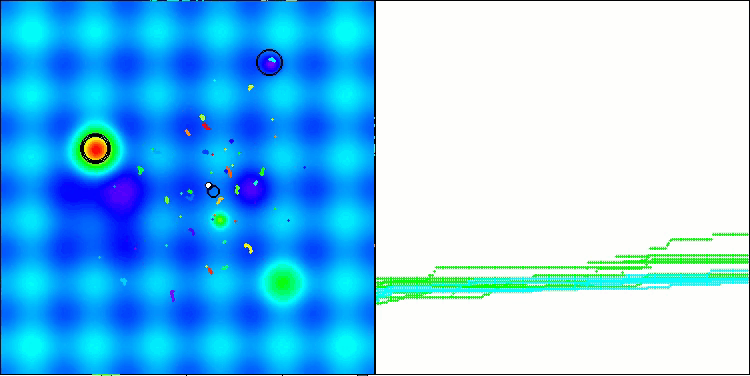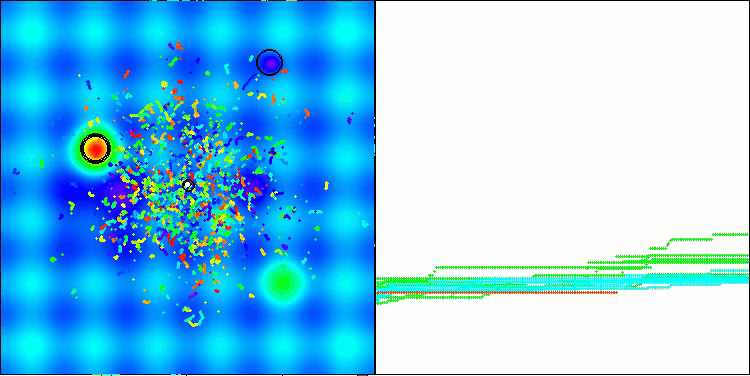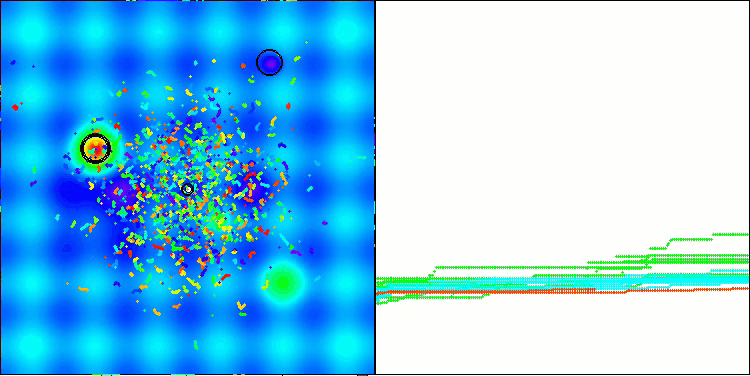
Hillyテスト関数のADAM
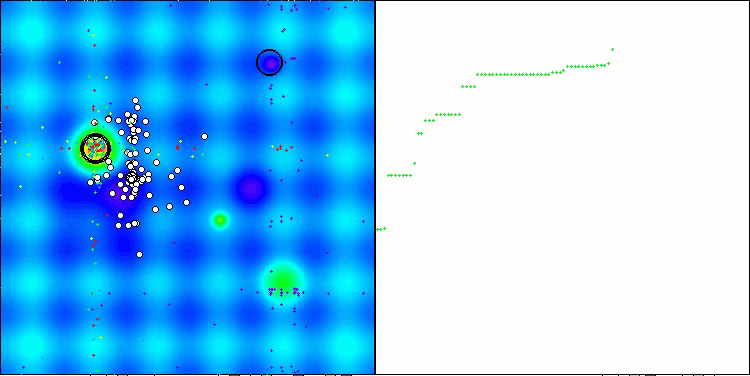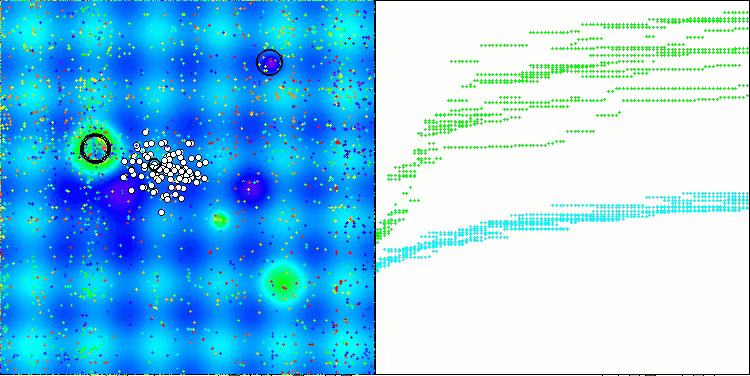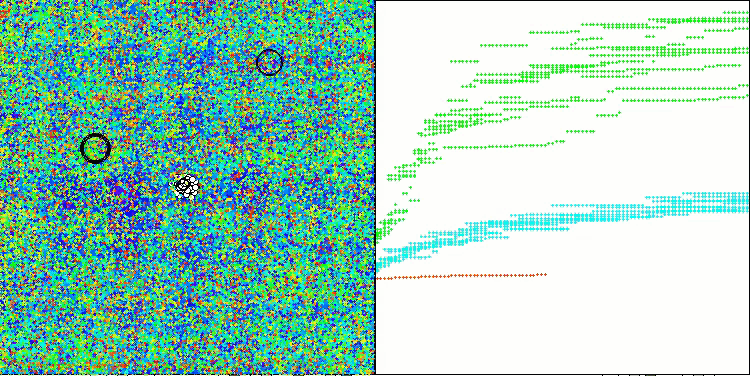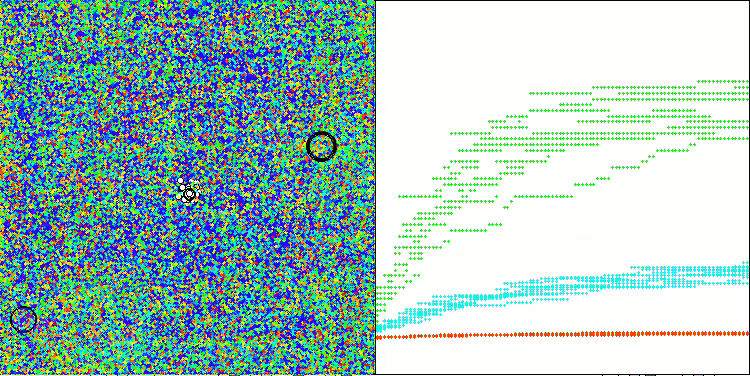
Hillyテスト関数のADAMm
Forestテスト関数のADAMm
Megacityテスト関数のADAMm
テスト結果に基づくと、確率的集団型ADAMはランキング表で32位にランクインしており、かなり良好な結果と言えます。元のバージョンは結果が振るわなかったため、ランキング表に含めることができませんでした。
| # | AO | 詳細 | Hilly | Hilly最終 | Forest | Forest最終 | Megacity(離散) | Megacity最終 | 最終結果 | MAXの% | ||||||
| 10p(5F) | 50p(25F) | 1000p(500F) | 10p(5F) | 50p(25F) | 1000p(500F) | 10p(5F) | 50p(25F) | 1000p(500F) | ||||||||
| 1 | ANS | across neighbourhood search | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | コードロックアルゴリズム(joo) | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | AMOm | 動物移動最適化m | 0.90358 | 0.84317 | 0.46284 | 2.20959 | 0.99001 | 0.92436 | 0.46598 | 2.38034 | 0.56769 | 0.59132 | 0.23773 | 1.39675 | 5.987 | 66.52 |
| 4 | (P+O)ES | (P+O)進化戦略 | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 5 | CTA | 彗星の尾アルゴリズム(joo) | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 6 | SDSm | 確率的拡散探索M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 7 | AAm | アーチェリーアルゴリズムM | 0.91744 | 0.70876 | 0.42160 | 2.04780 | 0.92527 | 0.75802 | 0.35328 | 2.03657 | 0.67385 | 0.55200 | 0.23738 | 1.46323 | 5.548 | 61.64 |
| 8 | ESG | 社会集団の進化(joo) | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 9 | SIA | 等方的焼きなまし(joo) | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 10 | ACS | 人工協調探索 | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 11 | ASO | 無政府社会最適化 | 0.84872 | 0.74646 | 0.31465 | 1.90983 | 0.96148 | 0.79150 | 0.23803 | 1.99101 | 0.57077 | 0.54062 | 0.16614 | 1.27752 | 5.178 | 57.54 |
| 12 | AOSm | 原子軌道探索M | 0.80232 | 0.70449 | 0.31021 | 1.81702 | 0.85660 | 0.69451 | 0.21996 | 1.77107 | 0.74615 | 0.52862 | 0.14358 | 1.41835 | 5.006 | 55.63 |
| 13 | TSEA | 亀甲進化アルゴリズム(joo) | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 14 | DE | 差分進化 | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 15 | CRO | 化学反応の最適化 | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 16 | BSA | 鳥群アルゴリズム | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 17 | HS | ハーモニー検索 | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 18 | SSG | 苗木の播種と育成 | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 19 | BCOm | 細菌走化性最適化M | 0.75953 | 0.62268 | 0.31483 | 1.69704 | 0.89378 | 0.61339 | 0.22542 | 1.73259 | 0.65385 | 0.42092 | 0.14435 | 1.21912 | 4.649 | 51.65 |
| 20 | ABO | アフリカ水牛の最適化 | 0.83337 | 0.62247 | 0.29964 | 1.75548 | 0.92170 | 0.58618 | 0.19723 | 1.70511 | 0.61000 | 0.43154 | 0.13225 | 1.17378 | 4.634 | 51.49 |
| 21 | (PO)ES | (PO)進化戦略 | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 22 | TSm | タブーサーチM | 0.87795 | 0.61431 | 0.29104 | 1.78330 | 0.92885 | 0.51844 | 0.19054 | 1.63783 | 0.61077 | 0.38215 | 0.12157 | 1.11449 | 4.536 | 50.40 |
| 23 | BSO | ブレインストーム最適化 | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 24 | WOAm | 鯨最適化アルゴリズムM | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 25 | AEFA | 人工電界アルゴリズム | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 26 | AEO | 人工生態系ベースの最適化アルゴリズム | 0.91380 | 0.46713 | 0.26470 | 1.64563 | 0.90223 | 0.43705 | 0.21400 | 1.55327 | 0.66154 | 0.30800 | 0.28563 | 1.25517 | 4.454 | 49.49 |
| 27 | ACOm | 蟻コロニー最適化M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 28 | BFO-GA | 細菌採食の最適化:Ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 29 | SOA | シンプル最適化アルゴリズム | 0.91520 | 0.46976 | 0.27089 | 1.65585 | 0.89675 | 0.37401 | 0.16984 | 1.44060 | 0.69538 | 0.28031 | 0.10852 | 1.08422 | 4.181 | 46.45 |
| 30 | ABHA | 人工蜂の巣アルゴリズム | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 31 | ACMO | 大気雲モデルの最適化 | 0.90321 | 0.48546 | 0.30403 | 1.69270 | 0.80268 | 0.37857 | 0.19178 | 1.37303 | 0.62308 | 0.24400 | 0.10795 | 0.97503 | 4.041 | 44.90 |
| 32 | アダム | 適応モーメント推定M | 0.88635 | 0.44766 | 0.26613 | 1.60014 | 0.84497 | 0.38493 | 0.16889 | 1.39880 | 0.66154 | 0.27046 | 0.10594 | 1.03794 | 4.037 | 44.85 |
| 33 | アシャ | 人工シャワーアルゴリズム | 0.89686 | 0.40433 | 0.25617 | 1.55737 | 0.80360 | 0.35526 | 0.19160 | 1.35046 | 0.47692 | 0.18123 | 0.09774 | 0.75589 | 3.664 | 40.71 |
| 34 | ASBO | 適応型社会行動最適化(ASBO) | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 35 | MEC | mind evolutionary computation | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 36 | IWO | 侵入雑草最適化 | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 37 | Micro-AIS | 微小人工免疫系 | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 38 | COAm | カッコウ最適化アルゴリズムM | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 39 | SDOm | 螺旋ダイナミクス最適化M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| 40 | NMm | ネルダー=ミード法M | 0.73807 | 0.50598 | 0.31342 | 1.55747 | 0.63674 | 0.28302 | 0.08221 | 1.00197 | 0.44667 | 0.18667 | 0.04028 | 0.67362 | 3.233 | 35.92 |
| 41 | FAm | ホタルアルゴリズムM | 0.58634 | 0.47228 | 0.32276 | 1.38138 | 0.68467 | 0.37439 | 0.10908 | 1.16814 | 0.28667 | 0.16467 | 0.04722 | 0.49855 | 3.048 | 33.87 |
| 42 | GSA | 重力探索法 | 0.64757 | 0.49197 | 0.30062 | 1.44016 | 0.53962 | 0.36353 | 0.09945 | 1.00260 | 0.32667 | 0.12200 | 0.01917 | 0.46783 | 2.911 | 32.34 |
| 43 | BFO | 細菌採餌最適化 | 0.61171 | 0.43270 | 0.31318 | 1.35759 | 0.54410 | 0.21511 | 0.05676 | 0.81597 | 0.42167 | 0.13800 | 0.03195 | 0.59162 | 2.765 | 30.72 |
| 44 | ABC | 人工蜂コロニー | 0.63377 | 0.42402 | 0.30892 | 1.36671 | 0.55103 | 0.21874 | 0.05623 | 0.82600 | 0.34000 | 0.14200 | 0.03102 | 0.51302 | 2.706 | 30.06 |
| 45 | BA | コウモリアルゴリズム | 0.59761 | 0.45911 | 0.35242 | 1.40915 | 0.40321 | 0.19313 | 0.07175 | 0.66810 | 0.21000 | 0.10100 | 0.03517 | 0.34617 | 2.423 | 26.93 |
まとめ
本稿では、従来ニューラルネットワークで用いられてきたよく知られた勾配法ADAMを、より一般的な最適化問題の解決に適応させる試みを紹介しました。この試みは成功しており、その結果得られた真に確率的な集団型ADAMmは、大域最適化問題における最強クラスのアルゴリズムと競合可能であることが示されました。本稿は、最適解探索問題に対する決定論的アプローチは、多次元探索空間では確率的手法ほど効果的でないことが多く、探索能力を拡張するには追加的なランダム要素が不可欠であることを示しています。
ただし、従来型のADAMのようなネットワーク統合型勾配法は、バックプロパゲーションで正確な勾配値を使用するため、ニューラルネットワークの学習において依然としてほぼ無敵の性能を発揮します。しかし、多くの機械学習論文の著者が指摘するように、誤差最小化関数以上に複雑な評価基準を用いたニューラルネットワークの学習では、勾配法が困難に直面し、局所最適解に陥ることがあります。
本稿で示したアプローチは、ニューラルネットワークにおける統合型手法の古典的な利用にも役立つ可能性があります。ニューロンの活性化関数の解析的形式を用いることで、高い精度と収束速度を維持しつつ、学習中のジャミングへの耐性を大幅に向上させることができます。これにより、学習時に非常に複雑な指標や評価基準を用いるタスクにおいても、古典的手法を活用できるようになります。本研究が、研究者や実務者に対して、一般的な最適化問題や機械学習手法を新しい視点から考えるきっかけとなることを願っています。
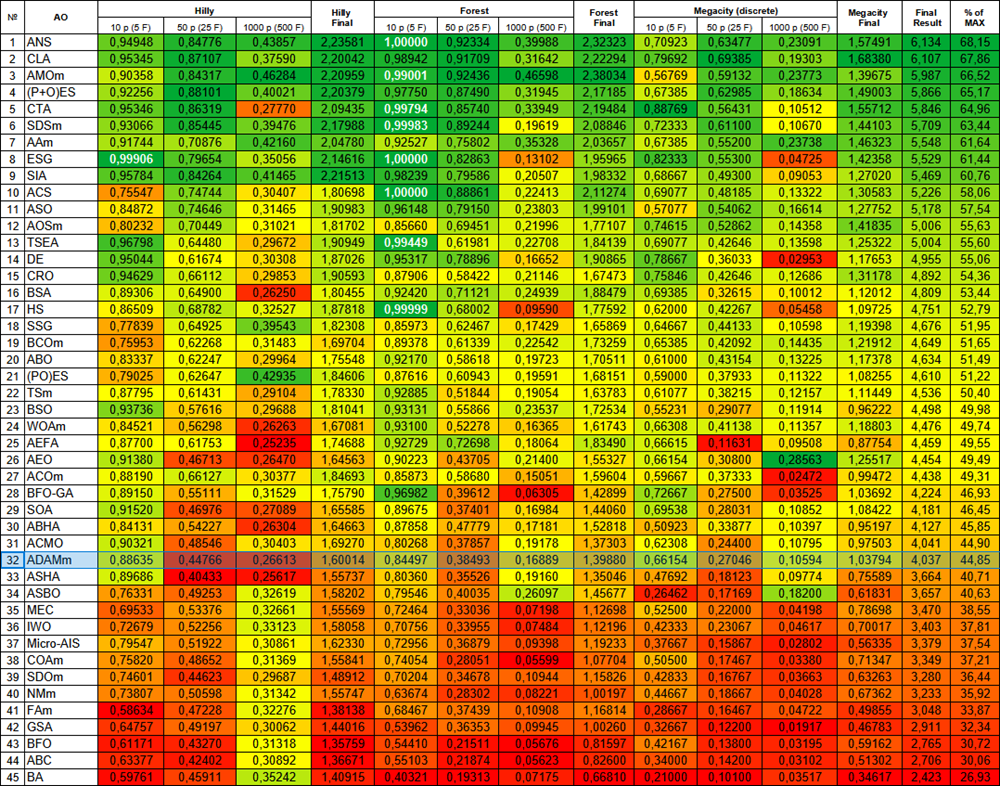
図1:関連するテスト結果に基づくアルゴリズムの色分け。0.99以上の結果は白色で強調表示されている
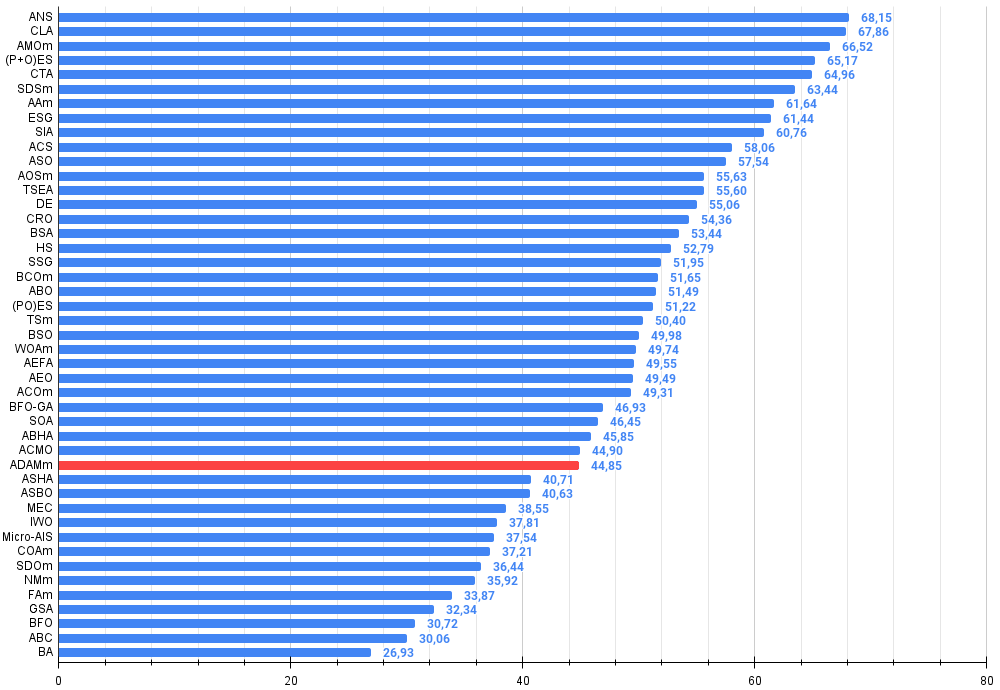
図2:アルゴリズムのテスト結果のヒストグラム(0から100までのスケールで、多ければ多いほど良い、
ここで、100は理論的に可能な最大の結果であり、アーカイブには評価表を計算するスクリプトが含まれている)
ADAMmの長所と短所
長所
- 低次元の問題で良好な結果が得られる
- 結果のばらつきが少ない
短所
- 外部パラメータが多い
この記事には、最新版のアルゴリズムコードを含むアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。
記事で使用されているプログラム
| # | 名前 | 種類 | 詳細 |
|---|---|---|---|
| 1 | #C_AO.mqh | インクルード | 集団最適化アルゴリズムの親クラス |
| 2 | #C_AO_enum.mqh | インクルード | 集団最適化アルゴリズムの列挙 |
| 3 | TestFunctions.mqh | インクルード | テスト関数のライブラリ |
| 4 | TestStandFunctions.mqh | インクルード | テストスタンド関数ライブラリ |
| 5 | Utilities.mqh | インクルード | 補助関数のライブラリ |
| 6 | CalculationTestResults.mqh | インクルード | 比較表の結果を計算するスクリプト |
| 7 | Testing AOs.mq5 | スクリプト | すべての集団最適化アルゴリズムの統一テストスタンド |
| 8 | Simple use of population optimization algorithms.mq5 | スクリプト | 可視化せずに集団最適化アルゴリズムを使用する簡単な例 |
| 9 | Test_AO_ADAM.mq5 | スクリプト | ADAMおよびADAMmテストスタンド |
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/16443
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。
この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。
 初級から中級まで:浮動小数点
初級から中級まで:浮動小数点
 汎用MLP近似器に基づくエキスパートアドバイザー
汎用MLP近似器に基づくエキスパートアドバイザー
 初級から中級まで:オーバーロード
初級から中級まで:オーバーロード
 外国為替におけるポートフォリオ最適化:VaRとマーコウィッツ理論の統合
外国為替におけるポートフォリオ最適化:VaRとマーコウィッツ理論の統合
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索