MetaTrader 5 / 例
English Русский 中文 Español Deutsch Português
preview
母集団最適化アルゴリズム：群鳥アルゴリズム(BSA)

母集団最適化アルゴリズム：群鳥アルゴリズム(BSA)

MetaTrader 5 — 例 | 30 8月 2024, 10:10
177 0
Andrey Dik
Andrey Dik

内容

1.  はじめに
2.  アルゴリズムの説明
3.  テスト結果


1. はじめに

鳥は自然や生態系の中で重要な位置を占める素晴らしい生き物です。鳥類は恐竜から進化したと考えられています。最も有名な例としては、約1億5000万年前に生息していた最古の鳥として知られる始祖鳥が挙げられます。数や行動の変化は、汚染、生息地の喪失、気候変動など、生態系における問題を示すことがあるため、鳥類はしばしば環境の健全性を示す指標として機能します。地球上で知られている鳥は10,000種以上あり、それぞれの鳥はその生活様式に独自の適応性を持っています。

ある鳥は長距離を飛ぶことができ、ある鳥は深海まで潜ることができ、またある鳥は驚くべき発声能力を持っています。鳥は生態系において重要な役割を果たしており、植物の種子を散布し、昆虫や他の動物の個体数を制御し、捕食者の食料源となります。多くの鳥は長距離の渡り鳥となり、群れで他の種と交流しながら一緒に生活し、餌や繁殖場所を求めて何千キロも一緒に移動します。この現象は、卓越したナビゲーション能力、持久力、グループ内での相互作用と協調性を浮き彫りにします。鳥類は私たちの地球にとって信じられないほど多様で重要な存在です。

群鳥アルゴリズム(Bird Swarm Algorithm: BSA)は、鳥の群れの社会的相互作用と行動に基づく群知能を利用した、バイオインスパイアされたエキサイティングな進化アルゴリズムです。2015年にMengらによって開発されたBSAは、鳥の行動の3つの重要な側面、すなわち飛行、採餌 、警戒を組み合わせた独自の最適化アプローチです。 それぞれ「鳥」が個別の戦術と戦略を持つ電子の群れの中で、アルゴリズムによる知性と創造性に満ちた、集団的相互作用のユニークなシステムが生まれます。ここで重要なのは、個体の努力だけでなく、最適化という共通の目標に向かって協力し、交流し、支え合う能力です。  

BSAの個人によって検索戦略は異なるかもしれません。鳥は飛行、警戒、採餌行動をランダムに切り替えることができます。バイオニックデザインアルゴリズムには、全体の適応度と個体の適応度に基づく採食が含まれます。鳥はまた、群れの中心に移動しようとしたり（これは他の鳥との競争につながる）、群れから離れようとしたりします。鳥の行動には、定期的な飛行や移動、生産者と乞食の役割の切り替えなどがあります。BSAの世界では、ある反復における各個体が独自の探索戦略を持つため、アルゴリズムが多面的になり、その力を発揮することができます。

しかし、多くの群知能アルゴリズムと同様に、BSAは早期収束に悩まされ、局所最適で立ち往生することがあります。群ベースの最適化アルゴリズムから高い精度でより速い収束を達成するために、搾取と探索のバランスをとる様々な手法が用いられてきました。

鳥の行動に基づくBSAアルゴリズムは、自然界における鳥の集団的な群れの相互作用に着想を得ており、その行動がこのアルゴリズムの基礎となっています。

  • 群れの行動： ムクドリ、ツバメ、ガンなど多くの鳥類は、一緒に飛ぶと群れ行動をとります。この行動は、移動中や採食中に空気抵抗を減らし、エネルギーを節約するのに役立ちます。
  • コミュニケーション： 鳥は鳴き声、身振り、姿勢など、さまざまな種類のコミュニケーションを使用して互いに意思疎通を図ります。これにより、彼らは行動を調整し、親類に危険を知らせ、餌を探す調整をすることができます。
  • 適応力： 鳥類は環境条件の変化に対して高度な適応力を持っています。危険や天候の変化、餌の有無に素早く対応し、状況に応じて行動や移動ルートを変えることができます。
  • リードとフォロー：鳥の群れには通常、飛ぶ方向を決めるリーダーがおり、他の鳥はリーダーに従います。これは、BSAアルゴリズムでも最適解を効果的に見つけるために考慮されている、先行と後続の原理を示しています。

BSAアルゴリズムは、このような鳥の行動原理を利用して、鳥の群れの集団行動をシミュレートし、様々な最適化問題を解く効率的な最適化手法を開発しました。BSAは単なるアルゴリズムではなく、鳥の社会的相互作用が複雑な問題を効率的に解決するためのインスピレーションの源となる、最適化の世界への魅力的な旅なのです。


2. アルゴリズム

BSAアルゴリズムのロジックをより詳しく見ていきましょう。一見、複雑でわかりにくいかもしれません。コードの実装を始める前に、実装の基礎となるアルゴリズムの擬似コードを作成しましょう。これによって、BSAの仕組みをより理解しやすくなるでしょう。

以下は、鳥の群れの行動をモデル化したアルゴリズムの高レベル記述である群鳥アルゴリズム(BSA)擬似コードです。

1. N個の解と関連パラメータの初期化
2. 新しい解を生み出す：
3. もし鳥が飛んでいたら：
    4. もし鳥が生産者なら：
        5. 新たな食料源を求めて
    6. その他の場合：
        7. 乞食鳥は生産者の後を追う
8. その他の場合：
    9. 鳥が食べている場合：
        10. 鳥が摂食している
    11. その他の場合：
        12. 鳥は用心深いままでいる
13. 新しい解の評価
14. 解の更新
15. 停止基準に達した場合：
    16. アルゴリズムの完成
17. その他の場合：
    18. ステップ2に戻る


以下は、新しい餌場を探す鳥の方程式です(5)。

 xn = RNDg (min, max, producerPower)

ここで

  • xn：新しい座標値
  • RNDg：現在の座標を分布の中心とする正規分布の乱数
  • minとmax：分配の境界
  • producerPower：生産者の標準偏差

この式によれば、繁殖期の鳥は探索空間のあらゆる方向に移動することができ、現在位置の近辺では確率が高くなります。そのため、鳥たちは餌を求めて新しい場所を探索することができます。

以下は、生産者を追う乞食鳥の方程式です(7)。

xn = x + (xK - x) * FL * RNDg (-1.0, 1.0, scroungerPower)

ここで

  • xn：新しい座標値
  • X：履歴における乞食の最良の座標
  • xK：履歴における生産者の最良の座標（母集団における位置Kを持つランダムな鳥が生産者として選ばれる）
  • RNDg：分布の中心を0、境界を「-1.0」と「 1.0」とする正規分布の乱数
  • scroungerPower：乞食の標準偏差

この方程式は、乞食鳥はその最良の座標と、群れの中で最も優れた個体の最良の座標によって導かれることを示しています（生産者はその最良の座標ではなく、現在の座標によって導かれる）。これは、群れの中でリーダーに従うという行動のモデルです。

以下は、飛行中以外の摂食期間中の鳥に適用される式です(10)。

xn = x + (p - x) * C * r1 + (g - x) * S * r2

ここで

  • xn：新しい座標値
  • x：現在の座標
  • p：履歴における鳥が餌を取る最良の座標
  • g：履歴における最良の母集団座標（最適大域解）
  • r1：[0.0 ...1.0]の範囲の一様乱数
  • r2：[0.0 ...1.0]の範囲の一様乱数
  • C：認知比率、外部パラメータ
  • S：社会的比率、外部パラメータ

この方程式は、鳥の行動が鳥自身の経験（現在の位置と過去の最良の位置）と群れの経験に基づく、餌を摂取する瞬間を記述しています。

以下は、警戒している鳥の方程式です(12）。

xn = x + A1 * (mean [c] - x) * r1 + A2 * (xK - x) * r2

ここで

  • xn：新しい座標値
  • X：履歴における最良の警戒している鳥の座標
  • r1：[0.0 ...1.0]の範囲の一様乱数
  • r2：[-1.0 ...1.0]の範囲の一様乱数
  • mean [c]：群れ内の全ての鳥の最良座標に基づく、c番目の座標の平均値

A1：群れの中心の平均座標の影響の補正比率

A1 = a1 * exp (-pFit * N / (sumFit + e)) 

ここで

  • a1：比率、外部パラメータ
  • e：DBL_MIN（0による除算を避けるため）
  • pFit：警戒している鳥の最良適応度
  • sumFit：群れの鳥の最良適応度
  • N：群れの鳥の数

A2：観察のために選択された鳥（警戒している鳥の視野に入った）の位置が、警戒している鳥の行動に与える影響を考慮した補正率。以下は、A2の方程式です。

A2 = a2 * exp (((pFit - pFitK) / (|pFitK - pFit| + e))* (N * pFitK / (sumFit + e)))

ここで

  • a2：レシオ、外部パラメータ
  • e：DBL_MIN（0による除算を避けるため）
  • pFit：警戒している鳥の最良適応度
  • pFitK：集団から無作為に選んだK番目の鳥（警戒している鳥の視野に入ってきた鳥）の最良適応度
  • sumFit：群れの鳥の最良適応度
  • N：群れの鳥の数

このように、警戒している鳥は周囲を監視しているため、身内に危険をタイムリーに知らせることができます。これはアルゴリズムで説明されている中で最も複雑な行動であり、集団内のすべての鳥の適応度、警戒している鳥自身と観察のために選ばれた鳥の適応度を考慮に入れています。要するに、警戒している鳥は、視野に入ってくる相手の位置がわかれば、個体群全体の適応度の方向に動くということです。

擬似コード中のハイライトされたテキストは、図1に示されたBSAロジック要素に対応します。

BSA

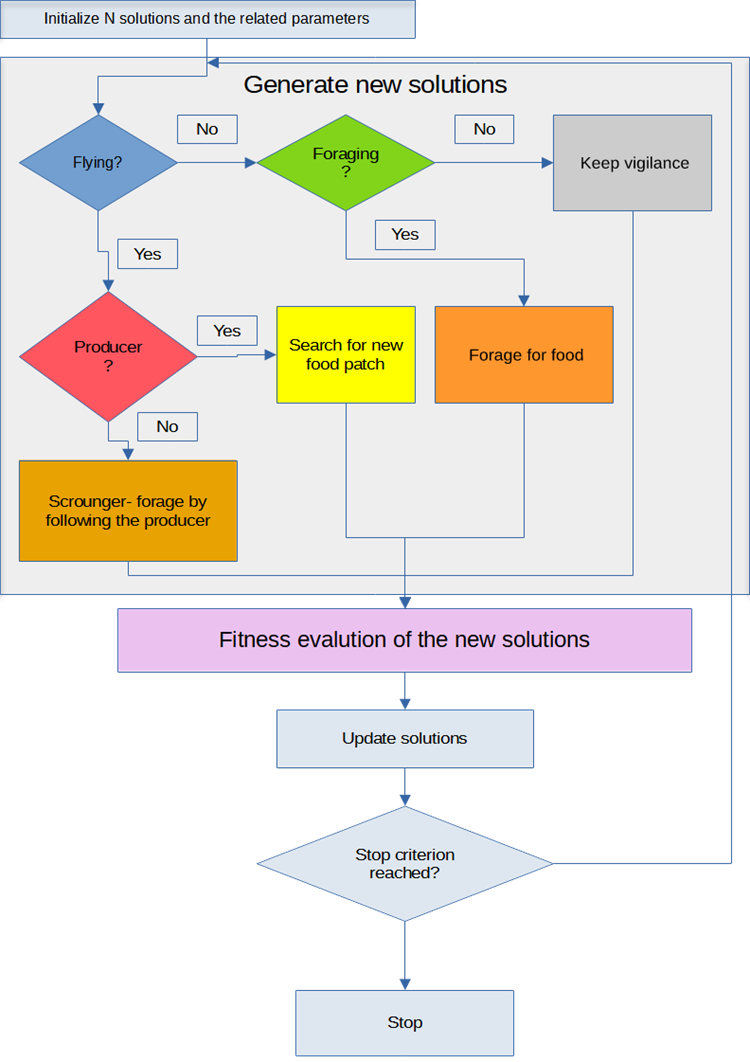
図1：BSAアルゴリズム論理図

図1の図は、BSAアルゴリズムを可視化したもので、鳥の群れの行動をモデル化しています。以下は、アルゴリズムの主な特徴です。

  1. 解の初期化：アルゴリズムは、解とそれに関連するパラメータのセットを初期化することから始まります。これは、探索空間における鳥（または解）の初期分布に関係します。
  2. 飛行行動：アルゴリズムの作動中、各鳥は「飛ぶ」ことも「飛ばない」こともできます。この状態は、鳥の新しい解決策を発見する能力に影響を与えます。 
  3. 採食行動：鳥が「飛んでいる」場合は、「生産者」になって餌のある新しい場所を探し始めることもできるし、「乞食」になって生産者の後を追うこともできます。
  4. 採食行動：鳥が「飛んでいない」場合は、摂食しているか、警戒を続けているかのどちらかです。これは予期している状態、あるいは環境を観察している状態を表しているのかもしれません。
  5. 評価と解の更新：新しい解を生成した後、その適応度や品質が評価されます。
  6. 停止基準：アルゴリズムは、ある停止基準に達するまで、解の生成と更新のサイクルを続けます。これは、一定の反復回数であったり、一定レベルの解の質を達成することであったり、あるいは別の基準であったりします。

BSAは最適解を探索する過程で適応し進化する動的アルゴリズムであることを強調したいとおもいます。

BSAアルゴリズムのコードを実装してみましょう。各エージェントについてS_BSA_Agent構造体を定義します。これは、最適化問題の個別の解となり、群れの中の鳥の記述となります。

この構造体には以下のフィールドが含まれます。

  • cBest[]：最良のエージェント座標を格納する配列
  • fBest：最良のエージェント適応度スコアを格納する変数
  • Init - 構造体フィールドを初期化するS_BSA_Agent構造体メソッド。ArrayResize関数を使用してcBest配列のサイズを変更するために使用されるcoords整数引数を取ります。

変数fBestの初期値を、可能な限り最小のdouble値、つまり最悪適応度に設定します。

//——————————————————————————————————————————————————————————————————————————————
struct S_BSA_Agent
{
    double cBest []; //best coordinates
    double fBest;    //best fitness

    void Init (int coords)
    {
      ArrayResize (cBest, coords);
      fBest = -DBL_MAX;
    }
};
//——————————————————————————————————————————————————————————————————————————————

BSAアルゴリズムのC_AO_BSAクラスを定義しましょう。このクラスはC_AO集団アルゴリズムの基本クラスを継承し、以下のフィールドとメソッドを含んでいます。

1. publicフィールド

  • ao_name：最適化アルゴリズム名
  • ao_desc：最適化アルゴリズムの説明
  • popSize：母集団のサイズ
  • params：アルゴリズムのパラメータの配列
  • flyingProb：飛行確率
  • producerProb：生産確率
  • foragingProb：採餌確率
  • a1：a1定数 [0...2]
  • a2：a2定数 [0...2]
  • C：認知的比率
  • S：社会的比率
  • FL：FL定数 [0...2]
  • producerPower：生産者の行動における標準偏差
  • scroungerPower：乞食の行動における標準偏差

2. オプション

  • C_AO_BSA：クラスフィールドを初期化するクラスコンストラクタ
  • SetParams：アルゴリズムのパラメータを設定するメソッド
  • Init：アルゴリズムを初期化するメソッド（最小検索範囲と最大検索範囲、検索ステップ、エポック数を受ける）
  • Moving：エージェントを移動させるメソッド
  • Revision：エージェントの改訂メソッド

//——————————————————————————————————————————————————————————————————————————————
class C_AO_BSA : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_BSA () { }
  C_AO_BSA ()
  {
    ao_name = "BSA";
    ao_desc = "Bird Swarm Algorithm";

    popSize        = 20;  //population size

    flyingProb     = 0.8;  //Flight probability
    producerProb   = 0.25; //Producer probability
    foragingProb   = 0.55; //Foraging probability
    a1             = 0.6;  //a1 constant [0...2]
    a2             = 0.05; //a2 constant [0...2]
    C              = 0.05; //Cognitive coefficient
    S              = 1.1;  //Social coefficient
    FL             = 1.75; //FL constant [0...2]
    producerPower  = 7.05; //Producer power
    scroungerPower = 2.60; //Scrounger power

    ArrayResize (params, 11);

    params [0].name = "popSize";         params [0].val  = popSize;

    params [1].name  = "flyingProb";     params [1].val  = flyingProb;
    params [2].name  = "producerProb";   params [2].val  = producerProb;
    params [3].name  = "foragingProb";   params [3].val  = foragingProb;
    params [4].name  = "a1";             params [4].val  = a1;
    params [5].name  = "a2";             params [5].val  = a2;
    params [6].name  = "C";              params [6].val  = C;
    params [7].name  = "S";              params [7].val  = S;
    params [8].name  = "FL";             params [8].val  = FL;
    params [9].name  = "producerPower";  params [9].val  = producerPower;
    params [10].name = "scroungerPower"; params [10].val = scroungerPower;
  }

  void SetParams ()
  {
    popSize        = (int)params [0].val;

    flyingProb     = params [1].val;
    producerProb   = params [2].val;
    foragingProb   = params [3].val;
    a1             = params [4].val;
    a2             = params [5].val;
    C              = params [6].val;
    S              = params [7].val;
    FL             = params [8].val;
    producerPower  = params [9].val;
    scroungerPower = params [10].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();
  void Injection (const int popPos, const int coordPos, const double value);

  //----------------------------------------------------------------------------
  double flyingProb;      //Flight probability
  double producerProb;    //Producer probability
  double foragingProb;    //Foraging probability
  double a1;              //a1 constant [0...2]
  double a2;              //a2 constant [0...2]
  double C;               //Cognitive coefficient
  double S;               //Social coefficient
  double FL;              //FL constant [0...2]
  double producerPower;   //Producer power
  double scroungerPower;  //Scrounger power

  S_BSA_Agent agent [];


  private: //-------------------------------------------------------------------
  double mean [];  //represents the element of the average position of the whole bird’s swarm
  double N;
  double e;        //epsilon

  void BirdProducer  (int pos);
  void BirdScrounger (int pos);
  void BirdForaging  (int pos);
  void BirdVigilance (int pos);
};
//——————————————————————————————————————————————————————————————————————————————

C_AO_BSAクラスのInitメソッドは、渡されたパラメータに基づいてクラス変数を初期化するために使用されます。このメソッドは、StandardInitメソッドを使用して標準的な初期化をおこない、最小検索範囲と最大検索範囲、検索ステップを受け取ります。

標準的な初期化が成功すれば、メソッドは変数Nとeの初期化を続けます。Nの値はpopSize母集団サイズに設定されます。eは最小のdouble値で初期化されたイプシロンです。

このメソッドは、agent配列をpopSizeのサイズにリサイズします。Initメソッドは、agentの各要素に対してcoordsパラメータを指定して呼び出されます。mean配列のサイズもcoordsのサイズに変更されます。この配列は、鳥の平均個体数座標を格納するために使用されます。

このメソッドは、初期化に成功すればtrueを返し、そうでなければfalseを返します。

このメソッドは、与えられたパラメータでBSA最適化アルゴリズムの初期設定をおこない、最適化を実行する準備をします。

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_BSA::Init (const double &rangeMinP  [], //minimum search range
                     const double &rangeMaxP  [], //maximum search range
                     const double &rangeStepP [], //step search
                     const int     epochsP = 0)  //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (agent, popSize);
  for (int i = 0; i < popSize; i++) agent [i].Init (coords);

  ArrayResize (mean, coords);

  N = popSize;
  e = DBL_MIN;

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_BSAクラスのMovingメソッドは、最適化中にエージェントを移動させるために使用されます。このメソッドは次をおこないます。

  • revisionがfalseの場合、エージェントの座標a[i].c[c]は、指定された範囲のランダムな値で初期化される。その後revisionフラグがtrueにセットされ、メソッドは終了します。
  • revisionがfalseでなければ、方程式と確率を用いて各エージェントの新しい座標が計算されます。

2回目以降のエポックでは、このメソッドは、満たされた確率に応じて群れの各鳥の行動を決定する関数を呼び出します。 

  • 飛ぶ確率(flyingProb)を満たせば、エージェントは「飛びます」。この場合、2つの動作オプションが考えられます。

  1. 確率がproducerProbより小さければ、エージェントは「生産者」であり、新しい食事場所を探しています。
  2. そうでなければ、エージェントは「乞食」となり、「生産者」に従うことになります。
  • もし「飛ばない」のであれば、以下の2つの動作オプションが考えられます。
  1. 確率がforagingProbより小さければ、エージェントは食物を「採集」します。 
  2. そうでなければ、エージェントは「警戒」状態にあります。

このメソッドは、BSA最適化アルゴリズムにおいて、現在のエポック、ランダム値、確率に従ってエージェントの座標を更新する役割を担います。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BSA::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    //bird is flying------------------------------------------------------------
    if (u.RNDprobab () < flyingProb)
    {
      //bird producer
      if (u.RNDprobab () < producerProb) BirdProducer  (i); //bird is looking for a new place to eat
      //bird is not a producer
      else                               BirdScrounger (i); //scrounger follows the  producer
    }
    //bird is not flying--------------------------------------------------------
    else
    {
      //bird foraging
      if (u.RNDprobab () < foragingProb) BirdForaging  (i); //bird feeds
      //bird is not foraging
      else                               BirdVigilance (i); //bird vigilance
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_BSAクラスのBirdProducerメソッドは、BSAアルゴリズムにおける「生産者」の振る舞いをシミュレートするために使用されます。このメソッドは次をおこないます。

  • 鳥の現在位置を格納するために使用されるx変数を初期化します。
  • 各エージェント座標に対して以下のアクションが実行されます。
    • x値は現在のエージェント座標に設定される
    • x値はガウス分布を使用して更新され、平均値は現在の座標、範囲と標準偏差は rangeMin、rangeMax、producerPower値によって決定される
    • エージェント座標の新しい値は、探索範囲とステップに従ってx値を調整するSeInDiSpメソッドを使用して設定される

このメソッドは、BSAアルゴリズムにおける「生産者」の行動をモデル化したもので、この「生産者」は、ガウス分布を使用して探索空間を探索し、新しい食物源の位置（すなわち新しい潜在的解）を探索します。

//——————————————————————————————————————————————————————————————————————————————
void  C_AO_BSA::BirdProducer  (int pos)
{
  double x = 0.0; //bird position

  for (int c = 0; c < coords; c++)
  {
    x = a [pos].c [c];
    x = u.GaussDistribution (x, rangeMin [c], rangeMax [c], producerPower);

    a [pos].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}
//——————————————————————————————————————————————————————————————————————————————

「乞食」の行動をモデル化したメソッドは、C_AO_BSAクラスのBirdScrounger関数です。これは以下の動作をおこないます。

  • 1. K、 x、 xK変数を初期化：Kは群れの中で無作為に選ばれた鳥の位置、xはその鳥の最良の位置、xKは群れの中で無作為に選ばれた鳥の現在の最良の位置です。
  • 2. すべての座標をループする：
    • 現在の鳥ではないランダムな鳥を選択する
    • 現在の鳥とランダムに選ばれた鳥の最良の位置に基づいてxとxKを更新する
    • ガウス分布を使用してxを更新する
    • 最後に、SeInDiSpメソッドを使用して鳥の現在位置を更新し、検索範囲とステップに従ってx値を調整する

このメソッドは、BSAアルゴリズムにおける 「乞食」の振る舞いを、「生産者」に追従する（すなわち、生産者の位置に対して自身の位置を調整する）ガウス分布を使用してモデル化します。

//——————————————————————————————————————————————————————————————————————————————
void  C_AO_BSA::BirdScrounger (int pos)
{
  int    K  = 0;   //position of a randomly selected bird in a swarm
  double x  = 0.0; //best bird position
  double xK = 0.0; //current best position of a randomly selected bird in a swarm

  for (int c = 0; c < coords; c++)
  {
    do K = u.RNDminusOne (popSize);
    while (K == pos);

    x  = agent [pos].cBest [c];
    xK = agent   [K].cBest [c];

    x = x + (xK - x) * FL * u.GaussDistribution (0, -1.0, 1.0, scroungerPower);

    a [pos].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_BSAクラスのBirdForagingメソッドは、現在飛んでおらず、食事に忙しい鳥のためのものです。このメソッドは、すべての座標に対してループの中で次のことをおこないます。

  • 鳥の現在位置、最良の位置、最良の位置に基づいて、x、p、gを更新する
  • 2つの乱数r1とr2を生成する
  • これらの乱数と定数CとSを使用してxを更新する
  • SeInDiSp関数を使用して、得られた鳥の位置を調整する
//——————————————————————————————————————————————————————————————————————————————
void  C_AO_BSA::BirdForaging  (int pos)
{
  double x  = 0.0; //current bird position
  double p  = 0.0; //best bird position
  double g  = 0.0; //best global position
  double r1 = 0.0; //uniform random number [0.0 ... 1.0]
  double r2 = 0.0; //uniform random number [0.0 ... 1.0]

  for (int c = 0; c < coords; c++)
  {
    x = a     [pos].c     [c];
    p = agent [pos].cBest [c];
    g = cB                [c];

    r1 = u.RNDprobab ();
    r2 = u.RNDprobab ();

    x = x + (p - x) * C * r1 + (g - x) * S * r2;

    a [pos].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}
//——————————————————————————————————————————————————————————————————————————————

警戒している鳥の行動をシミュレートする、最新かつ最も複雑なメソッドがBirdVigilanceです。これは以下の動作をおこないます。

  • 群れ内の全ての鳥の最良適応度値の合計を計算します。
  • 群れ内のすべての鳥の各座標の平均値を計算します。
  • 現在の鳥ではないランダムな鳥を選択します。
  • 現在の鳥とランダムに選ばれた鳥の最良適応度値に基づいて、pFitとpFitKを更新します。
  • pFit、pFitK、N、sumFit、eに依存する指数関数を用いてA1とA2を計算します。
  • すべての座標をループします。 
    • 2つの乱数r1とr2を生成する
    • 現在の鳥とランダムに選ばれた鳥の最良の位置に基づいてxとxKを更新する
    • A1、A2、r1、r2を使用してxを更新する
    • SeInDiSp関数を使用して現在の鳥の位置を調整する
//——————————————————————————————————————————————————————————————————————————————
void  C_AO_BSA::BirdVigilance (int pos)
{
  int    K      = 0;   //position of a randomly selected bird in a swarm
  double sumFit = 0.0; //best birds fitness sum
  double pFitK  = 0.0; //best fitness of a randomly selected bird
  double pFit   = 0.0; //best bird fitness
  double A1     = 0.0;
  double A2     = 0.0;
  double r1     = 0.0; //uniform random number [ 0.0 ... 1.0]
  double r2     = 0.0; //uniform random number [-1.0 ... 1.0]
  double x      = 0.0; //best bird position
  double xK     = 0.0; //best position of a randomly selected bird in a swarm

  ArrayInitialize (mean, 0.0);

  for (int i = 0; i < popSize; i++) sumFit += agent [i].fBest;

  for (int c = 0; c < coords; c++)
  {
    for (int i = 0; i < popSize; i++) mean [c] += a [i].c [c];

    mean [c] /= popSize;
  }

  do K = u.RNDminusOne (popSize);
  while (K == pos);

  pFit  = agent [pos].fBest;
  pFitK = agent   [K].fBest;

  A1 = a1 * exp (-pFit * N / (sumFit + e));
  A2 = a2 * exp (((pFit - pFitK) / (fabs (pFitK - pFit) + e)) * (N * pFitK / (sumFit + e)));

  for (int c = 0; c < coords; c++)
  {
    r1 = u.RNDprobab ();
    r2 = u.RNDfromCI (-1, 1);

    x  = agent [pos].cBest [c];
    xK = agent   [K].cBest [c];

    x = x + A1 * (mean [c] - x) * r1 + A2 * (xK - x) * r2;

    a [pos].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_BSAクラスのRevisionメソッドは、最適な大域解を更新し、エージェントの最適な位置を更新するために使用されます。このメソッドは次をおこないます。

  • 大域解を更新します。
  • 前回の最良適応度関数値とエージェント座標を更新します。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BSA::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB) ind = i;
  }

  if (ind != -1)
  {
    fB = a [ind].f;
    ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > agent [i].fBest)
    {
      agent [i].fBest = a [i].f;
      ArrayCopy (agent [i].cBest, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————


3. テスト結果

BSAアルゴリズムの様々な関数集合に対する結果について、もう少し詳しく述べたいと思います。すべてのテスト関数における総合BSAスコアは4.80947で、これは最大可能スコアの53.44%に相当します。この結果は、アルゴリズムの全体的な効率を示しています。群鳥アルゴリズムは、さまざまな関数に関する最適化問題をうまく解決できる可能性を秘めています。

BSA|Bird Swarm Algorithm|20.0|0.8|0.25|0.55|0.6|0.05|0.05|1.1|1.75|7.05|2.6|
=============================
5 Hilly's; Func runs:10000; result:0.8930600046782612
25 Hilly's; Func runs:10000; result:0.6489975525320968
500 Hilly's; Func runs:10000; result:0.262496551797822
=============================
5 Forest's; Func runs:10000; result:0.9241962617798402
25 Forest's; Func runs:10000; result:0.7112057472851052
500 Forest's; Func runs:10000; result:0.24938963509983267
=============================
5 Megacity's; Func runs:10000; result:0.6938461538461538
25 Megacity's; Func runs:10000; result:0.3261538461538461
500 Megacity's; Func runs:10000; result:0.1001230769230778
=============================
All score:4.80947 (53.44%)

アルゴリズムの動作を可視化すると、さまざまなテスト関数にわたって結果が大きく広がっていることがわかります。局所的な表面領域の探索に成功しても、アルゴリズムは局所的な罠にはまるという問題に遭遇することがあります。このため、大域的最適解を達成する能力が制限され、最適解探索の安定性を欠く可能性があります。

Skinテスト関数の可視化は、アルゴリズム操作の一例であり、評価表の作成には関与しません。

Hilly

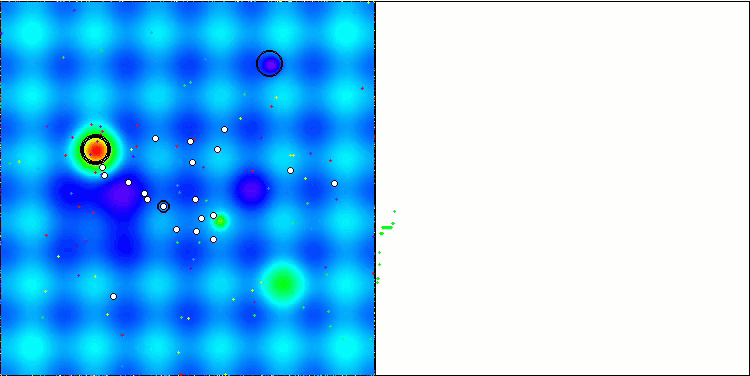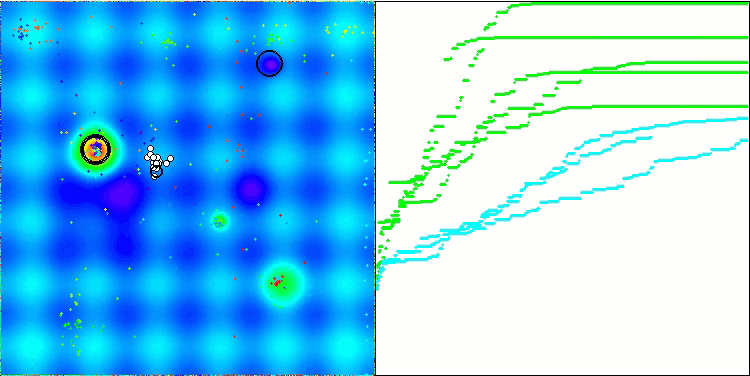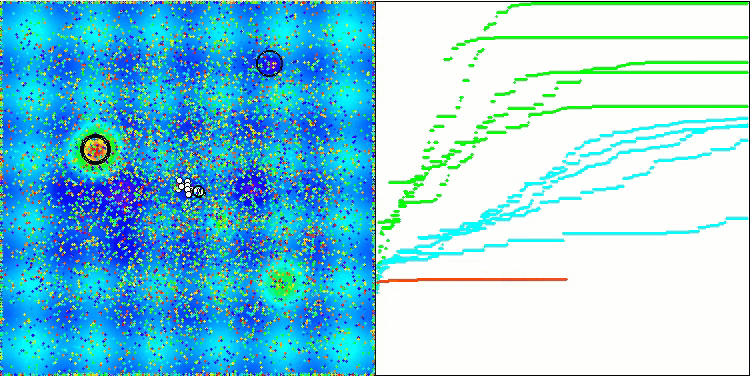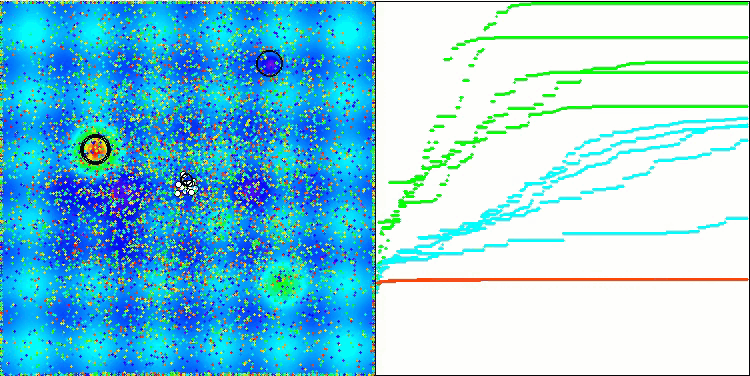
  Hillyテスト関数のBSA

Forest

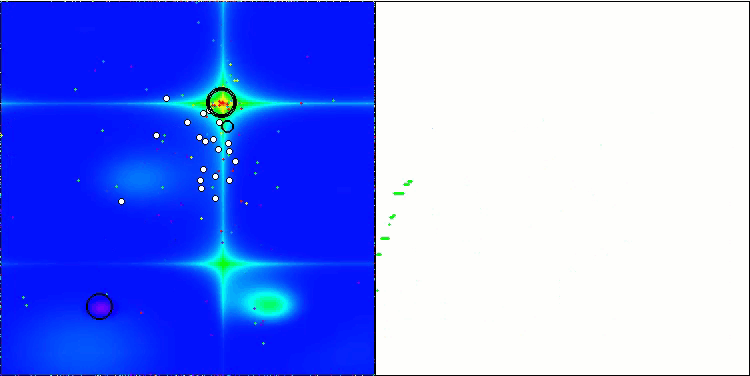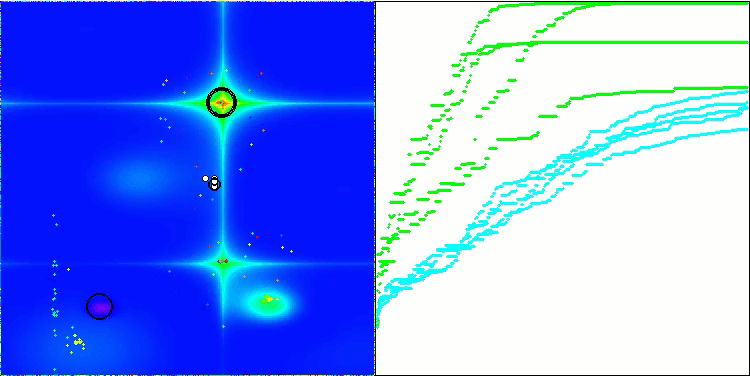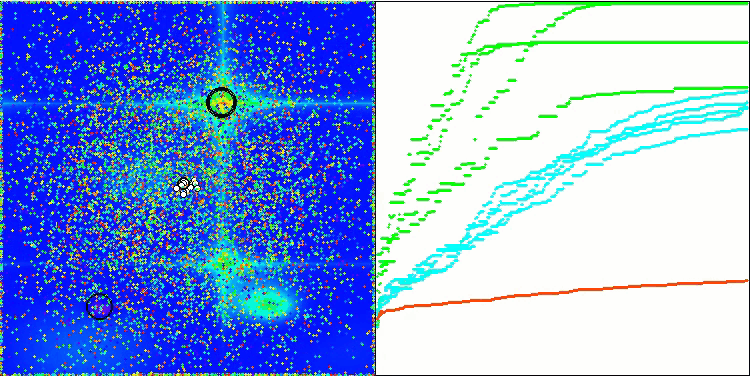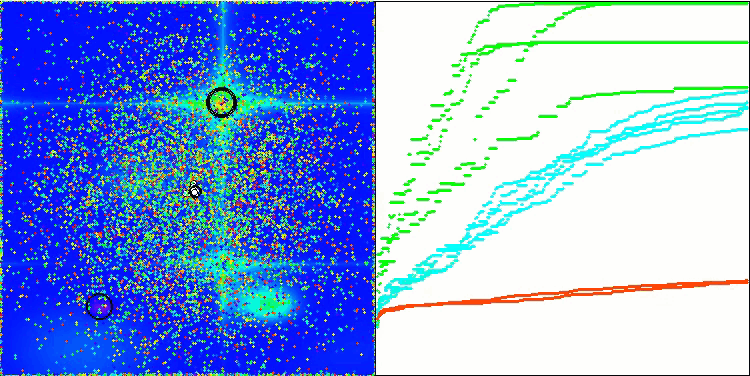
   Forestテスト関数のBSA

Megacity

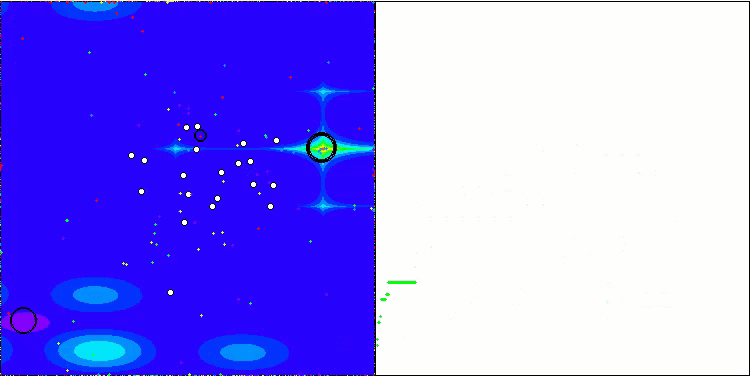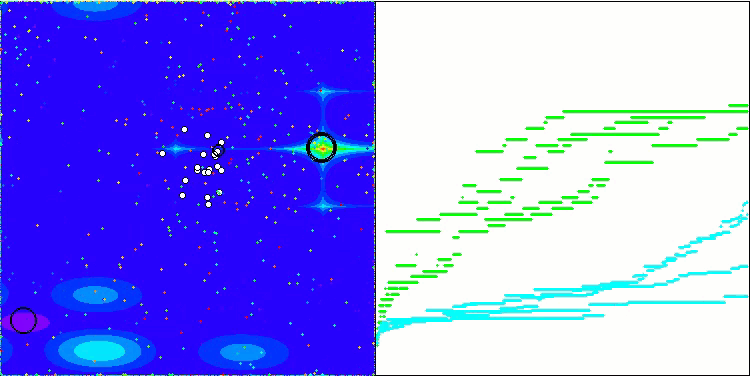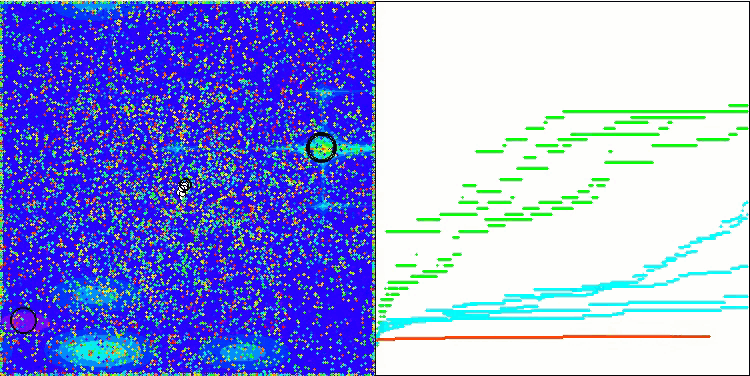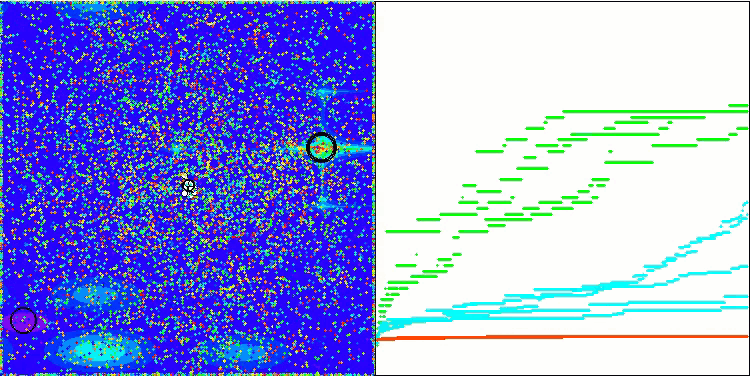
Megacityテスト関数のBSA

Skin

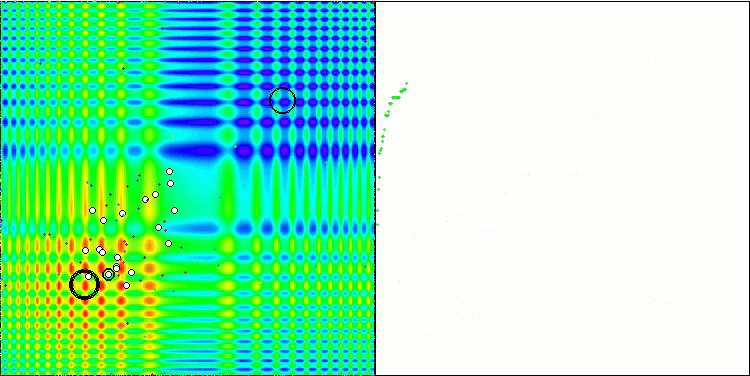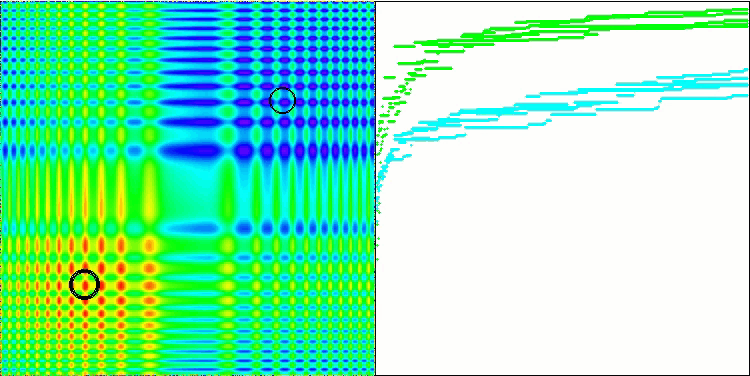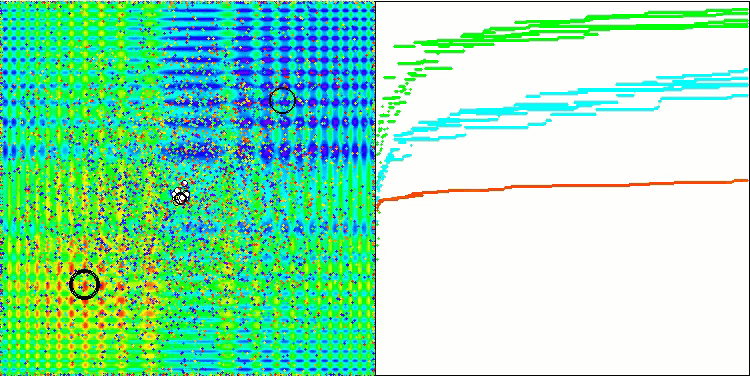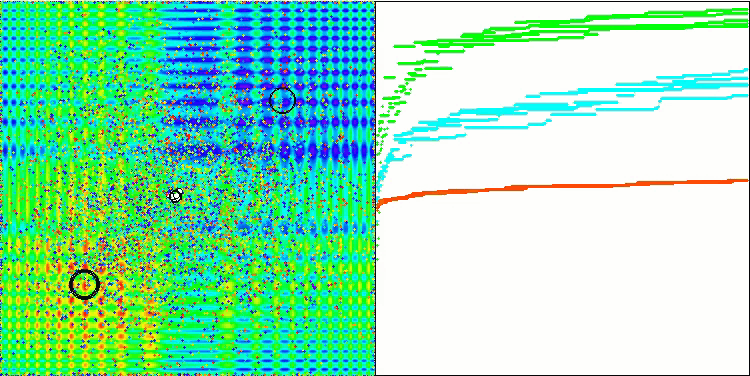
Skinテスト関数のBSA

重要なことは、変数の数が多い滑らかなHillyテスト関数では、このアルゴリズムは、検討したすべてのアルゴリズムの中で、評価表で最低の結果を示し、極めて非効率的であることが判明したことです。高次元のForestおよび離散Megacity関数では、BSAは、表の上位に位置するものも含め、他のアルゴリズムと比較しても、まずまずの結果を示しています。

# AO 詳細 Hilly Hilly最終 Forest Forest最終 Megacity（離散） Megacity最終 最終結果 MAXの%
10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F)
1 BGA バイナリ遺伝的アルゴリズム 0.99992 0.99484 0.50483 2.49959 1.00000 0.99975 0.32054 2.32029 0.90667 0.96400 0.23035 2.10102 6.921 76.90
2 (P+O)ES (P+O）進化戦略 0.99934 0.91895 0.56297 2.48127 1.00000 0.93522 0.39179 2.32701 0.83167 0.64433 0.21155 1.68755 6.496 72.18
3 SDSm 確率的拡散探索M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
4 ESG 社会集団の進化 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
5 SIA 等方的焼きなまし 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
6 DE 差分進化 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
7 BSA 鳥群アルゴリズム 0.90857 0.73661 0.25767 1.90285 0.90437 0.81619 0.16401 1.88457 0.61692 0.54154 0.10951 1.26797 5.055 56.17
8 HS ハーモニー検索 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
9 SSG 苗木の播種と育成 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
10 (PO)ES (PO）進化戦略 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
11 WOAm 鯨最適化アルゴリズム M 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
12 ACOm 蟻コロニー最適化M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
13 BFO-GA 細菌採食の最適化：Ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
14 MEC Mind Evolutionary Computation 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
15 IWO 侵入雑草最適化 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
16 Micro-AIS 微小人工免疫系 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54
17 COAm カッコウ最適化アルゴリズムM 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21
18 SDOm 螺旋ダイナミクス最適化M 0.74601 0.44623 0.29687 1.48912 0.70204 0.34678 0.10944 1.15826 0.42833 0.16767 0.03663 0.63263 3.280 36.44
19 NMm ネルダー=ミード法M 0.73807 0.50598 0.31342 1.55747 0.63674 0.28302 0.08221 1.00197 0.44667 0.18667 0.04028 0.67362 3.233 35.92
20 FAm ホタルアルゴリズムM 0.58634 0.47228 0.32276 1.38138 0.68467 0.37439 0.10908 1.16814 0.28667 0.16467 0.04722 0.49855 3.048 33.87
21 GSA 重力探索法 0.64757 0.49197 0.30062 1.44016 0.53962 0.36353 0.09945 1.00260 0.32667 0.12200 0.01917 0.46783 2.911 32.34
22 BFO 細菌採餌の最適化 0.61171 0.43270 0.31318 1.35759 0.54410 0.21511 0.05676 0.81597 0.42167 0.13800 0.03195 0.59162 2.765 30.72
23 ABC 人工蜂コロニー 0.63377 0.42402 0.30892 1.36671 0.55103 0.21874 0.05623 0.82600 0.34000 0.14200 0.03102 0.51302 2.706 30.06
24 BA コウモリアルゴリズム 0.59761 0.45911 0.35242 1.40915 0.40321 0.19313 0.07175 0.66810 0.21000 0.10100 0.03517 0.34617 2.423 26.93
25 SA 焼きなまし 0.55787 0.42177 0.31549 1.29513 0.34998 0.15259 0.05023 0.55280 0.31167 0.10033 0.02883 0.44083 2.289 25.43
26 IWDm intelligent water drops M 0.54501 0.37897 0.30124 1.22522 0.46104 0.14704 0.04369 0.65177 0.25833 0.09700 0.02308 0.37842 2.255 25.06
27 PSO 粒子群最適化 0.59726 0.36923 0.29928 1.26577 0.37237 0.16324 0.07010 0.60572 0.25667 0.08000 0.02157 0.35823 2.230 24.77
28 MA モンキーアルゴリズム 0.59107 0.42681 0.31816 1.33604 0.31138 0.14069 0.06612 0.51819 0.22833 0.08567 0.02790 0.34190 2.196 24.40
29 SFL Shuffled Frog-Leaping 0.53925 0.35816 0.29809 1.19551 0.37141 0.11427 0.04051 0.52618 0.27167 0.08667 0.02402 0.38235 2.104 23.38
30 FSS 魚群検索 0.55669 0.39992 0.31172 1.26833 0.31009 0.11889 0.04569 0.47467 0.21167 0.07633 0.02488 0.31288 2.056 22.84
31 RND ランダム 0.52033 0.36068 0.30133 1.18234 0.31335 0.11787 0.04354 0.47476 0.25333 0.07933 0.02382 0.35648 2.014 22.37
32 GWO 灰色オオカミオプティマイザ 0.59169 0.36561 0.29595 1.25326 0.24499 0.09047 0.03612 0.37158 0.27667 0.08567 0.02170 0.38403 2.009 22.32
33 CSS 荷電系探索 0.44252 0.35454 0.35201 1.14907 0.24140 0.11345 0.06814 0.42299 0.18333 0.06300 0.02322 0.26955 1.842 20.46
34 EM 電磁気学的アルゴリズム 0.46250 0.34594 0.32285 1.13129 0.21245 0.09783 0.10057 0.41085 0.15667 0.06033 0.02712 0.24412 1.786 19.85


まとめ

鳥群アルゴリズム（BSA）は、鳥の群れの多様な状態や戦略を具現化する豊かなロジックで想像力をかき立てる魅力的な研究ツールです。このアルゴリズムに取り組んだのは、鳥の個体行動や集団行動がさまざまな条件や組み合わせに左右されるという、複雑な力学が内包されている点が興味深かったからです。

BSAの複雑さは、最適な結果を得るために慎重なチューニングを必要とするパラメータの多さにも表れています。アルゴリズムパラメータを最適化するには、標準のMetaTrader 5テスターの数学的計算モードで動作するEAを作成し、アルゴリズムの評価で7位を確保する適切な外部パラメータを見つける必要がありました。さらなる改良の可能性があるかもしれないので、興味のある方はぜひこのアルゴリズムで実験してみてください。鳥の行動（記事では4種類の行動）を実行する順序やシーケンスの組み合わせには多くのバリエーションがあるため、より良い結果を得るための未開拓の可能性を秘めていると私は考えています。 

タブ

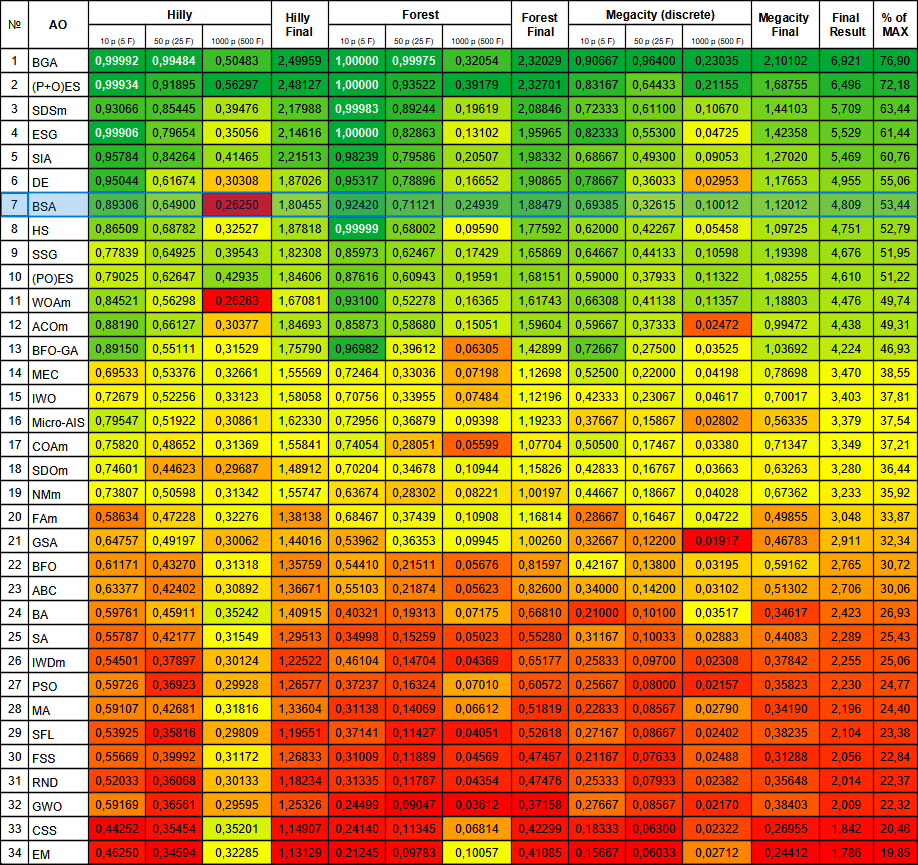
図2：関連テストに応じたアルゴリズムのカラーグラデーション0.99以上の結果は白で強調表示

チャート

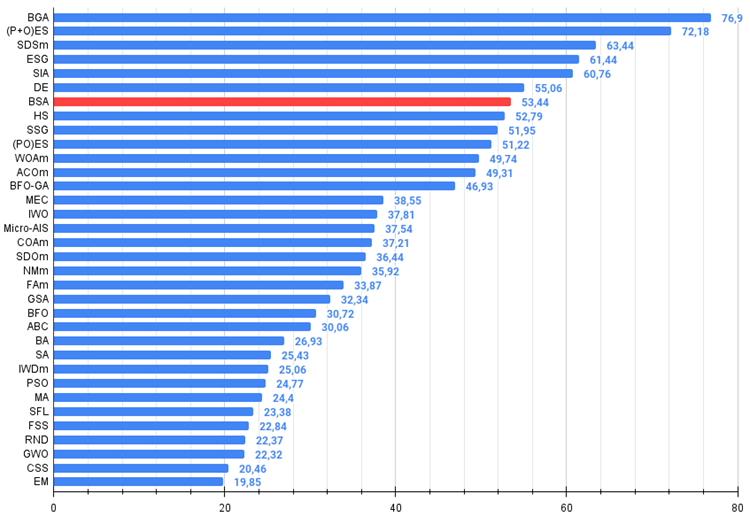
図3：アルゴリズムのテスト結果のヒストグラム（0から100までのスケールで、多ければ多いほど良いです。

ここで、100は理論的に可能な最大の結果であり、アーカイブにはレーティング表を計算するスクリプトが含まれている)

BSAの長所と短所

長所

  1. シャープなForest関数と高次元の離散Megacityでの良い結果

短所

  1. 実装が複雑
  2. 収束性が低い
  3. Hillyのような滑らかな関数ではスケーラビリティが低い（高次元タスクの問題）

この記事には、現在のコードバージョンのアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/14491

添付されたファイル |
ZIPをダウンロード
BSA.zip (28.34 KB)
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動
非定常過程と偽回帰 非定常過程と偽回帰
この記事では、モンテカルロシミュレーションを用いて非定常過程に回帰分析を適用しようとすると、偽回帰が発生することを示しています。
ニューラルネットワークの実践：割線 ニューラルネットワークの実践：割線
理論的な部分ですでに説明したように、ニューラルネットワークを扱う場合、線形回帰と導関数を使用する必要があります。なぜでしょうか。その理由は、線形回帰は現存する最も単純な公式の1つだからです。本質的に、線形回帰は単なるアフィン関数です。しかし、ニューラルネットワークについて語るとき、私たちは直接線形回帰の効果には興味がありません。この直線を生み出す方程式に興味があるのです。作られた線にはそれほど興味がありません。私たちが理解すべき主要な方程式をご存じですか。ご存じでなければ、この記事を読んで理解することをお勧めします。
MQLプロジェクトでJSON Data APIを使用する MQLプロジェクトでJSON Data APIを使用する
MetaTraderにはないデータを使用できることを想像してみてください。価格分析とテクニカル分析による指標からデータを得るだけです。取引力を一段と高めるデータにアクセスできることを想像してみてください。APIデータを通して他のソフトウェア、マクロ分析手法、超高度ツールの出力をMetaTraderを通じてミックスすれば、MetaTraderソフトウェアのパワーを倍増させることができます。この記事では、APIの使い方を教え、便利で価値のあるAPIデータサービスを紹介します。
データサイエンスと機械学習（第25回）：回帰型ニューラルネットワーク(RNN)を用いたFX時系列予測 データサイエンスと機械学習（第25回）：回帰型ニューラルネットワーク(RNN)を用いたFX時系列予測
回帰型ニューラルネットワーク(Recurrent Neural Network: RNN)は、過去の情報を活用して将来の出来事を予測することに優れています。その驚くべき予測能力は、さまざまな領域で応用され、大きな成功を収めています。この記事では、外為市場のトレンドを予測するためにRNNモデルを導入し、外為取引における予測精度を高める可能性を示します。