母集団最適化アルゴリズム：Spiral Dynamics Optimization (SDO)アルゴリズム

内容

1. はじめに
2.アルゴリズム
3.テスト結果

1. はじめに

科学文献には、自然や個体群のさまざまな側面に基づく、多種多様なメタヒューリスティクス最適化アルゴリズムが紹介されています。これらのアルゴリズムは、例えば、群知能、物理学、化学、社会的人間行動、植物、動物など、いくつかのカテゴリに分類されます。群知能に基づくメタヒューリスティクス最適化アルゴリズムは数多く存在します。物理現象に基づくアルゴリズムも広く提案され、さまざまな分野で活用されています。

群知能に基づくアルゴリズムは、最適解を見つけるプロセスに知能の要素を組み込んでいます。個々のエージェントが情報を交換し、共通の目標を達成するために協力します。これらのアルゴリズムは、大域的な探索と変化する条件への適応性を必要とする問題において効率的です。

一方、物理ベースのアルゴリズムは、最適化問題を解くために物理学の法則と原理に依存しています。重力、電磁気学、熱力学などの物理現象をシミュレーションし、これらの原理を使って最適解を見つけるのです。物理に基づいたアルゴリズムの主な利点の1つは、その解釈のしやすさです。検索エリア全体にわたって、正確かつ一貫したダイナミクスを表示することができます。

さらに、物理学に基づくアルゴリズムの中には、黄金比を使用するものがあります。黄金比は数学的かつ自然な比率で、特別な性質を持ち、最適解に素早く効率的に収束するのに役立ちます。黄金比は、人工ニューラルネットワークの最適化や資源配分など、さまざまな分野で研究応用されています。

このように、物理学に基づくメタヒューリスティクス最適化アルゴリズムは、複雑な最適化問題を解くための強力なツールとなります。その精度と基本的な物理原理の応用は、最適解の効率的な探索が求められる様々な分野で魅力的なものとなっています。

Spiral Dynamics Optimization (SDO)は、2011年に田村健一と安田恵一郎によって提案された、自然界の対数螺旋現象を利用して開発された最も単純な物理アルゴリズムの1つです。アルゴリズムはシンプルで、制御パラメータもほとんどありません。さらに、このアルゴリズムは計算速度が高く、局所的な探索が可能で、初期段階では多様化し、後期段階では強化することができます。

銀河、オーロラ、動物の角、竜巻、貝殻、カタツムリ、アンモナイト、カメレオンの尻尾、タツノオトシゴなど、自然界にはたくさんの螺旋があります。螺旋は、人類がその黎明期に創り出した古代美術にも見られます。長年にわたり、何人かの研究者が螺旋のシーケンスと複雑さを理解し、螺旋の方程式とアルゴリズムを開発するために努力してきました。自然界で頻繁に起こる螺旋現象は、銀河や熱帯低気圧で観察される対数螺旋です。離散対数螺旋生成過程は、メタヒューリスティックスの効率的な探索動作として実装され、これが螺旋力学最適化アルゴリズムの開発のきっかけとなりました。

自然界に見られる可視螺旋列と呼ばれるパターンは、植物、樹木、波、その他多くの形を表しています。自然界の視覚的パターンは、カオス理論、フラクタル、螺旋、その他の数学的概念を用いてモデル化することができます。自然のパターンには、螺旋とフラクタルが密接に関係しているものがあります。例えば、フィボナッチ螺旋は黄金比とフィボナッチ数に基づく対数螺旋の変形です。対数であるため、曲線はどのスケールでも同じように見え、フラクタルとみなすこともできます。

以上のようなパターンから、研究者たちは最適化アルゴリズムの開発に取り組んできました。螺旋軌道にはさまざまな種類がありますが、ここでは主なものを紹介します。

• 代数螺旋
• サイクロイド螺旋
• 外トロコイドヘリックス
• 内トロコイド螺旋
• 対数螺旋
• ローズ螺旋
• フェルマー螺旋

これらの種類の螺旋はそれぞれ独自の特性を持っており、さまざまな自然のパターンをモデル化するのに使うことができます。特に、螺旋経路の概念に基づく、自然から着想を得た様々な最適化アルゴリズムが注目されています。長年にわたり、研究者たちは螺旋運動を利用したさまざまな新しい最適化アルゴリズムを開発してきました。

さらに、最適解の精度を向上させるために、上部構造や補完として螺旋経路を使用することで、非螺旋アルゴリズムの動作を変更することができます。

田村と安田が提案した2次元螺旋最適化アルゴリズムは、2次元連続最適化問題に対する多点メタヒューリスティクス探索手法です。そして田村と安田は、2次元最適化の思想を用いてn次元最適化を提案しました。

2.アルゴリズム

著者らによって説明された多次元空間を探索するためのSDOアルゴリズムには、限界と欠点があります。

• 1次元やその他の奇数次元の最適化問題には適用できません。
• アルゴリズムによって座標をペアでリンクすると、特定の問題での解の質に影響を与え、合成テストでは偽陽性の結果を示すことがあります。

多次元空間における螺旋軌道の構築には、ある種の困難が伴います。したがって、問題が1次元空間に限定される場合、螺旋は少なくとも2次元の動きを必要とするため、通常の意味での螺旋は構築できません。この場合、螺旋を使わなくても、単純な関数を使って座標値を経時的に変化させることができます。1次元の最適化問題については、螺旋は使用されません。螺旋に沿った移動に追加の次元がないためです。

多次元空間では、各座標の組に対して螺旋を構成することができますが、残りの1つの座標に対しては螺旋を定義することができません。例えば、13次元空間の場合、6組の座標に対して螺旋を構成することが可能だが、1つの座標は螺旋の要素を持たずに移動します。

多次元空間で螺旋を構成するには、「多次元螺旋」または「ハイパー螺旋」法を使うことができます。この方法では、追加の仮想座標を導入し、各次元で螺旋形状を定義します。超螺旋を構成するには、回転行列と多次元空間の幾何学に基づくアルゴリズムを使用することができます。しかし、このアプローチはより複雑な計算を必要とし、現実的な最適化問題への導入は難しいかもしれません。

この記事では、2次元の関数が繰り返し複製される形で多次元関数が使用されているため、元のSDOは不当に高い結果を示す可能性があります。したがって、螺旋アルゴリズムは、座標が互いに何ら関連していない他の多次元問題では貧弱な結果を示すことになります。言い換えれば、この場合、螺旋アルゴリズムにとって、複製された関数に関する完璧な条件を意図せず作り出してしまうことになります。

螺旋アルゴリズムにおける上記の問題を回避するために、2次元螺旋の1つの座標軸への投影に基づくアプローチを提案します。二次元螺旋上の点の運動を振り子の運動と考えれば、点の運動を2つの座標それぞれに投影すると、振り子の運動をそれぞれの座標に投影したものと一致します。このように、振り子の点運動を多次元空間の各軸に投影することで、2次元空間における点の螺旋運動をシミュレーションすることができます。

多次元空間の各座標で振り子の挙動をシミュレーションする螺旋を構成する方法を使う場合、それぞれの「仮想」螺旋の半径は異なることがあります。いくつかの座標は既知の最適値に近く、大きく変更する必要がないため、これは最適化の質に良い影響を与える可能性があります。

減衰を伴うあらゆる調和振動の法則を、2次元の螺旋を1次元の軸に投影したものとしてとらえることができます。以下の式の単純な減衰調和振動子（点の位置の時間依存性）を選択しました。

x(t) = A*e^(-γt)*cos(ωt + φ)

ここで

• A：振動の振幅
• γ：減衰比
• ω：振動子の固有振動数
• φ：振動の初期位相

この式から明らかなように、減衰比、周波数、初期位相は定数であり、アルゴリズム入力として使用できますが、ここでは3つではなく、2つのパラメータを使用します。各反復では、振動の初期位相を無作為成分として使用します（各座標は他の座標に対して位相がわずかにずれる）。そうでなければ、アルゴリズムは完全に決定論的であり、空間内の点の初期配置にのみ依存します。

このアイデアは、新しい最良の大域的極限が発見されるとすぐに、大域的極限の座標と対応する点の座標との差である新しい振幅がすべての点に対して計算されるというものです。この時点から、新しいより良い極限が発見され、新しい振幅が決定されるまで、座標に沿った振幅は個々に、各点のメモリに保存されます。

振幅を決定した後、各点は減衰とともに振動し始め、振動の対称軸は大域的最適解の既知の座標となります。減衰比と周波数（外部パラメータ）の影響を評価するには、図1と図2を使うと視覚的に便利です。

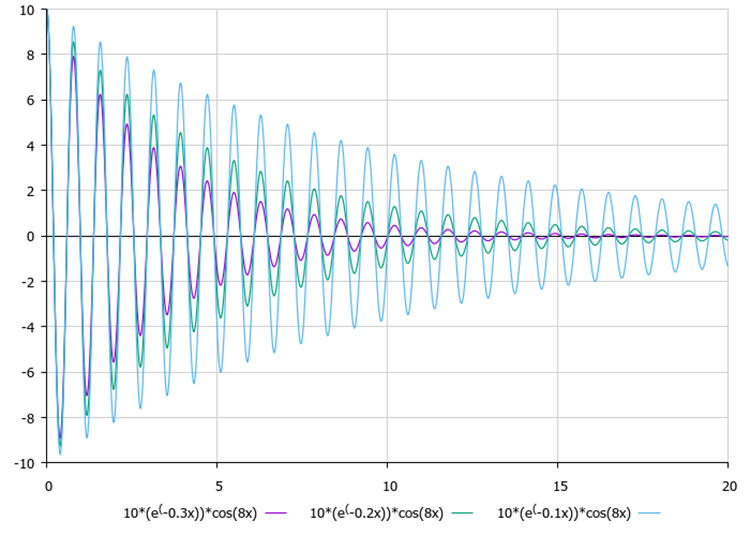
図1：振動の性質に及ぼす振幅の影響

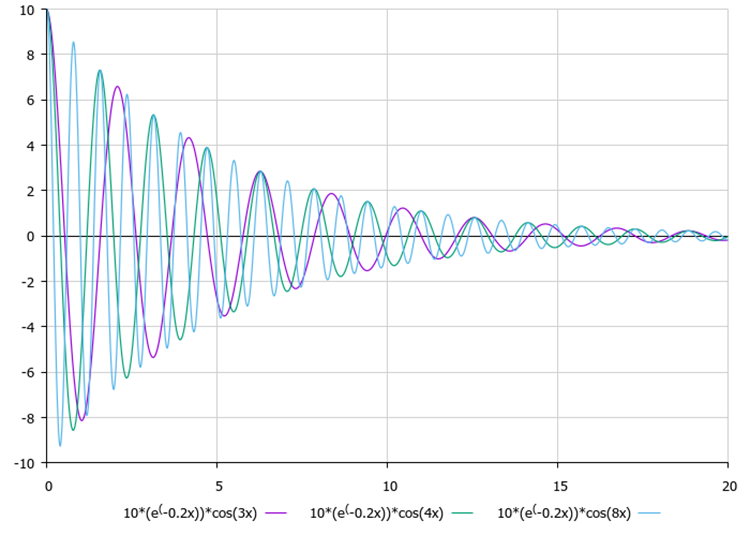
図2：振動の性質に及ぼす周波数の影響

私たちのアルゴリズムでは、すべての座標は絶対的に独立していますが、前述のように、螺旋を構築するためのロジックでは、対になる組み合わせや座標間のつながりは存在しません。ある点の動きを2次元平面上で構成すると、図3のような螺旋になります。

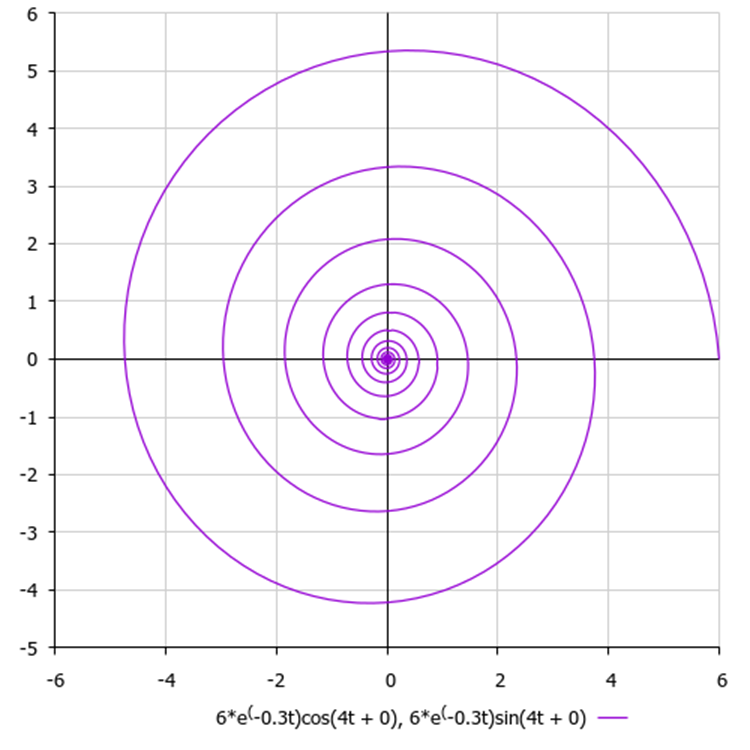
図3：デフォルトのアルゴリズムパラメータを使用した仮想スパイラル（6が振幅値、0.3が減衰比、4が周波数）

実際、本当の問題では、テスト関数と同様に、各座標に沿った振幅は同じである必要はありません（元のアルゴリズムとは異なる）。振幅の差は、平坦化された螺旋を生み出します。振幅が小さいほど、対応する座標は既知の最適値に近くなるため、より速く精緻化されます。

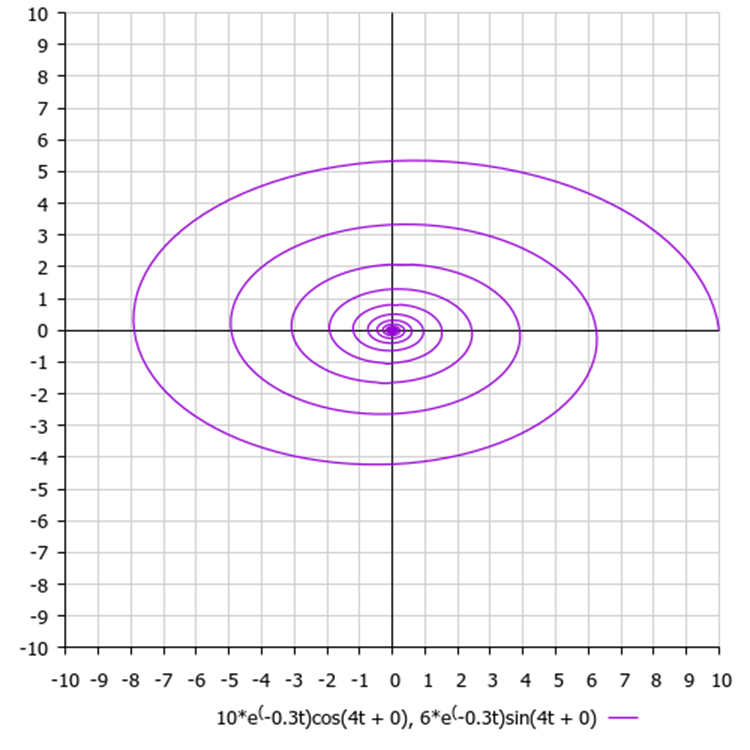
図4：Y座標に沿った点の値は既知の値に近く、その振動振幅はX軸に沿ったものより小さくなる

グラフ上のプロットはすべてゼロを基準にしています。なぜなら、既知の最適値の値との相対的な差を考えるからです。

コードの説明に移りましょう。まず、アルゴリズムの構造を決め、擬似コードを作成しましょう。

1. 点集団を初期化する
2. 適応度関数の値を計算する
3. 新たな最適値が現れたときの各点座標の振幅を計算する
4. 新たな最適点が現れたら、最適点を無作為な方向に「捨てる」
   
5. 減衰調和振動の方程式を用いて、点の新しい位置を計算する
6. P2から繰り返す

点4は特別に追加されたもので、ある局所的な極限に「螺旋」状に収束し、そこで立ち往生しないように、立ち往生に対する抵抗力を高めることを意図しています。アルゴリズムの著者はこのトピックを取り上げていません。

エージェント（粒子、点）を記述するには、以下の変数を含むS_Particle構造体が適しています。

• c []：粒子座標の配列
  
• cD[]：粒子速度の配列
• t：反復ステップ、式中では「時間」の役割を果たす
  
• f：粒子適応度関数の値
  

この構造体はまた、構造体変数の初期化に使われるInit関数も定義しています。coordsパラメータは粒子座標の数を指定します。

//——————————————————————————————————————————————————————————————————————————————
struct S_Particle
{
  void Init (int coords)
  {
    ArrayResize (c,    coords);
    ArrayResize (cD,   coords);
    t = 0;
    f = -DBL_MAX;
  }

  double c  []; //coordinates
  double cD []; //coordinates
  int    t;     //iteration (time)
  double f;     //fitness
};
//——————————————————————————————————————————————————————————————————————————————

SDOmアルゴリズムクラスC_AO_SDOmを定義してみましょう。このクラスには以下の変数とメソッドがあります。

• cB []：最適座標の配列
• fB：最適座標の適応度関数値
• p []：粒子の配列，データ型 - S_Particle.
• rangeMax []：検索範囲の最大値の配列
  
• rangeMin []：検索範囲の最小値の配列
  
• rangeStep []：検索ステップの配列
  
• Init：クラスのパラメータを初期化するメソッド（受け取るパラメータ： coordinatesNumberP - 座標の数、 populationSize - 母集団のサイズ、 dampingFactorP - 減衰比、frequencyP - 周波数、precisionP - 精度）
• Moving：探索空間内で粒子を移動させるメソッド
• Revision：最適座標を修正更新するメソッド
• coords：座標の数
• popSiz：母集団のサイズ
• A、e、γ、ω、φ：減衰調和振動方程式の成分
  
• precision、revision：クラス内部で使用されるprivate変数
• SeInDiSp：指定されたステップで、指定された範囲の新しい座標値を計算するメソッド
  
• RNDfromCI：指定した範囲の乱数を生成するメソッド

このコードでは、C_AO_SDOmクラスについて説明します。C_AO_SDOmクラスは、最適座標の修正と更新のための追加関数を備えたアルゴリズムの実装を表しています。

クラスの最初の3つの変数は、最良の座標を格納するcB配列、最良の座標の適応度関数の値を格納するfB変数、母集団の候補（粒子）を格納するp配列です。

次の3つのクラス変数はrangeMax、rangeMin、rangeStep配列で、それぞれ検索範囲と検索ステップの最大値と最小値を格納します。

さらに、このクラスにはInit、Moving、Revisionの3つのpublicメソッドがあります。Initは、クラスのパラメータを初期化し、粒子の初期集団を作成するために使用されます。移動は探索空間内で粒子を移動させるために使われる。Revisionは、最適な座標を修正し、その値を更新するために適用されます。

このクラスには、クラス内で使用されるいくつかのprivate変数も含まれています。これらはそれぞれ座標の数と母集団のサイズを格納する変数coordsとpopSizeです。Movingメソッドで使用されるA変数、精度値を格納するprecision変数、最適座標の修正の必要性を担当するrevision変数です。

このクラスにはいくつかのprivateメソッドがあります。Research、SeInDiSp、RNDfromCIです。Researchは新しい粒子座標を調査するために使用され、SeInDiSpとRNDfromCIは与えられた範囲内で無作為な値を計算するために使用されます。

precisionはアルゴリズムの外部パラメータで、減衰振動の軌道に沿った運動の離散性を担当します。値が大きいほど軌跡が正確に再現され、値が小さいほど軌跡が「ぼろぼろ」になります（これは結果に悪影響があるという意味ではなく、タスクに依存する）。一連の実験の結果、デフォルトの設定が最適と判断されます。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_SDOm
{
  //----------------------------------------------------------------------------
  public: double     cB []; //best coordinates
  public: double     fB;    //FF of the best coordinates
  public: S_Particle p  []; //particles

  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search

  public: void Init (const int    coordinatesNumberP,   //coordinates number
                     const int    populationSizeP,      //population size
                     const double dampingFactorP,       //damping factor
                     const double frequencyP,           //frequency
                     const double precisionP);          //precision

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coords;   //coordinates number
  private: int    popSize;  //population size

  private: double A;
  private: double e;
  private: double γ;
  private: double ω;
  private: double φ;
  private: double precision;

  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
};
//——————————————————————————————————————————————————————————————————————————————

C_AO_SDOmクラスのInitメソッドは、クラスのパラメータを初期化し、粒子の初期集団を作成するために使用されます。

まず、MathSrandを使用して乱数発生器をリセットし、GetMicrosecondCount関数を使用して発生器を初期化します。

次に、fB変数とrevision変数に初期値を設定し、減衰振動方程式に参加する定数変数に値を割り当てます。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_SDOm::Init (const int    coordinatesNumberP,   //coordinates number
                      const int    populationSizeP,      //population size
                      const double dampingFactorP,       //damping factor
                      const double frequencyP,           //frequency
                      const double precisionP)           //precision
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coords  = coordinatesNumberP;
  popSize = populationSizeP;

  e = M_E;
  γ = dampingFactorP;
  ω = frequencyP;
  φ = 0.0;
  precision = precisionP;

  ArrayResize (rangeMax,  coords);
  ArrayResize (rangeMin,  coords);
  ArrayResize (rangeStep, coords);
  ArrayResize (cB,        coords);

  ArrayResize (p, popSize);

  for (int i = 0; i < popSize; i++)
  {
    p [i].Init (coords);
  }
}
//——————————————————————————————————————————————————————————————————————————————

探索空間内で粒子を移動させるには、Movingメソッドを使用します。

最初のコードブロック（if (!revision)）は最初の反復でのみ実行され、探索空間に粒子を無作為に配置するためのものです。次にこのメソッドは、revisionの値をtrueに設定し、次回からは通常のコードブロックが使用されるようにします。

メソッドコードの次の部分は、集団粒子を移動させる役割を担っています。現在の粒子のフィットネス値がベスト座標の適応度値と等しい場合（p[i].f == fB）、最初のコードブロックと同じ方法で粒子座標が更新されます。これは、すべての粒子が一点に収束するのを防ぐために、粒子がその位置から無作為な方向に投げ出されることを意味します。

そうでない場合、このメソッドはt変数を使用して、反復カウンタ（最良のグローバル解が更新されるとリセットされる）を使用して各粒子の現在時刻をシミュレーションします。その後、減衰調和振動の方程式を用いて各粒子の座標を計算します。

コードのコメントアウトされた部分は、方程式によって計算された座標値に無作為なインクリメントを追加するもので、美しい視覚的な花火効果を生み出すために使用できます。しかし、この効果には実用的な価値はなく、結果も改善されないため、コードはコメントアウトされています。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_SDOm::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        p [i].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
        p [i].c [c] = SeInDiSp (p [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  int t = 0.0;

  for (int i = 0; i < popSize; i++)
  {
    if  (p [i].f == fB)
    {
      for (int c = 0; c < coords; c++)
      {
        p [i].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
        p [i].c [c] = SeInDiSp (p [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }

      continue;
    }

    p [i].t++;
    t = p [i].t;

    for (int c = 0; c < coords; c++)
    {
      A = p [i].cD [c];
      φ = RNDfromCI (0.0, 2.0);

      p [i].c [c] = p [i].c [c] + A * pow (e, -γ * t / precision) * cos (ω * t / (precision) + φ);// + RNDfromCI (-0.01, 0.01) * (rangeMax [c] - rangeMin [c]);
      p [i].c [c] = SeInDiSp (p [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Revisionクラスメソッドは、最適座標を更新し、粒子座標と既知の最適解との差を計算するために使用されます。この差が初期振幅となり、新しいより良い解が見つかると、粒子はこれらの動きの中心に位置する最もよく知られた座標の周りを振動し始めます。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_SDOm::Revision ()
{
  //----------------------------------------------------------------------------
  bool flag = false;
  for (int i = 0; i < popSize; i++)
  {
    if (p [i].f > fB)
    {
      flag = true;
      fB = p [i].f;
      ArrayCopy (cB, p [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  if (flag)
  {
    for (int i = 0; i < popSize; i++)
    {
      p [i].t = 0;

      for (int c = 0; c < coords; c++)
      {
        p [i].cD [c] = (cB [c] - p [i].c [c]);

      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

3.テスト結果

テストスタンドの結果は良好のようです。

C_AO_SDOm:100;0.3;4.0;10000.0
=============================
5 Rastrigin's; Func runs 10000 result:76.22736727464056
Score:0.94450
25 Rastrigin's; Func runs 10000 result:64.5695106264092
Score:0.80005
500 Rastrigin's; Func runs 10000 result:47.607500083305425
Score:0.58988
=============================
5 Forest's; Func runs 10000 result:1.3265635010116805
Score:0.75037
25 Forest's; Func runs 10000 result:0.5448141810532924
Score:0.30817
500 Forest's; Func runs 10000 result:0.12178250603909949
Score:0.06889
=============================
5 Megacity's; Func runs 10000 result:5.359999999999999
Score:0.44667
25 Megacity's; Func runs 10000 result:1.552
Score:0.12933
500 Megacity's; Func runs 10000 result:0.38160000000000005
Score:0.03180
=============================
All score:4.06967

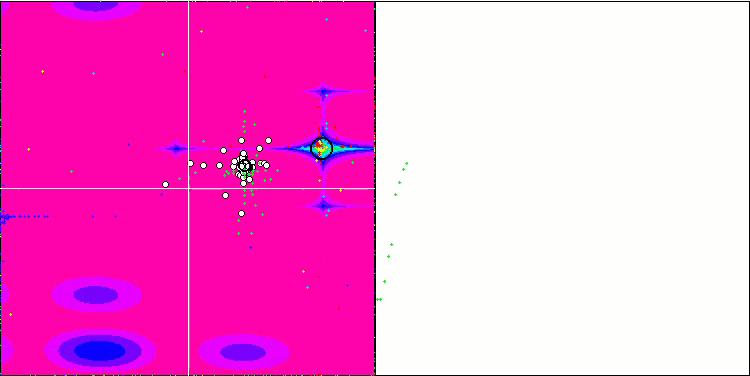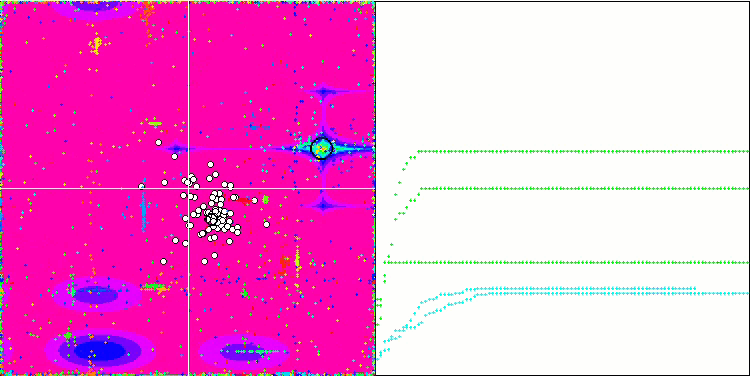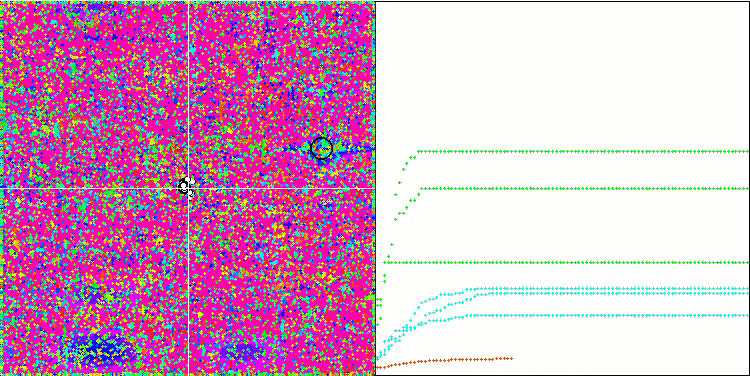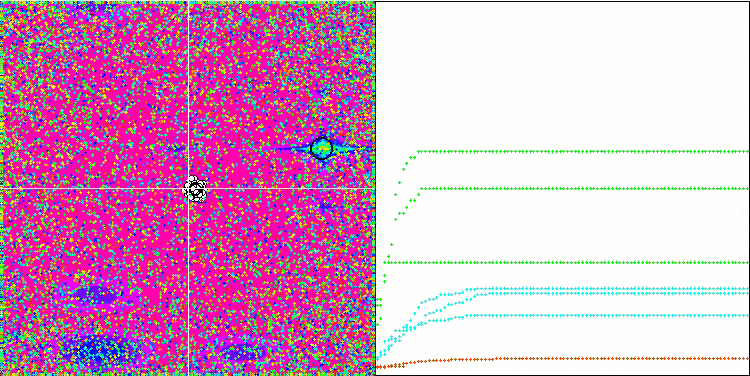
すべてのテスト関数の収束グラフは不安定であり、収束曲線の性質はすべての反復を通じて変化します。これでは結果に対する信頼感は増しません。Megacity関数の視覚化では、テストごとの結果の不安定さを示すために、特にいくつかのテストを繰り返し表示します（通常、GIFが大きくなりすぎないように、ビデオでは1つしか表示されない）。結果の広がりは非常に大きいです。

粒子の座標がはっきりと見える線で並ぶシャープForestと離散的なMegacityを除いて、粒子の動きの性質に特徴は見られませんでした。これが良いか悪いかの判断は難しいです。例えば、ACOmアルゴリズムの場合は質的な収束の兆候でありましたが、SDOmの場合はおそらくそうではありません。

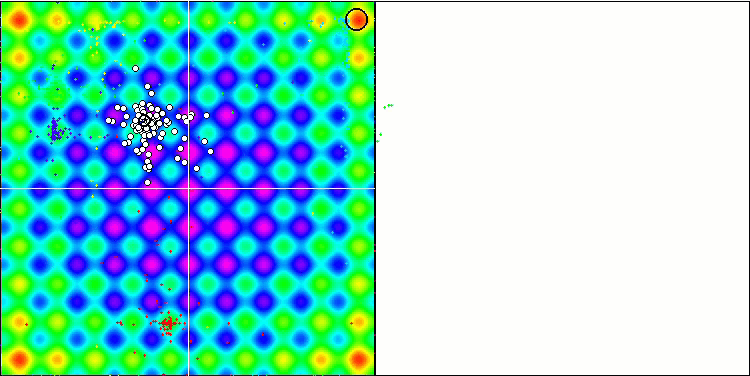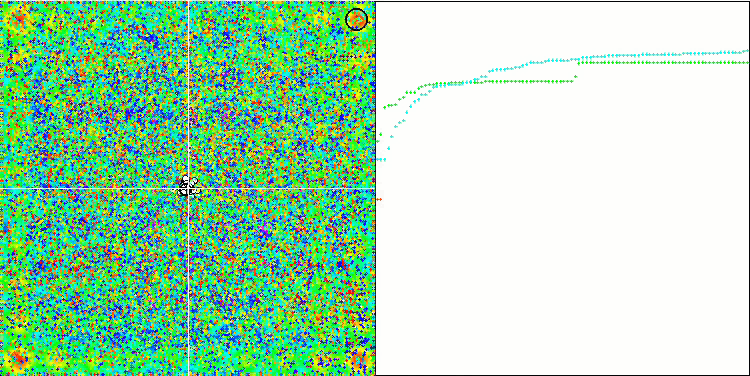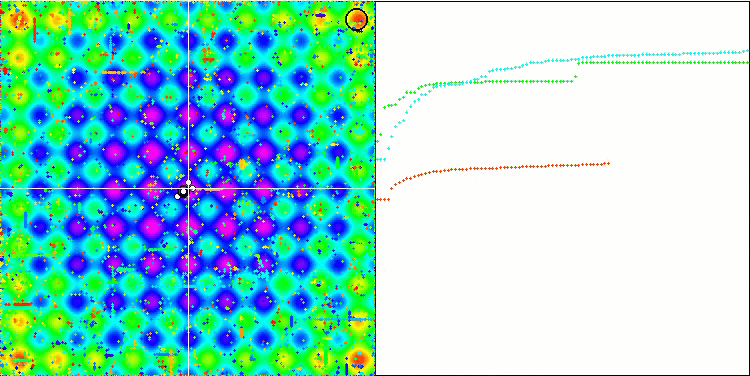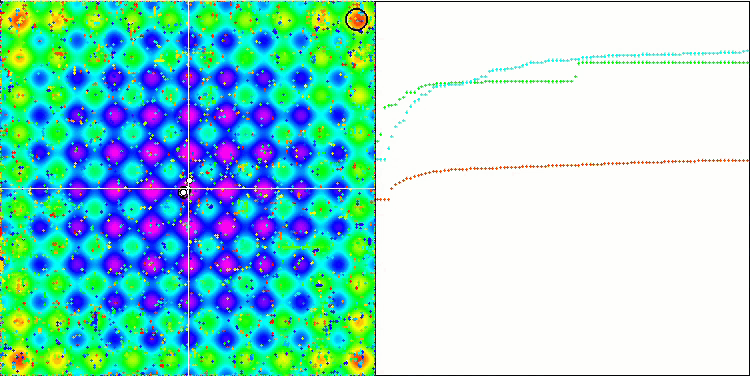
  Rastriginテスト関数のSDOm

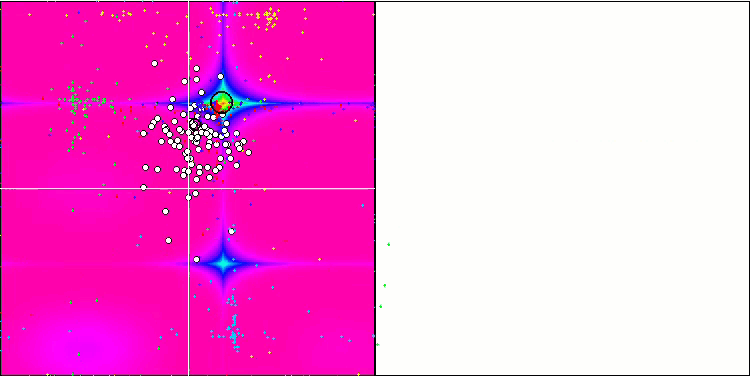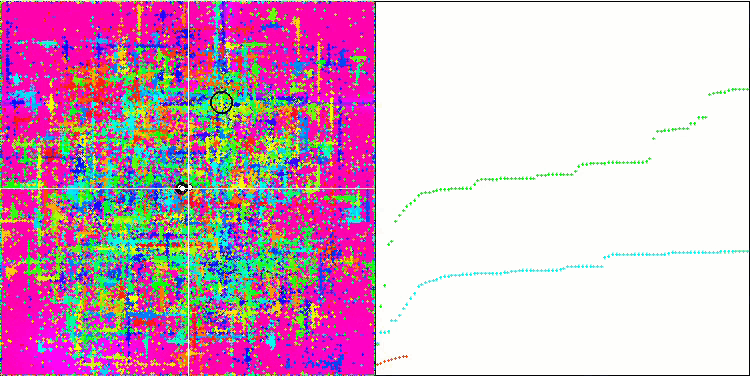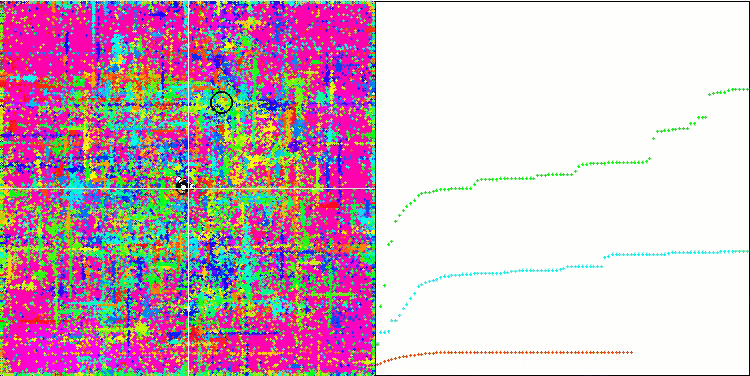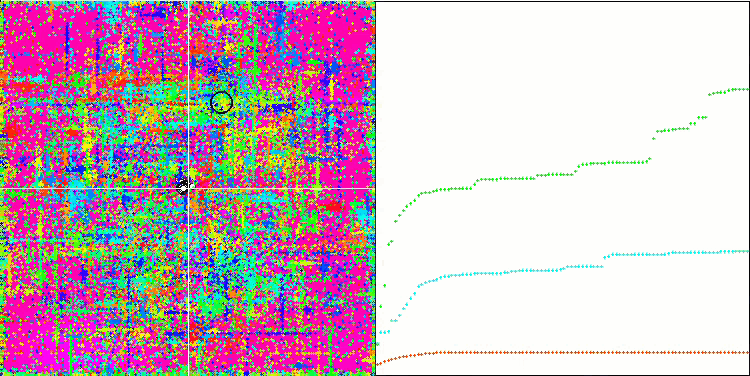
  Forestテスト関数のSDOm

  Megacityテスト関数のSDOm

Movingメソッドでコメントアウトされている、粒子座標に無作為なノイズを加える役割を持つコードを使用すると、花火に似た興味深い現象が起こる一方、振動の位相の無作為な変化は使用されません。私は、粒子が既知の解に大量に収束した後、異なる方向に放出され、これがアルゴリズムが行き詰まった瞬間に発揮される美しい効果の理由だと推測しています。このことは、花火の爆発と収束グラフの水平セクションの始まりが一致していることからもわかります。

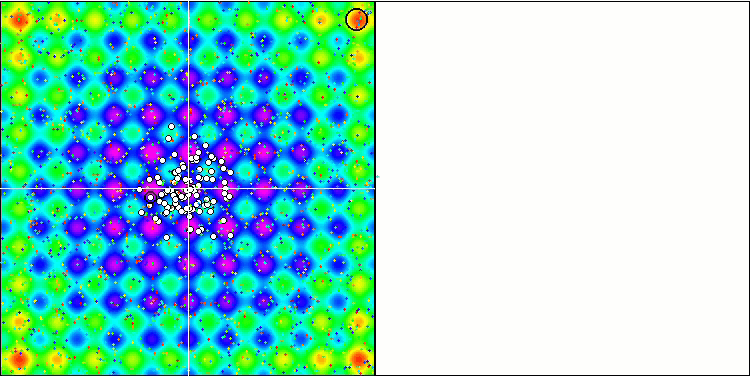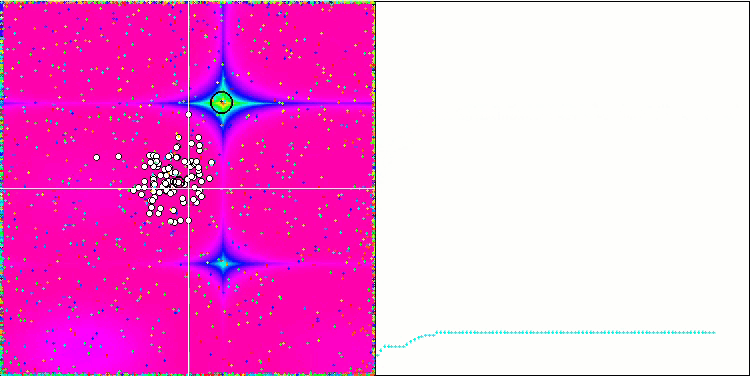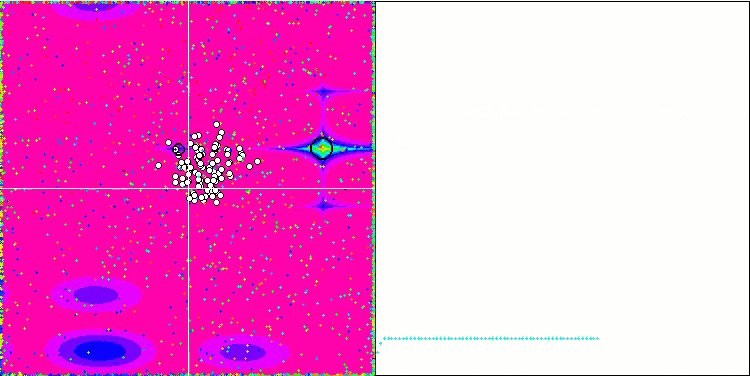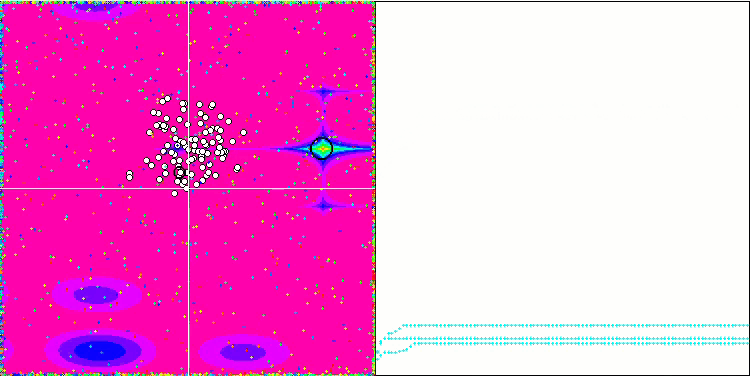
無駄だが美しい花火のデモンストレーション

SDOmアルゴリズムは、全体的にかなり良好な結果を示しており、格付け表のレビューに参加した23個中8位に位置しています。SDOmは平滑Rastrigin関数で顕著に良い結果を示しました。スタックする傾向は、複雑なForestとMegacity関数の結果に干渉します。

#	AO	詳細	Rastrigin			Rastrigin最終	Forest			Forest最終	Megacity（離散）			Megacity最終	最終結果
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	SDSm	確率的拡散探索M	0.99809	1.00000	0.69149	2.68958	1.00000	1.00000	1.00000	3.00000	1.00000	1.00000	1.00000	3.00000	100000
2	SDS	Stochastic Diffusion Search	0.99737	0.97322	0.58904	2.55963	0.96778	0.93572	0.79649	2.69999	0.78696	0.93815	0.71804	2.44315	88.208
3	SSG	苗木の播種と育成	1.00000	0.92761	0.51630	2.44391	0.72654	0.65201	0.83760	2.21615	0.54782	0.61841	0.99522	2.16146	77.678
4	HS	ハーモニー検索	0.99676	0.88385	0.44686	2.32747	0.99882	0.68242	0.37529	2.05653	0.71739	0.71842	0.41338	1.84919	70.647
5	IWO	侵入雑草最適化	0.95828	0.62227	0.27647	1.85703	0.70690	0.31972	0.26613	1.29275	0.57391	0.30527	0.33130	1.21048	48.267
6	ACOm	蟻コロニー最適化M	0.34611	0.16683	0.15808	0.67103	0.86785	0.68980	0.64798	2.20563	0.71739	0.63947	0.05579	1.41265	47.419
7	MEC	Mind Evolutionary Computation	0.99270	0.47345	0.21148	1.67763	0.60691	0.28046	0.21324	1.10061	0.66957	0.30000	0.26045	1.23002	44.061
8	SDOm	螺旋ダイナミクス最適化 M	0.81076	0.56474	0.35334	1.72884	0.72333	0.30644	0.30985	1.33963	0.43479	0.13289	0.14695	0.71463	41.370
9	COAm	カッコウ最適化アルゴリズムM	0.92400	0.43407	0.24120	1.59927	0.58309	0.23477	0.13842	0.95629	0.52174	0.24079	0.17001	0.93254	37.845
10	FAm	ホタルアルゴリズムM	0.59825	0.31520	0.15893	1.07239	0.51012	0.29178	0.41704	1.21894	0.24783	0.20526	0.35090	0.80398	33.152
11	ABC	人工蜂コロニー	0.78170	0.30347	0.19313	1.27829	0.53774	0.14799	0.11177	0.79750	0.40435	0.19474	0.13859	0.73768	29.784
12	BA	コウモリアルゴリズム	0.40526	0.59145	0.78330	1.78002	0.20817	0.12056	0.21769	0.54641	0.21305	0.07632	0.17288	0.46225	29.488
13	CSS	荷電系探索	0.56605	0.68683	1.00000	2.25289	0.14065	0.01853	0.13638	0.29555	0.07392	0.00000	0.03465	0.10856	27.914
14	GSA	重力探索法	0.70167	0.41944	0.00000	1.12111	0.31623	0.25120	0.27812	0.84554	0.42609	0.25525	0.00000	0.68134	27.807
15	BFO	細菌採餌の最適化	0.67203	0.28721	0.10957	1.06881	0.39655	0.18364	0.17298	0.75317	0.37392	0.24211	0.18841	0.80444	27.549
16	EM	電磁気学的アルゴリズム	0.12235	0.42928	0.92752	1.47915	0.00000	0.02413	0.29215	0.31628	0.00000	0.00527	0.10872	0.11399	18.981
17	SFL	ShuffledFrog-Leaping	0.40072	0.22021	0.24624	0.86717	0.20129	0.02861	0.02221	0.25211	0.19565	0.04474	0.06607	0.30646	13.201
18	MA	モンキーアルゴリズム	0.33192	0.31029	0.13582	0.77804	0.10000	0.05443	0.07482	0.22926	0.15652	0.03553	0.10669	0.29874	11.771
19	FSS	魚群検索	0.46812	0.23502	0.10483	0.80798	0.12825	0.03458	0.05458	0.21741	0.12175	0.03947	0.08244	0.24366	11.329
20	IWDm	インテリジェント水滴M	0.26459	0.13013	0.07500	0.46972	0.28568	0.05445	0.05112	0.39126	0.22609	0.05659	0.05054	0.33322	10.434
21	PSO	粒子群最適化	0.20449	0.07607	0.06641	0.34696	0.18873	0.07233	0.18207	0.44313	0.16956	0.04737	0.01947	0.23641	8.431
22	RND	ランダム	0.16826	0.09038	0.07438	0.33302	0.13480	0.03318	0.03949	0.20747	0.12175	0.03290	0.04898	0.20363	5.056
23	GWO	灰色オオカミオプティマイザ	0.00000	0.00000	0.02093	0.02093	0.06562	0.00000	0.00000	0.06562	0.23478	0.05789	0.02545	0.31812	1.000

まとめ

修正版の実装に対する独自のアプローチでは、原著者のアルゴリズムのような重い行列計算を回避することを可能にし、またn次元空間の座標間の関係を参照することなく普遍化することを可能になりました。

私は、減衰調和振動の方程式に「質量」の概念を用いることで、粒子の挙動をその適応度に依存するものにしようと試みてきました。このアイデアは、質量の大きい（適応度関数の値が良い）粒子の振幅と周波数を小さくする一方、軽い粒子は振幅が大きく周波数が高い動きをしなければならないというものでした。これにより、既知の最適解をより高度に洗練させることができると同時に、光の粒子の「幅広い」運動により、探索能力を高めることができます。残念ながら、このアイデアは期待されたような成績の向上をもたらしませんでした。

アルゴリズムにおける粒子軌道の物理シミュレーションは、速度、加速度、慣性などの物理的概念を使用する可能性を示唆しています。これは今後の研究課題です。

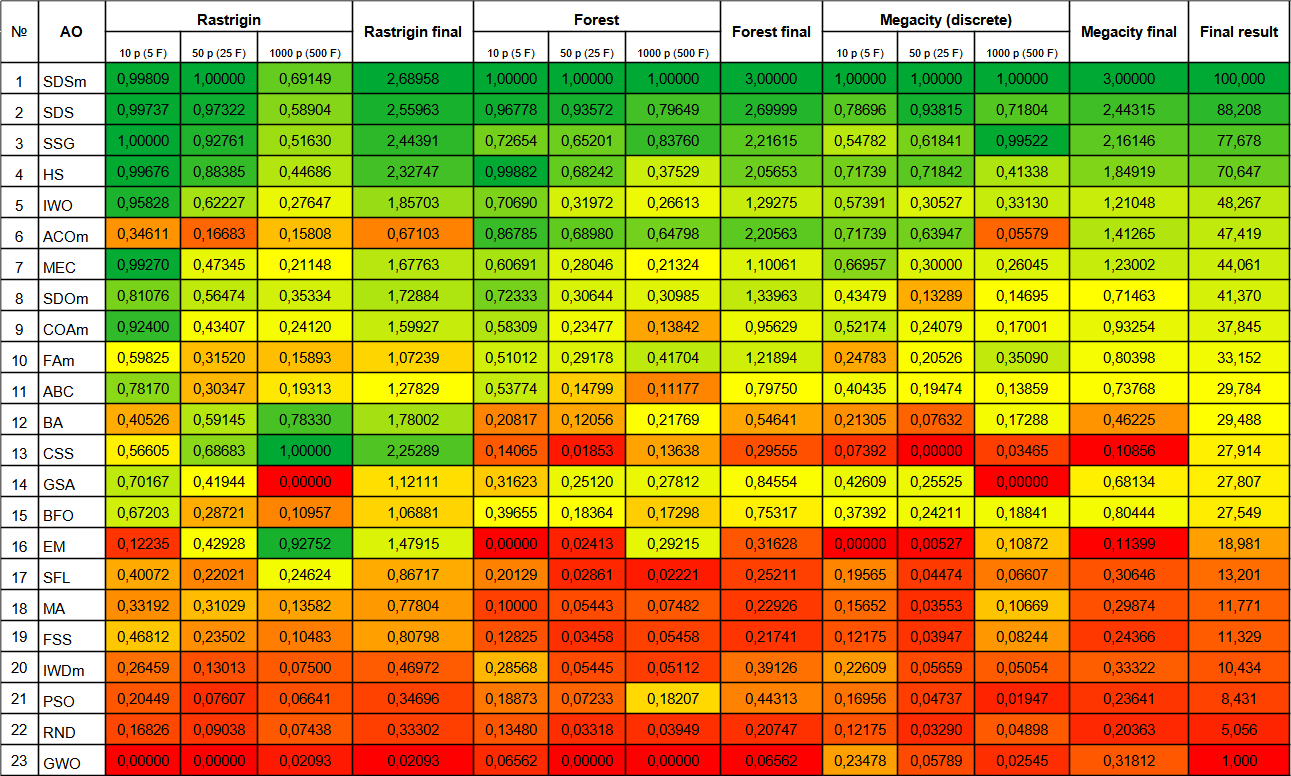
図5：関連テストによるアルゴリズムのカラーグラデーション

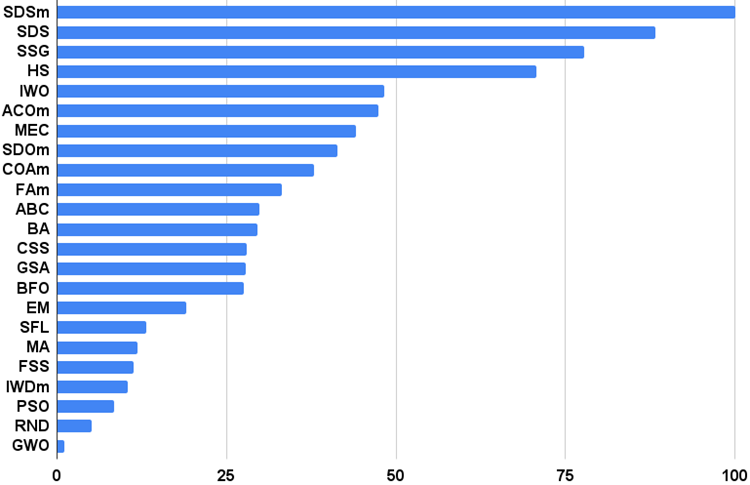
図6：アルゴリズムのテスト結果のヒストグラム（0から100までのスケールで、多ければ多いほど良いです。

アーカイブには、記事で適用されている方法で格付けを計算するためのスクリプトが含まれています）。

修正螺旋ダイナミクス最適化（SDOm）アルゴリズムの長所と短所：

長所
1. 外部パラメータが少ない
2.実装がシンプル
3.動作速度

短所
1. 結果のばらつきが大きい
2.局所的な極端さから抜け出せない傾向がある

この記事には、過去の記事で説明したアルゴリズムコードの最新版を更新したアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。