MetaTrader 5 / 例
English Русский 中文 Español Deutsch Português
preview
人工電界アルゴリズム(AEFA)

人工電界アルゴリズム(AEFA)

MetaTrader 5 — 例 | 10 2月 2025, 11:41
79 0
Andrey Dik
Andrey Dik
内容
  1. はじめに
  2. アルゴリズムの実装
  3. テスト結果


はじめに

人工電界アルゴリズムは、テクノロジーと自然の調和を具現化した素晴らしい創造物です。クーロンの静電気力の法則に着想を得たこのアルゴリズムは、電気現象をモデル化し、複雑な最適化問題を解決する独自の能力で注目を集めています。自然法則に関連する既存のアルゴリズム（例：電荷システム探索(CSS)、電磁気学に似たアルゴリズム(EM)、重力探索アルゴリズム(GSA)など）と比較して、人工電界アルゴリズムは、研究者にとって非常に刺激的で興味深い革新です。

人工電界アルゴリズムは、クーロンの法則に基づいています。クーロンの法則によれば、2つの荷電粒子間の静電気力（引力または反発力）は、両者の電荷の積に正比例し、それらの間の距離の2乗に反比例します。提案されたアルゴリズムでは、エージェントを荷電粒子として扱い、その強さは電荷によって決まります。これらの粒子は、静電気力によって互いに引き寄せたり反発したりします。この力によって、物体は探索空間内を移動します。したがって、電荷は静電気力を通じた直接的なコミュニケーション手段として使用され、電荷の位置は問題の解に対応します。電荷は、候補解の適応度および集団の適応度に基づいて定義されます。提案されたアルゴリズムでは、最も高い電荷を持つ荷電粒子（「最良の」個体）が、より低い電荷を持つ他のすべての粒子を引き寄せ、探索空間内をゆっくりと移動する静電力の引力のみを考慮します。

このように、AEFAは、クーロンの静電気力の第1法則（同じ電荷を持つ粒子は互いに反発し、異なる電荷を持つ粒子は引き寄せ合う）およびクーロンの静電気力の第2法則（異なる電荷を持つ粒子間の引力または同じ電荷を持つ粒子間の反発力は、それらの電荷の積に正比例し、電荷の中心間の距離の2乗に反比例する）と運動の法則（任意の電荷の現在の速度は、以前の速度と速度変化の合計に等しい）に従う孤立した電荷システムとして考えることができます。あらゆる電荷の速度または加速度の変化は、システムに作用する力を粒子の質量で割ったものに等しくなります。

AEFA（人工電界アルゴリズム）は、以下の研究者によって開発されました。

1. Anita - Department of Sciences and Humanities, Uttarakhand National Institute of Technology, Srinagar（インド）
2. Anupam Yadav - Department of Mathematics, Dr.B.R.Ambedkar National Institute of Technology Jalandhar（インド）

AEFAは2019年に提案され、「Swarm and Evolutionary Computation」誌に掲載されました。記事の著者は、電場と荷電粒子の概念が、2つの荷電粒子間の引力や反発力のメカニズムを理解するための強力な理論を提供することを指摘しています。したがって、AEFAは静電気力の原理を利用して、母集団最適化アルゴリズムを開発しています。


アルゴリズムの実装

AEFA にはさまざまな数式が含まれていますが、それらを説明する前に、重要なポイントを整理しておきましょう。

  • 本アルゴリズムのエージェント（意思決定要素）は、静電気力の作用を受けて移動する荷電粒子として表されます。
  • 粒子の電荷は、その粒子自身の最良の結果と、現在の集団内での最良・最悪の結果に基づいて決まります（最適化の過程全体での最高値ではなく、あくまで現在の集団内の値を使用します）。
  • 粒子に作用する力は、粒子間の電荷と距離に依存します。
  • クーロン定数 K(t)は、反復が進むにつれて減少し、大域探索と局所最適化のバランスを調整します。

では、アルゴリズムの数式を詳しく見ていきましょう。

探索空間の次元数をd、粒子数をNとします。各粒子iの位置は、X_i = (x_1, x_2, ..., x_d)、i = 1, 2, ..., Nとして表されます。
各粒子がこれまでに発見した最良の位置をP_i、集団全体の最良の位置をP_bestとします。

1. クーロンの法則（静電気力）：F_ij = K * Q_i * Q_j / R^2、ここで

  • F_ij：粒子 iとjの間に働く静電気力
  • K：クーロン定数
  • Q_iとQ_j：それぞれ粒子iと粒子jの電荷
  • R：粒子iと粒子jの間の距離

2. Q_i電荷周辺の電場：E_i = F_ij / Q_i 、ここで

  • E_i：粒子iの周囲の電場
  • F_ij：粒子iに作用する静電気力

3. ニュートンの運動方程式（粒子の加速度）：a_i = F_ij / M、ここで

  • a_i：粒子iの加速度
  • F_ij：粒子に作用する力
  • M：粒子の質量

4. 電場による粒子加速の式：a_i = E_i * Q_i / M、ここで

  • a_i：粒子iの加速度
  • E_i：粒子周辺の電場
  • Q_i：粒子の電荷
  • M：粒子の質量

5. 最適な粒子位置の更新： p_di (t+1) = {p_di (t)（f (X_i (t+1)) > f (X_i (t))の場合）、X_i (t+1) = X_i (t)（その他の場合）}、ここで

  • p_di (t)：時刻tにおける粒子iの適応度
  • p_di (t+1)：時刻(t+1)における粒子i の適応度
  • X_i (t)：時刻tにおける粒子iの位置
  • X_i (t+1)：時刻(t+1)における粒子iの新しい位置
  • f(X_i (t))：時刻tにおける粒子iの前回の位置での評価関数値
  • f(X_i (t+1))：時刻(t+1)における粒子iの新しい位置での評価関数値

6. 粒子iに対する粒子jの力：F_dij (t) = K (t) * (Q_i (t) * Q_j (t) * (p_dj (t) - X_di (t))) / (R_ij (t)^2 + ε)、ここで

  • F_dij (t)：時刻tにおける粒子iにに対する粒子jの力
  • K (t)：時刻tにおけるクーロン定数
  • Q_i (t)とQ_j (t)：時刻tにおける粒子iと粒子jの電荷
  • p_dj (t)：時刻tにおける粒子jの最適位置
  • X_di (t)：時刻tにおける粒子iの位置
  • R_ij (t)：時刻tにおける粒子iと粒子j間のユークリッド距離
  • ε：ゼロ除算を防ぐための小さな定数

7. 粒子iと粒子jの間のユークリッド距離：R_ij (t) = (X_i (t) - X_j (t))^2

8. クーロン定数：K (t) = K_0 * exp (-α * t / maxiter)、ここで

  • K_0：初期クーロン定数
  • α：外部パラメータ
  • t：現在の時刻（エポック）
  • maxiter：最大反復回数

9. 粒子iに作用する合力：F_di (t) = Σ (rand () * F_dij (t))、j=(1からN)、 j≠i、ここで

  • F_di (t)：時刻tにおける粒子iに作用する合力
  • rand ()：[0, 1]の範囲の乱数
  • N ：探索空間内の粒子の数

10. 粒子iに作用する電場：E_di (t) = F_di (t) / Q_i (t)、ここで

  • E_di (t)：時刻tにおける粒子iに作用する電場
  • F_di (t)：粒子iに作用する合力
  • Q_i (t)：時刻tにおける粒子iの電荷

11. 時刻t+1における粒子速度iの更新：V_i (t+1) = rand () * V_i (t) + a_i (t)、ここで

  • V_i(t)：前回の速度
  • a_i(t)：粒子に影響を与える加速度
  • rand ()：[0, 1]の範囲の乱数

12. 粒子iの位置を次の時点に更新する：t+1:X_i (t+1) = X_i (t) + V_i (t+1)、ここで

  • V_i (t+1)：新しい速度

13. 集団内のすべての粒子の電荷が同じであり、すべてのi、j = 1、2、...、Nに対してQ_i (t) = Q_j (t)であることを指定する式

14. 時刻tにおける各粒子iの相対電荷 q_i (t)の計算：q_i (t) = exp ((fit_p_i (t) - worst (t)) / (best (t) - worst (t)))、ここで

  • fit_p_i (t)：粒子の個体的最適位置の適合度値
  • fit_best (t)：大域的最適位置の適合度値
  • fit_worst(t)：集団内の最悪の粒子の適応度値

15. 式：Q_i (t) = q_i (t) / Σ_j=1...N q_j (t)
この式は、すべての粒子の相対電荷q_i(t)を 正規化し、その合計が1になるようにします。このようにして、各粒子の正規化された電荷Q_i(t)が得られます。

16. 式：best (t) = max (fit_j (t))、j = 1, 2,..., N
この式は、すべての粒子の適応度の最大値として、時刻tにおける集団内のbest (t)値である現在の最良適応度値を計算します。

17. 式：worst (t) = min (fit_j (t)) for j = 1, 2,..., N
この式は、時刻tにおける集団内の現在の最悪の適応度値waste (t)を、すべての粒子の適応度値の最小値として計算します。

アルゴリズム内の粒子運動の法則の式がわかったので、将来MQL5でAEFA アルゴリズム コードを記述するのに役立つ疑似コードを作成できます。


AEFAの疑似コード

手順1：初期化

- 粒子の位置をランダムに初期化します。
- 各粒子の目的関数の値を計算します。
- 現在の反復を t = 0に設定します。

手順2：停止条件が満たされるまで粒子の位置を更新する

1. 式(8)に従ってクーロン定数K(t)を計算します。
2. 現在の反復における評価関数の最良値fit_best(t)と最悪値fit_worst(t)を計算します。
3. 各粒子i = 1, 2, ..., Nについて以下をおこないます。
   a. 式(14)に従って Q_i(t)粒子電荷を計算します。
   b. 式(6)に従って粒子jから粒子iに作用する力を計算します。
   c. 式(9)を用いて粒子iに作用する全力を計算します。
   d. 式(4)を用いて粒子iの加速度を計算します。
   （例：式(11)を使用して速度を更新し、式(12)を使用して粒子iの位置を更新します。
4. 反復カウンタt = t + 1を増やします。

手順3：停止条件。停止条件を確認します（例：最大反復回数に達した場合）。条件が満たされない場合は、手順2に進みます。

K0

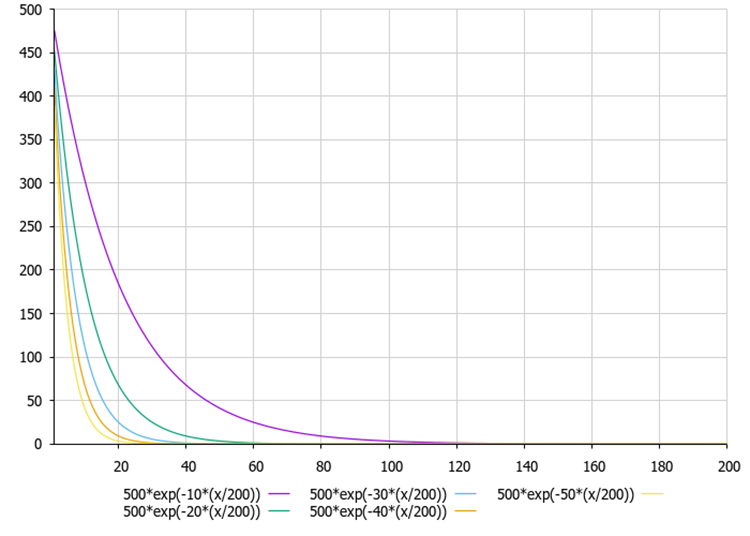
図1：クーロンの公式による静電力のα比 （外部パラメータ）への依存性

ついにアルゴリズムの説明、式、疑似コードが分かりました。次に、コードの生成に進みましょう。

アルゴリズム内のエージェントを記述するために使用されるS_AEFA_Agent構造体を実装します。この構造体には以下のフィールドが含まれます。

  • best_fitness：この変数はエージェントの最適な適応度を表します。
  • best_position[]：検索空間におけるエージェントの最適位置の座標の配列
  • velocity[]：粒子の速度ベクトルを表す配列
  • charge：エージェントの電荷
  • relative_charge：粒子の相対電荷

この構造体は、粒子（エージェント）を初期化するInit関数も定義します。これは、エージェント座標の数を示すcoordsパラメータを取り、それぞれbest_position配列とvelocity配列のサイズを変更します。その後、best_fitness～DBL_MAXの最小のdouble値に設定し、chargeとrelative_chargeを0に設定します。

このコードは、人工電界アルゴリズムでエージェントを記述するための基礎を提供し、この文脈でのさらなる作業に備えます。

//——————————————————————————————————————————————————————————————————————————————
struct S_AEFA_Agent
{
    double best_fitness;
    double best_position [];
    double velocity      [];
    double charge;
    double relative_charge;

    void Init (int coords)
    {
      ArrayResize (best_position, coords);
      ArrayResize (velocity,      coords);

      best_fitness    = -DBL_MAX;
      charge          = 0;
      relative_charge = 0;
    }
};
//——————————————————————————————————————————————————————————————————————————————

C_AOクラスから継承されたC_AO_AEFAクラスについて説明します。クラス内では次のメソッドと変数が定義されています。

  • C_AO_AEFA：変数とパラメータの値が設定されるコンストラクタ
  • SetParams：params配列に格納されている値に基づいてパラメータを設定するメソッド
  • Init：値のセットを受け取り、初期化を実行するメソッド
  • MovingおよびRevision：アルゴリズムの主なロジックを実行するメソッド
  • K0、alpha、particlesMass、epsilonなどのdouble型のいくつかの変数、agent配列および他のprivate変数
  • CalculateK、UpdateCharges、CalculateForces、CalculateDistance、UpdateVelocityAndPosition privateメソッドは検索空間内で粒子を移動する操作を実行します。
//——————————————————————————————————————————————————————————————————————————————
class C_AO_AEFA : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_AEFA () { }
  C_AO_AEFA ()
  {
    ao_name = "AEFA";
    ao_desc = "Artificial Electric Field Algorithm";
    ao_link = ""; //"https://www.mql5.com/ja/articles/15162";

    popSize      = 50;
    K0           = 500.0;
    alpha        = 20.0;
    particleMass = 1.0;

    ArrayResize (params, 4);

    params [0].name = "popSize";       params [0].val = popSize;
    params [1].name = "K0";            params [1].val = K0;
    params [2].name = "alpha";         params [2].val = alpha;
    params [3].name = "particleMass";  params [3].val = particleMass;
  }

  void SetParams ()
  {
    popSize      = (int)params [0].val;
    K0           = params      [1].val;
    alpha        = params      [2].val;
    particleMass = params      [3].val;
  }

  bool Init (const double &rangeMinP  [],
             const double &rangeMaxP  [],
             const double &rangeStepP [],
             const int     epochsP = 0);

  void Moving ();
  void Revision ();

  //----------------------------------------------------------------------------
  double K0;
  double alpha;
  double particleMass;
  double epsilon;

  S_AEFA_Agent agent [];

  private: //-------------------------------------------------------------------
  int    epochs;
  int    epochNow;
  double K;
  double CalculateK                (int t);
  void   UpdateCharges             (double best, double worst);
  void   CalculateForces           ();
  double CalculateDistance         (const double &x1 [], const double &x2 []);
  void   UpdateVelocityAndPosition (int i);
};
//——————————————————————————————————————————————————————————————————————————————

次に、C_AO_AEFAクラスのInitメソッドの実装に進みます。このメソッドは、指定されたパラメータを使用してAEFAアルゴリズムを初期化します。

以下は、Initメソッドの入力です。

  • rangeMinP：最小範囲境界の値の配列
  • rangeMaxP：最大範囲制限の値の配列
  • rangeStepP：範囲手順値の配列
  • epochsP：エポックの数（デフォルトは0）

以下は、Initメソッドで実行されるアクションです。

1. StandardInitメソッドが呼び出され、rangeMinP、rangeMaxP、rangeStepP配列を受け取ります。StandardInitメソッドがfalseを返した場合、Initはfalseを返します。
2. epochsおよびepochNow変数がそれぞれepochsPおよび0に設定されます。
3. agent配列がpopSizeにサイズ変更されます。
4. ループでは、agent配列の各要素は、coords配列を渡してInitメソッドを呼び出すことによって初期化されます。
5. epsilon変数は1e-10に設定されます。
6. メソッドがtrueを返します。

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_AEFA::Init (const double &rangeMinP  [],
                      const double &rangeMaxP  [],
                      const double &rangeStepP [],
                      const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  epochs   = epochsP;
  epochNow = 0;

  ArrayResize (agent, popSize);
  for (int i = 0; i < popSize; i++) agent [i].Init (coords);

  epsilon = 1e-10;

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_AEFAクラスの Moving()メソッドに移りましょう。このメソッドでは、最適化アルゴリズムで粒子の位置が更新されます。何が起こっているのかを簡単に説明します。

1. epochNow変数の値が増加されます。
2. revision変数がfalseに等しい場合、粒子の初期位置が初期化されます。各粒子の座標は指定された範囲内のランダムな値に設定され、この値は指定された手順に従って変換されます。
3. revisionがtrueに等しい場合、各粒子の最良および最悪の関数推定値とともにK値が計算されます。力が計算され、各粒子の速度と位置が電荷とともに更新されます。

このメソッドの一般的な考え方は、粒子の運動法則の式を計算するための特別な方法を使用して、最適化アルゴリズム内の粒子の位置を更新することです。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AEFA::Moving ()
{
  epochNow++;

  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  K            = CalculateK (epochNow);
  double best  = -DBL_MAX;
  double worst =  DBL_MAX;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > best)  best  = a [i].f;
    if (a [i].f < worst) worst = a [i].f;
  }

  UpdateCharges   (best, worst);
  CalculateForces ();

  for (int i = 0; i < popSize; i++)
  {
    UpdateVelocityAndPosition (i);
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_AEFAクラスのCalculateK()メソッドでは、t（現在のエポックインデックス）とその他のパラメータK0、alpha、epochsに基づいてKパラメータを計算します。このメソッドでは以下をおこないます。

1. このメソッドは、アルゴリズムの現在のエポックのインデックスを表すパラメータtを入力として受け取ります。
2. 次にK値が計算されます。
3. 式に基づいた計算結果がメソッド値として返されます。

//——————————————————————————————————————————————————————————————————————————————
double C_AO_AEFA::CalculateK (int t)
{
  return K0 * MathExp (-alpha * t / epochs);
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_AEFAクラスのUpdateCharges()メソッドで、最良および最悪の適合値に基づいて粒子の変化を更新します。以下は、メソッド内のアクションの簡単な説明です。

1. sum_q変数が作成され、0に設定されます。
2. 次に、0からpopSizeまでの範囲内のすべての粒子を反復処理します。
3. ループ内では、各粒子の相対電荷が式を使用して計算されます。
4. 相対電荷値がsum_q変数に追加されます。
5. 次に、すべての粒子に対して2番目のループが発生し、各粒子に、相対電荷をsum_qで割った値に等しい電荷値が割り当てられます。

したがって、このメソッドでは、粒子の適合度に基づいて粒子の電荷が更新され、最高および最悪の適合度値と比較した相対的な品質が反映されます。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AEFA::UpdateCharges (double best, double worst)
{
  double sum_q = 0;

  for (int i = 0; i < popSize; i++)
  {
    agent [i].relative_charge = MathExp ((a [i].f - worst) / (best - worst));
    sum_q += agent [i].relative_charge;
  }
  for (int i = 0; i < popSize; i++)
  {
    agent [i].charge = agent [i].relative_charge / sum_q;
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_AEFAクラスのCalculateForces()メソッドとCalculateDistance()メソッドを提供しましょう。

CalculateDistance()メソッドは、2つの粒子の座標を表す2つの配列x1[]とx2[]を受け入れ、それらの間の空間距離を計算します。これをおこなうには、配列のすべての座標を反復処理し、各座標に対して配列の対応する要素の差の二乗を計算し、その後これらの二乗を合計します。結果の合計の平方根が抽出され、この値が空間内の2点間の距離（ユークリッド距離）として返されます。

CalculateForces()メソッドは、各粒子に作用する力を計算します。各粒子について、他のすべての粒子との関係で力のベクトルが計算されます。同一の粒子を除く各粒子のペア(i != j)については、CalculateDistance()メソッドを使用してそれらの間の距離が計算されます。次に、空間内の各座標について、粒子の電荷、粒子の位置、粒子間の距離を含む式を使用して、粒子に作用する力が計算されます。結果は各座標ごとに合計され、結果として得られた力が粒子の電荷で割られ、粒子の速度への影響が考慮されます。

したがって、これらのメソッドは、アルゴリズム内の粒子間に作用する力と空間内の粒子間の距離をそれぞれ計算します。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AEFA::CalculateForces ()
{
  double force [];
  ArrayResize (force, coords);

  for (int i = 0; i < popSize; i++)
  {
    ArrayInitialize (force, 0);

    for (int j = 0; j < popSize; j++)
    {
      if (i != j)
      {
        double R = CalculateDistance (a [i].c, a [j].c);

        for (int d = 0; d < coords; d++)
        {
          force [d] += u.RNDprobab () * K *
                       (agent [i].charge * agent [j].charge * (agent [j].best_position [d] - a [i].c [d])) /
                       (R * R + epsilon);
        }
      }
    }

    for (int d = 0; d < coords; d++)
    {
      agent [i].velocity [d] = force [d] / agent [i].charge;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
double C_AO_AEFA::CalculateDistance (const double &x1 [], const double &x2 [])
{
  double sum = 0;
  for (int d = 0; d < coords; d++)
  {
    sum += (x1 [d] - x2 [d]) * (x1 [d] - x2 [d]);
  }
  return MathSqrt (sum);
}
//——————————————————————————————————————————————————————————————————————————————

次は、C_AO_AEFAクラスのUpdateVelocityAndPosition()メソッドです。このメソッドは、インデックスiの粒子の速度と位置を更新します。空間内の粒子の各座標に対して次のことが起こります。

1. 粒子の電荷、現在の速度、粒子の質量に応じて加速度が計算されます。
2. 粒子の速度は、現在の速度と加速度にランダムなコンポーネントを乗算して追加することによって更新されます。
3. 新しい速度を現在の位置に追加することによって、粒子の位置が更新されます。次に、u.SeInDiSp()を使用して、新しい位置が各座標に対して指定された最小値と最大値内に制限されます。

したがって、UpdateVelocityAndPosition()メソッドは、加速度、ランダム要因、および空間内の粒子の位置に対する制約を考慮して、最適化アルゴリズム内の粒子の速度と位置を更新します。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AEFA::UpdateVelocityAndPosition (int i)
{
  for (int d = 0; d < coords; d++)
  {
    double acceleration = (agent [i].charge * agent [i].velocity [d]) / particleMass;

    agent [i].velocity [d] = (u.RNDfromCI (0, 1)) * agent [i].velocity [d] + acceleration;

    a [i].c [d] += agent [i].velocity [d];
    a [i].c [d] = u.SeInDiSp (a [i].c [d], rangeMin [d], rangeMax [d], rangeStep [d]);
  }
}
//——————————————————————————————————————————————————————————————————————————————

最後に、C_AO_AEFAクラスのRevision()メソッドがあります。このメソッドでは、粒子の最適位置と最適適合値、およびfBの大域的最適解に関する情報が更新されます。このメソッドでは次をおこないます。

1. ind変数は、最適解配列内の位置のフラグとインデックスとして作成され、-1に設定されます。
2. 次に、0からpopSizeまでの範囲内のすべての粒子を反復処理します。
3. ループ内では、粒子の適応度関数の値が fB 値を超えているかどうかがチェックされます。超えている場合、fBが更新され、ind変数がiに設定されます。
4. 次に、粒子の適応度が、すべてのエポックにおけるその粒子の最良の適応度（agent[i].best_fitnessに格納）よりも大きいかどうかがチェックされます。大きい場合は、最高スコアと順位が更新されます。
5. 最後に、indが-1と等しくない場合、cBの位置はindインデックスを持つ粒子の位置をコピーすることによって更新されます。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AEFA::Revision ()
{
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }

    if (a [i].f > agent [i].best_fitness)
    {
      agent [i].best_fitness = a [i].f;
      ArrayCopy (agent [i].best_position, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);
}
//——————————————————————————————————————————————————————————————————————————————


3. テスト結果

以下は、AEFAテストスタンドの結果です。

AEFA|Artificial Electric Field Algorithm|20.0|1000.0|10.0|100.0|
=============================
5 Hilly's; Func runs:10000; result:0.8769988087850553
25 Hilly's; Func runs:10000; result:0.617530930198765
500 Hilly's; Func runs:10000; result:0.2523539056281608
=============================
5 Forest's; Func runs:10000; result:0.927287032866128
25 Forest's; Func runs:10000; result:0.7269761843712702
500 Forest's; Func runs:10000; result:0.18063577020760296
=============================
5 Megacity's; Func runs:10000; result:0.6661538461538462
25 Megacity's; Func runs:10000; result:0.11630769230769236
500 Megacity's; Func runs:10000; result:0.0950769230769239
=============================
All score:4.45932 (49.55%)

テストごとに結果に大きなばらつきがあることがわかります。さらに、このアルゴリズムは高次元関数を扱うときに検索能力が非常に弱いことが示されており、これは結果によっても確認されています。離散関数を扱う際に特別な問題が特定されています。

Hilly

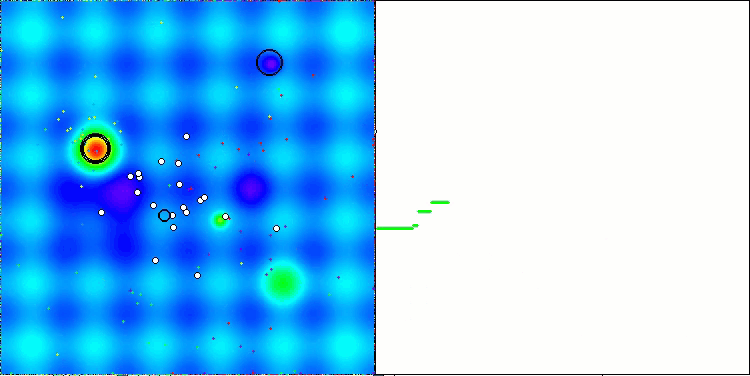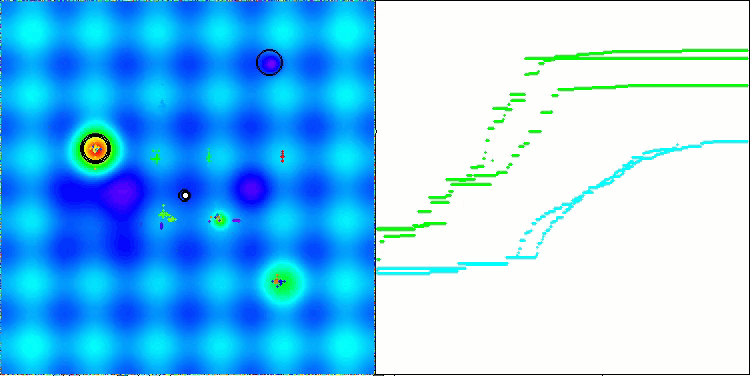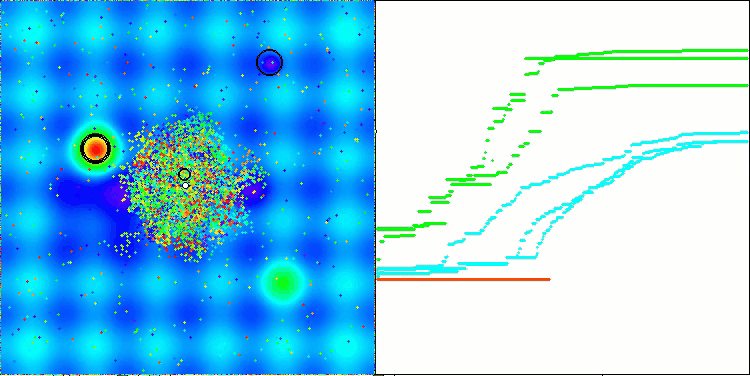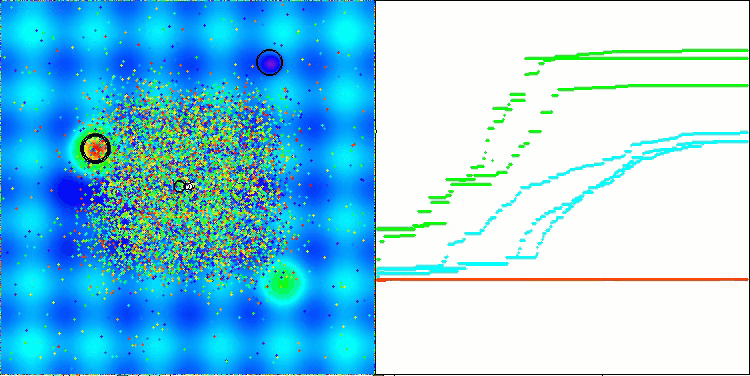
  Hillyテスト関数のAEFA

Forest

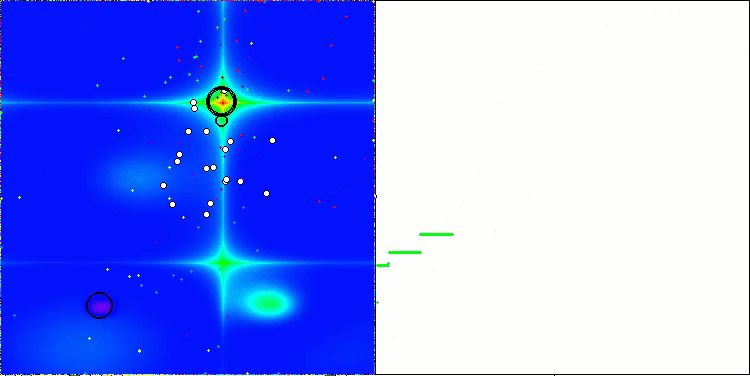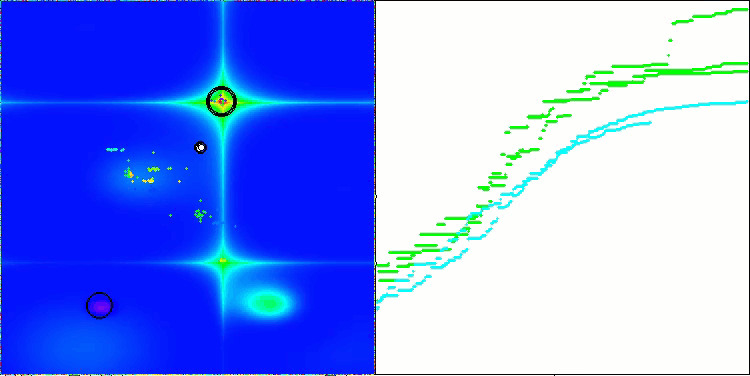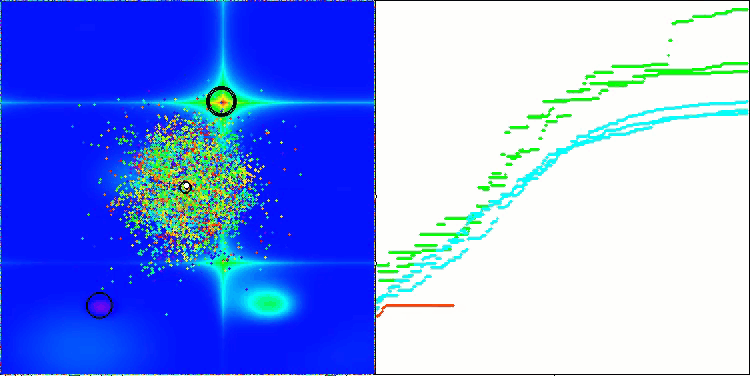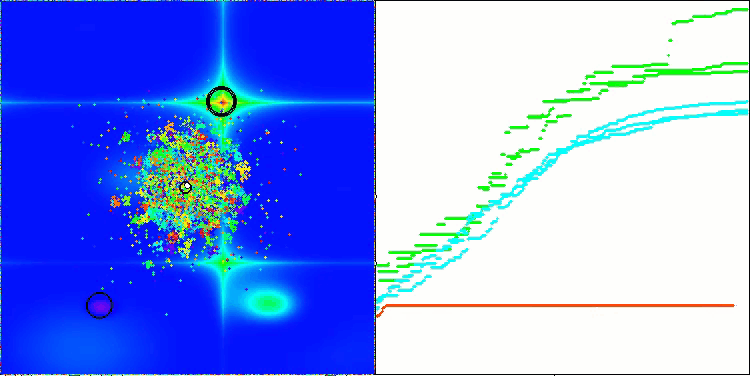
  Forestテスト関数のAEFA

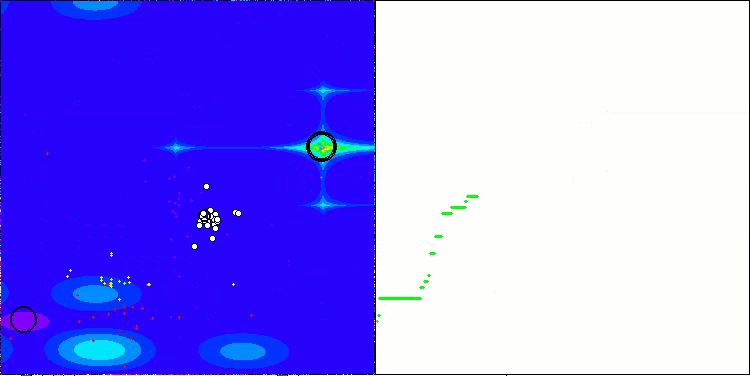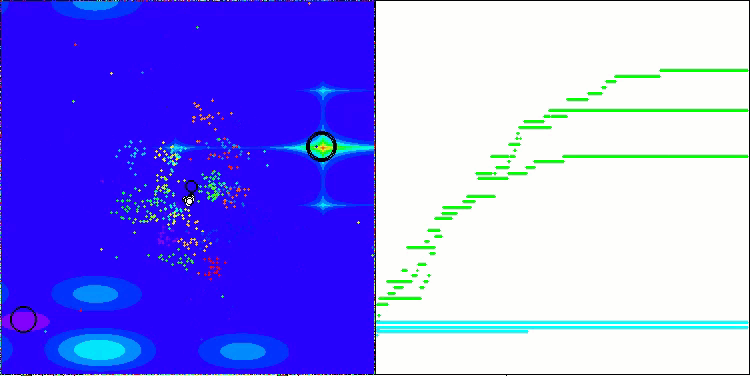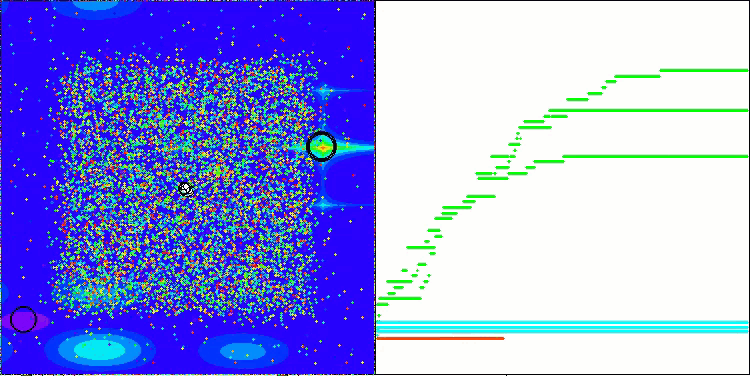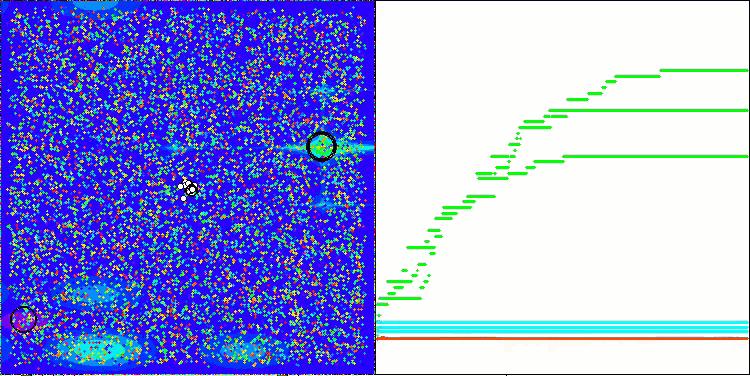
  Megacityテスト関数のAEFA

AEFAアルゴリズムの重要な特性について強調したい点があります。適応度関数を10,000回実行する標準テストを実施した後、実行回数を100,000回に増やして追加の実験をおこないました。その結果は期待を大きく上回るものでした。パラメータの少ない多くの関数において、適応度関数の実行回数を増やすことで、アルゴリズムは100%の収束を達成しました。ここで重要なのは、格付表に掲載されているすべてのアルゴリズムが、たとえ上位に位置するものであっても、実行回数を増やせば必ずしも100%の収束を達成できるわけではないという点です。多くのアルゴリズムは局所極値に陥りやすく、それ以上の探索が難しくなります。しかし、AEFA はこのような行き詰まりに対して耐性を持つことが示されました。一方で、本アルゴリズムも多次元空間での探索、特に離散関数に対する探索においては、他のアルゴリズムと同様の困難に直面することが確認されました。

以下は、100,000 回のテスト関数実行における AEFA テストスタンドの結果です。

SDSm|Stochastic Diffusion Search M|100.0|100.0|0.05|
=============================
5 Hilly's; Func runs:100000; result:0.9874670077970368
25 Hilly's; Func runs:100000; result:0.9355482229513405
500 Hilly's; Func runs:100000; result:0.5943074120378588
=============================
5 Forest's; Func runs:100000; result:0.994126703499673
25 Forest's; Func runs:100000; result:0.9627011069578397
500 Forest's; Func runs:100000; result:0.5628894538341265
=============================
5 Megacity's; Func runs:100000; result:0.9015384615384615
25 Megacity's; Func runs:100000; result:0.7264615384615385
500 Megacity's; Func runs:100000; result:0.37464615384615396
=============================
All score:7.03969 (78.22%)

このアルゴリズム収束の特徴は、以下の画像で確認できます。

MrunsHilly

MrunsForest

MrunsMegacity

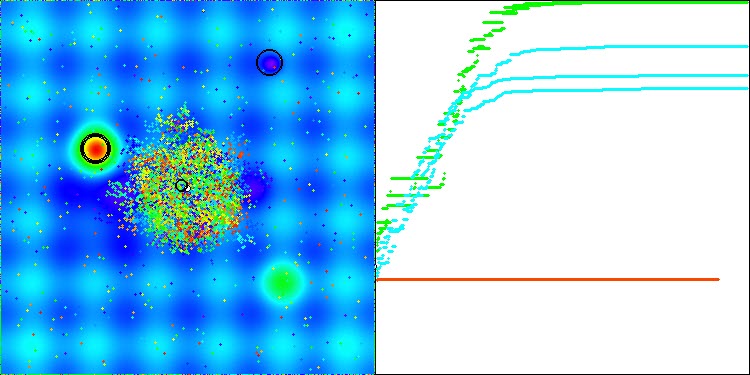
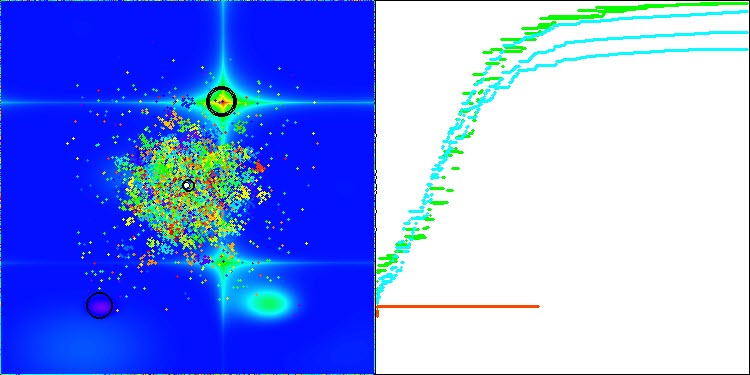
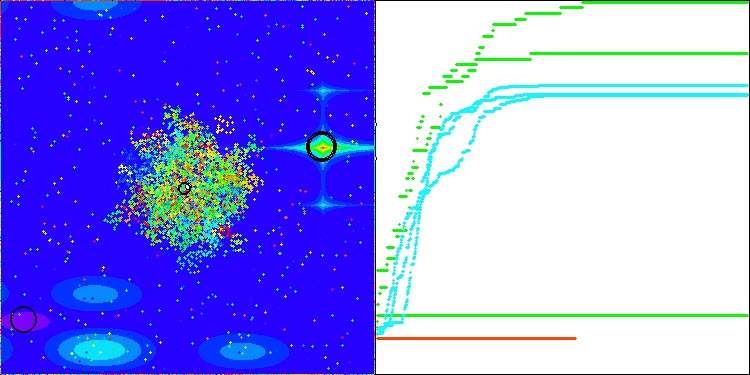
以下は、母集団最適化アルゴリズムの評価表です。

# AO 詳細 Hilly Hilly最終 Forest Forest最終 Megacity（離散） Megacity最終 最終結果 MAXの%
10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F)
1 BGA バイナリ遺伝的アルゴリズム 0.99989 0.99518 0.42835 2.42341 0.96153 0.96181 0.32027 2.24360 0.91385 0.95908 0.24220 2.11512 6.782 75.36
2 ANS across neighbourhood search 0.94948 0.84776 0.43857 2.23581 1.00000 0.92334 0.39988 2.32323 0.70923 0.63477 0.23091 1.57491 6.134 68.15
3 CLA コードロックアルゴリズム 0.95345 0.87107 0.37590 2.20042 0.98942 0.91709 0.31642 2.22294 0.79692 0.69385 0.19303 1.68380 6.107 67.86
4 (P+O)ES (P+O）進化戦略 0.92256 0.88101 0.40021 2.20379 0.97750 0.87490 0.31945 2.17185 0.67385 0.62985 0.18634 1.49003 5.866 65.17
5 CTA 彗尾アルゴリズム 0.95346 0.86319 0.27770 2.09435 0.99794 0.85740 0.33949 2.19484 0.88769 0.56431 0.10512 1.55712 5.846 64.96
6 SDSm 確率的拡散探索M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
7 ESG 社会母集団の進化 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
8 SIA 等方的焼きなまし 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
9 ACS 人工協調探索 0.75547 0.74744 0.30407 1.80698 1.00000 0.88861 0.22413 2.11274 0.69077 0.48185 0.13322 1.30583 5.226 58.06
10 TSEA 亀甲進化アルゴリズム 0.96798 0.64480 0.29672 1.90949 0.99449 0.61981 0.22708 1.84139 0.69077 0.42646 0.13598 1.25322 5.004 55.60
11 DE 差分進化 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
12 CRO 化学反応の最適化 0.94629 0.66112 0.29853 1.90593 0.87906 0.58422 0.21146 1.67473 0.75846 0.42646 0.12686 1.31178 4.892 54.36
13 BSA 鳥群アルゴリズム 0.89306 0.64900 0.26250 1.80455 0.92420 0.71121 0.24939 1.88479 0.69385 0.32615 0.10012 1.12012 4.809 53.44
14 HS ハーモニー検索 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
15 SSG 苗木の播種と育成 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
16 (PO)ES (PO）進化戦略 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
17 BSO ブレインストーム最適化 0.93736 0.57616 0.29688 1.81041 0.93131 0.55866 0.23537 1.72534 0.55231 0.29077 0.11914 0.96222 4.498 49.98
18 WOAm 鯨最適化アルゴリズムM 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
19 AEFA 人工電界アルゴリズム 0.87700 0.61753 0.25235 1.74688 0.92729 0.72698 0.18064 1.83490 0.66615 0.11631 0.09508 0.87754 4.459 49.55
20 ACOm 蟻コロニー最適化M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
21 BFO-GA 細菌採食の最適化：Ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
22 MEC Mind Evolutionary Computation 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
23 IWO 侵入雑草最適化 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
24 Micro-AIS 微小人工免疫系 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54
25 COAm カッコウ最適化アルゴリズムM 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21
26 SDOm 螺旋ダイナミクス最適化M 0.74601 0.44623 0.29687 1.48912 0.70204 0.34678 0.10944 1.15826 0.42833 0.16767 0.03663 0.63263 3.280 36.44
27 NMm ネルダー=ミード法M 0.73807 0.50598 0.31342 1.55747 0.63674 0.28302 0.08221 1.00197 0.44667 0.18667 0.04028 0.67362 3.233 35.92
28 FAm ホタルアルゴリズムM 0.58634 0.47228 0.32276 1.38138 0.68467 0.37439 0.10908 1.16814 0.28667 0.16467 0.04722 0.49855 3.048 33.87
29 GSA 重力探索法 0.64757 0.49197 0.30062 1.44016 0.53962 0.36353 0.09945 1.00260 0.32667 0.12200 0.01917 0.46783 2.911 32.34
30 BFO 細菌採餌最適化 0.61171 0.43270 0.31318 1.35759 0.54410 0.21511 0.05676 0.81597 0.42167 0.13800 0.03195 0.59162 2.765 30.72
31 ABC 人工蜂コロニー 0.63377 0.42402 0.30892 1.36671 0.55103 0.21874 0.05623 0.82600 0.34000 0.14200 0.03102 0.51302 2.706 30.06
32 BA コウモリアルゴリズム 0.59761 0.45911 0.35242 1.40915 0.40321 0.19313 0.07175 0.66810 0.21000 0.10100 0.03517 0.34617 2.423 26.93
33 SA 焼きなまし 0.55787 0.42177 0.31549 1.29513 0.34998 0.15259 0.05023 0.55280 0.31167 0.10033 0.02883 0.44083 2.289 25.43
34 IWDm intelligent water drops M 0.54501 0.37897 0.30124 1.22522 0.46104 0.14704 0.04369 0.65177 0.25833 0.09700 0.02308 0.37842 2.255 25.06
35 PSO 粒子群最適化 0.59726 0.36923 0.29928 1.26577 0.37237 0.16324 0.07010 0.60572 0.25667 0.08000 0.02157 0.35823 2.230 24.77
36 ボイド ボイドアルゴリズム 0.43340 0.30581 0.25425 0.99346 0.35718 0.20160 0.15708 0.71586 0.27846 0.14277 0.09834 0.51957 2.229 24.77
37 MA モンキーアルゴリズム 0.59107 0.42681 0.31816 1.33604 0.31138 0.14069 0.06612 0.51819 0.22833 0.08567 0.02790 0.34190 2.196 24.40
38 SFL Shuffled Frog-Leaping 0.53925 0.35816 0.29809 1.19551 0.37141 0.11427 0.04051 0.52618 0.27167 0.08667 0.02402 0.38235 2.104 23.38
39 FSS 魚群検索 0.55669 0.39992 0.31172 1.26833 0.31009 0.11889 0.04569 0.47467 0.21167 0.07633 0.02488 0.31288 2.056 22.84
40 RND ランダム 0.52033 0.36068 0.30133 1.18234 0.31335 0.11787 0.04354 0.47476 0.25333 0.07933 0.02382 0.35648 2.014 22.37
41 GWO 灰色オオカミオプティマイザ 0.59169 0.36561 0.29595 1.25326 0.24499 0.09047 0.03612 0.37158 0.27667 0.08567 0.02170 0.38403 2.009 22.32
42 CSS 荷電系探索 0.44252 0.35454 0.35201 1.14907 0.24140 0.11345 0.06814 0.42299 0.18333 0.06300 0.02322 0.26955 1.842 20.46
43 EM 電磁気学的アルゴリズム 0.46250 0.34594 0.32285 1.13129 0.21245 0.09783 0.10057 0.41085 0.15667 0.06033 0.02712 0.24412 1.786 19.85


まとめ

異なる次元のテスト関数に対する人工電界アルゴリズム(AEFA)の結果に基づいて、次の結論を導き出すことができます。

1. AEFAは、Hilly、Forest、Megacityなどのさまざまなテスト関数で満足のいく結果を示しました。ただし、離散Megacity関数に対する結果は他の関数と比べて劣っています。
2. 本アルゴリズムは、多数の関数評価（100,000回）において高い性能を発揮し、低次元空間における収束精度を最大100%まで向上させることができます。
3. AEFAの総合スコアは4.45932 (49.55%)であり、評価表では19位にランクインし、中程度の位置を占めています。

標準テストにおいてAEFAアルゴリズムは、異なる次元のテスト関数すべてにおいて最良の結果を示したわけではありません。しかし、追加の利点として、適応度関数の評価回数を増やすことで、総合スコア7.03969 (78.22%)という優れた結果を達成できます。特に、滑らかな表面を持つ低次元空間の問題において有用なアルゴリズムとなり得ます。

Tab

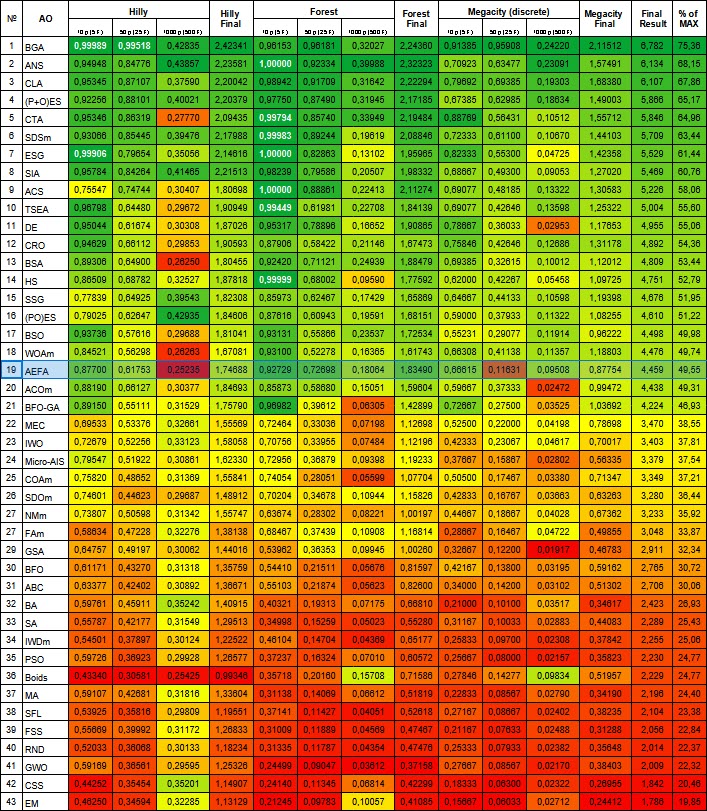
図2：関連テストによるアルゴリズムのカラーグラデーション 0.99以上の結果は白で強調表示される

チャート

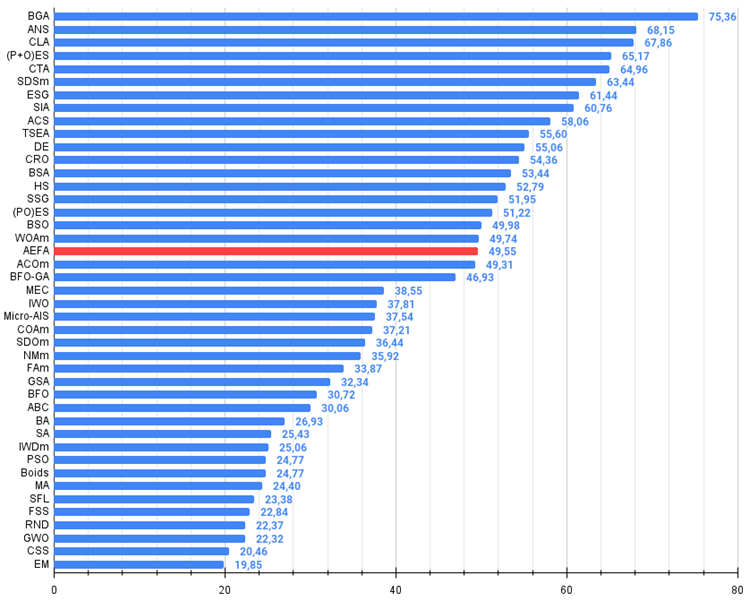
図3：アルゴリズムのテスト結果のヒストグラム（0から100までのスケールで、多ければ多いほど良い、

ここで、100は理論的に可能な最大の結果であり、アーカイブにはレーティング表を計算するスクリプトが含まれている）


AEFA の長所と短所

長所

  1. 十分な数の適合関数の実行による低次元の滑らかな関数で優れた収束を見せる。
  2. 外部パラメータの数が比較的少ない。

短所

  1. 標準テストで使用される関数に関する結果が広範囲である。
  2. 離散関数に関する結果が弱い。
  3. スケーラビリティが非常に低い。
  4. 実装が複雑

この記事には、最新版のアルゴリズムコードを含むアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/15162

添付されたファイル |
ZIPをダウンロード
AEFA.zip (26.78 KB)
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動
適応型社会行動最適化(ASBO):Schwefel、ボックス=ミュラー法 適応型社会行動最適化(ASBO):Schwefel、ボックス=ミュラー法
この記事は、生物の社会的行動の世界と、それが新たな数学モデルであるASBO（適応型社会的行動最適化、Adaptive Social Behavior Optimization）の構築に与える影響について、興味深い洞察を提供します。生物社会におけるリーダーシップ、近隣関係、協力の原則が、革新的な最適化アルゴリズムの開発にどのように着想を与えるのかを探ります。
取引におけるニューラルネットワーク：時空間ニューラルネットワーク(STNN) 取引におけるニューラルネットワーク：時空間ニューラルネットワーク(STNN)
この記事では、時空間変換を活用し、今後の価格変動を効果的に予測する手法について解説します。STNNの数値予測精度を向上させるために、データの重要な側面をより適切に考慮できる連続アテンションメカニズムが提案されています。
多通貨エキスパートアドバイザーの開発（第15回）：実際の取引のためのEAの準備 多通貨エキスパートアドバイザーの開発（第15回）：実際の取引のためのEAの準備
既製のエキスパートアドバイザー(EA)の完成に徐々に近づくにつれ、取引戦略のテスト段階では二次的に思える問題にも注意を払う必要があります。これらの問題は、実際の取引に移行する際に重要となります。
取引におけるニューラルネットワーク：二重アテンションベースのトレンド予測モデル 取引におけるニューラルネットワーク：二重アテンションベースのトレンド予測モデル
前回の記事で取り上げた時系列の区分線形表現の活用について、引き続き議論します。本日は、この手法を他の時系列分析手法と組み合わせることで、価格動向の予測精度を向上させる方法を探ります。