MetaTrader 5 / トレーディング
English Русский Español Deutsch Português
preview
中心力最適化(CFO)アルゴリズム

中心力最適化(CFO)アルゴリズム

MetaTrader 5 — トレーディング |
18 0
Andrey Dik
Andrey Dik


内容

  1. はじめに
  2. アルゴリズムの実装
  3. テスト結果


はじめに

自然は、数十億年にわたる進化の過程において、多くの効率的な最適化機構を生み出してきました。研究者はこれらに着想を得て、新しいアルゴリズムを開発しています。そのような自然現象のひとつが重力です。重力は、宇宙空間における天体の運動を支配する基本的な力です。これまでにも、類似のアルゴリズムについて多くの分析がおこなわれてきました。

中心力最適化(Central Force Optimization, CFO)アルゴリズムは、重力運動学の原理を数値最適化の分野に適用しようとする試みです。このメタヒューリスティックアルゴリズムは、決定論的な運動法則に基づいており、多次元の解空間における仮想粒子の相互作用をシミュレートします。各粒子は、重力に相当する影響を受けながら、目的関数の値がより良い領域へと移動します。

CFOは、シンプルで直感的なメタファーに基づいています。すなわち、可能な解空間に多数の試行点（エージェント）が分布していると仮定します。各エージェントは、それが表す解の品質、すなわち目的関数の値に比例した「質量」を持ちます。質量の大きい天体が質量の小さい天体を引き寄せるのと同様に、最良の解を持つエージェントは仮想的な重力場を形成し、他のエージェントを引き寄せます。

各エージェントの運動は、ニュートンの運動法則に類似した規則に従います。加速度は、他のエージェントから受ける引力の総和によって決定され、位置の更新は運動学の方程式に基づいておこなわれます。アルゴリズムの重要な特徴のひとつは、その決定論的性質にあります。多くの他のメタヒューリスティック手法とは異なり、CFOはアルゴリズムの主要なループにおいて乱数を使用しません。


アルゴリズムの実装

CFOアルゴリズムの着想は、研究者たちが、「物理法則を最適解探索に適用したらどうなるのか」という疑問を抱いたことから始まりました。各点の高さが解の品質に対応する、起伏に富んだ広大な地形を想像してください。丘が高いほど、その地点に対応する解の品質は高くなります。目的は最も高い地点を見つけることですが、問題は地形全体を一度に見渡すことができない点にあります。その代わりに、地形内を移動し、自身の現在位置の高度を報告できる複数の研究者（エージェント）が存在すると考えます。

初期状態では、エージェントは探索領域全体にランダムに配置されます。低地に位置するものもあれば、丘の斜面にあるもの、小さな丘の頂上に偶然到達するものもあります。各エージェントは、それが位置する点の高さに比例した「質量」を持ちます。地点が高いほど、エージェントは「重く」なります。そして、ここからが最も重要な部分です。エージェントはランダムにさまようのではなく、重力の法則に従って運動します。「重い」エージェント、すなわちより良い解を見つけたエージェントが、「軽い」エージェント、すなわち劣った位置にあるエージェントを引き寄せると考えます。さらに、この引力は一方向にのみ作用します。良い解は悪い解を引き寄せますが、その逆は起こりません。

引力の大きさは、ニュートンの万有引力の法則に類似した規則に基づいて計算されます。これは、エージェント間の「質量」の差（解の品質の差）と、それらの間の距離に依存します。適応度関数の値が高いエージェントは、近くにある値の低いエージェントを強く引き寄せますが、遠くにあるエージェントにはほとんど影響を与えません。これらの力の作用により、各エージェントは加速され、移動を開始します。小さく「軽い」エージェントは、「重い」エージェントに向かって移動し、まるで球が丘の斜面を転がって頂上へ向かうかのように振る舞います。アルゴリズムの各ステップにおいて、エージェントは引力を再計算し、その運動を更新します。エージェントが探索領域の境界を越えようとした場合には、反射機構が作動します。これは、領域の端に壁があり、エージェントがそこから跳ね返されて許可された領域内に戻される様子に例えられます。

時間の経過とともに、エージェントは地形内の高い地点の周囲に集まり始めます。多くのエージェントが最も有望な領域に集中し、反復を重ねるごとにピークの位置がより正確に特定されていきます。理想的には、十分な反復回数を与えれば、すべてのエージェントは地形全体における大域的最大値、すなわち最も高い地点の周囲に収束します。

CFOの特徴は、本質的に決定論的アルゴリズムである点にあります。同一の初期エージェント配置で2回実行した場合、常に同じ結果が得られます。この点が、乱数に依存する多くの他のメタヒューリスティックアルゴリズムとの大きな違いです。 

CFOアルゴリズム

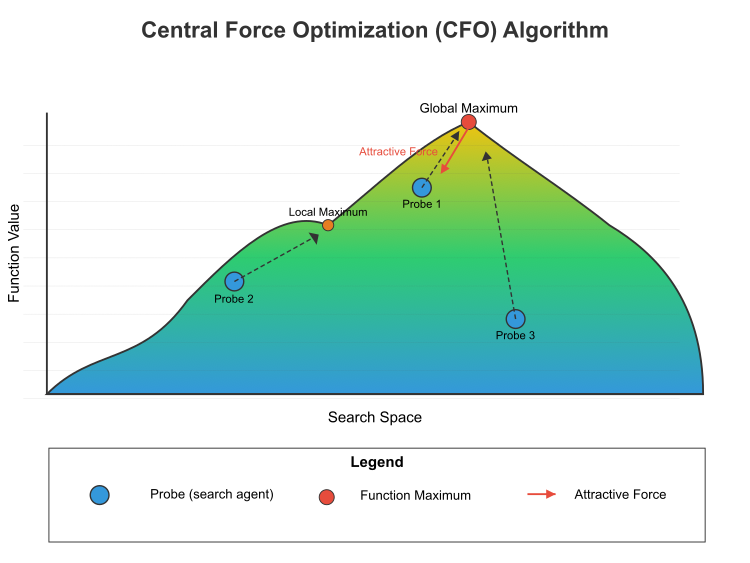
図1：中心力最適化アルゴリズムのフローチャート 

図1は、探索空間におけるCFOアルゴリズムの動作原理を示しています。目的関数のランドスケープが描かれており、青（低い値）から黄色（高い値）へのカラーグラデーションで表現されています。大域的最大値（最も高い点）および局所最大値（より低いピーク）が示されています。3つのエージェント（探索エージェント）が、Probe1、Probe2、Probe3として示されています。引力（赤い矢印）は、高い点がどのようにエージェントを引き寄せるかを表しています。 これはCFOの中心的な概念であり、良い解が悪い解を引き寄せるが、その逆は起こらないという一方向の引力を示しています。点線は、エージェントが最大値へ向かう軌跡を示しています。この過程を記述する数理モデルには、以下の要素が含まれます。

力の計算：任意の2つのエージェントiおよびjについて、jの関数値（質量）がiの関数値より大きい場合、jは次の式に従ってiに力を及ぼします。F = g × [(m_j - m_i)^α / d^β] × direction、ここで
  • g：重力定数
  • m_j、m_i：エージェントjおよびiの関数値（質量）
  • α：質量指数（通常は2）
  • d：エージェント間の距離
  • β：距離指数（通常は2）
  • direction：エージェントiからエージェントjへ向かう単位ベクトル
加速度の計算：エージェントiの加速度は、それに作用するすべての力の総和として計算されます。
位置の更新：各エージェントの位置は、「c: x_new = x_old + 0.5 × a」に従って更新されます。ここで、
  • x_new：新しい位置
  • x_old：現在の位置
  • a：加速度
境界処理：エージェントが探索範囲の外に出た場合、探索領域内に戻されます。

    アルゴリズムは、これらの計算をすべてのエージェントに対して反復的に適用し、探索空間内の最適解へ向かって徐々に移動させます。時間の経過とともに、エージェントは大域的最大値および局所最大値の周囲に集まる傾向を示し、通常は大域的最適解の周囲で最も高い集中度が観測されます。

    CFOの独自性は、その決定論的性質と一方向の引力機構にあります。この仕組みにより、基本形では乱数を用いることなく、探索が最良の解へと導かれます。CFOアルゴリズムの疑似コードを以下に示します。

    1. 初期化
      • 検索空間の境界を定義します。
      • パラメータとして、エージェント数、重力定数、質量および距離に関する指数、再配置係数を設定します。
      • 所定数のエージェントを生成し、探索空間内にランダムに配置します。
      • 各エージェントについて、目的関数の初期値を計算します。
    2. メインループ（指定されたエポック数だけ反復）
      • 各エージェントについて、以下の処理をおこないます。
        • 加速度ベクトルをゼロにリセットします。
        • 他のエージェントからの影響を考慮します。
          • 別のエージェントが、より良い目的関数値（より大きな「質量」）を持つ場合、そのエージェントは引力を生成します。
          • エージェント間の距離を計算します。
          • 引力は、「質量」の差のα乗に比例し、距離のβ乗に反比例します。
          • 力の方向は、現在のエージェントから「より重い」エージェントへ向かう方向です。
          • 目的関数値がより良いすべてのエージェントからの影響を合算します。
      • すべての加速度を計算した後、エージェントの位置を更新します。
        • 新しい位置＝現在の位置＋加速度の1/2
        • エージェントが探索空間の外に出た場合、再配置処理を適用します。
          • 下限境界を越えた場合は、再配置係数を考慮して空間内に反射させます。
          • 上限境界を越えた場合も同様に、反対側から反射させます。
      • 新しい位置におけるすべてのエージェントの目的関数値を再計算します。
      • 現在までの最良解の情報を更新します。
    3. 終了処理
      • 発見された最良解、すなわち目的関数値が最大となるエージェントの座標を返します。

    次に、アルゴリズムのコード実装に進みます。S_CFO_Agent構造体を定義します。この構造体はS_AO_Agentを継承しており、S_CFO_AgentはS_AO_Agentで定義されたすべてのプロパティおよびメソッドを引き継ぎます。 

    構造体フィールド：a[]は、加速度の値を格納するための動的配列です。Init()メソッドは構造体を初期化するために使用され、渡されたcoordsパラメータに基づいてc配列のサイズを変更し、同様に加速度配列aのサイズもcoordsに基づいて変更します。これにより、座標数に応じて配列サイズを動的に設定できます。また、使用前にa配列のすべての要素を0.0に初期化することで、加速度値をリセットします。さらに、f変数にはdouble型で取り得る最小値を設定し、適応度関数の初期値として使用します。これにより、その後に計算されるいかなる値も、現在の値より大きくなることが保証されます。

    //——————————————————————————————————————————————————————————————————————————————
//--- CFO probe structure
struct S_CFO_Agent : public S_AO_Agent
{
    double a []; // acceleration vector

    void Init (int coords)
    {
      ArrayResize (c, coords);   // coordinates
      ArrayResize (a, coords);   // acceleration
      ArrayInitialize (a, 0.0);  // reset accelerations
      f = -DBL_MAX;              // fitness function value
    }
};
//——————————————————————————————————————————————————————————————————————————————

    C_AO_CFOクラスはC_AOクラスを継承し、CFOアルゴリズムを定義します。コンストラクタとデストラクタを持ちますが、この場合、デストラクタは特定の処理をおこないません。C_AO_CFO()はコンストラクタであり、アルゴリズムの各種パラメータを初期化します。具体的には、以下の変数を設定します。

    • popSize、g、alpha、beta、initialFrep、finalFrep、noiseFactorは、アルゴリズムおよび最適化処理に関連するパラメータです。
    • frepは現在の再配置係数であり、initialFrepによって初期化されます。
    • params配列が初期化され、アルゴリズムのパラメータが格納されます。その後、対応する名前を持つ配列へ値がコピーされます。

    クラスメソッド

    • SetParams()は、params配列から値を取得してアルゴリズムのパラメータを設定します。同時に、現在の再配置係数をinitialFrepに設定します。
    • Init()は、パラメータの最小値および最大値、ならびにそれらを変更するためのステップを用いてアルゴリズムを初期化します。epochsPパラメータは、アルゴリズムを実行するエポック数を指定します。
    • Moving()は、アルゴリズム内でエージェント（エージェント）を移動させる処理を担当します。
    • Revision()は、エージェントの状態を監査または更新するために使用されます。

    クラスフィールド

    • S_CFO_Agent probe[]は、最適化に使用されるエージェント（エージェント）の配列です。
    • epochsおよびepochNowはprivateフィールドであり、それぞれ総エポック数と現在のエポックを表します。

    追加のprivateメソッド

    • InitialDistribution()は、探索空間内におけるエージェントの初期分布を設定します。
    • UpdateRepFactor()は、システムの現在状態に応じて再配置係数を更新します。
    • CalculateAccelerations()は、エージェントの位置および相互作用に基づいて加速度を計算します。
    • UpdatePositions()は、計算された加速度に基づいてエージェントの位置を更新します。
    • CalculateDistanceSquared()は、空間内の2点間の距離を計算し、エージェント間の相互作用を評価するためのメソッドです。

    //——————————————————————————————————————————————————————————————————————————————
//--- Main class of the CFO algorithm
class C_AO_CFO : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_CFO () { }
  C_AO_CFO ()
  {
    ao_name = "CFO";
    ao_desc = "Central Force Optimization";
    ao_link = "https://www.mql5.com/ja/articles/17167";

    popSize     = 30;          // number of probes
    g           = 1.0;         // gravitational constant
    alpha       = 0.1;         // mass power
    beta        = 0.1;         // degree for distance
    initialFrep = 0.9;         // initial repositioning factor
    finalFrep   = 0.1;         // final repositioning factor
    noiseFactor = 1.0;         // random noise factor

    frep        = initialFrep; // current repositioning factor

    ArrayResize (params, 7);
    params [0].name = "popSize";     params [0].val = popSize;
    params [1].name = "g";           params [1].val = g;
    params [2].name = "alpha";       params [2].val = alpha;
    params [3].name = "beta";        params [3].val = beta;
    params [4].name = "initialFrep"; params [4].val = initialFrep;
    params [5].name = "finalFrep";   params [5].val = finalFrep;
    params [6].name = "noiseFactor"; params [6].val = noiseFactor;
  }

  void SetParams ()
  {
    popSize     = (int)MathMax (1, params [0].val);
    g           = params [1].val;
    alpha       = params [2].val;
    beta        = params [3].val;
    initialFrep = params [4].val;
    finalFrep   = params [5].val;
    noiseFactor = params [6].val;

    frep        = initialFrep;
  }

  bool Init (const double &rangeMinP  [],  // minimum values
             const double &rangeMaxP  [],  // maximum values
             const double &rangeStepP [],  // step change
             const int     epochsP = 0);   // number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  double g;              // gravitational constant 
  double alpha;          // power for mass
  double beta;           // degree for distance
  double initialFrep;    // initial repositioning factor
  double finalFrep;      // final repositioning factor
  double noiseFactor;    // random noise factor

  S_CFO_Agent probe [];  // array of probes

  private: //-------------------------------------------------------------------
  int    epochs;         // total number of epochs
  int    epochNow;       // current epoch
  double frep;           // repositioning factor

  void   InitialDistribution      ();
  void   UpdateRepFactor          ();
  void   CalculateAccelerations   ();
  void   UpdatePositions          ();
  double CalculateDistanceSquared (const double &x1 [], const double &x2 []);
};
//——————————————————————————————————————————————————————————————————————————————

    C_AO_CFOクラスのInit()メソッドは、CFOアルゴリズムの初期化を担当します。このメソッドは、パラメータの最小値および最大値の配列、それらの値を変更するためのステップ幅、ならびにエポック数（デフォルトは0）を受け取ります。渡された値の範囲が妥当であるかを検証するためにStandardInitメソッドを呼び出します。この検証に失敗した場合、Init()メソッドはfalseを返します。検証が成功した場合、総エポック数および現在のエポック番号を設定します（現在のエポックは0に初期化されます）。その後、エージェント（エージェント）配列のサイズを、集団サイズを表すpopSizeに変更します。次に、probe配列内の各エージェントに対してInit()メソッドを呼び出し、座標数を渡して初期化をおこないます。すべてのエージェントが正しく初期化された場合、Init()メソッドはtrueを返します。このようにして、Init()メソッドは、アルゴリズムが動作を開始するために必要な初期パラメータおよび条件を設定します。

    //——————————————————————————————————————————————————————————————————————————————
//--- Initialization
bool C_AO_CFO::Init (const double &rangeMinP  [], // minimum values
                     const double &rangeMaxP  [], // maximum values
                     const double &rangeStepP [], // step change
                     const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  epochs   = epochsP;
  epochNow = 0;

  // Initialization of probes
  ArrayResize (probe, popSize);
  for (int i = 0; i < popSize; i++) probe [i].Init (coords);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

    C_AO_CFOクラスのMoving()メソッドは、CFOアルゴリズムの主要なステップを担当します。メソッドは、まず現在のエポックカウンタをインクリメントし、アルゴリズムの次のステップを示します。メソッドが初めて呼び出された場合、すなわちrevisionがfalseのときは、初期化処理をおこなった後、実行を終了します。これは、アルゴリズムが動作を開始するために必要な初期値および状態を設定するために必要です。次に、エージェント配列から適応度関数の値を一時配列にコピーし、以降の計算で最新の値を保持します。

    その後、探索空間におけるエージェントの再配置に関するパラメータを更新します。これはアルゴリズムの適応性を確保するために重要です。続いて、現在の状態に基づきエージェントの加速度を計算し、位置を更新します。これにより、探索空間内でエージェントが移動します。最後に、更新されたエージェントの位置をメイン配列に同期させ、変更を記録してデータの一貫性を確保します。Moving()メソッドは、アルゴリズム実行中にエージェントの状態を、適応度関数および現在の位置に基づいて体系的に更新する役割を果たします。

    //——————————————————————————————————————————————————————————————————————————————
//--- The main step of the algorithm
void C_AO_CFO::Moving ()
{
  epochNow++;

  // Initial initialization
  if (!revision)
  {
    InitialDistribution ();
    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  // Copy the fitness function values from the base class
  for (int p = 0; p < popSize; p++)
  {
    probe [p].f = a [p].f;
  }

  // Update the repositioning parameter
  UpdateRepFactor ();

  // Main CFO loop
  CalculateAccelerations ();
  UpdatePositions ();

  // Synchronize positions with the base class
  for (int p = 0; p < popSize; p++)
  {
    ArrayCopy (a [p].c, probe [p].c);
  }
}
//——————————————————————————————————————————————————————————————————————————————

    C_AO_CFOクラスのInitialDistributionメソッドは、探索空間におけるエージェント（エージェント）の初期分布を担当します。ソッドは、popSizeの集団内の各エージェントを順に処理します。各エージェントについて、a配列をゼロに初期化し、適応度関数fを最小値に設定することで初期化をおこないます。さらに、各エージェントの座標ごとに、指定された範囲（rangeMinおよびrangeMax）内でランダムな値を生成します。生成されたランダム値は、SeInDiSpメソッドを使用して特定の範囲とrangeStepステップに補正されます。最後に、エージェントの座標は一時的なc配列からメイン配列aにコピーされ、各エージェントの初期状態が固定されます。

    //——————————————————————————————————————————————————————————————————————————————
//--- Initial probe distribution
void C_AO_CFO::InitialDistribution ()
{
  for (int p = 0; p < popSize; p++)
  {
    ArrayInitialize (probe [p].a, 0.0);
    probe [p].f = -DBL_MAX;

    // Random distribution
    for (int c = 0; c < coords; c++)
    {
      probe [p].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
      probe [p].c [c] = u.SeInDiSp (probe [p].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }

    ArrayCopy (a [p].c, probe [p].c);
  }
}
//——————————————————————————————————————————————————————————————————————————————

    C_AO_CFOクラスのUpdateRepFactorメソッドは、アルゴリズム実行中にエージェントの再配置係数（または抑制係数）を更新する役割を担います。メソッドはまずチェックをおこないます。エポック数が0より大きい場合、現在のepochNowを総エポック数で割った割合に基づき、初期値initialFrepから最終値finalFrepまで線形に減少する形で新しいfrep値を計算します。エポック数が0の場合、frepはinitialFrepのままとなります。これは、アルゴリズムが初期段階にある場合でも再配置係数の安定性を確保するためです。メソッドの最後で、frepはMathMaxおよびMathMin関数を用いて0から1の範囲に制限されます。これにより、再配置係数が設定された限界を超えることがなくなり、アルゴリズムの安定性および正しい動作が保証されます。

    //——————————————————————————————————————————————————————————————————————————————
//--- Update the repositioning factor
void C_AO_CFO::UpdateRepFactor ()
{
  // Linearly decrease frep from the initial to the final value
  if (epochs > 0) frep = initialFrep - (initialFrep - finalFrep) * epochNow / epochs;
  else frep = initialFrep;

  // Value constraint
  frep = MathMax (0.0, MathMin (1.0, frep));
}
//——————————————————————————————————————————————————————————————————————————————

    C_AO_CFOクラスのCalculateAccelerationsメソッドは、集団内の各エージェントの加速度を、他のすべてのエージェントからの影響に基づいて計算するために設計されています。メソッドの主要なステップと処理の流れは以下の通りです。集団内の各エージェントについて（0からpopSizeまで）、probe[p].aの加速度値をゼロにリセットします。これは、計算を一から開始し、他のエージェントとの相互作用に基づく加速度を累積するためにおこなわれます。各エージェントについて、内部ループで他のすべてのエージェント（0からpopSizeまで）を順に処理します。現在のエージェントpのインデックスが他のエージェントkと一致する場合は、continueコマンドでその反復をスキップします。2つのエージェントの適応度値の差(massDiff = probe[k].f - probe[p].f)を計算します。この値は、どれだけ「強い」（または良い）エージェントかを判定するために使用されます。massDiffが0より大きい場合、すなわちkインデックスのエージェントがpインデックスのエージェントよりも適応度が高い場合は、以下の処理をおこないます。

    1. 距離の計算：CalculateDistanceSquared関数を用いて、2つのエージェントの現在座標間の距離の二乗を計算します。この距離が最小正値よりも小さい場合、反復はスキップされます。

    2. 力の方向の形成：距離がDBL_EPSILONより大きい場合、実際の距離を計算します。各座標cについて、現在のエージェントから適応度が高いエージェントへ向かう力の方向を決定します。

    3. 加速度の計算： 現在のエージェントの加速度は、式「probe[p].a[c] += g * MathPow(massDiff, alpha) * direction / MathPow(distance, beta)」に基づき更新されます。この式では、質量（適応度値）の差、エージェント間の距離、および相互作用の強さに影響するパラメータ（g、alpha、beta）が考慮されます。

    このメソッドにより、各エージェントは他のエージェントの影響を自身の加速度に反映させることができます。これはCFOアルゴリズムにおける最適化の重要な要素です。計算された加速度は、後続の処理で探索空間内のエージェントの位置更新に使用されます。

    //——————————————————————————————————————————————————————————————————————————————
//--- Calculate accelerations
void C_AO_CFO::CalculateAccelerations ()
{
  for (int p = 0; p < popSize; p++)
  {
    // Reset the acceleration for the current probe
    ArrayInitialize (probe [p].a, 0.0);

    // Summarize the influence of all other probes
    for (int k = 0; k < popSize; k++)
    {
      if (k == p) continue;

      // Difference in masses (fitness values)
      double massDiff = probe [k].f - probe [p].f;

      // Check the condition of the U(...) unit function
      if (massDiff > 0) // Strict condition for the unit function
      {
        // Calculate the distance between probes
        double distSquared = CalculateDistanceSquared (probe [k].c, probe [p].c);
        if (distSquared < DBL_EPSILON) continue;

        double distance = MathSqrt (distSquared);

        for (int c = 0; c < coords; c++)
        {
          // Force direction
          double direction = (probe [k].c [c] - probe [p].c [c]) / distance;

          // Acceleration equation
          probe [p].a [c] += g * MathPow (massDiff, alpha) * direction / MathPow (distance, beta);
        }
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

    C_AO_CFOクラスのUpdatePositionsメソッドは、加速度、ランダム要素、境界制約を考慮して、探索空間内のエージェント（またはエージェント）の位置を更新するために使用されます。このメソッドにはいくつかのステップが含まれます。

    ランダムノイズ係数の減衰
    • 現在のランダムノイズ比であるcurrentNoiseFactorを解析します。この比率は初期値noiseFactorで初期化されます。
    • エポック数が0より大きい場合、currentNoiseFactorは現在のepochNowに比例して減少します。これは、エポックが進むにつれてノイズが減少し、アルゴリズムが徐々に最適解により正確に収束できるようにするためです。

    次に、集団内のすべてのエージェント（0からpopSizeまで）を順に処理し、各エージェントについて全座標（0からcoordsまで）を処理します。エージェントの位置は、現在の加速度probe[p].a[c]を用いた式により更新されます。この場合、単純な式が使用され、新しい位置は現在の位置に加速度の半分を加えた値となります。 

    更新された位置には、currentNoiseFactor、重力定数g、および-1から1の範囲の乱数に基づく小さなランダムオフセットが加えられます。 元のアルゴリズムは厳密に決定論的ですが、ここでは局所解に陥るのを防ぐためにランダム性の要素を追加しています。新しい位置が指定された範囲（rangeMinおよびrangeMax）を超えた場合、位置は許可された範囲内に調整されます。また、サンプリングステップが指定されている場合、SeInDiSpメソッドを用いて位置をステップの最も近い倍数に補正します。 

    //——————————————————————————————————————————————————————————————————————————————
//--- Update positions
void C_AO_CFO::UpdatePositions ()
{
  // Random noise ratio decreases with increasing epoch number
  double currentNoiseFactor = noiseFactor;
  if (epochs > 0) currentNoiseFactor *= (1.0 - (double)epochNow / epochs);

  for (int p = 0; p < popSize; p++)
  {
    for (int c = 0; c < coords; c++)
    {
      // Update the position by equation
      probe [p].c [c] += 0.5 * probe [p].a [c];

      // Add a small random offset directly to the position
      probe [p].c [c] += currentNoiseFactor * g * u.RNDfromCI (-1.0, 1.0);

      // Reposition when going out of bounds
      if (probe [p].c [c] < rangeMin [c]) probe [p].c [c] = rangeMin [c];
      if (probe [p].c [c] > rangeMax [c]) probe [p].c [c] = rangeMax [c];

      // Discretization if step is specified
      probe [p].c [c] = u.SeInDiSp (probe [p].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

    C_AO_CFOクラスのCalculateDistanceSquaredメソッドは、多次元空間内の2点間の距離の二乗を計算する役割を担います。このメソッドは最適化処理で使用されます。距離の二乗を返すことで平方根の計算を省略でき、計算コストを大幅に削減できるためです。メソッドは2つのパラメータx1およびx2を受け取ります。これらは配列（const double &x1[]およびconst double &x2[]）で、空間内の2点の座標を表し、次元数はcoordの数と同じです。メソッドの冒頭で、変数sumを作成し0で初期化します。この変数は、座標ごとの差の二乗を累積するために使用されます。その後、すべての座標（0からcoords-1まで）をループ処理し、各座標について以下をおこないます。

    • x1配列とx2配列の対応する要素の差を計算します(diff = x1[i] - x2[i])。
    • 差の二乗を計算します(diff * diff)。
    • 差の二乗をsum変数に加算します。
    ループ処理が完了した後、sumには座標差の二乗和が格納されます。メソッドはこのsumを返し、これが2点間の距離の二乗となります。
    //——————————————————————————————————————————————————————————————————————————————
//--- Calculate distance (returns squared distance for optimization)
double C_AO_CFO::CalculateDistanceSquared (const double &x1 [], const double &x2 [])
{
  double sum = 0.0;
  for (int i = 0; i < coords; i++)
  {
    double diff = x1 [i] - x2 [i];
    sum += diff * diff;
  }
  return sum;
}
//——————————————————————————————————————————————————————————————————————————————

    C_AO_CFOクラスのRevision()メソッドは、最適化中に得られた最良解を更新する役割を担います。メソッドは、popSizeの集団内のすべてのエージェント（またはエージェント）を順に処理します。各エージェントについて、そのa[p].f適応度関数値が現在の最良値fBより大きいかどうかを確認します。大きい場合、fBの値を当該エージェントの適応度関数値に更新します。その後、当該エージェントのcB座標をコピーし、最良解として保存します。このようにして、Revision()メソッドは、すべてのエージェントの中から最良の解を検出し保存し、エージェントが結果を改善した場合にはグローバルパラメータを即座に更新します。

    //——————————————————————————————————————————————————————————————————————————————
//--- Update the best solution
void C_AO_CFO::Revision ()
{
  for (int p = 0; p < popSize; p++)
  {
    if (a [p].f > fB)
    {
      fB = a [p].f;
      ArrayCopy (cB, a [p].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————


    テスト結果

    元の厳密に決定論的なアルゴリズムの基本バージョンでは、次の結果が示されます。 

    CFO|Central Force Optimization|30.0|1.0|0.1|0.1|0.9|0.1|
    =============================
    5 Hilly's; Func runs:10000; result:0.34508431921321436
    25 Hilly's; Func runs:10000; result:0.2826594689557952
    500 Hilly's; Func runs:10000; result:0.25174636412054047
    =============================
    5 Forest's; Func runs:10000; result:0.26234538930351947
    25 Forest's; Func runs:10000; result:0.1852230195779629
    500 Forest's; Func runs:10000; result:0.15353213276989314
    =============================
    5 Megacity's; Func runs:10000; result:0.24923076923076923
    25 Megacity's; Func runs:10000; result:0.1261538461538462
    500 Megacity's; Func runs:10000; result:0.09492307692307768
    =============================
    All score:1.95090 (21.68%)

    このままでは、アルゴリズムの結果を評価表に含めることはできません。改善が必要です。そこで、前述の通り、この箇所にランダム性の要素を追加しました。これがない場合、探索は決定論的で解の多様性が不足してしまいます。

    // Add a small random offset directly to the position
probe [p].c [c] += currentNoiseFactor * g * u.RNDfromCI (-1.0, 1.0);

    各エージェントの移動にわずかなランダムバイアスを加えることで、アルゴリズムは予期しない方向への探索を開始できるようになりました。もう一度テストをおこなうと、まったく異なる結果が観察でき、これにより初めて評価表に記録できる結果となります。 

    CFO|Central Force Optimization|30.0|1.0|0.1|0.1|0.9|0.1|1.0|
    =============================
    5 Hilly's; Func runs:10000; result:0.6096110105488222
    25 Hilly's; Func runs:10000; result:0.5495761567207647
    500 Hilly's; Func runs:10000; result:0.27830861578120414
    =============================
    5 Forest's; Func runs:10000; result:0.6341793648294705
    25 Forest's; Func runs:10000; result:0.4683296629644541
    500 Forest's; Func runs:10000; result:0.22540930020804817
    =============================
    5 Megacity's; Func runs:10000; result:0.5723076923076923
    25 Megacity's; Func runs:10000; result:0.2347692307692307
    500 Megacity's; Func runs:10000; result:0.09586153846153929
    =============================
    All score:3.66835 (40.76%)

    これで、アルゴリズムの動作の可視化を見ることができます。ご覧の通り、アルゴリズムは中程度の次元を持つ関数では良好に動作しますが、低次元および高次元の関数では十分に性能が発揮されません。 

    Hilly

    Hillyテスト関数のCFO

    Forest

    Forestテスト関数のCFO

    Megacity 

    Megacityテスト関数のCFO

    テスト結果に基づくと、本アルゴリズムはトップクラスの集団最適化アルゴリズムのひとつに位置し、ランキングでは42位にランクされています。

    # AO 詳細 Hilly Hilly最終 Forest Forest最終 Megacity（離散） Megacity最終 最終結果 MAXの%
    10p(5F) 50p(25F) 1000p(500F) 10p(5F) 50p(25F) 1000p(500F) 10p(5F) 50p(25F) 1000p(500F)
    1 ANS across neighbourhood search 0.94948 0.84776 0.43857 2.23581 1.00000 0.92334 0.39988 2.32323 0.70923 0.63477 0.23091 1.57491 6.134 68.15
    2 CLA コードロックアルゴリズム(joo) 0.95345 0.87107 0.37590 2.20042 0.98942 0.91709 0.31642 2.22294 0.79692 0.69385 0.19303 1.68380 6.107 67.86
    3 AMOm 動物移動最適化m 0.90358 0.84317 0.46284 2.20959 0.99001 0.92436 0.46598 2.38034 0.56769 0.59132 0.23773 1.39675 5.987 66.52
    4 (P+O)ES (P+O)進化戦略 0.92256 0.88101 0.40021 2.20379 0.97750 0.87490 0.31945 2.17185 0.67385 0.62985 0.18634 1.49003 5.866 65.17
    5 CTA 彗星の尾アルゴリズム(joo) 0.95346 0.86319 0.27770 2.09435 0.99794 0.85740 0.33949 2.19484 0.88769 0.56431 0.10512 1.55712 5.846 64.96
    6 TETA 時間進化移動アルゴリズム(joo) 0.91362 0.82349 0.31990 2.05701 0.97096 0.89532 0.29324 2.15952 0.73462 0.68569 0.16021 1.58052 5.797 64.41
    7 SDSm 確率的拡散探索M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
    8 BOAm ビリヤード最適化アルゴリズムM 0.95757 0.82599 0.25235 2.03590 1.00000 0.90036 0.30502 2.20538 0.73538 0.52523 0.09563 1.35625 5.598 62.19
    9 AAm アーチェリーアルゴリズムM 0.91744 0.70876 0.42160 2.04780 0.92527 0.75802 0.35328 2.03657 0.67385 0.55200 0.23738 1.46323 5.548 61.64
    10 ESG 社会集団の進化(joo) 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
    11 SIA 等方的焼きなまし(joo) 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
    12 ACS 人工協調探索 0.75547 0.74744 0.30407 1.80698 1.00000 0.88861 0.22413 2.11274 0.69077 0.48185 0.13322 1.30583 5.226 58.06
    13 DA 弁証法的アルゴリズム 0.86183 0.70033 0.33724 1.89940 0.98163 0.72772 0.28718 1.99653 0.70308 0.45292 0.16367 1.31967 5.216 57.95
    14 BHAm ブラックホールアルゴリズムM 0.75236 0.76675 0.34583 1.86493 0.93593 0.80152 0.27177 2.00923 0.65077 0.51646 0.15472 1.32195 5.196 57.73
    15 ASO 無政府社会最適化 0.84872 0.74646 0.31465 1.90983 0.96148 0.79150 0.23803 1.99101 0.57077 0.54062 0.16614 1.27752 5.178 57.54
    16 RFO ロイヤルフラッシュ最適化(joo) 0.83361 0.73742 0.34629 1.91733 0.89424 0.73824 0.24098 1.87346 0.63154 0.50292 0.16421 1.29867 5.089 56.55
    17 AOSm 原子軌道探索M 0.80232 0.70449 0.31021 1.81702 0.85660 0.69451 0.21996 1.77107 0.74615 0.52862 0.14358 1.41835 5.006 55.63
    18 TSEA 亀甲進化アルゴリズム(joo) 0.96798 0.64480 0.29672 1.90949 0.99449 0.61981 0.22708 1.84139 0.69077 0.42646 0.13598 1.25322 5.004 55.60
    19 DE 差分進化 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
    20 SRA レストラン経営達人アルゴリズム(joo) 0.96883 0.63455 0.29217 1.89555 0.94637 0.55506 0.19124 1.69267 0.74923 0.44031 0.12526 1.31480 4.903 54.48
    21 CRO 化学反応の最適化 0.94629 0.66112 0.29853 1.90593 0.87906 0.58422 0.21146 1.67473 0.75846 0.42646 0.12686 1.31178 4.892 54.36
    22 BIO 血液型遺伝最適化(joo) 0.81568 0.65336 0.30877 1.77781 0.89937 0.65319 0.21760 1.77016 0.67846 0.47631 0.13902 1.29378 4.842 53.80
    23 BSA 鳥群アルゴリズム 0.89306 0.64900 0.26250 1.80455 0.92420 0.71121 0.24939 1.88479 0.69385 0.32615 0.10012 1.12012 4.809 53.44
    24 HS ハーモニー検索 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
    25 SSG 苗木の播種と育成 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
    26 BCOm 細菌走化性最適化M 0.75953 0.62268 0.31483 1.69704 0.89378 0.61339 0.22542 1.73259 0.65385 0.42092 0.14435 1.21912 4.649 51.65
    27 ABO アフリカ水牛の最適化 0.83337 0.62247 0.29964 1.75548 0.92170 0.58618 0.19723 1.70511 0.61000 0.43154 0.13225 1.17378 4.634 51.49
    28 (PO)ES (PO)進化戦略 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
    29 TSm タブーサーチM 0.87795 0.61431 0.29104 1.78330 0.92885 0.51844 0.19054 1.63783 0.61077 0.38215 0.12157 1.11449 4.536 50.40
    30 BSO ブレインストーム最適化 0.93736 0.57616 0.29688 1.81041 0.93131 0.55866 0.23537 1.72534 0.55231 0.29077 0.11914 0.96222 4.498 49.98
    31 WOAm 鯨最適化アルゴリズムM 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
    32 AEFA 人工電界アルゴリズム 0.87700 0.61753 0.25235 1.74688 0.92729 0.72698 0.18064 1.83490 0.66615 0.11631 0.09508 0.87754 4.459 49.55
    33 AEO 人工生態系ベースの最適化アルゴリズム 0.91380 0.46713 0.26470 1.64563 0.90223 0.43705 0.21400 1.55327 0.66154 0.30800 0.28563 1.25517 4.454 49.49
    34 ACOm 蟻コロニー最適化M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
    35 BFO-GA 細菌採食の最適化：Ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
    36 SOA シンプル最適化アルゴリズム 0.91520 0.46976 0.27089 1.65585 0.89675 0.37401 0.16984 1.44060 0.69538 0.28031 0.10852 1.08422 4.181 46.45
    37 ABHA 人工蜂の巣アルゴリズム 0.84131 0.54227 0.26304 1.64663 0.87858 0.47779 0.17181 1.52818 0.50923 0.33877 0.10397 0.95197 4.127 45.85
    38 ACMO 大気雲モデルの最適化 0.90321 0.48546 0.30403 1.69270 0.80268 0.37857 0.19178 1.37303 0.62308 0.24400 0.10795 0.97503 4.041 44.90
    39 ADAMm 適応モーメント推定M 0.88635 0.44766 0.26613 1.60014 0.84497 0.38493 0.16889 1.39880 0.66154 0.27046 0.10594 1.03794 4.037 44.85
    40 CGO カオスゲーム最適化 0.57256 0.37158 0.32018 1.26432 0.61176 0.61931 0.62161 1.85267 0.37538 0.21923 0.19028 0.78490 3.902 43.35
    41 ATAm 人工部族アルゴリズムM 0.71771 0.55304 0.25235 1.52310 0.82491 0.55904 0.20473 1.58867 0.44000 0.18615 0.09411 0.72026 3.832 42.58
    42 CFO 中心力最適化 0.60961 0.54958 0.27831 1.43750 0.63418 0.46833 0.22541 1.32792 0.57231 0.23477 0.09586 0.90294 3.668 40.76
    43 ASHA 人工シャワーアルゴリズム 0.89686 0.40433 0.25617 1.55737 0.80360 0.35526 0.19160 1.35046 0.47692 0.18123 0.09774 0.75589 3.664 40.71
    44 ASBO 適応型社会行動最適化(ASBO) 0.76331 0.49253 0.32619 1.58202 0.79546 0.40035 0.26097 1.45677 0.26462 0.17169 0.18200 0.61831 3.657 40.63
    45 MEC mind evolutionary computation 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
    RW ランダムウォーク 0.48754 0.32159 0.25781 1.06694 0.37554 0.21944 0.15877 0.75375 0.27969 0.14917 0.09847 0.52734 2.348 26.09


    まとめ

    CFOアルゴリズムは、物体間の重力引力の原理に基づき、物理法則を複雑な最適化問題の解法に応用しようとした興味深い試みです。標準的なテストセットで広範な検証をおこなった結果、CFOは理論上の最大効率のわずか40％強の性能を示し、集団型最適化アルゴリズム上位45種の中で42位にランクされました。なお、この控えめな結果であっても、元のアルゴリズムを修正し、もともと決定論的であった性質にランダム成分を導入したことによって初めて達成されました。

    性能指標は比較的低いものの、CFOにはいくつか魅力的な特徴があります。まず、極めて明快な物理的解釈を持ち、直感的である点です。基本概念の単純さ（潜在解を表すエージェントが、物質的な天体がより重い天体に引かれるのと同様に、より良い解に引き寄せられる）が、アルゴリズムの動作の透明性と実装の容易さを保証しています。

    一方で、テストにより、CFOには修正や改善が必要な重要な制限も明らかになりました。エージェントの初期分布に過度に依存する点は主要な問題の一つです。決定論的な移動メカニズムにより、エージェントの初期位置が最終的な探索結果を大きく左右してしまいます。 

    また、最良解のみが最劣解に影響を与え、逆は起こらない一方向の引力メカニズムは論理的には妥当ですが、探索空間を十分に探索する能力を大きく制限する可能性があります。探索初期において、劣った解からもある程度の影響を受けられる適応型メカニズムを導入することで、アルゴリズムが解空間内の有望な領域を検出する能力を向上させることが可能です。

    図2：対応するテストに応じたアルゴリズムのカラーグラデーション

    チャート

    図3：アルゴリズムテスト結果のヒストグラム（0から100のスケール、高いほど良い）100は理論上の最大値であり、アーカイブには評価表を計算するためのスクリプトがあります。

    CFOの長所と短所

    長所

    1. 中次元関数に適している

    短所

    1. 低次元および高次元関数では十分に機能しない
    2. 離散関数に対する検索能力が弱い

    この記事には、最新版のアルゴリズムコードを含むアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。


    記事で使用されているプログラム

    # 名前 種類 詳細
    1 #C_AO.mqh
    		 インクルード
    		 集団最適化の親クラス
    アルゴリズム
    2 #C_AO_enum.mqh
    		 インクルード
    		 集団最適化アルゴリズムの列挙
    3 TestFunctions.mqh
    		 インクルード
    		 テスト関数のライブラリ
    4 TestStandFunctions.mqh
    		 インクルード
    		 テストスタンド関数ライブラリ
    5 Utilities.mqh
    		 インクルード
    		 補助関数のライブラリ
    6 CalculationTestResults.mqh
    		 インクルード
    		 比較表の結果を計算するスクリプト
    7 Testing AOs.mq5
    		 スクリプト すべての集団最適化アルゴリズムの統一テストスタンド
    8 Simple use of population optimization algorithms.mq5
    		 スクリプト
    		 可視化せずに集団最適化アルゴリズムを使用する簡単な例
    9 Test_AO_CFO.mq5
    		 スクリプト CFOテストスタンド

    MetaQuotes Ltdによってロシア語から翻訳されました。
    元の記事: https://www.mql5.com/ru/articles/17167

    添付されたファイル |
    ZIPをダウンロード
    CFO.zip (179.39 KB)

    警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

    この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。

    この著者による他の記事

    ディスカッションに移動
    EAのサンプル EAのサンプル
    一般的なMACDを使ったEAを例として、MQL4開発の原則を紹介します。
    多通貨エキスパートアドバイザーの開発（第24回）：新しい戦略の追加(II) 多通貨エキスパートアドバイザーの開発（第24回）：新しい戦略の追加(II)
    本記事では、引き続き、作成済みの自動最適化システムに新しい戦略を連携する方法を見ていきます。最適化プロジェクト作成EAと、第2ステージおよび第3ステージのEAにどのような変更を加える必要があるかを見てみましょう。
    エラー 146 (「トレードコンテキスト ビジー」) と、その対処方法 エラー 146 (「トレードコンテキスト ビジー」) と、その対処方法
    この記事では、MT4において複数のEAの衝突をさける方法を扱います。ターミナルの操作、MQL4の基本的な使い方がわかる人にとって、役に立つでしょう。
    初心者からエキスパートへ：MQL5での可視化による地理的市場認識の強化 初心者からエキスパートへ：MQL5での可視化による地理的市場認識の強化
    セッションを意識せずに取引することは、まるでコンパスなしで航海するようなものです。移動してはいるものの、目的を持って移動していないのです。本稿では、トレーダーが市場のタイミングを認識する方法を革新し、通常のチャートを動的な地理的表示に変換する手法を紹介します。MQL5の強力な可視化機能を活用して、リアルタイムでアクティブな取引セッションを点灯させるライブ世界地図を構築します。これにより、抽象的な市場時間が直感的な視覚情報として理解可能になります。この手法は取引心理を鋭敏化すると同時に、複雑な市場構造と実用的な洞察を結びつけるプロフェッショナル向けのプログラミング技術も明らかにします。