MetaTrader 5 / テスター
English Русский 中文 Español Deutsch Português
preview
動物移動最適化(AMO)アルゴリズム

動物移動最適化(AMO)アルゴリズム

MetaTrader 5 — テスター | 24 3月 2025, 09:09
65 0
Andrey Dik
Andrey Dik

内容
  1. はじめに
  2. アルゴリズムの実装
  3. テスト結果


はじめに

渡り：自然の調和と自然戦略。動物は、何世紀にもわたる進化の過程で確立された経路に沿って、越冬地と繁殖地の間を移動します。これらの季節的な移動は、単なるランダムな放浪ではなく、生存と繁殖に最適な地域へ導く慎重に計画されたルートです。動物たちは、群れや個体の本能的な要求に従い、食物、避難場所、繁殖に適した環境を求めて移動します。こうした旅は、生存競争の一環であるだけでなく、自然との調和の表れでもあり、個々の動物が生態系全体の中で重要な役割を果たしています。

たとえば、トナカイはより良い放牧地を求めて長距離を移動し、ツルやガチョウなどの鳥は、世代から世代へと受け継がれた特定のルートをたどりながら、越冬地と営巣地の間を飛行します。こうした移動は、単に個々の種の生存を保証するだけでなく、植物の受粉や種子の拡散を促進し、生態系全体を支える役割も果たしています。

自然からのインスピレーション。AMO（Animal Migration Optimization、動物移動最適化）アルゴリズムは、2013年に研究者Xiantao Liによって提案されました。このアルゴリズムの核心となる考え方は、動物が生存と繁殖に最適な条件を求めて季節的に移動するプロセスをモデル化することです。鳥、魚、哺乳類などの渡り動物の行動を観察することで着想を得ており、動物が越冬地と繁殖地の間を移動する際に従う、自然界が生み出した一定の相互作用のルールを取り入れています。

AMOアルゴリズムは、動物が長距離を移動する際に見られる3つの主要な要素をシミュレートします。つまり、近隣の個体との衝突を避けること、群れ（グループ）と同じ方向に移動すること、そして互いの間に十分な距離を保つことです。これらの原則は、単に衝突を回避するだけでなく、野生環境での生存に不可欠な集団行動を維持する役割も果たします。

AMOアルゴリズムの最適化段階。このアルゴリズムでは、1回の反復内で2つの主要な最適化フェーズが含まれます。

  • 移行：この段階では、近隣の個体を考慮して個体の位置が更新されます。
  • 集団の更新：この段階では、個体は群れ内の位置に応じて確率に応じて部分的に新しい個体に置き換えられます。

渡り動物の集団行動をモデル化することは、複雑な最適化問題を解決するための効果的なアプローチとなり得ます。AMOアルゴリズムは、自然のプロセスを模倣することで、探索空間の広範な探索と最適解の活用のバランスを取ることを目的としています。


2. アルゴリズムの実装

この渡りアルゴリズムモデルの基本的な考え方は、各動物の周囲に同心円状の「ゾーン」を作成することです。たとえば、反発ゾーンでは、動物は衝突を避けるために近隣の動物から離れる傾向があります。著者によると、この渡りアルゴリズムは2つの主要なプロセスに分けられます。

1. 渡り。位相リングは、個体の限られた近傍を定義するための仕組みです。便宜上、各次元の近傍の長さは5に設定されています。近傍トポロジーは固定されており、集団内の各個体のインデックスに基づいて決定されます。たとえば、動物のインデックスがjの場合、その近隣の個体のインデックスは [j - 2, j - 1, j, j + 1, j + 2] になります。また、もし動物のインデックスが1であれば、その近傍の個体は [N - 1, N, 1, 2, 3] というように決定されます。近隣トポロジが形成された後、1つの近隣をランダムを選択し、その近隣の位置を反映するように個体の位置を更新します。このアルゴリズムの設計は、元のアルゴリズムの作成者によって提案されたものです。さらに、この近傍点の数をアルゴリズムのパラメータとして設定することで、実験を通じて最適な近傍点の数を特定し、アルゴリズムの効率を最大化することが可能になります。

2. 集団の更新。集団の更新フェーズでは、一部の動物が群れを離れ、新たな個体が加わる過程をモデル化します。個体は、適応度関数の品質に基づいて決定される確率「p」で新しい動物に置き換えられます。適応度関数値の降順で集団を並び替えます。つまり、最も適応度の高い個体を変更する確率は1/Nですが、最も適応度が低い個体を変更する確率は1です。

著者のバージョンによると、渡りと集団の更新は、以下に示すようにアルゴリズム的に記述できます。

渡り

1. それぞれの動物について a. 動物の位相的近傍を決定します（最も近い5つの近傍）。
   b. 近隣リストからランダムに近隣を選択します。    
   c. 次の式を使用して、選択した近隣動物の方向に動物の位置を更新します。
      x_j_new = x_j_old + r * (x_neighbor - x_j_old)、ここで
  • x_j_new：j番目の動物の新しい位置
  • x_j_old：現在の位置
  • x_neighbor：選択された隣接位置
  • r：正規分布からの乱数

   d. 目的関数を使用して動物の新しい位置を評価します。

集団の更新

1. 動物を目的関数の値で降順に並べ替えます。 2. それぞれの動物について a. 動物を新しいランダムな動物に置き換える確率を計算します。

      p = 1.0 - (1.0 / (x + 1)) 、ここでxは並び替えられたリスト内のi番目の動物の順位（インデックス）です。

   b. 乱数がp未満の場合、動物を置き換えます（座標を、集団からランダムに選択された 2 匹の動物の座標の平均値に変更します）。 c. それ以外の場合は、動物を変更せずにそのままにしておきます。

3. 目的関数を使用して新しい集団を推定します。

変更

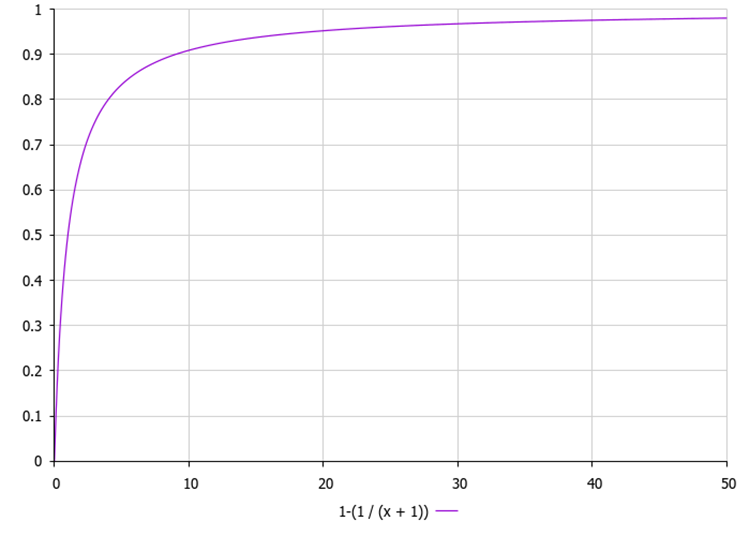
図1　集団内での位置に応じて個体の確率を変更します。ここで、「x」は集団内の個体のインデックスです。

AMO動物移動アルゴリズムの疑似コードを記述してみましょう。

1. 動物の集団をランダムな位置で初期化します。

2. メインループ

   a. それぞれの動物について

      位相的な近傍を定義します。
      ランダムな隣人を選択します。
      動物の位置を隣の動物の方向に更新します。
      新しいポジションを評価します。

   b. 目的関数の値によって集団を並び替えます。

   c. 劣った動物を新しい動物に確率的に置き換えます。

   d. 更新された集団を推定します。

   （例：最適なソリューションを更新します。

3. 停止基準を満たすまで、ステップ2から繰り返します。

アルゴリズムについて理解できたので、コードの記述に進むことができます。C_AO_AMOクラスのコードを詳しく見てみましょう。

1. C_AO_AMOクラスはC_AO基本クラスから継承され、その機能を使用したり拡張したりすることができます。

2. コンストラクタは、名前、説明、記事へのリンクなど、アルゴリズムの基本的な特性を指定します。集団のサイズ、バイアス、近隣の数などのアルゴリズム パラメータも初期化されます。

3. popSize、deviation、neighborsNumberOnSide変数は、移行時に考慮される集団サイズ、標準偏差、および片側の近隣集団の数を決定します。

4.SetParamsメソッドは、params 配列に格納されている値に基づいてアルゴリズムパラメータを更新する役割を担います。

5. Initは、最小および最大範囲値、ステップ、エポック数の配列を受け入れる初期化メソッドです。 

6. Moving ()メソッドは検索空間内でエージェントを移動させる役割を担い、Revision ()メソッドは集団内のエージェントの状態をチェックして更新します。

7. S_AO_Agent population []配列にはエージェント（動物）の現在の集団が格納されます。S_AO_Agent pTemp []は、集団を並び替えるときに使用する一時配列です。

8. GetNeighborsIndexは、特定のエージェントの隣接インデックスを取得するために使用されるprivateメソッドです。

C_AO_AMOクラスは、渡りに基づいた最適化アルゴリズムを実装し、アルゴリズムの設定と実行に必要なメソッドとパラメータを提供します。基底クラスから機能を継承し、タスクの要件に応じて動作を拡張および変更できます。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_AMOm : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_AMOm () { }
  C_AO_AMOm ()
  {
    ao_name = "AMOm";
    ao_desc = "Animal Migration Optimization M";
    ao_link = "https://www.mql5.com/ja/articles/15543";

    popSize               = 50;   // Population size
    deviation             = 8;
    neighborsNumberOnSide = 10;

    ArrayResize (params, 3);

    params [0].name = "popSize";               params [0].val = popSize;

    params [1].name = "deviation";             params [1].val = deviation;
    params [2].name = "neighborsNumberOnSide"; params [2].val = neighborsNumberOnSide;
  }

  void SetParams ()
  {
    popSize               = (int)params [0].val;

    deviation             = params      [1].val;
    neighborsNumberOnSide = (int)params [2].val;
  }

  bool Init (const double &rangeMinP  [],
             const double &rangeMaxP  [],
             const double &rangeStepP [],
             const int     epochsP = 0);

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  double deviation;
  int    neighborsNumberOnSide;

  S_AO_Agent population []; // Animal population
  S_AO_Agent pTemp      []; // Temporary animal population

  private: //-------------------------------------------------------------------
  int   GetNeighborsIndex (int i);
};
//——————————————————————————————————————————————————————————————————————————————

次に、C_AO_AMOクラスのInitメソッドコードを考えてみましょう。以下は、メソッドの各部分の説明です。

1. rangeMinP []、rangeMaxP []、rangeStepP []：最適化されたパラメータの最小範囲と最大範囲、およびそのステップを決定するための配列。

      2. StandardInitメソッドは、渡された範囲に基づいて標準の初期化を実行します。

      3. popSizeでpopulation配列とpTemp配列のサイズを変更します。

      4.エージェントの初期化は、population配列のすべての要素に対して実行されます。座標の数coordsを渡すInitメソッドを使用して各エージェントを初期化します。 

      5. すべての操作が成功した場合、メソッドはtrueを返します。

      C_AO_AMOクラスのInitメソッドは、指定された範囲とパラメータを考慮してエージェント集団を初期化する役割を担います。

      //——————————————————————————————————————————————————————————————————————————————
bool C_AO_AMO::Init (const double &rangeMinP  [],
                     const double &rangeMaxP  [],
                     const double &rangeStepP [],
                     const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (population, popSize);
  ArrayResize (pTemp,      popSize);

  for (int i = 0; i < popSize; i++) population [i].Init (coords);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

      次に、集団内のエージェントの移動を担当するC_AO_AMOクラスのMovingメソッドについて説明します。コードの主な部分:

      1. revisionステータスの確認

      • revisionがfalseの場合、メソッドは初めて、またはリセット後に呼び出されます。この場合、集団は初期化されます。
      • 集団内の各個体（0からpopSize）および各座標（0からcoords）に対して、指定された範囲（rangeMinおよびrangeMax）内でランダムな値が生成されます。
      • これらの値はSeInDiSp関数によって処理され、指定されたステップ(rangeStep)を考慮して調整されます。

      2. revisionフラグの設定:

      • 初期化後、revisionはtrueに設定され、メソッドは終了します。

      3. 基本的な移行サイクル

      • revisionがtrueに等しい場合、メソッドはメインの移行ロジックに切り替わります。
      • それぞれの個体について、座標の反復が再度発生します。
      • GetNeighborsIndex(i)は、現在の個体が比較される隣接個体のインデックスを取得するために使用されます。
      • 隣接個体と現在の個体の座標間の距離distが計算されます。
      • この距離に基づいて、新しい座標が配置される最小境界と最大境界（minとmax）が決定されます。
      4.値の調整
      • 計算された境界が許容範囲外の場合、rangeMinとrangeMaxを考慮して調整されます。
      • 次に、標準偏差(deviation)を考慮できる正規分布（GaussDistribution関数）を使用して新しい座標値が計算されます。
      • 最初のケースと同様に、新しい値もSeInDiSpを使用して処理されます。

      Movingメソッドは、近隣エージェントとランダム要因に応じてエージェントの位置を更新する役割を担います。 

      //——————————————————————————————————————————————————————————————————————————————
void C_AO_AMO::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  int    ind1    = 0;
  double dist    = 0.0;
  double x       = 0.0;
  double min     = 0.0;
  double max     = 0.0;

  for (int i = 0; i < popSize; i++)
  { 
    for (int c = 0; c < coords; c++)
    {
      //------------------------------------------------------------------------
      ind1 = GetNeighborsIndex (i);

      dist = fabs (population [ind1].c [c] - a [i].c [c]);

      x    = a [i].c [c];
      min  = x - dist;
      max  = x + dist;

      if (min < rangeMin [c]) min = rangeMin [c];
      if (max > rangeMax [c]) max = rangeMax [c];

      a [i].c [c] = u.GaussDistribution (x, min, max, deviation);
      a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

      次のコードはC_AO_AMOのRevisionメソッドです。1つずつ見ていきましょう。

      1. 最適な個体を見つける

      • ind変数は、最適な関数(f)を持つ個体のインデックスを格納するために使用されます。
      • コードは、集団全体（0からpopSizeまで）を通過し、現在の個体が最適な関数値を持っている場合、fB値を更新します。
      • 最適な個体が見つかった場合、その特性(coordinates)がcB配列にコピーされます。
      2. 集団変化の基本的なサイクル
      • 集団内の各個体（0からpopSizeまで）について、iインデックスに応じてprob確率が計算されます。
      • 各座標（0からcoordsまで）に対して、prob確率とのランダムな比較がおこなわれます。
      • 乱数がprobより小さい場合、2つのランダムな個体ind1とind2が選択されます。
      • 両方の個体が一致する場合、同じ個体が選択されないようにind2が増加します。
      • 現在の個体の新しい座標値は、ランダムに選ばれた2つの個体の座標の平均として計算され、その後、値を指定された範囲に制限するSeInDiSp関数を使用して調整されます。
      3. 集団の更新
      •    変更が完了すると、a配列から値をコピーして、集団全体が更新されます。
      •    次にSorting関数が呼び出されます。集団をf関数で並び替えます。
      確率条件と個体のランダム選択を使用して座標値を更新することは、この方法が近隣間の相互作用に基づいて最適なソリューションを見つけることを目的としていることを示唆しています。
      //——————————————————————————————————————————————————————————————————————————————
void C_AO_AMO::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB  = a [i].f;
      ind = i;
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  int    ind1 = 0;
  int    ind2 = 0;
  double dist = 0.0;
  double x    = 0.0;
  double min  = 0.0;
  double max  = 0.0;
  double prob = 0.0;
  
  for (int i = 0; i < popSize; i++)
  {
    prob = 1.0 - (1.0 / (i + 1));
    
    for (int c = 0; c < coords; c++)
    {  
      if (u.RNDprobab() < prob)
      {
        ind1 = u.RNDminusOne (popSize);
        ind2 = u.RNDminusOne (popSize);

        if (ind1 == ind2)
        {
          ind2++;
          if (ind2 > popSize - 1) ind2 = 0;
        }

        a [i].c [c] = (population [ind1].c [c] + population [ind2].c [c]) * 0.5;
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
  }
  
  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++) population [i] = a [i];

  u.Sorting (population, pTemp, popSize);
}
//——————————————————————————————————————————————————————————————————————————————

      最後に、配列の境界を考慮して、指定されたiインデックスのランダムな近傍のインデックスを取得するC_AO_AMOクラスのGetNeighborsIndexメソッドのコードを検討してみましょう。

      1. 変数の初期化

      • Ncount： neighborsNumberOnSide変数によって決定される隣接ノードの数
      • N：要素自体を含む隣接要素の総数は、Ncount * 2 + 1として定義される

      2. このメソッドは条件文を使用して、配列の境界に対するiインデックスの位置をチェックします。

      3. 最初のNcount要素 (左側の境界線) を処理します。iインデックスがNcountより小さい場合、配列の先頭にあることを意味します。この場合、このメソッドは0からN-1までのランダムな近傍インデックスを生成します。

      4.最後のNcount要素 (右側の境界線) を処理します。iインデックスがpopSize - Ncount以上の場合、配列の末尾にあることを意味します。このメソッドは、境界を考慮して、 popSize - Nから始まる隣接インデックスを生成します。

      5. その他すべての要素を処理します。iのインデックスが配列の中央のどこかにある場合、メソッドはNcountだけ左にオフセットされた隣接インデックスを生成し、0からN-1までのランダムな値を追加します。

      6. 最後に、メソッドは生成された隣接インデックスを返します。

      GetNeighborsIndexメソッドを使用すると、配列の境界を考慮して、指定されたインデックスiのランダムな近傍のインデックスを取得できます。

      //——————————————————————————————————————————————————————————————————————————————
int C_AO_AMO::GetNeighborsIndex (int i)
{
  int Ncount = neighborsNumberOnSide;
  int N = Ncount * 2 + 1;
  int neighborIndex;

  // Select a random neighbor given the array boundaries
  if (i < Ncount)
  {
    // For the first Ncount elements
    neighborIndex = MathRand () % N;
  }
  else
  {
    if (i >= popSize - Ncount)
    {
      // For the last Ncount elements
      neighborIndex = (popSize - N) + MathRand () % N;
    }
    else
    {
      // For all other elements
      neighborIndex = i - Ncount + MathRand () % N;
    }
  }

  return neighborIndex;
}
//——————————————————————————————————————————————————————————————————————————————

      さて、アルゴリズムの記述が完了したら、それがどのように動作するかを確認しましょう。以下は、アルゴリズムのオリジナルバージョンの結果です。

      AMO|Animal Migration Optimization|50.0|1.0|2.0|
      =============================
      5 Hilly's; Func runs:10000; result:0.43676335174918435
      25 Hilly's; Func runs:10000; result:0.28370099295372453
      500 Hilly's; Func runs:10000; result:0.25169663266864406
      =============================
      5 Forest's; Func runs:10000; result:0.312993148861033
      25 Forest's; Func runs:10000; result:0.23960515885149344
      500 Forest's; Func runs:10000; result:0.18938496103401775
      =============================
      5 Megacity's; Func runs:10000; result:0.18461538461538463
      25 Megacity's; Func runs:10000; result:0.12246153846153851
      500 Megacity's; Func runs:10000; result:0.10223076923076994
      =============================
      All score:2.12345 (23.59%)

      残念ながら、元のバージョンでは検索品質が弱いです。このような指標は評価表には含まれません。結果を分析すると、アルゴリズムと他の参加者の間に大きなギャップがあることが明らかになり、アルゴリズムを深く考え直すきっかけとなりました。

      この戦略を詳しく調査したところ、重大な欠陥が発見されました。集団選別は、最も優れた個体からの遺伝物質の蓄積に貢献していなかったのです。それは、本質に影響を与えることなく、トポロジカルな配置のみを変更しました。並び替えの影響は、探索空間内の個体の座標を変更する確率を調整することにのみ限定されており、この確率は個体の適応度に反比例します。

      注目すべきは、新しい座標が、ランダムに選択された2つの個体の値を平均することによって、集団内にすでに存在する座標のみに基づいて形成されたことです。これらのニュアンスを認識したことで、選別前に子孫を親グループに統合するために集団を拡大するという考えが生まれました。このアプローチは、最良の遺伝子の組み合わせを保存するだけでなく、適応度の低い個体を自然に排除することにもつながります。間違いなく、集団の遺伝子プールを更新するという問題は依然として重要ですが、提案された変更により、進化プロセスのダイナミクスが大幅に向上するはずです。このアイデアを実装するには、まず、集団のサイズを2倍にして初期化メソッドを変更します。

      初期化コード全体を示して、集団が2倍になっていることを確認します。

      //——————————————————————————————————————————————————————————————————————————————
bool C_AO_AMOm::Init (const double &rangeMinP  [],
                      const double &rangeMaxP  [],
                      const double &rangeStepP [],
                      const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (population, popSize * 2);
  ArrayResize (pTemp,      popSize * 2);

  for (int i = 0; i < popSize * 2; i++) population [i].Init (coords);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

      したがって、Revisionメソッドを修正する必要があります。

      //----------------------------------------------------------------------------
for (int i = 0; i < popSize; i++) population [i + popSize] = a [i];

u.Sorting (population, pTemp, popSize * 2);

      適切な調整をおこなった後、アルゴリズムを再度テストし、結果を比較します。

      AMOm|Animal Migration Optimization M|50.0|1.0|2.0|
      =============================
      5 Hilly's; Func runs:10000; result:0.4759595972704031
      25 Hilly's; Func runs:10000; result:0.31711543296080447
      500 Hilly's; Func runs:10000; result:0.2540492181444619
      =============================
      5 Forest's; Func runs:10000; result:0.40387880560608347
      25 Forest's; Func runs:10000; result:0.27049305409901064
      500 Forest's; Func runs:10000; result:0.19135802944407254
      =============================
      5 Megacity's; Func runs:10000; result:0.23692307692307696
      25 Megacity's; Func runs:10000; result:0.14461538461538465
      500 Megacity's; Func runs:10000; result:0.10109230769230851
      =============================
      All score:2.39548 (26.62%)

      この場合、全体的な結果が 3%改善され、選択したパスが成功する可能性が高いことがわかります。

      次に、順位に応じた個体の確率的な変化をMovingメソッドに渡してみます。これにより、最も近い隣人から新しい座標を受け取った直後に、個人の座標を変更できるようになります。

      //----------------------------------------------------------------------------
int    ind1 = 0;
int    ind2 = 0;
double dist = 0.0;
double x    = 0.0;
double min  = 0.0;
double max  = 0.0;
double prob = 0.0;

for (int i = 0; i < popSize; i++)
{
  prob = 1.0 - (1.0 / (i + 1));
    
  for (int c = 0; c < coords; c++)
  {
    //------------------------------------------------------------------------
    ind1 = GetNeighborsIndex (i);

    dist = fabs (population [ind1].c [c] - a [i].c [c]);

    x    = a [i].c [c];
    min  = x - dist;
    max  = x + dist;

    if (min < rangeMin [c]) min = rangeMin [c];
    if (max > rangeMax [c]) max = rangeMax [c];

    a [i].c [c] = u.GaussDistribution (x, min, max, deviation);
      
    //----------------------------------------------------------------------------
    if (u.RNDprobab() < prob)
    {
      ind1 = u.RNDminusOne (popSize);
      ind2 = u.RNDminusOne (popSize);

      if (ind1 == ind2)
      {
        ind2++;
        if (ind2 > popSize - 1) ind2 = 0;
      }

      a [i].c [c] = (population [ind1].c [c] + population [ind2].c [c]) * 0.5;
    }
      
    a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}

      結果をもう一度確認してみましょう:

      AMO|Animal Migration Optimization|50.0|1.0|2.0|
      =============================
      5 Hilly's; Func runs:10000; result:0.7204154413083147
      25 Hilly's; Func runs:10000; result:0.4480389094268583
      500 Hilly's; Func runs:10000; result:0.25286213277651365
      =============================
      5 Forest's; Func runs:10000; result:0.7097109421461968
      25 Forest's; Func runs:10000; result:0.3299544372347476
      500 Forest's; Func runs:10000; result:0.18667655927410348
      =============================
      5 Megacity's; Func runs:10000; result:0.41076923076923083
      25 Megacity's; Func runs:10000; result:0.204000000000000001
      500 Megacity's; Func runs:10000; result:0.09586153846153929
      =============================
      All score:3.35829 (37.31%)

      それははるかに良いので、続ける価値があります。コードをいくつか試した後、Movingメソッドの最終バージョンが完成しました。

      //----------------------------------------------------------------------------
  int    ind1    = 0;
  int    ind2    = 0;
  double dist    = 0.0;
  double x       = 0.0;
  double min     = 0.0;
  double max     = 0.0;
  double prob    = 0.0;

  for (int i = 0; i < popSize; i++)
  {
    prob = 1.0 - (1.0 / (i + 1));
    
    for (int c = 0; c < coords; c++)
    {
      //------------------------------------------------------------------------
      ind1 = GetNeighborsIndex (i);

      dist = fabs (population [ind1].c [c] - a [i].c [c]);

      x    = population [ind1].c [c];
      min  = x - dist;
      max  = x + dist;

      if (min < rangeMin [c]) min = rangeMin [c];
      if (max > rangeMax [c]) max = rangeMax [c];

      a [i].c [c] = u.GaussDistribution (x, min, max, deviation);
      a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);


      //------------------------------------------------------------------------
      if (u.RNDprobab() < prob)
      {
        if (u.RNDprobab() <= 0.01)
        {
          ind1 = u.RNDminusOne (popSize);
          ind2 = u.RNDminusOne (popSize);

          //if (ind1 == ind2)
          {
            //ind2++;
            //if (ind2 > popSize - 1) ind2 = 0;

            a [i].c [c] = (population [ind1].c [c] + population [ind2].c [c]) * 0.5;
            a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
          }
        }
        //ind1 = u.RNDminusOne (popSize);
        //a [i].c [c] = population [ind1].c [c];
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

      Movingメソッドから、エージェント集団の更新と並び替えを担当するC_AO_AMOのRevisionメソッドの最終バージョンに移りましょう。

      //——————————————————————————————————————————————————————————————————————————————
void C_AO_AMO::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB  = a [i].f;
      ind = i;
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  
  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++) population [popSize + i] = a [i];

  u.Sorting (population, pTemp, popSize * 2);
}
//——————————————————————————————————————————————————————————————————————————————
      コードが最終的に形成されたら、再びテストに進みます。


      3. テスト結果

      AMOテストスタンドの結果

      AMOm|Animal Migration Optimization|50.0|8.0|10.0|
      =============================
      5 Hilly's; Func runs:10000; result:0.9627642143272663
      25 Hilly's; Func runs:10000; result:0.8703754433240446
      500 Hilly's; Func runs:10000; result:0.467183248460726
      =============================
      5 Forest's; Func runs:10000; result:0.9681183408862706
      25 Forest's; Func runs:10000; result:0.9109372988714968
      500 Forest's; Func runs:10000; result:0.4719026790932256
      =============================
      5 Megacity's; Func runs:10000; result:0.6676923076923076
      25 Megacity's; Func runs:10000; result:0.5886153846153845
      500 Megacity's; Func runs:10000; result:0.23546153846153978
      =============================
      All score:6.14305 (68.26%)

      評価表では高い結果が見られます。ただし、その代償として、小次元関数の最終値のばらつきが大きくなります。通常の10回ではなく50回のテストを実行してみましょう。

      AMOm|Animal Migration Optimization|50.0|8.0|10.0|
      =============================
      5 Hilly's; Func runs:10000; result:0.903577388020872
      25 Hilly's; Func runs:10000; result:0.8431723262743616
      500 Hilly's; Func runs:10000; result:0.46284266807030283
      =============================
      5 Forest's; Func runs:10000; result:0.9900061169785055
      25 Forest's; Func runs:10000; result:0.9243600311397848
      500 Forest's; Func runs:10000; result:0.4659761237381695
      =============================
      5 Megacity's; Func runs:10000; result:0.5676923076923077
      25 Megacity's; Func runs:10000; result:0.5913230769230771
      500 Megacity's; Func runs:10000; result:0.23773230769230896
      =============================
      All score:5.98668 (66.52%)

      結果はより現実的になりましたが、効率もわずかに低下しました。

      Hilly

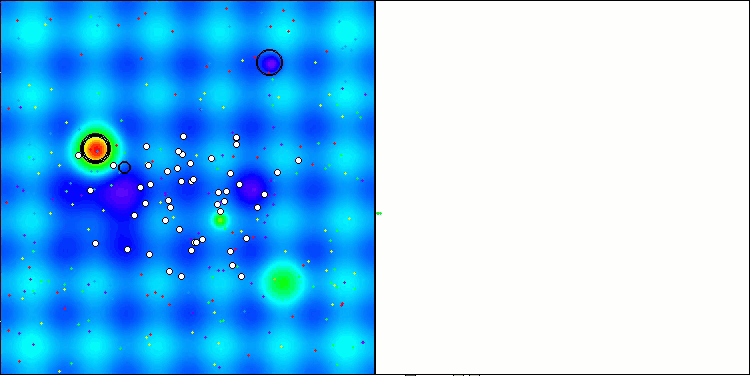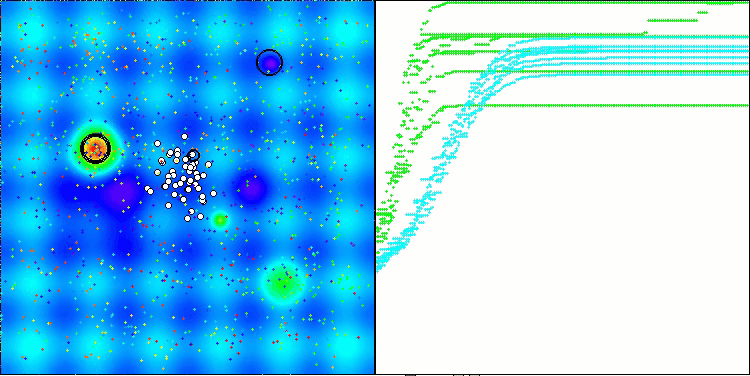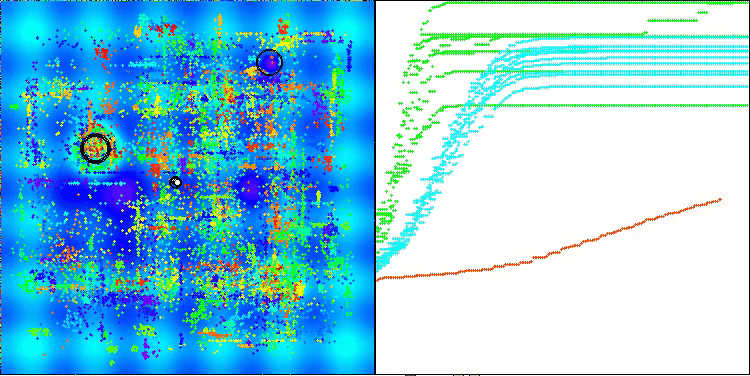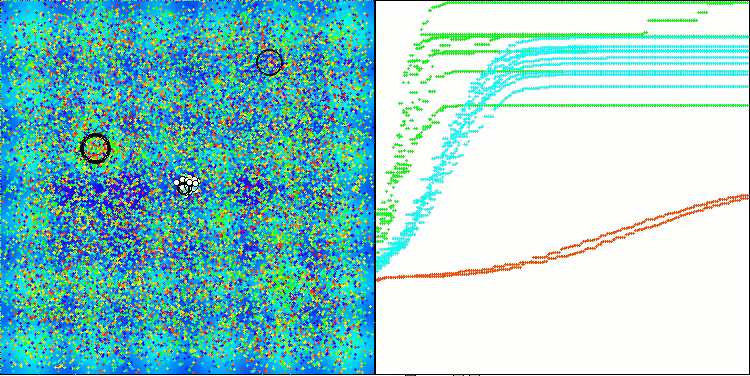
       Hilly関数のAMOm

      Forest

      Forest関数のAMOm

      Megacity

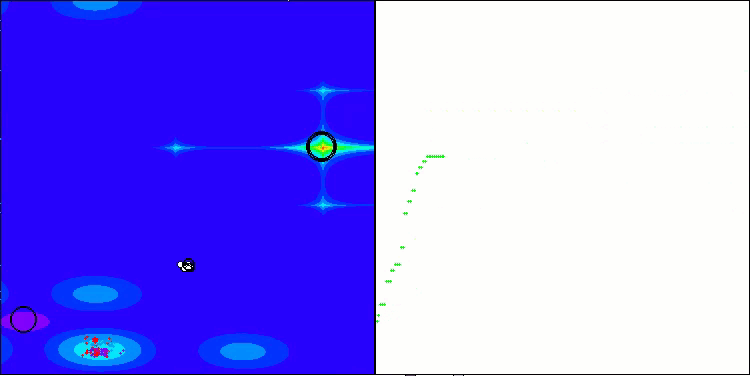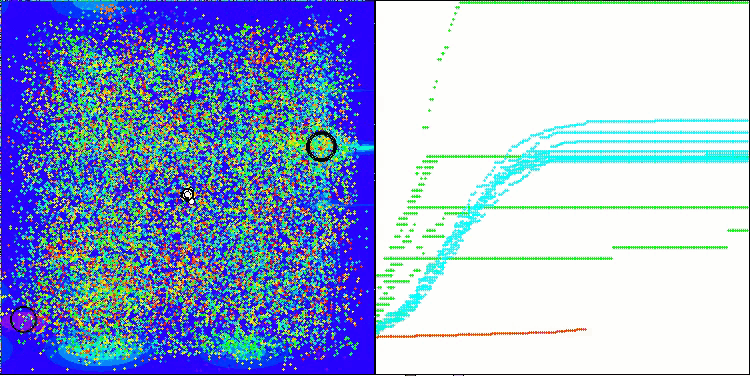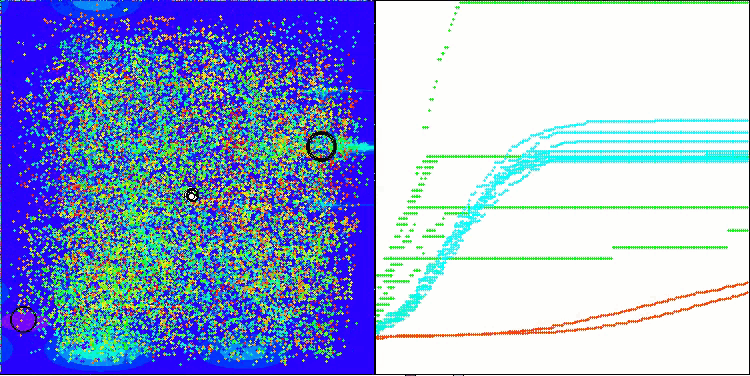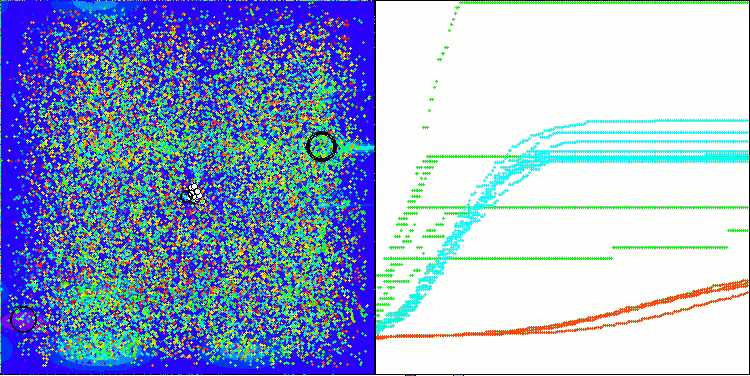
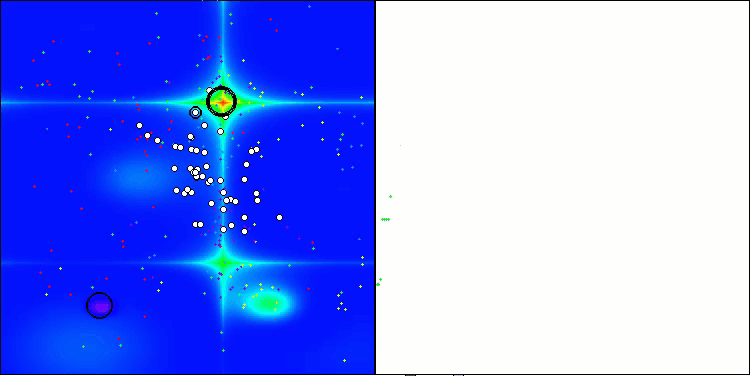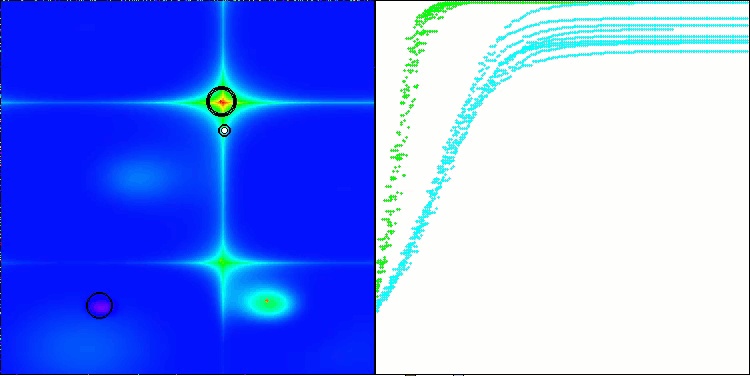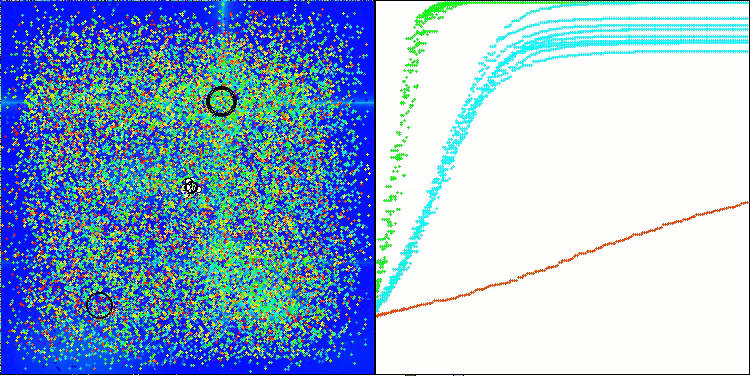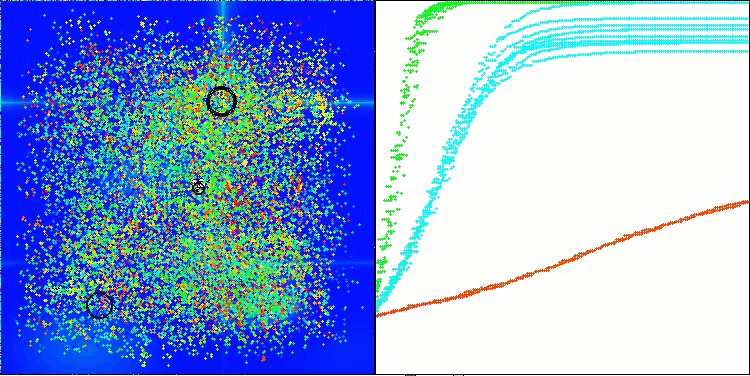
      Megacity関数のAMOm

      驚くべき変革を経て、アルゴリズムは自信を持って評価表の3位を獲得しました。

      # AO 詳細 Hilly Hilly最終 Forest Forest最終 Megacity（離散） Megacity最終 最終結果 MAXの%
      10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F)
      1 ANS Across Neighbourhood Search 0.94948 0.84776 0.43857 2.23581 1.00000 0.92334 0.39988 2.32323 0.70923 0.63477 0.23091 1.57491 6.134 68.15
      2 CLA コードロックアルゴリズム 0.95345 0.87107 0.37590 2.20042 0.98942 0.91709 0.31642 2.22294 0.79692 0.69385 0.19303 1.68380 6.107 67.86
      3 午前 渡り最適化M 0.90358 0.84317 0.46284 2.20959 0.99001 0.92436 0.46598 2.38034 0.56769 0.59132 0.23773 1.39675 5.987 66.52
      4 (P+O)ES (P+O）進化戦略 0.92256 0.88101 0.40021 2.20379 0.97750 0.87490 0.31945 2.17185 0.67385 0.62985 0.18634 1.49003 5.866 65.17
      5 CTA 彗尾アルゴリズム 0.95346 0.86319 0.27770 2.09435 0.99794 0.85740 0.33949 2.19484 0.88769 0.56431 0.10512 1.55712 5.846 64.96
      6 SDSm 確率的拡散探索M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
      7 ESG 社会母集団の進化 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
      8 SIA 等方的焼きなまし 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
      9 ACS 人工協調探索 0.75547 0.74744 0.30407 1.80698 1.00000 0.88861 0.22413 2.11274 0.69077 0.48185 0.13322 1.30583 5.226 58.06
      10 ASO 無政府社会の最適化 0.84872 0.74646 0.31465 1.90983 0.96148 0.79150 0.23803 1.99101 0.57077 0.54062 0.16614 1.27752 5.178 57.54
      11 TSEA 亀甲進化アルゴリズム 0.96798 0.64480 0.29672 1.90949 0.99449 0.61981 0.22708 1.84139 0.69077 0.42646 0.13598 1.25322 5.004 55.60
      12 DE 差分進化 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
      13 CRO 化学反応の最適化 0.94629 0.66112 0.29853 1.90593 0.87906 0.58422 0.21146 1.67473 0.75846 0.42646 0.12686 1.31178 4.892 54.36
      14 BSA 鳥群アルゴリズム 0.89306 0.64900 0.26250 1.80455 0.92420 0.71121 0.24939 1.88479 0.69385 0.32615 0.10012 1.12012 4.809 53.44
      15 HS ハーモニー検索 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
      16 SSG 苗木の播種と育成 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
      17 (PO)ES (PO）進化戦略 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
      18 BSO ブレインストーム最適化 0.93736 0.57616 0.29688 1.81041 0.93131 0.55866 0.23537 1.72534 0.55231 0.29077 0.11914 0.96222 4.498 49.98
      19 WOAm 鯨最適化アルゴリズムM 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
      20 AEFA 人工電界アルゴリズム 0.87700 0.61753 0.25235 1.74688 0.92729 0.72698 0.18064 1.83490 0.66615 0.11631 0.09508 0.87754 4.459 49.55
      21 ACOm 蟻コロニー最適化M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
      22 BFO-GA 細菌採食の最適化：Ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
      23 ABHA 人工蜂の巣アルゴリズム 0.84131 0.54227 0.26304 1.64663 0.87858 0.47779 0.17181 1.52818 0.50923 0.33877 0.10397 0.95197 4.127 45.85
      24 ASBO 適応型社会行動最適化(ASBO) 0.76331 0.49253 0.32619 1.58202 0.79546 0.40035 0.26097 1.45677 0.26462 0.17169 0.18200 0.61831 3.657 40.63
      25 MEC Mind Evolutionary Computation 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
      26 IWO 侵入雑草最適化 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
      27 Micro-AIS 微小人工免疫系 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54
      28 COAm カッコウ最適化アルゴリズムM 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21
      29 SDOm 螺旋ダイナミクス最適化M 0.74601 0.44623 0.29687 1.48912 0.70204 0.34678 0.10944 1.15826 0.42833 0.16767 0.03663 0.63263 3.280 36.44
      30 NMm ネルダー=ミード法M 0.73807 0.50598 0.31342 1.55747 0.63674 0.28302 0.08221 1.00197 0.44667 0.18667 0.04028 0.67362 3.233 35.92
      31 FAm ホタルアルゴリズムM 0.58634 0.47228 0.32276 1.38138 0.68467 0.37439 0.10908 1.16814 0.28667 0.16467 0.04722 0.49855 3.048 33.87
      32 GSA 重力探索法 0.64757 0.49197 0.30062 1.44016 0.53962 0.36353 0.09945 1.00260 0.32667 0.12200 0.01917 0.46783 2.911 32.34
      33 BFO 細菌採餌最適化 0.61171 0.43270 0.31318 1.35759 0.54410 0.21511 0.05676 0.81597 0.42167 0.13800 0.03195 0.59162 2.765 30.72
      34 ABC 人工蜂コロニー 0.63377 0.42402 0.30892 1.36671 0.55103 0.21874 0.05623 0.82600 0.34000 0.14200 0.03102 0.51302 2.706 30.06
      35 BA コウモリアルゴリズム 0.59761 0.45911 0.35242 1.40915 0.40321 0.19313 0.07175 0.66810 0.21000 0.10100 0.03517 0.34617 2.423 26.93
      36 SA 焼きなまし 0.55787 0.42177 0.31549 1.29513 0.34998 0.15259 0.05023 0.55280 0.31167 0.10033 0.02883 0.44083 2.289 25.43
      37 IWDm intelligent water drops M 0.54501 0.37897 0.30124 1.22522 0.46104 0.14704 0.04369 0.65177 0.25833 0.09700 0.02308 0.37842 2.255 25.06
      38 PSO 粒子群最適化 0.59726 0.36923 0.29928 1.26577 0.37237 0.16324 0.07010 0.60572 0.25667 0.08000 0.02157 0.35823 2.230 24.77
      39 Boids ボイドアルゴリズム 0.43340 0.30581 0.25425 0.99346 0.35718 0.20160 0.15708 0.71586 0.27846 0.14277 0.09834 0.51957 2.229 24.77
      40 MA モンキーアルゴリズム 0.59107 0.42681 0.31816 1.33604 0.31138 0.14069 0.06612 0.51819 0.22833 0.08567 0.02790 0.34190 2.196 24.40
      41 SFL Shuffled Frog-Leaping 0.53925 0.35816 0.29809 1.19551 0.37141 0.11427 0.04051 0.52618 0.27167 0.08667 0.02402 0.38235 2.104 23.38
      42 FSS 魚群検索 0.55669 0.39992 0.31172 1.26833 0.31009 0.11889 0.04569 0.47467 0.21167 0.07633 0.02488 0.31288 2.056 22.84
      43 RND ランダム 0.52033 0.36068 0.30133 1.18234 0.31335 0.11787 0.04354 0.47476 0.25333 0.07933 0.02382 0.35648 2.014 22.37
      44 GWO 灰色オオカミオプティマイザ 0.59169 0.36561 0.29595 1.25326 0.24499 0.09047 0.03612 0.37158 0.27667 0.08567 0.02170 0.38403 2.009 22.32
      45 CSS 荷電系探索 0.44252 0.35454 0.35201 1.14907 0.24140 0.11345 0.06814 0.42299 0.18333 0.06300 0.02322 0.26955 1.842 20.46



      まとめ

      テスト関数に対するAMOmアルゴリズムの結果に基づいて、次の結論を導き出すことができます。小さな次元の関数では値が広がっていますが、アルゴリズムは大きな次元の関数では優れたスケーラビリティを示します。アルゴリズムのオリジナルバージョンに大幅な変更が加えられたことで、パフォーマンスが大幅に向上しました。この場合、親集団を2倍にして（子個体と一緒に並び替えるため）、アルゴリズムステージの実行順序を変更することで、より広範囲の多様なソリューションを取得できるようになりました。このアルゴリズムは、アルゴリズムの変更に追加のテクニックを使用する可能性を明確に示す例となり、大幅な改善につながりました。これは、他の最適化アルゴリズムとの関係では必ずしも機能しないアルゴリズムロジック自体の改善によって可能になりました。 

      tab

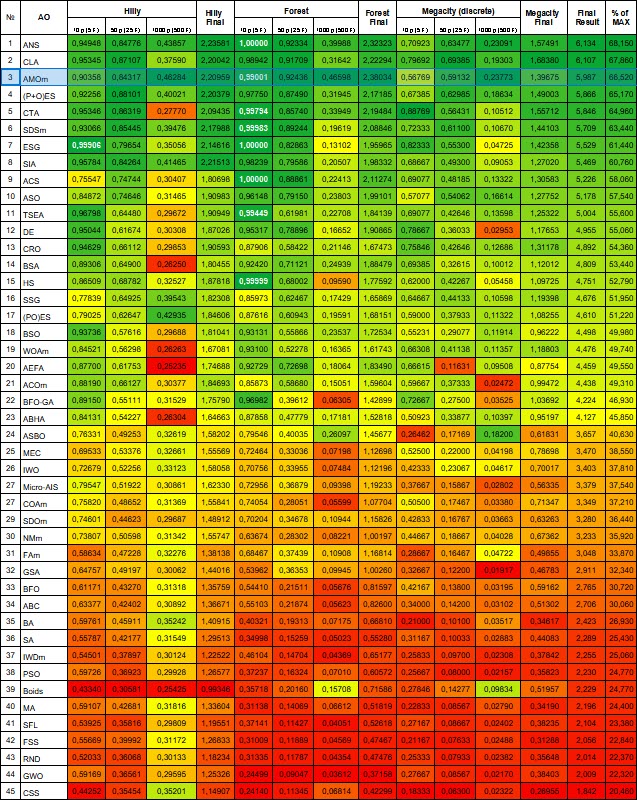
      図2：関連するテストに応じたアルゴリズムのカラーグラデーション結果は以上0.99は白で強調表示されます

      チャート

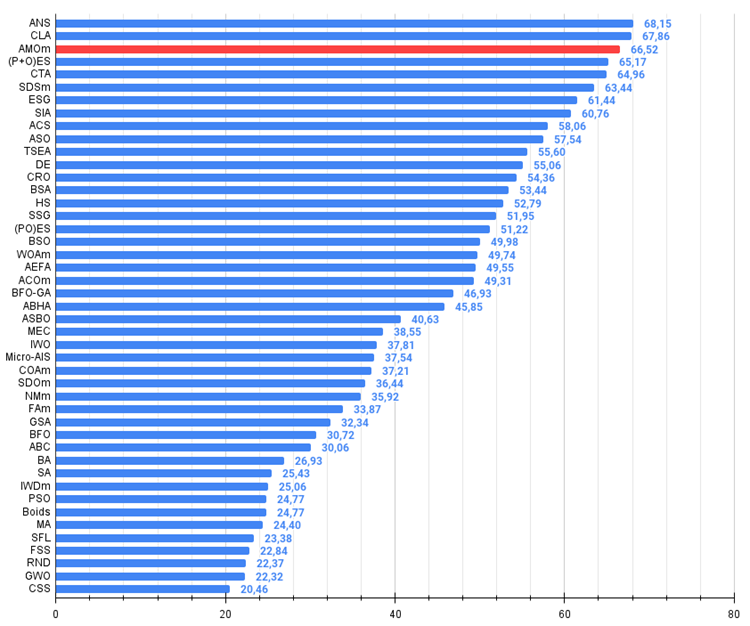
      図3：アルゴリズムテスト結果のヒストグラム（0～100のスケール、数値が高いほど良い

      100は理論上の最大結果であり、アーカイブには評価表を計算するためのスクリプトが含まれています)


      AMOmの長所と短所

      長所

      1. 収束が良好
      2. 拡張性が高い
      3. パラメータが少ない
      4. 実装がシンプル

      短所

      1. 低次元関数に関する結果が散らばる

      この記事には、最新版のアルゴリズムコードを含むアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。

      MetaQuotes Ltdによってロシア語から翻訳されました。
      元の記事: https://www.mql5.com/ru/articles/15543

      添付されたファイル |
      ZIPをダウンロード
      AMO.zip (31.3 KB)
      警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

      この著者による他の記事

      ディスカッションに移動
      ウィリアム・ギャンの手法（第1回）：ギャンアングルインジケーターの作成 ウィリアム・ギャンの手法（第1回）：ギャンアングルインジケーターの作成
      ギャン理論の本質は何でしょうか。ギャンアングルはどのように構築されるのでしょうか。本記事では、MetaTrader5向けのギャンアングルインジケーターを作成します。
      取引におけるニューラルネットワーク：独立したチャネルへのグローバル情報の注入(InjectTST) 取引におけるニューラルネットワーク：独立したチャネルへのグローバル情報の注入(InjectTST)
      最新のマルチモーダル時系列予測方法のほとんどは、独立チャネルアプローチを使用しています。これにより、同じ時系列の異なるチャネルの自然な依存関係が無視されます。2つのアプローチ（独立チャネルと混合チャネル）を賢く使用することが、モデルのパフォーマンスを向上させる鍵となります。
      初級から中級へ：演算子 初級から中級へ：演算子
      この記事では、主な演算子 について学んでいきます。このトピックは理解しやすいかもしれませんが、コードフォーマットに数式を含める際には非常に重要なポイントがいくつかあります。これらの細部を十分に理解していないと、経験の浅いプログラマーは最終的に自分で解決策を見つけることをあきらめてしまうかもしれません。
      クライアント端末での取引戦略の例の分析 クライアント端末での取引戦略の例の分析
      この記事では、ブロック図を使用して、端末のExperts\Free Robotsフォルダにあるローソク足ベースの訓練EAのロジックを調べます。