MetaTrader 5 / テスター
English Русский 中文 Español Deutsch Português
preview
アフリカ水牛最適化(ABO)

アフリカ水牛最適化(ABO)

MetaTrader 5 — テスター |
119 5
Andrey Dik
Andrey Dik


内容

  1. はじめに
  2. アルゴリズムの実装
  3. テスト結果


はじめに

アフリカ水牛最適化(ABO)アルゴリズムは、野生におけるアフリカ水牛の顕著な行動に着想を得て開発されたメタヒューリスティック手法です。このアルゴリズムは、アフリカ水牛の社会的相互作用および生存戦略を基盤として、Julius Beneoluchi Odili氏とMohd Nizam Kahar氏によって2015年に提案されました。

アフリカ水牛は、集団での防衛能力や、食料・水源を探索する際の高度な協調性で知られています。彼らは大規模な群れで生活し、捕食者からの防御に加えて、成獣が幼獣や弱い個体の保護にあたることで、緊密な社会構造を形成します。捕食者に襲われた際には、群れの弱者を囲むように輪を作る、防衛陣形を形成する、あるいは連携して反撃するなど、見事な協調行動を見せます。

ABOアルゴリズムの基本原理は、このような水牛の行動の重要な側面を反映しています。まず「通信」です。水牛は音声信号によって互いの行動を調整しており、これはアルゴリズムにおいてはエージェント間の情報共有に対応します。次に「学習」です。水牛は自身の経験だけでなく、群れの他個体の経験からも学習します。アルゴリズムでは、これがエージェントの位置を蓄積された情報に基づいて更新するという形で実装されています。

アフリカ水牛のこうした独特な行動は、最適化アルゴリズムの設計において極めて興味深いインスピレーションの源となります。これらの動物は、環境の変化に柔軟に適応し、食料や水を求めて季節的に長距離を移動します。その過程で、効率的に資源を探索し、危険を回避するための戦略を駆使します。移動中、水牛は資源を効率的に見つけて危険を回避できる探索戦略を採用します。

このように、アフリカ水牛の高度に協調的で適応力に富む行動は、ABOアルゴリズムの設計における強力な動機づけとなっています。これらの特徴により、ABOは複雑な問題に対する効果的な解決策を提供する、自然の生存戦略に着想を得た有望な最適化手法として位置づけられます。


アルゴリズムの実装

アフリカ水牛最適化(ABO)アルゴリズムは、アフリカ水牛に見られる協調性や社会的相互作用といった本能的な行動を活用し、最適化問題の解決を図る手法です。以下に、本アルゴリズムの動作原理を示します。

1. アルゴリズムは、解空間内における水牛の集団を初期化することから始まります。各水牛は1つの潜在的な解を表し、その位置はランダムに設定されます。

2. 各解（すなわち水牛の位置）は、適応度関数により評価されます。現在の適応度が過去の自己最良値(bp_max)を上回っていれば、その位置が維持されます。同様に、群れ全体の中での最良値(bg_max)を上回っている場合も、その位置が維持されます。

3. 水牛の位置は、「maaa（留まって活用する）」および「waaa（移動して探索する）」という2つの信号に基づいて更新されます。これらの信号は、水牛が食料源を効率的に探索する行動を模倣しています。 

4. 水牛の移動が、式W.k + 1 = W.k + lp * r1 * (bgmaxt.k - m.k) + lp * r2 * (bpmax.k - m.k)によって更新されます。ここで、W.kは探索を担う移動ベクトル、m.kは現在位置、lp1とlp2は学習係数、r1とr2は[0,1]の範囲の乱数です。bgmaxは群れ全体における最良の位置、bpmaxはその個体における最良の位置です。

bgmaxt.k - m.kは「maaa」信号、bpmax.k - m.kは「waaa」信号に相当します。

5. 次に、水牛kの位置は、自身の現在位置と前のステップで計算された移動量に基づいて、式m.k + 1 = λ * (W.k + m.k)によって更新されます。この式は水牛の新しい位置を決定します。ここで、λは移動率です。

6. 停止条件が満たされていない場合は、ステップ2に戻って、適応度の評価を再度おこないます。

7. 停止条件が満たされた時点でアルゴリズムは終了し、与えられた問題に対して見つかった最良の解を表す位置ベクトルを出力します。

アルゴリズムの基礎を実装するS_Buffalo構造体とC_AO_ABOクラスについて説明します。

  • S_Buffaloは、水牛を表す構造体であり、アルゴリズム内でエージェントの移動ベクトルを示すw配列を含みます。
  • コンストラクタでは、popSize（個体数）、lp1およびlp2（学習係数）、さらにアルゴリズムで使用されるlambdaが設定されます。
  • SetParamsメソッドは、params配列に格納された値に基づいてアルゴリズムのパラメータを設定します。
  • Initメソッドは、アルゴリズムの初期化をおこないます。このメソッドは、探索の最小・最大範囲、探索ステップ、エポック数を受け取ります。 
  • MovingメソッドとRevisionメソッドは、アルゴリズムの主要な処理ステップである移動（新しい解の探索）および修正（解の確認と更新）を実装します。 
  • クラスフィールドのlp1、lp2、およびlambdaは、アルゴリズムの挙動を制御するために使用されます。 
  • S_Buffalo型の配列bは、最適化に参加する水牛インスタンスを格納します。

//——————————————————————————————————————————————————————————————————————————————
struct S_Buffalo
{
    double w [];
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
class C_AO_ABO : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_ABO () { }
  C_AO_ABO ()
  {
    ao_name = "ABO";
    ao_desc = "African Buffalo Optimization";
    ao_link = "https://www.mql5.com/ja/articles/16024";

    popSize = 50;    // population size

    lp1     = 0.7;   // learning factor 1
    lp2     = 0.5;   // learning factor 2
    lambda  = 0.3;   // lambda for the movement equation

    ArrayResize (params, 4);

    params [0].name = "popSize"; params [0].val = popSize;
    params [1].name = "lp1";     params [1].val = lp1;
    params [2].name = "lp2";     params [2].val = lp2;
    params [3].name = "lambda";  params [3].val = lambda;
  }

  void SetParams ()
  {
    popSize = (int)params [0].val;
    lp1     = params      [1].val;
    lp2     = params      [2].val;
    lambda  = params      [3].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  double lp1;    // learning factor 1
  double lp2;    // learning factor 2
  double lambda; // lambda for the movement equation

  private: //-------------------------------------------------------------------
  S_Buffalo b [];
};
//——————————————————————————————————————————————————————————————————————————————

C_AO_ABOクラスのInitメソッドは、アルゴリズムパラメータを初期化する役割を担います。以下はメソッドパラメータです。

  • rangeMinP []：パラメータの範囲における最小値を指定する配列
  • rangeMaxP []：パラメータの範囲における最大値を指定する配列
  • rangeStepP []：パラメータ値の変更ステップを指定する配列
  • epochsP：エポック（反復）数。デフォルトは0です。最適化処理における反復回数を設定します。

 以下は、メソッドのロジックです。

1. 標準初期化：最初にStandardInitを呼び出し、渡された配列rangeMinP、rangeMaxP、rangeStepP使用して初期化をおこないます。初期化に失敗した場合には、falseを返します。

2. 集団の初期化

  • 配列bのサイズをpopSizeに設定します。これにより、探索エージェントの数が確保されます。
  • 集団内の各エージェント（0からpopSize−1までのループ処理）に対して、b [i].w配列をcoordsにサイズ変更します。ここでのcoordsは座標数（問題での最適化対象のパラメータ数）を表します。
  • b [i].w配列はArrayInitializeによってゼロで初期化されます。

3. すべての操作が成功した場合、メソッドは初期化が成功したことを示すtrueを返します。

Initメソッドは、アルゴリズムに必要なデータ構造を準備し、パラメータと集団を正しく初期化する役割を担います。これは、このデータを用いて最適化をおこなうメインアルゴリズムを実行する前の重要なステップです。

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_ABO::Init (const double &rangeMinP [],
                     const double &rangeMaxP [],
                     const double &rangeStepP [],
                     const int epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (b, popSize);
  for (int i = 0; i < popSize; i++)
  {
    ArrayResize(b [i].w, coords);
    ArrayInitialize (b [i].w, 0.0);
  }

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_ABOクラスのMovingメソッドは、最適化中に集団内の水牛を検索空間上で移動させる役割を担います。動作の詳細は以下の通りです。

1. まず、リビジョンが実行されたかどうかを確認します（if (!revision)）。まだ実行されていない場合、集団をランダムな値で初期化します。

  • 外側のループでpopSizeすべてを処理します。
  • 内側のループでcoords座標すべてを処理します。

     各パラメータについて以下をおこないます。

  • まず、u.RNDfromCIメソッドを使用してrangeMin [c]からrangeMax [c]の範囲でランダムな値を生成します。
  • この値はu.SeInDiSpを使用してチェックおよび調整され、rangeStep [c]ステップを考慮して値が指定された範囲に制限されます。
  • 初期化が完了すると、revisionがtrueに設定され、メソッドの実行が完了します。

2. 水牛の移動の基本的なロジック。既にリビジョンが実行されている場合、各水牛の位置を更新します。

  • w、m、r1、r2、bg、bpの変数を計算のために初期化します。
  • 外側のループでpopSizeすべてを処理します。
  • 内側のループでcoords座標すべてを処理します。
  • 2つの乱数r1、r2を生成し、水牛の行動にランダム性を導入します。
  • bgには群れ全体の最良位置cB [c]の座標を、bpには個体の最良位置a [i].cB [c]の座標を取得します。
  • mには現在の位置a [i].c [c]の座標を、wには現在の移動ベクトルb [i].w [c]の値を取得します。
  • 移動ベクトルb [i].w [c]の値は、水牛の大域および局所最良位置の両方を考慮した式 b [i].w [c] = w + r1 * (bg - m) + r2 * (bp - m)に従って更新されます。
  • 次に、対応するm座標による位置がλ比を使用して更新されます。
  • 最後に、u.SeInDiSpを使用して、検索エージェントの座標a [i].c [c]の新しい値が計算され、調整されます。

Movingメソッドは、位置の初期化および更新を担当し、最適化中に集団のメンバーの移動を実行します。このメソッドは、群れの動物たちの大域および局所の既知の最良位置の両方に基づいた乱数を使用して、水牛の位置を初期化および更新します。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ABO::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  double w  = 0.0;
  double m  = 0.0;
  double r1 = 0.0;
  double r2 = 0.0;
  double bg = 0.0;
  double bp = 0.0;

  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      r1 = u.RNDfromCI (0, lp1);
      r2 = u.RNDfromCI (0, lp2);

      bg = cB [c];
      bp = a [i].cB [c];

      m = a [i].c [c];
      w = b [i].w [c];

      b [i].w [c] = w + r1 * (bg - m) + r2 * (bp - m);

      m = lambda * (m + b [i].w [c]);

      a [i].c [c] = u.SeInDiSp (m, rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_ABOクラスのRevisionメソッドは、集団内の関数とパラメータの最良値を更新する役割を担います。以下がメソッドの説明です。

1. 変数indは-1で初期化されます。これは、今回の更新処理で見つかった最良の個体のインデックスを記録するために使用されます。

2. 大域的最良の個体を検索

  • forループを使って、全エージェント（集団サイズ popSize）を順に確認します。
  • 各エージェントの適応度a [i].fが、現在の大域最良値fBを上回っているかどうかを確認します。
  • もし上回っていれば、fBを更新し、そのエージェントのインデックスをindに記録します。
  • ループ完了後、より良いエージェントが見つかっていれば(ind != -1）、ArrayCopy関数を使って、そのエージェントのパラメータcを大域最良パラメータ配列cBにコピーします。

3. 局所最良値の更新

  • 続いて、再び全エージェントを対象にforループを実行します。
  • 各エージェントの適応度a [i].fが、現在の局所最良値a [i].fBを上回っているかどうかを確認します。
  • もし上回っていれば、a [i].fBを更新し、そのエージェントのインデックスを局所最良座標配列cBに記録します。

Revisionメソッドでは、主に次の2つのタスクが実行されます。

  • 大域最適解における適応度の評価値と対応するパラメータを特定・更新します。
  • さらに、集団内の各エージェントについて、局所最適解における適応度関数の値とパラメータを更新します。

このような処理は、多くの最適化アルゴリズム（例：PSO、ABOなど）において一般的であり、解探索の精度向上や多様性維持のために、大域最適解と局所最適解の両方を追跡することが重要です。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ABO::Revision ()
{
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > a [i].fB)
    {
      a [i].fB = a [i].f;
      ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

アルゴリズムの実装全体を検討しました。それは非常に簡単です。これでテスト段階に進むことができます。

オリジナルのABOバージョンのパフォーマンスを確認してみましょう。

ABO|African Buffalo Optimization|50.0|0.2|0.9|0.9|
=============================
5 Hilly's; Func runs:10000; result:0.8495807203797128
25 Hilly's; Func runs:10000; result:0.5186057937632769
500 Hilly's; Func runs:10000; result:0.2642792490546295
=============================
5 Forest's; Func runs:10000; result:0.6554510234450559
25 Forest's; Func runs:10000; result:0.41662244493546935
500 Forest's; Func runs:10000; result:0.21044033116304034
=============================
5 Megacity's; Func runs:10000; result:0.6015384615384616
25 Megacity's; Func runs:10000; result:0.26430769230769224
500 Megacity's; Func runs:10000; result:0.11120000000000112
=============================
All score:3.89203 (43.24%)

悪くありません。しかし、自分らしさを保つためには、アルゴリズムの改良に挑戦せずにはいられません。オリジナルのバージョンでは、水牛の新しい位置は、群れ全体の最良位置、自身の最良位置、そして現在位置に基づき、変位ベクトル（現在位置からの変位量）を予め計算して決定されます。この変位ベクトルは、動きにおける一種の慣性として機能しています。

そこで私は、慣性という概念を廃止し、自分自身と群れの最適位置の情報を直接用い、現在の状況に即した計算をおこなうことを思いつきました。これに伴い、著者のコード部分はコメントアウトし、外部パラメータであるλも削除して、よりシンプルな新コードを作成しました。新しいコードは緑色で強調表示されます。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ABO::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  double w  = 0.0;
  double m  = 0.0;
  double r1 = 0.0;
  double r2 = 0.0;
  double bg = 0.0;
  double bp = 0.0;

  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      /*
      r1 = u.RNDfromCI (0, lp1);
      r2 = u.RNDfromCI (0, lp2);

      bg = cB [c];
      bp = a [i].cB [c];

      m = a [i].c [c];
      w = b [i].w [c];

      b [i].w [c] = w + r1 * (bg - m) + r2 * (bp - m);

      m = lambda * (m + b [i].w [c]);

      a [i].c [c] = u.SeInDiSp (m, rangeMin [c], rangeMax [c], rangeStep [c]);
      */

      r1 = u.RNDfromCI (-lp1, lp1);
      r2 = u.RNDfromCI (-lp2, lp2);

      bg = cB [c];
      bp = a [i].cB [c];

      m = a [i].c [c];

      m = m + r1 * (bg - m) + r2 * (bp - m);

      a [i].c [c] = u.SeInDiSp (m, rangeMin [c], rangeMax [c], rangeStep [c]);

    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

水牛の移動のロジックを変更した後に得られた結果は次のとおりです。

ABO|African Buffalo Optimization|50.0|1.0|0.1|0.9|
=============================
5 Hilly's; Func runs:10000; result:0.833371781687727
25 Hilly's; Func runs:10000; result:0.6224659624836805
500 Hilly's; Func runs:10000; result:0.2996410968574058
=============================
5 Forest's; Func runs:10000; result:0.9217022975045926
25 Forest's; Func runs:10000; result:0.5861755787948962
500 Forest's; Func runs:10000; result:0.19722782275756043
=============================
5 Megacity's; Func runs:10000; result:0.6100000000000001
25 Megacity's; Func runs:10000; result:0.4315384615384614
500 Megacity's; Func runs:10000; result:0.13224615384615512
=============================
All score:4.63437 (51.49%)

結果は約10%改善されました。具体的には、51.49%対43.24%です。改善効果は特に、パラメータ数が50および1000の関数で顕著に表れています。一方で、パラメータ数が10の関数では変化がほとんど見られませんでした。これは、大規模問題に対するアルゴリズムのスケーラビリティが向上したことを示しています。

次に試してみたいアイデアがもう一つあります。現在の式では各水牛の最良位置を使っていますが、群れの中からランダムに選んだ水牛の最良位置を用い、その選択確率を集団リストの先頭側に偏らせる方法です。これはコードのわずかな修正で簡単に検証できます。確率を集団リストの先頭に寄せることで、乱数[0.0, 1.0]を累乗し、その結果の小数部分を切り捨てる操作がおこなわれます。今回の試みでは累乗の指数として「4」を使用しています。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ABO::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  double w  = 0.0;
  double m  = 0.0;
  double r1 = 0.0;
  double r2 = 0.0;
  double bg = 0.0;
  double bp = 0.0;

  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      /*
      r1 = u.RNDfromCI (0, lp1);
      r2 = u.RNDfromCI (0, lp2);

      bg = cB [c];
      bp = a [i].cB [c];

      m = a [i].c [c];
      w = b [i].w [c];

      b [i].w [c] = w + r1 * (bg - m) + r2 * (bp - m);

      m = lambda * (m + b [i].w [c]);

      a [i].c [c] = u.SeInDiSp (m, rangeMin [c], rangeMax [c], rangeStep [c]);
      */
      
      r1 = u.RNDfromCI (-lp1, lp1);
      r2 = u.RNDfromCI (-lp2, lp2);

      bg = cB [c];
      //bp = a [i].cB [c];
      
      
      double r = u.RNDprobab ();
      int ind = (int)pow (r - 1, 4);
      
      bp = a [ind].cB [c]; 

      m = a [i].c [c];

      m = m + r1 * (bg - m) + r2 * (bp - m);

      a [i].c [c] = u.SeInDiSp (m, rangeMin [c], rangeMax [c], rangeStep [c]);
      
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

最も優秀な水牛に偏った確率的選択を集団内の個体に適用するためには、Revisionメソッド内で個体を適応度の高い順に並べ替える必要があります。幸いにも、この目的に合ったSorting_fBメソッドは、以前の記事のいずれかで既に実装されています。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ABO::Revision ()
{
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > a [i].fB)
    {
      a [i].fB = a [i].f;
      ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  S_AO_Agent aT [];
  ArrayResize (aT, popSize);

  u.Sorting_fB (a, aT, popSize);
}
//——————————————————————————————————————————————————————————————————————————————

群れの中で最良の水牛の位置を確率的に選択し、それをABOアルゴリズムの新しい位置計算の式に適用した結果を見てみましょう。

ABO|African Buffalo Optimization|50.0|0.1|0.8|0.9|
=============================
5 Hilly's; Func runs:10000; result:0.841272551476775
25 Hilly's; Func runs:10000; result:0.5701677694693293
500 Hilly's; Func runs:10000; result:0.28850644933225034
=============================
5 Forest's; Func runs:10000; result:0.9015705858486595
25 Forest's; Func runs:10000; result:0.49493378365495344
500 Forest's; Func runs:10000; result:0.1919604395333699
=============================
5 Megacity's; Func runs:10000; result:0.5692307692307692
25 Megacity's; Func runs:10000; result:0.35261538461538455
500 Megacity's; Func runs:10000; result:0.12010769230769343
=============================
All score:4.33037 (48.12%)

アルゴリズムの全体的な性能は若干低下しましたが、それでも「純粋な」オリジナル版よりは高い結果となっています。そこで、アルゴリズム改良の最初の実験結果を記録し、評価表に反映させることにします。なお、アルゴリズムのロジック変更により探索空間での挙動が変わるため、各バージョンのアルゴリズムに対しては、すべてのテストで最大の性能を引き出せるように外部パラメータを調整している点をご留意ください。


テスト結果

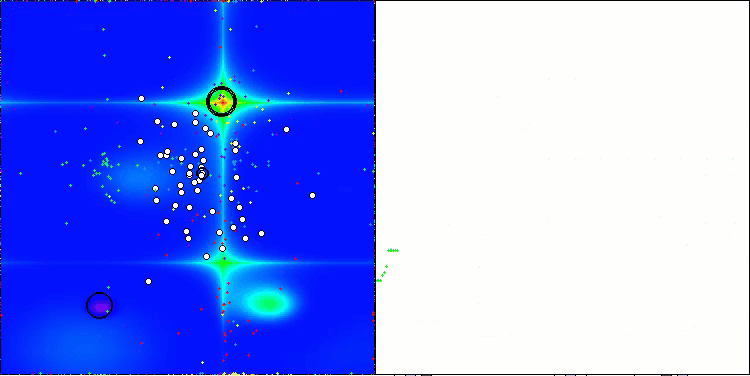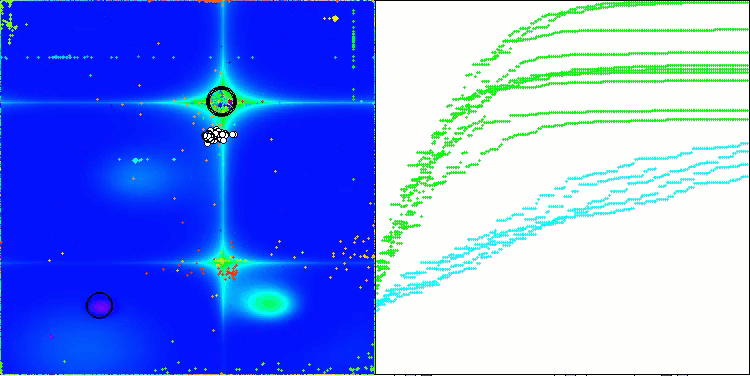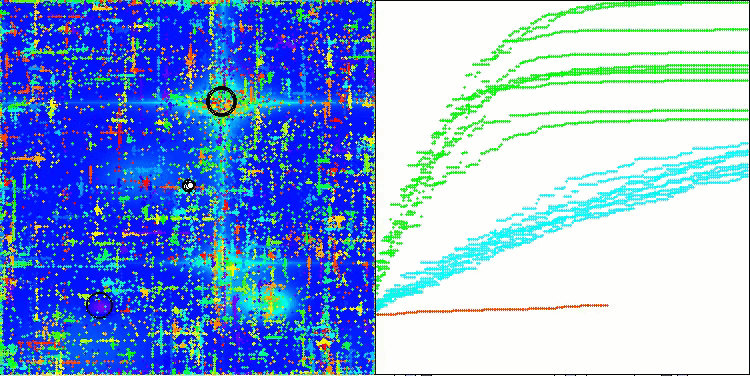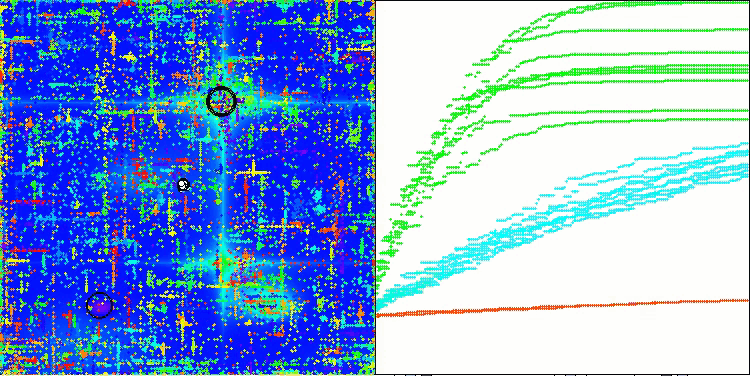
ABOアルゴリズムの可視化からは、ハイパースペースの重要な領域が丁寧に探索されていることがわかり、最適化対象関数の表面を精緻に調査する能力の高さを示しています。一方で、今回の小さな改良はアルゴリズムのスケーラビリティを向上させるものの、パラメータ次元が小さい問題では局所解に陥りやすくなる傾向があります。これは、可視化の収束グラフにおける緑色の線のばらつき（結果の散布）から確認できます。

Hilly

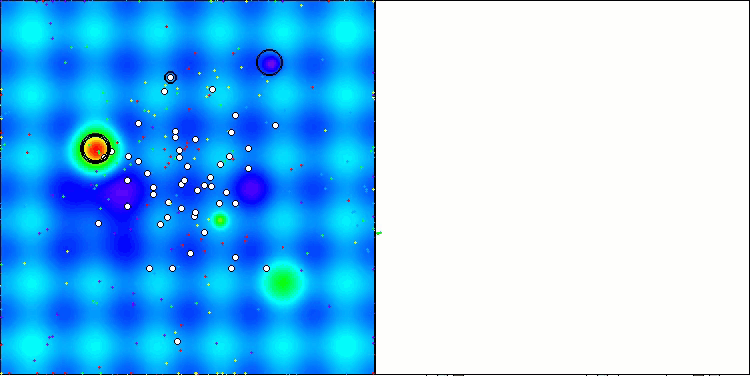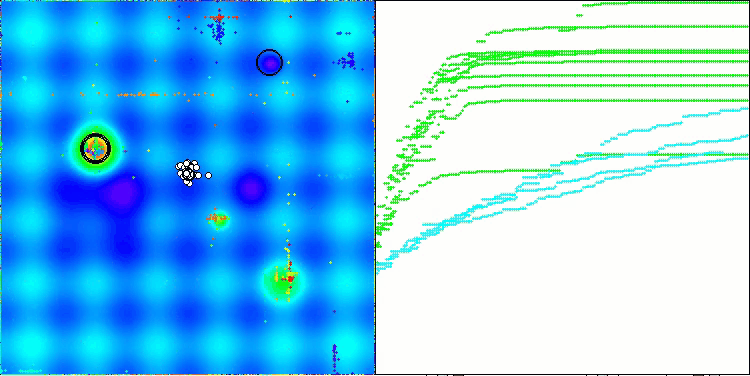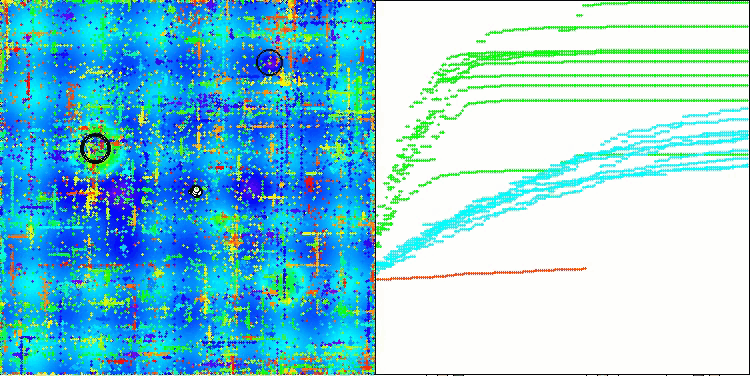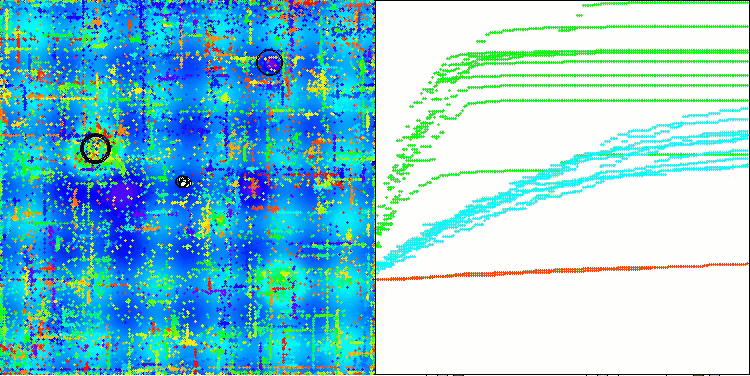
Hillyテスト関数のABO

Forest

Forestテスト関数のABO

Megacity

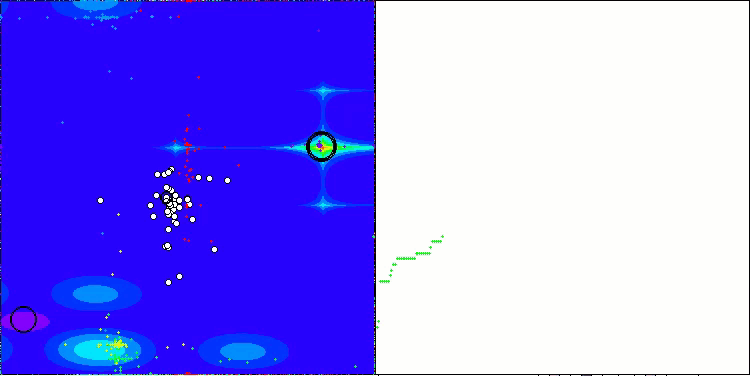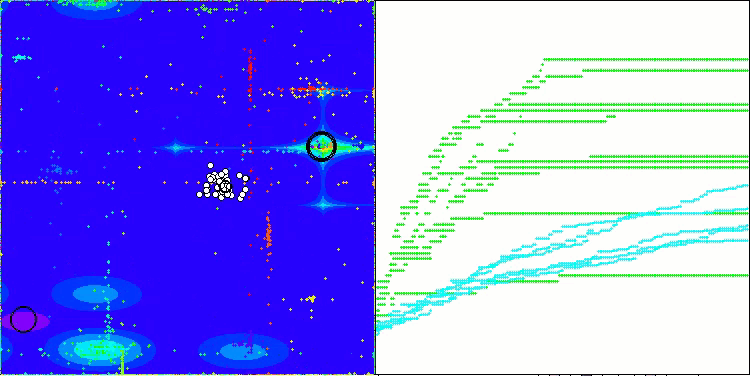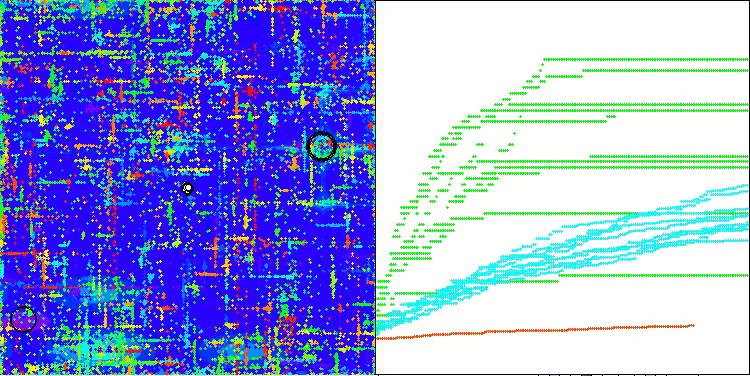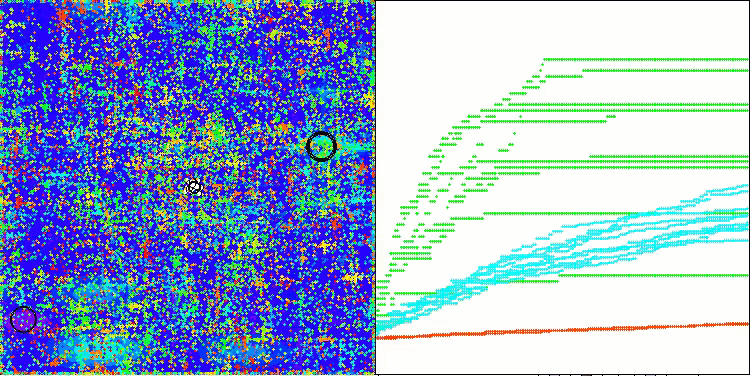
Megacityテスト関数のABO

テスト結果によると、このアルゴリズムは最適化アルゴリズムの総合ランキングで安定して19位を獲得しました。

# AO 詳細 Hilly Hilly最終 Forest Forest最終 Megacity（離散） Megacity最終 最終結果 MAXの%
10p(5F) 50p(25F) 1000p(500F) 10p(5F) 50p(25F) 1000p(500F) 10p(5F) 50p(25F) 1000p(500F)
1 ANS across neighbourhood search 0.94948 0.84776 0.43857 2.23581 1.00000 0.92334 0.39988 2.32323 0.70923 0.63477 0.23091 1.57491 6.134 68.15
2 CLA コードロックアルゴリズム 0.95345 0.87107 0.37590 2.20042 0.98942 0.91709 0.31642 2.22294 0.79692 0.69385 0.19303 1.68380 6.107 67.86
3 AMOm 動物移動最適化m 0.90358 0.84317 0.46284 2.20959 0.99001 0.92436 0.46598 2.38034 0.56769 0.59132 0.23773 1.39675 5.987 66.52
4 (P+O)ES (P+O)進化戦略 0.92256 0.88101 0.40021 2.20379 0.97750 0.87490 0.31945 2.17185 0.67385 0.62985 0.18634 1.49003 5.866 65.17
5 CTA 彗尾アルゴリズム 0.95346 0.86319 0.27770 2.09435 0.99794 0.85740 0.33949 2.19484 0.88769 0.56431 0.10512 1.55712 5.846 64.96
6 SDSm 確率的拡散探索M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
7 AAm アーチェリーアルゴリズムM 0.91744 0.70876 0.42160 2.04780 0.92527 0.75802 0.35328 2.03657 0.67385 0.55200 0.23738 1.46323 5.548 61.64
8 ESG 社会母集団の進化 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
9 SIA 等方的焼きなまし 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
10 ACS 人工協調探索 0.75547 0.74744 0.30407 1.80698 1.00000 0.88861 0.22413 2.11274 0.69077 0.48185 0.13322 1.30583 5.226 58.06
11 ASO 無政府社会最適化 0.84872 0.74646 0.31465 1.90983 0.96148 0.79150 0.23803 1.99101 0.57077 0.54062 0.16614 1.27752 5.178 57.54
12 TSEA 亀甲進化アルゴリズム 0.96798 0.64480 0.29672 1.90949 0.99449 0.61981 0.22708 1.84139 0.69077 0.42646 0.13598 1.25322 5.004 55.60
13 DE 差分進化 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
14 CRO 化学反応の最適化 0.94629 0.66112 0.29853 1.90593 0.87906 0.58422 0.21146 1.67473 0.75846 0.42646 0.12686 1.31178 4.892 54.36
15 BSA 鳥群アルゴリズム 0.89306 0.64900 0.26250 1.80455 0.92420 0.71121 0.24939 1.88479 0.69385 0.32615 0.10012 1.12012 4.809 53.44
16 HS ハーモニー検索 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
17 SSG 苗木の播種と育成 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
18 BCOm 細菌走化性最適化M 0.75953 0.62268 0.31483 1.69704 0.89378 0.61339 0.22542 1.73259 0.65385 0.42092 0.14435 1.21912 4.649 51.65
19 ABO アフリカ水牛の最適化 0.83337 0.62247 0.29964 1.75548 0.92170 0.58618 0.19723 1.70511 0.61000 0.43154 0.13225 1.17378 4.634 51.49
20 (PO)ES (PO)進化戦略 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
21 TSm タブーサーチM 0.87795 0.61431 0.29104 1.78330 0.92885 0.51844 0.19054 1.63783 0.61077 0.38215 0.12157 1.11449 4.536 50.40
22 BSO ブレインストーム最適化 0.93736 0.57616 0.29688 1.81041 0.93131 0.55866 0.23537 1.72534 0.55231 0.29077 0.11914 0.96222 4.498 49.98
23 WOAm 鯨最適化アルゴリズムM 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
24 AEFA 人工電界アルゴリズム 0.87700 0.61753 0.25235 1.74688 0.92729 0.72698 0.18064 1.83490 0.66615 0.11631 0.09508 0.87754 4.459 49.55
25 ACOm 蟻コロニー最適化M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
26 BFO-GA 細菌採食の最適化：Ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
27 ABHA 人工蜂の巣アルゴリズム 0.84131 0.54227 0.26304 1.64663 0.87858 0.47779 0.17181 1.52818 0.50923 0.33877 0.10397 0.95197 4.127 45.85
28 ACMO 大気雲モデルの最適化 0.90321 0.48546 0.30403 1.69270 0.80268 0.37857 0.19178 1.37303 0.62308 0.24400 0.10795 0.97503 4.041 44.90
29 アシャ 人工シャワーアルゴリズム 0.89686 0.40433 0.25617 1.55737 0.80360 0.35526 0.19160 1.35046 0.47692 0.18123 0.09774 0.75589 3.664 40.71
30 ASBO 適応型社会行動最適化(ASBO) 0.76331 0.49253 0.32619 1.58202 0.79546 0.40035 0.26097 1.45677 0.26462 0.17169 0.18200 0.61831 3.657 40.63
31 MEC mind evolutionary computation 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
32 IWO 侵入雑草最適化 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
33 Micro-AIS 微小人工免疫系 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54
34 COAm カッコウ最適化アルゴリズムM 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21
35 SDOm 螺旋ダイナミクス最適化M 0.74601 0.44623 0.29687 1.48912 0.70204 0.34678 0.10944 1.15826 0.42833 0.16767 0.03663 0.63263 3.280 36.44
36 NMm ネルダー=ミード法M 0.73807 0.50598 0.31342 1.55747 0.63674 0.28302 0.08221 1.00197 0.44667 0.18667 0.04028 0.67362 3.233 35.92
37 FAm ホタルアルゴリズムM 0.58634 0.47228 0.32276 1.38138 0.68467 0.37439 0.10908 1.16814 0.28667 0.16467 0.04722 0.49855 3.048 33.87
38 GSA 重力探索法 0.64757 0.49197 0.30062 1.44016 0.53962 0.36353 0.09945 1.00260 0.32667 0.12200 0.01917 0.46783 2.911 32.34
39 BFO 細菌採餌最適化 0.61171 0.43270 0.31318 1.35759 0.54410 0.21511 0.05676 0.81597 0.42167 0.13800 0.03195 0.59162 2.765 30.72
40 ABC 人工蜂コロニー 0.63377 0.42402 0.30892 1.36671 0.55103 0.21874 0.05623 0.82600 0.34000 0.14200 0.03102 0.51302 2.706 30.06
41 BA コウモリアルゴリズム 0.59761 0.45911 0.35242 1.40915 0.40321 0.19313 0.07175 0.66810 0.21000 0.10100 0.03517 0.34617 2.423 26.93
42 AAA 藻類適応アルゴリズム 0.50007 0.32040 0.25525 1.07572 0.37021 0.22284 0.16785 0.76089 0.27846 0.14800 0.09755 0.52402 2.361 26.23
43 SA 焼きなまし 0.55787 0.42177 0.31549 1.29513 0.34998 0.15259 0.05023 0.55280 0.31167 0.10033 0.02883 0.44083 2.289 25.43
44 IWDm intelligent water drops M 0.54501 0.37897 0.30124 1.22522 0.46104 0.14704 0.04369 0.65177 0.25833 0.09700 0.02308 0.37842 2.255 25.06
45 PSO 粒子群最適化 0.59726 0.36923 0.29928 1.26577 0.37237 0.16324 0.07010 0.60572 0.25667 0.08000 0.02157 0.35823 2.230 24.77


まとめ

本稿では、ABOアルゴリズムのオリジナル版と、若干の修正を加えた改良版を紹介しました。アルゴリズムのロジック変更により、各最適化ステップでの計算が簡素化され、外部パラメータ数は3つから2つに削減されました（集団サイズを決めるパラメータは除く）。これにより、全体的な性能が向上しています。新しいアルゴリズムでは、新たな探索空間の探索と既に発見された良好な解の活用とのバランスの取り方が変わりました。

改良版は低次元問題において局所解に陥りやすい傾向があるものの、実用面では高い効率性を発揮しています。アルゴリズムの動作を可視化した結果、ハイパースペースの重要領域を深く探索できることが確認され、探索能力の向上が示されました。結果として、新バージョンはオリジナル版に比べてより強力かつ効率的であり、離散関数を含む多様なテスト関数に対して優れたスケーラビリティを示しています。

Tab

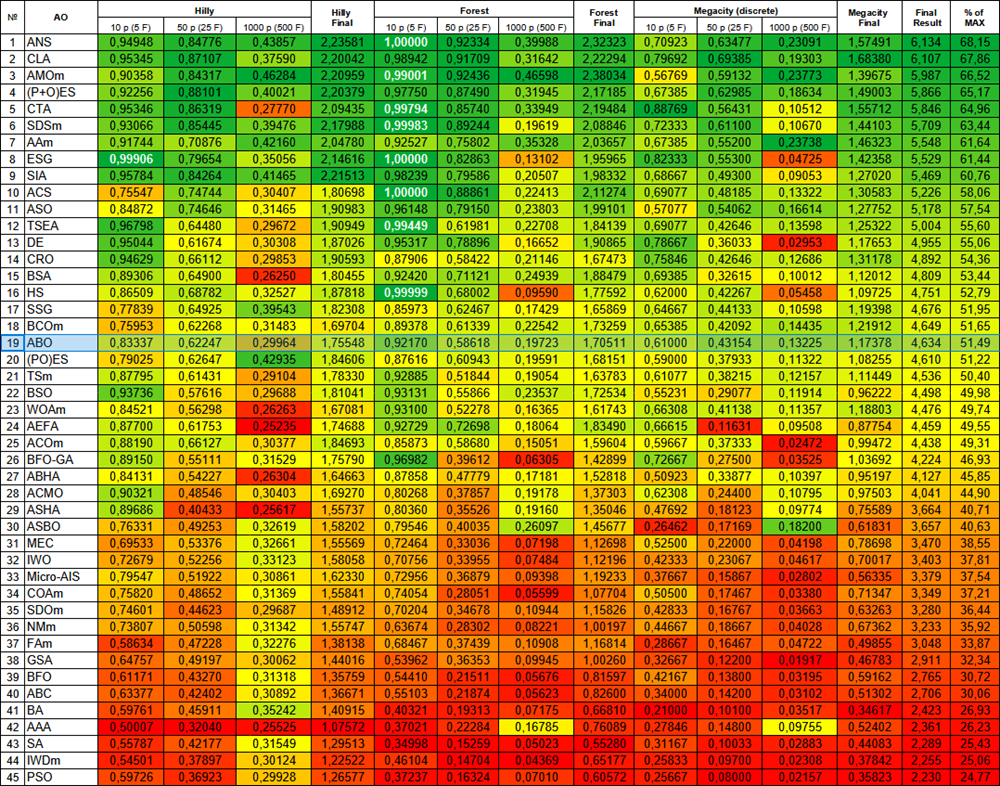
図1：関連するテスト結果に基づくアルゴリズムの色分け。0.99以上の結果は白色で強調表示されている

チャート

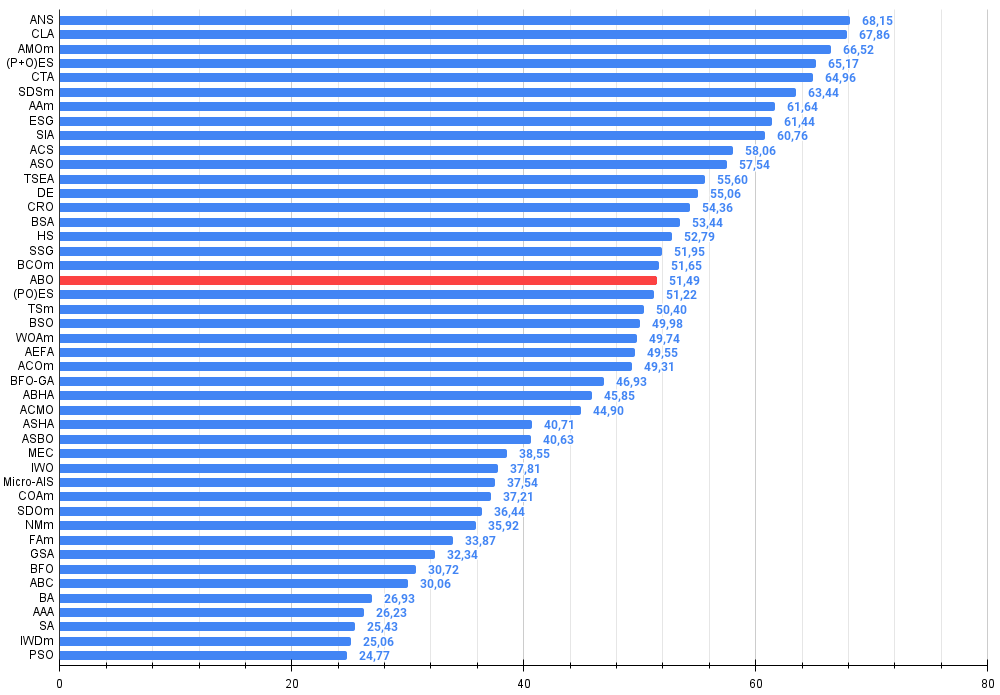
図2：アルゴリズムのテスト結果のヒストグラム（0から100までのスケールで、多ければ多いほど良い、

ここで、100は理論的に可能な最大の結果であり、アーカイブにはレーティングテーブルを計算するスクリプトが含まれている)


ABOの長所と短所

長所

  1. 迅速
  2. 実装が非常にシンプル
  3. 優れたスケーラビリティ
  4. 外部パラメータの数が少ない

短所

  1. 低次元関数では結果の散布度が高くなる
  2. 局所解に陥ることを防ぐ仕組みの欠如

この記事には、最新版のアルゴリズムコードを含むアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/16024

添付されたファイル |
ZIPをダウンロード
ABO.zip (35.98 KB)
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

最後のコメント | ディスカッションに移動 (5)
BeeXXI Corporation
Nikolai Semko | 10 10月 2024 において 16:14
とても興味深い記事だ。
アンドリューの努力と貢献に感謝する。
ジャンピング・バッタとアタック・パンサーの最適化方法についての記事を楽しみにしている。
Denis Kirichenko
Denis Kirichenko | 10 10月 2024 において 17:00

著者はとても素晴らしい！このトピックの全くの "ダミー "である私は、最適化の方法がこんなにたくさんあることに驚いている。おそらくパールボタンも？))

アンドレイ、どのようなソフトウェアで視覚化（例えばフォレストテスト関数のABO） されたのか教えてください。どこかに書いてあったかもしれませんが、見逃してしまいました......。

次の記事はインドゾウかメキシコのトゥシカン？))

Andrey Dik
Andrey Dik | 10 10月 2024 において 20:35
Nikolai Semko #:
とても興味深い記事だ。
アンドレイの労苦と貢献に感謝する。
ジャンピング・バッタとアタック・パンサーの最適化方法についての記事を楽しみにしている。

ニコライ、温かい言葉をありがとう。

ジャンピングバッタのアルゴリズムについては聞いたことがありませんが、猫の話題についてはいくつかあるようです：パンサー最適化アルゴリズム（POA）とマウンテンライオンアルゴリズム（MLA）だ。これらの検索戦略のロジックを再現するのに十分な記述が見つかれば、検討するかもしれない。

Andrey Dik
Andrey Dik | 10 10月 2024 において 20:39
Denis Kirichenko #:

著者はとても素晴らしい！このトピックの全くの "ダミー "である私は、最適化の方法がこんなにたくさんあることに驚いている。おそらくパールボタンも？))

アンドレイ、どのようなソフトウェアで視覚化（例えばフォレストテスト関数のABO） されたのか教えてください。どこかに書いてあったかもしれませんが、見逃してしまいました。

次の記事はインドゾウかメキシコのトゥシカンか？))

ありがとう、デニス。

私はmql5.comの記事でMQL5言語のみを使用しており、視覚化は標準ツールを使用してMT5で構築されています。すべてのソースコードは記事の添付ファイルにあり、私の結果を再現することができます。

Andrey Dik
Andrey Dik | 11 10月 2024 において 00:01
私の記事には「パスフレーズ」が隠されているものもあるが、今のところ読者に発見されたものはない。
取引におけるニューラルネットワーク：制御されたセグメンテーション（最終部） 取引におけるニューラルネットワーク：制御されたセグメンテーション（最終部）
前回の記事で開始した、MQL5を使用したRefMask3Dフレームワークの構築作業を引き続き進めていきます。このフレームワークは、点群におけるマルチモーダルインタラクションと特徴量解析を包括的に研究し、自然言語で提供される説明に基づいてターゲットオブジェクトを特定・識別することを目的としています。
従来の機械学習手法を使用した為替レートの予測：ロジットモデルとプロビットモデル 従来の機械学習手法を使用した為替レートの予測：ロジットモデルとプロビットモデル
この記事では、為替レートの予測を目的とした取引用EAの構築を試みます。アルゴリズムは、ロジスティック回帰およびプロビット回帰といった古典的な分類モデルに基づいています。取引シグナルのフィルターとして、尤度比検定が用いられます。
リプレイシステムの開発（第69回）：正しい時間を知る(II) リプレイシステムの開発（第69回）：正しい時間を知る(II)
今日は、iSpread機能がなぜ必要なのかについて考察します。同時に、ティックが1つも存在しない状況で、システムがどのようにバーの残り時間を通知するのかについても理解を深めていきます。ここで提示されるコンテンツは、教育目的のみに使用されることを意図しています。いかなる状況においても、提示された概念を学習し習得する以外の目的でアプリケーションを利用することは避けてください。
取引におけるニューラルネットワーク：一般化3次元指示表現セグメンテーション 取引におけるニューラルネットワーク：一般化3次元指示表現セグメンテーション
市場の状況を分析する際には、それを個別のセグメントに分割し、主要なトレンドを特定します。しかし、従来の分析手法は一つの側面に偏りがちで、全体像の適切な把握を妨げます。この記事では、複数のオブジェクトを選択できる手法を通じて、状況をより包括的かつ多層的に理解する方法を紹介します。