MetaTrader 5 / テスター
English Русский 中文 Español Português
preview
ビリヤード最適化アルゴリズム(BOA)

ビリヤード最適化アルゴリズム(BOA)

MetaTrader 5 — テスター |
20 0
Andrey Dik
Andrey Dik

内容

  1. はじめに
  2. アルゴリズムの実装
  3. テスト結果


はじめに

数学的精度と現実世界からの着想が交差する最適化アルゴリズムの世界では、驚くほど独創的なアプローチが生まれることがあります。その一例がビリヤード最適化アルゴリズム(BOA)です。この方法は、古典的なビリヤードの力学から探索戦略のアイデアを引き出しています。

プール台を思い浮かべてみてください。それぞれの穴は潜在的な解を表し、玉は可能性の空間を移動する解探索者です。熟練したビリヤードプレイヤーが玉の軌道を計算して正確に穴に落とすのと同じように、BOAは探索と改善の反復プロセスを通じて最適解に向かって意思決定を導きます。このアルゴリズムは、2023年に研究者のHadi GiviとMarie Hubálovskáによって開発され、最適化問題を解く上で興味深く独特なアプローチを示しています。

本記事では、BOAの概念的基礎に迫り、その数学モデルを探り、マルチモーダル問題の解決における効率を分析します。概念的なシンプルさと数学的精度を兼ね備えたこのアルゴリズムは、計算最適化の分野に新たな可能性を切り開き、現代の最適化手法の重要な一翼を担う存在となっています。


アルゴリズムの実装

BOAアルゴリズムは、ビリヤードに着想を得た最適化手法です。ある問題の最適解を探すことを考えてみましょう。ビリヤード用語で言えば、それは「玉を穴に入れる」ことに似ています。プール台には8つの穴があり、多くの玉があります。アルゴリズムの開始時には、ランダムな解の集合（集団）が作られます。これらの解はプール台の玉のようなものです。各解に対して、目的関数の値が計算され、その良さが評価されます。

アルゴリズムの各反復で、集団の中から上位8つの解が「穴」（目標）として選ばれます。残りの解は、これらの穴に向かって導くべき玉として扱われます。それぞれの玉（解）について、穴（最良解）の1つをランダムに選びます。その後、玉の新しい位置が計算されます。選ばれた穴の方向に向かって移動する新しい解です。新しい位置の目的関数の値が改善されれば玉はその位置に移動し、改善されなければ元の位置に留まります。

数学的には次のように表されます。

X_new = X + rnd [0.0; 1.0] × (P - I × X)

ここで

  • X_new：玉の新しい位置
  • X：玉の現在の位置
  • P：穴の位置（または現在の玉が目指す玉の位置）
  • I：1または2のランダム選択

このプロセスを何度も繰り返すことで、最終的に玉（解）は問題の最適解に近づきます。

BOAの利点は、方程式中の係数が1つだけで、理論上「大域探索」と「局所探索」のバランスをうまく取れる点にあります。これはランダム比率Iを使うことで実現され、玉の「アンダーシュート」（良好な点付近の解を精緻化）や「オーバーシュート」（解空間の異なる領域を探索）を可能にします。

boaアルゴリズムダイアグラム

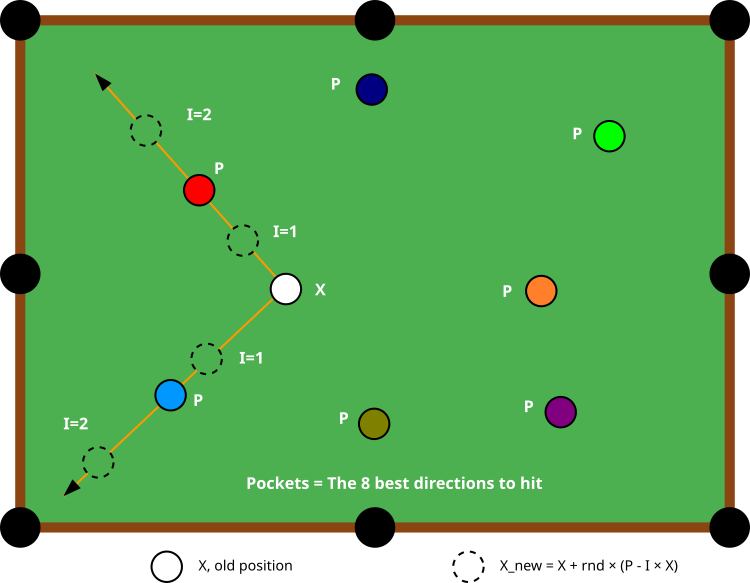
図1：BOAアルゴリズムのフローチャート

図1はBOAアルゴリズムの動作原理を模式的に示しています。中央の白い玉Xは、探索空間におけるエージェントの現在位置を表します。その周りには色付きの玉Pがあり、これらはこれまでに見つかった8つの最良解（穴）です。図は、エージェント（白い玉）が異なる穴に向かって位置を更新する様子を示しています。各ステップで、エージェントは8つの穴のうち1つをランダムに目標方向として選びます。

オレンジの矢印付き線は、エージェントが異なる穴（例：赤と青）に移動する可能な軌道を示しています。点線の円は、エージェントが移動中に取る中間位置を表しており、I（1または2）の値によって変化します。Iの値によって、「打撃の強さ」と動きの性質が変わります。I=1の場合は選ばれた穴方向に位置が移動し、I=2の場合は、より鋭い動きが可能となり、解空間の広い範囲を探索します。

アルゴリズムの仕組みを完全に理解できたので、BOAの疑似コードの作成を開始します。

初期化
    玉の数(popSize)と穴の数(numPockets)を決定します。
    玉（エージェント）の集団を作成します。
    探索空間の最小値と最大値を設定します。

基本アルゴリズム
第1段階：初期化（1回のみ実行）
    集団内の各玉について
        探索空間に玉をランダムに配置します。
        初期位置を保存します。
        適応度関数の初期値を最小値として初期化します。

第2段階：玉の移動
    集団内の各玉について
        玉の各座標について
            ランダムに穴を選択（numPocketsの最良解のうち1つ）します。
            次の式を使用して玉の位置を更新します。X_new = X + rnd [0.0; 1.0] × (P - I × X)
            新しい位置が許容範囲内であることを確認します。

第3段階：最良解の更新
    各玉について
        適応度が大域最良解より良ければ、大域最良値を更新します。
        適応度が自身の最良値より良ければ、自身の最良値を更新します。
    玉を適応度順にソートします。
        ソート後の最初のnumPockets個が次の反復の穴となります。

玉の移動と最良解更新のステップを、停止条件（例：最大反復回数）に達するまで繰り返します。

それでは、アルゴリズムコードの記述を始めましょう。C_AO_BOAクラスは、C_AOクラス（集団最適化アルゴリズムの基底クラス）を継承し、BOA最適化アルゴリズムを実装します。主な要素は以下の通りです。

    C_AO_BOA()コンストラクタはインスタンス変数の値を初期化します。
    • popSizeは50に設定されており、これはアルゴリズム内の玉（エージェント）の数を表します。
    • numPocketsは8に設定され、ビリヤード台の穴の数を形成します。
    • params配列のサイズが変更され、2つのパラメータ（popSizeとnumPockets）がparams配列に追加されます。
    メソッド
    • SetParams ()：params配列からpopSizeとnumPocketsをローカル変数に設定します。
    • Init ()：探索の最小値と最大値やステップ、エポック数を設定します。
    • Moving ()：アルゴリズム内で玉の移動を管理します。
    • Revision ()：エージェントの位置や決定を確認して修正します。
    //——————————————————————————————————————————————————————————————————————————————
class C_AO_BOA : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_BOA () { }
  C_AO_BOA ()
  {
    ao_name = "BOA";
    ao_desc = "Billiards Optimization Algorithm";
    ao_link = "https://www.mql5.com/ja/articles/17325";

    popSize    = 50;  // number of balls (agents)
    numPockets = 8;   // number of pockets on a billiard table

    ArrayResize (params, 2);

    params [0].name = "popSize";    params [0].val = popSize;
    params [1].name = "numPockets"; params [1].val = numPockets;
  }

  void SetParams ()
  {
    popSize    = (int)params [0].val;
    numPockets = (int)params [1].val;
  }

  bool Init (const double &rangeMinP  [],  // minimum values
             const double &rangeMaxP  [],  // maximum values
             const double &rangeStepP [],  // step change
             const int     epochsP = 0);   // number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  int numPockets;       // number of pockets (best solutions)

  private: //-------------------------------------------------------------------
};
//——————————————————————————————————————————————————————————————————————————————

    C_AO_BOAクラスのInitメソッドは、BOAアルゴリズムの初期化を担当します。 メソッドの冒頭では、最小値と最大値の配列および探索ステップを引数としてStandardInit()関数が呼び出されます。この関数は、すべての最適化アルゴリズム派生クラスに共通して必要となる処理や初期化（初期探索範囲の設定を含む）を実行するとともに、アルゴリズム内部で使用される探索エージェントの準備をおこないます。StandardInit ()がfalse（初期化失敗）を返した場合、Initメソッドも同様にfalseを返します。すべての処理が正常に完了した場合には、メソッドはtrueを返します。

    //——————————————————————————————————————————————————————————————————————————————
//--- Initialization
bool C_AO_BOA::Init (const double &rangeMinP  [],
                     const double &rangeMaxP  [],
                     const double &rangeStepP [],
                     const int epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  return true;
}
//——————————————————————————————————————————————————————————————————————————————

    Movingメソッドは、BOAアルゴリズムの主要ステップを実装し、解空間におけるエージェント（玉）の移動を制御します。まず、if (!revision)という条件を確認し、このメソッドが初めて呼び出されたかどうかを判定します。revision = falseの場合は、エージェントの位置を初期化する必要があります。そのため、popSizeで定義されたすべてのエージェントに対してループを実行し、その内部で、各エージェントの決定変数を定義する座標ごとのネストされたループが実行されます。

    初期位置の生成段階では、各エージェントの各座標に対して、指定された範囲内でランダムな値が選択されます。その後、u.SeInDiSp()関数によって、その値はステップ幅を考慮した許容値に調整されます。エージェントの初期位置は、玉の個体最良解としてa[p].cB[c]に保存されます（最初の反復では、初期解がそのまま既知の最良解に相当します）。初期化が完了するとrevision = trueが設定され、値の再初期化を防ぐためにメソッドは終了します。

    2回目以降の反復では、すべてのエージェントを移動させるためのループが開始されます。座標更新の過程では、すべてのエージェントおよびその座標に対してネストされたループが実行され、利用可能な最良穴の中から1つがランダムに選択され、エージェントの現在位置の更新に用いられます。位置は、直前の位置に対して、選択された穴の位置に基づくランダムな変化を加えることで更新されます。ここで、u.RNDprobab()関数は区間[0.0,1.0]のランダム値を返し、ランダムノイズの付加に使用されます。一方、u.RNDintInRange(1, 2)関数は、1または2のランダムな整数を返し、それをエージェントの位置に乗算することで移動量を変化させます。

    位置更新後、最小値と最大値の制約および変更ステップを考慮して値が調整され、更新された位置が指定された探索範囲内に収まるように修正されます。

    //——————————————————————————————————————————————————————————————————————————————
//--- The main step of the algorithm
void C_AO_BOA::Moving ()
{
  //----------------------------------------------------------------------------
  // Initial initialization
  if (!revision)
  {
    for (int p = 0; p < popSize; p++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [p].c  [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [p].c  [c] = u.SeInDiSp (a [p].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
        a [p].cB [c] = a [p].c [c];  // Save the initial position
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  for (int p = 0; p < popSize; p++)
  {
    for (int c = 0; c < coords; c++)
    {
      int pocketID = u.RNDminusOne (numPockets);

      a [p].c [c] = a [p].cB [c] + u.RNDprobab () * (a [pocketID].cB [c] - u.RNDintInRange (1, 2) * a [p].cB [c]);
      a [p].c [c] = u.SeInDiSp (a [p].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————
    Revisionメソッドは、BOAアルゴリズムにおける大域最良解の更新を担当するとともに、各玉（エージェント）の個体最良解を更新します。メソッドの最後では、玉はそれぞれの個体最良解の評価値に基づいてソートされます。

    //——————————————————————————————————————————————————————————————————————————————
//--- Update the best solution taking into account greedy selection and the probability of making worse decisions
void C_AO_BOA::Revision ()
{
  int bestIND = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      bestIND = i;
    }

    if (a [i].f > a [i].fB)
    {
      a [i].fB = a [i].f;
      ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  if (bestIND != -1) ArrayCopy (cB, a [bestIND].c, 0, 0, WHOLE_ARRAY);

  S_AO_Agent aT []; ArrayResize (aT, popSize);
  u.Sorting_fB (a, aT, popSize);
}
//——————————————————————————————————————————————————————————————————————————————


    テスト結果

    それでは、BOAアルゴリズムがどのように機能するかを見てみましょう。
    BOA|Billiards Optimization Algorithm|50.0|8.0|
    =============================
    5 Hilly's; Func runs:10000; result:0.63960620766331
    25 Hilly's; Func runs:10000; result:0.3277725645995603
    500 Hilly's; Func runs:10000; result:0.2514878043770147
    =============================
    5 Forest's; Func runs:10000; result:0.3885662762060409
    25 Forest's; Func runs:10000; result:0.1955657530616877
    500 Forest's; Func runs:10000; result:0.15336230733273673
    =============================
    5 Megacity's; Func runs:10000; result:0.5415384615384615
    25 Megacity's; Func runs:10000; result:0.19046153846153846
    500 Megacity's; Func runs:10000; result:0.10530769230769324
    =============================
    All score:2.79367 (31.04%)

    ご覧のとおり、このアルゴリズムの性能はかなり弱く、ランキング表にも入っていません。そのため、私はアルゴリズムをより詳しく分析し、どのようにすれば改善できるかについていくつかのアイデアを考えました。まず、玉の移動を表す式をもう一度見てみましょう。

    X_new = X + rnd [0.0; 1.0] × (P - I × X)

    この式では、係数Iが玉の現在座標の値に直接乗算されていますが、これは物理的解釈が困難です。実際には、座標の絶対値に対してスケーリングがおこなわれていることになります。より自然なのは、この係数を外に出し、穴と玉の座標値の差分に対してスケーリングを行うことです。そうすることで、「玉が穴に届かない」あるいは「穴を飛び越える」といった、より物理的に意味のある挙動を表現できるようになります。また、[0.0,1.0]の範囲の乱数を用いた追加のノイズ項によって、動きの多様性が確保されます。

    その結果、次のような玉の移動式が得られます。

    X_new = X + rnd [0.0; 1.0] × (P -X) × I

    以下に示すのは、修正版のMoving()メソッドの完全なコードです。そこでは、まず著者による元の式がコメントアウトされ、その直後に、私が提案する修正版の式が記述されています。

    //——————————————————————————————————————————————————————————————————————————————
//--- The main step of the algorithm
void C_AO_BOA::Moving ()
{
  //----------------------------------------------------------------------------
  // Initial initialization
  if (!revision)
  {
    for (int p = 0; p < popSize; p++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [p].c  [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [p].c  [c] = u.SeInDiSp (a [p].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
        a [p].cB [c] = a [p].c [c];  // Save the initial position as the best individual solution 
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  for (int p = 0; p < popSize; p++)
  {
    for (int c = 0; c < coords; c++)
    {
      int pocketID = u.RNDminusOne (numPockets);

      //a [p].c [c] = a [p].cB [c] + u.RNDprobab () * (a [pocketID].cB [c] - u.RNDintInRange (1, 2) * a [p].cB [c]);
      a [p].c [c] = a [p].cB [c] + u.RNDprobab () * (a [pocketID].cB [c] - a [p].cB [c]) * u.RNDintInRange (1, 2);
      a [p].c [c] = u.SeInDiSp (a [p].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

    それでは、これらの変更を加えた後、著者らのオリジナル版で最も良い結果を示したパラメータを用いて、アルゴリズムがどのように動作するかを見ていきましょう。

    BOA|Billiards Optimization Algorithm|50.0|8.0|
    =============================
    5 Hilly's; Func runs:10000; result:0.8727603657603271
    25 Hilly's; Func runs:10000; result:0.7117647027521633
    500 Hilly's; Func runs:10000; result:0.25339119302510993
    =============================
    5 Forest's; Func runs:10000; result:0.9228482722678735
    25 Forest's; Func runs:10000; result:0.7601448268715335
    500 Forest's; Func runs:10000; result:0.3498925749480034
    =============================
    5 Megacity's; Func runs:10000; result:0.6184615384615385
    25 Megacity's; Func runs:10000; result:0.45876923076923076
    500 Megacity's; Func runs:10000; result:0.14586153846153965
    =============================
    All score:5.09389 (56.60%)

    さらにいくつかの実験をおこなった後、さらに良い結果を生み出すパラメータを思いつきました。

    BOA|Billiards Optimization Algorithm|50.0|25.0|
    =============================
    5 Hilly's; Func runs:10000; result:0.957565927297626
    25 Hilly's; Func runs:10000; result:0.8259872884790693
    500 Hilly's; Func runs:10000; result:0.2523458952211869
    =============================
    5 Forest's; Func runs:10000; result:0.9999999999999929
    25 Forest's; Func runs:10000; result:0.900362056289584
    500 Forest's; Func runs:10000; result:0.305018130407844
    =============================
    5 Megacity's; Func runs:10000; result:0.7353846153846153
    25 Megacity's; Func runs:10000; result:0.5252307692307692
    500 Megacity's; Func runs:10000; result:0.09563076923077005
    =============================
    All score:5.59753 (62.19%)

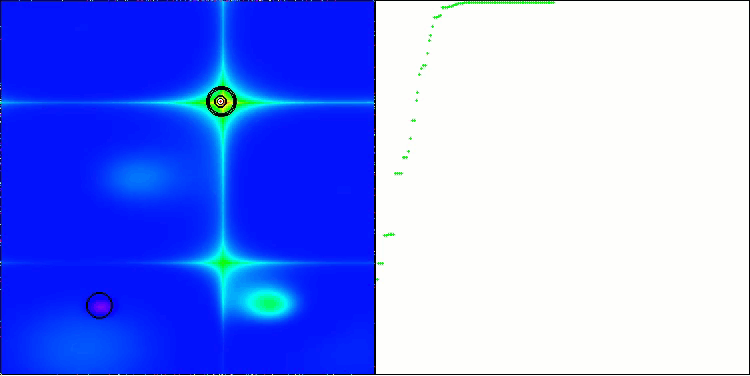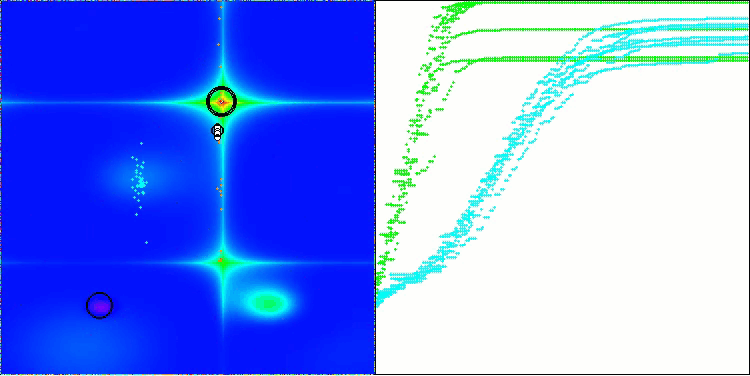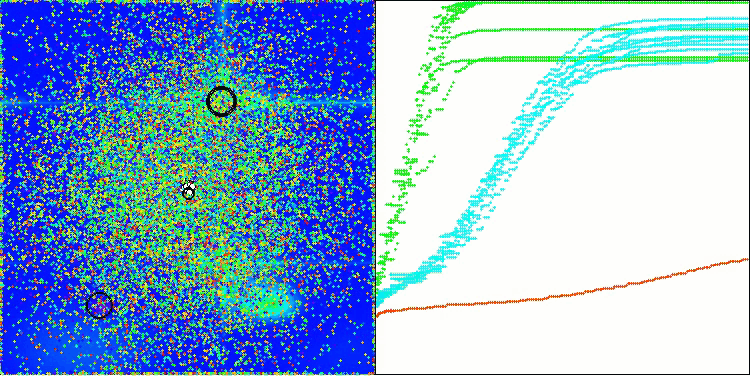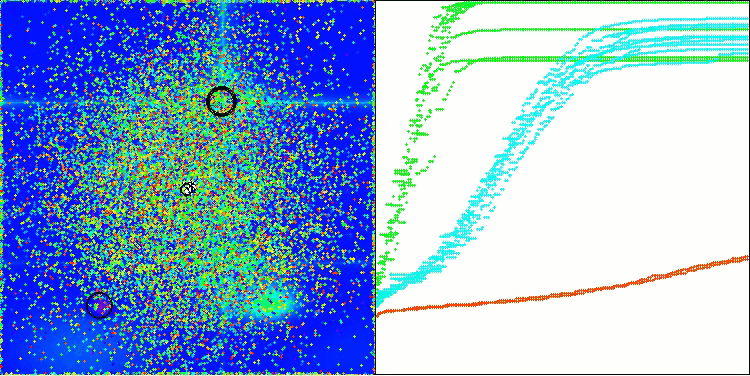
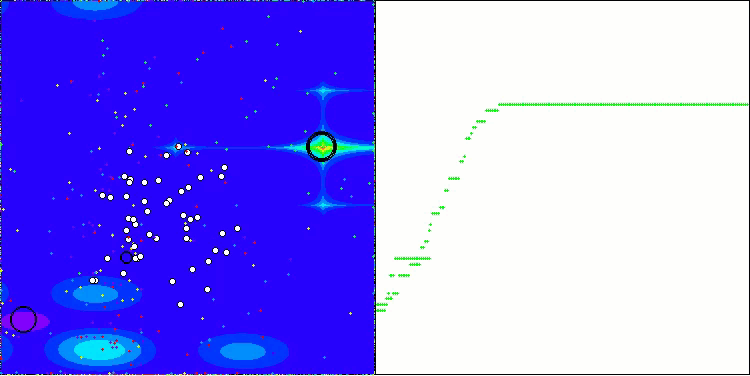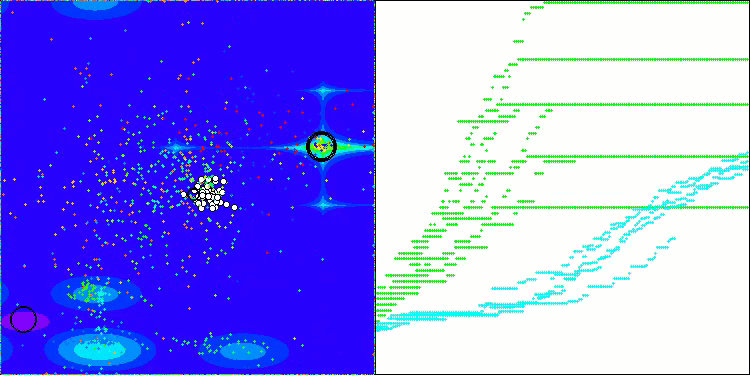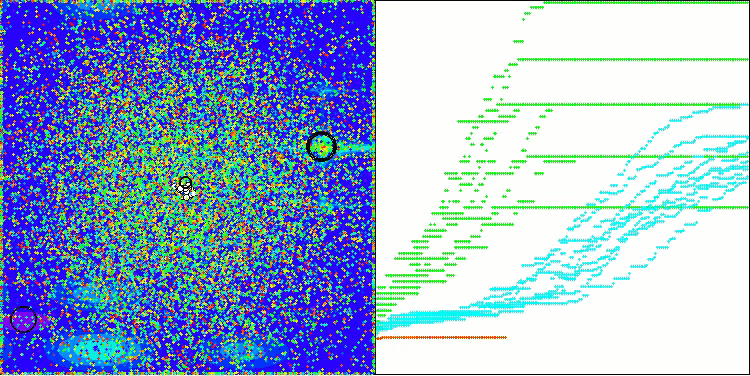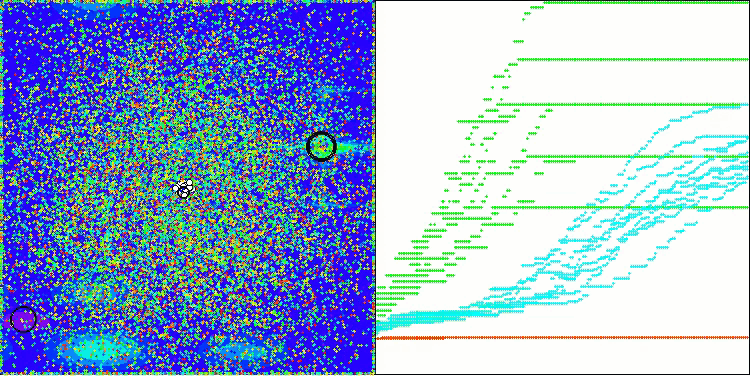
    テスト関数上で動作するBOAアルゴリズムの可視化を見てみましょう。探索空間において、特に特徴的な挙動は観察されず、「玉」の動きは全体的にカオス的に見えます。特に注目すべき点として、このアルゴリズムは小規模および中規模の次元の問題には比較的うまく対処できる一方で、高次元問題では収束性に問題が生じることが分かります。この傾向は、滑らかなHilly関数において顕著であり、他の多くの集団ベース最適化アルゴリズムと比較しても極めて珍しく、離散的なMegacity関数よりも性能が悪化するという結果が観測されます。さらに、小次元問題を解く際にも、アルゴリズムが局所最小値に陥りやすい傾向を示す点は注目に値します。

    Hilly

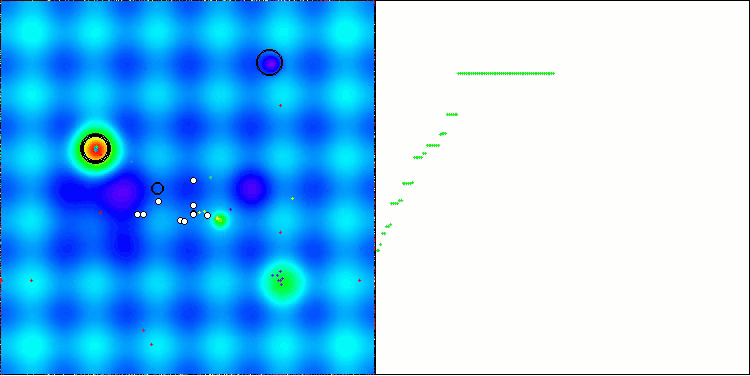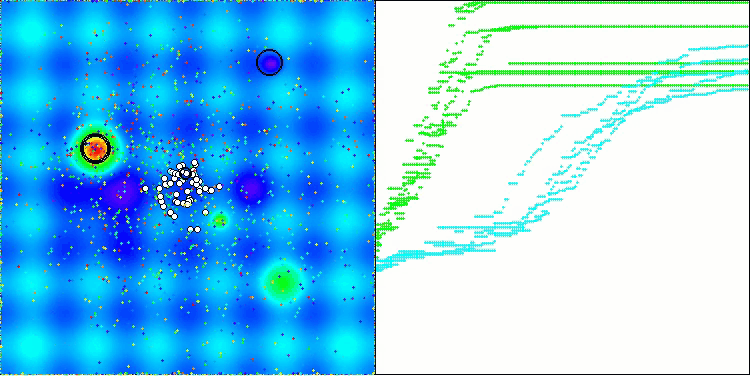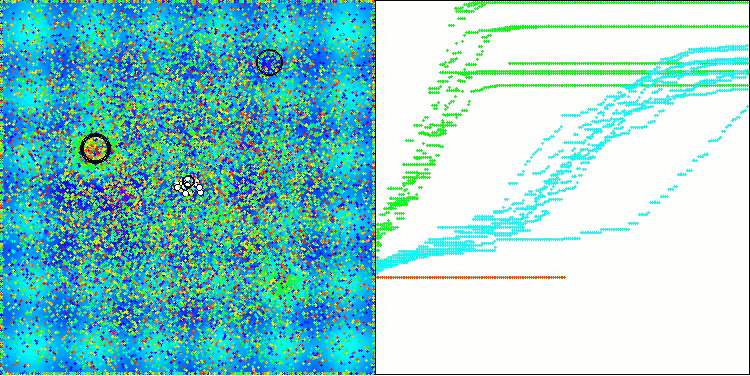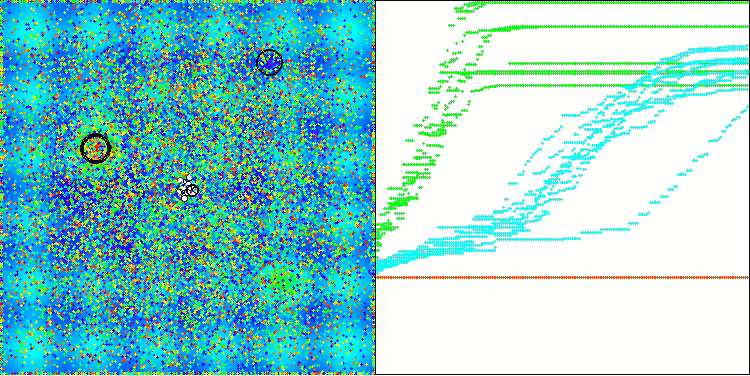
    Hillyテスト関数のBOA

    Forest

    Forestテスト関数BOA

    Megacity

    Megacityテスト関数のBOA

    それでは、テスト結果を総括し、アルゴリズムの効率について考察してみましょう。本アルゴリズムは深刻な欠点を抱えているにもかかわらず、最適化アルゴリズムのランキングにおいて第8位を獲得しており、全体としては比較的高い効率を示したと言えます。

    # AO 詳細 Hilly Hilly最終 Forest Forest最終 Megacity（離散） Megacity最終 最終結果 MAXの%
    10p(5F) 50p(25F) 1000p(500F) 10p(5F) 50p(25F) 1000p(500F) 10p(5F) 50p(25F) 1000p(500F)
    1 ANS across neighbourhood search 0.94948 0.84776 0.43857 2.23581 1.00000 0.92334 0.39988 2.32323 0.70923 0.63477 0.23091 1.57491 6.134 68.15
    2 CLA コードロックアルゴリズム(joo) 0.95345 0.87107 0.37590 2.20042 0.98942 0.91709 0.31642 2.22294 0.79692 0.69385 0.19303 1.68380 6.107 67.86
    3 AMOm 動物移動最適化m 0.90358 0.84317 0.46284 2.20959 0.99001 0.92436 0.46598 2.38034 0.56769 0.59132 0.23773 1.39675 5.987 66.52
    4 (P+O)ES (P+O)進化戦略 0.92256 0.88101 0.40021 2.20379 0.97750 0.87490 0.31945 2.17185 0.67385 0.62985 0.18634 1.49003 5.866 65.17
    5 CTA 彗星の尾アルゴリズム(joo) 0.95346 0.86319 0.27770 2.09435 0.99794 0.85740 0.33949 2.19484 0.88769 0.56431 0.10512 1.55712 5.846 64.96
    6 TETA 時間進化移動アルゴリズム（joo） 0.91362 0.82349 0.31990 2.05701 0.97096 0.89532 0.29324 2.15952 0.73462 0.68569 0.16021 1.58052 5.797 64.41
    7 SDSm 確率的拡散探索M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
    8 BOAm ビリヤード最適化アルゴリズムM 0.95757 0.82599 0.25235 2.03590 1.00000 0.90036 0.30502 2.20538 0.73538 0.52523 0.09563 1.35625 5.598 62.19
    9 AAm アーチェリーアルゴリズムM 0.91744 0.70876 0.42160 2.04780 0.92527 0.75802 0.35328 2.03657 0.67385 0.55200 0.23738 1.46323 5.548 61.64
    10 ESG 社会集団の進化(joo) 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
    11 SIA 等方的焼きなまし(joo) 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
    12 ACS 人工協調探索 0.75547 0.74744 0.30407 1.80698 1.00000 0.88861 0.22413 2.11274 0.69077 0.48185 0.13322 1.30583 5.226 58.06
    13 DA 弁証法的アルゴリズム 0.86183 0.70033 0.33724 1.89940 0.98163 0.72772 0.28718 1.99653 0.70308 0.45292 0.16367 1.31967 5.216 57.95
    14 BHAm ブラックホールアルゴリズムM 0.75236 0.76675 0.34583 1.86493 0.93593 0.80152 0.27177 2.00923 0.65077 0.51646 0.15472 1.32195 5.196 57.73
    15 ASO 無政府社会最適化 0.84872 0.74646 0.31465 1.90983 0.96148 0.79150 0.23803 1.99101 0.57077 0.54062 0.16614 1.27752 5.178 57.54
    16 RFO ロイヤルフラッシュ最適化（joo） 0.83361 0.73742 0.34629 1.91733 0.89424 0.73824 0.24098 1.87346 0.63154 0.50292 0.16421 1.29867 5.089 56.55
    17 AOSm 原子軌道探索M 0.80232 0.70449 0.31021 1.81702 0.85660 0.69451 0.21996 1.77107 0.74615 0.52862 0.14358 1.41835 5.006 55.63
    18 TSEA 亀甲進化アルゴリズム(joo) 0.96798 0.64480 0.29672 1.90949 0.99449 0.61981 0.22708 1.84139 0.69077 0.42646 0.13598 1.25322 5.004 55.60
    19 DE 差分進化 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
    20 CRO 化学反応の最適化 0.94629 0.66112 0.29853 1.90593 0.87906 0.58422 0.21146 1.67473 0.75846 0.42646 0.12686 1.31178 4.892 54.36
    21 BIO 血液型遺伝最適化(joo) 0.81568 0.65336 0.30877 1.77781 0.89937 0.65319 0.21760 1.77016 0.67846 0.47631 0.13902 1.29378 4.842 53.80
    22 BSA 鳥群アルゴリズム 0.89306 0.64900 0.26250 1.80455 0.92420 0.71121 0.24939 1.88479 0.69385 0.32615 0.10012 1.12012 4.809 53.44
    23 HS ハーモニー検索 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
    24 SSG 苗木の播種と育成 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
    25 BCOm 細菌走化性最適化M 0.75953 0.62268 0.31483 1.69704 0.89378 0.61339 0.22542 1.73259 0.65385 0.42092 0.14435 1.21912 4.649 51.65
    26 ABO アフリカ水牛の最適化 0.83337 0.62247 0.29964 1.75548 0.92170 0.58618 0.19723 1.70511 0.61000 0.43154 0.13225 1.17378 4.634 51.49
    27 (PO)ES (PO)進化戦略 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
    28 TSm タブーサーチM 0.87795 0.61431 0.29104 1.78330 0.92885 0.51844 0.19054 1.63783 0.61077 0.38215 0.12157 1.11449 4.536 50.40
    29 BSO ブレインストーム最適化 0.93736 0.57616 0.29688 1.81041 0.93131 0.55866 0.23537 1.72534 0.55231 0.29077 0.11914 0.96222 4.498 49.98
    30 WOAm 鯨最適化アルゴリズムM 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
    31 AEFA 人工電界アルゴリズム 0.87700 0.61753 0.25235 1.74688 0.92729 0.72698 0.18064 1.83490 0.66615 0.11631 0.09508 0.87754 4.459 49.55
    32 AEO 人工生態系ベースの最適化アルゴリズム 0.91380 0.46713 0.26470 1.64563 0.90223 0.43705 0.21400 1.55327 0.66154 0.30800 0.28563 1.25517 4.454 49.49
    33 ACOm 蟻コロニー最適化M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
    34 BFO-GA 細菌採食の最適化：Ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
    35 SOA シンプル最適化アルゴリズム 0.91520 0.46976 0.27089 1.65585 0.89675 0.37401 0.16984 1.44060 0.69538 0.28031 0.10852 1.08422 4.181 46.45
    36 ABHA 人工蜂の巣アルゴリズム 0.84131 0.54227 0.26304 1.64663 0.87858 0.47779 0.17181 1.52818 0.50923 0.33877 0.10397 0.95197 4.127 45.85
    37 ACMO 大気雲モデルの最適化 0.90321 0.48546 0.30403 1.69270 0.80268 0.37857 0.19178 1.37303 0.62308 0.24400 0.10795 0.97503 4.041 44.90
    38 ADAMm 適応モーメント推定M 0.88635 0.44766 0.26613 1.60014 0.84497 0.38493 0.16889 1.39880 0.66154 0.27046 0.10594 1.03794 4.037 44.85
    39 CGO カオスゲーム最適化 0.57256 0.37158 0.32018 1.26432 0.61176 0.61931 0.62161 1.85267 0.37538 0.21923 0.19028 0.78490 3.902 43.35
    40 ATAm 人工部族アルゴリズムM 0.71771 0.55304 0.25235 1.52310 0.82491 0.55904 0.20473 1.58867 0.44000 0.18615 0.09411 0.72026 3.832 42.58
    41 ASHA 人工シャワーアルゴリズム 0.89686 0.40433 0.25617 1.55737 0.80360 0.35526 0.19160 1.35046 0.47692 0.18123 0.09774 0.75589 3.664 40.71
    42 ASBO 適応型社会行動最適化(ASBO) 0.76331 0.49253 0.32619 1.58202 0.79546 0.40035 0.26097 1.45677 0.26462 0.17169 0.18200 0.61831 3.657 40.63
    43 MEC mind evolutionary computation 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
    44 CSA 円探索アルゴリズム 0.66560 0.45317 0.29126 1.41003 0.68797 0.41397 0.20525 1.30719 0.37538 0.23631 0.10646 0.71815 3.435 38.17
    45 IWO 侵入雑草最適化 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
    RW ランダムウォーク 0.48754 0.32159 0.25781 1.06694 0.37554 0.21944 0.15877 0.75375 0.27969 0.14917 0.09847 0.52734 2.348 26.09


    まとめ

    修正版ビリヤード最適化アルゴリズム(BOAm)は、テスト関数において興味深い結果を示しました。提示されたデータの分析から、このアルゴリズムは小規模および中規模の問題において最良の性能を発揮することが分かります。10,000回の反復に到達した時点で、Hilly (0.957)、Forest (0.999)、Megacity (0.735)の各テストにおいて最大値を獲得しており、中程度の複雑さを持つ問題に対して高い最適解探索能力を有していることが示されています。一方で、問題の次元が大きくなるにつれて性能は大きく低下します。1000変数のケースでは、スコアがそれぞれ0.252、0.305、0.095まで落ち込んでおり、高次元問題に対する課題が明確に表れています。

    特に注目すべき点は、アルゴリズムの修正版における顕著な性能向上です。BOAmは、理論上の最大値に対して62.19%を達成しており、これはオリジナル版の31.04%のほぼ2倍に相当します。この印象的な改善は、玉の位置更新式に関するわずか1行のコード変更によって実現されました。

    本アルゴリズムのシンプルさは、長所であると同時に制約でもあります。直感的で実装が容易であり、ビリヤードという洗練された概念に基づいている一方で、高次元問題を効率的に処理するためには、さらなる改良が必要となる可能性があります。それでもなお、ランキング表においてトップ10にランクインしていることから、BOAmは探索と活用のバランスに優れた、有望なメタヒューリスティック手法であると言えるでしょう。

    表

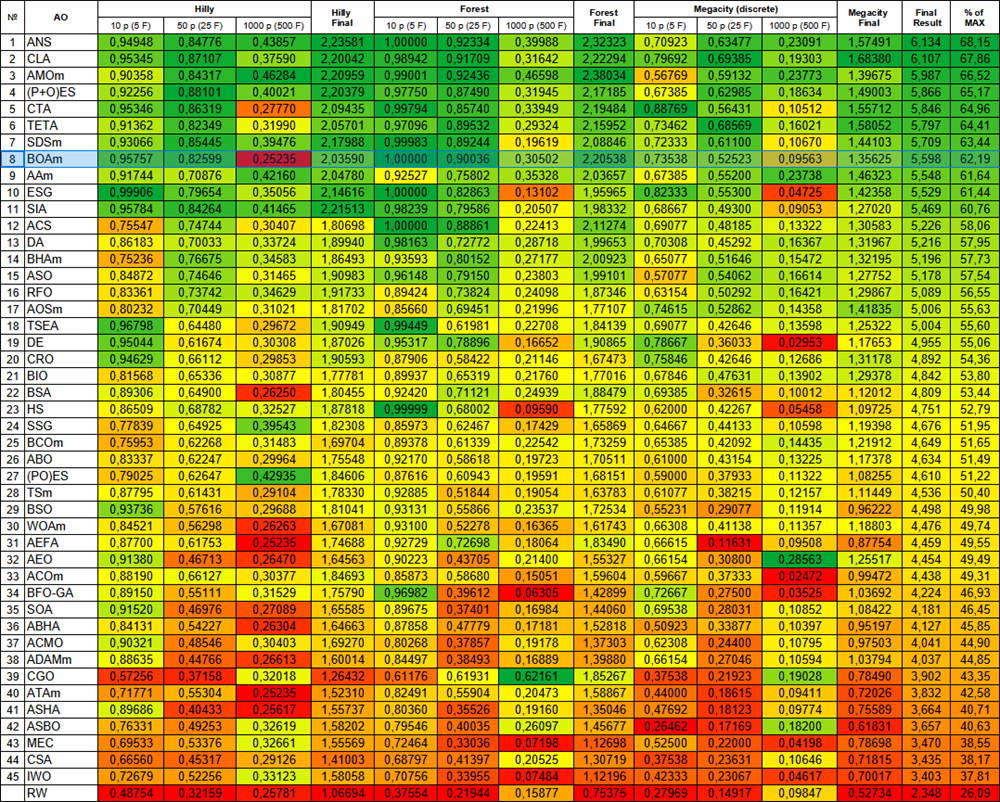
    図2：対応するテストに応じたアルゴリズムのカラーグラデーション

    グラフ

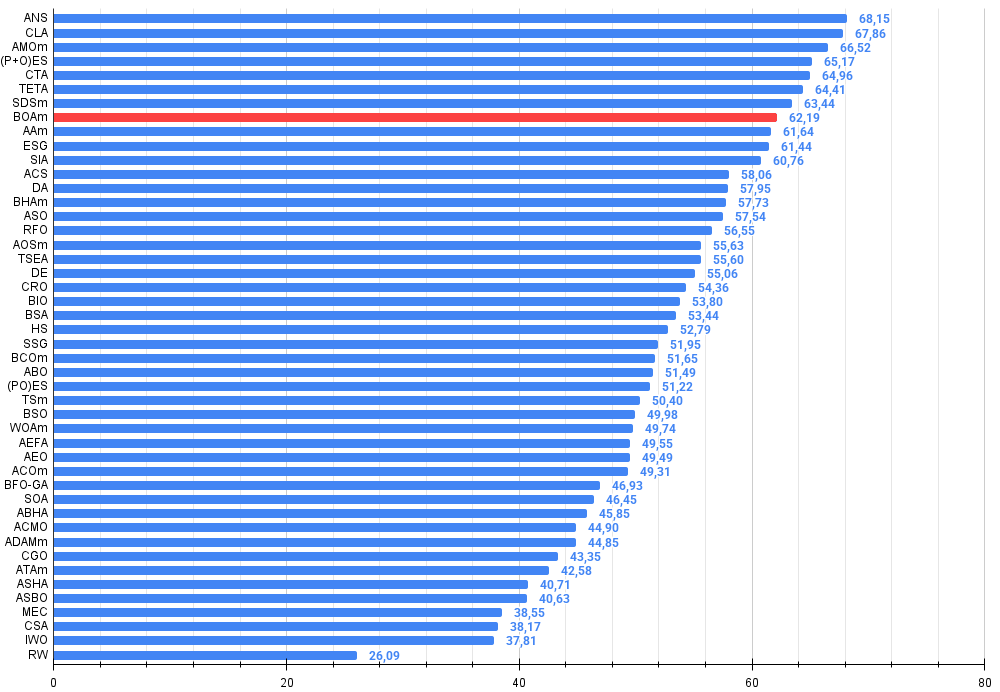
    図3：アルゴリズムテスト結果のヒストグラム（0から100のスケール、高いほど良い）100は理論上の最大値であり、アーカイブには評価表を計算するためのスクリプトがあります。

    BOAの長所と短所

    長所

    1. 外部パラメータが非常に少ない
    2. 実装がシンプル
    3. 小規模から中規模の問題に優れたパフォーマンスを発揮する
    4. 「鋭い」極値を持つ問題（Forest関数など）で優れた結果が得られる

    短所

    1. 低次元の問題では、局所的な極値に行き詰まってしまう
    2. 高次元の「滑らかな」問題（Hilly関数など）における収束の速度と精度が非常に低くなる

    この記事には、最新版のアルゴリズムコードを含むアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。


    記事で使用されているプログラム

    # 名前 種類 詳細
    1 #C_AO.mqh
    		 インクルード
    		 集団最適化の親クラス
    アルゴリズム
    2 #C_AO_enum.mqh
    		 インクルード
    		 集団最適化アルゴリズムの列挙
    3 TestFunctions.mqh
    		 インクルード
    		 テスト関数のライブラリ
    4
    		 TestStandFunctions.mqh
    		 インクルード
    		 テストスタンド関数ライブラリ
    5
    		 Utilities.mqh
    		 インクルード
    		 補助関数のライブラリ
    6
    		 CalculationTestResults.mqh
    		 インクルード
    		 比較表の結果を計算するスクリプト
    7
    		 Testing AOs.mq5
    		 スクリプト すべての集団最適化アルゴリズムの統一テストスタンド
    8
    		 Simple use of population optimization algorithms.mq5
    		 スクリプト
    		 可視化せずに集団最適化アルゴリズムを使用する簡単な例
    9
    		 Test_AO_BOAm.mq5
    		 スクリプト BOAmテストスタンド

    MetaQuotes Ltdによってロシア語から翻訳されました。
    元の記事: https://www.mql5.com/ru/articles/17325

    添付されたファイル |
    ZIPをダウンロード
    BOAm.zip (170.91 KB)

    警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

    この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。

    この著者による他の記事

    ディスカッションに移動
    EAのサンプル EAのサンプル
    一般的なMACDを使ったEAを例として、MQL4開発の原則を紹介します。
    多通貨エキスパートアドバイザーの開発（第24回）：新しい戦略の追加(I) 多通貨エキスパートアドバイザーの開発（第24回）：新しい戦略の追加(I)
    本記事では、作成済みの自動最適化システムに新しい戦略を連携する方法を見ていきます。どのようなEAを作成する必要があるのか、EAライブラリのファイルを変更せずにできるのか、必要な変更を最小限に抑えられるかを確認してみましょう。
    エラー 146 (「トレードコンテキスト ビジー」) と、その対処方法 エラー 146 (「トレードコンテキスト ビジー」) と、その対処方法
    この記事では、MT4において複数のEAの衝突をさける方法を扱います。ターミナルの操作、MQL4の基本的な使い方がわかる人にとって、役に立つでしょう。
    カオスゲーム最適化(CGO) カオスゲーム最適化(CGO)
    本記事では、新しいメタヒューリスティックアルゴリズムであるカオスゲーム最適化(CGO)を紹介します。CGOは、高次元問題に対しても高い効率を維持できるという独自の特性を示しています。ほとんどの最適化アルゴリズムとは異なり、CGOは問題の規模が大きくなると性能が低下するどころか、場合によっては向上することさえあり、これがこのアルゴリズムの主要な特徴です。