ブラックホールアルゴリズム(BHA)

MetaTrader 5 — 例 | YYYY年10月DD日, 08:41

Andrey Dik

内容

はじめに

ブラックホールアルゴリズム(BHA: Black Hole Algorithm)は、最適化問題に対して独自の視点を提供するメタヒューリスティック手法です。このアルゴリズムは、2013年にA. Hatamlouによって提案され、宇宙でもっとも神秘的かつ強力な存在であるブラックホールの性質にインスピレーションを受けています。ブラックホールが周囲のあらゆる物質を重力によって引き寄せるように、BHAも「最良の解」を中心に他の候補解を引き寄せ、質の低い解を淘汰していきます。

広大な探索空間を想像してみてください。そこには多数の解が存在し、それぞれが最適な位置を求めて動いています。その中心には「ブラックホール」と呼ばれる最良解があり、強力な引力を発揮しています。アルゴリズムは各ステップで、どの「星」（候補解）がブラックホールに吸い込まれるか、あるいは探索を続けるかを判断していきます。

BHAはランダム性の要素を取り入れることで、未知の探索領域を広く調べ、局所解に閉じ込められることを防ぎます。この特性により、関数最適化、組合せ最適化、さらには機械学習におけるハイパーパラメータチューニングなど、さまざまな分野で有効に活用されています。本記事では、ブラックホールアルゴリズムの仕組みと実装手法、そしてその利点と限界について詳しく解説します。科学とアートが交差する最適化の世界を、ぜひご体験ください。

アルゴリズムの実装

ブラックホールアルゴリズム(BHA)は、星がブラックホールとどのように相互作用するかという考えに基づき、与えられた探索空間内で最適解を見つけるための手法です。アルゴリズムの動作は初期化から始まり、まずランダムな「星」の初期集団を生成します。各星は最適化問題における潜在的な解を表します。これらの星は上限および下限によって制約された探索空間内に配置されます。アルゴリズムの反復中、各ステップで最良の解が選択され、それが「ブラックホール」として指定されます。残りの星は次の式を用いてブラックホールに近づくように移動します。

Xi(t+1) = Xi(t) + rand × (XBH - Xi(t))

ここで

Xi(t)：i番目の星の現在位置
XBH：ブラックホールの位置
rand：0から1までの乱数

アルゴリズムの重要な要素の1つが、次の式で計算される事象の地平線（イベントホライゾン）です。

R = fitBH / Σfiti

この地平線を越えた星はブラックホールに「吸い込まれ」、新しいランダムな星に置き換えられます。このメカニズムにより集団の多様性が維持され、探索空間のさらなる探索が促進されます。

BHAには、いくつかの重要な特徴があります。構造が単純であり、集団サイズを除いてまったくパラメータを必要としないため、非常に扱いやすいという利点があります。チューニングを必要としない点は、他の最適化アルゴリズムではほとんど見られない特性です。

BHAは他の集団ベースのアルゴリズムと似ています。つまり、最初のステップとしてランダムな解（初期星）の集団を生成し、目的関数を計算して各解の評価値を求めます。各反復において最良解がブラックホールとして選ばれ、他の候補解（星）をその周囲に引き寄せ始めます。他の候補解が最良解に近づくと、それらは最良解に「吸収」されます。

以下の図は、BHAの探索戦略を示したものです。ブラックホールの事象の地平線を越えたすべての星はその中心へと移動し、地平線を超えた星は吸収されます。つまり、星の物質は探索空間の新しい領域へとテレポートされることになります。

BHA_2

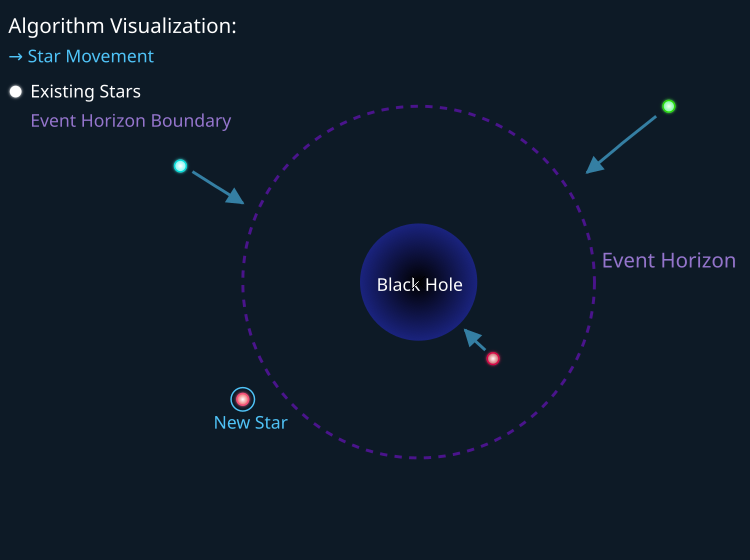
図1：BHA検索戦略。緑と青の星はブラックホールの中心へ向かって移動し、赤い星は「新星」の位置へテレポートします。

次に、BHAの擬似コードを示します。

// 入力
N：星の数（集団サイズ）
tmax：最大反復回数

// 初期化
1. N個の星の初期位置を作成します。
   For i = 1 to N:
       Xi = LB + rand × (UB - LB)

2. t = 1

// メインループ
3. While t ≤ tmax:

    // 各星の目的関数の値を計算する
    4. 各Xiについてfitiを計算します。

    // ブラックホールを定義する
    5. 最良のfiti値を持つ星をXBHとします。
       fitBH = 最良のfiti値

    // 星の位置を更新する
    6. 各Xi星ごとに:
       Xi(t+1) = Xi(t) + rand × (XBH - Xi(t))

    // 事象の地平線の半径を計算する
    7.R = fitBH / ∑(i=1 ～ N) fiti

    // 星の吸収を確認する
    8. 各Xi星ごとに:
       XiとXBH間の距離がR未満の場合
           Xiの新しい位置をランダムに生成する
           Xi = LB + rand × (UB - LB)

    9. t = t + 1

// 見つかった最良解を返す
XBHを返す

BHA

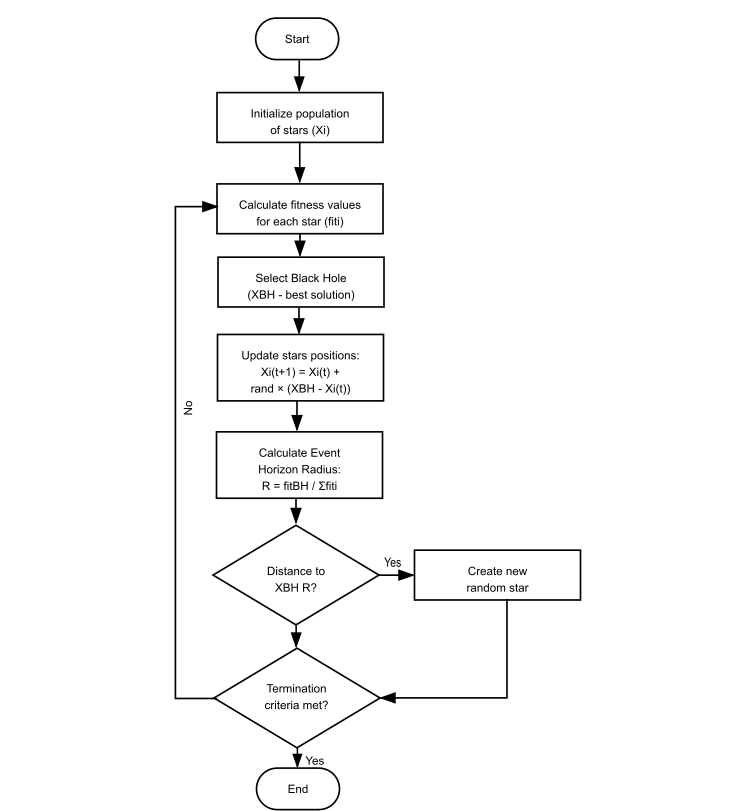
図2：BHA演算の論理構造

C_AO_BHAクラスは、C_AO基底クラスを継承する派生クラスです。クラス構造は以下のとおりです。

コンストラクタとデストラクタ

コンストラクタはアルゴリズムの基本パラメータを初期化します。

以下はpublicメソッドです。

SetParams()：パラメータ配列から集団サイズを設定する
Init()：与えられた境界およびステップで探索空間を初期化する
Moving()：星がブラックホールに向かって移動する動作を実装する
Revision()：最良解（ブラックホール）を更新する

以下はPrivateメンバーです。

blackHoleIndex：集団内で最良解のインデックスを保持する

最適化パラメータは配列経由で渡されます。

rangeMinP []：各座標の最小値
rangeMaxP []：各座標の最大値
rangeStepP []：各座標の離散化ステップ
epochsP：アルゴリズムの反復回数

これは、BHAを実装するための基本的なフレームワークであり、主なロジックはMoving()およびRevision()メソッド内で実装されます。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_BHA : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_BHA () { }
  C_AO_BHA ()
  {
    ao_name = "BHA";
    ao_desc = "Black Hole Algorithm";
    ao_link = "https://www.mql5.com/ja/articles/16655";

    popSize = 50;   // Population size

    ArrayResize (params, 1);

    // Initialize parameters
    params [0].name = "popSize"; params [0].val = popSize;
  }

  void SetParams () // Method for setting parameters
  {
    popSize = (int)params [0].val;
  }

  bool Init (const double &rangeMinP  [], // Minimum search range
             const double &rangeMaxP  [], // Maximum search range
             const double &rangeStepP [], // Search step
             const int     epochsP = 0);  // Number of epochs

  void Moving   ();       // Moving method
  void Revision ();       // Revision method

  private: //-------------------------------------------------------------------
  int blackHoleIndex;    // Black hole index (best solution)
};

Initメソッドはシンプルであり、そのタスクは次のとおりです。

アルゴリズムを初期化する
StandardInitを呼び出して探索範囲とステップを設定する
ブラックホールの初期インデックスを0に設定する
初期化が正常に完了した場合はtrueを返し、エラーが発生した場合はfalseを返す

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_BHA::Init (const double &rangeMinP  [],
                     const double &rangeMaxP  [],
                     const double &rangeStepP [],
                     const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  blackHoleIndex = 0; // Initialize black hole index
  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Movingメソッドは、いくつかの主要なブロックで構成されています。

a) 初期初期化（revision=falseの場合）

ランダムな位置を持つ星の初期集団を生成する
位置は指定された範囲内で生成され、離散グリッドに丸められる
revisionフラグをtrueに設定する

b) 基本アルゴリズム（revision = trueの場合）

すべての星の適応度関数値の合計を計算する
事象の地平線の半径を次の式で計算する：R = fitBH / Σfiti

c) 星の位置更新

ブラックホール以外の各星について次を実行する
1. ブラックホールまでのユークリッド距離を計算する
2. 距離が地平線半径より小さい場合
  - 新しいランダムな星を生成する
3. それ以外の場合
  - 次の式を使用して位置を更新する：Xi(t+1) = Xi(t) + rand × (XBH - Xi(t))
  - 新しい位置を許容範囲および離散グリッド内に収める

すべての計算は、探索空間の制約および離散化ステップを考慮して実行されます。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BHA::Moving ()
{
  // Initial random positioning on first run
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        // Generate a random position within the allowed range
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        // Convert to discrete values according to step
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
    revision = true;
    return;
  }

  // Calculate the sum of fitness values for the radius of the event horizon
  double sumFitness = 0.0;
  for (int i = 0; i < popSize; i++)
  {
    sumFitness += a [i].f;
  }

  // Calculate the radius of the event horizon
  // R = fitBH / Σfiti
  double eventHorizonRadius = a [blackHoleIndex].f / sumFitness;

  // Update star positions
  for (int i = 0; i < popSize; i++)
  {
    // Skip the black hole
    if (i == blackHoleIndex) continue;

    // Calculate the distance to the black hole
    double distance = 0.0;
    for (int c = 0; c < coords; c++)
    {
      double diff = a [blackHoleIndex].c [c] - a [i].c [c];
      distance += diff * diff;
    }
    distance = sqrt (distance);

    // Check for event horizon crossing
    if (distance < eventHorizonRadius)
    {
      // Star is consumed - create a new random star
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
    else
    {
      // Update the star position using the equation:
      // Xi(t+1) = Xi(t) + rand × (XBH - Xi(t))
      for (int c = 0; c < coords; c++)
      {
        double rnd = u.RNDfromCI (0.0, 1.0);
        double newPosition = a [i].c [c] + rnd * (a [blackHoleIndex].c [c] - a [i].c [c]);

        // Check and correct the boundaries
        newPosition = u.SeInDiSp (newPosition, rangeMin [c], rangeMax [c], rangeStep [c]);
        a [i].c [c] = newPosition;
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Revisionメソッドは次の機能を実行します。

最良解の探索

集団内のすべての星を反復処理する
各星の適応度値(a[i].f)を現在の最良値(fB)と比較する
最良解を見つけた場合
- 最良の適応度関数値(fB)を更新する
- ブラックホールのインデックス(blackHoleIndex)を保存する
- 最適解の座標をcB配列にコピーする

このメソッドの主な目的は、最適化の過程で見つかった最良解（ブラックホール）を追跡し、保存することです。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BHA::Revision ()
{
  // Find the best solution (black hole)
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      blackHoleIndex = i;
      ArrayCopy (cB, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

BHAをテストすると、次の結果が得られました。

BHA|Black Hole Algorithm|50.0|
=============================
5 Hilly's; Func runs:10000; result:0.6833993073000924
25 Hilly's; Func runs:10000; result:0.47275633991339616
500 Hilly's; Func runs:10000; result:0.2782882943201518
=============================
5 Forest's; Func runs:10000; result:0.6821776337288085
25 Forest's; Func runs:10000; result:0.3878950941651221
500 Forest's; Func runs:10000; result:0.20702263338385946
=============================
5 Megacity's; Func runs:10000; result:0.39461538461538465
25 Megacity's; Func runs:10000; result:0.20076923076923076
500 Megacity's; Func runs:10000; result:0.1076846153846164
=============================
All score:3.41461 (37.94%)

表によると、結果は平均を下回っています。しかし、このアルゴリズムの明確な利点は、集団サイズ以外のパラメータを持たないことです。このため、結果は十分に満足できるものと考えられます。動作中にすぐに気づいたのは、集団内の解の多様性が欠如しているために局所最適解に陥る傾向があるということです。さらに、各星についてブラックホールまでのユークリッド距離を計算する必要があり、これは計算リソースを多く消費します。この状況は、既存の欠点を修正するための可能な方法について考察するきっかけとなりました。

元のアルゴリズムでは、各反復ごとに星は移動しますが、ブラックホールはその位置に留まります。しかし、実際の宇宙ではすべての天体が運動しています。そこで私はいくつかの変更を加えることにしました。具体的には、ブラックホールをその中心を基準としたガウス分布に基づく距離で移動させ、さらに冪乗則分布も試しました。この適応の目的は、新しい探索領域を探る能力を維持しつつ、収束精度を向上させることにありました。しかし、これらの変更にもかかわらず、結果に改善は見られませんでした。これは、ブラックホールの安定した位置（特にこの探索戦略において）がアルゴリズムの効率にとって重要であり、星が最も有望な領域に集中することを保証している可能性を示しています。より良い結果を得るためには、他のアプローチや手法の組み合わせを検討する価値があるかもしれません。

そこで、ユークリッド距離の計算をやめ、ブラックホールの事象の地平線を実際の交差の基準ではなく、確率的吸収の指標として使用するというアイデアが生まれました。星全体の動きを適用する代わりに、この確率を各座標に個別に適用します。

以上の考察に基づき、新しいバージョンのMovingメソッドを作成します。変更は事象の地平線の計算方法に影響を与えています。ここでは、集団の平均適応度値が、集団内の最小および最大適応度値の差に対して正規化されます。現在、事象の地平線は星の各座標における吸収確率を表し、吸収が発生しない場合は、著者の式に従って銀河のブラックモンスターの中心へ向かう通常の移動を実行します。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BHAm::Moving ()
{
  // Initial random positioning on first run
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        // Generate a random position within the allowed range
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        // Convert to discrete values according to step
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  // Calculate the average fitness values for the event horizon radius
  double aveFit = 0.0;
  double maxFit = fB;
  double minFit = a [0].f;

  for (int i = 0; i < popSize; i++)
  {
    aveFit += a [i].f;
    if (a [i].f < minFit) minFit = a [i].f;
  }
  aveFit /= popSize;

  // Calculate the radius of the event horizon
  double eventHorizonRadius = (aveFit - minFit) / (maxFit - minFit);

  // Update star positions
  for (int i = 0; i < popSize; i++)
  {
    // Skip the black hole
    if (i == blackHoleIndex) continue;

    for (int c = 0; c < coords; c++)
    {
      if (u.RNDprobab () < eventHorizonRadius * 0.01)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
      else
      {
        double rnd = u.RNDfromCI (0.0, 1.0);
        double newPosition = a [i].c [c] + rnd * (a [blackHoleIndex].c [c] - a [i].c [c]);

        // Check and correct the boundaries
        newPosition = u.SeInDiSp (newPosition, rangeMin [c], rangeMax [c], rangeStep [c]);
        a [i].c [c] = newPosition;
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

アルゴリズムの2つのバージョンの主な違いを分析しましょう。まず、事象の地平線半径の計算から見ていきます。最初のバージョン(BHA)では、半径は最良解とすべての解の合計の比として定義されます。これにより、集団が大きくなると半径が非常に小さくなり、適応度関数の絶対値に強く依存する結果となります。一方、2番目のバージョン(BHAm)では、半径が[0,1]の範囲で正規化され、最小値と最大値の間における平均の相対的な位置を示すことができます。これにより、集団サイズおよび適応度関数の絶対値に依存しない特性が維持されます。

次に、星の吸収メカニズムを見てみましょう。アルゴリズムの最初のバージョンでは、ブラックホールまでのユークリッド距離を確認し、吸収が発生した場合、その星をランダムな位置に完全に置き換えます。これにより、集団内により劇的な変化が生じます。2番目のバージョンでは、各座標ごとに確率的な吸収を使用し、これにより集団内の変化がより滑らかになります。ここで、0.01という比率が急激な変化の確率を低減させています。

結果として、最初のバージョンは探索空間をより積極的に利用します。そのため、局所領域での高速な収束が得られますが、早期収束のリスクが高まり、解を完全に置き換えることによって有望な領域を見逃す可能性もあります。これに対して、2番目のバージョンはより穏やかな探索戦略を提供し、探索と利用のバランスがより良く、局所最適に陥るリスクが少なく、収束は遅いものの、より信頼性の高い結果が得られる可能性があります。また、集団の多様性をより良く維持できる点も特徴です。

結論として、最初のバージョンは明確に定義された最適解を持つ問題、すなわち高速な収束と小規模な探索空間が求められる場合により適しています。一方、2番目のバージョンは、グローバル最適解の探索の信頼性が重要な複雑な多極最適化問題や、より徹底的な探索を必要とする高次元問題において、より効果的です。

アルゴリズムの動作の可視化について、私の考えを共有したいと思います。可視化によって、アルゴリズム内部で発生しているプロセスをより深く理解し、その隠れたメカニズムを明らかにするためのユニークな機会を提供します。特定の設定をおこなうことで、カオス的なイメージが徐々に構造化されたパターンへと変化していく様子を観察することができます。このプロセスは、アルゴリズムの動作における技術的な側面を示すだけでなく、その最適化に関する新しいアイデアやアプローチをもたらすきっかけにもなります。

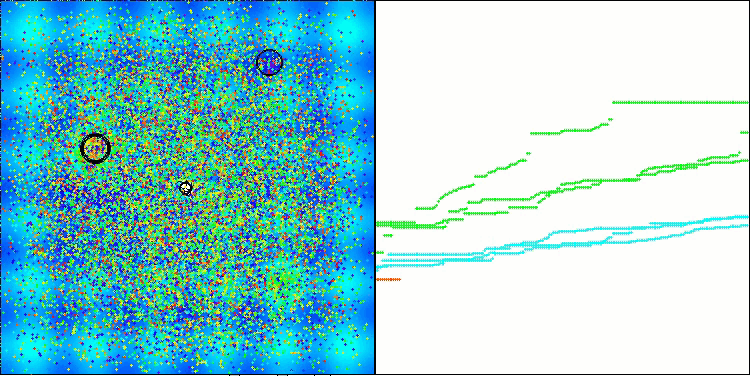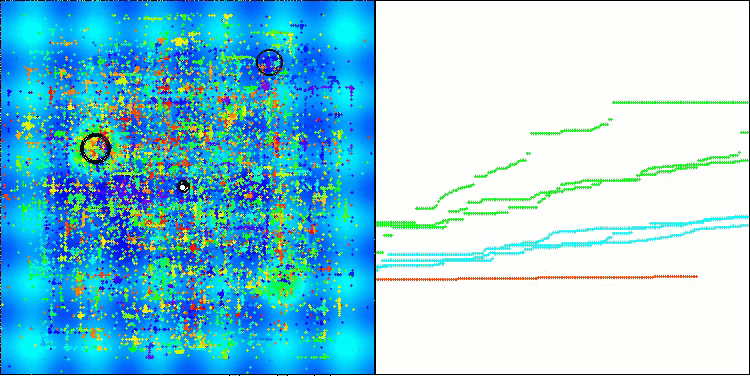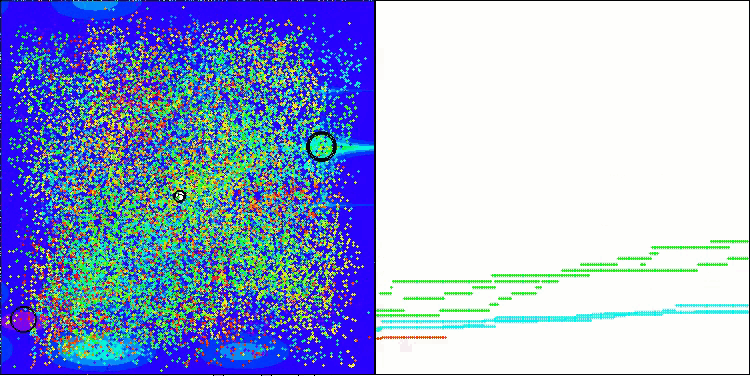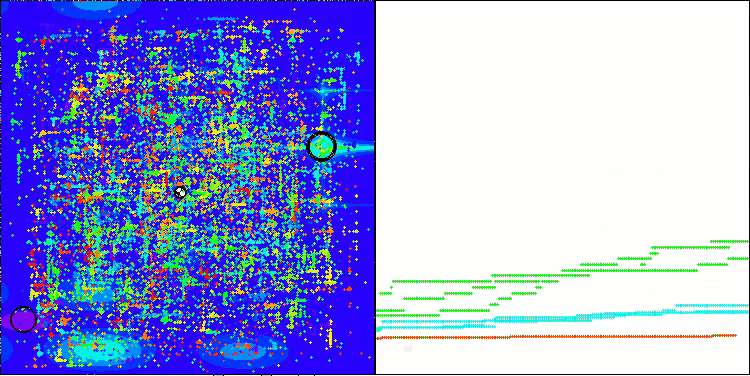
BHAmアルゴリズムにおける、[0.0;0.1]の範囲で星の移動のランダム成分を生成する例

可視化によって、アルゴリズムの効率を評価するだけでなく、従来のデータ分析では明らかにならないパターンを特定できることは重要です。これにより、アルゴリズムの動作をより深く理解し、新しい解決策やイノベーションを生み出すきっかけとなります。したがって、可視化は科学と創造性を結びつけ、複雑なプロセスの探索と理解のための新たな地平を開く強力なツールとなるのです。

テスト結果

BHAmアルゴリズムの修正版の結果

BHAm|Black Hole Algorithm M|50.0|
=============================
5 Hilly's; Func runs:10000; result:0.752359491007831
25 Hilly's; Func runs:10000; result:0.7667459889455067
500 Hilly's; Func runs:10000; result:0.34582657277589457
=============================
5 Forest's; Func runs:10000; result:0.9359337849703726
25 Forest's; Func runs:10000; result:0.801524710041611
500 Forest's; Func runs:10000; result:0.2717683112397725
=============================
5 Megacity's; Func runs:10000; result:0.6507692307692307
25 Megacity's; Func runs:10000; result:0.5164615384615385
500 Megacity's; Func runs:10000; result:0.154715384615386
=============================
All score:5.19611 (57.73%)

テスト結果に基づくと、BHAmアルゴリズムは印象的な成果を示しています。これは、元のバージョンとの比較だけでなく、全体の表においても顕著です。可視化の結果からも、「m」接尾辞を持つ新しいバージョンが、元のアルゴリズムに特有の欠点から実際に解放されていることが確認できます。すなわち、行き詰まりの傾向がほとんど完全に排除され、収束精度が大幅に向上し、結果のばらつきも減少しています。同時に、元のアルゴリズムの「ファミリー的特徴」は保持されています。すなわち、空間内での星の特有の凝集（クランプ）形成や、解空間内の特定のアトラクタへの引き寄せといった性質です。

Hilly

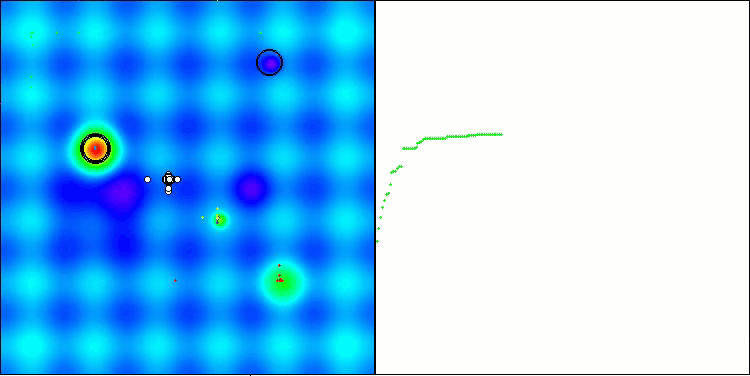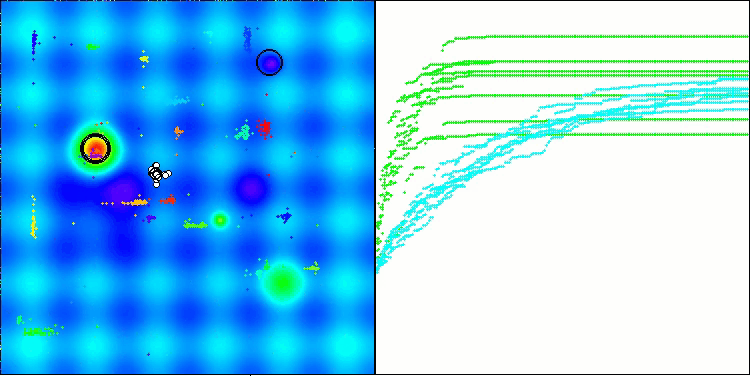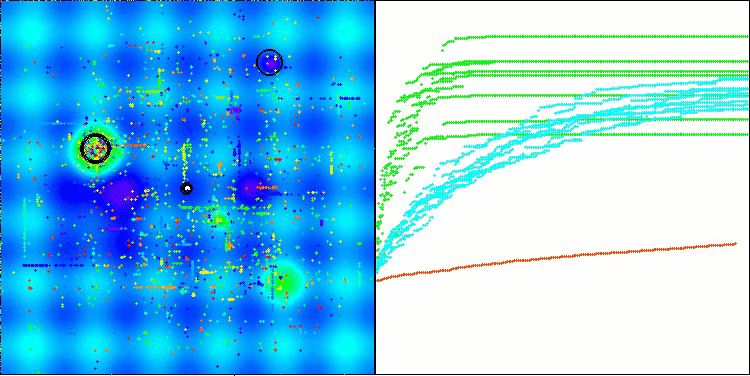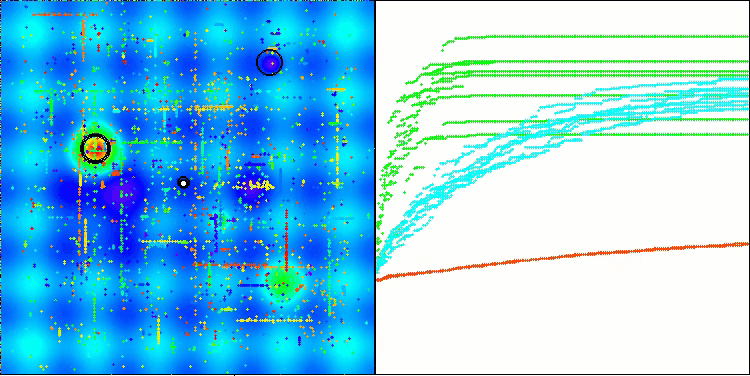
Hillyテスト関数のBHAm

Forest

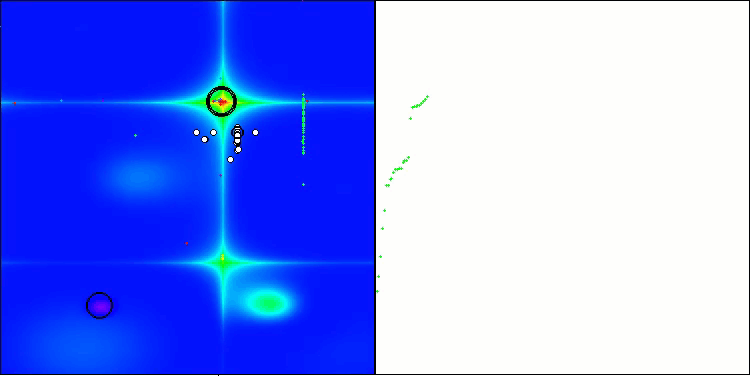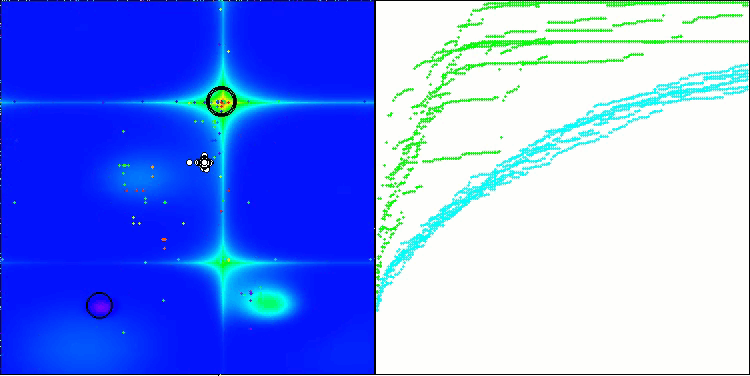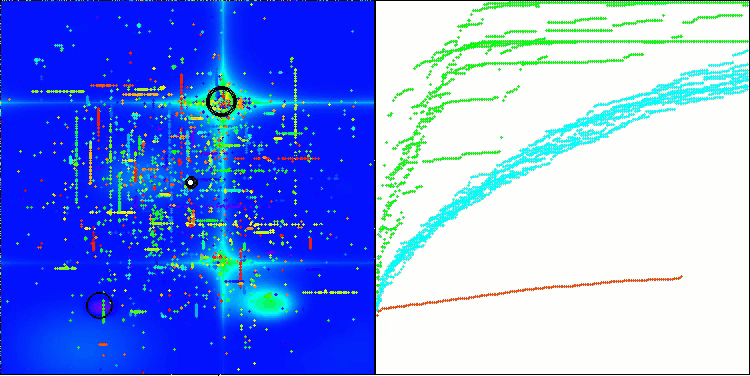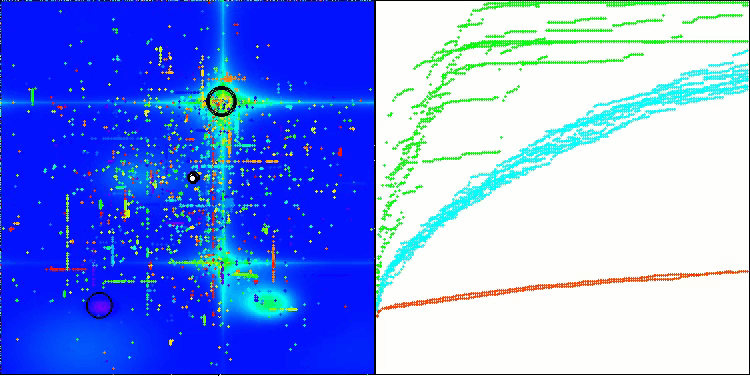
Forestテスト関数のBHAm

Megacity

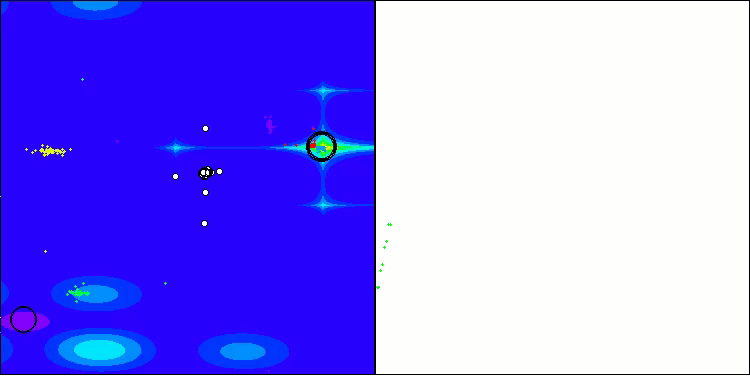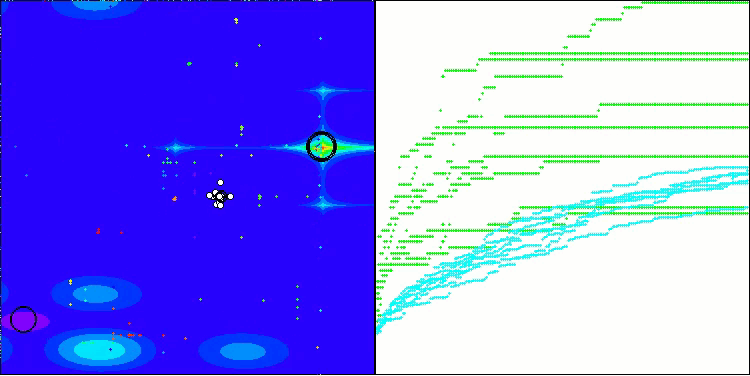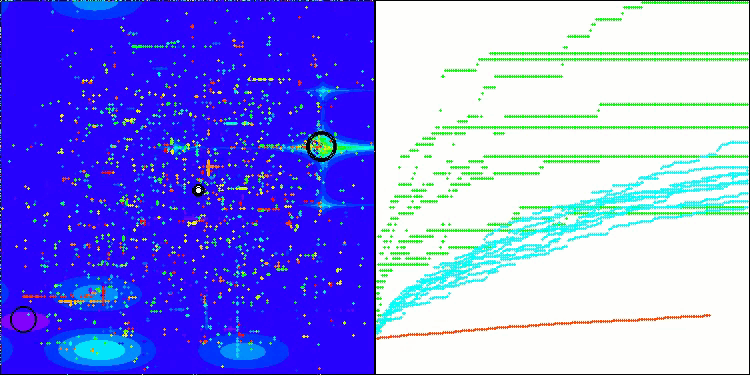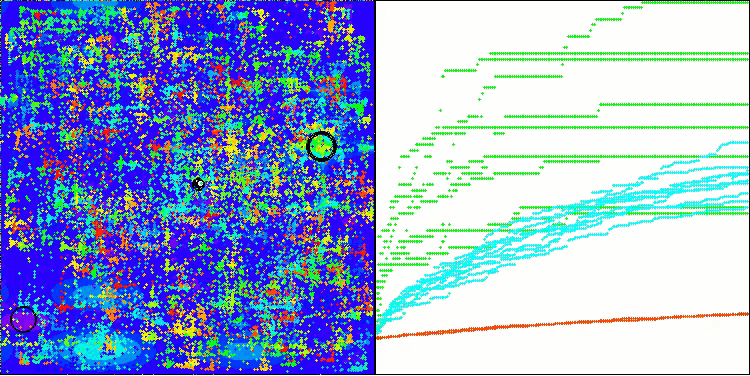
Megacityテスト関数のBHAm

テスト結果に基づくと、BHAmアルゴリズムは第11位という好成績を収めました。これは、既知の最も強力なアルゴリズムが競合相手として存在することを考慮すれば、非常に良好な結果です。

#	AO	詳細	Hilly			Hilly最終	Forest			Forest最終	Megacity（離散）			Megacity最終	最終結果	MAXの%
#	AO	詳細	10p(5F)	50p(25F)	1000p(500F)	Hilly最終	10p(5F)	50p(25F)	1000p(500F)	Forest最終	10p(5F)	50p(25F)	1000p(500F)	Megacity最終	最終結果	MAXの%
1	ANS	across neighbourhood search	0.94948	0.84776	0.43857	2.23581	1.00000	0.92334	0.39988	2.32323	0.70923	0.63477	0.23091	1.57491	6.134	68.15
2	CLA	コードロックアルゴリズム(joo)	0.95345	0.87107	0.37590	2.20042	0.98942	0.91709	0.31642	2.22294	0.79692	0.69385	0.19303	1.68380	6.107	67.86
3	AMOm	動物移動最適化m	0.90358	0.84317	0.46284	2.20959	0.99001	0.92436	0.46598	2.38034	0.56769	0.59132	0.23773	1.39675	5.987	66.52
4	(P+O)ES	(P+O)進化戦略	0.92256	0.88101	0.40021	2.20379	0.97750	0.87490	0.31945	2.17185	0.67385	0.62985	0.18634	1.49003	5.866	65.17
5	CTA	彗星の尾アルゴリズム(joo)	0.95346	0.86319	0.27770	2.09435	0.99794	0.85740	0.33949	2.19484	0.88769	0.56431	0.10512	1.55712	5.846	64.96
6	SDSm	確率的拡散探索M	0.93066	0.85445	0.39476	2.17988	0.99983	0.89244	0.19619	2.08846	0.72333	0.61100	0.10670	1.44103	5.709	63.44
7	AAm	アーチェリーアルゴリズムM	0.91744	0.70876	0.42160	2.04780	0.92527	0.75802	0.35328	2.03657	0.67385	0.55200	0.23738	1.46323	5.548	61.64
8	ESG	社会集団の進化(joo)	0.99906	0.79654	0.35056	2.14616	1.00000	0.82863	0.13102	1.95965	0.82333	0.55300	0.04725	1.42358	5.529	61.44
9	SIA	等方的焼きなまし(joo)	0.95784	0.84264	0.41465	2.21513	0.98239	0.79586	0.20507	1.98332	0.68667	0.49300	0.09053	1.27020	5.469	60.76
10	ACS	人工協調探索	0.75547	0.74744	0.30407	1.80698	1.00000	0.88861	0.22413	2.11274	0.69077	0.48185	0.13322	1.30583	5.226	58.06
11	BHAm	ブラックホールアルゴリズムM	0.75236	0.76675	0.34583	1.86493	0.93593	0.80152	0.27177	2.00923	0.65077	0.51646	0.15472	1.32195	5.196	57.73
12	ASO	無政府社会最適化	0.84872	0.74646	0.31465	1.90983	0.96148	0.79150	0.23803	1.99101	0.57077	0.54062	0.16614	1.27752	5.178	57.54
13	AOSm	原子軌道探索M	0.80232	0.70449	0.31021	1.81702	0.85660	0.69451	0.21996	1.77107	0.74615	0.52862	0.14358	1.41835	5.006	55.63
14	TSEA	亀甲進化アルゴリズム(joo)	0.96798	0.64480	0.29672	1.90949	0.99449	0.61981	0.22708	1.84139	0.69077	0.42646	0.13598	1.25322	5.004	55.60
15	DE	差分進化	0.95044	0.61674	0.30308	1.87026	0.95317	0.78896	0.16652	1.90865	0.78667	0.36033	0.02953	1.17653	4.955	55.06
16	CRO	化学反応の最適化	0.94629	0.66112	0.29853	1.90593	0.87906	0.58422	0.21146	1.67473	0.75846	0.42646	0.12686	1.31178	4.892	54.36
17	BSA	鳥群アルゴリズム	0.89306	0.64900	0.26250	1.80455	0.92420	0.71121	0.24939	1.88479	0.69385	0.32615	0.10012	1.12012	4.809	53.44
18	HS	ハーモニー検索	0.86509	0.68782	0.32527	1.87818	0.99999	0.68002	0.09590	1.77592	0.62000	0.42267	0.05458	1.09725	4.751	52.79
19	SSG	苗木の播種と育成	0.77839	0.64925	0.39543	1.82308	0.85973	0.62467	0.17429	1.65869	0.64667	0.44133	0.10598	1.19398	4.676	51.95
20	BCOm	細菌走化性最適化M	0.75953	0.62268	0.31483	1.69704	0.89378	0.61339	0.22542	1.73259	0.65385	0.42092	0.14435	1.21912	4.649	51.65
21	ABO	アフリカ水牛の最適化	0.83337	0.62247	0.29964	1.75548	0.92170	0.58618	0.19723	1.70511	0.61000	0.43154	0.13225	1.17378	4.634	51.49
22	(PO)ES	(PO)進化戦略	0.79025	0.62647	0.42935	1.84606	0.87616	0.60943	0.19591	1.68151	0.59000	0.37933	0.11322	1.08255	4.610	51.22
23	TSm	タブーサーチM	0.87795	0.61431	0.29104	1.78330	0.92885	0.51844	0.19054	1.63783	0.61077	0.38215	0.12157	1.11449	4.536	50.40
24	BSO	ブレインストーム最適化	0.93736	0.57616	0.29688	1.81041	0.93131	0.55866	0.23537	1.72534	0.55231	0.29077	0.11914	0.96222	4.498	49.98
25	WOAm	鯨最適化アルゴリズムM	0.84521	0.56298	0.26263	1.67081	0.93100	0.52278	0.16365	1.61743	0.66308	0.41138	0.11357	1.18803	4.476	49.74
26	AEFA	人工電界アルゴリズム	0.87700	0.61753	0.25235	1.74688	0.92729	0.72698	0.18064	1.83490	0.66615	0.11631	0.09508	0.87754	4.459	49.55
27	AEO	人工生態系ベースの最適化アルゴリズム	0.91380	0.46713	0.26470	1.64563	0.90223	0.43705	0.21400	1.55327	0.66154	0.30800	0.28563	1.25517	4.454	49.49
28	ACOm	蟻コロニー最適化M	0.88190	0.66127	0.30377	1.84693	0.85873	0.58680	0.15051	1.59604	0.59667	0.37333	0.02472	0.99472	4.438	49.31
29	BFO-GA	細菌採食の最適化：Ga	0.89150	0.55111	0.31529	1.75790	0.96982	0.39612	0.06305	1.42899	0.72667	0.27500	0.03525	1.03692	4.224	46.93
30	SOA	シンプル最適化アルゴリズム	0.91520	0.46976	0.27089	1.65585	0.89675	0.37401	0.16984	1.44060	0.69538	0.28031	0.10852	1.08422	4.181	46.45
31	ABHA	人工蜂の巣アルゴリズム	0.84131	0.54227	0.26304	1.64663	0.87858	0.47779	0.17181	1.52818	0.50923	0.33877	0.10397	0.95197	4.127	45.85
32	ACMO	大気雲モデルの最適化	0.90321	0.48546	0.30403	1.69270	0.80268	0.37857	0.19178	1.37303	0.62308	0.24400	0.10795	0.97503	4.041	44.90
33	ADAMm	適応モーメント推定M	0.88635	0.44766	0.26613	1.60014	0.84497	0.38493	0.16889	1.39880	0.66154	0.27046	0.10594	1.03794	4.037	44.85
34	ATAm	人工部族アルゴリズムM	0.71771	0.55304	0.25235	1.52310	0.82491	0.55904	0.20473	1.58867	0.44000	0.18615	0.09411	0.72026	3.832	42.58
35	ASHA	人工シャワーアルゴリズム	0.89686	0.40433	0.25617	1.55737	0.80360	0.35526	0.19160	1.35046	0.47692	0.18123	0.09774	0.75589	3.664	40.71
36	ASBO	適応型社会行動最適化(ASBO)	0.76331	0.49253	0.32619	1.58202	0.79546	0.40035	0.26097	1.45677	0.26462	0.17169	0.18200	0.61831	3.657	40.63
37	MEC	mind evolutionary computation	0.69533	0.53376	0.32661	1.55569	0.72464	0.33036	0.07198	1.12698	0.52500	0.22000	0.04198	0.78698	3.470	38.55
38	IWO	侵入雑草最適化	0.72679	0.52256	0.33123	1.58058	0.70756	0.33955	0.07484	1.12196	0.42333	0.23067	0.04617	0.70017	3.403	37.81
39	Micro-AIS	微小人工免疫系	0.79547	0.51922	0.30861	1.62330	0.72956	0.36879	0.09398	1.19233	0.37667	0.15867	0.02802	0.56335	3.379	37.54
40	COAm	カッコウ最適化アルゴリズムM	0.75820	0.48652	0.31369	1.55841	0.74054	0.28051	0.05599	1.07704	0.50500	0.17467	0.03380	0.71347	3.349	37.21
41	SDOm	螺旋ダイナミクス最適化M	0.74601	0.44623	0.29687	1.48912	0.70204	0.34678	0.10944	1.15826	0.42833	0.16767	0.03663	0.63263	3.280	36.44
42	NMm	ネルダー=ミード法M	0.73807	0.50598	0.31342	1.55747	0.63674	0.28302	0.08221	1.00197	0.44667	0.18667	0.04028	0.67362	3.233	35.92
43	FAm	ホタルアルゴリズムM	0.58634	0.47228	0.32276	1.38138	0.68467	0.37439	0.10908	1.16814	0.28667	0.16467	0.04722	0.49855	3.048	33.87
44	GSA	重力探索法	0.64757	0.49197	0.30062	1.44016	0.53962	0.36353	0.09945	1.00260	0.32667	0.12200	0.01917	0.46783	2.911	32.34
45	BFO	細菌採餌最適化	0.61171	0.43270	0.31318	1.35759	0.54410	0.21511	0.05676	0.81597	0.42167	0.13800	0.03195	0.59162	2.765	30.72

まとめ

ブラックホールアルゴリズム(BHA)は、自然界の基本法則がいかにして効率的な最適化ツールへと変換され得るかを示す、非常に優れた例です。このアルゴリズムは、中心となる最良解（ブラックホール）への重力的引力という、シンプルで直感的なアイデアに基づいています。アルゴリズムの進化の過程において、私たちは驚くべき現象を観察します。すなわち、解の星々が銀河の中心に向かって移動する過程で、新たでより強力な引力中心、すなわちより良い解を発見し、探索空間の構造が動的に変化するというものです。これは、自然界の自己組織化メカニズムがアルゴリズム的最適化においていかに効果的に利用できるかを明確に示しています。

実践は、興味深いパターンを示しています。しばしば、基本的なアイデアを複雑化するのではなく、単純化し再考することこそが、予想外に印象的な結果を導くのです。アルゴリズム最適化の世界では、探索ロジックを複雑化することで性能が大幅に向上するケースはほとんど存在しません。

この例は、重要な原則を明確に示しています。すなわち、アルゴリズムの開発者の権威や手法の人気は、その効率性を保証する最終的な根拠として受け取るべきではないということです。どんな手法でも、たとえ非常に成功したものであっても、計算効率や得られる結果の品質の両面で改良することが可能です。修正版アルゴリズム(BHAm)は、このような改良の優れた例です。元の手法の概念的な単純さと外部調整パラメータの欠如を維持しながらも、性能と収束速度の両面で顕著な改善を示しています。

この経験は、根本的な結論へと導きます。すなわち、イノベーションと実験精神は、あらゆる専門的活動において不可欠な要素であるということです。機械学習アルゴリズムの開発であれ、取引戦略の構築であれ、新しいアプローチを探求する勇気と、既存の手法を再考する意欲こそが、しばしば画期的な成果を達成する鍵となります。

最終的に、最適化の進歩は、他のどの分野においても同様に、権威への盲目的な追従によってではなく、基本原理の深い理解と創造的な実験への意志に基づく、より新しく効率的な解を絶えず探求することによって推進されるのです。

Tab

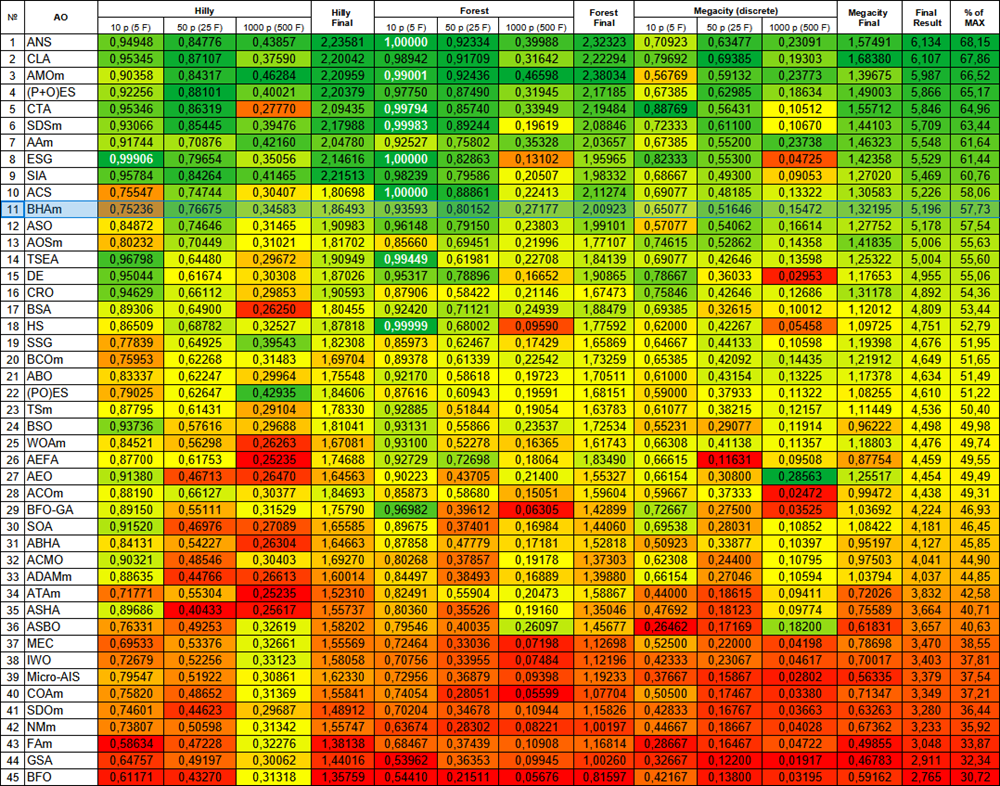
図3：関連するテスト結果に基づくアルゴリズムの色分け。0.99以上の結果は白色で強調表示されている

チャート

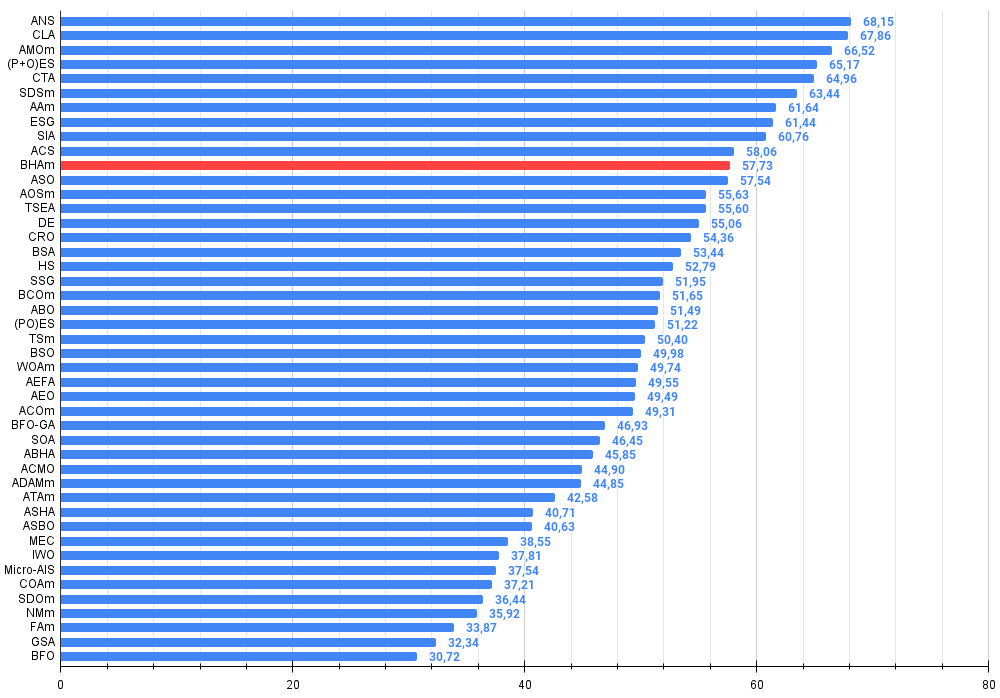
図4：アルゴリズムテスト結果のヒストグラム（0から100のスケール、高いほど良い）100は理論上の最大値であり、アーカイブには評価表を計算するためのスクリプトがあります。

BHAmの長所と短所

長所

集団規模が唯一の外部パラメータ
実装がシンプル
EAが非常に高速
大規模な問題に適している

短所

小次元問題では結果のばらつきが大きい
低次元問題では局所解に陥りやすい傾向がある

この記事には、最新版のアルゴリズムコードを含むアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。

github：https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5

記事で使用されているプログラム

#	名前	種類	詳細
1	#C_AO.mqh	インクルード	集団最適化アルゴリズムの親クラス
2	#C_AO_enum.mqh	インクルード	集団最適化アルゴリズムの列挙
3	TestFunctions.mqh	インクルード	テスト関数のライブラリ
4	TestStandFunctions.mqh	インクルード	テストスタンド関数ライブラリ
5	Utilities.mqh	インクルード	補助関数のライブラリ
6	CalculationTestResults.mqh	インクルード	比較表の結果を計算するスクリプト
7	Testing AOs.mq5	スクリプト	すべての集団最適化アルゴリズムの統一テストスタンド
8	Simple use of population optimization algorithms.mq5	スクリプト	可視化せずに集団最適化アルゴリズムを使用する簡単な例
9	Test_AO_BHAm.mq5	スクリプト	BHAmテストスタンド

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/16655

添付されたファイル |

ZIPをダウンロード

BHAm.zip (147.71 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。

この著者による他の記事

ディスカッションに移動

取引におけるニューラルネットワーク：予測符号化を備えたハイブリッド取引フレームワーク（最終回）

予測符号化と強化学習アルゴリズムを組み合わせた金融時系列分析用のハイブリッド取引システム「StockFormer」の検討を引き続きおこないます。本システムは、複雑なパターンや資産間の相互依存関係を捉えることを可能にするDiversified Multi-Head Attention (DMH-Attn)機構を備えた、3つのTransformerブランチに基づいています。前回は、フレームワークの理論的な側面に触れ、DMH-Attn機構を実装しました。今回は、モデルのアーキテクチャと学習について解説します。

PythonとMQL5で構築するマルチモジュール型取引ロボット（第1回）：基本アーキテクチャと最初のモジュールの作成

Pythonによるデータ分析とMQL5による取引執行を組み合わせたモジュール型の取引システムを開発します。このシステムは、4つの独立したモジュールによって市場の異なる側面（ボリューム、アービトラージ、経済、リスク）を並行して監視します。ランダムフォレストを400本の決定木で構成したモデルを用いて市場データを分析します。特に本システムでは、リスク管理に重点を置いています。どれほど高度なアルゴリズムであっても、適切なリスク管理がなければ意味がありません。

市場シミュレーション（第2回）：両建て注文(II)

前回の記事とは異なり、今回はエキスパートアドバイザー(EA)を用いて選択オプションをテストしてみます。最終的な解決策ではありませんが、現時点では十分な内容となっています。本記事を通じて、1つの実現可能な解決方法の実装手順を理解できます。

取引におけるトレンド基準

トレンドは多くの取引戦略において重要な要素です。本記事では、トレンドを識別するために使用されるいくつかのツールとその特性にを見ていきます。トレンドを理解し正しく解釈することは、取引効率を大幅に高め、リスクを最小限に抑えることにつながります。