MetaTrader 5 / 例
English Русский 中文 Español Deutsch Português
preview
細菌走化性最適化(BCO)

細菌走化性最適化(BCO)

MetaTrader 5 — 例 | 6 5月 2025, 10:12
79 0
Andrey Dik
Andrey Dik

内容

  1. はじめに
  2. アルゴリズムの実装
  3. テスト結果


はじめに

最適化の分野では、多くの研究者や開発者が、進化、社会的相互作用、食物を探す生物の行動など、自然界で起こる生物学的プロセスからインスピレーションを得ています。これにより、まったく新しい革新的な最適化手法が開発されます。研究によって、これらの方法が、特にマルチモーダル、微分不可能、離散的な問題を解決する際に、従来のヒューリスティックおよび勾配ベースのアプローチよりも優れていることが示されています。そのような方法のひとつが、Bremermann氏とその同僚によって最初に提案された走化性アルゴリズムです。細菌採餌の最適化(BFO)アルゴリズムについては、すでに取り上げたことがあります。このアルゴリズムは、濃度勾配中の化学誘引物質に対する細菌の反応をシミュレートします。Bremermannは三次元の勾配における走化性を分析し、それをニューラルネットワークの学習に適用しました。このアルゴリズムは細菌の走化性の原理に基づいていますが、新たな生物学的発見によって、このプロセスのより詳細なモデルを構築できるようになっています。

この記事では、このモデルを新たな最適化戦略として検討します。新しいモデルと従来の走化性アルゴリズムとの主な違いは以下のとおりです。

  1. 新しいモデルでは、細菌が濃度値に関する情報を使用します。
  2. 化学誘引物質の濃度が増加しても、細菌は一方向に移動し続けるわけではありません。

細菌は単細胞生物であり、地球上で最も単純な生命体のひとつです。にもかかわらず、彼らは環境から情報を受け取り、空間を移動し、その情報を生存に活用することができます。環境変化に対する細菌の反応は、近年、集中的に研究されており、最適化を研究する科学者たちからも注目を集めています。最適化アルゴリズムは、関数のランドスケープに関する情報を収集し、それを用いて最適値を見つけるシステムと考えられます。細菌の走化性というアイデアは、その単純さゆえに、こうしたアルゴリズムを構築する出発点として魅力的です。

さまざまな研究によって、細菌同士が情報を交換していることが明らかになっていますが、その通信のメカニズムについてはあまり分かっていません。一般的に、モデルでは細菌は個々の存在として扱われ、社会的相互作用は考慮されません。この点が、アリ、ハチ、スズメバチ、シロアリなどの社会性昆虫の行動を記述する相互作用モデルとは異なります。社会性昆虫は、集団的知能を備えたシステムとして機能し、さまざまな問題に対して新たな可能性を提供します。

適応も走化性の重要な側面です。細菌は、一定の化学的条件に対する感受性を変化させることができ、環境の変化に効果的に対応できます。この特性により、彼らは単に丈夫であるだけでなく、資源探索においても非常に効率的です。

本研究では、コロニーの動きを分析するマクロモデルではなく、個々の細菌の走化性に着目したミクロモデルに基づいています。このアルゴリズムは、S. D. MüllerとP. Koumatsakasによって開発され、その主なアイデアは2002年に発表されました。


アルゴリズムの実装

細菌走化性最適化アルゴリズム（BCO）の考え方は、細菌の行動において観察される生物学的原理を用いて最適化問題を解決することです。このアルゴリズムは、細菌が環境内の化学勾配にどのように反応するかをモデル化し、細菌がより好ましい生存条件を見つけることを可能にします。アルゴリズムの主なアイデアは以下の通りです。

  1. アルゴリズムは、細菌の動きを瞬間的な回転でつながれた一連の直線的な軌道として記述します。それぞれの動きは、速度、方向、および持続時間によって特徴づけられます。
  2. 細菌の回転方向は確率分布によって決定され、これにより動きにおけるランダムな変化を考慮することができます。
  3. アルゴリズムは関数の勾配に関する情報を利用して、細菌を最適解へと導き、目標に到達するために必要な反復回数を最小限に抑えます。

細菌走化性最適化(BCO)アルゴリズムの詳細な疑似コードでは、初期化、移動および修正ステップを含む主要な最適化ループ、補助関数など、アルゴリズムの主なステップが説明されています。

初期化

1. パラメータを設定します。

  • popSize：集団のサイズ（細菌の数）
  • hs：平均変化を計算するステップ数
  • T0：初期温度
  • b：パラメータ
  • tau_c：パラメータ
  • v：スピード

2. popSizeの細菌配列を作成します。

3. 0からpopSize-1までの各i個の細菌について次をおこないます。

  • fPrevを「-DBL_MAX」に初期化する
  • hsサイズのfHistory配列を作成し、ゼロで埋める

基本的な最適化ループ： 停止条件に達するまで繰り返します。

0からpopSize-1までの各i個の細菌の移動段階

1. 目的関数「f_tr」の現在の値を取得します。

2. bacterium [i].fPrevから目的関数「f_pr」の以前の値を取得します。

3. f_tr <= f_prの場合：T = T0

    それ以外の場合：calculate b_corr = CalculateCorrectedB (f_tr, f_pr, i)

  • T = T0 * exp (b_corr * (f_tr - f_pr))

4. Tパラメータを用いて指数分布から「tau」を生成します。

5. coords：1次元のnew_angles []を計算します。0からcoords - 2までの各j角度について次をおこないます。

  • theta = CalculateRotationAngle ()
  • mu = 62 * (1 - cos (theta)) * π / 180
  • sigma = 26 * (1 - cos (theta)) * π / 180
  • new_angles [j] = パラメータ(mu、mu-π、mu+π) に基づく正規分布から生成された乱数

6. 新しい位置を計算します。

  • l = v * tau
  • CalculateNewPosition (l, new_angles, new_position, current_position)

7. rangeMinとrangeMax内の値を制限して細菌の位置を更新します。

8. bacterium [i].fPrevをf_trの値で更新します。

修正段階

1. cBグローバル最適解をfB適合値で更新します。

2. 0から「popSize - 1」までの各細菌「i」について。目的関数「fHistory」の値の履歴を更新します。

  • すべての値を1つ左にシフトする
  • 目的関数の現在の値を履歴の末尾に追加する

以下は補助関数です。

CalculateCorrectedB (f_tr, f_pr, bacteriumIndex)

1. delta_f_tr = f_tr - f_prを計算します。

2. delta_f_pr = 最後のhsステップの平均変化を計算します。

3. |delta_f_pr| < epsilonの場合：bを返します。

   そうでない場合：b * (1 / (|delta_f_tr / delta_f_pr| + 1) + 1 / (|f_pr| + 1))を返します。

CalculateRotationAngle ()

1. cos_theta = exp (-tau_c / T0)を計算します。

2. arccos (cos_theta)を返します。

CalculateNewPosition (l, angles, new_position, current_position)

1. すべての角度を考慮してnew_position[0]を計算します。

2. 1からcoords-1までの各i座標について

   対応する角度からnew_position[i]を計算します。

3. 各座標にランダムな方向（1または-1）を適用します。

GenerateFromExponentialDistribution (T)

-T*ln（0から1の間の乱数）を返します。

アルゴリズムコードの記述に移りましょう。最適化問題の解決策として細菌を表すには、S_BCO_Bacterium構造体を記述します。

1. 構造体フィールド

  • fPrev：目的関数の以前の値
  • fHistory[]：目的関数の値の履歴の配列

2. Init初期化メソッドは以下の操作をおこないます。

  • fHistory配列のサイズをhistorySizeに変更する
  • fHistory配列のすべての要素を0.0で初期化する
  • fPrev：目的関数の以前の値を可能な限り最小の値に設定する

細菌は、目的関数の値が指定された回数（個々の動き）にわたる反復の中でどのように変化するかを追跡する構造体の形式で表現されます。

//——————————————————————————————————————————————————————————————————————————————
struct S_BCO_Bacterium
{
    double fPrev;        // previous value of the objective function
    double fHistory [];  // history of objective function values

    void Init (int coords, int historySize)
    {
      ArrayResize     (fHistory, historySize);
      ArrayInitialize (fHistory, 0.0);
      fPrev = -DBL_MAX;
    }
};
//——————————————————————————————————————————————————————————————————————————————

C_AO_BCOアルゴリズムクラスについて説明します。このクラスを段階的に分けて説明します。

1. アルゴリズムの外部パラメータはコンストラクタで初期化されます。

2. SetParamsメソッドは、params配列からパラメータ値を更新します。

3. MovingメソッドとRevisionメソッドは、細菌の移動とその位置の修正を担当します。

4. このクラスは、アルゴリズムに関連するさまざまな計算に使用されるいくつかのprivateメソッドを定義します：CalculateAverageDeltaFpr、CalculateNewAngles、CalculateNewPosition、GenerateFromExponentialDistribution、CalculateCorrectedB、CalculateRotationAngle、RNDdir、bacterium ：最近の配列（集団）。 以下は、クラスパラメータです。

  • hs：平均変化を計算するためのステップ数
  • T0：初期温度
  • b：パラメータ
  • tau_c：パラメータ
  • v：スピード
//——————————————————————————————————————————————————————————————————————————————
class C_AO_BCO : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_BCO () { }
  C_AO_BCO ()
  {
    ao_name = "BCO";
    ao_desc = "Bacterial Chemotaxis Optimization";
    ao_link = "https://www.mql5.com/ja/articles/15711";

    popSize = 50;     // population size (number of bacteria)
    hs      = 10;     // number of steps to calculate average change
    T0      = 1.0;    // initial temperature
    b       = 0.5;    // parameter b
    tau_c   = 1.0;    // parameter tau_c
    v       = 1.0;    // velocity

    ArrayResize (params, 6);

    params [0].name = "popSize"; params [0].val = popSize;
    params [1].name = "hs";      params [1].val = hs;
    params [2].name = "T0";      params [2].val = T0;
    params [3].name = "b";       params [3].val = b;
    params [4].name = "tau_c";   params [4].val = tau_c;
    params [5].name = "v";       params [5].val = v;
  }

  void SetParams ()
  {
    popSize = (int)params [0].val;
    hs      = (int)params [1].val;
    T0      = params      [2].val;
    b       = params      [3].val;
    tau_c   = params      [4].val;
    v       = params      [5].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving ();
  void Revision ();

  //----------------------------------------------------------------------------
  int    hs;
  double T0;
  double b;
  double tau_c;
  double v;

  S_BCO_Bacterium bacterium [];

  private: //-------------------------------------------------------------------
  double CalculateAverageDeltaFpr            (int bacteriumIndex);
  void   CalculateNewAngles                  (double &angles []);
  void   CalculateNewPosition                (double l, const double &angles [], double &new_position [], const double &current_position []);
  double GenerateFromExponentialDistribution (double T);
  double CalculateCorrectedB                 (double f_tr, double f_pr, int bacteriumIndex);
  double CalculateRotationAngle              ();
  int    RNDdir                              ();
};

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_BCO::Init (const double &rangeMinP  [], //minimum search range
                     const double &rangeMaxP  [], //maximum search range
                     const double &rangeStepP [], //step search
                     const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (bacterium, popSize);
  for (int i = 0; i < popSize; i++) bacterium [i].Init (coords, hs);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_BCOクラスのMovingメソッドは、探索空間における細菌の移動を担当します。以下にその動作を説明します。

1. revisionがfalseの場合、細菌は初期位置を持つことを意味します。

  • 各細菌a [i]に対して、指定された範囲内でランダムな座標が生成されます。
  • 関数u.RNDfromCIはランダムな値を生成し、関数u.SeInDiSpは指定されたステップを考慮してその値を調整します。

2. revisionがtrueの場合の基本的な移動ループ。このメソッドは、細菌の動きの基本的なロジックを実装します。温度Tを以下のように定義します。

  • 現在の関数値f_trが、前回のf_prより良好または同等であれば、初期温度T0が使用されます。
  • それ以外の場合は、CalculateCorrectedB関数を使って温度が調整されます。これは現在と前回の適応度関数の差を考慮します。 
  • tau移動時間は指数分布を使って生成されます。
  • 移動角度と新しい位置は、移動距離lと新しい角度に基づいて計算されます。
  • 新しい位置は、指定された範囲とステップを考慮して調整されます。
  • ループの最後に、各細菌の適応度関数の前回の値が更新されます。

Movingメソッドは、探索空間における細菌の移動の基本的なロジックを実装しており、前の反復の結果に応じて行動を適応させます。ランダム要素と適応メカニズムを組み合わせて最適解の探索をおこないます。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BCO::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    double f_tr = a [i].f;
    double f_pr = bacterium [i].fPrev;

    double T;
    
    if (f_tr <= f_pr)
    {
      T = T0;
    }
    else
    {
      double b_corr = CalculateCorrectedB (f_tr, f_pr, i);
      
      T = T0 * exp (b_corr * (f_tr - f_pr));
    }

    double tau = GenerateFromExponentialDistribution (T);

    double new_angles [];
    ArrayResize (new_angles, coords - 1);
    CalculateNewAngles (new_angles);

    double l = v * tau;
    double new_position [];
    ArrayResize (new_position, coords);
    CalculateNewPosition (l, new_angles, new_position, a [i].c);

    for (int c = 0; c < coords; c++)
    {
      a [i].c [c] = u.SeInDiSp (new_position [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }

    bacterium [i].fPrev = a [i].f;
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_BCOクラスのRevisionメソッドは、見つかった最適解に関する情報と、各細菌の適応関数の値の履歴を更新する役割を担います。

1. 変数indは-1で初期化され、最良の関数値を持つ細菌のインデックスを格納するために使用されます。

2. 最適な関数値を見つけます。

  • このメソッドは、popSize集団内のすべての細菌を走査し、現在の最良値fBよりも大きい関数値fを持つ細菌を探します。
  • より高い関数値を持つ細菌が見つかった場合fBはその値に更新され、その細菌のインデックスがindに保存されます。

3. indが-1でない場合（つまり、より良い細菌が見つかった場合）、そのインデックスの細菌の座標がcB配列にコピーされます。cBは現在の最良解の座標を表します。

4. 各細菌に対して適応度関数の履歴(fHistory)が更新されます。このメソッドでは、各fHistory要素を左に1つずつシフトさせて、新しい値を挿入するスペースを作ります。各反復の最後には、fHistory配列の最後の要素に、その細菌の現在の適応度値a [i].fが代入されます。

まとめると、Revisionメソッドは主に2つの機能を実行します。

  • 最良の適応度関数値と対応する座標の更新
  • 各細菌の適応度関数値の履歴を更新し、移動の過程での状態変化を追跡できるようにする 
//——————————————————————————————————————————————————————————————————————————————
void C_AO_BCO::Revision ()
{
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }
  }

  if (ind != -1)
  {
    ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);
  }

  for (int i = 0; i < popSize; i++)
  {
    for (int j = 1; j < hs; j++)
    {
      bacterium [i].fHistory [j - 1] = bacterium [i].fHistory [j];
    }

    bacterium [i].fHistory [hs - 1] = a [i].f;
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_BCOクラスのCalculateAverageDeltaFprメソッドは、適応度の履歴に基づいて、特定の細菌の2つの隣接する位置間の適応度関数値(デルタ)の平均変化を計算するように設計されています。

//——————————————————————————————————————————————————————————————————————————————
double C_AO_BCO::CalculateAverageDeltaFpr (int bacteriumIndex)
{
  double sum = 0;

  for (int i = 1; i < hs; i++)
  {
    sum += bacterium [bacteriumIndex].fHistory [i] - bacterium [bacteriumIndex].fHistory [i - 1];
  }

  return sum / (hs - 1);
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_BCOクラスのCalculateNewAnglesメソッドは、回転および分布に関するロジックに基づいて新しい角度を計算するために設計されており、以下の処理をおこないます。

  • 新しい角度の配列を反復処理し、それぞれの角度に対して新しい値を計算する
  • 角度の余弦に依存するパラメータを使用して、正規分布を用いた値を生成する
//——————————————————————————————————————————————————————————————————————————————
void C_AO_BCO::CalculateNewAngles (double &angles [])
{
  for (int i = 0; i < coords - 1; i++)
  {
    double theta = CalculateRotationAngle ();
    double mu    = 62 * (1 - MathCos (theta)) * M_PI / 180.0;
    double sigma = 26 * (1 - MathCos (theta)) * M_PI / 180.0;

    angles [i] = u.GaussDistribution (mu, mu - M_PI, mu + M_PI, 8);
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_BCOクラスのCalculateNewPositionメソッドは、現在の座標、角度、およびパラメーターlに基づいて新しい位置座標を計算するように設計されています。 

1. メソッドの入力パラメータ:

  • l：位置の変化に影響を与える比率
  • angles[]：新しい位置の計算に使用される角度の配列
  • new_position[]：新しい座標が格納される配列
  • current_position[]：現在の座標を保持する配列

2. 最初の座標new_position[0]は、現在の座標current_position[0]に、rangeMax [0]とrangeMin [0]の差にlを掛けたものを加算して計算されます。

3. 次に、この最初の座標に、angles配列の先頭から最後の一つ手前までの角度の余弦を順に掛けていきます。

4. 結果に対して、ランダムな方向（「-1」または「1」）を生成する RNDdir ()関数の戻り値を掛けます。

5. 次の各座標new_position [i]（iは1からcoords - 2まで）については、対応する角度の正弦（sin）を用いて現在の位置から新しい位置を計算します。

6. それぞれの新しい座標にも、現在のインデックスiから最後の一つ手前までの角度の余弦を順に掛けていきます。

7. 残りの座標にもランダムな方向が適用され、結果にRNDdir ()の戻り値を掛けます。

8. 最後の座標の処理では、座標の数が1より大きい場合、最後の座標new_position [coords - 1]は、最後の角度の正弦（sin）を用いて現在の位置から新しい位置を計算します。

このように、CalculateNewPositionメソッドは以下の処理を行います。

  • 現在の座標と角度に基づいて新しい座標を計算する
  • 各座標に対してランダムな方向の影響を考慮する
  • 角度を考慮するために三角関数（正弦、余弦）を使用する

したがって、このメソッドは、細菌が空間内を移動する様子を、現在位置と与えられた角度を考慮してシミュレーションするために使用されます。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BCO::CalculateNewPosition (double l, const double &angles [], double &new_position [], const double &current_position [])
{
  new_position [0] = current_position [0] + l * (rangeMax [0] - rangeMin [0]);
 
  for (int k = 0; k < coords - 1; k++)
  {
    new_position [0] *= MathCos (angles [k]);
  }
 
  new_position [0] *= RNDdir ();

  for (int i = 1; i < coords - 1; i++)
  {
    new_position [i] = current_position [i] + l * MathSin (angles [i - 1]) * (rangeMax [0] - rangeMin [0]);
    
    for (int k = i; k < coords - 1; k++)
    {
      new_position [i] *= MathCos (angles [k]);
    }
    
    new_position [i] *= RNDdir ();
  }

  if (coords > 1)
  {
    new_position [coords - 1] = current_position [coords - 1] + l * MathSin (angles [coords - 2]);
  }
 
}
//——————————————————————————————————————————————————————————————————————————————

次に、C_AO_BCOクラスのRNDdirメソッドについて簡単に説明します。このメソッドは、ランダムな方向を生成するために設計されたメソッドで、「-1」または「1」のいずれかの値をランダムに返します。

//——————————————————————————————————————————————————————————————————————————————
int C_AO_BCO::RNDdir ()
{
  if (u.RNDbool () < 0.5) return -1;
 
  return 1;
}
//——————————————————————————————————————————————————————————————————————————————

では、C_AO_BCOクラスのメソッドについて簡単に見ていきましょう。

GenerateFromExponentialDistributionメソッドでは次がおこなわれます。

  • パラメータ Tを用いて指数分布に従う乱数を生成する
  • (0, 1) の範囲からランダムな数値を取得し、その値の対数を計算し、-Tを掛ける
  • 結果として、指数分布に従うランダムな数値が得られる

 CalculateCorrectedBメソッドは次の処理を実行します。

  • f_trとf_pr（現在の適応度と以前の適応度）の差に基づいて調整されたb値を計算する
  • f_trとf_prの差を計算し、細菌の平均値を取得し、調整されたb値を返す
//——————————————————————————————————————————————————————————————————————————————
double C_AO_BCO::GenerateFromExponentialDistribution (double T)
{
  return -T * MathLog (u.RNDprobab ());
}

double C_AO_BCO::CalculateCorrectedB (double f_tr, double f_pr, int bacteriumIndex)
{
  double delta_f_tr = f_tr - f_pr;
  double delta_f_pr = CalculateAverageDeltaFpr (bacteriumIndex);

  if (MathAbs (delta_f_pr) < DBL_EPSILON)
  {
    return b;
  }
  else
  {
    return b * (1 / (MathAbs (delta_f_tr / delta_f_pr) + 1) + 1 / (MathAbs (f_pr) + 1));
  }
}
//——————————————————————————————————————————————————————————————————————————————

最後はC_AO_BCOクラスのCalculateRotationAngleメソッドです。このメソッドは、指定されたパラメータに基づいて回転角度を計算し、ラジアン単位で値を返します。

//——————————————————————————————————————————————————————————————————————————————
double C_AO_BCO::CalculateRotationAngle ()
{
  double cos_theta = MathExp (-tau_c / T0);
  return MathArccos (cos_theta);
}
//——————————————————————————————————————————————————————————————————————————————

アルゴリズムのオリジナルバージョンをテストして、結果を見てみましょう。

BCO|Bacterial Chemotaxis Optimization|50.0|10.0|1.0|0.5|1.0|1.0|
=============================
5 Hilly's; Func runs:10000; result:0.42924491510564006
25 Hilly's; Func runs:10000; result:0.282259866768426
500 Hilly's; Func runs:10000; result:0.2515386629014219
=============================
5 Forest's; Func runs:10000; result:0.2476662231845009
25 Forest's; Func runs:10000; result:0.17824381036550777
500 Forest's; Func runs:10000; result:0.15324081202657283
=============================
5 Megacity's; Func runs:10000; result:0.2430769230769231
25 Megacity's; Func runs:10000; result:0.11415384615384619
500 Megacity's; Func runs:10000; result:0.09444615384615461
=============================
All score:1.99387 (22.15%)

得られた結果は非常に弱く、評価表に含める意味はありませんでした。著者の文章による説明に基づいてアルゴリズムを設計しコードを記述する際に、いくつかの数式を修正する必要がありました。中には数学的に意味を成さないもの（たとえば、数値をベクトルで割る操作）もありましたし、他のものは極端に小さい、または非常に大きい値になってしまい、問題の次元とは釣り合わない結果に退化してしまいました。そのため、各数式の関数出力を出力して分析を行いました。これらの理由から、著者が記述した形式のままでは、アルゴリズムは正常に機能しないと判断しました。

さらに、正規分布を用いた角度の操作についても見直しが可能です。というのも、これらの操作の物理的意味は、各座標において細菌の現在位置から新しい変化量を単に設定すれば十分であるため、処理を大幅に簡素化できるのです。以上の検討を踏まえ、私はアルゴリズムの基本的な概念と考え方には忠実でありつつ、細菌走化性の独自実装を開発することにしました。

以下に、私のバージョンのアルゴリズムの疑似コードを示します。

初期化
1. popSize細菌の集団を作成する
2. 各細菌について：
    hsサイズの目的関数f_history[i]の値の履歴を初期化する
    初期値f_prev[i]=-DBL_MAXを設定する

メインループ
停止条件に達するまで:

1. これが最初の反復である場合：
   各細菌について：
     探索空間内のx[i]の位置をランダムに初期化する
     各j座標についてx[i].[j]∈[x_min[j],x_max[j]]

2. そうでない場合：
   各細菌について：
     a. 目的関数の平均変化を計算する
        delta_ave [i] = (1 / (hs - 1)) * sum (f_history [i].[k] - f_history [i].[k-1]、kは1..hs-1の範囲) + epsilon
     
     b. 適応度の相対的な変化を計算する
        delta [i] = 1 - |f (x [i]) - f_prev [i]| / delta_ave [i]
        delta [i] = max (delta [i], 0.0001)
     
     c. 各j座標について：
        確率0.5の場合：
          dist [j] = (x_max [j] - x_min [j]) * delta [i]
          x [i].[j] = N (x [i].[j], x [i].[j] - dist [j], x [i].[j] + dist [j])
          Limit x [i].[j] within [x_min [j], x_max [j]]
        そうでない場合：
          x [i].[j] = x_best [j]
     
     d. f_prev [i] = f (x [i])を更新する

3. 各細菌の目的関数f (x [i])を評価する

4. 見つかった最適解を更新する
   iが存在する場合： f (x [i]) > f (x_best)、x_best = x [i]

5. 各細菌の目的関数値の履歴を更新する
   f_historyの値をシフトする[i]
   新しい値を追加する： f_history [i].[hs - 1] = f (x [i])

完了
見つかった最適解x_bestを返す

ここで、

  • x [i]：i番目の細菌の位置
  • f (x)：目的関数
  • hs：履歴サイズ
  • epsilon：ゼロ除算を防ぐための小さな定数
  • N (μ, a, b)：平均μ、境界[a,b]の切断正規分布

したがって、私が修正した疑似コードは、BCOアルゴリズムの基本構造とロジックを反映しています。主なポイントに焦点を当ててみましょう。

  • このアルゴリズムでは、各細菌が潜在的な解決策を表す集団を用います。
  • 各反復ステップにおいて、細菌は過去の結果に関する情報をもとに探索空間を移動します。
  • 移動の判断は目的関数の相対的な変化に基づいており、アルゴリズムが最適化の地形に適応できるようになっています。
  • 各細菌について目的関数の履歴が記録されており、それを用いて平均的な変化量が計算されます。
  • 細菌は一定の確率で、新たな領域を探索する代わりに、既知の最良解に向かって移動することがあります（これは遺伝的形質の継承に類似しています）。
  • 各移動の後には新しい位置が評価され、発見された最適解が更新されます。

BCOmバージョンは、局所探索（個々の細菌の移動）と大域探索（最良解を通じた情報共有）の両要素を組み合わせた構成になっています。

続いて、オリジナル版と改良版の主な違いを見てみましょう。まず、細菌の移動メカニズムを大幅に簡素化しました。回転角や温度といった複雑な仕組みは排除しています。次に、新バージョンでは細菌の行動を調整するために変更履歴に過度に依存せず、位置更新により直接的なアプローチを採用しています。従来の指数分布と正規分布の併用に代えて、正規分布のみを用いて座標を更新するようにしました。これにより、アルゴリズムの動作を制御するパラメータが1つ（集団サイズを除く）にまで削減され、最適化プロセスの構成と管理がより簡潔になりました。

全体として、新しい疑似コードでは各最適化ステップの計算がより簡単になっており、その結果としてタスクの実行速度も向上することが期待されます（従来のバージョンでは、各細菌の各座標に対して複数回の正弦・余弦計算が必要でした）。私のアプローチは、新たな解探索と既知の良好な解の活用の間でバランスをとる形で設計されています。

これらのロジックの変更により、アルゴリズムはよりシンプルになり、（テスト結果次第ではありますが）より効率的になると考えられます。では、コードの作成に進みましょう。

各細菌を表す構造体S_BCO_Bacteriumは変更せずそのまま使用します。この構造体は、細菌とその目的関数値の履歴に関する情報を保持するために設計されています。

C_AO_BCOmクラスのInitメソッドは、アルゴリズムのパラメータを初期化する役割を担っています。ここでは、各座標ごとの許容移動距離の定義を追加します。

このように、C_AO_BCOmクラスのInitメソッドは、最適化アルゴリズムのパラメータ初期化を担当し、標準的な初期化条件を確認しつつ、必要な配列を作成し、それらに値を設定します。

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_BCOm::Init (const double &rangeMinP  [], //minimum search range
                      const double &rangeMaxP  [], //maximum search range
                      const double &rangeStepP [], //step search
                      const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (bacterium, popSize);
  for (int i = 0; i < popSize; i++) bacterium [i].Init (coords, hs);

  ArrayResize (allowedDispl, coords);
  for (int c = 0; c < coords; c++) allowedDispl [c] = rangeMax [c] - rangeMin [c];

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

探索空間における細菌の移動を担当するC_AO_BCOmクラスのMovingメソッドを見ていきましょう。このクラスを段階的に分けて説明します。

1. 初回の反復では、メソッドの挙動に変更はなく、細菌の座標は指定された範囲内でランダムに初期化されます。

2. 移動の基本的なロジックでは、Δ、ΔAve、distなどの変数を宣言し、各個体に対して以下の処理をおこないます。

  • CalculateAverageDeltaFpr(i)関数を用いて、ΔAve（平均変化量）を算出する
  • 細菌の位置の変化の度合いを示すΔ（相対変化量）を計算する
  • Δが小さすぎる場合は、最小値として0.0001に設定する

3. 座標を変更します。

  • 各座標に対してランダムな確率(50%)で更新をおこなうかどうかを判定する
  • 条件が満たされた場合、allowedDispl[c]とΔに基づいてdist（変位量）を計算する
  • GaussDistribution関数を使って、新しい値xを生成する（xMinおよびxMaxの範囲を考慮）
  • xが範囲外に出た場合は、RNDfromCIを使用して範囲内に補正する
  • 最終的に、rangeStepを考慮して新しい座標値を保存する

4. 適応度関数の以前の値fを、各細菌のbacterium配列内に保存します。この処理には、a配列とbacterium配列を使用します。RNDfromCI、SeInDiSp、GaussDistribution各関数は、乱数生成・分布処理・座標値の正規化などを担当します。

このように、Moving()メソッドはアルゴリズム内で個体の位置の初期化と更新を担っています。ランダムな確率や確率分布を用いて細菌の移動を制御しています。ただし、オリジナル版との主な違いは、適応度関数の勾配（変化量）をよりシンプルかつ効率的に扱う実装方法にあります。細菌の「健康状態（適応度）」が前回よりも改善しなくなると、その移動速度は加速します。逆に、外部環境が良好であればあるほど、細菌の活動は鈍化します。これは、生物学的に見ると逆の挙動です。自然界の細菌は、過酷な環境では活動を抑制し、仮死状態になる傾向があります。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BCOm::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  double x    = 0.0;
  double xMin = 0.0;
  double xMax = 0.0;
  double Δ    = 0.0;
  double ΔAve = 0.0;
  double dist = 0.0;

  for (int i = 0; i < popSize; i++)
  {
    ΔAve = CalculateAverageDeltaFpr (i) + DBL_EPSILON;

    Δ = fabs (a [i].f - bacterium [i].fPrev) / ΔAve;

    Δ = 1.0 - Δ;

    if (Δ < 0.0001) Δ = 0.0001;

    for (int c = 0; c < coords; c++)
    {
      if (u.RNDprobab () < 0.5)
      {
        dist = allowedDispl [c] * Δ;

        x    = a [i].c [c];
        xMin = x - dist;
        xMax = x + dist;

        x = u.GaussDistribution (x, xMin, xMax, 8);

        if (x > rangeMax [c]) x = u.RNDfromCI (xMin, rangeMax [c]);
        if (x < rangeMin [c]) x = u.RNDfromCI (rangeMin [c], xMax);

        a [i].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]);
      }
      else a [i].c [c] = cB [c];
    }

    bacterium [i].fPrev = a [i].f;
  }
}
//——————————————————————————————————————————————————————————————————————————————

目的関数の集団と値の履歴に関する情報を更新する役割を担うC_AO_BCOmクラスのRevision()メソッドは変更されていません。


テスト結果

それでは、BCOmアルゴリズムの新しいバージョンのパフォーマンスを見てみましょう。

BCO|Bacterial Chemotaxis Optimization|50.0|10.0|
=============================
5 Hilly's; Func runs:10000; result:0.759526049526603
25 Hilly's; Func runs:10000; result:0.6226756163411526
500 Hilly's; Func runs:10000; result:0.31483373090540534
=============================
5 Forest's; Func runs:10000; result:0.8937814268120954
25 Forest's; Func runs:10000; result:0.6133909133246214
500 Forest's; Func runs:10000; result:0.22541842289630293
=============================
5 Megacity's; Func runs:10000; result:0.653846153846154
25 Megacity's; Func runs:10000; result:0.42092307692307684
500 Megacity's; Func runs:10000; result:0.14435384615384755
=============================
All score:4.64875 (51.65%)

おそらく、これまでに蓄積された経験と、元のバージョンに関する情報を批判的に精査したことが功を奏し、アルゴリズムの新しいバージョンは、実際の応用において元のバージョンよりも優れた性能を発揮することが実証されました。

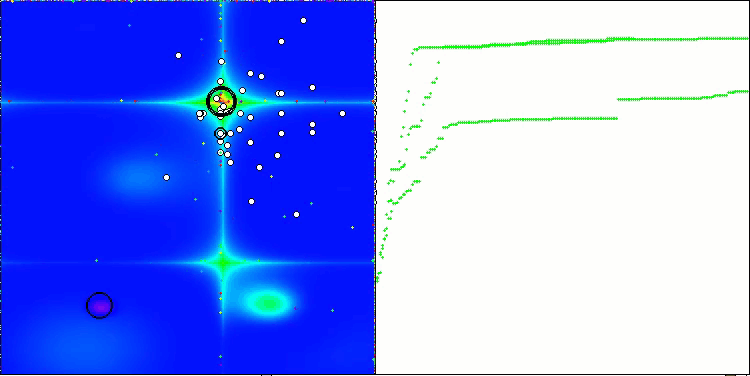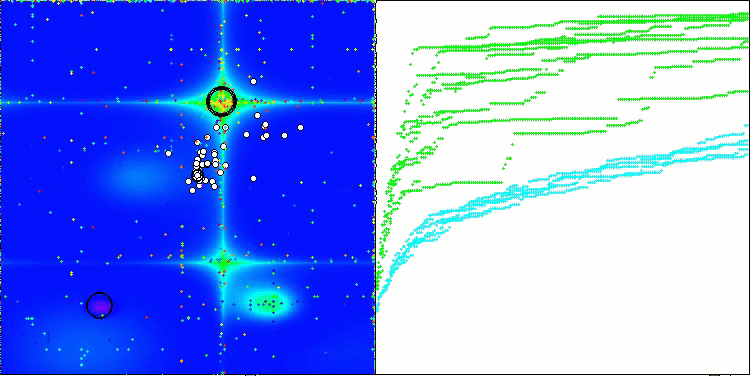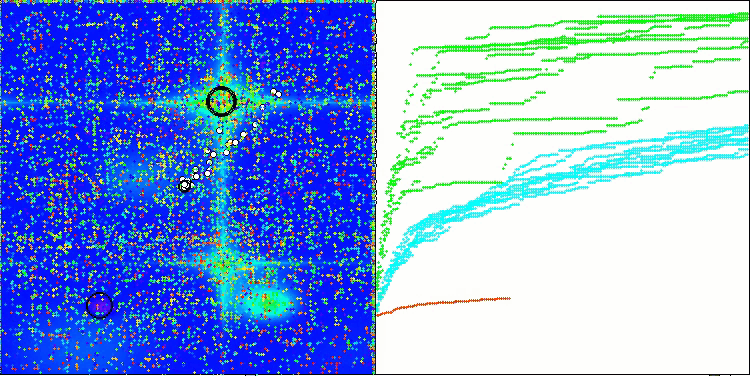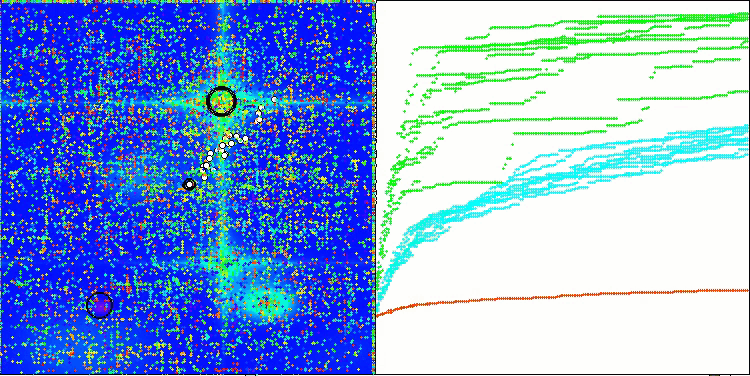
BCOmアルゴリズムの可視化では、ハイパースペース内の重要な領域が精密に探索されている様子が確認でき、これは最適化対象の関数の表面を詳細に調査する高い能力を示しています。

Hilly

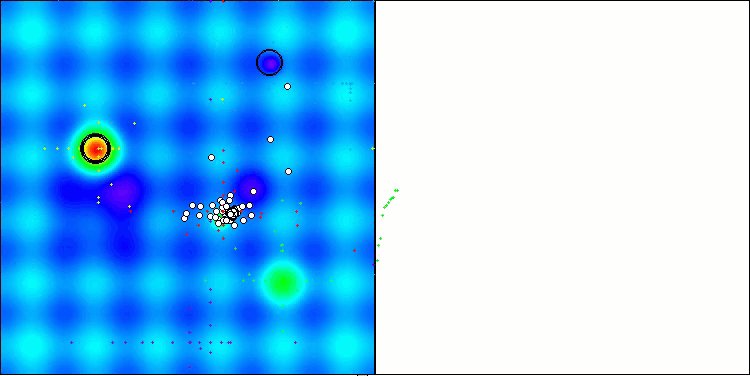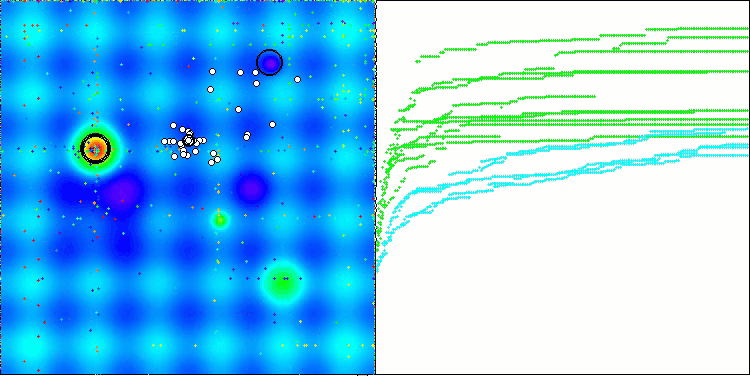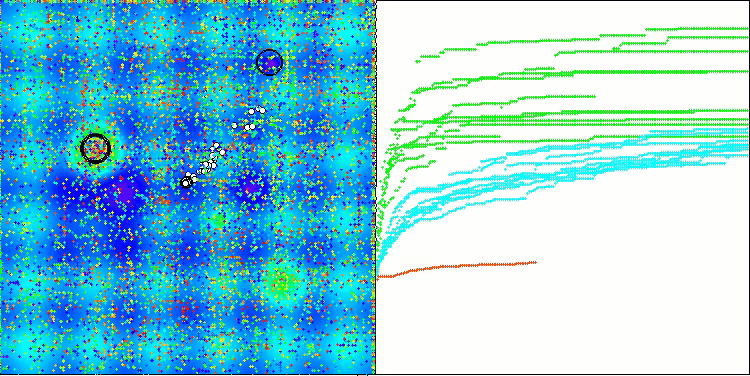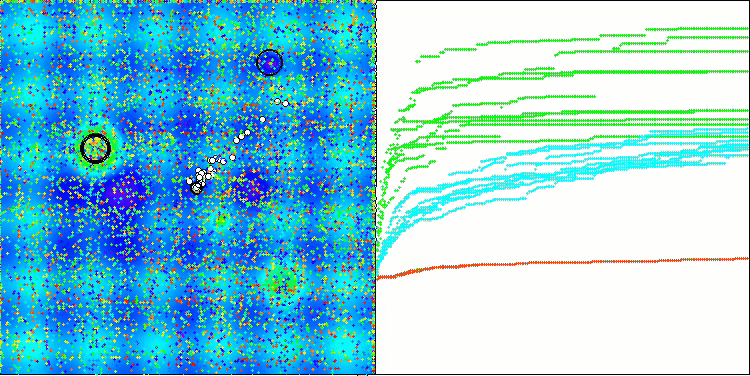
Hillyテスト関数のBCOm

Forest

Forestテスト関数のBCom

Megacity

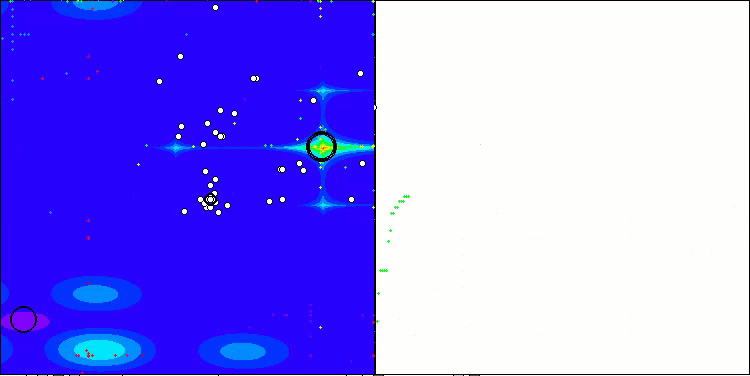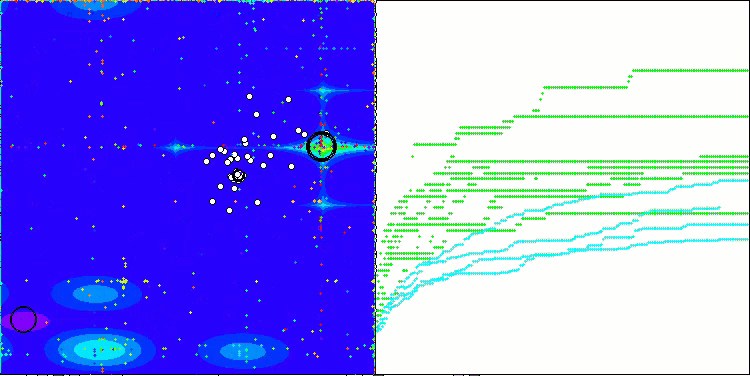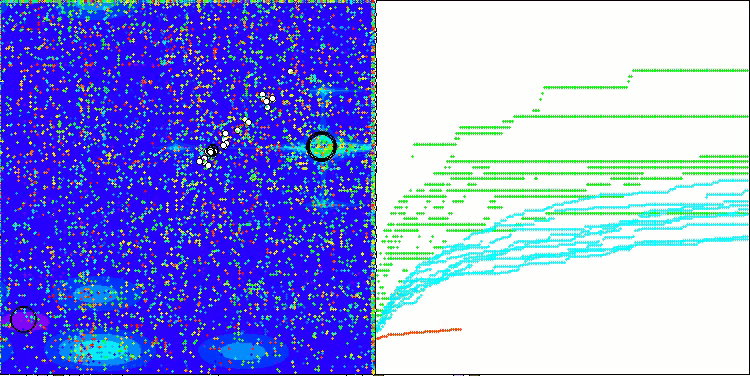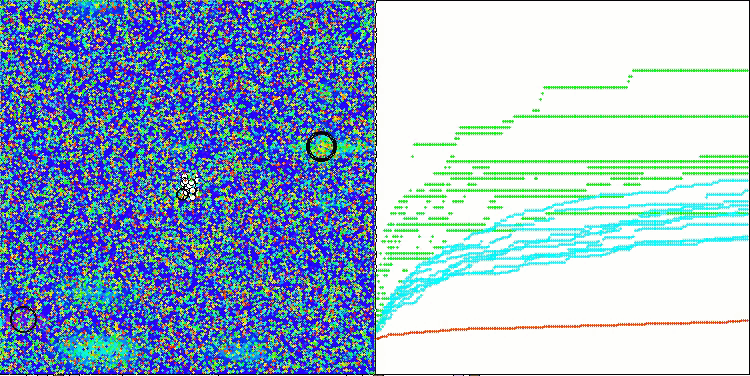
Megacityテスト関数のBCOm

テスト結果によると、このアルゴリズムは最適化アルゴリズムの総合ランキングで安定して17位を獲得しました。

# AO 詳細 Hilly Hilly最終 Forest Forest最終 Megacity（離散） Megacity最終 最終結果 MAXの%
10p(5F) 50p(25F) 1000p(500F) 10p(5F) 50p(25F) 1000p(500F) 10p(5F) 50p(25F) 1000p(500F)
1 ANS acrossneighbourhoodsearch 0.94948 0.84776 0.43857 2.23581 1.00000 0.92334 0.39988 2.32323 0.70923 0.63477 0.23091 1.57491 6.134 68.15
2 CLA コードロックアルゴリズム 0.95345 0.87107 0.37590 2.20042 0.98942 0.91709 0.31642 2.22294 0.79692 0.69385 0.19303 1.68380 6.107 67.86
3 AMOm 動物移動最適化m 0.90358 0.84317 0.46284 2.20959 0.99001 0.92436 0.46598 2.38034 0.56769 0.59132 0.23773 1.39675 5.987 66.52
4 (P+O)ES (P+O）進化戦略 0.92256 0.88101 0.40021 2.20379 0.97750 0.87490 0.31945 2.17185 0.67385 0.62985 0.18634 1.49003 5.866 65.17
5 CTA 彗尾アルゴリズム 0.95346 0.86319 0.27770 2.09435 0.99794 0.85740 0.33949 2.19484 0.88769 0.56431 0.10512 1.55712 5.846 64.96
6 SDSm 確率的拡散探索M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
7 ESG 社会母集団の進化 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
8 SIA 等方的焼きなまし 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
9 ACS 人工協調探索 0.75547 0.74744 0.30407 1.80698 1.00000 0.88861 0.22413 2.11274 0.69077 0.48185 0.13322 1.30583 5.226 58.06
10 ASO 無政府社会最適化 0.84872 0.74646 0.31465 1.90983 0.96148 0.79150 0.23803 1.99101 0.57077 0.54062 0.16614 1.27752 5.178 57.54
11 TSEA 亀甲進化アルゴリズム 0.96798 0.64480 0.29672 1.90949 0.99449 0.61981 0.22708 1.84139 0.69077 0.42646 0.13598 1.25322 5.004 55.60
12 DE 差分進化 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
13 CRO 化学反応の最適化 0.94629 0.66112 0.29853 1.90593 0.87906 0.58422 0.21146 1.67473 0.75846 0.42646 0.12686 1.31178 4.892 54.36
14 BSA 鳥群アルゴリズム 0.89306 0.64900 0.26250 1.80455 0.92420 0.71121 0.24939 1.88479 0.69385 0.32615 0.10012 1.12012 4.809 53.44
15 HS ハーモニー検索 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
16 SSG 苗木の播種と育成 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
17 BCOm 細菌走化性最適化M 0.75953 0.62268 0.31483 1.69704 0.89378 0.61339 0.22542 1.73259 0.65385 0.42092 0.14435 1.21912 4.649 51.65
18 (PO)ES (PO)進化戦略 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
19 TSm タブーサーチM 0.87795 0.61431 0.29104 1.78330 0.92885 0.51844 0.19054 1.63783 0.61077 0.38215 0.12157 1.11449 4.536 50.40
20 BSO ブレインストーム最適化 0.93736 0.57616 0.29688 1.81041 0.93131 0.55866 0.23537 1.72534 0.55231 0.29077 0.11914 0.96222 4.498 49.98
21 WOAm 鯨最適化アルゴリズムM 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
22 AEFA 人工電界アルゴリズム 0.87700 0.61753 0.25235 1.74688 0.92729 0.72698 0.18064 1.83490 0.66615 0.11631 0.09508 0.87754 4.459 49.55
23 ACOm 蟻コロニー最適化M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
24 BFO-GA 細菌採食の最適化：Ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
25 ABHA 人工蜂の巣アルゴリズム 0.84131 0.54227 0.26304 1.64663 0.87858 0.47779 0.17181 1.52818 0.50923 0.33877 0.10397 0.95197 4.127 45.85
26 ASBO 適応型社会行動最適化(ASBO) 0.76331 0.49253 0.32619 1.58202 0.79546 0.40035 0.26097 1.45677 0.26462 0.17169 0.18200 0.61831 3.657 40.63
27 MEC mindevolutionarycomputation 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
28 IWO 侵入雑草最適化 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
29 Micro-AIS 微小人工免疫系 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54
30 COAm カッコウ最適化アルゴリズムM 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21
31 SDOm 螺旋ダイナミクス最適化M 0.74601 0.44623 0.29687 1.48912 0.70204 0.34678 0.10944 1.15826 0.42833 0.16767 0.03663 0.63263 3.280 36.44
32 NMm ネルダー=ミード法M 0.73807 0.50598 0.31342 1.55747 0.63674 0.28302 0.08221 1.00197 0.44667 0.18667 0.04028 0.67362 3.233 35.92
33 FAm ホタルアルゴリズムM 0.58634 0.47228 0.32276 1.38138 0.68467 0.37439 0.10908 1.16814 0.28667 0.16467 0.04722 0.49855 3.048 33.87
34 GSA 重力探索法 0.64757 0.49197 0.30062 1.44016 0.53962 0.36353 0.09945 1.00260 0.32667 0.12200 0.01917 0.46783 2.911 32.34
35 BFO 細菌採餌最適化 0.61171 0.43270 0.31318 1.35759 0.54410 0.21511 0.05676 0.81597 0.42167 0.13800 0.03195 0.59162 2.765 30.72
36 ABC 人工蜂コロニー 0.63377 0.42402 0.30892 1.36671 0.55103 0.21874 0.05623 0.82600 0.34000 0.14200 0.03102 0.51302 2.706 30.06
37 BA コウモリアルゴリズム 0.59761 0.45911 0.35242 1.40915 0.40321 0.19313 0.07175 0.66810 0.21000 0.10100 0.03517 0.34617 2.423 26.93
38 AAA 藻類適応アルゴリズム 0.50007 0.32040 0.25525 1.07572 0.37021 0.22284 0.16785 0.76089 0.27846 0.14800 0.09755 0.52402 2.361 26.23
39 SA 焼きなまし 0.55787 0.42177 0.31549 1.29513 0.34998 0.15259 0.05023 0.55280 0.31167 0.10033 0.02883 0.44083 2.289 25.43
40 IWDm intelligentwaterdropsm 0.54501 0.37897 0.30124 1.22522 0.46104 0.14704 0.04369 0.65177 0.25833 0.09700 0.02308 0.37842 2.255 25.06
41 PSO 粒子群最適化 0.59726 0.36923 0.29928 1.26577 0.37237 0.16324 0.07010 0.60572 0.25667 0.08000 0.02157 0.35823 2.230 24.77
42 ボイド ボイドアルゴリズム 0.43340 0.30581 0.25425 0.99346 0.35718 0.20160 0.15708 0.71586 0.27846 0.14277 0.09834 0.51957 2.229 24.77
43 MA モンキーアルゴリズム 0.59107 0.42681 0.31816 1.33604 0.31138 0.14069 0.06612 0.51819 0.22833 0.08567 0.02790 0.34190 2.196 24.40
44 SFL shuffledfrog-leaping 0.53925 0.35816 0.29809 1.19551 0.37141 0.11427 0.04051 0.52618 0.27167 0.08667 0.02402 0.38235 2.104 23.38
45 FSS 魚群検索 0.55669 0.39992 0.31172 1.26833 0.31009 0.11889 0.04569 0.47467 0.21167 0.07633 0.02488 0.31288 2.056 22.84




まとめ

本稿では、BCOアルゴリズムのオリジナルバージョンと修正版を検討しました。オープンソースから再現したオリジナルバージョンは、三角関数に基づく複雑な計算により処理が重く、探索性能も弱く、さらに数学的な誤りが含まれていることが判明しました。これを受けて、アルゴリズム全体の再考と、探索戦略の綿密な分析、そして新たな修正版の設計が必要となりました。アルゴリズムロジックの見直しにより、各最適化ステップでの計算が簡略化され、コードの実行速度が向上しました。新しいアルゴリズムでは、新しい探索空間の開拓と、既に得られた有望な解の活用との間で、異なるバランスが取られています。

この新しいアプローチは、細菌の自然な行動とはやや異なるものの、実用上は高い効率性を示しました。アルゴリズムの動作を可視化した結果、ハイパースペース内の重要な領域を深く探索できる能力が確認され、探索性能の向上が示されました。その結果、修正版のアルゴリズムは、オリジナル版と比べて、より強力かつ効率的であることが明らかになりました。


Tab

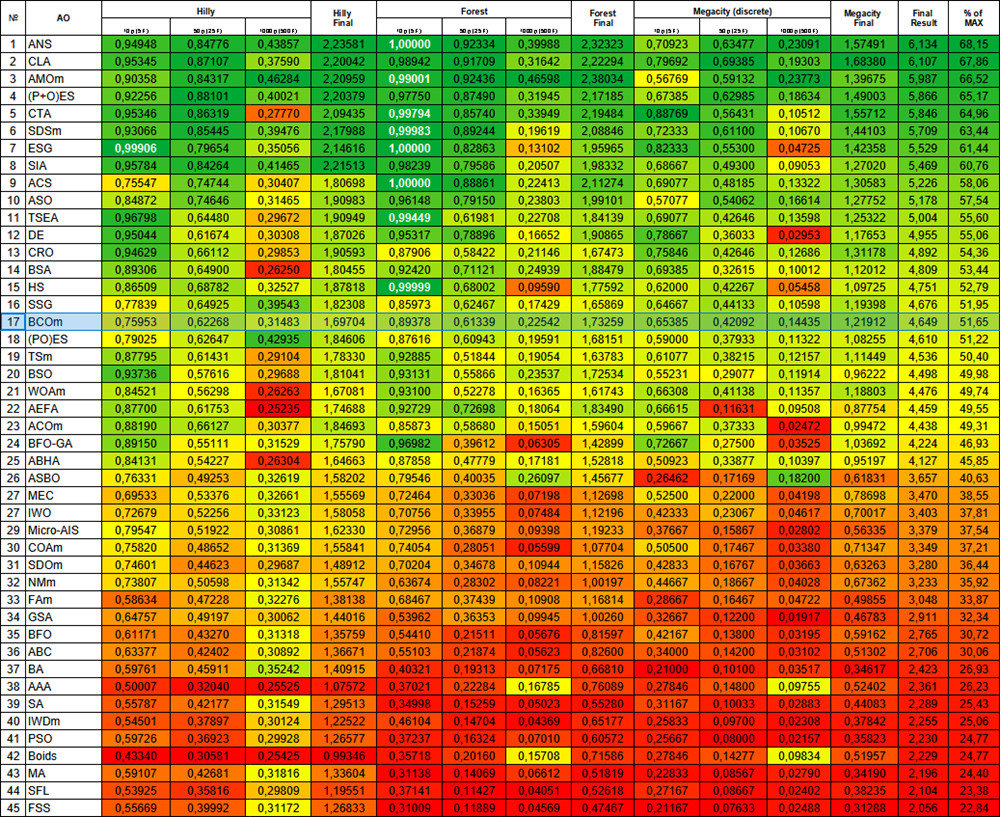
図1：アルゴリズムのテスト結果に応じた色分け： 該当するテストにおいて、結果が0.99以上の場合は白で強調表示される

チャート

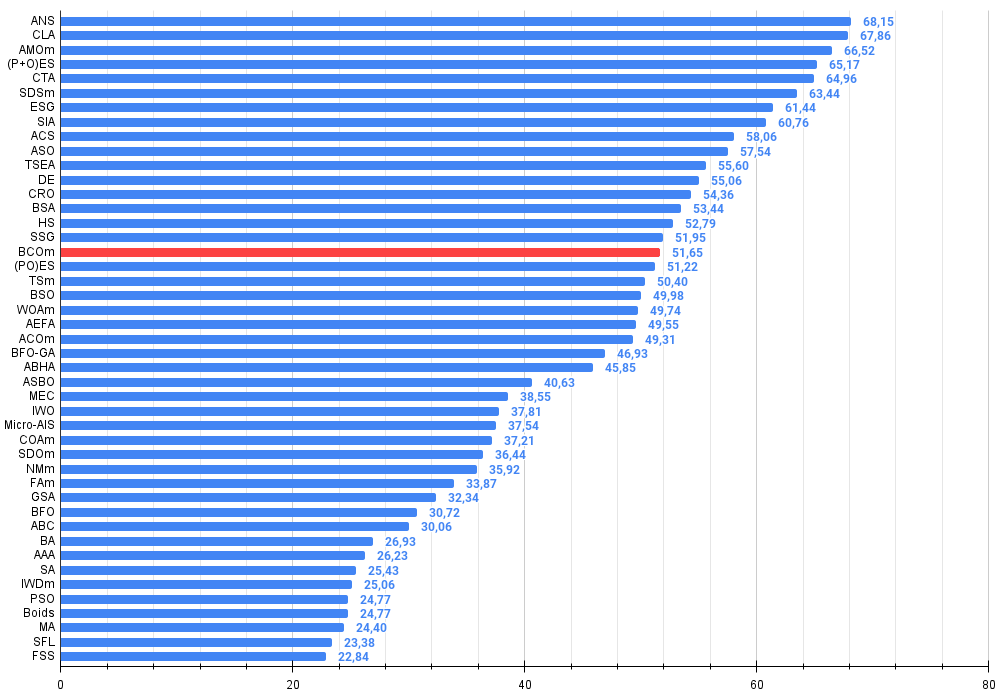
図2：アルゴリズムのテスト結果のヒストグラム（0から100までのスケールで、多ければ多いほど良い、

ここで、100は理論的に可能な最大の結果であり、アーカイブにはレーティングテーブルを計算するスクリプトが含まれている)


BCOmの長所と短所:

長所

  1. 迅速
  2. 自己適応。
  3. 優れたスケーラビリティ
  4. 外部パラメータは1つだけ

短所

  1. 低次元関数では結果の散布度が高くなる

この記事には、最新版のアルゴリズムコードを含むアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/15711

添付されたファイル |
ZIPをダウンロード
BCOm.zip (36.35 KB)
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動
リプレイシステムの開発（第63回）：サービスの再生(IV) リプレイシステムの開発（第63回）：サービスの再生(IV)
この記事では、1分足のティックシミュレーションに関する問題を最終的に解決し、実際のティックと共存できるようにします。これにより、将来的なトラブルを回避することが可能になります。ここで提示される資料は教育目的のみに使用されます。いかなる状況においても、提示された概念を学習し習得する以外の目的でアプリケーションを閲覧することは避けてください。
注文板に基づいた取引システムの開発（第1回）：インジケーター 注文板に基づいた取引システムの開発（第1回）：インジケーター
市場の厚みは、特に高頻度取引(HFT)アルゴリズムにおいて、高速な取引を実行するために不可欠な要素です。本連載では、多くの取引可能な銘柄に対してブローカー経由で取得できるこの種の取引イベントについて取り上げます。まずは、チャート上に直接表示されるヒストグラムのカラーパレット、位置、サイズをカスタマイズ可能なインジケーターから始めます。次に、特定の条件下でこのインジケーターをテストするためのBookEventイベントの生成方法について解説します。今後の記事では、価格分布データの保存方法や、そのデータをストラテジーテスターで活用する方法などのトピックも取り上げる予定です。
取引におけるニューラルネットワーク：点群の階層的特徴量学習 取引におけるニューラルネットワーク：点群の階層的特徴量学習
点群から特徴量を抽出するアルゴリズムの研究を続けます。この記事では、PointNet手法の効率を高めるメカニズムについて解説します。
取引におけるニューラルネットワーク：点群解析（PointNet） 取引におけるニューラルネットワーク：点群解析（PointNet）
直接的な点群解析は、不要なデータの増加を避け、分類やセグメンテーションタスクにおけるモデルの性能を向上させます。このような手法は、元データの摂動に対して高い性能と堅牢性を示します。