母集団最適化アルゴリズム：クジラ最適化アルゴリズム(WOA)

MetaTrader 5 — 例 | 27 8月 2024, 17:07

202

Andrey Dik

内容

1. はじめに
2. アルゴリズム
3. テスト結果

1. はじめに

ザトウクジラは雄大な海の巨人であり、海の支配者です。ザトウクジラが狩りのダンスを始めるとき、時間は止まっているように見えます。そのすべての動きは優雅さと正確さに満ちています。バブルネットの名手は、水のカーテンのような泡を作り、獲物を輪の中央に閉じ込めて集めます。このユニークな給餌法は、狩猟過程における彼らの知性と戦略的思考を強調します。

他の個体、さらには見知らぬ個体との行動の同期は、深い相互理解と団結を意味し、状況に関係なく集団で作業し調整する能力を示すものです。

1日に1.4トンもの餌を消費する彼らの能力は、海洋生態系における彼らの役割が、海洋で最も強力な消費者のひとつであることを強調するものです。豊かな狩猟期と平和な断食期を交互に繰り返す彼らの生活リズムは、彼らが君臨する海の偉大さと予測不可能さを物語っています。ザトウクジラがほとんど餌を食べない冬は、彼らの驚くべき生存能力の証拠となります。豊かな漁獲で蓄えた脂肪を頼りに、餌が乏しくなった期間を生き延びるのです。これは、自然がいかに動物たちに資源の節約と賢明な利用を教えるかを思い起こさせます。

ザトウクジラは生存と適応の生きた記録であり、知恵の象徴であり、海の力と美の体現であり、私たちに無尽蔵のインスピレーションを与えてくれます。

クジラ最適化アルゴリズムは、2016年にMirjaliliとLewisによって提案されたメタヒューリスティクス最適化アルゴリズムです。クジラの狩猟行動から着想を得たといいます。

クジラは「バブルネット」や「スパイラルペネトレーション」など、さまざまな狩猟戦略を用います。「バブルネット」では、クジラが獲物を取り囲むように泡の「網」を作り、獲物を混乱させ、怯えさせます。「スパイラルペネトレーション」とは、クジラが深海から獲物を捕獲するために螺旋状に上昇することです。

これらの狩猟戦略は、WOAアルゴリズムで抽象的にモデル化されました。WOAアルゴリズムでは、「クジラ」は最適化問題の解を表し、「狩猟」は最適解の探索を表します。

2. アルゴリズム

WOAアルゴリズムは、ランダムな位置を持つクジラの集団を初期化することから始まります。そして、リーダーが選択されます。目的関数の値が最も良いクジラ（実際には最適大域解）です。残りのクジラの位置は、リーダーの位置を考慮して更新されます。これは、探索モードと搾取モードの2つのモードで発生します。探索モードでは、クジラは現在の大域的最適解を中心にランダム探索をおこない、位置を更新します。搾取モードでは、クジラは自分の位置を更新し、現在の最適解に近づいていきます。

WOAアルゴリズムは、多くの最適化問題の解決に適用され、良好な結果を示しています。ただし、他の最適化アルゴリズムと同様、これにも長所と短所があります。例えば、局所最適に陥りやすく、収束速度が比較的遅い場合があります。

ザトウクジラに関する興味深い事実を、WOAアルゴリズムの原則と関連付ける方法を紹介しましょう。

協力と調整：ザトウクジラは群れで狩りをすることが多く、互いに協力し合って狩りを成功させます。これはWOAアルゴリズムの原理を彷彿とさせるもので、個々のエージェント（クジラ）が協力し、情報を交換し、最適解を得るために行動を調整します。

知能的な戦略：ザトウクジラは、バブルネットの形成や群れの連携など、さまざまな知的狩猟戦略を用います。WOAアルゴリズムは、最適解の発見や状況の変化への適応など、知能的な最適化戦略にも基づいています。

適応性と効率性：ザトウクジラは狩りの過程で適応性と効率性を発揮し、状況に応じて方法を変えます。WOAアルゴリズムはまた、様々な最適化戦略を適用し、より良い結果を得るために動作を修正することで、適応性と効率性を追求しています。

このように、WOAアルゴリズムはザトウクジラのユニークな狩猟戦略と行動からインスピレーションを得ており、様々な領域の最適化問題を効率的かつ知的に解くのに役立っています。

改良型WOAm (Whale Optimization Algorithm)最適化アルゴリズムには、いくつかの主要段階があります。

1. 大域解に向けた動き：
- アルゴリズムの初期段階では、各「クジラ」（解）は大域的最適解に向かって移動します。これは解空間を探索し、最適に向かう大まかな方向を見つけるのに役立ちます。

2. 自己の位置を向上させる：
- 各クジラは現在の位置を改善し、より良い解決策に近づこうとします。個体は、より良いパフォーマンスを達成するために、パラメータや戦略を変更することができます。

3. スパイラル運動：
- この段階は、WOAアルゴリズムの重要なメカニズムです。クジラは最適解の周りをらせん状に移動することができるため、探索空間をより効率的に探索し、最適解に近づくことができます。

4.移動：
- このステップでは、多様性を提供し、局所最適から抜け出せなくなるのを防ぐために、個体の位置をランダムに変更します。移動は、アルゴリズムが十分でない解に早期に収束するのを避けるのに役立ちます。

これらのステップを組み合わせることで、最適化問題の空間における最適解を効率的に探索することができます。アルゴリズムのスタックに対する耐性を向上させるため、第4ステージを追加して変更を加えました。野生のクジラが餌を求めて新たな領土へと移動するのをモデル化することは、以前の供給源が枯渇した場合に必要となります。この追加は、アルゴリズムにさらなる柔軟性を与え、自然界における生存戦略や適応戦略を反映して、より効率的に解空間を探索するのに役立ちます。

probab

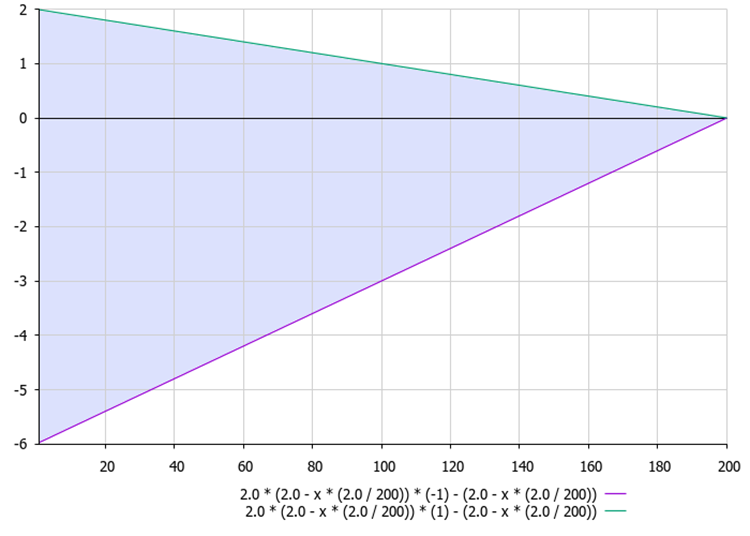
図1：現在のエポックによるA = 2.0 * aKo * r - aKoの式におけるA比の値の範囲

鯨探索最適化アルゴリズム(WOAm)の擬似コードは次の通りです。

1. ランダムな位置で集団を初期化します。
2. 適応度を計算します。
3. aKo比を計算します：aKo = 2.0 - epochNow * (2.0 / epochs)。
4. r乱数を-1から1の範囲の一様分布から生成します。
5. AとCの変数を計算します
   - A = 2.0 * aKo * r - aKo （図1）
   - C = 2.0 * r
6. spiralCoeff、一様分布からの乱数l、乱数確率pの値を設定します。
7. pがrefProbより小さい場合
   - Aの絶対値が1.0より大きい場合：X = Xbest - A * |Xbest - Xprev|
   - そうでなければ、leaderIndランダムインデックスを0からpopSizeの範囲で選択します：X = Xlead - A * |Xlead - Xprev|
8. それ以外の場合で、ランダム確率がspiralProbより小さい場合：X = Xprev + | Xprev - X| * exp (b * l) * cos (2 * M_PI * l)
9. その他の場合、X = PowerDistribution (cB [c], rangeMin [c], rangeMin [c], 30)
10. 適応度を計算します。
11. 大域解を更新します。
12. 停止基準が満たされるまで、ステップ3から繰り返します。

WOA

図2：WOA最適化アルゴリズムにインスピレーションを与えたクジラの「バブル」狩猟

次に、WOAmアルゴリズムのコードを書きましょう。

各クジラを記述する構造体S_WOA_Agent を定義します。ここで何が起こっているのかを見てみましょう。

1. この構造体には以下のフィールドが含まれます。
- cPrev[]：エージェントの前の座標を保存する配列
- fPrev：エージェントの前回の評価（適応度）を格納する変数

2. Init：S_WOA_Agent構造体メソッドで、構造体フィールドを初期化します。ArrayResize関数を使用してcPrev配列のサイズを変更するために使用されるcoords整数引数を取ります。

3. fPrev = -DBL_MAX：変数fPrevの初期値をdouble数値の可能な最小値に等しく設定します。

このコードは、WOAm最適化アルゴリズムにおけるエージェントの基本的なデータ構造体を表し、新しいエージェントが作成されたときにそのフィールドを初期化します。

//——————————————————————————————————————————————————————————————————————————————
struct S_WOA_Agent
{
    double cPrev []; //previous coordinates
    double fPrev;    //previous fitness

    void Init (int coords)
    {
      ArrayResize (cPrev, coords);
      fPrev = -DBL_MAX;
    }
};
//——————————————————————————————————————————————————————————————————————————————

WOAmアルゴリズムのC_AO_WOAmクラスを定義しましょう。このクラスはC_AO母集団アルゴリズムの基本クラスを継承し、以下のフィールドとメソッドを含んでいます。

1. publicフィールド

ao_name：最適化アルゴリズム名
ao_desc：最適化アルゴリズムの説明
popSize：母集団のサイズ
params：アルゴリズムのパラメータの配列
refProb：精製確率
spiralCoeff：スパイラル比
spiralProb：スパイラル確率
agent：エージェントのベクトル

2. オプション

C_AO_WOAm：クラスフィールドを初期化するクラスコンストラクタ
SetParams：アルゴリズムのパラメータを設定するメソッド
Init：アルゴリズムを初期化するメソッド（最小検索範囲と最大検索範囲、検索ステップ、エポック数を受け取る）
Moving：エージェントを移動させるメソッド
Revision：エージェントの改訂メソッド

3. privateフィールド

epochs：エポック数
epochNow：現在のエポック

//——————————————————————————————————————————————————————————————————————————————
class C_AO_WOAm : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_WOAm () { }
  C_AO_WOAm ()
  {
    ao_name = "WOAm";
    ao_desc = "Whale Optimization Algorithm M";

    popSize = 100;   //population size


    ArrayResize (params, 4);

    params [0].name = "popSize";     params [0].val = popSize;
    params [1].name = "refProb";     params [1].val = refProb;
    params [2].name = "spiralCoeff"; params [2].val = spiralCoeff;
    params [3].name = "spiralProb";  params [3].val = spiralProb;
  }

  void SetParams ()
  {
    popSize     = (int)params [0].val;
    refProb     = params      [1].val;
    spiralCoeff = params      [2].val;
    spiralProb  = params      [3].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  double refProb;     //refinement probability
  double spiralCoeff; //spiral coefficient
  double spiralProb;  //spiral probability


  S_WOA_Agent agent []; //vector

  private: //-------------------------------------------------------------------
  int  epochs;
  int  epochNow;
};
//——————————————————————————————————————————————————————————————————————————————

C_AO_WOAmクラスのInitメソッドは、渡されたパラメータに基づいてクラス変数を初期化するために使用されます。このメソッドは、StandardInitメソッドを使用して標準的な初期化をおこない、最小検索範囲と最大検索範囲、検索ステップを受け取ります。

標準的な初期化が成功した場合、メソッドはepochs変数とepochNow変数の初期化を続けます。epochsの値は、パラメータとして渡されたepochsPに設定され、epochNowは0に初期化されます。

このメソッドは、agent配列をpopSizeサイズにリサイズします。Initメソッドは、agentの各要素に対してcoordsパラメータを指定して呼び出されます。

このメソッドは、初期化に成功すればtrueを返し、そうでなければfalseを返します。

このメソッドは、与えられたパラメータでWOAm最適化アルゴリズムの初期設定をおこない、与えられたエポック数の最適化を実行する準備をします。

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_WOAm::Init (const double &rangeMinP  [], //minimum search range
                     const double &rangeMaxP  [], //maximum search range
                     const double &rangeStepP [], //step search
                     const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  epochs   = epochsP;
  epochNow = 0;

  ArrayResize (agent, popSize);
  for (int i = 0; i < popSize; i++) agent [i].Init (coords);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_WOAmクラスのMovingメソッドは、最適化中にエージェントを移動させるために使用されます。このメソッドは次をおこないます。

epochNow++;：現在のエポック値が増加します

if (!revision)：revisionがfalseであるかどうかをチェックします。

もしrevisionがfalseなら

エージェントの座標 a[i].c[c]は、指定された範囲のランダムな値を用いて初期化されます。
revisionフラグがtrueに設定されます。
メソッドはその仕事を完了します。

もしrevisionがfalseでないなら

各エージェントについて、ある方程式と確率を用いて新しい座標が計算されます。
エージェントの新しい座標を決定するために、さまざまな数学的計算、乱数、確率が使用されます。
新しいx座標は、条件と確率に従って計算されます。
新しい座標a[i].c[c]は、検索範囲とステップに従って値を調整するためにSeInDiSpメソッドを使用して設定されます。

このメソッドは、WOAm最適化アルゴリズムにおいて、現在のエポック、ランダム値、確率に従ってエージェントの座標を更新する役割を担います。クジラのさまざまな行動パターンを説明するコードの該当箇所を色分けしてみましょう。

大域解の改善：新しいエポックごとに、クジラは線形則と計算されたA比に従って、発見された大域解の近傍をより注意深く探索し、大域的最適解に近づこうとします。

母集団「リーダー」の周辺の探索：A比を考慮して、クジラは一様分布法則に従って無作為に選ばれた集団「リーダー」の周辺を探索します。そのため、クジラが生息しているすべての地域で調査が続けられています。

スパイラル運動と「バブル」ネットワーク:クジラは、個々の最適な位置と現在地を考慮しながら、らせん状に移動します。これにより、魚が密集して集まり、餌が一か所に集中します。

クジラの回遊：クジラの回遊は、べき法則大域的最適解から突然離れることによってシミュレートされます。このプロセスによって、大域解の近傍にいる確率は高く、大域解から非常に離れている確率は小さいがゼロではないことが決定されます。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_WOAm::Moving ()
{
  epochNow++;

  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      double aKo = 2.0 - epochNow * (2.0 / epochs);
      double r = u.RNDfromCI (-1, 1);
      double A = 2.0 * aKo * r - aKo;
      double C = 2.0 * r;
      double b = spiralCoeff;
      double l = u.RNDfromCI (-1, 1);
      double p = u.RNDprobab ();
      double x;

      if (p < refProb)
      {
        if (MathAbs (A) > 1.0)
        {
          x = cB [c] - A * MathAbs (cB [c] - agent [i].cPrev [c]);                                                      //Xbest - A * |Xbest - X|
        }
        else
        {
          int leaderInd = u.RNDminusOne (popSize);
          x = agent [leaderInd].cPrev [c] - A * MathAbs (agent [leaderInd].cPrev [c] - agent [i].cPrev [c]);            //Xlid - A * |Xlid - X|;
        }
      }
      else
      {
        if (u.RNDprobab () < spiralProb)
        {
          x = agent [i].cPrev [c] + MathAbs (agent [i].cPrev [c] - a [i].c [c]) * MathExp (b * l) * cos (2 * M_PI * l); //XbestPrev + |XbestPrev - X| * MathExp (b * l) * cos (2 * M_PI * l)
        }
        else
        {
          x = u.PowerDistribution (cB [c], rangeMin [c], rangeMin [c], 30);
        }
      }

      a [i].c [c] = u.SeInDiSp (x, rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_WOAmクラスのRevisionメソッドは、大域的最適解の更新とクジラ自身の最適位置の更新に使用されます。このメソッドは次をおこないます。

1. 大域解を更新する：forループの中で、メソッドはすべての個体を繰り返し処理します。現在の個体の適応度関数の値が、適応度関数の現在の最適値を超えている場合、最適値が更新され、現在の個体の座標の配列が最適解の座標の配列にコピーされます。

2. 以前の適応度関数の値とエージェントの座標を更新します。forループの中で、メソッドはすべての個体を繰り返し処理します。もし現在の個体の適応度関数がエージェントの適応度関数の前の値を超えていれば、適応度関数の前の値が更新され、現在の個体の座標の配列がエージェントの前の座標の配列にコピーされます。

Revisionメソッドは、WOAm最適化アルゴリズムの一部として、以前の特徴量値とエージェント座標を更新するだけでなく、その特徴量値に基づいて最適なエージェントを更新する役割を担っています。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_WOAm::Revision ()
{
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB) ind = i;
  }

  if (ind != -1)
  {
    fB = a [ind].f;
    ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);
  }

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > agent [i].fPrev)
    {
      agent [i].fPrev = a [i].f;
      ArrayCopy (agent [i].cPrev, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

3. テスト結果

著者によって提案されたアルゴリズムの基本バージョンは、残念ながら、以下に示すような比較的弱い結果を示し、大いに不満が残ります。

WOA|Whale Optimization Algorithm|100.0|0.1|0.5|0.8|
=============================
5 Hilly's; Func runs:10000; result:0.45323929163422483
25 Hilly's; Func runs:10000; result:0.3158990997230676
500 Hilly's; Func runs:10000; result:0.25544320870775555
=============================
5 Forest's; Func runs:10000; result:0.43485195446891795
25 Forest's; Func runs:10000; result:0.2454326019188397
500 Forest's; Func runs:10000; result:0.1557433572339264
=============================
5 Megacity's; Func runs:10000; result:0.3400000000000001
25 Megacity's; Func runs:10000; result:0.18800000000000003
500 Megacity's; Func runs:10000; result:0.10146153846153938
=============================
All score:2.49007 (27.67%)

しかし、努力と創意工夫によって、移動やべき乗分布などの要素を含め、大幅な改善がなされました。さらに、クジラの現在位置を出発点として次の位置を計算する代わりに、過去の最良のクジラの位置が使用されるようになりました。これらの修正によってアルゴリズムが変化し、新たな品質が与えられ、修正版の結果が大幅に改善されました。こうして、アルゴリズムはより効率的になり、与えられた問題を解く上でより大きな成功を収めることができるようになりました。

以下はWOAmの改良版で、22%以上の改善が見られた結果です（0%は可能な限り最悪の結果、100%は達成可能な最高の理論結果）。

WOAm|Whale Optimization Algorithm|100.0|0.1|0.5|0.8|
=============================
5 Hilly's; Func runs:10000; result:0.8452089588169466
25 Hilly's; Func runs:10000; result:0.562977678943021
500 Hilly's; Func runs:10000; result:0.262626056156147
=============================
5 Forest's; Func runs:10000; result:0.9310009723200832
25 Forest's; Func runs:10000; result:0.5227806126625986
500 Forest's; Func runs:10000; result:0.1636489301696601
=============================
5 Megacity's; Func runs:10000; result:0.6630769230769229
25 Megacity's; Func runs:10000; result:0.41138461538461535
500 Megacity's; Func runs:10000; result:0.11356923076923182
=============================
All score:4.47627 (49.74%)

修正版操作の可視化では、Hilly関数では結果のばらつきが大きく、離散Megacityではばらつきが小さいことがわかります。通常、ほとんどのアルゴリズムにおいて、Megacity関数はより複雑で、結果のばらつきが大きいことに注意することは興味深いです。さらに驚くべきことに、WOAmはこの関数で非常に安定した良好な結果を示しています。

このアルゴリズムは、探索空間の様々な領域で局所的な表面領域を探索し、有望な方向性を強調することに成功しています。これは、個体群の一般的な群れ行動を個々の動物の行動段階に分割することで、各クジラの状況を個々に改善することを目的としています。

このアプローチにより、アルゴリズムは、パック内の個々のエージェントのポジションを向上させることに焦点を当てながら、最適解の探索空間を効果的に探索することができます。これにより、潜在的に有望な領域をより正確かつ詳細に探索することが容易になり、ひいてはアルゴリズム全体のパフォーマンスが向上します。

基本版は、この可視化では表示されていません。さらに、Ackleyテスト関数に対するアルゴリズムの動作の可視化も提供されています。この関数は評価表の計算には関与しません。

Hilly

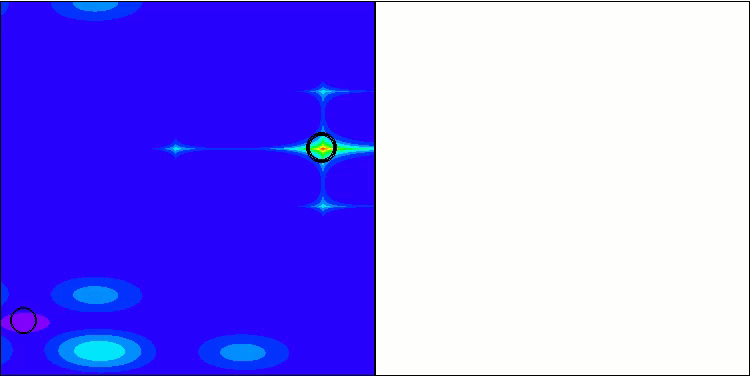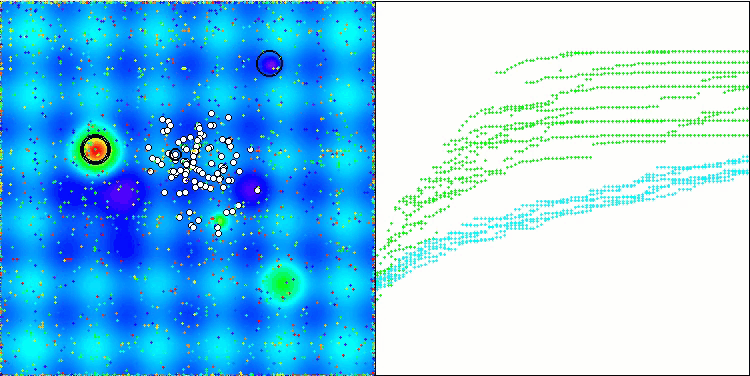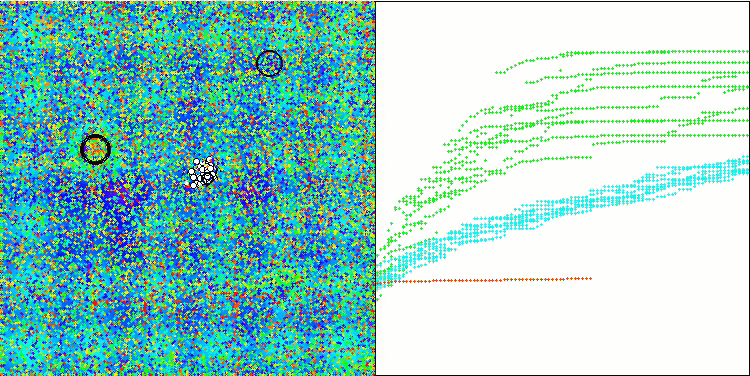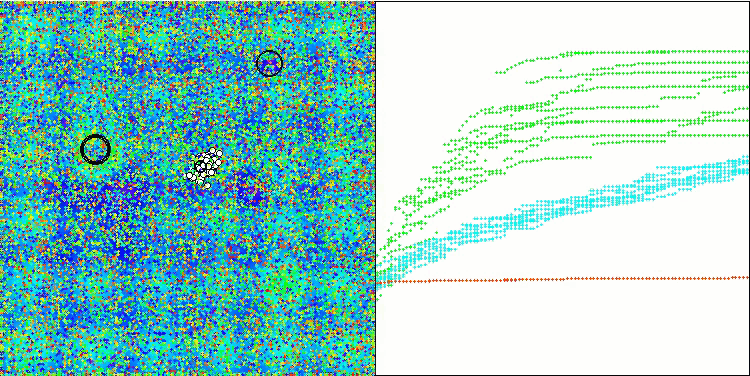
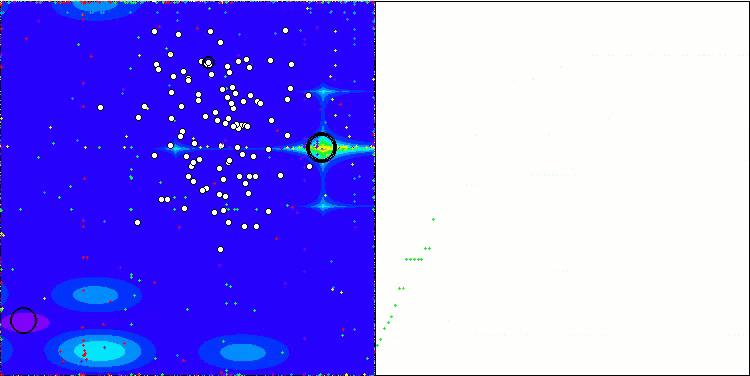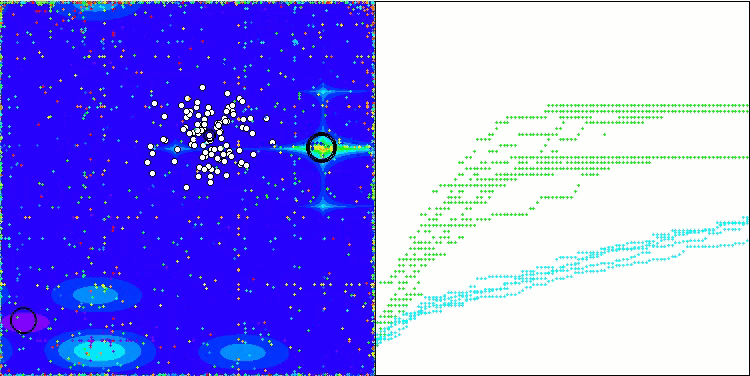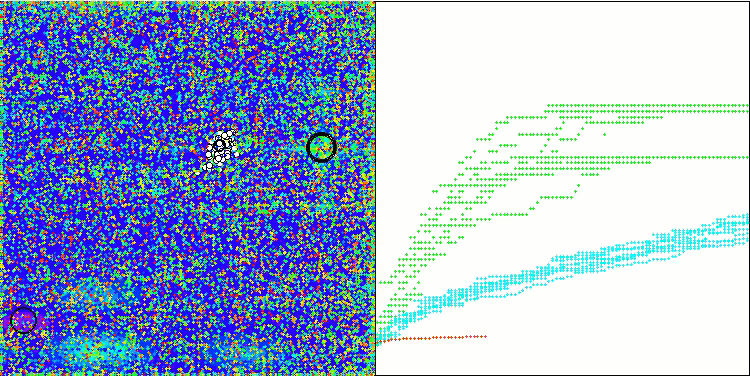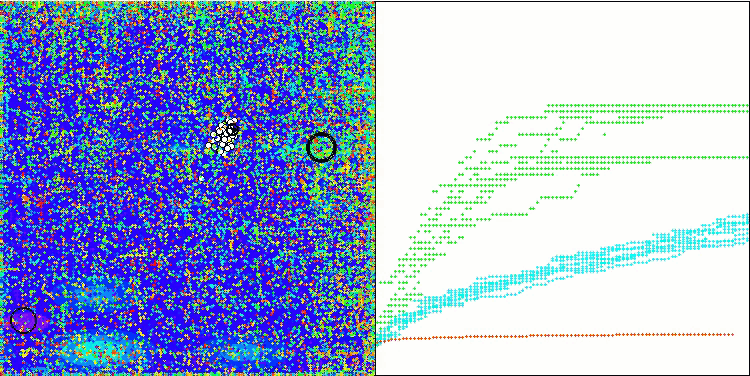
Hillyテスト関数のWOAm

Forest

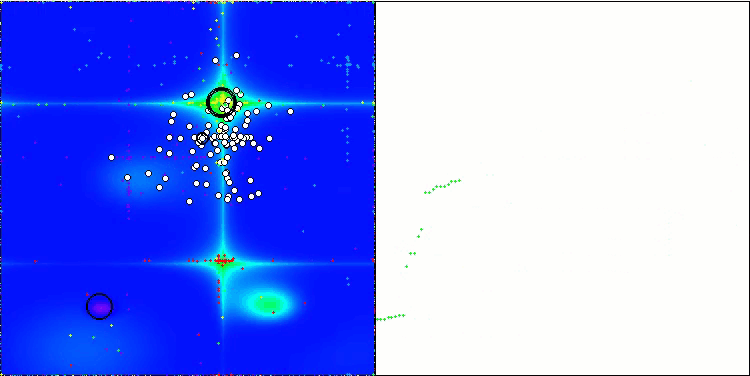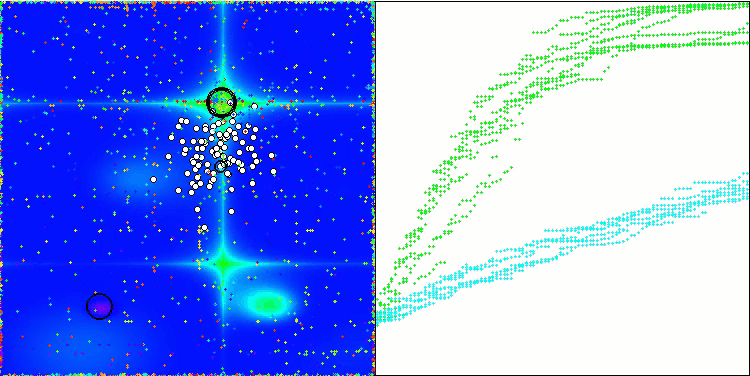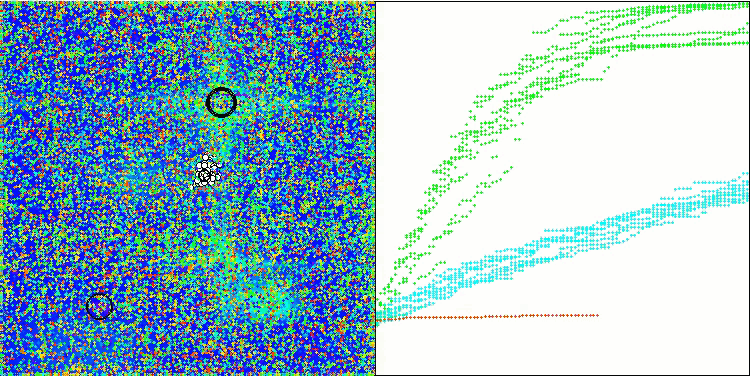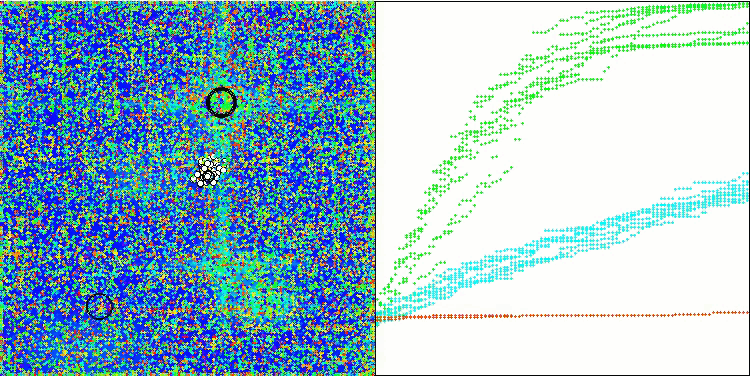
Forestテスト関数のWOAm

Megacity

Megacityテスト関数のWOAm

Ackley

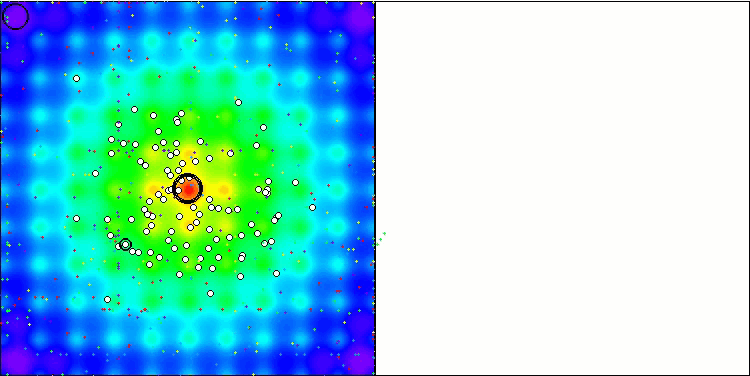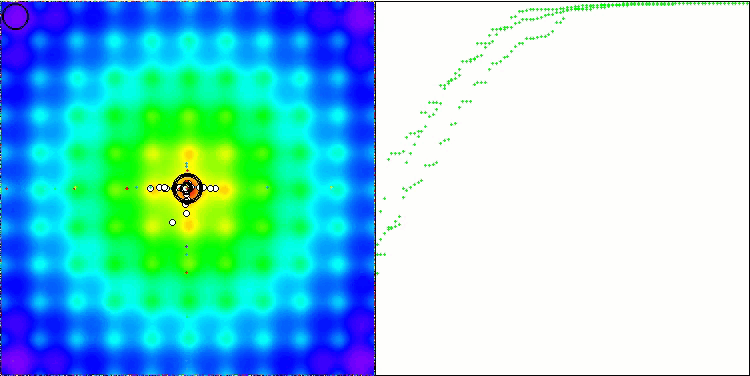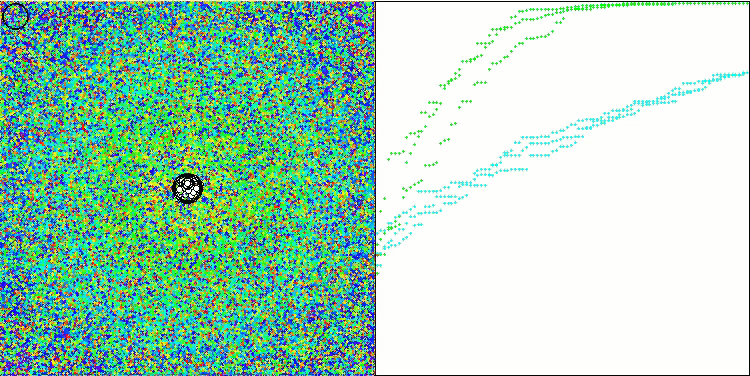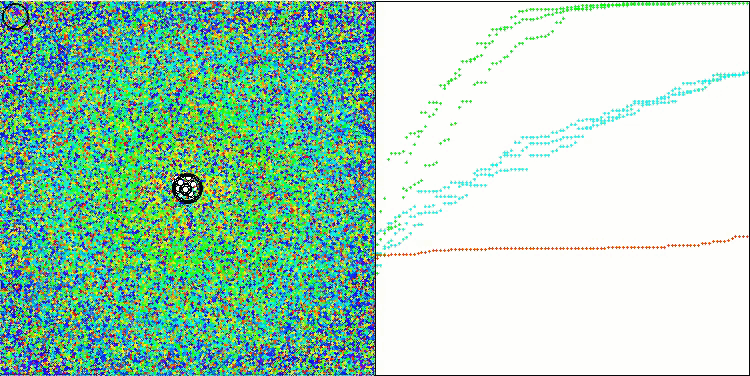
Ackleyテスト関数のWOAm

修正WOAmアルゴリズムは、上位10位という栄誉に輝き、良好で安定した総合結果を示しました。

#	AO	詳細	Hilly			Hilly最終	Forest			Forest最終	Megacity（離散）			Megacity最終	最終結果	MAXの%
#	AO	詳細	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Hilly最終	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Forest最終	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Megacity最終	最終結果	MAXの%
1	BGA	バイナリ遺伝的アルゴリズム	0.99992	0.99484	0.50483	2.49959	1.00000	0.99975	0.32054	2.32029	0.90667	0.96400	0.23035	2.10102	6.921	76.90
2	(P+O)ES	(P+O）進化戦略	0.99934	0.91895	0.56297	2.48127	1.00000	0.93522	0.39179	2.32701	0.83167	0.64433	0.21155	1.68755	6.496	72.18
3	SDSm	確率的拡散探索M	0.93066	0.85445	0.39476	2.17988	0.99983	0.89244	0.19619	2.08846	0.72333	0.61100	0.10670	1.44103	5.709	63.44
4	ESG	社会集団の進化	0.99906	0.79654	0.35056	2.14616	1.00000	0.82863	0.13102	1.95965	0.82333	0.55300	0.04725	1.42358	5.529	61.44
5	SIA	等方的焼きなまし	0.95784	0.84264	0.41465	2.21513	0.98239	0.79586	0.20507	1.98332	0.68667	0.49300	0.09053	1.27020	5.469	60.76
6	DE	差分進化	0.95044	0.61674	0.30308	1.87026	0.95317	0.78896	0.16652	1.90865	0.78667	0.36033	0.02953	1.17653	4.955	55.06
7	HS	ハーモニー検索	0.86509	0.68782	0.32527	1.87818	0.99999	0.68002	0.09590	1.77592	0.62000	0.42267	0.05458	1.09725	4.751	52.79
8	SSG	苗木の播種と育成	0.77839	0.64925	0.39543	1.82308	0.85973	0.62467	0.17429	1.65869	0.64667	0.44133	0.10598	1.19398	4.676	51.95
9	(PO)ES	(PO）進化戦略	0.79025	0.62647	0.42935	1.84606	0.87616	0.60943	0.19591	1.68151	0.59000	0.37933	0.11322	1.08255	4.610	51.22
10	WOAm	鯨最適化アルゴリズム M	0.84521	0.56298	0.26263	1.67081	0.93100	0.52278	0.16365	1.61743	0.66308	0.41138	0.11357	1.18803	4.476	49.74
11	ACOm	蟻コロニー最適化M	0.88190	0.66127	0.30377	1.84693	0.85873	0.58680	0.15051	1.59604	0.59667	0.37333	0.02472	0.99472	4.438	49.31
12	BFO-GA	細菌採食の最適化：Ga	0.89150	0.55111	0.31529	1.75790	0.96982	0.39612	0.06305	1.42899	0.72667	0.27500	0.03525	1.03692	4.224	46.93
13	MEC	Mind Evolutionary Computation	0.69533	0.53376	0.32661	1.55569	0.72464	0.33036	0.07198	1.12698	0.52500	0.22000	0.04198	0.78698	3.470	38.55
14	IWO	侵入雑草最適化	0.72679	0.52256	0.33123	1.58058	0.70756	0.33955	0.07484	1.12196	0.42333	0.23067	0.04617	0.70017	3.403	37.81
15	Micro-AIS	微小人工免疫系	0.79547	0.51922	0.30861	1.62330	0.72956	0.36879	0.09398	1.19233	0.37667	0.15867	0.02802	0.56335	3.379	37.54
16	COAm	カッコウ最適化アルゴリズムM	0.75820	0.48652	0.31369	1.55841	0.74054	0.28051	0.05599	1.07704	0.50500	0.17467	0.03380	0.71347	3.349	37.21
17	SDOm	螺旋ダイナミクス最適化M	0.74601	0.44623	0.29687	1.48912	0.70204	0.34678	0.10944	1.15826	0.42833	0.16767	0.03663	0.63263	3.280	36.44
18	NMm	ネルダー=ミード法M	0.73807	0.50598	0.31342	1.55747	0.63674	0.28302	0.08221	1.00197	0.44667	0.18667	0.04028	0.67362	3.233	35.92
19	FAm	ホタルアルゴリズムM	0.58634	0.47228	0.32276	1.38138	0.68467	0.37439	0.10908	1.16814	0.28667	0.16467	0.04722	0.49855	3.048	33.87
20	GSA	重力探索法	0.64757	0.49197	0.30062	1.44016	0.53962	0.36353	0.09945	1.00260	0.32667	0.12200	0.01917	0.46783	2.911	32.34
21	BFO	細菌採餌の最適化	0.61171	0.43270	0.31318	1.35759	0.54410	0.21511	0.05676	0.81597	0.42167	0.13800	0.03195	0.59162	2.765	30.72
22	ABC	人工蜂コロニー	0.63377	0.42402	0.30892	1.36671	0.55103	0.21874	0.05623	0.82600	0.34000	0.14200	0.03102	0.51302	2.706	30.06
23	BA	コウモリアルゴリズム	0.59761	0.45911	0.35242	1.40915	0.40321	0.19313	0.07175	0.66810	0.21000	0.10100	0.03517	0.34617	2.423	26.93
24	SA	焼きなまし	0.55787	0.42177	0.31549	1.29513	0.34998	0.15259	0.05023	0.55280	0.31167	0.10033	0.02883	0.44083	2.289	25.43
25	IWDm	intelligent water drops M	0.54501	0.37897	0.30124	1.22522	0.46104	0.14704	0.04369	0.65177	0.25833	0.09700	0.02308	0.37842	2.255	25.06
26	PSO	粒子群最適化	0.59726	0.36923	0.29928	1.26577	0.37237	0.16324	0.07010	0.60572	0.25667	0.08000	0.02157	0.35823	2.230	24.77
27	MA	モンキーアルゴリズム	0.59107	0.42681	0.31816	1.33604	0.31138	0.14069	0.06612	0.51819	0.22833	0.08567	0.02790	0.34190	2.196	24.40
28	SFL	Shuffled Frog-Leaping	0.53925	0.35816	0.29809	1.19551	0.37141	0.11427	0.04051	0.52618	0.27167	0.08667	0.02402	0.38235	2.104	23.38
29	FSS	魚群検索	0.55669	0.39992	0.31172	1.26833	0.31009	0.11889	0.04569	0.47467	0.21167	0.07633	0.02488	0.31288	2.056	22.84
30	RND	ランダム	0.52033	0.36068	0.30133	1.18234	0.31335	0.11787	0.04354	0.47476	0.25333	0.07933	0.02382	0.35648	2.014	22.37
31	GWO	灰色オオカミオプティマイザ	0.59169	0.36561	0.29595	1.25326	0.24499	0.09047	0.03612	0.37158	0.27667	0.08567	0.02170	0.38403	2.009	22.32
32	CSS	荷電系探索	0.44252	0.35454	0.35201	1.14907	0.24140	0.11345	0.06814	0.42299	0.18333	0.06300	0.02322	0.26955	1.842	20.46
33	EM	電磁気学的アルゴリズム	0.46250	0.34594	0.32285	1.13129	0.21245	0.09783	0.10057	0.41085	0.15667	0.06033	0.02712	0.24412	1.786	19.85

まとめ

全体として、この記事で紹介したようにこのアルゴリズムが改善されたことに満足しています。しかし、このバージョンを修正するためのより深い研究があり、このトピックに情熱を持ち、さらなる実験に意欲的な人にとっては、検討する価値があります。これらのテクニックに飛び込むことで、新たな地平が開かれ、与えられたアルゴリズムに対するさらに優れた解決策がひらめくかもしれません。

ここでは、クジラ探索最適化アルゴリズム(WOA)を改善し、局所的な極端さで立ち往生する可能性を減らすのに役立ついくつかの戦略を紹介します。

1. 母集団の多様化：母集団の多様性は、局所最適にはまり込むことを避けるのに役立ちます。突然変異、交叉、解の近傍研究などのメカニズムなど、集団の多様性を維持するための方法を検討します。

2.エリート戦略：この戦略では、世代ごとにいくつかの異なる最適解（エリート）を維持することで、集団の多様性の低下を回避します。

3. マルチ戦略メカニズム：このアプローチでは、複数の探索戦略を同時に使用することで、アルゴリズムが解空間をより良く探索し、局所的な落とし穴を回避することができます。

4. 他のアルゴリズムとのハイブリッド化：WOAを他の最適化アルゴリズムとハイブリッド化することによっても、その性能を向上させることができます。例えば、アルゴリズムの探索段階を改善するために、差分進化や粒子群を使用することができます。

tab

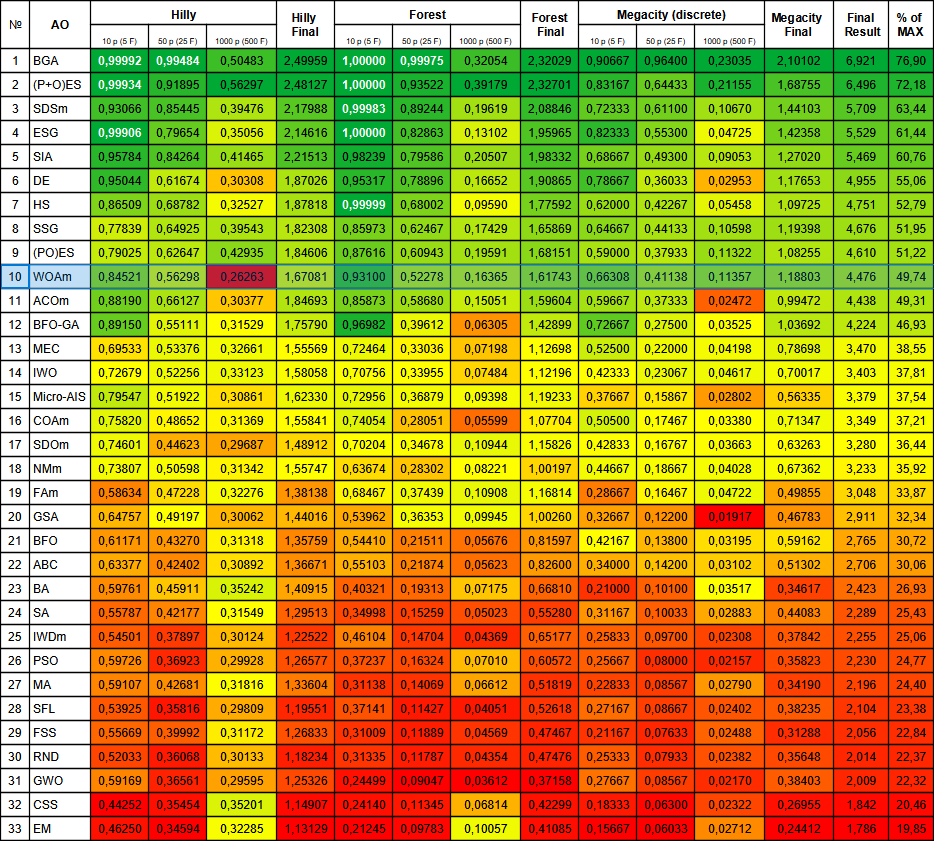
図3：関連テストに応じたアルゴリズムのカラーグラデーション0.99以上の結果は白で強調表示

1000個の変数を持つ滑らかなHilly関数の値セルの色は注目すべきもので、この結果は表に示したすべてのアルゴリズムの中で最悪であることを示しています。また、5つの変数を持つForest関数の高いパフォーマンス指標と、Forest関数とMegacity関数の概ね良好なパフォーマンスにも注目するべきです。

チャート

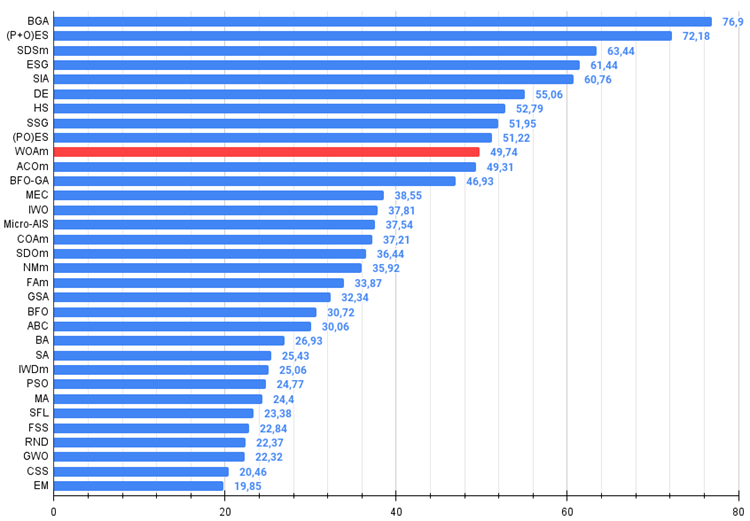
図4：アルゴリズムのテスト結果のヒストグラム（0から100までのスケールで、多ければ多いほど良いです。

ここで、100は理論的に可能な最大の結果であり、アーカイブにはレーティング表を計算するスクリプトが含まれている)

WOAmの長所と短所

長所

シンプルなアーキテクチャと実装
シャープForest関数と離散Megacityに関する安定した良好な結果
コンピューティングリソースに負荷をかけない

短所

収束性が低い（100%に近い結果が得られない）
Hillyのような滑らかな関数ではスケーラビリティが低い（高次元タスクの問題）

この記事には、最新版のアルゴリズムコードを含むアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/14414

添付されたファイル |

ZIPをダウンロード

WOAm.zip (24.34 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動

MQL5でインタラクティブなグラフィカルユーザーインターフェイスを作成する（第1回）：パネルの製作

この記事では、MetaQuotes Language 5 (MQL5)を使用して、グラフィカルユーザーインターフェイス(GUI)パネルを作成し、実装するための基本的な手順について説明します。カスタムユーティリティパネルは、一般的なタスクを簡素化し、重要な取引情報を可視化することで、取引におけるユーザーのインタラクションを向上させます。カスタムパネルを作成することで、トレーダーはワークフローを合理化し、取引操作の時間を節約することができます。

知っておくべきMQL5ウィザードのテクニック（第25回）：多時間枠のテストと取引

アセンブリクラスで使用されているMQL5コードアーキテクチャの制限によって、複数の時間枠に基づく戦略は、デフォルトではウィザードで組み立てられたEAではテストできません。今回は、二次移動平均を使用したケーススタディで、複数の時間枠を使用する戦略について、この制限を回避する可能性を探ります。

PatchTST機械学習アルゴリズムによる24時間の値動きの予測

この記事では、PatchTSTと呼ばれる2023年にリリースされた比較的複雑なニューラルネットワークアルゴリズムを適用し、今後24時間の値動きを予測します。公式リポジトリを使用し、若干の修正を加え、EURUSDのモデルを訓練し、PythonとMQL5の両方で将来の予測をおこなうために適用します。

Candlestick Trend Constraintモデルの構築（第5回）：通知システム（パート3）

本稿ではWhatsAppとMetaTrader 5を統合して通知する方法を紹介します。理解を容易にするためにフローチャートを掲載し、統合におけるセキュリティ対策の重要性について説明します。指標の主な目的は、自動化によって分析を簡素化することであり、特定の条件が満たされたときにユーザーに警告するための通知方法を含むべきです。詳しくは本稿で説明します。