MetaTrader 5 / 例
English Русский 中文 Español Deutsch Português
preview
彗尾アルゴリズム(CTA)

彗尾アルゴリズム(CTA)

MetaTrader 5 — 例 | 16 10月 2024, 10:18
127 0
Andrey Dik
Andrey Dik

内容

1. はじめに
2. アルゴリズムの実装
3.テスト結果


1. はじめに

天文学の世界において、彗星は常に科学者や研究者の特別な関心を集めてきました。主に氷、塵、ガスからなるこれらのユニークな宇宙天体は、宇宙空間で起こるプロセスに関する重要な情報源です。彗星の最も顕著で印象的な特徴の1つは、太陽に接近する際に形成される尾です。

太陽は彗星の尾の形成において重要な役割を果たしています。太陽からの放射線と太陽風は、彗星表面の物質の蒸発と破壊を引き起こし、このプロセスが、太陽風や太陽の重力によって彗星から押し流される塵、ガス、電離粒子から成る彗星の尾の形成につながります。

この記事では、このユニークな天文現象に着想を得たCTA（彗尾アルゴリズム）最適化アルゴリズムについて考察します。CTAアルゴリズムは、彗星の運動とその尾の概念を利用して、最適化問題の最適解を見つけ出します。彗星とその尾の動き、さらにはこれらの過程における太陽の役割について詳しく探求し、これらの概念がどのようにCTAアルゴリズムに適用され、効果的に最適解を導き出すかについても議論します。

彗星は太陽系内の小天体で、太陽に近づくと蒸発し、ガスを放出します。このプロセスは「昇華」と呼ばれます。彗星は通常、楕円形の軌道を描き、その軌道周期は数年から数百万年と幅広いものです。

彗星とその尾の動きは、太陽の影響と密接に関連しています。太陽の熱によって彗星の氷が気体に変わり、コマ（彗星核を取り囲む気体の甲羅）が膨張します。太陽放射と高速の太陽粒子（太陽風）による圧力は、コマの塵やガスを太陽から吹き飛ばし、時には長く明るい尾を形成します。さらに、太陽放射と太陽風によって彗星の尾のガスが電離し、光を放ちます。

CTAアルゴリズムの文脈においては、各解を解空間を移動する彗星の尾の粒子と捉えることができます。彗星の核は最良解を表し、尾部の粒子は核から放出される解の誘導体です。この表現により、アルゴリズムは解空間を「学習」し、その特徴に適応することが可能となります。


2. アルゴリズムの実装

このアルゴリズムの重要な要素である彗星とその尾の動き、そしてこれらのプロセスにおける太陽の役割を詳しく見てみましょう。

彗星の動き

  • 彗星は太陽の周りを楕円軌道で回っています。
  • 太陽に近づくと、彗星はガスと塵を放出し始め、彗星の尾を形成します。
  • 彗星の運動は、太陽の引力、太陽風、そして太陽放射による斥力によって決定されます。
  • 彗星は軌道に沿って移動し、その尾は常に太陽と反対方向を向いています。

彗星の尾の動き

  • 彗星のガス尾は、太陽風によって彗星核から「投げ出された」電離ガスで構成されています。
  • 太陽風は、太陽から放出される荷電粒子の流れであり、これが彗星のガスの尾を「吹き飛ばし」、太陽と反対方向に向ける要因となります。
  • 一方、彗星の塵の尾は、太陽放射によって彗星核から「投げ出された」大きな粒子で構成されています。
  • 太陽放射は塵の粒子に圧力をかけ、彗星の進行方向からわずかに偏らせることで湾曲した塵の尾を形成します。

太陽の役割

  • 太陽は彗星が公転する軌道の中心天体です。
  • 太陽の引力によって、彗星は楕円軌道に沿って運動します。
  • 太陽風と太陽放射は彗星の尾を「形作り」、太陽と反対方向に向ける役割を果たします。

    彗星

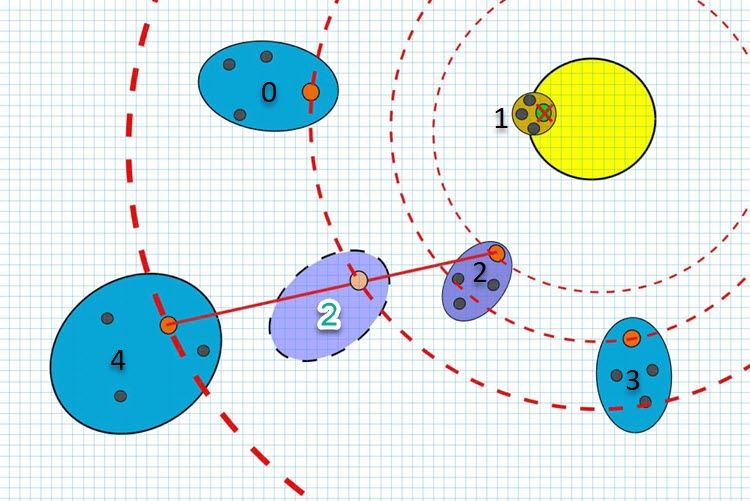
    図1：CTAアルゴリズムにおける彗星の形状とサイズの恒星までの距離の関数（最良大域解）

    図1は、このアルゴリズムにおける彗星の特性を示しています。それぞれの彗星は、配列のインデックスに対応する固有の番号を持っています。図は、恒星に対する彗星の条件付き軌道を示しており、恒星からの距離が長くなるにつれて、彗星の尾は長くなり、球形に近い形状をとります。同時に、尾部粒子の雲は彗星核との相対的な位置関係が小さくなります。彗星が恒星に近づくほど、尾の確率領域は小さくなり、細長くなります。


    彗星1は太陽に近づきすぎて蒸発しましたが、アルゴリズムでは彗星の破壊は実際には起こりません。代わりに、恒星の中心に対応する中心を持つ尾雲の形成が続きます。これは、尾雲が小さくなるほど、彗星の領域での解の精密化がより集中的におこなわれることを意味します。逆に、尾が大きい場合は探索空間がより広く探索されます。この場合、すべての彗星の楕円の軸は常に恒星から離れる方向、つまり現在の最良の大域解から離れる方向を向いています。

    アルゴリズムの論理は、恒星からの距離に応じて膨張する方向と減少する方向の両方で、彗星雲の膨張係数を調整できることを可能にします。また、彗星の軌道半径によって楕円の平坦度を調整することもできます。さらに、彗星の尾を恒星から離すのではなく、恒星に向けることも可能です（望む場合）。

    図1では、彗星2が条件付きで新しい軌道に移動する瞬間も示されています（丸2）。これは、2つの彗星の核間で物質が交換される際に発生します。図では、彗星2は彗星4から物質を借りています。彗星間の物質交換の過程でより良い解が見つかれば、その時点で物質が形成されていた対応する彗星は新しい軌道に移動します。

    彗星の尾の大きさと、恒星までの距離に応じた核に対するその変位は、線形法則に従って条件付きで計算できます。この場合、1に等しい最大距離は、問題の対応する最適化座標の最小値と最大値の範囲に対応します。このアプローチによって、恒星までの距離による彗星の尾のパラメータの変化をシンプルかつ明快に表現することができます。

    グラフ

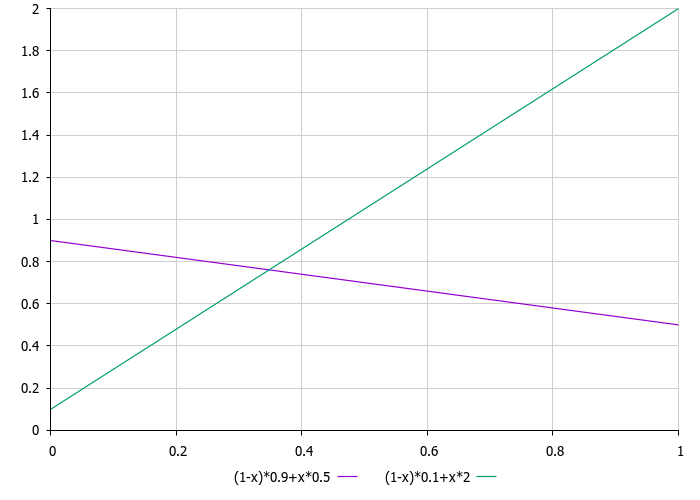
    図2：彗星のトレイルの変位比（紫）とトレイルの大きさ（緑）の恒星までの距離依存性のグラフ

    そこで、彗星の粒子雲の形と大きさの変化の法則を開発したので、アルゴリズムの可能な特性についての結論をまとめることができます。太陽からの尾の方向（大域的最適解）と、最適解とそうでない解の両方を探索することを考慮に入れた、彗星の軌跡に着想を得たアルゴリズムの主な特性は以下の通りです。

    1. 溶液の蒸発と進化：このアルゴリズムは、最適解領域とそうでない領域の両方を探索できる、解の蒸発と進化のプロセスを用いることができます。
    2. 多変量：アルゴリズムは、彗星の尾における組成の多様性と同様に、最適性の異なるレベルを反映する様々な解の選択肢を生成するように努めることができます。
    3. 外的要因への適応性：彗星は太陽照射に反応するため、アルゴリズムは環境や目的関数の変化に適応することができます。
    4.大域的最適解の検索：太陽から遠ざかる尾の方向は、大域的な最適解を求めると同時に、局所最適への早すぎる収束を避けるために、最適でない解も考慮に入れるというアルゴリズムの欲求を象徴しているのかもしれません。

    アルゴリズムのスケッチを擬似コードで書いてみましょう。

    1. 彗星核をランダムに生成します。
    2. 彗星の核は、その尾部、つまり彗星核を中心とする正規分布の粒子を作り出します。
    3. 彗星粒子の適応度を計算します。
    4. 大域解を更新します。
    5. 対応する彗星の最良の粒子を核に割り当てます。
    6. 彗星粒子の各座標について、以下を実行します。
       確率は0.6です。
          彗星核を中心とした正規分布の粒子を作ります。
       または
          ランダムに選んだ2つの彗星の核の座標を使って彗星粒子を作ります。
    7. 大域解を更新します。
    8. 対応する彗星の最良の粒子を核に割り当てます。
    9. 停止基準が満たされるまで、6から繰り返します。

    CTAアルゴリズムに特定の構造を書く必要はありません。アルゴリズムと実行プログラムの間で意思決定を交換するために使われるエージェントの基本構造は、彗星とその粒子を記述するのに十分です。この構造がどのようなものか思い出してみましょう。

    S_AO_Agent構造体には2つのフィールドがあります。

    • c[]：解決空間内のエージェント座標を格納する配列
    • f：解の質を評価するためのエージェント適応度

    CTAアルゴリズムの文脈では、彗星そのものとその尾の粒子の両方を記述するためにこの構造を使用します。

    //——————————————————————————————————————————————————————————————————————————————
struct S_AO_Agent
{
    double c []; //coordinates
    double f;    //fitness
};
//——————————————————————————————————————————————————————————————————————————————

    C_AOクラスを継承するC_AO_CTAクラスを定義しましょう。

    • C_AO_CTA ()：コンストラクタは、定義済みの値でクラスオブジェクトを初期化します。また、母集団サイズ(popSize)、彗星数(cometsNumb)、尾長係数(tailLengthKo)、最大最小シフト係数(maxShiftCoefと minShiftCoef)、最大最小サイズ係数(maxSizeCoefとminSizeCoef)などのアルゴリズムのパラメータも設定します。
    • SetParams()は、params配列の値に基づいてアルゴリズムパラメータを設定します。
    • Init()は、指定された探索範囲とエポック数でアルゴリズムを初期化します。
    • Moving()メソッドとRevision()メソッドは、アルゴリズムの主要なロジックを実装しています。

    comets[]フィールドはS_AO_Agent型のオブジェクトの配列で、アルゴリズムにおける彗星を表します。

    tailLength[]、maxSpaceDistance[]、partNumberの各privateフィールドは、アルゴリズムの内部演算に使用されます。

    //——————————————————————————————————————————————————————————————————————————————
class C_AO_CTA : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_CTA () { }

  C_AO_CTA ()
  {
    ao_name = "CTA";
    ao_desc = "Comet Tail Algorithm";
    ao_link = "https://www.mql5.com/ru/articles/14841";

    popSize      = 50;   //population size
    cometsNumb   = 5;    //number of comets
    tailLengthKo = 0.2;  //tail length coefficient
    maxShiftCoef = 0.9;
    minShiftCoef = 0.5;
    maxSizeCoef  = 0.1;
    minSizeCoef  = 1.5;

    ArrayResize (params, 7);

    params [0].name = "popSize";       params [0].val = popSize;
    params [1].name = "cometsNumb";    params [1].val = cometsNumb;
    params [2].name = "tailLengthKo";  params [2].val = tailLengthKo;
    params [3].name = "maxShiftCoef";  params [3].val = maxShiftCoef;
    params [4].name = "minShiftCoef";  params [4].val = minShiftCoef;
    params [5].name = "maxSizeCoef";   params [5].val = maxSizeCoef;
    params [6].name = "minSizeCoef";   params [6].val = minSizeCoef;
  }

  void SetParams ()
  {
    popSize      = (int)params [0].val;
    cometsNumb   = (int)params [1].val;
    tailLengthKo = params      [2].val;
    maxShiftCoef = params      [3].val;
    minShiftCoef = params      [4].val;
    maxSizeCoef  = params      [5].val;
    minSizeCoef  = params      [6].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();
  void Injection (const int popPos, const int coordPos, const double value);

  //----------------------------------------------------------------------------
  int    cometsNumb;    //number of comets
  double tailLengthKo;  //tail length coefficient
  double maxShiftCoef;  //maximum shift coefficient
  double minShiftCoef;  //minimum shift coefficient
  double maxSizeCoef;   //maximum size coefficient
  double minSizeCoef;   //minimum size coefficient

  S_AO_Agent comets [];

  private: //-------------------------------------------------------------------
  int    epochs;
  int    epochNow;
  double tailLength       [];
  double maxSpaceDistance []; //maximum distance in space
  int    partNumber; //number of particles
};
//——————————————————————————————————————————————————————————————————————————————

    C_AO_CTAクラスにInitメソッドを定義します。このメソッドは、与えられた探索範囲とエポック数でアルゴリズムを初期化します。各ステップの説明は、次の通りです。

    1.「if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;」：このコードは、指定された検索範囲でStandardInitメソッドを呼び出します。StandardInitがfalseを返した場合、Initメソッドも即座にfalseを返します。

    2. 「ArrayResize (comets, cometsNumb);」彗星の数に応じて、彗星の配列サイズを変更します。

    3. 座標と適応度関数の値は、forループ内で各彗星に対して初期化されます。

    4. 「ArrayResize (tailLength, coords); ArrayResize (maxSpaceDistance, coords);」：座標の数に応じて、tailLength配列とmaxSpaceDistance配列のサイズを変更します。

    5. 以下のforループの中で、各座標について空間内の最大距離と尾の長さが計算されます。

    6.「partNumber = popSize / cometsNumb;」：それぞれの彗星の尾の粒子の数を計算します。

    //——————————————————————————————————————————————————————————————————————————————
bool C_AO_CTA::Init (const double &rangeMinP [], //minimum search range
                     const double &rangeMaxP  [], //maximum search range
                     const double &rangeStepP [], //step search
                     const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  epochs   = epochsP;
  epochNow = 0;

  ArrayResize (comets, cometsNumb);
  for (int i = 0; i < cometsNumb; i++)
  {
    ArrayResize (comets [i].c, coords);
    comets [i].f = -DBL_MAX;
  }

  ArrayResize (tailLength,       coords);
  ArrayResize (maxSpaceDistance, coords);

  for (int i = 0; i < coords; i++)
  {
    maxSpaceDistance [i] = rangeMax [i] - rangeMin [i];
    tailLength       [i] = maxSpaceDistance [i] * tailLengthKo;
  }

  partNumber = popSize / cometsNumb;

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

    彗星の尾の粒子の形成は、C_AO_CTAクラスのMoving()メソッドでおこなわれます。以下は、このメソッドの主なステップです。

    1. まず、エポックカウンタepochNowをインクリメントし、ローカル変数cnt、min、maxを初期化します。
    2. revisionがfalseの場合、彗星の座標は指定されたrangeMin～rangeMaxの範囲内で初期化されます。粒子（エージェント）は、tailLengthで決定された範囲内で、ガウス分布を使って各彗星の周りに作成されます。
    3. revisionがtrueの場合、粒子（エージェント）の位置が更新されます。coefTail係数とcoefSize係数は各粒子について計算されます。これらは、cB中心点までの距離に応じて彗星の尾の変位と大きさを定義しています。これらの係数は、尾の長さによって制限される範囲内で粒子の新しい位置を決定するために使用されます。
    4. u.RNDprobab()の確率が0.6より小さい場合は、ガウス分布を使って粒子の新しい位置を計算します。そうでなければ、粒子の新しい位置は、ランダムに選択された他の2つの彗星の核の座標の線形結合として計算されます。
    5. すべての場合において、粒子の新しい座標はrangeMinとrangeMaxに制限され、rangeStep のステップで離散化されます。

    このメソッドの一般的な考え方は、彗星の運動と振る舞いをCTAアルゴリズムでモデル化することであり、粒子（エージェント）は彗星の尾を表し、その座標と尾の大きさは大域的最適解（太陽）までの距離に依存します。

    //——————————————————————————————————————————————————————————————————————————————
void C_AO_CTA::Moving ()
{
  epochNow++;
  int    cnt = 0;
  double min = 0.0;
  double max = 0.0;

  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < cometsNumb; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        comets [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        comets [i].c [c] = u.SeInDiSp  (comets [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    for (int i = 0; i < cometsNumb; i++)
    {
      for (int p = 0; p < partNumber; p++)
      {
        for (int c = 0; c < coords; c++)
        {
          min = comets [i].c [c] - tailLength [c] * 0.5; if (min < rangeMin [c]) min = rangeMin [c];
          max = comets [i].c [c] + tailLength [c] * 0.5; if (max > rangeMax [c]) max = rangeMax [c];

          a [cnt].c [c] = u.GaussDistribution (comets [i].c [c], min, max, 1);
          a [cnt].c [c] = u.SeInDiSp  (a [cnt].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
        }

        cnt++;
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  cnt             = 0;
  double coefTail = 0.0;
  double coefSize = 0.0;

  for (int i = 0; i < cometsNumb; i++)
  {
    for (int p = 0; p < partNumber; p++)
    {
      for (int c = 0; c < coords; c++)
      {
        if (u.RNDprobab () < 0.6)
        {
          coefTail = fabs (comets [i].c [c] - cB [c]) / maxSpaceDistance [c];
          coefSize = coefTail;

          //(1-x)*0.9+x*0.5
          coefTail = (1 - coefTail) * maxShiftCoef + coefTail * minShiftCoef;

          //(1-x)*0.1+x*0.9
          coefSize = (1 - coefSize) * maxSizeCoef + coefSize * minSizeCoef;

          if (cB [c] * Dir > comets [i].c [c] * Dir)
          {
            min = comets [i].c [c] - tailLength [c] * coefTail         * coefSize;
            max = comets [i].c [c] + tailLength [c] * (1.0 - coefTail) * coefSize;
          }
          if (cB [c] * Dir < comets [i].c [c] * Dir)
          {
            min = comets [i].c [c] - tailLength [c] * (1.0 - coefTail) * coefSize;
            max = comets [i].c [c] + tailLength [c] * (coefTail)*coefSize;
          }
          if (cB [c] == comets [i].c [c])
          {
            min = comets [i].c [c] - tailLength [c] * 0.1;
            max = comets [i].c [c] + tailLength [c] * 0.1;
          }

          if (min < rangeMin [c]) min = rangeMin [c];
          if (max > rangeMax [c]) max = rangeMax [c];

          a [cnt].c [c] = u.GaussDistribution (comets [i].c [c], min, max, Power);
          a [cnt].c [c] = u.SeInDiSp  (a [cnt].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
        }
        else
        {
          int    r   = 0;
          int    r1  = 0;
          int    r2  = 0;

          do
          {
            r = u.RNDminusOne (cometsNumb);
            r1 = r;
          }
          while (r1 == i);

          do
          {
            r = u.RNDminusOne (cometsNumb);
            r2 = r;
          }
          while (r2 == i || r2 == r1);

          a [cnt].c [c] = comets [r1].c [c] + 0.1 * (comets [r2].c [c] - comets [i].c [c]) * u.RNDprobab();
          a [cnt].c [c] = u.SeInDiSp (a [cnt].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
        }
      }

      cnt++;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

    次に、彗尾アルゴリズム(CTA)で彗星の位置を修正するC_AO_CTAクラスのRevision()メソッドを実装します。

    以下は、このメソッドの主なステップです。

    1. 母集団の中から最適解を見つけます。

    • このメソッドはpopSize個の母集団内のすべての解を調べ、fB目的関数の最良の値を持つ解を見つけます。
    • より良い解が見つかった場合、そのa[ind].cの位置がcBベクトルにコピーされます。このベクトルは最良解を格納します。

    2. 彗星位置を更新します。

    • このメソッドは、すべてのcometNumb彗星に沿って移動し、そのpartNumber彗星に関連する粒子の中から各彗星の最適解を探索します。
    • ある彗星の最適解が見つかった場合、その彗星のcomets[i].cの位置は、見つかった最適解a[ind].cの位置に更新されます。

    このメソッドは、CTAアルゴリズムの重要なステップを実装しており、彗星の尾で見つかった最適解に基づいて彗星の位置を修正します。これにより、より高い目的関数値を持つ領域へ探索を向けることができます。

    //——————————————————————————————————————————————————————————————————————————————
void C_AO_CTA::Revision ()
{
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //set a new kernel------------------------------------------------------------
  int cnt = 0;

  for (int i = 0; i < cometsNumb; i++)
  {
    ind = -1;

    for (int p = 0; p < partNumber;  p++)
    {
      if (a [cnt].f > comets [i].f)
      {
        comets [i].f = a [cnt].f;
        ind = cnt;
      }

      cnt++;
    }

    if (ind != -1) ArrayCopy (comets [i].c, a [ind].c, 0, 0, WHOLE_ARRAY);
  }
}
//——————————————————————————————————————————————————————————————————————————————


    3. テスト結果

    CTAテストスタンドの結果：

    CTA|Comet Tail Algorithm|80.0|40.0|4.0|-1.0|0.2|1.0|0.5|0.1|15.0|
    =============================
    5 Hilly's; Func runs:10000; result:0.9534613588697962
    25 Hilly's; Func runs:10000; result:0.863192334000326
    500 Hilly's; Func runs:10000; result:0.27769783965091077
    =============================
    5 Forest's; Func runs:10000; result:0.997942251272262
    25 Forest's; Func runs:10000; result:0.857403562283056
    500 Forest's; Func runs:10000; result:0.33949224947400775
    =============================
    5 Megacity's; Func runs:10000; result:0.8876923076923078
    25 Megacity's; Func runs:10000; result:0.5643076923076924
    500 Megacity's; Func runs:10000; result:0.10512307692307787
    =============================
    All score:5.84631 (64.96%)

    テストに基づき、CTAの操作について以下の結論が得られます。

    アルゴリズムの総合スコアは5.84631で、これは可能な最大スコアの64.96%に相当します。これはCTAアルゴリズムの優れた性能を示しています。

    Hilly

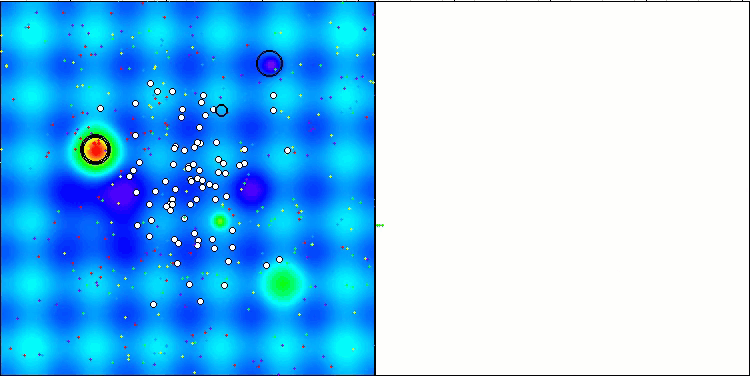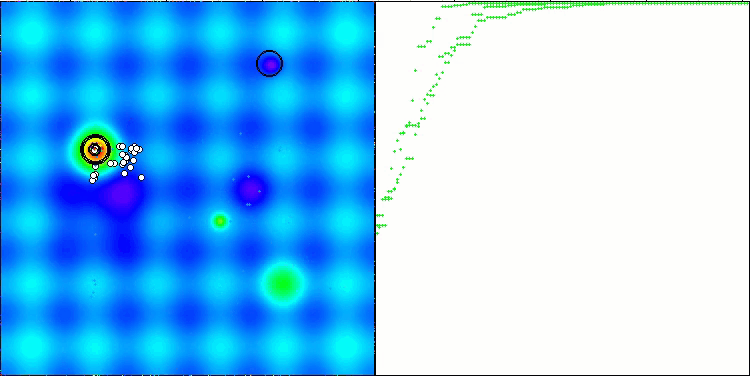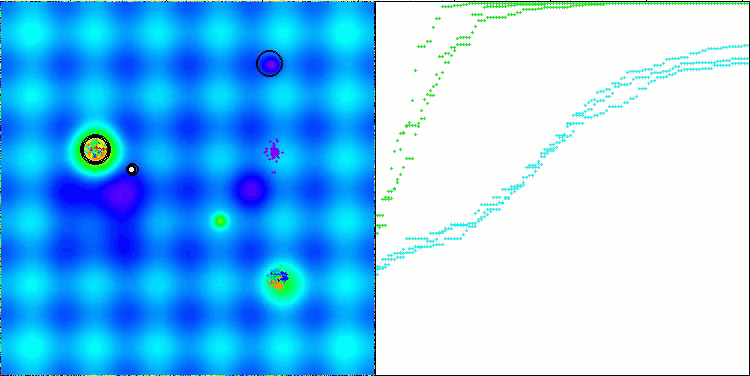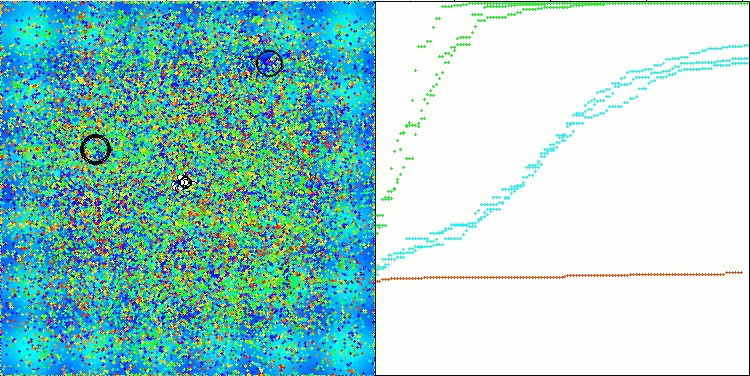
      Hillyテスト関数のCTA

    Forest

      Forestテスト関数のCTA

    Megacity

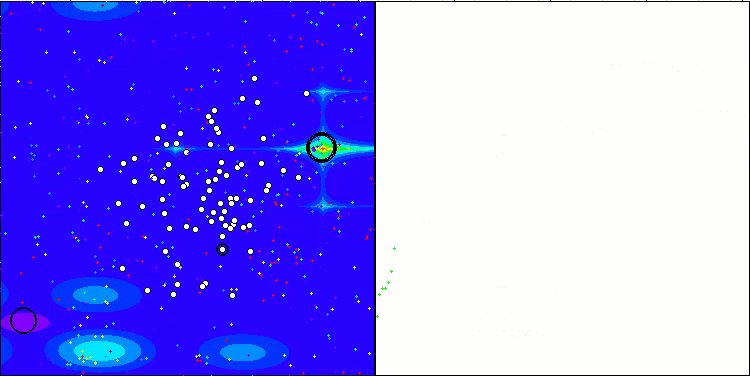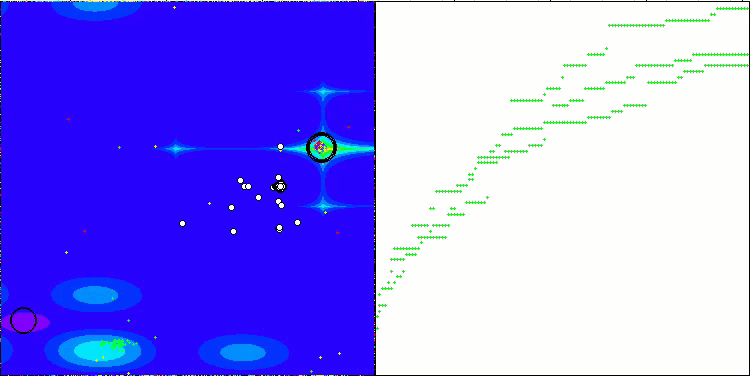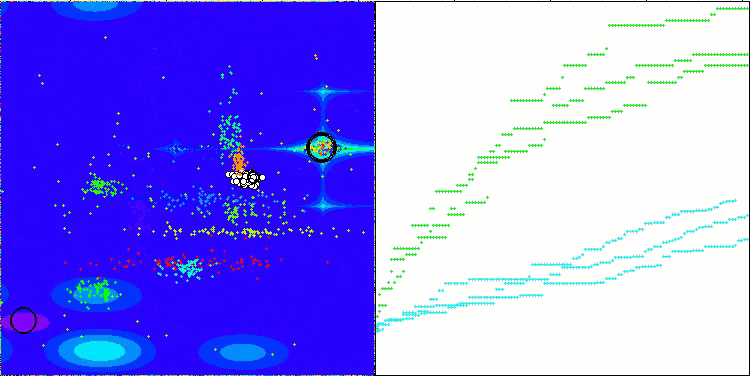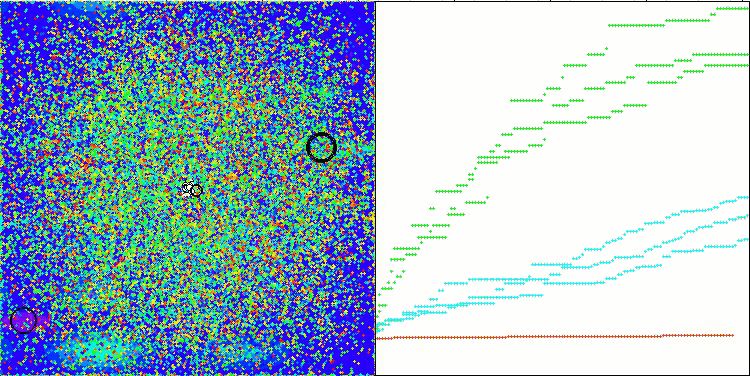
      Megacityテスト関数のCTA

    テスト結果によると、CTAアルゴリズムは評価表の3位に値します。

    # AO 詳細 Hilly Hilly最終 Forest Forest最終 Megacity（離散） Megacity最終 最終結果 MAXの%
    10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F)
    1 BGA バイナリ遺伝的アルゴリズム 0.99992 0.99484 0.50483 2.49959 1.00000 0.99975 0.32054 2.32029 0.90667 0.96400 0.23035 2.10102 6.921 76.90
    2 (P+O)ES (P+O）進化戦略 0.99934 0.91895 0.56297 2.48127 1.00000 0.93522 0.39179 2.32701 0.83167 0.64433 0.21155 1.68755 6.496 72.18
    3 CTA 彗尾アルゴリズム 0.95346 0.86319 0.27770 2.09435 0.99794 0.85740 0.33949 2.19484 0.88769 0.56431 0.10512 1.55712 5.846 64.96
    4 SDSm 確率的拡散探索M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
    5 ESG 社会集団の進化 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
    6 SIA 等方的焼きなまし 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
    7 TSEA 亀甲進化アルゴリズム 0.96798 0.64480 0.29672 1.90949 0.99449 0.61981 0.22708 1.84139 0.69077 0.42646 0.13598 1.25322 5.004 55.60
    8 DE 差分進化 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
    9 BSA 鳥群アルゴリズム 0.90857 0.73661 0.25767 1.90285 0.90437 0.81619 0.16401 1.88457 0.61692 0.54154 0.10951 1.26797 5.055 56.17
    10 HS ハーモニー検索 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
    11 SSG 苗木の播種と育成 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
    12 (PO)ES (PO）進化戦略 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
    13 BSO ブレインストーム最適化 0.91301 0.56222 0.30047 1.77570 0.97162 0.57162 0.23449 1,77772 0.60462 0.27138 0.12011 0.99611 4.550 50.55
    14 WOAm 鯨最適化アルゴリズムM 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
    15 ACOm 蟻コロニー最適化M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
    16 BFO-GA 細菌採食の最適化：Ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
    17 MEC Mind Evolutionary Computation 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
    18 IWO 侵入雑草最適化 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
    19 Micro-AIS 微小人工免疫系 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54
    20 COAm カッコウ最適化アルゴリズムM 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21
    21 SDOm 螺旋ダイナミクス最適化M 0.74601 0.44623 0.29687 1.48912 0.70204 0.34678 0.10944 1.15826 0.42833 0.16767 0.03663 0.63263 3.280 36.44
    22 NMm ネルダー=ミード法M 0.73807 0.50598 0.31342 1.55747 0.63674 0.28302 0.08221 1.00197 0.44667 0.18667 0.04028 0.67362 3.233 35.92
    23 FAm ホタルアルゴリズムM 0.58634 0.47228 0.32276 1.38138 0.68467 0.37439 0.10908 1.16814 0.28667 0.16467 0.04722 0.49855 3.048 33.87
    24 GSA 重力探索法 0.64757 0.49197 0.30062 1.44016 0.53962 0.36353 0.09945 1.00260 0.32667 0.12200 0.01917 0.46783 2.911 32.34
    25 BFO 細菌採餌最適化 0.61171 0.43270 0.31318 1.35759 0.54410 0.21511 0.05676 0.81597 0.42167 0.13800 0.03195 0.59162 2.765 30.72
    26 ABC 人工蜂コロニー 0.63377 0.42402 0.30892 1.36671 0.55103 0.21874 0.05623 0.82600 0.34000 0.14200 0.03102 0.51302 2.706 30.06
    27 BA コウモリアルゴリズム 0.59761 0.45911 0.35242 1.40915 0.40321 0.19313 0.07175 0.66810 0.21000 0.10100 0.03517 0.34617 2.423 26.93
    28 SA 焼きなまし 0.55787 0.42177 0.31549 1.29513 0.34998 0.15259 0.05023 0.55280 0.31167 0.10033 0.02883 0.44083 2.289 25.43
    29 IWDm intelligent water drops M 0.54501 0.37897 0.30124 1.22522 0.46104 0.14704 0.04369 0.65177 0.25833 0.09700 0.02308 0.37842 2.255 25.06
    30 PSO 粒子群最適化 0.59726 0.36923 0.29928 1.26577 0.37237 0.16324 0.07010 0.60572 0.25667 0.08000 0.02157 0.35823 2.230 24.77
    31 ボイド ボイドアルゴリズム 0.43340 0.30581 0.25425 0.99346 0.35718 0.20160 0.15708 0.71586 0.27846 0.14277 0.09834 0.51957 2.229 24.77
    32 MA モンキーアルゴリズム 0.59107 0.42681 0.31816 1.33604 0.31138 0.14069 0.06612 0.51819 0.22833 0.08567 0.02790 0.34190 2.196 24.40
    33 SFL Shuffled Frog-Leaping 0.53925 0.35816 0.29809 1.19551 0.37141 0.11427 0.04051 0.52618 0.27167 0.08667 0.02402 0.38235 2.104 23.38
    34 FSS 魚群検索 0.55669 0.39992 0.31172 1.26833 0.31009 0.11889 0.04569 0.47467 0.21167 0.07633 0.02488 0.31288 2.056 22.84
    35 RND ランダム 0.52033 0.36068 0.30133 1.18234 0.31335 0.11787 0.04354 0.47476 0.25333 0.07933 0.02382 0.35648 2.014 22.37
    36 GWO 灰色オオカミオプティマイザ 0.59169 0.36561 0.29595 1.25326 0.24499 0.09047 0.03612 0.37158 0.27667 0.08567 0.02170 0.38403 2.009 22.32
    37 CSS 荷電系探索 0.44252 0.35454 0.35201 1.14907 0.24140 0.11345 0.06814 0.42299 0.18333 0.06300 0.02322 0.26955 1.842 20.46
    38 EM 電磁気学的アルゴリズム 0.46250 0.34594 0.32285 1.13129 0.21245 0.09783 0.10057 0.41085 0.15667 0.06033 0.02712 0.24412 1.786 19.85


    まとめ

    考慮されているCTAアルゴリズムは、彗星運動の概念に基づいており、彗星の物理法則や進化に矛盾する多くの特徴を持っています。これらの特徴がアルゴリズムの最終的な結果に与える影響については、より詳細に検討する必要があります。


    矛盾の1つは、彗星の尾の方向に関するものです。CTAアルゴリズムでは、一般的に恒星に向かう尾の方向（Dir_P = -1）を使用することで、性能が大幅に向上します。この方向を利用することで、アルゴリズムの空間探索能力も改善されます。最適化を志向する方は、現在のエポックに応じて動的な尾方向係数を使用することを検討すると良いでしょう。特に注目すべきは、尾の向きを恒星から遠ざけると低次元の問題での収束が良くなり、逆に恒星に向けると高次元の問題でより効果的になるという点です。

    もう1つの論点は、彗星の尾の大きさです。CTAアルゴリズムでは、尾の大きさを動的に変更すること（恒星までの距離が長くなるにつれて尾を大きくすること）が、アルゴリズムの効率を向上させることがわかりました。現実には、彗星の尾の大きさは太陽に近づくにつれて増加します。しかし、尾の大きさがこのように動的に変化することで、彗星核周辺の解空間の研究領域を大域解から離れた領域に広げることができ、有望な解を発見する可能性が高まり、局所的な極限にはまり込むリスクを減らすことができます。恒星に近づくにつれて、彗星の尾は縮小し、解の微細化の強度が増します。

    CTAアルゴリズムは、彗星が他の彗星から取り残された粒子を捕獲する際に自然界で発生するように、彗星間の情報交換も含んでいます。これは解空間を探索するためのアルゴリズムの追加機能です。恒星からのコロナ質量放出をモデル化したり、いくつかの彗星の座標を他の彗星から借りることで、アルゴリズムの組み合わせ特性を利用し、個体群の多様性を高める手法が試みられてきました。

    CTA（彗尾アルゴリズム）は、彗星の動きの概念を用いた最適化に対する興味深い新しいアプローチです。このアルゴリズムは、滑らかな関数と離散関数の両方において良好な収束を示し、実装が非常に簡単です（アルゴリズムの構造が単純なため、ソフトウェア実装が簡素化されます）。また、大きなコンピューティングリソースを必要とせず、幅広い問題に適用可能です。離散関数での結果のばらつきも小さく、取引システムの最適化のように、離散ターゲット関数で作業する際の結果の安定性と再現性が高まります。しかし同時に、このアルゴリズムには多くの外部パラメータ（彗星の尾のサイズ、尾の係数、方向シフトなど）が存在します。高次元の滑らかな関数においては、このアルゴリズムが最高の結果を示さない場合もあります。

    一般に、CTAの特質は解空間の探索と、発見された大域的最適解の精密化との間の動的なバランスにあります。

    したがって、CTAアルゴリズムは、彗星運動の物理法則に完全には一致しない多くの単純化や仮定を使用しています。しかし、この現実からの乖離によって、実装の単純さを維持しながら、最適化問題を解くアルゴリズムの効率を高めることが可能となります。


    タブ

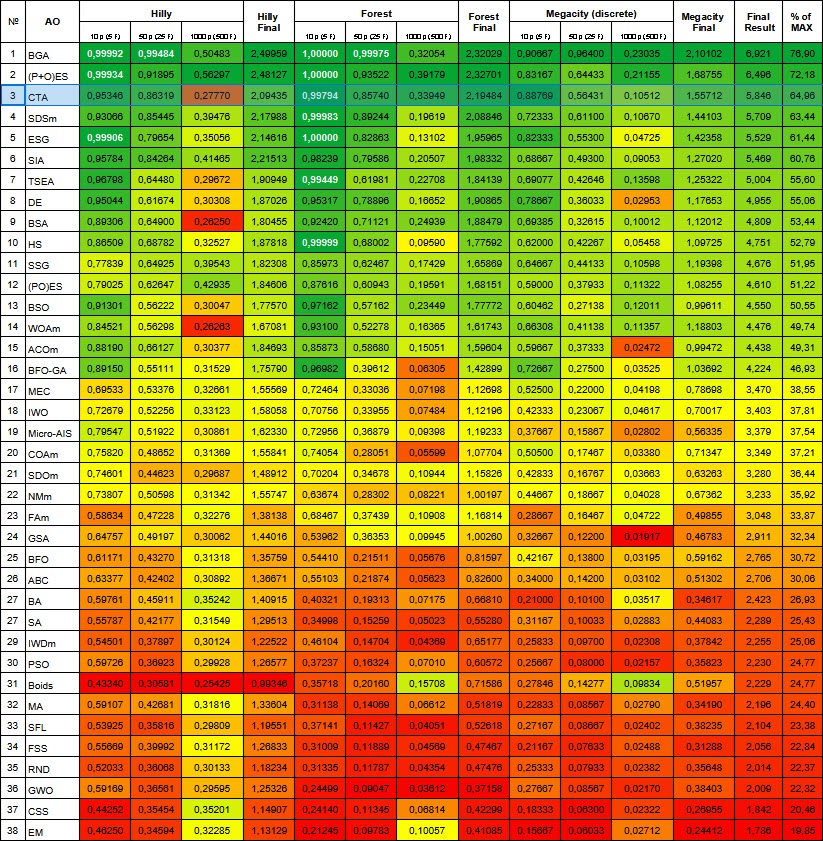
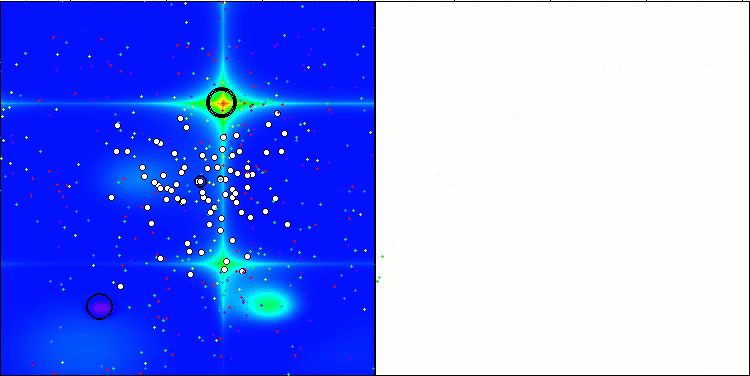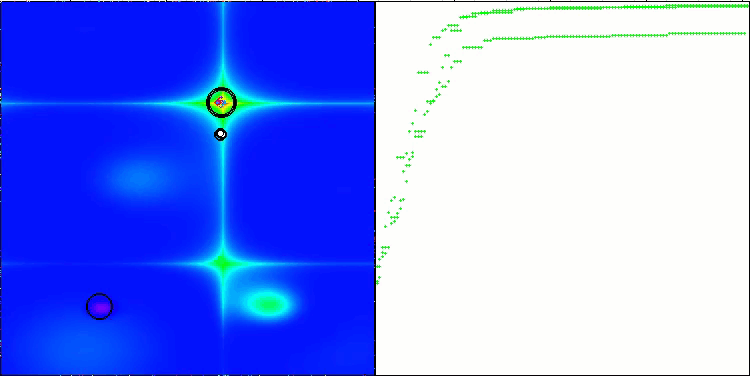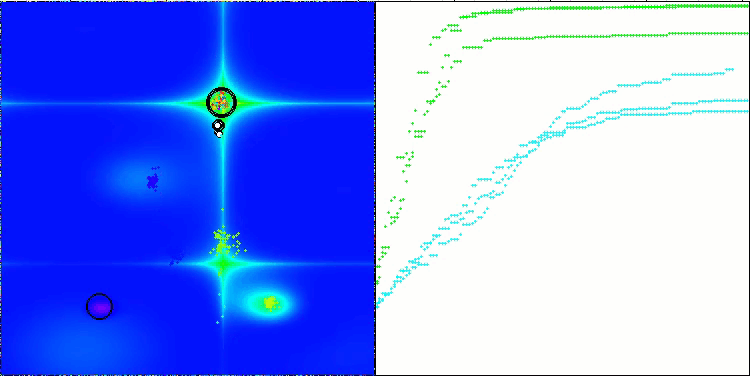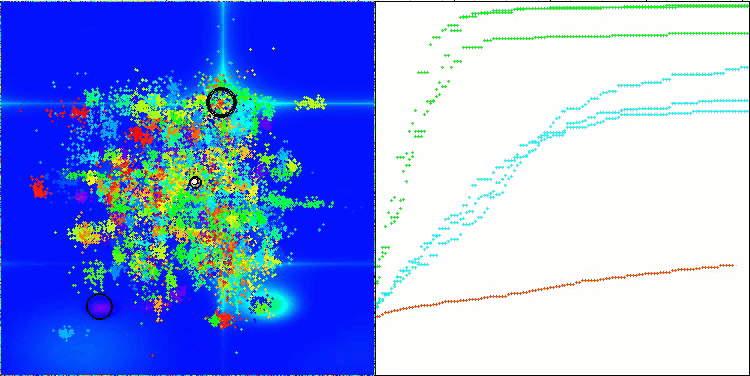
    図3：関連テストに応じたアルゴリズムのカラー勾配0.99以上の結果は白で強調表示

    チャート

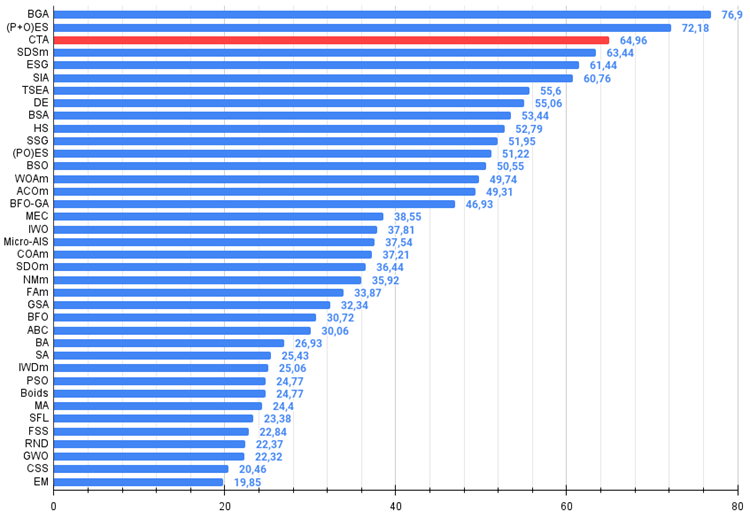
    図4：アルゴリズムのテスト結果のヒストグラム（0から100までのスケールで、多ければ多いほど良いです。

    ここで、100は理論的に可能な最大の結果であり、アーカイブにはレーティング表を計算するスクリプトが含まれている）


    CTAの長所と短所

    長所：

    1. 様々な種類の関数に対して収束性が良い
    2. 実装がシンプル
    3. コンピューティングリソースに負担をかけない
    4. 離散関数に関する結果のばらつきが小さい

    短所

    1. 外部パラメータが多い
    2. 滑らかな高次元関数に関する結果が悪い


    ソースコード

      この記事には、最新版のアルゴリズムコードを含むアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。

      MetaQuotes Ltdによってロシア語から翻訳されました。
      元の記事: https://www.mql5.com/ru/articles/14841

      添付されたファイル |
      ZIPをダウンロード
      CTA.zip (25.65 KB)
      警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

      この著者による他の記事

      ディスカッションに移動
      アルゴリズム取引のリスクマネージャー アルゴリズム取引のリスクマネージャー
      本稿の目的は、リスクマネージャーを利用する必要性を証明し、アルゴリズム取引におけるリスク管理の原則を別クラスで実践することで、金融市場におけるデイ取引と投資におけるリスク標準化アプローチの有効性を誰もが検証できるようにすることです。この記事では、アルゴリズム取引用のリスクマネージャークラスを作成します。これは、手動取引のリスクマネージャーの作成について述べた前回の記事の論理的な続きです。
      亀甲進化アルゴリズム(TSEA) 亀甲進化アルゴリズム(TSEA)
      これは、亀の甲羅の進化にインスパイアされたユニークな最適化アルゴリズムです。TSEAアルゴリズムは、問題に対する最適解を表す構造化された皮膚領域が徐々に形成される様子をエミュレートします。最良の解は「硬く」なり、外側に近い位置に配置され、成功しなかった解は「柔らかい」ままで内側に留まります。このアルゴリズムは、質と距離に基づく解のクラスタリングを利用し、成功率の低い選択肢を保持しながら、柔軟性と適応性を提供します。
      あらゆるタイプのトレーリングストップを開発してEAに接続する方法 あらゆるタイプのトレーリングストップを開発してEAに接続する方法
      この記事では、様々なトレーリングストップを簡単に作成するためのクラスと、トレーリングストップを任意のEAに接続する方法について説明します。
      リプレイシステムの開発（第46回）：Chart Tradeプロジェクト(V) リプレイシステムの開発（第46回）：Chart Tradeプロジェクト(V)
      アプリケーションを動作させるために必要なファイルを探すのに時間を浪費していませんか。すべてを実行ファイルに含めてみてはどうでしょうか。そうすれば、ファイルを探す必要がなくなります。多くの人がこのような配布・保管方法を採用していることは知っていますが、少なくとも、実行ファイルの配布や保管に関してはもっと適切な方法があります。ここで紹介する方法は、MQL5だけでなく、MetaTrader 5そのものを優れたアシスタントとして使うことができるので、非常に便利です。しかも、理解するのはそれほど難しくありません。