ニューロボイド最適化アルゴリズム(NOA)

MetaTrader 5 — テスター | YYYY年02月DD日, 07:13

Andrey Dik

内容

はじめに

最適化アルゴリズムを研究する中で、私は常に、可能な限りシンプルでありながら最も効率的な解法を作りたいという考えに惹かれてきました。自然界において単純な個体同士の相互作用によって複雑な問題が解決される様子を観察する中で、私は新しい最適化アルゴリズム「Neuroboids Optimization Algorithm (NOA)」を開発しました。

このアルゴリズムは、最小限のニューラルエージェント（ニューロボイド）という概念に基づいています。各ニューロボイドは、2層のニューロンを持つシンプルなニューラルネットワークであり、ADAMアルゴリズムを用いて学習されます。このアプローチの独自性は、個々のエージェントが極めて単純であるにもかかわらず、集団行動により複雑な最適化問題の探索空間を効果的に探索できる点にあります。

NOAの着想は、自然システムにおける自己組織化のプロセスにあります。そこでは、単純な単位が基本ルールに従うことで、複雑で適応的な構造を形成します。本記事では、アルゴリズムの理論的根拠、数学モデル、および標準的な最適化テスト関数を用いた実験的効率検証の結果を紹介します。

アルゴリズムの実装

雨上がりの庭を歩いていると想像してください。そこにはミミズが無数にいます。単純な神経系を持つ生き物です。私たちの意味で「考える」能力はありませんが、難しい地形を進み、危険を避け、食べ物や配偶者を見つけます。小さな脳にはわずか数千個のニューロンしかありませんが、何百万年も生き延びてきました。こうして「ニューロボイド」のアイデアが生まれました。

ミミズの単純さと集合知の力を組み合わせたらどうなるでしょうか。自然界では、単純な生物が協力することで驚くべき成果を達成します。アリは複雑なコロニーを作り、ミツバチは蜜を集める際に最適化問題を解決し、鳥の群れは中央制御なしで複雑な動的構造を形成します。

私のニューロボイドは、これらのミミズのようなものです。各ニューロボイドは小さなニューラルネットワークを持ちます。何百万ものパラメータを持つ巨大なアーキテクチャではなく、入力と出力にわずか数個のニューロンを備えています。彼らは探索空間全体を知りません。見えるのは自身の局所環境だけです。1匹のミミズが栄養豊富な土壌の場所を見つけると、他のミミズも徐々にその場所に引き寄せられます。しかし盲目的に従うわけではなく、それぞれが独自性と移動戦略を保持します。ニューロボイドは最適化の背後にあるすべての数学を知る必要はありません。試行錯誤を通じて自ら学習します。1匹が良い解を見つけても、他は単に座標をコピーするのではなく、その解がなぜ良いのかを理解し、独自にそこへ到達する方法を学びます。

海辺の夕日を覚えていますか。太陽は波に反射して無数のきらめきを生み、それぞれが光と水の相互作用の小さな物語です。ニューロボイドも同じで、それぞれが解の一部を反映し、集団で完全な像を作ります。遠目には動きがカオスに見えるかもしれません。しかし、この一見混沌とした中に秩序が生まれます。最適解を探索する自己組織化システムです。

ニューロボイドには中央の指揮者もいません。各個体は、自身の小さなニューラルネットワークを用いて、最良解に従うか新しい領域を探索するか、隣の成功戦略をコピーするか、それとも独自の戦略を試すかを決定します。

複雑さやスケールに取り憑かれた世界において、ニューロボイドは最も偉大なシステムは最も単純な要素から構築されることを思い出させてくれます。砂粒が浜辺や山を作り、水滴が海を形作るように、小さなデジタルミミズであるニューロボイドたちも、巨大でモノリシックなアルゴリズムでは解決できない問題を協力して解きます。

noaアルゴリズムダイアグラム

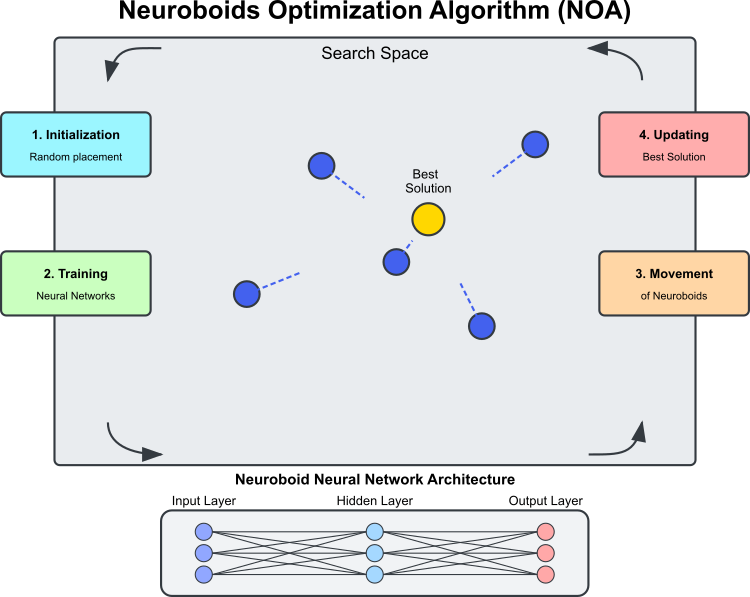
図1：NOAアルゴリズムの動作

図1はNOAアルゴリズムの主要コンポーネントと動作原理を示しています。探索空間はニューロボイド（青色の円）が最適解を探索する領域です。ニューロボイドはそれぞれ独自のニューラルネットワークを持つ最適化エージェントです。最良解は現時点で見つかっている最適解（黄金の円）で、ニューロボイドはそれに向かって移動します。ニューラルネットワークのアーキテクチャは以下の通りです。各ニューロボイドは、自身のニューラルネットワークで移動方向を決定します。アルゴリズムの周期的プロセスは、初期化（ランダムな配置）、ニューラルネットワーク学習（最良解に基づく学習）、訓練済みネットワークによる移動、より良い解が見つかれば最良解の更新、の各ステージで構成されます。点線はニューロボイドの移動方向を示し、ニューラルネットワークの出力と最良解へのランダム性の要素によって決定されます。

「ニューロボイド」という用語は、ニューラルネットワークとボイド（集団行動モデルの人工「鳥」）の概念を組み合わせたものです。各ニューロボイドエージェントは、探索空間内の位置と、
移動戦略を決定する個別のニューラルネットワークで構成されます。

従来のメタヒューリスティックアルゴリズム（遺伝的アルゴリズムや群知能法など）では、エージェントの挙動は固定ルールで決定されますが、NOAでは各ニューロボイドが独自のニューラルネットワークを持ち、最適化中に学習します。ニューラルネットワークは、最良解（ターゲットベクトル）に基づき、有望な探索方向を徐々に学習します。結果として、この最適化アルゴリズムには2つの探索戦略が存在します。1つはNOA自体、もう1つはニューラルネットワーク内に組み込まれたADAMです。バックプロパゲーションにより、ADAMは各ニューロボイドのニューラルネットワーク重みの調整ツールとして独立して使用されます。その結果、すべてのニューロボイドの重み総数は問題次元より大きくなる可能性があります。ニューラルネットワーク全体の重みを直接最適化する必要はなく、これは自然かつ自動的におこなわれます。

ニューロボイドの挙動には、自然界の社会学習（成功した個体の観察）、神経可塑性（神経系の適応能力）、集合知（多数の単純なエージェントの相互作用による創発的最適化）との類似点があります。

NOAアルゴリズムの主な技術的特徴は以下の通りです。

最適化内での誤差の順伝播と逆伝播
複数ニューラルネットワークの分散学習、各ネットワークが独自戦略を形成
現在の探索状態に基づく適応的行動調整
ニューラルネットワークの活性化関数を用いた非線形探索ダイナミクスの作成

この組み合わせにより、NOAは機械学習と最適化パラダイムを組み合わせた興味深いハイブリッドアプローチとなります。ニューラルネットワークを目的関数近似に使うのではなく（サロゲートモデルのように）、探索自体を間接的に導くために利用し、最適化問題解決のための一種の「メタラーニング」を実現しています。

これで、NOAアルゴリズムの疑似コードを記述することができます。

初期化

N個のニューラルネットワーク（ニューロボイド）の集団を作成します。
各ニューラルネットワークは、最適化問題の次元と同じ数の入力と出力を持つ構造を持ちます。
パラメータを設定します。
- popSize（集団規模）
- actFunc（ニューロンの活性化関数）
- dispScale（座標変位のスケール）
- eliteProb（エリート座標をコピーする確率）

アルゴリズム

最初の反復の場合(revision=false)
- 集団内の各ニューロボイドについて
  - 探索空間内で座標をランダムに初期化する
  - 座標を許容される離散値に変換する
- 「revision = true」に設定し、現在の反復を終了する
後続の反復の場合
- ほとんどのニューロボイド（最後の5体を除く）について
  - 各座標について
    - eliteProbの確率で、座標値を最良解からの値(cB)で置き換える
- 集団内の各ニューロボイドについて
  - 最良解(cB)と現在のニューロボイド位置を[-1, 1]の範囲にスケーリングする
  - 現在のニューロボイドのニューラルネットワークで順伝播を実行する
  - 目標値（cBによるスケーリング）とニューラルネットワーク出力の誤差を計算する
  - 誤差逆伝播によりニューラルネットワークを学習させる
  - ニューロボイドの座標を、ニューラルネットワーク出力で決定される方向に移動させて更新する
  - 座標を許容される離散値に変換する
評価と更新
- 集団内の各ニューロボイドについて
  - 現在の座標に対する目的関数の値を計算する
  - 値がこれまでの最良値(fB)より良ければ
    - 最良値(fB)を更新する
    - 現在の座標を最良座標(cB)として保存する

それでは、アルゴリズムコードの記述を始めましょう。C_AO_NOAクラスを定義します。このクラスはC_AOクラスを継承しており、C_AOのプロパティやメソッドを持つと同時に、独自の機能も追加します。クラスの主要要素は以下の通りです。

~C_AO_NOA ()デストラクタ：nn配列の各要素（ニューロボイド個体の個別ニューラルネットワーク）の動的に割り当てられた活性化関数オブジェクトを削除します。これによりメモリリークを防ぎます。

C_AO_NOA ()コンストラクタ

最適化アルゴリズムのパラメータを初期化します。
パラメータの初期値を設定します（popSize：集団サイズ、actFunc：ニューロンの活性化関数、dispScale：移動スケール、エリート座標をコピーする確率）。
パラメータを格納するparams配列を確保します。

SetParams ()メソッド：params配列に格納された値に基づき、パラメータを設定します。

Init ()メソッド：クラスを初期化するために定義されます。rangeMinP、rangeMaxP、rangeStepPの値範囲、およびepochsPのエポック数を設定します。

Moving ()およびRevision ()：集団内の個体を移動させたり、意思決定の評価と更新をおこなうために使用されます。

nn配列：各ニューロボイドのニューラルネットワーククラスのインスタンスの配列です。

privateメソッド：ScaleInp ()およびScaleOut ()：入力データと出力データのスケーリングをおこなうメソッドです。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_NOA : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_NOA ()
  {
    for (int i = 0; i < ArraySize (nn); i++) if (CheckPointer (nn [i].actFunc)) delete nn [i].actFunc;
  }
  C_AO_NOA ()
  {
    ao_name = "NOA";
    ao_desc = "Neuroboids Optimization Algorithm (joo)";
    ao_link = "https://www.mql5.com/ja/articles/16992";

    popSize   = 50;   // population size
    actFunc   = 0;    // neuron activation function
    dispScale = 0.01; // scale of movements
    eliteProb = 0.1;  // probability of copying elite coordinates

    ArrayResize (params, 4);
    params [0].name = "popSize";   params [0].val  = popSize;
    params [1].name = "actFunc";   params [1].val  = actFunc;
    params [2].name = "dispScale"; params [2].val  = dispScale;
    params [3].name = "eliteProb"; params [3].val  = eliteProb;
  }

  void SetParams ()
  {
    popSize   = (int)params [0].val;
    actFunc   = (int)params [1].val;
    dispScale = params      [2].val;
    eliteProb = params      [3].val;
  }

  bool Init (const double &rangeMinP  [],  // minimum values
             const double &rangeMaxP  [],  // maximum values
             const double &rangeStepP [],  // step change
             const int     epochsP = 0);   // number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  int    actFunc;   // neuron activation function
  double dispScale; // scale of movements
  double eliteProb; // probability of copying elite coordinates

  private: //-------------------------------------------------------------------
  C_MLPa nn [];

  void ScaleInp (double &inp [], double &out []);
  void ScaleOut (double &inp [], double &out []);
};
//——————————————————————————————————————————————————————————————————————————————

Initメソッドは、C_AO_NOAクラスのインスタンスを初期化するために用いられます。複数のパラメータを受け取り、値の範囲やエポック数を指定し、アルゴリズムを調整するために必要な操作を実行します。

メソッドシグネチャ：初期化が成功したかどうかを示します。パラメータは次のとおりです。

MinP []：パラメータの最小値
MaxP []：パラメータの最大値
StepP []：パラメータの変更ステップ
epochsP：エポックの数

標準初期化：メソッドの最初の行で、渡された範囲を用いてStandardInit関数が呼び出されます。

ニューラルネットワーク設定の準備

nnConf配列を作成し、ニューラルネットワークの入力層と出力層のサイズを格納します。
ArrayResizeを呼び出して、nnConf配列を2要素（入力層と出力層）にリサイズします。
両方の配列要素は、入力データの次元に対応するcoords値で初期化されます。

E_Act列挙型の宣言：ニューロン活性化関数の種類（eActTanh、eActAlgSigm、eActRatSigmなど）を定義します。

ニューロン配列のバックアップ：nn配列（ニューロンの配列）を、コンストラクタで設定されたpopSizeにリサイズします。

ニューロンの初期化

cnt変数を0で初期化します。各ニューロンに一意のランダムシードを渡すために使用され、各ニューラルネットワークの重みがユニークに初期化されます。
forループ内で各ニューロンを初期化します。nn[i].Init()メソッドを呼び出し、nnConf構成、actFunc活性化関数、および現在のcnt値とシステム起動後の経過ミリ秒数に基づくシードを渡します。
ループの各反復でcntをインクリメントし、各ニューロン初期化に一意のシードが生成されるようにします。

戻り値：すべての操作が成功した場合、trueを返し、初期化が成功したことを示します。

C_AO_NOAクラスのInitメソッドは、ニューラルネットワークおよび関連パラメータの初期化をおこない、最適化アルゴリズムをセットアップする重要な役割を果たします。

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_NOA::Init (const double &rangeMinP  [], // minimum values
                     const double &rangeMaxP  [], // maximum values
                     const double &rangeStepP [], // step change
                     const int     epochsP = 0)   // number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  int nnConf [];
  ArrayResize (nnConf, 2);
  nnConf [0] = coords;
  nnConf [1] = coords;

  enum E_Act
  {
    eActTanh,      //0
    eActAlgSigm,   //1
    eActRatSigm,   //2

    eActSoftPlus,  //3
    eActBentIdent, //4
    eActSiLU,      //5

    eActACON,      //6
    eActSERF,      //7
    eActSnake      //8
  };

  ArrayResize (nn, popSize);
  int cnt = 0;
  for (int i = 0; i < popSize; i++)
  {
    nn [i].Init (nnConf, actFunc, (int)GetTickCount64 () + cnt);
    cnt++;
  }

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Moving()メソッドは、ニューロンのような最適化アルゴリズムの枠組みで、集団内の個体を移動させる役割を担います。ステップごとに分解して説明します。

初期値の初期化：revisionがfalseの場合、メソッドは最初の初期化をおこないます。popSizeの集団の各要素、およびcoordsの各次元に対して、探索エージェントを表すa[i].c[c]配列に初期値を設定します。

u.RNDfromCI()はrangeMin[c]からrangeMax[c]の範囲でランダムな値を生成します。
u.SeInDiSp()はステップ変化を用いて、a[i].c[c]の値を有効範囲内に調整する関数です。
初期化が完了すると、revisionはtrueに設定され、メソッドから制御が戻ります。

座標の更新：個体の座標はエリート確率(eliteProb)に基づいて更新されます。集団の最初の「popSize - 5」個体について、ランダムチェックをおこない、ランダム値がeliteProb未満の場合、a[i].c[c]はエリート座標cB[c]と同じ値に設定されます。

ニューラルネットワークデータの処理：入力データ、出力データ、目標値、誤差の配列を作成し、coordsサイズに準備します。集団の各要素について次をおこないます。

ScaleInp ()はcBの目標座標をスケーリングし、targValに格納します。
ScaleInp ()は集団の現在の座標をスケーリングし、inpDataに格納します。
nn [i].ForwProp ()はニューラルネットワークで順伝播をおこない、出力を生成します。
誤差（目標値と出力の差）を各座標ごとに計算します。
nn [i].BackProp (err)により誤差を逆伝播させ、重みを調整します。
a [i].c [c]の座標を、ニューラルネットワークの出力、スケーリング、ランダムサンプル要素を考慮して更新します。
最後に、a[i].c[c]の値はu.SeInDiSp関数で正規化されます。

このように、Moving()メソッドはモデル内の個体を移動させる責任を持ち、初期化時の配置と、ニューラルネットワーク出力および確率的選択に基づく位置の更新をおこないます。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NOA::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    // Initialize the initial values of anchors in all parallel universes
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  double rnd  = 0.0;
  double val  = 0.0;
  int    pair = 0.0;

  for (int i = 0; i < popSize - 5; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      if (u.RNDprobab () < eliteProb)
      {
        a [i].c [c] = cB [c];
      }
    }
  }

  double inpData []; ArrayResize (inpData, coords);
  double outData []; ArrayResize (outData, coords);
  double targVal []; ArrayResize (targVal, coords);
  double err     []; ArrayResize (err,     coords);

  for (int i = 0; i < popSize; i++)
  {
    ScaleInp (cB,      targVal);
    ScaleInp (a [i].c, inpData);

    nn [i].ForwProp (inpData, outData);

    for (int c = 0; c < coords; c++) err [c] = targVal [c] - outData [c];

    nn [i].BackProp (err);

    for (int c = 0; c < coords; c++)
    {
      a [i].c [c] += outData [c] * (rangeMax [c] - rangeMin [c]) * dispScale * u.RNDprobab ();
      a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

次に、Revisionメソッドは、集団内の現在の「最良解」を評価および更新する役割を担います。集団内の各個体について、目的関数の値を現在の「最良値」と比較し、より良い解が見つかれば、現在の「最良値」を更新します。このようにして、メソッドは集団内で現在の最良解が常に維持されることを保証します。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NOA::Revision ()
{
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ArrayCopy (cB, a [i].c);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

ScaleInpメソッドは、rangeMinおよびrangeMaxで指定された範囲の入力データを、-1から1の区間へスケーリングする役割を担います。inp[c]の各値は、線形スケーリングをおこなうu.Scale関数を用いて変換され、-1から1の範囲に正規化されます。ScaleInpメソッドは、後続の計算に備えてデータを準備し、所定の範囲への正規化を保証します。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NOA::ScaleInp (double &inp [], double &out [])
{
  for (int c = 0; c < coords; c++) out [c] = u.Scale (inp [c], rangeMin [c], rangeMax [c], -1, 1);
}
//——————————————————————————————————————————————————————————————————————————————

ScaleOutメソッドはScaleInpと同様に機能しますが、逆方向のスケーリングをおこないます。-1から1の範囲にある値を、rangeMinからrangeMaxで定義された元の範囲へ変換します。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NOA::ScaleOut (double &inp [], double &out [])
{
  for (int c = 0; c < coords; c++) out [c] = u.Scale (inp [c], -1, 1, rangeMin [c], rangeMax [c]);
}
//——————————————————————————————————————————————————————————————————————————————

テスト結果

アルゴリズムは、低次元および中程度の次元を持つ関数に対して興味深い結果を示しています。一方で、問題規模が1000変数に達すると計算時間が許容できないほど大きくなるため、これらのテスト結果は提示していません。テストの結果、9件中6件（約45%）のテストで最適値に到達しました。

NOA|Neuroboids Optimization Algorithm (joo)|50.0|0.0|0.01|0.1|
=============================
5 Hilly's; Func runs:10000; result:0.7013521128826248
25 Hilly's; Func runs:10000; result:0.40128968110640306
=============================
5 Forest's; Func runs:10000; result:0.6222984295200933
25 Forest's; Func runs:10000; result:0.30830340651626337
=============================
5 Megacity's; Func runs:10000; result:0.4523076923076924
25 Megacity's; Func runs:10000; result:0.20892307692307693
=============================
All score:2.69447 (44.91%)

ここで、NOAアルゴリズムの可視化について少し触れたいと思います。ご覧のとおり、このアルゴリズムは興味深い扇形の構造を形成します。本質的には、これらの構造はニューロボイド内のニューラルネットワークの出力結果を可視化したものです。

Hilly

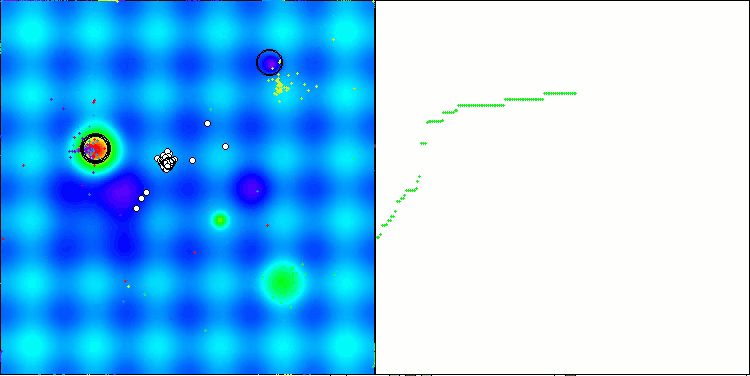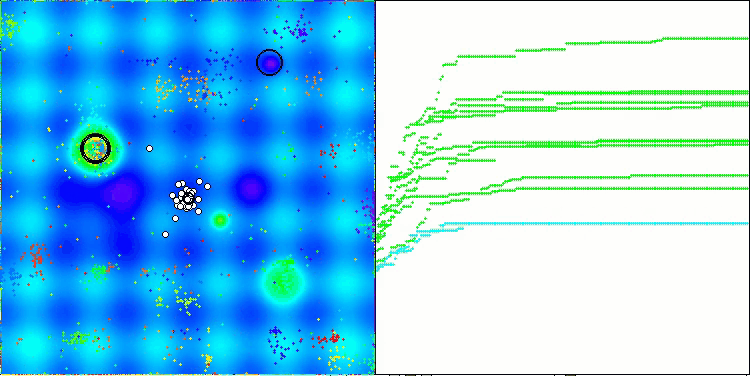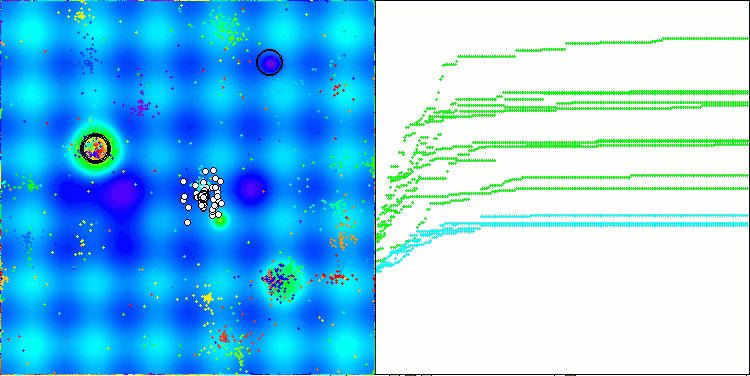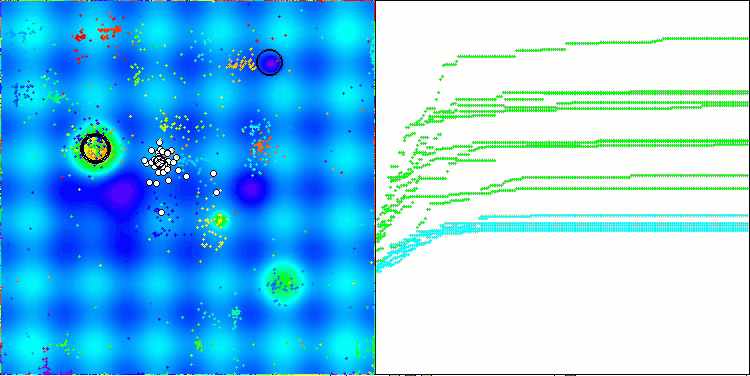
Hillyテスト関数のNOA

Forest

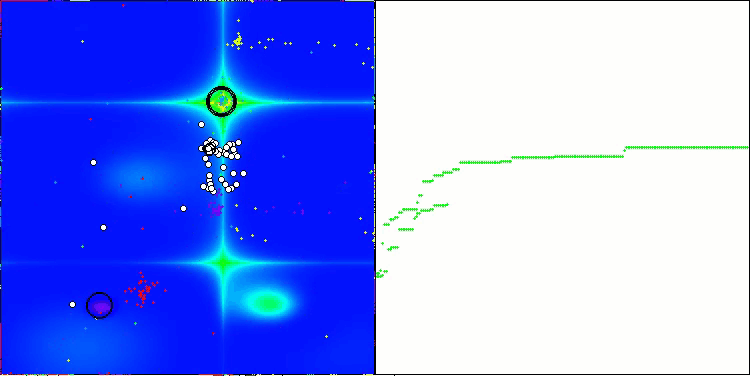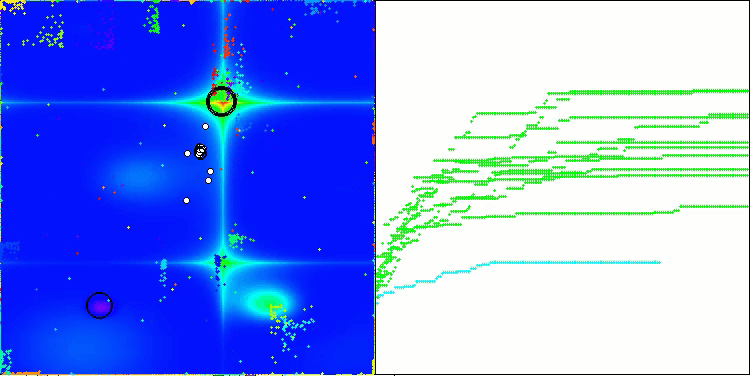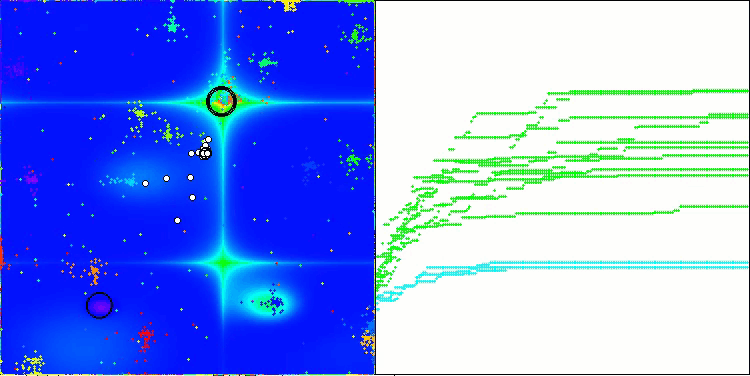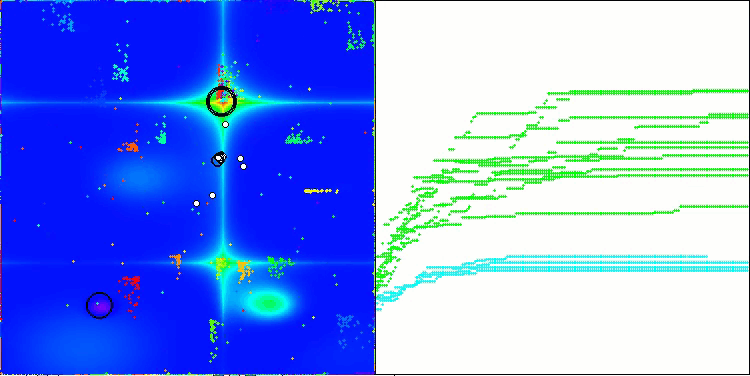
Forestテスト関数NOA

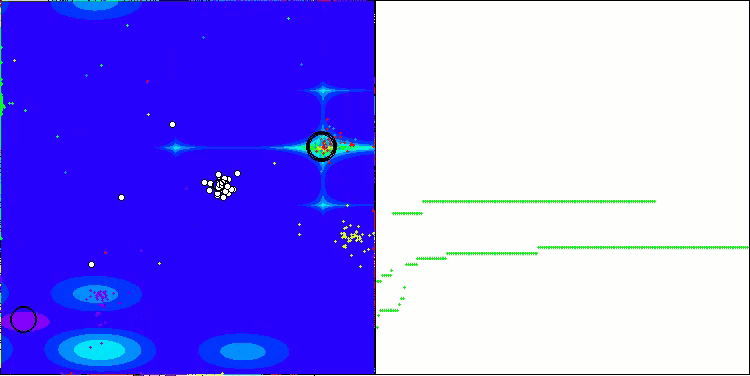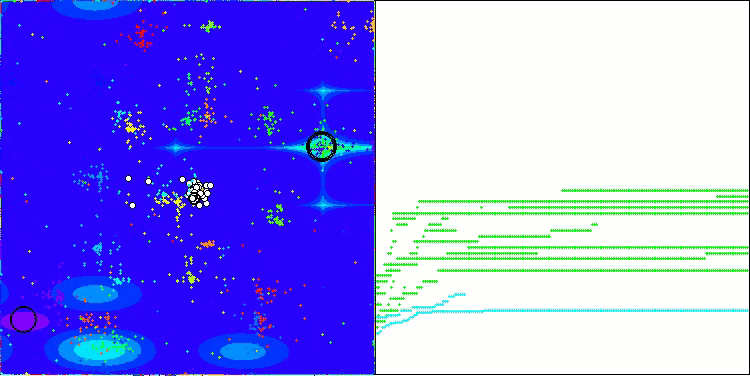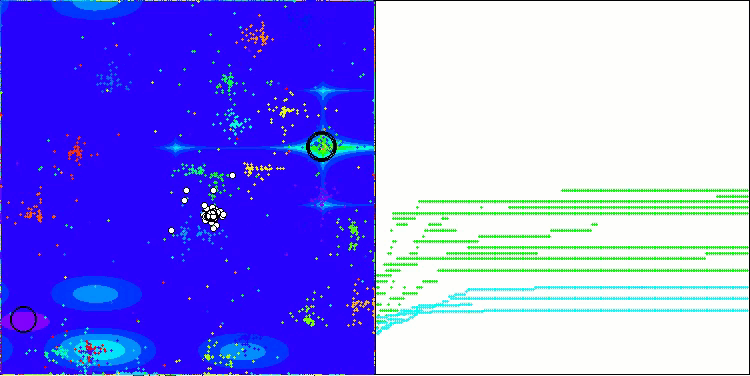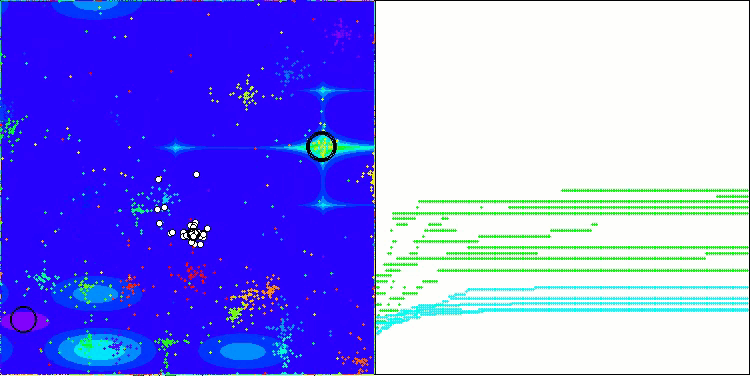
Megacityテスト関数のNOA

テストの結果、NOAアルゴリズムは高次元関数に対するテスト結果が得られていないため、別枠（通し番号なし）で記載されています。以下の表は、評価表に参加している他のアルゴリズムとの結果を比較分析するために提示されています。

#	AO	詳細	Hilly			Hilly最終	Forest			Forest最終	Megacity（離散）			Megacity最終	最終結果	MAXの%
#	AO	詳細	10p(5F)	50p(25F)	1000p(500F)	Hilly最終	10p(5F)	50p(25F)	1000p(500F)	Forest最終	10p(5F)	50p(25F)	1000p(500F)	Megacity最終	最終結果	MAXの%
1	ANS	across neighbourhood search	0.94948	0.84776	0.43857	2.23581	1.00000	0.92334	0.39988	2.32323	0.70923	0.63477	0.23091	1.57491	6.134	68.15
2	CLA	コードロックアルゴリズム(joo)	0.95345	0.87107	0.37590	2.20042	0.98942	0.91709	0.31642	2.22294	0.79692	0.69385	0.19303	1.68380	6.107	67.86
3	AMOm	動物移動最適化m	0.90358	0.84317	0.46284	2.20959	0.99001	0.92436	0.46598	2.38034	0.56769	0.59132	0.23773	1.39675	5.987	66.52
4	(P+O)ES	(P+O)進化戦略	0.92256	0.88101	0.40021	2.20379	0.97750	0.87490	0.31945	2.17185	0.67385	0.62985	0.18634	1.49003	5.866	65.17
5	CTA	彗星の尾アルゴリズム(joo)	0.95346	0.86319	0.27770	2.09435	0.99794	0.85740	0.33949	2.19484	0.88769	0.56431	0.10512	1.55712	5.846	64.96
6	TETA	時間進化移動アルゴリズム（joo）	0.91362	0.82349	0.31990	2.05701	0.97096	0.89532	0.29324	2.15952	0.73462	0.68569	0.16021	1.58052	5.797	64.41
7	SDSm	確率的拡散探索M	0.93066	0.85445	0.39476	2.17988	0.99983	0.89244	0.19619	2.08846	0.72333	0.61100	0.10670	1.44103	5.709	63.44
8	BOAm	ビリヤード最適化アルゴリズムM	0.95757	0.82599	0.25235	2.03590	1.00000	0.90036	0.30502	2.20538	0.73538	0.52523	0.09563	1.35625	5.598	62.19
9	AAm	アーチェリーアルゴリズムM	0.91744	0.70876	0.42160	2.04780	0.92527	0.75802	0.35328	2.03657	0.67385	0.55200	0.23738	1.46323	5.548	61.64
10	ESG	社会集団の進化(joo)	0.99906	0.79654	0.35056	2.14616	1.00000	0.82863	0.13102	1.95965	0.82333	0.55300	0.04725	1.42358	5.529	61.44
11	SIA	等方的焼きなまし(joo)	0.95784	0.84264	0.41465	2.21513	0.98239	0.79586	0.20507	1.98332	0.68667	0.49300	0.09053	1.27020	5.469	60.76
12	ACS	人工協調探索	0.75547	0.74744	0.30407	1.80698	1.00000	0.88861	0.22413	2.11274	0.69077	0.48185	0.13322	1.30583	5.226	58.06
13	DA	弁証法的アルゴリズム	0.86183	0.70033	0.33724	1.89940	0.98163	0.72772	0.28718	1.99653	0.70308	0.45292	0.16367	1.31967	5.216	57.95
14	BHAm	ブラックホールアルゴリズムM	0.75236	0.76675	0.34583	1.86493	0.93593	0.80152	0.27177	2.00923	0.65077	0.51646	0.15472	1.32195	5.196	57.73
15	ASO	無政府社会最適化	0.84872	0.74646	0.31465	1.90983	0.96148	0.79150	0.23803	1.99101	0.57077	0.54062	0.16614	1.27752	5.178	57.54
16	RFO	ロイヤルフラッシュ最適化（joo）	0.83361	0.73742	0.34629	1.91733	0.89424	0.73824	0.24098	1.87346	0.63154	0.50292	0.16421	1.29867	5.089	56.55
17	AOSm	原子軌道探索M	0.80232	0.70449	0.31021	1.81702	0.85660	0.69451	0.21996	1.77107	0.74615	0.52862	0.14358	1.41835	5.006	55.63
18	TSEA	亀甲進化アルゴリズム(joo)	0.96798	0.64480	0.29672	1.90949	0.99449	0.61981	0.22708	1.84139	0.69077	0.42646	0.13598	1.25322	5.004	55.60
19	DE	差分進化	0.95044	0.61674	0.30308	1.87026	0.95317	0.78896	0.16652	1.90865	0.78667	0.36033	0.02953	1.17653	4.955	55.06
20	SRA	レストラン経営達人アルゴリズム(SRA)	0.96883	0.63455	0.29217	1.89555	0.94637	0.55506	0.19124	1.69267	0.74923	0.44031	0.12526	1.31480	4.903	54.48
21	CRO	化学反応の最適化	0.94629	0.66112	0.29853	1.90593	0.87906	0.58422	0.21146	1.67473	0.75846	0.42646	0.12686	1.31178	4.892	54.36
22	BIO	血液型遺伝最適化(joo)	0.81568	0.65336	0.30877	1.77781	0.89937	0.65319	0.21760	1.77016	0.67846	0.47631	0.13902	1.29378	4.842	53.80
23	BSA	鳥群アルゴリズム	0.89306	0.64900	0.26250	1.80455	0.92420	0.71121	0.24939	1.88479	0.69385	0.32615	0.10012	1.12012	4.809	53.44
24	HS	ハーモニー検索	0.86509	0.68782	0.32527	1.87818	0.99999	0.68002	0.09590	1.77592	0.62000	0.42267	0.05458	1.09725	4.751	52.79
25	SSG	苗木の播種と育成	0.77839	0.64925	0.39543	1.82308	0.85973	0.62467	0.17429	1.65869	0.64667	0.44133	0.10598	1.19398	4.676	51.95
26	BCOm	細菌走化性最適化M	0.75953	0.62268	0.31483	1.69704	0.89378	0.61339	0.22542	1.73259	0.65385	0.42092	0.14435	1.21912	4.649	51.65
27	ABO	アフリカ水牛の最適化	0.83337	0.62247	0.29964	1.75548	0.92170	0.58618	0.19723	1.70511	0.61000	0.43154	0.13225	1.17378	4.634	51.49
28	(PO)ES	(PO)進化戦略	0.79025	0.62647	0.42935	1.84606	0.87616	0.60943	0.19591	1.68151	0.59000	0.37933	0.11322	1.08255	4.610	51.22
29	TSm	タブーサーチM	0.87795	0.61431	0.29104	1.78330	0.92885	0.51844	0.19054	1.63783	0.61077	0.38215	0.12157	1.11449	4.536	50.40
30	BSO	ブレインストーム最適化	0.93736	0.57616	0.29688	1.81041	0.93131	0.55866	0.23537	1.72534	0.55231	0.29077	0.11914	0.96222	4.498	49.98
31	WOAm	鯨最適化アルゴリズムM	0.84521	0.56298	0.26263	1.67081	0.93100	0.52278	0.16365	1.61743	0.66308	0.41138	0.11357	1.18803	4.476	49.74
32	AEFA	人工電界アルゴリズム	0.87700	0.61753	0.25235	1.74688	0.92729	0.72698	0.18064	1.83490	0.66615	0.11631	0.09508	0.87754	4.459	49.55
33	AEO	人工生態系ベースの最適化アルゴリズム	0.91380	0.46713	0.26470	1.64563	0.90223	0.43705	0.21400	1.55327	0.66154	0.30800	0.28563	1.25517	4.454	49.49
34	ACOm	蟻コロニー最適化M	0.88190	0.66127	0.30377	1.84693	0.85873	0.58680	0.15051	1.59604	0.59667	0.37333	0.02472	0.99472	4.438	49.31
35	BFO-GA	細菌採食の最適化：Ga	0.89150	0.55111	0.31529	1.75790	0.96982	0.39612	0.06305	1.42899	0.72667	0.27500	0.03525	1.03692	4.224	46.93
36	SOA	シンプル最適化アルゴリズム	0.91520	0.46976	0.27089	1.65585	0.89675	0.37401	0.16984	1.44060	0.69538	0.28031	0.10852	1.08422	4.181	46.45
37	ABHA	人工蜂の巣アルゴリズム	0.84131	0.54227	0.26304	1.64663	0.87858	0.47779	0.17181	1.52818	0.50923	0.33877	0.10397	0.95197	4.127	45.85
38	ACMO	大気雲モデルの最適化	0.90321	0.48546	0.30403	1.69270	0.80268	0.37857	0.19178	1.37303	0.62308	0.24400	0.10795	0.97503	4.041	44.90
39	ADAMm	適応モーメント推定M	0.88635	0.44766	0.26613	1.60014	0.84497	0.38493	0.16889	1.39880	0.66154	0.27046	0.10594	1.03794	4.037	44.85
40	CGO	カオスゲーム最適化	0.57256	0.37158	0.32018	1.26432	0.61176	0.61931	0.62161	1.85267	0.37538	0.21923	0.19028	0.78490	3.902	43.35
41	ATAm	人工部族アルゴリズムM	0.71771	0.55304	0.25235	1.52310	0.82491	0.55904	0.20473	1.58867	0.44000	0.18615	0.09411	0.72026	3.832	42.58
42	ASHA	人工シャワーアルゴリズム	0.89686	0.40433	0.25617	1.55737	0.80360	0.35526	0.19160	1.35046	0.47692	0.18123	0.09774	0.75589	3.664	40.71
43	ASBO	適応型社会行動最適化(ASBO)	0.76331	0.49253	0.32619	1.58202	0.79546	0.40035	0.26097	1.45677	0.26462	0.17169	0.18200	0.61831	3.657	40.63
44	MEC	mind evolutionary computation	0.69533	0.53376	0.32661	1.55569	0.72464	0.33036	0.07198	1.12698	0.52500	0.22000	0.04198	0.78698	3.470	38.55
45	CSA	円探索アルゴリズム	0.66560	0.45317	0.29126	1.41003	0.68797	0.41397	0.20525	1.30719	0.37538	0.23631	0.10646	0.71815	3.435	38.17
	NOA	ニューロボイド最適化アルゴリズム(joo)	0.70135	0.40129	0.00000	1.10264	0.62230	0.30830	0.00000	0.93060	0.45231	0.20892	0.00000	0.66123	2.694	29.94
	RW	ランダムウォーク	0.48754	0.32159	0.25781	1.06694	0.37554	0.21944	0.15877	0.75375	0.27969	0.14917	0.09847	0.52734	2.348	26.09

まとめ

NOAの開発にあたり、ニューラルネットワークと最適化アルゴリズムという2つの世界を融合させることを目標としました。その結果は、ある意味では予想通りであり、同時に予想外でもありました。

このアルゴリズムにおいて私が最も魅力を感じている点は、その生物学的妥当性です。私たちはしばしば複雑なモデルを作ろうとしますが、自然界は何百万年もの間、単純な生物の集合知によって効率的な解を示してきました。ニューロボイドは、この自然の知恵をアルゴリズムとして具現化しようとする試みです。

さまざまな関数に対するテストでは、有望な結果が得られました。約45%の効率は、概念的に新しいアプローチとしては十分に良い出発点だと考えています。アルゴリズムは中程度の複雑さを持つタスクにおいて良好に機能することが確認されました。一方で、重大な制約も存在します。問題規模が大きくなるとスケーラビリティの問題が顕著になり、1000変数では複数のニューラルネットワークを学習させる必要があるため、計算負荷が現実的ではなくなります。

NOAの特に興味深い点は、探索戦略を自己学習できる能力です。固定ルールに基づく従来のメタヒューリスティックとは異なり、ニューロボイドは学習を通じて行動を適応させます。

実行ごとの結果にばらつきが見られる点には二面性があります。一方では予測性の欠如を意味しますが、他方では探索戦略の多様性を示しており、複雑な最適化ランドスケープでは利点となり得ます。

NOAアルゴリズムの今後の発展方向として、以下の点が考えられます。

計算負荷を低減するためのニューラルネットワーク構造の最適化
ニューロボイド間での知識転移メカニズムの実装

最終的に、NOAは単なる新しい最適化手法ではありません。単純なシステムがいかにして複雑な振る舞いを生み出すかを理解するための一歩です。これは、機械学習とメタヒューリスティック最適化、個の知能と集合知の境界を探る試みでもあります。

このアプローチは、関数最適化にとどまらず、適応行動のモデリングや、根本的に新しい人工知能アーキテクチャの探索といった、より広い分野での可能性を秘めていると私は考えています。複雑さが当たり前となりつつある世界において、適切に構成された単純さが、予想外に興味深い解を生み出すこともあるのです。

総じて、NOAアルゴリズムは最適化問題に対する完成された解として捉えるべきではなく、研究の出発点となる基盤、そして最適化全般および機械学習分野における有望な解法創出のための足がかりとして位置づけるべきものです。

Tab

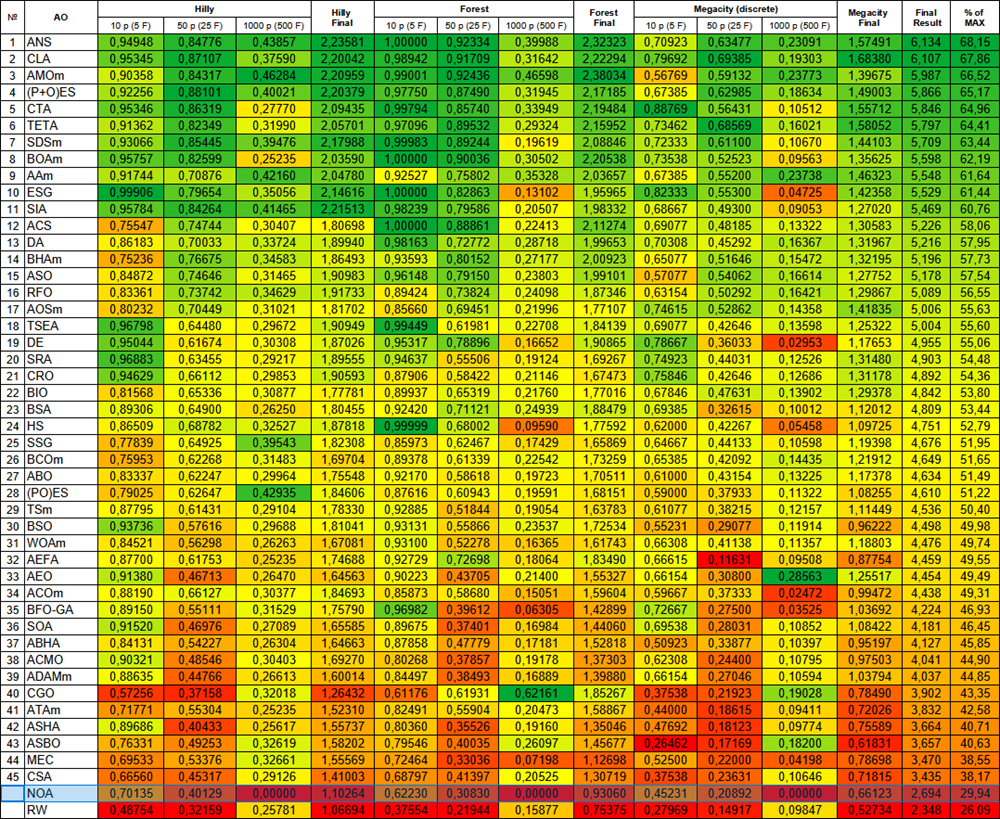
図2：対応するテストに応じたアルゴリズムのカラーグラデーション

チャート

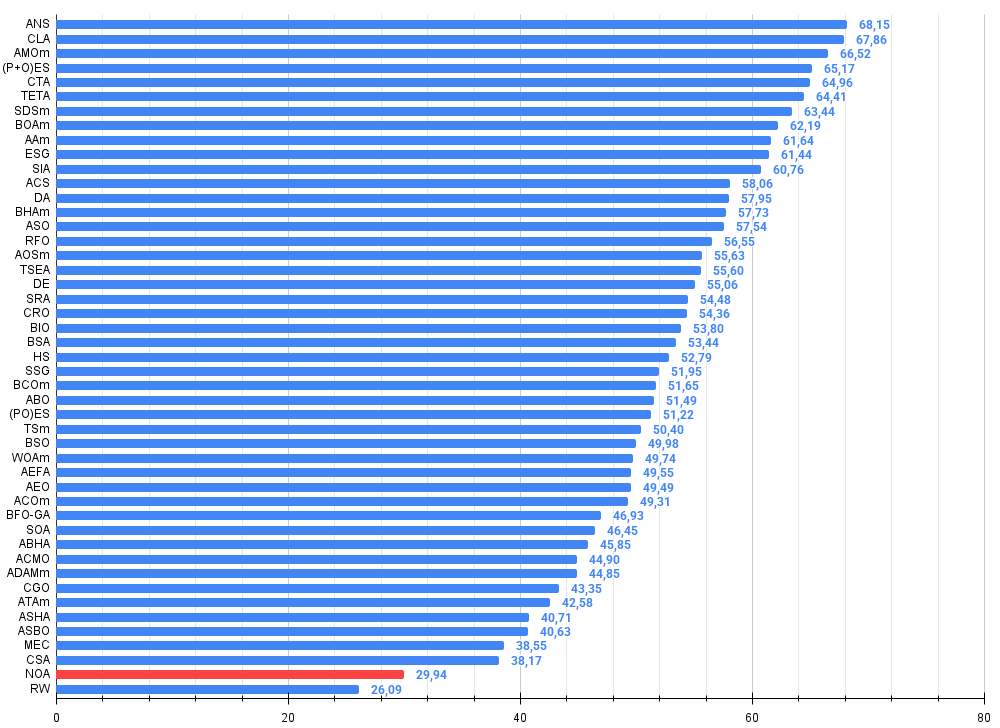
図3：アルゴリズムテスト結果のヒストグラム（0から100のスケール、高いほど良い）100は理論上の最大値であり、アーカイブには評価表を計算するためのスクリプトがあります。

NOAの長所と短所

長所

実装がシンプル
興味深い結果

短所

実行時間が長いため、多次元空間の結果は得られなかった

この記事には、最新版のアルゴリズムコードを含むアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。

github：https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5

記事で使用されているプログラム

#	名前	種類	詳細
1	#C_AO.mqh	インクルード	集団最適化の親クラスアルゴリズム
2	#C_AO_enum.mqh	インクルード	集団最適化アルゴリズムの列挙
3	MLPa.mqh	インクルード	ADAMを用いたMLPニューラルネットワーク
4	TestFunctions.mqh	インクルード	テスト関数のライブラリ
5	TestStandFunctions.mqh	インクルード	テストスタンド関数ライブラリ
6	Utilities.mqh	インクルード	補助関数のライブラリ
7	CalculationTestResults.mqh	インクルード	比較表の結果を計算するスクリプト
8	Testing AOs.mq5	スクリプト	すべての集団最適化アルゴリズムの統一テストスタンド
9	Simple use of population optimization algorithms.mq5	スクリプト	可視化せずに集団最適化アルゴリズムを使用する簡単な例
10	Test_AO_NOA.mq5	スクリプト	NOAテストスタンド

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/16992

添付されたファイル |

ZIPをダウンロード

NOA.zip (181.52 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。

この著者による他の記事

ディスカッションに移動

EAのサンプル

一般的なMACDを使ったEAを例として、MQL4開発の原則を紹介します。

PythonでリモートFXリスク管理システムを構築する

Pythonで動作するリモートの外国為替リスク管理システムを構築しており、サーバーにも段階的に展開しています。本記事を通して、プログラムでFXのリスクを管理する方法や、FXの資金を無駄にしない方法を学んでいきます。

エラー 146 (「トレードコンテキストビジー」) と、その対処方法

この記事では、MT4において複数のEAの衝突をさける方法を扱います。ターミナルの操作、MQL4の基本的な使い方がわかる人にとって、役に立つでしょう。

レストラン経営達人アルゴリズム(SRA)

レストラン経営達人アルゴリズム(SRA)は、レストラン経営の原則に着想を得た革新的な最適化手法です。従来のアプローチとは異なり、SRAは弱い解を破棄するのではなく、成功した解の要素と組み合わせて改善します。このアルゴリズムは競争力のある結果を示し、最適化問題における探索と活用のバランスに関する新しい視点を提供します。