MetaTrader 5 / トレーディングシステム
English Русский 中文 Español Português
preview
ロイヤルフラッシュ最適化(RFO)

ロイヤルフラッシュ最適化(RFO)

MetaTrader 5 — トレーディングシステム |
30 2
Andrey Dik
Andrey Dik

内容

  1. はじめに
  2. アルゴリズムの実装
  3. テスト結果


はじめに

最適化問題を解決するためのアプローチは数多く存在しますが、その中でも遺伝的アルゴリズムは、自然進化の過程を模倣することで探索空間を効率的に探索できる点から、特別な位置を占めています。従来の遺伝的アルゴリズムでは、解を二進数で符号化する方法が用いられており、実数値を二進形式へ変換する必要があります。この変換は、追加の複雑さをもたらすだけでなく、アルゴリズム全体を大幅に重くしてしまいます。現代においては計算コストの最小化が決定的な役割を果たしており、手法の生産性はその処理速度にほぼ比例すると言えます。こうした問題を解決する過程で、遺伝的演算子を保持しつつ、実数値を変換する最も計算負荷の高い処理を、より単純で計算負荷の少ない操作に置き換えるというアイデアに至りました。

私の提案するロイヤルフラッシュ最適化(RFO)アルゴリズムは、遺伝的アルゴリズムの主要な利点を維持しながら、解をより直接的に表現する新しい最適化手法です。その中核となるアイデアは、探索空間の各座標をセクターに分割することであり、これはポーカーの手札が特定のランクを持つカードで構成されることに似ています。ビット列を扱う代わりに、本アルゴリズムではマップ上のランク（セクター番号）を操作するため、探索空間のトポロジーを自然な形で保持することが可能になります。

私の意見では、提案されたアプローチの主な利点は、実装の単純さと直感的な明快さ（「マップ」での作業はビット文字列よりも視覚的です）、そして遺伝的アルゴリズムの組み合わせ特性を維持しながら実数をエンコードおよびデコードする必要がないことです。本記事では、アルゴリズムの実装と意思決定の修正演算子の特徴について詳しく検討します。

ポーカーの比喩は、アルゴリズムの名称を与えているだけでなく、その本質を的確に表現しています。ポーカーにおいてプレイヤーが最良のカードの組み合わせを集めようとするように、このアルゴリズムも異なる解のセクターを組み合わせ、徐々に最適な「手札」を形成していきます。ポーカーでは各カードが固有のランクとスートを持つのと同様に、アルゴリズムにおいても各セクターは探索空間内で固有の値と位置を持っています。この場合も実際のゲームと同じく、個々のカードの価値だけでなく、全体の組み合わせにおける相互作用が重要となります。

なお、このアプローチは、離散最適化の考え方を連続空間へ一般化したものと捉えることができ、理論的解析および実用的応用の両面で興味深い展望を開くものです。ポーカーが偶然性と戦略性を組み合わせたゲームであるのと同様に、RFOはランダム探索と指向的最適化を融合させており、複雑な多変量問題に対して高い有効性を発揮します。


アルゴリズムの実装

ロイヤルフラッシュ最適化(RFO)アルゴリズムは、探索空間を離散的なセクターとして表現するという考え方に基づいています。これは、ポーカーにおいてカードが特定のランクを持つことに類似しています。従来の遺伝的アルゴリズムでは、すべての座標に対応する値（最適化対象のパラメータ）を二進コードに変換し、それらを染色体のようなシーケンスにまとめますが、この処理には追加の計算コストが必要となります。RFOでは、このアプローチを放棄し、より単純で直感的な表現方法を採用しています。

二進符号化の代わりに、探索空間の各座標をセクターに分割し、それぞれにポーカーのカードになぞらえた値、すなわちジャック、クイーン、キング、エース（J、Q、K、A）のようなランクを割り当てます。ランク（セクター）の数は、アルゴリズムの外部パラメータとして指定され、任意の整数値を取ることができます。これにより、探索空間内の任意の点はランクの組み合わせとして表現され、各マップはその座標に対応する特定のセクターを示します。この手法は計算を単純化するだけでなく、遺伝的アルゴリズムが持つ組み合わせ的な特性をそのまま保持します。

最適化の過程において、アルゴリズムは「手札」、すなわち異なる解を表すカードの集合を扱います。交叉および突然変異の演算子は、二進変換をおこなうことなく、これらの「手札」（カード集合）に直接適用されます。各手札は染色体に相当し、この仕組みによって探索空間を効率的に探索することが可能になります。

以下の図（図1）は、この原理を明確に示しています。X、Y、Zの3つの座標を持つ3次元探索空間が描かれており、各座標はカードデッキのランクに対応するセクターに分割されています。右側には「手札」の例が示されており、アルゴリズムが最適解を探索する過程で形成するさまざまなカードの組み合わせが表現されています。

RFO

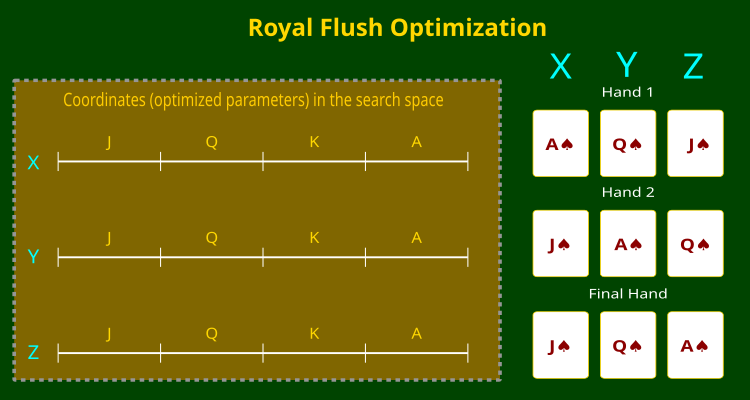
図1：RFOアルゴリズムとカードデッキのランクによる座標分割

ロイヤルフラッシュ最適化(RFO)アルゴリズムの擬似コードの作成に進みます。

  • 初期
    • 「ポーカーテーブル」のプレイヤー数（集団サイズ）を設定する
    • 「デッキ」のサイズ（各次元のセクター数）を決定する
    • 「ブラフ」の確率（突然変異）を設定する
    • 初期の「手札」を作成する：各座標のカードランクをランダムに生成する
    • ランクをセクター内のランダムオフセットで実数値に変換する
  • メインゲームループ
    • テーブル上の各ポジションについて繰り返す
      • 二次選択法を用いて「対戦相手」を選ぶ（強い「手札」の方が選ばれる確率が高い）
      • 現在の「手札」（解）をコピーする
      • 3点カード交換をおこなう
        • 3つの「カット」ポイントをランダムに選ぶ
        • 「カット」ポイントをソートする
        • 開始ポイント（0または1）をランダムに選び
        • 現在の手札と対戦相手の手札の間でカードを交換する
        • 「ブラフ」（突然変異確率）が可能：与えられた確率でカードランクをランダムに変更する
      • 得られたマップランクを実際の座標値に変換する
  • 評価と更新
    • 各「手札」の値（目的関数値）を計算する
    • 見つかった最良の組み合わせ（大域最適解）を記録する
    • 現在の手札と前のデッキを組み合わせる
    • すべての「手札」を値順にソートする
    • 最良の「手札」が次世代に進む
  • 停止条件に達したらアルゴリズムを終了する

    • 次に、アルゴリズムコードの作成に進みます。ゲームプレイの文脈で「手札」に関する情報を持つオブジェクトを表すS_RFO_Agent構造体のコードを作成します。

    構造体フィールド

    • card []：カードの実数値を格納する配列
    • f：手札の値（適合度関数の値）
    • cardRanks []：「カードランク」（セクター番号）を整数で表す配列

    Init()メソッドは構造体を初期化します。coordsというパラメータを1つ取り、これは「手札」のカード数を指定します。

    //——————————————————————————————————————————————————————————————————————————————
// Structure for representing a single "hand"
struct S_RFO_Agent
{
    double card [];       // cards
    double f;             // value of the fitness function ("hand value")
    int    cardRanks [];  // sector numbers ("map ranks") 

    void Init (int coords)
    {
      ArrayResize (cardRanks, coords);
      ArrayResize (card,      coords);
      f = -DBL_MAX;       // initialization with minimum value
    }
};
//——————————————————————————————————————————————————————————————————————————————

    C_AO_RFOクラスはアルゴリズムを実装しており、C_AO基底クラスからプロパティとメソッドを継承しています。詳しく見てみましょう。

    C_AO_RFO()コンストラクタはクラス変数の値を設定し、パラメータを初期化します。
    • popSize：集団サイズ（ポーカーテーブル）は50に設定される
    • deckSize：デッキ内のカード数（またはセクター数）は1000に設定される
    • dealerBluff：ブラフの確率（突然変異）は3％ (0.03)に設定される
    • params配列：パラメータを格納するために使用され、3要素にリサイズされ、popSize、deckSize、dealerBluffに対応する値で埋められる

    SetParams ()メソッド：params配列から値を取り出し、対応するクラス変数に割り当てる

    Init()メソッド：最適化するパラメータの最小値と最大値、およびそれらのステップなど、渡されたパラメータを使用してクラスを初期化するように設計されている

    Moving ()メソッドとRevision()メソッド：手札のカードをシャッフルしたり、最良の組み合わせを更新したりする操作をおこなう

    クラスフィールド
    • deckSize：次元内のセクター数
    • dealerBluff：突然変異の確率
    • deck []、tempDeck []、hand []：S_RFO_Agent型の配列で、順にメインデッキ、ソート用の一時デッキ、現在の手札（子孫）を表す
    privateクラスメンバ
    • cutPoints：手札のカードセットの「カット」ポイントの数で、カードセットの組み合わせに使用される
    • tempCuts []とfinalCuts []：一時的および最終的な「カット」ポイントのインデックスを格納する配列
    • 使用されるメソッドには、Evolution()、DealCard()、ShuffleRanks()があります。Evolution()はカードの順列の基本的な進化を実行する役割があります。DealCard()はセクターを実際の値に変換する役割があります。ShuffleRanks()はランクを突然変異させる役割があり、利用可能なランクの中からランダムに選択します。
      //——————————————————————————————————————————————————————————————————————————————
class C_AO_RFO : public C_AO
{
  public:
  C_AO_RFO ()
  {
    ao_name = "RFO";
    ao_desc = "Royal Flush Optimization";
    ao_link = "https://www.mql5.com/ja/articles/17063";

    popSize      = 50;      // "poker table" (population) size
    deckSize     = 1000;    // number of "cards" in the deck (sectors)
    dealerBluff  = 0.03;    // "bluff" (mutation) probability

    ArrayResize (params, 3);

    params [0].name = "popSize";      params [0].val = popSize;
    params [1].name = "deckSize";     params [1].val = deckSize;
    params [2].name = "dealerBluff";  params [2].val = dealerBluff;
  }

  void SetParams ()
  {
    popSize     = (int)params [0].val;
    deckSize    = (int)params [1].val;
    dealerBluff = params      [2].val;
  }

  bool Init (const double &rangeMinP  [],  // minimum values
             const double &rangeMaxP  [],  // maximum values
             const double &rangeStepP [],  // step change
             const int     epochsP = 0);   // number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  int    deckSize;         // number of sectors in the dimension
  double dealerBluff;      // mutation probability

  S_RFO_Agent deck [];     // main deck (population)
  S_RFO_Agent tempDeck []; // temporary deck for sorting
  S_RFO_Agent hand [];     // current hand (descendants)

  private: //-------------------------------------------------------------------
  int cutPoints;           // number of cutting points
  int tempCuts  [];        // temporary indices of cutting points
  int finalCuts [];        // final indices taking the beginning and end into account

  void   Evolution ();     // main process of evolution
  double DealCard (int rank, int suit);  // convert sector to real value
  void   ShuffleRanks (int &ranks []);   // rank mutation
};
//——————————————————————————————————————————————————————————————————————————————

      Initメソッドは、C_AO_RFOクラスのオブジェクトを初期化するために使用されます。

      メソッドはまず、最小値や最大値、パラメータの変化ステップなど、与えられたパラメータの標準的な初期化をおこなう関数を呼び出すことから始まります。この初期化に失敗した場合、メソッドは終了し、falseを返します。パラメータの初期化が成功した後、メソッドは「手札」と「デッキ」に関する情報を格納するためのデータ構造の準備をおこないます。具体的には、手札やデッキを格納する配列のサイズを集団サイズに合わせて変更します。

      次に、手札配列の各要素を、指定された座標に基づいて設定する特別なメソッドを使って初期化します。同様に、デッキ配列および一時デッキ配列も準備され、初期化されます。メソッドは交叉アルゴリズムに必要なカットポイントの数を設定します。この場合、実験により最適とされた3つのカットポイントが設定されます。その後、一時的および最終的なカットポイントを格納するための配列が用意されます。最後に、メソッドはtrueを返し、初期化が正常に完了したことを確認します。

      //——————————————————————————————————————————————————————————————————————————————
bool C_AO_RFO::Init (const double &rangeMinP  [],
                     const double &rangeMaxP  [],
                     const double &rangeStepP [],
                     const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  // Initialize structures for storing "hands" and "decks"
  ArrayResize (hand, popSize);
  for (int i = 0; i < popSize; i++) hand [i].Init (coords);

  ArrayResize (deck,     popSize * 2);
  ArrayResize (tempDeck, popSize * 2);
  for (int i = 0; i < popSize * 2; i++)
  {
    deck     [i].Init (coords);
    tempDeck [i].Init (coords);
  }

  // Initialize arrays for cutting points
  cutPoints = 3;  // three cutting points for a "three-card" crossover
  ArrayResize (tempCuts,  cutPoints);
  ArrayResize (finalCuts, cutPoints + 2);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

      Movingメソッドは、RFOアルゴリズムにおける集団の状態を「移動」させたり更新したりする処理を担当します。

      ステータスの確認：メソッドはまず、初期のカード配布が完了しているかどうかを確認する条件をチェックすることから開始します。初期化が完了していない場合(revision == false)、メソッドは初期化をおこないます。

      初期分布の初期化：初期分布の初期化では、集団のすべての要素を順に処理します。各要素（各「手札」）に対して、必要な枚数のカードセットを作成します。内側のループでは、必要なカード枚数ごとに次の処理をおこないます。

      • デッキからランダムにカードランクを選択する
      • 生成されたランクに基づいてカードを配るためのメソッドを呼び出す
      • 得られたマップが指定範囲内に収まっているかをチェックし、必要に応じて指定パラメータに従って調整する
      • 取得したマップの値をa配列に設定する

      状態の更新：初期化が完了した後、状態を更新するためにrevisionフラグはtrueに設定され、初期分布が完了しており、追加の再初期化が不要であることを示します。

      すでに初期配布がおこなわれている場合、メソッドはEvolution()メソッドを呼び出し、手札のシャッフルおよびカードを配る進化的なプロセスを実行します。

      //——————————————————————————————————————————————————————————————————————————————
void C_AO_RFO::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    // Initialize the initial "distribution"
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        hand [i].cardRanks [c] = u.RNDminusOne (deckSize);
        hand [i].card      [c] = DealCard (hand [i].cardRanks [c], c);
        hand [i].card      [c] = u.SeInDiSp (hand [i].card [c], rangeMin [c], rangeMax [c], rangeStep [c]);

        a [i].c [c] = hand [i].card [c];
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  Evolution ();
}
//——————————————————————————————————————————————————————————————————————————————

      Revisionメソッドは、「手札」の最良な「組み合わせ」を見つけ、それらの適合度を評価し、全体のデッキを更新する役割を担います。

      最適な組み合わせを見つける

      • メソッドはまず、集団内で最良の手札のインデックスを保持するためのbestHand変数を初期化することから始まります。
      • 次に、0からpopSizeまでのすべての集団要素を順に走査するループを実行します。このループの中で、各手札の適合度値を現在の最良値fBと比較します。
      • 現在の手札の適合度がfBより大きい場合には、最良値を更新し、その手札のインデックスをbestHand変数に代入します。

      最良の手札が見つかると、そのカード情報はcB配列にコピーされます。これにより、最良の組み合わせ、すなわち大域最適解の状態が保存されます。その後、hand配列内の各手札について、適合度値を対応するa配列の値と同一に更新します。これは、各手札の適合度情報を常に最新の状態に保つために必要な処理です。適合度の更新が完了した後、hand配列に含まれる現在の手札は、集団サイズpopSizeの位置から全体デッキであるdeck配列に追加されます。これは、deck配列の後半、すなわち集団の第2半分に相当します。

      最後に、tempDeckという一時配列を用いてdeck配列全体をソートし、組み合わせの値に基づいてデッキを整列させます。この処理により、価値の高いカードの組み合わせが、以降の選択で高い確率で選ばれ、その後の組み合わせ処理に有利に働くようになります。

      //——————————————————————————————————————————————————————————————————————————————
void C_AO_RFO::Revision ()
{
  // Search for the best "combination"
  int bestHand = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      bestHand = i;
    }
  }

  if (bestHand != -1) ArrayCopy (cB, a [bestHand].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  // Update fitness values
  for (int i = 0; i < popSize; i++)
  {
    hand [i].f = a [i].f;
  }

  // Add current hands to the general deck
  for (int i = 0; i < popSize; i++)
  {
    deck [popSize + i] = hand [i];
  }

  // Sort the deck by combination value
  u.Sorting (deck, tempDeck, popSize * 2);
}
//——————————————————————————————————————————————————————————————————————————————

      Evolutionメソッドはアルゴリズムの中核となるロジックを担当しており、テーブル上のプレイヤーの「手札」間でカードの交換をおこない、「ブラフ」が発生し、カードの実数値が更新されます。

      メソッドはまず、集団内のすべての要素を順に処理するループから開始します。このループ内で、以下の処理が実行されます。

      対戦相手の選択

      • 対戦相手を選択するために乱数が生成され、その値を二乗することで選択圧を高めます。これにより、対戦相手が選ばれる確率はその評価値と関連付けられ、より優れた手札が選択されやすくなります。
      • 生成された乱数はu.Scale関数によってスケーリングされ、対戦相手のインデックスが取得されます。

      その後、現在の手札はdeck配列からhand配列にコピーされます。次に、カード交換に使用するランダムな「カット」ポイントが生成されます。これらのポイントは、2つの手札間でどのカードを交換するかを決定するためのものです。カットポイントはソートされ、その前後に境界が追加されます。最初の境界は0に設定され、最後の境界はcoords-1に設定されます。続いて、u.RNDbool()を用いてカード交換を開始するランダムな開始点が選択されます。カード交換が完了した後、指定された確率に基づいて「ブラフ」がおこなわれる可能性があります。

      ランクを実際の値に変換する
      • 最後のループでは、カードランクがDealCardメソッドを用いて実数値に変換され、その値が設定された境界内に収まっているかが確認されます。
      • その後、最終的なカード情報を格納するa配列の値が更新されます。

      //——————————————————————————————————————————————————————————————————————————————
void C_AO_RFO::Evolution ()
{
  // For each position at the table
  for (int i = 0; i < popSize; i++)
  {
    // Select an opponent based on their rating (probability squared to enhance selection)
    double rnd = u.RNDprobab ();
    rnd *= rnd;
    int opponent = (int)u.Scale (rnd, 0.0, 1.0, 0, popSize - 1);

    // Copy the current hand
    hand [i] = deck [i];

    // Define cutting points for card exchange
    for (int j = 0; j < cutPoints; j++)
    {
      tempCuts [j] = u.RNDminusOne (coords);
    }

    // Sort cutting points and add borders
    ArraySort (tempCuts);
    ArrayCopy (finalCuts, tempCuts, 1, 0, WHOLE_ARRAY);
    finalCuts [0] = 0;
    finalCuts [cutPoints + 1] = coords - 1;

    // Random selection of a starting point for exchange
    int startPoint = u.RNDbool ();

    // Exchange cards between hands
    for (int j = startPoint; j < cutPoints + 2; j += 2)
    {
      if (j < cutPoints + 1)
      {
        for (int len = finalCuts [j]; len < finalCuts [j + 1]; len++) hand [i].cardRanks [len] = deck [opponent].cardRanks [len];
      }
    }

    // Possibility of "bluffing" (mutation)
    ShuffleRanks (hand [i].cardRanks);

    // Convert ranks to real values
    for (int c = 0; c < coords; c++)
    {
      hand [i].card [c] = DealCard (hand [i].cardRanks [c], c);
      hand [i].card [c] = u.SeInDiSp (hand [i].card [c], rangeMin [c], rangeMax [c], rangeStep [c]);

      a [i].c [c] = hand [i].card [c];
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

      DealCardメソッドは、ロイヤルフラッシュ最適化アルゴリズムにおける重要な要素であり、探索空間の離散的なセクターを連続的な座標値に変換します。このメソッドは2つのパラメータを入力として受け取ります。rankはカードのランクを表し、suitは座標インデックス（スート）を表します。

      この変換は2つの段階で構成されます。まず、探索空間全体の範囲をセクター数で割ることで、1つのセクターの大きさであるsuitRangeを計算します。次に、選択されたセクター内で具体的な値を生成します。u.RNDprobab()によるランダムオフセットは、各セクター内での空間探索を一様におこなうことを保証し、rankは探索空間における基準位置を決定します。

      この手法により、セクターによる解の離散的な表現と連続的な探索空間を組み合わせることが可能となり、大域探索と局所探索のバランスが実現されます。

      //——————————————————————————————————————————————————————————————————————————————
double C_AO_RFO::DealCard (int rank, int suit)
{
  // Convert the map rank to a real value with a random offset within the sector
  double suitRange = (rangeMax [suit] - rangeMin [suit]) / deckSize;
  return rangeMin [suit] + (u.RNDprobab () + rank) * suitRange;
}
//——————————————————————————————————————————————————————————————————————————————

      ShuffleRanksメソッドは、ロイヤルフラッシュ最適化アルゴリズムにおける突然変異メカニズムを実装しており、カードランクを扱う際の「ブラフ」として機能します。このメソッドは、ランク配列を参照渡しで受け取り、各座標について順に処理をおこないます。そして、dealerBluffで指定された確率に基づいて、現在のランクをデッキ内の有効なランク範囲からランダムに選択された値に置き換えます。この処理は、ポーカーにおいてプレイヤーが予期せず手札のカードを入れ替える状況に例えることができ、ゲームに不確実性の要素を導入します。この突然変異メカニズムは、アルゴリズムが局所最適解に陥るのを防ぎ、最適化の過程において解の多様性を維持することを目的としています。

      //——————————————————————————————————————————————————————————————————————————————
void C_AO_RFO::ShuffleRanks (int &ranks [])
{
  // Rank shuffle (mutation)
  for (int i = 0; i < coords; i++)
  {
    if (u.RNDprobab () < dealerBluff) ranks [i] = (int)MathRand () % deckSize;
  }
}
//——————————————————————————————————————————————————————————————————————————————


      テスト結果

      RFOアルゴリズムのテスト結果

      RFO|Royal Flush Optimization|50.0|1000.0|0.03|
      =============================
      5 Hilly's; Func runs:10000; result:0.8336125672709654
      25 Hilly's; Func runs:10000; result:0.7374210861383783
      500 Hilly's; Func runs:10000; result:0.34629436610445113
      =============================
      5 Forest's; Func runs:10000; result:0.8942431024645086
      25 Forest's; Func runs:10000; result:0.7382367793268382
      500 Forest's; Func runs:10000; result:0.24097956383750824
      =============================
      5 Megacity's; Func runs:10000; result:0.6315384615384616
      25 Megacity's; Func runs:10000; result:0.5029230769230771
      500 Megacity's; Func runs:10000; result:0.16420769230769366
      =============================
      All score:5.08946 (56.55%)

      最終スコアの56.55%は非常に立派な結果です。可視化においては、アルゴリズムは特定の挙動を示しておらず、個々の点が混沌とした挙動を示しているように見えます。

      Hilly

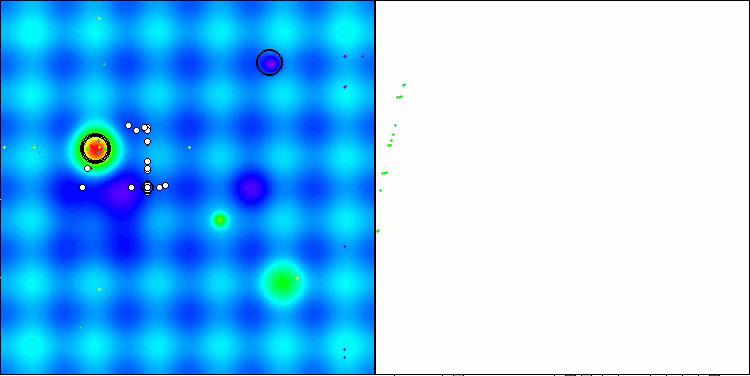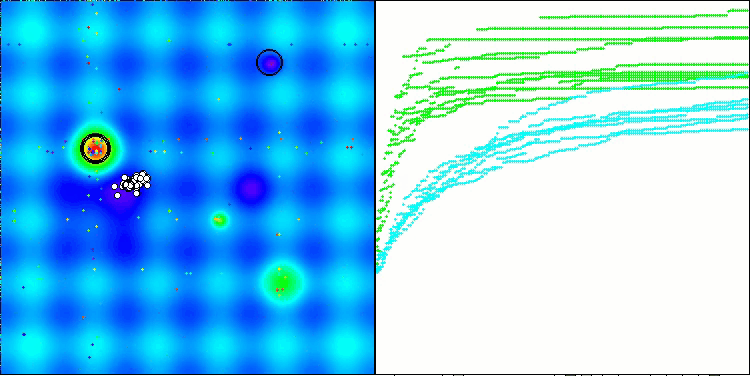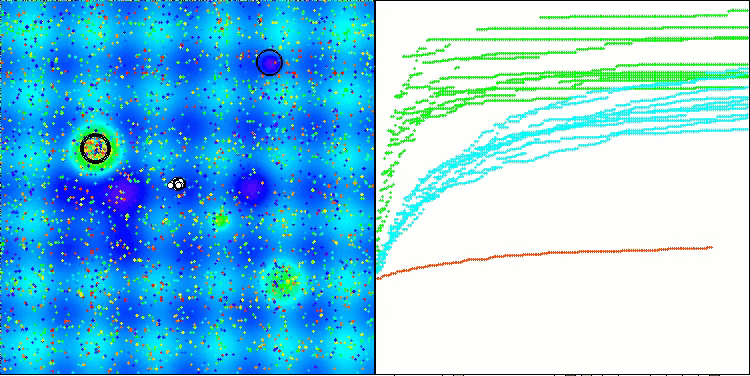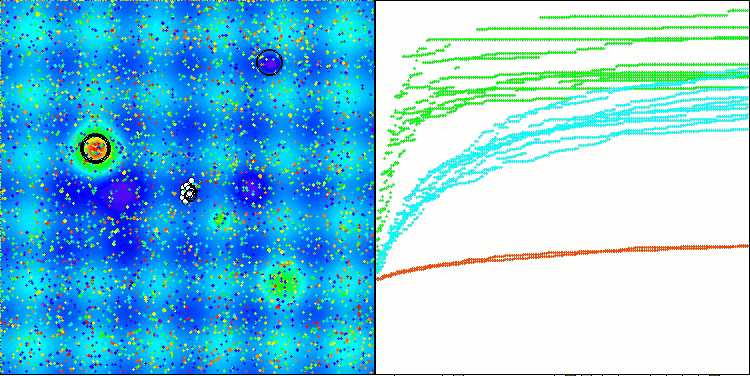
        Hillyテスト関数のRFO

      Forest

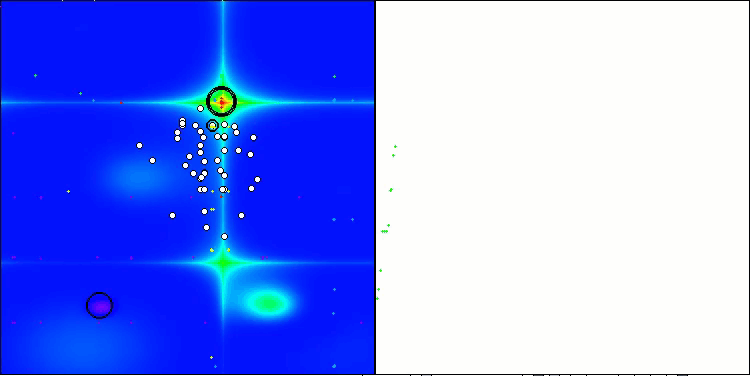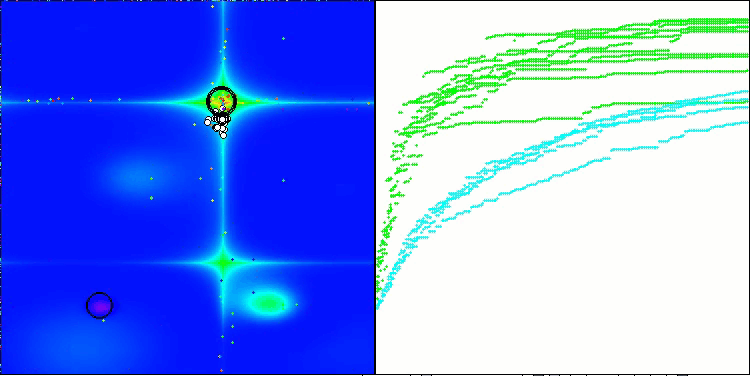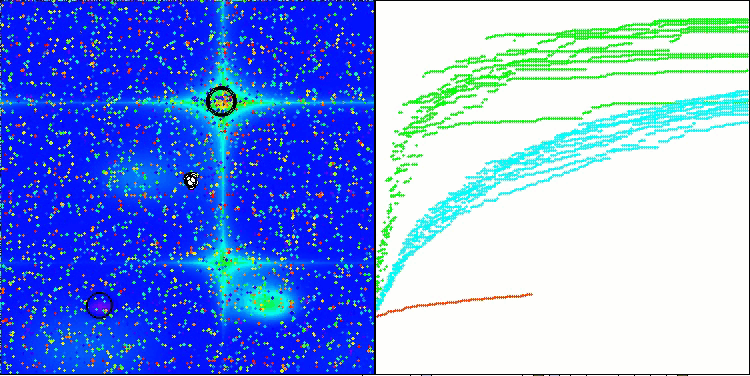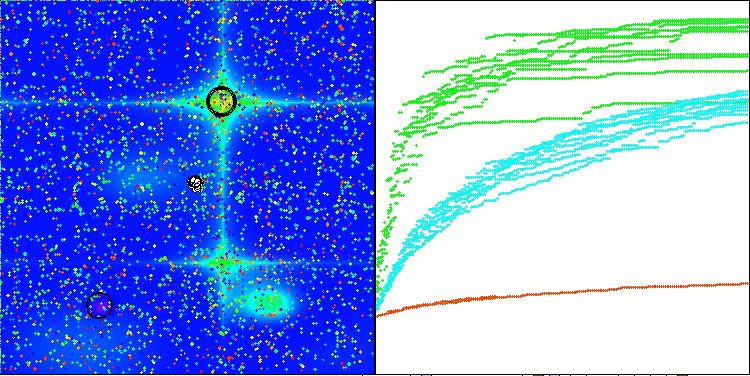
      Forestテスト関数のRFO

      Megacity

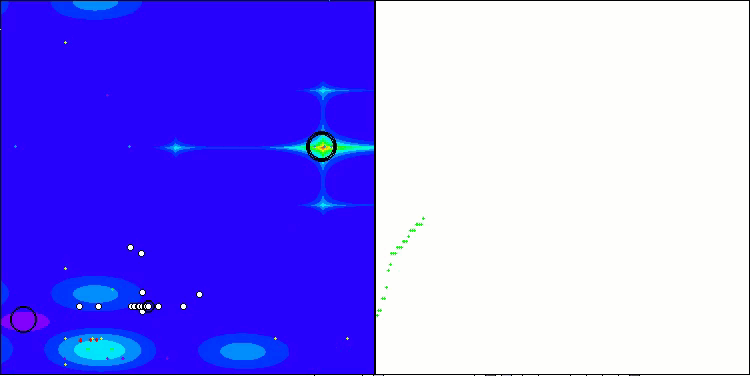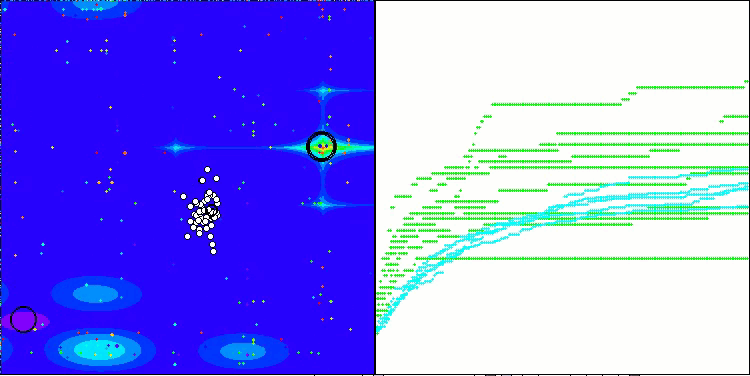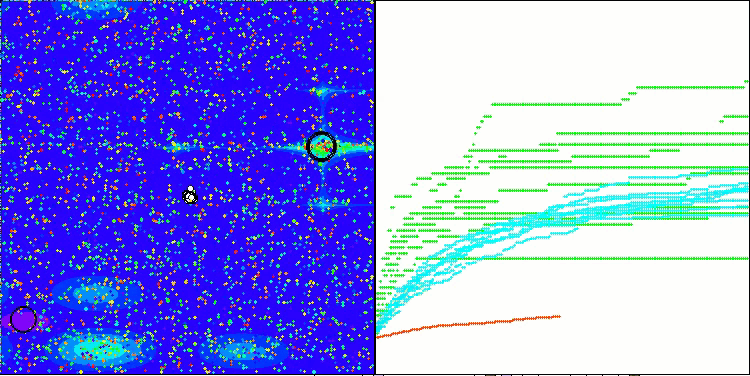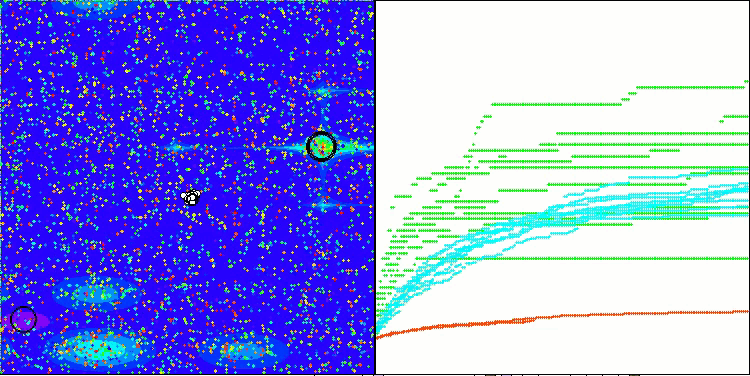
      Megacityテスト関数のRFO

      テスト結果に基づくと、RFO最適化アルゴリズムは15位にランクインしており、既知の最も強力なアルゴリズムの一覧に加わっています。

      # AO 詳細 Hilly Hilly最終 Forest Forest最終 Megacity（離散） Megacity最終 最終結果 MAXの%
      10p(5F) 50p(25F) 1000p(500F) 10p(5F) 50p(25F) 1000p(500F) 10p(5F) 50p(25F) 1000p(500F)
      1 ANS across neighbourhood search 0.94948 0.84776 0.43857 2.23581 1.00000 0.92334 0.39988 2.32323 0.70923 0.63477 0.23091 1.57491 6.134 68.15
      2 CLA コードロックアルゴリズム(joo) 0.95345 0.87107 0.37590 2.20042 0.98942 0.91709 0.31642 2.22294 0.79692 0.69385 0.19303 1.68380 6.107 67.86
      3 AMOm 動物移動最適化m 0.90358 0.84317 0.46284 2.20959 0.99001 0.92436 0.46598 2.38034 0.56769 0.59132 0.23773 1.39675 5.987 66.52
      4 (P+O)ES (P+O)進化戦略 0.92256 0.88101 0.40021 2.20379 0.97750 0.87490 0.31945 2.17185 0.67385 0.62985 0.18634 1.49003 5.866 65.17
      5 CTA 彗星の尾アルゴリズム(joo) 0.95346 0.86319 0.27770 2.09435 0.99794 0.85740 0.33949 2.19484 0.88769 0.56431 0.10512 1.55712 5.846 64.96
      6 TETA 時間進化移動アルゴリズム（joo） 0.91362 0.82349 0.31990 2.05701 0.97096 0.89532 0.29324 2.15952 0.73462 0.68569 0.16021 1.58052 5.797 64.41
      7 SDSm 確率的拡散探索M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
      8 AAm アーチェリーアルゴリズムM 0.91744 0.70876 0.42160 2.04780 0.92527 0.75802 0.35328 2.03657 0.67385 0.55200 0.23738 1.46323 5.548 61.64
      9 ESG 社会集団の進化(joo) 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
      10 SIA 等方的焼きなまし(joo) 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
      11 ACS 人工協調探索 0.75547 0.74744 0.30407 1.80698 1.00000 0.88861 0.22413 2.11274 0.69077 0.48185 0.13322 1.30583 5.226 58.06
      12 DA 弁証法的アルゴリズム 0.86183 0.70033 0.33724 1.89940 0.98163 0.72772 0.28718 1.99653 0.70308 0.45292 0.16367 1.31967 5.216 57.95
      13 BHAm ブラックホールアルゴリズムM 0.75236 0.76675 0.34583 1.86493 0.93593 0.80152 0.27177 2.00923 0.65077 0.51646 0.15472 1.32195 5.196 57.73
      14 ASO 無政府社会最適化 0.84872 0.74646 0.31465 1.90983 0.96148 0.79150 0.23803 1.99101 0.57077 0.54062 0.16614 1.27752 5.178 57.54
      15 RFO ロイヤルフラッシュ最適化（joo） 0.83361 0.73742 0.34629 1.91733 0.89424 0.73824 0.24098 1.87346 0.63154 0.50292 0.16421 1.29867 5.089 56.55
      16 AOSm 原子軌道探索M 0.80232 0.70449 0.31021 1.81702 0.85660 0.69451 0.21996 1.77107 0.74615 0.52862 0.14358 1.41835 5.006 55.63
      17 TSEA 亀甲進化アルゴリズム(joo) 0.96798 0.64480 0.29672 1.90949 0.99449 0.61981 0.22708 1.84139 0.69077 0.42646 0.13598 1.25322 5.004 55.60
      18 DE 差分進化 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
      19 CRO 化学反応の最適化 0.94629 0.66112 0.29853 1.90593 0.87906 0.58422 0.21146 1.67473 0.75846 0.42646 0.12686 1.31178 4.892 54.36
      20 BSA 鳥群アルゴリズム 0.89306 0.64900 0.26250 1.80455 0.92420 0.71121 0.24939 1.88479 0.69385 0.32615 0.10012 1.12012 4.809 53.44
      21 HS ハーモニー検索 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
      22 SSG 苗木の播種と育成 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
      23 BCOm 細菌走化性最適化M 0.75953 0.62268 0.31483 1.69704 0.89378 0.61339 0.22542 1.73259 0.65385 0.42092 0.14435 1.21912 4.649 51.65
      24 ABO アフリカ水牛の最適化 0.83337 0.62247 0.29964 1.75548 0.92170 0.58618 0.19723 1.70511 0.61000 0.43154 0.13225 1.17378 4.634 51.49
      25 (PO)ES (PO)進化戦略 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
      26 TSm タブーサーチM 0.87795 0.61431 0.29104 1.78330 0.92885 0.51844 0.19054 1.63783 0.61077 0.38215 0.12157 1.11449 4.536 50.40
      27 BSO ブレインストーム最適化 0.93736 0.57616 0.29688 1.81041 0.93131 0.55866 0.23537 1.72534 0.55231 0.29077 0.11914 0.96222 4.498 49.98
      28 WOAm 鯨最適化アルゴリズムM 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
      29 AEFA 人工電界アルゴリズム 0.87700 0.61753 0.25235 1.74688 0.92729 0.72698 0.18064 1.83490 0.66615 0.11631 0.09508 0.87754 4.459 49.55
      30 AEO 人工生態系ベースの最適化アルゴリズム 0.91380 0.46713 0.26470 1.64563 0.90223 0.43705 0.21400 1.55327 0.66154 0.30800 0.28563 1.25517 4.454 49.49
      31 ACOm 蟻コロニー最適化M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
      32 BFO-GA 細菌採食の最適化：Ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
      33 SOA シンプル最適化アルゴリズム 0.91520 0.46976 0.27089 1.65585 0.89675 0.37401 0.16984 1.44060 0.69538 0.28031 0.10852 1.08422 4.181 46.45
      34 ABHA 人工蜂の巣アルゴリズム 0.84131 0.54227 0.26304 1.64663 0.87858 0.47779 0.17181 1.52818 0.50923 0.33877 0.10397 0.95197 4.127 45.85
      35 ACMO 大気雲モデルの最適化 0.90321 0.48546 0.30403 1.69270 0.80268 0.37857 0.19178 1.37303 0.62308 0.24400 0.10795 0.97503 4.041 44.90
      36 ADAMm 適応モーメント推定M 0.88635 0.44766 0.26613 1.60014 0.84497 0.38493 0.16889 1.39880 0.66154 0.27046 0.10594 1.03794 4.037 44.85
      37 ATAm 人工部族アルゴリズムM 0.71771 0.55304 0.25235 1.52310 0.82491 0.55904 0.20473 1.58867 0.44000 0.18615 0.09411 0.72026 3.832 42.58
      38 ASHA 人工シャワーアルゴリズム 0.89686 0.40433 0.25617 1.55737 0.80360 0.35526 0.19160 1.35046 0.47692 0.18123 0.09774 0.75589 3.664 40.71
      39 ASBO 適応型社会行動最適化(ASBO) 0.76331 0.49253 0.32619 1.58202 0.79546 0.40035 0.26097 1.45677 0.26462 0.17169 0.18200 0.61831 3.657 40.63
      40 MEC mind evolutionary computation 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
      41 IWO 侵入雑草最適化 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
      42 Micro-AIS 微小人工免疫系 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54
      43 COAm カッコウ最適化アルゴリズムM 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21
      44 SDOm 螺旋ダイナミクス最適化M 0.74601 0.44623 0.29687 1.48912 0.70204 0.34678 0.10944 1.15826 0.42833 0.16767 0.03663 0.63263 3.280 36.44
      45 NMm ネルダー=ミード法M 0.73807 0.50598 0.31342 1.55747 0.63674 0.28302 0.08221 1.00197 0.44667 0.18667 0.04028 0.67362 3.233 35.92
      RW ランダムウォーク 0.48754 0.32159 0.25781 1.06694 0.37554 0.21944 0.15877 0.75375 0.27969 0.14917 0.09847 0.52734 2.348 26.09


      まとめ

      新しい最適化手法の研究や開発をおこなう中で、効率と実装の複雑さのバランスを取る必要にしばしば直面します。ロイヤルフラッシュ最適化(RFO)アルゴリズムの研究は、最適化の本質やその改良方法について考えさせられる興味深い結果をもたらしました。

      理論上の最大値の約57%に到達したアルゴリズムの性能を観察すると、時には複雑化よりも単純化の方が価値を持つという興味深い現象が見えてきます。RFOは、複雑な二進符号化を放棄し、より単純なセクターベースのアプローチを採用することで、解の品質を十分に保ちながらアルゴリズムの性能を大きく向上させられることを示しています。これは、ポーカーにおいて複雑で計算に時間のかかる戦略よりも、単純で素早い戦略の方が有効な場合がある状況に似ています。

      最適化アルゴリズム群の中でのRFOの位置づけを考えると、乗り物の進化との類比を引くことができます。高性能なスポーツカーと並んで燃費の良い都市型自動車が必要とされるように、最適化アルゴリズムの世界においても、異なる優先事項に焦点を当てた手法が存在する余地があります。RFOは、性能と資源効率の間で合理的なトレードオフを提供する、遺伝的アルゴリズムの「低コスト」な変種として捉えることができます。

      結論として、RFOの開発は今後の研究に向けた興味深い展望を開くものだと言えます。これは、セクターベースの最適化アプローチに基づくアルゴリズム群の発展に向けた第一歩に過ぎないかもしれません。この手法の単純さと洗練性、そして実用的な有効性の組み合わせは、性能と計算効率のバランスを取った新しいアルゴリズムを創出するための着想源となり得ます。

      なお、セクターへの分割は配列としてメモリを確保することなく、仮想的におこなわれている点にも注意する価値があります。このRFOフレームワークは、改良版ポーカーアルゴリズムのさらなる発展に向けた非常に優れた出発点です。

      Tab

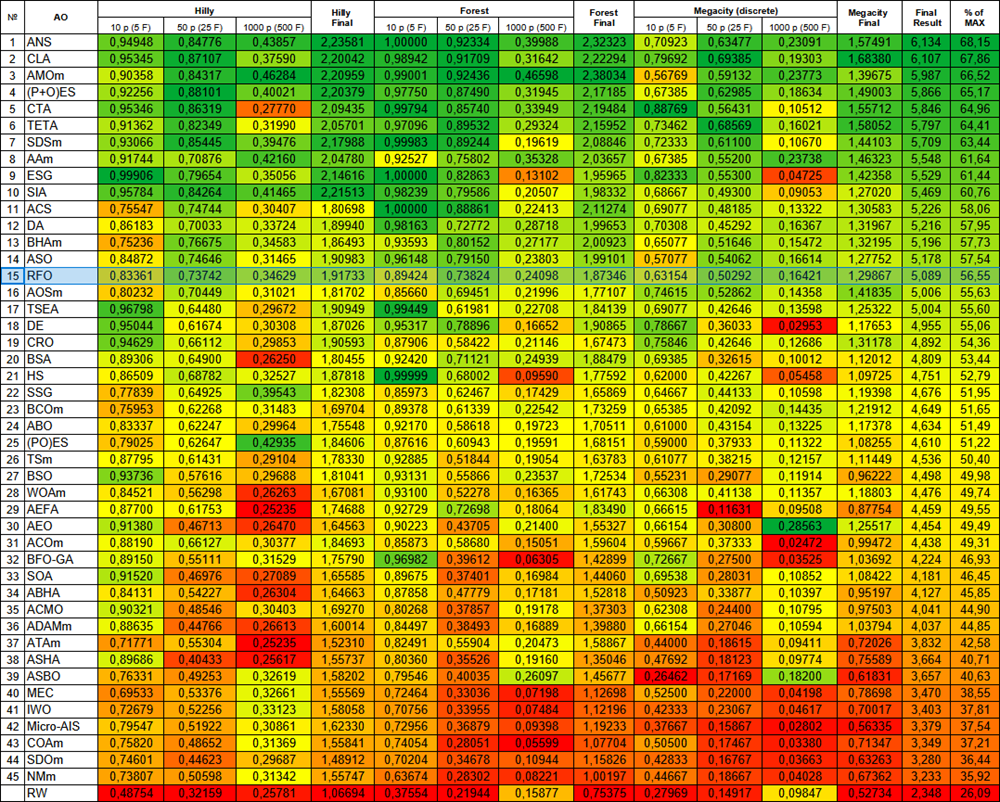
      図2：対応するテストに応じたアルゴリズムのカラーグラデーション

      チャート

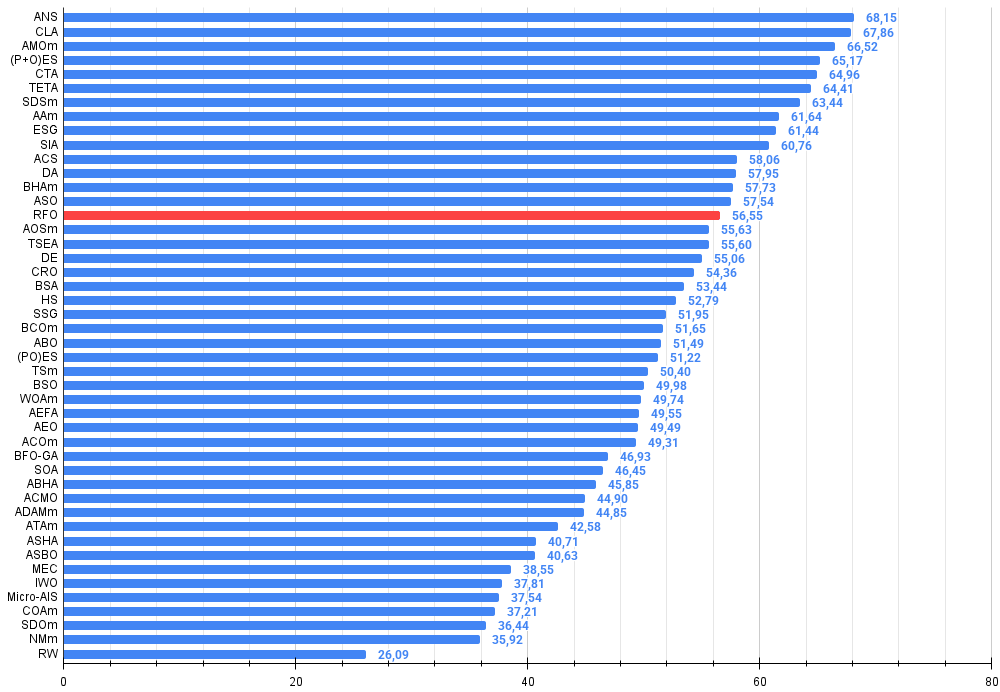
      図3：アルゴリズムテスト結果のヒストグラム（0から100のスケール、高いほど良い）100は理論上の最大値であり、アーカイブには評価表を計算するためのスクリプトがあります。


      RFOの長所と短所

      長所

      1. 外部パラメータは少なく、集団サイズを除けば2つだけ
      2. 実装がシンプル
      3. 迅速
      4. バランスがよく、さまざまな次元のタスクで優れたパフォーマンスを発揮する

      短所：

      1. 平均収束精度

      この記事には、最新版のアルゴリズムコードを含むアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。

      記事で使用されているプログラム

      # 名前 種類 詳細
      1 #C_AO.mqh
      		 インクルード
      		 集団最適化アルゴリズムの親クラス
      2 #C_AO_enum.mqh
      		 インクルード
      		 集団最適化アルゴリズムの列挙
      3 TestFunctions.mqh
      		 インクルード
      		 テスト関数のライブラリ
      4
      		 TestStandFunctions.mqh
      		 インクルード
      		 テストスタンド関数ライブラリ
      5
      		 Utilities.mqh
      		 インクルード
      		 補助関数のライブラリ
      6
      		 CalculationTestResults.mqh
      		 インクルード
      		 比較表の結果を計算するスクリプト
      7
      		 Testing AOs.mq5
      		 スクリプト すべての集団最適化アルゴリズムの統一テストスタンド
      8
      		 Simple use of population optimization algorithms.mq5
      		 スクリプト
      		 可視化せずに集団最適化アルゴリズムを使用する簡単な例
      9
      		 Test_AO_RFO.mq5
      		 スクリプト RFOテストステンド

      MetaQuotes Ltdによってロシア語から翻訳されました。
      元の記事: https://www.mql5.com/ru/articles/17063

      添付されたファイル |
      ZIPをダウンロード
      RFO.zip (161.58 KB)

      警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

      この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。

      この著者による他の記事

      最後のコメント | ディスカッションに移動 (2)
      Alex-4
      Alex-4 | 12 2月 2025 において 03:57

      また、具体的に（アイデアとして）どのように
      EAでの計算を
      EAでの計算をBPのために特別に適応させることができるのでしょうか？私は
      mqlのウェブサイトをざっと見ただけでは、具体的なことはわかりませんでした。
      Andrey Dik
      Andrey Dik | 12 2月 2025 において 05:08
      blef #:

      そして、具体的にどのように（アイデアという点で）
      計算を適応させることができるのか
      EAでの計算をBPのために特別に適応させることができるのでしょうか？を見てみると
      をざっと見ただけで、mqlのウェブサイトでも具体的なことはわかりませんでした。

      多くの可能性の中から最適な解決策を見つける必要がある場合はすべてそうです。例えば、自己最適化を 行うアドバイザー。

      市場シミュレーション（第7回）：ソケット(I) 市場シミュレーション（第7回）：ソケット(I)
      ソケットについてご存じでしょうか。また、MetaTrader 5でどのように使用するかをご存じでしょうか。もし答えが「いいえ」であれば、ここから一緒に学んでいきましょう。本日の記事では、その基礎について解説します。同じことを実現する方法はいくつも存在しますが、私たちが常に重視するのは結果です。そこで、MetaTrader 5からExcelのような他のプログラムへデータを転送するための、実際にシンプルな方法が存在することを示したいと思います。ただし、本来の主な目的は、MetaTrader 5からExcelへデータを送ることではなく、その逆、つまりExcelやその他のプログラムからMetaTrader 5へデータを転送することにあります。
      取引におけるニューラルネットワーク：階層型ダブルタワーTransformer（最終回） 取引におけるニューラルネットワーク：階層型ダブルタワーTransformer（最終回）
      複雑な多変量時系列の分析および予測を目的に設計された、Hidformer階層型ダブルタワーTransformerモデルの構築を引き続き進めます。本記事では、これまでに着手した作業を論理的な結論へと導き、実際の履歴データを用いてモデルを検証します。
      エラー 146 (「トレードコンテキスト ビジー」) と、その対処方法 エラー 146 (「トレードコンテキスト ビジー」) と、その対処方法
      この記事では、MT4において複数のEAの衝突をさける方法を扱います。ターミナルの操作、MQL4の基本的な使い方がわかる人にとって、役に立つでしょう。
      弁証法的探索(DA) 弁証法的探索(DA)
      本記事では、弁証法の考え方に着想を得た大域最適化手法である弁証法的アルゴリズム(Dialectical Algorithm, DA)を紹介します。このアルゴリズムは、集団を「思索的思考者(speculative thinkers)」と「実践的思考者(practical thinkers)」に独自に分割する点が特徴です。テストでは、低次元問題において最大98%の高い性能を示し、全体的な効率は57.95%に達しました。本記事ではこれらの指標を解説し、アルゴリズムの詳細な説明とさまざまな関数に対する実験結果を提示します。