MetaTrader 5 / トレーディングシステム
English Русский 中文 Español Português
preview
弁証法的探索(DA)

弁証法的探索(DA)

MetaTrader 5 — トレーディングシステム |
12 0
Andrey Dik
Andrey Dik

内容

  1. はじめに
  2. アルゴリズムの実装
  3. テスト結果


はじめに

唯物弁証法は、自然、社会、思考に存在する対立関係の統一と相互作用を基本原理としています。これは、発展は相反する力や傾向の衝突を通じて起こるという考えに基づき、あらゆる現象には内在する矛盾が含まれていると考えます。このアプローチの重要な原理は、量的変化から質的変化への移行です。すなわち、緩やかな量的変化の蓄積が、ある時点で質的な転換を引き起こします。発展は「否定の否定」の法則に従い、ある「正」（テーゼ）が「反」（アンチテーゼ）に置き換わることで、以前の状態の最良部分を保持した新たな質としての「合」（シンテーゼ）が生まれます。

最適化アルゴリズムの世界において、数学的精密さと哲学的知恵が出会った結果、唯物弁証法に着想を得た独自の手法が誕生しました。それが弁証法的アルゴリズム(DA)です。このアルゴリズムは、古典的弁証法と現代最適化手法を統合したシンテーゼとして提示され、テーゼとアンチテーゼという哲学的対立の観点から最適解探索を再構築します。DAの基本理念は、あらゆる解（テーゼ）が、その対立する解（アンチテーゼ）との相互作用を通じて改善の可能性を内包している、というものです。

この考え方は、アルゴリズム上では次のように実装されています。思索的思考者は既存の解から離れて新たな探索をおこない、実践的思考者は有望な解の周辺を集中的に探索します。唯物弁証法の物質的側面は、客観的基準に基づく意思決定評価や結果の実践的検証として現れます。発展は循環的に起こり、得られた解は新たな矛盾を生み、それが次の探索ラウンドにつながります。このプロセスは、知識と改善の連続性を反映しています。

このアルゴリズムは、3つの重要なステップを通じてこの原理を実現します。まず理解の段階では、解の評価と分類がおこなわれます。次に弁証法的相互作用では、解がそれぞれのアンチテーゼを見つけます。そしてシンテーゼの段階では、新しく改善された解が形成されます。アルゴリズムの特徴として、集団を2種類の思考者に分ける点があります。思索的思考者(k1)は類似した解の間で品質は類似しているが、探索空間上では離れた位置を移動し、広範囲の探索をおこないます。一方、実践的思考者(p-k1)は品質は大きく異なるが、探索空間上では近接した位置で局所探索をおこないます。この分割は、対立の統一と闘争という哲学的原理を反映しており、それぞれのグループが最適化に独自の貢献をします。

弁証法的探索(DA)は2009年にSerdar KadiogluとMeinolf Sellmannによって導入されました。この手法は制約付き最適化問題の解決に弁証法的アプローチを用いており、新しい解の探索という点で唯物弁証法の伝統を継承しています。


アルゴリズムの実装

このアルゴリズムは、探索空間内の座標ベクトルとして表されるp個の解（通常は50個）からなる集団に基づいています。この集団は、k1の思索的思考者（最良解）とp-k1の実践的思考者の2つのグループに分けられます。

第1段階は「理解」のフェーズです。まず、すべての解は目的関数f(x)によって評価されます。解は品質順にソートされ、最良のk1個の解が思索的思考者となり、残りは実践的思考者となります。この段階では、新しい解も、前回のイテレーションでの各思考者の最良解と比較して、品質が良ければ受け入れられ、そうでなければ却下されます。

第2段階は、「弁証法的な」フェーズです。この段階では、各解のアンチテーゼ（対立する解）が探索されます。思索的思考者の場合、アンチテーゼは「品質は維持しつつ、探索空間内でできるだけ遠くにある解」を選ぶことで決定されます（理想主義的弁証法）。具体的には、最良の解に対しては2番目に良い解、最後の解に対しては最後から2番目の解、それ以外は距離が最も遠い隣接解が選ばれます。一方、実践的思考者は「品質に十分差がありつつ、探索空間内では近い解」をアンチテーゼとして選びます（唯物論的弁証法）。

第3段階は思索的および実践的フェーズ（更新フェーズ）です。ここでは、すべての解の位置が見つかったアンチテーゼを用いて更新されます。思索的思考者は一様分布を使用し、探索空間全体を広く探索できるようにします。実践的思考者は正規分布を使用しますが、私の実験では両方のタイプに対して一様分布の方が性能が良いことがわかりました。

位置更新の式はすべての解に共通です。X(i) = X(i) + μ⊙(Xanti(i) - X(i))、ここで、μは対応する分布から生成されるランダムベクトル、⊙は要素ごとの乗算を表します。これにより、思索的思考者による探索と、実践的思考者による局所解の改善のバランスが保たれます。

弁証法的アルゴリズム(DA)の位置更新の考え方は、差分進化(DE)の更新式と似ています。DEでは、新しいベクトルは、ターゲットベクトルに他の2つのベクトルのスケーリングされた差を加えることによって作成されます(x_new = x_target + F(x_r1 - x_r2))。一方、DAでは同様の原理を用いますが、アンチテーゼと適応比率を用いています(x_new = x + μ(x_anti - x))。

しかし、両者の最も大きな違いは、新しい解を生成する際のベクトルの選択方法にあります。DEでは、差分ベクトルをランダムに選択することで、探索の確率性が確保されます。一方、DAでは、解間の距離と品質に基づき、アンチテーゼを決定する決定論的アプローチが採用されています。また、集団を思索的思考者と実践的思考者に分け、それぞれ異なる探索戦略を適用する点も特徴です。DAアルゴリズムは、ユークリッド距離の計算により計算量は増加しますが、多くの最適化問題において高い探索効率を示します。

図1は、思索的（赤、最良）テーゼと実践的（青）テーゼのアンチテーゼ選択の原理を示しています。思索的思考者は、品質では近く、探索空間ではより遠い解をアンチテーゼとして選択します。一方、実践的思考者は、品質ではより遠く、探索空間では近い解をアンチテーゼとして選択します。 

弁証法的探索

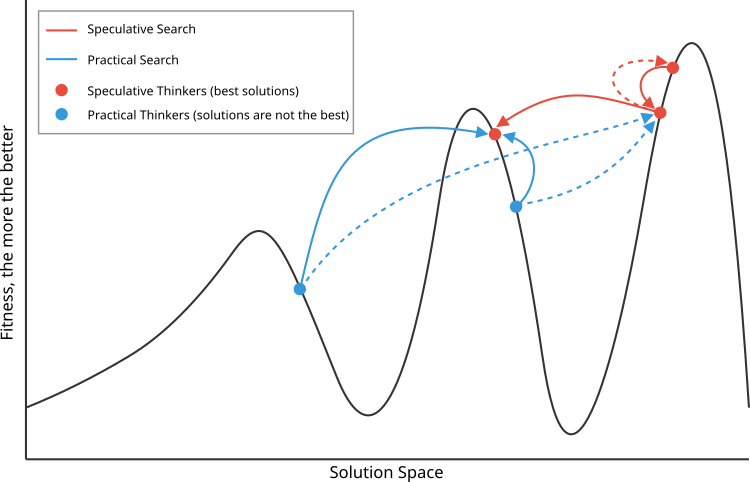
図1：DAアルゴリズムの動作原理の模式図。実線は優先的に選ばれたアンチテーゼとの相互作用を示し、破線はあまり優先されないアンチテーゼとの相互作用を示している


弁証法的アルゴリズムフロー

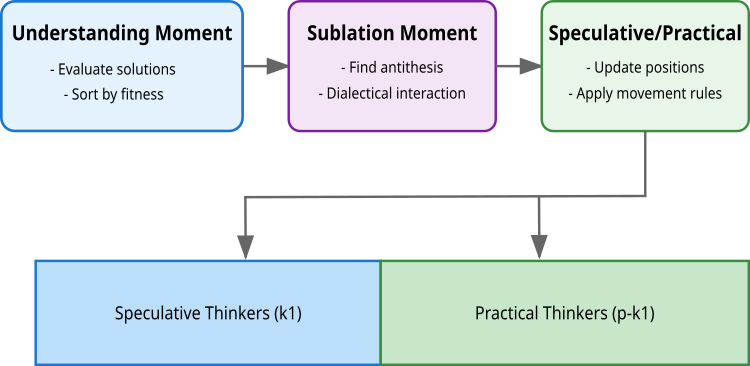
図2：DAアルゴリズムのステージ別処理フロー

続いて、アルゴリズムの疑似コードを示します。

初回イテレーション：エージェントをランダムに配置します(position[i] = random(min, max))。

個体最良解に基づき集団をソートします。

エージェントを3種類に分類します。

  • 最良の思想家（1エージェント）
  • 思索的思考者（k1=3エージェント）
  • 実践的思考者（47エージェント）
次回以降のイテレーション

    A.最良の思考者は2番目に良い解に向かって移動します。

    position[0] = best[0] + rand(0,1) * (position[1] - position[0])

    B. 思索的思考者

    • ユークリッド距離を使用して最も遠い近傍を見つけます。

    distance = √Σ(x₁-x₂)²

    • 最も遠い位置を基準に位置を更新します。

    position[i] = best[i] + rand(0,1) * (position[furthest] - position[i])

    C.実践的思考者

    • 思索的思考者2人をランダムに選びます。
    • 最も近い解に向かって移動します。

    position[i] = best[i] + rand(0,1) * (position[nearest] - position[i])

    各移動後の処理

      • 個体最良解を更新します。
      • 大域最良解を更新します。
      • 個体解の品質に基づきエージェントをソートします。

      このプロセスを停止条件に達するまで繰り返します。

      アルゴリズムの全体を把握した後は、コードでの実装に移ります。次に、C_AO基底クラスの機能を継承して、弁証法的最適化アルゴリズム用のC_AO_DAクラスを作成します。

      アルゴリズムパラメータ

      • 集団サイズ：最適化に参加するエージェントの数を決定します。
      • 思索的思考者：解の探索により自由に動ける優れたエージェントの数を示します。
      • 分析用近傍：各思索的思考者（エージェント）が情報交換や戦略改善のために相互作用する、最も近い近傍エージェントの数を決定します。

      メソッド

      • C_AO_DA ()：コンストラクタで主要パラメータを初期化するとともに、これらを格納する配列を作成します。
      • SetParams ()：パラメータを設定することで、アルゴリズム実行中に値を更新できるようにします。
      • Moving()とRevision ()：エージェントを探索空間で移動させたり、得られた解を修正したりするための関数です。
      • EuclideanDistance ()：探索空間内で2つのベクトル間の距離を計算します。これは、思索的思考者の近傍や実践的思考者の最遠の類似解を選択する際に必要です。
      //——————————————————————————————————————————————————————————————————————————————
// Class implementing the dialectical optimization algorithm
class C_AO_DA : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_DA () { }
  C_AO_DA ()
  {
    ao_name = "DA";
    ao_desc = "Dialectical Algorithm";
    ao_link = "https://www.mql5.com/ja/articles/16999";

    popSize = 50;       // population size
    k1      = 3;        // speculative thinkers
    k2      = 10;       // neighbours

    ArrayResize (params, 3);
    params [0].name = "popSize"; params [0].val = popSize;
    params [1].name = "k1";      params [1].val = k1;
    params [2].name = "k2";      params [2].val = k2;
  }

  // Setting algorithm parameters
  void SetParams ()
  {
    popSize = (int)params [0].val;
    k1      = (int)params [1].val;
    k2      = (int)params [2].val;
  }

  bool Init (const double &rangeMinP  [], // minimum search range
             const double &rangeMaxP  [], // maximum search range
             const double &rangeStepP [], // search step
             const int     epochsP = 0);  // number of epochs

  void Moving   ();    // Moving agents in the search space
  void Revision ();    // Review and update the best solutions found

  //----------------------------------------------------------------------------
  int k1;       // number of speculative thinkers
  int k2;       // number of neighbors to analyze

  private: //-------------------------------------------------------------------
  // Calculate the Euclidean distance between two vectors
  double EuclideanDistance (const double &vec1 [], const double &vec2 [], const int dim)
  {
    double sum  = 0;
    double diff = 0.0;

    for (int i = 0; i < dim; i++)
    {
      diff = vec1 [i] - vec2 [i];
      sum += diff * diff;
    }
    return MathSqrt (sum);
  }
};
//——————————————————————————————————————————————————————————————————————————————

      C_AO_DAクラスのInitメソッドは、最適化アルゴリズムのパラメータを初期化することを目的としています。このメソッドは、探索範囲の最小値および最大値の配列、探索ステップ、さらに必要に応じて最適化を実行するエポック数を受け取ります。メソッドはまず標準的なパラメータの初期化をおこないます。初期化に失敗した場合は、falseを返します。初期化が成功した場合は、trueを返し、アルゴリズムが実行可能な状態であることを確認します。

      //——————————————————————————————————————————————————————————————————————————————
bool C_AO_DA::Init (const double &rangeMinP  [], // minimum search range
                    const double &rangeMaxP  [], // maximum search range
                    const double &rangeStepP [], // search step
                    const int     epochsP = 0)   // number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  return true;
}
//——————————————————————————————————————————————————————————————————————————————

      Movingメソッドは、探索空間内でのエージェントの移動を実装したものです。このメソッドの動作の詳細な説明は以下に記載されています。

      初期化

      • 初回呼び出し時(!revision)、各エージェントの初期位置は、与えられた座標ごとの最小値と最大値の範囲を用いてランダムに設定されます。各エージェントa[i]は、指定された範囲内でランダムに座標を割り当てられ、一定のステップに従います。
      • 初期化後、revisionはtrueに設定されます。これにより、後続のMovingメソッド呼び出しで再初期化されることはありません。

      最良思考者の位置更新

      • 最良思考者は、前回の最良位置とランダムな確率に基づき座標を更新します。この更新には、最も近い隣接エージェントa[1]を使用します。

      思索的思考者の位置更新

      • 思索的思考者（エージェント）は、k2からk1の範囲で順に処理されます。メソッドは、最も遠い前方の隣接エージェント(antiPrevIND)と次の隣接エージェント(antiNextIND)を探索します。
      • 思索的思考者の座標は、アンチテーゼを考慮して、最も遠い隣接エージェントに基づき更新されます。

      実践的思考者の位置更新

      • 実践的思考者（エージェント）は、k1からpopSizeの範囲で処理されます。
      • コードはランダムに2人の思索的思考者を選択し、それぞれまでの距離を計算します。実践的思考者は、選択した2人のうち最も近い思索的思考者を基準に座標を更新します。
      • 各座標は、選ばれた隣接エージェントに基づいて更新されます。

      補助関数

      • EuclideanDistance：多次元空間における2点aとbのユークリッド距離を計算する
      • u.RNDfromCI：指定された区間からランダムな数値を返す
      • u.SeInDiSp：範囲に応じてvalueを適切なステップに変換する
      • u.RNDprobab：一様確率分布に従うランダム数値を返す
      //——————————————————————————————————————————————————————————————————————————————
// Implement agent movement in the search space
void C_AO_DA::Moving ()
{
  //----------------------------------------------------------------------------
  // Initialize the agents' positions randomly
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  //  Update the best thinker's position
  for (int c = 0; c < coords; c++)
  {
    a [0].c [c] = a [0].cB [c] + u.RNDprobab () * (a [1].c [c] - a [0].c [c]);
    a [0].c [c] = u.SeInDiSp (a [0].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }

  //----------------------------------------------------------------------------
  double dist_next   = -DBL_MAX;  // maximum distance to the next neighbor
  double dist_prev   = -DBL_MAX;  // maximum distance to the previous neighbor
  double dist        = 0.0;       // current distance
  int    antiNextIND = 0;         // index of the most distant next neighbor
  int    antiPrevIND = 0;         // index of the most distant previous neighbor
  int    antiIND     = 0;         // selected index to update position

  // Update the positions of speculative thinkers -------------------------------
  for (int i = k2; i < k1; i++)
  {
    // Find the most distant previous neighbor
    for (int j = 1; j <= k2; j++)
    {
      dist = EuclideanDistance (a [i].cB, a [i - j].cB, coords);
      if (dist > dist_prev)
      {
        dist_prev   = dist;
        antiPrevIND = i - j;
      }
    }

    // Find the farthest next neighbor
    for (int j = 1; j <= k2; j++)
    {
      dist = EuclideanDistance (a [i].cB, a [i + j].cB, coords);
      if (dist > dist_next)
      {
        dist_next = dist;
        antiNextIND  = i + j;
      }
    }

    // Select the most distant neighbor to update position
    if (dist_prev > dist_next) antiIND = antiPrevIND;
    else                       antiIND = antiNextIND;

    // Update the speculative thinker's coordinates
    for (int c = 0; c < coords; c++)
    {
      a [i].c [c] = a [i].cB [c] + u.RNDbool () * (a [antiIND].c [c] - a [i].c [c]);
      //a [i].c [c] = a [i].cB [c] + u.RNDprobab () * (a [antiIND].c [c] - a [i].c [c]);
      a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }

  // Update the positions of practical thinkers --------------------------------
  for (int i = k1; i < popSize; i++)
  {
    // Random selection of two speculative thinkers
    antiNextIND = u.RNDintInRange (0, k1 - 1);
    antiPrevIND = u.RNDintInRange (0, k1 - 1);

    if (antiNextIND == antiPrevIND) antiNextIND = antiPrevIND + 1;

    // Calculate distances to selected thinkers
    dist_next = EuclideanDistance (a [i].cB, a [antiNextIND].cB, coords);
    dist_prev = EuclideanDistance (a [i].cB, a [antiPrevIND].cB, coords);

    // Select the closest thinker to update the position
    if (dist_prev < dist_next) antiIND = antiPrevIND;
    else                       antiIND = antiNextIND;

    // Update the coordinates of the practical thinker
    for (int c = 0; c < coords; c++)
    {
      a [i].c [c] = a [i].cB [c] + u.RNDprobab () * (a [antiIND].c [c] - a [i].c [c]);
      a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

      Revisionメソッドは、エージェントが見つけた最良解を改訂・更新する役割を担っています。以下にメソッドの動作を詳細に説明します。

      最良解の更新：forループ内で、集団の各エージェントを順に処理します。各エージェントの現在の適応度関数値a[i].fが比較され、まず大域最良解と照合されます。

      • 大域最良解：エージェントのf値が現在の大域最良解fBより大きい場合、そのエージェントの解が新たな大域最良解として更新され、最良解を見つけたエージェントのインデックスindが保存されます。
      • 個体最良解：各エージェントのf値は個体最良解fBと比較されます。現在の値がより良ければ、個体最良値が更新され、現在の座標cが個体最良座標cBにコピーされます。

      大域最良解の座標更新：大域最良解となったエージェントのインデックス（ind != -1）が見つかった場合、そのエージェントの座標が大域的最良座標cBにコピーされます。

      エージェントのソート：メソッドの最後で、aT配列が作成され、サイズは集団の大きさに合わせて変更されます。その後、u.Sorting_fB関数が呼び出され、各エージェントの見つけた最良解（fB値）に基づきエージェントがソートされます。

      //——————————————————————————————————————————————————————————————————————————————
// Review and update the best solutions found
void C_AO_DA::Revision ()
{
  int ind = -1;

  // Update the best solutions found for each agent
  for (int i = 0; i < popSize; i++)
  {
    // Update the global best solution
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }

    // Update the agent's personal best solution
    if (a [i].f > a [i].fB)
    {
      a [i].fB = a [i].f;
      ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  // Update the global best solution coordinates
  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  // Sort agents by their best found solutions
  static S_AO_Agent aT []; ArrayResize (aT, popSize);
  u.Sorting_fB (a, aT, popSize);
}
//——————————————————————————————————————————————————————————————————————————————


      テスト結果

      いよいよ、DAのテスト結果に目を通す時が来ました。ここで再びMovingメソッドに注目してみましょう。著者の意図を反映した行はコメントアウトされ、緑色で強調されています。以下が結果です。

      DA|Dialectical Algorithm|50.0|30.0|1.0|
      =============================
      5 Hilly's; Func runs:10000; result:0.749254786734898
      25 Hilly's; Func runs:10000; result:0.36669693350810206
      500 Hilly's; Func runs:10000; result:0.2532075139007539
      =============================
      5 Forest's; Func runs:10000; result:0.7626421292861323
      25 Forest's; Func runs:10000; result:0.4144802592253075
      500 Forest's; Func runs:10000; result:0.2006796312431603
      =============================
      5 Megacity's; Func runs:10000; result:0.36
      25 Megacity's; Func runs:10000; result:0.15969230769230774
      500 Megacity's; Func runs:10000; result:0.0952000000000008
      =============================
      All score:3.36185 (37.35%)

      これらの結果は決して最良とは言えませんが、ランキング表に載る可能性はありました。しかし、実は私のミスで、[0.0;1.0]の範囲で乱数を使うところを、コードにランダムなブール値を返す関数を挿入してしまいました（赤でマークされています）。

      論理上のランダムな変更の本質は次の通りです。50%の確率で、対応する座標はそのまま残るか、あるいはアンチテーゼの座標に置き換えられます。私の考えでは、これは著者が意図した「テーゼとアンチテーゼの対立」の考え方と、むしろ一致していると言えます。実践的思考者の場合はこれまで通りで、最終的なテーゼは現在のテーゼと思索的思考者から取ったアンチテーゼとの共生関係となります。こうして、幸運な偶然により以下の結果が得られました。

      DA|Dialectical Algorithm|50.0|40.0|1.0|
      =============================
      5 Hilly's; Func runs:10000; result:0.8618313952293774
      25 Hilly's; Func runs:10000; result:0.700333708747176
      500 Hilly's; Func runs:10000; result:0.3372386732170054
      =============================
      5 Forest's; Func runs:10000; result:0.9816317765399738
      25 Forest's; Func runs:10000; result:0.7277214130784131
      500 Forest's; Func runs:10000; result:0.28717629901518305
      =============================
      5 Megacity's; Func runs:10000; result:0.7030769230769229
      25 Megacity's; Func runs:10000; result:0.4529230769230769
      500 Megacity's; Func runs:10000; result:0.16366923076923204
      =============================
      All score:5.21560 (57.95%)

      これは本当に印象的な結果です。これほど大幅な性能向上が無意識のうちに起こったため、修正版に「m」を付けることはできません。ランキング表では、アルゴリズムは従来通りDAとして扱います。こうして、弁証法的アルゴリズムは優れた性能を示し、全体効率は57.95%に達しました。アルゴリズムの重要な特徴は、思索的思考者と実践的思考者への分割によって、大域探索と局所探索のバランスを効果的に取れる点にあります。

      可視化結果からも、アルゴリズムは重要な局所最適解を比較的素早く見つけることがわかりますが、収束精度が十分ではないため、完璧とは言えません。それにもかかわらず、いずれのテストケースにおいても十分に良好な結果が得られています。

      Hilly

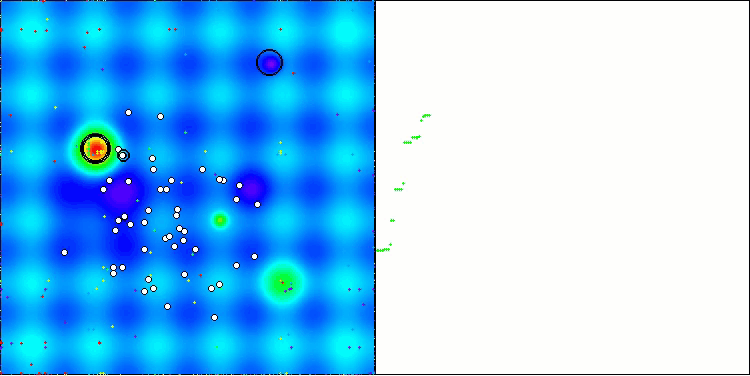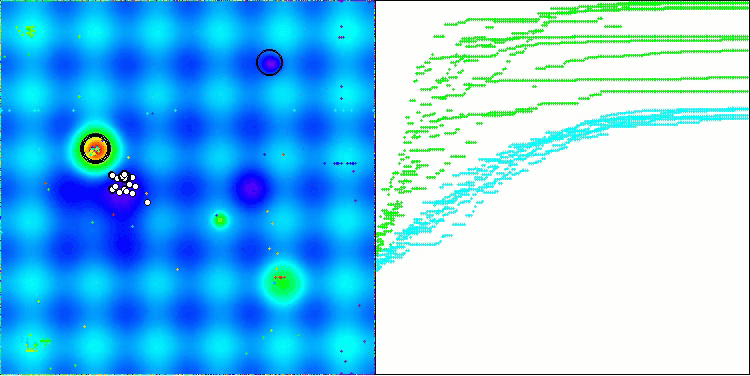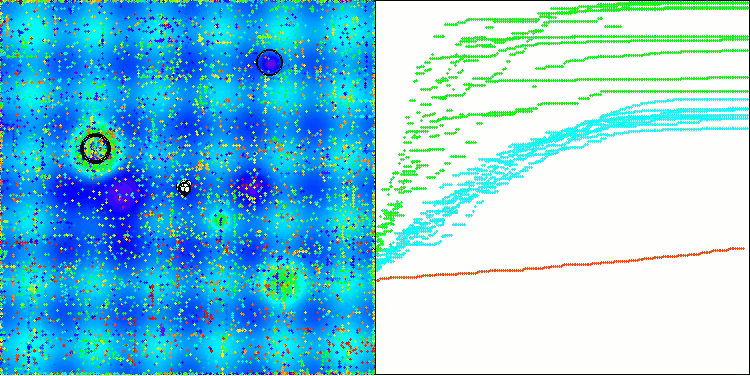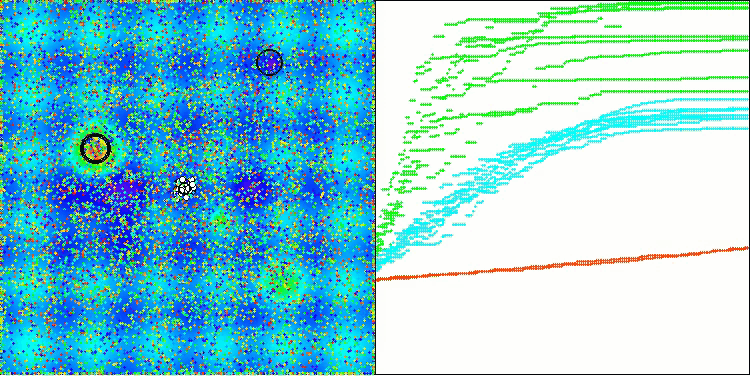
        Hillyテスト関数のDA

      Forest

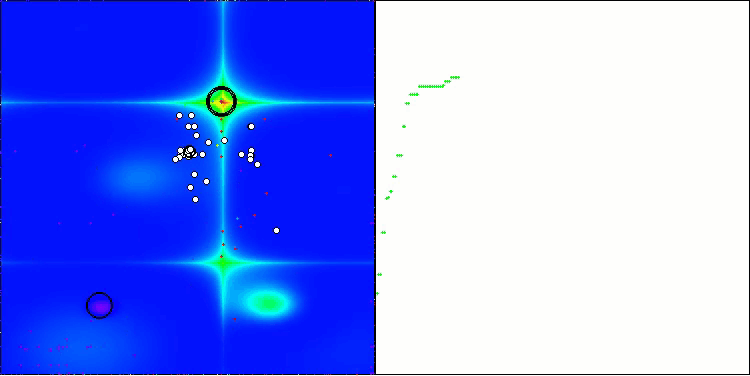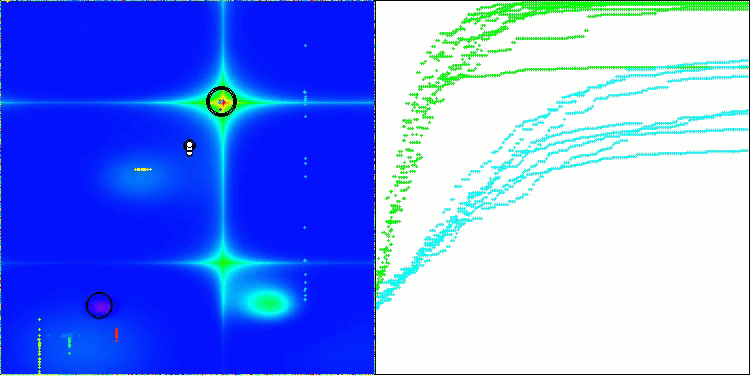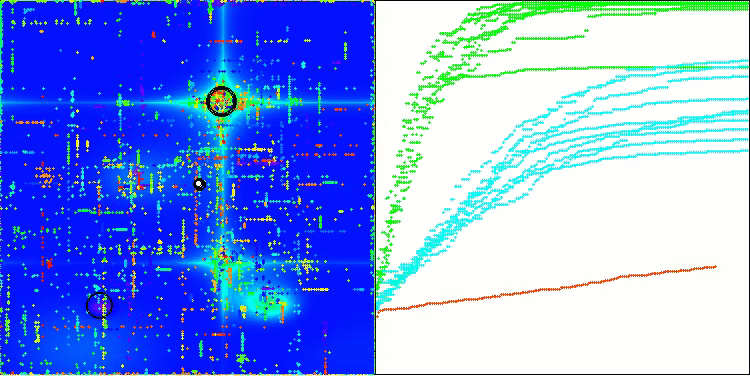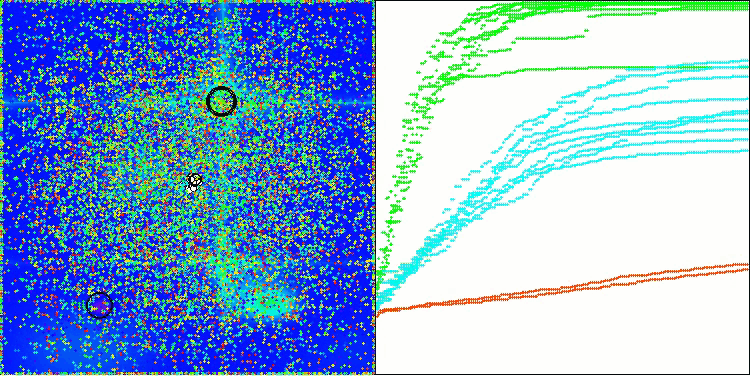
      Forestテスト関数のDA

      Megacity

      Megacityテスト関数のDA

      テスト結果によると、DAアルゴリズムはランキング表で12位に入り、良好かつ安定した結果を示しました。

      # AO 詳細 Hilly Hilly最終 Forest Forest最終 Megacity（離散） Megacity最終 最終結果 MAXの%
      10p(5F) 50p(25F) 1000p(500F) 10p(5F) 50p(25F) 1000p(500F) 10p(5F) 50p(25F) 1000p(500F)
      1 ANS across neighbourhood search 0.94948 0.84776 0.43857 2.23581 1.00000 0.92334 0.39988 2.32323 0.70923 0.63477 0.23091 1.57491 6.134 68.15
      2 CLA コードロックアルゴリズム(joo) 0.95345 0.87107 0.37590 2.20042 0.98942 0.91709 0.31642 2.22294 0.79692 0.69385 0.19303 1.68380 6.107 67.86
      3 AMOm 動物移動最適化m 0.90358 0.84317 0.46284 2.20959 0.99001 0.92436 0.46598 2.38034 0.56769 0.59132 0.23773 1.39675 5.987 66.52
      4 (P+O)ES (P+O)進化戦略 0.92256 0.88101 0.40021 2.20379 0.97750 0.87490 0.31945 2.17185 0.67385 0.62985 0.18634 1.49003 5.866 65.17
      5 CTA 彗星の尾アルゴリズム(joo) 0.95346 0.86319 0.27770 2.09435 0.99794 0.85740 0.33949 2.19484 0.88769 0.56431 0.10512 1.55712 5.846 64.96
      6 TETA 時間進化移動アルゴリズム（joo） 0.91362 0.82349 0.31990 2.05701 0.97096 0.89532 0.29324 2.15952 0.73462 0.68569 0.16021 1.58052 5.797 64.41
      7 SDSm 確率的拡散探索M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
      8 AAm アーチェリーアルゴリズムM 0.91744 0.70876 0.42160 2.04780 0.92527 0.75802 0.35328 2.03657 0.67385 0.55200 0.23738 1.46323 5.548 61.64
      9 ESG 社会集団の進化(joo) 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
      10 SIA 等方的焼きなまし(joo) 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
      11 ACS 人工協調探索 0.75547 0.74744 0.30407 1.80698 1.00000 0.88861 0.22413 2.11274 0.69077 0.48185 0.13322 1.30583 5.226 58.06
      12 ダ 弁証法的アルゴリズム 0.86183 0.70033 0.33724 1.89940 0.98163 0.72772 0.28718 1.99653 0.70308 0.45292 0.16367 1.31967 5.216 57.95
      13 BHAm ブラックホールアルゴリズムM 0.75236 0.76675 0.34583 1.86493 0.93593 0.80152 0.27177 2.00923 0.65077 0.51646 0.15472 1.32195 5.196 57.73
      14 ASO 無政府社会最適化 0.84872 0.74646 0.31465 1.90983 0.96148 0.79150 0.23803 1.99101 0.57077 0.54062 0.16614 1.27752 5.178 57.54
      15 AOSm 原子軌道探索M 0.80232 0.70449 0.31021 1.81702 0.85660 0.69451 0.21996 1.77107 0.74615 0.52862 0.14358 1.41835 5.006 55.63
      16 TSEA 亀甲進化アルゴリズム(joo) 0.96798 0.64480 0.29672 1.90949 0.99449 0.61981 0.22708 1.84139 0.69077 0.42646 0.13598 1.25322 5.004 55.60
      17 DE 差分進化 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
      18 CRO 化学反応の最適化 0.94629 0.66112 0.29853 1.90593 0.87906 0.58422 0.21146 1.67473 0.75846 0.42646 0.12686 1.31178 4.892 54.36
      19 BSA 鳥群アルゴリズム 0.89306 0.64900 0.26250 1.80455 0.92420 0.71121 0.24939 1.88479 0.69385 0.32615 0.10012 1.12012 4.809 53.44
      20 HS ハーモニー検索 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
      21 SSG 苗木の播種と育成 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
      22 BCOm 細菌走化性最適化M 0.75953 0.62268 0.31483 1.69704 0.89378 0.61339 0.22542 1.73259 0.65385 0.42092 0.14435 1.21912 4.649 51.65
      23 ABO アフリカ水牛の最適化 0.83337 0.62247 0.29964 1.75548 0.92170 0.58618 0.19723 1.70511 0.61000 0.43154 0.13225 1.17378 4.634 51.49
      24 (PO)ES (PO)進化戦略 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
      25 TSm タブーサーチM 0.87795 0.61431 0.29104 1.78330 0.92885 0.51844 0.19054 1.63783 0.61077 0.38215 0.12157 1.11449 4.536 50.40
      26 BSO ブレインストーム最適化 0.93736 0.57616 0.29688 1.81041 0.93131 0.55866 0.23537 1.72534 0.55231 0.29077 0.11914 0.96222 4.498 49.98
      27 WOAm 鯨最適化アルゴリズムM 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
      28 AEFA 人工電界アルゴリズム 0.87700 0.61753 0.25235 1.74688 0.92729 0.72698 0.18064 1.83490 0.66615 0.11631 0.09508 0.87754 4.459 49.55
      29 AEO 人工生態系ベースの最適化アルゴリズム 0.91380 0.46713 0.26470 1.64563 0.90223 0.43705 0.21400 1.55327 0.66154 0.30800 0.28563 1.25517 4.454 49.49
      30 ACOm 蟻コロニー最適化M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
      31 BFO-GA 細菌採食の最適化：Ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
      32 SOA シンプル最適化アルゴリズム 0.91520 0.46976 0.27089 1.65585 0.89675 0.37401 0.16984 1.44060 0.69538 0.28031 0.10852 1.08422 4.181 46.45
      33 ABHA 人工蜂の巣アルゴリズム 0.84131 0.54227 0.26304 1.64663 0.87858 0.47779 0.17181 1.52818 0.50923 0.33877 0.10397 0.95197 4.127 45.85
      34 ACMO 大気雲モデルの最適化 0.90321 0.48546 0.30403 1.69270 0.80268 0.37857 0.19178 1.37303 0.62308 0.24400 0.10795 0.97503 4.041 44.90
      35 ADAMm 適応モーメント推定M 0.88635 0.44766 0.26613 1.60014 0.84497 0.38493 0.16889 1.39880 0.66154 0.27046 0.10594 1.03794 4.037 44.85
      36 ATAm 人工部族アルゴリズムM 0.71771 0.55304 0.25235 1.52310 0.82491 0.55904 0.20473 1.58867 0.44000 0.18615 0.09411 0.72026 3.832 42.58
      37 ASHA 人工シャワーアルゴリズム 0.89686 0.40433 0.25617 1.55737 0.80360 0.35526 0.19160 1.35046 0.47692 0.18123 0.09774 0.75589 3.664 40.71
      38 ASBO 適応型社会行動最適化(ASBO) 0.76331 0.49253 0.32619 1.58202 0.79546 0.40035 0.26097 1.45677 0.26462 0.17169 0.18200 0.61831 3.657 40.63
      39 MEC mind evolutionary computation 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
      40 IWO 侵入雑草最適化 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
      41 Micro-AIS 微小人工免疫系 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54
      42 COAm カッコウ最適化アルゴリズムM 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21
      43 SDOm 螺旋ダイナミクス最適化M 0.74601 0.44623 0.29687 1.48912 0.70204 0.34678 0.10944 1.15826 0.42833 0.16767 0.03663 0.63263 3.280 36.44
      44 NMm ネルダー=ミード法M 0.73807 0.50598 0.31342 1.55747 0.63674 0.28302 0.08221 1.00197 0.44667 0.18667 0.04028 0.67362 3.233 35.92
      45 BBBC ビッグバンビッグクランチアルゴリズム 0.60531 0.45250 0.31255 1.37036 0.52323 0.35426 0.20417 1.08166 0.39769 0.19431 0.11286 0.70486 3.157 35.08
      RW ランダムウォーク 0.48754 0.32159 0.25781 1.06694 0.37554 0.21944 0.15877 0.75375 0.27969 0.14917 0.09847 0.52734 2.348 26.09


      まとめ

      弁証法的アルゴリズムは、哲学の弁証法の概念に基づく革新的な最適化手法であり、対立する要素の相互作用によって解の改善を実現します。このアルゴリズムは、集団を思索的思考者と実践的思考者に分ける独自の方式によって、大域探索と局所探索の概念をうまく組み合わせており、探索と活用のバランスを効果的に取ることが可能です。

      アルゴリズムは3つの主要ステップで構成されており、体系的な最適化手法を提供します。作業の中で、思索的思考者は探索空間の広範な探索をおこないます（ただし一般に最適化アルゴリズムでは、解は「散らす」のではなく精緻化されることが多いです）。一方、実践的思考者は、有望な領域の局所最適化に注力します。この分割により、アルゴリズムは探索空間を効果的に探索し、局所最適解に陥ることを避けることができます。特に、私のおこなったランダムな誤差によってアルゴリズムの論理がより弁証法的な対立のテーマに近づいた点も興味深い特徴です。

      テスト結果は、バランスの取れた探索能力によって高い効率性を示すことを確認しています。さまざまなタイプのタスクに対しても十分な性能レベルを維持しています。他のアルゴリズムと比較しても、DAは極端に良くなったり悪くなったりすることはなく、表上の色のグラデーションでも均一かつ安定した結果を示しています。全体の性能指標は、既存の最適化手法と比較してもアルゴリズムの競争力を示しています。このように、哲学的原理と数学的手法を組み合わせることで、複雑な最適化問題を解くための強力なツールが生まれます。

      Tab

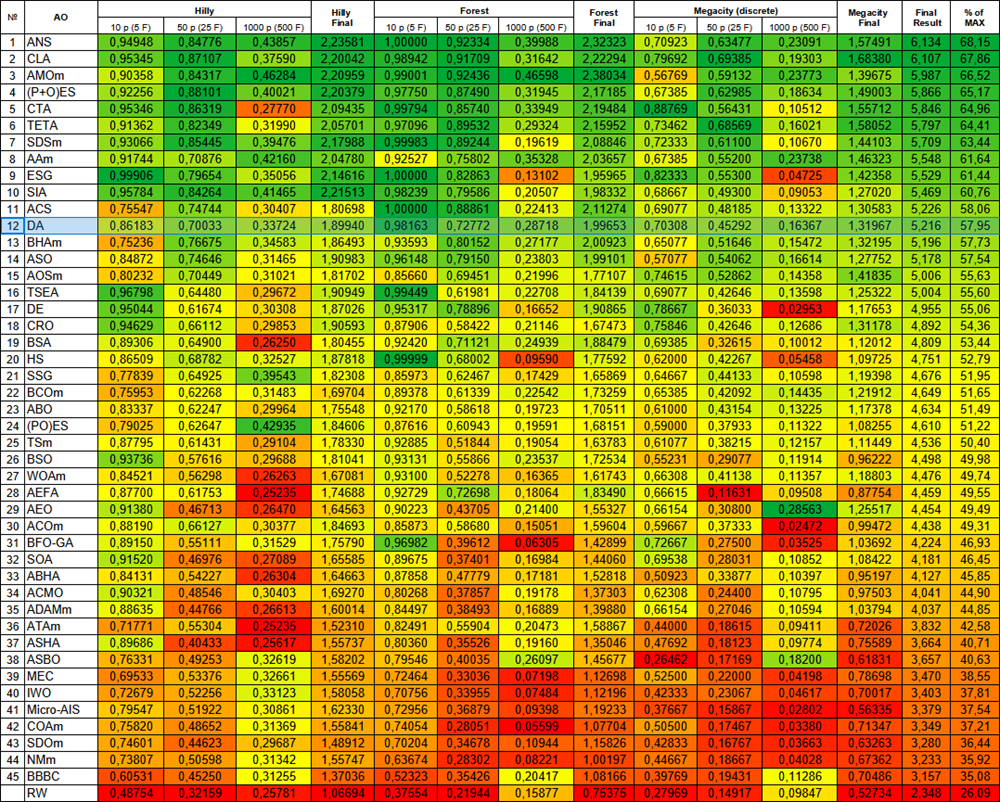
      図3：対応するテストに応じたアルゴリズムのカラーグラデーション

      チャート

      図4：アルゴリズムテスト結果のヒストグラム（0から100のスケール、高いほど良い）100は理論上の最大値であり、アーカイブには評価表を計算するためのスクリプトがあります。


      DAの長所と短所

      長所

      1. 外部パラメータは少なく、集団サイズを除けば2つだけ
      2. 実装がシンプル
      3. かなり早い
      4. 小規模な問題と大規模な問題の両方においてバランスの取れた優れたパフォーマンスを発揮

      短所

      1. 結果がばらばら

      この記事には、最新版のアルゴリズムコードを含むアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。

      記事で使用されているプログラム

      # 名前 種類 詳細
      1 #C_AO.mqh
      		 インクルード
      		 集団最適化アルゴリズムの親クラス
      2 #C_AO_enum.mqh
      		 インクルード
      		 集団最適化アルゴリズムの列挙
      3 TestFunctions.mqh
      		 インクルード
      		 テスト関数のライブラリ
      4
      		 TestStandFunctions.mqh
      		 インクルード
      		 テストスタンド関数ライブラリ
      5
      		 Utilities.mqh
      		 インクルード
      		 補助関数のライブラリ
      6
      		 CalculationTestResults.mqh
      		 インクルード
      		 比較表の結果を計算するスクリプト
      7
      		 Testing AOs.mq5
      		 スクリプト すべての集団最適化アルゴリズムの統一テストスタンド
      8
      		 Simple use of population optimization algorithms.mq5
      		 スクリプト
      		 可視化せずに集団最適化アルゴリズムを使用する簡単な例
      9
      		 Test_AO_DA.mq5
      		 スクリプト DAテストスタンド

      MetaQuotes Ltdによってロシア語から翻訳されました。
      元の記事: https://www.mql5.com/ru/articles/16999

      添付されたファイル |
      ZIPをダウンロード
      DA.zip (158.45 KB)

      警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

      この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。

      この著者による他の記事

      ディスカッションに移動
      EAのサンプル EAのサンプル
      一般的なMACDを使ったEAを例として、MQL4開発の原則を紹介します。
      金融時系列予測のための生物学的ニューロン 金融時系列予測のための生物学的ニューロン
      時系列予測のために生物学的に正しいニューロンシステムを構築します。ニューラルネットワークのアーキテクチャにプラズマ的な環境を導入することで、一種の「集合知」が生まれます。そこでは、各ニューロンが直接的な結合だけでなく、長距離の電磁相互作用を通じてもシステム全体の動作に影響を与えます。このようなニューラル脳モデリングシステムが市場においてどのような性能を発揮するのかを見ていきます。
      エラー 146 (「トレードコンテキスト ビジー」) と、その対処方法 エラー 146 (「トレードコンテキスト ビジー」) と、その対処方法
      この記事では、MT4において複数のEAの衝突をさける方法を扱います。ターミナルの操作、MQL4の基本的な使い方がわかる人にとって、役に立つでしょう。
      取引におけるニューラルネットワーク：階層型ダブルタワーTransformer (Hidformer) 取引におけるニューラルネットワーク：階層型ダブルタワーTransformer (Hidformer)
      階層型ダブルタワーTransformer (Hidformer: Hierarchical Double-Tower Transformer)フレームワークについて紹介します。このフレームワークは時系列予測およびデータ分析向けに開発されました。Hidformerの開発者は、Transformerアーキテクチャに対して複数の改良を提案しており、その結果、予測精度の向上と計算リソースの削減を実現しています。