亀甲進化アルゴリズム(TSEA)

内容

1. はじめに
2. アルゴリズムの実装
3.テスト結果

1. はじめに

亀は、最も古く、驚くべき自然の創造物のひとつです。彼らの甲羅は弾力性と保護、そして生存の象徴です。亀の一生を通じて形成されるこの壮大な盾は、物理的な保護だけでなく、絶え間ない成長や障害の克服を象徴しています。

甲羅に描かれたデザインは、その成長の道のりのユニークさを示す証拠であり、時間と生物そのものとの調和を象徴しています。 甲羅は「臍帯」と呼ばれる中心点から成長し、既存の甲羅に新しい層が追加されることで、さまざまな模様が形成されます。模様の各セグメントは、亀の成長の異なる年や季節を表しています。毎年、甲羅は亀とともに成熟し、新しい模様を持ちながら、動物の経験と成長を反映した独自のクラスタを形成します。

亀の甲羅は、上部の「カラパス」と下部の「プラストロンという2つの部分から構成されています。亀の甲羅の成長は、変態の結果として起こります。甲羅の模様は、遺伝、環境、甲羅自体の成長など、さまざまな要因が複雑に絡み合った結果です。

亀の甲羅は生体組織とカルシウム、マグネシウムなどの炭酸塩から成り立っています。甲羅の炭酸塩構造は強度を高め、亀の内臓を保護します。若い亀の甲羅は柔らかい軟骨で構成されており、時間の経過とともに固まって骨になります。甲羅は、亀の皮膚の下に新しい骨組織が定期的に堆積することで成長します。このプロセスにより、亀の成長に伴って甲羅が大きくなり、新しい模様が現れたり、既存の模様が時間とともに変化したりします。

亀の甲羅の模様はランダムではなく、特定の生物学的プロセスの結果として形成されます。これらの模様は、形状、色、位置に基づいて異なるグループまたは「クラスタ」に分類できます。たとえば、星型の模様を持つ亀もいれば、ヒョウの皮のような模様を持つ亀もいます。亀の甲羅は成長するにつれて模様が変化し、進化します。その結果、模様が属するクラスタが変更されることもあります。例えば、当初は「星」と分類されていた模様が、時間の経過とともに複雑化することがあります。

それぞれの亀の甲羅には独特の模様があり、それは環境への適応、カモフラージュ、さらには繁殖のために仲間を引き寄せるなど、重要な機能を果たしています。

私は、亀の甲羅の模様にインスピレーションを得て、独自の最適化アルゴリズムを作成しました。亀の甲羅の進化は、データの結合とクラスタリングの過程の比喩となり、経験と知識に基づいて適応し進化できる新しいツールの創出を決定づけました。

2. アルゴリズムの実装

亀甲進化アルゴリズムの背後にある考え方は、最適化問題の解を表す新しい角質化した皮膚の領域を徐々に形成することで、甲羅の成長をエミュレートすることです。このモデルでは、最良の解は硬くなり、外面に近い位置に配置され、成功しなかった解は柔らかいままで内側に留まります。

ここでの甲羅は、その表面に模様を形成するクラスタに分割され、これらの層はクラスタに垂直に分割されることでシミュレートされます。アルゴリズムにおける甲羅の成長をエミュレートするプロセスには、上方（外側）への動き、下方（内側）への動き、そして伸長が含まれます。この最適化アルゴリズムのユニークな特徴は、成功率の低い解を保存する点であり、これは甲羅の内側への成長に現れます。甲羅の内側の層だけが両方向に拡張し、他の層は外側にのみ拡張します。また、最悪の解は新しいものに置き換えられます。各垂直クラスタ（層）の解の容量には制限があり、最大数に達していない場合は解が単純に追加され、最大数に達した場合には、説明された原則に従って解が置き換えられます。

図1は、解の質と解間の距離によるクラスタリングを明確に示しています。理解を深めるために、1次元の解空間を持つ仮想的な例を用います。この図を参照することで、解の質と近さによってどのようにクラスタが形成されるかがよく理解できるでしょう。

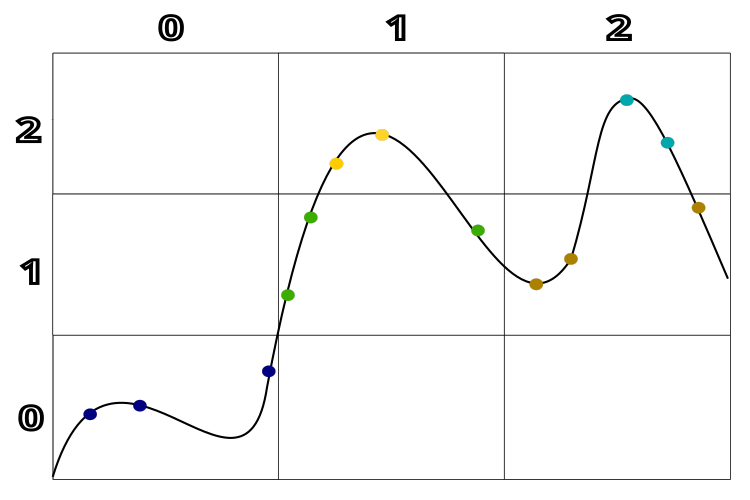
図1：TSEAアルゴリズムにおける解の質と解間の距離によるクラスタリング

TSEAアルゴリズムの擬似コードを以下に示します。

1.  母集団に対してランダムな個体を生成します。
2.  FF（適応度関数）を計算します。
3. 母集団を垂直方向にクラスタリングした初期状態を作成します。
4.  初期K-Means集団は水平方向にクラスタリングします。
5.  母集団を甲羅に配置します。
6.  甲羅のデータに基づいて新しい集団を生成します。
     6.1.0.8の確率で
          クラスタを垂直に選択します。
          セル内の最良のエージェントを選択するか、0.5の確率で任意のエージェントを選びます。
          セル内で選択されたエージェントを使用するか、0.6の確率で最良の大域解を使用します。
          べき分布を用いて新しいエージェントの座標を作成します。
     6.2 または
          クラスタを垂直に選択します。
          縦に2つのクラスタを選び、その中からランダムにエージェントを選びます。
          選択したエージェントの座標の平均値を新しい座標として作成します。
7.    FF（適応度関数）を計算します。
8.   母集団の垂直クラスタリングを実施します。
9.    K-NN（k近傍法）による甲羅へのエージェントの帰属を定義します。
10. 50エポックごとに甲羅の垂直クラスタリングをおこないます。
11. 母集団を甲羅に配置します。
12. P6から繰り返します。

二次方程式 (図 2) に従ってクラスタを垂直に選択します。この方程式では、リストの最後の（最良）クラスターが0番目（最悪）のクラスタよりも選択される確率が高くなります。

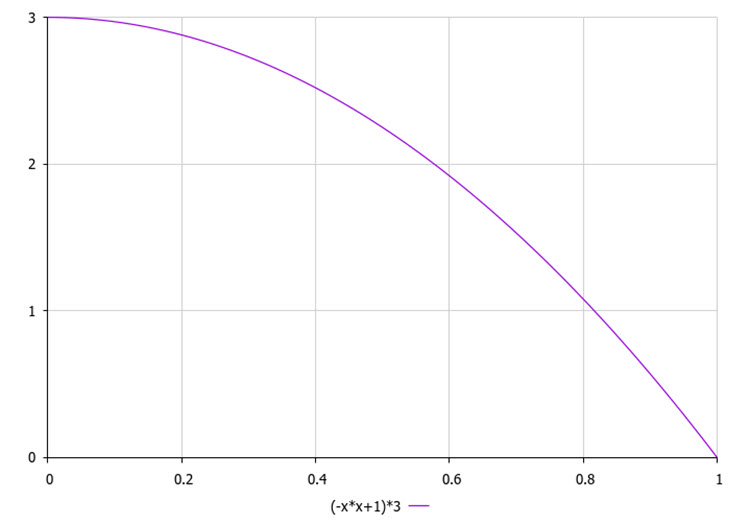
図2：クラスタを垂直方向に選択する確率の法則（質別）：３はクラスタ数

したがって、甲羅の新しいセクション（エージェント - 最適化問題の解）を作成するロジックは次のようになります。

1. 甲羅層（垂直クラスタ）を選択します。上部の硬い層を選ぶ確率は、下部の柔らかい層を選ぶ確率よりも高く設定します。
2. 選択された層の水平クラスタから甲羅部分を選択します。
3. 選択したセクションを「融合」します。

このプロセスにおいて、「融合」（硬化）する確率は、下層よりも上層の方が高いです。

擬似コードと親集団におけるエージェント選択の法則が整ったので、タスクは99%完了しました。もちろん、これは冗談です。まだコードを書く必要があります。

TSEAアルゴリズムの最適化エージェントを、S_TSEA_Agent構造体として定義します。この構造体には、縦と横のクラスタラベルが必要です。

1. この構造体には以下のフィールドが含まれます。

• c[]：エージェント座標を格納する配列
• f：エージェントのスコア（適応度）を格納する変数
• label：クラスタメンバーシップラベル
• labelClustV：垂直クラスタリング
• minDist ：最も近い重心までの最小距離

2. Initは、構造体フィールドを初期化する S_TSEA_Agent構造体のメソッドです。このメソッドは、ArrayResize関数を使用して「c」配列のサイズを変更するために使用されるcoords整数引数を受け取ります。
3.f = -DBL_MAX：変数「f」の初期値をdouble型の可能な最小値に設定します。
4.label = -1およびlabelClustV = -1：クラスタメンバーシップラベルを-1に初期化します。
5.minDist = DBL_MAX：変数minDistの初期値をdouble型の可能な最大値に設定します。

このコードは、TSEA最適化アルゴリズムにおけるエージェントの基本的なデータ構造を表しており、新しいエージェントが作成される際にそのフィールドを初期化します。これにより、エージェントは現在の状態に関する情報を保存し、アルゴリズムの実行中にそれを更新することが可能になります。

//——————————————————————————————————————————————————————————————————————————————
struct S_TSEA_Agent
{
    double c     [];     //coordinates
    double f;            //fitness
    int    label;        //cluster membership label
    int    labelClustV;  //clusters vertically
    double minDist;      //minimum distance to the nearest centroid

    void Init (int coords)
    {
      ArrayResize (c,     coords);
      f           = -DBL_MAX;
      label       = -1;
      labelClustV = -1;
      minDist     = DBL_MAX;
    }
};
//——————————————————————————————————————————————————————————————————————————————

亀の甲羅を記述する必要があります。亀の甲羅は2次元配列で構成されており、適応度クラスタが縦に、ロケーションクラスタが横に配置されています。二次元配列の各セルには、0からアルゴリズムの外部パラメータで指定された最大値までの値が含まれます。

水平クラスタを記述するために、次のフィールドを含むS_TSEA_horizontal構造体を使用します。

• indBest：セル内の最良エージェントのインデックス
  
• agent[]：エージェントを格納するためのS_TSEA_Agent構造体の配列

また、垂直クラスタを記述するためには、次のフィールドを含むS_TSEA_horizontal構造体を使用します。

• cell[]：S_TSEA_horizontal構造体の配列
  

このようにして、このコードでは2次元配列の両方向で亀の甲羅を表現できます。各セルに最適化エージェントを格納することができ、亀の甲羅は、子エージェントを作成する際に便利にアクセスできる特別に構造化された親集団として機能します。

//——————————————————————————————————————————————————————————————————————————————
struct S_TSEA_horizontal
{
    int indBest;
    S_TSEA_Agent agent [];
};

struct S_TSEA_vertical
{
    S_TSEA_horizontal cell [];
};

//——————————————————————————————————————————————————————————————————————————————

クラスタリングを実行するために、TSEAアルゴリズムはK-MeansとK-NNの2つのクラスタリング手法を適用します。K-Meansについては、BSOアルゴリズムに関する記事で既に検討しました。ここでは、クラスタの構造がどのようなものかを思い出してみましょう。

• centroid[]：セルの重心の座標を格納する配列
• f：セントロイドのスコア（適応度）を格納する変数
• count：クラスタ内のエージェント数
• agentList[]：クラスタ内のエージェントのリスト
• Init ：構造体のフィールドを初期化するS_Cluster構造体のメソッド
  

//——————————————————————————————————————————————————————————————————————————————
struct S_Cluster
{
    double centroid [];  //cluster centroid
    double f;            //centroid fitness
    int    count;        //number of points in the cluster

    void Init (int coords)
    {
      ArrayResize (centroid, coords);
      f     = -DBL_MAX;
      count = 0;
      ArrayResize (ideasList, 0, 100);
    }
};
//——————————————————————————————————————————————————————————————————————————————

子エージェントの対応するクラスタへの帰属を決定するために、K-NN法（k近傍法）を用います。

K-Meansメソッドに加えて、C_TSEA_clustersクラスには以下があります。

1. VectorDistanceメソッド

• double数の配列で表現されたv1とv2ベクトル間のユークリッド距離を計算します。
• ユークリッド距離の方程式(alteucleuclalt)を使用します。
• 算出された距離を返します。

2. DistanceIndex構造体

• distanceとindexという2つの値のペアを表します。
• ある点から他の点までの距離とそのインデックスを格納するのに使われます。

3. BubbleSortメソッド

• DistanceIndex型のオブジェクトの配列を、バブルソートメソッドを用いて距離の昇順に並び替えます。
• 一時的なtemp変数が配列要素の交換に使われます。

4. KNNメソッドは、「point」を分類するためのk-最近傍アルゴリズムを実装しています。

• 「point」から「data 」配列内のすべての点までの距離を計算し、これらの距離を並び替え、その点がn_clusters（k個の最近傍に基づくクラスタ）のいずれかに属するかを決定します。
• votes配列は、各クラスタの得票数を計算するために使用されます。
• 最も投票数の多いクラスタのインデックスが返されます。

//——————————————————————————————————————————————————————————————————————————————
class C_TSEA_clusters
{
  public:

  double VectorDistance (double &v1 [], double &v2 [])
  {
    double distance = 0.0;
    for (int i = 0; i < ArraySize (v1); i++)
    {
      distance += (v1 [i] - v2 [i]) * (v1 [i] - v2 [i]);
    }
    return MathSqrt (distance);
  }

  struct DistanceIndex
  {
      double distance;
      int index;
  };

  void BubbleSort (DistanceIndex &arr [], int start, int end)
  {
    for (int i = start; i < end; i++)
    {
      for (int j = start; j < end - i; j++)
      {
        if (arr [j].distance > arr [j + 1].distance)
        {
          DistanceIndex temp = arr [j];
          arr [j] = arr [j + 1];
          arr [j + 1] = temp;
        }
      }
    }
  }

  int KNN (S_TSEA_Agent &data [], S_TSEA_Agent &point, int k_neighbors, int n_clusters)
  {
    int n = ArraySize (data);
    DistanceIndex distances_indices [];

    // Calculate the distances from a point to all other points
    for (int i = 0; i < n; i++)
    {
      DistanceIndex dist;
      dist.distance = VectorDistance (point.c, data [i].c);
      dist.index = i;
      ArrayResize (distances_indices, n);
      distances_indices [i] = dist;
    }

    // Sort the distances
    BubbleSort (distances_indices, 0, n - 1);

    // Define the cluster for the point
    int votes [];
    ArrayResize (votes, n_clusters);
    ArrayInitialize (votes, 0);

    for (int j = 0; j < k_neighbors; j++)
    {
      int label = data [distances_indices [j].index].label;

      if (label != -1 && label < n_clusters)
      {
        votes [label]++;
      }
    }

    int max_votes = 0;
    int max_votes_cluster = -1;

    for (int j = 0; j < n_clusters; j++)
    {
      if (votes [j] > max_votes)
      {
        max_votes = votes [j];
        max_votes_cluster = j;
      }
    }

    return max_votes_cluster;
  }
};
//——————————————————————————————————————————————————————————————————————————————

C_AO基本クラスから派生したC_AO_TSEAクラスの説明に移りましょう。このクラスは亀甲進化アルゴリズム(TSEA: Turtle Shell Evolution Algorithm)を実装しています。以下はクラスフィールドとメソッドです。

1. C_AO_TSEA：コンストラクタはクラスフィールドを初期化します。アルゴリズムの名前、説明、アルゴリズムに関する記事へのリンクが設定されています。また、母集団サイズ、垂直水平クラスタ数、最近接数、セル内の最大エージェント数などのアルゴリズムパラメータも設定します。

2. SetParams：このメソッドは、配列paramsの値に基づいてアルゴリズムのパラメータを設定します。

3. Init ：このメソッドはアルゴリズムを初期化します。最小検索範囲と最大検索範囲、検索ステップ、エポック数を取ります。

4. MovingメソッドとRevisionメソッドは、TSEAアルゴリズムの主要なメソッドであり、基本的なロジックを実装しています。

5. vClusters、hClusters、neighborNumb、maxAgentsInCell各フィールドは、コンストラクタで設定されるアルゴリズムパラメータで、SetParamsメソッドを使って変更できます。

6. agent、cell、clusters各配列はアルゴリズムが使用するデータ構造です。これらはそれぞれエージェント、セル、クラスタに関する情報を含んでいます。

7. C_TSEA_clustersクラスのkmオブジェクトは、クラスタリング操作の実行に使用されます。

8. minFval、stepF、epochs、epochsNow各privateフィールドは内部変数です。クラス外からのアクセスを意図していません。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_TSEA : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_TSEA () { }
  C_AO_TSEA ()
  {
    ao_name = "TSEA";
    ao_desc = "Turtle Shell Evolution Algorithm";
    ao_link = "https://www.mql5.com/ru/articles/14789";

    popSize         = 100; //population size

    vClusters       = 3;   //number of vertical clusters
    hClusters       = 10;  //number of horizontal clusters
    neighbNumb      = 5;   //number of nearest neighbors
    maxAgentsInCell = 3;   //max agents in cell

    ArrayResize (params, 5);

    params [0].name = "popSize";          params [0].val  = popSize;

    params [1].name = "vClusters";        params [1].val  = vClusters;
    params [2].name = "hClusters";        params [2].val  = hClusters;
    params [3].name = "neighbNumb";       params [3].val  = neighbNumb;
    params [4].name = "maxAgentsInCell";  params [4].val  = maxAgentsInCell;
  }

  void SetParams ()
  {
    popSize         = (int)params [0].val;

    vClusters       = (int)params [1].val;
    hClusters       = (int)params [2].val;
    neighbNumb      = (int)params [3].val;
    maxAgentsInCell = (int)params [4].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving    ();
  void Revision  ();
  void Injection (const int popPos, const int coordPos, const double value);

  //----------------------------------------------------------------------------
  int    vClusters;      //number of vertical clusters
  int    hClusters;      //number of horizontal clusters
  int    neighbNumb;     //number of nearest neighbors
  int    maxAgentsInCell;

  S_TSEA_Agent    agent   [];
  S_TSEA_vertical cell    [];

  S_Cluster      clusters [];
  C_TSEA_clusters km;

  private: //-------------------------------------------------------------------
  double minFval;
  double stepF;

  int    epochs;
  int    epochsNow;
};
//——————————————————————————————————————————————————————————————————————————————

C_AO_TSEAクラスのInitメソッドは、TSEAアルゴリズムを初期化します。以下に、その動作の詳細を記します。

1. StandardInit (rangeMinP, rangeMaxP, rangeStepP)：このメソッドは、アルゴリズムの標準的な初期化のために呼び出されます。最小、最大の検索範囲と検索ステップを取ります。初期化に失敗した場合はfalseを返します。

2.ArrayResize (agent, popSize)：agent配列のサイズをpopSize母集団のサイズに変更します。その後、Init(coords)メソッドが各エージェントに対して呼び出され、初期化されます。

3. ArrayResize (clusters, hClusters)：clusters配列のサイズをhClusters水平クラスタ数に変更します。次にInit(coords)メソッドが各クラスタに対して呼び出され、初期化されます。

4.ArrayResize (cell, vClusters)：cell配列のサイズをvClusters垂直クラスタ数に変更します。次に、cell[i].cell 配列と各セル内のエージェントの配列が、各セルごとに初期化されます。

5. minFval = DBL_MAX、stepF = 0.0、 epochs = epochsP、epochsNow = 0：アルゴリズム内部変数を初期化します。

6. 最後に、このメソッドは初期化が成功したことを示すtrueを返します。

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_TSEA::Init (const double &rangeMinP  [], //minimum search range
                      const double &rangeMaxP  [], //maximum search range
                      const double &rangeStepP [], //step search
                      const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (agent, popSize);
  for (int i = 0; i < popSize; i++) agent [i].Init (coords);

  ArrayResize (clusters, hClusters);
  for (int i = 0; i < hClusters; i++) clusters [i].Init (coords);

  ArrayResize (cell, vClusters);

  for (int i = 0; i < vClusters; i++)
  {
    ArrayResize (cell [i].cell, hClusters);

    for (int c = 0; c < hClusters; c++) ArrayResize (cell [i].cell [c].agent, 0, maxAgentsInCell);
  }

  minFval   = DBL_MAX;
  stepF     = 0.0;
  epochs    = epochsP;
  epochsNow = 0;

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_TSEAクラスのMovingメソッドは、TSEAアルゴリズムにおけるエージェント移動の基本ロジックを実装しています。以下は、主なステップの簡単な説明です。

1. 母集団の初期化

• これが最初の反復である場合(revision == false)、ランダムな個体が母集団に生成されます。
• そうでない場合は、既存の決定に基づいて母集団が更新されます。

2. 母集団の更新

• 各クラスタ(vClusters х hClusters)ごとに最適解が求められます。
• 新しい解は次のように形成されます。
• 最適解は、0.5の確率で、ある偏りを持ったランダムなクラスタからコピーされます。
• 0.2の確率で、異なるクラスタからの2つのランダムな解の平均として新しい解が形成されます。
• 新しい解の座標は、べき乗分布を使って生成され、最適解に近い状態を維持します。

3. 集団内エージェント（個体）の更新

このメソッドは、亀の甲羅の進化という基本的な考え方を実装しています。最良の解は「硬く」なり、外側の表面に近い位置に配置され、成功しなかった解は「柔らかい」ままで内側に位置します。このようにして解をクラスタリングし、あまり成功しなかった変種を保持することで、アルゴリズムの柔軟性と適応性を確保します。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_TSEA::Moving ()
{
  epochsNow++;

  //----------------------------------------------------------------------------
  //1. Generate random individuals for the population
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);

        agent [i].c [c] = a [i].c [c];
      }
    }

    return;
  }

  //----------------------------------------------------------------------------
  int    vPos = 0;
  int    hPos = 0;
  int    pos  = 0;
  int    size = 0;
  double val  = 0.0;
  double rnd  = 0.0;
  double min  = 0.0;
  double max  = 0.0;

  for (int v = 0; v < vClusters; v++)
  {
    for (int h = 0; h < hClusters; h++)
    {
      size = ArraySize (cell [v].cell [h].agent);

      if (size > 0)
      {
        max = -DBL_MAX;
        pos = -1;

        for (int c = 0; c < size; c++)
        {
          if (cell [v].cell [h].agent [c].f > max)
          {
            max = cell [v].cell [h].agent [c].f;
            pos = c;
            cell [v].cell [h].indBest = c;
          }
        }
      }
    }
  }

  for (int i = 0; i < popSize; i++)
  {
    if (u.RNDprobab () < 0.8)
    {
      while (true)
      {
        rnd = u.RNDprobab ();
        rnd = (-rnd * rnd + 1.0) * vClusters;

        vPos = (int)rnd;
        if (vPos > vClusters - 1) vPos = vClusters - 1;

        hPos = u.RNDminusOne (hClusters);

        size = ArraySize (cell [vPos].cell [hPos].agent);

        if (size > 0) break;
      }

      pos = u.RNDminusOne (size);

      if (u.RNDprobab () < 0.5) pos = cell [vPos].cell [hPos].indBest;

      for (int c = 0; c < coords; c++)
      {
        if (u.RNDprobab () < 0.6) val = cell [vPos].cell [hPos].agent [pos].c [c];
        else                      val = cB [c];

        double dist = (rangeMax [c] - rangeMin [c]) * 0.1;
        min = val - dist; if (min < rangeMin [c]) min = rangeMin [c];
        max = val + dist; if (max > rangeMax [c]) max = rangeMax [c];

        val = u.PowerDistribution (val, min, max, 30);

        a [i].c [c] = u.SeInDiSp  (val, rangeMin [c], rangeMax [c], rangeStep [c]);

        agent [i].c [c] = a [i].c [c];
      }
    }
    else
    {
      int size2 = 0;
      int hPos2 = 0;
      int pos2  = 0;

      while (true)
      {
        rnd = u.RNDprobab ();
        rnd = (-rnd * rnd + 1.0) * vClusters;

        vPos = (int)rnd;
        if (vPos > vClusters - 1) vPos = vClusters - 1;

        hPos = u.RNDminusOne (hClusters);
        size = ArraySize (cell [vPos].cell [hPos].agent);

        hPos2 = u.RNDminusOne (hClusters);
        size2 = ArraySize (cell [vPos].cell [hPos2].agent);

        if (size > 0 && size2 > 0) break;
      }

      pos  = u.RNDminusOne (size);
      pos2 = u.RNDminusOne (size2);

      for (int c = 0; c < coords; c++)
      {
        val = (cell [vPos].cell [hPos ].agent [pos ].c [c] +
               cell [vPos].cell [hPos2].agent [pos2].c [c]) * 0.5;

        a [i].c [c] = u.SeInDiSp  (val, rangeMin [c], rangeMax [c], rangeStep [c]);

        agent [i].c [c] = a [i].c [c];
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

C_AO_TSEAクラスのRevisionメソッドは、TSEAアルゴリズムにおける亀甲セクションの再配分の段階を実装しています。

エージェント集団を修正（更新）し、最良の大域解を更新する役割を担います。

アルゴリズムのこの部分の主なステップは以下の通りです。

1. 各エージェントの「適応度」を計算し、最良の「fB」解を決定します。
2. エージェントの適応度に基づいて、エージェントを垂直方向の「labelClustV」クラスタにラベル付けします。
3. これが最初の反復である場合(revision == false)、エージェントのクラスタリングはK-Meansアルゴリズムを使って初期化されます。
4. これが最初の反復でない場合は、以下のように実行されます。

- すべてのエージェントは、単一の「データ」配列に集められます。
- 母集団内の各エージェントについて、K-最近傍アルゴリズムを用いて水平方向の「ラベル」クラスタが決定されます。
- クラスタに分割されたエージェントを格納する「セル」構造は、50エポックごとに更新されます。

5. 各エージェントを適切なセルに配置します。もしそのセルが既に埋まっていれば、エージェントはそのセルの中で最も適応度が低い（セルが最下層にある場合は最も適応度が高い）ものと入れ替わります。

この段階の主な考え方は、甲羅の構造を維持することであり、最良解は外面に近く、成功しなかった解決策は内側に位置します。エージェントのクラスタリングと甲羅構造の動的な更新は、アルゴリズムの柔軟性と適応性を保証します。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_TSEA::Revision ()
{
  //get fitness--------------------------------------------------
  int pos = -1;

  for (int i = 0; i < popSize; i++)
  {
    agent [i].f = a [i].f;

    if (a [i].f > fB)
    {
      fB = a [i].f;
      pos = i;
    }

    if (a [i].f < minFval) minFval = a [i].f;
  }

  if (pos != -1) ArrayCopy (cB, a [pos].c, 0, 0, WHOLE_ARRAY);

  stepF = (fB - minFval) / vClusters;

  //Vertical layout of the child population-----------------------------------
  for (int i = 0; i < popSize; i++)
  {
    if (agent [i].f == fB) agent [i].labelClustV = vClusters - 1;
    else
    {
      agent [i].labelClustV = int((agent [i].f - minFval) / stepF);
      if (agent [i].labelClustV > vClusters - 1) agent [i].labelClustV = vClusters - 1;
    }
  }

  //----------------------------------------------------------------------------
  if (!revision)
  {
    km.KMeansPlusPlusInit (agent, popSize, clusters);
    km.KMeans             (agent, popSize, clusters);

    revision = true;
  }
  //----------------------------------------------------------------------------
  else
  {
    static S_TSEA_Agent data [];
    ArrayResize (data, 0, 1000);
    int size = 0;

    for (int v = 0; v < vClusters; v++)
    {
      for (int h = 0; h < hClusters; h++)
      {
        for (int c = 0; c < ArraySize (cell [v].cell [h].agent); c++)
        {
          size++;
          ArrayResize (data, size);

          data [size - 1] = cell [v].cell [h].agent [c];
        }
      }
    }

    for (int i = 0; i < popSize; i++)
    {
      agent [i].label = km.KNN (data, agent [i], neighbNumb, hClusters);
    }
    
    if (epochsNow % 50 == 0)
    {
      for (int v = 0; v < vClusters; v++)
      {
        for (int h = 0; h < hClusters; h++)
        {
          ArrayResize (cell [v].cell [h].agent, 0);
        }
      }

      for (int i = 0; i < ArraySize (data); i++)
      {
        if (data [i].f == fB) data [i].labelClustV = vClusters - 1;
        else
        {
          data [i].labelClustV = int((data [i].f - minFval) / stepF);
          if (data [i].labelClustV > vClusters - 1) data [i].labelClustV = vClusters - 1;
        }

        int v = data [i].labelClustV;
        int h = data [i].label;

        int size = ArraySize (cell [v].cell [h].agent) + 1;
        ArrayResize (cell [v].cell [h].agent, size);

        cell [v].cell [h].agent [size - 1] = data [i];
      }
    }
  }

  //Place the population in the shell------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    int v = agent [i].labelClustV;
    int h = agent [i].label;

    int size = ArraySize (cell [v].cell [h].agent);
    int pos    = 0;
    int posMin = 0;
    int posMax = 0;

    if (size >= maxAgentsInCell)
    {
      double minF =  DBL_MAX;
      double maxF = -DBL_MAX;

      for (int c = 0; c < maxAgentsInCell; c++)
      {
        if (cell [v].cell [h].agent [c].f < minF)
        {
          minF = cell [v].cell [h].agent [c].f;
          posMin = c;
        }
        if (cell [v].cell [h].agent [c].f > maxF)
        {
          maxF = cell [v].cell [h].agent [c].f;
          posMax = c;
        }
      }

      if (v == 0)
      {
        if (agent [i].f < minF)
        {
          pos = posMin;
        }
        else
        {
          pos = posMax;
        }
      }
      else  pos = posMin;
    }
    else
    {
      ArrayResize (cell [v].cell [h].agent, size + 1);
      pos = size;
    }

    cell [v].cell [h].agent [pos] = agent [i];
  }
}
//——————————————————————————————————————————————————————————————————————————————

3. テスト結果

TSEAの結果

亀甲進化アルゴリズム|100.0|3.0|10.0|5.0|3.0|TSEA
=============================
5 Hilly's; Func runs:10000; result:0.811921100517765
25 Hilly's; Func runs:10000; result:0.5537631430428238
500 Hilly's; Func runs:10000; result:0.2813575513298344
=============================
5 Forest's; Func runs:10000; result:0.9564485273109922
25 Forest's; Func runs:10000; result:0.481362270824773
500 Forest's; Func runs:10000; result:0.181400891410298
=============================
5 Megacity's; Func runs:10000; result:0.6676923076923076
25 Megacity's; Func runs:10000; result:0.3633846153846153
500 Megacity's; Func runs:10000; result:0.11670769230769343
=============================
All score:4.41404 (49.04%)

全テスト関数の合計スコアは4.41404で、理論最適解の49.04%に相当します。

テストベンチの動作を視覚化すると、アルゴリズムが良好に収束していることがわかります。すべてのテスト関数について、収束グラフ上に軌跡の散らばりが見られます。しかし、自由度が大きくなると、このばらつきは小さくなります。アルゴリズムにクラスタリングを用いるとともに、各セルのエージェント数を一定に保つことで、アルゴリズムは適応度関数の重要な領域を効果的に探索することができます。

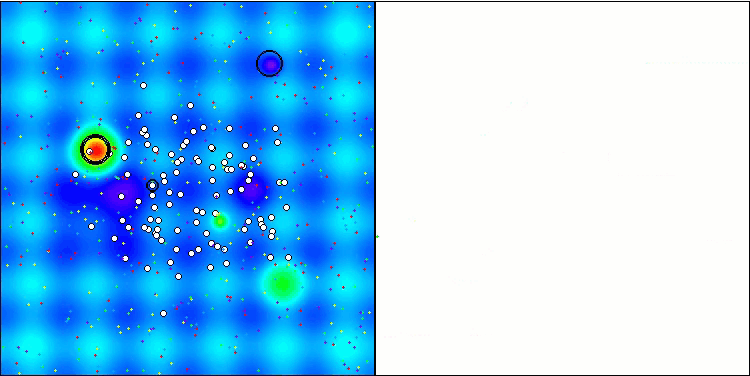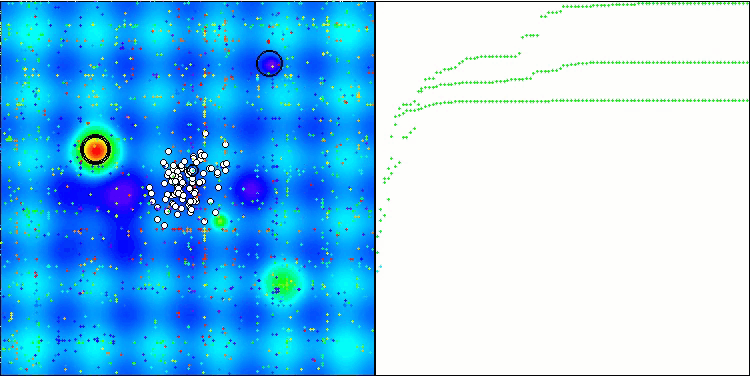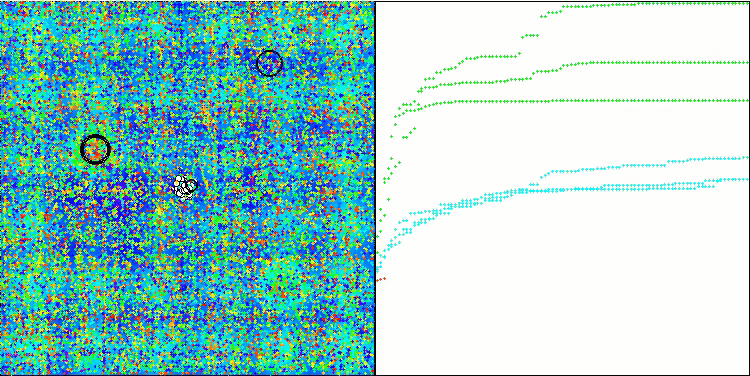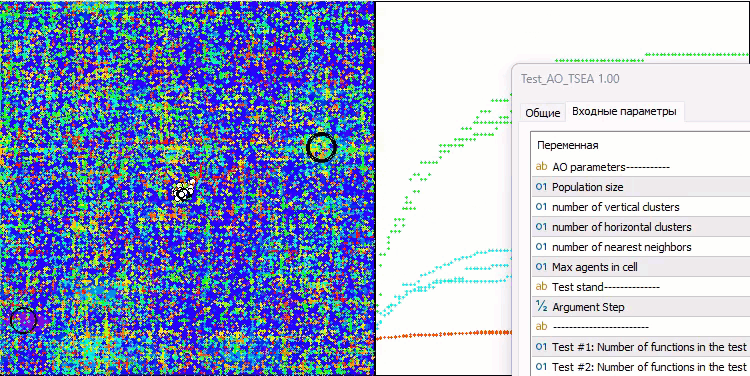
  Hillyテスト関数のTSEA

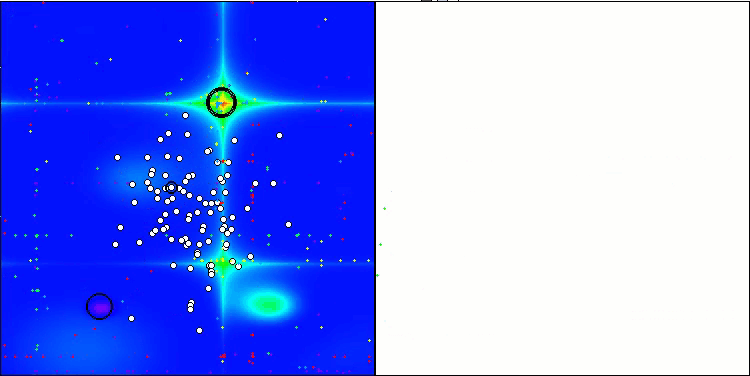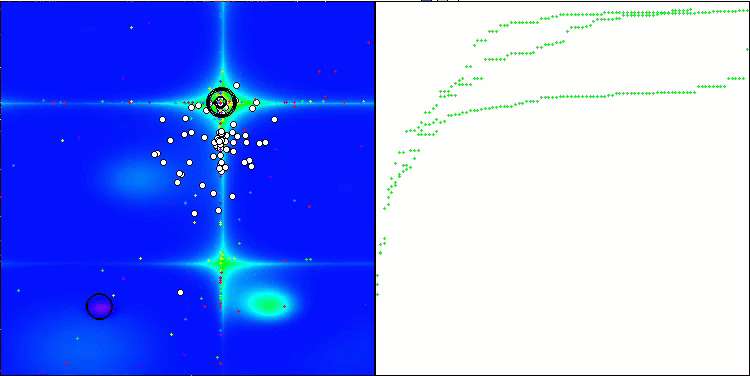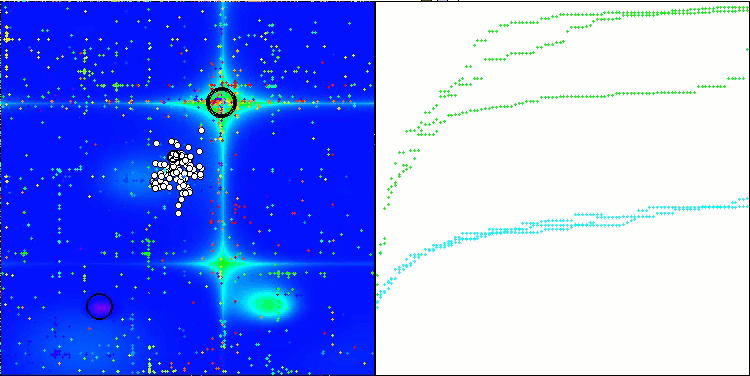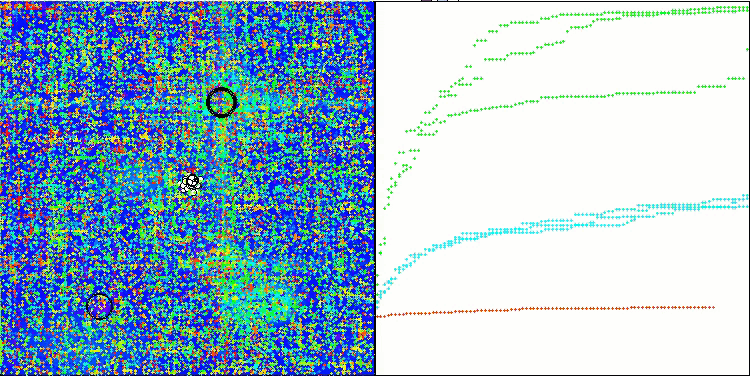
  Hillyテスト関数のTSEA

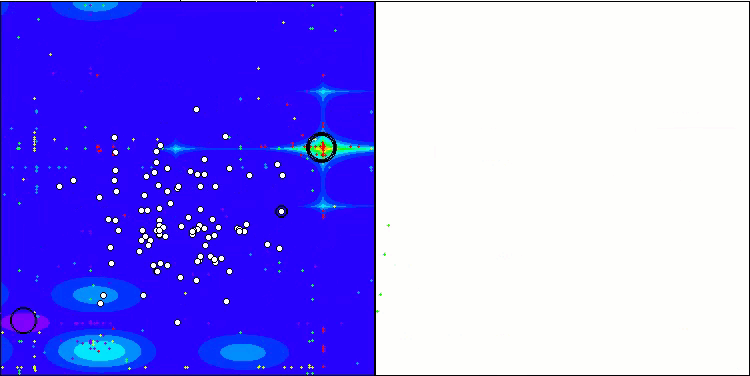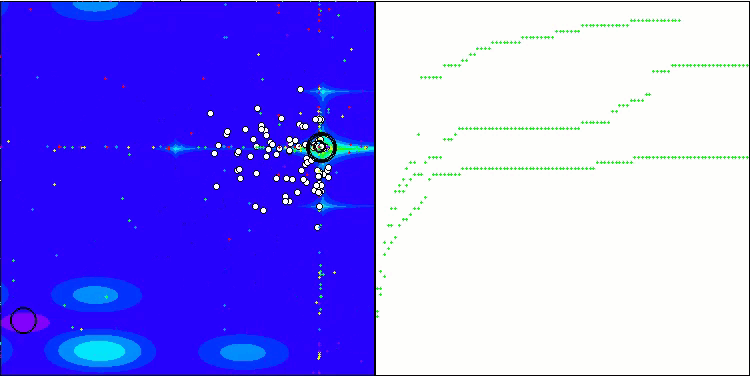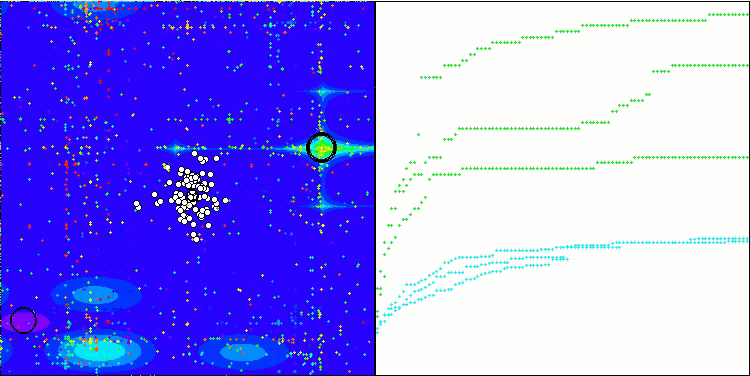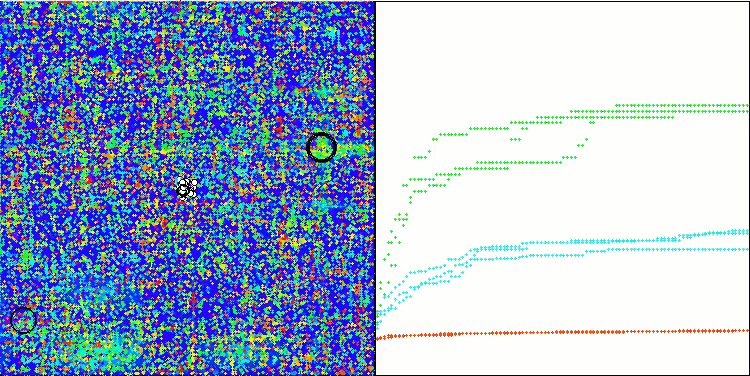
  Megacityテスト関数のTSEA

テスト関数をチェックした結果、このアルゴリズムは最終評価表の最上位6位を占めました。

#	AO	詳細	Hilly			Hilly最終	Forest			Forest最終	Megacity（離散）			Megacity最終	最終結果	MAXの%
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	BGA	バイナリ遺伝的アルゴリズム	0.99992	0.99484	0.50483	2.49959	1.00000	0.99975	0.32054	2.32029	0.90667	0.96400	0.23035	2.10102	6.921	76.90
2	(P+O)ES	(P+O）進化戦略	0.99934	0.91895	0.56297	2.48127	1.00000	0.93522	0.39179	2.32701	0.83167	0.64433	0.21155	1.68755	6.496	72.18
3	SDSm	確率的拡散探索M	0.93066	0.85445	0.39476	2.17988	0.99983	0.89244	0.19619	2.08846	0.72333	0.61100	0.10670	1.44103	5.709	63.44
4	ESG	社会集団の進化	0.99906	0.79654	0.35056	2.14616	1.00000	0.82863	0.13102	1.95965	0.82333	0.55300	0.04725	1.42358	5.529	61.44
5	SIA	等方的焼きなまし	0.95784	0.84264	0.41465	2.21513	0.98239	0.79586	0.20507	1.98332	0.68667	0.49300	0.09053	1.27020	5.469	60.76
6	TSEA	亀甲進化アルゴリズム	0.96798	0.64480	0.29672	1.90949	0.99449	0.61981	0.22708	1.84139	0.69077	0.42646	0.13598	1.25322	5.004	55.60
7	DE	差分進化	0.95044	0.61674	0.30308	1.87026	0.95317	0.78896	0.16652	1.90865	0.78667	0.36033	0.02953	1.17653	4.955	55.06
8	BSA	鳥群アルゴリズム	0.90857	0.73661	0.25767	1.90285	0.90437	0.81619	0.16401	1.88457	0.61692	0.54154	0.10951	1.26797	5.055	56.17
9	HS	ハーモニー検索	0.86509	0.68782	0.32527	1.87818	0.99999	0.68002	0.09590	1.77592	0.62000	0.42267	0.05458	1.09725	4.751	52.79
10	SSG	苗木の播種と育成	0.77839	0.64925	0.39543	1.82308	0.85973	0.62467	0.17429	1.65869	0.64667	0.44133	0.10598	1.19398	4.676	51.95
11	(PO)ES	(PO）進化戦略	0.79025	0.62647	0.42935	1.84606	0.87616	0.60943	0.19591	1.68151	0.59000	0.37933	0.11322	1.08255	4.610	51.22
12	BSO	ブレインストーム最適化	0.91301	0.56222	0.30047	1.77570	0.97162	0.57162	0.23449	1,77772	0.60462	0.27138	0.12011	0.99611	4.550	50.55
13	WOAm	鯨最適化アルゴリズムM	0.84521	0.56298	0.26263	1.67081	0.93100	0.52278	0.16365	1.61743	0.66308	0.41138	0.11357	1.18803	4.476	49.74
14	ACOm	蟻コロニー最適化M	0.88190	0.66127	0.30377	1.84693	0.85873	0.58680	0.15051	1.59604	0.59667	0.37333	0.02472	0.99472	4.438	49.31
15	BFO-GA	細菌採食の最適化：Ga	0.89150	0.55111	0.31529	1.75790	0.96982	0.39612	0.06305	1.42899	0.72667	0.27500	0.03525	1.03692	4.224	46.93
16	MEC	Mind Evolutionary Computation	0.69533	0.53376	0.32661	1.55569	0.72464	0.33036	0.07198	1.12698	0.52500	0.22000	0.04198	0.78698	3.470	38.55
17	IWO	侵入雑草最適化	0.72679	0.52256	0.33123	1.58058	0.70756	0.33955	0.07484	1.12196	0.42333	0.23067	0.04617	0.70017	3.403	37.81
18	Micro-AIS	微小人工免疫系	0.79547	0.51922	0.30861	1.62330	0.72956	0.36879	0.09398	1.19233	0.37667	0.15867	0.02802	0.56335	3.379	37.54
19	COAm	カッコウ最適化アルゴリズムM	0.75820	0.48652	0.31369	1.55841	0.74054	0.28051	0.05599	1.07704	0.50500	0.17467	0.03380	0.71347	3.349	37.21
20	SDOm	螺旋ダイナミクス最適化M	0.74601	0.44623	0.29687	1.48912	0.70204	0.34678	0.10944	1.15826	0.42833	0.16767	0.03663	0.63263	3.280	36.44
21	NMm	ネルダー=ミード法M	0.73807	0.50598	0.31342	1.55747	0.63674	0.28302	0.08221	1.00197	0.44667	0.18667	0.04028	0.67362	3.233	35.92
22	FAm	ホタルアルゴリズムM	0.58634	0.47228	0.32276	1.38138	0.68467	0.37439	0.10908	1.16814	0.28667	0.16467	0.04722	0.49855	3.048	33.87
23	GSA	重力探索法	0.64757	0.49197	0.30062	1.44016	0.53962	0.36353	0.09945	1.00260	0.32667	0.12200	0.01917	0.46783	2.911	32.34
24	BFO	細菌採餌最適化	0.61171	0.43270	0.31318	1.35759	0.54410	0.21511	0.05676	0.81597	0.42167	0.13800	0.03195	0.59162	2.765	30.72
25	ABC	人工蜂コロニー	0.63377	0.42402	0.30892	1.36671	0.55103	0.21874	0.05623	0.82600	0.34000	0.14200	0.03102	0.51302	2.706	30.06
26	BA	コウモリアルゴリズム	0.59761	0.45911	0.35242	1.40915	0.40321	0.19313	0.07175	0.66810	0.21000	0.10100	0.03517	0.34617	2.423	26.93
27	SA	焼きなまし	0.55787	0.42177	0.31549	1.29513	0.34998	0.15259	0.05023	0.55280	0.31167	0.10033	0.02883	0.44083	2.289	25.43
28	IWDm	intelligent water drops M	0.54501	0.37897	0.30124	1.22522	0.46104	0.14704	0.04369	0.65177	0.25833	0.09700	0.02308	0.37842	2.255	25.06
29	PSO	粒子群最適化	0.59726	0.36923	0.29928	1.26577	0.37237	0.16324	0.07010	0.60572	0.25667	0.08000	0.02157	0.35823	2.230	24.77
30	ボイド	ボイドアルゴリズム	0.43340	0.30581	0.25425	0.99346	0.35718	0.20160	0.15708	0.71586	0.27846	0.14277	0.09834	0.51957	2.229	24.77
31	MA	モンキーアルゴリズム	0.59107	0.42681	0.31816	1.33604	0.31138	0.14069	0.06612	0.51819	0.22833	0.08567	0.02790	0.34190	2.196	24.40
32	SFL	Shuffled Frog-Leaping	0.53925	0.35816	0.29809	1.19551	0.37141	0.11427	0.04051	0.52618	0.27167	0.08667	0.02402	0.38235	2.104	23.38
33	FSS	魚群検索	0.55669	0.39992	0.31172	1.26833	0.31009	0.11889	0.04569	0.47467	0.21167	0.07633	0.02488	0.31288	2.056	22.84
34	RND	ランダム	0.52033	0.36068	0.30133	1.18234	0.31335	0.11787	0.04354	0.47476	0.25333	0.07933	0.02382	0.35648	2.014	22.37
35	GWO	灰色オオカミオプティマイザ	0.59169	0.36561	0.29595	1.25326	0.24499	0.09047	0.03612	0.37158	0.27667	0.08567	0.02170	0.38403	2.009	22.32
36	CSS	荷電系探索	0.44252	0.35454	0.35201	1.14907	0.24140	0.11345	0.06814	0.42299	0.18333	0.06300	0.02322	0.26955	1.842	20.46
37	EM	電磁気学的アルゴリズム	0.46250	0.34594	0.32285	1.13129	0.21245	0.09783	0.10057	0.41085	0.15667	0.06033	0.02712	0.24412	1.786	19.85

まとめ

亀の甲羅の成長に基づく最適化アルゴリズムというアイデアは非常に興味深く、自然が提供する「技術的」解決策のインスピレーションとなることを示しています。このような鈍重な動物でさえ、自然が大量に提供する「技術的」解決策のインスピレーションや見本となり得るのです。TSEA (Turtle Shell Evolution Algorithm)テストに基づき、アルゴリズムの主な特徴を明確に定義することができました。

このアルゴリズムのユニークな特徴は、成功率の低い解を保存する点です。れは、あまり成功しなかった変種が甲羅の内層に保存されることで明らかです。このアプローチにより、母集団の多様性を維持し、局所最適への早期収束を防ぐことが可能になります。最悪解に見える極小値が大域的最適解に近い可能性があることを考慮し、その周辺を探査し続けることは理にかなっています。アルゴリズムは、より有望な場所よりもそのような場所を集中的に探索しないかもしれませんが、注目すべき対象であることに変わりはありません。

解を縦方向には甲羅の層を模擬したクラスタに、横方向には表面の特徴的な模様を模擬したクラスタに分けることで、解空間の領域を効率的に分離し、それらを別々に研究することができます。同時に、甲羅の模様は可動性を保ち、適応度関数の表面に合わせて変化し、適応することが可能です。

亀の甲羅を何層にも重ねることで、それぞれの層で新しい解を形成できます。上層の硬い層は下層の柔らかい層と相互作用せず、逆もまた同様です。これは、生きている亀の甲羅が成長する過程に似ており、定期的な再クラスタリングによって、下層の硬い部分が上層に移動することができます。この過程は、古い甲羅を脱ぎ捨て、より強く、より優れた新しい甲羅を形成することに例えられます。

このアルゴリズムは、異なる次元数の問題に対して良好な性能（スケーラビリティ）を示し、その柔軟性を発揮しています。

全体として、TSEAは進化的アルゴリズムとクラスタリングメカニズムを組み合わせた興味深いアプローチです。しかし、アルゴリズムの可能性はまだまだ尽きないと確信しています。この時点では、以前に記事で取り上げた膨大な種類の中から、新たな解決策を生み出すさまざまな方法のほんの一部しか利用されていません。このアルゴリズムは私の焦点であり、さらなる改良の余地があります。おそらく、PSOや他の有名なアルゴリズムで起こったような新たな改良の基礎となることでしょう。

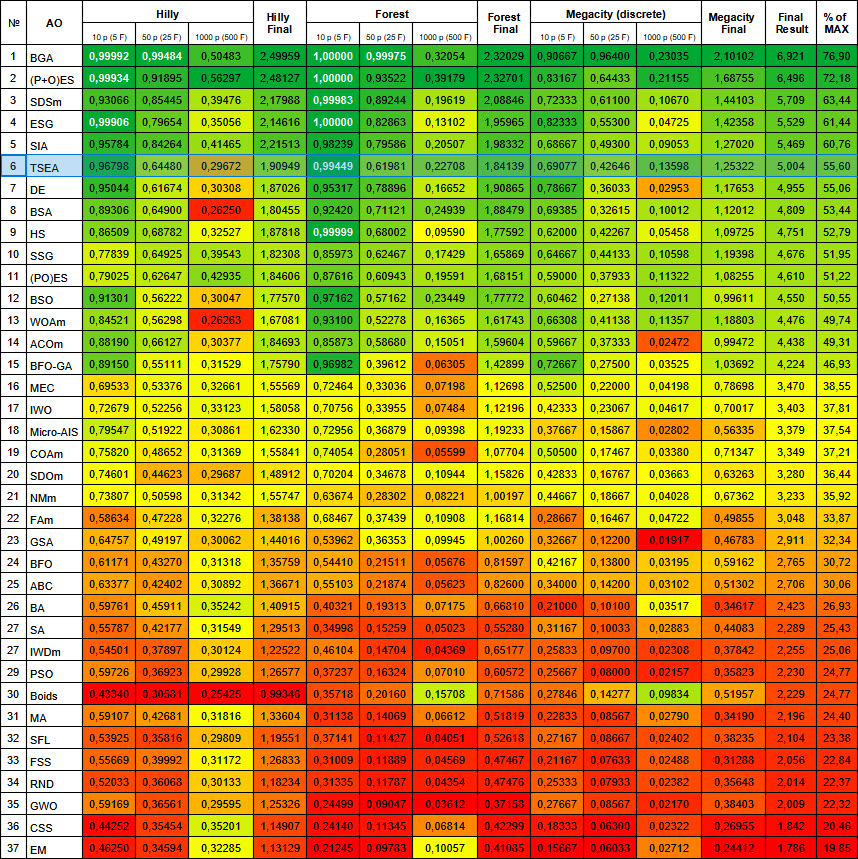
図3：関連テストに応じたアルゴリズムのカラーグラデーション 0.99以上の結果は白で強調表示

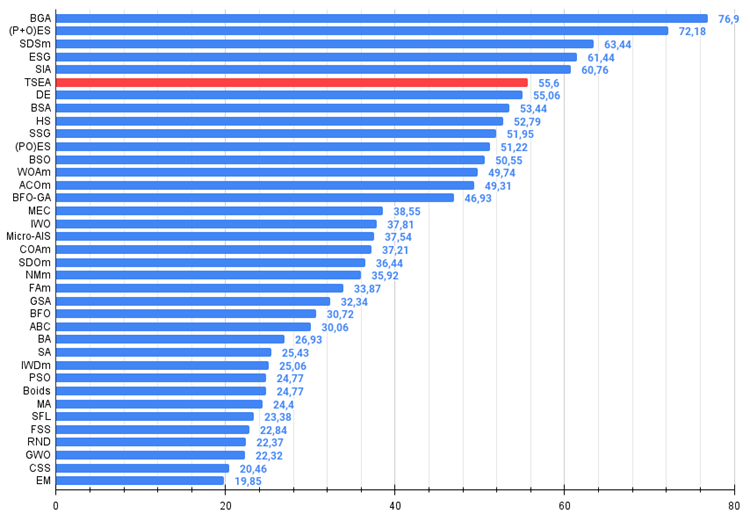
図4：アルゴリズムのテスト結果のヒストグラム（0から100までのスケールで、多ければ多いほど良い、

ここで、100は理論的に可能な最大の結果であり、アーカイブにはレーティング表を計算するスクリプトが含まれている）

TSEAの長所と短所

長所：

1. 様々な種類の関数で良好な収束を示す
2. 外部パラメータの数が少ない
   

短所

1. 低次元関数に関する結果のばらつきが大きい
   
2. コンピューティングリソースへの負荷が高い

この記事には、最新版のアルゴリズムコードを含むアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。

github：https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5

コードベース：https://www.mql5.com/ru/code/49355