Algoritmo de busca circular — Circle Search Algorithm (CSA)
53
0
Conteúdo
Introdução
O algoritmo de otimização de busca circular (Circle Search Algorithm, CSA) é um novo método de otimização inspirado nas propriedades geométricas do círculo. Sua singularidade está no uso de relações trigonométricas e princípios geométricos para explorar o espaço de busca.
A base do CSA é uma ideia interessante onde cada ponto de busca se move por uma trajetória determinada por uma tangente ao círculo, criando um equilíbrio entre a diversificação global e o refinamento local da solução. Essa abordagem é original porque o círculo possui propriedades matemáticas únicas — raio constante e derivada contínua — o que garante movimentação suave dos agentes no espaço de busca.
O algoritmo combina duas fases: intensificação e diversificação. Na fase de intensificação, os agentes se concentram em regiões promissoras, movendo-se de forma mais direcionada, enquanto na fase de diversificação eles realizam saltos mais ousados para áreas inexploradas do espaço de soluções. A transição entre as fases é regulada por um mecanismo baseado na iteração atual e em um parâmetro especial "c".
O que torna o CSA especialmente atraente é sua capacidade de operar de forma eficiente em espaços multidimensionais, mantendo uma interpretação geométrica intuitiva. Cada agente da população segue sua trajetória única, determinada por um ângulo θ, que é ajustado dinamicamente durante o processo de busca.
O algoritmo Circle Search Algorithm (CSA) foi desenvolvido pelos pesquisadores Mohammad H. Kaiys, Hany M. Hasanien e outros, e foi publicado em 2022.
Implementação do algoritmo
O algoritmo CSA (Circle Search Algorithm) tem como objetivo encontrar a solução ideal em círculos aleatórios, buscando expandir a zona de busca. Ele utiliza o centro do círculo como ponto-alvo. O processo começa com a redução gradual do ângulo entre a tangente e o círculo, o que permite que a tangente se aproxime do centro (figura 1).
Para garantir diversidade na busca e evitar que o algoritmo fique preso em ótimos locais, o ângulo de contato tangencial também é modificado de forma aleatória. No contexto do algoritmo, o ponto de contato "Xt" atua como agente de busca, enquanto o ponto central "Xc" representa a melhor solução encontrada.
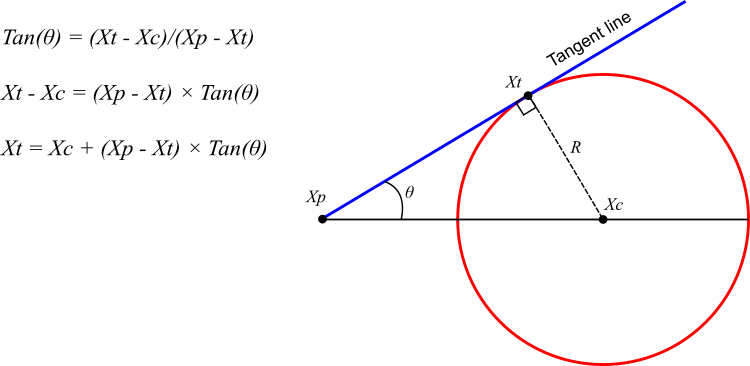
Figura 1. Propriedades geométricas do círculo e sua tangente
O algoritmo CSA adapta a posição do agente de busca em resposta ao movimento do ponto de contato em direção ao centro. Isso permite melhorar a qualidade da solução, enquanto a atualização aleatória do ângulo de contato tangencial funciona como um mecanismo importante para evitar quedas em mínimos locais. Os principais estágios de funcionamento do otimizador CSA estão ilustrados abaixo no esquema.
Figura 2. Esquema de funcionamento do algoritmo CSA
Em seguida, é definido um ângulo para cada agente. Se a iteração atual for maior que o produto entre o limiar e o número máximo de iterações, o agente está na fase de diversificação; caso contrário, aplica-se a fase de intensificação (ver figura 2). As posições dos agentes são atualizadas, e realiza-se a avaliação da adaptabilidade de cada um deles. Os resultados são comparados com a melhor solução atual e, se for encontrada uma melhor, a posição é atualizada. A iteração termina com o incremento do contador de iterações. Quando o algoritmo conclui sua execução, ele retorna a melhor posição encontrada e seu valor de adaptabilidade.
O algoritmo utiliza o conceito de movimentação de pontos ao longo de tangentes ao círculo, onde cada agente de busca se move em um determinado ângulo θ em relação à melhor solução atual. Esse movimento é regulado por diversos parâmetros (w, a, p), que variam ao longo do tempo. Como mencionado anteriormente, o funcionamento do algoritmo é dividido em duas fases: diversificação, ou sejas, quando os agentes realizam deslocamentos mais amplos para buscar regiões promissoras, e intensificação, isto é, quando os agentes se concentram no refinamento das soluções encontradas.
Na versão final, que proponho, há algumas diferenças que melhoram significativamente as capacidades de busca do algoritmo. A fórmula de atualização do "w" foi modificada:
- Na versão original: w = w × rand - w
- No código final: w = π × (1 - epochNow/epochs) Isso tornou a variação do parâmetro "w" mais previsível e linear, o que melhora a convergência do algoritmo.
- Na versão original: Xi = Xc + (Xc - Xi) × tan(θ)
- Na versão final: Xi = Xc + rand × (Xc - Xi) × tan(θ) A adição do fator aleatório "rand [0.0; 1.0]" introduz estocasticidade extra na busca e melhora o desempenho em relação à versão original.
- Adicionado o processo de atualização da melhor solução local para cada agente
- Melhorada a estratégia de equilíbrio entre busca global e local
A principal diferença conceitual está no fato de que a versão final tornou o algoritmo mais "suave" e previsível em seu comportamento, mantendo ainda assim sua capacidade de busca. O algoritmo original era mais "caótico" em seu funcionamento, enquanto a versão final proporciona um processo de otimização mais controlado, especialmente na transição entre as fases de diversificação e intensificação.
Agora podemos prosseguir com a escrita do pseudocódigo do algoritmo.
Pseudocódigo do algoritmo Circle Search Algorithm (CSA):
- Inicialização:
- Definir o tamanho da população (popSize = 50)
- Definir a constante da fase de diversificação (constC = 0.8)
- Inicializar os parâmetros:
- w = π (parâmetro do ângulo)
- a = π
- p = 1.0
- θ = 0 (ângulo inicial)
- Se for a primeira iteração (revision = false):
- Para cada agente "i" na população:
- Inicializar aleatoriamente as coordenadas dentro dos limites definidos
- Ajustar as coordenadas de acordo com o passo de variação
- Definir revision = true
- Retornar ao início
- Para cada agente "i" na população:
- Caso contrário (laço principal de otimização):
- Incrementar o contador de iterações (epochNow++)
- Atualizar os parâmetros:
- w = π × (1 - epochNow/epochs) // diminuição linear
- a = π - π × (epochNow/epochs)²
- p = 1 - 0.9 × √(epochNow/epochs)
- Para cada agente na população:
- Determinar a fase atual:
- Se epochNow ≤ constC × epochs: → Fase de diversificação: θ = w × random [0.0; 1.0]
- Caso contrário: → Fase de intensificação: θ = w × p
- Atualizar a posição do agente:
- Para cada coordenada j: → new_pos = best_pos + random [0.0; 1.0] × (best_pos - current_pos) × tan(θ) → Ajustar new_pos dentro dos limites definidos
- Determinar a fase atual:
- Revisão dos resultados:
- Para cada agente:
- Se a adaptabilidade do agente > melhor adaptabilidade global: → Atualizar a melhor solução global
- Se a adaptabilidade do agente > melhor adaptabilidade local: → Atualizar a melhor solução local do agente
- Para cada agente:
- Repetir os passos 3–5 até atingir o critério de parada
Vamos agora à implementação. A classe "C_AO_CSA" representa a implementação do algoritmo CSA e herda da classe base "C_AO". Vamos analisar seus principais elementos e estrutura:
Construtor inicializa os parâmetros do algoritmo. Ele define o nome e a descrição do algoritmo, além de estabelecer os valores dos parâmetros:- popSize — tamanho da população, fixado em 50.
- constC — constante com valor 0.8, usada na fase de diversificação.
- w, aParam, p, theta — valores iniciais dos parâmetros que serão usados no algoritmo.
- SetParams() — método usado para definir os valores dos parâmetros com base no array de dados "params".
- Init() — este método é implementado para inicializar os parâmetros relacionados aos limites dos valores e à quantidade de épocas nas quais o algoritmo será executado.
- Moving() — utilizado para movimentar as partículas e executar as iterações do algoritmo.
- Revision() — para analisar e ajustar o estado da população.
Métodos privados:
- CalculateW(), CalculateA(), CalculateP(), CalculateTheta() — métodos responsáveis por calcular os respectivos parâmetros.
- IsExplorationPhase() — método que determina se o algoritmo está na fase de diversificação.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_CSA : public C_AO { public: //-------------------------------------------------------------------- C_AO_CSA () { ao_name = "CSA"; ao_desc = "Circle Search Algorithm"; ao_link = "https://www.mql5.com/ru/articles/17143"; popSize = 50; // размер популяции constC = 0.8; // оптимальное значение для фазы исследования w = M_PI; // начальное значение w aParam = M_PI; // начальное значение a p = 1.0; // начальное значение p theta = 0; // начальное значение угла ArrayResize (params, 2); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "constC"; params [1].val = constC; } void SetParams () { popSize = (int)params [0].val; constC = params [1].val; } bool Init (const double &rangeMinP [], // минимальные значения const double &rangeMaxP [], // максимальные значения const double &rangeStepP [], // шаг изменения const int epochsP = 0); // количество эпох void Moving (); void Revision (); //---------------------------------------------------------------------------- double constC; // константа для определения фазы поиска [0,1] private: //------------------------------------------------------------------- int epochs; // максимальное число итераций int epochNow; // текущая итерация // Параметры для CSA double w; // параметр для вычисления угла double aParam; // параметр a из формулы (8) double p; // параметр p из формулы (9) double theta; // угол поиска double CalculateW (); double CalculateA (); double CalculateP (); double CalculateTheta (double currentW, double currentP); bool IsExplorationPhase (); }; //——————————————————————————————————————————————————————————————————————————————
O método "Init" é destinado à inicialização dos parâmetros do algoritmo CSA. Seus parâmetros incluem o array de valores mínimos do espaço de busca "rangeMinP []", o array de valores máximos "rangeMaxP []", o array de passos de variação dos valores "rangeStepP []", além da quantidade de épocas, especificada pelo parâmetro "epochsP", que por padrão é igual a 0.
Durante a execução do método, é chamado "StandardInit", cuja finalidade é tentar inicializar os parâmetros padrão. Em caso de sucesso na inicialização, os valores das variáveis "epochs" e "epochNow" são definidos. A variável "epochs" recebe o valor de "epochsP", enquanto "epochNow" é zerado. O método finaliza sua execução retornando "true", indicando que a inicialização dos parâmetros do algoritmo foi bem-sucedida.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_CSA::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- epochs = epochsP; epochNow = 0; return true; } //——————————————————————————————————————————————————————————————————————————————
O método "Moving" na classe "C_AO_CSA" implementa a lógica de atualização das posições dos agentes dentro do algoritmo CSA. No início do método, ocorre o incremento do contador da época atual, o que permite acompanhar quantas iterações já foram realizadas (e esse dado é usado nas fórmulas de cálculo). Em seguida, é verificada a necessidade de inicializar as coordenadas dos agentes. Se for a primeira execução do método, são geradas coordenadas aleatórias para todos os agentes dentro dos limites definidos. Essas coordenadas são então ajustadas considerando os passos de variação estabelecidos. Após isso, o sinalizador de revisão é ativado, sendo definido como verdadeiro.
Caso o método não esteja sendo chamado pela primeira vez, então os parâmetros principais do algoritmo, como "w", "aParam" e "p", são atualizados. Depois disso, para cada agente é calculado o ângulo "theta", que é utilizado para atualizar suas coordenadas. Cada coordenada é atualizada levando em conta as coordenadas do melhor agente, a influência de um fator aleatório e o ângulo "theta". Em seguida, os resultados são ajustados para garantir que permaneçam dentro dos limites definidos.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_CSA::Moving () { epochNow++; //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { a [i].c [j] = u.RNDfromCI (rangeMin [j], rangeMax [j]); a [i].c [j] = u.SeInDiSp (a [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]); } } revision = true; return; } //---------------------------------------------------------------------------- w = CalculateW (); // Обновляем w по линейному закону aParam = CalculateA (); // Обновляем a p = CalculateP (); // Обновляем p for (int i = 0; i < popSize; i++) { theta = CalculateTheta (w, p); for (int j = 0; j < coords; j++) { a [i].c [j] = cB [j] + u.RNDprobab () * (cB [j] - a [i].c [j]) * tan (theta); a [i].c [j] = u.SeInDiSp (a [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]); } } } //——————————————————————————————————————————————————————————————————————————————
O método "Revision" é responsável por atualizar as melhores soluções dentro da população. Ele verifica os valores atuais das funções-objetivo dos agentes e atualiza os respectivos parâmetros quando encontra soluções melhores.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_CSA::Revision () { for (int i = 0; i < popSize; i++) { // Обновляем лучшее глобальное решение if (a [i].f > fB) { fB = a [i].f; ArrayCopy (cB, a [i].c, 0, 0, WHOLE_ARRAY); } } } //——————————————————————————————————————————————————————————————————————————————
O método "CalculateW" serve para calcular o valor do parâmetro "w", que diminui de forma linear a partir do valor inicial (M_PI) até "0", conforme o número atual de épocas (epochNow) aumenta em relação ao total de épocas (epochs), retornando o valor calculado de "w". Esse parâmetro calculado participa da fórmula de cálculo do ângulo "Theta".
//—————————————————————————————————————————————————————————————————————————————— double C_AO_CSA::CalculateW () { // Линейное уменьшение w от начального значения (M_PI) до 0 return M_PI * (1.0 - (double)epochNow / epochs); //return w * u.RNDprobab () - w; } //——————————————————————————————————————————————————————————————————————————————O método "CalculateA" calcula o valor de "aParam", que diminui de "M_PI" até "0" com o aumento de "epochNow", seguindo uma dependência quadrática em relação ao total de épocas "epochs".
//—————————————————————————————————————————————————————————————————————————————— double C_AO_CSA::CalculateA () { return M_PI - M_PI * MathPow ((double)epochNow / epochs, 2); } //——————————————————————————————————————————————————————————————————————————————
O método "CalculateP" calcula o valor de "p", que diminui de "1.0" para "0.1" à medida que "epochNow" aumenta, ou seja, depende da época atual.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_CSA::CalculateP () { return 1.0 - 0.9 * MathPow ((double)epochNow / epochs, 0.5); } //——————————————————————————————————————————————————————————————————————————————
O método "CalculateTheta" calcula o valor de "Theta" usando os parâmetros atuais "currentW" e "currentP".
- Se a fase atual for de diversificação, retorna o produto de "currentW" por um número aleatório.
- Caso contrário, retorna o produto de "currentW" por "currentP".
//—————————————————————————————————————————————————————————————————————————————— double C_AO_CSA::CalculateTheta (double currentW, double currentP) { // Используем параметр aParam для регулировки угла if (IsExplorationPhase ()) return currentW * u.RNDprobab (); else return currentW * currentP; } //——————————————————————————————————————————————————————————————————————————————
O método "IsExplorationPhase" verifica se a iteração atual está na fase de diversificação.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_CSA::IsExplorationPhase () { // Исследование в первой части итераций(constC обычно 0.8) return (epochNow <= constC * epochs); } //——————————————————————————————————————————————————————————————————————————————
Resultados dos testes
Os autores do algoritmo o apresentam como um método de otimização altamente eficaz, no entanto, após sua implementação, algumas melhorias e a realização de testes finais, os resultados obtidos não impressionam. O algoritmo conseguiu entrar na tabela de classificação, mas seus indicadores ficaram bem abaixo dos melhores algoritmos atuais.CSA|Circle Search Algorithm|50.0|0.8|
=============================
5 Hilly's; Func runs: 10000; result: 0.6656012653478078
25 Hilly's; Func runs: 10000; result: 0.4531682514562617
500 Hilly's; Func runs: 10000; result: 0.2912586479936386
=============================
5 Forest's; Func runs: 10000; result: 0.6879687203647712
25 Forest's; Func runs: 10000; result: 0.41397289345600924
500 Forest's; Func runs: 10000; result: 0.2052507546137296
=============================
5 Megacity's; Func runs: 10000; result: 0.3753846153846153
25 Megacity's; Func runs: 10000; result: 0.2363076923076922
500 Megacity's; Func runs: 10000; result: 0.10646153846153927
=============================
All score: 3.43537 (38.17%)
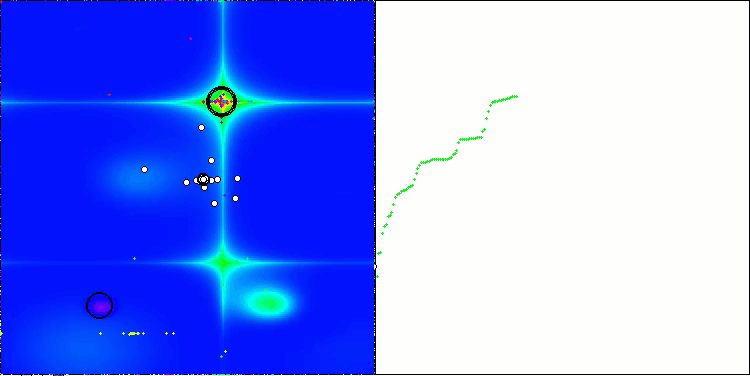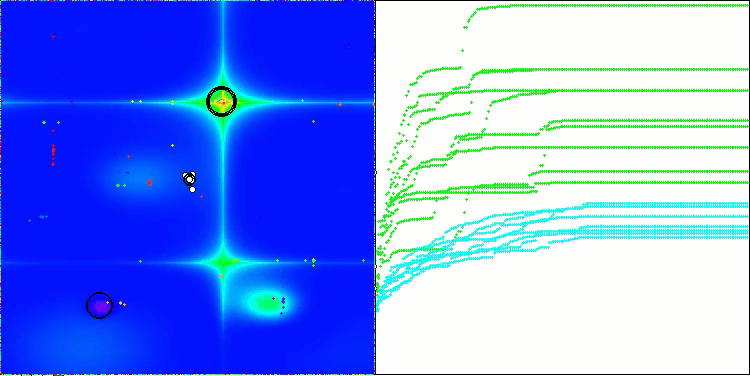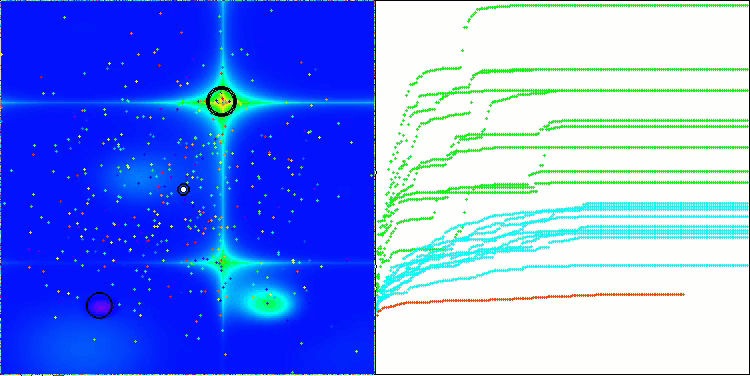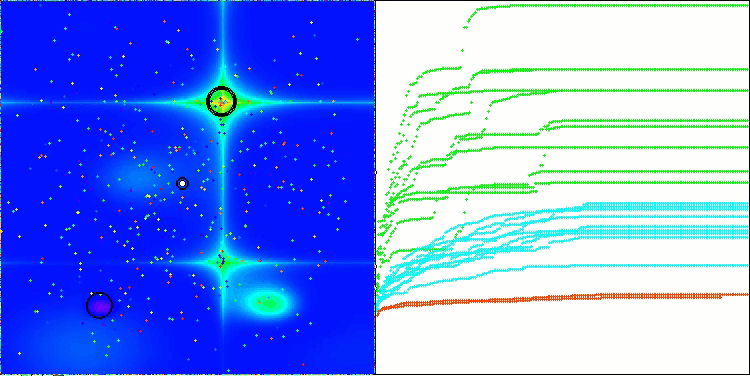
Na visualização do funcionamento do algoritmo, observam-se problemas de convergência e travamento em extremos locais. Tem não obstante, o algoritmo tenta trabalhar ao máximo de suas capacidades. Apesar dos problemas de aprisionamento em armadilhas (claramente visíveis nos longos trechos horizontais no gráfico de convergência), destaca-se sua capacidade de operar com desempenho razoável em problemas de alta dimensionalidade.
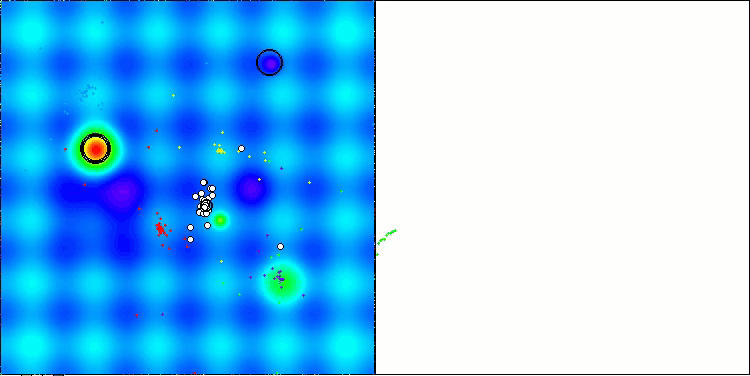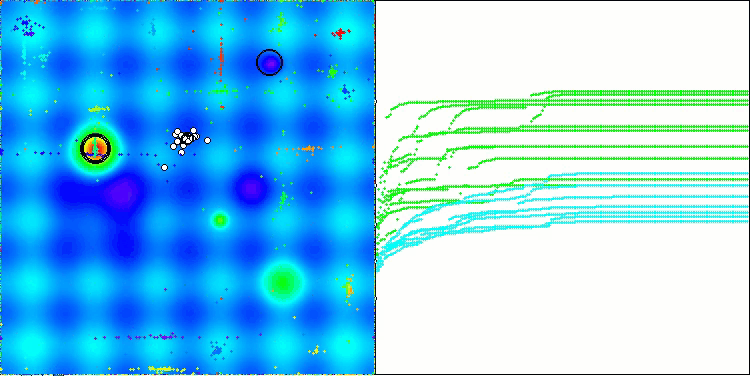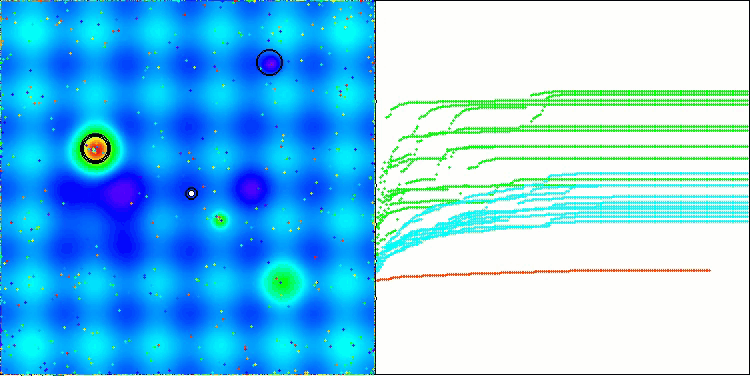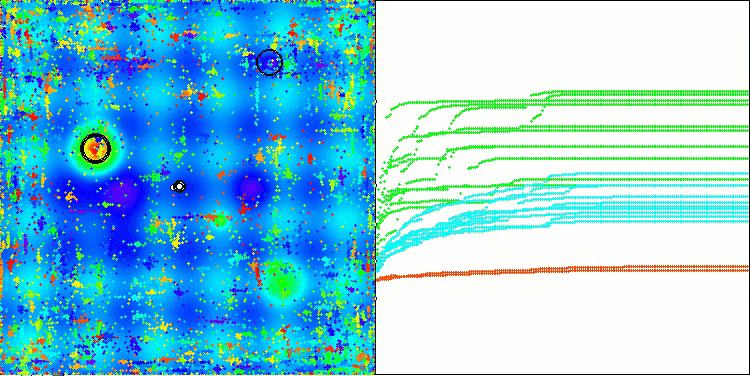
CSA na função de teste Hilly
CSA na função de teste Forest
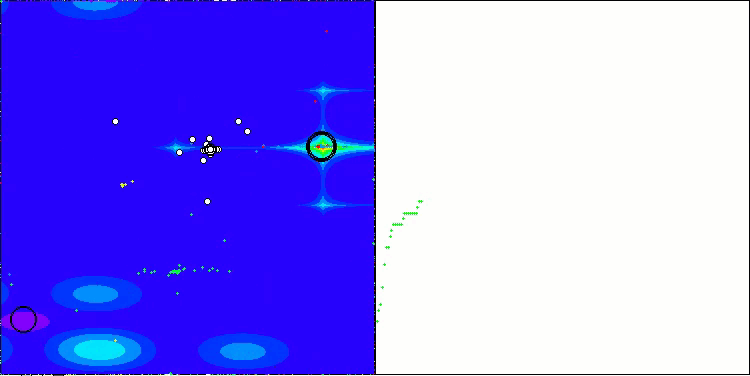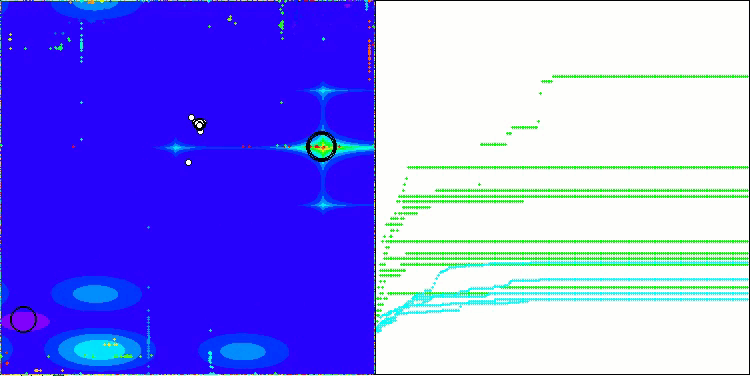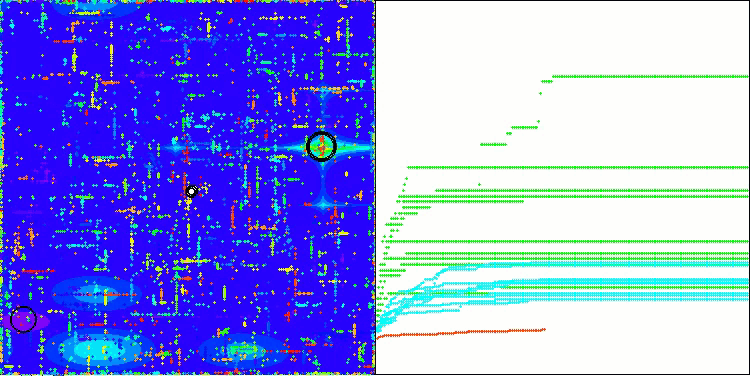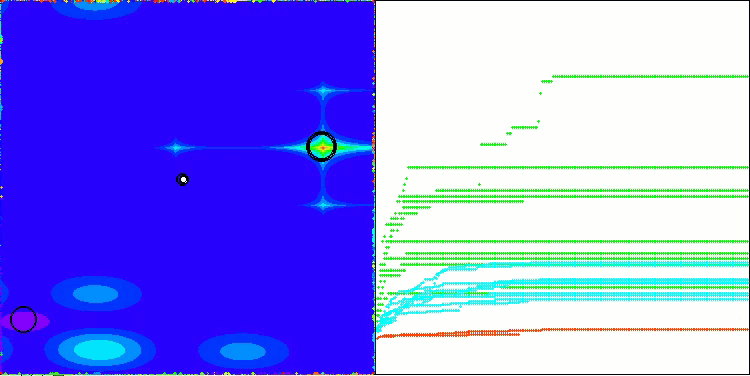
CSA na função de teste Megacity
Com base nos resultados dos testes, o algoritmo CSA ocupa a 41ª posição na tabela de classificação.
| № | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration ptimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | TETA | time evolution travel algorithm (joo) | 0,91362 | 0,82349 | 0,31990 | 2,05701 | 0,97096 | 0,89532 | 0,29324 | 2,15952 | 0,73462 | 0,68569 | 0,16021 | 1,58052 | 5,797 | 64,41 |
| 7 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 8 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 9 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 10 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 11 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 12 | DA | dialectical algorithm | 0,86183 | 0,70033 | 0,33724 | 1,89940 | 0,98163 | 0,72772 | 0,28718 | 1,99653 | 0,70308 | 0,45292 | 0,16367 | 1,31967 | 5,216 | 57,95 |
| 13 | BHAm | black hole algorithm M | 0,75236 | 0,76675 | 0,34583 | 1,86493 | 0,93593 | 0,80152 | 0,27177 | 2,00923 | 0,65077 | 0,51646 | 0,15472 | 1,32195 | 5,196 | 57,73 |
| 14 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 15 | RFO | royal flush optimization (joo) | 0,83361 | 0,73742 | 0,34629 | 1,91733 | 0,89424 | 0,73824 | 0,24098 | 1,87346 | 0,63154 | 0,50292 | 0,16421 | 1,29867 | 5,089 | 56,55 |
| 16 | AOSm | atomic orbital search M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| 17 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 18 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 19 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 20 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 21 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 22 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 23 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 24 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 25 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 26 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 27 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 28 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 29 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 30 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 31 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 32 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 33 | SOA | simple optimization algorithm | 0,91520 | 0,46976 | 0,27089 | 1,65585 | 0,89675 | 0,37401 | 0,16984 | 1,44060 | 0,69538 | 0,28031 | 0,10852 | 1,08422 | 4,181 | 46,45 |
| 34 | ABHA | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4,127 | 45,85 |
| 35 | ACMO | atmospheric cloud model optimization | 0,90321 | 0,48546 | 0,30403 | 1,69270 | 0,80268 | 0,37857 | 0,19178 | 1,37303 | 0,62308 | 0,24400 | 0,10795 | 0,97503 | 4,041 | 44,90 |
| 36 | ADAMm | adaptive moment estimation M | 0,88635 | 0,44766 | 0,26613 | 1,60014 | 0,84497 | 0,38493 | 0,16889 | 1,39880 | 0,66154 | 0,27046 | 0,10594 | 1,03794 | 4,037 | 44,85 |
| 37 | ATAm | artificial tribe algorithm M | 0,71771 | 0,55304 | 0,25235 | 1,52310 | 0,82491 | 0,55904 | 0,20473 | 1,58867 | 0,44000 | 0,18615 | 0,09411 | 0,72026 | 3,832 | 42,58 |
| 38 | ASHA | artificial showering algorithm | 0,89686 | 0,40433 | 0,25617 | 1,55737 | 0,80360 | 0,35526 | 0,19160 | 1,35046 | 0,47692 | 0,18123 | 0,09774 | 0,75589 | 3,664 | 40,71 |
| 39 | ASBO | adaptive social behavior optimization | 0,76331 | 0,49253 | 0,32619 | 1,58202 | 0,79546 | 0,40035 | 0,26097 | 1,45677 | 0,26462 | 0,17169 | 0,18200 | 0,61831 | 3,657 | 40,63 |
| 40 | MEC | mind evolutionary computation | 0,69533 | 0,53376 | 0,32661 | 1,55569 | 0,72464 | 0,33036 | 0,07198 | 1,12698 | 0,52500 | 0,22000 | 0,04198 | 0,78698 | 3,470 | 38,55 |
| 41 | CSA | circle search algorithm | 0,66560 | 0,45317 | 0,29126 | 1,41003 | 0,68797 | 0,41397 | 0,20525 | 1,30719 | 0,37538 | 0,23631 | 0,10646 | 0,71815 | 3,435 | 38,17 |
| 42 | IWO | invasive weed optimization | 0,72679 | 0,52256 | 0,33123 | 1,58058 | 0,70756 | 0,33955 | 0,07484 | 1,12196 | 0,42333 | 0,23067 | 0,04617 | 0,70017 | 3,403 | 37,81 |
| 43 | Micro-AIS | micro artificial immune system | 0,79547 | 0,51922 | 0,30861 | 1,62330 | 0,72956 | 0,36879 | 0,09398 | 1,19233 | 0,37667 | 0,15867 | 0,02802 | 0,56335 | 3,379 | 37,54 |
| 44 | COAm | cuckoo optimization algorithm M | 0,75820 | 0,48652 | 0,31369 | 1,55841 | 0,74054 | 0,28051 | 0,05599 | 1,07704 | 0,50500 | 0,17467 | 0,03380 | 0,71347 | 3,349 | 37,21 |
| 45 | SDOm | spiral dynamics optimization M | 0,74601 | 0,44623 | 0,29687 | 1,48912 | 0,70204 | 0,34678 | 0,10944 | 1,15826 | 0,42833 | 0,16767 | 0,03663 | 0,63263 | 3,280 | 36,44 |
| RW | random walk | 0,48754 | 0,32159 | 0,25781 | 1,06694 | 0,37554 | 0,21944 | 0,15877 | 0,75375 | 0,27969 | 0,14917 | 0,09847 | 0,52734 | 2,348 | 26,09 | |
Considerações finais
A partir da análise e dos testes realizados com o algoritmo Circle Search Algorithm (CSA), é possível tirar as seguintes conclusões: apesar da elegância da proposta geométrica e do mecanismo de busca intuitivo baseado em movimentação tangencial ao círculo, o algoritmo apresenta desempenho relativamente fraco na comparação com outros métodos, ocupando o 41º lugar entre 45 na tabela de algoritmos de otimização. Essa colocação indica limitações significativas em sua implementação atual.
Os principais problemas do algoritmo estão relacionados à sua tendência de ficar preso em extremos locais, o que é especialmente notável ao lidar com tarefas simples de baixa dimensionalidade. Isso pode estar ligado a diversos fatores: em primeiro lugar, o mecanismo de busca baseado em ângulos, embora promissor em teoria, na prática se mostra pouco eficaz para escapar de ótimos locais. Em segundo lugar, o equilíbrio entre as fases de diversificação e intensificação, regulado pelo parâmetro "constC", não garante diversificação suficiente da busca. Toda a população acaba convergindo para soluções pseudo-ótimas, ou seja, para um único ponto, e nem mesmo as tentativas de "sacudir" a população com um componente aleatório na fórmula principal de atualização da posição dos agentes no espaço de soluções foram eficazes.
A tentativa de melhorar o algoritmo por meio da adição de um multiplicador aleatório à fórmula de atualização das posições dos agentes, embora tenha levado a um comportamento mais previsível do algoritmo, não conseguiu aumentar significativamente sua eficácia. Isso pode indicar que a ideia base do algoritmo, fundamentada nas propriedades geométricas do círculo, ou não foi completamente explorada pelos autores na implementação atual, ou possui limitações fundamentais dentro do contexto da otimização global.
Apesar disso, o algoritmo demonstra certas capacidades de busca e pode ser eficaz para algumas tarefas específicas, especialmente aquelas em que o relevo da função-objetivo seja relativamente simples. Para melhorar a eficiência do algoritmo, posso recomendar aos usuários a continuidade das pesquisas no sentido de aprimorar o mecanismo de escape dos ótimos locais, possivelmente através da introdução de mecanismos adicionais de diversificação da busca ou pela hibridização com outros métodos de otimização (como direção prioritária, o uso dessa estratégia de busca em outros algoritmos de otimização como componente).
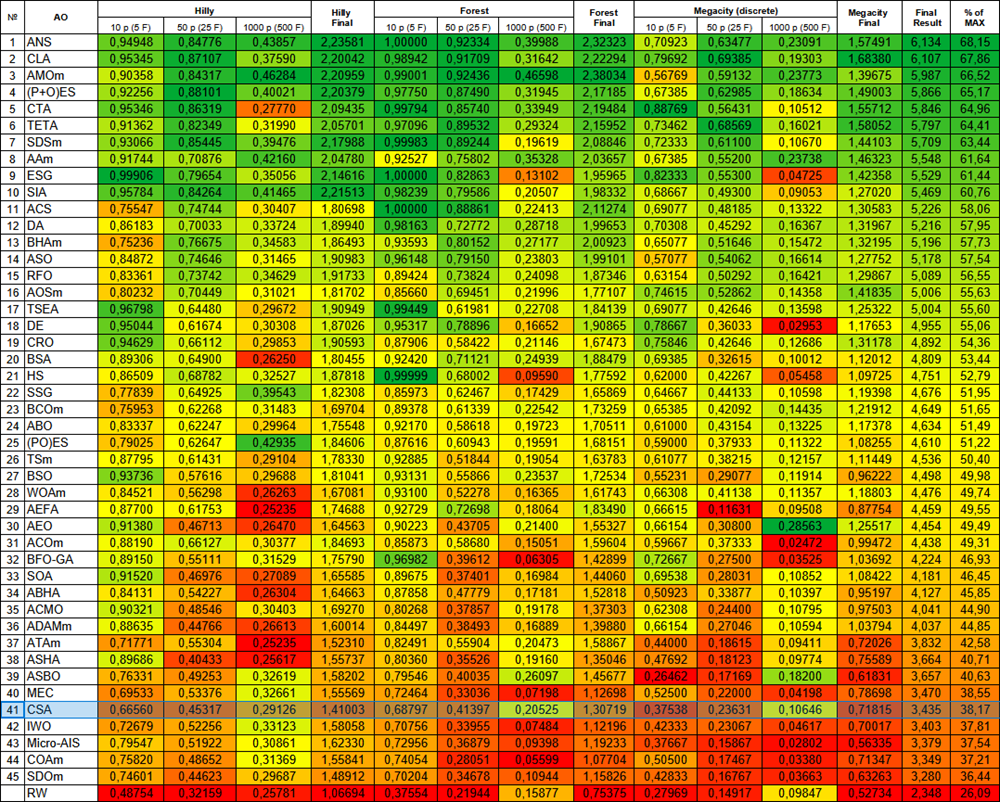
Figura 3. Gradação de cores dos algoritmos nos testes correspondentes
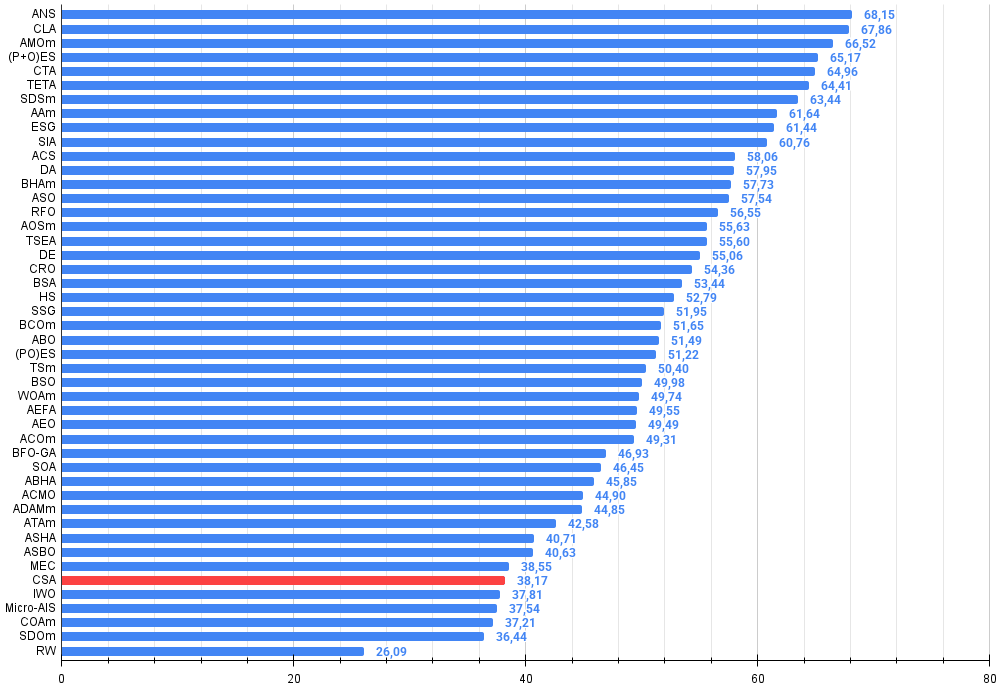
Figura 4. Histograma dos resultados de teste dos algoritmos (em uma escala de 0 a 100, quanto maior, melhor, onde 100 é o resultado teórico máximo possível, no arquivo está o script para cálculo da tabela de classificação)
Pontos fortes e fracos do algoritmo CSA:
Pontos fortes:
- Pouquíssimos parâmetros externos
- Implementação simples
- Ideia interessante baseada nas propriedades geométricas do círculo
Pontos fracos:
- Baixa precisão de convergência
- Fica preso em extremos locais
Está anexado ao artigo um arquivo com as versões atualizadas dos códigos dos algoritmos. O autor do artigo não se responsabiliza pela precisão absoluta na descrição dos algoritmos canônicos, pois muitos deles foram modificados para aprimorar suas capacidades de busca. As conclusões e opiniões apresentadas nos artigos baseiam-se nos resultados dos experimentos realizados.
Programas utilizados no artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | C_AO.mqh | Arquivo incluído | Classe base para algoritmos populacionais de otimização |
| 2 | C_AO_enum.mqh | Arquivo incluído | Enumeração dos algoritmos populacionais de otimização |
| 3 | TestFunctions.mqh | Arquivo incluído | Biblioteca de funções de teste |
| 4 | TestStandFunctions.mqh | Arquivo incluído | Biblioteca de funções da bancada de testes |
| 5 | Utilities.mqh | Arquivo incluído | Biblioteca de funções auxiliares |
| 6 | CalculationTestResults.mqh | Arquivo incluído | Script para cálculo dos resultados na tabela comparativa |
| 7 | Testing AOs.mq5 | Script | Bancada unificada de testes para todos os algoritmos populacionais de otimização |
| 8 | Simple use of population optimization algorithms.mq5 | Script | Exemplo simples de uso dos algoritmos populacionais de otimização sem visualização |
| 9 | Test_AO_CSA.mq5 | Script | Bancada de testes para o CSA |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/17143
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
Desenvolvendo um EA multimoeda (Parte 22): Início da transição para substituição dinâmica de configurações
Fibonacci no Forex (Parte I): Testando relações entre preço e tempo
Redes neurais em trading: Modelos bidimensionais do espaço de conexões (Chimera)
Redes neurais em trading: Treinamento multitarefa baseado no modelo ResNeXt (Conclusão)
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso