MetaTrader 5 / 例
English Русский 中文 Español Deutsch Português
preview
Across Neighbourhood Search (ANS)

Across Neighbourhood Search (ANS)

MetaTrader 5 — 例 | 8 1月 2025, 15:33
182 0
Andrey Dik
Andrey Dik
内容
  1. はじめに
  2. アルゴリズムの実装
  3. テスト結果


1. はじめに

現代社会において、効率的な最適化手法の開発は、エンジニアリングアプリケーションから機械学習や人工知能の分野における科学研究に至るまで、幅広い課題を解決する上で重要な役割を果たしています。このような背景の中で、メタヒューリスティック進化アルゴリズムは、複雑な最適化問題を解決するための強力なツールとして注目されています。しかし、パフォーマンスと効率をさらに向上させるには、既存の手法の継続的な改良と修正、さらには新しいアルゴリズムの開発が不可欠です。

この記事では、数値最適化のための母集団探索に基づく最適化アルゴリズムである Across Neighborhood Search (ANS)を紹介します。このアルゴリズムは、2014年にGuohua Wu氏によって提案されました。ANSアルゴリズムは、最適化分野における大きな進展を示すものであり、高い効率と精度をもって現実世界のさまざまな課題を解決する可能性を秘めています。本稿では、その真偽を以下で検証します。ANSの基本的なアイデアは、複数のエージェントが解空間を移動し、近隣のエージェントと相互作用して情報を交換するマルチエージェントシステムの挙動をモデル化することです。このアプローチにより、局所最適化と大域最適化を組み合わせることで、解空間を効果的に最適化することが可能になります。

この記事では、ANSアルゴリズムの構造や動作原理の詳細を解説するとともに、既存の最適化手法との比較分析をおこないます。開発されたANSアルゴリズムは、最適化の分野に新たな可能性を切り開き、幅広い問題を高いパフォーマンスで解決することを可能にします。さらに、人工知能の進化という文脈において、ANSアルゴリズムが、問題の特性や環境の変化に柔軟に対応できる、より高度でインテリジェントな最適化手法の構築に向けた重要な一歩であることも注目すべき点です。

2. アルゴリズムの実装

ANS (Across Neighborhood Search)アルゴリズムは、進化アルゴリズムおよびメタヒューリスティックの分野のアイデアを活用し、問題のパラメータ空間における最適解を見つけるために設計された最適化手法です。

ANSの主な特徴は次のとおりです。

  • 近傍探索：エージェントが現在の解の近傍を探索し、局所的な最適解を効率的に発見します。
  • 正規分布の活用：アルゴリズムが複数の有望な方向性を同時に探ることを可能にする、最適解のコレクションを利用します。
  • 解コレクション：ANSは、アルゴリズムを複数の有望な方向に同時に向けるのに役立つ最適解のコレクションを使用します。

ANSでは、個体のグループが協力して解空間を探索し、取り組んでいる最適化問題を効率的かつ効果的に解決します。アルゴリズムの基本的な概念は、個体がこれまでに発見した優れた解をコレクションとして保持し、それを動的に更新することです。各世代において、個体は正規確率分布に従って近傍を探索し、複数の異なる解を試みます。このアプローチにより、事前にどれが最適解であるかを知らなくても、複数の有望な解を同時に探索することができます。

以下では、著者の概念に基づき、方程式とステップを含むANSアルゴリズムの詳細な説明をおこないます。ANSは以下の手順で実行されます。

1. パラメータの初期化

  • 母集団サイズm
  • 最適解セットのコレクションc
  • ガウス分布の標準偏差sigma
  • 探索空間の次元数D
  • 最大世代数MaxG

2. 母集団の初期化：探索空間内の母集団の各個体の位置をランダムに初期化します。

3. 最適解の更新：母集団内の各個体は、正規分布を使用してコレクション内の最適解の近傍を探索し、その結果に基づいて現在の位置を更新します。

4. 検索する座標の選択：ランダムな数値n（検索範囲の度合い）を選択し、解空間内の個体の現在位置の座標を決定します。

5. 個体の位置の更新：前のステップに従って個体iの位置を更新します。

方程式と操作

1. i番目の個体の位置pos_iを更新します（コレクションからの解の近傍を探索）

  • 個体iの位置はガウス分布を使用して更新されます：pos_i =r_g + G (r_g - pos_i)、ここで
  • G：ガウス分布からのランダム値
  • r_g：コレクションからの最適な解の位置

2. i番目の個体の位置pos_iを更新します（個体自身の最適解の近傍を探索）

  • 個体iの位置はガウス分布を使用して更新されます：pos_i = r_i + G (r_i - pos_i)、ここで
  • G：ガウス分布からのランダム値
  • r_i：個体の最適解の位置

3. 最適解のセットを更新します

  • 最適解のコレクションは、個体の新しい位置に基づいて更新されます。

したがって、方程式は、i番目の個体をその最適解r_iの近傍で、またRコレクションからの他の最適解r_gの近傍で探すメカニズムを表しています。アルゴリズムのこれらのステップは、最適化問題を解決するためのANS (Across Neighborhood Search)法の基本ロジックを表します。これには、パラメータの初期化、個々の位置のランダムな初期化、最適解の近傍を指定した個々の位置の更新、および最適解のコレクションの更新が含まれます。アルゴリズムは停止条件が満たされるまで実行され続けます。

最適解または個体に基づいた検索は、母集団戦略アルゴリズムで一般的に用いられる手法ですが、具体的な実装プロセスは最適化アルゴリズムごとに異なります。このアルゴリズムでは、エージェントの母集団に加えて、新たに「最適解のコレクション」という母集団が導入されています。このコレクションのサイズは、アルゴリズムの外部パラメータとして定義され、母集団のサイズより大きくも小さくも設定できます。

ANSアルゴリズムの検索戦略は、まず最適解コレクションを埋めることから始まり、次にコレクション内の最適解や各エージェントの最良の個別解の近傍探索へと進みます。標準偏差sigmaの大きさは、探索空間全体の探索と解の洗練化のバランスにおいて重要な役割を果たします。低いsigmaは広範囲の探索を可能にし、高いsigmaは近傍探索を精緻化します。このパラメータは、探索の強化(intensification)と多様化(diversification)のバランスを調整します。一部のアルゴリズムでは、このバランスを動的に調整できるようエポック数に関連付けていますが、本アルゴリズムでは外部パラメータとして事前に定義されています。

したがって、ANSアルゴリズムは、見つかった最適解の利用（近傍の検索による）と解空間の探索（個々の最適解の近傍の検索による）を組み合わせています。これにより、理論的には検索の強化と多様化の間で適切なバランスが実現されるはずです。

それでは、ANSアルゴリズムコードの作成と解析に移りましょう。ANSアルゴリズムでエージェントを表すために使用されるS_ANS_Agent構造体を定義します。構造体フィールド

  • c：エージェントの座標を格納する配列
  • cBest：最適なエージェント座標を格納する配列
  • f：エージェントの適応度値
  • fBest：エージェントの最適な適応度値
  • Init(int coords)：初期化メソッド（cおよびcBest配列のサイズを設定し、fおよびfBestの初期値を設定）

コードのこの部分はエージェントの基本構造を表します。エージェントの配列は、ANSアルゴリズムの主な母集団を表します。

//——————————————————————————————————————————————————————————————————————————————
struct S_ANS_Agent
{
    double c     []; //coordinates
    double cBest []; //best coordinates
    double f;        //fitness
    double fBest;    //best fitness

    void Init (int coords)
    {
      ArrayResize (c,     coords);
      ArrayResize (cBest, coords);
      f     = -DBL_MAX;
      fBest = -DBL_MAX;
    }
};
//—————————————————————————————————————————————————————————————————————————————

最適解のコレクションを記述するには、検索空間内の最適な座標と対応する適合値に関する情報を格納するために使用される構造体S_Collectionを設定します。この構造体には以下のフィールドが含まれます。

  • c：座標を格納するための配列
  • f：コレクション内の問題に対する特定の解の適合値
  • Init(int coords)：初期化メソッド（c配列のサイズと初期f値をdouble型の最小可能値に設定）
//——————————————————————————————————————————————————————————————————————————————
struct S_Collection
{
    double c []; //coordinates
    double f;    //fitness

    void Init (int coords)
    {
      ArrayResize (c, coords);
      f = -DBL_MAX;
    }
};
//——————————————————————————————————————————————————————————————————————————————

C_AO基本クラスの継承であり、Across Neighbourhood Search (ANS)アルゴリズムの実装であるC_AO_ANSクラスを宣言します。重要なポイントは次のとおりです。

  • ao_name、ao_desc、ao_link：ANSアルゴリズムを記述するプロパティ
  • popSize：母集団サイズ
  • collectionSize、sigma、range、collChoiceProbab：ANSアルゴリズムパラメータ
  • SetParams()：パラメータを設定するメソッド
  • Init()、Moving()、Revision()：エージェントを初期化、移動し、母集団と解のコレクションを更新するためのメソッド
  • S_ANS_Agent、S_Collection：エージェントデータとコレクションを格納するための構造体
//——————————————————————————————————————————————————————————————————————————————
class C_AO_ANS : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_ANS () { }
  C_AO_ANS ()
  {
    ao_name = "ANS";
    ao_desc = "Across Neighbourhood Search";
    ao_link = "https://www.mql5.com/ja/articles/15049";

    popSize          = 50;   //population size

    collectionSize   = 20;   //Best solutions collection
    sigma            = 3.0;  //Form of normal distribution
    range            = 0.5;  //Range of values dispersed
    collChoiceProbab = 0.8;  //Collection choice probab

    ArrayResize (params, 5);

    params [0].name = "popSize";          params [0].val = popSize;
    params [1].name = "collectionSize";   params [1].val = collectionSize;
    params [2].name = "sigma";            params [2].val = sigma;
    params [3].name = "range";            params [3].val = range;
    params [4].name = "collChoiceProbab"; params [4].val = collChoiceProbab;
  }

  void SetParams ()
  {
    popSize          = (int)params [0].val;
    collectionSize   = (int)params [1].val;
    sigma            = params      [2].val;
    range            = params      [3].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  int    collectionSize;    //Best solutions collection
  double sigma;             //Form of normal distribution
  double range;             //Range of values dispersed
  double collChoiceProbab;  //Collection choice probab

  S_ANS_Agent agent [];

  private: //-------------------------------------------------------------------
  S_Collection coll     [];
  S_Collection collTemp [];
};
//——————————————————————————————————————————————————————————————————————————————

Initメソッドは、ANSアルゴリズムのパラメータを初期化します。

  • rangeMinP、rangeMaxP、rangeStepP：検索範囲の最小値、最大値、ステップを表す配列
  • epochsP：エポック（世代）の数

メソッド内では次がおこなわれます。

  • StandardInitを使用して、標準パラメータの初期化が成功したかどうかが確認されます。
  • エージェント(agent)とコレクション(coll)の配列（最適解を格納するための2番目の母集団）、collTemp（コレクションを並び替えるための一時配列）が作成されます。
  • 各エージェントとコレクションに対して、Initメソッドが呼び出され、初期値が設定されます。

このメソッドは、最適化を実行するためのANSアルゴリズムを準備する上で重要な役割を果たします。coll配列とcollTemp配列は、collectionSizeパラメータの2倍のサイズで初期化されることに注意することが重要です。 これは、コレクションに追加された新しいエージェントが配列の後半に配置されるようにします。その後の並び替えはコレクション全体にわたっておこなわれ、最適なエージェントを含む最初の半分だけが以降の作業に使用されます。

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_ANS::Init (const double &rangeMinP  [], //minimum search range
                     const double &rangeMaxP  [], //maximum search range
                     const double &rangeStepP [], //step search
                     const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (agent, popSize);
  for (int i = 0; i < popSize; i++) agent [i].Init (coords);

  ArrayResize (coll,     collectionSize * 2);
  ArrayResize (collTemp, collectionSize * 2);
  for (int i = 0; i < collectionSize * 2; i++)
  {
    coll     [i].Init (coords);
    collTemp [i].Init (coords);
  }

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Movingメソッドは、ANSアルゴリズムでエージェントの移動を実行します。このコードを詳しく見てみましょう。

1. 初期化（revisionがfalseの場合）

  • これが最初のステップ（最初のエポック）の場合、各エージェントに対して次の処理がおこなわれます。
    • rangeMin[c]からrangeMax[c]の範囲でvalランダム値が生成されます。
    • ステップrangeStep[c]を考慮するためにSeInDiSp演算子が適用されます。
    • val値がagent[i].c[c]エージェント座標に割り当てられます。
    • val値がagent[i].cBest[c]エージェントの最適座標にも割り当てられます（この段階ではエージェントの適応度値は不明であるため、最適座標は現在の初期座標と同じになります）。
    • val値がa[i].c[c]エージェント配列に割り当てられます。

2. エージェントの移動（revisionがtrueの場合）

  • 各エージェントと各座標について
    • 乱数がcollChoiceProbabより小さい場合、コレクションからランダムな解が選択されます。
      • コレクションからランダムなインデックスindが選択されます（空でない解が見つかるまで）。
      • 現在のエージェント座標からp値が取得されます。
      • コレクションから選択された解からr値が取得されます。
    • それ以外の場合は、最適なエージェント座標が使用されます。
      • 現在のエージェント座標からp値が取得されます。
      • 最適なエージェント座標からr値が取得されます。
    • 移動の距離(dist)と（minとmax）範囲が計算されます。
    • minとmaxの値はrangeMin[c]とrangeMax[c]の範囲に制限されます。
    • r、min、max、sigmaパラメータを持つ正規分布
    • val値がagent[i].c[c]エージェント座標に割り当てられます。
    • val値はa[i].c[c]エージェント配列にも割り当てられます。

以下のコードは、コレクション内のエージェントと解の最適な座標を考慮して、ANSアルゴリズム内のエージェントの座標を更新します。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ANS::Moving ()
{
  double val = 0.0;

  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        val = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        val = u.SeInDiSp  (val, rangeMin [c], rangeMax [c], rangeStep [c]);

        agent [i].c     [c] = val;
        agent [i].cBest [c] = val;

        a [i].c [c] = val;
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  double min  = 0.0;
  double max  = 0.0;
  double dist = 0.0;
  int    ind  = 0;
  double r    = 0.0;
  double p    = 0.0;

  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      if (u.RNDprobab () < collChoiceProbab)
      {
        do ind = u.RNDminusOne (collectionSize);
        while (coll [ind].f == -DBL_MAX);

        p = agent [i].c   [c];
        r = coll  [ind].c [c];

      }
      else
      {
        p = agent [i].c     [c];
        r = agent [i].cBest [c];
      }

      dist = fabs (p - r) * range;
      min  = r - dist;
      max  = r + dist;

      if (min < rangeMin [c]) min = rangeMin [c];
      if (max > rangeMax [c]) max = rangeMax [c];

      val = u.GaussDistribution (r, min, max, sigma);
      val = u.SeInDiSp (val, rangeMin [c], rangeMax [c], rangeStep [c]);

      agent [i].c [c] = val;
      a     [i].c [c] = val;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Revisionメソッドは、ANSアルゴリズム内のエージェントとコレクションのリビジョン（更新）を実行します。要点は次のとおりです。

  • メソッドの最初の部分：適応度がfBの大域解よりも優れているエージェントを検索し、その座標を配列cBに保存します。
  • メソッドの2番目の部分：エージェントの現在の適応度a[i].fに基づいて、エージェントの最適な座標agent[i].cBestを更新します。
  • メソッドの3番目の部分：エージェントの最適な座標に基づいてcollコレクションを更新します。
  • コレクションを並べ替えます。

このメソッドは、アルゴリズムの実行中にエージェントと解のコレクションを更新する上で重要な役割を果たします。エージェントの母集団はコレクションの2番目の部分に配置され、コレクションが並び替えられ、最適解を含むコレクションの前半が使用されます。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ANS::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > agent [i].fBest)
    {
      agent [i].fBest = a [i].f;
      ArrayCopy (agent [i].cBest, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  //----------------------------------------------------------------------------
  int cnt = 0;
  for (int i = collectionSize; i < collectionSize * 2; i++)
  {
    if (cnt < popSize)
    {
      coll [i].f = agent [cnt].fBest;
      ArrayCopy (coll [i].c, agent [cnt].cBest, 0, 0, WHOLE_ARRAY);
      cnt++;
    }
    else break;
  }

  u.Sorting (coll, collTemp, collectionSize * 2);
}
//——————————————————————————————————————————————————————————————————————————————


3. テスト結果

以下は、ANSテストの結果です。

ANS|Across Neighbourhood Search|50.0|100.0|8.0|1.0|0.6|
=============================
5 Hilly's; Func runs:10000; result:0.9494753644543816
25 Hilly's; Func runs:10000; result:0.8477633752716718
500 Hilly's; Func runs:10000; result:0.43857039929159747
=============================
5 Forest's; Func runs:10000; result:0.9999999999988883
25 Forest's; Func runs:10000; result:0.9233446583489741
500 Forest's; Func runs:10000; result:0.3998822848099108
=============================
5 Megacity's; Func runs:10000; result:0.709230769230769
25 Megacity's; Func runs:10000; result:0.6347692307692309
500 Megacity's; Func runs:10000; result:0.2309076923076936
=============================
All score:6.13394 (68.15%)

ANSはすべてのテスト関数で優れた結果を示しています。このアルゴリズムの動作をテスト環境で視覚化したものを見てみましょう。ANSの結果は非常に素晴らしいものですが、視覚化するといくつかの疑問が浮かび上がります。特に、母集団の挙動は非常に印象的で、まるで視界から消えてしまうように見えます。解空間が空になり、関数のランドスケープにはエージェントが一切存在しなくなります。これはただ一つのことを意味します。アルゴリズムの優れた成果にもかかわらず、母集団が退化しやすいということです。優れた解のコレクションが非常に似通った解で埋め尽くされ、新しい解を生成することができなくなります。なぜなら、すべての解が既存の解の派生にすぎないからです。

このような母集団の動態は、母集団の多様性を維持するためのメカニズムを改良する必要性を示唆しています。 最適化中に解の多様性を保つのに役立つ突然変異演算子の導入や、その他の多様性維持のためのメカニズムを検討する価値があるかもしれません。これにより、母集団の退化を防ぎ、アルゴリズムのより安定した動作を実現することができるでしょう。

Hilly

  Hillyテスト関数のANS

Forest

  Forestテスト関数のANS

Megacity

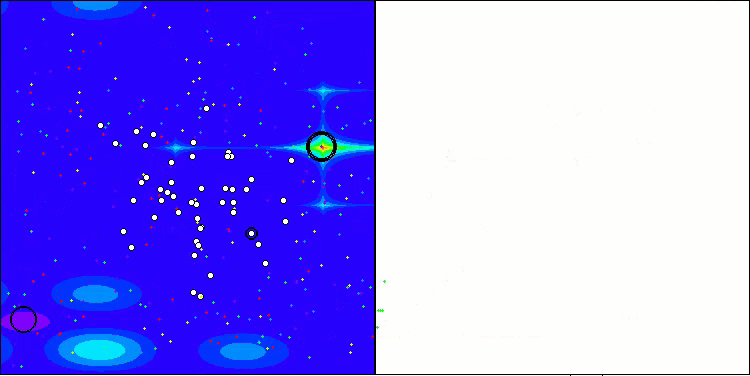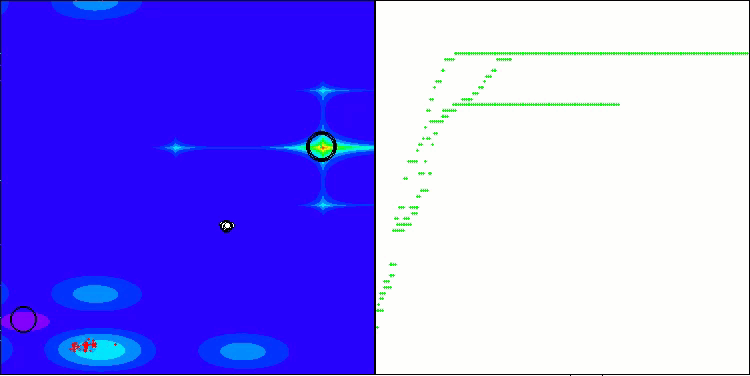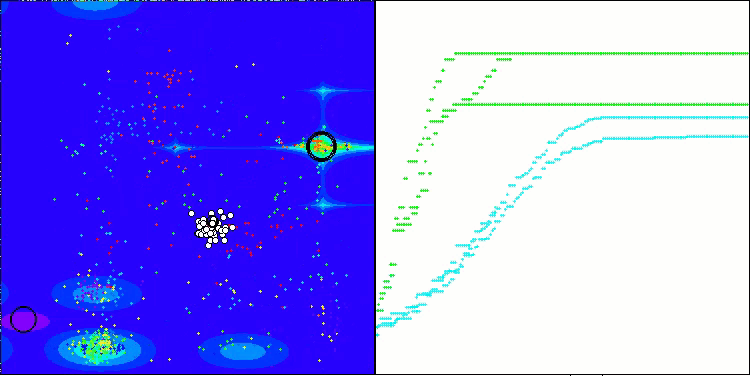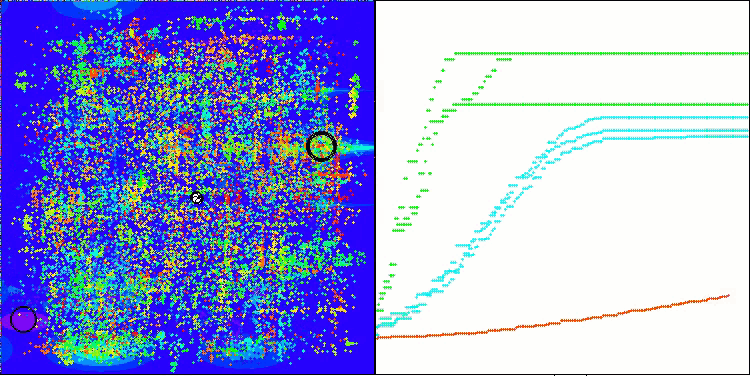
  Megacityテスト関数のANS

この記事で検討したアルゴリズムは、評価表で堂々と2位を獲得しました。このアルゴリズムは優れたスケーラビリティを示し、大規模次元の問題でも検索能力を維持します。 

# AO 詳細 Hilly Hilly最終 Forest Forest最終 Megacity（離散） Megacity最終 最終結果 MAXの%
10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F)
1 BGA バイナリ遺伝的アルゴリズム 0.99989 0.99518 0.42835 2.42341 0.96153 0.96181 0.32027 2.24360 0.91385 0.95908 0.24220 2.11512 6.782 75.36
2 ANS across neighbourhood search 0.94948 0.84776 0.43857 2.23581 1.00000 0.92334 0.39988 2.32323 0.70923 0.63477 0.23091 1.57491 6.134 68.15
3 CLA コードロックアルゴリズム 0.95345 0.87107 0.37590 2.20042 0.98942 0.91709 0.31642 2.22294 0.79692 0.69385 0.19303 1.68380 6.107 67.86
4 (P+O)ES (P+O）進化戦略 0.92256 0.88101 0.40021 2.20379 0.97750 0.87490 0.31945 2.17185 0.67385 0.62985 0.18634 1.49003 5.866 65.17
5 CTA 彗尾アルゴリズム 0.95346 0.86319 0.27770 2.09435 0.99794 0.85740 0.33949 2.19484 0.88769 0.56431 0.10512 1.55712 5.846 64.96
6 SDSm 確率的拡散探索M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
7 ESG 社会母集団の進化 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
8 SIA 等方的焼きなまし 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
9 ACS 人工協調探索 0.75547 0.74744 0.30407 1.80698 1.00000 0.88861 0.22413 2.11274 0.69077 0.48185 0.13322 1.30583 5.226 58.06
10 TSEA 亀甲進化アルゴリズム 0.96798 0.64480 0.29672 1.90949 0.99449 0.61981 0.22708 1.84139 0.69077 0.42646 0.13598 1.25322 5.004 55.60
11 DE 差分進化 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
12 CRO 化学反応の最適化 0.94629 0.66112 0.29853 1.90593 0.87906 0.58422 0.21146 1.67473 0.75846 0.42646 0.12686 1.31178 4.892 54.36
13 BSA 鳥群アルゴリズム 0.89306 0.64900 0.26250 1.80455 0.92420 0.71121 0.24939 1.88479 0.69385 0.32615 0.10012 1.12012 4.809 53.44
14 HS ハーモニー検索 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
15 SSG 苗木の播種と育成 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
16 (PO)ES (PO）進化戦略 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
17 BSO ブレインストーム最適化 0.93736 0.57616 0.29688 1.81041 0.93131 0.55866 0.23537 1.72534 0.55231 0.29077 0.11914 0.96222 4.498 49.98
18 WOAm 鯨最適化アルゴリズムM 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
19 ACOm 蟻コロニー最適化M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
20 BFO-GA 細菌採食の最適化：Ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
21 MEC Mind Evolutionary Computation 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
22 IWO 侵入雑草最適化 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
23 Micro-AIS 微小人工免疫系 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54
24 COAm カッコウ最適化アルゴリズムM 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21
25 SDOm 螺旋ダイナミクス最適化M 0.74601 0.44623 0.29687 1.48912 0.70204 0.34678 0.10944 1.15826 0.42833 0.16767 0.03663 0.63263 3.280 36.44
26 NMm ネルダー=ミード法M 0.73807 0.50598 0.31342 1.55747 0.63674 0.28302 0.08221 1.00197 0.44667 0.18667 0.04028 0.67362 3.233 35.92
27 FAm ホタルアルゴリズムM 0.58634 0.47228 0.32276 1.38138 0.68467 0.37439 0.10908 1.16814 0.28667 0.16467 0.04722 0.49855 3.048 33.87
28 GSA 重力探索法 0.64757 0.49197 0.30062 1.44016 0.53962 0.36353 0.09945 1.00260 0.32667 0.12200 0.01917 0.46783 2.911 32.34
29 BFO 細菌採餌最適化 0.61171 0.43270 0.31318 1.35759 0.54410 0.21511 0.05676 0.81597 0.42167 0.13800 0.03195 0.59162 2.765 30.72
30 ABC 人工蜂コロニー 0.63377 0.42402 0.30892 1.36671 0.55103 0.21874 0.05623 0.82600 0.34000 0.14200 0.03102 0.51302 2.706 30.06
31 BA コウモリアルゴリズム 0.59761 0.45911 0.35242 1.40915 0.40321 0.19313 0.07175 0.66810 0.21000 0.10100 0.03517 0.34617 2.423 26.93
32 SA 焼きなまし 0.55787 0.42177 0.31549 1.29513 0.34998 0.15259 0.05023 0.55280 0.31167 0.10033 0.02883 0.44083 2.289 25.43
33 IWDm intelligent water drops M 0.54501 0.37897 0.30124 1.22522 0.46104 0.14704 0.04369 0.65177 0.25833 0.09700 0.02308 0.37842 2.255 25.06
34 PSO 粒子群最適化 0.59726 0.36923 0.29928 1.26577 0.37237 0.16324 0.07010 0.60572 0.25667 0.08000 0.02157 0.35823 2.230 24.77
35 ボイド ボイドアルゴリズム 0.43340 0.30581 0.25425 0.99346 0.35718 0.20160 0.15708 0.71586 0.27846 0.14277 0.09834 0.51957 2.229 24.77
36 MA モンキーアルゴリズム 0.59107 0.42681 0.31816 1.33604 0.31138 0.14069 0.06612 0.51819 0.22833 0.08567 0.02790 0.34190 2.196 24.40
37 SFL Shuffled Frog-Leaping 0.53925 0.35816 0.29809 1.19551 0.37141 0.11427 0.04051 0.52618 0.27167 0.08667 0.02402 0.38235 2.104 23.38
38 FSS 魚群検索 0.55669 0.39992 0.31172 1.26833 0.31009 0.11889 0.04569 0.47467 0.21167 0.07633 0.02488 0.31288 2.056 22.84
39 RND ランダム 0.52033 0.36068 0.30133 1.18234 0.31335 0.11787 0.04354 0.47476 0.25333 0.07933 0.02382 0.35648 2.014 22.37
40 GWO 灰色オオカミオプティマイザ 0.59169 0.36561 0.29595 1.25326 0.24499 0.09047 0.03612 0.37158 0.27667 0.08567 0.02170 0.38403 2.009 22.32
41 CSS 荷電系探索 0.44252 0.35454 0.35201 1.14907 0.24140 0.11345 0.06814 0.42299 0.18333 0.06300 0.02322 0.26955 1.842 20.46
42 EM 電磁気学的アルゴリズム 0.46250 0.34594 0.32285 1.13129 0.21245 0.09783 0.10057 0.41085 0.15667 0.06033 0.02712 0.24412 1.786 19.85


記事のこの部分には通常、結論が含まれます。しかし、この場合、最終的な結論を出すのは時期尚早であるように思われます。最後に、まずは結果の従来の視覚的表現、つまり色分けされた評価表と、理論上の最大値の100%スケールでアルゴリズムの相対的な位置を示すヒストグラムを見てみましょう。これらの視覚データは、他の方法と比較したANSの効率をよりよく理解し、評価するのに役立ちます。

Tab

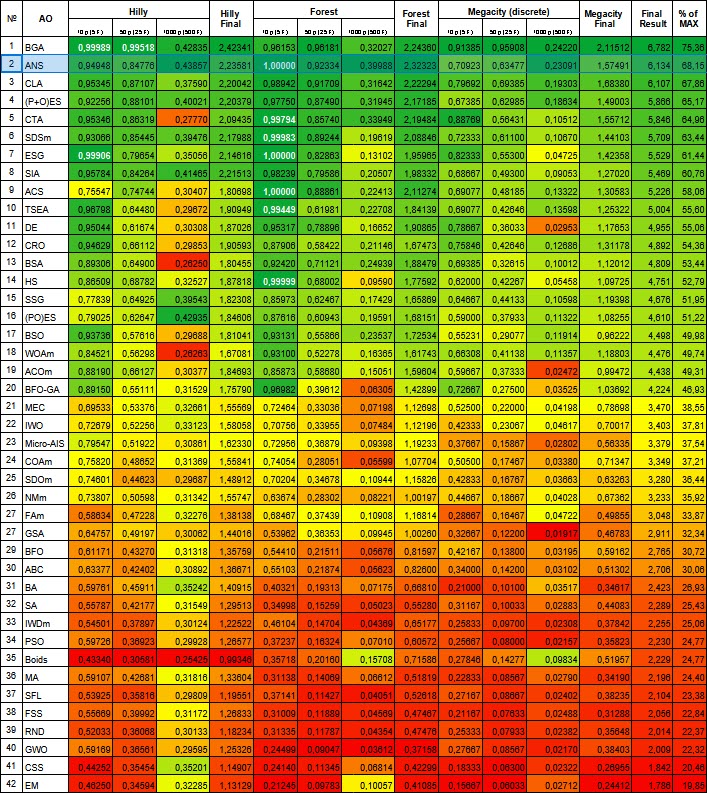
図1：関連テストによるアルゴリズムのカラーグラデーション0.99以上の結果は白で強調表示される

チャート

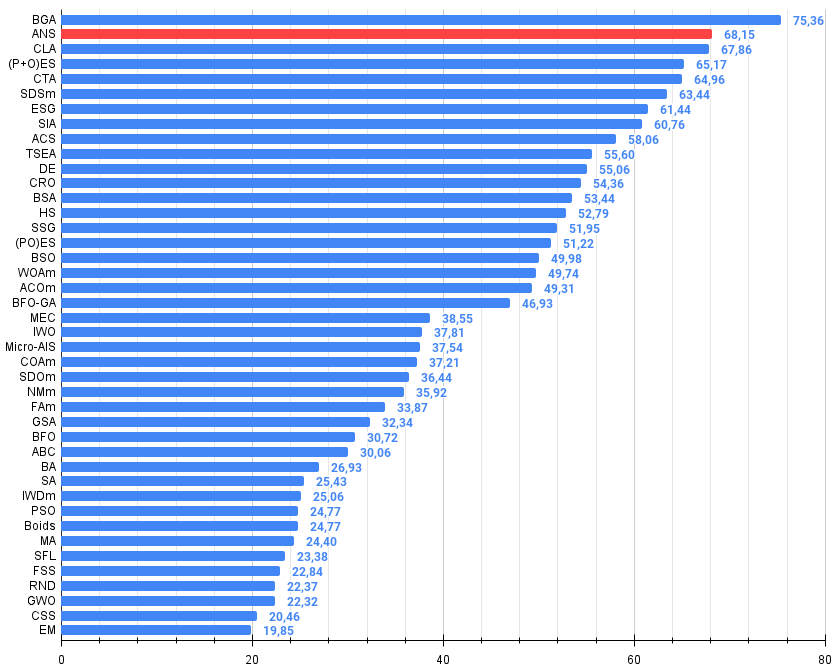
図2：アルゴリズムのテスト結果のヒストグラム（0から100までのスケールで、多ければ多いほど良い、

ここで、100は理論的に可能な最大の結果であり、アーカイブにはレーティング表を計算するスクリプトが含まれている）

この記事の前半で、ANSアルゴリズムの母集団が退化する傾向があることを指摘しました。この重大な欠点に対処するため、私はアルゴリズムに突然変異演算子を追加することで改良を試みました。この場合、突然変異は、エージェントの最適解の近傍で発生し、対応する座標の最小許容値から最大許容値の範囲内で新しい座標を取得するガウス分布に基づく確率として実装されます。この変更をおこなうためには、Movingメソッドにいくつかの改修を加える必要があります。

以下に、コードに加えた変更点と、メソッドのロジックを簡単に説明します。

  • 乱数が0.005未満の場合、正規分布を使用して突然変異が発生します。
  • それ以外の場合は、コレクションからランダムに選択された解、またはエージェントの最適座標が使用されます。
  • 正規分布のための距離と範囲が計算されます。
  • 新しい座標値を取得するために正規分布が適用されます。
//----------------------------------------------------------------------------
double min  = 0.0;
double max  = 0.0;
double dist = 0.0;
int    ind  = 0;
double r    = 0.0;
double p    = 0.0;

for (int i = 0; i < popSize; i++)
{
  for (int c = 0; c < coords; c++)
  {
    if (u.RNDprobab () < 0.005)
    {
      val = u.GaussDistribution (agent [i].cBest [c], rangeMin [c], rangeMax [c], sigma);
      val = u.SeInDiSp (val, rangeMin [c], rangeMax [c], rangeStep [c]);
    }
    else
    {
      if (u.RNDprobab () < collChoiceProbab)
      {
        do ind = u.RNDminusOne (collectionSize);
        while (coll [ind].f == -DBL_MAX);

        p = agent [i].c   [c];
        r = coll  [ind].c [c];
 
      }
      else
      {
        p = agent [i].c     [c];
        r = agent [i].cBest [c];
      }

      dist = fabs (p - r) * range;
      min  = r - dist;
      max  = r + dist;

      if (min < rangeMin [c]) min = rangeMin [c];
      if (max > rangeMax [c]) max = rangeMax [c];

      val = u.GaussDistribution (r, min, max, sigma);
      val = u.SeInDiSp (val, rangeMin [c], rangeMax [c], rangeStep [c]);
    }
      
    agent [i].c [c] = val;
    a     [i].c [c] = val;
  }
}

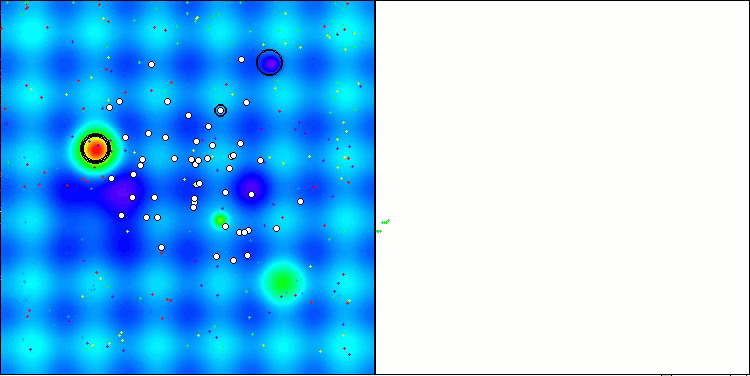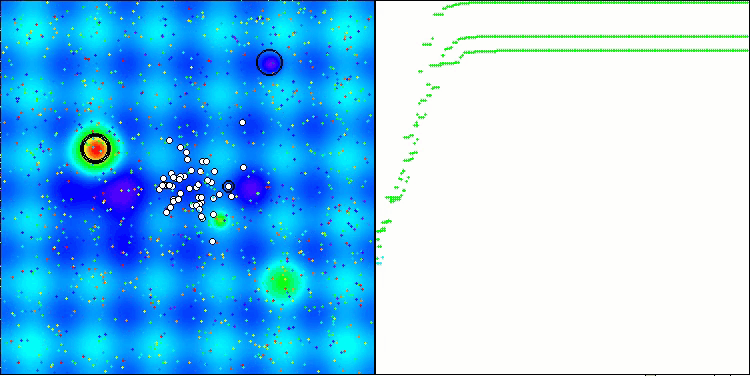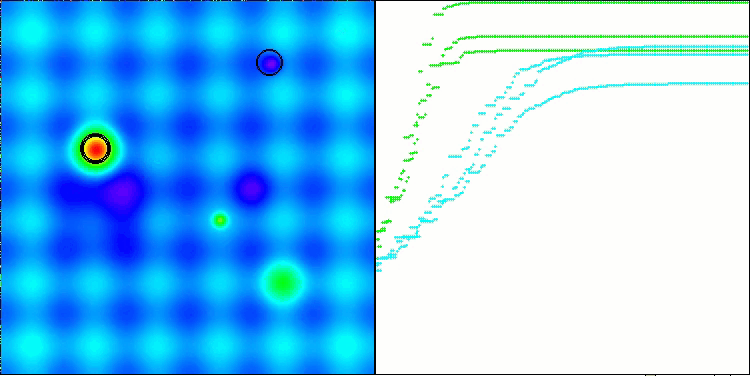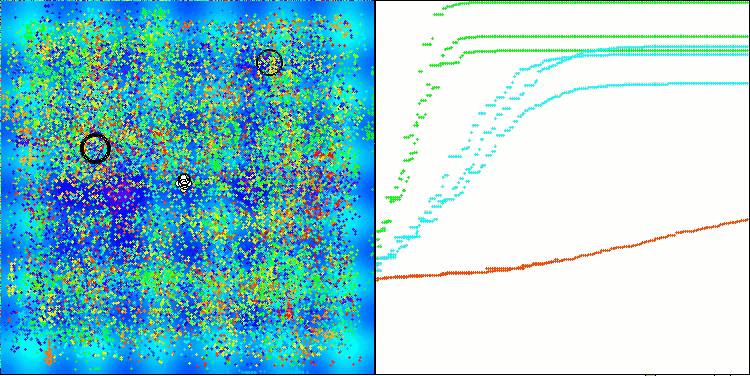
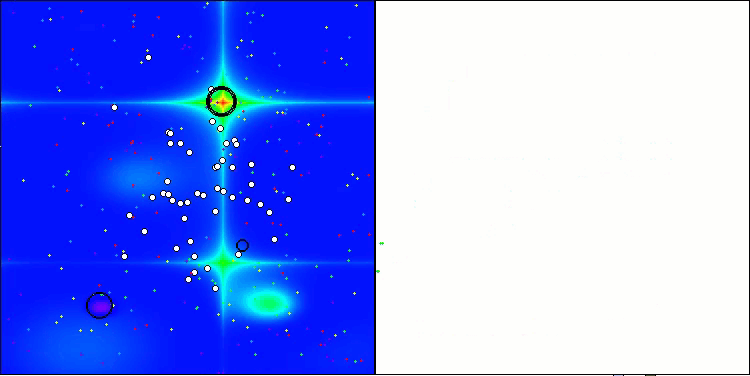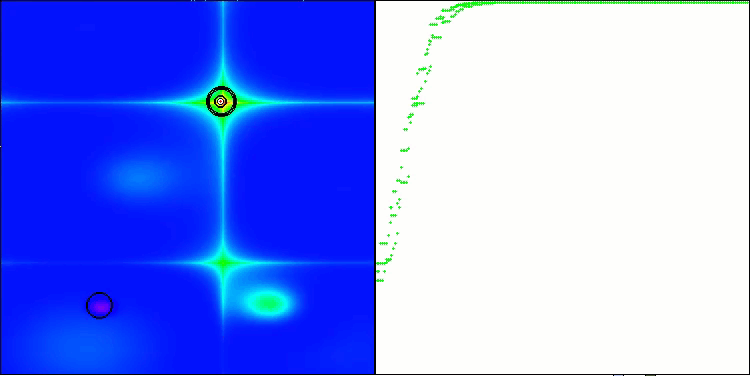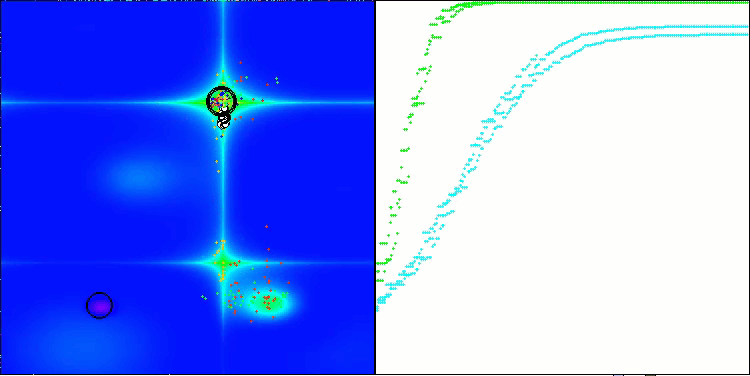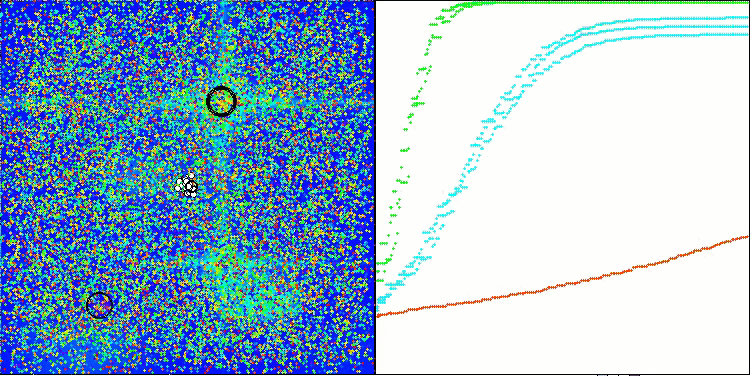
突然変異演算子を追加した後、アルゴリズムは、図3（アルゴリズムの視覚化のスクリーンショット）に示すように、任意の数のエポックにわたって検索空間の探索を続けます。

エージェン去った

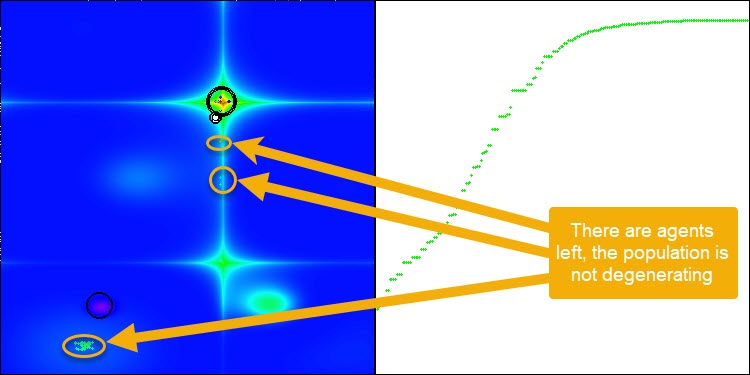
図3：エージェントは残されており、母集団は退化していない（パラメータmut = 0.005）

異なる座標数と突然変異演算子(mut)の異なる値を持つテスト関数に対するANSアルゴリズムの結果から、次の結論を導き出すことができます。
  • mutの値が0.1の突然変異演算子は、全体的な結果に悪影響を与えます。このような大きな突然変異率（各座標における操作総数の10%）では、アルゴリズムのパフォーマンスが低下することが確認されました。そのため、このパラメータを徐々に減少させることにしました。パラメータの値を下げた結果、パフォーマンスが改善されたため、最終的に0.005という値に落ち着きました。この比率は、以下に示すように、母集団の退化を防ぎつつ、アルゴリズムのパフォーマンスを向上させるのに十分であることが判明しました。

以下は、突然変異確率mut = 0.1でのアルゴリズム操作の結果です。

500 Megacity's; Func runs:10000; result:0.19352307692307838

=============================
All score:6.05103 (67.23%)
ANS|Across Neighbourhood Search|50.0|100.0|8.0|1.0|0.6|
=============================
5 Hilly's; Func runs:10000; result:0.9534829314854332
25 Hilly's; Func runs:10000; result:0.8136803288623282
500 Hilly's; Func runs:10000; result:0.31144979106165716
=============================
5 Forest's; Func runs:10000; result:0.9996561274415626
25 Forest's; Func runs:10000; result:0.81670393859872
500 Forest's; Func runs:10000; result:0.25620559379918284
=============================
5 Megacity's; Func runs:10000; result:0.8753846153846153
25 Megacity's; Func runs:10000; result:0.5778461538461539
500 Megacity's; Func runs:10000; result:0.13375384615384744
=============================
All score:5.73816 (63.76%)

以下は、突然変異確率mut = 0.01でのアルゴリズム操作の結果です。

ANS|Across Neighbourhood Search|50.0|100.0|8.0|1.0|0.6|

=============================
5 Hilly's; Func runs:10000; result:0.9073657389037575
25 Hilly's; Func runs:10000; result:0.871278233418226
500 Hilly's; Func runs:10000; result:0.3960769225373809
=============================
5 Forest's; Func runs:10000; result:0.989394440004635
25 Forest's; Func runs:10000; result:0.9513150500729907
500 Forest's; Func runs:10000; result:0.35407610928209116
=============================
5 Megacity's; Func runs:10000; result:0.7492307692307691
25 Megacity's; Func runs:10000; result:0.6387692307692309
500 Megacity's; Func runs:10000; result:0.19352307692307838
=============================
All score:6.05103 (67.23%)

以下は、突然変異確率mut = 0.005でのアルゴリズム操作の結果です。

ANS|Across Neighbourhood Search|50.0|100.0|8.0|1.0|0.6|
=============================
5 Hilly's; Func runs:10000; result:0.949632264944664
25 Hilly's; Func runs:10000; result:0.871206955779846
500 Hilly's; Func runs:10000; result:0.40738389742274217
=============================
5 Forest's; Func runs:10000; result:0.9924803131691761
25 Forest's; Func runs:10000; result:0.9493489251290264
500 Forest's; Func runs:10000; result:0.3666276564633121
=============================
5 Megacity's; Func runs:10000; result:0.8061538461538461
25 Megacity's; Func runs:10000; result:0.6732307692307691
500 Megacity's; Func runs:10000; result:0.20844615384615534
=============================
All score:6.22451 (69.16%)


まとめ

突然変異演算子を連携させた結果を確認したところ、次のような結論を導き出すことができます。

1. シンプルで実装が簡単。
2. 探索と開発のバランス。
3. さまざまな種類の問題を解決する効率性。
4. さまざまなタスクへの適応性。
5. さらなる改善の可能性あり。

したがって、ANSは、幅広い問題に対して競争力のある結果を示し、さらなる発展の可能性を秘めた、シンプルでありながら効果的な最適化アルゴリズムです。

ANSの一般的な長所と短所

長所：

  1. 様々な種類の関数に対して収束性が良い
  2. EAが非常に高速
  3. 実装がシンプル
  4. 優れたスケーラビリティ

短所

  1. 時々、極値にはまってしまうことがある

この記事には、最新版のアルゴリズムコードを含むアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/15049

添付されたファイル |
ZIPをダウンロード
ANS.zip (26.81 KB)
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動
ニューラルネットワークが簡単に（第96回）：マルチスケール特徴量抽出(MSFformer) ニューラルネットワークが簡単に（第96回）：マルチスケール特徴量抽出(MSFformer)
長期的な依存関係と短期的な特徴量の効率的な抽出と統合は、時系列分析において依然として重要な課題です。正確で信頼性の高い予測モデルを作成するためには、それらを適切に理解し、統合することが必要です。
スマートマネーコンセプト（オーダーブロック）とフィボナッチ指標を組み合わせた最適な取引エントリー方法 スマートマネーコンセプト（オーダーブロック）とフィボナッチ指標を組み合わせた最適な取引エントリー方法
SMC（オーダーブロック）は、機関投資家トレーダーが大規模なな売買を開始する主要領域です。価格が大きく動いた後、フィボナッチは直近のスイングハイからスイングローへの潜在的なリトレースメントを特定し、最適な取引エントリーを特定するのに役立ちます。
古典的な戦略を再構築する（第10回）：AIはMACDを強化できるか？ 古典的な戦略を再構築する（第10回）：AIはMACDを強化できるか？
MACDインジケーターを経験的に分析し、インジケーターを含む戦略にAIを適用することで、EURUSDの予測精度が向上するかどうかをテストします。さらに、インジケーター自体が価格より予測しやすいのか、またインジケーターの値が将来の価格水準を予測できるのかも同時に評価します。これにより、AI取引戦略にMACDを統合することに投資する価値があるかどうかを判断するための情報を提供します。
Controlsクラスを使用してインタラクティブなMQL5ダッシュボード/パネルを作成する方法（第1回）：パネルの設定 Controlsクラスを使用してインタラクティブなMQL5ダッシュボード/パネルを作成する方法（第1回）：パネルの設定
この記事では、取引操作を効率化するために設計されたMQL5のControlsクラスを使用して、インタラクティブな取引ダッシュボードを作成します。パネルには、タイトル、[Trade]、[Close]、[Information]のナビゲーションボタン、取引の実行とポジションの管理用の専用アクションボタンが表示されます。この記事を読み終える頃には、今後の記事でさらに機能強化するための基礎パネルが完成しているはずです。