Busca dialética — Dialectic Search (DA)
83
0
Conteúdo
Introdução
O materialismo dialético baseia-se no princípio da unidade e da luta dos opostos na natureza, na sociedade e no pensamento. Seu fundamento está na ideia de que o desenvolvimento ocorre por meio do conflito entre forças e tendências opostas, onde cada fenômeno contém contradições internas. O princípio-chave dessa abordagem é a transição de mudanças quantitativas em qualitativas, quando mudanças graduais se acumulam e resultam em saltos qualitativos abruptos. O processo de desenvolvimento segue a lei da "negação da negação", em que uma tese é sucedida por uma antítese, gerando uma síntese como nova qualidade que preserva o melhor dos estados anteriores.
No mundo dos algoritmos de otimização, onde a precisão matemática se encontra com a sabedoria filosófica, surgiu um método único inspirado no materialismo dialético, o Dialectical Algorithm (DA). Este algoritmo, apresentado como uma síntese entre a dialética clássica e os métodos modernos de otimização, reformula o processo de busca por soluções ótimas através da lente do confronto filosófico entre tese e antítese. A essência do DA está na ideia de que toda solução (tese) contém em si o potencial de ser aprimorada por meio da interação com sua contraposição (antítese).
Na implementação algorítmica, esse princípio se manifesta na interação entre pensadores especulativos, que buscam novas soluções se afastando das conhecidas, e pensadores práticos, que se concentram em soluções já verificadas. O aspecto materialista do materialismo dialético se revela na confiança em critérios objetivos para avaliar soluções e na verificação prática dos resultados. O desenvolvimento ocorre de forma cíclica: as soluções encontradas geram novas contradições, o que leva ao próximo ciclo de busca, refletindo a continuidade do processo de conhecimento e aprimoramento.
O algoritmo implementa esse princípio por meio de três momentos-chave: compreensão, onde ocorre a avaliação e ordenação das soluções; interação dialética, em que as soluções encontram suas antíteses; e o momento de síntese, onde se formam novas soluções aprimoradas. A particularidade do algoritmo está na divisão da população em dois tipos de pensadores: especulativos (k1), que exploram o espaço de soluções com grandes saltos (por meio da interação de soluções semelhantes em qualidade, mas distantes entre si no espaço de busca), e práticos (p-k1), que realizam uma busca local (soluções diferentes em qualidade, mas próximas no espaço). Essa divisão reflete o princípio filosófico da unidade e luta dos opostos, em que cada grupo traz uma contribuição única ao processo de otimização.
A busca dialética (Dialectic Search, DA) foi apresentada por Serdar Kadioglu e Meinolf Sellmann em 2009. Esse método adota a abordagem dialética para resolver tarefas de otimização com restrições, dando continuidade às tradições estabelecidas pelo materialismo dialético na investigação e busca por novas soluções.
Implementação do algoritmo
Na base do algoritmo está uma população com p soluções (geralmente 50), cada uma representando um vetor de coordenadas no espaço de busca. Essa população é dividida em dois grupos: k1 pensadores especulativos (as melhores soluções) e (p-k1) pensadores práticos.
A primeira etapa é o Momento de Compreensão. Aqui ocorre a avaliação de todas as soluções através da função objetivo f(x). As soluções são classificadas por qualidade, e as melhores k1 tornam-se pensadores especulativos, enquanto as demais tornam-se práticos. Nesta etapa também ocorre a aceitação ou rejeição de novas soluções, com base em sua qualidade em relação às iterações anteriores (a melhor solução individual para cada pensador).
A segunda etapa é o Momento Dialético. Nesta fase, cada solução busca sua antítese, o oposto com o qual irá interagir. Para os pensadores especulativos, a busca pela antítese baseia-se na maximização da distância com manutenção da qualidade da solução (dialética idealista). Para a primeira solução, a antítese é a segunda melhor; para a última, é a penúltima; para as demais, escolhe-se o vizinho com a maior distância. Já os pensadores práticos buscam a antítese minimizando a distância, desde que haja diferença suficiente na qualidade (dialética materialista).
A terceira etapa é o Momento Especulativo/Prático (Momento de Atualização). Aqui ocorre a atualização das posições de todas as soluções usando as antíteses encontradas. Os pensadores especulativos usam uma distribuição uniforme, que garante uma ampla exploração do espaço de soluções. Os pensadores práticos utilizam uma distribuição normal. Meus experimentos mostraram que, para ambos os tipos de pensadores, a distribuição uniforme oferece os melhores resultados.
A fórmula de atualização das posições é a mesma para todos: X(i) = X(i) + μ⊙(Xanti(i) - X(i)), onde μ é um vetor aleatório do respectivo tipo de distribuição, e ⊙ representa a multiplicação elemento a elemento. Isso garante um equilíbrio entre a exploração do espaço de soluções pelos pensadores especulativos e o refinamento das soluções encontradas pelos pensadores práticos.
O Algoritmo Dialético (DA) possui semelhanças com o algoritmo de evolução diferencial DE, no que diz respeito à fórmula de atualização das soluções. No DE, um novo vetor é criado adicionando-se ao vetor alvo a diferença escalada entre dois outros vetores (x_new = x_target + F(x_r1 - x_r2)), enquanto o DA usa um princípio semelhante, mas com uma antítese e um coeficiente adaptativo (x_new = x + μ(x_anti - x)).
No entanto, a principal diferença está no modo como os vetores são escolhidos para gerar novas soluções. O DE depende da seleção aleatória de vetores para formar a diferença, o que caracteriza sua natureza estocástica. O DA, por outro lado, adota uma abordagem determinística na escolha das antíteses, baseada na distância entre as soluções e sua qualidade, ao mesmo tempo em que divide a população entre pensadores especulativos e práticos, cada qual com estratégias de busca distintas. O algoritmo DA apresenta uma complexidade computacional ligeiramente maior (devido ao cálculo de distância euclidiana), mas mostra uma eficiência mais elevada em diversas tarefas de otimização.
Na Figura 1 é ilustrado o princípio de escolha das antíteses para as teses especulativas (vermelhas, as melhores) e materiais (azuis). Os especulativos escolhem antíteses vizinhas em qualidade, mas distantes no espaço de busca; já os materiais escolhem soluções distantes em qualidade, mas próximas no espaço de busca.
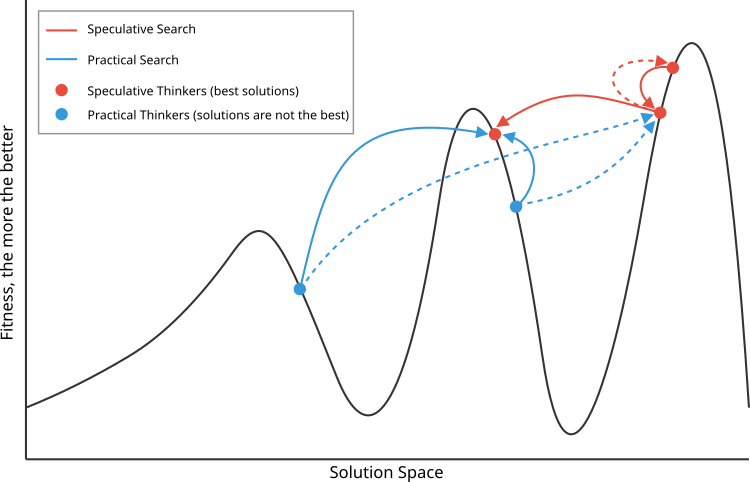
Imagem 1. Representação esquemática do princípio de funcionamento do algoritmo DA. Linhas contínuas - interação com antíteses preferenciais, diferente das menos preferenciais, indicadas por linhas tracejadas
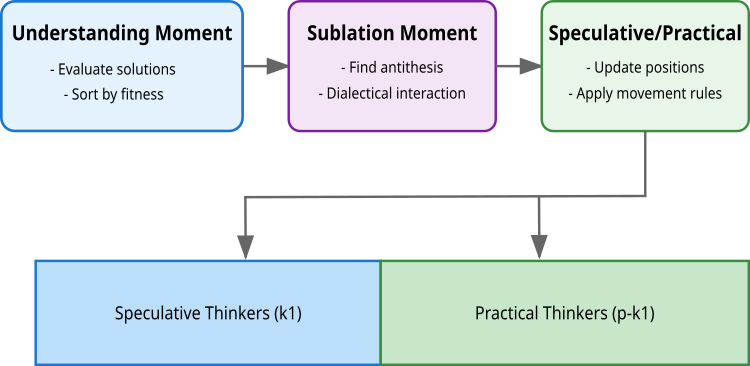
Imagem 2. Etapas da lógica do algoritmo DA
Prosseguimos agora com a escrita do pseudocódigo do algoritmo:
Na primeira iteração: os agentes são posicionados aleatoriamente: position[i] = random(min, max)
A população é ordenada com base nas melhores soluções individuais
Cria-se uma população com três tipos de agentes:
- Melhor pensador (1 agente)
- Pensadores especulativos (k1 = 3 agentes)
- Pensadores práticos (os demais dos 50 agentes)
A. O melhor pensador move-se em direção ao segundo melhor:
position[0] = best[0] + rand(0,1) * (position[1] - position[0])B. Pensadores especulativos:
- Identificam os vizinhos mais distantes com base na distância euclidiana:
- Atualizam a posição em relação ao mais distante:
C. Pensadores práticos:
- Selecionam dois pensadores especulativos aleatórios
- Movem-se em direção ao mais próximo:
position[i] = best[i] + rand(0,1) * (position[nearest] - position[i])
Após cada movimento:- Atualizamos as melhores soluções individuais
- Atualizamos a melhor solução global
- Ordenamos os agentes com base na qualidade de suas soluções individuais
O processo se repete até que o critério de parada seja atingido
Após a análise completa do algoritmo, passamos à implementação em código. Vamos escrever a classe "C_AO_DA" do algoritmo dialético de otimização, herdando a funcionalidade da classe base "C_AO".
Parâmetros do algoritmo:
- Tamanho da população— as antíteses determinam a quantidade de agentes que participarão do processo de otimização.
- Pensadores especulativos — indica a quantidade de melhores agentes capazes de realizar uma busca mais livre por soluções.
- Vizinhos para análise — define quantos vizinhos mais próximos cada pensador especulativo (agente) irá considerar para trocar informações e aprimorar sua estratégia.
Métodos:
- C_AO_DA () — o construtor inicializa os parâmetros principais e também cria um array para armazenar os parâmetros.
- SetParams () — a definição de parâmetros permite atualizar os valores dos parâmetros do algoritmo durante a execução.
- Moving () e Revision () — funções responsáveis pelo deslocamento dos agentes no espaço de busca e pela revisão das soluções encontradas.
- EuclideanDistance () — cálculo da distância no espaço de busca entre dois vetores, necessário para escolher o vizinho mais próximo (para os especulativos) e o mais distante (para os práticos), de acordo com a semelhança entre as soluções encontradas pelos agentes.
//—————————————————————————————————————————————————————————————————————————————— // Класс реализующий диалектический алгоритм оптимизации class C_AO_DA : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_DA () { } C_AO_DA () { ao_name = "DA"; ao_desc = "Dialectical Algorithm"; ao_link = "https://www.mql5.com/ru/articles/16999"; popSize = 50; // размер популяции k1 = 3; // спекулятивные мыслители k2 = 10; // соседи ArrayResize (params, 3); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "k1"; params [1].val = k1; params [2].name = "k2"; params [2].val = k2; } // Установка параметров алгоритма void SetParams () { popSize = (int)params [0].val; k1 = (int)params [1].val; k2 = (int)params [2].val; } bool Init (const double &rangeMinP [], // минимальный диапазон поиска const double &rangeMaxP [], // максимальный диапазон поиска const double &rangeStepP [], // шаг поиска const int epochsP = 0); // количество эпох void Moving (); // Перемещение агентов в пространстве поиска void Revision (); // Пересмотр и обновление лучших найденных решений //---------------------------------------------------------------------------- int k1; // количество спекулятивных мыслителей int k2; // количество соседей для анализа private: //------------------------------------------------------------------- // Вычисление евклидового расстояния между двумя векторами double EuclideanDistance (const double &vec1 [], const double &vec2 [], const int dim) { double sum = 0; double diff = 0.0; for (int i = 0; i < dim; i++) { diff = vec1 [i] - vec2 [i]; sum += diff * diff; } return MathSqrt (sum); } }; //——————————————————————————————————————————————————————————————————————————————
O método "Init" da classe "C_AO_DA" é destinado à inicialização dos parâmetros do algoritmo de otimização. Ele recebe arrays com os valores mínimos e máximos do intervalo de busca, os passos de busca e, opcionalmente, o número de épocas para executar a otimização. O método realiza primeiro a inicialização padrão dos parâmetros; se essa inicialização falhar, ele retorna "false". Caso a inicialização seja bem-sucedida, o método retorna "true", confirmando que o algoritmo está pronto para ser executado.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_DA::Init (const double &rangeMinP [], // минимальный диапазон поиска const double &rangeMaxP [], // максимальный диапазон поиска const double &rangeStepP [], // шаг поиска const int epochsP = 0) // количество эпох { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- return true; } //——————————————————————————————————————————————————————————————————————————————
O método "Moving" implementa o deslocamento dos agentes no espaço de busca. Abaixo está uma descrição detalhada do funcionamento do método:
Inicialização:
- No início (!revision), as posições iniciais dos agentes são definidas aleatoriamente, usando os limites mínimos e máximos definidos para cada coordenada. Cada agente "a[i]" recebe coordenadas aleatórias dentro dos intervalos especificados e de acordo com o passo definido.
- Após a inicialização, "revision" é definido como "true", o que impede nova inicialização nas próximas chamadas ao método "Moving".
Atualização da posição do melhor pensador:
- O melhor pensador (agente) atualiza suas coordenadas com base em sua melhor posição anterior e uma probabilidade aleatória, utilizando o vizinho mais próximo "a[1]" para realizar a atualização.
Atualização das posições dos pensadores especulativos:
- Para cada pensador especulativo (agente) no intervalo de "k2" até "k1", o método procura o vizinho anterior mais distante (antiPrevIND) e o vizinho seguinte mais distante (antiNextIND).
- Em seguida, a coordenada do pensador especulativo é atualizada com base no vizinho mais distante considerado como antítese.
Atualização das posições dos pensadores práticos:
- Os pensadores práticos (agentes) estão no intervalo de "k1" até "popSize".
- O código seleciona aleatoriamente dois pensadores especulativos e calcula a distância até eles. O pensador prático escolhe o mais próximo (entre os dois selecionados) para atualizar sua posição.
- Cada coordenada é atualizada com base no vizinho escolhido.
Funções auxiliares
- EuclideanDistance — função que calcula a distância euclidiana entre dois pontos "a" e "b" em um espaço multidimensional.
- u.RNDfromCI — retorna um número aleatório dentro de um intervalo especificado.
- u.SeInDiSp — ajusta o "value" ao passo adequado de acordo com o intervalo.
- u.RNDprobab — retorna um número aleatório com distribuição uniforme de probabilidade.
//—————————————————————————————————————————————————————————————————————————————— // Реализация движения агентов в пространстве поиска void C_AO_DA::Moving () { //---------------------------------------------------------------------------- // Начальная инициализация позиций агентов случайным образом if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- // Обновление позиции лучшего мыслителя for (int c = 0; c < coords; c++) { a [0].c [c] = a [0].cB [c] + u.RNDprobab () * (a [1].c [c] - a [0].c [c]); a [0].c [c] = u.SeInDiSp (a [0].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } //---------------------------------------------------------------------------- double dist_next = -DBL_MAX; // максимальное расстояние до следующего соседа double dist_prev = -DBL_MAX; // максимальное расстояние до предыдущего соседа double dist = 0.0; // текущее расстояние int antiNextIND = 0; // индекс наиболее удаленного следующего соседа int antiPrevIND = 0; // индекс наиболее удаленного предыдущего соседа int antiIND = 0; // выбранный индекс для обновления позиции // Обновление позиций спекулятивных мыслителей ------------------------------- for (int i = k2; i < k1; i++) { // Поиск наиболее удаленного предыдущего соседа for (int j = 1; j <= k2; j++) { dist = EuclideanDistance (a [i].cB, a [i - j].cB, coords); if (dist > dist_prev) { dist_prev = dist; antiPrevIND = i - j; } } // Поиск наиболее удаленного следующего соседа for (int j = 1; j <= k2; j++) { dist = EuclideanDistance (a [i].cB, a [i + j].cB, coords); if (dist > dist_next) { dist_next = dist; antiNextIND = i + j; } } // Выбор наиболее удаленного соседа для обновления позиции if (dist_prev > dist_next) antiIND = antiPrevIND; else antiIND = antiNextIND; // Обновление координат спекулятивного мыслителя for (int c = 0; c < coords; c++) { a [i].c [c] = a [i].cB [c] + u.RNDbool () * (a [antiIND].c [c] - a [i].c [c]); //a [i].c [c] = a [i].cB [c] + u.RNDprobab () * (a [antiIND].c [c] - a [i].c [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } // Обновление позиций практических мыслителей -------------------------------- for (int i = k1; i < popSize; i++) { // Случайный выбор двух спекулятивных мыслителей antiNextIND = u.RNDintInRange (0, k1 - 1); antiPrevIND = u.RNDintInRange (0, k1 - 1); if (antiNextIND == antiPrevIND) antiNextIND = antiPrevIND + 1; // Расчет расстояний до выбранных мыслителей dist_next = EuclideanDistance (a [i].cB, a [antiNextIND].cB, coords); dist_prev = EuclideanDistance (a [i].cB, a [antiPrevIND].cB, coords); // Выбор ближайшего мыслителя для обновления позиции if (dist_prev < dist_next) antiIND = antiPrevIND; else antiIND = antiNextIND; // Обновление координат практического мыслителя for (int c = 0; c < coords; c++) { a [i].c [c] = a [i].cB [c] + u.RNDprobab () * (a [antiIND].c [c] - a [i].c [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
O método "Revision" é responsável pela revisão e atualização das melhores soluções encontradas pelos agentes. Abaixo está uma análise detalhada do funcionamento deste método:
Atualização das melhores soluções encontradas: no laço "for", o método percorre cada agente na população. Para cada agente, o valor atual da função de adaptabilidade "a[i].f" é comparado:
- Melhor solução global — se o valor da função "f" do agente for maior do que o atual melhor valor global "fB", então a solução global é atualizada e o índice do agente (ind) que encontrou essa melhor solução é armazenado.
- Melhor solução pessoal — cada valor "f" do agente também é comparado com seu melhor valor pessoal "fB". Se o valor atual for melhor, o valor pessoal é atualizado e suas coordenadas atuais "c" são copiadas para as coordenadas pessoais "cB".
Atualização das coordenadas da melhor solução global: se foi encontrado o índice de um agente que passou a representar a melhor solução global (ind != -1), então as coordenadas desse agente são copiadas para as coordenadas globais "cB".
Ordenação dos agentes: No final do método, é criado um array "aT" e seu tamanho é ajustado ao tamanho da população. Em seguida, a função "u.Sorting_fB" é chamada para ordenar os agentes com base em suas melhores soluções encontradas (valores de fB).
//—————————————————————————————————————————————————————————————————————————————— // Пересмотр и обновление лучших найденных решений void C_AO_DA::Revision () { int ind = -1; // Обновление лучших найденных решений для каждого агента for (int i = 0; i < popSize; i++) { // Обновление глобального лучшего решения if (a [i].f > fB) { fB = a [i].f; ind = i; } // Обновление личного лучшего решения агента if (a [i].f > a [i].fB) { a [i].fB = a [i].f; ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY); } } // Обновление координат глобального лучшего решения if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); // Сортировка агентов по их лучшим найденным решениям static S_AO_Agent aT []; ArrayResize (aT, popSize); u.Sorting_fB (a, aT, popSize); } //——————————————————————————————————————————————————————————————————————————————
Resultados dos testes
Chegou o momento de conhecer os resultados dos testes com o DA. Ainda mais, vamos destacar o método "Moving", onde a linha que deveria estar conforme a proposta dos autores está destacada em verde e comentada no código. Pois bem, os resultados foram os seguintes:
=============================
5 Hilly's; Func runs: 10000; result: 0.749254786734898
25 Hilly's; Func runs: 10000; result: 0.36669693350810206
500 Hilly's; Func runs: 10000; result: 0.2532075139007539
=============================
5 Forest's; Func runs: 10000; result: 0.7626421292861323
25 Forest's; Func runs: 10000; result: 0.4144802592253075
500 Forest's; Func runs: 10000; result: 0.2006796312431603
=============================
5 Megacity's; Func runs: 10000; result: 0.36
25 Megacity's; Func runs: 10000; result: 0.15969230769230774
500 Megacity's; Func runs: 10000; result: 0.0952000000000008
=============================
All score: 3.36185 (37.35%)
Esses resultados estão longe de serem os melhores, mas poderiam ter entrado na tabela de classificação. Ocorre que cometi um erro, e em vez de usar números aleatórios no intervalo [0.0;1.0], inseri no código uma função de geração de valores booleanos aleatórios (destacado em vermelho).
A lógica da mudança aleatória consiste no seguinte: com 50% de probabilidade, a coordenada correspondente permanece a mesma, ou será substituída pela coordenada da antítese. Na minha opinião, isso se alinha até mais com a ideia dos autores sobre o confronto entre tese e antítese. No caso dos pensadores práticos, tudo permanece como antes — seus teses finais são um híbrido entre a tese atual e a antítese, retirados dos pensadores especulativos. Assim, por um feliz acaso, obtive os seguintes resultados:
DA|Dialectical Algorithm|50.0|40.0|1.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.8618313952293774
25 Hilly's; Func runs: 10000; result: 0.700333708747176
500 Hilly's; Func runs: 10000; result: 0.3372386732170054
=============================
5 Forest's; Func runs: 10000; result: 0.9816317765399738
25 Forest's; Func runs: 10000; result: 0.7277214130784131
500 Forest's; Func runs: 10000; result: 0.28717629901518305
=============================
5 Megacity's; Func runs: 10000; result: 0.7030769230769229
25 Megacity's; Func runs: 10000; result: 0.4529230769230769
500 Megacity's; Func runs: 10000; result: 0.16366923076923204
=============================
All score: 5.21560 (57.95%)
São resultados realmente impressionantes! Como essa melhora significativa nos indicadores ocorreu de forma não intencional, não posso atribuir à versão modificada o índice "m". Na nossa tabela de classificação, o algoritmo permanecerá com o nome "DA". Dessa forma, o algoritmo dialético demonstra excelente desempenho, atingindo um índice de eficiência geral de 57,95%. A característica central do algoritmo é sua capacidade de equilibrar com eficácia a busca global e a busca local, graças à divisão entre pensadores especulativos e práticos.
Na visualização, é possível perceber que o algoritmo encontra rapidamente ótimos locais relevantes, embora careça de precisão na convergência para ser considerado ideal. Ainda assim, os resultados são, de qualquer forma, bastante sólidos.
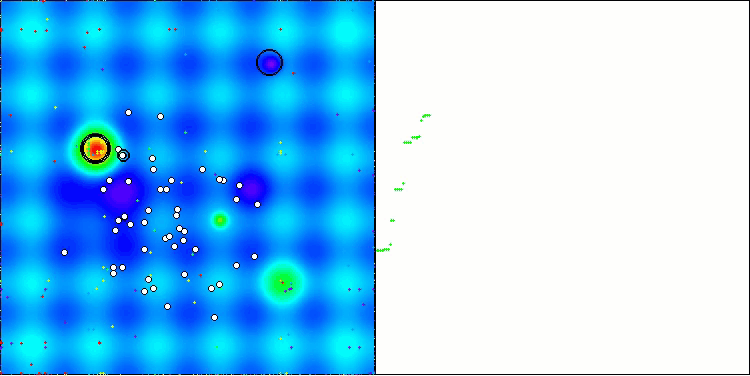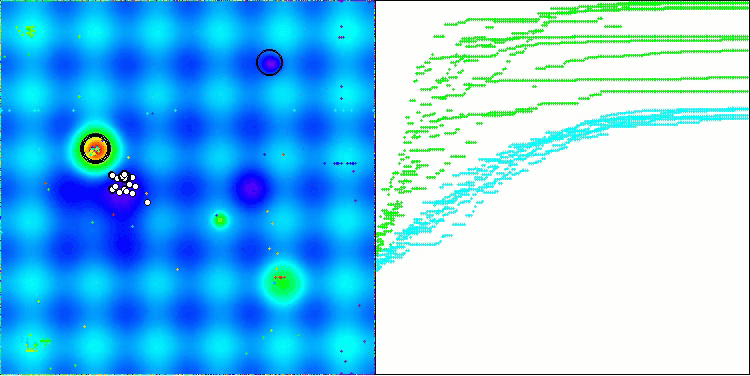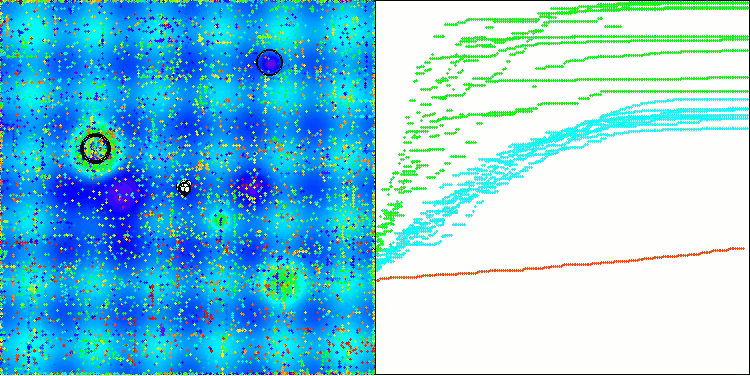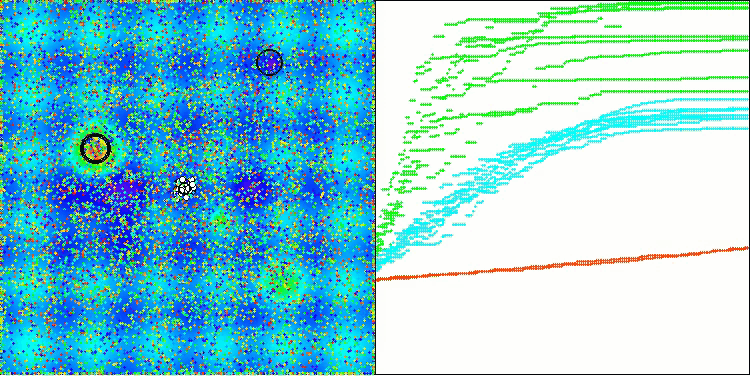
DA na função de teste Hilly
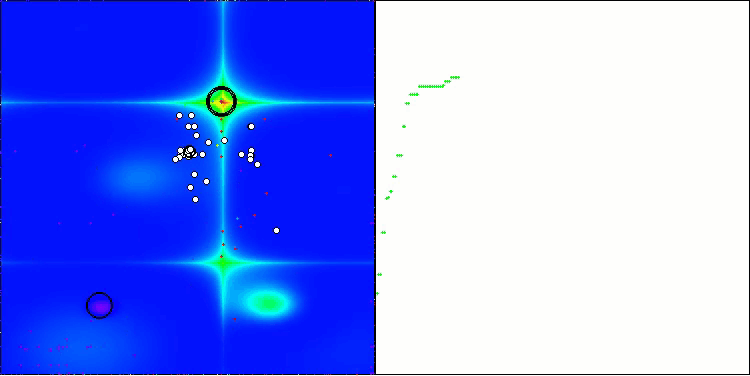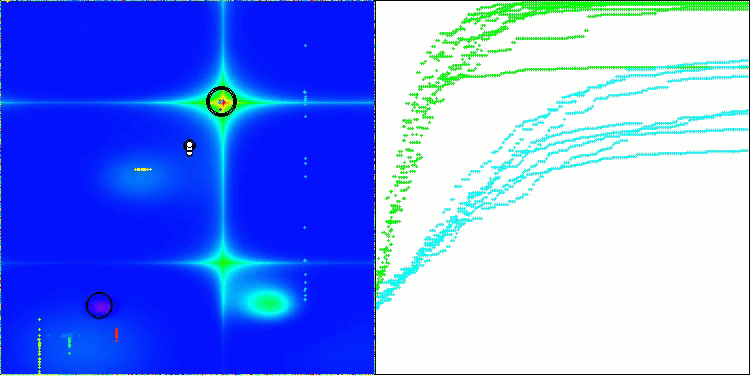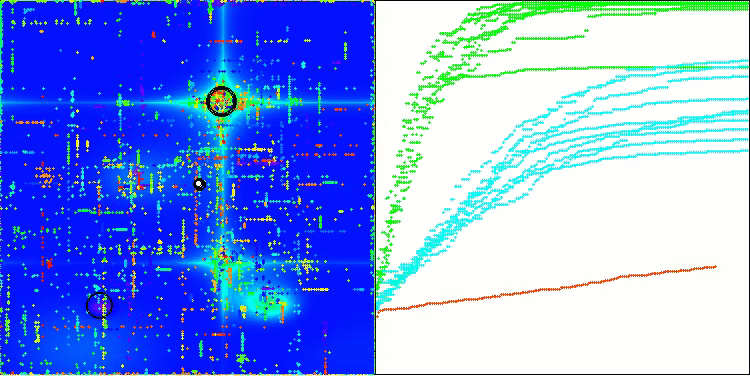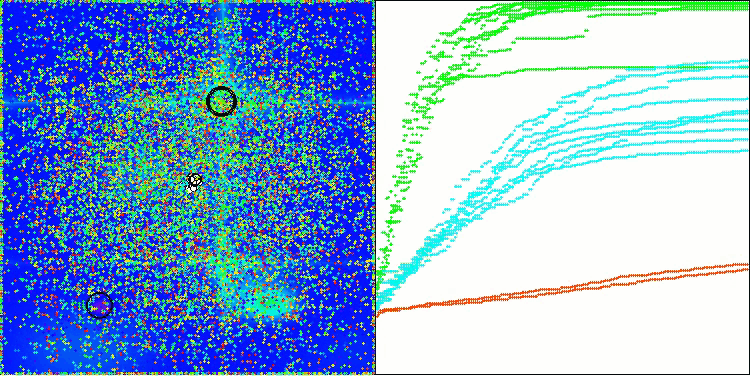
DA na função de teste Forest
DA na função de teste Megacity
De acordo com os resultados dos testes, o algoritmo DA ficou na 12ª posição da nossa tabela de classificação — um resultado bom e estável.
| № | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration ptimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | TETA | time evolution travel algorithm (joo) | 0,91362 | 0,82349 | 0,31990 | 2,05701 | 0,97096 | 0,89532 | 0,29324 | 2,15952 | 0,73462 | 0,68569 | 0,16021 | 1,58052 | 5,797 | 64,41 |
| 7 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 8 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 9 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 10 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 11 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 12 | DA | dialectical algorithm | 0,86183 | 0,70033 | 0,33724 | 1,89940 | 0,98163 | 0,72772 | 0,28718 | 1,99653 | 0,70308 | 0,45292 | 0,16367 | 1,31967 | 5,216 | 57,95 |
| 13 | BHAm | black hole algorithm M | 0,75236 | 0,76675 | 0,34583 | 1,86493 | 0,93593 | 0,80152 | 0,27177 | 2,00923 | 0,65077 | 0,51646 | 0,15472 | 1,32195 | 5,196 | 57,73 |
| 14 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 15 | AOSm | atomic orbital search M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| 16 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 17 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 18 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 19 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 20 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 21 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 22 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 23 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 24 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 25 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 26 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 27 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 28 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 29 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 30 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 31 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 32 | SOA | simple optimization algorithm | 0,91520 | 0,46976 | 0,27089 | 1,65585 | 0,89675 | 0,37401 | 0,16984 | 1,44060 | 0,69538 | 0,28031 | 0,10852 | 1,08422 | 4,181 | 46,45 |
| 33 | ABHA | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4,127 | 45,85 |
| 34 | ACMO | atmospheric cloud model optimization | 0,90321 | 0,48546 | 0,30403 | 1,69270 | 0,80268 | 0,37857 | 0,19178 | 1,37303 | 0,62308 | 0,24400 | 0,10795 | 0,97503 | 4,041 | 44,90 |
| 35 | ADAMm | adaptive moment estimation M | 0,88635 | 0,44766 | 0,26613 | 1,60014 | 0,84497 | 0,38493 | 0,16889 | 1,39880 | 0,66154 | 0,27046 | 0,10594 | 1,03794 | 4,037 | 44,85 |
| 36 | ATAm | artificial tribe algorithm M | 0,71771 | 0,55304 | 0,25235 | 1,52310 | 0,82491 | 0,55904 | 0,20473 | 1,58867 | 0,44000 | 0,18615 | 0,09411 | 0,72026 | 3,832 | 42,58 |
| 37 | ASHA | artificial showering algorithm | 0,89686 | 0,40433 | 0,25617 | 1,55737 | 0,80360 | 0,35526 | 0,19160 | 1,35046 | 0,47692 | 0,18123 | 0,09774 | 0,75589 | 3,664 | 40,71 |
| 38 | ASBO | adaptive social behavior optimization | 0,76331 | 0,49253 | 0,32619 | 1,58202 | 0,79546 | 0,40035 | 0,26097 | 1,45677 | 0,26462 | 0,17169 | 0,18200 | 0,61831 | 3,657 | 40,63 |
| 39 | MEC | mind evolutionary computation | 0,69533 | 0,53376 | 0,32661 | 1,55569 | 0,72464 | 0,33036 | 0,07198 | 1,12698 | 0,52500 | 0,22000 | 0,04198 | 0,78698 | 3,470 | 38,55 |
| 40 | IWO | invasive weed optimization | 0,72679 | 0,52256 | 0,33123 | 1,58058 | 0,70756 | 0,33955 | 0,07484 | 1,12196 | 0,42333 | 0,23067 | 0,04617 | 0,70017 | 3,403 | 37,81 |
| 41 | Micro-AIS | micro artificial immune system | 0,79547 | 0,51922 | 0,30861 | 1,62330 | 0,72956 | 0,36879 | 0,09398 | 1,19233 | 0,37667 | 0,15867 | 0,02802 | 0,56335 | 3,379 | 37,54 |
| 42 | COAm | cuckoo optimization algorithm M | 0,75820 | 0,48652 | 0,31369 | 1,55841 | 0,74054 | 0,28051 | 0,05599 | 1,07704 | 0,50500 | 0,17467 | 0,03380 | 0,71347 | 3,349 | 37,21 |
| 43 | SDOm | spiral dynamics optimization M | 0,74601 | 0,44623 | 0,29687 | 1,48912 | 0,70204 | 0,34678 | 0,10944 | 1,15826 | 0,42833 | 0,16767 | 0,03663 | 0,63263 | 3,280 | 36,44 |
| 44 | NMm | Nelder-Mead method M | 0,73807 | 0,50598 | 0,31342 | 1,55747 | 0,63674 | 0,28302 | 0,08221 | 1,00197 | 0,44667 | 0,18667 | 0,04028 | 0,67362 | 3,233 | 35,92 |
| 45 | BBBC | big bang-big crunch algorithm | 0,60531 | 0,45250 | 0,31255 | 1,37036 | 0,52323 | 0,35426 | 0,20417 | 1,08166 | 0,39769 | 0,19431 | 0,11286 | 0,70486 | 3,157 | 35,08 |
| RW | random walk | 0,48754 | 0,32159 | 0,25781 | 1,06694 | 0,37554 | 0,21944 | 0,15877 | 0,75375 | 0,27969 | 0,14917 | 0,09847 | 0,52734 | 2,348 | 26,09 | |
Considerações finais
O algoritmo dialético representa uma abordagem inovadora de otimização, fundamentada no conceito filosófico da dialética, onde a melhoria das soluções é alcançada por meio da interação entre opostos. O algoritmo combina com sucesso conceitos de busca global e local através da divisão única da população entre pensadores especulativos e práticos, o que garante um equilíbrio eficaz entre diversificação e intensificação do espaço de soluções.
A estrutura do algoritmo, composta por três etapas-chave, garante uma abordagem sistemática para a otimização. Durante a execução, os pensadores especulativos realizam uma busca ampla no espaço de soluções (ainda que, em geral, algoritmos de otimização tendam a refinar as melhores soluções em vez de “espalhá-las” pelo espaço de busca), enquanto os pensadores práticos concentram-se na otimização local de regiões promissoras. Essa divisão permite que o algoritmo explore eficientemente o espaço de soluções e evite ficar preso em ótimos locais, ainda mais considerando que, devido a um erro acidental que cometi, a lógica do algoritmo acabou se aproximando ainda mais da ideia de opostos dialéticos.
Os resultados dos testes confirmam a alta eficiência do algoritmo com capacidades de busca equilibradas, que se mantêm em bom nível em diferentes tipos de tarefas. Em comparação com outros algoritmos, o DA não apresenta desvios acentuados nem para pior nem para melhor, mantendo um desempenho estável e uniforme conforme a gradação de cores na tabela. O indicador geral de eficiência demonstra a competitividade do algoritmo em relação aos métodos de otimização existentes. Essa combinação de princípios filosóficos com métodos matemáticos forma uma ferramenta poderosa para resolver problemas complexos de otimização.
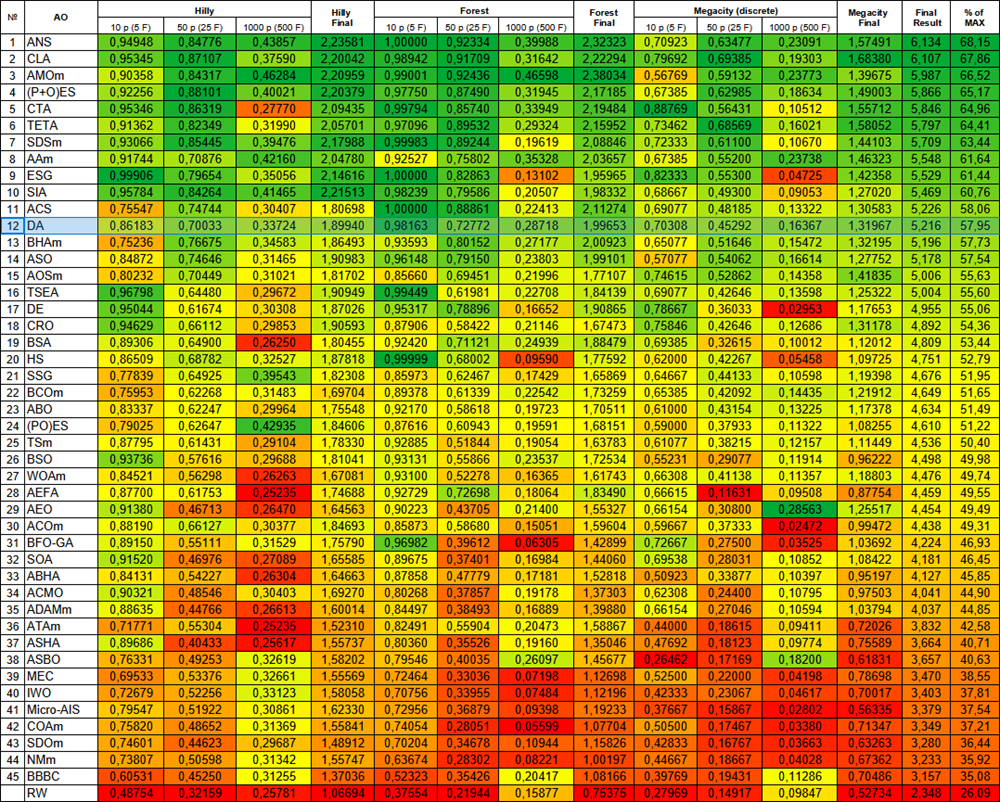
Imagem 3. Graduação de cores dos algoritmos conforme os respectivos testes
Imagem 4. Histograma dos resultados de teste dos algoritmos (em uma escala de 0 a 100, quanto maior, melhor, onde 100 é o resultado teórico máximo possível, no arquivo compactado está o script para cálculo da tabela de classificação)
Pontos positivos e negativos do algoritmo DA:
Pontos positivos:
- Poucos parâmetros externos, apenas dois além do tamanho da população.
- Implementação simples.
- Bastante rápido.
- Indicadores equilibrados e bons em tarefas de baixa e alta dimensionalidade.
Pontos negativos:
- Variação dos resultados.
Um arquivo compactado com as versões atuais dos códigos dos algoritmos está anexado ao artigo. O autor do artigo não se responsabiliza pela exatidão absoluta na descrição dos algoritmos canônicos, pois muitos deles foram modificados para melhorar as capacidades de busca. As conclusões e julgamentos apresentados nos artigos baseiam-se nos resultados dos experimentos realizados.
Programas utilizados no artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | C_AO.mqh | Arquivo incluído | Classe pai dos algoritmos populacionais de otimização |
| 2 | C_AO_enum.mqh | Arquivo incluído | Enumeração dos algoritmos populacionais de otimização |
| 3 | TestFunctions.mqh | Arquivo incluído | Biblioteca de funções de teste |
| 4 | TestStandFunctions.mqh | Arquivo incluído | Biblioteca de funções do ambiente de teste |
| 5 | Utilities.mqh | Arquivo incluído | Biblioteca de funções auxiliares |
| 6 | CalculationTestResults.mqh | Arquivo incluído | Script para cálculo dos resultados na tabela comparativa |
| 7 | Testing AOs.mq5 | Script | Ambiente de teste unificado para todos os algoritmos populacionais de otimização |
| 8 | Simple use of population optimization algorithms.mq5 | Script | Exemplo simples de uso dos algoritmos populacionais de otimização sem visualização |
| 9 | Test_AO_DA.mq5 | Script | Ambiente de teste para o DA |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/16999
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
Redes neurais em trading: Transformador hierárquico de duas torres (Hidformer)
Neurônio biológico para previsão de séries temporais financeiras
Redes neurais em trading: Transformador hierárquico com duas torres (Conclusão)
Indicador de previsão de volatilidade usando Python
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso