
Dialektische Suche (DA)
Inhalt
Einführung
Der dialektische Materialismus beruht auf dem Prinzip der Einheit und des Kampfes der Gegensätze in der Natur, der Gesellschaft und im Denken. Sie beruht auf der Vorstellung, dass Entwicklung durch den Konflikt gegensätzlicher Kräfte und Tendenzen entsteht, wobei jedes Phänomen innere Widersprüche enthält. Das Schlüsselprinzip dieses Ansatzes ist der Übergang von quantitativen zu qualitativen Veränderungen, wenn sich allmähliche Veränderungen akkumulieren und zu starken qualitativen Sprüngen führen. Die Entwicklung folgt dem Gesetz der „Negation der Negation“, bei dem die These durch die Antithese ersetzt wird, wodurch die Synthese als neue Qualität entsteht, die das Beste der vorherigen Zustände bewahrt.
In der Welt der Optimierungsalgorithmen, in der mathematische Präzision auf philosophische Weisheit trifft, hat sich eine einzigartige, vom dialektischen Materialismus inspirierte Methode entwickelt: Dialektischer Algorithmus (DA). Dieser Algorithmus, der eine Synthese aus klassischer Dialektik und modernen Optimierungsmethoden darstellt, überdenkt die Suche nach optimalen Lösungen durch das Prisma des philosophischen Gegensatzes von These und Antithese. Die Grundlage der DA ist die Idee, dass jede Lösung (These) das Potenzial für eine Verbesserung durch die Interaktion mit ihrem Gegenteil (Antithese) enthält.
In seiner algorithmischen Umsetzung spiegelt sich dieses Prinzip in der Interaktion zwischen spekulativen Denkern (thinker), die nach neuen Lösungen suchen und sich dabei vom Bekannten entfernen, und praktischen Denkern, die nach bewährten Lösungen streben, wider. Der materialistische Aspekt des dialektischen Materialismus zeigt sich darin, dass man sich auf objektive Kriterien zur Bewertung von Entscheidungen und zur praktischen Überprüfung von Ergebnissen stützt. Die Entwicklung verläuft zyklisch: Die gefundenen Lösungen führen zu neuen Widersprüchen, die zu einer neuen Runde der Suche führen und die Kontinuität des Wissens und der Verbesserung widerspiegelt.
Der Algorithmus setzt dieses Prinzip durch drei Schlüsselpunkte um: das Verstehen, bei dem die Lösungen bewertet und sortiert werden; die dialektische Interaktion, bei der die Lösungen ihre Gegensätze finden; und der Moment der Synthese, bei dem neue, verbesserte Lösungen entstehen. Die Besonderheit des Algorithmus ist die Aufteilung der Population in zwei Arten von Denkern: spekulative (k1), die den Lösungsraum in großen Schritten erkunden (durch die Interaktion von qualitativ ähnlichen, aber im Suchraum voneinander entfernten Lösungen), und praktische (p-k1), die eine lokale Suche durchführen (qualitativ entfernt, aber im Lösungsraum nahe). Diese Aufteilung spiegelt das philosophische Prinzip der Einheit und des Kampfes der Gegensätze wider, bei dem jede Gruppe ihren eigenen, einzigartigen Beitrag zur Optimierung leistet.
Die Dialektische Suche (DA) wurde 2009 von Serdar Kadioglu und Meinolf Sellmann eingeführt. Diese Methode verwendet einen dialektischen Ansatz zur Lösung von Optimierungsproblemen und setzt damit die Tradition fort, die der dialektische Materialismus bei der Untersuchung und Suche nach neuen Lösungen begründet hat.
Implementierung des Algorithmus
Der Algorithmus basiert auf einer Population von p Lösungen (in der Regel 50), von denen jede ein Vektor von Koordinaten im Suchraum ist. Diese Bevölkerung wird in zwei Gruppen unterteilt: k1 spekulative Denker (beste Lösungen) und (p-k1) praktische Denker.
Die erste Phase ist der Moment des Verstehens. Hier werden alle Entscheidungen anhand der Zielfunktion f(x) bewertet. Die Lösungen werden nach Qualität sortiert, und die besten k1-Lösungen werden zu spekulativen Denkern, während die übrigen zu praktischen Lösungen werden. In dieser Phase werden auch neue Lösungen auf der Grundlage ihrer Qualität im Vergleich zu früheren Iterationen akzeptiert oder verworfen (die beste individuelle Lösung für den Denker).
Die zweite Phase ist das dialektische Moment. In dieser Phase wird nach dem Gegenpol jeder Lösung gesucht – dem Gegenstück, mit dem die Lösung interagieren wird. Für spekulative Denker basiert die Suche nach der Antithese auf der Maximierung der Distanz bei gleichzeitiger Wahrung der Qualität der Lösung (idealistische Dialektik). Für die erste Lösung ist die Antithese die zweitbeste, für die letzte – die vorletzte, für die übrigen wird der Nachbar mit dem größten Abstand gewählt. Praktische Denker suchen die Antithese, indem sie den Abstand mit einem ausreichenden Qualitätsunterschied minimieren (materialistische Dialektik).
Die dritte Stufe ist der spekulativ-praktische Moment (Moment der Erneuerung). Hier werden die Positionen aller Lösungen anhand der gefundenen Antithesen aktualisiert. Spekulative Denker verwenden eine Gleichverteilung, die eine breite Suche im Lösungsraum ermöglicht. Praktische Denker verwenden die Normalverteilung. Meine Experimente haben gezeigt, dass für beide Arten von Denkern eine gleichmäßige Verteilung am besten funktioniert.
Die Gleichung für die Aktualisierung der Positionen ist für alle dieselbe: X(i) = X(i) + μ⊙(Xanti(i) – X(i)), wobei μ ein Zufallsvektor aus der entsprechenden Verteilung ist, ⊙ bedeutet elementweise Multiplikation. Dies gewährleistet ein Gleichgewicht zwischen der Erkundung des Lösungsraums durch spekulative Denker und der Verfeinerung der gefundenen Lösungen durch praktische Denker.
Der Dialektische Algorithmus (DA) hat Ähnlichkeiten mit dem Algorithmus der Differentiellen Evolution (DE) in der Gleichung zur Aktualisierung der Lösung. Bei DE wird ein neuer Vektor erzeugt, indem die skalierte Differenz zweier anderer Vektoren zum Zielvektor addiert wird (x_neu = x_Ziel + F(x_r1 – x_r2)), während DA ein ähnliches Prinzip verwendet, jedoch mit einer Antithese und einem adaptiven Verhältnis (x_neu = x + μ(x_anti – x)).
Der entscheidende Unterschied liegt jedoch in der Art und Weise, wie die Vektoren ausgewählt werden, um neue Lösungen zu generieren. DE beruht auf einer zufälligen Auswahl von Differenzvektoren, wodurch der stochastische Charakter der Suche gewährleistet wird. DA hingegen verwendet einen deterministischen Ansatz zur Auswahl von Antithesen auf der Grundlage des Abstands zwischen den Lösungen und ihrer Qualität, wobei die Bevölkerung in spekulative und praktische Denker mit unterschiedlichen Suchstrategien unterteilt wird. Der DA-Algorithmus weist eine etwas höhere Rechenkomplexität auf (Berechnung des euklidischen Abstands), aber DA zeigt eine höhere Effizienz bei verschiedenen Optimierungsproblemen.
Abbildung 1 zeigt das Prinzip der Auswahl von Antithesen für spekulative (rot, am besten) und materielle (blau) Thesen. Die spekulativen wählen Antithesen, die qualitativ benachbart, aber im Suchraum weiter entfernt sind, während die materiellen Antithesen im Gegensatz dazu Antithesen wählen, die qualitativ weiter entfernt, aber im Suchraum nahe sind.
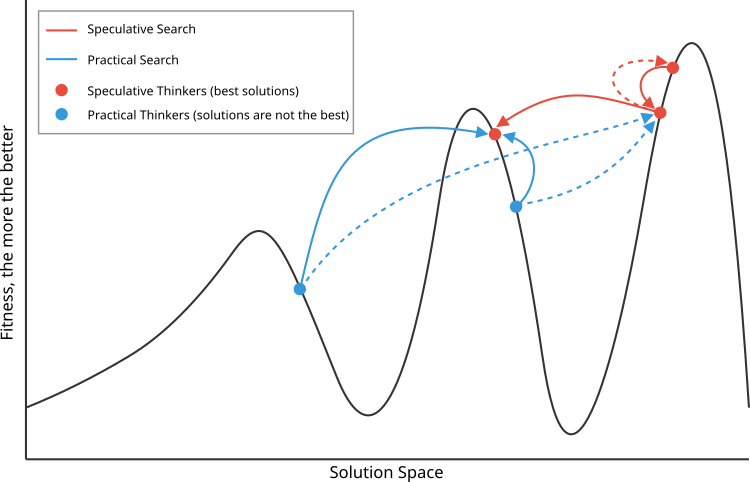
Abbildung 1. Schematische Darstellung des Funktionsprinzips des DA-Algorithmus. Durchgehende Linien – Interaktion mit bevorzugten Antithesen, im Gegensatz zu weniger bevorzugten Antithesen, die durch gestrichelte Linien angezeigt werden
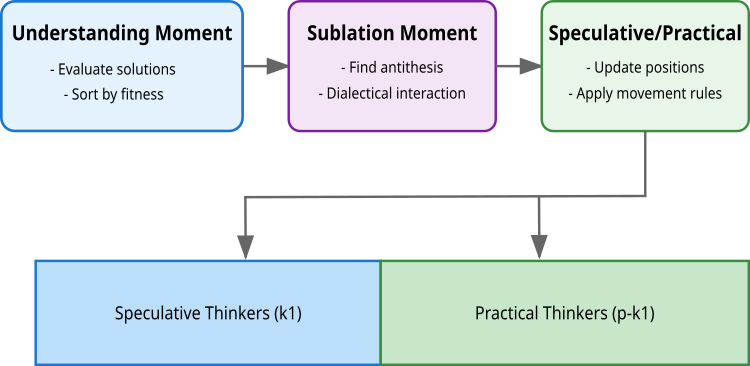
Abbildung 2. Stufen der Logik des DA-Algorithmus
Gehen wir nun dazu über, den Pseudocode des Algorithmus zu schreiben:
Bei der ersten Iteration: Platziere Agenten nach dem Zufallsprinzip: position[i] = random(min, max);
Sortiere die Population nach den besten individuellen Lösungen;
Erstelle eine Population von drei Arten von Agenten:
- Bester Denker (1 Agent),
- Spekulative Denker (k1 = 3 Agenten),
- Praktische Denker (der Rest der 50 Agenten).
A. Der beste Denker bewegt sich auf den zweitbesten zu:
position[0] = best[0] + rand(0,1) * (position[1] - position[0])B. Spekulative Denker:
- Finde die am weitesten entfernten Nachbarn mit Hilfe des euklidischen Abstands:
- Aktualisiere die Position relativ zur weitesten Entfernung:
C. Praktische Denker:
- Wähle zwei spekulative Denker nach dem Zufallsprinzip
- Gehe zum Nächstgelegenen:
position[i] = best[i] + rand(0,1) * (position[nearest] - position[i])
Nach jeder Bewegung:- Aktualisiere die besten persönlichen Lösungen
- Aktualisiere die beste globale Lösung
- Sortiere die Agenten nach der Qualität der persönlichen Entscheidungen
Der Vorgang wird so lange wiederholt, bis das Abbruchkriterium erreicht ist.
Nach einer vollständigen Analyse des Algorithmus gehen wir zur Implementierung in Code über. Schreiben wir die Klasse C_AO_DA des dialektischen Optimierungsalgorithmus, die die Funktionalität von der Basisklasse C_AO erbt.
Parameter des Algorithmus:
- Populationsgröße – Die Antithesen bestimmen die Anzahl der Agenten, die an der Optimierung teilnehmen.
- Spekulative Denker weisen auf die Anzahl besserer Agenten hin, die in der Lage sind, freier nach Lösungen zu suchen.
- Nachbarn für die Analyse bestimmen die Anzahl der nächsten Nachbarn, mit denen jeder spekulative Denker (Agent) interagieren wird, um Informationen auszutauschen und seine Strategie zu verbessern.
Methoden:
- C_AO_DA () – der Konstruktor initialisiert die Hauptparameter und erstellt ein Array, um sie zu speichern.
- SetParams () – das Setzen von Parametern ermöglicht die Aktualisierung der Werte der Algorithmusparameter während des Betriebs.
- Moving () und Revision () – Funktionen zum Verschieben von Agenten im Suchraum und zum Überarbeiten der gefundenen Lösungen.
- EuklidischerAbstand () – berechnet den Abstand im Suchraum zwischen zwei Vektoren, der für die Auswahl der engsten (für spekulative) und weitesten (für praktische) Ähnlichkeit der von den Agenten gefundenen Lösungen erforderlich ist.
//—————————————————————————————————————————————————————————————————————————————— // Class implementing the dialectical optimization algorithm class C_AO_DA : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_DA () { } C_AO_DA () { ao_name = "DA"; ao_desc = "Dialectical Algorithm"; ao_link = "https://www.mql5.com/en/articles/16999"; popSize = 50; // population size k1 = 3; // speculative thinkers k2 = 10; // neighbours ArrayResize (params, 3); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "k1"; params [1].val = k1; params [2].name = "k2"; params [2].val = k2; } // Setting algorithm parameters void SetParams () { popSize = (int)params [0].val; k1 = (int)params [1].val; k2 = (int)params [2].val; } bool Init (const double &rangeMinP [], // minimum search range const double &rangeMaxP [], // maximum search range const double &rangeStepP [], // search step const int epochsP = 0); // number of epochs void Moving (); // Moving agents in the search space void Revision (); // Review and update the best solutions found //---------------------------------------------------------------------------- int k1; // number of speculative thinkers int k2; // number of neighbors to analyze private: //------------------------------------------------------------------- // Calculate the Euclidean distance between two vectors double EuclideanDistance (const double &vec1 [], const double &vec2 [], const int dim) { double sum = 0; double diff = 0.0; for (int i = 0; i < dim; i++) { diff = vec1 [i] - vec2 [i]; sum += diff * diff; } return MathSqrt (sum); } }; //——————————————————————————————————————————————————————————————————————————————
Die Methode Init der Klasse C_AO_DA dient der Initialisierung der Parameter des Optimierungsalgorithmus. Sie akzeptiert Arrays von minimalen und maximalen Suchbereichswerten, Suchschritten und optional die Anzahl der Epochen zur Durchführung der Optimierung. Die Methode führt zunächst die Standardinitialisierung der Parameter durch; schlägt diese fehl, gibt sie „false“ zurück. Ist die Initialisierung erfolgreich, gibt die Methode „true“ zurück und bestätigt damit, dass der Algorithmus einsatzbereit ist.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_DA::Init (const double &rangeMinP [], // minimum search range const double &rangeMaxP [], // maximum search range const double &rangeStepP [], // search step const int epochsP = 0) // number of epochs { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- return true; } //——————————————————————————————————————————————————————————————————————————————
Die Methode Moving ist eine Implementierung der Agentenbewegung im Suchraum. Im Folgenden wird die Funktionsweise der Methode ausführlich beschrieben:
Initialisierung:
- Zu Beginn (!revision) werden die Anfangspositionen der Agenten nach dem Zufallsprinzip festgelegt, wobei die vorgegebenen minimalen und maximalen Grenzwerte für jede Koordinate verwendet werden. Jeder Agent „a[i]“ erhält zufällige Koordinaten in bestimmten Bereichen und mit einer bestimmten Schrittweite.
- Nach der Initialisierung wird „revision“ auf „true“ gesetzt, was eine Neuinitialisierung bei zukünftigen Aufrufen der Methode Moving verhindert.
Aktualisieren der Position des besten Denkers:
- Der beste Denker (Agent) aktualisiert seine Koordinaten auf der Grundlage seiner vorherigen besten Position und einer Zufallswahrscheinlichkeit, wobei er seinen nächsten Nachbarn „a[1]“ für die Aktualisierung verwendet.
Aktualisierung der Positionen der spekulativen Denker:
- Für jeden spekulativen Denker (Agent) im Bereich von „k2“ bis „k1“ sucht die Methode nach dem am weitesten entfernten vorherigen (antiPrevIND) und nächsten Nachbarn (antiNextIND).
- Die Koordinate des spekulativen Denkers wird dann anhand des am weitesten entfernten Nachbarn aktualisiert, wenn er die Antithese betrachtet.
Aktualisieren der Positionen der praktischen Denker:
- Praktische Denker (Agenten) reichen von „k1“ bis „popSize“.
- Der Code wählt zufällig zwei spekulative Denker aus und berechnet die Entfernungen zu ihnen. Der praktische Denker wählt dann den nächstgelegenen (der beiden gewählten) Denker aus, um seine Position zu aktualisieren.
- Jede Koordinate wird auf der Grundlage des ausgewählten Nachbarn aktualisiert.
Hilfsfunktionen
- EuclideanDistance – Funktion, die den euklidischen Abstand zwischen zwei Punkten „a“ und „b“ in einem mehrdimensionalen Raum berechnet.
- u.RNDfromCI – gibt eine Zufallszahl aus dem angegebenen Intervall zurück.
- u.SeInDiSp – konvertiert „value“ in die entsprechende Stufe je nach Bereich.
- u.RNDprobab – liefert eine Zufallszahl mit gleichmäßiger Wahrscheinlichkeitsverteilung.
//—————————————————————————————————————————————————————————————————————————————— // Implement agent movement in the search space void C_AO_DA::Moving () { //---------------------------------------------------------------------------- // Initialize the agents' positions randomly if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- // Update the best thinker's position for (int c = 0; c < coords; c++) { a [0].c [c] = a [0].cB [c] + u.RNDprobab () * (a [1].c [c] - a [0].c [c]); a [0].c [c] = u.SeInDiSp (a [0].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } //---------------------------------------------------------------------------- double dist_next = -DBL_MAX; // maximum distance to the next neighbor double dist_prev = -DBL_MAX; // maximum distance to the previous neighbor double dist = 0.0; // current distance int antiNextIND = 0; // index of the most distant next neighbor int antiPrevIND = 0; // index of the most distant previous neighbor int antiIND = 0; // selected index to update position // Update the positions of speculative thinkers ------------------------------- for (int i = k2; i < k1; i++) { // Find the most distant previous neighbor for (int j = 1; j <= k2; j++) { dist = EuclideanDistance (a [i].cB, a [i - j].cB, coords); if (dist > dist_prev) { dist_prev = dist; antiPrevIND = i - j; } } // Find the farthest next neighbor for (int j = 1; j <= k2; j++) { dist = EuclideanDistance (a [i].cB, a [i + j].cB, coords); if (dist > dist_next) { dist_next = dist; antiNextIND = i + j; } } // Select the most distant neighbor to update position if (dist_prev > dist_next) antiIND = antiPrevIND; else antiIND = antiNextIND; // Update the speculative thinker's coordinates for (int c = 0; c < coords; c++) { a [i].c [c] = a [i].cB [c] + u.RNDbool () * (a [antiIND].c [c] - a [i].c [c]); //a [i].c [c] = a [i].cB [c] + u.RNDprobab () * (a [antiIND].c [c] - a [i].c [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } // Update the positions of practical thinkers -------------------------------- for (int i = k1; i < popSize; i++) { // Random selection of two speculative thinkers antiNextIND = u.RNDintInRange (0, k1 - 1); antiPrevIND = u.RNDintInRange (0, k1 - 1); if (antiNextIND == antiPrevIND) antiNextIND = antiPrevIND + 1; // Calculate distances to selected thinkers dist_next = EuclideanDistance (a [i].cB, a [antiNextIND].cB, coords); dist_prev = EuclideanDistance (a [i].cB, a [antiPrevIND].cB, coords); // Select the closest thinker to update the position if (dist_prev < dist_next) antiIND = antiPrevIND; else antiIND = antiNextIND; // Update the coordinates of the practical thinker for (int c = 0; c < coords; c++) { a [i].c [c] = a [i].cB [c] + u.RNDprobab () * (a [antiIND].c [c] - a [i].c [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Die Revisionsmethode ist für die Überarbeitung und Aktualisierung der für die Agenten gefundenen besten Lösungen zuständig. Im Folgenden wird die Funktionsweise dieser Methode eingehend analysiert:
Aktualisierung der gefundenen besten Lösungen: In der „for“-Schleife durchläuft die Methode jeden Agenten der Population. Für jeden Agenten wird der aktuelle Wert der Fitnessfunktion „a [i].f“ verglichen:
- Globale beste Lösung – wenn der Wert der Funktion f des Agenten größer ist als die aktuelle globale beste Lösung fB, dann wird die globale Lösung aktualisiert und der Index des Agenten (ind), der diese beste Lösung gefunden hat, wird gespeichert.
- Persönlich beste Entscheidung – auch hier wird der f-Wert jedes Agenten mit seinem persönlich besten fB-Wert verglichen. Wenn der aktuelle Wert besser ist, wird der persönliche Bestwert des Agenten aktualisiert und seine aktuellen c-Koordinaten werden in seine persönlichen cB-Koordinaten kopiert.
Aktualisierung der Koordinaten der besten globalen Lösung: Wenn der Index eines Agenten, der die beste globale Lösung wurde (ind != -1), gefunden wurde, werden die Koordinaten dieses Agenten in die globalen Koordinaten von cB kopiert.
Sortierende Agenten: Am Ende der Methode wird das Array aT erstellt und seine Größe an die Größe der Population angepasst. Dann wird die Funktion u.Sorting_fB aufgerufen, die die Agenten nach ihren besten gefundenen Lösungen (fB-Werten) sortiert.
//—————————————————————————————————————————————————————————————————————————————— // Review and update the best solutions found void C_AO_DA::Revision () { int ind = -1; // Update the best solutions found for each agent for (int i = 0; i < popSize; i++) { // Update the global best solution if (a [i].f > fB) { fB = a [i].f; ind = i; } // Update the agent's personal best solution if (a [i].f > a [i].fB) { a [i].fB = a [i].f; ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY); } } // Update the global best solution coordinates if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); // Sort agents by their best found solutions static S_AO_Agent aT []; ArrayResize (aT, popSize); u.Sorting_fB (a, aT, popSize); } //——————————————————————————————————————————————————————————————————————————————
Testergebnisse
Es ist an der Zeit, sich mit den Ergebnissen der DA-Prüfung vertraut zu machen. Schauen wir uns noch einmal die Methode „Moving“ an. Der Text, der die Vision der Autoren widerspiegelt, ist auskommentiert und grün hervorgehoben. Die Ergebnisse lauten also wie folgt:
=============================
5 Hilly's; Func runs: 10000; result: 0.749254786734898
25 Hilly's; Func runs: 10000; result: 0.36669693350810206
500 Hilly's; Func runs: 10000; result: 0.2532075139007539
=============================
5 Forest's; Func runs: 10000; result: 0.7626421292861323
25 Forest's; Func runs: 10000; result: 0.4144802592253075
500 Forest's; Func runs: 10000; result: 0.2006796312431603
=============================
5 Megacity's; Func runs: 10000; result: 0.36
25 Megacity's; Func runs: 10000; result: 0.15969230769230774
500 Megacity's; Func runs: 10000; result: 0.0952000000000008
=============================
All score: 3.36185 (37.35%)
Diese Ergebnisse sind bei weitem nicht die besten, aber sie hätten es in die Rangliste schaffen können. Aber die Sache ist die, dass ich einen Fehler gemacht habe und anstatt Zufallszahlen im Bereich [0.0;1.0] zu verwenden, habe ich eine zufällige boolesche Zahlenfunktion in den Code eingefügt (in rot markiert).
Das Wesen einer zufälligen Änderung in der Logik ist folgendes: Mit einer Wahrscheinlichkeit von 50 % bleibt die entsprechende Koordinate gleich oder sie wird durch die Koordinate der Antithese ersetzt. Dies entspricht meines Erachtens noch mehr der Vorstellung der Autoren vom Gegensatz von Thesen und Antithesen. Bei den praktischen Denkern bleibt alles beim Alten; ihre abschließenden Thesen sind eine Symbiose zwischen der aktuellen These und der von den spekulativen Denkern übernommenen Antithese. Durch einen glücklichen Zufall wurden die folgenden Ergebnisse erzielt:
DA|Dialectical Algorithm|50.0|40.0|1.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.8618313952293774
25 Hilly's; Func runs: 10000; result: 0.700333708747176
500 Hilly's; Func runs: 10000; result: 0.3372386732170054
=============================
5 Forest's; Func runs: 10000; result: 0.9816317765399738
25 Forest's; Func runs: 10000; result: 0.7277214130784131
500 Forest's; Func runs: 10000; result: 0.28717629901518305
=============================
5 Megacity's; Func runs: 10000; result: 0.7030769230769229
25 Megacity's; Func runs: 10000; result: 0.4529230769230769
500 Megacity's; Func runs: 10000; result: 0.16366923076923204
=============================
All score: 5.21560 (57.95%)
Das sind wirklich beeindruckende Ergebnisse! Da eine so deutliche Leistungsverbesserung unbewusst erfolgte, kann ich der geänderten Version nicht den Index m zuordnen. In unserer Rangliste bleibt der Algorithmus als DA erhalten. Der dialektische Algorithmus zeigt also eine hervorragende Leistung und erreicht eine Gesamteffizienz von 57,95 %. Ein wesentliches Merkmal des Algorithmus ist seine Fähigkeit, dank der Aufteilung in spekulative und praktische Denker ein effektives Gleichgewicht zwischen globaler und lokaler Suche herzustellen.
Aus der Visualisierung ist ersichtlich, dass der Algorithmus recht schnell signifikante lokale Optima findet, obwohl er nicht die Konvergenzgenauigkeit besitzt, um als perfekt zu gelten. Die Ergebnisse sind jedoch in jedem Fall recht ordentlich.
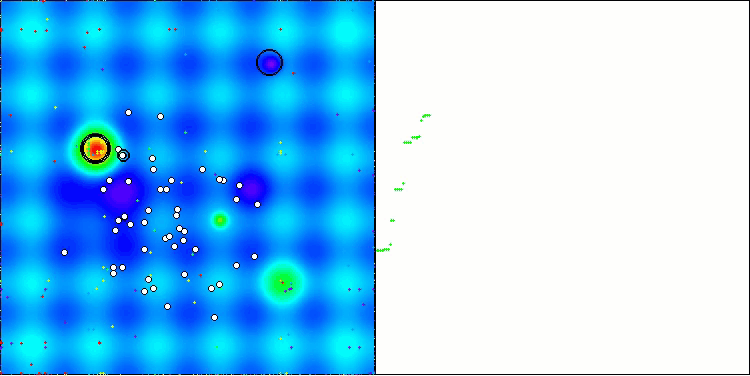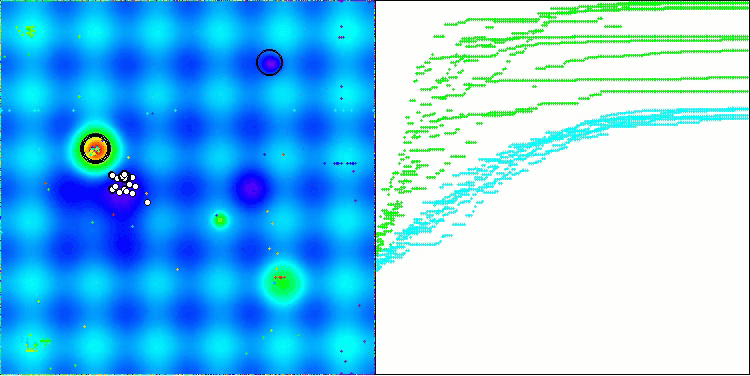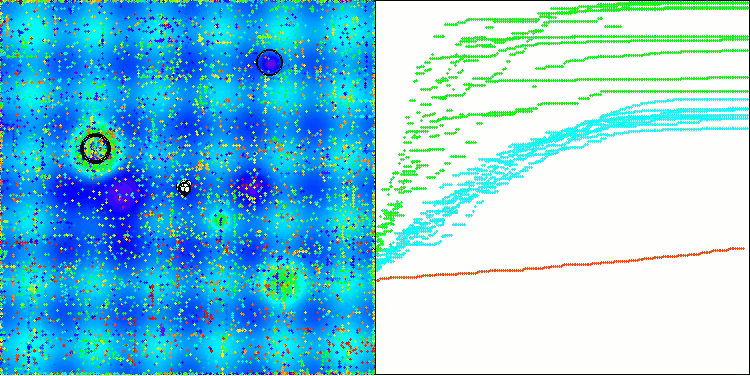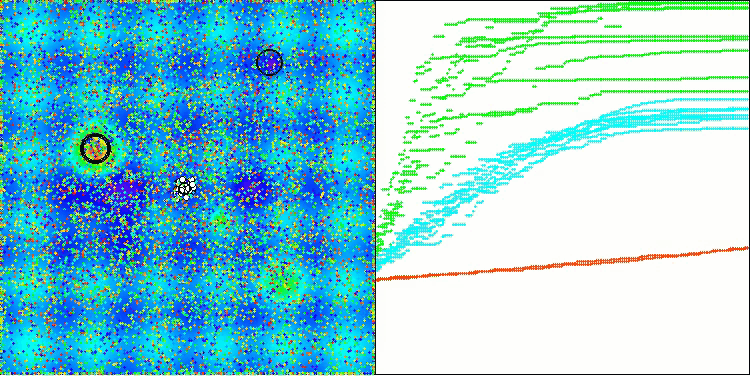
DA mit der Testfunktion Hilly
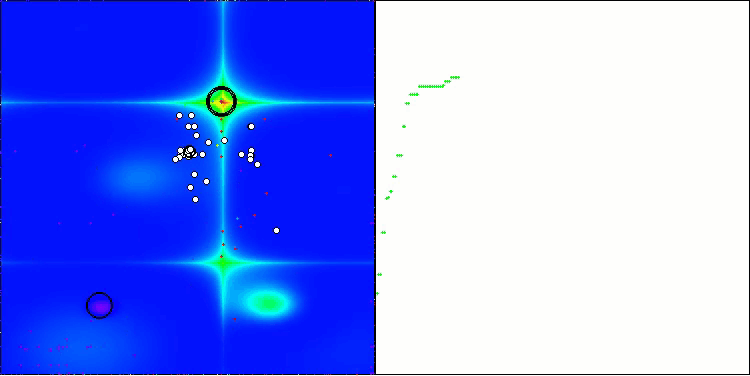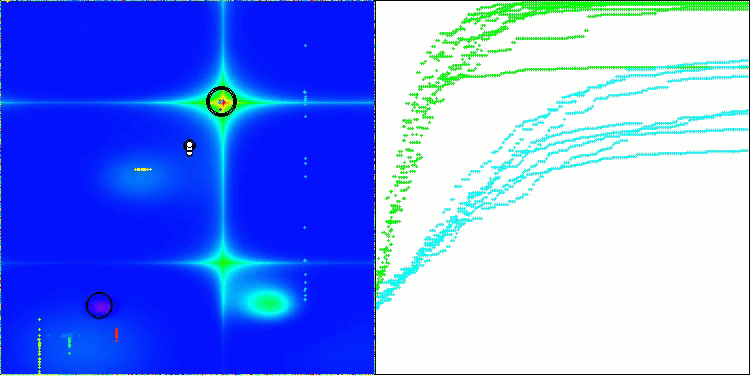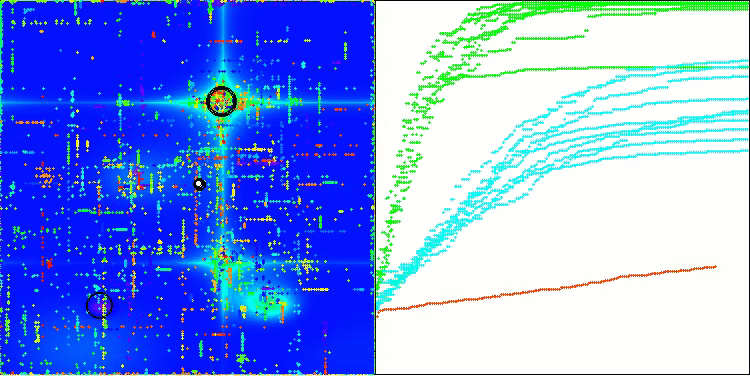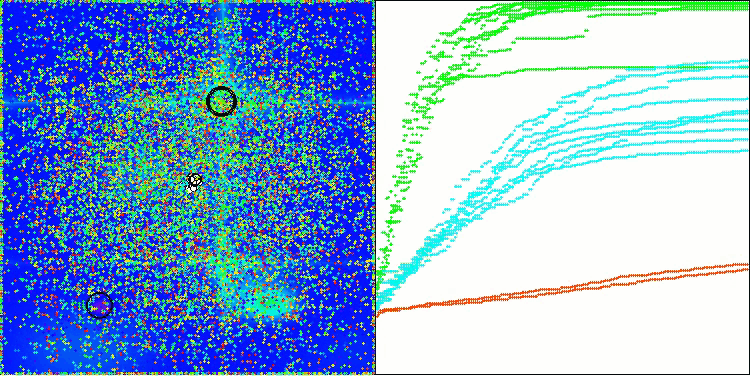
DA mit der Testfunktion Forest

DA mit der Testfunktion Megacity
Der DA-Algorithmus rangiert den Testergebnissen zufolge in unserer Tabelle auf Platz 12, was ein gutes und stabiles Ergebnis darstellt.
| # | AO | Beschreibung | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | Suche über die gesamte Nachbarschaft | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | Code-Sperr-Algorithmus (joo) | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | AMOm | Optimierung der Tiermigration M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5.987 | 66,52 |
| 4 | (P+O)ES | (P+O) Entwicklungsstrategien | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 5 | CTA | Kometenschweif-Algorithmus (joo) | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 6 | TETA | Zeit-Evolutions-Reise-Algorithmus (Joo) | 0.91362 | 0.82349 | 0.31990 | 2.05701 | 0.97096 | 0.89532 | 0.29324 | 2.15952 | 0.73462 | 0.68569 | 0.16021 | 1.58052 | 5.797 | 64.41 |
| 7 | SDSm | stochastische Diffusionssuche M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 8 | AAm | Algorithmus für das Bogenschießen M | 0.91744 | 0.70876 | 0.42160 | 2.04780 | 0.92527 | 0.75802 | 0.35328 | 2.03657 | 0.67385 | 0.55200 | 0.23738 | 1.46323 | 5.548 | 61.64 |
| 9 | ESG | Entwicklung sozialer Gruppen (joo) | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 10 | SIA | Simuliertes isotropes Glühen (Joo) | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 11 | ACS | künstliche, kooperative Suche | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 12 | DA | dialektischer Algorithmus | 0.86183 | 0.70033 | 0.33724 | 1.89940 | 0.98163 | 0.72772 | 0.28718 | 1.99653 | 0.70308 | 0.45292 | 0.16367 | 1.31967 | 5.216 | 57.95 |
| 13 | BHAm | Algorithmus für schwarze Löcher M | 0.75236 | 0.76675 | 0.34583 | 1.86493 | 0.93593 | 0.80152 | 0.27177 | 2.00923 | 0.65077 | 0.51646 | 0.15472 | 1.32195 | 5.196 | 57.73 |
| 14 | ASO | Anarchische Gesellschaftsoptimierung | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5.178 | 57,54 |
| 15 | AOSm | Suche nach atomaren Orbitalen M | 0.80232 | 0.70449 | 0.31021 | 1.81702 | 0.85660 | 0.69451 | 0.21996 | 1.77107 | 0.74615 | 0.52862 | 0.14358 | 1.41835 | 5.006 | 55.63 |
| 16 | TSEA | Schildkrötenpanzer-Evolutionsalgorithmus (joo) | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 17 | DE | differentielle Evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 18 | CRO | Optimierung chemischer Reaktionen | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 19 | BSA | Vogelschwarm-Algorithmus | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 20 | HS | Harmoniesuche | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 21 | SSG | Setzen, Säen und Wachsen | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 22 | BCOm | Optimierung mit der bakteriellen Chemotaxis M | 0.75953 | 0.62268 | 0.31483 | 1.69704 | 0.89378 | 0.61339 | 0.22542 | 1.73259 | 0.65385 | 0.42092 | 0.14435 | 1.21912 | 4.649 | 51.65 |
| 23 | ABO | Optimierung des afrikanischen Büffels | 0.83337 | 0.62247 | 0.29964 | 1.75548 | 0.92170 | 0.58618 | 0.19723 | 1.70511 | 0.61000 | 0.43154 | 0.13225 | 1.17378 | 4.634 | 51.49 |
| 24 | (PO)ES | (PO) Entwicklungsstrategien | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 25 | TSm | Tabu-Suche M | 0.87795 | 0.61431 | 0.29104 | 1.78330 | 0.92885 | 0.51844 | 0.19054 | 1.63783 | 0.61077 | 0.38215 | 0.12157 | 1.11449 | 4.536 | 50.40 |
| 26 | BSO | Brainstorming-Optimierung | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 27 | WOAm | Wal-Optimierungsalgorithmus M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 28 | AEFA | Algorithmus für künstliche elektrische Felder | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 29 | AEO | Algorithmus zur Optimierung auf der Grundlage künstlicher Ökosysteme | 0.91380 | 0.46713 | 0.26470 | 1.64563 | 0.90223 | 0.43705 | 0.21400 | 1.55327 | 0.66154 | 0.30800 | 0.28563 | 1.25517 | 4.454 | 49.49 |
| 30 | ACOm | Ameisen-Kolonie-Optimierung M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 31 | BFO-GA | Optimierung der bakteriellen Futtersuche — ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 32 | SOA | einfacher Optimierungsalgorithmus | 0.91520 | 0.46976 | 0.27089 | 1.65585 | 0.89675 | 0.37401 | 0.16984 | 1.44060 | 0.69538 | 0.28031 | 0.10852 | 1.08422 | 4.181 | 46.45 |
| 33 | ABHA | Algorithmus für künstliche Bienenstöcke | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 34 | ACMO | Optimierung atmosphärischer Wolkenmodelle | 0.90321 | 0.48546 | 0.30403 | 1.69270 | 0.80268 | 0.37857 | 0.19178 | 1.37303 | 0.62308 | 0.24400 | 0.10795 | 0.97503 | 4.041 | 44.90 |
| 35 | ADAMm | adaptive Momentabschätzung M | 0.88635 | 0.44766 | 0.26613 | 1.60014 | 0.84497 | 0.38493 | 0.16889 | 1.39880 | 0.66154 | 0.27046 | 0.10594 | 1.03794 | 4.037 | 44.85 |
| 36 | ATAm | Algorithmus für künstliche Stämme M | 0.71771 | 0.55304 | 0.25235 | 1.52310 | 0.82491 | 0.55904 | 0.20473 | 1.58867 | 0.44000 | 0.18615 | 0.09411 | 0.72026 | 3.832 | 42.58 |
| 37 | ASHA | Algorithmus für künstliches Duschen | 0.89686 | 0.40433 | 0.25617 | 1.55737 | 0.80360 | 0.35526 | 0.19160 | 1.35046 | 0.47692 | 0.18123 | 0.09774 | 0.75589 | 3.664 | 40.71 |
| 38 | ASBO | Optimierung des adaptiven Sozialverhaltens | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 39 | MEC | Evolutionäre Berechnung des Geistes | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 40 | IWO | Optimierung mit invasiven Unkräutern | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 41 | Micro-AIS | Künstliches Mikro-Immunsystem | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 42 | COAm | Kuckuck-Optimierungsalgorithmus M | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 43 | SDOm | Optimierung der Spiraldynamik M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| 44 | NMm | Nelder-Mead-Verfahren M | 0.73807 | 0.50598 | 0.31342 | 1.55747 | 0.63674 | 0.28302 | 0.08221 | 1.00197 | 0.44667 | 0.18667 | 0.04028 | 0.67362 | 3.233 | 35.92 |
| 45 | BBBC | Big-Bang-Big-Crunch-Algorithmus | 0.60531 | 0.45250 | 0.31255 | 1.37036 | 0.52323 | 0.35426 | 0.20417 | 1.08166 | 0.39769 | 0.19431 | 0.11286 | 0.70486 | 3.157 | 35.08 |
| RW | Random Walk | 0.48754 | 0.32159 | 0.25781 | 1.06694 | 0.37554 | 0.21944 | 0.15877 | 0.75375 | 0.27969 | 0.14917 | 0.09847 | 0.52734 | 2.348 | 26.09 | |
Zusammenfassung
Der dialektische Algorithmus ist ein innovativer Optimierungsansatz, der auf dem philosophischen Konzept der Dialektik basiert, bei dem die Interaktion von Gegensätzen zu besseren Lösungen führt. Der Algorithmus kombiniert erfolgreich die Konzepte der globalen und lokalen Suche durch eine einzigartige Aufteilung der Population in spekulative und praktische Denker, die ein effektives Gleichgewicht zwischen Erkundung und Ausbeutung des Lösungsraums gewährleistet.
Die Struktur des Algorithmus, die aus drei Schlüsselschritten besteht, bietet einen systematischen Ansatz zur Optimierung. Spekulative Denker führen eine breite Suche im Lösungsraum durch (obwohl bei Optimierungsalgorithmen in der Regel die besten Lösungen eher verfeinert als über den Suchraum „verstreut“ werden), während praktische Denker sich auf die lokale Optimierung vielversprechender Bereiche konzentrieren. Diese Aufteilung ermöglicht es dem Algorithmus, den Lösungsraum effektiv zu erkunden und zu vermeiden, dass er in lokalen Optima stecken bleibt, zumal die Logik des Algorithmus durch den zufälligen Fehler, den ich gemacht habe, noch näher an das Thema der dialektischen Gegensätze herangeführt wurde.
Die Testergebnisse bestätigen die hohe Effizienz des Algorithmus mit ausgewogenen Suchfähigkeiten, die ein ausreichend hohes Leistungsniveau bei verschiedenen Aufgabentypen bieten. Im Vergleich zu anderen Algorithmen weist DA keine starken Abweichungen zum Schlechteren oder Besseren auf und zeigt ein gleichmäßig stabiles Ergebnis für die Farbabstufung in der Tabelle. Der Gesamtleistungsindikator zeigt die Wettbewerbsfähigkeit des Algorithmus im Vergleich zu bestehenden Optimierungsmethoden. Diese Kombination aus philosophischen Prinzipien und mathematischen Methoden schafft ein leistungsfähiges Werkzeug zur Lösung komplexer Optimierungsprobleme.
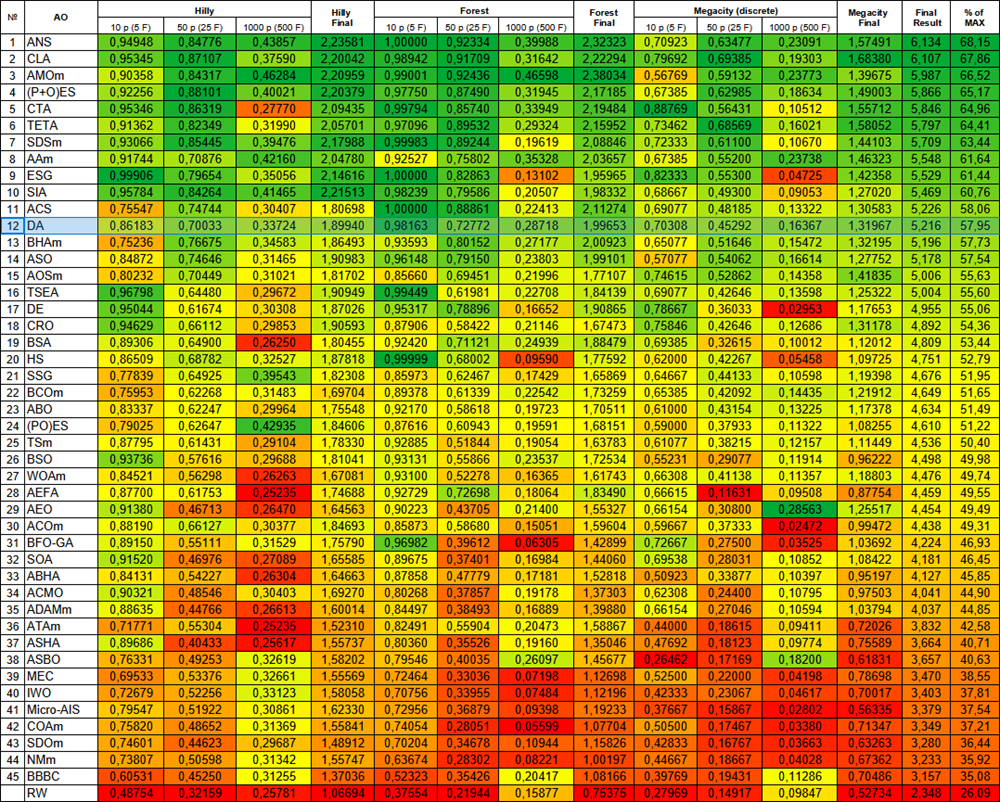
Abbildung 3. Farbabstufung der Algorithmen nach den entsprechenden Tests

Abbildung 4. Histogramm der Algorithmus-Testergebnisse (Skala von 0 bis 100, je höher, desto besser, wobei 100 das maximal mögliche theoretische Ergebnis ist; im Archiv befindet sich ein Skript zur Berechnung der Bewertungstabelle)
DA Pro und Kontra:
Vorteile:
- Es gibt nur wenige externe Parameter, nur zwei, wenn man die Bevölkerungsgröße nicht mitzählt.
- Einfache Umsetzung.
- Ziemlich schnell.
- Ausgewogene, gute Leistung sowohl bei kleinen als auch bei großen Problemen.
Nachteile:
- Verstreute Ergebnisse.
Der Artikel wird von einem Archiv mit den aktuellen Versionen der Codes der Algorithmen begleitet. Der Autor des Artikels übernimmt keine Verantwortung für die absolute Richtigkeit der Beschreibung der kanonischen Algorithmen. An vielen von ihnen wurden Änderungen vorgenommen, um die Suchmöglichkeiten zu verbessern. Die in den Artikeln dargelegten Schlussfolgerungen und Urteile beruhen auf den Ergebnissen der Versuche.
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | #C_AO.mqh | Include | Übergeordnete Klasse von Populationsoptimierungsalgorithmen |
| 2 | #C_AO_enum.mqh | Include | Enumeration der Algorithmen zur Populationsoptimierung |
| 3 | TestFunctions.mqh | Include | Bibliothek mit Testfunktionen |
| 4 | TestStandFunctions.mqh | Include | Bibliothek mit Funktionen für den Prüfstand |
| 5 | Utilities.mqh | Include | Bibliothek mit Hilfsfunktionen |
| 6 | CalculationTestResults.mqh | Include | Skript zur Berechnung der Ergebnisse in der Vergleichstabelle |
| 7 | Testing AOs.mq5 | Skript | Der einheitliche Prüfstand für alle Algorithmen zur Populationsoptimierung |
| 8 | Simple use of population optimization algorithms.mq5 | Skript | Ein einfaches Beispiel für die Verwendung von Algorithmen zur Populationsoptimierung ohne Visualisierung |
| 9 | Test_AO_DA.mq5 | Skript | DA-Prüfstand |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/16999
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Die Übertragung der Trading-Signale in einem universalen Expert Advisor.
Die Übertragung der Trading-Signale in einem universalen Expert Advisor.
 Neuronale Netze im Handel: Ein Multi-Agenten-System mit konzeptioneller Verstärkung (letzter Teil)
Neuronale Netze im Handel: Ein Multi-Agenten-System mit konzeptioneller Verstärkung (letzter Teil)
 Eine alternative Log-datei mit der Verwendung der HTML und CSS
Eine alternative Log-datei mit der Verwendung der HTML und CSS
 Marktsimulation (Teil 06): Übertragen von Informationen von MetaTrader 5 nach Excel
Marktsimulation (Teil 06): Übertragen von Informationen von MetaTrader 5 nach Excel
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.