Búsqueda dialéctica - Dialectic Search (DA)
22
0
Contenido
Introducción
El materialismo dialéctico se basa en el principio de unidad y lucha de opuestos en la naturaleza, la sociedad y el pensamiento. Se fundamenta en la noción de que el desarrollo se produce a través del conflicto de fuerzas y tendencias contrarias, donde cada fenómeno contiene contradicciones internas. El principio clave de este enfoque es la transición de los cambios cuantitativos a los cualitativos, cuando los cambios graduales se acumulan y provocan saltos cualitativos bruscos. El proceso de desarrollo sigue la ley de la "negación de la negación", en la que la tesis es sustituida por la antítesis, dando lugar a la síntesis como nueva cualidad que mantiene lo mejor de los estados anteriores.
En el mundo de los algoritmos de optimización, donde la precisión matemática se une a la sabiduría filosófica, ha surgido un método único inspirado en el materialismo dialéctico: el Algoritmo Dialéctico (DA). Este algoritmo, presentado como una síntesis de la dialéctica clásica y los métodos modernos de optimización, replantea el proceso de búsqueda de soluciones óptimas usando el prisma de la oposición filosófica entre tesis y antítesis. El DA se basa en la idea de que cualquier solución (tesis) contiene el potencial de mejora a través de la interacción con su opuesto (antítesis).
En la realización algorítmica, este principio se refleja mediante la interacción entre los pensadores especulativos que buscan nuevas soluciones alejándose de las soluciones conocidas y los pensadores prácticos que buscan soluciones probadas. El aspecto materialista del materialismo dialéctico se manifiesta en la confianza en criterios objetivos para evaluar las decisiones y la verificación práctica de los resultados. El desarrollo se produce de manera cíclica: las soluciones encontradas dan lugar a nuevas contradicciones, lo que conduce a la siguiente ronda de búsqueda, reflejando la continuidad del proceso de cognición y mejora.
El algoritmo materializa este principio a través de tres momentos clave: la percepción, en la que se evalúan y clasifican las soluciones; la interacción dialéctica, en la que las soluciones encuentran sus antítesis; y el momento de síntesis, en el que se forman soluciones nuevas y mejoradas. Una característica del algoritmo consiste en la división de la población en dos tipos de pensadores: especulativos (k1), que exploran el espacio de soluciones en pasos amplios (mediante la interacción de soluciones similares en calidad pero distantes entre sí en el espacio de búsqueda), y prácticos (p-k1), que buscan de manera local (soluciones distantes en calidad pero cercanas en el espacio de soluciones). Esta división refleja el principio filosófico de la unidad y lucha de contrarios, donde cada grupo realiza una contribución única al proceso de optimización.
La búsqueda dialéctica (DA) fue introducida por Serdar Kadioglu y Meinolf Sellmann en 2009. Este método usa un enfoque dialéctico para resolver problemas de optimización con restricciones, continuando la tradición establecida por el materialismo dialéctico de investigar y encontrar nuevas soluciones.
Implementación del algoritmo
El algoritmo se basa en una población de soluciones p (normalmente 50), cada una de las cuales representa un vector de coordenadas en el espacio de búsqueda. Esta población se divide en dos grupos: k1 pensadores especulativos (mejores soluciones) y (p-k1) pensadores prácticos.
La primera etapa es el momento de comprensión. Aquí, todas las soluciones se evalúan a través de la función objetivo f(x). Las soluciones se clasifican por calidad, y las mejores soluciones k1 se convierten en pensadores especulativos, mientras que el resto se convierte en pensadores prácticos. En esta etapa también se toman o rechazan nuevas decisiones según su calidad en comparación con las iteraciones anteriores (la mejor decisión individual para el pensador).
La segunda etapa es el momento dialéctico. En esta fase, a cada solución se le busca una antítesis, un opuesto con el que la solución interactuará. Para los pensadores especulativos, la búsqueda de la antítesis se basa en la maximización de la distancia manteniendo la calidad de la solución (dialéctica idealista). Para la primera solución, la antítesis se convierte en la segunda mejor solución, para la última, en la penúltima, y para el resto, se selecciona al vecino con la mayor distancia. Los pensadores prácticos buscan la antítesis valiéndose de la minimización de la distancia con la suficiente diferencia de calidad (dialéctica materialista).
La tercera etapa es el momento especulativo/práctico (momento de actualización). Aquí se actualizan las posiciones de todas las soluciones usando la antítesis encontrada. Los pensadores especulativos usan una distribución uniforme que proporciona una búsqueda amplia en el espacio de soluciones. Los pensadores prácticos usan la distribución normal. Mis experimentos han demostrado que una distribución uniforme funciona mejor para ambos tipos de pensadores.
La fórmula para actualizar las posiciones será la misma para todos: X(i) = X(i) + μ⊙(Xanti(i) - X(i)), donde μ es un vector aleatorio de la distribución correspondiente, y ⊙ denota multiplicación por partes. Esto ofrece un equilibrio entre la exploración del espacio de soluciones a través de pensadores especulativos y el perfeccionamiento de las soluciones encontradas a través de pensadores prácticos.
El algoritmo dialéctico (DA) tiene similitudes con el algoritmo de evolución diferencial DE, en la fórmula de actualización de soluciones. En el DE, se crea un nuevo vector añadiendo la diferencia escalada de otros dos vectores al vector objetivo (x_new = x_target + F(x_r1 - x_r2)), mientras que el DA utiliza un principio similar pero con antítesis y coeficiente adaptativo (x_new = x + μ(x_anti - x)).
No obstante, la diferencia clave radica en la forma en que se seleccionan los vectores para generar nuevas soluciones. El DE se basa en una selección aleatoria de vectores de diferencias para garantizar la naturaleza estocástica de la búsqueda. El DA, por el contrario, adopta un enfoque determinista para la selección de antítesis basado en la distancia entre soluciones y su calidad, al tiempo que divide la población en pensadores especulativos y prácticos con diferentes estrategias de búsqueda. El algoritmo DA presenta una complejidad computacional ligeramente superior (cálculo de la distancia euclidiana), pero el DA muestra una mayor eficacia en diversos problemas de optimización.
La figura 1 muestra el principio de selección de antítesis para las tesis especulativas (rojas, las mejores) y las tesis materiales (azules). Las especulativas seleccionan las antítesis vecinas en calidad pero más distantes en el espacio de búsqueda, mientras que las materiales seleccionan a la inversa, las más distantes en calidad pero cercanas en el espacio de búsqueda.
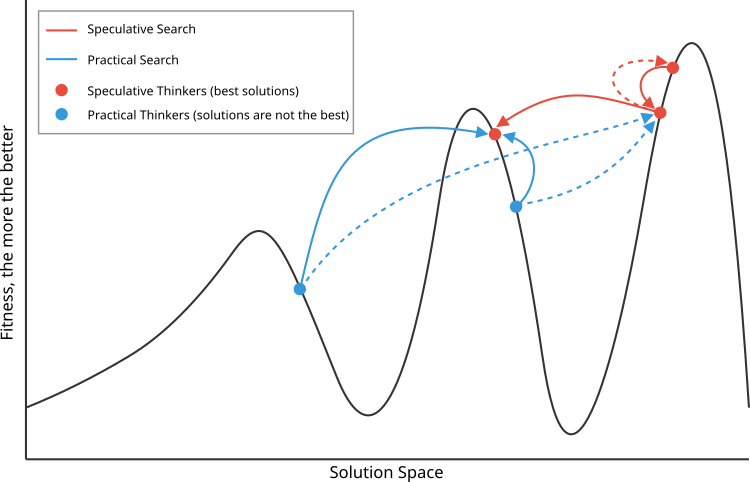
Figura 1. Representación esquemática del principio de funcionamiento del algoritmo DA. Las líneas continuas corresponden a las interacciones con las antítesis preferidas, frente a las menos preferidas, indicadas con líneas discontinuas
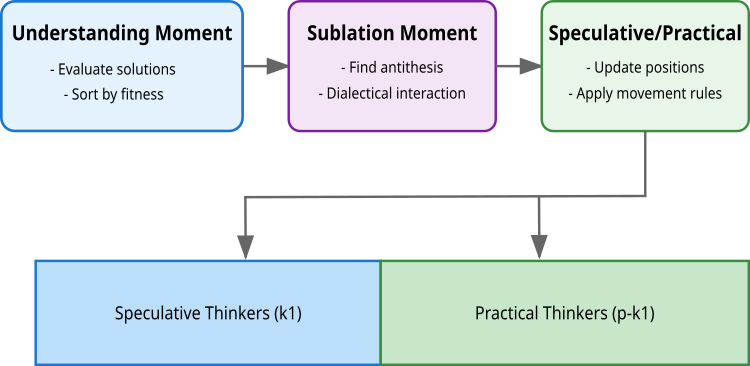
Figura 2. Etapas de la lógica del algoritmo DA
Vamos a escribir ahora el pseudocódigo del algoritmo:
En la primera iteración: Colocamos agentes aleatoriamente: position[i] = random(min, max)
Clasificamos la población según las mejores soluciones personalizadas
Creamos una población de tres tipos de agentes:
- Mejor pensador (1 agente)
- Pensadores especulativos (k1 = 3 agentes)
- Pensadores prácticos (el resto de los 50 agentes)
A. El mejor pensador se acerca al segundo mejor pensador:
position[0] = best[0] + rand(0,1) * (position[1] - position[0])B. Pensadores especulativos:
- Encuentran los vecinos más cercanos mediante la distancia euclidiana:
- Actualizan su posición respecto al más lejano:
В. Pensadores prácticos:
- Se seleccionan dos pensadores especulativos al azar
- Avanzan hacia el más cercano:
position[i] = best[i] + rand(0,1) * (position[nearest] - position[i])
Después de cada movimiento:- Actualizamos las mejores soluciones personales
- Actualizamos de la mejor solución global
- Clasificamos los agentes según la calidad de sus decisiones personales
El proceso se repite hasta alcanzar el criterio de parada
Una vez analizado el algoritmo, podemos pasar a su implementación en código. Vamos a escribir la clase "C_AO_DA" del algoritmo de optimización dialéctica, heredando funcionalidad de la clase base "C_AO".
Parámetros del algoritmo:
- Antítesis del tamaño de la población — determina el número de agentes que participarán en el proceso de optimización.
- Pensadores especulativos — indica el número de mejores agentes capaces de soluciones más fluidas.
- Vecinos para el análisis — define el número de vecinos inmediatos con los que cada pensador (agente) especulativo interactuará para intercambiar información y mejorar su estrategia.
Métodos:
- C_AO_DA () — el constructor inicializa los parámetros principales, y crea un array para almacenar los parámetros.
- SetParams () — la parametrización permite actualizar los valores de los parámetros del algoritmo durante el funcionamiento.
- Moving () н Revision () — funciones para mover agentes en el espacio de búsqueda y revisar las soluciones encontradas.
- EuclideanDistance () — calcula la distancia en el espacio de búsqueda entre dos vectores, lo que resulta necesario para seleccionar la similitud más cercana (para la especulación) y la más lejana (para la práctica) de las soluciones encontradas por los agentes.
//—————————————————————————————————————————————————————————————————————————————— // Класс реализующий диалектический алгоритм оптимизации class C_AO_DA : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_DA () { } C_AO_DA () { ao_name = "DA"; ao_desc = "Dialectical Algorithm"; ao_link = "https://www.mql5.com/es/articles/16999"; popSize = 50; // размер популяции k1 = 3; // спекулятивные мыслители k2 = 10; // соседи ArrayResize (params, 3); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "k1"; params [1].val = k1; params [2].name = "k2"; params [2].val = k2; } // Установка параметров алгоритма void SetParams () { popSize = (int)params [0].val; k1 = (int)params [1].val; k2 = (int)params [2].val; } bool Init (const double &rangeMinP [], // минимальный диапазон поиска const double &rangeMaxP [], // максимальный диапазон поиска const double &rangeStepP [], // шаг поиска const int epochsP = 0); // количество эпох void Moving (); // Перемещение агентов в пространстве поиска void Revision (); // Пересмотр и обновление лучших найденных решений //---------------------------------------------------------------------------- int k1; // количество спекулятивных мыслителей int k2; // количество соседей для анализа private: //------------------------------------------------------------------- // Вычисление евклидового расстояния между двумя векторами double EuclideanDistance (const double &vec1 [], const double &vec2 [], const int dim) { double sum = 0; double diff = 0.0; for (int i = 0; i < dim; i++) { diff = vec1 [i] - vec2 [i]; sum += diff * diff; } return MathSqrt (sum); } }; //——————————————————————————————————————————————————————————————————————————————
El método "Init" de la clase "C_AO_DA" está diseñado para inicializar los parámetros del algoritmo de optimización. Admite arrays de valores mínimos y máximos del rango de búsqueda, los pasos de búsqueda y, opcionalmente, el número de épocas para realizar la optimización. El método ejecuta primero la inicialización estándar de los parámetros; si falla, retorna "false". Si la inicialización se realiza correctamente, el método retorna "true", confirmando que el algoritmo está listo para ejecutarse.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_DA::Init (const double &rangeMinP [], // минимальный диапазон поиска const double &rangeMaxP [], // максимальный диапазон поиска const double &rangeStepP [], // шаг поиска const int epochsP = 0) // количество эпох { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- return true; } //——————————————————————————————————————————————————————————————————————————————
El método "Moving" supone una implementación del movimiento de los agentes en el espacio de búsqueda, una descripción detallada de cómo funciona el método:
Inicialización:
- Al principio (!revision), se establecen las posiciones iniciales de los agentes de forma aleatoria, utilizando los límites mínimo y máximo dados para cada coordenada. Cada agente "a[i]" recibe coordenadas aleatorias en los rangos dados y con un paso determinado.
- Tras la inicialización, "revision" se establece en "true", lo cual evita la reinicialización en futuras llamadas al método "Moving".
Actualización de la posición del mejor pensador:
- El mejor pensador (agente) actualiza sus coordenadas basándose en su mejor posición anterior y la probabilidad aleatoria, usando el vecino más cercano "a [1]" para actualizarse.
Actualización de las posiciones de los pensadores especulativos:
- Para cada pensador (agente) especulativo en el rango de "k2" a "k1", el método busca el vecino anterior más distante (antiPrevIND) y el vecino siguiente (antiNextIND).
- La coordenada del pensador especulativo se actualiza entonces usando el vecino más lejano al considerar la antítesis.
Actualización de las posiciones de los pensadores prácticos:
- Los pensadores (agentes) prácticos van de "k1" a "popSize".
- El código selecciona aleatoriamente dos pensadores especulativos y calcula las distancias a ellos. El pensador práctico selecciona entonces al pensador más cercano (de los dos elegidos) para actualizar su posición.
- Cada coordenada se actualiza para reflejar el vecino seleccionado.
Funciones auxiliares
- EuclideanDistance — función que calcula la distancia euclidiana entre dos puntos "a" y "b" en un espacio multidimensional.
- u.RNDfromCI — devuelve un número aleatorio del intervalo especificado.
- u.SeInDiSp — lleva "value" a un paso adecuado en función del rango.
- u.RNDprobab — retorna un número aleatorio con distribución de probabilidad uniforme.
//—————————————————————————————————————————————————————————————————————————————— // Реализация движения агентов в пространстве поиска void C_AO_DA::Moving () { //---------------------------------------------------------------------------- // Начальная инициализация позиций агентов случайным образом if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- // Обновление позиции лучшего мыслителя for (int c = 0; c < coords; c++) { a [0].c [c] = a [0].cB [c] + u.RNDprobab () * (a [1].c [c] - a [0].c [c]); a [0].c [c] = u.SeInDiSp (a [0].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } //---------------------------------------------------------------------------- double dist_next = -DBL_MAX; // максимальное расстояние до следующего соседа double dist_prev = -DBL_MAX; // максимальное расстояние до предыдущего соседа double dist = 0.0; // текущее расстояние int antiNextIND = 0; // индекс наиболее удаленного следующего соседа int antiPrevIND = 0; // индекс наиболее удаленного предыдущего соседа int antiIND = 0; // выбранный индекс для обновления позиции // Обновление позиций спекулятивных мыслителей ------------------------------- for (int i = k2; i < k1; i++) { // Поиск наиболее удаленного предыдущего соседа for (int j = 1; j <= k2; j++) { dist = EuclideanDistance (a [i].cB, a [i - j].cB, coords); if (dist > dist_prev) { dist_prev = dist; antiPrevIND = i - j; } } // Поиск наиболее удаленного следующего соседа for (int j = 1; j <= k2; j++) { dist = EuclideanDistance (a [i].cB, a [i + j].cB, coords); if (dist > dist_next) { dist_next = dist; antiNextIND = i + j; } } // Выбор наиболее удаленного соседа для обновления позиции if (dist_prev > dist_next) antiIND = antiPrevIND; else antiIND = antiNextIND; // Обновление координат спекулятивного мыслителя for (int c = 0; c < coords; c++) { a [i].c [c] = a [i].cB [c] + u.RNDbool () * (a [antiIND].c [c] - a [i].c [c]); //a [i].c [c] = a [i].cB [c] + u.RNDprobab () * (a [antiIND].c [c] - a [i].c [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } // Обновление позиций практических мыслителей -------------------------------- for (int i = k1; i < popSize; i++) { // Случайный выбор двух спекулятивных мыслителей antiNextIND = u.RNDintInRange (0, k1 - 1); antiPrevIND = u.RNDintInRange (0, k1 - 1); if (antiNextIND == antiPrevIND) antiNextIND = antiPrevIND + 1; // Расчет расстояний до выбранных мыслителей dist_next = EuclideanDistance (a [i].cB, a [antiNextIND].cB, coords); dist_prev = EuclideanDistance (a [i].cB, a [antiPrevIND].cB, coords); // Выбор ближайшего мыслителя для обновления позиции if (dist_prev < dist_next) antiIND = antiPrevIND; else antiIND = antiNextIND; // Обновление координат практического мыслителя for (int c = 0; c < coords; c++) { a [i].c [c] = a [i].cB [c] + u.RNDprobab () * (a [antiIND].c [c] - a [i].c [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
El método "Revision" se encarga de revisar y actualizar las mejores soluciones encontradas para los agentes. A continuación le presentamos un análisis detallado del rendimiento de este método:
Actualización de las mejores soluciones encontradas: en un ciclo "for", el método recorre cada agente de la población. Para cada agente, se compara el valor actual de la función de aptitud "a[i].f":
- Mejor solución global — si el valor de la función del agente "f" es mayor que la mejor solución global actual "fB", se actualiza la solución global y se recuerda el índice del agente (ind) que encontró esta mejor solución.
- Mejor criterio personal — igualmente, se compara el valor f de cada agente con su mejor valor fB personal. Si el valor actual es mejor, se actualiza el mejor valor personal del agente y sus coordenadas actuales "c" se copian en sus coordenadas personales "cB".
Actualización de las coordenadas de la mejor solución global — si se ha encontrado el índice del agente que se ha convertido en la mejor solución global (ind != -1), las coordenadas de este agente se copian en las coordenadas globales "cB ".
Clasificación de agentes: Al final del método, se crea un array "aT" y se redimensiona para ajustarse al tamaño de la población. A continuación se llama a la función "u.Sorting_fB", que clasifica los agentes según sus mejores soluciones encontradas (valores fB).
//—————————————————————————————————————————————————————————————————————————————— // Пересмотр и обновление лучших найденных решений void C_AO_DA::Revision () { int ind = -1; // Обновление лучших найденных решений для каждого агента for (int i = 0; i < popSize; i++) { // Обновление глобального лучшего решения if (a [i].f > fB) { fB = a [i].f; ind = i; } // Обновление личного лучшего решения агента if (a [i].f > a [i].fB) { a [i].fB = a [i].f; ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY); } } // Обновление координат глобального лучшего решения if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); // Сортировка агентов по их лучшим найденным решениям static S_AO_Agent aT []; ArrayResize (aT, popSize); u.Sorting_fB (a, aT, popSize); } //——————————————————————————————————————————————————————————————————————————————
Resultados de las pruebas
Ya es hora de familiarizarnos con los resultados de las pruebas del DA. Una vez más, prestaremos atención al método "Move", en él la línea está marcada y comentada en verde, como debe ser según la idea de los autores. Los resultados son los siguientes:
=============================
5 Hilly's; Func runs: 10000; result: 0.749254786734898
25 Hilly's; Func runs: 10000; result: 0.36669693350810206
500 Hilly's; Func runs: 10000; result: 0.2532075139007539
=============================
5 Forest's; Func runs: 10000; result: 0.7626421292861323
25 Forest's; Func runs: 10000; result: 0.4144802592253075
500 Forest's; Func runs: 10000; result: 0.2006796312431603
=============================
5 Megacity's; Func runs: 10000; result: 0.36
25 Megacity's; Func runs: 10000; result: 0.15969230769230774
500 Megacity's; Func runs: 10000; result: 0.0952000000000008
=============================
All score: 3.36185 (37.35%)
Estos resultados están lejos de ser los mejores, aunque podrían entrar en la tabla de clasificación. Pero el caso es que cometí un error y en lugar de utilizar números aleatorios en el rango [0,0;1,0], inserté en el código una función de números booleanos aleatorios (marcados en rojo).
La esencia de un cambio aleatorio en la lógica es la siguiente: con una probabilidad del 50%, la coordenada correspondiente seguirá siendo la misma, o será sustituida por la coordenada de antítesis. En mi opinión, esto concuerda aún más con la idea de los autores de contraponer tesis y antítesis. En el caso de los pensadores prácticos, las cosas siguen igual, sus tesis finales son una simbiosis entre la tesis actual y la antítesis tomada de los pensadores especulativos. Así pues, resultó una feliz coincidencia que se obtuvieran estos resultados:
DA|Dialectical Algorithm|50.0|40.0|1.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.8618313952293774
25 Hilly's; Func runs: 10000; result: 0.700333708747176
500 Hilly's; Func runs: 10000; result: 0.3372386732170054
=============================
5 Forest's; Func runs: 10000; result: 0.9816317765399738
25 Forest's; Func runs: 10000; result: 0.7277214130784131
500 Forest's; Func runs: 10000; result: 0.28717629901518305
=============================
5 Megacity's; Func runs: 10000; result: 0.7030769230769229
25 Megacity's; Func runs: 10000; result: 0.4529230769230769
500 Megacity's; Func runs: 10000; result: 0.16366923076923204
=============================
All score: 5.21560 (57.95%)
Estos resultados son realmente impresionantes. Como esta mejora tan significativa en el rendimiento me ocurrió sin saberlo, no puedo asignar a la versión modificada un índice "m". El algoritmo permanecerá como "DA" en nuestra tabla de clasificación. De esta forma, el algoritmo dialéctico muestra un excelente rendimiento, alcanzando una eficacia global del 57,95%. Una característica clave del algoritmo es su capacidad para equilibrar eficazmente la búsqueda global y local, gracias a su separación entre pensadores especulativos y prácticos.
En la visualización, podemos ver que el algoritmo encuentra óptimos locales significativos con bastante rapidez, si bien le falta precisión de convergencia para considerarse perfecto. No obstante, los resultados son bastante decentes en ambos casos.
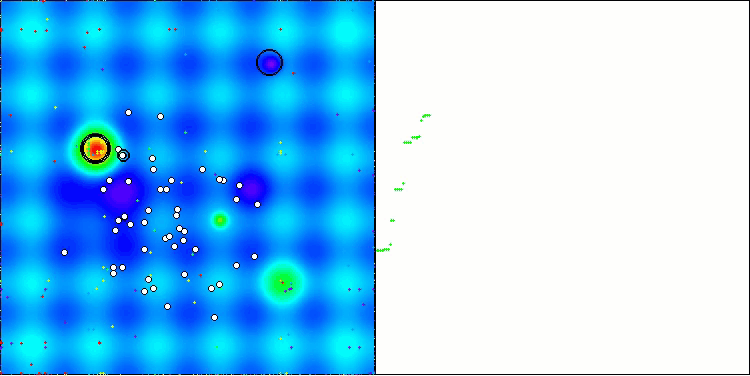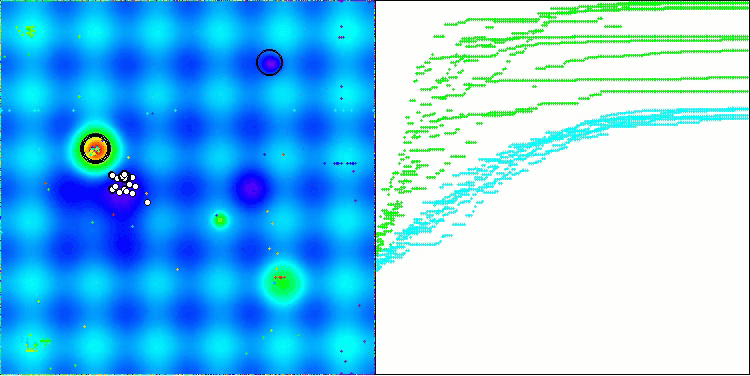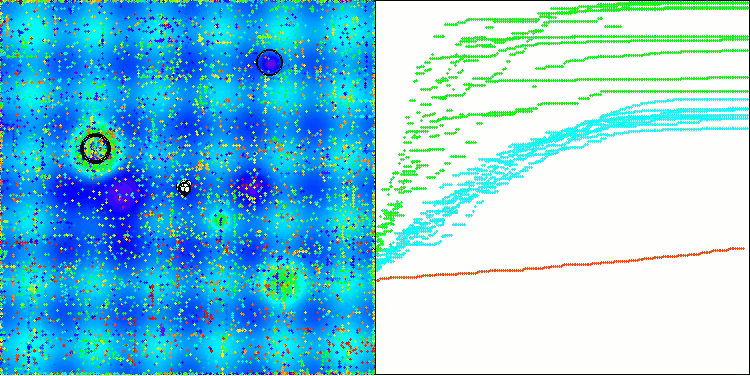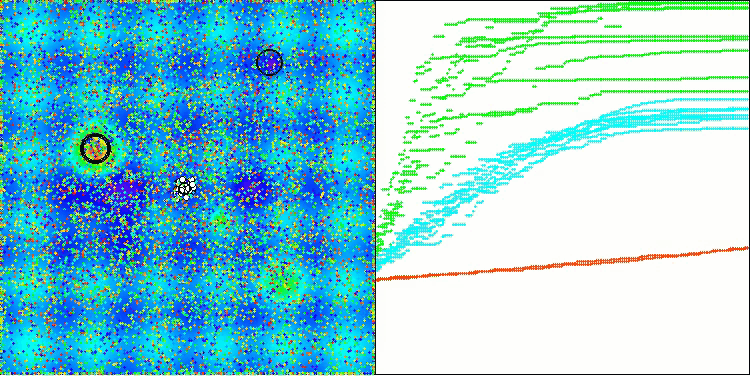
DA en la función de prueba Hilly
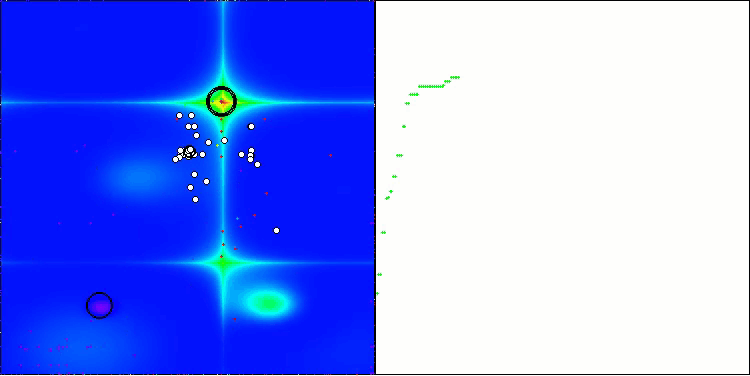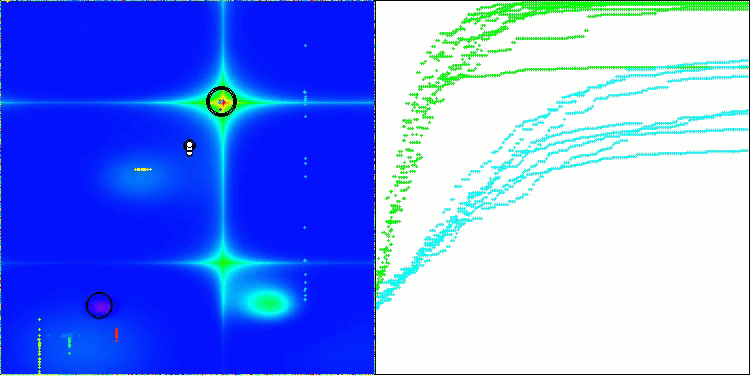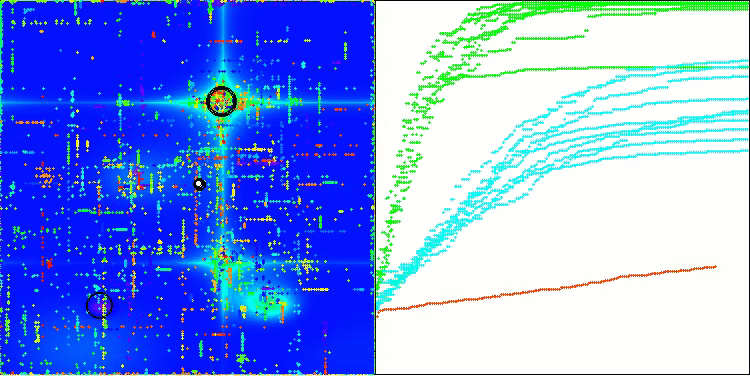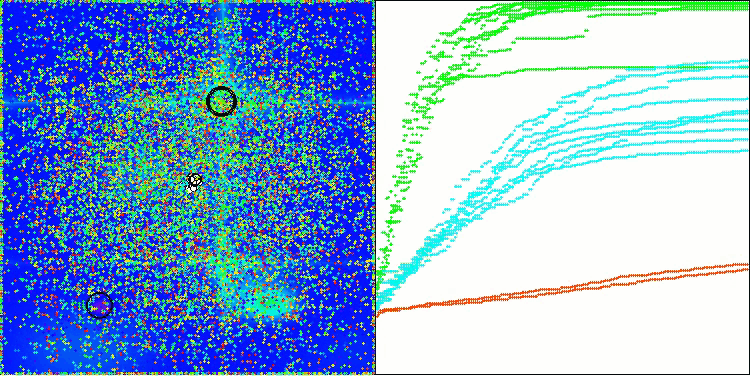
DA en la función de prueba Forest
DA en la función de prueba Megacity
El algoritmo DA, según los resultados de la prueba, se sitúa en nuestra tabla de clasificación en el puesto 12, un indicador bueno y estable.
| № | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % de MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration optimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | TETA | time evolution travel algorithm (joo) | 0,91362 | 0,82349 | 0,31990 | 2,05701 | 0,97096 | 0,89532 | 0,29324 | 2,15952 | 0,73462 | 0,68569 | 0,16021 | 1,58052 | 5,797 | 64,41 |
| 7 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 8 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 9 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 10 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | /0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 11 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 12 | DA | dialectical algorithm | 0,86183 | 0,70033 | 0,33724 | 1,89940 | 0,98163 | 0,72772 | 0,28718 | 1,99653 | 0,70308 | 0,45292 | 0,16367 | 1,31967 | 5,216 | 57,95 |
| 13 | BHAm | black hole algorithm M | 0,75236 | 0,76675 | 0.34583 | 1,86493 | 0.93593 | 0.80152 | 0,27177 | 2,00923 | 0.65077 | 0.51646 | 0,15472 | 1,32195 | 5.196 | 57.73 |
| 14 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 15 | AOSm | búsqueda de orbitales atómicos M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| 16 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 17 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 18 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 19 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 20 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 21 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 22 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 23 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 24 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 25 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 26 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 27 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 28 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 29 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 30 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 31 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 32 | SOA | simple optimization algorithm | 0.91520 | 0.46976 | 0.27089 | 1,65585 | 0.89675 | 0.37401 | 0.16984 | 1,44060 | 0.69538 | 0.28031 | 0.10852 | 1,08422 | 4.181 | 46,45 |
| 33 | ABH | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4.127 | 45,85 |
| 34 | ACMO | atmospheric cloud model optimization | 0,90321 | 0,48546 | 0,30403 | 1,69270 | 0,80268 | 0,37857 | 0,19178 | 1,37303 | 0,62308 | 0,24400 | 0,10795 | 0,97503 | 4,041 | 44,90 |
| 35 | ADAMm | adaptive moment estimation M | 0.88635 | 0.44766 | 0,26613 | 1.60014 | 0.84497 | 0.38493 | 0.16889 | 1,39880 | 0,66154 | 0.27046 | 0.10594 | 1,03794 | 4.037 | 44.85 |
| 36 | ATAm | artificial tribe algorithm M | 0.71771 | 0.55304 | 0,25235 | 1,52310 | 0.82491 | 0.55904 | 0,20473 | 1,58867 | 0,44000 | 0,18615 | 0.09411 | 0.72026 | 3.832 | 42.58 |
| 37 | ASHA | artificial showering algorithm | 0,89686 | 0,40433 | 0,25617 | 1,55737 | 0,80360 | 0,35526 | 0,19160 | 1,35046 | 0,47692 | 0,18123 | 0,09774 | 0,75589 | 3,664 | 40,71 |
| 38 | ASBO | adaptive social behavior optimization | 0,76331 | 0,49253 | 0,32619 | 1,58202 | 0,79546 | 0,40035 | 0,26097 | 1,45677 | 0,26462 | 0,17169 | 0,18200 | 0,61831 | 3.657 | 40,63 |
| 39 | MEC | mind evolutionary computation | 0,69533 | 0,53376 | 0,32661 | 1,55569 | 0,72464 | 0,33036 | 0,07198 | 1,12698 | 0,52500 | 0,22000 | 0,04198 | 0,78698 | 3,470 | 38,55 |
| 40 | IWO | invasive weed optimization | 0,72679 | 0,52256 | 0,33123 | 1,58058 | 0,70756 | 0,33955 | 0,07484 | 1,12196 | 0,42333 | 0,23067 | 0,04617 | 0,70017 | 3,403 | 37,81 |
| 41 | Micro-AIS | micro artificial immune system | 0,79547 | 0,51922 | 0,30861 | 1,62330 | 0,72956 | 0,36879 | 0,09398 | 1,19233 | 0,37667 | 0,15867 | 0,02802 | 0,56335 | 3,379 | 37,54 |
| 42 | COAm | cuckoo optimization algorithm M | 0,75820 | 0,48652 | 0,31369 | 1,55841 | 0,74054 | 0,28051 | 0,05599 | 1,07704 | 0,50500 | 0,17467 | 0,03380 | 0,71347 | 3,349 | 37,21 |
| 43 | SDOm | spiral dynamics optimization M | 0,74601 | 0,44623 | 0,29687 | 1,48912 | 0,70204 | 0,34678 | 0,10944 | 1,15826 | 0,42833 | 0,16767 | 0,03663 | 0,63263 | 3,280 | 36,44 |
| 44 | NMm | Nelder-Mead method M | 0,73807 | 0,50598 | 0,31342 | 1,55747 | 0,63674 | 0,28302 | 0,08221 | 1,00197 | 0,44667 | 0,18667 | 0,04028 | 0,67362 | 3,233 | 35,92 |
| 45 | BBC | big bang-big crunch algorithm | 0.60531 | 0.45250 | 0.31255 | 1,37036 | 0.52323 | 0.35426 | 0,20417 | 1,08166 | 0.39769 | 0,19431 | 0.11286 | 0.70486 | 3.157 | 35.08 |
| R.W. | random walk | 0.48754 | 0.32159 | 0.25781 | 1,06694 | 0.37554 | 0,21944 | 0,15877 | 0,75375 | 0.27969 | 0,14917 | 0.09847 | 0.52734 | 2.348 | 26.09 | |
Conclusiones
El algoritmo dialéctico supone un enfoque innovador de la optimización basado en el concepto filosófico de la dialéctica, según el cual las soluciones mejoradas se consiguen mediante la interacción de los opuestos. El algoritmo integra con éxito los conceptos de búsqueda global y local mediante una separación única de la población en pensadores especulativos y prácticos, lo que ofrece un equilibrio eficaz entre la exploración y la explotación del espacio de soluciones.
La estructura del algoritmo, que consta de tres pasos clave, posibilita un enfoque sistemático de la optimización. En el proceso, los pensadores especulativos buscan ampliamente en el espacio de soluciones (aunque normalmente, en los algoritmos de optimización, las mejores soluciones se refinan en lugar de "repartirse" por el espacio de búsqueda), mientras que los pensadores prácticos se centran en la optimización local de áreas más prometedoras. Esta separación permite al algoritmo explorar de forma eficaz el espacio de soluciones y evitar quedarse atascado en óptimos locales, sobre todo porque el error aleatorio que cometí hizo que la lógica del algoritmo se acercara aún más al tema de los opuestos dialécticos.
Los resultados de las pruebas confirman la alta eficiencia del algoritmo con capacidades de búsqueda equilibradas, que posibilitan un nivel bastante alto en diferentes tipos de tareas. Comparado con otros algoritmos, el DA no muestra fuertes desviaciones para peor o mejor y muestra un resultado uniformemente consistente en la gradación de colores de la tabla. La medida del rendimiento global muestra la competitividad del algoritmo frente a los métodos de optimización existentes. Esta combinación de principios filosóficos y métodos matemáticos crea una potente herramienta para resolver complejos problemas de optimización.
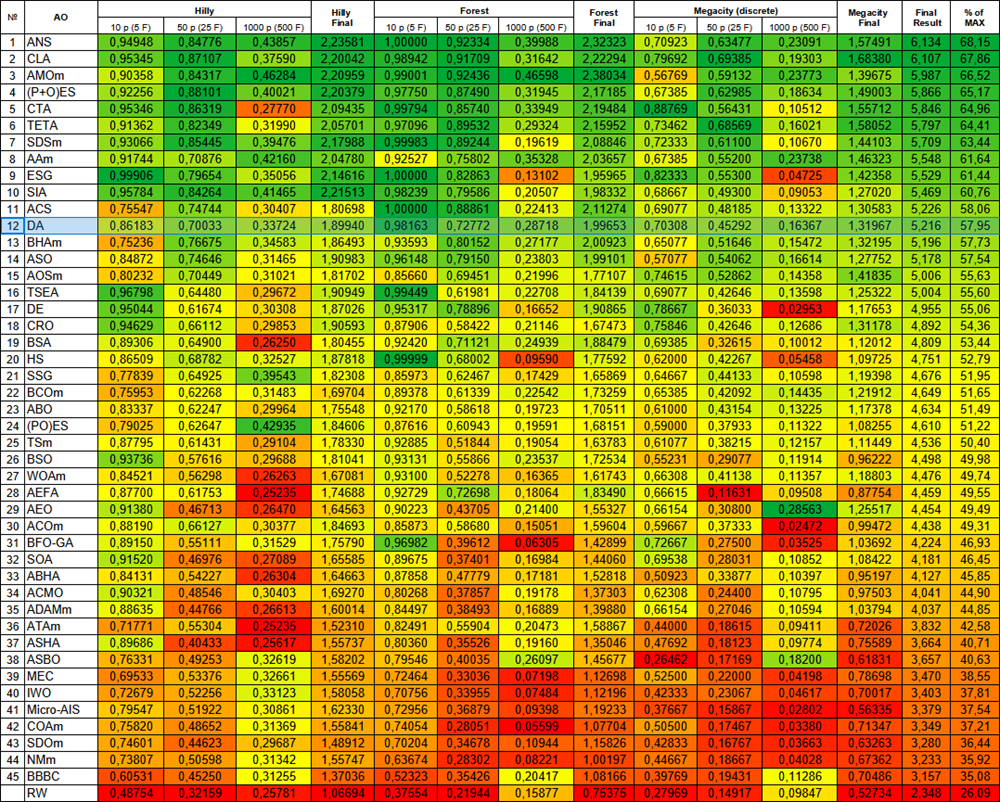
Figura 3. Clasificación por colores de los algoritmos según las pruebas respectivas
Figura 4. Histograma con los resultados de las pruebas de los algoritmos (en una escala de 0 a 100, cuanto más mejor, donde 100 es el máximo resultado teórico posible, el script para calcular la tabla de puntuación está en el archivo)
Ventajas e inconvenientes del algoritmo DA:
Ventajas:
- Pocos parámetros externos, solo dos, sin contar el tamaño de la población.
- Aplicación relativamente sencilla.
- Bastante rápido.
- Equilibrado, buen rendimiento en tareas de pequeñas y grandes dimensionalidades.
Desventajas:
- Dispersión de los resultados.
Adjuntamos al artículo un archivo con las versiones actuales de los códigos de los algoritmos. El autor de este artículo no se responsabiliza de la exactitud absoluta de la descripción de los algoritmos canónicos, muchos de ellos han sido modificados para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos realizados.
Programas usados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | #C_AO.mqh | Archivo de inclusión | Clase padre de algoritmos de optimización basados en la población |
| 2 | #C_AO_enum.mqh | Archivo de inclusión | Enumeración de los algoritmos de optimización basados en la población |
| 3 | TestFunctions.mqh | Archivo de inclusión | Biblioteca de funciones de prueba |
| 4 | TestStandFunctions.mqh | Archivo de inclusión | Biblioteca de funciones del banco de pruebas |
| 5 | Utilities.mqh | Archivo de inclusión | Biblioteca de funciones auxiliares |
| 6 | CalculationTestResults.mqh | Archivo de inclusión | Script para calcular los resultados en una tabla comparativa |
| 7 | Testing AOs.mq5 | Script | Banco de pruebas único para todos los algoritmos de optimización basados en la población |
| 8 | Simple use of population optimization algorithms.mq5 | Script | Ejemplo sencillo de utilización de algoritmos de optimización basados en la población sin visualización |
| 9 | Test_AO_DA.mq5 | Script | Banco de pruebas para DA |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/16999
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
Utilizando redes neuronales en MetaTrader
Añadimos un LLM personalizado a un robot comercial (Parte 5): Desarrollar y probar la estrategia de negociación con LLMs (III) Ajuste del adaptador
Particularidades del trabajo con números del tipo double en MQL4
Neurona biológica para la previsión de series temporales financieras
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso