MetaTrader 5 / 交易系统
English Русский Español Português
preview
辩证搜索（DA）

辩证搜索（DA）

MetaTrader 5 — 交易系统 |
189 0
Andrey Dik
Andrey Dik

目录

  1. 概述
  2. 算法的实现
  3. 测试结果


概述

辩证唯物主义是建立在自然界、社会和思维的对立统一和斗争的原则之上的。它基于这样一种观点，即发展是通过对立力量和趋势的冲突来实现的，每种现象都包含着内在矛盾。这种方法的关键原则是从量变到质变的过渡，即渐进的变化积累并导致急剧的质变。这一发展遵循“否定之否定”的规律，即命题被对立所取代，从而产生了一种新的性质，即综合，它保留了先前状态的最佳状态。

在数学精度与哲学智慧相结合的优化算法领域，出现了一种受辩证唯物主义启发的独特方法：辩证算法（DA）。该算法是经典辩证法和现代优化方法的综合，通过论题和对偶的哲学对立的棱镜重新思考了寻找最优解的问题。DA的基础是这样一种观点，即任何解决方案（正题）都包含通过与其对立面（反题）的相互作用而改进的潜力。

在其算法实现中，这一原则通过寻求新解决方案的思辨思想者与追求经过验证的解决方案的务实思想者之间的互动得到了体现。辩证唯物主义的唯物主义方面表现在对评价决策和实际验证结果的客观标准的依赖上。发展是周期性的：找到的解决方案会引发新的矛盾，从而导致下一轮的搜索，反映了知识的连续性和改进。

该算法通过三个关键点实现了这一原则：理解，解决方案的评估和排序发生在哪里；辩证互动，解决方案在其中找到了对立；以及形成新的改进解决方案的合成时刻。该算法的特点是将群体划分为两种类型的思考者：推测型（k1），以广泛的步骤探索解决方案空间（通过质量相似但在搜索空间中彼此相距较远的解决方案的相互作用）；实践型（p-k1），进行局部搜索（质量相距较远，但在解决方案空间中接近）。这种划分反映了对立统一和斗争的哲学原则，每个群体都为优化做出了自己独特的贡献。

辩证搜索 (DA) 由 Serdar Kadioglu 和 Meinolf Sellmann 于 2009 年提出。这种方法采用辩证的方法来解决约束优化问题，延续了辩证唯物主义在研究和寻找新解决方案方面建立的传统。


算法的实现

该算法基于 p 个解决方案（通常为 50 个）的总体，每个解决方案都是搜索空间中的坐标向量。这个群体被分为两组：k1 推测型思考者（最佳解决方案）和（p-k1）实践型思考者。

第一阶段是理解的时刻。这里，所有决策都通过目标函数 f(x) 来评估。解决方案按质量排序，最好的 k1 个解决方案成为推测型思考者，而其余的则成为实践型思考者。在这个阶段，新的解决方案也会根据其与之前迭代的质量（对思考者来说是最佳的个人解决方案）而被接受或拒绝。

第二阶段是辩证时刻。在此阶段，将搜索每个解决方案的对立面 —— 即与解决方案相互作用的对立面。对于推测思想者来说，对立面的探索是基于最大化距离，同时保持解决方案的质量（理想主义辩证法）。对于第一个解决方案，对立面是第二好的，对于最后一个解决方案，对立面是倒数第二个，对于其余的解决方案，选择距离最大的邻居。实用思想者通过最小化具有足够质量差异的距离来寻求对立（唯物辩证法）。

第三阶段是思辨/实践时刻（更新时刻）。这里使用找到的对立面来更新所有解决方案的位置。推测型思考者使用均匀分布，这允许在解决方案空间中进行广泛的搜索。实践型思考者使用正态分布。我的实验表明，对于两种类型的思考者来说，均匀分布效果最好。

更新位置的公式对所有人来说都是相同的：X(i) = X(i) + μ⊙(Xanti(i) - X(i))，其中 μ 是来自相应分布的随机向量，⊙ 表示逐元素乘法。这确保了通过推测型思考者探索解决方案空间与通过实践型思考者完善找到的解决方案之间的平衡。

辩证算法（DA）与差分进化（ DE ）算法在解更新方程上有相似之处。在 DE 中，通过将另外两个向量的缩放差异添加到目标向量来创建一个新向量（x_new = x_target + F(x_r1 - x_r2)），而 DA 使用类似的原理，但具有对立面和自适应比率（x_new = x + μ(x_anti - x)）。

然而，关键的区别在于选择向量来生成新解的方式。DE 依赖于差分向量的随机选择，这确保了搜索的随机性。另一方面，DA 使用确定性方法根据解决方案之间的距离及其质量来选择对比，同时将种群分为具有不同搜索策略的推测型和实践型思考者。DA 算法的计算复杂度（计算欧氏距离）稍高，但 DA 在各种优化问题中表现出更高的效率。

图 1 显示了推测型（红色，最佳）论点和实践型（蓝色）论点选择对立论点的原则。推测型的对立面选择在质量上相邻但在搜索空间中较远的对立面，而实践型的对立面则相反，选择在质量上较远但在搜索空间中较近的对立面。 

辩证搜索

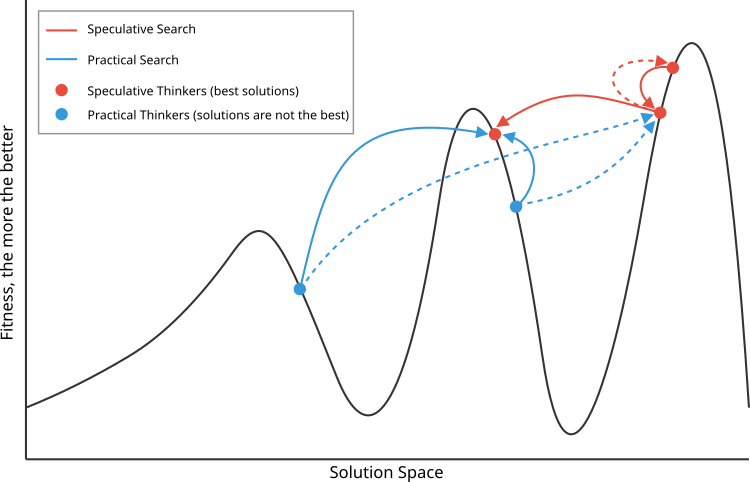
图1.DA 算法工作原理的示意图。实线 - 与首选对立面的相互作用，与不太首选的对立面形成对比，用虚线表示


辩证算法流

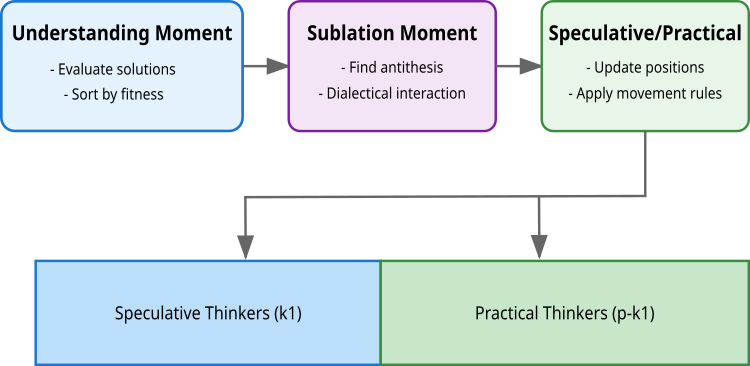
图 2.DA 算法逻辑的阶段

让我们继续编写算法的伪代码：

在第一次迭代中：随机放置代理：position[i] = random(min, max)

按最佳个体解决方案对群体进行排序

创建三种类型的代理群体：

  • 最佳思考者（1 个代理）
  • 推测型思考者（k1 = 3 个代理）
  • 实践型思考者（其余 50 个代理）
在后续迭代中：

    A.最好的思考者会向第二好的思考者迈进：

    position[0] = best[0] + rand(0,1) * (position[1] - position[0])

    B.推测型思考者：

    • 使用欧几里得距离找到最远的最近邻居：

    distance = √Σ(x₁-x₂)²

    • 更新相对于最远的位置：

    position[i] = best[i] + rand(0,1) * (position[furthest] - position[i])

    C.实用型思考者：

    • 随机选择两个推测型思考者
    • 移向最近的一个：

    position[i] = best[i] + rand(0,1) * (position[nearest] - position[i])

    每次移动后：

      • 更新最佳个体解决方案
      • 更新全局最优解
      • 根据个体决策的质量对代理进行分类

      重复该过程直到达到停止标准。

      在对算法进行完整分析之后，我们继续进行代码实现。让我们编写辩证优化算法的 C_AO_DA 类，从 C_AO 基类继承功能。

      算法参数：

      • 种群规模 ——对立面决定了参与优化的代理数量。
      • 推测型思考者指定了更多更优秀的代理能够更自由地寻找解决方案的数量。
      • 用于分析的邻居决定了每个推测型思考者（代理）与之交互以交换信息和改进其策略的最近邻居的数量。

      方法：

      • C_AO_DA () — 构造函数初始化主要参数并创建一个数组来存储它们。
      • SetParams () — 设置参数允许在操作期间更新算法参数的值。
      • Moving () 和 Revision () —— 用于在搜索空间中移动代理并修改找到的解决方案的函数。
      • EuclideanDistance () — 计算搜索空间中两个向量之间的距离，这对于选择代理找到的解决方案中最接近（推测型）和最远（实践型）的相似性是必要的。
      //——————————————————————————————————————————————————————————————————————————————
// Class implementing the dialectical optimization algorithm
class C_AO_DA : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_DA () { }
  C_AO_DA ()
  {
    ao_name = "DA";
    ao_desc = "Dialectical Algorithm";
    ao_link = "https://www.mql5.com/en/articles/16999";

    popSize = 50;       // population size
    k1      = 3;        // speculative thinkers
    k2      = 10;       // neighbours

    ArrayResize (params, 3);
    params [0].name = "popSize"; params [0].val = popSize;
    params [1].name = "k1";      params [1].val = k1;
    params [2].name = "k2";      params [2].val = k2;
  }

  // Setting algorithm parameters
  void SetParams ()
  {
    popSize = (int)params [0].val;
    k1      = (int)params [1].val;
    k2      = (int)params [2].val;
  }

  bool Init (const double &rangeMinP  [], // minimum search range
             const double &rangeMaxP  [], // maximum search range
             const double &rangeStepP [], // search step
             const int     epochsP = 0);  // number of epochs

  void Moving   ();    // Moving agents in the search space
  void Revision ();    // Review and update the best solutions found

  //----------------------------------------------------------------------------
  int k1;       // number of speculative thinkers
  int k2;       // number of neighbors to analyze

  private: //-------------------------------------------------------------------
  // Calculate the Euclidean distance between two vectors
  double EuclideanDistance (const double &vec1 [], const double &vec2 [], const int dim)
  {
    double sum  = 0;
    double diff = 0.0;

    for (int i = 0; i < dim; i++)
    {
      diff = vec1 [i] - vec2 [i];
      sum += diff * diff;
    }
    return MathSqrt (sum);
  }
};
//——————————————————————————————————————————————————————————————————————————————

      C_AO_DA 类的 Init 方法用于初始化优化算法的参数。它接受最小和最大搜索范围值、搜索步长以及执行优化的时期数（可选）的数组。该方法首先执行标准参数初始化；如果失败，则返回 “false”。如果初始化成功，该方法返回 “true”，确认算法已准备好运行。

      //——————————————————————————————————————————————————————————————————————————————
bool C_AO_DA::Init (const double &rangeMinP  [], // minimum search range
                    const double &rangeMaxP  [], // maximum search range
                    const double &rangeStepP [], // search step
                    const int     epochsP = 0)   // number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  return true;
}
//——————————————————————————————————————————————————————————————————————————————

      Moving 方法是代理在搜索空间中移动的一种实现。该方法的操作的详细描述如下：

      初始化：

      • 在开始时（!revision），使用每个坐标给定的最小和最大边界随机设置代理的初始位置。每个 “a[i]” 代理在给定范围内以一定的步长接收随机坐标。
      • 初始化后，“revision” 设置为 “true”，以防止在将来调用 Moving 方法时重新初始化。

      更新最佳思考者的位置：

      • 最佳思考者（代理）根据其先前的最佳位置和随机概率更新其坐标，并使用其最近邻居 “a[1]” 进行更新。

      更新推测型思考者的位置：

      • 对于 “k2” 到 “k1” 范围内的每个推测性思考者（代理），该方法搜索最远的前一个（antiPrevIND）和下一个邻居（antiNextIND）。
      • 然后，在考虑对立面时，使用最远的邻居来更新推测型思考者的坐标。

      更新实践型思考者的位置：

      • 实践型思考者（代理）的范围从 “k1” 到 “popSize”。
      • 代码随机选择两个推测型思考者并计算与它们的距离。然后，实践型思考者选择最接近的（两个选定的）思考者来更新其位置。
      • 每个坐标都根据所选邻居进行更新。

      辅助函数

      • EuclideanDistance — 计算多维空间中两点 “a” 和 “b” 之间的欧几里得距离的函数。
      • u.RNDfromCI — 从指定间隔返回一个随机数。
      • u.SeInDiSp — 根据范围将 “value” 转换为适当的步长。
      • u.RNDprobab — 返回具有均匀概率分布的随机数。
      //——————————————————————————————————————————————————————————————————————————————
// Implement agent movement in the search space
void C_AO_DA::Moving ()
{
  //----------------------------------------------------------------------------
  // Initialize the agents' positions randomly
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  //  Update the best thinker's position
  for (int c = 0; c < coords; c++)
  {
    a [0].c [c] = a [0].cB [c] + u.RNDprobab () * (a [1].c [c] - a [0].c [c]);
    a [0].c [c] = u.SeInDiSp (a [0].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }

  //----------------------------------------------------------------------------
  double dist_next   = -DBL_MAX;  // maximum distance to the next neighbor
  double dist_prev   = -DBL_MAX;  // maximum distance to the previous neighbor
  double dist        = 0.0;       // current distance
  int    antiNextIND = 0;         // index of the most distant next neighbor
  int    antiPrevIND = 0;         // index of the most distant previous neighbor
  int    antiIND     = 0;         // selected index to update position

  // Update the positions of speculative thinkers -------------------------------
  for (int i = k2; i < k1; i++)
  {
    // Find the most distant previous neighbor
    for (int j = 1; j <= k2; j++)
    {
      dist = EuclideanDistance (a [i].cB, a [i - j].cB, coords);
      if (dist > dist_prev)
      {
        dist_prev   = dist;
        antiPrevIND = i - j;
      }
    }

    // Find the farthest next neighbor
    for (int j = 1; j <= k2; j++)
    {
      dist = EuclideanDistance (a [i].cB, a [i + j].cB, coords);
      if (dist > dist_next)
      {
        dist_next = dist;
        antiNextIND  = i + j;
      }
    }

    // Select the most distant neighbor to update position
    if (dist_prev > dist_next) antiIND = antiPrevIND;
    else                       antiIND = antiNextIND;

    // Update the speculative thinker's coordinates
    for (int c = 0; c < coords; c++)
    {
      a [i].c [c] = a [i].cB [c] + u.RNDbool () * (a [antiIND].c [c] - a [i].c [c]);
      //a [i].c [c] = a [i].cB [c] + u.RNDprobab () * (a [antiIND].c [c] - a [i].c [c]);
      a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }

  // Update the positions of practical thinkers --------------------------------
  for (int i = k1; i < popSize; i++)
  {
    // Random selection of two speculative thinkers
    antiNextIND = u.RNDintInRange (0, k1 - 1);
    antiPrevIND = u.RNDintInRange (0, k1 - 1);

    if (antiNextIND == antiPrevIND) antiNextIND = antiPrevIND + 1;

    // Calculate distances to selected thinkers
    dist_next = EuclideanDistance (a [i].cB, a [antiNextIND].cB, coords);
    dist_prev = EuclideanDistance (a [i].cB, a [antiPrevIND].cB, coords);

    // Select the closest thinker to update the position
    if (dist_prev < dist_next) antiIND = antiPrevIND;
    else                       antiIND = antiNextIND;

    // Update the coordinates of the practical thinker
    for (int c = 0; c < coords; c++)
    {
      a [i].c [c] = a [i].cB [c] + u.RNDprobab () * (a [antiIND].c [c] - a [i].c [c]);
      a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

      Revision 方法负责修改和更新为代理找到的最佳解决方案。以下是该方法工作原理的详细分析：

      更新找到的最佳解决方案：在 “for” 循环中，该方法遍历群体中的每个代理。对于每个代理，比较适应度函数 “a [i].f” 的当前值：

      • 全局最佳解决方案 —— 如果代理的 f 函数的值大于当前 fB 全局最佳解决方案，则更新全局解决方案并保存找到此最佳解决方案的代理 (ind) 的索引。
      • 个人最佳决策 —— 每个代理的 f 值也与其个体最佳 fB 值进行比较。如果当前值更好，则更新代理的个体最佳值，并将其当前 c 坐标复制到其个体 cB 坐标。

      更新全局最佳解决方案的坐标：如果找到了成为全局最佳解决方案（ind != -1）的代理的索引，则将该代理的坐标复制到 cB 全局坐标。

      代理排序：在方法结束时，创建 aT 数组并更改其大小以匹配种群规模。然后调用 u.Sorting_fB 函数，该函数根据找到的最佳解决方案（fB 值）对代理进行排序。

      //——————————————————————————————————————————————————————————————————————————————
// Review and update the best solutions found
void C_AO_DA::Revision ()
{
  int ind = -1;

  // Update the best solutions found for each agent
  for (int i = 0; i < popSize; i++)
  {
    // Update the global best solution
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }

    // Update the agent's personal best solution
    if (a [i].f > a [i].fB)
    {
      a [i].fB = a [i].f;
      ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  // Update the global best solution coordinates
  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  // Sort agents by their best found solutions
  static S_AO_Agent aT []; ArrayResize (aT, popSize);
  u.Sorting_fB (a, aT, popSize);
}
//——————————————————————————————————————————————————————————————————————————————


      测试结果

      现在是时候取得 DA 测试的结果了。我们再来关注一下 Moving 方法。反映作者观点的字符串被注释掉并以绿色突出显示。因此，结果如下：

      DA|Dialectical Algorithm|50.0|30.0|1.0|
      =============================
      5 Hilly's; Func runs:10000; result：0.749254786734898
      25 Hilly's；Func runs：10000; result：0.36669693350810206
      500 Hilly's；Func runs：10000; result：0.2532075139007539
      =============================
      5 Forest's; Func runs：10000; result：0.7626421292861323
      25 Forest's; Func runs：10000; result：0.4144802592253075
      500 Forest's; Func runs：10000; result：0.2006796312431603
      =============================
      5 Megacity's; Func runs:10000; result：0.36
      25 Megacity's; Func runs:10000; result：0.15969230769230774
      500 Megacity's；Func runs：10000; result：0.0952000000000008
      =============================
      All score:3.36185（37.35%）

      这些结果远非最佳，但它们本可以进入排名表。但问题是我犯了一个错误，我没有使用 [0.0;1.0] 范围内的随机数，而是在代码中插入了一个随机布尔数函数（标记为红色）。

      随机变化的逻辑本质是：有 50% 的概率，对应的坐标保持不变，或者被对立面的坐标所取代。在我看来，这更符合作者关于正题和反题对立的思想。对于实践型思考者来说，一切都保持不变；他们的最终论点是当前论点与推测型思考者的对立论点之间的共生关系。于是，机缘巧合之下，得到了如下结果：

      DA|Dialectical Algorithm|50.0|40.0|1.0|
      =============================
      5 Hilly's; Func runs:10000; result：0.8618313952293774
      25 Hilly's；Func runs：10000; result：0.700333708747176
      500 Hilly's；Func runs：10000; result：0.3372386732170054
      =============================
      5 Forest's; Func runs：10000; result：0.9816317765399738
      25 Forest's; Func runs：10000; result：0.7277214130784131
      500 Forest's; Func runs：10000; result：0.28717629901518305
      =============================
      5 Megacity's; Func runs:10000; result：0.7030769230769229
      25 Megacity's; Func runs:10000; result：0.4529230769230769
      500 Megacity's；Func runs：10000; result：0.16366923076923204
      =============================
      All score:5.21560（57.95%）

      这些成果确实令人印象深刻！由于性能的显著提高是在不知不觉中发生的，我无法将 m 索引分配给修改后的版本。在我们的排名表中，算法将保持为 DA。由此可见，辩证算法表现出了优异的性能，总体有效率达到了 57.95%。该算法的一个关键特征是它能够在全局和局部搜索之间有效地平衡，这要归功于它将思考者分为推测型思考者和实践型思考者。

      从可视化中可以看出，该算法很快就找到了显著的局部最优解，尽管它缺乏被认为是完美的收敛精度。然而，无论如何，结果都相当不错。

      Hilly

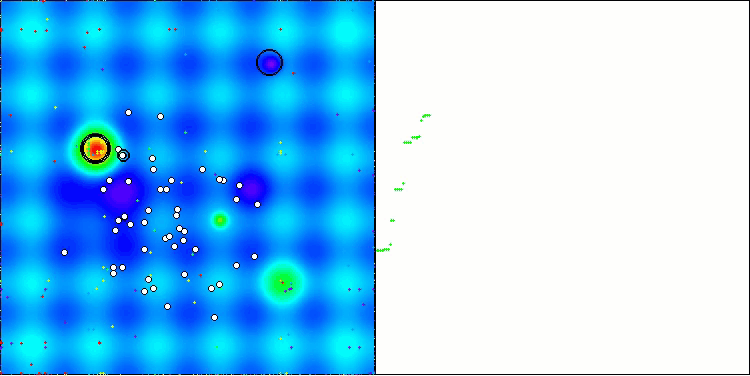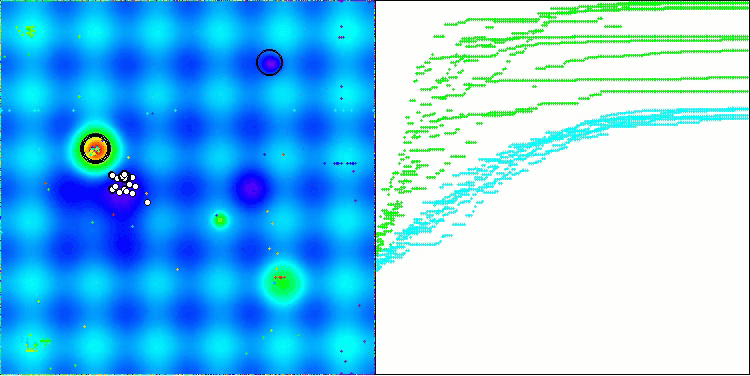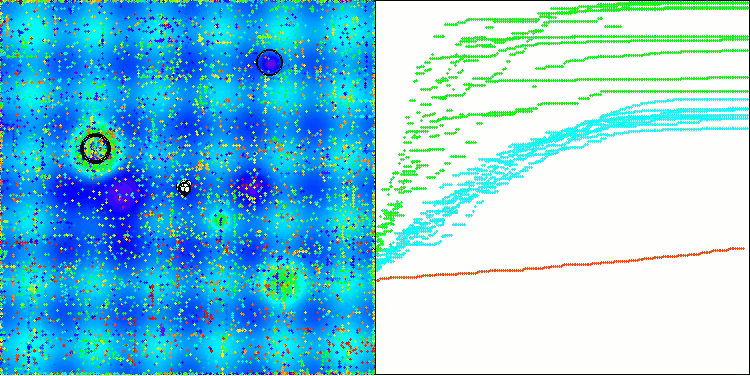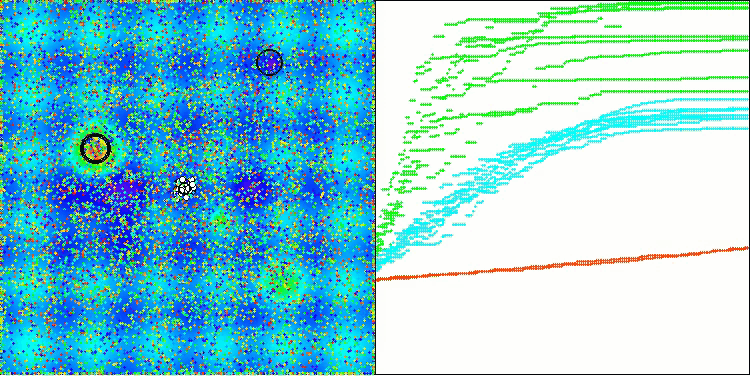
        Hilly 测试函数上的 DA

      Forest

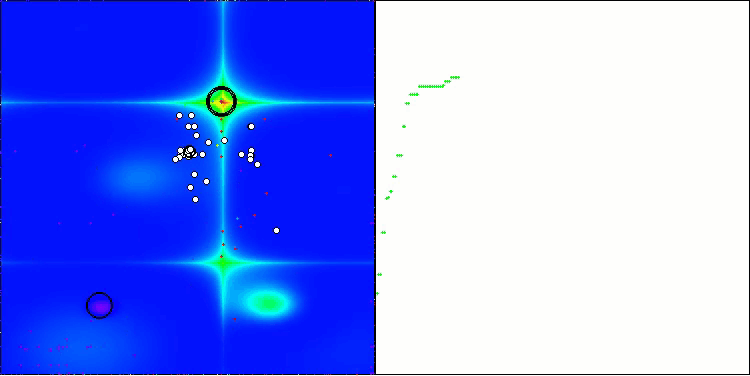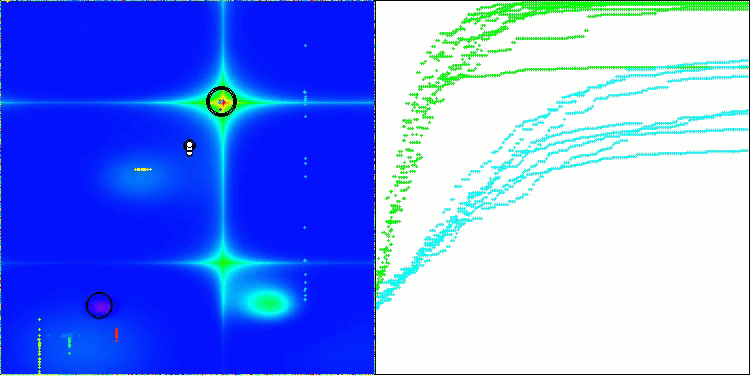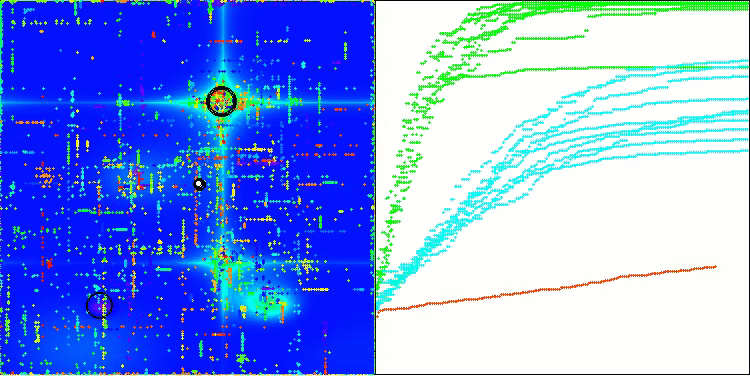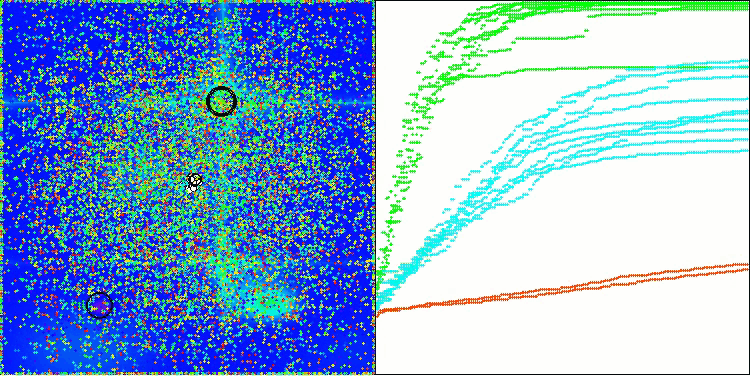
      Forest 测试函数上的 DA

      Megacity

      Megacity 测试函数上的 DA

      根据测试结果，DA 算法在我们的表中排名第 12 位，这是一个良好而稳定的结果。

      # 算法 描述 Hilly Hilly 最终 Forest Forest 最终 Megacity (discrete) Megacity 最终 最终结果 最大值的百分比
      10 p（5 F） 50 p（25 F） 1000 p（500 F） 10 p（5 F） 50 p（25 F） 1000 p（500 F） 10 p（5 F） 50 p（25 F） 1000 p（500 F）
      1 ANS 跨邻里搜索（across neighbourhood search） 0.94948 0.84776 0.43857 2.23581 1.00000 0.92334 0.39988 2.32323 0.70923 0.63477 0.23091 1.57491 6.134 68.15
      2 CLA 密码锁算法（joo） 0.95345 0.87107 0.37590 2.20042 0.98942 0.91709 0.31642 2.22294 0.79692 0.69385 0.19303 1.68380 6.107 67.86
      3 AMOm 动物迁徙优化 M（animal migration optimization M） 0.90358 0.84317 0.46284 2.20959 0.99001 0.92436 0.46598 2.38034 0.56769 0.59132 0.23773 1.39675 5.987 66.52
      4 (P+O)ES (P+O) 演进战略（(P+O) evolution strategies） 0.92256 0.88101 0.40021 2.20379 0.97750 0.87490 0.31945 2.17185 0.67385 0.62985 0.18634 1.49003 5.866 65.17
      5 CTA 彗尾算法（joo） 0.95346 0.86319 0.27770 2.09435 0.99794 0.85740 0.33949 2.19484 0.88769 0.56431 0.10512 1.55712 5.846 64.96
      6 TETA 时间演化旅行算法（joo） 0.91362 0.82349 0.31990 2.05701 0.97096 0.89532 0.29324 2.15952 0.73462 0.68569 0.16021 1.58052 5.797 64.41
      7 SDSm 随机扩散搜索 M（stochastic diffusion search M） 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
      8 AAm 射箭算法 M（archery algorithm M） 0.91744 0.70876 0.42160 2.04780 0.92527 0.75802 0.35328 2.03657 0.67385 0.55200 0.23738 1.46323 5.548 61.64
      9 ESG 社会群体的进化（joo） 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
      10 SIA 模拟各向同性退火（joo） 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
      11 ACS 人工协同搜索（artificial cooperative search） 0.75547 0.74744 0.30407 1.80698 1.00000 0.88861 0.22413 2.11274 0.69077 0.48185 0.13322 1.30583 5.226 58.06
      12 DA 辩证算法 0.86183 0.70033 0.33724 1.89940 0.98163 0.72772 0.28718 1.99653 0.70308 0.45292 0.16367 1.31967 5.216 57.95
      13 BHAm 黑洞算法 M 0.75236 0.76675 0.34583 1.86493 0.93593 0.80152 0.27177 2.00923 0.65077 0.51646 0.15472 1.32195 5.196 57.73
      14 ASO 无政府社会优化（anarchy society optimization） 0.84872 0.74646 0.31465 1.90983 0.96148 0.79150 0.23803 1.99101 0.57077 0.54062 0.16614 1.27752 5.178 57.54
      15 AOSm 原子轨道搜索 M 0.80232 0.70449 0.31021 1.81702 0.85660 0.69451 0.21996 1.77107 0.74615 0.52862 0.14358 1.41835 5.006 55.63
      16 TSEA 龟壳进化算法（joo） 0.96798 0.64480 0.29672 1.90949 0.99449 0.61981 0.22708 1.84139 0.69077 0.42646 0.13598 1.25322 5.004 55.60
      17 DE 差分进化（differential evolution） 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
      18 CRO 化学反应优化（chemical reaction optimization） 0.94629 0.66112 0.29853 1.90593 0.87906 0.58422 0.21146 1.67473 0.75846 0.42646 0.12686 1.31178 4.892 54.36
      19 BSA 鸟群算法（bird swarm algorithm） 0.89306 0.64900 0.26250 1.80455 0.92420 0.71121 0.24939 1.88479 0.69385 0.32615 0.10012 1.12012 4.809 53.44
      20 HS 和声搜索（harmony search） 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
      21 SSG 树苗播种和生长（saplings sowing and growing） 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
      22 BCOm 细菌趋化性优化 M（bacterial chemotaxis optimization M） 0.75953 0.62268 0.31483 1.69704 0.89378 0.61339 0.22542 1.73259 0.65385 0.42092 0.14435 1.21912 4.649 51.65
      23 ABO 非洲水牛优化 0.83337 0.62247 0.29964 1.75548 0.92170 0.58618 0.19723 1.70511 0.61000 0.43154 0.13225 1.17378 4.634 51.49
      24 (PO)ES (PO) 进化策略（(PO) evolution strategies） 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
      25 TSm 禁忌搜索 M（tabu search M） 0.87795 0.61431 0.29104 1.78330 0.92885 0.51844 0.19054 1.63783 0.61077 0.38215 0.12157 1.11449 4.536 50.40
      26 BSO 头脑风暴优化（brain storm optimization） 0.93736 0.57616 0.29688 1.81041 0.93131 0.55866 0.23537 1.72534 0.55231 0.29077 0.11914 0.96222 4.498 49.98
      27 WOAm Wale 优化算法 M（wale optimization algorithm M） 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
      28 AEFA 人工电场算法（artificial electric field algorithm） 0.87700 0.61753 0.25235 1.74688 0.92729 0.72698 0.18064 1.83490 0.66615 0.11631 0.09508 0.87754 4.459 49.55
      29 AEO 基于人工生态系统的优化算法 0.91380 0.46713 0.26470 1.64563 0.90223 0.43705 0.21400 1.55327 0.66154 0.30800 0.28563 1.25517 4.454 49.49
      30 ACOm 蚁群优化M（ant colony optimization M） 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
      31 BFO-GA 细菌觅食优化 - ga（bacterial foraging optimization - ga） 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
      32 SOA 简单优化算法 0.91520 0.46976 0.27089 1.65585 0.89675 0.37401 0.16984 1.44060 0.69538 0.28031 0.10852 1.08422 4.181 46.45
      33 ABHA 人工蜂巢算法（artificial bee hive algorithm） 0.84131 0.54227 0.26304 1.64663 0.87858 0.47779 0.17181 1.52818 0.50923 0.33877 0.10397 0.95197 4.127 45.85
      34 ACMO 大气云模型优化（atmospheric cloud model optimization） 0.90321 0.48546 0.30403 1.69270 0.80268 0.37857 0.19178 1.37303 0.62308 0.24400 0.10795 0.97503 4.041 44.90
      35 ADAMm 自适应矩估计 M 0.88635 0.44766 0.26613 1.60014 0.84497 0.38493 0.16889 1.39880 0.66154 0.27046 0.10594 1.03794 4.037 44.85
      36 ATAm 人工部落算法 M 0.71771 0.55304 0.25235 1.52310 0.82491 0.55904 0.20473 1.58867 0.44000 0.18615 0.09411 0.72026 3.832 42.58
      37 ASHA 人工喷淋算法（artificial showering algorithm） 0.89686 0.40433 0.25617 1.55737 0.80360 0.35526 0.19160 1.35046 0.47692 0.18123 0.09774 0.75589 3.664 40.71
      38 ASBO 适应性社会行为优化（adaptive social behavior optimization） 0.76331 0.49253 0.32619 1.58202 0.79546 0.40035 0.26097 1.45677 0.26462 0.17169 0.18200 0.61831 3.657 40.63
      39 MEC 思维进化计算（mind evolutionary computation） 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
      40 IWO 入侵性杂草优化（invasive weed optimization） 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
      41 Micro-AIS 微型人工免疫系统（micro artificial immune system） 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54
      42 COAm 布谷鸟优化算法 M（cuckoo optimization algorithm M） 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21
      43 SDOm 螺旋动力学优化 M（spiral dynamics optimization M） 0.74601 0.44623 0.29687 1.48912 0.70204 0.34678 0.10944 1.15826 0.42833 0.16767 0.03663 0.63263 3.280 36.44
      44 NMm Nelder-Mead 方法 M 0.73807 0.50598 0.31342 1.55747 0.63674 0.28302 0.08221 1.00197 0.44667 0.18667 0.04028 0.67362 3.233 35.92
      45 BBBC 大爆炸-大挤压算法 0.60531 0.45250 0.31255 1.37036 0.52323 0.35426 0.20417 1.08166 0.39769 0.19431 0.11286 0.70486 3.157 35.08
      RW 随机游走 0.48754 0.32159 0.25781 1.06694 0.37554 0.21944 0.15877 0.75375 0.27969 0.14917 0.09847 0.52734 2.348 26.09


      总结

      辩证算法是一种基于辩证法哲学概念的创新优化方法，其中对立面的相互作用实现了改进的解决方案。该算法通过将人群独特地划分为推测型思考者和实践型思考者，成功地结合了全局搜索和局部搜索的概念，从而确保了解决方案空间的探索和利用之间的有效平衡。

      该算法结构由三个关键步骤组成，提供了一种系统的优化方法。在他们的工作中，推测型思考者对解决方案空间进行了广泛的搜索（尽管通常在优化算法中，最佳解决方案是经过改进的，而不是“分散”在搜索空间中），而实践型思考者则专注于有前景领域的局部优化。这种划分使算法能够有效地探索解空间，避免陷入局部最优，特别是由于我犯的随机错误，算法逻辑变得更加接近辩证对立的主题。

      测试结果证实了该算法的高效性，具有平衡的搜索能力，在各种类型的任务上提供了足够高的性能。与其他算法相比，DA 没有显示出明显的偏差，无论是好是坏，并且在表中显示了均匀稳定的颜色渐变结果。总体性能指标表明了该算法与现有优化方法相比的竞争力。这种哲学原理和数学方法的结合为解决复杂的优化问题创造了一个强大的工具。

      Tab

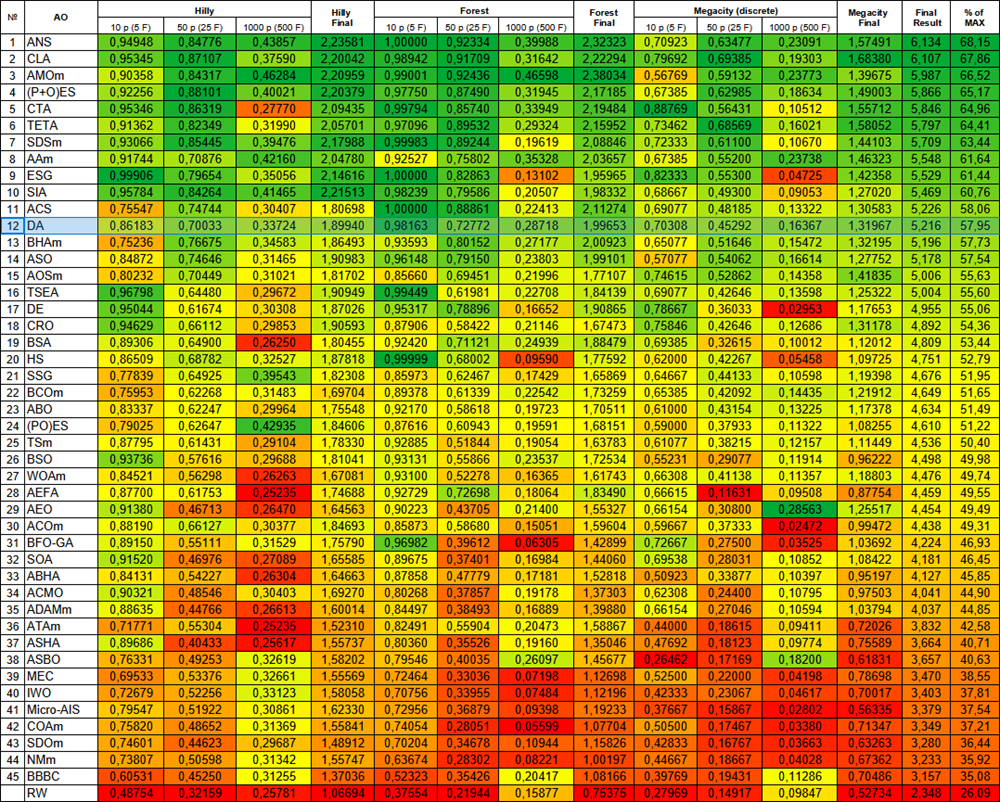
      图 3.根据相应测试的算法颜色分级

      图表

      图 4.算法测试结果直方图（范围从 0 到 100，越高越好，其中 100 是可能的最大理论结果，存档中有一个用于计算评级表的脚本）


      DA 的优缺点：

      优点：

      1. 外部参数很少，只有两个，不包括种群规模。
      2. 实现简单。
      3. 相当快。
      4. 平衡，在小型和大型问题上都有良好的表现。

      缺点：

      1. 结果分散。

      这篇文章附有一个归档，其中包含当前版本的算法代码。文章作者不对规范算法描述的绝对准确性负责。为提高搜索能力，已对其中多项功能进行了修改。文章中提出的结论和判断都是基于实验结果。

      本文中用到的程序

      # 名称 类型 描述
      1 #C_AO.mqh
      		 包含文件
      		 种群优化算法的父类
      2 #C_AO_enum.mqh
      		 包含文件
      		 种群优化算法的枚举
      3 TestFunctions.mqh
      		 包含文件
      		 测试函数库
      4
      		 TestStandFunctions.mqh
      		 包含文件
      		 试验台函数库
      5
      		 Utilities.mqh
      		 包含文件
      		 辅助函数库
      6
      		 CalculationTestResults.mqh
      		 包含文件
      		 用于计算比较表中结果的脚本
      7
      		 Testing AOs.mq5
      		 脚本 所有种群优化算法的统一测试平台
      8
      		 Simple use of population optimization algorithms.mq5
      		 脚本
      		 使用不带可视化的种群优化算法的简单示例
      9
      		 Test_AO_DA.mq5
      		 脚本 DA 试验台

      本文由MetaQuotes Ltd译自俄文
      原文地址： https://www.mql5.com/ru/articles/16999

      附加的文件 |
      下载ZIP
      DA.zip (158.45 KB)

      注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

      本文由网站的一位用户撰写，反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责，也不对因使用所述解决方案、策略或建议而产生的任何后果负责。

      该作者的其他文章

      前往讨论
      交易中的神经网络：配备注意力机制（MASAAT）的智代融汇 交易中的神经网络：配备注意力机制（MASAAT）的智代融汇
      我们概述多智代自适应投资组合优化框架（MASAAT），其结合了注意力机制和时间序列分析。MASAAT 生成一组智代，分析价格序列和方向变化，能够在不同细节层次识别资产价格的明显波动。
      血液遗传优化算法（BIO） 血液遗传优化算法（BIO）
      我向大家介绍我的新种群优化算法——血液遗传优化算法（Blood Inheritance Optimization，BIO），该算法的灵感源自人类血型遗传系统。在该算法中，每个解都有其自身的“血型”，这一血型决定了其进化方式。正如自然界中，孩子的血型是依据特定规则遗传而来，在BIO算法中，新解通过一套遗传与变异机制来获取自身特性。
      接受者操作特征（ROC）曲线入门 接受者操作特征（ROC）曲线入门
      ROC 曲线是用于评估分类器性能的图形工具。尽管 ROC 图形相对简单，但在实践中使用它们时，仍存在一些常见的误解和误区。本文旨在为那些希望理解分类器性能评估的交易者提供一份关于 ROC 图形的入门介绍。
      用于预测金融时间序列的生物神经元 用于预测金融时间序列的生物神经元
      我们将为时间序列预测建立一个生物学上正确的神经元系统。在神经网络架构中引入类似等离子体的环境创造了一种“集体智能”，其中每个神经元不仅通过直接连接，还通过长距离电磁相互作用影响系统的运行。让我们看看神经大脑建模系统在市场上的表现。