
Диалектический поиск — Dialectic Search (DA)
Содержание
Введение
Диалектический материализм основывается на принципе единства и борьбы противоположностей в природе, обществе и мышлении. В его основе лежит представление о том, что развитие происходит через конфликт противоположных сил и тенденций, где каждое явление содержит внутренние противоречия. Ключевой принцип данного подхода — переход количественных изменений в качественные, когда постепенные изменения накапливаются и приводят к резким качественным скачкам. Процесс развития следует закону "отрицание отрицания", при котором тезис сменяется антитезисом, порождая синтез, как новое качество, сохраняющее лучшее из предыдущих состояний.
В мире оптимизационных алгоритмов, где математическая точность встречается с философской мудростью, появился уникальный метод, черпающий вдохновение из диалектического материализма — Dialectical Algorithm (DA). Этот алгоритм, представленный как синтез классической диалектики и современных методов оптимизации, переосмысливает процесс поиска оптимальных решений через призму философского противостояния тезиса и антитезиса. В основе DA лежит идея о том, что любое решение (тезис) содержит в себе потенциал для улучшения через взаимодействие со своей противоположностью (антитезисом).
В алгоритмической реализации этот принцип отражается через взаимодействие спекулятивных мыслителей, которые ищут новые решения, отдаляясь от известных, и практических мыслителей, стремящихся к проверенным решениям. Материалистический аспект диалектического материализма проявляется в опоре на объективные критерии оценки решений и практическую проверку результатов. Развитие происходит циклически: найденные решения порождают новые противоречия, что ведет к следующему витку поиска, отражая непрерывность процесса познания и совершенствования.
Алгоритм реализует этот принцип через три ключевых момента: понимание, где происходит оценка и сортировка решений; диалектическое взаимодействие, в котором решения находят свои антитезисы; и момент синтеза, где формируются новые, улучшенные решения. Особенность алгоритма заключается в разделении популяции на два типа мыслителей: спекулятивных (k1), которые исследуют пространство решений широкими шагами (через взаимодействие схожих решений по качеству, но удаленных друг от друга в пространстве поиска), и практических (p-k1), осуществляющих локальный поиск (далеких по качеству, но близких в пространстве решений). Это разделение отражает философский принцип единства и борьбы противоположностей, где каждая группа вносит свой уникальный вклад в процесс оптимизации.
Диалектический поиск (Dialectic Search, DA) был представлен Serdar Kadioglu и Meinolf Sellmann в 2009 году. Этот метод использует диалектический подход для решения задач оптимизации с ограничениями, продолжая традиции, заложенные диалектическим материализмом в исследовании и поиске новых решений.
Реализация алгоритма
В основе алгоритма лежит популяция из p решений (обычно 50), каждое из которых представляет собой вектор координат в пространстве поиска. Эта популяция разделяется на две группы: k1 спекулятивных мыслителей (лучшие решения) и (p-k1) практических мыслителей.
Первый этап — Момент понимания. Здесь происходит оценка всех решений через целевую функцию f(x). Решения сортируются по качеству, и лучшие k1 решений становятся спекулятивными мыслителями, а остальные — практическими. На этом этапе также происходит принятие или отклонение новых решений, на основе их качества по сравнению с предыдущими итерациями (наилучшее индивидуальное решение для мыслителя).
Второй этап — Диалектический момент. На этом этапе к каждому решению ведется поиск антитезиса — противоположности, с которой решение будет взаимодействовать. Для спекулятивных мыслителей поиск антитезиса основан на максимизации расстояния при сохранении качества решения (идеалистическая диалектика). Для первого решения антитезисом становится второе лучшее, для последнего — предпоследнее, для остальных выбирается сосед с наибольшим расстоянием. Практические мыслители ищут антитезис через минимизацию расстояния при достаточной разнице в качестве (материалистическая диалектика).
Третий этап — Спекулятивный/Практический Момент (Момент обновления). Здесь происходит обновление позиций всех решений с использованием найденных антитезисов. Спекулятивные мыслители используют равномерное распределение, что обеспечивает широкий поиск в пространстве решений. Практические мыслители используют нормальное распределение. Мои эксперименты показали, что для обоих типов мыслителей лучше всего работает равномерное распределение.
Формула обновления позиций одинакова для всех: X(i) = X(i) + μ⊙(Xanti(i) - X(i)), где μ — случайный вектор из соответствующего распределения, ⊙ означает поэлементное умножение. Это обеспечивает баланс между исследованием пространства решений через спекулятивных мыслителей и уточнением найденных решений с помощью практических мыслителей.
Диалектический алгоритм (DA) имеет сходства с алгоритмом дифференциальной эволюции DE, в формуле обновления решений. В DE новый вектор создается путем добавления к целевому вектору масштабированной разности двух других векторов (x_new = x_target + F(x_r1 - x_r2)), в то время как DA использует схожий принцип, но с антитезисом и адаптивным коэффициентом (x_new = x + μ(x_anti - x)).
Однако ключевое различие заключается в способе выбора векторов для генерации новых решений. DE полагается на случайный выбор векторов разности, что обеспечивает стохастическую природу поиска. DA, напротив, использует детерминированный подход к выбору антитезисов, основанный на расстоянии между решениями и их качестве, при этом разделяя популяцию на спекулятивных и практических мыслителей с различными стратегиями поиска. Алгоритм DA демонстрируют вычислительную сложность немного больше (вычисление евклидова расстояние), но DA демонстрирует более высокую эффективность в различных задачах оптимизации.
На рисунке 1 показан принцип выбора антитезисов для спекулятивных (красные, лучшие) тезисов и материальных (синие). Спекулятивные выбирают антитезисы соседние по качеству, но более удаленные в пространстве поиска, а материальные наоборот, более дальние по качеству, но близкие в пространстве поиска.
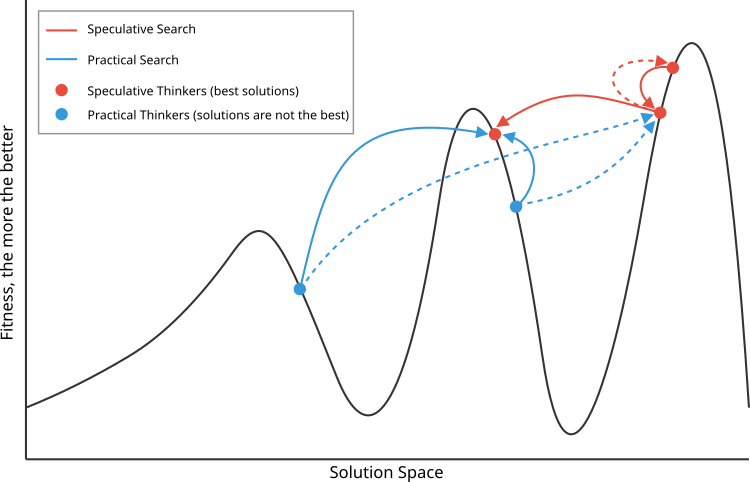
Рисунок 1. Схематичное представление принципа работы алгоритма DA. Сплошные линии - взаимодействие с предпочтительными антитезисами, в отличие от менее предпочтительных, обозначенных пунктирными линиями
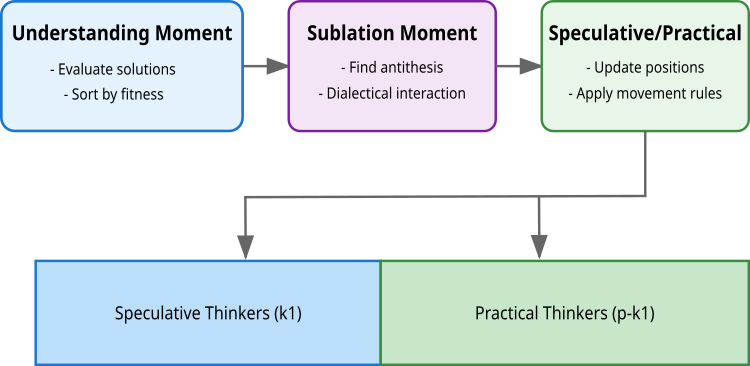
Рисунок 2. Этапы логики алгоритма DA
Переходим к написанию псевдокода алгоритма:
На первой итерации: Случайно размещаем агентов: position[i] = random(min, max)
Сортируем популяцию по лучшим индивидуальным решениям
Создаём популяцию из трёх типов агентов:
- Лучший мыслитель (1 агент)
- Спекулятивные мыслители (k1 = 3 агента)
- Практические мыслители (остальные из 50 агентов)
А. Лучший мыслитель движется в сторону второго лучшего:
position[0] = best[0] + rand(0,1) * (position[1] - position[0])Б. Спекулятивные мыслители:
- Находят самых далёких ближайших соседей через евклидово расстояние:
- Обновляют позицию относительно самого далёкого:
В. Практические мыслители:
- Выбирают двух случайных спекулятивных мыслителей
- Движутся к ближайшему:
position[i] = best[i] + rand(0,1) * (position[nearest] - position[i])
После каждого движения:- Обновляем лучшие личные решения
- Обновляем глобальное лучшее решение
- Сортируем агентов по качеству личных решений
Процесс повторяется до достижения критерия остановки
После полного разбора алгоритма, переходим к реализации в коде. Напишем класс "C_AO_DA" диалектического алгоритма оптимизации, наследуя функциональность от базового класса "C_AO".
Параметры алгоритма:
- Размер популяции— антитезисы определяют количество агентов, которые будут участвовать в процессе оптимизации.
- Спекулятивные мыслители — указывает количество лучших агентов, способных к более свободному поиску решений.
- Соседи для анализа — определяет количество ближайших соседей, с которыми каждый из спекулятивных мыслителей (агентов) будет взаимодействовать для обмена информацией и улучшения своей стратегии.
Методы:
- C_AO_DA () — конструктор инициализирует основные параметры, а также создаёт массив для хранения параметров.
- SetParams () — установка параметров позволяет обновлять значения параметров алгоритма в процессе работы.
- Moving () и Revision () — функции для перемещения агентов в пространстве поиска и пересмотра найденных решений.
- EuclideanDistance () — вычисление расстояния в пространстве поиска между двумя векторами, что необходимо для выбора ближайшего (для спекулятивных) и дальнего (для практических) сходства решений, найденных агентами.
//—————————————————————————————————————————————————————————————————————————————— // Класс реализующий диалектический алгоритм оптимизации class C_AO_DA : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_DA () { } C_AO_DA () { ao_name = "DA"; ao_desc = "Dialectical Algorithm"; ao_link = "https://www.mql5.com/ru/articles/16999"; popSize = 50; // размер популяции k1 = 3; // спекулятивные мыслители k2 = 10; // соседи ArrayResize (params, 3); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "k1"; params [1].val = k1; params [2].name = "k2"; params [2].val = k2; } // Установка параметров алгоритма void SetParams () { popSize = (int)params [0].val; k1 = (int)params [1].val; k2 = (int)params [2].val; } bool Init (const double &rangeMinP [], // минимальный диапазон поиска const double &rangeMaxP [], // максимальный диапазон поиска const double &rangeStepP [], // шаг поиска const int epochsP = 0); // количество эпох void Moving (); // Перемещение агентов в пространстве поиска void Revision (); // Пересмотр и обновление лучших найденных решений //---------------------------------------------------------------------------- int k1; // количество спекулятивных мыслителей int k2; // количество соседей для анализа private: //------------------------------------------------------------------- // Вычисление евклидового расстояния между двумя векторами double EuclideanDistance (const double &vec1 [], const double &vec2 [], const int dim) { double sum = 0; double diff = 0.0; for (int i = 0; i < dim; i++) { diff = vec1 [i] - vec2 [i]; sum += diff * diff; } return MathSqrt (sum); } }; //——————————————————————————————————————————————————————————————————————————————
Метод "Init" класса "C_AO_DA" предназначен для инициализации параметров алгоритма оптимизации. Он принимает массивы минимальных и максимальных значений диапазона поиска, шаги поиска, а также опционально количество эпох для выполнения оптимизации. Метод сначала выполняет стандартную инициализацию параметров; если она не проходит успешно, он возвращает значение "false". Если инициализация успешна, метод возвращает "true", подтверждая готовность алгоритма к работе.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_DA::Init (const double &rangeMinP [], // минимальный диапазон поиска const double &rangeMaxP [], // максимальный диапазон поиска const double &rangeStepP [], // шаг поиска const int epochsP = 0) // количество эпох { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- return true; } //——————————————————————————————————————————————————————————————————————————————
Метод "Moving" представляет собой реализацию движения агентов в пространстве поиска, подробное описание работы метода:
Инициализация:
- В начале (!revision) задаются начальные позиции агентов случайным образом, используя заданные минимальные и максимальные границы для каждой координаты. Каждый агент "a [i]" получает случайные координаты в заданных диапазонах и с определённым шагом.
- После инициализации "revision" устанавливается в "true", что предотвращает повторную инициализацию при будущих вызовах метода "Moving".
Обновление позиции лучшего мыслителя:
- Лучший мыслитель (агент) обновляет свои координаты, основываясь на своей предыдущей лучшей позиции и случайной вероятности, используя ближайшего соседа "a [1]" для обновления.
Обновление позиций спекулятивных мыслителей:
- Для каждого спекулятивного мыслителя (агента) в диапазоне от "k2" до "k1", метод ищет наиболее удаленного предыдущего (antiPrevIND) и следующего соседа (antiNextIND).
- Затем обновляется координата спекулятивного мыслителя с использованием наиболее удаленного соседа при рассмотрении антитезиса.
Обновление позиций практических мыслителей:
- Практические мыслители (агенты) находятся в диапазоне от "k1" до "popSize".
- Код случайным образом выбирает двух спекулятивных мыслителей и вычисляет расстояния до них. Затем практический мыслитель выбирает ближайшего (из выбранных двух) мыслителя для обновления своей позиции.
- Каждая координата обновляется с учетом выбранного соседа.
Вспомогательные функции
- EuclideanDistance — функция, вычисляющая евклидово расстояние между двумя точками "a" и "b" в многомерном пространстве.
- u.RNDfromCI — возвращает случайное число из указанного интервала.
- u.SeInDiSp — приводит "value" к подходящему шагу в зависимости от диапазона.
- u.RNDprobab — возвращает случайное число с равномерным распределением вероятности.
//—————————————————————————————————————————————————————————————————————————————— // Реализация движения агентов в пространстве поиска void C_AO_DA::Moving () { //---------------------------------------------------------------------------- // Начальная инициализация позиций агентов случайным образом if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- // Обновление позиции лучшего мыслителя for (int c = 0; c < coords; c++) { a [0].c [c] = a [0].cB [c] + u.RNDprobab () * (a [1].c [c] - a [0].c [c]); a [0].c [c] = u.SeInDiSp (a [0].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } //---------------------------------------------------------------------------- double dist_next = -DBL_MAX; // максимальное расстояние до следующего соседа double dist_prev = -DBL_MAX; // максимальное расстояние до предыдущего соседа double dist = 0.0; // текущее расстояние int antiNextIND = 0; // индекс наиболее удаленного следующего соседа int antiPrevIND = 0; // индекс наиболее удаленного предыдущего соседа int antiIND = 0; // выбранный индекс для обновления позиции // Обновление позиций спекулятивных мыслителей ------------------------------- for (int i = k2; i < k1; i++) { // Поиск наиболее удаленного предыдущего соседа for (int j = 1; j <= k2; j++) { dist = EuclideanDistance (a [i].cB, a [i - j].cB, coords); if (dist > dist_prev) { dist_prev = dist; antiPrevIND = i - j; } } // Поиск наиболее удаленного следующего соседа for (int j = 1; j <= k2; j++) { dist = EuclideanDistance (a [i].cB, a [i + j].cB, coords); if (dist > dist_next) { dist_next = dist; antiNextIND = i + j; } } // Выбор наиболее удаленного соседа для обновления позиции if (dist_prev > dist_next) antiIND = antiPrevIND; else antiIND = antiNextIND; // Обновление координат спекулятивного мыслителя for (int c = 0; c < coords; c++) { a [i].c [c] = a [i].cB [c] + u.RNDbool () * (a [antiIND].c [c] - a [i].c [c]); //a [i].c [c] = a [i].cB [c] + u.RNDprobab () * (a [antiIND].c [c] - a [i].c [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } // Обновление позиций практических мыслителей -------------------------------- for (int i = k1; i < popSize; i++) { // Случайный выбор двух спекулятивных мыслителей antiNextIND = u.RNDintInRange (0, k1 - 1); antiPrevIND = u.RNDintInRange (0, k1 - 1); if (antiNextIND == antiPrevIND) antiNextIND = antiPrevIND + 1; // Расчет расстояний до выбранных мыслителей dist_next = EuclideanDistance (a [i].cB, a [antiNextIND].cB, coords); dist_prev = EuclideanDistance (a [i].cB, a [antiPrevIND].cB, coords); // Выбор ближайшего мыслителя для обновления позиции if (dist_prev < dist_next) antiIND = antiPrevIND; else antiIND = antiNextIND; // Обновление координат практического мыслителя for (int c = 0; c < coords; c++) { a [i].c [c] = a [i].cB [c] + u.RNDprobab () * (a [antiIND].c [c] - a [i].c [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Метод "Revision" отвечает за пересмотр и обновление лучших найденных решений для агентов. Ниже представлен подробный анализ работы этого метода:
Обновление лучших найденных решений: в цикле "for", метод проходит по каждому агенту в популяции. Для каждого агента сравнивается текущее значение функции приспособленности "a [i].f":
- Глобальное лучшее решение — если значение функции "f" агента больше текущего глобального лучшего решения "fB", то глобальное решение обновляется и запоминается индекс агента (ind), который нашел это лучшее решение.
- Личное лучшее решение — также каждое значение "f" агента сравнивается с его личным лучшим значением "fB". Если текущее значение лучше, то обновляется личное лучшее значение агента и копируются его текущие координаты "c" в личные координаты "cB".
Обновление координат глобального лучшего решения: если был найден индекс агента, который стал глобальным лучшим решением (ind != -1), то координаты этого агента копируются в глобальные координаты "cB ".
Сортировка агентов: В конце метода создается массив "aT" и изменяется его размер под размер популяции. Затем вызывается функция "u.Sorting_fB", которая сортирует агентов по их лучшим найденным решениям (значения fB).
//—————————————————————————————————————————————————————————————————————————————— // Пересмотр и обновление лучших найденных решений void C_AO_DA::Revision () { int ind = -1; // Обновление лучших найденных решений для каждого агента for (int i = 0; i < popSize; i++) { // Обновление глобального лучшего решения if (a [i].f > fB) { fB = a [i].f; ind = i; } // Обновление личного лучшего решения агента if (a [i].f > a [i].fB) { a [i].fB = a [i].f; ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY); } } // Обновление координат глобального лучшего решения if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); // Сортировка агентов по их лучшим найденным решениям static S_AO_Agent aT []; ArrayResize (aT, popSize); u.Sorting_fB (a, aT, popSize); } //——————————————————————————————————————————————————————————————————————————————
Результаты тестов
Настало время познакомиться с результатами тестирования DA. Еще раз обратим внимание на метод "Moving", в нем зеленым цветом обозначено и закомментирована строка, как оно должно быть согласно задумке авторов. Так вот, результаты получились следующие:
=============================
5 Hilly's; Func runs: 10000; result: 0.749254786734898
25 Hilly's; Func runs: 10000; result: 0.36669693350810206
500 Hilly's; Func runs: 10000; result: 0.2532075139007539
=============================
5 Forest's; Func runs: 10000; result: 0.7626421292861323
25 Forest's; Func runs: 10000; result: 0.4144802592253075
500 Forest's; Func runs: 10000; result: 0.2006796312431603
=============================
5 Megacity's; Func runs: 10000; result: 0.36
25 Megacity's; Func runs: 10000; result: 0.15969230769230774
500 Megacity's; Func runs: 10000; result: 0.0952000000000008
=============================
All score: 3.36185 (37.35%)
Такие результаты далеко не самые лучшие, но они могли попасть в рейтинговую таблицу. Но дело в том, что я допустил ошибку и вместо использования случайных чисел в диапазоне [0.0;1.0] вставил в код функцию случайных булевых чисел (отмечено красным цветом).
Суть случайного изменения в логике заключается в следующем: с вероятностью 50% соответствующая координата останется прежней, либо она будет заменена координатой антитезиса. На мой взгляд, это даже больше соответствует идее авторов о противостоянии тезисов и антитезисов. В случае практических мыслителей, все остается по-прежнему, их итоговые тезисы являются симбиозом между текущем тезисом и антитезисом, взятых у спекулятивных мыслителей. Таким образом, получились по счастливой случайности такие результаты:
DA|Dialectical Algorithm|50.0|40.0|1.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.8618313952293774
25 Hilly's; Func runs: 10000; result: 0.700333708747176
500 Hilly's; Func runs: 10000; result: 0.3372386732170054
=============================
5 Forest's; Func runs: 10000; result: 0.9816317765399738
25 Forest's; Func runs: 10000; result: 0.7277214130784131
500 Forest's; Func runs: 10000; result: 0.28717629901518305
=============================
5 Megacity's; Func runs: 10000; result: 0.7030769230769229
25 Megacity's; Func runs: 10000; result: 0.4529230769230769
500 Megacity's; Func runs: 10000; result: 0.16366923076923204
=============================
All score: 5.21560 (57.95%)
Это действительно впечатляющие результаты! Поскольку столь значительное улучшение показателей произошло у меня неосознанно, я не могу присвоить модифицированной версии индекс "m". В нашей рейтинговой таблице алгоритм останется как "DA". Таким образом, диалектический алгоритм демонстрирует отличную производительность, достигая общего показателя эффективности 57.95%. Ключевой особенностью алгоритма является его способность эффективно балансировать между глобальным и локальным поиском, благодаря разделению на спекулятивных и практических мыслителей.
На визуализации можно заметить, что алгоритм довольно быстро находит значимые локальные оптимумы, хотя ему не хватает точности сходимости, чтобы считаться идеальным. Тем не менее, результаты в любом случае весьма достойны.
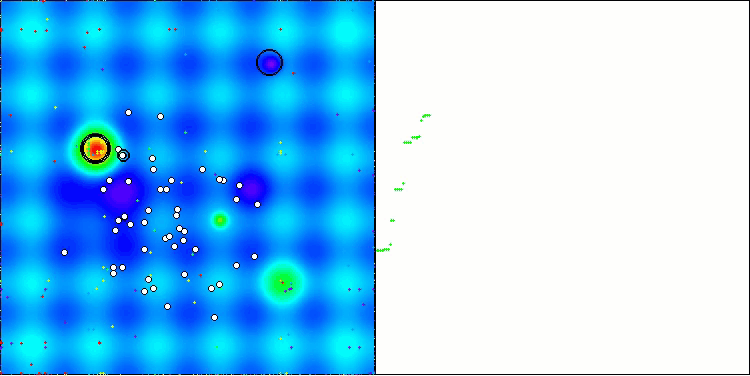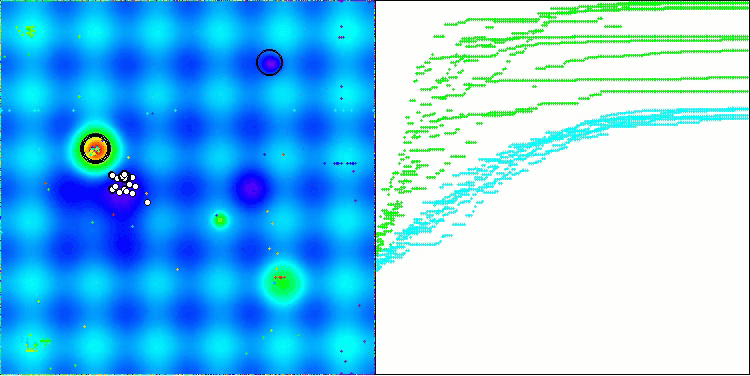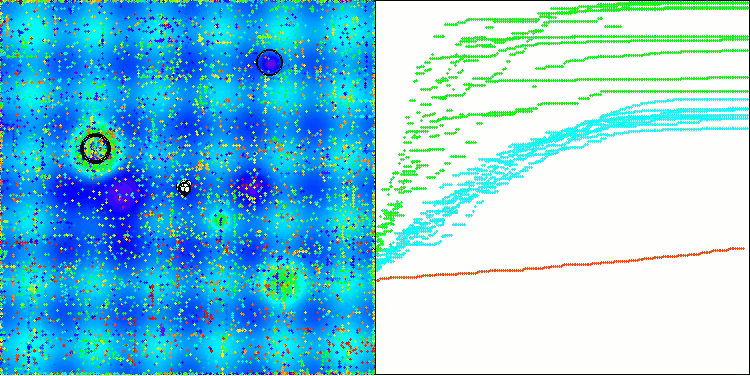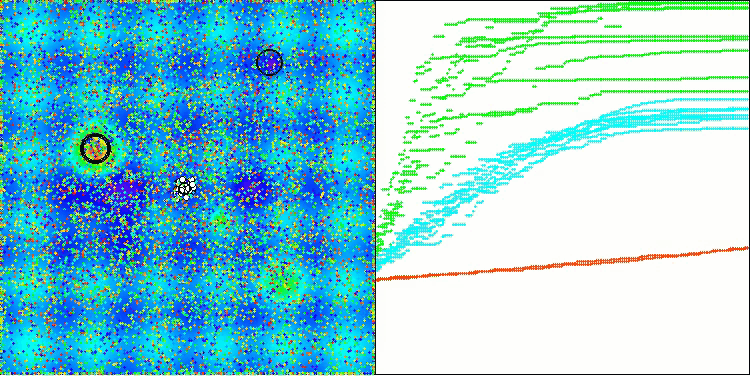
DA на тестовой функции Hilly
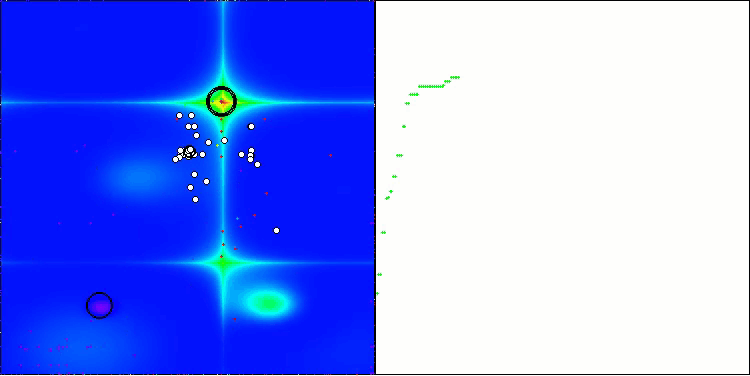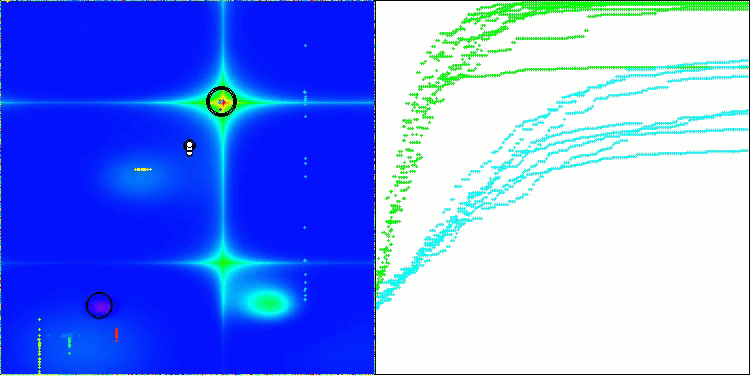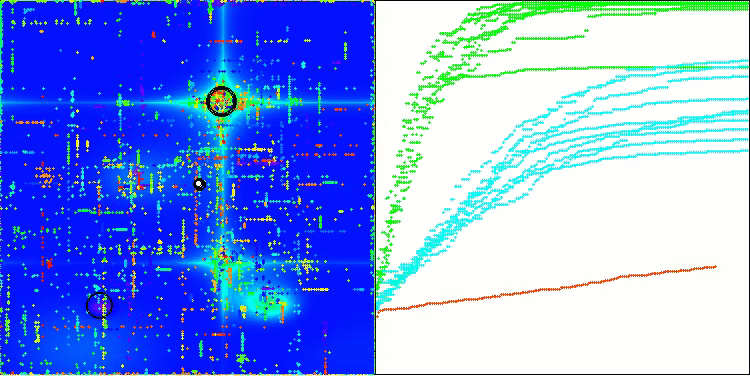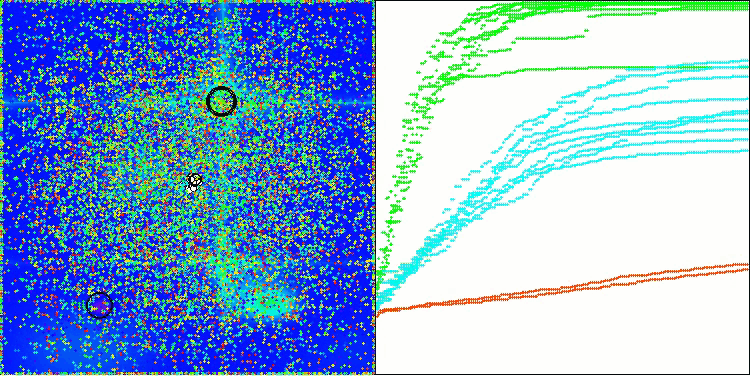
DA на тестовой функции Forest

DA на тестовой функции Megacity
Алгоритм DA, согласно результатам тестирования, поместился в нашей рейтинговой таблице на 12-ое место, хороший и стабильный показатель.
| № | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration ptimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | TETA | time evolution travel algorithm (joo) | 0,91362 | 0,82349 | 0,31990 | 2,05701 | 0,97096 | 0,89532 | 0,29324 | 2,15952 | 0,73462 | 0,68569 | 0,16021 | 1,58052 | 5,797 | 64,41 |
| 7 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 8 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 9 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 10 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 11 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 12 | DA | dialectical algorithm | 0,86183 | 0,70033 | 0,33724 | 1,89940 | 0,98163 | 0,72772 | 0,28718 | 1,99653 | 0,70308 | 0,45292 | 0,16367 | 1,31967 | 5,216 | 57,95 |
| 13 | BHAm | black hole algorithm M | 0,75236 | 0,76675 | 0,34583 | 1,86493 | 0,93593 | 0,80152 | 0,27177 | 2,00923 | 0,65077 | 0,51646 | 0,15472 | 1,32195 | 5,196 | 57,73 |
| 14 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 15 | AOSm | atomic orbital search M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| 16 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 17 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 18 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 19 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 20 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 21 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 22 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 23 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 24 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 25 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 26 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 27 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 28 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 29 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 30 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 31 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 32 | SOA | simple optimization algorithm | 0,91520 | 0,46976 | 0,27089 | 1,65585 | 0,89675 | 0,37401 | 0,16984 | 1,44060 | 0,69538 | 0,28031 | 0,10852 | 1,08422 | 4,181 | 46,45 |
| 33 | ABHA | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4,127 | 45,85 |
| 34 | ACMO | atmospheric cloud model optimization | 0,90321 | 0,48546 | 0,30403 | 1,69270 | 0,80268 | 0,37857 | 0,19178 | 1,37303 | 0,62308 | 0,24400 | 0,10795 | 0,97503 | 4,041 | 44,90 |
| 35 | ADAMm | adaptive moment estimation M | 0,88635 | 0,44766 | 0,26613 | 1,60014 | 0,84497 | 0,38493 | 0,16889 | 1,39880 | 0,66154 | 0,27046 | 0,10594 | 1,03794 | 4,037 | 44,85 |
| 36 | ATAm | artificial tribe algorithm M | 0,71771 | 0,55304 | 0,25235 | 1,52310 | 0,82491 | 0,55904 | 0,20473 | 1,58867 | 0,44000 | 0,18615 | 0,09411 | 0,72026 | 3,832 | 42,58 |
| 37 | ASHA | artificial showering algorithm | 0,89686 | 0,40433 | 0,25617 | 1,55737 | 0,80360 | 0,35526 | 0,19160 | 1,35046 | 0,47692 | 0,18123 | 0,09774 | 0,75589 | 3,664 | 40,71 |
| 38 | ASBO | adaptive social behavior optimization | 0,76331 | 0,49253 | 0,32619 | 1,58202 | 0,79546 | 0,40035 | 0,26097 | 1,45677 | 0,26462 | 0,17169 | 0,18200 | 0,61831 | 3,657 | 40,63 |
| 39 | MEC | mind evolutionary computation | 0,69533 | 0,53376 | 0,32661 | 1,55569 | 0,72464 | 0,33036 | 0,07198 | 1,12698 | 0,52500 | 0,22000 | 0,04198 | 0,78698 | 3,470 | 38,55 |
| 40 | IWO | invasive weed optimization | 0,72679 | 0,52256 | 0,33123 | 1,58058 | 0,70756 | 0,33955 | 0,07484 | 1,12196 | 0,42333 | 0,23067 | 0,04617 | 0,70017 | 3,403 | 37,81 |
| 41 | Micro-AIS | micro artificial immune system | 0,79547 | 0,51922 | 0,30861 | 1,62330 | 0,72956 | 0,36879 | 0,09398 | 1,19233 | 0,37667 | 0,15867 | 0,02802 | 0,56335 | 3,379 | 37,54 |
| 42 | COAm | cuckoo optimization algorithm M | 0,75820 | 0,48652 | 0,31369 | 1,55841 | 0,74054 | 0,28051 | 0,05599 | 1,07704 | 0,50500 | 0,17467 | 0,03380 | 0,71347 | 3,349 | 37,21 |
| 43 | SDOm | spiral dynamics optimization M | 0,74601 | 0,44623 | 0,29687 | 1,48912 | 0,70204 | 0,34678 | 0,10944 | 1,15826 | 0,42833 | 0,16767 | 0,03663 | 0,63263 | 3,280 | 36,44 |
| 44 | NMm | Nelder-Mead method M | 0,73807 | 0,50598 | 0,31342 | 1,55747 | 0,63674 | 0,28302 | 0,08221 | 1,00197 | 0,44667 | 0,18667 | 0,04028 | 0,67362 | 3,233 | 35,92 |
| 45 | BBBC | big bang-big crunch algorithm | 0,60531 | 0,45250 | 0,31255 | 1,37036 | 0,52323 | 0,35426 | 0,20417 | 1,08166 | 0,39769 | 0,19431 | 0,11286 | 0,70486 | 3,157 | 35,08 |
| RW | random walk | 0,48754 | 0,32159 | 0,25781 | 1,06694 | 0,37554 | 0,21944 | 0,15877 | 0,75375 | 0,27969 | 0,14917 | 0,09847 | 0,52734 | 2,348 | 26,09 | |
Выводы
Диалектический алгоритм представляет собой инновационный подход к оптимизации, основанный на философской концепции диалектики, где через взаимодействие противоположностей достигается улучшение решений. Алгоритм успешно объединяет концепции глобального и локального поиска через уникальное разделение популяции на спекулятивных и практических мыслителей, что обеспечивает эффективный баланс между исследованием и эксплуатацией пространства решений.
Структура алгоритма, состоящая из трех ключевых этапов, обеспечивает систематический подход к оптимизации. В процессе работы спекулятивные мыслители осуществляют широкий поиск в пространстве решений (хотя, как правило, в алгоритмах оптимизации наилучшие решения уточняются, а не "распыляются" по пространству поиска), в то время как практические мыслители фокусируются на локальной оптимизации перспективных областей. Это разделение позволяет алгоритму эффективно исследовать пространство решений и избегать застревания в локальных оптимумах, тем более, что из-за допущенной мной случайной ошибки логика алгоритма стала еще ближе теме диалектических противоположностей.
Результаты тестирования подтверждают высокую эффективность алгоритма со сбалансированными поисковыми возможностями, которые обеспечивают на достаточно высоком уровне на различных типах задач. По сравнению с другими алгоритмами DA не проявляет сильных отклонений в худшую или лучшую сторону и показывает равномерно устойчивый результат по цветовой градации в таблице. Общий показатель эффективности демонстрирует конкурентоспособность алгоритма в сравнении с существующими методами оптимизации. Эта комбинация философских принципов и математических методов создает мощный инструмент для решения сложных оптимизационных задач.
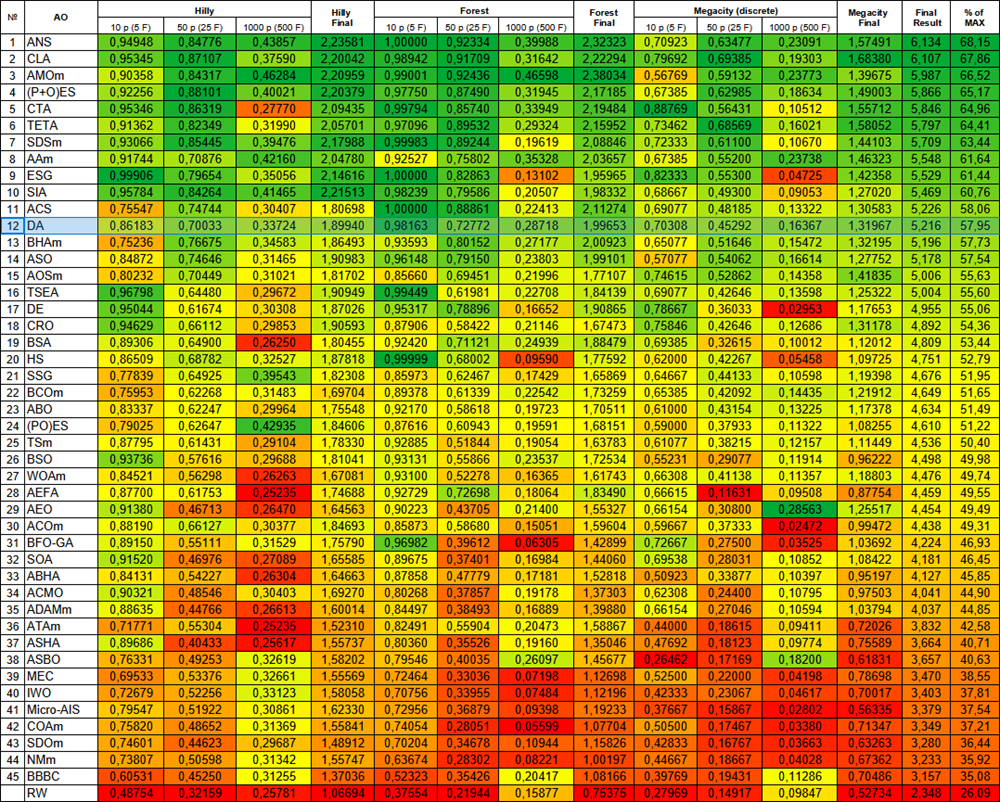
Рисунок 3. Цветовая градация алгоритмов по соответствующим тестам

Рисунок 4. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше, где 100 - максимально возможный теоретический результат, в архиве скрипт для расчета рейтинговой таблицы)
Плюсы и минусы алгоритма DA:
Плюсы:
- Мало внешних параметров, только два, не считая размер популяции.
- Несложная реализация.
- Достаточно быстрый.
- Сбалансированные, хорошие показатели на задачах как малых, так и больших размерностей.
Минусы:
- Разброс результатов.
К статье прикреплён архив с актуальными версиями кодов алгоритмов. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | #C_AO.mqh | Включаемый файл | Родительский класс популяционных алгоритмов оптимизации |
| 2 | #C_AO_enum.mqh | Включаемый файл | Перечисление популяционных алгоритмов оптимизации |
| 3 | TestFunctions.mqh | Включаемый файл | Библиотека тестовых функций |
| 4 | TestStandFunctions.mqh | Включаемый файл | Библиотека функций тестового стенда |
| 5 | Utilities.mqh | Включаемый файл | Библиотека вспомогательных функций |
| 6 | CalculationTestResults.mqh | Включаемый файл | Скрипт для расчета результатов в сравнительную таблицу |
| 7 | Testing AOs.mq5 | Скрипт | Единый испытательный стенд для всех популяционных алгоритмов оптимизации |
| 8 | Simple use of population optimization algorithms.mq5 | Скрипт | Простой пример использования популяционных алгоритмов оптимизации без визуализации |
| 9 | Test_AO_DA.mq5 | Скрипт | Испытательный стенд для DA |
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 От начального до среднего уровня: Директива Include
От начального до среднего уровня: Директива Include
 От начального до среднего уровня: Операторы BREAK и CONTINUE
От начального до среднего уровня: Операторы BREAK и CONTINUE
 Нейросети в трейдинге: Иерархический двухбашенный трансформер (Окончание)
Нейросети в трейдинге: Иерархический двухбашенный трансформер (Окончание)
 Интеграция MQL5 с пакетами обработки данных (Часть 1): Расширенный анализ данных и статистическая обработка
Интеграция MQL5 с пакетами обработки данных (Часть 1): Расширенный анализ данных и статистическая обработка
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования