Dialectic Search (DA)

Contents

1. Introduction
2. Implementation of the algorithm
3. Test results

Introduction

Dialectical materialism is based on the principle of the unity and struggle of opposites in nature, society and thinking. It is based on the idea that development occurs through the conflict of opposing forces and tendencies, where each phenomenon contains internal contradictions. The key principle of this approach is the transition from quantitative to qualitative changes, when gradual changes accumulate and lead to sharp qualitative leaps. The development follows the law of "negation of negation", in which the thesis is replaced by antithesis, giving rise to synthesis as a new quality that preserves the best of the previous states.

In the world of optimization algorithms, where mathematical precision meets philosophical wisdom, a unique method inspired by dialectical materialism has emerged: Dialectical Algorithm (DA). This algorithm, presented as a synthesis of classical dialectics and modern optimization methods, rethinks the search for optimal solutions through the prism of the philosophical opposition of thesis and antithesis. The basis of DA is the idea that any solution (thesis) contains the potential for improvement through interaction with its opposite (antithesis).

In its algorithmic implementation, this principle is reflected through the interaction between speculative thinkers, who seek new solutions, moving away from the known, and practical thinkers, who strive for proven solutions. The materialistic aspect of dialectical materialism is manifested in the reliance on objective criteria for evaluating decisions and practical verification of results. Development occurs cyclically: the solutions found give rise to new contradictions, which leads to the next round of search, reflecting the continuity of knowledge and improvement.

The algorithm implements this principle through three key points: understanding, where the evaluation and sorting of solutions occurs; dialectical interaction, in which solutions find their antitheses; and the moment of synthesis, where new, improved solutions are formed. The peculiarity of the algorithm is the division of the population into two types of thinkers: speculative (k1), which explore the solution space in broad steps (through the interaction of similar solutions in quality, but distant from each other in the search space), and practical (p-k1), which carry out a local search (distant in quality, but close in the solution space). This division reflects the philosophical principle of the unity and struggle of opposites, where each group makes its own unique contribution to the optimization.

Dialectic Search (DA) was introduced by Serdar Kadioglu and Meinolf Sellmann in 2009. This method uses a dialectical approach to solving constrained optimization problems, continuing the tradition established by dialectical materialism in the study and search for new solutions.

Implementation of the algorithm

The algorithm is based on a population of p solutions (usually 50), each of which is a vector of coordinates in the search space. This population is divided into two groups: k1 speculative thinkers (best solutions) and (p-k1) practical thinkers.

The first stage is the Moment of understanding. Here, all decisions are evaluated through the objective function f(x). Solutions are sorted by quality, and the best k1 solutions become speculative thinkers, while the rest become practical ones. At this stage, new solutions are also accepted or rejected based on their quality compared to previous iterations (the best individual solution for the thinker).

The second stage is the Dialectical moment. At this stage, a search is conducted for each solution's antithesis — the opposite with which the solution will interact. For speculative thinkers, the search for antithesis is based on maximizing distance while maintaining the quality of the solution (idealistic dialectic). For the first solution, the antithesis is the second best, for the last one - the penultimate one, for the rest, the neighbor with the greatest distance is chosen. Practical thinkers seek antithesis by minimizing the distance with a sufficient difference in quality (materialistic dialectic).

The third stage is the Speculative/Practical moment (Moment of renewal). Here the positions of all solutions are updated using the found antitheses. Speculative thinkers use a uniform distribution, which allows for a broad search across the solution space. Practical thinkers use the normal distribution. My experiments have shown that for both types of thinkers, a uniform distribution works best.

The equation for updating positions is the same for all: X(i) = X(i) + μ⊙(Xanti(i) - X(i)), where μ is a random vector from the corresponding distribution, ⊙ means element-wise multiplication. This ensures a balance between exploring the solution space through speculative thinkers and refining the solutions found through practical thinkers.

The Dialectical Algorithm (DA) has similarities with the Differential Evolution (DE) algorithm in the solution updating equation. In DE, a new vector is created by adding the scaled difference of two other vectors to the target vector (x_new = x_target + F(x_r1 - x_r2)), while DA uses a similar principle but with an antithesis and an adaptive ratio (x_new = x + μ(x_anti - x)).

However, the key difference lies in the way vectors are selected to generate new solutions. DE relies on random selection of difference vectors, which ensures the stochastic nature of the search. DA, on the other hand, uses a deterministic approach to choosing antitheses based on the distance between solutions and their quality, while dividing the population into speculative and practical thinkers with different search strategies. DA algorithm exhibits slightly more computational complexity (calculating Euclidean distance), but DA demonstrates higher efficiency in various optimization problems.

Figure 1 shows the principle of choosing antitheses for speculative (red, best) theses and material (blue) ones. Speculative ones choose antitheses that are adjacent in quality, but more distant in the search space, while material ones, on the contrary, choose antitheses that are more distant in quality, but close in the search space. 

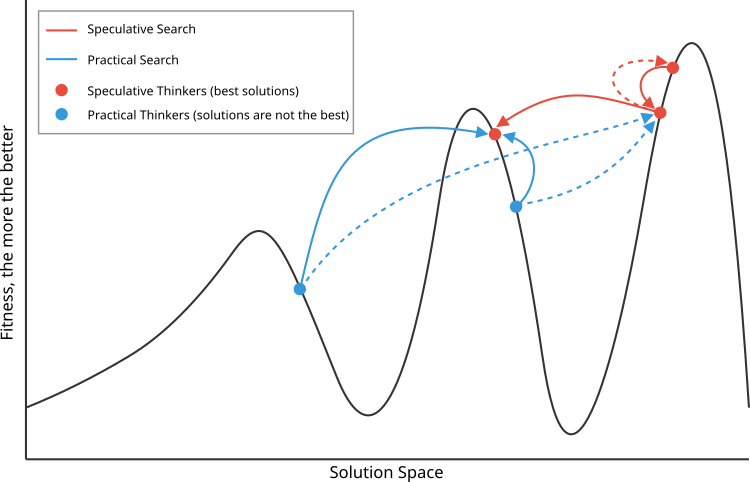
Figure 1. Schematic representation of the DA algorithm operating principle. Solid lines - interaction with preferred antitheses, in contrast to less preferred ones, indicated by dashed lines

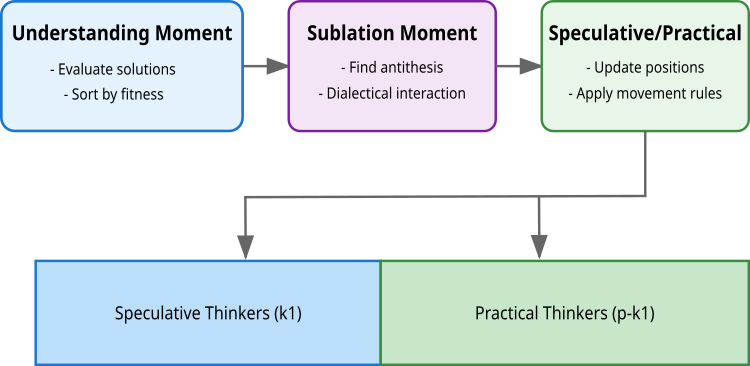
Figure 2. Stages of the DA algorithm logic

Let's move on to writing the pseudocode of the algorithm:

On the first iteration: Randomly place agents: position[i] = random(min, max)

Sort the population by the best individual solutions

Create a population of three types of agents:

• Best thinker (1 agent)
• Speculative thinkers (k1 = 3 agents)
• Practical thinkers (the rest of the 50 agents)

In subsequent iterations:

A. The best thinker moves towards the second best:

position[0] = best[0] + rand(0,1) * (position[1] - position[0])

B. Speculative thinkers:

• Find the farthest nearest neighbors using the Euclidean distance:

distance = √Σ(x₁-x₂)²

• Update the position relative to the farthest:

position[i] = best[i] + rand(0,1) * (position[furthest] - position[i])

C. Practical thinkers:

• Choose two speculative thinkers at random
• Move towards the nearest one:

position[i] = best[i] + rand(0,1) * (position[nearest] - position[i])

After each movement:

• Update the best personal solutions
• Update the global best solution
• Sort agents by the quality of personal decisions

The process is repeated until the stopping criterion is reached.

After a complete analysis of the algorithm, we move on to implementation in code. Let's write the C_AO_DA class of the dialectical optimization algorithm, inheriting the functionality from the C_AO base class.

Algorithm parameters:

• Population size—  antitheses determine the number of agents that will participate in the optimization.
• Speculative thinkers indicate the number of better agents capable of more free search for solutions.
• Neighbors for analysis determine the number of nearest neighbors with which each speculative thinker (agent) will interact to exchange information and improve their strategy.

Methods:

• C_AO_DA () — the constructor initializes the main parameters and also creates an array to store them.
• SetParams () — setting parameters allows updating the values of the algorithm parameters during operation.
• Moving () and Revision () — functions for moving agents in the search space and revising the solutions found.
• EuclideanDistance () — calculate the distance in the search space between two vectors, which is necessary for selecting the closest (for speculative) and furthest (for practical) similarity of solutions found by agents.

//——————————————————————————————————————————————————————————————————————————————
// Class implementing the dialectical optimization algorithm
class C_AO_DA : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_DA () { }
  C_AO_DA ()
  {
    ao_name = "DA";
    ao_desc = "Dialectical Algorithm";
    ao_link = "https://www.mql5.com/en/articles/16999";

    popSize = 50;       // population size
    k1      = 3;        // speculative thinkers
    k2      = 10;       // neighbours

    ArrayResize (params, 3);
    params [0].name = "popSize"; params [0].val = popSize;
    params [1].name = "k1";      params [1].val = k1;
    params [2].name = "k2";      params [2].val = k2;
  }

  // Setting algorithm parameters
  void SetParams ()
  {
    popSize = (int)params [0].val;
    k1      = (int)params [1].val;
    k2      = (int)params [2].val;
  }

  bool Init (const double &rangeMinP  [], // minimum search range
             const double &rangeMaxP  [], // maximum search range
             const double &rangeStepP [], // search step
             const int     epochsP = 0);  // number of epochs

  void Moving   ();    // Moving agents in the search space
  void Revision ();    // Review and update the best solutions found

  //----------------------------------------------------------------------------
  int k1;       // number of speculative thinkers
  int k2;       // number of neighbors to analyze

  private: //-------------------------------------------------------------------
  // Calculate the Euclidean distance between two vectors
  double EuclideanDistance (const double &vec1 [], const double &vec2 [], const int dim)
  {
    double sum  = 0;
    double diff = 0.0;

    for (int i = 0; i < dim; i++)
    {
      diff = vec1 [i] - vec2 [i];
      sum += diff * diff;
    }
    return MathSqrt (sum);
  }
};
//——————————————————————————————————————————————————————————————————————————————

The Init method of the C_AO_DA class is intended to initialize the parameters of the optimization algorithm. It accepts arrays of minimum and maximum search range values, search steps, and optionally the number of epochs to perform optimization. The method first performs standard parameter initialization; if this fails, it returns 'false'. If initialization is successful, the method returns 'true', confirming that the algorithm is ready to run.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_DA::Init (const double &rangeMinP  [], // minimum search range
                    const double &rangeMaxP  [], // maximum search range
                    const double &rangeStepP [], // search step
                    const int     epochsP = 0)   // number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  return true;
}
//——————————————————————————————————————————————————————————————————————————————

The Moving method is an implementation of agent movement in the search space. A detailed description of the method's operation is provided below:

Initialization:

• At the beginning (!revision), the initial positions of the agents are set randomly using the given minimum and maximum bounds for each coordinate. Each "a[i]" agent receives random coordinates in given ranges and with a certain step.
• After initialization, "revision" is set to 'true', which prevents reinitialization on future calls to the Moving method.

Update the best thinker's position:

• The best thinker (agent) updates its coordinates based on its previous best position and a random probability, using its nearest neighbor "a[1]" for updating.

Update positions of speculative thinkers:

• For each speculative thinker (agent) in the range from "k2" to "k1", the method searches for the most distant previous (antiPrevIND) and next neighbor (antiNextIND).
• The speculative thinker's coordinate is then updated using the most distant neighbor when considering the antithesis.
  

Update positions of practical thinkers:

• Practical thinkers (agents) range from "k1" to "popSize".
• The code randomly selects two speculative thinkers and calculates the distances to them. The practical thinker then selects the closest (of the two chosen) thinker to update its position.
• Each coordinate is updated based on the selected neighbor.

Auxiliary functions

• EuclideanDistance — function that calculates the Euclidean distance between two points "a" and "b" in a multidimensional space.
• u.RNDfromCI — return a random number from the specified interval.
• u.SeInDiSp — convert "value" to the appropriate step depending on the range.
• u.RNDprobab — return a random number with uniform probability distribution.

//——————————————————————————————————————————————————————————————————————————————
// Implement agent movement in the search space
void C_AO_DA::Moving ()
{
  //----------------------------------------------------------------------------
  // Initialize the agents' positions randomly
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  //  Update the best thinker's position
  for (int c = 0; c < coords; c++)
  {
    a [0].c [c] = a [0].cB [c] + u.RNDprobab () * (a [1].c [c] - a [0].c [c]);
    a [0].c [c] = u.SeInDiSp (a [0].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }

  //----------------------------------------------------------------------------
  double dist_next   = -DBL_MAX;  // maximum distance to the next neighbor
  double dist_prev   = -DBL_MAX;  // maximum distance to the previous neighbor
  double dist        = 0.0;       // current distance
  int    antiNextIND = 0;         // index of the most distant next neighbor
  int    antiPrevIND = 0;         // index of the most distant previous neighbor
  int    antiIND     = 0;         // selected index to update position

  // Update the positions of speculative thinkers -------------------------------
  for (int i = k2; i < k1; i++)
  {
    // Find the most distant previous neighbor
    for (int j = 1; j <= k2; j++)
    {
      dist = EuclideanDistance (a [i].cB, a [i - j].cB, coords);
      if (dist > dist_prev)
      {
        dist_prev   = dist;
        antiPrevIND = i - j;
      }
    }

    // Find the farthest next neighbor
    for (int j = 1; j <= k2; j++)
    {
      dist = EuclideanDistance (a [i].cB, a [i + j].cB, coords);
      if (dist > dist_next)
      {
        dist_next = dist;
        antiNextIND  = i + j;
      }
    }

    // Select the most distant neighbor to update position
    if (dist_prev > dist_next) antiIND = antiPrevIND;
    else                       antiIND = antiNextIND;

    // Update the speculative thinker's coordinates
    for (int c = 0; c < coords; c++)
    {
      a [i].c [c] = a [i].cB [c] + u.RNDbool () * (a [antiIND].c [c] - a [i].c [c]);
      //a [i].c [c] = a [i].cB [c] + u.RNDprobab () * (a [antiIND].c [c] - a [i].c [c]);
      a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }

  // Update the positions of practical thinkers --------------------------------
  for (int i = k1; i < popSize; i++)
  {
    // Random selection of two speculative thinkers
    antiNextIND = u.RNDintInRange (0, k1 - 1);
    antiPrevIND = u.RNDintInRange (0, k1 - 1);

    if (antiNextIND == antiPrevIND) antiNextIND = antiPrevIND + 1;

    // Calculate distances to selected thinkers
    dist_next = EuclideanDistance (a [i].cB, a [antiNextIND].cB, coords);
    dist_prev = EuclideanDistance (a [i].cB, a [antiPrevIND].cB, coords);

    // Select the closest thinker to update the position
    if (dist_prev < dist_next) antiIND = antiPrevIND;
    else                       antiIND = antiNextIND;

    // Update the coordinates of the practical thinker
    for (int c = 0; c < coords; c++)
    {
      a [i].c [c] = a [i].cB [c] + u.RNDprobab () * (a [antiIND].c [c] - a [i].c [c]);
      a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

The Revision method is responsible for revising and updating the best solutions found for agents. Below is a detailed analysis of how this method works:

Updating the best solutions found: in the "for" loop, the method iterates through each agent in the population. For each agent, the current value of the fitness function "a [i].f" is compared:

• Global best solution — if the value of the agent's f function is greater than the current fB global best solution, then the global solution is updated and the index of the agent (ind) that found this best solution is saved.
• Personal best decision — also each agent's f value is compared with its personal best fB value. If the current value is better, then the agent's personal best value is updated and its current c coordinates are copied to its personal cB coordinates.

Updating the coordinates of the global best solution: if the index of an agent that became the global best solution (ind != -1), was found, then the coordinates of this agent are copied to the cB global coordinates.

Sorting agents: At the end of the method, the aT array is created and its size is changed to match the population size. Then the u.Sorting_fB function is called, which sorts the agents by their best found solutions (fB values).

//——————————————————————————————————————————————————————————————————————————————
// Review and update the best solutions found
void C_AO_DA::Revision ()
{
  int ind = -1;

  // Update the best solutions found for each agent
  for (int i = 0; i < popSize; i++)
  {
    // Update the global best solution
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }

    // Update the agent's personal best solution
    if (a [i].f > a [i].fB)
    {
      a [i].fB = a [i].f;
      ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }

  // Update the global best solution coordinates
  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  // Sort agents by their best found solutions
  static S_AO_Agent aT []; ArrayResize (aT, popSize);
  u.Sorting_fB (a, aT, popSize);
}
//——————————————————————————————————————————————————————————————————————————————

Test results

It is time to get acquainted with the results of the DA testing. Let's pay attention to the Moving method again. The string reflecting the authors' vision is commented out and highlighted in green. So, the results are as follows:

DA|Dialectical Algorithm|50.0|30.0|1.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.749254786734898
25 Hilly's; Func runs: 10000; result: 0.36669693350810206
500 Hilly's; Func runs: 10000; result: 0.2532075139007539
=============================
5 Forest's; Func runs: 10000; result: 0.7626421292861323
25 Forest's; Func runs: 10000; result: 0.4144802592253075
500 Forest's; Func runs: 10000; result: 0.2006796312431603
=============================
5 Megacity's; Func runs: 10000; result: 0.36
25 Megacity's; Func runs: 10000; result: 0.15969230769230774
500 Megacity's; Func runs: 10000; result: 0.0952000000000008
=============================
All score: 3.36185 (37.35%)

These results are far from the best, but they could have made it into the ranking table. But the thing is that I made a mistake and instead of using random numbers in the range [0.0;1.0] I inserted a random boolean number function into the code (marked in red).

The essence of a random change in logic is the following: with a 50% probability, the corresponding coordinate will remain the same, or it will be replaced by the coordinate of the antithesis. In my opinion, this is even more consistent with the authors’ idea of the opposition of theses and antitheses. In the case of practical thinkers, everything remains the same; their final theses are a symbiosis between the current thesis and the antithesis taken from speculative thinkers. Thus, by a lucky chance, the following results were obtained:

DA|Dialectical Algorithm|50.0|40.0|1.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.8618313952293774
25 Hilly's; Func runs: 10000; result: 0.700333708747176
500 Hilly's; Func runs: 10000; result: 0.3372386732170054
=============================
5 Forest's; Func runs: 10000; result: 0.9816317765399738
25 Forest's; Func runs: 10000; result: 0.7277214130784131
500 Forest's; Func runs: 10000; result: 0.28717629901518305
=============================
5 Megacity's; Func runs: 10000; result: 0.7030769230769229
25 Megacity's; Func runs: 10000; result: 0.4529230769230769
500 Megacity's; Func runs: 10000; result: 0.16366923076923204
=============================
All score: 5.21560 (57.95%)

These are truly impressive results! Since such a significant improvement in performance occurred unconsciously, I cannot assign the m index to the modified version. In our ranking table the algorithm will remain as DA. Thus, the dialectical algorithm demonstrates excellent performance, achieving an overall efficiency rate of 57.95%. A key feature of the algorithm is its ability to effectively balance between global and local search, thanks to the division into speculative and practical thinkers.

From the visualization, one can see that the algorithm finds significant local optima quite quickly, although it lacks the convergence accuracy to be considered perfect. However, the results are quite decent in any case.

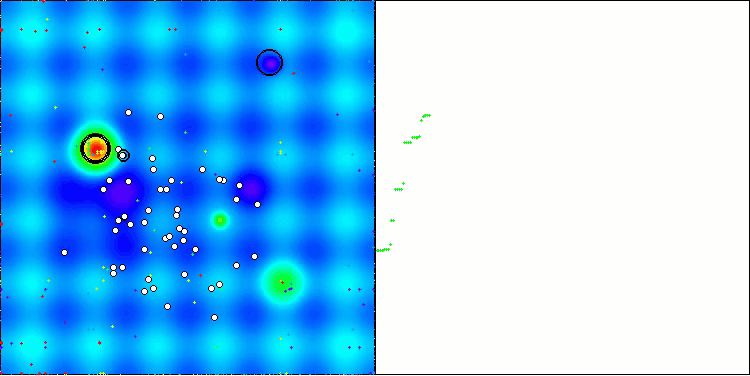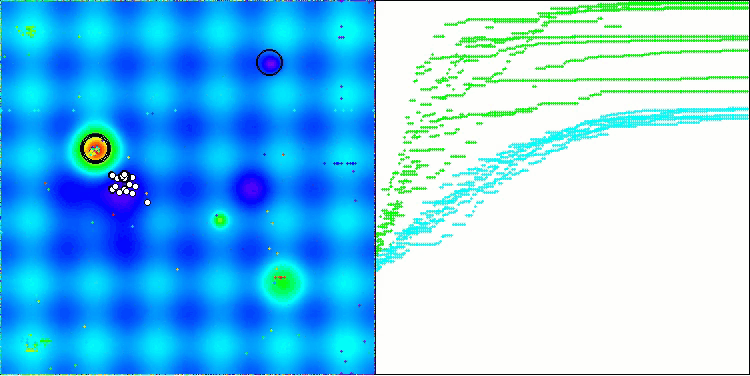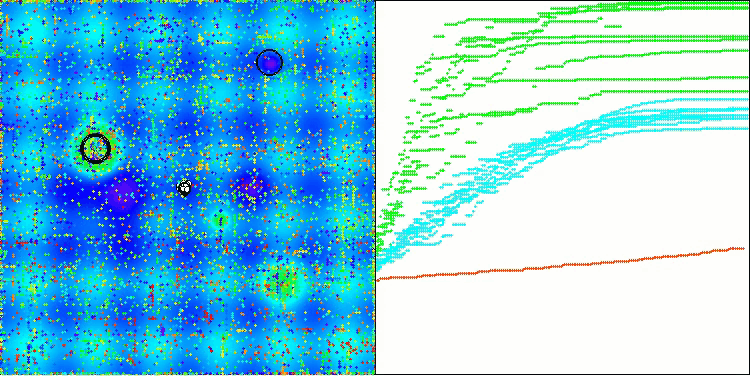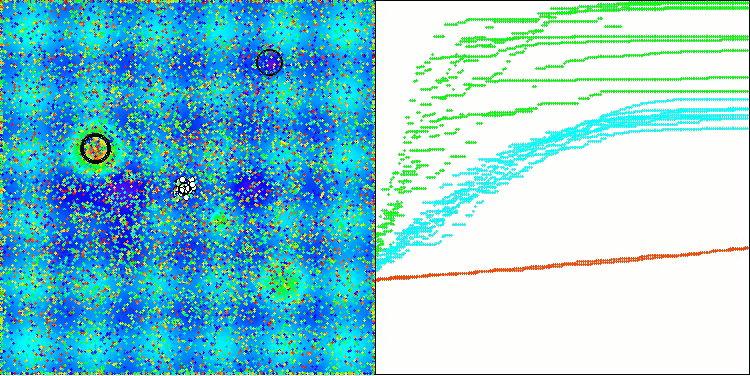
  DA on the Hilly test function

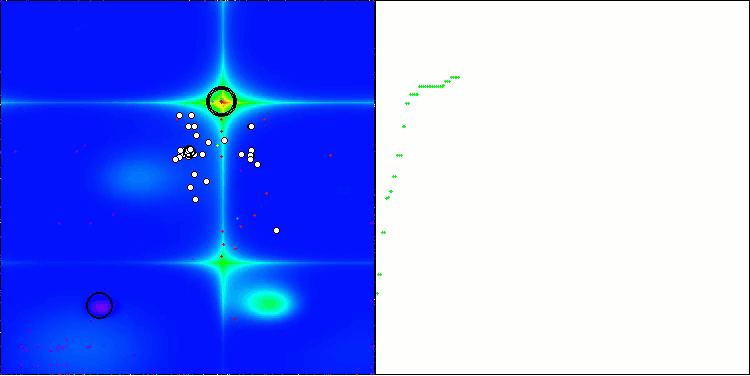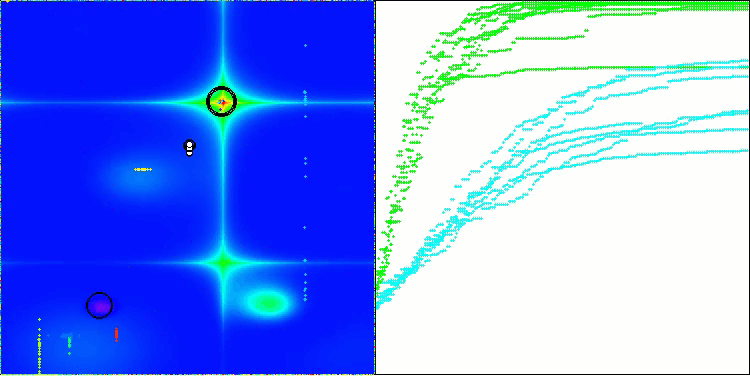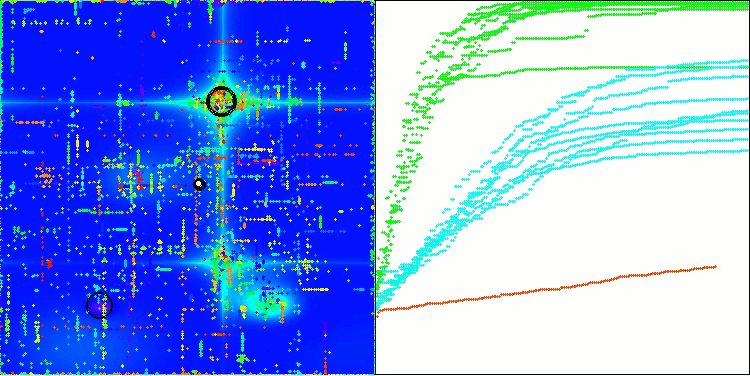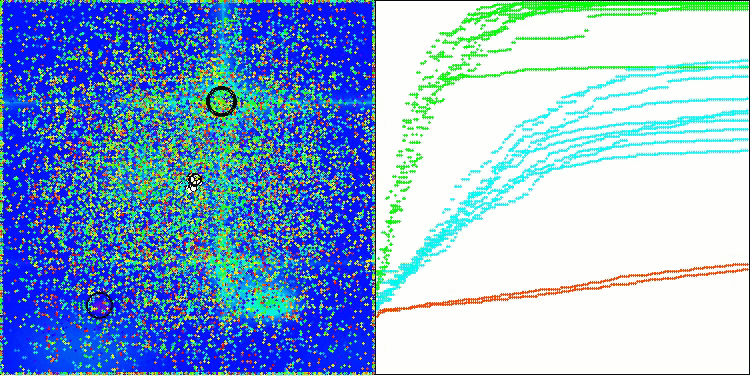
DA on the Forest test function

DA on the Megacity test function

The DA algorithm, according to the test results, ranked 12th in our table, which is a good and stable result.

#	AO	Description	Hilly			Hilly final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result	% of MAX
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	ANS	across neighbourhood search	0.94948	0.84776	0.43857	2.23581	1.00000	0.92334	0.39988	2.32323	0.70923	0.63477	0.23091	1.57491	6.134	68.15
2	CLA	code lock algorithm (joo)	0.95345	0.87107	0.37590	2.20042	0.98942	0.91709	0.31642	2.22294	0.79692	0.69385	0.19303	1.68380	6.107	67.86
3	AMOm	animal migration ptimization M	0.90358	0.84317	0.46284	2.20959	0.99001	0.92436	0.46598	2.38034	0.56769	0.59132	0.23773	1.39675	5.987	66.52
4	(P+O)ES	(P+O) evolution strategies	0.92256	0.88101	0.40021	2.20379	0.97750	0.87490	0.31945	2.17185	0.67385	0.62985	0.18634	1.49003	5.866	65.17
5	CTA	comet tail algorithm (joo)	0.95346	0.86319	0.27770	2.09435	0.99794	0.85740	0.33949	2.19484	0.88769	0.56431	0.10512	1.55712	5.846	64.96
6	TETA	time evolution travel algorithm (joo)	0.91362	0.82349	0.31990	2.05701	0.97096	0.89532	0.29324	2.15952	0.73462	0.68569	0.16021	1.58052	5.797	64.41
7	SDSm	stochastic diffusion search M	0.93066	0.85445	0.39476	2.17988	0.99983	0.89244	0.19619	2.08846	0.72333	0.61100	0.10670	1.44103	5.709	63.44
8	AAm	archery algorithm M	0.91744	0.70876	0.42160	2.04780	0.92527	0.75802	0.35328	2.03657	0.67385	0.55200	0.23738	1.46323	5.548	61.64
9	ESG	evolution of social groups (joo)	0.99906	0.79654	0.35056	2.14616	1.00000	0.82863	0.13102	1.95965	0.82333	0.55300	0.04725	1.42358	5.529	61.44
10	SIA	simulated isotropic annealing (joo)	0.95784	0.84264	0.41465	2.21513	0.98239	0.79586	0.20507	1.98332	0.68667	0.49300	0.09053	1.27020	5.469	60.76
11	ACS	artificial cooperative search	0.75547	0.74744	0.30407	1.80698	1.00000	0.88861	0.22413	2.11274	0.69077	0.48185	0.13322	1.30583	5.226	58.06
12	DA	dialectical algorithm	0.86183	0.70033	0.33724	1.89940	0.98163	0.72772	0.28718	1.99653	0.70308	0.45292	0.16367	1.31967	5.216	57.95
13	BHAm	black hole algorithm M	0.75236	0.76675	0.34583	1.86493	0.93593	0.80152	0.27177	2.00923	0.65077	0.51646	0.15472	1.32195	5.196	57.73
14	ASO	anarchy society optimization	0.84872	0.74646	0.31465	1.90983	0.96148	0.79150	0.23803	1.99101	0.57077	0.54062	0.16614	1.27752	5.178	57.54
15	AOSm	atomic orbital search M	0.80232	0.70449	0.31021	1.81702	0.85660	0.69451	0.21996	1.77107	0.74615	0.52862	0.14358	1.41835	5.006	55.63
16	TSEA	turtle shell evolution algorithm (joo)	0.96798	0.64480	0.29672	1.90949	0.99449	0.61981	0.22708	1.84139	0.69077	0.42646	0.13598	1.25322	5.004	55.60
17	DE	differential evolution	0.95044	0.61674	0.30308	1.87026	0.95317	0.78896	0.16652	1.90865	0.78667	0.36033	0.02953	1.17653	4.955	55.06
18	CRO	chemical reaction optimization	0.94629	0.66112	0.29853	1.90593	0.87906	0.58422	0.21146	1.67473	0.75846	0.42646	0.12686	1.31178	4.892	54.36
19	BSA	bird swarm algorithm	0.89306	0.64900	0.26250	1.80455	0.92420	0.71121	0.24939	1.88479	0.69385	0.32615	0.10012	1.12012	4.809	53.44
20	HS	harmony search	0.86509	0.68782	0.32527	1.87818	0.99999	0.68002	0.09590	1.77592	0.62000	0.42267	0.05458	1.09725	4.751	52.79
21	SSG	saplings sowing and growing	0.77839	0.64925	0.39543	1.82308	0.85973	0.62467	0.17429	1.65869	0.64667	0.44133	0.10598	1.19398	4.676	51.95
22	BCOm	bacterial chemotaxis optimization M	0.75953	0.62268	0.31483	1.69704	0.89378	0.61339	0.22542	1.73259	0.65385	0.42092	0.14435	1.21912	4.649	51.65
23	ABO	african buffalo optimization	0.83337	0.62247	0.29964	1.75548	0.92170	0.58618	0.19723	1.70511	0.61000	0.43154	0.13225	1.17378	4.634	51.49
24	(PO)ES	(PO) evolution strategies	0.79025	0.62647	0.42935	1.84606	0.87616	0.60943	0.19591	1.68151	0.59000	0.37933	0.11322	1.08255	4.610	51.22
25	TSm	tabu search M	0.87795	0.61431	0.29104	1.78330	0.92885	0.51844	0.19054	1.63783	0.61077	0.38215	0.12157	1.11449	4.536	50.40
26	BSO	brain storm optimization	0.93736	0.57616	0.29688	1.81041	0.93131	0.55866	0.23537	1.72534	0.55231	0.29077	0.11914	0.96222	4.498	49.98
27	WOAm	wale optimization algorithm M	0.84521	0.56298	0.26263	1.67081	0.93100	0.52278	0.16365	1.61743	0.66308	0.41138	0.11357	1.18803	4.476	49.74
28	AEFA	artificial electric field algorithm	0.87700	0.61753	0.25235	1.74688	0.92729	0.72698	0.18064	1.83490	0.66615	0.11631	0.09508	0.87754	4.459	49.55
29	AEO	artificial ecosystem-based optimization algorithm	0.91380	0.46713	0.26470	1.64563	0.90223	0.43705	0.21400	1.55327	0.66154	0.30800	0.28563	1.25517	4.454	49.49
30	ACOm	ant colony optimization M	0.88190	0.66127	0.30377	1.84693	0.85873	0.58680	0.15051	1.59604	0.59667	0.37333	0.02472	0.99472	4.438	49.31
31	BFO-GA	bacterial foraging optimization - ga	0.89150	0.55111	0.31529	1.75790	0.96982	0.39612	0.06305	1.42899	0.72667	0.27500	0.03525	1.03692	4.224	46.93
32	SOA	simple optimization algorithm	0.91520	0.46976	0.27089	1.65585	0.89675	0.37401	0.16984	1.44060	0.69538	0.28031	0.10852	1.08422	4.181	46.45
33	ABHA	artificial bee hive algorithm	0.84131	0.54227	0.26304	1.64663	0.87858	0.47779	0.17181	1.52818	0.50923	0.33877	0.10397	0.95197	4.127	45.85
34	ACMO	atmospheric cloud model optimization	0.90321	0.48546	0.30403	1.69270	0.80268	0.37857	0.19178	1.37303	0.62308	0.24400	0.10795	0.97503	4.041	44.90
35	ADAMm	adaptive moment estimation M	0.88635	0.44766	0.26613	1.60014	0.84497	0.38493	0.16889	1.39880	0.66154	0.27046	0.10594	1.03794	4.037	44.85
36	ATAm	artificial tribe algorithm M	0.71771	0.55304	0.25235	1.52310	0.82491	0.55904	0.20473	1.58867	0.44000	0.18615	0.09411	0.72026	3.832	42.58
37	ASHA	artificial showering algorithm	0.89686	0.40433	0.25617	1.55737	0.80360	0.35526	0.19160	1.35046	0.47692	0.18123	0.09774	0.75589	3.664	40.71
38	ASBO	adaptive social behavior optimization	0.76331	0.49253	0.32619	1.58202	0.79546	0.40035	0.26097	1.45677	0.26462	0.17169	0.18200	0.61831	3.657	40.63
39	MEC	mind evolutionary computation	0.69533	0.53376	0.32661	1.55569	0.72464	0.33036	0.07198	1.12698	0.52500	0.22000	0.04198	0.78698	3.470	38.55
40	IWO	invasive weed optimization	0.72679	0.52256	0.33123	1.58058	0.70756	0.33955	0.07484	1.12196	0.42333	0.23067	0.04617	0.70017	3.403	37.81
41	Micro-AIS	micro artificial immune system	0.79547	0.51922	0.30861	1.62330	0.72956	0.36879	0.09398	1.19233	0.37667	0.15867	0.02802	0.56335	3.379	37.54
42	COAm	cuckoo optimization algorithm M	0.75820	0.48652	0.31369	1.55841	0.74054	0.28051	0.05599	1.07704	0.50500	0.17467	0.03380	0.71347	3.349	37.21
43	SDOm	spiral dynamics optimization M	0.74601	0.44623	0.29687	1.48912	0.70204	0.34678	0.10944	1.15826	0.42833	0.16767	0.03663	0.63263	3.280	36.44
44	NMm	Nelder-Mead method M	0.73807	0.50598	0.31342	1.55747	0.63674	0.28302	0.08221	1.00197	0.44667	0.18667	0.04028	0.67362	3.233	35.92
45	BBBC	big bang-big crunch algorithm	0.60531	0.45250	0.31255	1.37036	0.52323	0.35426	0.20417	1.08166	0.39769	0.19431	0.11286	0.70486	3.157	35.08
	RW	random walk	0.48754	0.32159	0.25781	1.06694	0.37554	0.21944	0.15877	0.75375	0.27969	0.14917	0.09847	0.52734	2.348	26.09

Summary

The dialectical algorithm is an innovative approach to optimization based on the philosophical concept of dialectics, where the interaction of opposites achieves improved solutions. The algorithm successfully combines the concepts of global and local search through a unique division of the population into speculative and practical thinkers, which ensures an effective balance between exploration and exploitation of the solution space.

The algorithm structure, consisting of three key steps, provides a systematic approach to optimization. In their work, speculative thinkers conduct a broad search of the solution space (although, as a rule, in optimization algorithms the best solutions are refined rather than "scattered" across the search space), while practical thinkers focus on local optimization of promising areas. This division allows the algorithm to effectively explore the solution space and avoid getting stuck in local optima, especially since, due to the random error I made, the algorithm logic became even closer to the theme of dialectical opposites.

The test results confirm the high efficiency of the algorithm with balanced search capabilities, which provide a sufficiently high level of performance on various types of tasks. Compared to other algorithms, DA does not show strong deviations for the worse or better and shows a uniformly stable result for color gradation in the table. The overall performance indicator demonstrates the competitiveness of the algorithm in comparison with existing optimization methods. This combination of philosophical principles and mathematical methods creates a powerful tool for solving complex optimization problems.

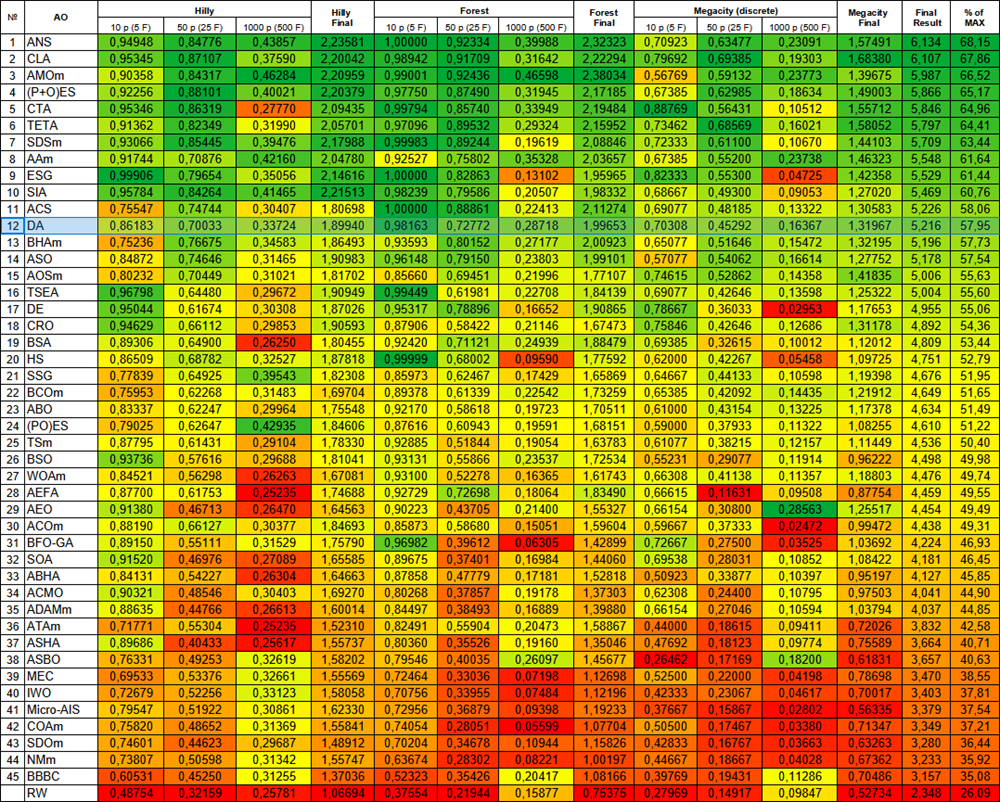
Figure 3. Color gradation of algorithms according to the corresponding tests

Figure 4. Histogram of algorithm testing results (scale from 0 to 100, the higher the better, where 100 is the maximum possible theoretical result, in the archive there is a script for calculating the rating table)

DA pros and cons:

Pros:

1. There are few external parameters, only two, not counting the population size.
   
2. Simple implementation.
3. Quite fast.
4. Balanced, good performance on both small and large-scale problems.
   

Disadvantages:

1. Scattered results.
   

The article is accompanied by an archive with the current versions of the algorithm codes. The author of the article is not responsible for the absolute accuracy in the description of canonical algorithms. Changes have been made to many of them to improve search capabilities. The conclusions and judgments presented in the articles are based on the results of the experiments.

• github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5

Programs used in the article

#	Name	Type	Description
1	#C_AO.mqh	Include	Parent class of population optimization algorithms
2	#C_AO_enum.mqh	Include	Enumeration of population optimization algorithms
3	TestFunctions.mqh	Include	Library of test functions
4	TestStandFunctions.mqh	Include	Test stand function library
5	Utilities.mqh	Include	Library of auxiliary functions
6	CalculationTestResults.mqh	Include	Script for calculating results in the comparison table
7	Testing AOs.mq5	Script	The unified test stand for all population optimization algorithms
8	Simple use of population optimization algorithms.mq5	Script	A simple example of using population optimization algorithms without visualization
9	Test_AO_DA.mq5	Script	DA test stand