金融時系列予測のための生物学的ニューロン

現代の取引は革命の真っ只中にあります。ニューラルネットワーク、遺伝的アルゴリズム、ディープラーニングなどの技術は目覚ましい成果を上げていますが、多くの場合、重大な欠点を抱えています。それは、これらの手法があまりにも「機械的」であり、市場変動の微妙な性質を捉えきれないという点です。市場変動の本質は、生きた市場参加者による集合的な行動の結果だからです。

このような背景のもとで、生物学的に妥当なニューラルモデルの利用が特に重要になります。抽象的な数学モデルを構築する代わりに、私たちは観測可能な宇宙で最も高度なコンピュータである人間の脳に目を向けました。私たちの研究グループは、Hodgkin-Huxleyモデルに基づき、神経プロセスの機能だけでなく、その物理的本質までも再現する独自のシステムを開発しました。

ノーベル賞を受賞したHodgkin-Huxleyモデルは、細胞レベルにおける神経インパルスの生成および伝播のメカニズムを記述しています。しかし、なぜこのモデルが金融市場を理解する鍵となり得るのでしょうか。その答えは、脳内での神経インパルスの伝播と、市場における情報の拡散との間に驚くほどの類似性が見られる点にあります。ニューロンがシナプス結合を通じて電気信号を交換するように、市場参加者も取引を通じて情報を交換しています。

本アプローチの革新性は、古典的モデルにプラズマ的要素を追加した点にあります。私たちはニューラルネットワークを、市場情報という「プラズマ」に浸された動的システムとして捉えています。この環境では、各ニューロンが直接的な結合だけでなく、自らが生成する電磁場を通じても他のニューロンの挙動に影響を及ぼします。これにより、従来のアルゴリズムでは見過ごされがちな微細な相関関係や構造を捉えることが可能になります。

本記事では、システムのアーキテクチャ、動作原理、そしてさまざまな金融商品への実践的な適用結果について詳しく解説します。生物学的発想に基づくアプローチが、金融時系列予測という課題に対して新たな視点を提供し、アルゴリズムトレーディングの分野に新たな地平を切り開くことを示していきます。

Hodgkin-Huxleyモデル：生物学と金融が出会うとき

ニューロンを想像してみてください。ニューロンは、電気インパルスを通じて情報を処理し伝達できる驚くべき細胞です。まさにこの脳の基本単位を、Alan HodgkinとAndrew Huxleyは画期的な研究の中で記述しました。この業績により、彼らは後にノーベル賞を受賞しています。このモデルは神経科学における真のブレークスルーでしたが、さらに想像してみてください。同じモデルが金融市場の動きを理解し、予測する助けにもなり得るのです。

このモデルの中核には、ニューロンがどのようにして電気インパルスを生成するのかを記述した数学的表現があります。トレーダーが市場から入ってくる情報に反応するように、ニューロンも入力信号に反応し、独自の活動パターンを生み出します。それでは、この驚くべきプロセスを記述するコードを見ていきましょう。

class HodgkinHuxleyNeuron:
    def __init__(self):
        self.V = -65.0  # Initial resting potential
        self.m = 0.05   # Activation of sodium channels
        self.h = 0.6    # Inactivation of sodium channels
        self.n = 0.32   # Activation of potassium channels
        self.last_spike_time = float('-inf')

イオンの踊り：ニューロンはいかにして意思決定をおこなうのか

Hodgkin-Huxleyモデルで最も印象的なのは、イオンがニューロン膜を越えて「踊る」様子を記述している点です。この分子バレエの主役となるナトリウムとカリウムは、特殊なチャネルを通って移動し、電気的な電位を生み出します。これは、市場において注文の流れが価格変動を生み出す仕組みと非常によく似ています。私たちの取引システムでは、この類推を活用し、市場データをイオン電流へと変換しています。

def ion_currents(self, V):
    I_Na = self.g_Na * (self.m ** 3) * self.h * (V - self.E_Na)  # Sodium current
    I_K = self.g_K * (self.n ** 4) * (V - self.E_K)             # Potassium current
    I_L = self.g_L * (V - self.E_L)                             # Leakage current
    return I_Na, I_K, I_L

プラズマの影響：ニューラルネットワークの新たな視点

私たちは古典的なモデルを超え、プラズマ的環境という概念を追加しました。ニューロンが単にシナプスによって結合されているのではなく、市場の「情報プラズマ」に浸されていると想像してください。各ニューロンのスパイクは影響の波を生み出し、その波は時間とともに減衰していきます。これは、市場におけるニュースが徐々に価格への影響力を失っていく様子とよく似ています。

def plasma_influence(self, current_time):
    time_since_spike = current_time - self.last_spike_time
    influence = self.plasma_strength * np.exp(-time_since_spike / self.plasma_decay)
    return influence * self.get_market_correlation()

時間を通じた学習：STDPメカニズム

私たちのシステムで最も刺激的な要素のひとつが、ニューロンスパイク間の時間的依存関係に基づく学習メカニズム(Spike-Timing-Dependent Plasticity, STDP)です。トレーダーが経験から学習するのと同様に、私たちのニューロンも市場の動きをどれだけうまく予測できたかに応じて、結合の強さを調整します。

def update_synaptic_weights(self, pre_spike, post_spike, weight):
    delta_t = post_spike - pre_spike
    if delta_t > 0:
        return weight * (1 + self.A_plus * np.exp(-delta_t / self.tau_plus))
    else:
        return weight * (1 - self.A_minus * np.exp(delta_t / self.tau_minus))

この生物学的着想に基づくアーキテクチャにより、私たちのシステムは単に市場データを処理するだけでなく、熟練トレーダーのように市場を「感じ取る」ことが可能になります。各ニューロンは市場ダイナミクスの特定の側面に特化したミニ専門家となり、それらの集合的な働きによって、驚くほど高精度な予測が生み出されます。

システムアーキテクチャ：生物学から取引判断へ

市場を分析するトレーダーの脳を想像してみてください。価格、出来高、インジケーター、ニュースといった情報を、何千ものニューロンが同時に処理しています。私たちはこの自然なアーキテクチャをシステム内に再現し、さらにプラズマや電磁相互作用という独自の特性を加えました。

システムの眼：入力データ構造

人間の脳が感覚を通じて情報を受け取るように、私たちのシステムも多数の市場シグナルを収集し処理します。すべてのティック、すべての価格変動がニューラルインパルスへと変換されます。それでは、データ前処理のコードを見ていきましょう。

class MarketFeatures:
    def __init__(self, window_size=20):
        self.window_size = window_size
        self.scaler = StandardScaler()
        
    def add_price(self, price: float, ohlc_data: pd.DataFrame) -> Dict[str, float]:
        features = {}
        
        # Technical indicators
        features['sma_10'] = self._calculate_sma(ohlc_data['close'], window=10)
        features['ema_20'] = self._calculate_ema(ohlc_data['close'], window=20)
        features['rsi'] = self._calculate_rsi(ohlc_data['close'], window=14)
        
        # Volumetric characteristics
        features['volume_sma'] = self._calculate_sma(ohlc_data['tick_volume'], window=10)
        
        # Temporal patterns
        features['hour'] = ohlc_data.index[-1].hour
        features['day_of_week'] = ohlc_data.index[-1].dayofweek
        
        return self.scaler.fit_transform(np.array(list(features.values())).reshape(1, -1))

ニューラルネットワーク：生物学と数学の架け橋

私たちのシステムの中核には、古典的なニューラルネットワークと生物学的に妥当なHodgkin-Huxleyモデルを融合させたハイブリッドアーキテクチャがあります。ここでの各ニューロンは、単なる数学的関数ではなく、小さな生きたシステムとして振る舞います。

class BioTradingModel(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super(BioTradingModel, self).__init__()
        self.layers = nn.ModuleList([
            nn.Linear(input_size, hidden_size),
            nn.Tanh(),
            nn.Linear(hidden_size, hidden_size),
            nn.Tanh(),
            nn.Linear(hidden_size, output_size)
        ])
        
        # Biological neurons
        self.bio_neurons = [HodgkinHuxleyNeuron() for _ in range(hidden_size)]
        self.plasma_field = PlasmaField(hidden_size)

プラズマフィールド：神経相互作用の新たな次元

私たちのシステムの独自性は、ニューロンが浸されるプラズマ的環境にあります。電磁場が空間に浸透するように、私たちのプラズマはニューロン間に追加の相互作用レベルを生み出します。

class PlasmaField:
    def __init__(self, size):
        self.field_strength = np.zeros(size)
        self.decay_rate = 0.95
        
    def update(self, neuron_activities):
        # Update the field based on neuron activity
        self.field_strength = self.field_strength * self.decay_rate
        self.field_strength += neuron_activities
        
    def get_influence(self, neuron_index):
        # Calculate the influence of a field on a specific neuron
        return np.sum(self.field_strength * np.exp(-self.distance_matrix[neuron_index]))

学習メカニズム：ニューロンとプラズマのダンス

私たちのシステムでは、学習が複数のレベルで同時におこなわれます。古典的な勾配降下法は、生物学的STDPやプラズマダイナミクスと組み合わせて用いられます。

def train_step(self, inputs, target):
    # Straight pass
    predictions = self.forward(inputs)
    loss = self.criterion(predictions, target)
    
    # Backpropagation
    self.optimizer.zero_grad()
    loss.backward()
    
    # Biological education
    for i, neuron in enumerate(self.bio_neurons):
        # STDP update
        neuron.update_weights(self.last_spike_times)
        
        # Plasma modulation
        plasma_influence = self.plasma_field.get_influence(i)
        neuron.modulate_weights(plasma_influence)
    
    self.optimizer.step()
    return loss.item()

この多層的なアーキテクチャにより、システムはデータ中の明白なパターンだけでなく、市場ダイナミクスの異なる側面間に存在する微妙でほとんど気づかれない関係性も捉えることができます。システムの各コンポーネントはそれぞれ固有の役割を果たし、それらの相乗効果によって単なる部品の合計以上のものが生まれます──まさに金融市場を分析するための人工脳です。

テクニカル指標：システムのデジタル感覚

私たちのニューラルシステムをトレーダーの人工脳と考えるなら、テクニカル指標はその感覚器官に相当します。人間が視覚、聴覚、触覚を使って世界を認識するように、システムもさまざまな指標を用いて市場のあらゆる側面を「感知」します。

基本指標：システムの視覚

まずは最も基本的な指標である移動平均から始めます。これはシステムの視覚のようなもので、市場のノイズの中から基調となるトレンドを見極めることを可能にします。

def calculate_moving_averages(self, prices):
    def sma(window):
        return np.convolve(prices, np.ones(window)/window, mode='valid')
    
    def ema(window):
        alpha = 2 / (window + 1)
        kernel = alpha * (1 - alpha)**np.arange(window)
        return np.convolve(prices, kernel[::-1], mode='valid')
    
    return {
        'sma_fast': sma(10),  # Fast SMA for short-term trends 
        'sma_slow': sma(20),  # Slow SMA for long-term trends
        'ema_fast': ema(10),  # Exponential MA for fast response
        'ema_slow': ema(20)   # Slow EMA for sorting out noise
    }

オシレーター：市場の瞬間を感知する

RSI、モメンタム、ストキャスティクスは、システムの触覚受容器に相当します。これらにより、価格変動の強さや反転の可能性のあるポイントを「感じ取る」ことができます。

def calculate_oscillators(self, data):
    def rsi(prices, period=14):
        delta = np.diff(prices)
        gain = np.where(delta > 0, delta, 0)
        loss = np.where(delta < 0, -delta, 0)
        
        avg_gain = np.mean(gain[:period])
        avg_loss = np.mean(loss[:period])
        
        for i in range(period, len(gain)):
            avg_gain = (avg_gain * 13 + gain[i]) / 14
            avg_loss = (avg_loss * 13 + loss[i]) / 14
            
        rs = avg_gain / avg_loss
        return 100 - (100 / (1 + rs))
    
    return {
        'rsi': rsi(data['close']),
        'momentum': data['close'] - np.roll(data['close'], 10),
        'stoch_k': self._calculate_stochastic_k(data)
    }

ボラティリティと出来高：システムの聴覚

ボラティリティや出来高の指標は、システムの耳のような役割を果たします──市場の「ノイズ」や値動きの強さを感知します。ボリンジャーバンドやATRは変動の振幅を評価するのに役立ち、出来高指標はその重要性を判断するのに役立ちます。

def measure_market_dynamics(self, data):
    def bollinger_bands(prices, window=20):
        sma = np.mean(prices[-window:])
        std = np.std(prices[-window:])
        return {
            'upper': sma + 2 * std,
            'lower': sma - 2 * std,
            'width': 4 * std / sma  # Normalized strip width
        }
    
    def volume_profile(volumes, prices):
        return {
            'volume_ma': np.mean(volumes[-10:]),
            'volume_trend': np.corrcoef(volumes[-20:], prices[-20:])[0,1],
            'volume_oscillator': (np.mean(volumes[-5:]) / np.mean(volumes[-20:]) - 1) * 100
        }
    
    volatility = bollinger_bands(data['close'])
    volume = volume_profile(data['volume'], data['close'])
    return {**volatility, **volume}

正規化：感度の調整

人間の脳が環境条件に応じて感覚の感度を調整するように、私たちのシステムも入力データのスケールを動的に調整します。これはニューラルネットワークを安定して動作させる上で非常に重要です。

def normalize_features(self, features: dict) -> dict:
    class AdaptiveNormalizer:
        def __init__(self, window=100):
            self.window = window
            self.history = {}
            
        def update(self, feature_name, value):
            if feature_name not in self.history:
                self.history[feature_name] = []
            
            self.history[feature_name].append(value)
            if len(self.history[feature_name]) > self.window:
                self.history[feature_name].pop(0)
            
            mean = np.mean(self.history[feature_name])
            std = np.std(self.history[feature_name])
            return (value - mean) / (std + 1e-8)  # Avoid zero divide
    
    normalizer = AdaptiveNormalizer()
    return {name: normalizer.update(name, value) 
            for name, value in features.items()}

これらすべての指標や機能は密接に連携して動作し、市場の現実を多次元的に描き出します。人間の脳がすべての感覚からの情報を統合するように、私たちのシステムもすべての指標からのデータを統合し、市場状況の単一の表現としてまとめます。これにより、単にトレンドを追ったり個別のシグナルに反応したりするだけでなく、市場ダイナミクスを包括的に理解することが可能になります。

実験結果

テスト方法

調査では、EUR/USD通貨ペアの履歴データを用いてシステムの包括的なテストを実施しました。対象期間は5年で、日足(D1)を使用しました。一般的な機械学習の原則に従い、データは学習用とテスト用に80/20の比率で分割しました。その結果、学習には1659データポイント、テストには415データポイントが使用されました。モデルは異なる重みの初期化を用いて20回の学習イテレーションをおこない、最適な構成を探索しました。

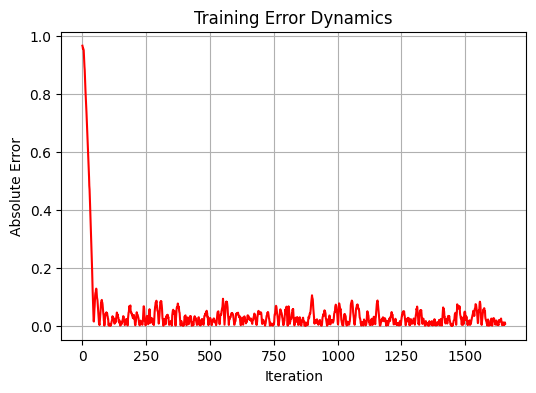
パフォーマンス分析

結果を分析する中で、モデルの興味深い特徴が明らかになりました。システムは短期的な価格変動を予測しようとするのではなく、通貨ペアの「公正価格」のようなものを判断することを目指しているように見えます。この観察は学習サンプルで比較的高い相関(0.583)と、標準誤差の低さ(0.012346)によって確認されます。しかし、テストサンプルではモデルの性能は大幅に低下し、相関はマイナス値(-0.108)に落ち込み、MSEは90倍以上に増加し、1.156584に達しました。

従来手法との比較

生物学的着想に基づくモデルは、従来のテクニカル指標や標準的なニューラルネットワークとは明らかに異なる挙動を示します。予測は大幅に変動しやすい傾向があります。 

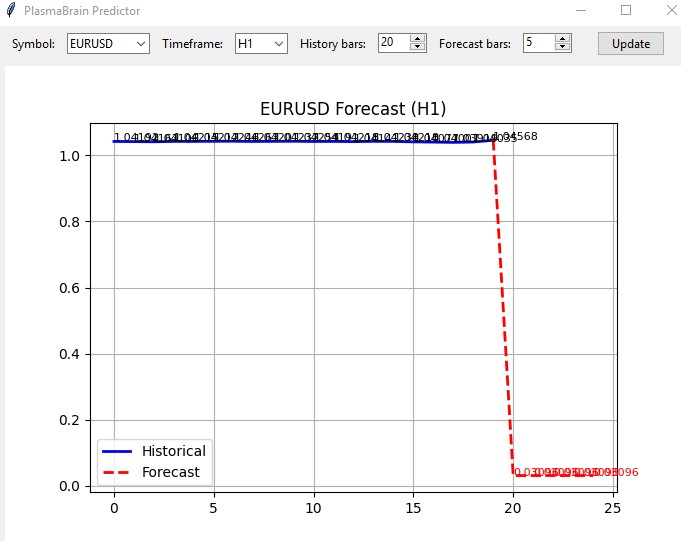
ここではテストサンプルに対する予測で、予測期間は15バーとしています。

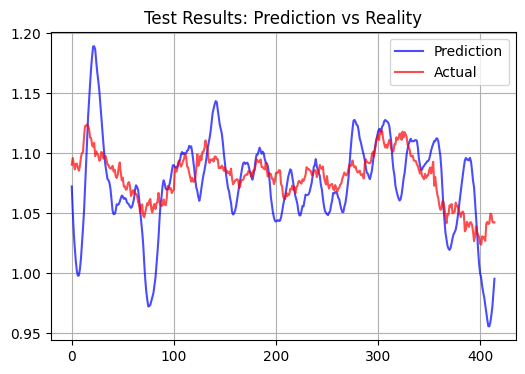
統計的パフォーマンス指標

モデル性能で最も顕著な結果は、テストサンプルにおける決定係数(R²)が非常に低く、約0.01であったことです。興味深いことに、学習サンプルでは比較的高い相関が見られ、データの長期的パターンを捉える能力があることを示しています。さらに、モデルの予測には明確に見えるスパイクが含まれることが多く、これらのスパイクが最小の価格変動に対応しているかどうか、またスキャルピングに適しているかどうかは今後の検証が必要です。

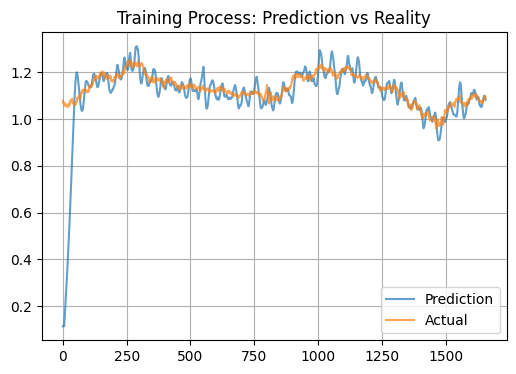
特徴と実用性

モデルの観察された挙動は、その生物学的性質によって説明できます。プラズマ的なニューラルシステムは強力なフィルターとして機能し、市場シグナルを大幅に増幅するようです。その結果、モデルは誇張された増分的予測を生成します。理論的には、STDPメカニズムにより安定した活性パターンが形成され、予測の平均化が進み、テスト状態と実際の状態に異なる結果が現れるはずです。さらに、入力として多くのテクニカル指標を用いていることが、過剰な正則化効果を生んでいる可能性もあります。

実務的観点から見ると、このモデルは通貨ペアの短期的な公正価値レベルを判断するために活用できます。 

結論

金融市場予測のための生物学的着想に基づくニューラルシステムに関する私たちの研究は、当初の想定とは異なる、しかし興味深い結果をもたらしました。人間の脳が資産の「公正価値」を直感的に感じ取れるように、生きたニューロンの動作原理に基づく私たちのモデルも、根本的に健全な価格レベルを識別する顕著な能力を示しました。

ニューラルネットワークのアーキテクチャにプラズマ的な環境を導入することで、一種の「集合知」が生まれました。ここでは、各ニューロンが直接的な結合だけでなく、長距離の電磁相互作用を通じてもシステムの動作に影響を与えます。このメカニズムは、市場ノイズの整理や長期的なトレンドの特定において特に有効であることが確認されました。 

おそらく、そこにはより深い意味があるのかもしれません。生物学的システムが長期的な生存のために進化したように、その姿を模して構築された私たちのニューラルネットワークも、安定して根本的に健全なパターンを特定することを目指しているのです。

最後まで読んでくださった方へのボーナス

私はこのモデルに基づいたインジケーターも作成しました。このインジケーターは、システムの残りの部分をモジュールとして読み込み、以下のようなシンプルなウィンドウで表示されます。

まだ実際の取引では試していませんが、他のすべてのシステムが概ね同じ方向を予測することを考えると、このインジケーターも期待通りに機能する可能性があります。