Алгоритм эволюционного путешествия во времени — Time Evolution Travel Algorithm (TETA)

MetaTrader 5 — Примеры | 29 января 2025, 08:40

329

Andrey Dik

Содержание

Введение

Мы рассмотрели много алгоритмов основанных на физических законах, таких как CSS, EM, GSA, AEFA, AOSm, однако, вселенная нас постоянно радует новыми явлениями и наполняет разными гипотезами и идеями. Один из основополагающих компонентов вселенной, такой как время, натолкнул меня на идею создания нового алгоритма оптимизации. Время не только вдохновляет на новые открытия, но и остаётся таинственной сущностью, которую трудно постигнуть. Оно течёт, словно река, унося с собой моменты нашей жизни и оставляя лишь воспоминания. Путешествия во времени всегда были предметом человеческого восхищения и фантазий. Чтобы лучше понять идею алгоритма, представим себе историю одного ученого.

Жил-был ученый-физик, одержимый идеей перемещения в светлое будущее, подальше от совершённых ошибок. Погрузившись в изучение потоков времени, он столкнулся с горьким открытием — путешествие в будущее невозможно. Не отчаявшись, он переключился на исследование перемещений в прошлое, надеясь исправить свои ошибки, но и здесь его ждало разочарование.

Однако, исследование гипотетических временных потоков привело его к поразительному открытию — существованию параллельных вселенных. Разработав теоретическую модель машины перемещения между мирами, он обнаружил нечто удивительное: хоть прямое путешествие во времени и невозможно, можно выбирать последовательность событий, ведущую к той или иной параллельной вселенной.

Каждое действие любого человека порождало новую параллельную реальность, но ученого интересовали только те вселенные, которые касались непосредственно его жизни. Для навигации между ними он установил в системе уравнений особые якоря (чтобы отличать миры между собой) — ключевые точки своей судьбы: семья, карьера, научные открытия, дружеские связи, значимые события. Эти якоря стали переменными в его машине перемещения, позволяя выбирать оптимальный путь между вероятностными мирами.

Запустив свое изобретение, он начал путешествие по параллельным мирам, но больше не стремился попасть в готовое светлое будущее. Он понял нечто более важное — возможность создавать это будущее своими руками, принимая решения в настоящем. Каждый новый выбор прокладывал путь к той версии реальности, которую он сам хотел воплотить в жизнь. Так он перестал быть пленником мечты об идеальном будущем, превратившись в его архитектора. Его машина стала не средством бегства от реальности, а инструментом осознанного творения собственной судьбы через выбор оптимальных решений в каждый момент времени.

В данной статье мы рассмотрим Алгоритм Эволюционного Путешествия во Времени (TETA), который реализует концепцию перемещения во времени и отличается тем, что не имеет никаких параметров или изменяемых переменных. Этот алгоритм естественным образом сохраняет баланс между поиском наилучшего решения и его уточнением. Обычно алгоритмы, не обладающие внешними параметрами, все же имеют внутренние параметры в виде констант, влияющих на эффективность работы. Однако в TETA нет даже таких констант, что делает его уникальным в своем роде.

Реализация алгоритма

В представленной истории ученый открыл способ перемещения между параллельными вселенными через изменение ключевых переменных своей жизни. Эта метафора ложится в основу предлагаемого алгоритма оптимизации, и, для наглядности понимания этого, рассмотрим рисунок ниже, который иллюстрирует идею алгоритма о параллельных вселенных, возникающих каждый раз при принятии решений. Каждая вселенная, имеющая завершенное пространство, определяется наличием признаков в виде якорей: семья, карьера, достижения и т.д.

Комбинируя свойства этих якорей, можно создавать новую вселенную, представляющую собой решение задачи оптимизации, в которой якоря — это оптимизируемые параметры.

TETA

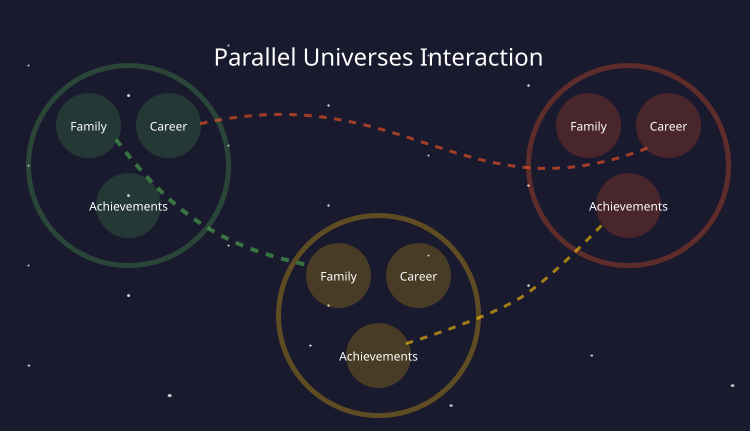
Рисунок 1. Параллельные вселенные со своими уникальными якорями (признаками)

В основе алгоритма TETA лежит концепция множественных параллельных вселенных, каждая из которых представляет собой потенциальное решение оптимизационной задачи. В техническом воплощении каждая такая вселенная описывается вектором координат (a[i].c), где каждая координата является якорем — ключевой переменной, определяющей конфигурацию данной реальности. Эти якоря можно представить как важнейшие параметры, настройка которых влияет на общее качество решения.

Для оценки качества каждой вселенной используется фитнес-функция (a[i].f), которая определяет "комфортность существования" в данной реальности. Чем выше значение этой функции, тем более благоприятной считается вселенная. Каждая вселенная хранит информацию не только о своем текущем состоянии, но и о лучшей известной конфигурации (a[i].cB), что можно сравнить с "памятью" о наиболее успешном варианте развития событий. Кроме того, алгоритм поддерживает глобальное лучшее состояние (cB), представляющее самую благоприятную конфигурацию среди всех обнаруженных вариантов.

Популяция из N особей формирует множество параллельных вселенных, каждая из которых описывается своим набором значений якорей. Эти вселенные постоянно ранжируются по значению фитнес-функции, что создает своеобразную иерархию от наименее до наиболее благоприятных состояний. Каждый якорь реальности является оптимизируемой переменной, и любое изменение этих переменных порождает новую конфигурацию вселенной. Полный набор якорей образует вектор переменных x = (x₁, x₂, ..., xₙ), полностью описывающий конкретную реальность. При этом, для каждой переменной определены границы допустимых значений, что можно интерпретировать, как физические законы, ограничивающие возможные изменения в каждой вселенной.

Оценка благоприятности каждой вселенной производится через фитнес-функцию f(x), отображающую конфигурацию вселенной в действительное число. Чем выше это значение, тем более предпочтительной считается данная реальность. Таким образом создается математически строгий механизм оценки и сравнения различных вариантов развития событий во множестве параллельных вселенных.

Ключевой особенностью алгоритма является единый вероятностный коэффициент (rnd *= rnd), который определяет как вероятность выбора вселенной для взаимодействия, так и силу изменения якорей. Это создает естественный механизм самобалансировки системы: лучшие вселенные имеют больший шанс быть выбранными, но их якоря изменяются слабее (пропорционально rnd), в то время как худшие вселенные, хотя и выбираются реже, подвергаются более сильным изменениям (пропорционально 1.0 - rnd).

Такой подход отражает глубокую философскую идею о том, что в жизни невозможно достичь идеала во всем сразу. Улучшение происходит через постоянную балансировку различных аспектов: иногда лучшие якоря могут немного ухудшиться ради общего баланса, в то время как худшие стремятся к улучшению. Сила изменений пропорциональна тому, насколько "хороша" вселенная, что отражает реальную жизнь, где кардинальные изменения чаще происходят тогда, когда что-то идет не так.

В результате, алгоритм не просто оптимизирует значения, а моделирует процесс поиска баланса в сложной многомерной системе жизненных обстоятельств, стремясь найти не идеальную, а наиболее гармоничную версию реальности через тонкую балансировку всех её аспектов.

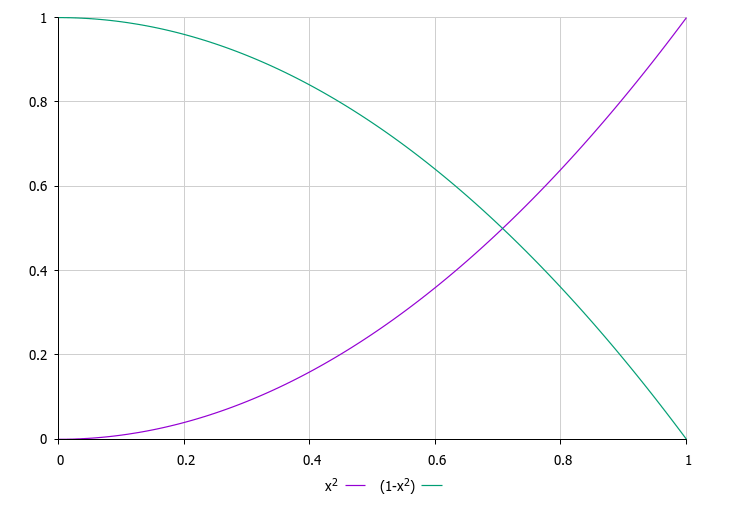
Рисунок 2. Красная линия — функция вероятности выбора вселенных в зависимости от их качества, зеленая линия — степень изменения якорей для соответствующих вселенных

Псевдокод алгоритма:

Инициализация:
1. Создать популяцию из N параллельных вселенных
2. Для каждой вселенной:
   - Случайно инициализировать значения якорей (координат) в допустимых пределах
   - Установить начальные лучшие значения равными текущим

Основной цикл:
1. Сортировка вселенных по качеству (фитнес-функции)
   - Лучшие вселенные получают меньшие индексы
   - Худшие вселенные получают большие индексы

2. Для каждой вселенной i из N:
   Для каждого якоря (координаты):

   а) Выбор вселенной для взаимодействия:
      - Генерировать случайное число rnd от 0 до 1
      - Возвести rnd в квадрат для усиления приоритета лучших вселенных
      - Выбрать индекс pair пропорционально rnd

   б) Если текущая вселенная не совпадает с выбранной (i ≠ pair):

      Если текущая вселенная лучше выбранной (i < pair):
         - Слабое изменение якоря пропорционально rnd
         - Новое_значение = текущее + rnd * (значение_выбранной - текущее)

      Иначе (текущая вселенная хуже выбранной):
         Если (случайное_число > rnd):
            - Сильное изменение якоря пропорционально (1 - rnd)
            - Новое_значение = текущее + (1-rnd) * (значение_выбранной - текущее)
         Иначе:
            - Полное копирование значения якоря из лучшей вселенной
            - Новое_значение = значение_выбранной

   в) Иначе (взаимодействие с собой):
      - Локальный поиск через гауссово распределение
      - Новое_значение = GaussDistribution(текущее_лучшее)

   г) Коррекция нового значения якоря в допустимых пределах

3. Обновление лучших значений:
   Для каждой вселенной:
   - Если текущее решение лучше личного лучшего, обновить личное лучшее
   - Если текущее решение лучше глобального лучшего, обновить глобальное лучшее

4. Повторять основной цикл до выполнения критерия остановки

Теперь у нас все готово для реализации машины перемещения по параллельным вселенным в коде. Напишем класс "C_AO_TETA", который будет являться производным от класса "C_AO". Вот его краткое описание:

Конструктор — инициализирует имя, описание и ссылку на алгоритм, а также устанавливает размер популяции.
Метод SetParams — устанавливает параметры, используя значения из массива "params".
Методы Init, Moving,Revision — объявлены, но будут реализованы в другом фрагменте кода.

class C_AO_TETA : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_TETA () { }
  C_AO_TETA ()
  {
    ao_name = "TETA";
    ao_desc = "Time Evolution Travel Algorithm";
    ao_link = "https://www.mql5.com/ru/articles/16963";

    popSize = 50; // количество параллельных вселенных в популяции

    ArrayResize (params, 1);
    params [0].name = "popSize"; params [0].val = popSize;
  }

  void SetParams ()
  {
    popSize = (int)params [0].val;
  }

  bool Init (const double &rangeMinP  [],  // минимальные значения для якорей
             const double &rangeMaxP  [],  // максимальные значения для якорей
             const double &rangeStepP [],  // шаг изменения якорей
             const int     epochsP = 0);   // количество эпох поиска

  void Moving ();
  void Revision ();

  private: //-------------------------------------------------------------------
};
//——————————————————————————————————————————————————————————————————————————————

Инициализация метода "Init" класса "C_AO_TETA" выполняет начальную настройку алгоритма.

Параметры метода:

rangeMinP — массив минимальных значений для якорей.
rangeMaxP — массив максимальных значений для якорей.
rangeStepP — массив шагов изменения якорей.
epochsP — количество эпох поиска по умолчанию 0).

Стандартная инициализация:

Метод вызывает "StandardInit", выполняет проверку и настройку диапазонов для якорей. Если эта инициализация не удалась (возвращает false).

Возврат значения:

Если все проверки и настройки прошли успешно, метод возвращает "true", указывая на успешную инициализацию алгоритма.

//——————————————————————————————————————————————————————————————————————————————
// TETA - Time Evolution Travel Algorithm
// Алгоритм оптимизации, основанный на концепции перемещения между параллельными вселенными
// через изменение ключевых якорей (событий) жизни

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_TETA::Init (const double &rangeMinP  [], // минимальные значения для якорей
                      const double &rangeMaxP  [], // максимальные значения для якорей
                      const double &rangeStepP [], // шаг изменения якорей
                      const int     epochsP = 0)   // количество эпох поиска
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Метод "Moving" класса "C_AO_TETA" отвечает за изменение якорей в параллельных вселенных для создания новых в рамках алгоритма.

Проверка состояния ревизии:

Если "revision" равен "false", метод инициализирует начальные значения якорей для всех параллельных вселенных, используя случайные значения из заданного диапазона и применяя функции для приведения к допустимым значениям (на основе шага).

Обновление значений якорей:

Если ревизия уже была проведена, происходит итерация по всем параллельным вселенным. Для каждого якоря генерируется вероятность и вычисляется его новое значение:
- Если текущая вселенная более благоприятна, то якорь немного изменяется в положительную сторону, чтобы найти лучший баланс.
- Если текущая вселенная менее благоприятна, проверка вероятности может привести к значительному изменению якоря или полному принятию его из более успешной вселенной.
- Если вселенные совпадают, происходит локальная настройка якоря с использованием гауссового распределения.
После вычисления нового значения, якорь приводится к допустимому диапазону.

Этот метод на практике отвечает за адаптацию и улучшение решений (параллельных вселенных), что является ключевой частью алгоритма оптимизации.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_TETA::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    // Инициализация начальных значений якорей во всех параллельных вселенных
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  double rnd  = 0.0;
  double val  = 0.0;
  int    pair = 0.0;

  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      // Генерация вероятности, которая определяет как шанс выбора вселенной,
      // так и силу изменения якорей
      rnd  = u.RNDprobab ();
      rnd *= rnd;

      // Выбор вселенной для обмена опытом
      pair = (int)u.Scale (rnd, 0.0, 1.0, 0, popSize - 1);

      if (i != pair)
      {
        if (i < pair)
        {
          // Если текущая вселенная более благоприятна:
          // Небольшое изменение якоря (пропорционально rnd) для поиска лучшего баланса
          val = a [i].c [c] + (rnd)*(a [pair].cB [c] - a [i].cB [c]);
        }
        else
        {
          if (u.RNDprobab () > rnd)
          {
            // Если текущая вселенная менее благоприятна:
            // Значительное изменение якоря (пропорционально 1.0 - rnd)
            val = a [i].cB [c] + (1.0 - rnd) * (a [pair].cB [c] - a [i].cB [c]);
          }
          else
          {
            // Полное принятие конфигурации якоря из более успешной вселенной
            val = a [pair].cB [c];
          }
        }
      }
      else
      {
        // Локальная настройка якоря через гауссово распределение
        val = u.GaussDistribution (cB [c], rangeMin [c], rangeMax [c], 1);
      }

      a [i].c [c] = u.SeInDiSp  (val, rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Метод "Revision" класса "C_AO_TETA" отвечает за обновление конфигураций якорей в параллельных вселенных и сортировку этих вселенных по их качеству, подробнее:

Обновление глобально лучшей конфигурации:

Метод проходит по всем параллельным вселенным (от 0 до popSize).
Если значение функции f текущей вселенной (a[i].f) больше глобального лучшего значения "fB", то:
- Обновляется "fB" на значение (a[i].f).
- Конфигурация якорей текущей вселенной копируется в глобальную конфигурацию "cB".

Обновление лучшей известной конфигурации для каждой вселенной:

Если значение функции "f" текущей вселенной больше её лучшего известного значения (a[i].fB), то:
- Обновляется (a[i].fB) на значение (a[i].f).
- Конфигурация якорей текущей вселенной копируется в её лучшую известную конфигурацию (a[i].cB).

Сортировка вселенных:

Объявляется статический массив "aT" для хранения агентов.
Размер массива изменяется на "popSize".
Вселенные сортируются по их лучшему из известных индивидуальных свойств с помощью функции "u.Sorting_fB".

//——————————————————————————————————————————————————————————————————————————————
void C_AO_TETA::Revision ()
{
  for (int i = 0; i < popSize; i++)
  {
    // Обновление глобально лучшей конфигурации якорей
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ArrayCopy (cB, a [i].c);
    }

    // Обновление лучшей известной конфигурации якорей для каждой вселенной
    if (a [i].f > a [i].fB)
    {
      a [i].fB = a [i].f;
      ArrayCopy (a [i].cB, a [i].c);
    }
  }

  // Сортировка вселенных по степени их благоприятности
  static S_AO_Agent aT []; ArrayResize (aT, popSize);
  u.Sorting_fB (a, aT, popSize);
}
//——————————————————————————————————————————————————————————————————————————————

Результаты тестов

Результаты работы алгоритма TETA:

TETA|Time Evolution Travel Algorithm|50.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.9136198796338938
25 Hilly's; Func runs: 10000; result: 0.8234856192574587
500 Hilly's; Func runs: 10000; result: 0.3199003852163246
=============================
5 Forest's; Func runs: 10000; result: 0.970957820488216
25 Forest's; Func runs: 10000; result: 0.8953189778250419
500 Forest's; Func runs: 10000; result: 0.29324457646900925
=============================
5 Megacity's; Func runs: 10000; result: 0.7346153846153844
25 Megacity's; Func runs: 10000; result: 0.6856923076923078
500 Megacity's; Func runs: 10000; result: 0.16020769230769372
=============================
All score: 5.79704 (64.41%)

Итоговый результат: 5.79704 (64.41%). Учитывая сложность тестовых функций, это отличный показатель. Алгоритм очень быстро обнаруживает важные участки поверхности с перспективными оптимумами и тут же приступает к их уточнению, что можно проследить на каждой визуализации работы алгоритма.

Hilly

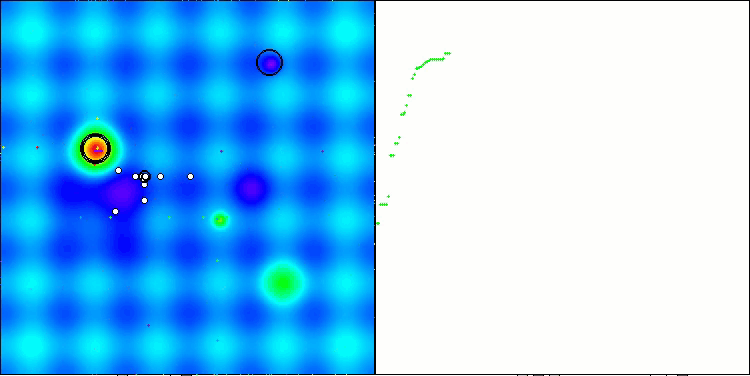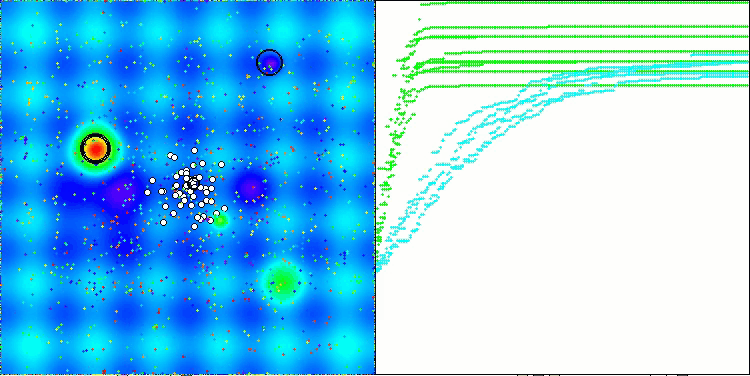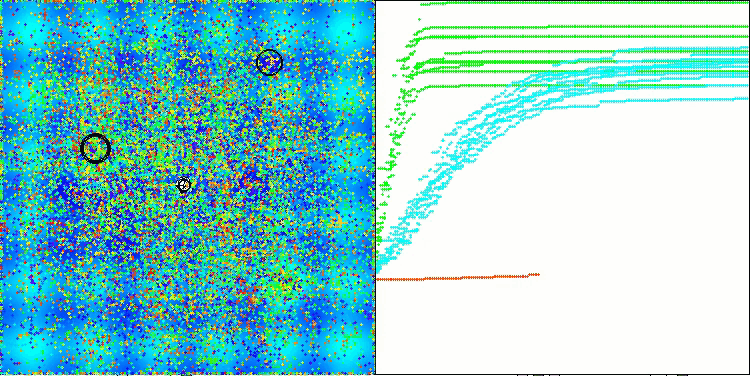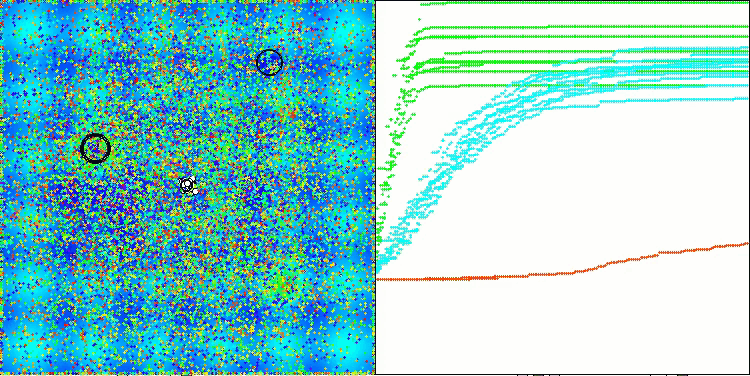
TETA на тестовой функции Hilly

Forest

TETA на тестовой функции Forest

Megacity

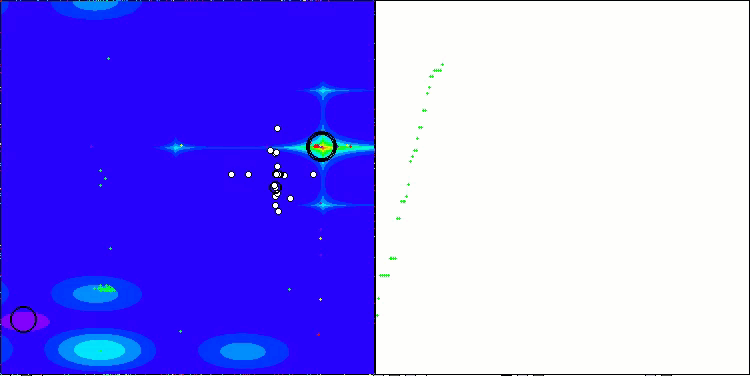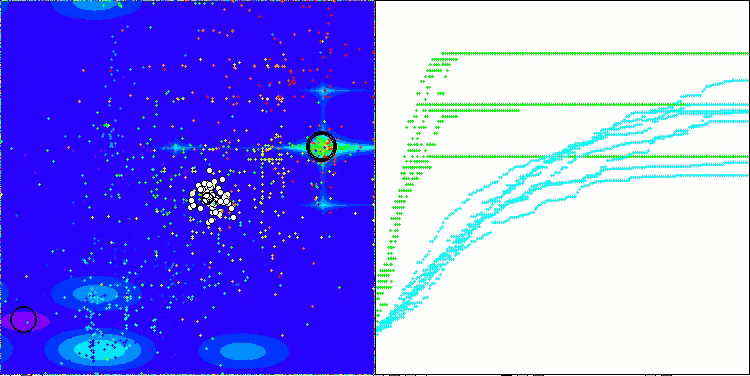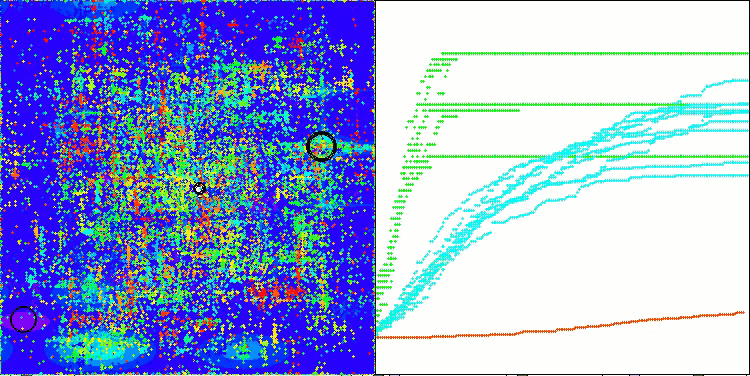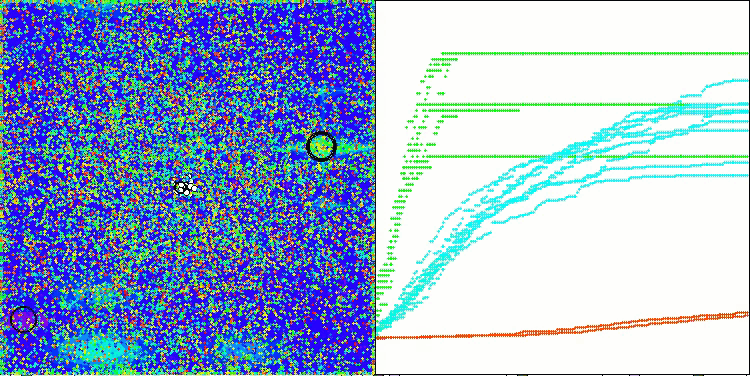
TETA на тестовой функции Megacity

Хотелось бы отметить, что по результатам работы на функции GoldsteinPrice, входящей в набор примеров тестовых функций, на которых можно тестировать алгоритмы оптимизации, набирает наилучший результат среди всех алгоритмов оптимизации, обгоняя лидера группы популяционных алгоритмов - ANS.

GoldsteinPrice

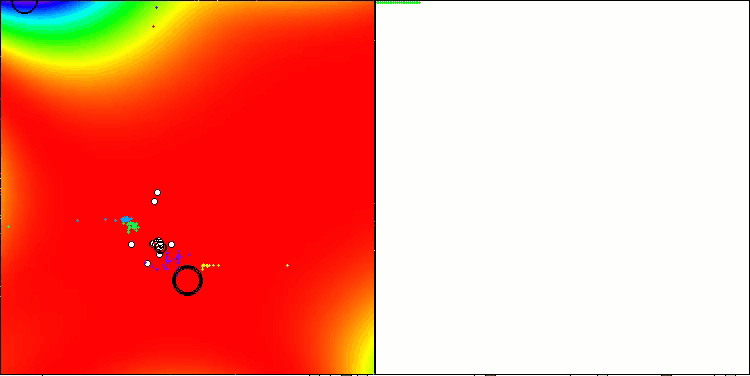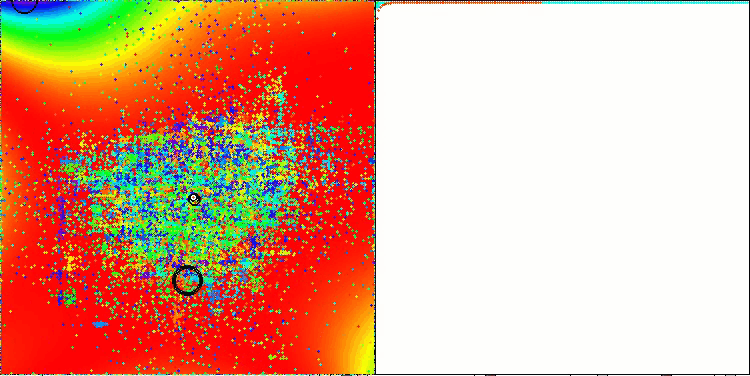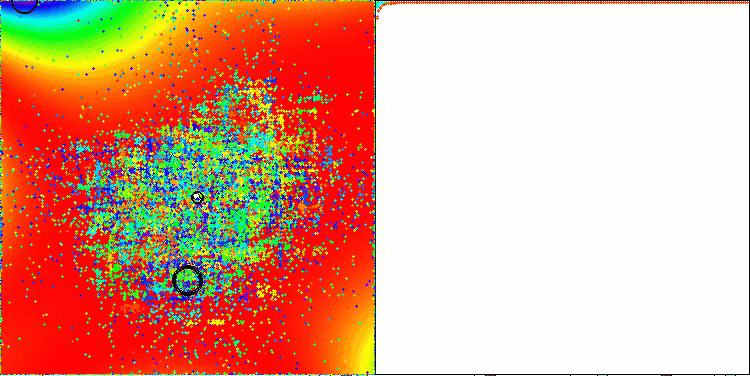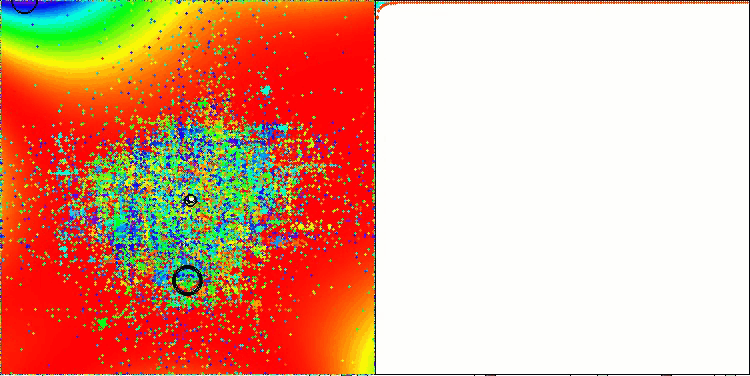
TETA на тестовой функции GoldsteinPrice (доступна для выбора из списка тестовых функций)

Результаты на GoldsteinPrice:

5 GoldsteinPrice's; Func runs: 10000; result: 0.9999786723616957
25 GoldsteinPrice's; Func runs: 10000; result: 0.9999750431600845
500 GoldsteinPrice's; Func runs: 10000; result: 0.9992343490683104

Алгоритм TETA при завершении тестирования входит в первую десятку лучших алгоритмов оптимизации и занимает почетное 6 место.

№	AO	Description	Hilly			Hilly final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result	% of MAX
№	AO	Description	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Hilly final	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Forest final	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Megacity final	Final result	% of MAX
1	ANS	across neighbourhood search	0,94948	0,84776	0,43857	2,23581	1,00000	0,92334	0,39988	2,32323	0,70923	0,63477	0,23091	1,57491	6,134	68,15
2	CLA	code lock algorithm (joo)	0,95345	0,87107	0,37590	2,20042	0,98942	0,91709	0,31642	2,22294	0,79692	0,69385	0,19303	1,68380	6,107	67,86
3	AMOm	animal migration ptimization M	0,90358	0,84317	0,46284	2,20959	0,99001	0,92436	0,46598	2,38034	0,56769	0,59132	0,23773	1,39675	5,987	66,52
4	(P+O)ES	(P+O) evolution strategies	0,92256	0,88101	0,40021	2,20379	0,97750	0,87490	0,31945	2,17185	0,67385	0,62985	0,18634	1,49003	5,866	65,17
5	CTA	comet tail algorithm (joo)	0,95346	0,86319	0,27770	2,09435	0,99794	0,85740	0,33949	2,19484	0,88769	0,56431	0,10512	1,55712	5,846	64,96
6	TETA	time evolution travel algorithm (joo)	0,91362	0,82349	0,31990	2,05701	0,97096	0,89532	0,29324	2,15952	0,73462	0,68569	0,16021	1,58052	5,797	64,41
7	SDSm	stochastic diffusion search M	0,93066	0,85445	0,39476	2,17988	0,99983	0,89244	0,19619	2,08846	0,72333	0,61100	0,10670	1,44103	5,709	63,44
8	AAm	archery algorithm M	0,91744	0,70876	0,42160	2,04780	0,92527	0,75802	0,35328	2,03657	0,67385	0,55200	0,23738	1,46323	5,548	61,64
9	ESG	evolution of social groups (joo)	0,99906	0,79654	0,35056	2,14616	1,00000	0,82863	0,13102	1,95965	0,82333	0,55300	0,04725	1,42358	5,529	61,44
10	SIA	simulated isotropic annealing (joo)	0,95784	0,84264	0,41465	2,21513	0,98239	0,79586	0,20507	1,98332	0,68667	0,49300	0,09053	1,27020	5,469	60,76
11	ACS	artificial cooperative search	0,75547	0,74744	0,30407	1,80698	1,00000	0,88861	0,22413	2,11274	0,69077	0,48185	0,13322	1,30583	5,226	58,06
12	BHAm	black hole algorithm M	0,75236	0,76675	0,34583	1,86493	0,93593	0,80152	0,27177	2,00923	0,65077	0,51646	0,15472	1,32195	5,196	57,73
13	ASO	anarchy society optimization	0,84872	0,74646	0,31465	1,90983	0,96148	0,79150	0,23803	1,99101	0,57077	0,54062	0,16614	1,27752	5,178	57,54
14	AOSm	atomic orbital search M	0,80232	0,70449	0,31021	1,81702	0,85660	0,69451	0,21996	1,77107	0,74615	0,52862	0,14358	1,41835	5,006	55,63
15	TSEA	turtle shell evolution algorithm (joo)	0,96798	0,64480	0,29672	1,90949	0,99449	0,61981	0,22708	1,84139	0,69077	0,42646	0,13598	1,25322	5,004	55,60
16	DE	differential evolution	0,95044	0,61674	0,30308	1,87026	0,95317	0,78896	0,16652	1,90865	0,78667	0,36033	0,02953	1,17653	4,955	55,06
17	CRO	chemical reaction optimisation	0,94629	0,66112	0,29853	1,90593	0,87906	0,58422	0,21146	1,67473	0,75846	0,42646	0,12686	1,31178	4,892	54,36
18	BSA	bird swarm algorithm	0,89306	0,64900	0,26250	1,80455	0,92420	0,71121	0,24939	1,88479	0,69385	0,32615	0,10012	1,12012	4,809	53,44
19	HS	harmony search	0,86509	0,68782	0,32527	1,87818	0,99999	0,68002	0,09590	1,77592	0,62000	0,42267	0,05458	1,09725	4,751	52,79
20	SSG	saplings sowing and growing	0,77839	0,64925	0,39543	1,82308	0,85973	0,62467	0,17429	1,65869	0,64667	0,44133	0,10598	1,19398	4,676	51,95
21	BCOm	bacterial chemotaxis optimization M	0,75953	0,62268	0,31483	1,69704	0,89378	0,61339	0,22542	1,73259	0,65385	0,42092	0,14435	1,21912	4,649	51,65
22	ABO	african buffalo optimization	0,83337	0,62247	0,29964	1,75548	0,92170	0,58618	0,19723	1,70511	0,61000	0,43154	0,13225	1,17378	4,634	51,49
23	(PO)ES	(PO) evolution strategies	0,79025	0,62647	0,42935	1,84606	0,87616	0,60943	0,19591	1,68151	0,59000	0,37933	0,11322	1,08255	4,610	51,22
24	TSm	tabu search M	0,87795	0,61431	0,29104	1,78330	0,92885	0,51844	0,19054	1,63783	0,61077	0,38215	0,12157	1,11449	4,536	50,40
25	BSO	brain storm optimization	0,93736	0,57616	0,29688	1,81041	0,93131	0,55866	0,23537	1,72534	0,55231	0,29077	0,11914	0,96222	4,498	49,98
26	WOAm	wale optimization algorithm M	0,84521	0,56298	0,26263	1,67081	0,93100	0,52278	0,16365	1,61743	0,66308	0,41138	0,11357	1,18803	4,476	49,74
27	AEFA	artificial electric field algorithm	0,87700	0,61753	0,25235	1,74688	0,92729	0,72698	0,18064	1,83490	0,66615	0,11631	0,09508	0,87754	4,459	49,55
28	AEO	artificial ecosystem-based optimization algorithm	0,91380	0,46713	0,26470	1,64563	0,90223	0,43705	0,21400	1,55327	0,66154	0,30800	0,28563	1,25517	4,454	49,49
29	ACOm	ant colony optimization M	0,88190	0,66127	0,30377	1,84693	0,85873	0,58680	0,15051	1,59604	0,59667	0,37333	0,02472	0,99472	4,438	49,31
30	BFO-GA	bacterial foraging optimization - ga	0,89150	0,55111	0,31529	1,75790	0,96982	0,39612	0,06305	1,42899	0,72667	0,27500	0,03525	1,03692	4,224	46,93
31	SOA	simple optimization algorithm	0,91520	0,46976	0,27089	1,65585	0,89675	0,37401	0,16984	1,44060	0,69538	0,28031	0,10852	1,08422	4,181	46,45
32	ABHA	artificial bee hive algorithm	0,84131	0,54227	0,26304	1,64663	0,87858	0,47779	0,17181	1,52818	0,50923	0,33877	0,10397	0,95197	4,127	45,85
33	ACMO	atmospheric cloud model optimization	0,90321	0,48546	0,30403	1,69270	0,80268	0,37857	0,19178	1,37303	0,62308	0,24400	0,10795	0,97503	4,041	44,90
34	ADAMm	adaptive moment estimation M	0,88635	0,44766	0,26613	1,60014	0,84497	0,38493	0,16889	1,39880	0,66154	0,27046	0,10594	1,03794	4,037	44,85
35	ATAm	artificial tribe algorithm M	0,71771	0,55304	0,25235	1,52310	0,82491	0,55904	0,20473	1,58867	0,44000	0,18615	0,09411	0,72026	3,832	42,58
36	ASHA	artificial showering algorithm	0,89686	0,40433	0,25617	1,55737	0,80360	0,35526	0,19160	1,35046	0,47692	0,18123	0,09774	0,75589	3,664	40,71
37	ASBO	adaptive social behavior optimization	0,76331	0,49253	0,32619	1,58202	0,79546	0,40035	0,26097	1,45677	0,26462	0,17169	0,18200	0,61831	3,657	40,63
38	MEC	mind evolutionary computation	0,69533	0,53376	0,32661	1,55569	0,72464	0,33036	0,07198	1,12698	0,52500	0,22000	0,04198	0,78698	3,470	38,55
39	IWO	invasive weed optimization	0,72679	0,52256	0,33123	1,58058	0,70756	0,33955	0,07484	1,12196	0,42333	0,23067	0,04617	0,70017	3,403	37,81
40	Micro-AIS	micro artificial immune system	0,79547	0,51922	0,30861	1,62330	0,72956	0,36879	0,09398	1,19233	0,37667	0,15867	0,02802	0,56335	3,379	37,54
41	COAm	cuckoo optimization algorithm M	0,75820	0,48652	0,31369	1,55841	0,74054	0,28051	0,05599	1,07704	0,50500	0,17467	0,03380	0,71347	3,349	37,21
42	SDOm	spiral dynamics optimization M	0,74601	0,44623	0,29687	1,48912	0,70204	0,34678	0,10944	1,15826	0,42833	0,16767	0,03663	0,63263	3,280	36,44
43	NMm	Nelder-Mead method M	0,73807	0,50598	0,31342	1,55747	0,63674	0,28302	0,08221	1,00197	0,44667	0,18667	0,04028	0,67362	3,233	35,92
44	BBBC	big bang-big crunch algorithm	0,60531	0,45250	0,31255	1,37036	0,52323	0,35426	0,20417	1,08166	0,39769	0,19431	0,11286	0,70486	3,157	35,08
45	CPA	cyclic parthenogenesis algorithm	0,71664	0,40014	0,25502	1,37180	0,62178	0,33651	0,19264	1,15093	0,34308	0,16769	0,09455	0,60532	3,128	34,76
	RW	random walk	0,48754	0,32159	0,25781	1,06694	0,37554	0,21944	0,15877	0,75375	0,27969	0,14917	0,09847	0,52734	2,348	26,09

Выводы

Работая над алгоритмом TETA, я постоянно стремился создать что-то простое и эффективное. Метафора параллельных вселенных и путешествий во времени изначально казалась просто красивой идеей, но в процессе разработки она органично воплотилась в эффективный механизм оптимизации.

Ключевой особенностью алгоритма стала идея о том, что невозможно достичь идеала во всем сразу — нужно искать баланс. В жизни мы постоянно балансируем между семьей, карьерой и личными достижениями, и именно эту концепцию я заложил в основу алгоритма через систему якорей. Каждый якорь представляет собой важный аспект, который нужно оптимизировать, но не в ущерб другим.

Наиболее интересным техническим решением стала связь между вероятностью выбора вселенной и силой её влияния на другие вселенные. Это создало естественный механизм, где лучшие решения имеют больший шанс быть выбранными, и их влияние зависит от качества. Такой подход обеспечивает баланс между исследованием новых возможностей и использованием уже найденных хороших решений.

Тестирование алгоритма принесло неожиданно отличные результаты. Это делает алгоритм особенно ценным для практических задач с ограниченными вычислительными ресурсами. При этом алгоритм показывает стабильно замечательные результаты на разных типах функций, демонстрируя свою универсальность. Что особенно радует — это компактность реализации. Всего около 50 строк ключевого кода, отсутствие настраиваемых параметров, и при этом такая эффективность. Это действительно удачное решение, когда простота реализации сочетается с высокой производительностью.

В конечном итоге, TETA превзошел мои первоначальные ожидания. Из метафоры о путешествиях во времени родился практичный и эффективный инструмент оптимизации, который может найти применение в самых разных областях. Это показывает, что иногда простые решения, основанные на понятных природных аналогиях, могут быть очень эффективными. Алгоритм был создан буквально на одном дыхании — от идеи до реализации, и я очень доволен проделанной работой над алгоритмом, который может стать хорошим помощником для исследователей и практиков в быстром поиске оптимальных решений.

Tab

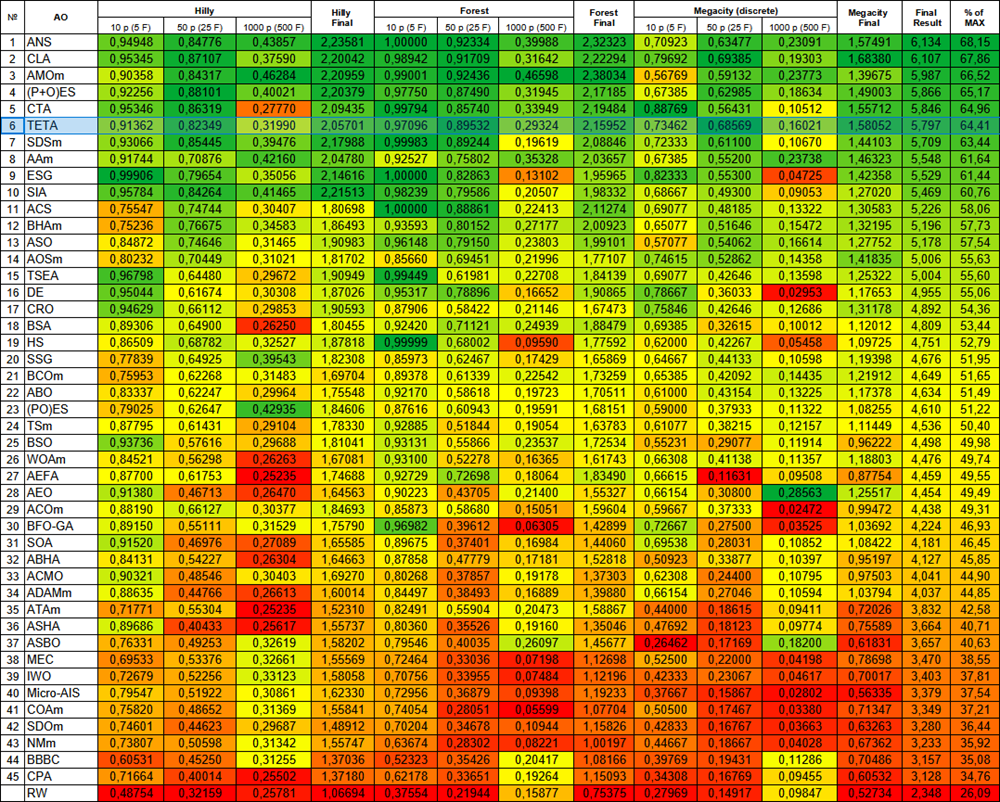
Рисунок 3. Цветовая градация алгоритмов по соответствующим тестам

Chart

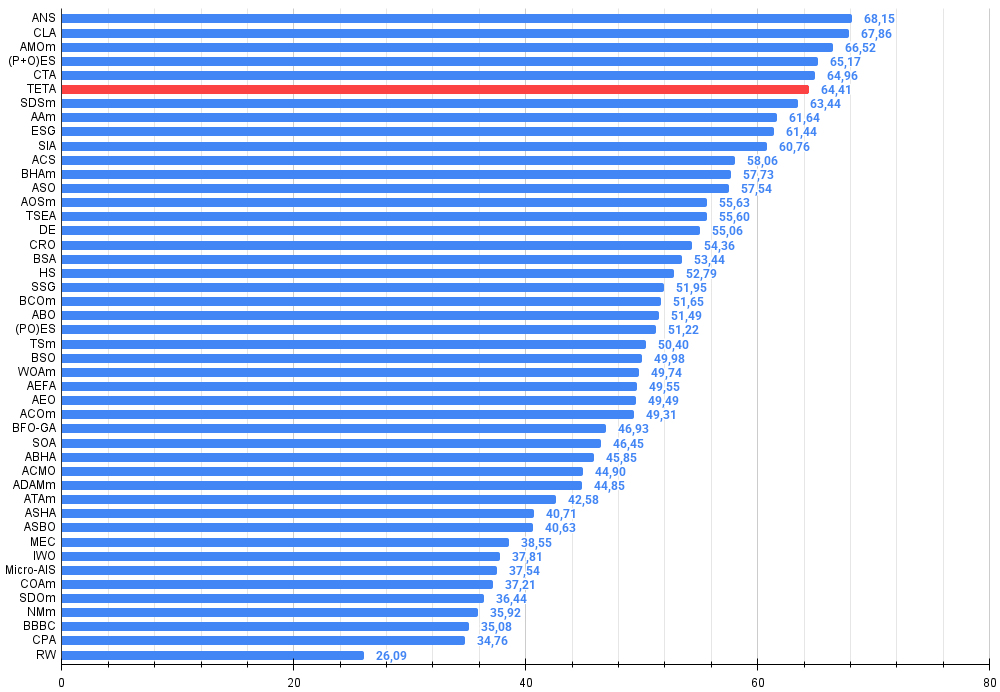
Рисунок 4. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше, где 100 - максимально возможный теоретический результат, в архиве скрипт для расчета рейтинговой таблицы)

Плюсы и минусы алгоритма TETA:

Плюсы:

Из внешних параметров только размер популяции.
Простая реализация.
Очень быстрый.
Сбалансированные показатели на задачах как малых, так и больших размерностей.

Минусы:

Разброс результатов на дискретных задачах малой размерности.

К статье прикреплён архив с актуальными версиями кодов алгоритмов. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.

github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5

Программы, используемые в статье

#	Имя	Тип	Описание
1	#C_AO.mqh	Включаемый файл	Родительский класс популяционных алгоритмов оптимизации
2	#C_AO_enum.mqh	Включаемый файл	Перечисление популяционных алгоритмов оптимизации
3	TestFunctions.mqh	Включаемый файл	Библиотека тестовых функций
4	TestStandFunctions.mqh	Включаемый файл	Библиотека функций тестового стенда
5	Utilities.mqh	Включаемый файл	Библиотека вспомогательных функций
6	CalculationTestResults.mqh	Включаемый файл	Скрипт для расчета результатов в сравнительную таблицу
7	Testing AOs.mq5	Скрипт	Единый испытательный стенд для всех популяционных алгоритмов оптимизации
8	Simple use of population optimization algorithms.mq5	Скрипт	Простой пример использования популяционных алгоритмов оптимизации без визуализации
9	Test_AO_TETA.mq5	Скрипт	Испытательный стенд для TETA

Прикрепленные файлы |

Загрузить ZIP

TETA.ZIP (154.13 KB)

Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Другие статьи автора

Перейти к обсуждению на форуме трейдеров

Собственные векторы и собственные значения: Разведочный анализ данных в MetaTrader 5

В статье мы рассмотрим различные способы применения собственных векторов и собственных значений в разведочном анализе данных для выявления в них уникальных взаимосвязей.

Создаем динамическую мультисимвольную мультипериодную панель индекса относительной силы (RSI) в MQL5

В статье рассмотрена разработка динамической мультисимвольной мультипериодной панели индикатора RSI в MQL5. Панель призвана предоставлять трейдерам значения RSI в реальном времени по различным символам и таймфреймам. Панель будет оснащена интерактивными кнопками, обновлениями в реальном времени и цветовыми индикаторами, помогающими трейдерам принимать обоснованные решения.

Разработка системы репликации (Часть 61): Нажатие кнопки воспроизведения в сервисе (II)

В данной статье мы рассмотрим изменения, которые позволят системе репликации/моделирования работать более эффективно и безопасно. Также я не оставлю без внимания тех, кто хочет извлечь максимум пользы из использования классов. Кроме того, рассмотрим специфическую проблему в MQL5, которая снижает производительность кода при работе с классами, и объясним, как ее решить.

Методы дискретизации ценовых движений на Python

Мы рассмотрим методы дискретизации цен на Python + MQL5. В этой статье я поделюсь практическим опытом разработки библиотеки на Python, которая реализует целый спектр подходов к формированию баров — от классических Volume и Range bars до более экзотических методов вроде Renko и Kagi.ары, свечи трехлинейного прорыва, рэйндж бары — какова их статистика, как еще можно представить цены дискретно?