Algoritmo de viaje evolutivo en el tiempo — Time Evolution Travel Algorithm (TETA)

Contenido

1. Introducción
2. Implementación del algoritmo
3. Resultados de las pruebas

Introducción

Ya hemos analizado muchos algoritmos basados en leyes físicas, tales como el CSS, el EM, el GSA, el AEFA o el AOSm, sin embargo, el universo nos entretiene constantemente con nuevos fenómenos y nos llena de diferentes hipótesis e ideas. Uno de los componentes fundamentales del universo, como es el tiempo, me llevó a la idea de crear un nuevo algoritmo de optimización. El tiempo no solo inspira nuevos descubrimientos, sino que sigue siendo una entidad misteriosa difícil de comprender. Fluye como un río, llevándose consigo los momentos de nuestra vida y dejando solo los recuerdos. Los viajes en el tiempo siempre han sido objeto de la fascinación y las fantasía humanas. Para entender mejor la idea de algoritmo, deberemos imaginar la historia de un científico.

Érase una vez un científico dedicado a la física, que estaba obsesionado con la idea de avanzar hacia un futuro brillante, lejos de los errores cometidos. Tras sumergirse en el estudio de los flujos temporales, se enfrentó a un amargo descubrimiento: resulta imposible viajar al futuro. Para no desanimarse, pasó a investigar los viajes atrás en el tiempo, con la esperanza de corregir sus errores, pero también aquí se llevó una decepción.

Sin embargo, su estudio de las corrientes temporales hipotéticas le llevó a un descubrimiento sorprendente: la existencia de universos paralelos. Tras desarrollar un modelo teórico de máquina para viajar entre mundos, descubrió algo sorprendente: aunque el viaje directo en el tiempo resultaba imposible, sí que era posible elegir una secuencia de acontecimientos que conduzcan a uno u otro universo paralelo.

Cada acción de cualquier persona generaba una nueva realidad paralela, pero al científico solo le interesaban los universos que afectaban directamente a su vida. Para navegar entre ellos, fijó anclas especiales en el sistema de ecuaciones (para distinguir los mundos entre sí): los puntos clave de su destino: su familia, su carrera, algunos descubrimientos científicos, sus amistades y otros acontecimientos significativos. Estas anclas se convirtieron en variables de su máquina de movimiento, permitiéndole seleccionar el mejor camino entre mundos probabilísticos.

Tras poner en marcha su invento, empezó a viajar por mundos paralelos, pero ya no aspiraba a un futuro brillante ya preparado. Se dio cuenta de algo más importante: existía la capacidad de crear ese futuro con sus propias manos tomando decisiones en el presente. Cada nueva selección allanaba el camino hacia la versión de la realidad que él mismo quería realizar. Así dejó de ser prisionero del sueño de un futuro ideal para convertirse en su arquitecto. Su máquina no se convirtió en un medio de evasión de la realidad, sino en un instrumento de creación consciente de su propio destino gracias a la elección de decisiones óptimas en cada momento.

En este artículo analizaremos el algoritmo de viaje evolutivo en el tiempo (TETA), que implementa el concepto de viaje en el tiempo y se caracteriza por no tener parámetros ni variables modificables. Este algoritmo mantiene de forma natural un equilibrio entre la búsqueda de la mejor solución y su clarificación. Normalmente, los algoritmos que no poseen parámetros externos siguen teniendo parámetros internos en forma de constantes que afectan al rendimiento. Sin embargo, el TETA ni siquiera tiene esas constantes, lo que lo hace único en su género.

Implementación del algoritmo

En la historia presentada, el científico descubrió una forma de viajar entre universos paralelos cambiando las variables clave de su vida. Esta metáfora constituye la base del algoritmo de optimización propuesto y, para que quede claro, analizaremos la siguiente figura, que ilustra la idea del algoritmo de universos paralelos que surgen cada vez que se toman decisiones. Cada universo con un espacio completo se define por la presencia de características en forma de anclas: familia, carrera, logros, etc.

Combinando las propiedades de estas anclas, podemos crear un nuevo universo que supondrá una solución a un problema de optimización en el que las anclas serán los parámetros a optimizar.

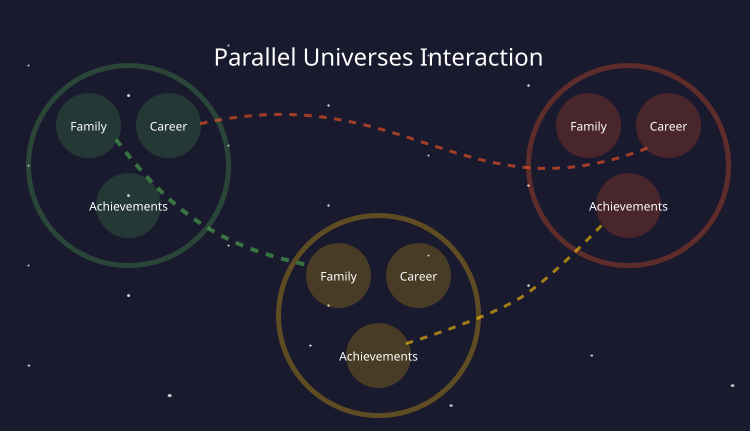
Figura 1. Universos paralelos con sus propias anclas (características) únicas

El algoritmo TETA se basa en el concepto de múltiples universos paralelos, cada uno de los cuales representará una solución potencial a un problema de optimización. En su realización técnica, cada universo de este tipo se describe usando un vector de coordenadas (a[i].c), donde cada coordenada es un ancla, una variable clave que define la configuración de una realidad dada. Estas anclas pueden considerarse parámetros críticos cuyo ajuste afecta a la calidad global de la solución.

Para evaluar la calidad de cada universo, se usa una función de aptitud (a[i].f) que determina la "comodidad de la existencia" en una realidad determinada. Cuanto mayor sea el valor de esta función, más favorable se considerará el universo. Cada universo almacena información no solo sobre su estado actual, sino también sobre la mejor configuración conocida (a[i].cB), que puede compararse con la "memoria" de la versión más acertada de los eventos. Además, el algoritmo mantiene un mejor estado global (cB) que representa la configuración más favorable entre todas las variantes detectadas.

Una población de N individuos forma un conjunto de universos paralelos, cada uno de los cuales se describe según su propio conjunto de valores de ancla. Estos universos se clasifican continuamente según su valor de aptitud, lo que crea una especie de jerarquía de los estados menos favorables a los más favorables. Cada ancla de la realidad es una variable optimizable, y cualquier cambio en estas variables generará una nueva configuración del universo. El conjunto completo de anclas forma un vector de variables x = (x₁, x₂, ..., xₙ) que describe por entero una realidad concreta. Al mismo tiempo, para cada variable se definen los límites de los valores aceptables, que podemos interpretar como leyes físicas que limitan los posibles cambios en cada universo.

La favorabilidad de cada universo se evalúa usando una función de aptitud f(x), que asigna la configuración del universo a un número real. Cuanto más alto sea este valor, más favorable se considerará una realidad determinada. De este modo, se crea un mecanismo matemáticamente riguroso para evaluar y comparar distintas variantes de desarrollo de eventos en un conjunto de universos paralelos.

Una característica clave del algoritmo es el único coeficiente de probabilidad (rnd *= rnd) que determina tanto la probabilidad de elegir un universo con el que interactuar como la fuerza del cambio de anclas. Esto crea un mecanismo natural de autoequilibrio para el sistema: los mejores universos tienen más posibilidades de ser seleccionados, pero sus anclas cambian de forma más débil (proporcional a rnd), mientras que los peores universos, aunque se seleccionan con menos frecuencia, sufren cambios más fuertes (proporcional a 1,0 - rnd).

Este planteamiento refleja la profunda idea filosófica de que en la vida es imposible alcanzar la perfección en todo al mismo tiempo. La mejora se produce gracias al equilibrio constante de distintos aspectos: a veces, las mejores anclas pueden deteriorarse un poco para lograr el equilibrio general, mientras que las peores anclas tienden a mejorar. El poder del cambio es proporcional a lo "bueno" que sea el universo, lo cual refleja la vida real, donde es más probable que se produzcan cambios drásticos cuando algo va mal.

Como resultado, el algoritmo no se limita a optimizar valores, sino que modela el proceso de búsqueda del equilibrio en un complejo sistema multidimensional de circunstancias vitales, tratando de encontrar no un ideal, sino la versión más armoniosa de la realidad mediante un delicado equilibrio de todos sus aspectos.

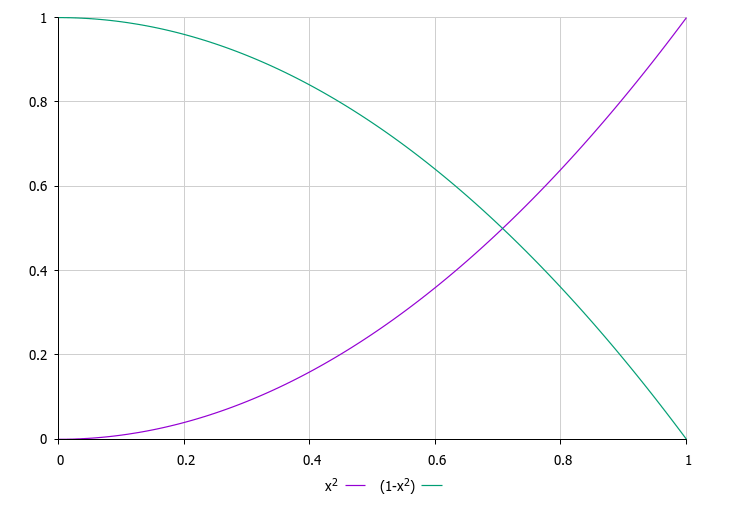
Figura 2. La línea roja es la función de probabilidad de seleccionar universos dependiendo de su calidad, la línea verde es el grado de cambio en las anclas para los respectivos universos

Pseudocódigo del algoritmo:

Inicialización:
1. Creamos una población de N universos paralelos
2. Para cada universo:
   - Inicializamos aleatoriamente los valores de las anclas (coordenadas) dentro de límites aceptables.
   - Fijamos los mejores valores iniciales como iguales a los actuales

Ciclo principal:
1. Clasificación de los universos según su calidad (función de aptitud)
   - Los mejores universos reciben índices más pequeños
   - Los peores universos reciben índices más grandes

2. Para cada universo i de N:
   Para cada ancla (coordenadas):
   
   (a) Se selecciona el universo para la interacción:
      - Se genera un número aleatorio rnd de 0 a 1
      - Se cuadra rnd para reforzar la priorización de los mejores universos
      - Se selecciona un índice de pares proporcional a rnd
   
   b) Si el universo actual no coincide con el universo seleccionado (i ≠ pair):
      
      Si el universo actual es mejor que el universo seleccionado (i < pair):
         - El cambio de ancla débil será proporcional a rnd
         - Nuevo_valor = actual + rnd * (valor_seleccionado - actual)
      
      En caso contrario (el universo actual es peor que el universo elegido):
         Si (número_aleatorio > rnd):
            - El cambio de ancla fuerte será proporcional a (1 - rnd)
            - Nuevo_valor = actual + (1-rnd) * (valor_seleccionado - actual)
         De lo contrario:
            - Se copiará al completo el valor de ancla del universo mejor
            - Nuevo_valor = valor_seleccionado
   
   c) De otro modo (interacción con uno mismo):
      - Se realizará la búsqueda local mediante una distribución gaussiana
      - Nuevo_valor = GaussDistribution(mejor_actual)
   
   d) Se corregirá el nuevo valor del ancla dentro de los límites permitidos

3. Actualización de los mejores valores:
   Para cada universo:
   - Si la solución actual es mejor que la mejor personal, se actualizará la mejor personal
   - Si la solución actual es mejor que la mejor solución global, se actualizará la mejor solución global

4. El ciclo principal se repetirá hasta que se cumpla el criterio de parada

Ahora estamos listos para implementar una máquina para viajar por universos paralelos en código. Vamos a escribir la clase "C_AO_TETA", que derivará de la clase "C_AO". He aquí una breve descripción de la misma:

• Constructor — inicializa el nombre, la descripción y la referencia al algoritmo, y establece el tamaño de la población.
• Método SetParams — establece los parámetros usando los valores del array "params".
• Métodos Init, Moving,Revision — están declarados, pero serán implementados en otro fragmento de código.

class C_AO_TETA : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_TETA () { }
  C_AO_TETA ()
  {
    ao_name = "TETA";
    ao_desc = "Time Evolution Travel Algorithm";
    ao_link = "https://www.mql5.com/es/articles/16963";

    popSize = 50; // количество параллельных вселенных в популяции

    ArrayResize (params, 1);
    params [0].name = "popSize"; params [0].val = popSize;
  }

  void SetParams ()
  {
    popSize = (int)params [0].val;
  }

  bool Init (const double &rangeMinP  [],  // минимальные значения для якорей
             const double &rangeMaxP  [],  // максимальные значения для якорей
             const double &rangeStepP [],  // шаг изменения якорей
             const int     epochsP = 0);   // количество эпох поиска

  void Moving ();
  void Revision ();

  private: //-------------------------------------------------------------------
};
//——————————————————————————————————————————————————————————————————————————————

La inicialización del método "Init" de la clase "C_AO_TETA" realizará el ajuste inicial del algoritmo. 

Parámetros del método:

• rangeMinP — array de valores mínimos para las anclas.
• rangeMaxP — array de valores máximos para las anclas.
• rangeStepP — array de pasos de cambio de anclas.
• epochsP — número de épocas de búsqueda, por defecto es 0).

Inicialización estándar:

• El método llama a "StandardInit" y efectúa la validación y el establecimiento de rangos para los anclas. Si esta inicialización falla (retorna false).

Valor de retorno:

• Si todas las comprobaciones y ajustes se realizan correctamente, el método retornará "true", lo cual indicará que el algoritmo se ha inicializado correctamente.

//——————————————————————————————————————————————————————————————————————————————
// TETA - Time Evolution Travel Algorithm
// Алгоритм оптимизации, основанный на концепции перемещения между параллельными вселенными
// через изменение ключевых якорей (событий) жизни

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_TETA::Init (const double &rangeMinP  [], // минимальные значения для якорей
                      const double &rangeMaxP  [], // максимальные значения для якорей
                      const double &rangeStepP [], // шаг изменения якорей
                      const int     epochsP = 0)   // количество эпох поиска
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  return true;
}
//——————————————————————————————————————————————————————————————————————————————

El método "Moving" de la clase "C_AO_TETA" se encargará de cambiar las anclas en universos paralelos para crear otras nuevas dentro del algoritmo.

Comprobación del estado de la revisión:

• Si "revision" es "false", el método inicializará los valores de ancla iniciales para todos los universos paralelos utilizando valores aleatorios del rango dado y aplicando funciones para convertirlos a valores válidos (basados en el paso).

Actualización de los valores de ancla:

• Si la revisión ya se ha realizado, se iterará por todos los universos paralelos. Para cada ancla, se generará una probabilidad y se calculará su nuevo valor:
  • Si el universo actual es más favorable, el ancla cambiará ligeramente en sentido positivo para encontrar un mejor equilibrio.
  • Si el universo actual es menos favorable, la comprobación de probabilidades podría dar lugar a un cambio significativo del ancla o a su adopción completa a partir de un universo más exitoso.
  • Si los universos coinciden, se producirá un ajuste local del ancla mediante una distribución gaussiana.
• Tras calcular el nuevo valor, el ancla se situará en el intervalo admisible.

En la práctica, este método se encarga de adaptar y mejorar las soluciones (universos paralelos), lo cual constituye una parte fundamental del algoritmo de optimización. 

//——————————————————————————————————————————————————————————————————————————————
void C_AO_TETA::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    // Инициализация начальных значений якорей во всех параллельных вселенных
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  double rnd  = 0.0;
  double val  = 0.0;
  int    pair = 0.0;

  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      // Генерация вероятности, которая определяет как шанс выбора вселенной,
      // так и силу изменения якорей
      rnd  = u.RNDprobab ();
      rnd *= rnd;

      // Выбор вселенной для обмена опытом
      pair = (int)u.Scale (rnd, 0.0, 1.0, 0, popSize - 1);

      if (i != pair)
      {
        if (i < pair)
        {
          // Если текущая вселенная более благоприятна:
          // Небольшое изменение якоря (пропорционально rnd) для поиска лучшего баланса
          val = a [i].c [c] + (rnd)*(a [pair].cB [c] - a [i].cB [c]);
        }
        else
        {
          if (u.RNDprobab () > rnd)
          {
            // Если текущая вселенная менее благоприятна:
            // Значительное изменение якоря (пропорционально 1.0 - rnd)
            val = a [i].cB [c] + (1.0 - rnd) * (a [pair].cB [c] - a [i].cB [c]);
          }
          else
          {
            // Полное принятие конфигурации якоря из более успешной вселенной
            val = a [pair].cB [c];
          }
        }
      }
      else
      {
        // Локальная настройка якоря через гауссово распределение
        val = u.GaussDistribution (cB [c], rangeMin [c], rangeMax [c], 1);
      }

      a [i].c [c] = u.SeInDiSp  (val, rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

El método "Revision" de la clase "C_AO_TETA" se encarga de actualizar las configuraciones de ancla en universos paralelos y de clasificar dichos universos según su calidad; concretamente:

Actualización de la mejor configuración a nivel global:

• El método itera todos los universos paralelos (de 0 a popSize).
• Si el valor de la función f del universo actual (a[i].f) es mayor que el mejor valor global "fB", entonces:
  • "fB" se actualizará al valor de (a[i].f).
  • La configuración de ancla del universo actual se copiará en la configuración global "cB".

Actualización de la mejor configuración conocida para cada universo:

• Si el valor de la función "f" del universo actual es mayor que su mejor valor conocido (a[i].fB), entonces:
  • (a[i].fB) se actualizará al valor de (a[i].f).
  • La configuración de ancla del universo actual se copiará en su mejor configuración conocida (a[i].cB).

Clasificación de universos:

• Se declara un array estático "aT" para almacenar agentes.
• El tamaño del array se cambia a "popSize".
• Los universos se clasifican según su mejor propiedad individual conocida mediante la función "u.Sorting_fB".

//——————————————————————————————————————————————————————————————————————————————
void C_AO_TETA::Revision ()
{
  for (int i = 0; i < popSize; i++)
  {
    // Обновление глобально лучшей конфигурации якорей
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ArrayCopy (cB, a [i].c);
    }

    // Обновление лучшей известной конфигурации якорей для каждой вселенной
    if (a [i].f > a [i].fB)
    {
      a [i].fB = a [i].f;
      ArrayCopy (a [i].cB, a [i].c);
    }
  }

  // Сортировка вселенных по степени их благоприятности
  static S_AO_Agent aT []; ArrayResize (aT, popSize);
  u.Sorting_fB (a, aT, popSize);
}
//——————————————————————————————————————————————————————————————————————————————

Resultados de las pruebas

Resultados del algoritmo TETA:

TETA|Time Evolution Travel Algorithm|50.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.9136198796338938
25 Hilly's; Func runs: 10000; result: 0.8234856192574587
500 Hilly's; Func runs: 10000; result: 0.3199003852163246
=============================
5 Forest's; Func runs: 10000; result: 0.970957820488216
25 Forest's; Func runs: 10000; result: 0.8953189778250419
500 Forest's; Func runs: 10000; result: 0.29324457646900925
=============================
5 Megacity's; Func runs: 10000; result: 0.7346153846153844
25 Megacity's; Func runs: 10000; result: 0.6856923076923078
500 Megacity's; Func runs: 10000; result: 0.16020769230769372
=============================
All score: 5.79704 (64.41%)

Conclusión: 5.79704 (64.41%). Teniendo en cuenta la complejidad de las funciones de la prueba, se trata de una puntuación excelente. El algoritmo detecta con gran rapidez área importantes de la superficie con óptimos prometedores y comienza inmediatamente a afinarlos, lo cual puede apreciarse en cada visualización del funcionamiento del algoritmo.

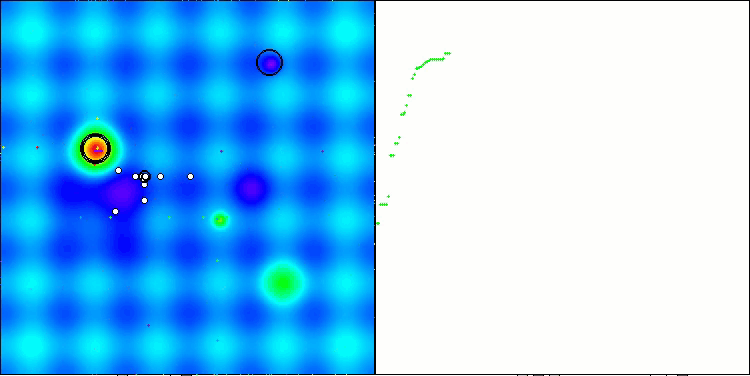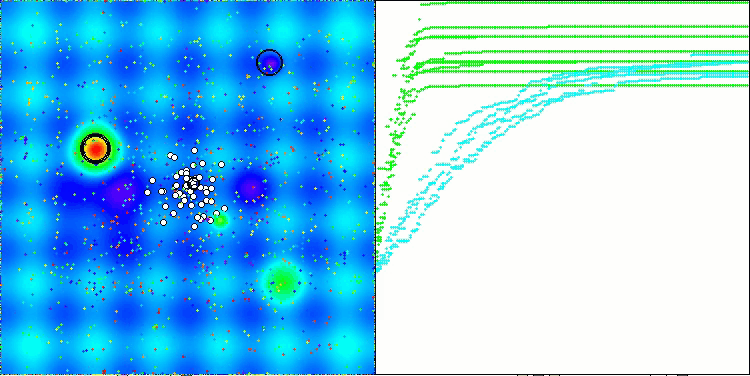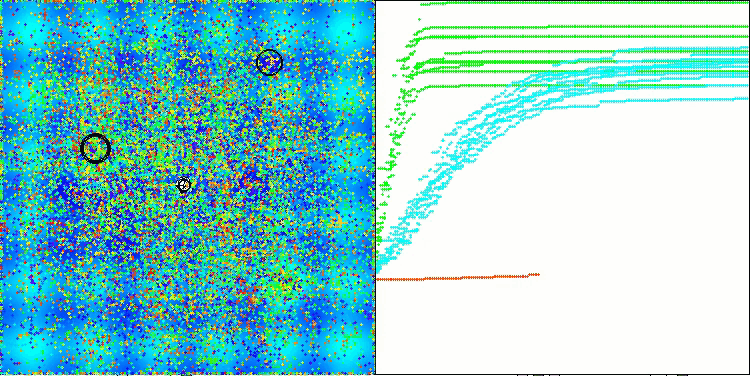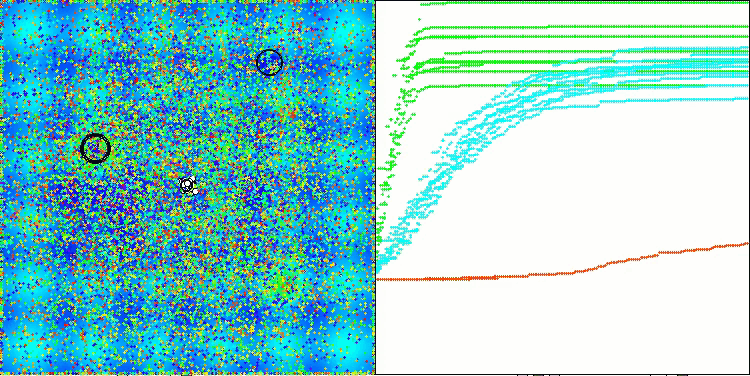
TETA en la función de prueba Hilly

  TETA en la función de prueba Forest

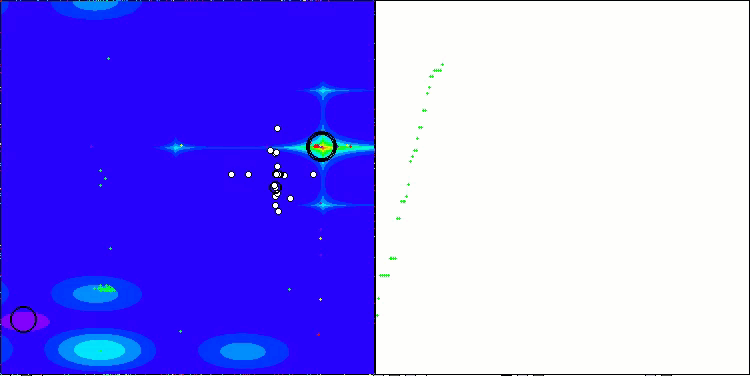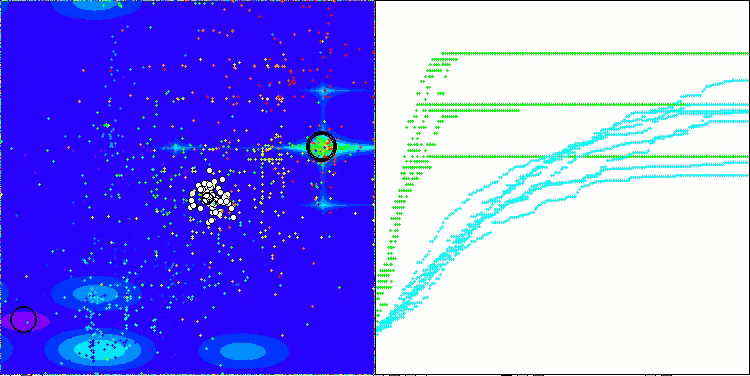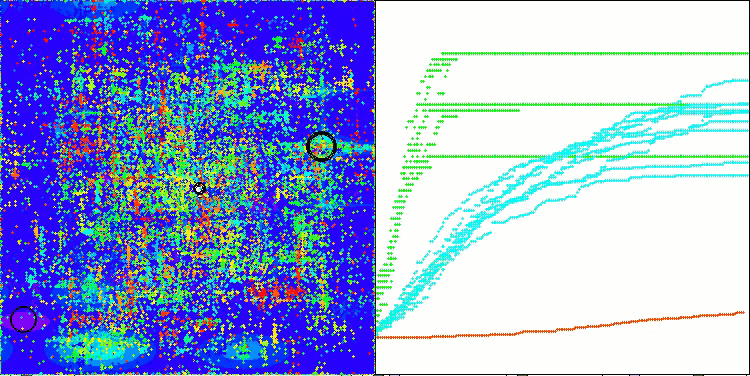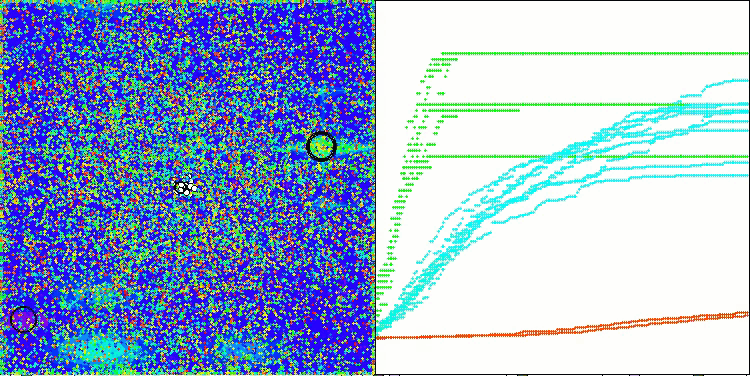
TETA en la función de prueba Megacity

Nos gustaría señalar que, según los resultados, la función GoldsteinPrice, incluida de ejemplo en el conjunto de funciones de prueba sobre las que se pueden probar algoritmos de optimización, obtiene el mejor resultado entre todos los algoritmos de optimización, superando al líder del grupo de algoritmos poblacionales: el ANS.

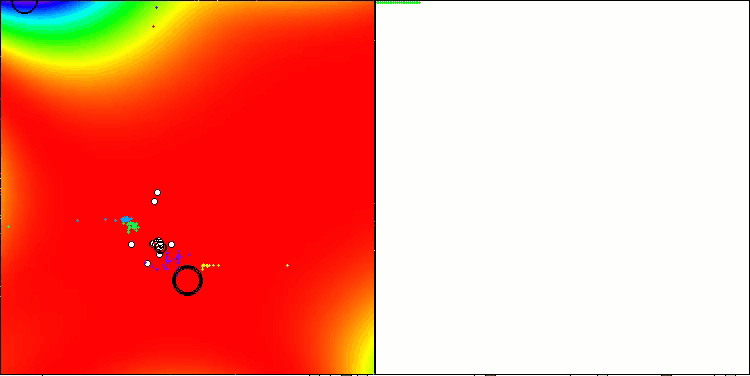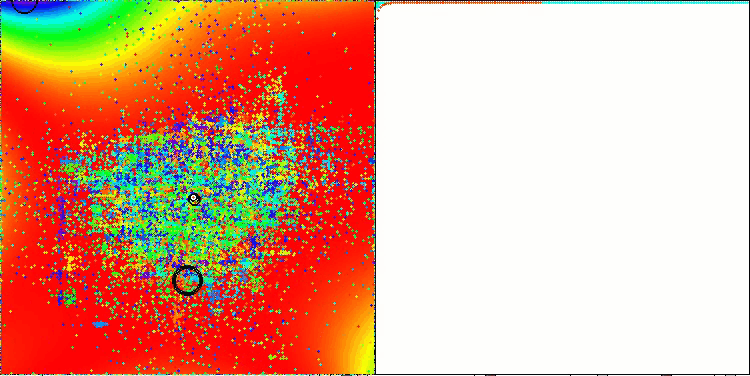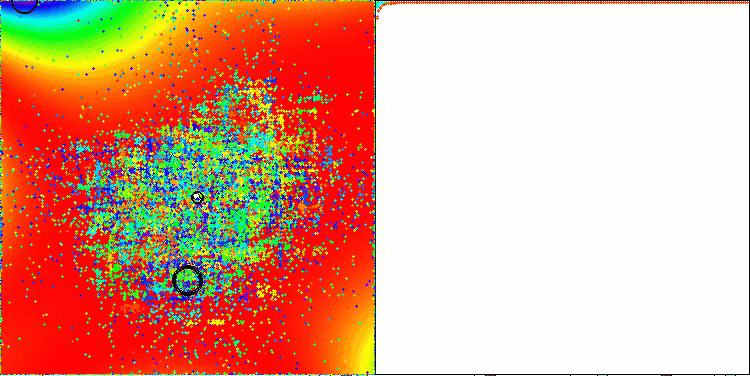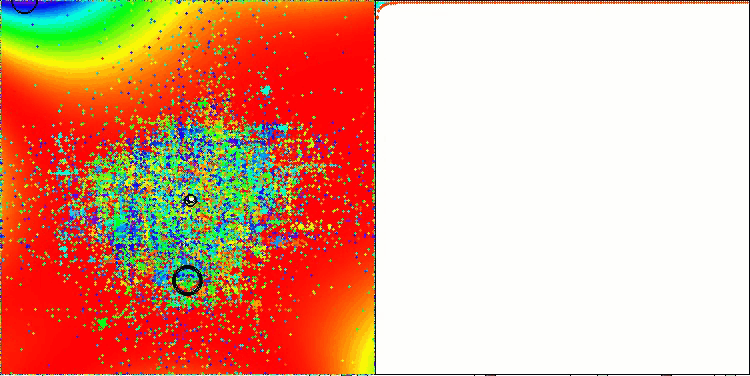
TETA en la función de prueba GoldsteinPrice (disponible para la selección en la lista de funciones de prueba)

Resultados en GoldsteinPrice:

5 GoldsteinPrice's; Func runs: 10000; result: 0.9999786723616957
25 GoldsteinPrice's; Func runs: 10000; result: 0.9999750431600845
500 GoldsteinPrice's; Func runs: 10000; result: 0.9992343490683104

Al final de las pruebas, el algoritmo TETA se encuentra entre los diez mejores algoritmos de optimización y ocupa un honroso sexto puesto.

№	AO	Description	Hilly			Hilly final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result	% de MAX
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	ANS	across neighbourhood search	0,94948	0,84776	0,43857	2,23581	1,00000	0,92334	0,39988	2,32323	0,70923	0,63477	0,23091	1,57491	6,134	68,15
2	CLA	code lock algorithm (joo)	0,95345	0,87107	0,37590	2,20042	0,98942	0,91709	0,31642	2,22294	0,79692	0,69385	0,19303	1,68380	6,107	67,86
3	AMOm	animal migration optimization M	0,90358	0,84317	0,46284	2,20959	0,99001	0,92436	0,46598	2,38034	0,56769	0,59132	0,23773	1,39675	5,987	66,52
4	(P+O)ES	(P+O) evolution strategies	0,92256	0,88101	0,40021	2,20379	0,97750	0,87490	0,31945	2,17185	0,67385	0,62985	0,18634	1,49003	5,866	65,17
5	CTA	comet tail algorithm (joo)	0,95346	0,86319	0,27770	2,09435	0,99794	0,85740	0,33949	2,19484	0,88769	0,56431	0,10512	1,55712	5,846	64,96
6	TETA	time evolution travel algorithm (joo)	0,91362	0,82349	0,31990	2,05701	0,97096	0,89532	0,29324	2,15952	0,73462	0,68569	0,16021	1,58052	5,797	64,41
7	SDSm	stochastic diffusion search M	0,93066	0,85445	0,39476	2,17988	0,99983	0,89244	0,19619	2,08846	0,72333	0,61100	0,10670	1,44103	5,709	63,44
8	AAm	archery algorithm M	0,91744	0,70876	0,42160	2,04780	0,92527	0,75802	0,35328	2,03657	0,67385	0,55200	0,23738	1,46323	5,548	61,64
9	ESG	evolution of social groups (joo)	0,99906	0,79654	0,35056	2,14616	1,00000	0,82863	0,13102	1,95965	0,82333	0,55300	0,04725	1,42358	5,529	61,44
10	SIA	simulated isotropic annealing (joo)	0,95784	0,84264	0,41465	2,21513	0,98239	0,79586	0,20507	1,98332	0,68667	0,49300	0,09053	1,27020	5,469	60,76
11	ACS	artificial cooperative search	0,75547	0,74744	0,30407	1,80698	1,00000	0,88861	0,22413	2,11274	0,69077	0,48185	0,13322	1,30583	5,226	58,06
12	BHAm	black hole algorithm M	0,75236	0,76675	0.34583	1,86493	0.93593	0.80152	0,27177	2,00923	0.65077	0.51646	0,15472	1,32195	5.196	57.73
13	ASO	anarchy society optimization	0,84872	0,74646	0,31465	1,90983	0,96148	0,79150	0,23803	1,99101	0,57077	0,54062	0,16614	1,27752	5,178	57,54
14	AOSm	búsqueda de orbitales atómicos M	0,80232	0,70449	0,31021	1,81702	0,85660	0,69451	0,21996	1,77107	0,74615	0,52862	0,14358	1,41835	5,006	55,63
15	TSEA	turtle shell evolution algorithm (joo)	0,96798	0,64480	0,29672	1,90949	0,99449	0,61981	0,22708	1,84139	0,69077	0,42646	0,13598	1,25322	5,004	55,60
16	DE	differential evolution	0,95044	0,61674	0,30308	1,87026	0,95317	0,78896	0,16652	1,90865	0,78667	0,36033	0,02953	1,17653	4,955	55,06
17	CRO	chemical reaction optimisation	0,94629	0,66112	0,29853	1,90593	0,87906	0,58422	0,21146	1,67473	0,75846	0,42646	0,12686	1,31178	4,892	54,36
18	BSA	bird swarm algorithm	0,89306	0,64900	0,26250	1,80455	0,92420	0,71121	0,24939	1,88479	0,69385	0,32615	0,10012	1,12012	4,809	53,44
19	HS	harmony search	0,86509	0,68782	0,32527	1,87818	0,99999	0,68002	0,09590	1,77592	0,62000	0,42267	0,05458	1,09725	4,751	52,79
20	SSG	saplings sowing and growing	0,77839	0,64925	0,39543	1,82308	0,85973	0,62467	0,17429	1,65869	0,64667	0,44133	0,10598	1,19398	4,676	51,95
21	BCOm	bacterial chemotaxis optimization M	0,75953	0,62268	0,31483	1,69704	0,89378	0,61339	0,22542	1,73259	0,65385	0,42092	0,14435	1,21912	4,649	51,65
22	ABO	african buffalo optimization	0,83337	0,62247	0,29964	1,75548	0,92170	0,58618	0,19723	1,70511	0,61000	0,43154	0,13225	1,17378	4,634	51,49
23	(PO)ES	(PO) evolution strategies	0,79025	0,62647	0,42935	1,84606	0,87616	0,60943	0,19591	1,68151	0,59000	0,37933	0,11322	1,08255	4,610	51,22
24	TSm	tabu search M	0,87795	0,61431	0,29104	1,78330	0,92885	0,51844	0,19054	1,63783	0,61077	0,38215	0,12157	1,11449	4,536	50,40
25	BSO	brain storm optimization	0,93736	0,57616	0,29688	1,81041	0,93131	0,55866	0,23537	1,72534	0,55231	0,29077	0,11914	0,96222	4,498	49,98
26	WOAm	wale optimization algorithm M	0,84521	0,56298	0,26263	1,67081	0,93100	0,52278	0,16365	1,61743	0,66308	0,41138	0,11357	1,18803	4,476	49,74
27	AEFA	artificial electric field algorithm	0,87700	0,61753	0,25235	1,74688	0,92729	0,72698	0,18064	1,83490	0,66615	0,11631	0,09508	0,87754	4,459	49,55
28	AEO	artificial ecosystem-based optimization algorithm	0,91380	0,46713	0,26470	1,64563	0,90223	0,43705	0,21400	1,55327	0,66154	0,30800	0,28563	1,25517	4,454	49,49
29	ACOm	ant colony optimization M	0,88190	0,66127	0,30377	1,84693	0,85873	0,58680	0,15051	1,59604	0,59667	0,37333	0,02472	0,99472	4,438	49,31
30	BFO-GA	bacterial foraging optimization - ga	0,89150	0,55111	0,31529	1,75790	0,96982	0,39612	0,06305	1,42899	0,72667	0,27500	0,03525	1,03692	4,224	46,93
31	SOA	simple optimization algorithm	0.91520	0.46976	0.27089	1,65585	0.89675	0.37401	0.16984	1,44060	0.69538	0.28031	0.10852	1,08422	4.181	46,45
32	ABH	artificial bee hive algorithm	0,84131	0,54227	0,26304	1,64663	0,87858	0,47779	0,17181	1,52818	0,50923	0,33877	0,10397	0,95197	4.127	45,85
33	ACMO	atmospheric cloud model optimization	0,90321	0,48546	0,30403	1,69270	0,80268	0,37857	0,19178	1,37303	0,62308	0,24400	0,10795	0,97503	4,041	44,90
34	ADAMm	adaptive moment estimation M	0.88635	0.44766	0,26613	1.60014	0.84497	0.38493	0.16889	1,39880	0,66154	0.27046	0.10594	1,03794	4.037	44.85
35	ATAm	artificial tribe algorithm M	0.71771	0.55304	0,25235	1,52310	0.82491	0.55904	0,20473	1,58867	0,44000	0,18615	0.09411	0.72026	3.832	42.58
36	ASHA	artificial showering algorithm	0,89686	0,40433	0,25617	1,55737	0,80360	0,35526	0,19160	1,35046	0,47692	0,18123	0,09774	0,75589	3,664	40,71
37	ASBO	adaptive social behavior optimization	0,76331	0,49253	0,32619	1,58202	0,79546	0,40035	0,26097	1,45677	0,26462	0,17169	0,18200	0,61831	3.657	40,63
38	MEC	mind evolutionary computation	0,69533	0,53376	0,32661	1,55569	0,72464	0,33036	0,07198	1,12698	0,52500	0,22000	0,04198	0,78698	3,470	38,55
39	IWO	invasive weed optimization	0,72679	0,52256	0,33123	1,58058	0,70756	0,33955	0,07484	1,12196	0,42333	0,23067	0,04617	0,70017	3,403	37,81
40	Micro-AIS	micro artificial immune system	0,79547	0,51922	0,30861	1,62330	0,72956	0,36879	0,09398	1,19233	0,37667	0,15867	0,02802	0,56335	3,379	37,54
41	COAm	cuckoo optimization algorithm M	0,75820	0,48652	0,31369	1,55841	0,74054	0,28051	0,05599	1,07704	0,50500	0,17467	0,03380	0,71347	3,349	37,21
42	SDOm	spiral dynamics optimization M	0,74601	0,44623	0,29687	1,48912	0,70204	0,34678	0,10944	1,15826	0,42833	0,16767	0,03663	0,63263	3,280	36,44
43	NMm	Nelder-Mead method M	0,73807	0,50598	0,31342	1,55747	0,63674	0,28302	0,08221	1,00197	0,44667	0,18667	0,04028	0,67362	3,233	35,92
44	BBC	big bang-big crunch algorithm	0.60531	0.45250	0.31255	1,37036	0.52323	0.35426	0,20417	1,08166	0.39769	0,19431	0.11286	0.70486	3.157	35.08
45	CPA	cyclic parthenogenesis algorithm	0,71664	0,40014	0,25502	1,37180	0,62178	0,33651	0,19264	1,15093	0,34308	0,16769	0,09455	0,60532	3,128	34,76
	R.W.	random walk	0.48754	0.32159	0.25781	1,06694	0.37554	0,21944	0,15877	0,75375	0.27969	0,14917	0.09847	0.52734	2.348	26.09

Conclusiones

Mientras trabajaba en el algoritmo TETA, me esforzaba constantemente por crear algo sencillo y eficiente. La metáfora de los universos paralelos y los viajes en el tiempo parecía al principio solo una bella idea, pero durante el desarrollo se convirtió orgánicamente en un eficaz mecanismo de optimización.

La característica clave del algoritmo era la idea de que resulta imposible alcanzar la perfección en todo a la vez: hay que buscar un equilibrio. En la vida, estamos constantemente conciliando la familia, la carrera profesional y los logros personales, y es en este concepto en el que he basado el algoritmo a través del sistema de anclas. Cada ancla representa un aspecto importante que hay que optimizar, pero no en detrimento de los demás.

La solución técnica más interesante era la relación entre la probabilidad de seleccionar un universo y la fuerza de su influencia en otros universos. Esto ha creado un mecanismo natural en el que las mejores soluciones tienen más posibilidades de ser seleccionadas, y su impacto depende de la calidad. Este planteamiento establece un equilibrio entre la exploración de nuevas oportunidades y el uso de las buenas soluciones ya encontradas.

Las pruebas del algoritmo arrojan resultados inesperadamente excelentes. Esto hace que el algoritmo resulte especialmente valioso para problemas prácticos con recursos computacionales limitados. Al mismo tiempo, el algoritmo muestra resultados notables y constantes en diferentes tipos de funciones, lo cual demuestra su versatilidad. Lo que resulta especialmente agradable es el carácter compacto de la aplicación. Solo unas 50 líneas de código clave, sin parámetros personalizables y, sin embargo, los resultados son ya eficaces. De hecho, supone una solución acertada cuando la sencillez de la aplicación se combina con un alto rendimiento.

Al final, el TETA ha superado mis expectativas iniciales. De la metáfora del viaje en el tiempo ha surgido una herramienta de optimización práctica y eficaz que puede utilizarse en campos muy diversos. Esto demuestra que a veces las soluciones sencillas basadas en analogías naturales comprensibles pueden resultar muy eficaces. El algoritmo se ha creado literalmente en un suspiro: de la idea a la aplicación. Estoy muy satisfecho con el trabajo realizado sobre el algoritmo, que puede ser un buen ayudante para que investigadores y profesionales encuentren rápidamente soluciones óptimas. 

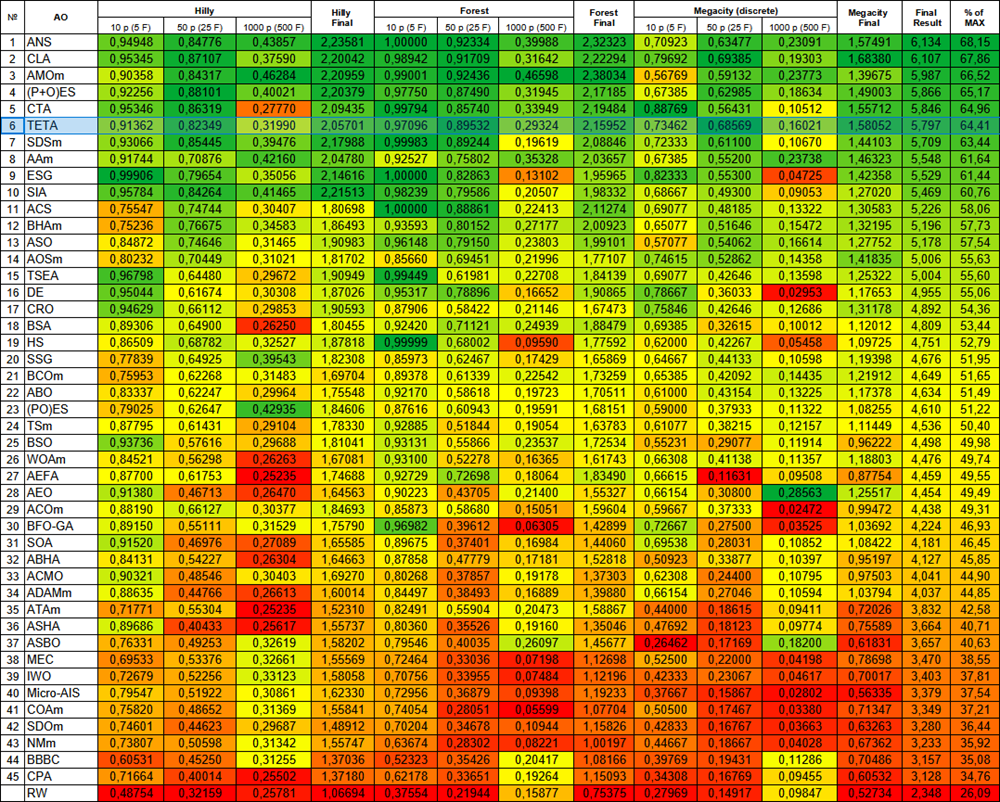
Figura 3. Clasificación por colores de los algoritmos según las pruebas respectivas

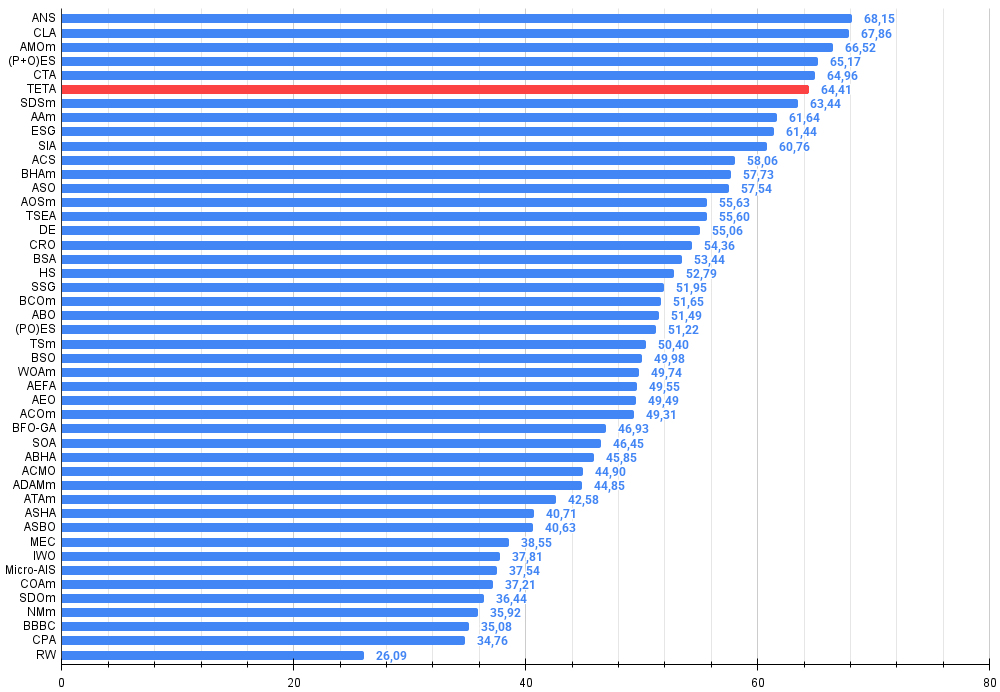
Figura 4. Histograma con los resultados de las pruebas de los algoritmos (en una escala de 0 a 100, cuanto más mejor, donde 100 es el máximo resultado teórico posible, el script para calcular la tabla de puntuación está en el archivo)

Ventajas e inconvenientes del algoritmo TETA:

Ventajas:

1. El único parámetro externo es el tamaño de la población.
   
2. Implementación sencilla.
3. Gran rapidez.
4. Rendimiento equilibrado en tareas de pequeñas y grandes dimensionalidades.
   

Desventajas:

1. Dispersión de resultados en problemas discretos de baja dimensionalidad.
   

Adjuntamos al artículo un archivo con las versiones actuales de los códigos de los algoritmos. El autor de este artículo no se responsabiliza de la exactitud absoluta de la descripción de los algoritmos canónicos, muchos de ellos han sido modificados para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos realizados.

• github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5

Programas usados en el artículo

#	Nombre	Tipo	Descripción
1	#C_AO.mqh	Archivo de inclusión	Clase padre de algoritmos de optimización basados en la población
2	#C_AO_enum.mqh	Archivo de inclusión	Enumeración de los algoritmos de optimización basados en la población
3	TestFunctions.mqh	Archivo de inclusión	Biblioteca de funciones de prueba
4	TestStandFunctions.mqh	Archivo de inclusión	Biblioteca de funciones del banco de pruebas
5	Utilities.mqh	Archivo de inclusión	Biblioteca de funciones auxiliares
6	CalculationTestResults.mqh	Archivo de inclusión	Script para calcular los resultados en una tabla comparativa
7	Testing AOs.mq5	Script	Banco de pruebas único para todos los algoritmos de optimización basados en la población
8	Simple use of population optimization algorithms.mq5	Script	Ejemplo sencillo de utilización de algoritmos de optimización basados en la población sin visualización
9	Test_AO_TETA.mq5	Script	Banco de pruebas para TETA