母集団最適化アルゴリズム：重力探索アルゴリズム(GSA)

内容

1.はじめに
2.アルゴリズム
3.テスト結果

1.はじめに

GSA（Gravitational Search Algorithm、重力探索アルゴリズム）は、最適化問題、特に非線形問題を、ニュートンの重力の法則の原理に従って解くために、E. Rashediによって提案されました。提案されているアルゴリズムでは、粒子を物体として捉え、その質量を考慮してそのパフォーマンスを推定します。重力とは、質量が互いに加速し合う傾向のことで、自然界に存在する4つの基本的な力の1つです（他は電磁気力、弱い核力、強い核力）。

宇宙のあらゆる粒子は、他のあらゆる粒子を引き寄せます。重力はどこにでも存在します。最も弱い力でありながら、最も目に見える力です。重力のおかげで、人は地球の上を歩くことができ、惑星は太陽の周りを回ることができます。あらゆる物体の重力は、その質量に比例します。したがって、質量が大きい物ほど重力が大きくなります。重力が持つ必然性は、他のあらゆる自然の力と一線を画しています。ニュートンの引力のふるまいは、遠隔作用と呼ばれています。アイザック・ニュートンが帰納的推論と呼んだように、これは、経験的証拠から演繹される一般的な物理法則で、1687年7月5日に出版されたニュートンの「自然哲学の数学的諸原理」（プリンキピア）で定式化された古典力学の一部です。

1686年4月、ニュートンが王立協会に初めて未発表の本を提出したとき、ロバート・フックは、ニュートンが自分から逆2乗の法則を受け取ったと主張しました。今日の言葉で言えば、これは、「すべての質点は、2点と交差する線に沿って作用する力によって、他のすべての質点を引き寄せる」という法則です。

2.アルゴリズム

この記事では、ニュートンの万有引力の法則「宇宙のすべての粒子は、それらの質量の積に正比例し、それらの間の距離の二乗に反比例する力で、他のすべての粒子を引き寄せる」に基づいた最適化アルゴリズムを紹介します。提案されたアルゴリズムでは、検索エージェントは、ニュートンの万有引力とニュートン力学の法則に基づき、互いに相互作用する質量の集合体です。同時に、すべてのエージェントは、質量（目的関数の値から計算）と距離に依存する引力によって、探索空間のどこにいても、互いに情報を交換することができます。

エージェントは物体として扱われ、その適応度は質量で測定されます。一般論として（実際の物理法則に近いアルゴリズム設定で）、これらの物体はすべて重力で引き寄せられ、この力によってすべての物体はより大きな質量を持つ物体に向かって大移動します。したがって、質量は重力による直接的な接続形態で相互作用します。

古典的なGSAでは、各粒子は3種類の質量を持ちます。

a）能動的質量
b）受動的質量
c）慣性質量

多くの場合、これらの概念の等価性を利用して、コードや計算を簡略化し、アルゴリズム検索機能の効率を高めることが便利で好都合です。したがって、アルゴリズムの質量は3つではなく、1つになります。GSAで使用する物理法則の方程式を図1に示します。

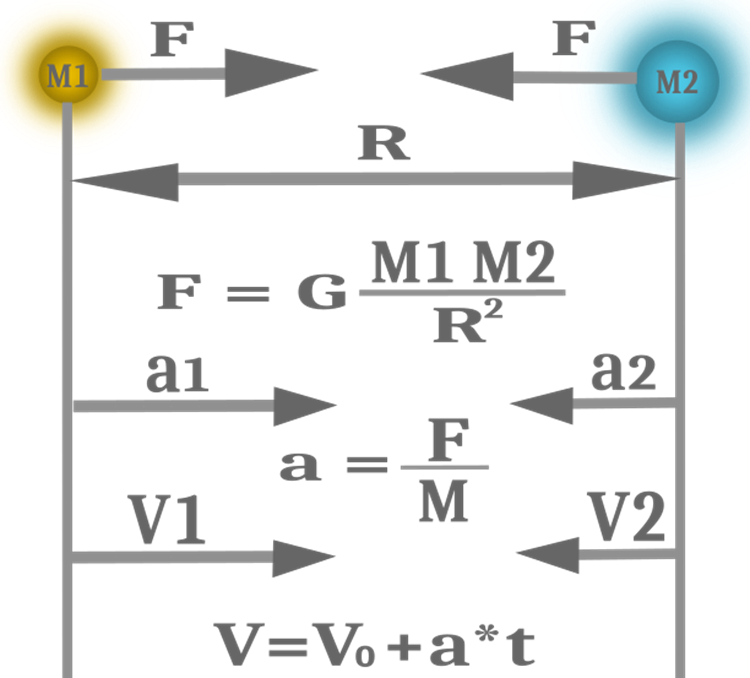
図1：重力、加速度、速度

粒子の位置が問題の解を提供し、適応度関数が質量を計算するために使用されます。このアルゴリズムには、探索と利用の2つの段階があります。局所最適値にはまり込まないように、最初のうちは知能機能を使い、その後は極値領域を利用するのです。

重力探索アルゴリズムでは、空間を移動する粒子を、ある質量を持つ物体に変える必要があります。これらの物体は、互いの重力相互作用によって引き寄せられ、空間内のあらゆる粒子は、粒子同士の相互引力によって引き寄せられて加速度を生み出すことになります。各粒子は他の粒子に引き寄せられ、力の方向に移動します。質量の小さい粒子は質量の大きい粒子に向かって移動します。質量の大きい物体も移動しますが、質量に反比例して低速で移動します。最適解は「大きい」物体で見つかります。速く動く「小さい」物体に比べ、低速で動くことで解を洗練させていきます。GSAは、オブジェクト間の相互作用による情報の伝達を実装しています。

GSAの手順は以下の通りです。

1.エージェントの初期化
2.適応度の進化
3.重力定数の計算
4.エージェントの質量の算出

1.エージェントの初期化
すべてのエージェントはランダムに初期化されます。各エージェントは、解の候補として考慮されます。安定性解析を有意義かつ信頼性の高いものにするためには、平衡初期条件の特定が極めて重要です。元の物体の「円盤」が平衡状態でなければ、シミュレーションの最初の時間ステップでその緩和が不安定を引き起こし、「円盤銀河」の安定性を理解する上であまり重要ではなくなってしまうからです。ダークマターハローや恒星円盤の外部ポテンシャルで静水圧平衡にある3次元ガス状円盤の密度、速度場、温度については、残念ながら分析的解法は知られていません。

2.適応度の進化
GSAの信頼性と有効性は、研究能力と利用能力のバランスに依存します。解探索プロセスの初期反復では、探索空間の探索が優先されます。これは、エージェントが初期の反復で大きなステップサイズを使用できるようにすることで実現できます。後の繰り返しでは、大域的最適解が欠落する事態を避けるために、探索空間の精密化が必要です。したがって、候補となる解は、その後の繰り返しで使用するために、小さなステップサイズを持つ必要があります。

3.重力定数の計算
重力定数（万有引力定数、ニュートン重力定数、キャベンディッシュ重力定数とも呼ばれる）は、Gで表記され、アイザック・ニュートンの万有引力の法則やアルベルト・アインシュタインの一般相対性理論において、重力効果の計算に関わる経験的物理定数です。ニュートンの法則では、これは、2つの物体間の引力をその質量と距離の逆二乗の積で結ぶ比例定数です。アインシュタイン方程式では、時空の幾何学とエネルギー運動量テンソルとの関係を定量化します。

4.エージェントの質量の算出
質量とは、空間内に存在する物質の量のことです。

アルゴリズムの擬似コードは次の通りです。

1. 物体のシステムをランダムに生成する
2. 各物体の適応度を決定する
3. 重力定数の値を更新し、質量を計算し、最良の物体と最悪の物体を算出する
4. 各座標に作用する力を計算する
5. 物体の加速度と速度を計算する
6. 物体の位置を更新する
7. 各物体の適応度を決定する
8. 終了基準を満たすまで、3から繰り返す

GSAコードについて考えてみましょう。S_Object構造体は重力相互作用のシステムにおける物体を記述するために必要です。これは重力探索をおこなうのに十分な物体の必要な物理特性をすべて記述することになります。c []は探索空間における座標、v []は各座標の速度ベクトル（配列次元は座標数）、Mは物体の質量（GSAでは質量は相対値であり、物体のシステム全体にわたる最大・最小適応度の値に依存して計算される値）、fは適応度の値、R[]は他の物体とのユークリッド距離（配列次元は物体数）、F[]は各座標の力のベクトル（配列次元は座標数）です。

//——————————————————————————————————————————————————————————————————————————————
struct S_Object
{
  double c  [];   //coordinates
  double v  [];   //velocity
  double M;       //mass
  double f;       //fitness
  double R  [];   //euclidean distance to other objects
  double F  [];   //force vector
};
//——————————————————————————————————————————————————————————————————————————————

重力探索アルゴリズムC_AO_GSAのクラスを宣言しましょう。エージェントとしてアルゴリズムに参加する物体の物理的特性のうち、必要なのはただ1つ、最適解を表す座標、つまりfBの値です。クラスは探索空間座標の有効範囲とステップを宣言します。重力的に結合した物体の系は、S_Object構造体の配列として表現されます。古典的なアルゴリズムでは、外部パラメータは3つしかありません。物体の重力相互作用の特性を決めるG_constant、a_constant、e_constantです。それ以外の定数は計算式に含まれていますが、これらの定数をアルゴリズムの外部パラメータに移動することで、アルゴリズム全体としての特性をより柔軟に調整できることが適切であると考えました。すべてのパラメータはアルゴリズムの動作に大きく影響するため、もう少し後で詳しく検討することにします。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_GSA
{
  //----------------------------------------------------------------------------
  public: S_Object o       []; //object
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: double cB        []; //best coordinates
  public: double fB;           //FF of the best coordinates

  public: void Init (const int    coordinatesNumberP, //coordinates number
                     const int    objectsNumberP,     //objects number
                     const double PowerOfdistanceP,   //power of distance
                     const double GraviPert_MinP,     //gravitational perturbation Min
                     const double GraviPert_MaxP,     //gravitational perturbation Min
                     const double VelocityPert_MinP,  //Velocity perturbation Min
                     const double VelocityPert_MaxP,  //Velocity perturbation Max
                     const double G_constantP,        //G constant
                     const double a_constantP,        //a constant
                     const double e_constantP,        //e constant
                     const int    maxIterationsP);    //max Iterations

  public: void Moving   (int iter);
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coordinatesNumber; //coordinates number
  private: int    objectsNumber;     //objects number
  private: double PowerOfdistance;   //power of distance
  private: double GraviPert_Min;     //gravitational perturbation Min
  private: double GraviPert_Max;     //gravitational perturbation Min
  private: double VelocPert_Min;     //velocity perturbation Min
  private: double VelocPert_Max;     //velocity perturbation Max
  private: double G_constant;        //G constant
  private: double a_constant;        //a constant
  private: double e_constant;        //e constant
  private: int    maxIterations;
  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
  private: double Scale     (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
};
//——————————————————————————————————————————————————————————————————————————————

Init ()アルゴリズムのpublicメソッドは、アルゴリズムの外部パラメータを内部定数に渡して、サービス変数の初期化や配列へのサイズ割り当てをおこなうことを目的としています。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_GSA::Init (const int    coordinatesNumberP, //coordinates number
                     const int    objectsNumberP,     //objects number
                     const double PowerOfdistanceP,   //power of distance
                     const double GraviPert_MinP,     //gravitational perturbation Min
                     const double GraviPert_MaxP,     //gravitational perturbation Min
                     const double VelocityPert_MinP,  //Velocity perturbation Min
                     const double VelocityPert_MaxP,  //Velocity perturbation Max
                     const double G_constantP,        //G constant
                     const double a_constantP,        //a constant
                     const double e_constantP,        //e constant
                     const int    maxIterationsP)     //max Iterations
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coordinatesNumber = coordinatesNumberP;
  objectsNumber     = objectsNumberP;
  PowerOfdistance   = PowerOfdistanceP;
  GraviPert_Min     = GraviPert_MinP;
  GraviPert_Max     = GraviPert_MaxP;
  VelocPert_Min     = VelocityPert_MinP;
  VelocPert_Max     = VelocityPert_MaxP;
  G_constant        = G_constantP;
  a_constant        = a_constantP;
  e_constant        = e_constantP;
  maxIterations     = maxIterationsP;

  ArrayResize (rangeMax,  coordinatesNumber);
  ArrayResize (rangeMin,  coordinatesNumber);
  ArrayResize (rangeStep, coordinatesNumber);

  ArrayResize (o,  objectsNumber);

  for (int i = 0; i < objectsNumber; i++)
  {
    ArrayResize (o [i].c,  coordinatesNumber);
    ArrayResize (o [i].v,  coordinatesNumber);
    ArrayResize (o [i].R,  objectsNumber);
    ArrayResize (o [i].F,  coordinatesNumber);
    o [i].f  = -DBL_MAX;
  }

  ArrayResize (cB, coordinatesNumber);
}
//——————————————————————————————————————————————————————————————————————————————

Moving ()の各反復で最初のpublicメソッドが呼び出されます。このメソッドには、GSAアルゴリズムのすべての物理とロジックが含まれています。かなり大きいので、部分に分けながら考えてみましょう。なお、このメソッドは現在の反復をパラメータとし、そのパラメータは重力定数の計算に関与し、研究と利用のバランスを調整します。

最初の反復で、物体の初期化段階が発生します。物体のすべての座標について、許容範囲内のランダムな値を一様分布で割り当てるとともに、範囲外でないことを確認します。最適化処理の開始時には、すべての物体の速度はゼロです。つまり、物体は座標に関して探索空間内で動かない状態です。なお、物体は質量を持たないので、光速で移動しなければなりませんが、この瞬間はある程度ビッグバンに相当するので、最初の反復では物理法則を破ってみます。この瞬間のオブジェクトの適応度は、「double'」の数で可能な最小値です。アルゴリズムのデバッグ時に、質量ゼロに関連するバグを見つけるのが難しかったのですが、以下で解決策をご覧いただけます。

//----------------------------------------------------------------------------
if (!revision)
{
  fB = -DBL_MAX;

  for (int obj = 0; obj < objectsNumber; obj++)
  {
    for (int c = 0; c < coordinatesNumber; c++)
    {
      o [obj].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      o [obj].c [c] = SeInDiSp (o [obj].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      o [obj].v [c] = 0.0;
      o [obj].M     = 0.0;
      o [obj].f     = -DBL_MAX;
    }
  }

  revision = true;
}

Moving ()メソッドの残りのコードは、物体が質量、速度、加速度を獲得する2回目以降の反復処理について言及しています。

まず、質量を計算する必要があります。前述のように、物体の質量（定義上は正のスカラー値）は適応度関数の値から計算されるので、得られた値に基づいて質量を計算する前に、適応度の最小値と最大値を決定する必要があります。このとき、適応度関数の値は、すでに前の反復で得られています。

//find the minimum and maximum fitness==========================================
for (int obj = 0; obj < objectsNumber; obj++)
{
  if (o [obj].f < Fmin) Fmin = o [obj].f;
  if (o [obj].f > Fmax) Fmax = o [obj].f;
}

コードのこの時点で、質量は、Mo=(Fo-Fmin)/(Fmax-Fmin)という式を使って計算されます。ここで、

• Mo：物体の質量
• Fo：体の適応度
• Fmax：すべての物体の適応度の最大値（最良値）
• Fmin：すべての物体の適応度の最値（最悪値）
  

式からわかるように、質量は0から1までの範囲で正の値しかとることができません。質量が0であった場合に速度が光速に等しくなることは先に述べたとおりなので、質量の下限を0.1に制限することにします。上限値は1に等しくしましょう。また、適応度関数の最小値と最大値が等しければ、すべての物体の質量はすべて同じになり、1に等しくなることに留意してください。これは、探索空間が物体のある領域で均質であり、すべての物体が適応度関数の質において平等であり、かつどの方向への移動も等しく優先される場合に対応します。この場合、すべての物体は共通の質量中心に向かって徐々に移動し、集中するはずだと思われますが、重力の非線形作用のため、そうはなりません。

//calculating the mass of objects===========================================
for (int obj = 0; obj < objectsNumber; obj++)
{
  Fo = o [obj].f;
  if (Fmax == Fmin) Mo = 1.0;
  else Mo = (Fo - Fmin) / (Fmax - Fmin);
  o [obj].M = Scale (Mo, 0.0, 1.0, 0.1, 1.0, false);
}

物体の質量を計算しました。次に、R方程式のもう一つの要素である、各物体から他の物体までのユークリッド距離を計算する必要があります。計算は、物体の列挙と各座標の計算の2サイクルで構成されています。ユークリッド距離は、座標差の2乗の和の根であることは記憶に新しいと思います。

//calculation of Euclidean distances between all objects====================
for (int obj = 0; obj < objectsNumber; obj++) ArrayInitialize (o [obj].R, 0.0);

for (int obj = 0; obj < objectsNumber; obj++)
{
  for (int obj2 = 0; obj2 < objectsNumber; obj2++)
  {
    if (obj != obj2)
    {
      if (o [obj].R [obj2] == 0.0)
      {
        for (int c = 0; c < coordinatesNumber; c++)
        {
          diffDist = o [obj].c [c] - o [obj2].c [c];
          o [obj].R [obj2] += diffDist * diffDist;
        }

        o [obj].R [obj2] = sqrt (o [obj].R [obj2]);
        o [obj2].R [obj] = o [obj].R [obj2];
      }
    }
  }
}

これで、物体の力ベクトルを計算できるようになりました。そのためには、速度が各座標ごとに別々に計算されるため、すべての物体を2サイクル、座標を1サイクルで通過させる必要もあります。物体のインデックスの一致を除外する条件を追加して、物体が力の計算で自分自身を計算しないようにしなければなりません。ここでは、ニュートンの有名な方程式を用いて、2つの物体（図1）の重力を計算し、距離をe_constant比で補正します。まず、重力定数Gを計算してみましょう。最適化が終わるまでにアルゴリズムが強まると仮定すると、この重力定数Gは、反復するたびに下方に変化するはずです。

//calculate the force vector for each object================================
for (int obj = 0; obj < objectsNumber; obj++) ArrayInitialize (o [obj].F, 0.0);

double G = G_constant * exp (-a_constant * (iter / maxIterations));

for (int obj = 0; obj < objectsNumber; obj++)
{
  for (int obj2 = 0; obj2 < objectsNumber; obj2++)
  {
    if (obj != obj2)
    {
      for (int c = 0; c < coordinatesNumber; c++)
      {
        diffDist = o [obj2].c [c] - o [obj].c [c];

        if (o [obj].R [obj2] != 0.0)
        {
          o [obj] .F [c] += G * o [obj].M * o [obj2].M * diffDist / (pow (o [obj].R [obj2], PowerOfdistance) + e_constant);
        }
      }
    }
  }
}

あとは、物体が動き出すための速度を計算するだけです。図1の式から、速度の計算には加速度が伴うことがわかります。加速度は、物体に作用する力を質量で割ったものに等くなります。この式には、時間V=V0+a*tも含まれています。私たちのアルゴリズムでは、反復が時間の役割を果たすので、速度の変化は1回の反復での加速にほかなりません。速度ベクトルはすでに上記で計算済みです。あとは質量で割ればいいだけです。さらに、著者らは力の摂動と速度の摂動についても紹介しています。摂動は、0から1の間の一様分布の乱数です。これは、物体の動きにランダムな要素を加えるもので、これがなければ動きは厳密に決定され、物体の初期位置にのみ依存することになります。私は、摂動指標をアルゴリズムの外部パラメータに導入することで、物体の動きを完全に決定論的なものから完全にランダムなものまで調整できるようにすることが合理的だと考えました。

//calculation of acceleration and velocity for all objects==================
double a = 0.0; //acceleration

for (int obj = 0; obj < objectsNumber; obj++)
{
  for (int c = 0; c < coordinatesNumber; c++)
  {
    r = RNDfromCI (GraviPert_Min, GraviPert_Max);
    a = o [obj].F [c] * r / o [obj].M;
    r = RNDfromCI (GraviPert_Min, GraviPert_Max);
    o [obj].v [c] = o [obj].v [c] * r + a;
    o [obj].c [c] = o [obj].c [c] + o [obj].v [c];

    if (o [obj].c [c] > rangeMax [c]) o [obj].c [c] = rangeMin [c];
    if (o [obj].c [c] < rangeMin [c]) o [obj].c [c] = rangeMax [c];

    o [obj].c [c] = SeInDiSp (o [obj].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}

2番目のRevision ()メソッドは、各反復時で実行が必須となります。このメソッドは、現在の反復で最良の適応度値を決定するように設計されています。ループの中で、すべてのオブジェクトを調べ、グローバルな最適解を置き換えます。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_GSA::Revision ()
{
  for (int s = 0; s < objectsNumber; s++)
  {
    if (o [s].f > fB)
    {
      fB = o [s].f;
      ArrayCopy (cB, o [s].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

3.テスト結果

それでは、テスト結果に移りましょう。以下は、私が見つけた最良のGSAパラメータを用いたテストスタンドの結果です。

2023.02.03 14:12:43.440 Test_AO_GSA (EURUSD,M1) C_AO_GSA:10;2.0;0.2;0.6;0.0;1.0;2.0;20.0;0.01
2023.02.03 14:12:43.440    Test_AO_GSA (EURUSD,M1)    =============================
2023.02.03 14:12:52.198 Test_AO_GSA (EURUSD,M1) 5 Rastrigin's; Func runs 10000 result：73.64619475145881
2023.02.03 14:12:52.198 Test_AO_GSA (EURUSD,M1) Score：0.91252
2023.02.03 14:13:06.105 Test_AO_GSA (EURUSD,M1) 25 Rastrigin's; Func runs 10000 result：59.4327218024363
2023.02.03 14:13:06.105 Test_AO_GSA (EURUSD,M1) Score：0.73640
2023.02.03 14:14:16.529 Test_AO_GSA (EURUSD,M1) 500 Rastrigin's; Func runs 10000 result：37.550565227034724
2023.02.03 14:14:16.529 Test_AO_GSA (EURUSD,M1) Score：0.46527
2023.02.03 14:14:16.529    Test_AO_GSA (EURUSD,M1)    =============================
2023.02.03 14:14:30.577 Test_AO_GSA (EURUSD,M1) 5 Forest's; Func runs 10000 result：0.741456333008312
2023.02.03 14:14:30.577    Test_AO_GSA (EURUSD,M1)    Score:0.41941
2023.02.03 14:14:50.281 Test_AO_GSA (EURUSD,M1) 25 Forest's; Func runs 10000 result：0.46894018717768426
2023.02.03 14:14:50.282 Test_AO_GSA (EURUSD,M1) Score：0.26526
2023.02.03 14:16:01.856 Test_AO_GSA (EURUSD,M1) 500 Forest's; Func runs 10000 result：0.11382493516764165
2023.02.03 14:16:01.856 Test_AO_GSA (EURUSD,M1) Score：0.06439
2023.02.03 14:16:01.856    Test_AO_GSA (EURUSD,M1)    =============================
2023.02.03 14:16:18.195 Test_AO_GSA (EURUSD,M1) 5 Megacity's; Func runs 10000 result：5.279999999999999
2023.02.03 14:16:18.195 Test_AO_GSA (EURUSD,M1) Score：0.44000
2023.02.03 14:16:34.536 Test_AO_GSA (EURUSD,M1) 25 Megacity's; Func runs 10000 result：2.296
2023.02.03 14:16:34.536 Test_AO_GSA (EURUSD,M1) Score：0.19133
2023.02.03 14:17:46.887 Test_AO_GSA (EURUSD,M1) 500 Megacity's; Func runs 10000 result：0.23399999999999999
2023.02.03 14:17:46.887 Test_AO_GSA (EURUSD,M1) Score：0.01950

アルゴリズムのパラメータは次の通りです。

input double PowerOfdistance_P = 2.0; //距離の累乗
input double GraviPert_Min_P = 0.2; //重力摂動最小値
input double GraviPert_Max_P = 0.6; //重力摂動最大値
input double VelocityPert_Min_P = 0.0; //速度摂動最小値
input double VelocityPert_Max_P = 1.0; //速度摂動最大値
input double G_constant_P = 2.0; //G定数
input double a_constant_P = 20.0; //a定数
input double e_constant_P = 0.01; //e定数

PowerOfdistance_P（物体間の距離を累乗する値）が、重力的に結合した物体の形成に影響します。式中のべき乗が高いほど、物体が他の物体に与える影響は少なくなります。

• GraviPert_Min_P：重力摂動範囲の下限値
• GraviPert_Max_P：重力摂動範囲の上限値
• GraviPert_Min_P = 1.0およびGraviPert_Max_P = 1.0 の場合、重力外乱が発生しません。
• VelocityPert_Min_P：速度摂動範囲の下限値
• VelocityPert_Max_P：速度摂動範囲の上限値

VelocityPert_Min_P = 1.0およびVelocityPert_Max_P = 1.0の場合、速度摂動は発生しません

• G_constant_P：重力定数はスケール因子として機能します。値が大きいほど、重力が強く作用し、物体の速度が速く変化します
• a_constant_P：検出された極値を精緻化するために最適化全体において検索フィールドを縮小するための重力定数の補正係数
• e_constant_P：オブジェクト間の距離に対する補正係数

それでは、可視化テストの結果を見てみましょう。テスト関数に対するアルゴリズムの挙動は、非常に独特で興味深いものです。実は、この実験は重力の働きを示しています。物体の動きや得られた最適化結果は、アルゴリズムの外部パラメータに強く影響されます。最初は速度がゼロの物体が探索空間にランダムに分布し、次の反復で移動を開始します。テストで使用した設定（私が見つけたベスト）は、物体を共通の質量中心に向かって移動させるものです。

各物体の重力は、アルゴリズムで十分に高い精度で記述された運動法則を持つ他の物体に影響を与えることを忘れてはなりません。共通の重心に近づくと、物体は高速で移動し続けます。それは、粒子の塊が共通の質量中心に向かって、脈動するように動いているように見えます。ある回数繰り返した後、物体の質量に影響を与える重力不均一性として作用する適応度関数の空間レリーフの影響を受けて、物体移動の軌道が変化します。先ほど説明したように、オブジェクトの質量は適応度関数の値から計算されます。しかし、軸に沿って対称なRastrigin関数は、物体の動きに対してかなり均一な影響を与え、グループへの分解は特に顕著ではありません。

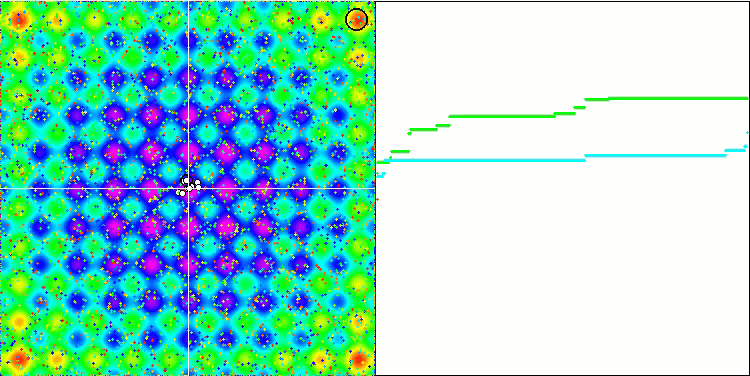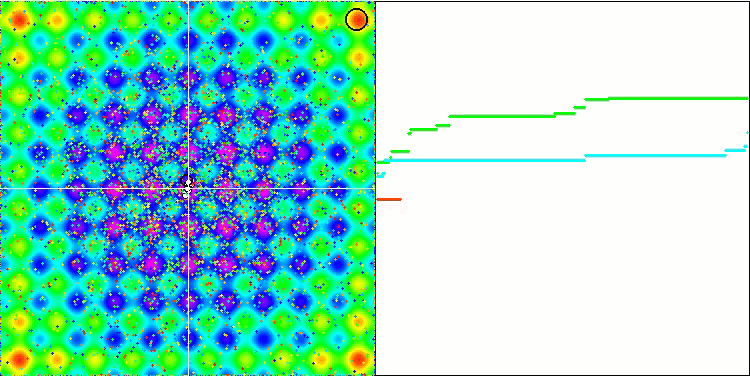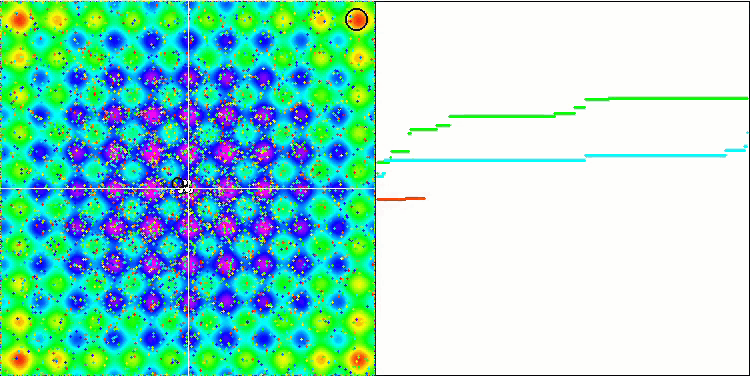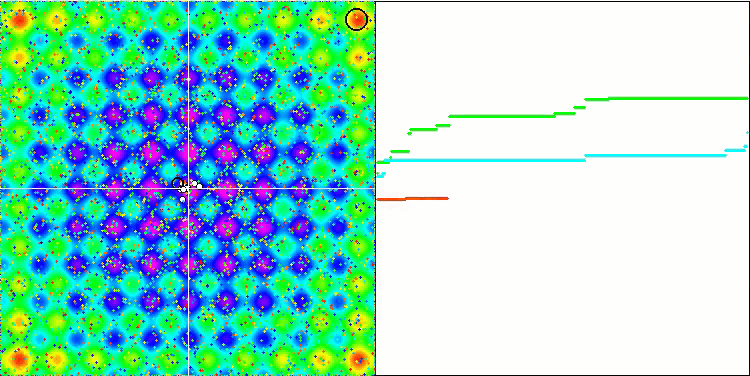
  Rastriginテスト関数のGSA

Forest関数とMegacity関数では、物体はさらに興味深い挙動を示します。これらの関数は対称ではないため、物体のグループ全体に対して不均一な効果をもたらします。

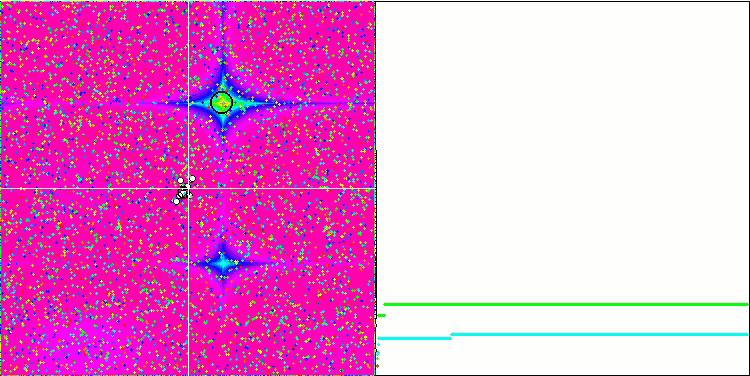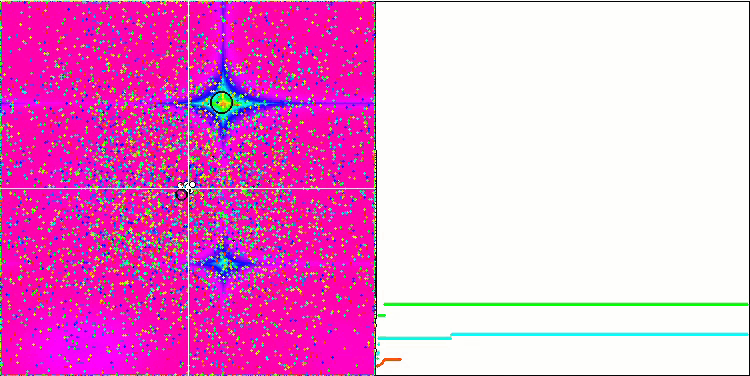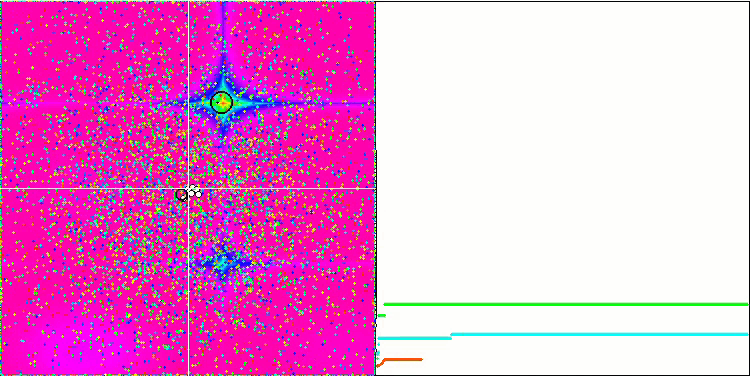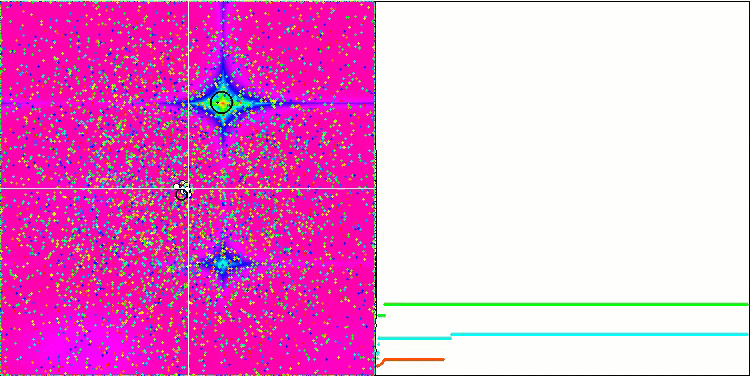
  Forestテスト関数のGSA

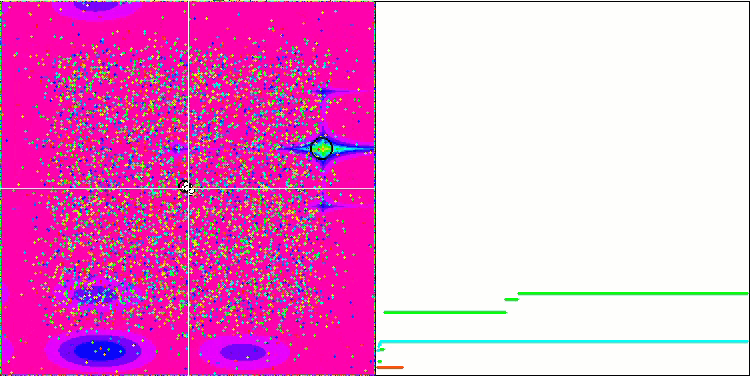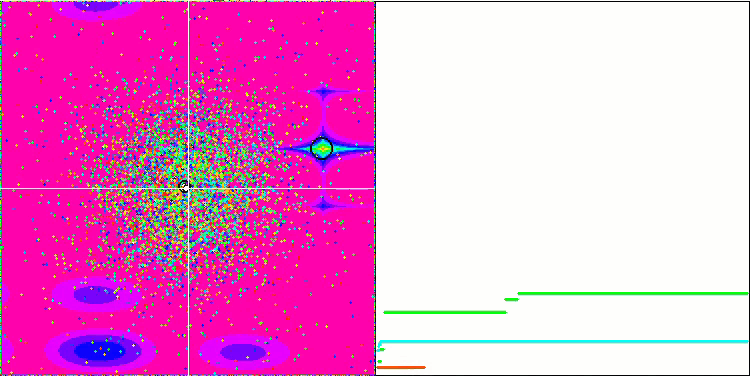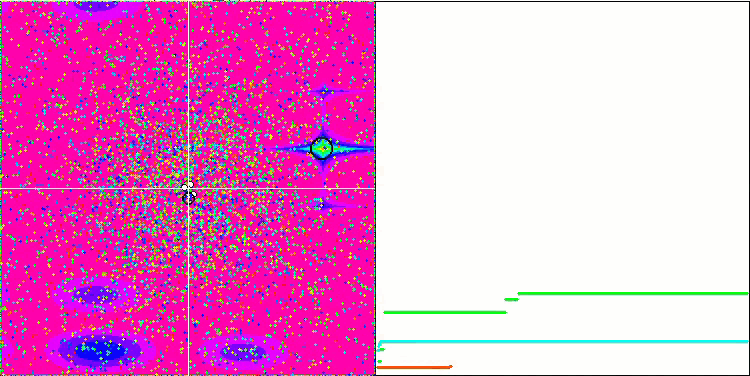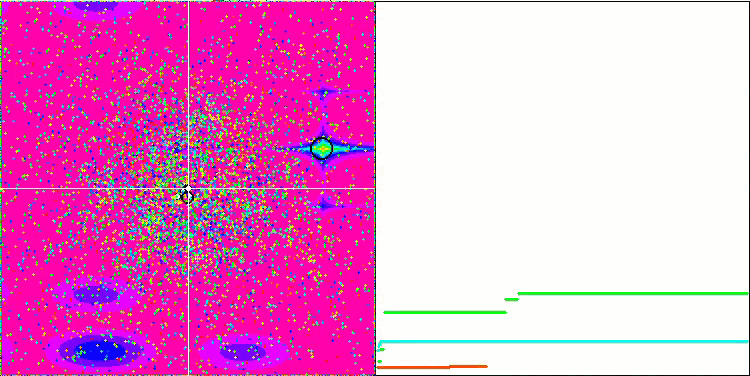
Megacityテスト関数のGSA

GSAでいろいろ試した結果、宇宙物体の動きのシミュレータを作ることを思いつきました。実用的な価値はありませんが、惑星系や恒星系に作用する物理法則を知ることができます。シミュレータは、GSAのランダム性を無効にしたバージョンです。さらに、3つの星（青色巨星、黄色星、白色矮星）を模した3つの天体を紹介します。質量パラメータは、それに対する設定で別々に表示されます。

シミュレータのために、均一な空間を持つUniverse適応度関数を新たに作成しました。シミュレータでは、物体間の距離のべき乗（パラメータ）が、相互の動きにどのような影響を与えるかを明確に示しています。下の可視化では、ニュートンの法則の標準値である2の代わりに3のべき乗を適用しています。その度合いが、対星系や三重星系などの重力的結合系の形成にどのような影響を与えるかが明らかになります。

私たちの宇宙での距離のべき乗が大きければ、銀河の形成は現実よりも遥かに早かったはずです。このアニメーションは、最初の反復で、共通の質量を中心に循環する対の物体が出現することを明確に示しています。予想通り、青色巨星は自らの周りにある天体を最も多く集めました。

GSAアルゴリズムに基づく宇宙物体移動シミュレータの可視化

それでは、GSAのテスト結果の分析に移りましょう。アルゴリズムに使われている独自の機能により、私たちのテストでは強い結果を得ることができませんでした。パラメーターのバリエーションを数多く試しましたが、アルゴリズムの収束は改善されませんでした。このアルゴリズムは、10個の変数とMegacityを持つ滑らかなRastrigin関数において、他のテスト参加者と比較して、いくつかの肯定的な結果を示しました。その他のテストでは、GSAは12位中8位と、平均を下回る結果となっています。

AO	詳細	Rastrigin			Rastrigin最終	Forest			Forest最終	Megacity(discrete)			Megacity最終	最終結果
		10パラメータ(5F)	50パラメータ(25F)	1000パラメータ（500F）		10パラメータ(5F)	50パラメータ(25F)	1000パラメータ（500F）		10パラメータ(5F)	50パラメータ(25F)	1000パラメータ（500F）
IWO	侵入雑草最適化	1.00000	1.00000	0.35295	2.35295	0.79937	0.46349	0.41071	1.67357	0.75912	0.44903	0.94416	2.15231	100.000
ACOm	蟻コロニー最適化M	0.36118	0.26810	0.20182	0.83110	1.00000	1.00000	1.00000	3.00000	1.00000	1.00000	0.15901	2.15901	96.805
COAm	カッコウ最適化アルゴリズムM	0.96423	0.69756	0.30792	1.96971	0.64504	0.34034	0.21362	1.19900	0.67153	0.34273	0.48451	1.49877	74.417
FAm	ホタルアルゴリズムM	0.62430	0.50653	0.20290	1.33373	0.55408	0.42299	0.64360	1.62067	0.21167	0.28416	1.00000	1.49583	70.740
BA	コウモリアルゴリズム	0.42290	0.95047	1.00000	2.37337	0.17768	0.17477	0.33595	0.68840	0.15329	0.07158	0.49268	0.71755	59.383
ABC	人工蜂コロニー	0.81573	0.48767	0.24656	1.54996	0.58850	0.21455	0.17249	0.97554	0.47444	0.26681	0.39496	1.13621	57.393
BFO	細菌採餌の最適化	0.70129	0.46155	0.13988	1.30272	0.41251	0.26623	0.26695	0.94569	0.42336	0.34491	0.53694	1.30521	55.563
GSA	重力探索法	0.73222	0.67404	0.00000	1.40626	0.31238	0.36416	0.42921	1.10575	0.51095	0.36658	0.00000	0.87753	52.786
FSS	魚群検索	0.48850	0.37769	0.13383	1.00002	0.78060	0.05013	0.08423	0.91496	0.00000	0.01084	0.23493	0.24577	20.094
PSO	粒子群最適化	0.21339	0.12224	0.08478	0.42041	0.15345	0.10486	0.28099	0.53930	0.08028	0.02385	0.05550	0.15963	14.358
RND	ランダム	0.17559	0.14524	0.09495	0.41578	0.08623	0.04810	0.06094	0.19527	0.00000	0.00000	0.13960	0.13960	8.117
GWO	灰色オオカミオプティマイザ	0.00000	0.00000	0.02672	0.02672	0.00000	0.00000	0.00000	0.00000	0.18977	0.04119	0.07252	0.30348	1.000

一般に、GSAアルゴリズムは、最適化される関数に勾配がある場合に顕著な影響を受けます。拡張性が低いため、多くの変数を含む重大なタスクに使用することはできません。したがって、このアルゴリズムをニューラルネットワークや取引システムの最適化に使用することはお勧めしません。重力探索アルゴリズムの可能性を十分に検討したわけではありません。さらなる研究により、この非常に興味深く珍しいアルゴリズムの未知の肯定的な特徴が開かれるかもしれません。このアルゴリズムの主な利点は、現在の最良の発見された大域解からの独立性と、すべてのエージェントが相互に作用する能力です。 

図2は、本アルゴリズムのテスト結果です。

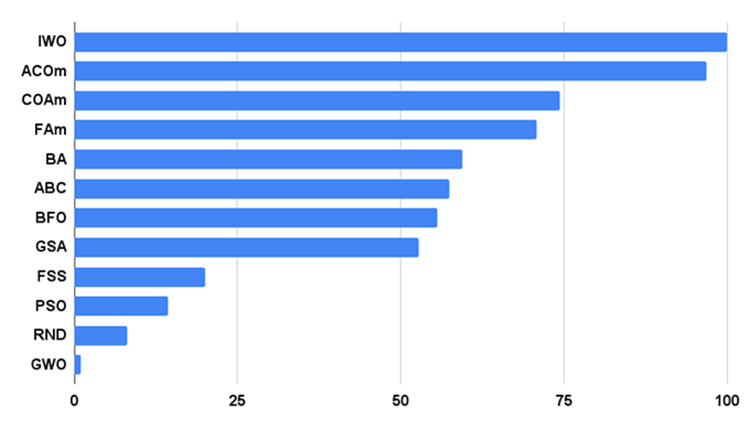
図2：アルゴリズムのテスト結果のヒストグラム

重力探索アルゴリズム（GSA）の特性に関する結論：

賛成：
1.簡単に実装できる。
2.変数の少ない滑らかな関数で良好な性能を発揮する。

反対：
1.計算量が多い。
2.離散関数の結果が悪い。
3.スケーラビリティが悪い。