母集団最適化アルゴリズム：荷電系探索（Charged System Search、CSS）アルゴリズム

内容

1. はじめに
2.アルゴリズム
3.テスト結果

1. はじめに

物理学では、電荷の周囲の空間には電場として知られる性質があります。この場は他の帯電した物体に力を及ぼします。点電荷の周囲の電場はクーロンの法則によって決まります。クーロンは、2 つの小さな帯電球間の電気力は、粒子を結ぶ線に沿った粒子間の距離の2乗に反比例し、2つの粒子の電荷の積に比例することを確認しました。さらに、帯電球内の点における電場の大きさは、粒子間の距離に比例するというガウスの法則を使用して取得できます。これらの原理を使用して、CSSは荷電粒子と呼ばれる一連の可能な解決策を定義します。各粒子は帯電した球体とみなされ（粒子が1次元の点である電磁アルゴリズムEMとは対照的）、他のエージェント（帯電粒子）に電気的な影響を与えることができます。

一方、ニュートンの第2法則は、物体の加速度がその物体に作用する正味の力に正比例することを説明します。したがって、結果的に粒子に作用する電気力により粒子が加速されます。ニュートン力学によれば、微小サイズの点質量とみなされる粒子の位置は、空間内での位置、速度、加速度が事前にわかっていれば、いつでも完全にわかります。CSSは、ニュートン力学の運動法則を使用して、粒子の位置を決定します。これらの法則を適用すると、理論的には、アルゴリズムの探索と活用の間で適切なバランスが得られるはずです。

荷電系探索(CSS)は、2010年にA. KavehとS. Talatahariによって初めて提案されました。

最適化は、数学的モデリングと機械学習の問題を解決する上で重要かつ不可欠な部分です。メタヒューリスティック アルゴリズムは、効果的で人気のある種類の最適化手法です。メタヒューリスティックは、特定の条件が満たされるか、指定された反復回数に達するまで、最適に近い問題の可能な解決策を確率的に検索するアルゴリズムとして理解できます。

科学文献では、メタヒューリスティックは、基本的なヒューリスティック手法をより効率的な検索空間の探索と意思決定を可能にする高レベルのアルゴリズムスキームに結合すると考えられています。これは通常、新しい特殊なヒューリスティックを開発するよりも少ない作業で済みます。課題は、一般的なメタヒューリスティック スキームを適応させて、困難な最適化問題を解決することです。さらに、メタヒューリスティックを効果的に実装すると、最適な解に近い解を許容可能な時間内に確実に見つけることができます。メタヒューリスティックを理解するためのさまざまなアプローチにより、メタヒューリスティックを特徴付けるいくつかの基本的な特性を定式化することが可能になります。近年、メタヒューリスティック手法の使用が増加し、アルゴリズムの能力を高め、最適化時間を短縮するための努力がおこなわれています。

2.アルゴリズム

CSSアルゴリズムは、荷電粒子を球の形で操作します。球の最小サイズは外部パラメータによって決定され（探索空間のすべての座標に沿った最大可能なユークリッド距離の一部です）、粒子が球の半径よりも短い距離で接近すると、反発力が粒子に作用します。同時に、粒子間の力の方向は、粒子間の電荷の違いによって影響を受けます。このアルゴリズムでは、前回の反復での座標値が考慮され、それによって粒子の速度がシミュレーションされます。加速度（粒子の運動の構成要素）は、電荷とその相互距離の影響を受けます。

上記を考慮して、アルゴリズムの疑似コード 手順を書き留めてみましょう。

1. 検索空間内の最初の無作為な位置で粒子を初期化し、前の反復の空間内の無作為な位置も設定します（前の反復があったと仮定）。

2.適応度関数の値を計算します。

3.方程式を使用して粒子の次の位置を計算します。

4.すべての粒子の中での適応度関数の最良の値と最悪の値を決定します。

5.停止条件が成立するまで手順2からの手順を繰り返します。

粒子の相互運動を計算する式を見てみましょう。荷電粒子の主な特徴はその電荷です。

q = (φp - φw) / (φb - φw)

ここで

• q：現在の粒子の電荷
• φp：粒子の適応度関数の値
• φb：すべての粒子の中での適応度関数の最良の値
• φw ：すべての粒子の中での適応度関数の最悪の値

粒子間の距離を決定するには、次の方程式を使用します。

r(i,j) = (|Xi - Xj|) / (|(Xi - Xj) * 0.5 - Xb|)

ここで

• ||：ユークリッド距離
• r(i,j)：粒子iとjの間の距離
• XiおよびXj：iおよびj粒子の対応する座標
• Xb：すべての反復で見つかった最適な位置の対応する座標

ここで、明らかに、著者のアイデアは、最適なグローバル座標に対する粒子の位置を考慮することでした。これは良いアイデアかもしれませんが、私の実験によると、このアルゴリズムの最適な解決策は、方程式の分子を計算するだけであることがわかりました。

電磁EMアルゴリズムと同様、相互作用力は引力または反発力のいずれかになります。変数cの方向の符号を表しましょう。力の方向を考慮するには、次の条件式を使用します。

φi < φjの場合はc = -1、それ以外の場合はc = 1

ここで

• c：相互作用力の方向の符号
• φiおよびφj：iおよびj粒子の適応度関数値

力の方向の符号は、適応度関数の値が小さい粒子は反発し、値が大きい粒子は引き合うように解釈できます。

EMアルゴリズムとは異なり、粒子は半径が0（アルゴリズムの外部パラメータ）より大きい球であることに同意したため、粒子にかかる力は対応する座標と同一線上にあります（アルゴリズムでは、合計の力は粒子上の はベクトルのセット）、方程式として表すことができます。

F = qi * Q * c * (Xj - Xi)

ここで

• F：粒子に影響を与える作用力
• qi：作用力が計算される粒子
• Q：互いの球の侵入に応じて考慮中の2つの粒子の相対位置を考慮するコンポーネント。Q の方程式は次のとおりです。

Q = ((qj * r(i,j) * b1) / a^3) + (qj * b2) / r(i,j)^2

ここで

• qj：考慮されている粒子に影響を与える粒子の電荷
• b1とb2は、対応する表現用語を「有効化/無効化」します。 r >= 粒子半径の場合、b1 = 0およびb2 = 1。それ以外の場合、b1 = 1およびb2 = 0。

最後に、次の方程式を使用して粒子の動きの新しい座標を計算できます。

Xn = X + λ1 * U * V + λ2 * U * coordinatesNumber * (F / qi)

ここで

• Xn：新しい座標
• λ1：重み係数（外部パラメータ）は、第2項（速度）の影響度を決定
• λ2：重み係数（外部パラメータ）は、第3項（加速度）の影響の度合いを決定
• U：[0;1]の範囲の乱数
• V：現在の反復での座標と前の反復での座標の差
• coordinatesNumber：座標の数。このratioは元の式には含まれていません。探索空間の次元が増加するにつれて、λ2比を増加する必要があるため、これを導入しました（したがって、粒子の「凍結」の影響を回避するために導入）。

λ1とλ2の相対値によって、多様化と検索強化のバランスが決まります。λ1パラメータの値を増やすと、粒子の前の位置の影響が強化され、アルゴリズムの研究特性が向上します。λ2の値が大きいと引力の強い影響が生じ、アルゴリズムの早期収束が発生する可能性があります。逆に、値が小さいとアルゴリズムの収束速度が遅くなり、検索領域がより広範囲に探索されます。

CSSアルゴリズムコードの分析を始めましょう。アルゴリズムの検索エージェントは粒子であり、S_Particle構造体として簡単に表すことができます。

粒子構造体には次のフィールドが含まれます。

• c：粒子座標の配列この配列には、空間内の粒子の現在の座標が含まれます。
• cPrev：前の粒子座標の配列この配列には、空間内の粒子の以前の座標が含まれています。
• cNew：新しい粒子座標の配列この配列には、アルゴリズムの次の反復で使用される新しい粒子座標が含まれています。
• q：粒子の電荷この値は、その粒子に割り当てられた電荷を表します。Chargeは0以外の正の値のみを取ることができます。
• f：粒子の適応度関数の値

粒子の構造体とその電荷に新しい座標の配列が存在することで、その特徴によりアルゴリズムを簡素化することができましたが、これらの量はすべての粒子で一般的に使用できる変数の形で保持できました（一見すると、これは論理的だと思われる）。 

//——————————————————————————————————————————————————————————————————————————————
struct S_Particle
{
  double c     [];  //coordinates
  double cPrev [];  //coordinates
  double cNew  [];  //coordinates
  double q;         //particle charge
  double f;         //fitness
};
//——————————————————————————————————————————————————————————————————————————————

以下を含むC_AO_CSSクラスを宣言します。

クラスのプロパティ

• p：粒子配列
• rangeMax：各座標の最大検索範囲値を含む配列
• rangeMin：各座標の最小検索範囲値を含む配列
• rangeStep：各座標の検索手順 サイズを含む配列
• cB：見つかった最良の座標を含む配列
• fB：最適座標の適応度関数値
• fW：最悪の座標に対する適応度関数の値

クラスのメソッド

• Init：アルゴリズムのパラメータ（座標の数、粒子の数、半径のサイズ、速度と加速度の比率）を初期化
• Moving：粒子の移動を実行
• Revision：最適な座標の更新を実行

privateクラスプロパティ

• coordinatesNumber：座標の数
• particlesNumber：粒子の数
• radius：半径のサイズ
• speedCo：速度比
• accelCo：加速度比
• F：力ベクトル
• revision：リビジョンの必要性を示すフラグ

privateクラスメソッド

• SeInDiSp：指定された手順で指定された範囲内の新しい座標値を計算
• RNDfromCI：指定された間隔で乱数を生成

//——————————————————————————————————————————————————————————————————————————————
class C_AO_CSS
{
  //----------------------------------------------------------------------------
  public: S_Particle p     []; //particles
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: double cB        []; //best coordinates
  public: double fB;           //FF of the best coordinates
  public: double fW;           //FF of the worst coordinates

  public: void Init (const int    coordinatesNumberP, //coordinates number
                     const int    particlesNumberP,   //particles number
                     const double radiusSizeP,        //radius size
                     const double speedCoP,           //speed coefficient
                     const double accelCoP);          //acceleration coefficient

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coordinatesNumber; //coordinates number
  private: int    particlesNumber;   //particles number
  private: double radius;            //radius size
  private: double speedCo;           //speed coefficient
  private: double accelCo;           //acceleration coefficient
  private: double F       [];        //force vector
  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
};
//——————————————————————————————————————————————————————————————————————————————

C_AO_CSSメソッドは、クラスオブジェクトのパラメータを初期化します。座標の数、粒子の数、半径のサイズ、速度、加速度の比率を引数として受け取ります。

メソッド内で、乱数生成器がリセットされ、fB変数とrevision変数の初期値が設定されます。次に、引数値が対応するオブジェクト変数に割り当てられます。
次に、rangeMax、rangeMin、rangeStep、F、p、cB 配列のサイズが座標と粒子の数に応じて変化します。
次に、ループ内で各粒子の配列のサイズが変更され、変数fの初期値が各粒子に設定されます。
メソッドの最後では、cB配列のサイズが座標の数に応じて変化します。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_CSS::Init (const int    coordinatesNumberP, //coordinates number
                     const int    particlesNumberP,   //particles number
                     const double radiusSizeP,        //radius size
                     const double speedCoP,           //speed coefficient
                     const double accelCoP)           //acceleration coefficient
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coordinatesNumber = coordinatesNumberP;
  particlesNumber   = particlesNumberP;
  radius            = radiusSizeP;
  speedCo           = speedCoP;
  accelCo           = accelCoP;

  ArrayResize (rangeMax,  coordinatesNumber);
  ArrayResize (rangeMin,  coordinatesNumber);
  ArrayResize (rangeStep, coordinatesNumber);
  ArrayResize (F,         coordinatesNumber);

  ArrayResize (p,  particlesNumber);

  for (int i = 0; i < particlesNumber; i++)
  {
    ArrayResize (p [i].c,     coordinatesNumber);
    ArrayResize (p [i].cPrev, coordinatesNumber);
    ArrayResize (p [i].cNew,  coordinatesNumber);
    p [i].f  = -DBL_MAX;
  }

  ArrayResize (cB, coordinatesNumber);
}
//——————————————————————————————————————————————————————————————————————————————

粒子（検索エージェント）を移動するためのメインロジックは、Moving()メソッドに実装されています。

最初の反復で、粒子座標の初期値をrangeMinからrangeMaxまでの範囲の乱数で初期化し、値「-DBL_MAX」に等しい粒子の適応度値を取得します。

RadiusSize_Pアルゴリズムの外部パラメータは、すべての座標の最大可能ユークリッド距離の一部の粒子サイズを決定します。これは、各座標の最大許容値と最小許容値の差の二乗和の平方根です。
コードの最後で、revision変数がtrueに設定されます。

//----------------------------------------------------------------------------
if (!revision)
{
  fB = -DBL_MAX;

  for (int obj = 0; obj < particlesNumber; obj++)
  {
    for (int c = 0; c < coordinatesNumber; c++)
    {
      p [obj].c     [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      p [obj].cPrev [c] = RNDfromCI (rangeMin [c], rangeMax [c]);

      p [obj].c     [c] = SeInDiSp (p [obj].c     [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      p [obj].cPrev [c] = SeInDiSp (p [obj].cPrev [c], rangeMin [c], rangeMax [c], rangeStep [c]);

      p [obj].f         = -DBL_MAX;
    }
  }

  double r = 0.0;
  double t = 0.0;

  for (int c = 0; c < coordinatesNumber; c++)
  {
    t = rangeMax [c] - rangeMin [c];
    r += t * t;
  }

  radius *= sqrt (r);
  revision = true;
}

Moving()メソッドコードの残りの部分は2回目以降の反復で実行され、検索空間内で粒子を移動します。

適応度関数のfB値とfW値の差が最初に計算され（すべての反復で見つかった最良の座標と、現在の反復での粒子間の最悪の座標について）、difference変数に格納されます。differenceが0.0の場合、値1.0が割り当てられます。

これにループが続き、粒子ごとに新しい値が計算されます。各粒子iについて、電荷qの新しい値が計算されます。

次に、変数summ1、summ2、q、e、c、b1、b2、X、Q、U、V、t1、t2が宣言され、上で説明した式で使用するために初期化されます。

ループでは、粒子ごとに、母集団内の他のすべての粒子の部分に作用する合計の力Fを計算します。粒子iごとにループし、summ1とsumm2の合計が計算されます。次に、i粒子とj粒子の間の距離rが計算されます。rが0.0の場合、0による除算を避けるために0.01の値が割り当てられます。b1とb2の値は、rとradiusの値に応じて計算されます。次に、問題の2つの粒子の適応度値に応じて、力cの方向の値が計算されます。次にQ値を計算します。そして、ｋ座標ごとに力の値F[k]を計算します。

粒子に作用する力のベクトルの値がわかったら、その動きの新しい座標の値を計算できます。次に、ループで粒子iの以前の座標の値と現在の座標の値が更新します。

このコードでは、元の方程式の一部がコメント化された要素として保存され、CSS作成者がどのようにおこなったかを示しています。

double difference = fB - fW;
if (difference == 0.0) difference = 1.0;

for (int i = 0; i < particlesNumber; i++)
{
  p [i].q = ((p [i].f - fW) / difference) + 0.1;
}

double summ1 = 0.0;
double summ2 = 0.0;
double q     = 0.1;
double e     = 0.001;
double c     = 0.0;
double b1    = 0.0;
double b2    = 0.0;
double X     = 0.0;
double Q     = 0.0;
double U     = 0.0;
double V     = 0.0;
double t1    = 0.0;
double t2    = 0.0;

for (int i = 0; i < particlesNumber && !IsStopped (); i++)
{
  ArrayInitialize (F, 0.0);

for (int j = 0; j < particlesNumber && !IsStopped (); j++)
{
  if (i == j) continue;

  summ1 = 0.0;
  summ2 = 0.0;

  for (int k = 0; k < coordinatesNumber && !IsStopped (); k++)
  {
    t1 = p [i].c [k] - p [j].c [k];
    summ1 += t1 * t1;

    //t2 = t1 * 0.5 - cB [k];
    //summ2 += t2 * t2;
  }

  //r = sqrt (summ1) / (sqrt (summ2) + e);
  r = sqrt (summ1);
        
  if (r == 0.0) r = 0.01;

  if (r >= radius)
  {
    b1 = 0.0;
    b2 = 1.0;
  }
  else
  {
    b1 = 1.0;
    b2 = 0.0;
  }

  c = p [i].f < p [j].f ? -1.0 : 1.0;

  q = p [j].q;

  Q = ((q * r * b1 / (radius * radius * radius)) + (q * b2 / (r * r))) * c;

  for (int k = 0; k < coordinatesNumber && !IsStopped (); k++)
  {
    F [k] += /*p [i].q */ Q * (p [j].c [k] - p [i].c [k]);
  }
}

  for (int k = 0; k < coordinatesNumber && !IsStopped (); k++)
  {
    V = p [i].c [k] - p [i].cPrev [k];
    U = RNDfromCI (0.0, 1.0);

    X = p [i].c [k] + speedCo * U * V + accelCo * U * coordinatesNumber * (F [k] / p [i].q);
        
    p [i].cNew [k] = SeInDiSp (X, rangeMin [k], rangeMax [k], rangeStep [k]);
  }
}

for (int i = 0; i < particlesNumber && !IsStopped (); i++)
{
  for (int k = 0; k < coordinatesNumber && !IsStopped (); k++)
  {
    p [i].cPrev [k] = p [i].c [k];
    p [i].c [k] = p [i].cNew [k];
  }
}

最後に、Revision()メソッドが登場します。
メソッドの開始時に、変数fWにdouble型の最大値(DBL_MAX)が割り当てられるため、その後、適応度関数の最小値を使用して最悪の粒子を決定できます。
その後、システムのすべての粒子を通じてループします。次のアクションが粒子ごとに実行されます。
- 現在の粒子のf値がfB（すべての粒子の最良の適応度関数）より大きい場合、fB値は現在の粒子のf値で更新され、cB配列（最良の位置）が現在の粒子の位置からコピーされます。
- 現在の粒子のf値がfW値（すべての粒子の最小の適応度関数）より小さい場合、fW値は現在の粒子のf値で更新されます。

したがって、このコードはすべての粒子の中から最良および最悪の適応度関数を見つけて、対応する値を更新します。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_CSS::Revision ()
{
  fW  = DBL_MAX;

  for (int i = 0; i < particlesNumber; i++)
  {
    if (p [i].f > fB)
    {
      fB = p [i].f;
      ArrayCopy (cB, p [i].c, 0, 0, WHOLE_ARRAY);
    }

    if (p [i].f < fW)
    {
      fW = p [i].f;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

3.テスト結果

次は、テストベンチでの荷電系探索アルゴリズムの出力です。

C_AO_CSS:50;0.1;0.7;0.01
=============================
5 Rastrigin's; Func runs 10000 result:70.43726076935499
Score:0.87276
25 Rastrigin's; Func runs 10000 result:68.88569793414477
Score:0.85353
500 Rastrigin's; Func runs 10000 result:66.01225385184436
Score:0.81793
=============================
5 Forest's; Func runs 10000 result:0.4891262437640296
Score:0.27667
25 Forest's; Func runs 10000 result:0.1494549763925046
Score:0.08454
500 Forest's; Func runs 10000 result:0.07829232143185726
Score:0.04429
=============================
5 Megacity's; Func runs 10000 result:2.04
Score:0.17000
25 Megacity's; Func runs 10000 result:0.744
Score:0.06200
500 Megacity's; Func runs 10000 result:0.26880000000000004
Score:0.02240
=============================
All score:3.20412

アルゴリズムの演算結果の出力は、全体的な結果が低いことを示しています。10、50、1000個の変数に対するRastrigin関数の場合、適応度関数値の結果はそれほど変わらないという事実にご注目ください。以下では、これが何を意味するのかを理解していきます。

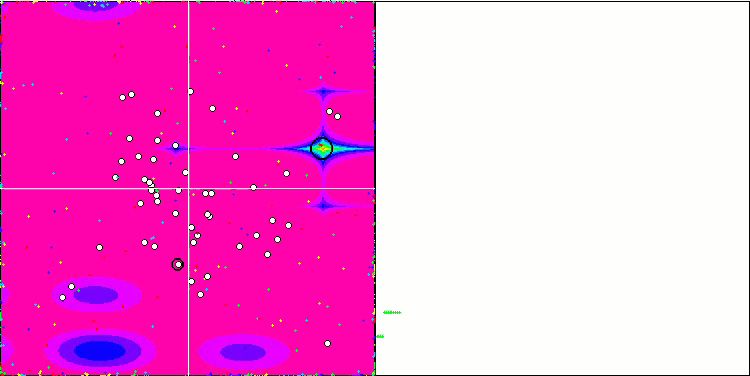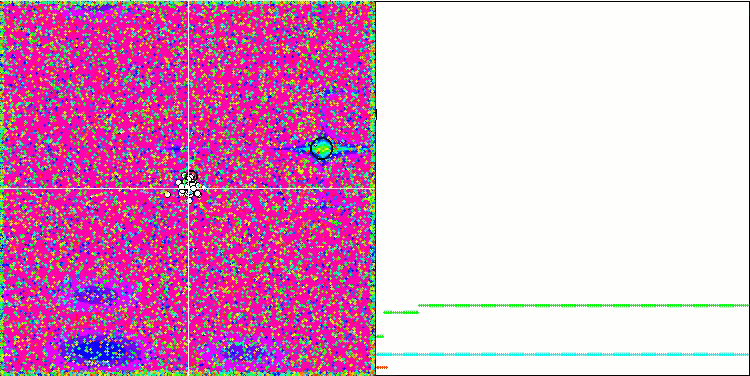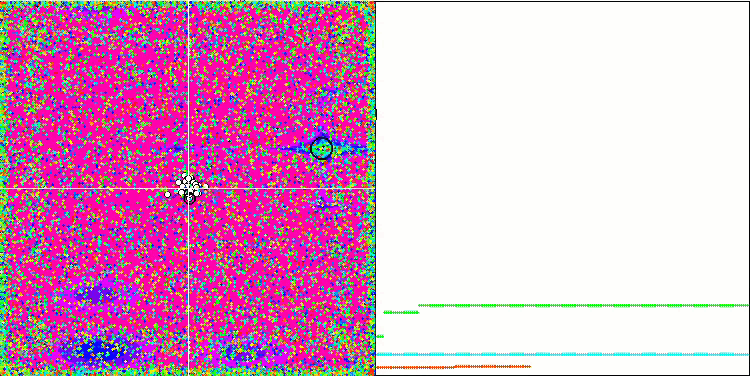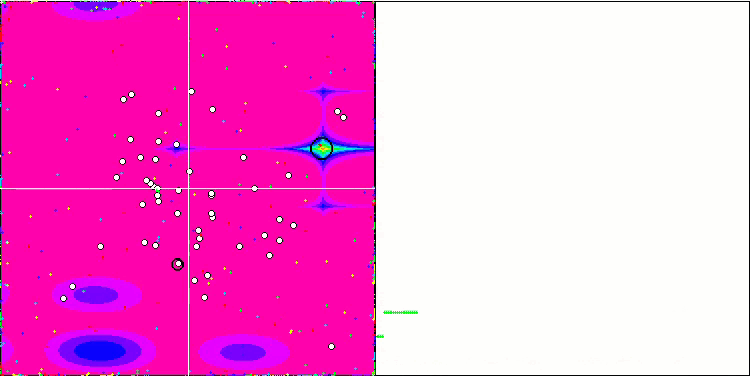
Rastriginテスト関数の視覚化では、重要な局所極値に沿った粒子母集団の明確な可視分割が示されており、これは局所領域の優れた研究を意味しますが、Forest関数とMegacity関数では同様の動作は観察されず、母集団は形のない雲のように動作します。収束グラフの長い水平セクションは、アルゴリズムが局所的な極値で行き詰まる傾向を示していますが、この重大な欠点は、平滑Rastrigin関数の優れたスケーラビリティによってある程度補われます。

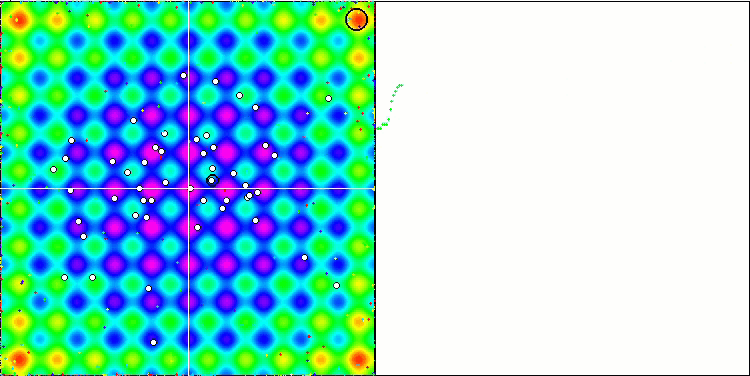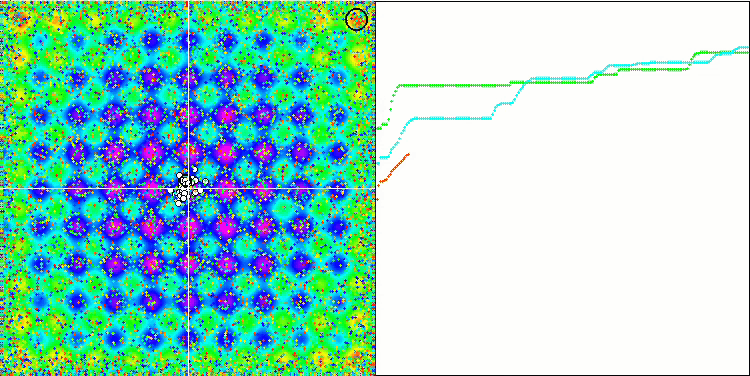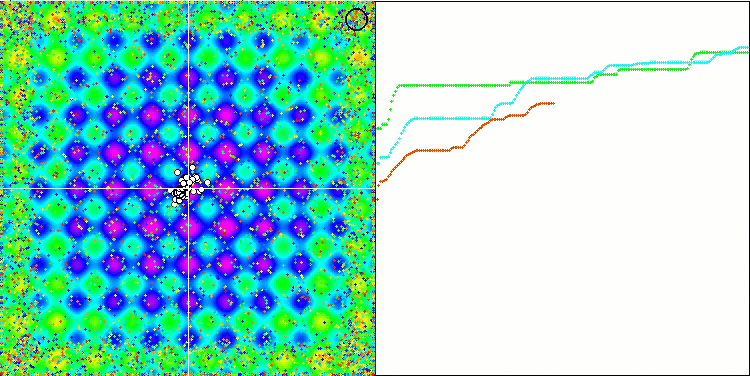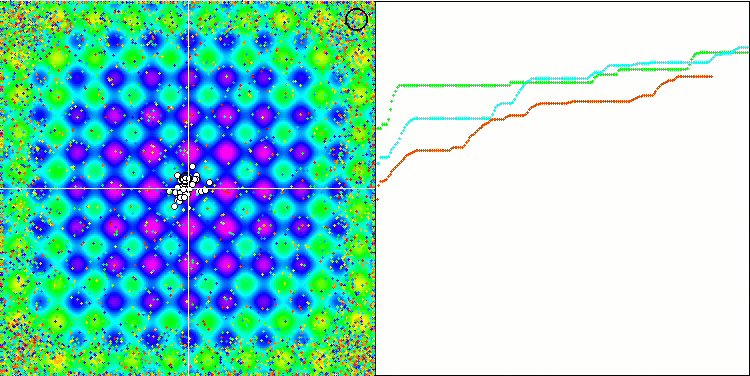
  Rastriginテスト関数のCSS

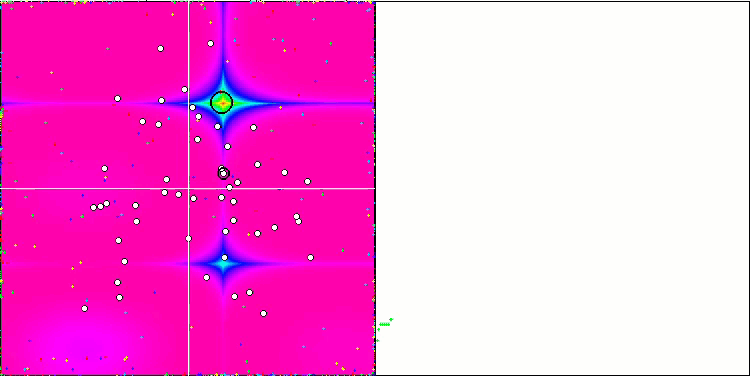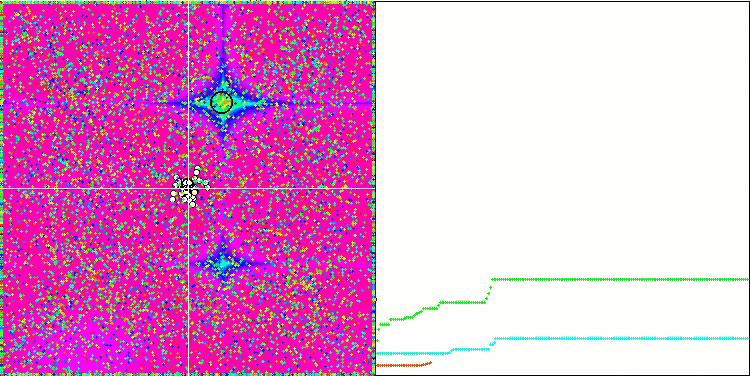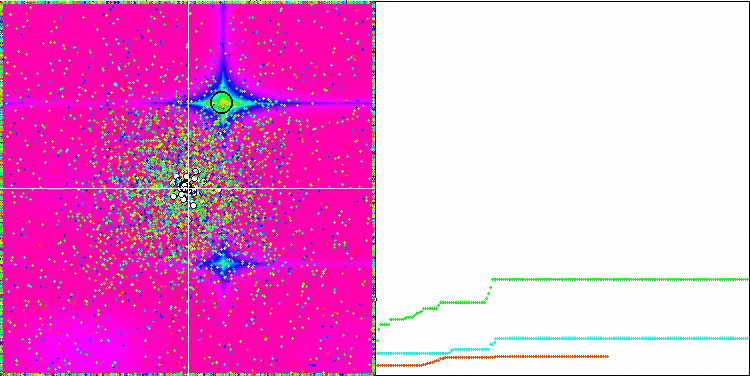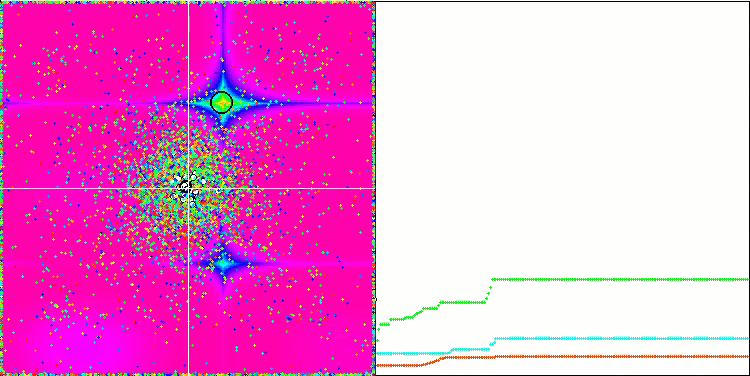
  Forestテスト関数のCSS

  Megacityテスト関数のCSS

CSSアルゴリズムのテストにより、平滑関数を最適化するための新しいリーダーが特定されました。Rastrigin 関数の以前のリーダーも、無生物の自然からインスピレーションを得たアルゴリズム、電磁探索(EM)でした。今回の新記録は前回の記録を10%近く上回ります。残念ながら、このアルゴリズムは、鋭い大域的極限を持つForest関数と離散Megacity関数で最悪の結果の一部を示しています。1,000個の変数を使用したRastriginでの素晴らしい結果のおかげで、このアルゴリズムは合計パラメータに基づいて20中13位に入ることができました。テスト規則によって割り当てられたCSSアルゴリズムの10,000回の実行中、CSSは大域的極限に90%よりも近づくことができませんでした（上記のテストベンチのプリントを参照）。   

#	AO	詳細	Rastrigin			Rastrigin最終	Forest			Forest最終	Megacity（離散）			Megacity最終	最終結果
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	SDS	Stochastic Diffusion Search	0.99737	1.00000	0.58904	2.58641	0.96893	1.00000	0.95092	2.91985	1.00000	1.00000	0.72149	2.72149	100000
2	SSG	苗木の播種と育成	1.00000	0.95313	0.51630	2.46944	0.72740	0.69680	1.00000	2.42421	0.69612	0.65918	1.00000	2.35531	87.506
3	HS	ハーモニー検索	0.99676	0.90817	0.44686	2.35179	1.00000	0.72930	0.44806	2.17736	0.91159	0.76578	0.41537	2.09274	79.501
4	ACOm	蟻コロニー最適化M	0.34611	0.17142	0.15808	0.67562	0.86888	0.73719	0.77362	2.37968	0.91159	0.68163	0.05606	1.64929	55.026
5	IWO	侵入雑草最適化	0.95828	0.63939	0.27647	1.87415	0.70773	0.34168	0.31773	1.36714	0.72927	0.32539	0.33289	1.38756	54.060
6	MEC	Mind Evolutionary Computation	0.99270	0.48648	0.21148	1.69066	0.60762	0.29973	0.25459	1.16194	0.85083	0.31978	0.26170	1.43231	49.669
7	COAm	カッコウ最適化アルゴリズムM	0.92400	0.44601	0.24120	1.61121	0.58378	0.25090	0.16526	0.99994	0.66298	0.25666	0.17083	1.09047	42.223
8	FAm	ホタルアルゴリズムM	0.59825	0.32387	0.15893	1.08106	0.51073	0.31182	0.49790	1.32045	0.31491	0.21880	0.35258	0.88629	36.941
9	ABC	人工蜂コロニー	0.78170	0.31182	0.19313	1.28664	0.53837	0.15816	0.13344	0.82998	0.51381	0.20758	0.13926	0.86064	32.977
10	BA	コウモリアルゴリズム	0.40526	0.60773	0.78330	1.79629	0.20841	0.12884	0.25989	0.59714	0.27073	0.08135	0.17371	0.52579	32.236
11	GSA	重力探索法	0.70167	0.43098	0.00000	1.13265	0.31660	0.26845	0.33204	0.91710	0.54144	0.27208	0.00000	0.81352	31.522
12	BFO	細菌採餌の最適化	0.67203	0.29511	0.10957	1.07671	0.39702	0.19626	0.20652	0.79980	0.47514	0.25807	0.18932	0.92253	30.702
13	CSS	荷電系探索	0.56605	0.70573	1.00000	2.27178	0.14081	0.01980	0.16282	0.32343	0.09393	0.00000	0.03481	0.12874	29.743
14	EM	電磁気学的アルゴリズム	0.12235	0.44109	0.92752	1.49096	0.00000	0.02578	0.34880	0.37458	0.00000	0.00562	0.10924	0.11486	20.252
15	SFL	ShuffledFrog-Leaping	0.40072	0.22627	0.24624	0.87323	0.20153	0.03057	0.02652	0.25862	0.24862	0.04769	0.06639	0.36270	14.050
16	MA	モンキーアルゴリズム	0.33192	0.31883	0.13582	0.78658	0.10012	0.05817	0.08932	0.24762	0.19889	0.03787	0.10720	0.34396	12.564
17	FSS	魚群検索	0.46812	0.24149	0.10483	0.81445	0.12840	0.03696	0.06516	0.23052	0.15471	0.04208	0.08283	0.27961	11.880
18	PSO	粒子群最適化	0.20449	0.07816	0.06641	0.34906	0.18895	0.07730	0.21738	0.48363	0.21547	0.05049	0.01957	0.28553	9.246
19	RND	ランダム	0.16826	0.09287	0.07438	0.33551	0.13496	0.03546	0.04715	0.21757	0.15471	0.03507	0.04922	0.23900	5.083
20	GWO	灰色オオカミオプティマイザ	0.00000	0.00000	0.02093	0.02093	0.06570	0.00000	0.00000	0.06570	0.29834	0.06170	0.02557	0.38561	1.000

まとめ

粒子が「くっついて」「固まる」ことなくフィールド上を強制的に移動させるには、多くの実験とコード編集をおこなう必要がありました。アルゴリズムの作成者は、最適化パラメータの数が最適化の品質に及ぼす影響を考慮していませんでした（問題の次元が増加するにつれて、収束は不釣り合いに急速に悪化しました）。方程式にさらに多くの座標を追加することで、加速の効果を強化し、CSS のパフォーマンスを向上させることができました（これらの変更をおこなわないと、アルゴリズムは非常に悪い結果を示した）。粒子の動きに固有の法則は、研究目的での変更にはあまりにも気まぐれであるため、この興味深い最適化アルゴリズムのパフォーマンスを向上させる試みが複雑になります。

このアルゴリズムは、平滑関数を最適化するための効果的な方法です。クーロン力によって相互接続された荷電粒子の雲を適用します。この興味深いアルゴリズムを使用する場合、離散探索空間フィールドの問題に対する適合性が低いことを考慮する必要があります。ただし、これは、以前に検討した変数のうち複数の変数を含む平滑関数にとっては最適な最適化アルゴリズムです。CSSは、多数の変数を使用した最適化のあらゆる領域で使用できます。勾配情報も検索空間の連続性も必要ありません。

個々のアルゴリズムの長所と短所をより視覚的に表現するには、図 1 のカラー スケールを使用して上の表を表すことができます。テーブルの色のグラデーションにより、特定の最適化問題に応じて、個々のアルゴリズムを使用する可能性をより明確に表現できます。今のところ、あらゆる問題に対する最適な解決策となる完全に普遍的なアルゴリズムを見つけることはできていません（おそらく、今後の研究で見つけることができるでしょう）。

例えば、評価の最初のアルゴリズム(SDS)を考慮すると、それは個々のテスト問題では最高ではありません（表では、複数の変数を持つ平滑関数が平均として示されています）。ACOmアルゴリズムに関しては、その個々の結果は表の平均をはるかに下回っています（平滑関数の解決が驚くほど不十分です）が、Forestおよび離散Megacityには非常によく対応します（もともと、巡回セールスマン問題などの離散問題を解決するように設計されていた）。ただし、スケーラビリティにはまだ多くの点が残されています。

最後に提示されたアルゴリズム(CSS)は、1,000個の変数をもつRastrigin関数でうまく機能し（多くのパラメータを使用してニューラルネットワークを訓練する場合に適している可能性がある）、これまでに検討されたすべての最適化アルゴリズムの中で最良の結果を示していますが、合計の結果に基づくと、表の中で最高のものとは思えません。したがって、問題の詳細に応じてアルゴリズムを正しく選択することが非常に重要です。

さまざまな検索戦略を使用した最適化アルゴリズムの大規模テストにより、予期せぬ事実が明らかになりました。- この戦略は、最良の結果を選択した単純な無作為検索を使用した場合よりもさらに悪い結果になる可能性があります。- 最下位に予想されたRNDが代わりに下から2つ目になりました。GWOは10パラメータを持つ離散Megacityを除き、無作為検索よりも悪いことが判明しました。

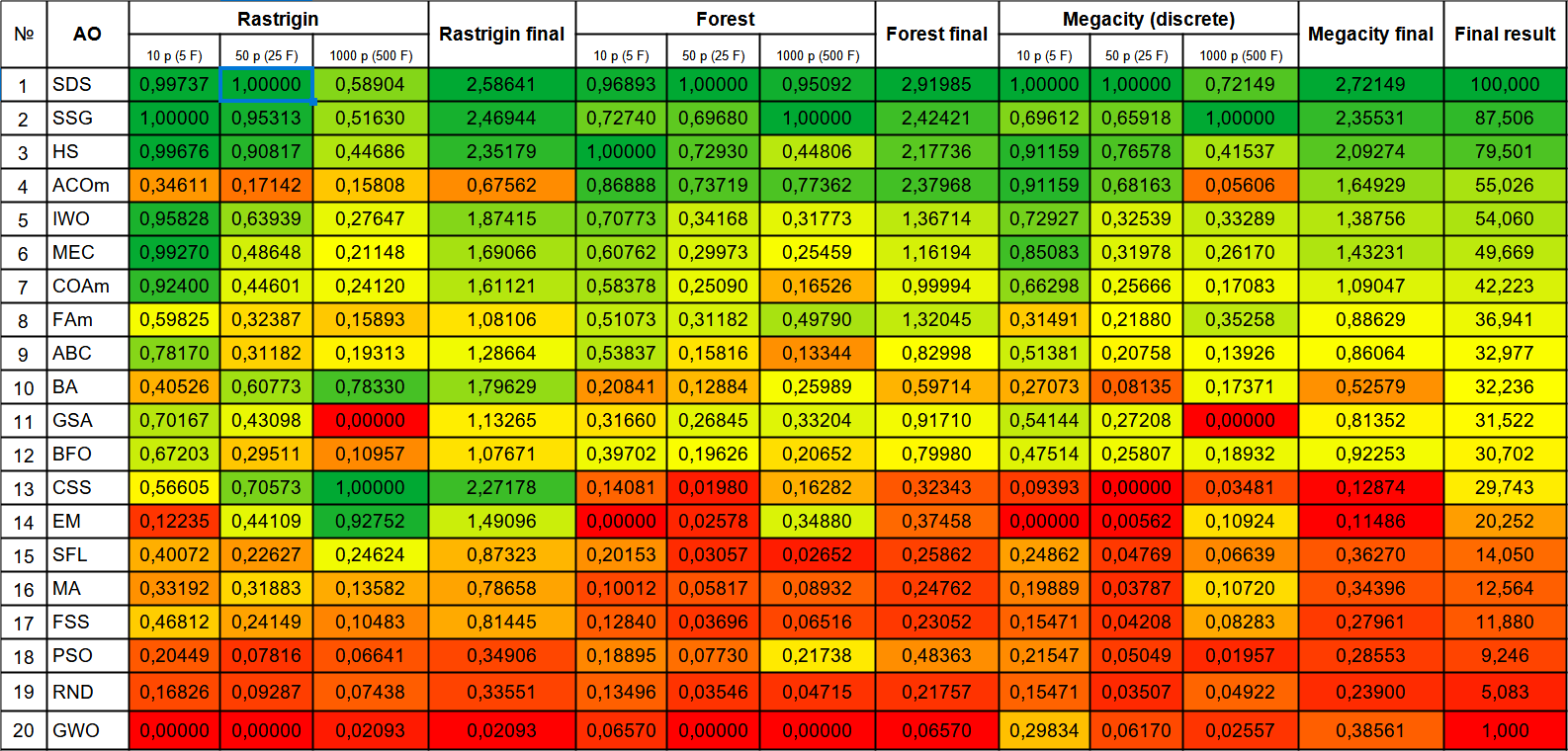
図1：関連テストによるアルゴリズムのカラーグラデーション

アルゴリズムのテスト結果のヒストグラムを以下に示します（0から100までのスケールで、多ければ多いほど良い。アーカイブには、この記事で説明した方法で格付け表を計算するスクリプトがある）。

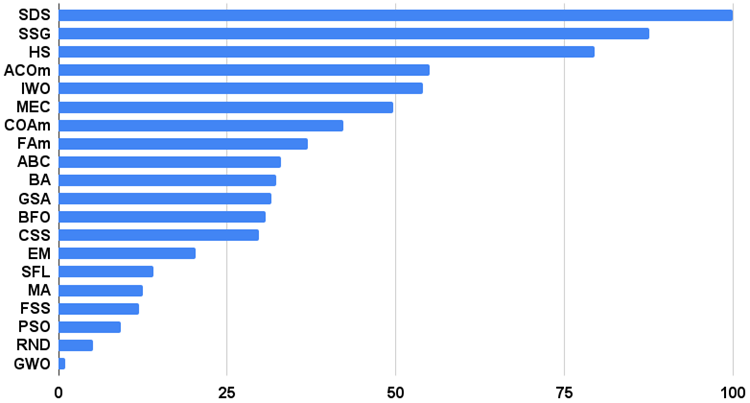
図2：テストアルゴリズムの最終結果のヒストグラム

荷電系探索(CSS)アルゴリズムの長所と短所

長所
1. 平滑関数で拡張性が高い
2.外部パラメータが少ない

短所
1. 離散関数の結果が低い
2.収束性が低い
3.局所的な極端な状況に陥る傾向

各記事には、以前の記事で説明したアルゴリズムコードの更新された最新バージョンを含むアーカイブが付属しています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。