MetaTrader 5 / テスター
English Русский 中文 Español Deutsch Português
preview
循環単為生殖アルゴリズム(CPA)

循環単為生殖アルゴリズム(CPA)

MetaTrader 5 — テスター |
75 0
Andrey Dik
Andrey Dik

内容

  1. はじめに
  2. アルゴリズムの実装
  3. テスト結果


はじめに

自然現象に着想を得た最適化アルゴリズムは、複雑な最適化問題の解決において依然として重要な役割を果たしています。特に注目されるのは、アリやハチ、アブラムシなどの社会性昆虫の行動に基づくアルゴリズムです。これまでに、COmやABHAなどの類似アルゴリズムについても議論してきました。 本記事では、アブラムシ特有の繁殖戦略を模倣した循環単為生殖アルゴリズム(CPA: Cyclic Parthenogenesis Algorithm)を紹介します。

アブラムシは、単為生殖と有性生殖の両方を含む特異な生活環により、非常に高い適応能力を示します。環境条件が良好な場合、アブラムシは単為生殖によって繁殖し、急速な個体数増加を可能にします。一方、環境が悪化すると、有性生殖に切り替わり、遺伝的多様性を促進するとともに、変化する環境下での生存率を高めます。

CPAは、これらの生物学的メカニズムを数学的にシミュレーションし、既存の解の利用（単為生殖による）と探索（有性生殖による新たな探索領域の開拓）のバランスを作り出します。さらに、アブラムシの社会的行動を模倣し、コロニー内での意思決定を組織化するとともに、コロニー間での移動メカニズムを実装することで情報交換を促進します。

これらの特徴により、CPAは局所探索と大域探索のバランスが求められる多次元最適化問題において特に効率的であると考えられます。本記事では、アルゴリズムの原理、数学モデル、実際の実装方法について詳細に検討します。なお、CPAはAli KavehとA. Zolghadrによって提案され、2019年に初めて発表されました。


アルゴリズムの実装

庭でアブラムシの群れを観察しているところを想像してください。これらの小さな生物は、2種類の繁殖方法を駆使し、環境に非常に効果的に適応します。CPAは、まさにこの行動をシミュレーションして複雑な最適化問題を解決します。どのように動作するのでしょうか。まず初期段階では、複数の解のグループ（コロニー）が作られ、それぞれに「雌」と「雄」の個体が含まれます。

アルゴリズムでは、新しい解を生成する方法として2つの手法が提案されています。
    • 自己複製：最良解が、自身のコピーにわずかな修正を加えて生成する
    • 従来の有性繁殖：2つの異なる解を組み合わせて新しい解を生成する

    さらに、あるコロニーの最良解が別のコロニーに「飛行」する場合があります。アルゴリズムは常にどの解が最良かを評価し、最良の成果を保存し、成功したオプションを組み合わせながら探索を進めます。すべては最適解を見つけるためです。アルゴリズムの重要な特徴は、すでに見つかった良好な解の利用と、全く新しい解の探索とのバランスを見つける点にあり、これはアブラムシが環境変化に適応する方法に似ています。

    CPA

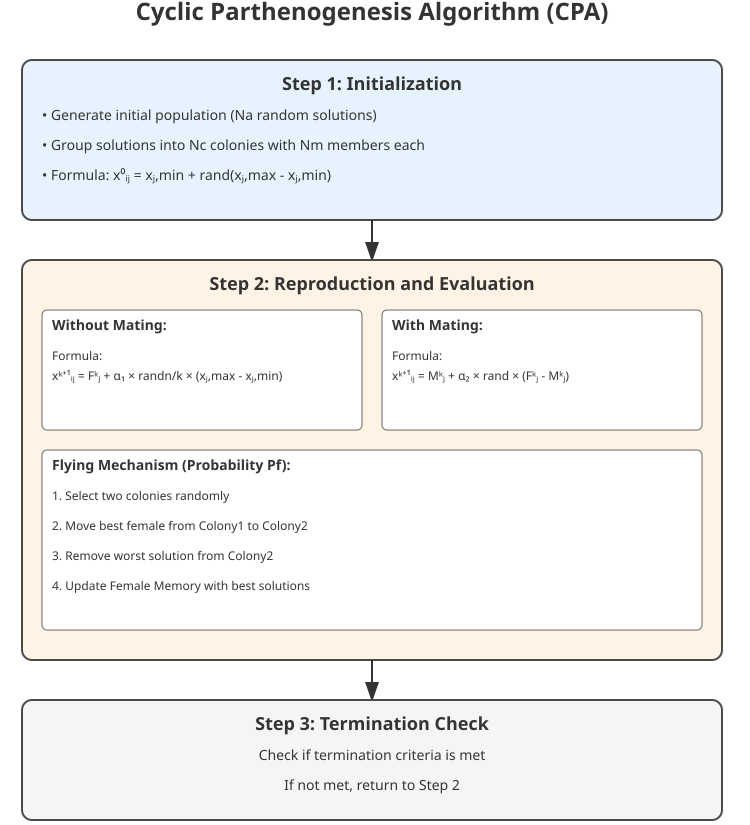
    図1：CPAアルゴリズムの構造と基本方程式

    次に、CPAアルゴリズムの視覚的表現を見てみましょう。図中の主な要素は、コロニー、ピンクの四角：雌個体（解）、青の四角：雄個体（解）、点線：コロニー間の飛行経路です。この図は、コロニーの構造、繁殖メカニズム、コロニー間の飛行、コロニー内での個体間の相互作用を示しています。実際のアブラムシを用いた視覚的な比喩を通じて、アルゴリズムの原理をより理解しやすくしています。

    CPAアルゴリズム図

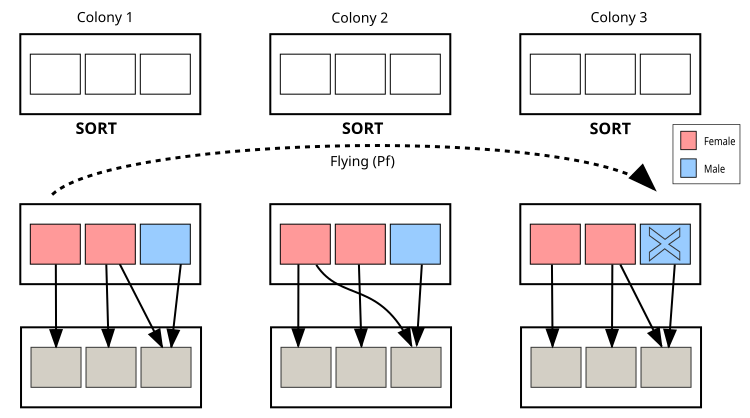
    図2：CPAアルゴリズムにおけるアブラムシコロニーとその相互作用

    アルゴリズムの説明に少し慣れてきたので、擬似コードの記述に移りましょう。

    初期化：
    個体数Naの集団を作成
    集団をNcのコロニーに分割

    各コロニー内：
    雌の個体数を決定(Fr * Nm)
    残りを雄とする

    初期パラメータの設定：
    α1（単為生殖比）
    α2（交配比率）
    Pf（飛行確率）

    メインサイクル（各エポックごとに実行）：
    各コロニーについて：
    雌：

    単為生殖による位置更新：
    new_position = current_position + alpha1 * k * N(0,1) * (max_range - min_range)
    ここで、k = (total_epochs - current_epoch) / total_epochs、
    N(0,1)は正規分布

    雄：
    コロニー内のランダムな雌を選択
    交配による位置更新：
    new_position = current_position + alpha2 * random[0,1] * (female_position - current_position)

    位置の改訂：
    最良解を更新
    現在の位置を保存
    コロニー内の個体を目的関数の値でソート

    移動（確率Pf）：
    2つのランダムなコロニーを選択
    最良解を比較
    最良解を最悪のコロニーに移動
    コロニー内の個体を再ソート

    これで、アルゴリズムのコードを記述する準備が整いました。次に、C_AO_CPAクラスを作成します。このクラスはC_AOクラスを継承し、アルゴリズム全体を実装します。主なコンポーネントは以下の通りです。

    C_AO_CPAコンストラクタ

    • 集団サイズ、コロニー数、雌比率、飛行確率、単為生殖・交配のスケーリング係数などのパラメータを設定
    • パラメータ配列を確保し、値を格納

    SetParamsメソッドは、params配列から値を取得し、適切な型に変換して設定 

    Init、Moving、Revisionメソッド

    • Init：指定範囲とエポック数でアルゴリズムを初期化
    • MovingおよびRevision：アルゴリズム内の移動と改訂のロジックを実装

    クラスメンバー：コロニー数、雌雄比率、プロセス制御パラメータなど、アルゴリズムに必要な変数を保持

    privateメンバー：現在のエポック、コロニー内の個体数、エージェントの一時配列などを追跡

    //——————————————————————————————————————————————————————————————————————————————
// Class implementing the Cyclic Parthenogenesis Algorithm (CPA)
// Inherited from the optimization base class
class C_AO_CPA : public C_AO
{
  public:
  C_AO_CPA (void)
  {
    ao_name = "CPA";
    ao_desc = "Cyclic Parthenogenesis Algorithm";
    ao_link = "https://www.mql5.com/ja/articles/16877";

    popSize = 50;       // total population size Na

    Nc      = 10;       // number of colonies
    Fr      = 0.2;      // ratio of female individuals
    Pf      = 0.9;      // probability of flight between colonies
    alpha1  = 0.3;      // scaling factor for parthenogenesis
    alpha2  = 0.9;      // scaling factor for pairing

    ArrayResize (params, 6);

    // Setting algorithm parameters
    params [0].name = "popSize";     params [0].val = popSize;
    params [1].name = "Nc";          params [1].val = Nc;
    params [2].name = "Fr";          params [2].val = Fr;
    params [3].name = "Pf";          params [3].val = Pf;
    params [4].name = "alpha1_init"; params [4].val = alpha1;
    params [5].name = "alpha2_init"; params [5].val = alpha2;
  }

  void SetParams ()
  {
    popSize = (int)params [0].val;

    Nc      = (int)params [1].val;
    Fr      = params      [2].val;
    Pf      = params      [3].val;
    alpha1  = params      [4].val;
    alpha2  = params      [5].val;
  }

  bool Init (const double &rangeMinP  [], // minimum search range
             const double &rangeMaxP  [], // maximum search range
             const double &rangeStepP [], // search step
             const int     epochsP = 0);  // number of epochs

  void Moving   ();         // function for moving individuals
  void Revision ();         // function for reviewing and updating positions

  //----------------------------------------------------------------------------
  int    Nc;                // number of colonies
  double Fr;                // ratio of female individuals
  double Pf;                // probability of flight between colonies

  private: //-------------------------------------------------------------------
  int    epochs;            // total number of epochs
  int    epochNow;          // current epoch
  int    Nm;                // number of individuals in each colony
  double alpha1;            // scaling factor for parthenogenesis
  double alpha2;            // scaling factor for pairing
  int    fNumber;           // number of females in the colony
  int    mNumber;           // number of males in the colony

  S_AO_Agent aT [];         // temporary colony for sorting
  void SortFromTo (S_AO_Agent &p [], S_AO_Agent &pTemp [], int from, int count); // agent sorting function
};
//——————————————————————————————————————————————————————————————————————————————

    C_AO_CPAクラスのInitメソッドの実装とその機能

    メソッドパラメータ

    • rangeMinP、rangeMaxP、rangeStepP：探索範囲の最小値と最大値、およびステップ幅を定義する配列
    • epochsP：エポック数（デフォルトは0）
    メソッドのロジック
    • まずStandardInitを呼び出し、渡された範囲で標準初期化を実行します。初期化に失敗した場合はfalseを返します。
    • エポック数と現在のエポック(epochNow)を設定します。
    • 集団サイズとコロニー数に基づき、1コロニーあたりのメンバー数(Nm)を計算します。
    • コロニー内の雌の数(fNumber)を決定します。この値は必ず1以上になるように制御します。雄の数(mNumber)は、個体の総数から雌の数を引くことで算出されます。
    • 一時的なコロニーエージェントを格納するために、aT配列を確保します。
    戻り値
    • 初期化が正常に完了した場合はtrueを返します。

      このメソッドは、アルゴリズムが動作するためのパラメータと構造を設定し、実行前に適切な初期化がおこなわれることを保証します。

      //——————————————————————————————————————————————————————————————————————————————
// Initialization of the algorithm with the given search parameters
bool C_AO_CPA::Init (const double &rangeMinP  [],
                     const double &rangeMaxP  [],
                     const double &rangeStepP [],
                     const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  epochs   = epochsP;
  epochNow = 0;
  // Calculating the colony size and the number of individuals of each gender
  Nm       = popSize / Nc;
  fNumber  = int(Nm * Fr); if (fNumber < 1) fNumber = 1;
  mNumber  = Nm - fNumber;

  ArrayResize (aT, Nm);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

      C_AO_CPAクラスのMovingメソッドは、解空間内でエージェントの座標を移動させ、特定のルールとランダム要素に基づいて位置を適応させます。順を追って説明します。

      エポックの増加： メソッドはまず現在のエポック(epochNow)をインクリメントします。これは、最適化または進化プロセスの次のステップが呼び出されたことを示します。

      第一段階（revisionがfalseの場合）：revisionフィールドがfalseに設定されている場合、個体群(popSize)内の各エージェントの座標を初期化します。

      • 各エージェントa[i]は、RNDfromCI関数を用いて、各次元(coords)におけるランダムな座標を[rangeMin[c], rangeMax[c]]の範囲で取得します。
      • その後、SeInDiSp関数により、離散化ステップ(rangeStep[c])に従って値が補正されます。
      • revisionフラグをtrueに設定し、メソッドを終了します。
        第二段階（revisionがtrueの場合）：revisionがtrueに設定されている場合、座標は前回の座標とランダム成分に基づいて適応されます。
        • 変数kは、残りエポック数と総エポック数の比として計算されます。これにより、最適化が進むにつれてエージェントの移動範囲が徐々に狭まります。
        • コロニー(col)と関数(fNumber)を順に処理し、コロニー内の最初のfNumberエージェントの座標を前回の座標(cP)に基づき更新します。この際、正規分布(GaussDistribution)から生成されたランダム値を加え、rangeMinとrangeMaxの範囲にスケーリングします。
        • 残りのエージェント（m = fNumberからNm）についても座標を更新しますが、ここではコロニー内の最良エージェントのランダムに選択された座標を使用します。さらにalpha2パラメータを考慮してランダム値を加えます。
        行動ロジック
        • このメソッドの全体的な目的は、エージェントを解空間内で移動させることです。前回の位置に基づく適応と、探索領域にランダム性を導入することで、大域最適解を見つける可能性を高めます。
        • alpha1やalpha2といったパラメータは、適応度とランダム性のレベルを制御する役割を果たします。

          まとめると、Movingメソッドは、個々のエージェントの過去の位置と他のエージェントの位置の両方を考慮しながら、解空間内でエージェントを動かす最適化アルゴリズムにおいて非常に重要な役割を担っています。

          //——————————————————————————————————————————————————————————————————————————————
// The main function for moving individuals in the search space
void C_AO_CPA::Moving ()
{
  epochNow++;
  //----------------------------------------------------------------------------
  // Initial random initialization of positions if this is the first iteration
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        // Generate a random position in a given range
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  // Calculate the search power decay rate over time
  double k    = (epochs - epochNow)/(double)epochs;
  int    ind  = 0;
  int    indF = 0;

  // Handling each colony
  for (int col = 0; col < Nc; col++)
  {
    // Updating the positions of female individuals (parthenogenesis)
    for (int f = 0; f < fNumber; f++)
    {
      ind = col * Nm + f;

      for (int c = 0; c < coords; c++)
      {
        // Parthenogenetic position update using normal distribution
        a [ind].c [c] = a [ind].cP [c] + alpha1 * k * u.GaussDistribution (0.0, -1.0, 1.0, 8) * (rangeMax [c] - rangeMin [c]);
      }
    }

    // Update positions of males (mating)
    for (int m = fNumber; m < Nm; m++)
    {
      ind = col * Nm + m;

      // Select a random female for mating
      indF = u.RNDintInRange (ind, col * Nm + fNumber - 1);

      for (int c = 0; c < coords; c++)
      {
        // Update position based on the selected female
        a [ind].c [c] = a [ind].cP [c] + alpha2 * u.RNDprobab () * (a [indF].cP [c] - a [ind].cP [c]);
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

          C_AO_CPAクラスのRevisionメソッドは、個体群内のエージェントの状態を、目的関数fの値に基づいて更新する役割を持ちます。詳しく見てみましょう。

          初期化：メソッドはまず、変数indを-1に初期化します。この変数は、f関数の最良値を持つエージェントのインデックスを格納するために使用されます。

          最良エージェントの探索：最初の orループで、個体群(popSize)内のすべてのエージェントを反復処理します。現在のエージェントa[i].fのf関数値が、現在の最良値fBより大きい場合、

          • fBをa[i].fに更新
          • 最良エージェントのインデックスをindに保存
          • ループ終了後、もしより良い値を持つエージェント(ind != -1)が見つかった場合、そのエージェントの座標cをcB配列にコピー

          現在の座標のコピー ：2つ目のforループで、各エージェントの現在の座標cを前回の座標cPにコピーします。これにより、エージェントの前回の状態が保存され、後続の分析に利用可能となります。

          エージェントのソート ：3つ目の「for」ループは、すべてのコロニー(Nc)を反復処理し、各コロニーに対してSortFromToメソッドを呼び出します。このメソッドは、f関数の値に基づいてコロニー内のエージェントをソートします。ソートのインデックスは「ind = col * Nm」として計算されます。

          確率的更新 ：このメソッドでは、u.RNDprobab()関数によって生成された乱数値が閾値Pfより小さいかどうかを確認します。

          • 条件が満たされた場合、2つの異なるランダムなコロニーインデックス（indCol_1とindCol_2）が選択されます。
          • その後、これら2つのコロニー内のエージェントにおけるf関数の値が比較されます。最初のコロニーの関数値が2番目のコロニーより小さい場合、インデックスが入れ替えられます。
          • 次に、最初のコロニー内の最初のエージェントの座標が、2番目のコロニー内の最後のエージェントの座標にコピーされます。
          • その後、SortFromToが再び呼び出され、2番目のコロニー内のエージェントの順序が更新されます。

          全体的なロジック

          Revisionメソッドは、エージェントの状態を更新するために使用されます。このメソッドは、最良エージェントの情報を保持し、コロニー間で情報交換をおこなう機能を提供します。

          //——————————————————————————————————————————————————————————————————————————————
// Function for revising positions and exchanging information between colonies
void C_AO_CPA::Revision ()
{
  // Find and update the best solution
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  // Save the current positions
  for (int i = 0; i < popSize; i++)
  {
    ArrayCopy (a [i].cP, a [i].c, 0, 0, WHOLE_ARRAY);
  }

  // Sort individuals in each colony by the target function value
  for (int col = 0; col < Nc; col++)
  {
    ind = col * Nm;
    SortFromTo (a, aT, ind, Nm);
  }

  // Mechanism of flight (migration) between colonies
  if (u.RNDprobab () < Pf)
  {
    int indCol_1 = 0;
    int indCol_2 = 0;

    // Select two random different colonies
    indCol_1 = u.RNDminusOne (Nc);
    do indCol_2 = u.RNDminusOne (Nc);
    while (indCol_1 == indCol_2);

    // Ensure that the best solution is in the first colony 
    if (a [indCol_1 * Nm].f < a [indCol_2 * Nm].f)
    {
      int temp = indCol_1;
      indCol_1 = indCol_2;
      indCol_2 = temp;
    }

    // Copy the best solution to the worst colony
    ArrayCopy (a [indCol_2 * Nm + Nm - 1].cP, a [indCol_1 * Nm].cP, 0, 0, WHOLE_ARRAY);

    // Re-sort the colony after migration
    SortFromTo (a, aT, indCol_2 * Nm, Nm);
  }
}
//——————————————————————————————————————————————————————————————————————————————

          C_AO_CPAクラスのSortFromToメソッドは、f関数の値に基づいてエージェントの配列を並べ替えるように設計されています。詳しく見てみましょう。

          変数の初期化

          • このメソッドは、エージェントの配列(p)、一時的な配列(pTemp)、ソートの開始インデックス(from)、ソート対象となる要素数(count)の4つのパラメータを受け取ります。
          • 変数cnt、t0、t1は、それぞれ交換回数のカウントおよび一時的な値の保持に使用されます。
          • また、ind配列およびval配列は、それぞれf適応度関数のインデックスと値を格納するために作成されます。

          インデックスおよび値の配列の作成 ：最初の「for」ループでは、ind配列とval配列が次のようにして埋められます。

          • ind[i]、元の配列内のエージェントのインデックス（fromから開始）を取得
          • val[i]は、対応するエージェントのf関数の値を取得

          ソート処理：メインの「while」ループは、交換が発生する限り（すなわちcnt > 0の間）実行されます。内側の「for」ループでは、val配列を走査して隣接する要素を比較します。

          • 現在の値が次の値より小さい場合（val[i] < val[i + 1]）、ind配列およびval配列内の要素を入れ替える
          • 交換がおこなわれたことを示すためにcntカウンタをインクリメントする
          • この処理は、交換が一度も発生しない完全な反復がおこなわれるまで続けられる

          ソート済み値のコピー：

          • ソートが完了すると、最初の「for」ループで、ソート済みのエージェントを一時配列「pTemp」から元の配列「p」へ、fromインデックスから順にコピーする
          • 続く「for」ループで、元のp配列を更新し、ソート後の値で置き換える
          //——————————————————————————————————————————————————————————————————————————————
// Auxiliary function for sorting agents by the value of the objective function
void C_AO_CPA::SortFromTo (S_AO_Agent &p [], S_AO_Agent &pTemp [], int from, int count)
{
  int    cnt = 1;
  int    t0  = 0;
  double t1  = 0.0;
  int    ind [];
  double val [];
  ArrayResize (ind, count);
  ArrayResize (val, count);

  // Copy values for sorting
  for (int i = 0; i < count; i++)
  {
    ind [i] = i + from;
    val [i] = p [i + from].f;
  }

  // Bubble sort in descending order
  while (cnt > 0)
  {
    cnt = 0;
    for (int i = 0; i < count - 1; i++)
    {
      if (val [i] < val [i + 1])
      {
        // Exchange of indices
        t0 = ind [i + 1];
        ind [i + 1] = ind [i];
        ind [i] = t0;

        // Exchange values
        t1 = val [i + 1];
        val [i + 1] = val [i];
        val [i] = t1;

        cnt++;
      }
    }
  }

  // Apply the sorting results
  for (int i = 0;    i < count; i++)        pTemp [i] = p [ind [i]];
  for (int i = from; i < from + count; i++) p     [i] = pTemp  [i - from];
}
//——————————————————————————————————————————————————————————————————————————————

          アルゴリズムコードを記述して徹底的に分析したので、CPAアルゴリズムのテスト結果に進みます。


          テスト結果

          アルゴリズムの興味深く独自なロジックを実装している際には、ランキング表の上位に入らないなどとはまったく考えておらず、CPAアルゴリズムのテスト結果を詳細に確認した際には、やや失望を感じました。テスト結果によると、本アルゴリズムは達成可能な最大結果のうち34.76%にとどまりました。

          CPA|Cyclic Parthenogenesis Algorithm|50.0|10.0|0.2|0.9|0.3|0.9|
          =============================
          5 Hilly's; Func runs:10000; result:0.7166412833856777
          25 Hilly's; Func runs:10000; result:0.4001377868508138
          500 Hilly's; Func runs:10000; result:0.25502012607456315
          =============================
          5 Forest's; Func runs:10000; result:0.6217765628284961
          25 Forest's; Func runs:10000; result:0.3365148812759322
          500 Forest's; Func runs:10000; result:0.192638189788532
          =============================
          5 Megacity's; Func runs:10000; result:0.34307692307692306
          25 Megacity's; Func runs:10000; result:0.16769230769230772
          500 Megacity's; Func runs:10000; result:0.09455384615384692
          =============================
          All score:3.12805 (34.76%)

          この可視化は、探索空間内で仮想アブラムシが移動するという、アルゴリズム特有の挙動を示しています。特に高次元の問題においてはその特徴が顕著であり、個々のコロニーやその内部で移動する仮想生物の動きを、視覚的にも識別することができます。

          Hilly

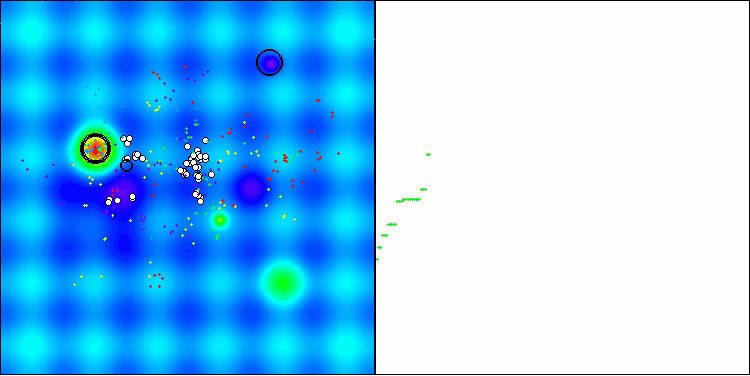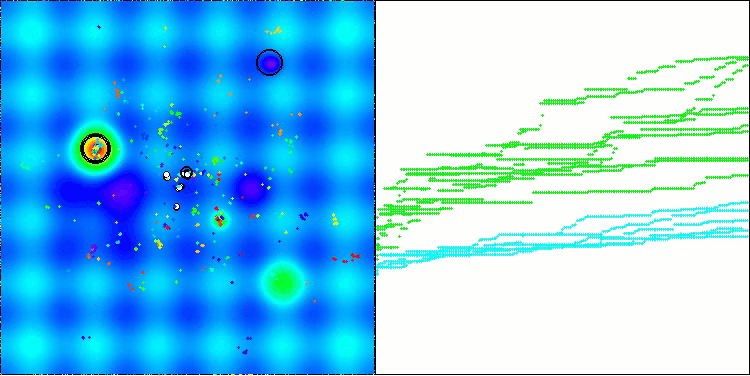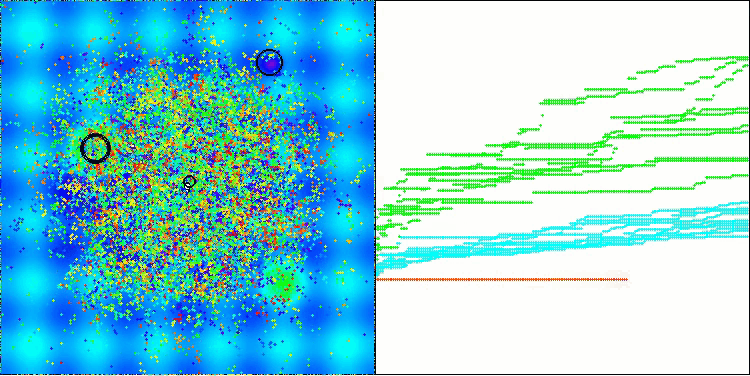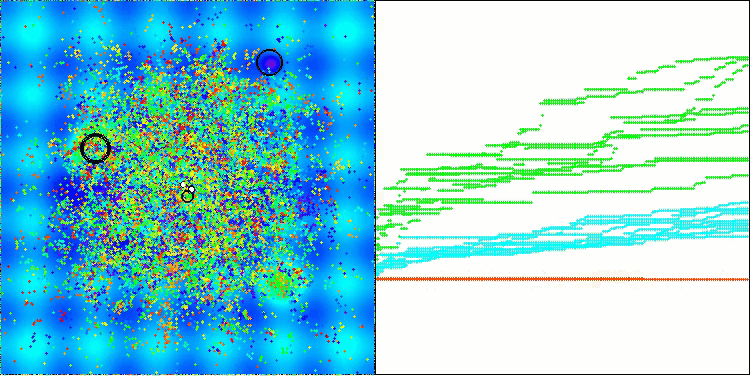
            Hillyテスト関数のCPA

          Forest

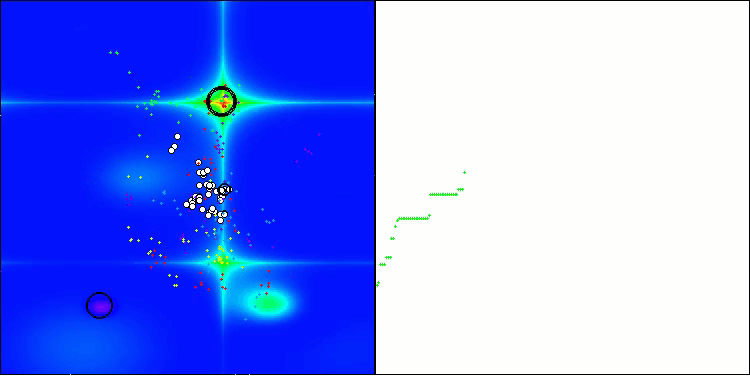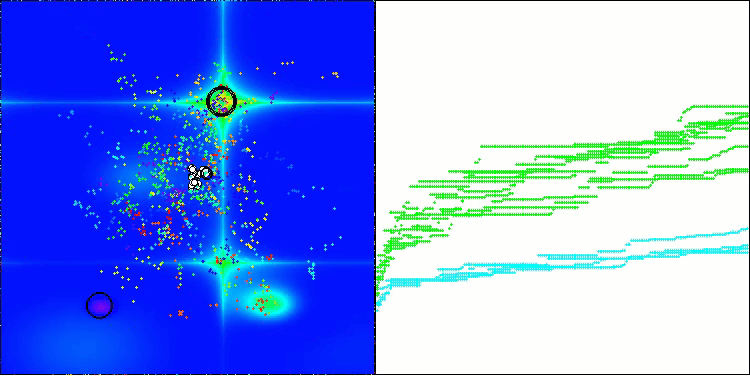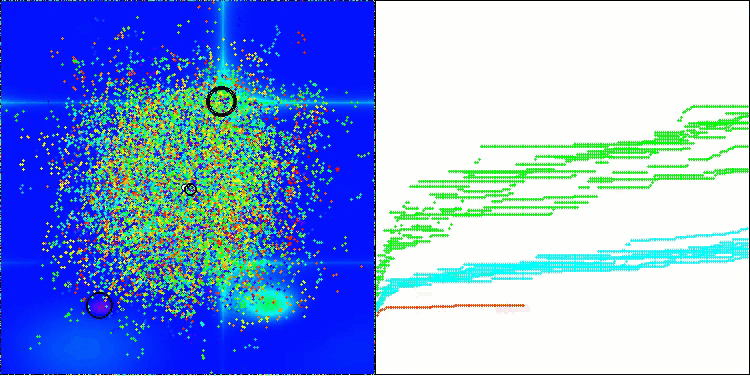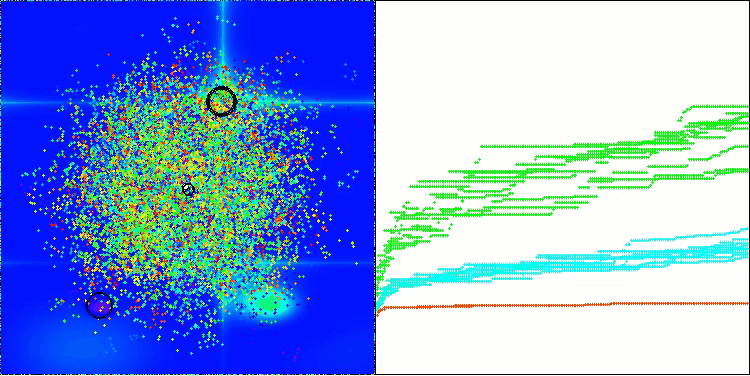
            Forestテスト関数のCPA

          Megacity

            Megacityテスト関数のCPA

          テストの結果、CPAアルゴリズムはランキング表で第44位に位置し、最優秀な集団最適化アルゴリズム45種類のグループに加わることができました。

          # AO 詳細 Hilly Hilly最終 Forest Forest最終 Megacity（離散） Megacity最終 最終結果 MAXの%
          10p(5F) 50p(25F) 1000p(500F) 10p(5F) 50p(25F) 1000p(500F) 10p(5F) 50p(25F) 1000p(500F)
          1 ANS across neighbourhood search 0.94948 0.84776 0.43857 2.23581 1.00000 0.92334 0.39988 2.32323 0.70923 0.63477 0.23091 1.57491 6.134 68.15
          2 CLA コードロックアルゴリズム(joo) 0.95345 0.87107 0.37590 2.20042 0.98942 0.91709 0.31642 2.22294 0.79692 0.69385 0.19303 1.68380 6.107 67.86
          3 AMOm 動物移動最適化m 0.90358 0.84317 0.46284 2.20959 0.99001 0.92436 0.46598 2.38034 0.56769 0.59132 0.23773 1.39675 5.987 66.52
          4 (P+O)ES (P+O)進化戦略 0.92256 0.88101 0.40021 2.20379 0.97750 0.87490 0.31945 2.17185 0.67385 0.62985 0.18634 1.49003 5.866 65.17
          5 CTA 彗星の尾アルゴリズム(joo) 0.95346 0.86319 0.27770 2.09435 0.99794 0.85740 0.33949 2.19484 0.88769 0.56431 0.10512 1.55712 5.846 64.96
          6 SDSm 確率的拡散探索M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
          7 AAm アーチェリーアルゴリズムM 0.91744 0.70876 0.42160 2.04780 0.92527 0.75802 0.35328 2.03657 0.67385 0.55200 0.23738 1.46323 5.548 61.64
          8 ESG 社会集団の進化(joo) 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
          9 SIA 等方的焼きなまし(joo) 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
          10 ACS 人工協調探索 0.75547 0.74744 0.30407 1.80698 1.00000 0.88861 0.22413 2.11274 0.69077 0.48185 0.13322 1.30583 5.226 58.06
          11 BHAm ブラックホールアルゴリズムM 0.75236 0.76675 0.34583 1.86493 0.93593 0.80152 0.27177 2.00923 0.65077 0.51646 0.15472 1.32195 5.196 57.73
          12 ASO 無政府社会最適化 0.84872 0.74646 0.31465 1.90983 0.96148 0.79150 0.23803 1.99101 0.57077 0.54062 0.16614 1.27752 5.178 57.54
          13 AOSm 原子軌道探索M 0.80232 0.70449 0.31021 1.81702 0.85660 0.69451 0.21996 1.77107 0.74615 0.52862 0.14358 1.41835 5.006 55.63
          14 TSEA 亀甲進化アルゴリズム(joo) 0.96798 0.64480 0.29672 1.90949 0.99449 0.61981 0.22708 1.84139 0.69077 0.42646 0.13598 1.25322 5.004 55.60
          15 DE 差分進化 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
          16 CRO 化学反応の最適化 0.94629 0.66112 0.29853 1.90593 0.87906 0.58422 0.21146 1.67473 0.75846 0.42646 0.12686 1.31178 4.892 54.36
          17 BSA 鳥群アルゴリズム 0.89306 0.64900 0.26250 1.80455 0.92420 0.71121 0.24939 1.88479 0.69385 0.32615 0.10012 1.12012 4.809 53.44
          18 HS ハーモニー検索 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
          19 SSG 苗木の播種と育成 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
          20 BCOm 細菌走化性最適化M 0.75953 0.62268 0.31483 1.69704 0.89378 0.61339 0.22542 1.73259 0.65385 0.42092 0.14435 1.21912 4.649 51.65
          21 ABO アフリカ水牛の最適化 0.83337 0.62247 0.29964 1.75548 0.92170 0.58618 0.19723 1.70511 0.61000 0.43154 0.13225 1.17378 4.634 51.49
          22 (PO)ES (PO)進化戦略 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
          23 TSm タブーサーチM 0.87795 0.61431 0.29104 1.78330 0.92885 0.51844 0.19054 1.63783 0.61077 0.38215 0.12157 1.11449 4.536 50.40
          24 BSO ブレインストーム最適化 0.93736 0.57616 0.29688 1.81041 0.93131 0.55866 0.23537 1.72534 0.55231 0.29077 0.11914 0.96222 4.498 49.98
          25 WOAm 鯨最適化アルゴリズムM 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
          26 AEFA 人工電界アルゴリズム 0.87700 0.61753 0.25235 1.74688 0.92729 0.72698 0.18064 1.83490 0.66615 0.11631 0.09508 0.87754 4.459 49.55
          27 AEO 人工生態系ベースの最適化アルゴリズム 0.91380 0.46713 0.26470 1.64563 0.90223 0.43705 0.21400 1.55327 0.66154 0.30800 0.28563 1.25517 4.454 49.49
          28 ACOm 蟻コロニー最適化M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
          29 BFO-GA 細菌採食の最適化：Ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
          30 SOA シンプル最適化アルゴリズム 0.91520 0.46976 0.27089 1.65585 0.89675 0.37401 0.16984 1.44060 0.69538 0.28031 0.10852 1.08422 4.181 46.45
          31 ABHA 人工蜂の巣アルゴリズム 0.84131 0.54227 0.26304 1.64663 0.87858 0.47779 0.17181 1.52818 0.50923 0.33877 0.10397 0.95197 4.127 45.85
          32 ACMO 大気雲モデルの最適化 0.90321 0.48546 0.30403 1.69270 0.80268 0.37857 0.19178 1.37303 0.62308 0.24400 0.10795 0.97503 4.041 44.90
          33 ADAMm 適応モーメント推定M 0.88635 0.44766 0.26613 1.60014 0.84497 0.38493 0.16889 1.39880 0.66154 0.27046 0.10594 1.03794 4.037 44.85
          34 ATAm 人工部族アルゴリズムM 0.71771 0.55304 0.25235 1.52310 0.82491 0.55904 0.20473 1.58867 0.44000 0.18615 0.09411 0.72026 3.832 42.58
          35 ASHA 人工シャワーアルゴリズム 0.89686 0.40433 0.25617 1.55737 0.80360 0.35526 0.19160 1.35046 0.47692 0.18123 0.09774 0.75589 3.664 40.71
          36 ASBO 適応型社会行動最適化(ASBO) 0.76331 0.49253 0.32619 1.58202 0.79546 0.40035 0.26097 1.45677 0.26462 0.17169 0.18200 0.61831 3.657 40.63
          37 MEC mind evolutionary computation 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
          38 IWO 侵入雑草最適化 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
          39 Micro-AIS 微小人工免疫系 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54
          40 COAm カッコウ最適化アルゴリズムM 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21
          41 SDOm 螺旋ダイナミクス最適化M 0.74601 0.44623 0.29687 1.48912 0.70204 0.34678 0.10944 1.15826 0.42833 0.16767 0.03663 0.63263 3.280 36.44
          42 NMm ネルダー=ミード法M 0.73807 0.50598 0.31342 1.55747 0.63674 0.28302 0.08221 1.00197 0.44667 0.18667 0.04028 0.67362 3.233 35.92
          43 BBBC ビッグバンビッグクランチアルゴリズム 0.60531 0.45250 0.31255 1.37036 0.52323 0.35426 0.20417 1.08166 0.39769 0.19431 0.11286 0.70486 3.157 35.08
          44 CPA 循環単為生殖アルゴリズム 0.71664 0.40014 0.25502 1.37180 0.62178 0.33651 0.19264 1.15093 0.34308 0.16769 0.09455 0.60532 3.128 34.76
          45 FAm ホタルアルゴリズムM 0.58634 0.47228 0.32276 1.38138 0.68467 0.37439 0.10908 1.16814 0.28667 0.16467 0.04722 0.49855 3.048 33.87
          RW ランダムウォーク 0.48754 0.32159 0.25781 1.06694 0.37554 0.21944 0.15877 0.75375 0.27969 0.14917 0.09847 0.52734 2.348 26.09




          まとめ

          CPAアルゴリズムの実装とテストに取り組んだことで、いくつか興味深い観察と結論が得られました。本アルゴリズムはアブラムシの行動に基づく集団ベースの最適化手法であり、アイデア自体は有望に思えるものの、テスト結果は他の集団ベースのアルゴリズムと比べて相対的に性能が低いことを示しています。

          本アルゴリズムの主な考え方は、配偶あり/なしの2種類の再生様式を用いることと、移住（コロニー間の移動）を許容したコロニー分割によって集団を構成することです。生物学的な比喩は洗練されており、アブラムシが実際に単為生殖と有性生殖の両方を用いて環境に適応する点をうまく取り入れています。しかしながら、これらの概念を数学的に実装した結果は、期待したほど効果的ではありませんでした。

          アルゴリズムの弱点は複数の側面で現れます。まず、個体を雌雄に分けることは、多様性や解の質の向上には十分でないことがわかりました。次に、探索空間の異なる領域を探索しやすくする目的で導入したコロニー分割は、実際には局所最適解への早期収束を招くことがしばしばありました。その抑制を意図したコロニー間飛行（移住）メカニズムの効率も低いことが確認されました。

          パラメータ調整も容易ではありません。コロニーサイズ(Nm)、雌の比率(Fr)、飛行確率(Pf)、スケーリング係数（alpha1、alpha2）といったパラメータはアルゴリズム性能に大きな影響を与え、最適値を見つけるのは困難です。適応的パラメータ導入による改善試みは一部の改善をもたらしましたが、効率を大幅に高めるには至りませんでした。これらの結果は、問題がより根本的でアルゴリズム構造自体に起因している可能性を示唆します。

          とはいえ、本アルゴリズムに取り組んだことは有益でした。第一に、生物由来アルゴリズムを解析・実装するうえで多くの実践的な経験が得られました。第二に、デバッグや最適化の過程を通じて、メタヒューリスティック手法における探索と活用のバランスの重要性を深く理解する助けになりました。第三に、美しい生物学的アナロジーが必ずしも効果的な最適化手法に直結しない良い例を示しました。 

          結論として、たとえ成功度の低いアルゴリズムであっても、新しい発想や手法を提示することでメタヒューリスティック最適化の分野発展に寄与します。制約はあるものの、CPAは異なる解探索戦略のバランスに関する興味深いアプローチを示しており、今後の研究の出発点として有望であると言えます。

          Tab

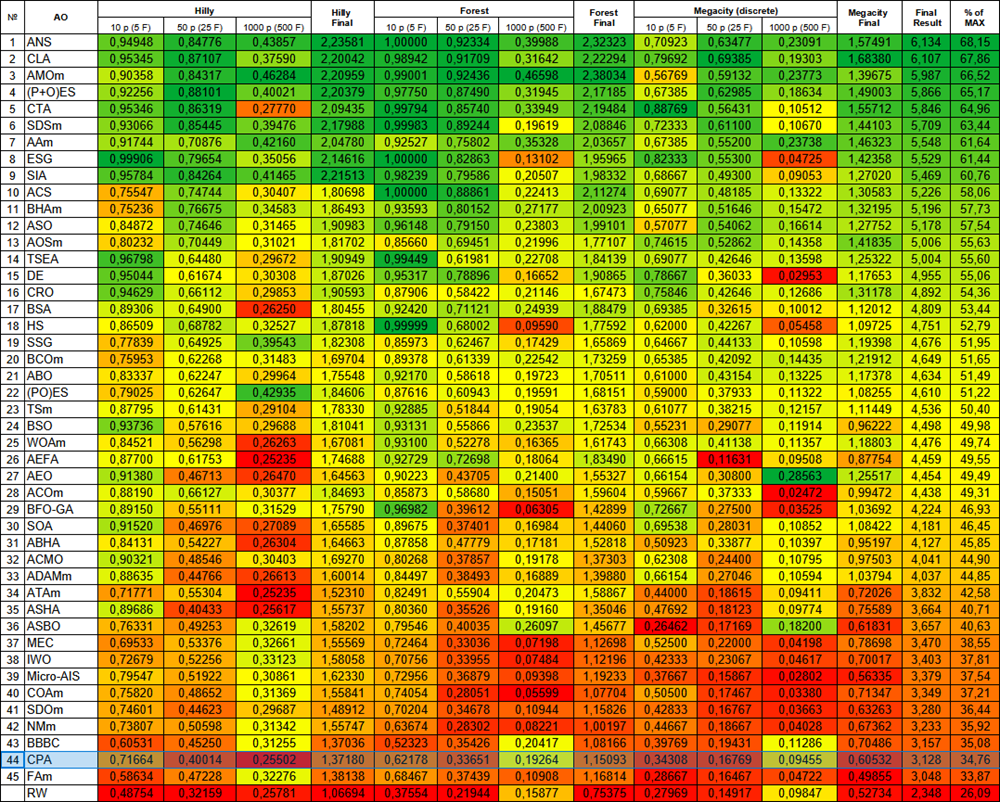
          図3：対応するテストに応じたアルゴリズムのカラーグラデーション

          チャート

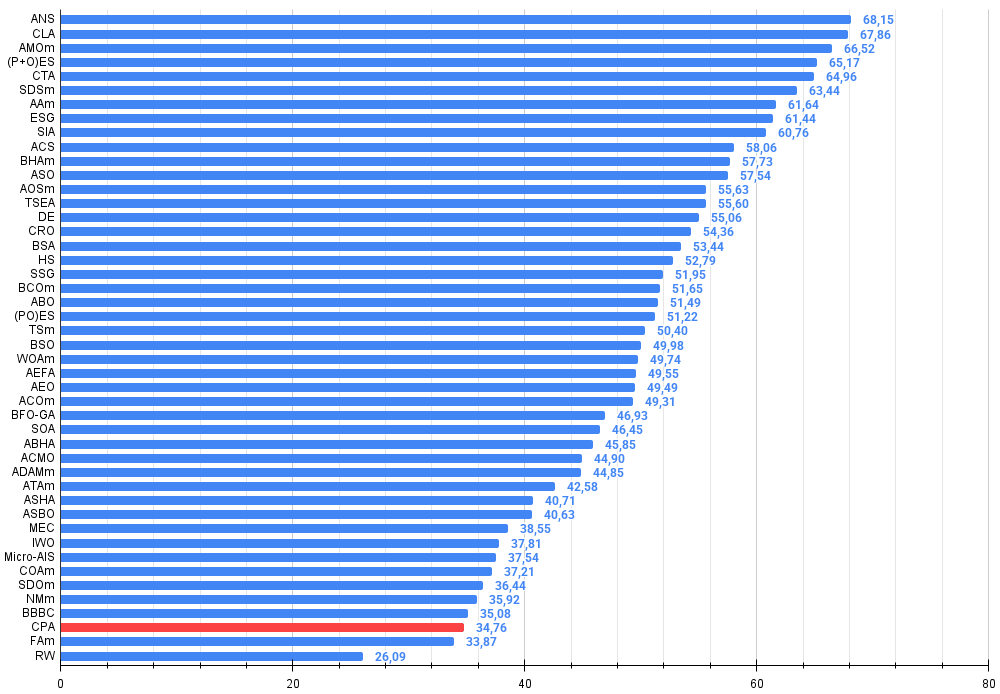
          図4：アルゴリズムテスト結果のヒストグラム（0から100のスケール、高いほど良い）100は理論上の最大値であり、アーカイブには評価表を計算するためのスクリプトがあります。

          CPAの長所と短所

          長所

          1. 興味深いアイディア
          2. 実装が非常にシンプル
          3. 大規模な問題に適している

          短所

          1. 外部パラメータが多い
          2. 速度と収束精度が低い。

          この記事には、最新版のアルゴリズムコードを含むアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。

          記事で使用されているプログラム

          # 名前 種類 詳細
          1 #C_AO.mqh
          		 インクルード
          		 集団最適化アルゴリズムの親クラス
          2 #C_AO_enum.mqh
          		 インクルード
          		 集団最適化アルゴリズムの列挙
          3 TestFunctions.mqh
          		 インクルード
          		 テスト関数のライブラリ
          4
          		 TestStandFunctions.mqh
          		 インクルード
          		 テストスタンド関数ライブラリ
          5
          		 Utilities.mqh
          		 インクルード
          		 補助関数のライブラリ
          6
          		 CalculationTestResults.mqh
          		 インクルード
          		 比較表の結果を計算するスクリプト
          7
          		 Testing AOs.mq5
          		 スクリプト すべての集団最適化アルゴリズムの統一テストスタンド
          8
          		 Simple use of population optimization algorithms.mq5
          		 スクリプト
          		 可視化せずに集団最適化アルゴリズムを使用する簡単な例
          9
          		 Test_AO_CPA.mq5
          		 スクリプト CPAテストスタンド

          MetaQuotes Ltdによってロシア語から翻訳されました。
          元の記事: https://www.mql5.com/ru/articles/16877

          添付されたファイル |
          ZIPをダウンロード
          CPA.zip (153.67 KB)

          警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

          この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。

          この著者による他の記事

          ディスカッションに移動
          MetaTrader 5での取引の視覚的な評価と調整 MetaTrader 5での取引の視覚的な評価と調整
          ストラテジーテスターは、単に自動売買ロボットのパラメータを最適化するだけでなく、さらに幅広い活用が可能です。本記事では、口座の取引履歴を事後に評価し、ストラテジーテスター上でポジションのストップロスを変更することで取引の調整をおこなう方法を紹介します。
          初級から中級まで：テンプレートとtypename(III) 初級から中級まで：テンプレートとtypename(III)
          本記事では、トピックの第一部について解説します。この内容は初心者にとって理解がやや難しい部分があります。さらなる混乱を避けて正しく理解していただくために、説明を段階的に分けて進めます。本記事ではその第一段階に焦点を当てます。ただし、記事の最後では行き詰まりに見えるかもしれませんが、実際には次の記事でより理解しやすくなる状況への一歩を踏み出す形になります。
          Pythonの価格変動離散化手法 Pythonの価格変動離散化手法
          Python + MQL5を使用した価格離散化手法を見ていきます。本記事では、バー生成に関する幅広い手法を実装したPythonライブラリの開発経験についご紹介します。クラシックなボリュームバーやレンジバーから、よりエキゾチックな練行足やカギ足といった手法までを網羅します。スリーラインブレイクローソク足やレンジバーの統計分析をおこないながら、価格を離散的に表現する新たな方法を探っていきます。
          アルゴリズム取引におけるニューロシンボリックシステム：シンボリックルールとニューラルネットワークを組み合わせる アルゴリズム取引におけるニューロシンボリックシステム：シンボリックルールとニューラルネットワークを組み合わせる
          本記事では、古典的なテクニカル分析とニューラルネットワークを組み合わせたハイブリッド型取引システムの開発経験について解説します。システムのアーキテクチャを、基本的なパターン分析やニューラルネットワーク構造から、実際の売買判断に至るメカニズムまで詳細に分析し、実際のコードや実務的な知見も共有します。