
Time Evolution Travel Algorithm (TETA)
Inhalt
Einführung
Wir haben uns viele Algorithmen angesehen, die auf physikalischen Gesetzen beruhen, wie CSS, EM, GSA, AEFA, AOSm, aber das Universum erfreut uns ständig mit neuen Phänomenen und erfüllt uns mit verschiedenen Hypothesen und Ideen. Eine der grundlegenden Komponenten des Universums, wie die Zeit, brachte mich auf die Idee, einen neuen Optimierungsalgorithmus zu entwickeln. Die Zeit inspiriert nicht nur zu neuen Entdeckungen, sondern bleibt auch ein geheimnisvolles Gebilde, das schwer zu begreifen ist. Sie fließt wie ein Fluss, der Momente unseres Lebens mit sich reißt und nur Erinnerungen zurücklässt. Zeitreisen waren schon immer ein Thema der menschlichen Faszination und Fantasie. Um die Idee des Algorithmus besser zu verstehen, sollten wir uns die Geschichte eines Wissenschaftlers vorstellen.
Es lebte einmal ein Physiker, der von der Idee besessen war, in eine strahlende Zukunft zu gehen, weg von den Fehlern, die er gemacht hatte. Nachdem er sich mit dem Studium der Zeitströme befasst hatte, musste er eine bittere Entdeckung machen: Reisen in die Zukunft sind unmöglich. Unbeirrt ging er dazu über, die Fähigkeit zu erforschen, in die Vergangenheit zu reisen, in der Hoffnung, seine Fehler zu korrigieren, aber auch hier wurde er enttäuscht.
Seine Untersuchung hypothetischer Zeitabläufe führte ihn jedoch zu einer verblüffenden Entdeckung: der Existenz von Paralleluniversen. Nachdem er ein theoretisches Modell einer Maschine entwickelt hatte, mit der man sich zwischen den Welten bewegen kann, entdeckte er etwas Erstaunliches: Obwohl direkte Zeitreisen unmöglich sind, ist es möglich, eine Abfolge von Ereignissen zu wählen, die zu dem einen oder anderen Paralleluniversum führt.
Jede Handlung eines Menschen ließ eine neue parallele Realität entstehen, aber der Wissenschaftler interessierte sich nur für die Universen, die sein Leben direkt beeinflussten. Um zwischen ihnen zu navigieren, hat er im Gleichungssystem besondere Ankerpunkte gesetzt (um zwischen den Welten zu unterscheiden) – Schlüsselpunkte seines Schicksals: Familie, Karriere, wissenschaftliche Entdeckungen, Freundschaften und bedeutende Ereignisse. Diese Anker wurden zu Variablen in seiner Maschine, die es ihm ermöglichten, den optimalen Weg zwischen probabilistischen Welten zu wählen.
Nachdem er seine Erfindung auf den Markt gebracht hatte, begann er eine Reise durch parallele Welten, wollte aber nicht mehr in eine vorgefertigte, strahlende Zukunft gelangen. Er erkannte etwas viel Wichtigeres: die Fähigkeit, diese Zukunft mit seinen eigenen Händen zu gestalten, indem er Entscheidungen in der Gegenwart traf. Jede neue Entscheidung ebnete den Weg zu der Version der Realität, die er selbst zum Leben erwecken wollte. So war er nicht länger Gefangener des Traums von einer idealen Zukunft, sondern wurde zu ihrem Architekten. Seine Maschine wurde nicht zu einem Mittel, um der Realität zu entfliehen, sondern zu einem Werkzeug, mit dem er sein eigenes Schicksal bewusst gestalten konnte, indem er zu jedem Zeitpunkt die optimalen Lösungen wählte.
In diesem Artikel betrachten wir den Time Evolution Travel Algorithm (TETA), der das Konzept der Zeitreise umsetzt und sich dadurch auszeichnet, dass er keine Parameter oder veränderbaren Variablen hat. Dieser Algorithmus hält natürlich ein Gleichgewicht zwischen der Suche nach der besten Lösung und deren Verfeinerung aufrecht. Typischerweise haben Algorithmen, die keine externen Parameter haben, dennoch interne Parameter in Form von Konstanten, die ihre Leistung beeinflussen. TETA verfügt jedoch auch nicht über solche Konstanten, was es in seiner Art einzigartig macht.
Implementierung des Algorithmus
In der vorgestellten Geschichte entdeckte ein Wissenschaftler eine Möglichkeit, zwischen Paralleluniversen zu reisen, indem er Schlüsselvariablen in seinem Leben veränderte. Diese Metapher bildet die Grundlage für den vorgeschlagenen Optimierungsalgorithmus. Um dies zu verdeutlichen, sehen Sie sich die folgende Abbildung an, die die Idee des Algorithmus von Paralleluniversen veranschaulicht, die bei jeder Entscheidung entstehen. Jedes Universum, das einen vollständigen Raum hat, wird durch das Vorhandensein von Merkmalen in Form von Ankern definiert: Familie, Karriere, Leistungen usw.
Durch die Kombination der Eigenschaften dieser Anker kann ein neues Universum geschaffen werden, das die Lösung eines Optimierungsproblems darstellt, bei dem die Anker die zu optimierenden Parameter sind.
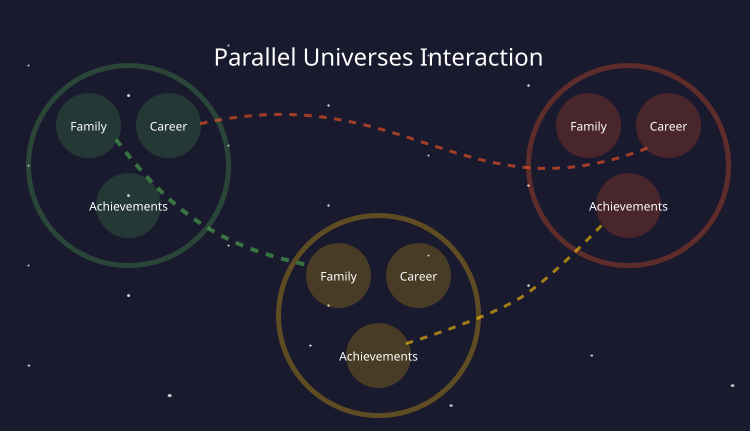
Abbildung 1. Parallele Universen mit ihren eigenen einzigartigen Ankern (Merkmalen)
Der TETA-Algorithmus basiert auf dem Konzept mehrerer paralleler Universen, von denen jedes eine mögliche Lösung für ein Optimierungsproblem darstellt. In seiner technischen Ausgestaltung wird jedes dieser Universen durch einen Koordinatenvektor (a[i].c) beschrieben, wobei jede Koordinate ein Anker ist – eine Schlüsselvariable, die die Konfiguration einer bestimmten Realität bestimmt. Diese Anker können als die wichtigsten Parameter betrachtet werden, deren Einstellungen die Gesamtqualität der Lösung beeinflussen.
Um die Qualität jedes Universums zu bewerten, wird eine Fitnessfunktion (a[i].f) verwendet, die den „Komfort des Daseins“ in einer bestimmten Realität bestimmt. Je höher der Wert dieser Funktion ist, desto günstiger wird das Universum eingeschätzt. Jedes Universum speichert nicht nur Informationen über seinen aktuellen Zustand, sondern auch über die beste bekannte Konfiguration (a[i].cB), die mit einem „Gedächtnis“ für das erfolgreichste Szenario verglichen werden kann. Darüber hinaus behält der Algorithmus einen globalen besten Zustand (cB) bei, der die günstigste Konfiguration unter allen entdeckten Optionen darstellt.
Eine Population von N Individuen bildet eine Reihe von Paralleluniversen, von denen jedes durch seinen eigenen Satz von Ankerwerten beschrieben wird. Diese Universen werden ständig nach dem Wert der Fitnessfunktion geordnet, wodurch eine Art Hierarchie vom ungünstigsten zum günstigsten Zustand entsteht. Jeder Anker der Realität ist eine optimierbare Variable, und jede Veränderung dieser Variablen erzeugt eine neue Konfiguration des Universums. Der vollständige Satz von Ankern bildet einen Vektor von Variablen x = (x₁, x₂, ..., xₙ), der eine bestimmte Realität vollständig beschreibt. Außerdem werden für jede Variable die Grenzen akzeptabler Werte definiert, die als physikalische Gesetze interpretiert werden können, die die möglichen Veränderungen in jedem Universum begrenzen.
Die Bewertung der Beliebtheit jedes Universums erfolgt durch die Fitnessfunktion f(x), die die Konfiguration des Universums auf eine reelle Zahl abbildet. Je höher dieser Wert ist, desto mehr wird eine bestimmte Realität als vorteilhaft angesehen. Auf diese Weise wird ein mathematisch strenger Mechanismus geschaffen, um verschiedene mögliche Entwicklungen in mehreren Paralleluniversen zu bewerten und zu vergleichen.
Das Hauptmerkmal des Algorithmus ist ein einziges Wahrscheinlichkeitsverhältnis (rnd *= rnd), das sowohl die Wahrscheinlichkeit der Auswahl eines Universums für die Interaktion als auch die Stärke der Veränderung der Anker bestimmt. Dadurch entsteht ein natürlicher Selbstausgleichsmechanismus für das System: Die besten Universen haben eine höhere Chance, ausgewählt zu werden, aber ihre Anker ändern sich weniger (proportional zu rnd), während die schlechtesten Universen, obwohl sie seltener ausgewählt werden, stärkeren Änderungen unterliegen (proportional zu 1,0 – rnd).
Dieser Ansatz spiegelt den tiefen philosophischen Gedanken wider, dass es unmöglich ist, in allen Bereichen gleichzeitig Perfektion zu erreichen. Die Verbesserung erfolgt durch ein ständiges Abwägen der verschiedenen Aspekte: Manchmal können sich die besten Anker im Interesse des Gesamtgleichgewichts etwas verschlechtern, während die schlechtesten nach Verbesserungen streben. Die Stärke der Veränderung ist proportional dazu, wie „gut“ das Universum ist, was das wirkliche Leben widerspiegelt, in dem dramatische Veränderungen wahrscheinlicher sind, wenn etwas schief läuft.
Infolgedessen optimiert der Algorithmus nicht einfach nur Werte, sondern simuliert den Prozess der Gleichgewichtsfindung in einem komplexen multidimensionalen System von Lebensumständen und strebt nicht nach einem Ideal, sondern nach der harmonischsten Version der Realität durch ein subtiles Gleichgewicht aller ihrer Aspekte.
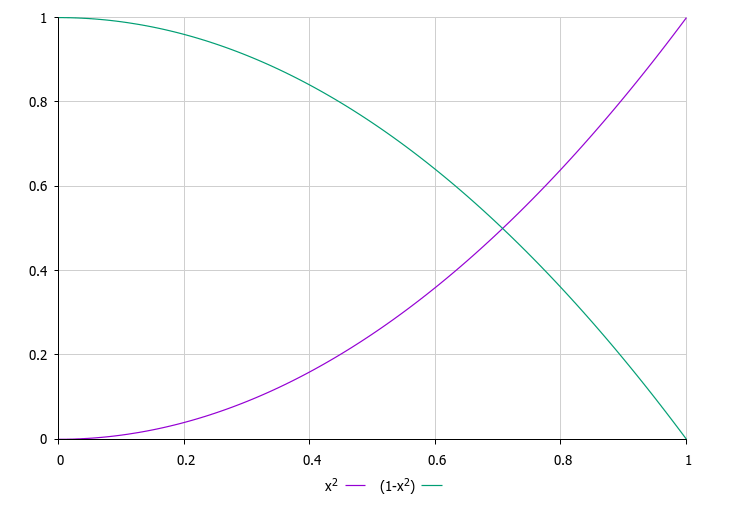
Abbildung 2. Die rote Linie ist die Wahrscheinlichkeitsfunktion für die Auswahl von Universen in Abhängigkeit von ihrer Qualität, die grüne Linie ist der Grad der Veränderung der Anker für die entsprechenden Universen
Pseudocode des Algorithmus:
1. Schaffen einer Population von N Paralleluniversen
2. Für jedes Universum:
- Zufällige Initialisierung der Ankerwerte (Koordinaten) innerhalb akzeptabler Grenzen
- Setzen der besten Anfangswerte gleich den aktuellen Werten
Hauptschleife:
1. Sortierung der Universen nach Qualität (Fitnessfunktionen)
- Die besten Universen erhalten niedrigere Indizes
- Schlechteste Universen erhalten höhere Indizes
2. Für jedes Universum i von N:
Für jeden Anker (Koordinate):
a) Wähle ein Universum für die Interaktion aus:
- Erzeuge eine Zufallszahl rnd von 0 bis 1
- Quadratisches rnd, um die Priorität der besten Universen zu erhöhen
- Wähle den Index von „pair“ proportional zu rnd
b) Wenn das aktuelle Universum nicht mit dem ausgewählten Universum übereinstimmt (i ≠ Paar):
Wenn das aktuelle Universum besser ist als das ausgewählte (i < Paar):
- Eine leichte Veränderung des Ankers ist proportional zu rnd
- New_value = current + rnd * (selected_value – current)
Andernfalls (das aktuelle Universum ist schlechter als das ausgewählte):
If (random_number > rnd):
- Starke Veränderung des Ankers proportional zu (1 – rnd)
- New_value = current + (1-rnd) * (selected_value – current)
Andernfalls:
- Vollständiges Kopieren des Ankerwertes aus dem besten Universum
- New_value = selected_value
c) Ansonsten (Interaktion mit sich selbst):
- Lokale Suche mit Gaußscher Verteilung
- New_value = GaussDistribution(current_best)
d) Korrektur des neuen Ankerwertes innerhalb akzeptabler Grenzen
3. Aktualisierung der besten Werte:
Für jedes Universum:
- Wenn die aktuelle Lösung besser ist als die persönliche Bestleistung, aktualisiere die persönliche Bestleistung
- Wenn die aktuelle Lösung besser ist als die global beste, aktualisiere die global beste
4. Wiederhole die Hauptschleife, bis das Abbruchkriterium erfüllt ist.
Jetzt haben wir alles vorbereitet, um die Paralleluniversums-Reisemaschine in Code umzusetzen. Schreiben wir die Klasse C_AO_TETA, die von der Klasse C_AO abgeleitet werden soll. Hier ist eine kurze Beschreibung:
- Konstruktor – initialisiert den Namen, die Beschreibung und den Link zum Algorithmus und legt die Populationsgröße fest
- SetParams-Parameter – setzt Parameter mit Werten aus dem Array „params“.
- Die Methoden Init, Moving und Revision sind deklariert, werden aber in einem anderen Teil des Codes implementiert.
class C_AO_TETA : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_TETA () { } C_AO_TETA () { ao_name = "TETA"; ao_desc = "Time Evolution Travel Algorithm"; ao_link = "https://www.mql5.com/en/articles/16963"; popSize = 50; // number of parallel universes in the population ArrayResize (params, 1); params [0].name = "popSize"; params [0].val = popSize; } void SetParams () { popSize = (int)params [0].val; } bool Init (const double &rangeMinP [], // minimum values for anchors const double &rangeMaxP [], // maximum values for anchors const double &rangeStepP [], // anchor change step const int epochsP = 0); // number of search epochs void Moving (); void Revision (); private: //------------------------------------------------------------------- }; //——————————————————————————————————————————————————————————————————————————————
Die Initialisierung der Init-Methode der Klasse C_AO_TETA führt die Ersteinrichtung des Algorithmus durch.
Parameter der Methode:- rangeMinP – Array der Mindestwerte der Anker.
- rangeMaxP – Array der Höchstwerte der Anker.
- rangeStepP – Array der Ankerwechselschritte.
- epochsP – Anzahl der Suchepochen (Standardwert 0).
- Die Methode ruft StandardInit auf, führt die Prüfung durch und setzt die Bereiche für die Anker. Wenn die Initialisierung fehlschlägt, wird „false“ zurückgegeben.
- Wenn alle Überprüfungen und Einstellungen erfolgreich sind, gibt die Methode „true“ zurück und zeigt damit die erfolgreiche Initialisierung des Algorithmus an.
//—————————————————————————————————————————————————————————————————————————————— // TETA - Time Evolution Travel Algorithm // An optimization algorithm based on the concept of moving between parallel universes // through changing the key anchors (events) of life //—————————————————————————————————————————————————————————————————————————————— bool C_AO_TETA::Init (const double &rangeMinP [], // minimum values for anchors const double &rangeMaxP [], // maximum values for anchors const double &rangeStepP [], // anchor change step const int epochsP = 0) // number of search epochs { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- return true; } //——————————————————————————————————————————————————————————————————————————————
Die Methode Moving der Klasse C_AO_TETA ist dafür zuständig, Anker in Paralleluniversen zu ändern, um neue innerhalb des Algorithmus zu schaffen.
Überprüfung des Revisionsstands:- Wenn „revision“ „false“ ist, initialisiert die Methode die anfänglichen Ankerwerte für alle Paralleluniversen mit Zufallswerten aus dem angegebenen Bereich und wendet Funktionen an, um sie auf gültige Werte zu bringen (basierend auf dem Schritt).
- Wurde die Revision bereits durchgeführt, erfolgt eine Iteration über alle Paralleluniversen hinweg. Für jeden Anker wird eine Wahrscheinlichkeit erzeugt und sein neuer Wert berechnet:
- Wenn das aktuelle Universum positiver ist, dann wird der Anker leicht in eine positive Richtung korrigiert, um ein besseres Gleichgewicht zu finden.
- Wenn die aktuelle Grundgesamtheit ungünstiger ist, kann ein Wahrscheinlichkeitstest zu einer signifikanten Änderung des Ankers oder zu einer vollständigen Übernahme des Ankers aus der günstigeren Grundgesamtheit führen.
- Wenn die Universen übereinstimmen, erfolgt eine lokale Ankeranpassung unter Verwendung einer Gaußschen Verteilung.
- Nach der Berechnung des neuen Wertes wird der Anker in den zulässigen Bereich gebracht.
Diese Methode ist in der Praxis für die Anpassung und Verbesserung von Lösungen (Paralleluniversen) verantwortlich, was ein wesentlicher Bestandteil des Optimierungsalgorithmus ist.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_TETA::Moving () { //---------------------------------------------------------------------------- if (!revision) { // Initialize the initial values of anchors in all parallel universes for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- double rnd = 0.0; double val = 0.0; int pair = 0.0; for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { // Generate a probability that determines the chance of choosing a universe, // as well as the anchor change force rnd = u.RNDprobab (); rnd *= rnd; // Selecting a universe for sharing experience pair = (int)u.Scale (rnd, 0.0, 1.0, 0, popSize - 1); if (i != pair) { if (i < pair) { // If the current universe is more favorable: // Slightly change the anchor (proportional to rnd) to find a better balance val = a [i].c [c] + (rnd)*(a [pair].cB [c] - a [i].cB [c]); } else { if (u.RNDprobab () > rnd) { // If the current universe is less favorable: // Significant change of anchor (proportional to 1.0 - rnd) val = a [i].cB [c] + (1.0 - rnd) * (a [pair].cB [c] - a [i].cB [c]); } else { // Full acceptance of the anchor configuration from a more successful universe val = a [pair].cB [c]; } } } else { // Local anchor adjustment via Gaussian distribution val = u.GaussDistribution (cB [c], rangeMin [c], rangeMax [c], 1); } a [i].c [c] = u.SeInDiSp (val, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Die Methode Revision der Klasse C_AO_TETA ist für die Aktualisierung der Ankerkonfigurationen in Paralleluniversen und die Sortierung dieser Universen nach ihrer Qualität zuständig. Weitere Einzelheiten:
- Die Methode durchläuft alle Paralleluniversen (von 0 bis popSize).
- Wenn der Wert der Funktion f des aktuellen Universums (a[i].f) größer ist als der globale Bestwert fB, dann:
- fB wird durch den Wert von (a[i].f) aktualisiert.
- Die Ankerkonfiguration des aktuellen Universums wird in die globale cB-Konfiguration kopiert.
- Wenn der Wert der Funktion f des aktuellen Universums größer ist als ihr bester bekannter Wert (a[i].fB), dann:
- (a[i].fB) wird durch den Wert von (a[i].f) aktualisiert.
- Die Ankerkonfiguration des aktuellen Universums wird in seine beste bekannte Konfiguration (a[i].cB) kopiert.
- Das statische Array aT wird zum Speichern von Bearbeitern deklariert.
- Die Arraygröße wird in popSize geändert.
- Die Universen werden mit Hilfe der Funktion u.Sorting_fB nach ihren besten bekannten individuellen Eigenschaften sortiert.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_TETA::Revision () { for (int i = 0; i < popSize; i++) { // Update globally best anchor configuration if (a [i].f > fB) { fB = a [i].f; ArrayCopy (cB, a [i].c); } // Update the best known anchor configuration for each universe if (a [i].f > a [i].fB) { a [i].fB = a [i].f; ArrayCopy (a [i].cB, a [i].c); } } // Sort universes by their degree of favorability static S_AO_Agent aT []; ArrayResize (aT, popSize); u.Sorting_fB (a, aT, popSize); } //——————————————————————————————————————————————————————————————————————————————
Testergebnisse
TETA-Ergebnisse:
TETA|Time Evolution Travel Algorithm|50.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.9136198796338938
25 Hilly's; Func runs: 10000; result: 0.8234856192574587
500 Hilly's; Func runs: 10000; result: 0.3199003852163246
=============================
5 Forest's; Func runs: 10000; result: 0.970957820488216
25 Forest's; Func runs: 10000; result: 0.8953189778250419
500 Forest's; Func runs: 10000; result: 0.29324457646900925
=============================
5 Megacity's; Func runs: 10000; result: 0.7346153846153844
25 Megacity's; Func runs: 10000; result: 0.6856923076923078
500 Megacity's; Func runs: 10000; result: 0.16020769230769372
=============================
All score: 5.79704 (64.41%)
Final result: 5.79704 (64.41%). In Anbetracht der Komplexität der Testfunktionen ist dies ein hervorragendes Ergebnis. Der Algorithmus erkennt sehr schnell wichtige Bereiche der Oberfläche mit vielversprechenden Optima und beginnt sofort mit deren Verfeinerung, was in jeder Visualisierung der Algorithmusoperation zu sehen ist.
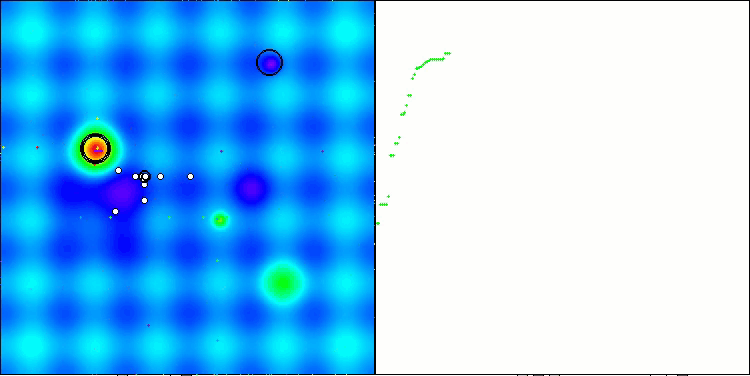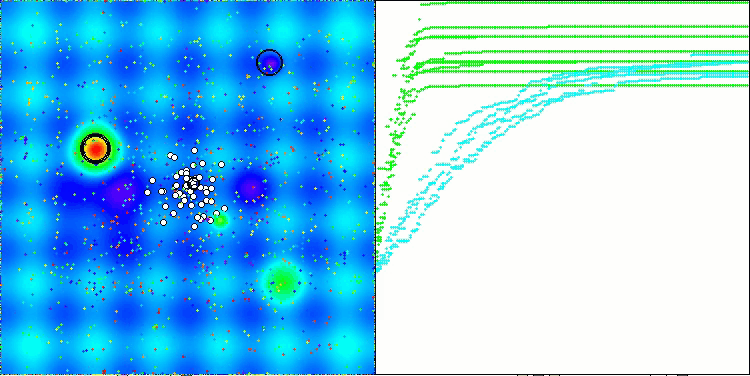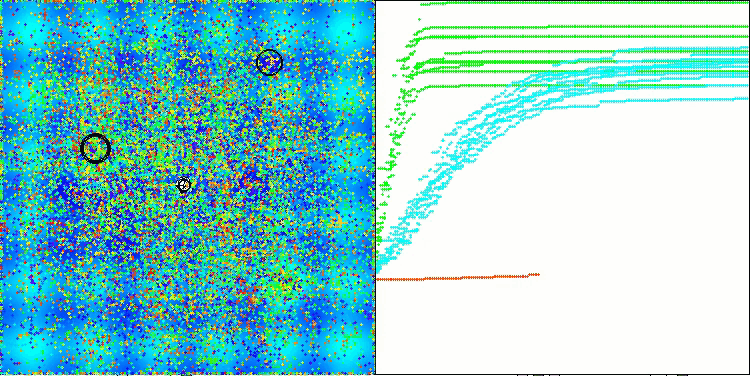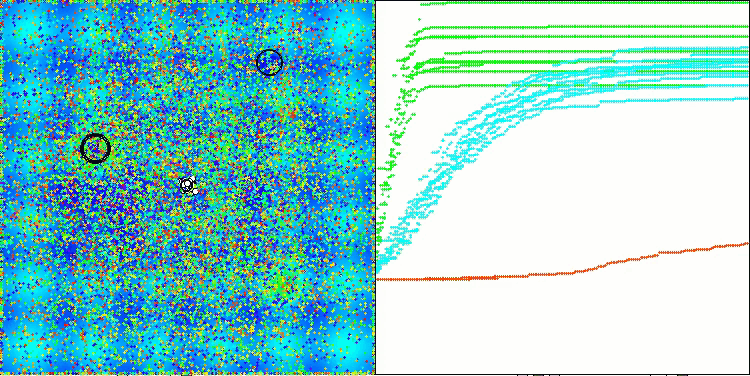
TETA mit der Testfunktion Hilly

TETA mit der Testfunktion Forest
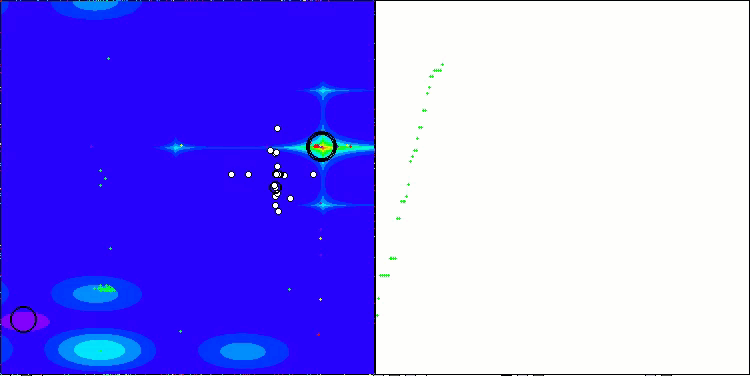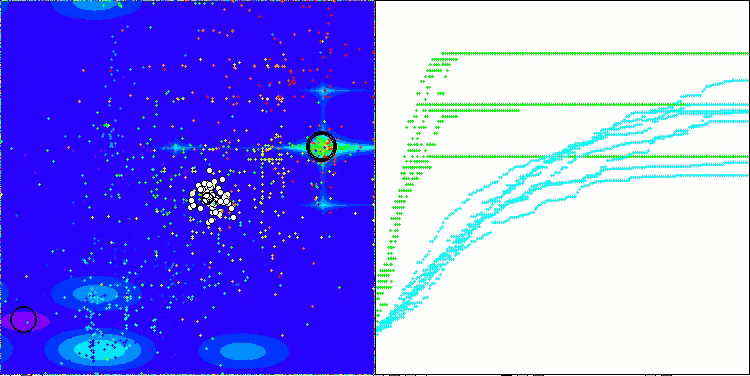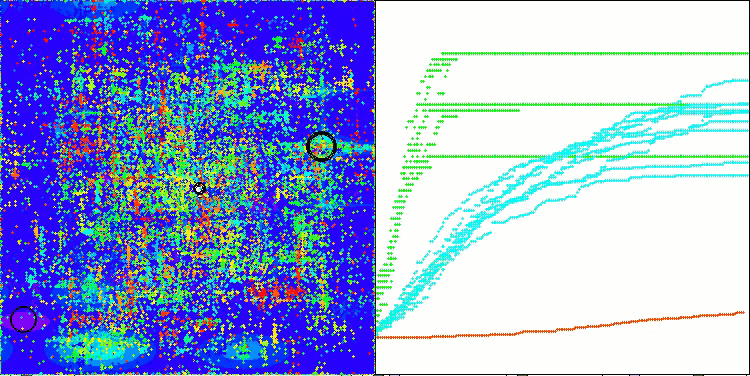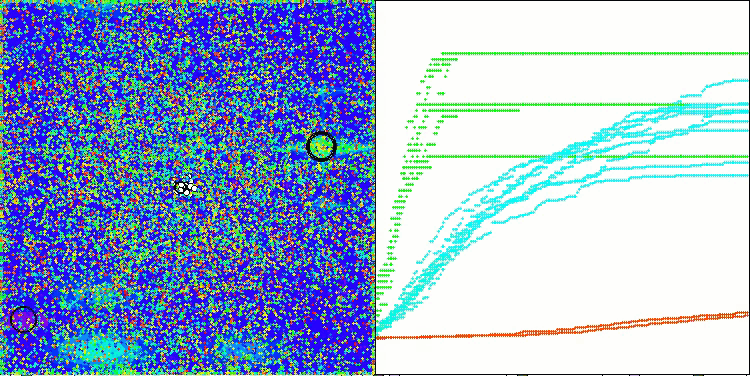
TETA mit der Testfunktion Megacity
Insbesondere erzielt der Algorithmus das beste Ergebnis unter allen Optimierungsalgorithmen und überholt den führenden Algorithmus der Gruppe der Populationsalgorithmen bei der Goldstein-Preis-Funktion, die in der Reihe der Testfunktionen enthalten ist, mit denen die Optimierungsalgorithmen getestet werden können.
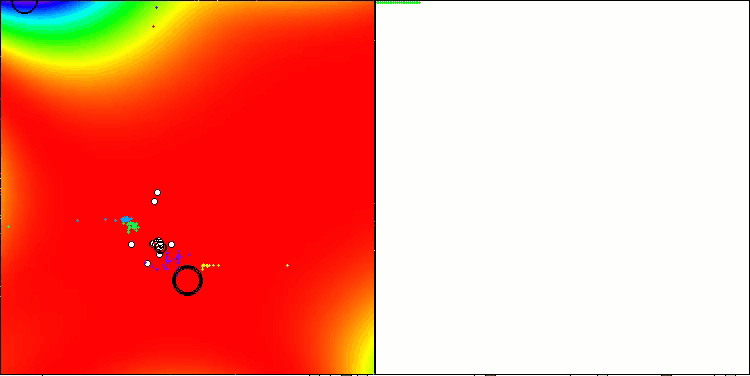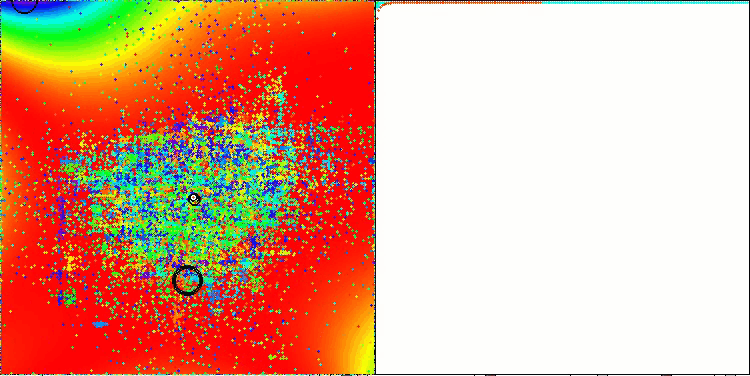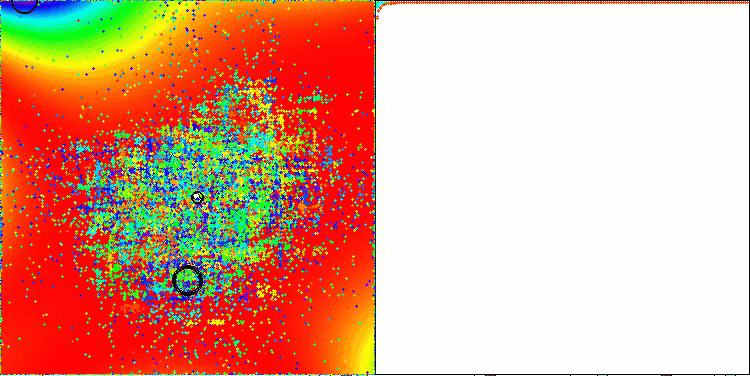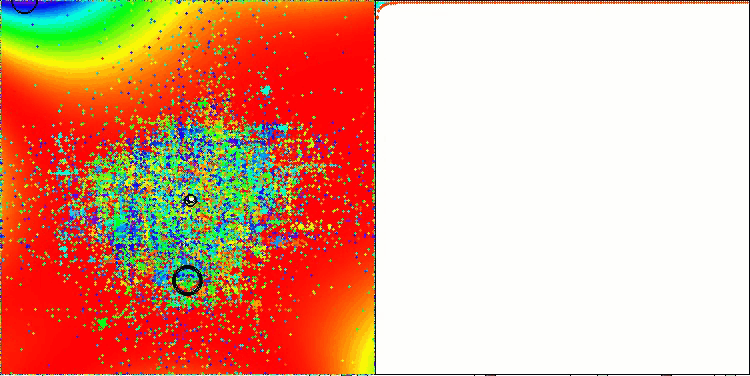
TETA auf GoldsteinPrice Testfunktion (verfügbar zur Auswahl aus der Liste der Testfunktionen)
Ergebnisse auf GoldsteinPrice:
5 GoldsteinPrice's; Func runs: 10000; result: 0.9999786723616957
25 GoldsteinPrice's; Func runs: 10000; result: 0.9999750431600845
500 GoldsteinPrice's; Func runs: 10000; result: 0.9992343490683104
Am Ende des Tests befand sich der TETA-Algorithmus unter den zehn besten Optimierungsalgorithmen und belegte einen respektablen sechsten Platz.
| # | AO | Beschreibung | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | Suche über die gesamte Nachbarschaft | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | Code-Sperr-Algorithmus (joo) | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | AMOm | Optimierung der Tiermigration M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5.987 | 66,52 |
| 4 | (P+O)ES | (P+O) Entwicklungsstrategien | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 5 | CTA | Kometenschweif-Algorithmus (joo) | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 6 | TETA | Zeit-Evolutions-Reise-Algorithmus (Joo) | 0.91362 | 0.82349 | 0.31990 | 2.05701 | 0.97096 | 0.89532 | 0.29324 | 2.15952 | 0.73462 | 0.68569 | 0.16021 | 1.58052 | 5.797 | 64.41 |
| 7 | SDSm | stochastische Diffusionssuche M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 8 | AAm | Algorithmus für das Bogenschießen M | 0.91744 | 0.70876 | 0.42160 | 2.04780 | 0.92527 | 0.75802 | 0.35328 | 2.03657 | 0.67385 | 0.55200 | 0.23738 | 1.46323 | 5.548 | 61.64 |
| 9 | ESG | Entwicklung sozialer Gruppen (joo) | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 10 | SIA | Simuliertes isotropes Glühen (Joo) | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 11 | ACS | künstliche, kooperative Suche | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 12 | BHAm | Algorithmus für schwarze Löcher M | 0.75236 | 0.76675 | 0.34583 | 1.86493 | 0.93593 | 0.80152 | 0.27177 | 2.00923 | 0.65077 | 0.51646 | 0.15472 | 1.32195 | 5.196 | 57.73 |
| 13 | ASO | Anarchische Gesellschaftsoptimierung | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5.178 | 57,54 |
| 14 | AOSm | Suche nach atomaren Orbitalen M | 0.80232 | 0.70449 | 0.31021 | 1.81702 | 0.85660 | 0.69451 | 0.21996 | 1.77107 | 0.74615 | 0.52862 | 0.14358 | 1.41835 | 5.006 | 55.63 |
| 15 | TSEA | Schildkrötenpanzer-Evolutionsalgorithmus (joo) | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 16 | DE | differentielle Evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 17 | CRO | Optimierung chemischer Reaktionen | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 18 | BSA | Vogelschwarm-Algorithmus | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 19 | HS | Harmoniesuche | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 20 | SSG | Setzen, Säen und Wachsen | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 21 | BCOm | Optimierung mit der bakteriellen Chemotaxis M | 0.75953 | 0.62268 | 0.31483 | 1.69704 | 0.89378 | 0.61339 | 0.22542 | 1.73259 | 0.65385 | 0.42092 | 0.14435 | 1.21912 | 4.649 | 51.65 |
| 22 | ABO | Optimierung des afrikanischen Büffels | 0.83337 | 0.62247 | 0.29964 | 1.75548 | 0.92170 | 0.58618 | 0.19723 | 1.70511 | 0.61000 | 0.43154 | 0.13225 | 1.17378 | 4.634 | 51.49 |
| 23 | (PO)ES | (PO) Entwicklungsstrategien | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 24 | TSm | Tabu-Suche M | 0.87795 | 0.61431 | 0.29104 | 1.78330 | 0.92885 | 0.51844 | 0.19054 | 1.63783 | 0.61077 | 0.38215 | 0.12157 | 1.11449 | 4.536 | 50.40 |
| 25 | BSO | Brainstorming-Optimierung | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 26 | WOAm | Wal-Optimierungsalgorithmus M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 27 | AEFA | Algorithmus für künstliche elektrische Felder | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 28 | AEO | Algorithmus zur Optimierung auf der Grundlage künstlicher Ökosysteme | 0.91380 | 0.46713 | 0.26470 | 1.64563 | 0.90223 | 0.43705 | 0.21400 | 1.55327 | 0.66154 | 0.30800 | 0.28563 | 1.25517 | 4.454 | 49.49 |
| 29 | ACOm | Ameisen-Kolonie-Optimierung M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 30 | BFO-GA | Optimierung der bakteriellen Futtersuche — ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 31 | SOA | einfacher Optimierungsalgorithmus | 0.91520 | 0.46976 | 0.27089 | 1.65585 | 0.89675 | 0.37401 | 0.16984 | 1.44060 | 0.69538 | 0.28031 | 0.10852 | 1.08422 | 4.181 | 46.45 |
| 32 | ABHA | Algorithmus für künstliche Bienenstöcke | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 33 | ACMO | Optimierung atmosphärischer Wolkenmodelle | 0.90321 | 0.48546 | 0.30403 | 1.69270 | 0.80268 | 0.37857 | 0.19178 | 1.37303 | 0.62308 | 0.24400 | 0.10795 | 0.97503 | 4.041 | 44.90 |
| 34 | ADAMm | adaptive Momentabschätzung M | 0.88635 | 0.44766 | 0.26613 | 1.60014 | 0.84497 | 0.38493 | 0.16889 | 1.39880 | 0.66154 | 0.27046 | 0.10594 | 1.03794 | 4.037 | 44.85 |
| 35 | ATAm | Algorithmus für künstliche Stämme M | 0.71771 | 0.55304 | 0.25235 | 1.52310 | 0.82491 | 0.55904 | 0.20473 | 1.58867 | 0.44000 | 0.18615 | 0.09411 | 0.72026 | 3.832 | 42.58 |
| 36 | ASHA | Algorithmus für künstliches Duschen | 0.89686 | 0.40433 | 0.25617 | 1.55737 | 0.80360 | 0.35526 | 0.19160 | 1.35046 | 0.47692 | 0.18123 | 0.09774 | 0.75589 | 3.664 | 40.71 |
| 37 | ASBO | Optimierung des adaptiven Sozialverhaltens | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 38 | MEC | Evolutionäre Berechnung des Geistes | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 39 | IWO | Optimierung mit invasiven Unkräutern | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 40 | Micro-AIS | Künstliches Mikro-Immunsystem | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 41 | COAm | Kuckuck-Optimierungsalgorithmus M | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 42 | SDOm | Optimierung der Spiraldynamik M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| 43 | NMm | Nelder-Mead-Verfahren M | 0.73807 | 0.50598 | 0.31342 | 1.55747 | 0.63674 | 0.28302 | 0.08221 | 1.00197 | 0.44667 | 0.18667 | 0.04028 | 0.67362 | 3.233 | 35.92 |
| 44 | BBBC | Big-Bang-Big-Crunch-Algorithmus | 0.60531 | 0.45250 | 0.31255 | 1.37036 | 0.52323 | 0.35426 | 0.20417 | 1.08166 | 0.39769 | 0.19431 | 0.11286 | 0.70486 | 3.157 | 35.08 |
| 45 | CPA | Algorithmus für die zyklische Parthenogenese | 0.71664 | 0.40014 | 0.25502 | 1.37180 | 0.62178 | 0.33651 | 0.19264 | 1.15093 | 0.34308 | 0.16769 | 0.09455 | 0.60532 | 3.128 | 34.76 |
| RW | Random Walk | 0.48754 | 0.32159 | 0.25781 | 1.06694 | 0.37554 | 0.21944 | 0.15877 | 0.75375 | 0.27969 | 0.14917 | 0.09847 | 0.52734 | 2.348 | 26.09 | |
Zusammenfassung
Während der Arbeit am TETA-Algorithmus war ich ständig bestrebt, etwas Einfaches und Effizientes zu schaffen. Die Metapher der Paralleluniversen und Zeitreisen schien zunächst eine einfache, nette Idee zu sein, aber während der Entwicklung entwickelte sie sich organisch zu einem effektiven Optimierungsmechanismus.
Das Hauptmerkmal des Algorithmus war die Idee, dass es unmöglich ist, in allem gleichzeitig Perfektion zu erreichen – man muss ein Gleichgewicht finden. Im Leben balancieren wir ständig zwischen Familie, Karriere und persönlichen Errungenschaften, und genau dieses Konzept habe ich mit dem Ankersystem zur Grundlage des Algorithmus gemacht. Jeder Anker stellt einen wichtigen Aspekt dar, der optimiert werden muss, aber nicht auf Kosten anderer.
Die interessanteste technische Lösung war der Zusammenhang zwischen der Wahrscheinlichkeit, ein Universum zu wählen, und der Stärke seines Einflusses auf andere Universen. So entstand ein natürlicher Mechanismus, bei dem die besten Lösungen eine höhere Chance haben, ausgewählt zu werden, und ihr Einfluss von ihrer Qualität abhängt. Dieser Ansatz bietet ein Gleichgewicht zwischen der Erkundung neuer Möglichkeiten und der Nutzung bereits gefundener guter Lösungen.
Die Erprobung des Algorithmus führte zu unerwartet guten Ergebnissen. Dies macht den Algorithmus besonders wertvoll für praktische Probleme mit begrenzten Berechnungsressourcen. Darüber hinaus zeigt der Algorithmus durchweg hervorragende Ergebnisse bei verschiedenen Arten von Funktionen, was seine Vielseitigkeit unter Beweis stellt. Besonders erfreulich ist die Kompaktheit der Umsetzung. Der Schlüsselcode benötigt nur etwa 50 Zeilen, keine anpassbaren Parameter, und ist doch so effektiv. Dies ist eine wirklich erfolgreiche Lösung, bei der eine einfache Implementierung mit hoher Leistung kombiniert wird.
Letztendlich hat TETA meine ursprünglichen Erwartungen übertroffen. Die Zeitreise-Metapher hat ein praktisches und effektives Optimierungsinstrument hervorgebracht, das in einer Vielzahl von Bereichen eingesetzt werden kann. Dies zeigt, dass manchmal einfache Lösungen, die auf klaren natürlichen Analogien beruhen, sehr effektiv sein können. Der Algorithmus wurde buchstäblich in einem Atemzug erstellt – vom Konzept bis zur Implementierung – und ich bin sehr zufrieden mit der Arbeit an dem Algorithmus, der Forschern und Praktikern bei der schnellen Suche nach optimalen Lösungen eine gute Hilfe sein kann.
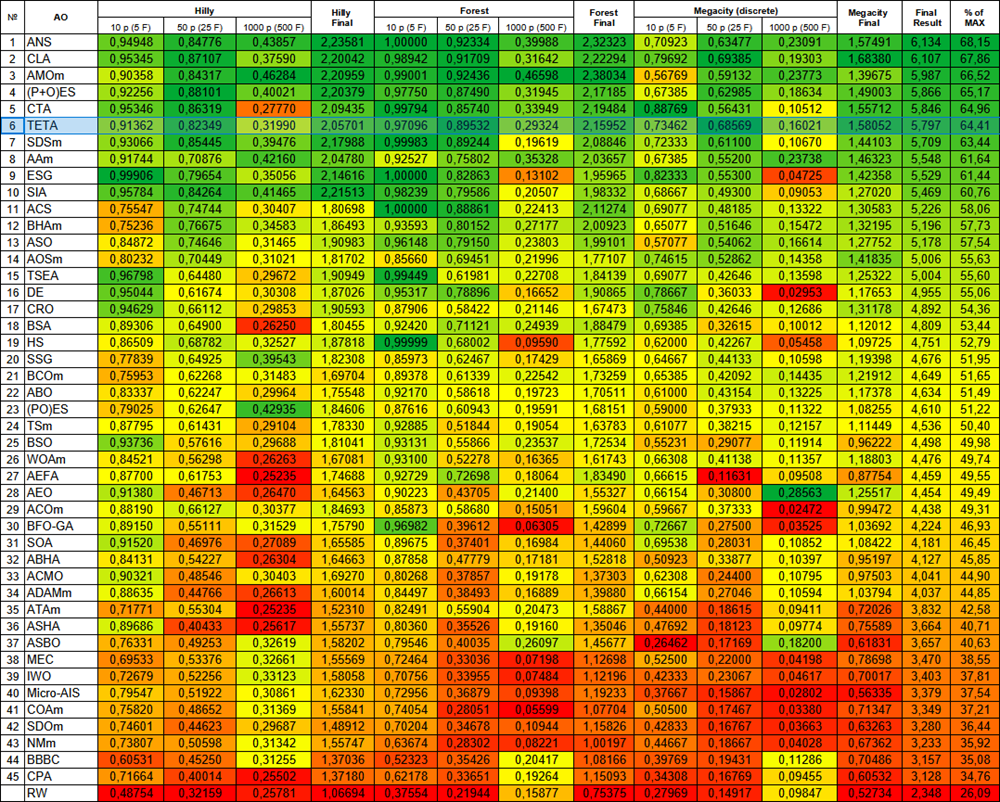
Abbildung 3. Farbabstufung der Algorithmen nach den entsprechenden Tests
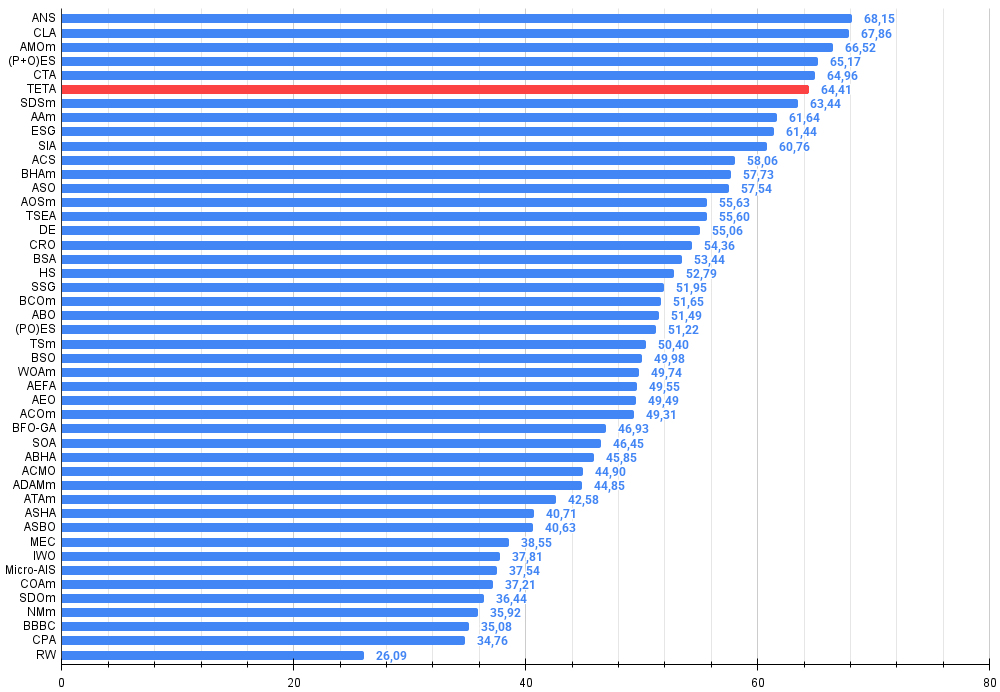
Abbildung 4. Histogramm der Algorithmus-Testergebnisse (Skala von 0 bis 100, je höher, desto besser, wobei 100 das maximal mögliche theoretische Ergebnis ist; im Archiv befindet sich ein Skript zur Berechnung der Bewertungstabelle)
Vor- und Nachteile von TETA:
Vorteile:
- Der einzige externe Parameter ist die Größe der Population.
- Einfache Umsetzung.
- Sehr schneller EA.
- Ausgewogene Metriken für klein- und großdimensionale Probleme.
Nachteile:
- Streuung der Ergebnisse bei niedrigdimensionalen diskreten Problemen.
Der Artikel wird von einem Archiv mit den aktuellen Versionen der Codes der Algorithmen begleitet. Der Autor des Artikels übernimmt keine Verantwortung für die absolute Richtigkeit der Beschreibung der kanonischen Algorithmen. An vielen von ihnen wurden Änderungen vorgenommen, um die Suchmöglichkeiten zu verbessern. Die in den Artikeln dargelegten Schlussfolgerungen und Urteile beruhen auf den Ergebnissen der Versuche.
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | #C_AO.mqh | Include | Übergeordnete Klasse von Populationsoptimierungsalgorithmen |
| 2 | #C_AO_enum.mqh | Include | Enumeration der Algorithmen zur Populationsoptimierung |
| 3 | TestFunctions.mqh | Include | Bibliothek mit Testfunktionen |
| 4 | TestStandFunctions.mqh | Include | Bibliothek mit Funktionen für den Prüfstand |
| 5 | Utilities.mqh | Include | Bibliothek mit Hilfsfunktionen |
| 6 | CalculationTestResults.mqh | Include | Skript zur Berechnung der Ergebnisse in der Vergleichstabelle |
| 7 | Testing AOs.mq5 | Skript | Der einheitliche Prüfstand für alle Algorithmen zur Populationsoptimierung |
| 8 | Simple use of population optimization algorithms.mq5 | Skript | Ein einfaches Beispiel für die Verwendung von Algorithmen zur Populationsoptimierung ohne Visualisierung |
| 9 | Test_AO_TETA.mq5 | Skript | TETA-Prüfstand |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/16963
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Entwicklung fortschrittlicher ICT-Handelssysteme: Implementierung von Signalen in den Indikator "Order Block"
Entwicklung fortschrittlicher ICT-Handelssysteme: Implementierung von Signalen in den Indikator "Order Block"
 Analyse des Binärcodes der Börsenkurse (Teil II): Umwandlung in BIP39 und Schreiben des GPT-Modells
Analyse des Binärcodes der Börsenkurse (Teil II): Umwandlung in BIP39 und Schreiben des GPT-Modells
 Automatisieren von Handelsstrategien in MQL5 (Teil 24): London Session Breakout System mit Risikomanagement und Trailing Stops
Automatisieren von Handelsstrategien in MQL5 (Teil 24): London Session Breakout System mit Risikomanagement und Trailing Stops
 Post-Factum-Handelsanalyse: Auswahl von Trailing-Stops und neuen Stoppstufen im Strategietester
Post-Factum-Handelsanalyse: Auswahl von Trailing-Stops und neuen Stoppstufen im Strategietester
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.