Algoritmo de Big Bang y Big Crunch
115
0
Contenido
Introducción
En la vasta extensión del universo, donde nacen y mueren las estrellas, existen misterios que la humanidad se esfuerza por desentrañar. El método BBBC (Big Bang-Big Crunch) es un algoritmo de optimización global inspirado en los procesos que tienen lugar en el espacio. Vamos a analizar este fascinante concepto.
La teoría del Big Bang y el Big Crunch fue propuesta como hipótesis alternativa del fin del universo por los físicos Alexander Friedman y Georges Lemaître a principios del siglo XX. Estos observaron que las ecuaciones de la teoría general de la relatividad de Einstein permiten tanto la expansión como la contracción del universo. Asimismo, Friedman demostró matemáticamente que el universo no puede permanecer estático y debe expandirse o contraerse. Distinguió tres posibles escenarios de su desarrollo: expansión perpetua, expansión seguida de contracción y modo oscilatorio.
A lo largo del siglo XX, muchos científicos desarrollaron la idea de combinar el Big Bang y el Big Crunch en un modelo cíclico. Hasta la fecha, la teoría del Big Crunch no es el principal modelo cosmológico, ya que las observaciones muestran que el universo se expande a un ritmo acelerado. No obstante, este concepto supone una idea interesante que sugiere la naturaleza cíclica de la evolución del universo. Etapas principales:
- El Big Bang, cuando el estado inicial con alta densidad y temperatura pasa a una etapa de rápida expansión y disipación de energía con formación de materia y espacio-tiempo con distribución caótica de partículas.
- El Big Crunch, cuando las fuerzas gravitatorias detienen la expansión y comienza el proceso inverso de compresión, toda la materia es arrastrada hacia un punto, volviendo a un estado de alta densidad.
- La ciclicidad se expresa en la secuencia de un nuevo Big Bang tras un Big Crunch, el proceso puede repetirse indefinidamente, y cada ciclo puede tener constantes físicas diferentes.
El algoritmo Big Bang-Big Crunch fue propuesto en 2006 por los científicos Osman K. Erol e Ibrahim Eksin de la Universidad Técnica de Estambul (Turquía).
Implementación del algoritmo
Al igual que en la teoría del Big Bang, donde el universo comienza su existencia con un potente estallido de energía, en el método BBBC observamos una fase inicial llena de aleatoriedad y variedad. En la fase de Big Bang, se crea una población de puntos aleatorios, cada uno de los cuales representa una solución candidata. Estos puntos están dispersos por el vasto espacio de búsqueda, listos para ser explorados, pero en cuanto el caos encuentra su lugar, comienza la fase del Big Crunch. Los puntos tienden hacia el "centro de masa", del mismo modo que las galaxias se atraen entre sí por efecto de la gravedad. Este momento supone el clímax, cuando se aúnan todos los esfuerzos para encontrar la mejor solución.
Aquí tenemos las etapas del algoritmo, el viaje del caos al orden:
1. La fase del Big Bang. En esta primera acción, se crea una población inicial de N puntos aleatorios. Cada punto ocupa su propio lugar en el espacio, distribuido de manera uniforme dentro de los límites dados.
2. La fase de Big Crunch, la transición hacia el cálculo del "centro de masa", el punto hacia el que tienden todos los demás. Utilizando la fórmula (fig. 1), encontramos las coordenadas del centro, que será el nuevo comienzo para los siguientes pasos.
3. Generación de nuevos puntos. Alrededor del centro de masas comienzan a existir nuevos puntos. Estos e forman con una distribución normal, siguiendo una fórmula que les da la dirección y la magnitud del movimiento.
El método BBBC busca la armonía entre investigación y refinamiento. Con cada nueva generación, la dispersión de los puntos durante la generación disminuye, lo cual permite al algoritmo refinar la solución óptima encontrada.
Al igual que en el espacio, donde cada movimiento importa, en el mundo de la optimización cada cálculo nos acerca a nuestro objetivo. Sumergiéndonos en este método, no solo descubrimos nuevos horizontes, sino que pasamos a formar parte de un gran proceso cósmico en busca de una solución mejor.
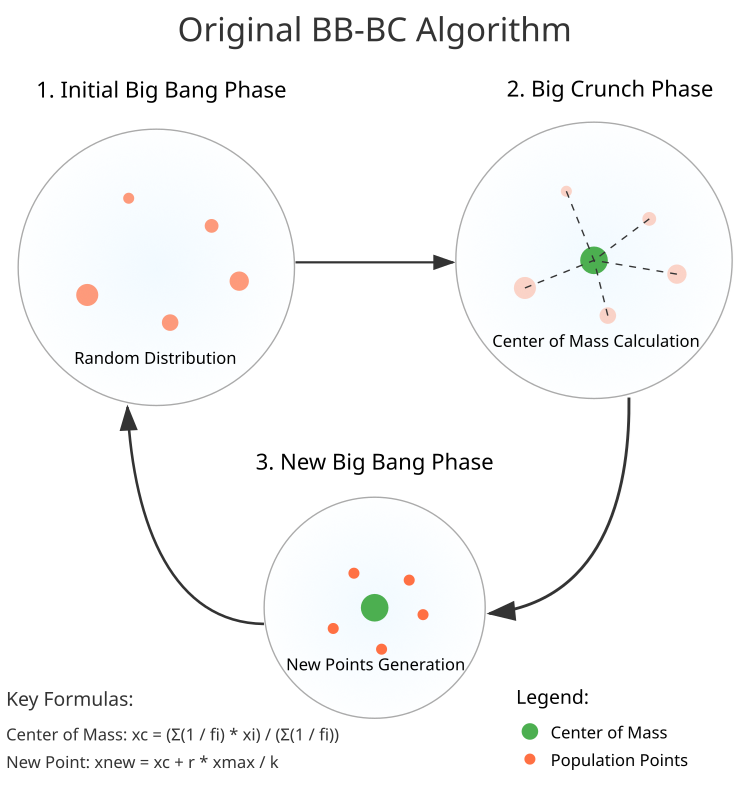
Figura 1. Esquema del algoritmo BBBC
Vamos a esbozar el pseudocódigo del algoritmo BBBC:
Aumentamos epochNow
// Inicialización (Big Bang)
Si revision == false
Para cada individuo i de 0 a popSize-1
Para cada coordenada c de 0 a coords-1
Nueva coordenada = Generación de números aleatorios (rangeMin[c], rangeMax[c])
Establecemos revision en true
Retorno
// Fase de Big Crunch
Si epochNow % bigBangPeriod != 0
Para cada coordenada c de 0 a coords-1
numerator = 0, denominator = 0
Para cada individuo i de 0 a popSize-1
adaptabilidad = Máximo (Valor absoluto (a [i].f), 1e-10)
peso = 1,0 / adaptabilidad
numerator += peso * coordenada del punto
denominator += peso
centerMass [c] = (denominator > 1e-10) ? numerator / denominator : cB [c]
Para cada individuo i de 0 a popSize-1
Para cada coordenada c de 0 a coords-1
r = Generación normal de números aleatorios (0, -1,0, 1,0, 1)
Nueva coordenada = centerMass [c] + r * rangeMax [c] / epochNow
// Fase de Big Bang
De lo contrario
Para cada individuo i de 0 a popSize-1
Para cada coordenada c de 0 a coords-1
Nueva coordenada = Generación normal de números aleatorios (cB [c], rangeMin [c], rangeMax [c], desviación estándar = 8)
Repetir hasta que se cumpla el criterio de parada de la Fase de Big Crunch.
Escribamos ahora el código. Ahora escribiremos la definición de la clase C_AO_BBBC, sucesora de C_AO:
Métodos públicos:- Constructor y destructor
- SetParams () — establecimiento de parámetros (tamaño de la población y periodicidad del Big Bang)
- Init () — inicialización del algoritmo con los límites de búsqueda especificados
- Moving () — método principal que implementa las fases Big Bang y Big Crunch.
- Revision () — método de actualización de la mejor solución encontrada
- epochs — número total de épocas de funcionamiento del algoritmo
- epochNow — época actual
- centreMass [] — array para almacenar las coordenadas del centro de masas
Esta clase supone una implementación del algoritmo BBBC, donde todos los cálculos básicos tienen lugar en los métodos Moving() y Revision(), mientras que los datos de población necesarios se almacenan en la clase base C_AO.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_BBBC : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_BBBC () { } C_AO_BBBC () { ao_name = "BBBC"; ao_desc = "Big Bang - Big Crunch Algorithm"; ao_link = "https://www.mql5.com/es/articles/16701"; popSize = 50; bigBangPeriod = 3; ArrayResize (params, 2); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "bigBangPeriod"; params [1].val = bigBangPeriod; } void SetParams () { popSize = (int)params [0].val; bigBangPeriod = (int)params [1].val; } bool Init (const double &rangeMinP [], // минимальный диапазон поиска const double &rangeMaxP [], // максимальный диапазон поиска const double &rangeStepP [], // шаг поиска const int epochsP = 0); // количество эпох void Moving (); void Revision (); //---------------------------------------------------------------------------- int bigBangPeriod; // периодичность большого взрыва private: //------------------------------------------------------------------- int epochs; // общее число эпох int epochNow; // текущая эпоха double centerMass []; // центр масс }; //——————————————————————————————————————————————————————————————————————————————
Método "Init" de la clase C_AO_BBBC:
El método realiza la inicialización del algoritmo y admite los parámetros:
- rangeMinP [] — array de valores mínimos para cada coordenada
- rangeMaxP [] — array de valores máximos para cada coordenada
- rangeStepP [] - array de pasos de discretización para cada coordenada
- epochsP — número de épocas de funcionamiento del algoritmo (0 por defecto)
Acciones del método:
- Llama a StandardInit () de la clase básica para inicializar los parámetros comunes
- Establece el número total de épocas (epochs) y pone a cero el contador de épocas actual (epochNow)
- Asigna memoria para el array del centro de masas VcentreMass) de tamaño "coords" (número de coordenadas).
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_BBBC::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { // Инициализация базового класса if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- epochs = epochsP; epochNow = 0; // Выделение памяти для массивов ArrayResize (centerMass, coords); return true; } //——————————————————————————————————————————————————————————————————————————————
El método Moving del algoritmo BB-BC consta de tres partes principales:
1. Primera inicialización (si revision = false):
- Crea una población inicial de puntos aleatorios
- Lleva a estos a una red de búsqueda discreta
2. Fase de Big Crunch (si epoch no es múltiplo de bigBangPeriod):
- Calcula el centro de masas usando la fórmula xc = (Σ(1/fi)*xi) / (Σ(1/fi))
- Genera nuevos puntos alrededor del centro de masas utilizando la fórmula: xnew = xc + r * xmax / epoch
- Usa la distribución normal para los números aleatorios
3. Fase del Big Bang (si la época es múltiplo de bigBangPeriod):
- Genera nuevos puntos usando una distribución normal
- Usa la mejor solución como media
- Utiliza una desviación = 8 para realizar una búsqueda amplia
Todos los puntos nuevos se limitan a los límites de búsqueda dados y se llevan a una cuadrícula discreta.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BBBC::Moving () { epochNow++; // Начальная инициализация (Big Bang) if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { // Генерация случайных начальных позиций a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); // Приведение к дискретной сетке поиска a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- // Фаза Big Crunch - большой коллапс if (epochNow % bigBangPeriod != 0) { for (int c = 0; c < coords; c++) { double numerator = 0; double denominator = 0; for (int i = 0; i < popSize; i++) { // Расчет веса как обратной величины от значения фитнес-функции double fitness = MathMax (MathAbs (a [i].f), 1e-10); double weight = 1.0 / fitness; // Суммирование для вычисления центра масс по формуле // xc = (Σ(1/fi)xi) / (Σ(1/fi)) numerator += weight * a [i].c [c]; denominator += weight; } // Определение координаты центра масс centerMass [c] = denominator > 1e-10 ? numerator / denominator : cB [c]; } for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { double r = u.GaussDistribution (0, -1.0, 1.0, 1); // Генерация новой точки по формуле // xnew = xc + r*xmax/k double newPoint = centerMass [c] + r * rangeMax [c] / epochNow; // Ограничение в пределах допустимой области и приведение к сетке a [i].c [c] = u.SeInDiSp (newPoint, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //---------------------------------------------------------------------------- // Фаза Big Bang - большой взрыв else { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.GaussDistribution (cB [c], rangeMin [c], rangeMax [c], 8); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } } //——————————————————————————————————————————————————————————————————————————————
El método Revision cumple dos funciones principales:
Hallar la mejor solución:- Inicializa el índice de la mejor solución (bestInd = -1)
- Itera todos los puntos de la población
- Si encuentra una solución mejor que la actual:
- Actualiza el valor de la mejor función de aptitud (fB)
- Memoriza el índice de la mejor solución (bestInd)
- Si se encuentra la mejor solución (bestInd != -1):
- Copia todas las coordenadas de la mejor solución del array al array de la mejor solución "cB"
- Copia todas las coordenadas de la mejor solución del array al array de la mejor solución "cB"
Este método garantiza la actualización de la información sobre la mejor solución global encontrada durante todo el tiempo de funcionamiento del algoritmo.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BBBC::Revision () { int bestInd = -1; // Поиск лучшего решения в текущей популяции for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; bestInd = i; } } // Обновление лучшего известного решения if (bestInd != -1) ArrayCopy (cB, a [bestInd].c, 0, 0, WHOLE_ARRAY); } //——————————————————————————————————————————————————————————————————————————————
Los autores del algoritmo BBBC afirman que es capaz de competir con otros algoritmos fuertes bien conocidos, como los algoritmos genéticos (AG), superando sus resultados en un número significativamente menor de épocas.
Como prueba, citan los resultados de pruebas realizadas con puntos de referencia sintéticos estándar y ampliamente usados, como la esfera (también conocida como paraboloide o elipsoide), Ackley y Rastrigin. Veamos una visualización del rendimiento del algoritmo con dos de estas pruebas.
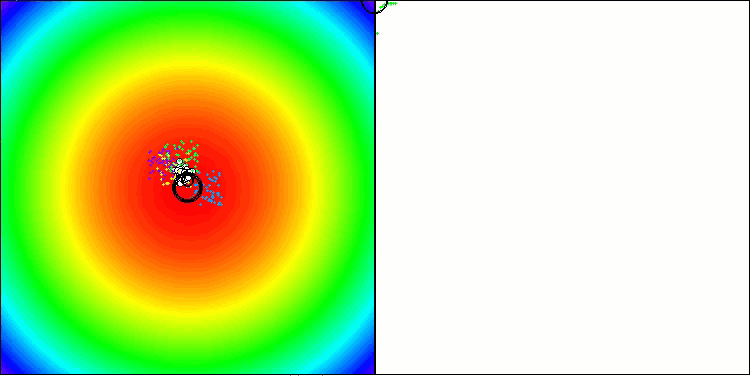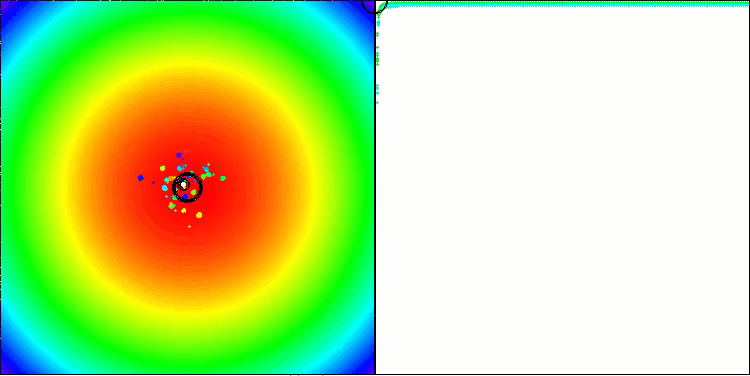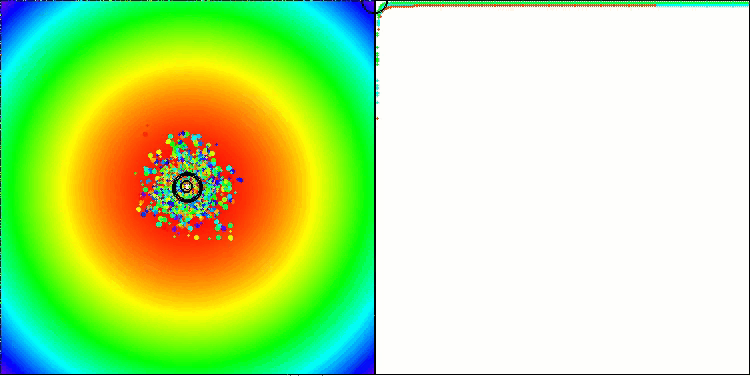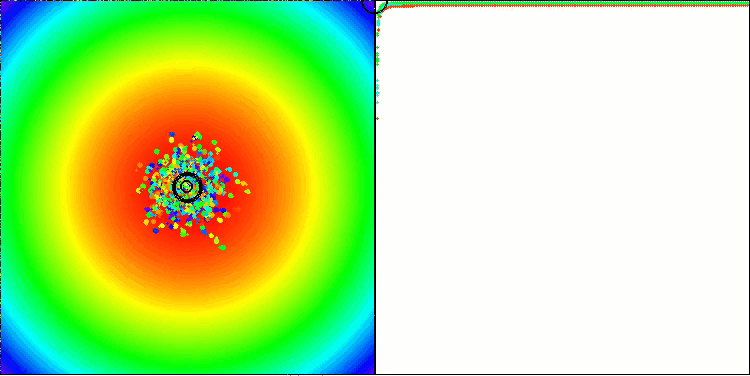
BBBC en la función de prueba Paraboloid
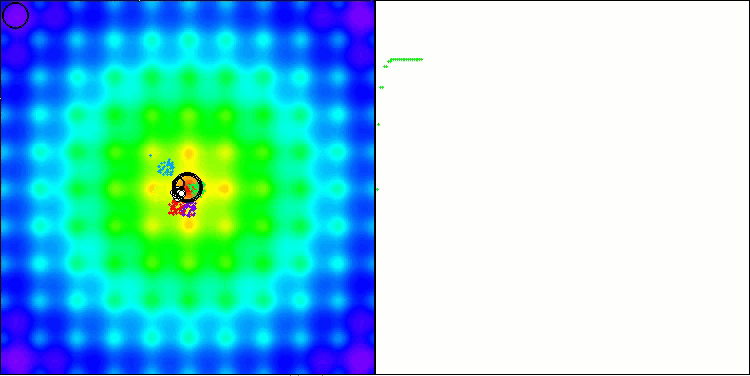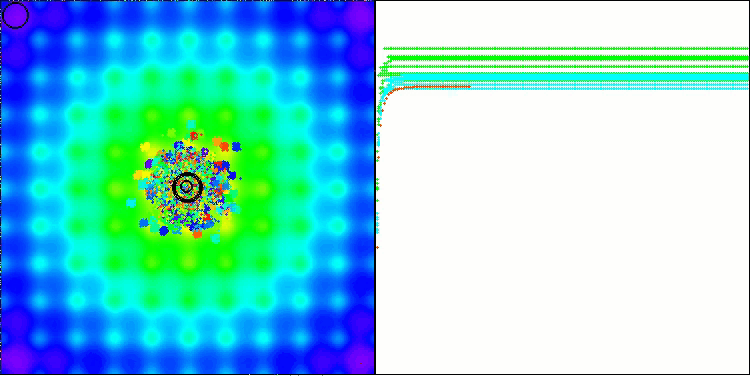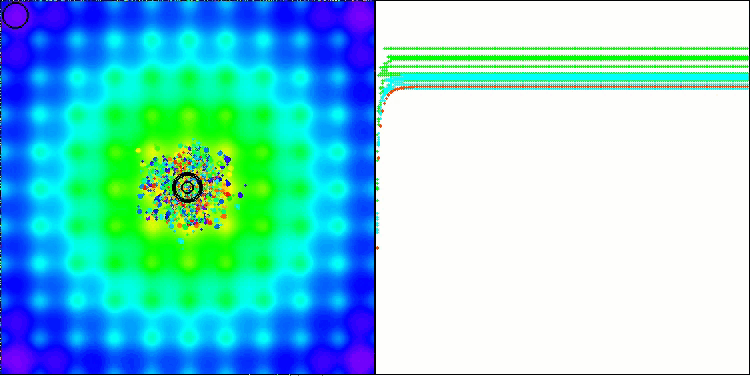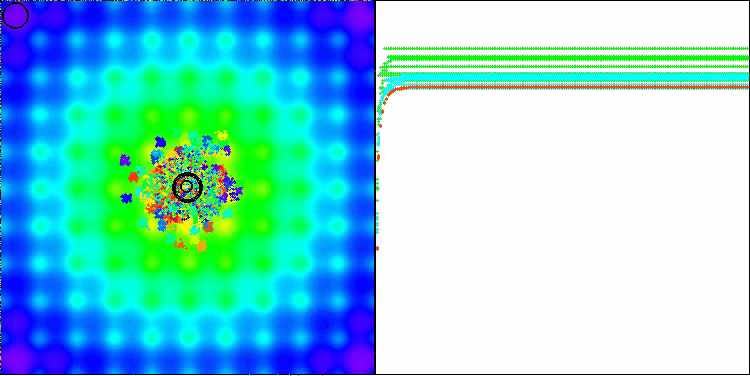
BBBC en la función de prueba de Ackley
De hecho, los resultados son impresionantes. Lo más notable es que los resultados en problemas de alta dimensionalidad (línea roja) no difieren mucho de los resultados en problemas de baja dimensionalidad (línea verde), lo cual indica la gran escalabilidad del algoritmo. Aunque la precisión de la convergencia no resulta perfecta en la función de Ackley, los resultados siguen siendo notables.
Vamos a examinar ahora los resultados del BBBC con nuestras funciones de prueba especialmente diseñadas para algoritmos de optimización.
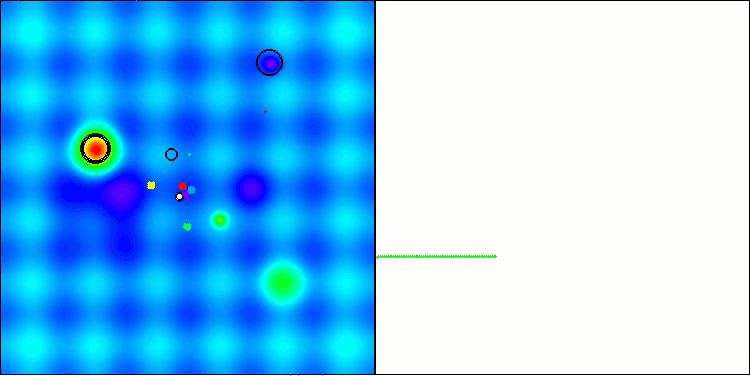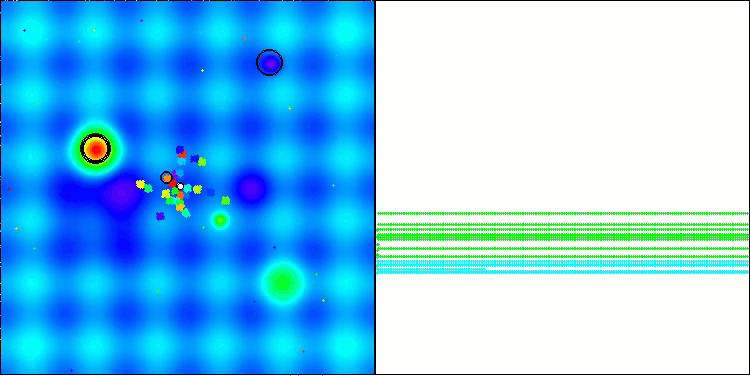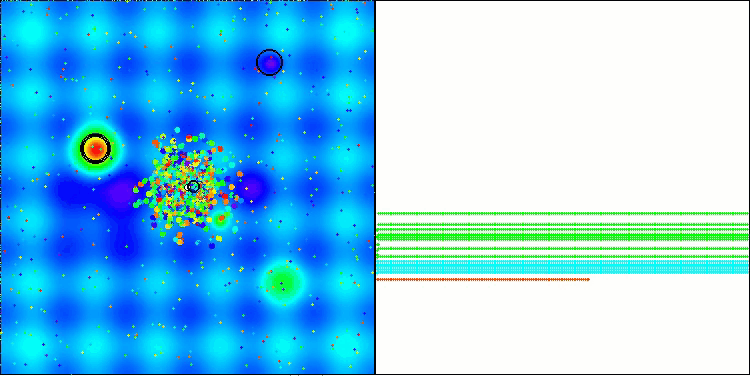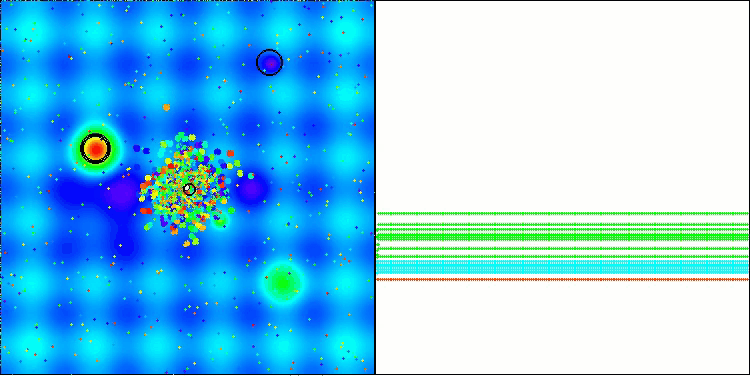
BBBC en la función de prueba Hilly
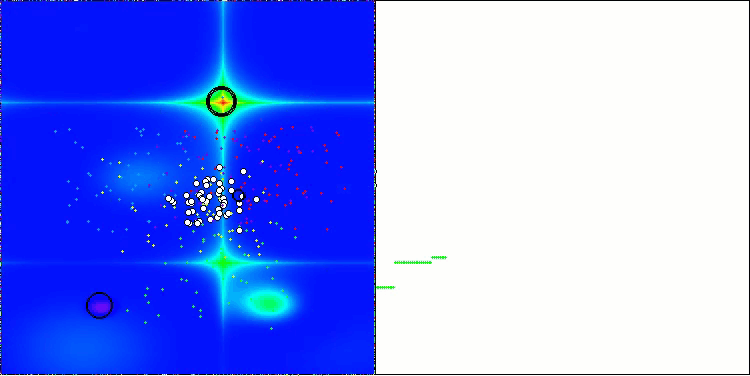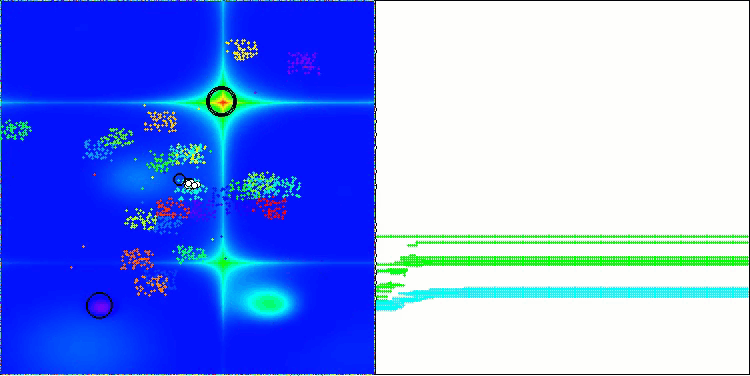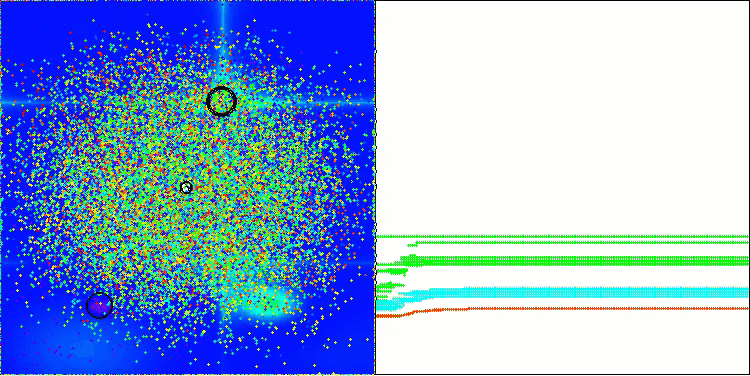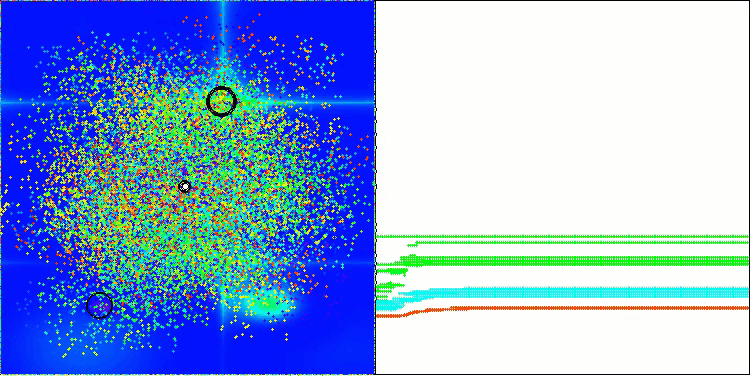
BBBC en la función de prueba de Forest
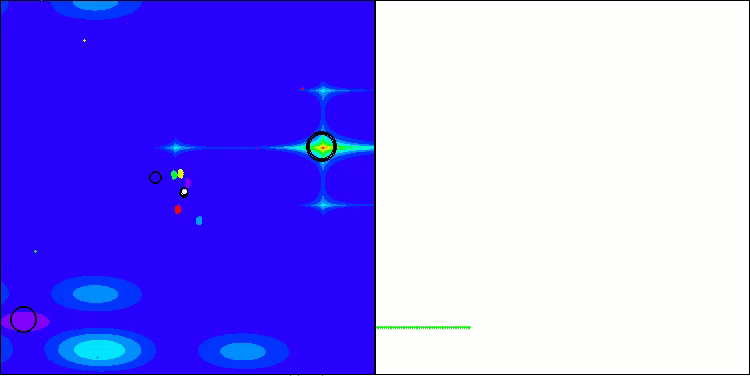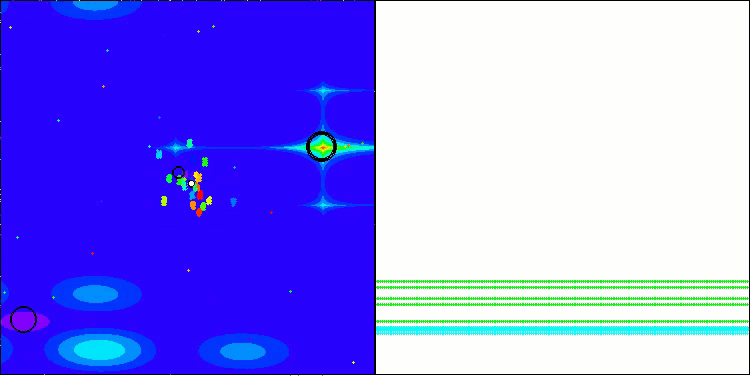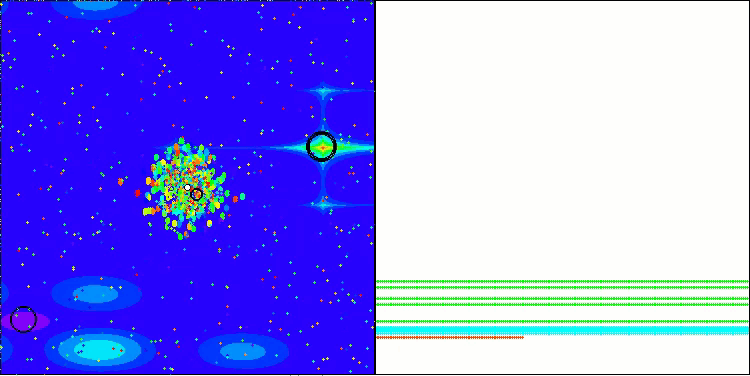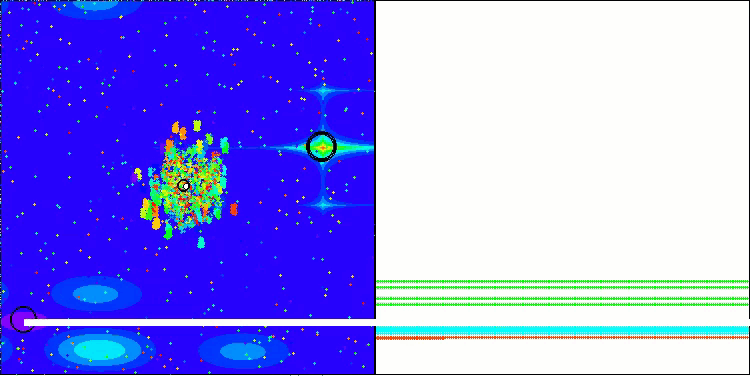
BBBC en la función de prueba de Megacity
Desafortunadamente, la magia del algoritmo ha dejado de funcionar en nuestros puntos de referencia. ¿Cuál es la razón? En primer lugar, cabe señalar que, al igual que en las características anteriores, en las pruebas Hilly, Forest y Megacity la población del algoritmo centra su "atención" en la parte central del espacio de búsqueda. Esta observación plantea ciertos interrogantes y parece bastante extraña.
Echemos un vistazo al interior del algoritmo BBBC y examinemos su funcionamiento. Veremos que utilizando el "centro de masas", los puntos distribuidos por el espacio tienden a colapsar en el centro del rango de la función. Esto ocurre porque el centro de masas de los puntos aparece exactamente en el centro, lo que crea una ilusión de eficacia del algoritmo. Esta coincidencia provoca que el algoritmo pueda encontrar con éxito óptimos para funciones de tipo esfera (con un óptimo global en el centro del rango). Sin embargo, esto no es en realidad el resultado de las extraordinarias capacidades de búsqueda del algoritmo, sino una afortunada coincidencia. Por ejemplo, si el algoritmo partiera de un punto con coordenadas 0,0, alcanzaría idealmente el óptimo global en la primera iteración. Ese es el secreto.
Cabe señalar que la mayoría de las funciones de prueba estándar ampliamente usadas para evaluar diversos algoritmos tienen un óptimo global situado en el centro del espacio de búsqueda. Estas pruebas no siempre son fiables y, en el caso de algunos algoritmos, como el BBBC, pueden provocar una impresión errónea sobre la capacidad real de búsqueda del algoritmo.
Para evitar falsos positivos en las pruebas, hemos desarrollado funciones de prueba especiales que:
- no son asimétricas
- tienen un óptimo global situado fuera del centro del espacio de búsqueda
- no son periódicas
- tienen una pequeña fracción de la superficie que se encuentra por encima de la línea media en altura.
Ahora nos centraremos en la impresión de los resultados del BBBC en las funciones de prueba, recogidos en la tabla siguiente. Esto es muy importante.
| Big bang en cada 2ª época | Big bang cada 3ª época | Big bang cada 10ª época |
|---|---|---|
| BBBC|Big Bang - Big Crunch Algorithm|50.0|2.0| ============================= 5 Hilly's; Func runs: 10000; result: 0.5789409521562645 25 Hilly's; Func runs: 10000; result: 0.36005433010965165 500 Hilly's; Func runs: 10000; result: 0.25650127842145554 ============================= 5 Forest's; Func runs: 10000; result: 0.5232991213500953 25 Forest's; Func runs: 10000; result: 0.293874681679014 500 Forest's; Func runs: 10000; result: 0.18830469994313143 ============================= 5 Megacity's; Func runs: 10000; result: 0.3269230769230769 25 Megacity's; Func runs: 10000; result: 0.15584615384615388 500 Megacity's; Func runs: 10000; result: 0.09743846153846236 ============================= All score: 2.78118 (30.90%) | BBBC|Big Bang - Big Crunch Algorithm|50.0|3.0| ============================= 5 Hilly's; Func runs: 10000; result: 0.5550785088841808 25 Hilly's; Func runs: 10000; result: 0.3605042956384694 500 Hilly's; Func runs: 10000; result: 0.25635343911025843 ============================= 5 Forest's; Func runs: 10000; result: 0.48703749499939086 25 Forest's; Func runs: 10000; result: 0.2897958021406425 500 Forest's; Func runs: 10000; result: 0.1865439156477803 ============================= 5 Megacity's; Func runs: 10000; result: 0.28307692307692306 25 Megacity's; Func runs: 10000; result: 0.15692307692307694 500 Megacity's; Func runs: 10000; result: 0.09701538461538546 ============================= All score: 2.67233 (29.69%) | BBBC|Big Bang - Big Crunch Algorithm|50.0|10.0| ============================= 5 Hilly's; Func runs: 10000; result: 0.4883607839451155 25 Hilly's; Func runs: 10000; result: 0.3344059754605514 500 Hilly's; Func runs: 10000; result: 0.25564528470980497 ============================= 5 Forest's; Func runs: 10000; result: 0.492293124748422 25 Forest's; Func runs: 10000; result: 0.28653857694657936 500 Forest's; Func runs: 10000; result: 0.1844110334128521 ============================= 5 Megacity's; Func runs: 10000; result: 0.3230769230769231 25 Megacity's; Func runs: 10000; result: 0.15261538461538465 500 Megacity's; Func runs: 10000; result: 0.09653846153846235 ============================= All score: 2.61389 (29.04%) |
Obsérvese que los resultados de las pruebas muestran diferencias insignificantes entre sí y se ajustan a la dispersión natural de los valores. Esto indica la escasa capacidad de búsqueda de la estrategia usada, que en esencia difiere poco de la búsqueda aleatoria. A este respecto, nos conviene ofrecer los resultados de la prueba del algoritmo de paseo aleatorio (RW - random walk). En artículos anteriores hemos mencionado este algoritmo, pero no hemos presentado sus resultados. Ahora es momento de hacerlo.
La presentación de los resultados del algoritmo RW resulta necesaria para evaluar la eficacia de las distintas estrategias de búsqueda en comparación con la simple dispersión aleatoria de puntos en el espacio. A continuación le mostramos el resultado medio de 100 ejecuciones de funciones de prueba (normalmente hacemos 10).
RW|Random Walk|50.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.48753502068617777
25 Hilly's; Func runs: 10000; result: 0.3215913699940513
500 Hilly's; Func runs: 10000; result: 0.2578113480890265
=============================
5 Forest's; Func runs: 10000; result: 0.3755402348403822
25 Forest's; Func runs: 10000; result: 0.21943566240362317
500 Forest's; Func runs: 10000; result: 0.15877419882827945
=============================
5 Megacity's; Func runs: 10000; result: 0.27969230769230796
25 Megacity's; Func runs: 10000; result: 0.14916923076923083
500 Megacity's; Func runs: 10000; result: 0.098473846153847
=============================
All score: 2.34802 (26.09%)
Aquí está el código para el algoritmo RW, es muy simple. La función "Moving" se encarga, como es habitual, de actualizar las coordenadas de cada individuo de la población. Para cada individuo, genera valores aleatorios dentro de un rango determinado y luego los ajusta usando la función "SeInDiSp" para que se correspondan con el paso de cambio.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_RW::Moving () { for (int w = 0; w < popSize; w++) { for (int c = 0; c < coords; c++) { a [w].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [w].c [c] = u.SeInDiSp (a [w].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
La función Revision comprueba todos los individuos de la población para encontrar el individuo con la mejor función de aptitud (fB). Si se encuentra un individuo así, sus coordenadas se copiarán en el mejor resultado global (cB).
//—————————————————————————————————————————————————————————————————————————————— void C_AO_RW::Revision () { int ind = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ind = i; } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); } //——————————————————————————————————————————————————————————————————————————————
Ahora vamos a modificar el algoritmo BBBC original para nivelar sus ventajas ilusorias en problemas con un óptimo global en el centro del rango de parámetros a optimizar, de forma que se puedan realizar pruebas objetivas. Veamos las diferencias en el código, hemos introducido cambios en el método "Moving":
- Cálculo del centro de masas suprimido
- Hemos cambiado la fase del Big Bang:
- Se utiliza la mejor solución (cB) en lugar del centro de masas (centreMass)
- Usa la fórmula xnew = cB + r*range/epochNow ("range" es ahora la diferencia entre "rangeMax" y "rangeMin")
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BBBC::Moving () { epochNow++; // Начальная инициализация (Big Bang) if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { // Генерация случайных начальных позиций a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); // Приведение к дискретной сетке поиска a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //-------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { //Фаза Big Crunch - большой коллапс if (epochNow % bigBangPeriod != 0) { for (int c = 0; c < coords; c++) { // Вычисление размера пространства поиска для текущей координаты double range = rangeMax [c] - rangeMin [c]; // Генерация случайного числа в диапазоне [-1, 1] double r = u.GaussDistribution (0, -1.0, 1.0, 1); // Генерация новой точки по формуле // xnew = xc + r*(xmax - xmin)/(k) double newPoint = cB [c] + r * range / epochNow; // Ограничение в пределах допустимой области и приведение к сетке a [i].c [c] = u.SeInDiSp (newPoint, rangeMin [c], rangeMax [c], rangeStep [c]); } } // Фаза Big Bang - большой взрыв else { for (int c = 0; c < coords; c++) { a [i].c [c] = u.GaussDistribution (cB [c], rangeMin [c], rangeMax [c], 8); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } } //——————————————————————————————————————————————————————————————————————————————
Resultados de las pruebas
Resultados de la versión corregida del algoritmo BBBC:
BBBC|Big Bang-Big Crunch Algorithm|50.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.6053080737014771
25 Hilly's; Func runs: 10000; result: 0.45249601882946056
500 Hilly's; Func runs: 10000; result: 0.31255376970202864
=============================
5 Forest's; Func runs: 10000; result: 0.5232283922331299
25 Forest's; Func runs: 10000; result: 0.354256711141388
500 Forest's; Func runs: 10000; result: 0.20417356281490023
=============================
5 Megacity's; Func runs: 10000; result: 0.3976923076923077
25 Megacity's; Func runs: 10000; result: 0.19430769230769235
500 Megacity's; Func runs: 10000; result: 0.11286153846153954
=============================
All score: 3.15688 (35.08%)
Los resultados de las pruebas muestran ahora las capacidades del algoritmo BBBC de manera objetiva. La visualización muestra una notable formación de las mismas "estrellas" que en el algoritmo original, pero ahora realiza la búsqueda en zonas realmente prometedoras, no solo predominantemente en el centro del espacio de búsqueda.
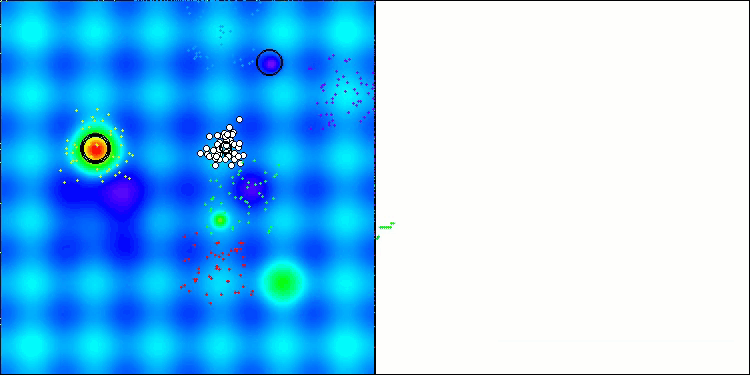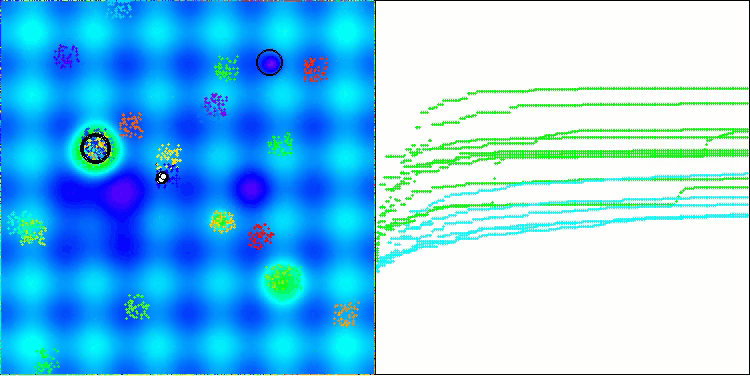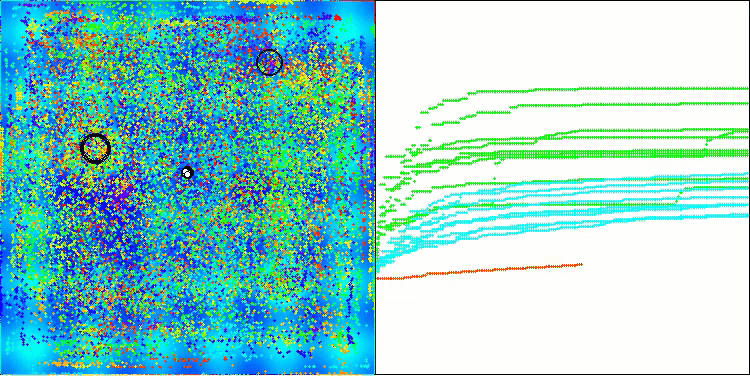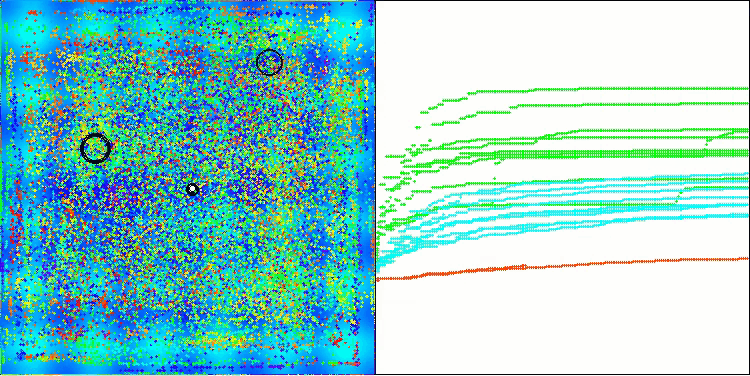
BHAm en la función de prueba Hilly
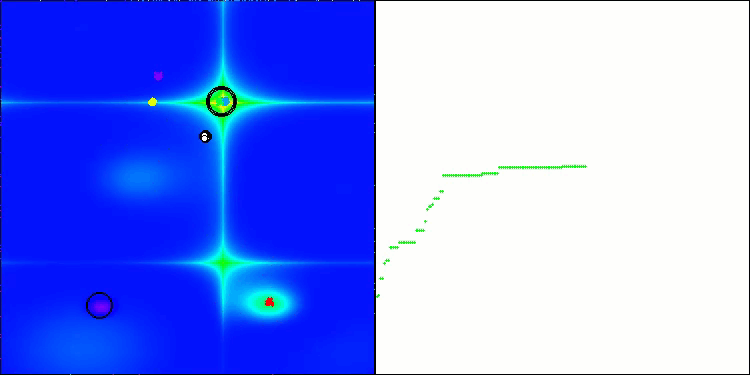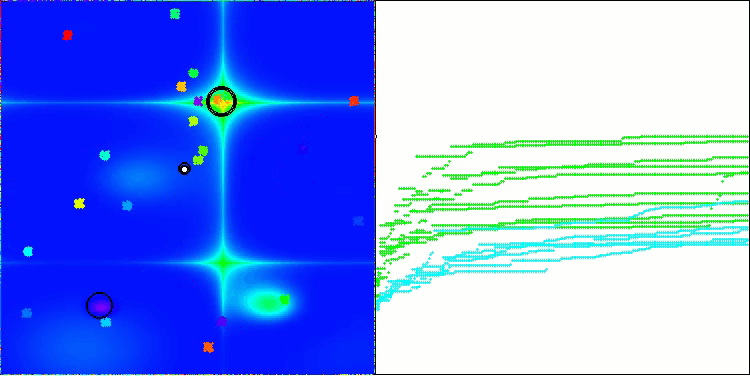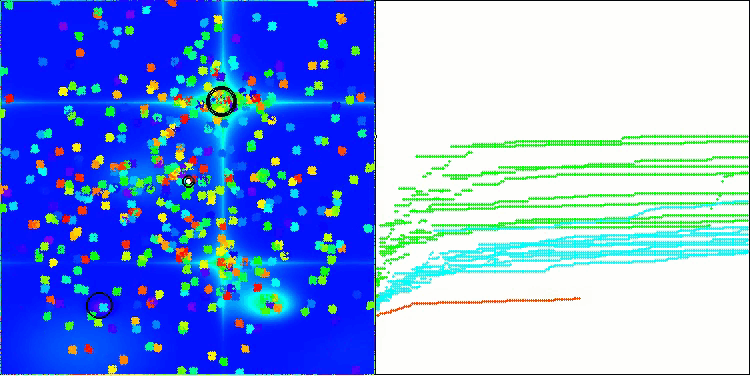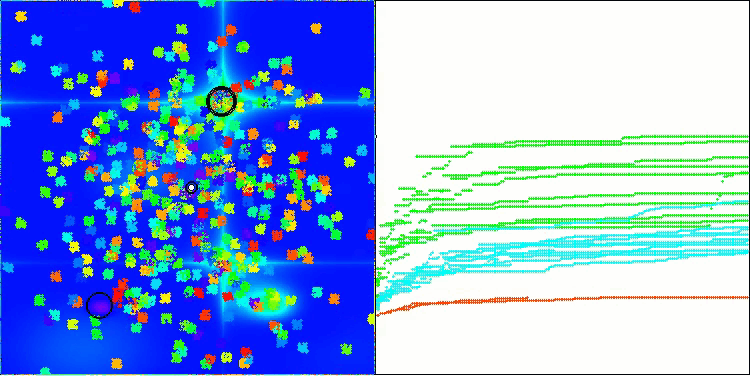
BHAm en la función de prueba Forest
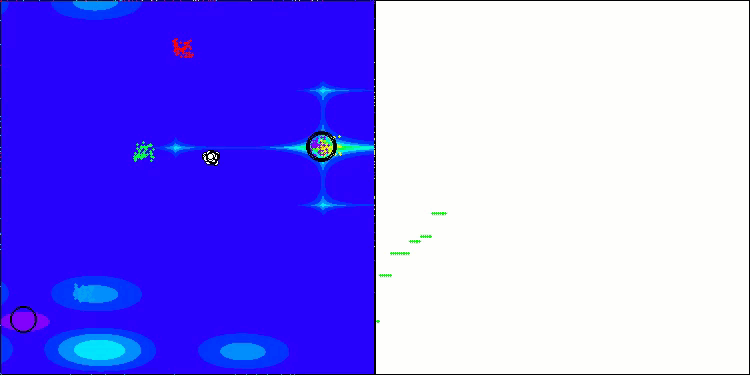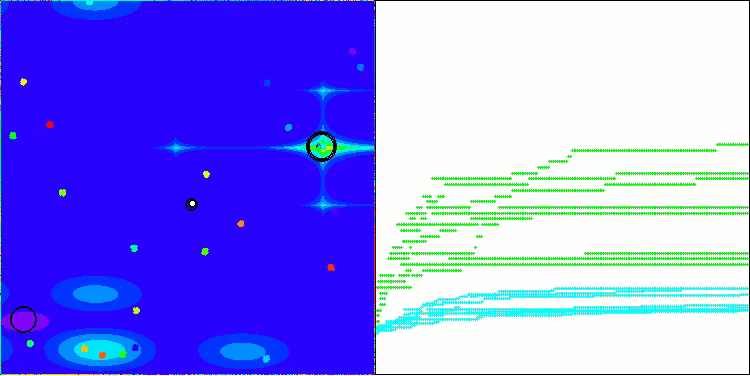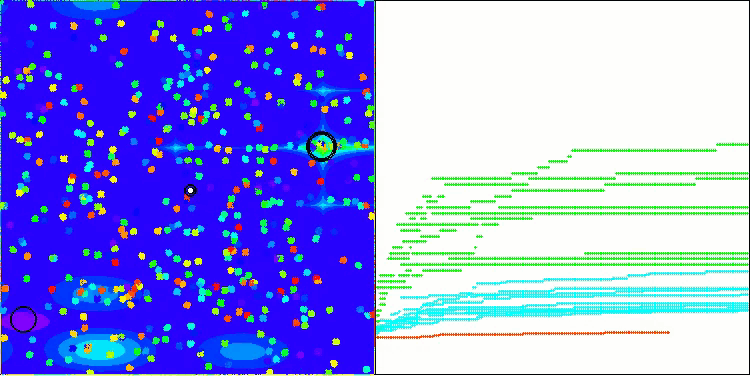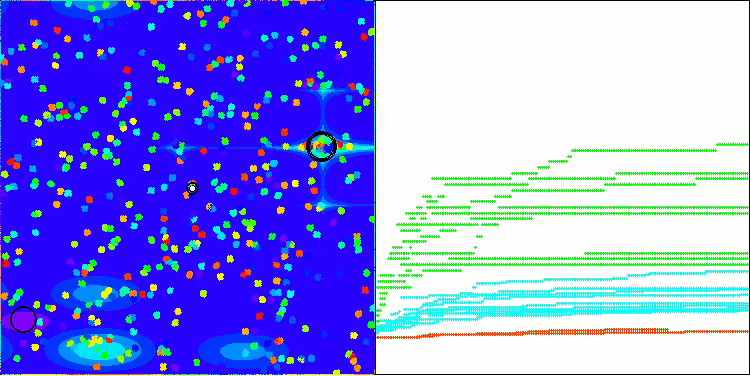
BHAm en la función de prueba Megacity
La versión corregida del BBBC ha ocupado el puesto 43 en la tabla de clasificación. El RW (el paseo aleatorio) no participa en la clasificación y se ofrece como referencia del límite inferior de "significatividad" de las estrategias de búsqueda.
| № | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % de MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration optimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 7 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 8 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 9 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 10 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 11 | BHAm | black hole algorithm M | 0,75236 | 0,76675 | 0.34583 | 1,86493 | 0.93593 | 0.80152 | 0,27177 | 2,00923 | 0.65077 | 0.51646 | 0,15472 | 1,32195 | 5.196 | 57.73 |
| 12 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 13 | AOSm | búsqueda de orbitales atómicos M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| 14 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 15 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 16 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 17 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 18 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 19 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 20 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 21 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 22 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 23 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 24 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 25 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 26 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 27 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 28 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 29 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 30 | SOA | simple optimization algorithm | 0.91520 | 0.46976 | 0.27089 | 1,65585 | 0.89675 | 0.37401 | 0.16984 | 1,44060 | 0.69538 | 0.28031 | 0.10852 | 1,08422 | 4.181 | 46,45 |
| 31 | ABH | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4.127 | 45,85 |
| 32 | ACMO | atmospheric cloud model optimization | 0,90321 | 0,48546 | 0,30403 | 1,69270 | 0,80268 | 0,37857 | 0,19178 | 1,37303 | 0,62308 | 0,24400 | 0,10795 | 0,97503 | 4,041 | 44,90 |
| 33 | ADAMm | adaptive moment estimation M | 0.88635 | 0.44766 | 0,26613 | 1.60014 | 0.84497 | 0.38493 | 0.16889 | 1,39880 | 0,66154 | 0.27046 | 0.10594 | 1,03794 | 4.037 | 44.85 |
| 34 | ATAm | artificial tribe algorithm M | 0.71771 | 0.55304 | 0,25235 | 1,52310 | 0.82491 | 0.55904 | 0,20473 | 1,58867 | 0,44000 | 0,18615 | 0.09411 | 0.72026 | 3.832 | 42.58 |
| 35 | ASHA | artificial showering algorithm | 0,89686 | 0,40433 | 0,25617 | 1,55737 | 0,80360 | 0,35526 | 0,19160 | 1,35046 | 0,47692 | 0,18123 | 0,09774 | 0,75589 | 3,664 | 40,71 |
| 36 | ASBO | adaptive social behavior optimization | 0,76331 | 0,49253 | 0,32619 | 1,58202 | 0,79546 | 0,40035 | 0,26097 | 1,45677 | 0,26462 | 0,17169 | 0,18200 | 0,61831 | 3.657 | 40,63 |
| 37 | MEC | mind evolutionary computation | 0,69533 | 0,53376 | 0,32661 | 1,55569 | 0,72464 | 0,33036 | 0,07198 | 1,12698 | 0,52500 | 0,22000 | 0,04198 | 0,78698 | 3,470 | 38,55 |
| 38 | IWO | invasive weed optimization | 0,72679 | 0,52256 | 0,33123 | 1,58058 | 0,70756 | 0,33955 | 0,07484 | 1,12196 | 0,42333 | 0,23067 | 0,04617 | 0,70017 | 3,403 | 37,81 |
| 39 | Micro-AIS | micro artificial immune system | 0,79547 | 0,51922 | 0,30861 | 1,62330 | 0,72956 | 0,36879 | 0,09398 | 1,19233 | 0,37667 | 0,15867 | 0,02802 | 0,56335 | 3,379 | 37,54 |
| 40 | COAm | cuckoo optimization algorithm M | 0,75820 | 0,48652 | 0,31369 | 1,55841 | 0,74054 | 0,28051 | 0,05599 | 1,07704 | 0,50500 | 0,17467 | 0,03380 | 0,71347 | 3,349 | 37,21 |
| 41 | SDOm | spiral dynamics optimization M | 0,74601 | 0,44623 | 0,29687 | 1,48912 | 0,70204 | 0,34678 | 0,10944 | 1,15826 | 0,42833 | 0,16767 | 0,03663 | 0,63263 | 3,280 | 36,44 |
| 42 | NMm | Nelder-Mead method M | 0,73807 | 0,50598 | 0,31342 | 1,55747 | 0,63674 | 0,28302 | 0,08221 | 1,00197 | 0,44667 | 0,18667 | 0,04028 | 0,67362 | 3,233 | 35,92 |
| 43 | BBC | big bang-big crunch algorithm | 0.60531 | 0.45250 | 0.31255 | 1,37036 | 0.52323 | 0.35426 | 0,20417 | 1,08166 | 0.39769 | 0,19431 | 0.11286 | 0.70486 | 3.157 | 35.08 |
| 44 | FAm | firefly algorithm M | 0,58634 | 0,47228 | 0,32276 | 1,38138 | 0,68467 | 0,37439 | 0,10908 | 1,16814 | 0,28667 | 0,16467 | 0,04722 | 0,49855 | 3,048 | 33,87 |
| 45 | GSA | gravitational search algorithm | 0,64757 | 0,49197 | 0,30062 | 1,44016 | 0,53962 | 0,36353 | 0,09945 | 1,00260 | 0,32667 | 0,12200 | 0,01917 | 0,46783 | 2,911 | 32,34 |
| R.W. | random walk | 0.48754 | 0.32159 | 0.25781 | 1,06694 | 0.37554 | 0,21944 | 0,15877 | 0,75375 | 0.27969 | 0,14917 | 0.09847 | 0.52734 | 2.348 | 26.09 | |
Conclusiones
El algoritmo BBBC (Big Bang-Big Crunch) supone un enfoque interesante para la optimización global inspirado en los procesos cosmológicos. Sin embargo, los resultados de las pruebas muestran que su supuesta eficacia se ha exagerado. Resulta importante señalar que el algoritmo concentra la búsqueda en el centro del espacio, lo que puede crear la ilusión de altas capacidades de búsqueda. Esto no indica que las capacidades del algoritmo sean sobresalientes, sino más bien que las condiciones del problema coinciden con sus características.
También vale la pena mencionar que muchas funciones de prueba estándar usadas para evaluar algoritmos tienen un óptimo global ubicado en el centro del espacio de búsqueda. Estas pruebas no siempre son fiables y pueden resultar engañosas respecto a las capacidades de búsqueda reales de algoritmos como el BBBC, que tienen características poco fiables en su estrategia de búsqueda. Por consiguiente, a veces las "verdades" ampliamente conocidas deben tratarse con cautela y pensamiento crítico.
Sin embargo, la versión modificada del algoritmo BBBC muestra buenos resultados en problemas de alta dimensionalidad, lo que resalta su potencial de desarrollo. Esto abre nuevas oportunidades para futuras investigaciones y mejoras que pueden aumentar su rendimiento en problemas de optimización más complejos y diversos, además de enriquecer nuestra base de conocimientos con nuevas técnicas para encontrar soluciones óptimas.
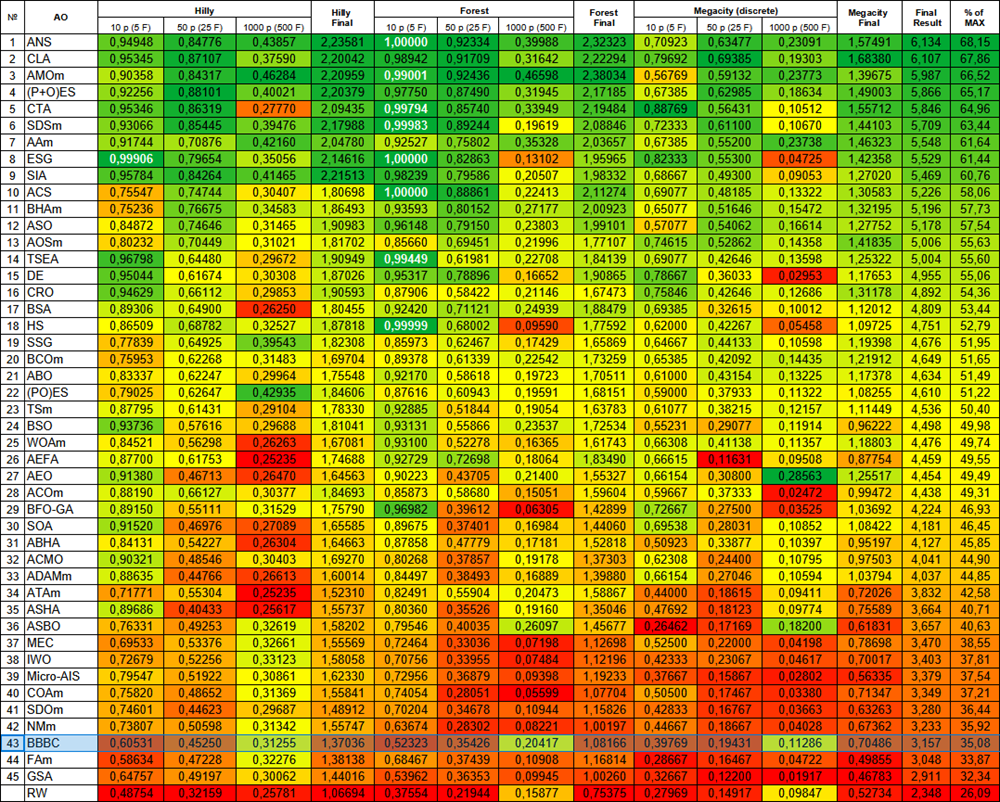
Figura 2. Gradación por colores de los algoritmos según sus respectivas pruebas. Los resultados superiores o iguales a 0.99 se resaltan en blanco.
La gradación de color en la tabla ilustra claramente que no todos los algoritmos de optimización resultan más eficientes que el paseo aleatorio simple (RW), especialmente para algunos tipos de problemas. Esto se ve especialmente bien en el contexto de los problemas multidimensionales, donde la complejidad del terreno y la dimensionalidad del espacio de búsqueda aumentan significativamente. En tales casos, muchas estrategias tradicionales pueden perder su eficacia y enfrentarse a problemas asociados a los extremos locales, la maldición de la dimensionalidad y otros factores. Sin embargo, esto no significa que recomendemos el uso de la búsqueda aleatoria como método principal, aunque sea importante compararla para comprender mejor las limitaciones y capacidades de las diferentes estrategias de optimización.
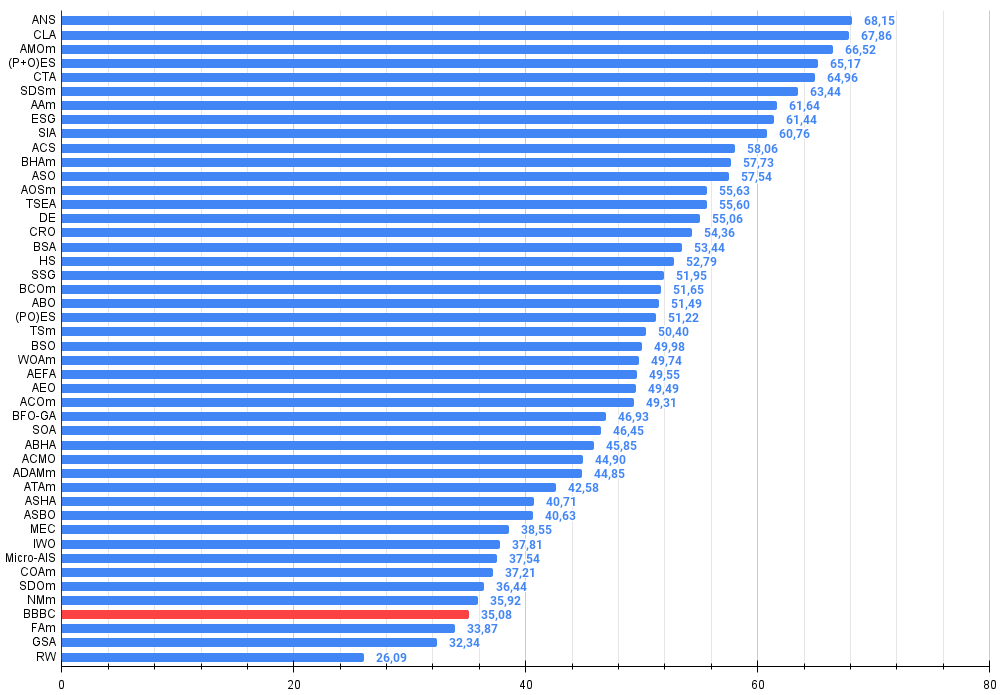
Figura 3. Histograma con los resultados de las pruebas de los algoritmos (en una escala de 0 a 100, cuanto más mejor, donde 100 es el máximo resultado teórico posible, el script para calcular la tabla de puntuación está en el archivo)
Ventajas y desventajas de la versión corregida del algoritmo BBBC:
Ventajas:
- El único parámetro externo es el tamaño de la población.
- Implementación sencilla.
- Gran rapidez.
- Funciona bien en problemas de gran escala.
Desventajas:
- Gran dispersión de resultados para problemas de pequeña dimensionalidad.
- Tiende a estancarse en problemas de baja dimensionalidad.
Adjuntamos al artículo un archivo con las versiones actuales de los códigos de los algoritmos. El autor de este artículo no se responsabiliza de la exactitud absoluta de la descripción de los algoritmos canónicos, muchos de ellos han sido modificados para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos realizados.
Programas usados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | #C_AO.mqh | Archivo de inclusión | Clase padre de algoritmos de optimización basados en la población |
| 2 | #C_AO_enum.mqh | Archivo de inclusión | Enumeración de los algoritmos de optimización basados en la población |
| 3 | TestFunctions.mqh | Archivo de inclusión | Biblioteca de funciones de prueba |
| 4 | TestStandFunctions.mqh | Archivo de inclusión | Biblioteca de funciones del banco de pruebas |
| 5 | Utilities.mqh | Archivo de inclusión | Biblioteca de funciones auxiliares |
| 6 | CalculationTestResults.mqh | Archivo de inclusión | Script para calcular los resultados en una tabla comparativa |
| 7 | Testing AOs.mq5 | Script | Banco de pruebas único para todos los algoritmos de optimización basados en la población |
| 8 | Simple use of population optimization algorithms.mq5 | Script | Ejemplo sencillo de utilización de algoritmos de optimización basados en la población sin visualización |
| 9 | Test_AO_BBBC.mq5 | Script | Banco de pruebas para el BBBC |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/16701
Del básico al intermedio: Struct (II)
Selección de características paso a paso en MQL5
Redes neuronales en el trading: Agente con memoria multinivel
Del básico al intermedio: Plantilla y Typename (IV)
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso