
Big Bang – Big Crunch (BBBC) Algorithmus
Inhalt
Einführung
In den unermesslichen Weiten des Universums, wo Sterne geboren werden und sterben, gibt es verborgene Geheimnisse, die die Menschheit zu enträtseln versucht. Die Methode Big Bang – Big Crunch (BBBC) ist ein globaler Optimierungsalgorithmus, der von Prozessen im Weltraum inspiriert ist. Lassen Sie uns dieses faszinierende Konzept erforschen.
Die Theorie von Big Bang und Big Crunch wurde Anfang des 20. Jahrhunderts von den Physikern Alexander Friedmann und Georges Lemaitre als alternatives Szenario für das Ende des Universums vorgeschlagen. Sie stellten fest, dass Einsteins Gleichungen der allgemeinen Relativitätstheorie sowohl eine Expansion als auch eine Kontraktion des Universums zulassen. Friedman bewies mathematisch, dass das Universum nicht statisch bleiben kann und sich entweder ausdehnen oder zusammenziehen muss. Er ermittelte drei mögliche Szenarien für ihre Entwicklung: ewige Expansion, Expansion gefolgt von Kontraktion und ein oszillierendes Regime.
Im Laufe des 20. Jahrhunderts entwickelten viele Wissenschaftler Ideen, die Big Bang und Big Crunch zu einem zyklischen Modell kombinierten. Heute ist die Theorie des Big Crunch nicht mehr das wichtigste kosmologische Modell, da Beobachtungen zeigen, dass sich das Universum immer schneller ausdehnt. Dieses Konzept ist jedoch eine interessante Idee, die eine zyklische Natur der Entwicklung des Universums nahelegt. Die wichtigsten Etappen:
- Der Big Bang, bei dem der anfängliche Zustand hoher Dichte und Temperatur in ein Stadium rascher Ausdehnung und Energieabgabe mit der Bildung von Materie und Raumzeit sowie einer chaotischen Verteilung von Teilchen übergeht.
- Beim Big Crunch, wenn die Gravitationskräfte die Expansion stoppen und die Kontraktion beginnt, wird die gesamte Materie in einen Punkt zurückgezogen und kehrt in einen Zustand hoher Dichte zurück.
- Der Kreislauf drückt sich in der Abfolge eines neuen Big Bang nach einem Big Crunch aus, der Prozess kann unendlich oft wiederholt werden, und jeder Zyklus kann unterschiedliche physikalische Konstanten haben.
Der Algorithmus von Big Bang – Big Crunch wurde 2006 von den Wissenschaftlern Osman K. Erol und Ibrahim Eksin von der Technischen Universität Istanbul (Türkei) vorgeschlagen.
Implementierung des Algorithmus
Wie beim Big Bang, bei der das Universum seine Existenz mit einem gewaltigen Energiestoß beginnt, beobachten wir auch bei der Methode BBBC eine Anfangsphase voller Zufälligkeit und Vielfalt. In der Phase des Big Bang entsteht eine Population von zufälligen Punkten. Jeder von ihnen ist ein Kandidat für eine Lösung. Diese Punkte sind über den riesigen Suchraum verstreut und warten darauf, erkundet zu werden, aber sobald das Chaos seinen Platz gefunden hat, beginnt die Big Crunch-Phase. Die Punkte neigen dazu, sich in Richtung des „Massenmittelpunkts“ zu bewegen, so wie Galaxien durch die Schwerkraft zueinander hingezogen werden. Dieser Moment ist der Höhepunkt, an dem alle Bemühungen auf der Suche nach der optimalen Lösung zusammenkommen.
Hier sind die Stufen des Algorithmus, der Weg vom Chaos zur Ordnung:
1. Die Phase des Big Bang. In diesem ersten Schritt wird eine Grundgesamtheit von N Zufallspunkten erstellt. Jeder Punkt nimmt seinen eigenen Platz im Raum ein, gleichmäßig verteilt innerhalb der vorgegebenen Grenzen.
2. Die Phase des Big Crunch. Übergang zur Berechnung des „Massenschwerpunkts“ – dem Punkt, den alle anderen anstreben. Mit Hilfe der Gleichung (Abb. 1) werden die Koordinaten des Mittelpunkts ermittelt, die der neue Ausgangspunkt für die nächsten Schritte sein wird.
3. Generierung neuer Punkte. Es entstehen neue Punkte um den Massenschwerpunkt herum. Sie werden mit einer Normalverteilung gebildet, die einer Gleichung folgt, die ihnen die Richtung und die Größe der Bewegung gibt.
Die Methode BBBC strebt nach Harmonie zwischen Exploration und Verfeinerung. Mit jeder neuen Generation nimmt die Streuung der Punkte bei der Erzeugung ab, wodurch der Algorithmus die gefundene optimale Lösung verfeinern kann.
Genau wie im Weltraum, wo jeder Schritt zählt, bringt uns in der Welt der Optimierung jede Berechnung unserem Ziel näher. Indem wir uns auf diese Methode einlassen, eröffnen wir nicht nur neue Horizonte, sondern werden auch Teil eines großen kosmischen Prozesses auf der Suche nach einer besseren Lösung.
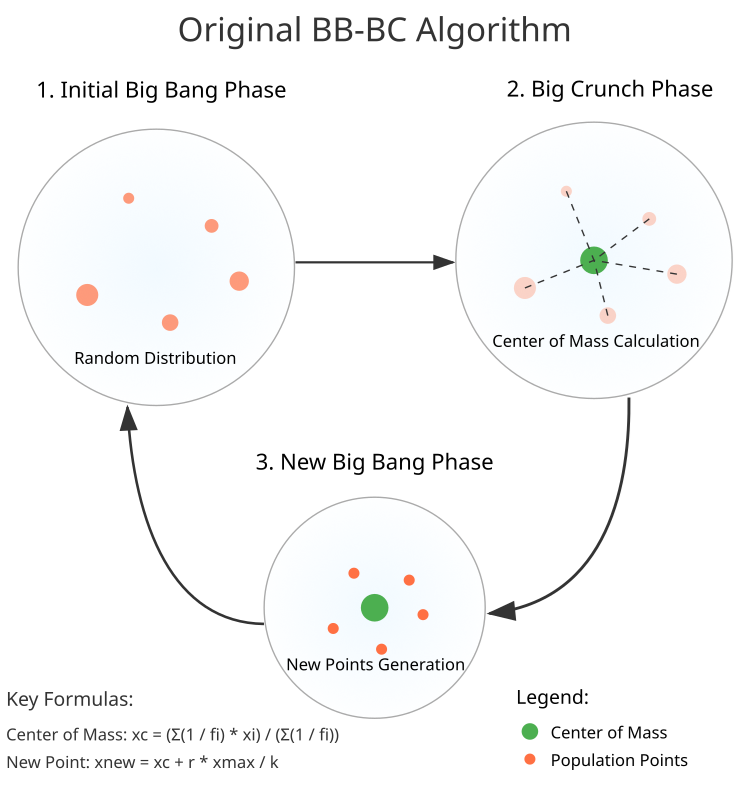
Abbildung 1. Struktur des BBBC-Algorithmus
Schreiben wir einen Pseudocode für den BBBC-Algorithmus:
epochNow erhöhen
// Initialisierung (Big Bang)
wenn Revision == false
Für jedes einzelne i von 0 bis popSize-1
Für jede Koordinate c von 0 bis coords-1
Neue Koordinate = Erzeugen einer Zufallszahl (rangeMin[c], rangeMax[c])
„Revision“ auf „true“ setzen
Rückkehr
// Big Crunch Phase
Wenn epochNow % bigBangPeriod != 0
Für jede Koordinate c von 0 bis coords-1
Zähler = 0, Nenner = 0
Für jedes einzelne i von 0 bis popSize-1
Fitness = Maximum (Absoluter Wert (a[i].f), 1e-10)
вес = 1,0 / Fitness
Zähler += Gewicht * Punktkoordinate
Nenner += Gewicht
centerMass[c] = (Nenner > 1e-10) ? Zähler / Nenner : cB[c]
Für jedes einzelne i von 0 bis popSize-1
Für jede Koordinate c von 0 bis coords-1
r = Erzeuge eine normalen Zufallszahl (0, -1,0, 1,0, 1)
Neue Koordinate = centerMass[c] + r * rangeMax[c] / epochNow
// Big Bang Phase
andernfalls
Für jedes einzelne i von 0 bis popSize-1
Für jede Koordinate c von 0 bis coords-1
Neue Koordinate = Erzeuge eine normale Zufallszahl (cB[c], rangeMin[c], rangeMax[c], Standardabweichung = 8)
Wiederhole den Vorgang, bis das Kriterium für das Ende der Big Crunch-Phase erfüllt ist.
Kommen wir nun zum Schreiben des Codes. Schreiben wir die Definition der Klasse C_AO_BBBC, einem Abkömmling von C_AO:
Öffentliche Methoden:- Konstruktor und Destruktor
- SetParams () – Parameter setzen (Populationsgröße und Periodizität des Big Bang)
- Init () – Initialisierung des Algorithmus mit vorgegebenen Suchgrenzen
- Moving () – Hauptmethode zur Umsetzung der Big Bang und Big Crunch Phasen
- Revision () – Methode zur Aktualisierung der besten gefundenen Lösung
- epochs – Gesamtzahl der Epochen, in denen der Algorithmus läuft
- epochNow – aktuelle Epoche
- centerMass[] – Array zum Speichern der Koordinaten des Massenschwerpunkts
Bei der Klasse handelt es sich um eine Implementierung des BBBC-Algorithmus, bei der alle wichtigen Berechnungen in den Methoden Moving() und Revision() durchgeführt werden und die erforderlichen Bevölkerungsdaten in der Basisklasse C_AO gespeichert sind.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_BBBC : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_BBBC () { } C_AO_BBBC () { ao_name = "BBBC"; ao_desc = "Big Bang - Big Crunch Algorithm"; ao_link = "https://www.mql5.com/en/articles/16701"; popSize = 50; bigBangPeriod = 3; ArrayResize (params, 2); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "bigBangPeriod"; params [1].val = bigBangPeriod; } void SetParams () { popSize = (int)params [0].val; bigBangPeriod = (int)params [1].val; } bool Init (const double &rangeMinP [], // minimum search range const double &rangeMaxP [], // maximum search range const double &rangeStepP [], // search step const int epochsP = 0); // number of epochs void Moving (); void Revision (); //---------------------------------------------------------------------------- int bigBangPeriod; // Big Bang periodicity private: //------------------------------------------------------------------- int epochs; // total number of epochs int epochNow; // current epoch double centerMass []; // center of mass }; //——————————————————————————————————————————————————————————————————————————————
Die Methode Init der Klasse C_AO_BBBC:
Die Methode initialisiert den Algorithmus und übernimmt die folgenden Parameter:
- rangeMinP[] – Array der Mindestwerte für jede Koordinate
- rangeMaxP[] – Array der Höchstwerte für jede Koordinate
- rangeStepP[] – Array der Diskretisierungsschritte für jede Koordinate
- epochsP – Anzahl der Epochen der Algorithmusoperationen (Standardwert 0)
Methodische Maßnahmen:
- Aufruf von StandardInit() der Basisklasse, um gemeinsame Parameter zu initialisieren.
- Zurücksetzten der Gesamtzahl der Epochen (epochs) und setzt den aktuellen Epochenzähler (epochNow) zurück.
- Speicheranforderung für das Massenschwerpunkt-Array (centerMass) der Größe coords (Anzahl der Koordinaten).
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_BBBC::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { // Initialize the base class if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- epochs = epochsP; epochNow = 0; // Allocate memory for arrays ArrayResize (centerMass, coords); return true; } //——————————————————————————————————————————————————————————————————————————————
Die MethodeMoving des BB-BC-Algorithmus besteht aus drei Hauptteilen:
1. Beginn der Initialisierung (wenn Revision = false):
- Erstelle eine Grundgesamtheit von Zufallspunkten
- Bringe sie zu einem diskreten Suchraster
2. Die Phase Big Crunch (wenn „epoch“ kein Vielfaches von bigBangPeriod ist):
- Berechne den Massenschwerpunkt nach folgender Gleichung: xc = (Σ(1/fi)*xi) / (Σ(1/fi))
- Erzeuge neue Punkte um den Massenschwerpunkt mit der Gleichung: xnew = xc + r * xmax / epoch
- Verwendung der Normalverteilung für Zufallszahlen
3. Die Phase des Big Bang (wenn „Epoche“ ein Vielfaches von bigBangPeriod ist):
- Neue Punkte mit der Normalverteilung generieren
- Verwenden der besten Lösung als Durchschnitt
- Verwendung von deviation = 8 für eine breite Suche
Alle neuen Punkte werden durch die angegebenen Suchgrenzen begrenzt und in ein diskretes Gitter umgewandelt.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BBBC::Moving () { epochNow++; // Starting initialization (Big Bang) if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { // Generate random starting dots a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); // Reduction to discrete search grid a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- // Big Crunch phase - big collapse if (epochNow % bigBangPeriod != 0) { for (int c = 0; c < coords; c++) { double numerator = 0; double denominator = 0; for (int i = 0; i < popSize; i++) { // Calculate weight as the inverse of the fitness function value double fitness = MathMax (MathAbs (a [i].f), 1e-10); double weight = 1.0 / fitness; // Summation to calculate the center of mass using the equation // xc = (Σ(1/fi)xi) / (Σ(1/fi)) numerator += weight * a [i].c [c]; denominator += weight; } // Determine the coordinates of the center of mass centerMass [c] = denominator > 1e-10 ? numerator / denominator : cB [c]; } for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { double r = u.GaussDistribution (0, -1.0, 1.0, 1); // Generate a new point using the equation // xnew = xc + r*xmax/k double newPoint = centerMass [c] + r * rangeMax [c] / epochNow; // Constrain within the allowed area and convert to grid a [i].c [c] = u.SeInDiSp (newPoint, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //---------------------------------------------------------------------------- // Big Bang phase - big bang else { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.GaussDistribution (cB [c], rangeMin [c], rangeMax [c], 8); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } } //——————————————————————————————————————————————————————————————————————————————
Die Methode Revision erfüllt zwei Hauptfunktionen:
Finden der besten Lösung:- Initialisierung des Index der besten Lösung (bestInd = -1)
- Iterieren über alle Punkte in der Grundgesamtheit
- Wenn eine bessere Lösung als die aktuelle gefunden wird:
- Aktualisiert den Wert der besten Fitnessfunktion (fB)
- Speichern des Index der besten Lösung (bestInd)
- Wenn eine bessere Lösung gefunden wird (bestInd != -1):
- Kopiere alle Koordinaten der besten Lösung aus dem Array in das Array cB der besten Lösungen.
- Kopiere alle Koordinaten der besten Lösung aus dem Array in das Array cB der besten Lösungen.
Die Methode liefert während der gesamten Dauer der Algorithmusoperation aktuelle Informationen über die gefundene global beste Lösung.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BBBC::Revision () { int bestInd = -1; // Find the best solution in the current population for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; bestInd = i; } } // Update the best known solution if (bestInd != -1) ArrayCopy (cB, a [bestInd].c, 0, 0, WHOLE_ARRAY); } //——————————————————————————————————————————————————————————————————————————————
Die Autoren von BBBC behaupten, dass er mit bekannten starken Algorithmen wie genetischen Algorithmen (GAs) konkurrieren kann und diese in deutlich weniger Epochen übertrifft.
Als Beweis führen sie Testergebnisse zu standardmäßigen und weit verbreiteten synthetischen Benchmarks an, wie die Sphäre (auch bekannt als Paraboloid oder Ellipsoid), Ackley und Rastrigin. Werfen wir einen Blick auf die Visualisierung der Algorithmusleistung bei zwei dieser Benchmarks.
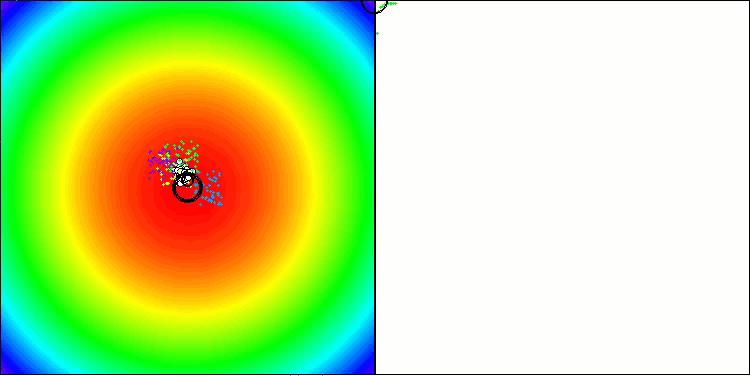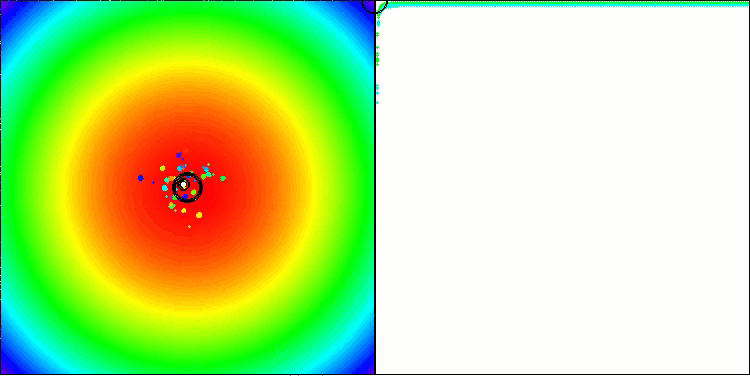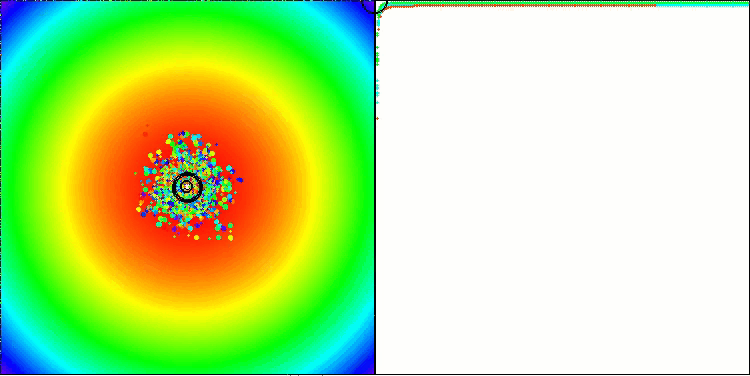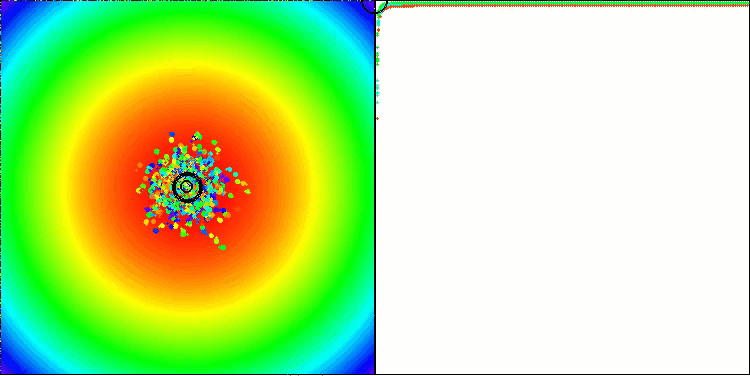
BBBC mit der Paraboloid-Testfunktion
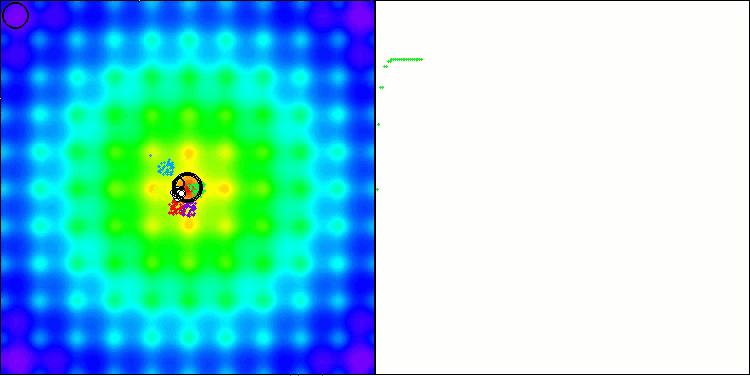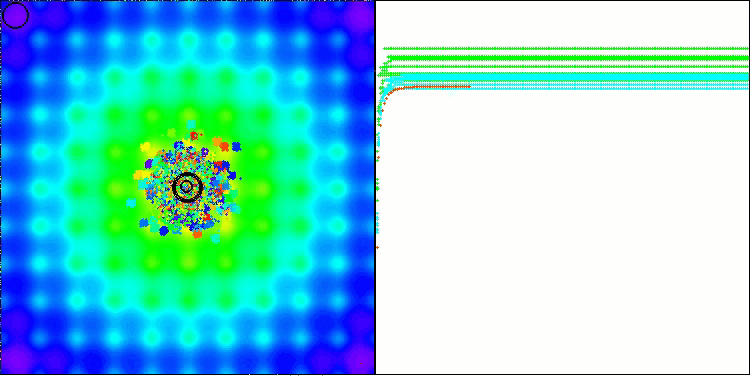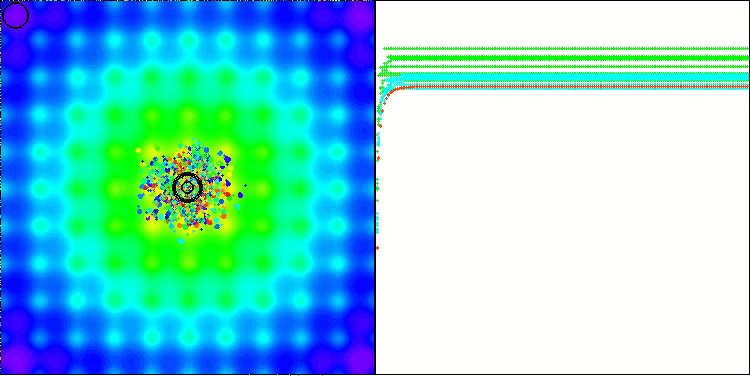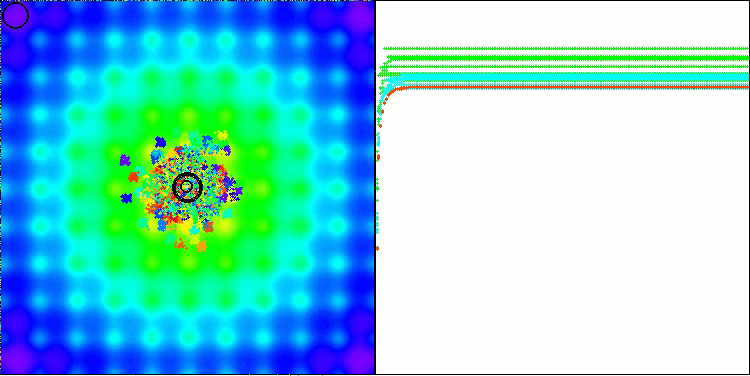
BBBC mit der Ackley-Testfunktion
Die Ergebnisse sind in der Tat beeindruckend. Besonders bemerkenswert ist, dass sich die Ergebnisse für hochdimensionale Probleme (rote Linie) kaum von den Ergebnissen für niedrigdimensionale Probleme (grüne Linie) unterscheiden, was auf die hohe Skalierbarkeit des Algorithmus hinweist. Obwohl die Konvergenzgenauigkeit bei der Ackley-Funktion nicht perfekt ist, sind die Ergebnisse dennoch bemerkenswert.
Betrachten wir nun die Ergebnisse der Arbeit von BBBC an unseren speziell für Optimierungsalgorithmen entwickelten Testfunktionen.
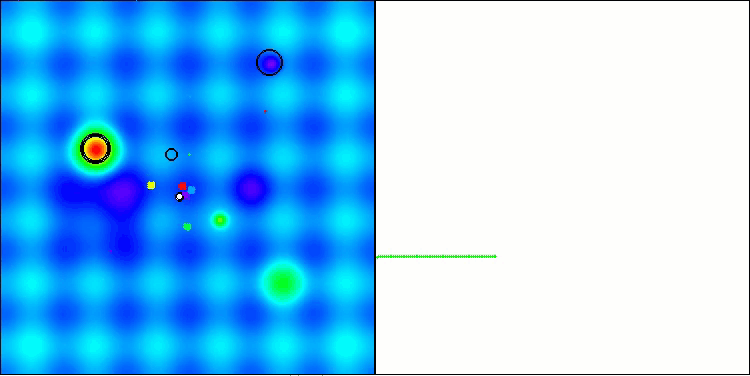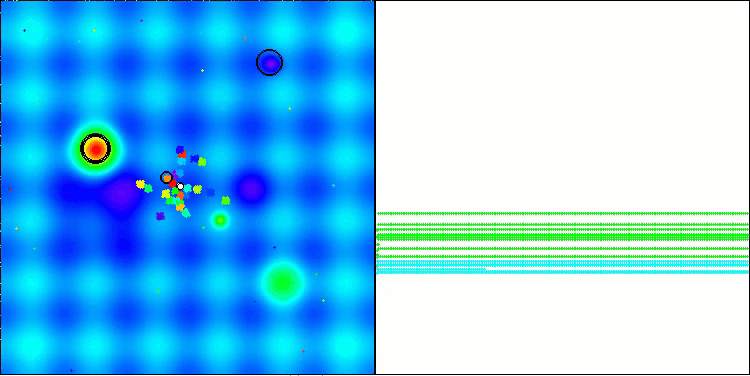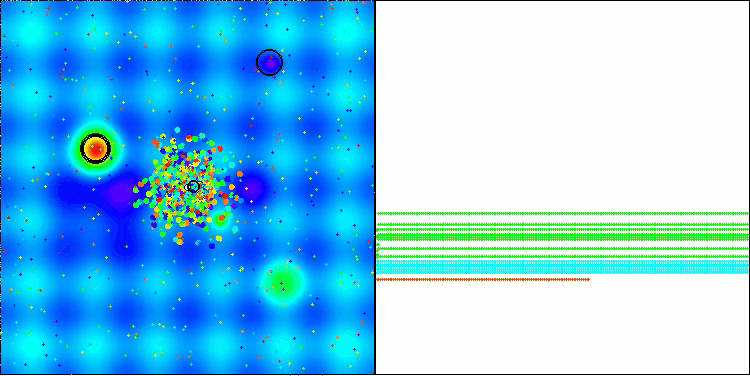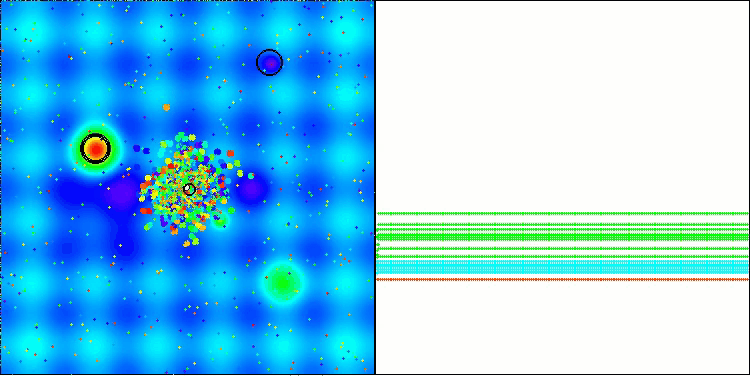
BBBC mit der Testfunktion Hilly
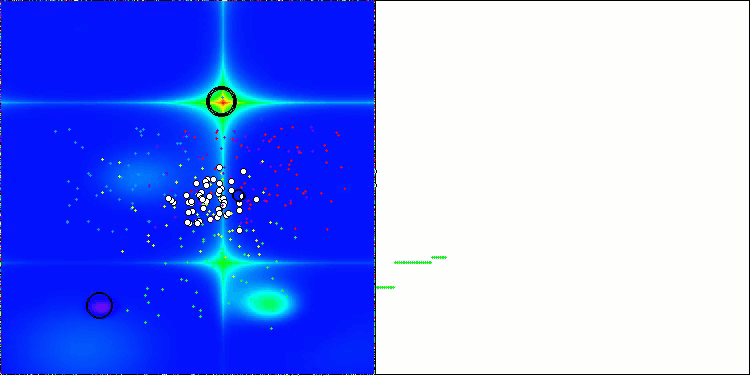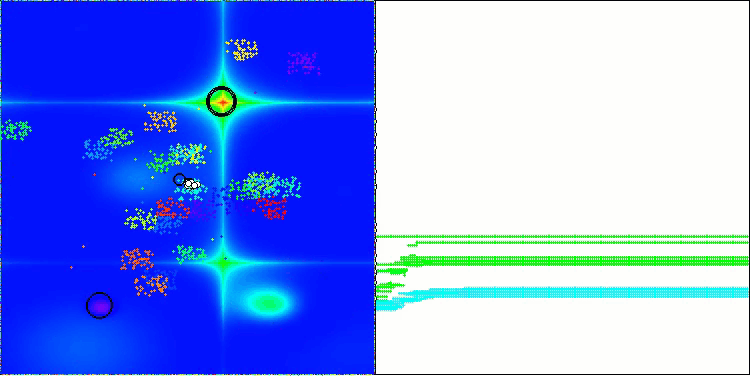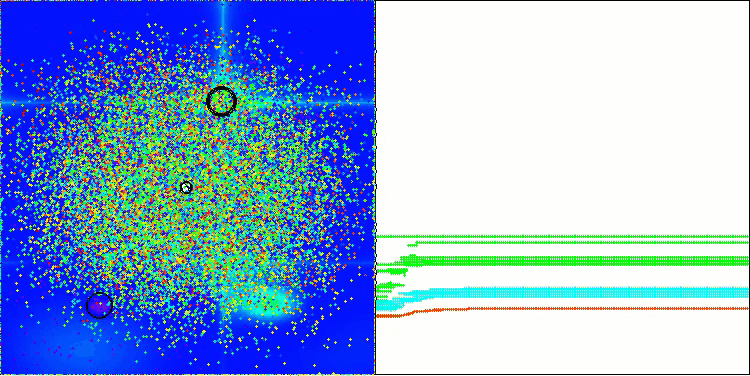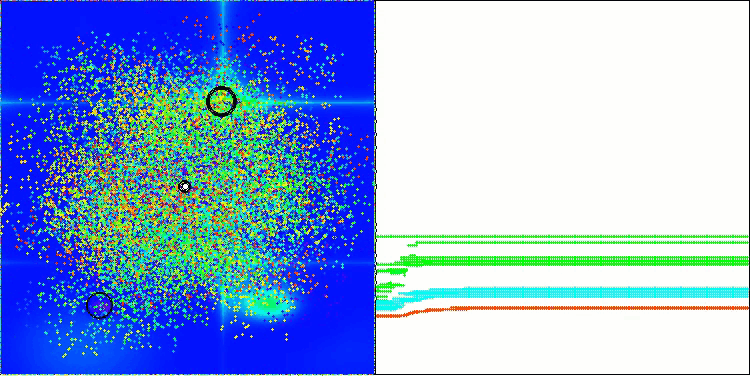
BBBC mit der Testfunktion Forest
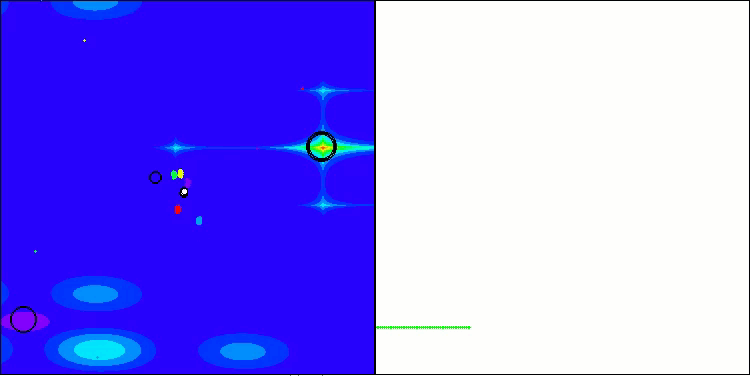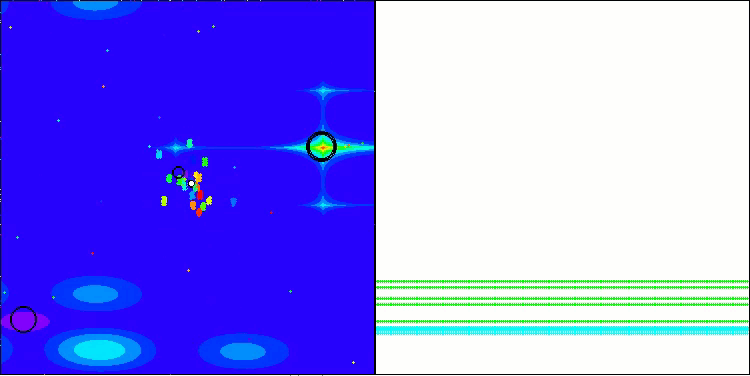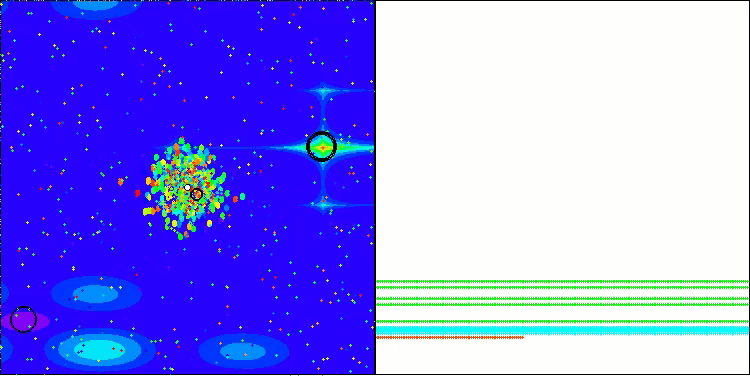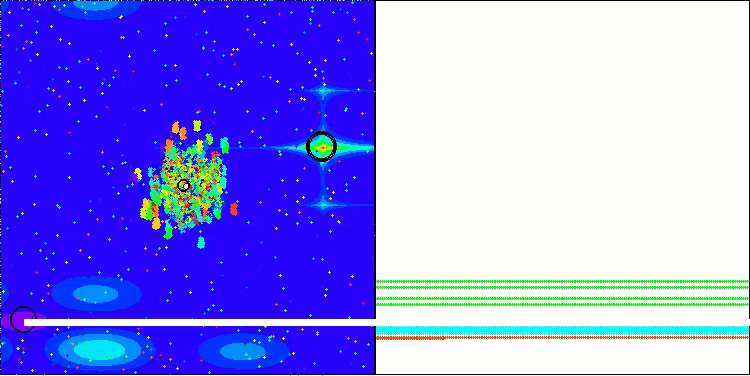
BBBC mit der Testfunktion Megacity
Leider funktionierte die Magie des Algorithmus bei unseren Benchmarks nicht mehr. Was ist der Grund dafür? Zunächst einmal ist zu beachten, dass die Algorithmuspopulation bei den Tests „Hilly“, „Forest“ und „Megacity“ wie bei den vorherigen Funktionen ihre „Aufmerksamkeit“ auf den zentralen Teil des Suchraums richtet. Diese Beobachtung wirft einige Fragen auf und erscheint recht merkwürdig.
Werfen wir einen Blick unter die Haube des BBBC-Algorithmus und untersuchen seine Funktionsweise. Wir werden sehen, dass bei Verwendung des „Massenschwerpunkts“ die im Raum verteilten Punkte dazu neigen, in der Mitte des Funktionsbereichs zusammenzufallen. Dies geschieht, weil der Massenschwerpunkt der Punkte genau in der Mitte liegt, was die Illusion der Effizienz des Algorithmus erzeugt. Diese Koinzidenz führt dazu, dass der Algorithmus in der Lage ist, erfolgreich Optima für kugelförmige Funktionen (mit dem globalen Optimum in der Mitte des Bereichs) zu finden. In Wirklichkeit ist dies jedoch nicht das Ergebnis der hervorragenden Suchfähigkeiten des Algorithmus, sondern ein glücklicher Zufall. Würde der Algorithmus beispielsweise bei der Koordinate 0,0 beginnen, würde er im Idealfall bei der ersten Iteration das globale Optimum erreichen.
Es ist anzumerken, dass die meisten Standard-Testfunktionen, die zur Bewertung verschiedener Algorithmen verwendet werden, ein globales Optimum in der Mitte des Suchraums aufweisen. Solche Tests sind nicht immer zuverlässig, und bei einigen Algorithmen, wie z. B. BBBC, können sie irreführend sein, was die tatsächlichen Suchfähigkeiten des Algorithmus betrifft.
Um falsch-positive Ergebnisse bei der Prüfung zu vermeiden, habe ich spezielle Testfunktionen entwickelt, die:
- nicht symmetrisch sind
- ein globales Optimum haben, das nicht in der Mitte des Suchraums liegt
- nicht periodisch sind
- einen kleinen Teil der Oberfläche oberhalb der Mittellinie haben.
Werfen wir nun einen Blick auf den Ausdruck der BBBC-Ergebnisse zu den in der nachstehenden Tabelle gesammelten Testfunktionen. Das ist sehr wichtig.
| Big Bang in jeder 2. Epoche | Big Bang in jeder 3. Epoche | Big Bang in jeder 10. Epoche |
|---|---|---|
| BBBC|Big Bang - Big Crunch Algorithm|50.0|2.0| ============================= 5 Hilly's; Func runs: 10000; result: 0.5789409521562645 25 Hilly's; Func runs: 10000; result: 0.36005433010965165 500 Hilly's; Func runs: 10000; result: 0.25650127842145554 ============================= 5 Forest's; Func runs: 10000; result: 0.5232991213500953 25 Forest's; Func runs: 10000; result: 0.293874681679014 500 Forest's; Func runs: 10000; result: 0.18830469994313143 ============================= 5 Megacity's; Func runs: 10000; result: 0.3269230769230769 25 Megacity's; Func runs: 10000; result: 0.15584615384615388 500 Megacity's; Func runs: 10000; result: 0.09743846153846236 ============================= All score: 2.78118 (30.90%) | BBBC|Big Bang - Big Crunch Algorithm|50.0|3.0| ============================= 5 Hilly's; Func runs: 10000; result: 0.5550785088841808 25 Hilly's; Func runs: 10000; result: 0.3605042956384694 500 Hilly's; Func runs: 10000; result: 0.25635343911025843 ============================= 5 Forest's; Func runs: 10000; result: 0.48703749499939086 25 Forest's; Func runs: 10000; result: 0.2897958021406425 500 Forest's; Func runs: 10000; result: 0.1865439156477803 ============================= 5 Megacity's; Func runs: 10000; result: 0.28307692307692306 25 Megacity's; Func runs: 10000; result: 0.15692307692307694 500 Megacity's; Func runs: 10000; result: 0.09701538461538546 ============================= All score: 2.67233 (29.69%) | BBBC|Big Bang - Big Crunch Algorithm|50.0|10.0| ============================= 5 Hilly's; Func runs: 10000; result: 0.4883607839451155 25 Hilly's; Func runs: 10000; result: 0.3344059754605514 500 Hilly's; Func runs: 10000; result: 0.25564528470980497 ============================= 5 Forest's; Func runs: 10000; result: 0.492293124748422 25 Forest's; Func runs: 10000; result: 0.28653857694657936 500 Forest's; Func runs: 10000; result: 0.1844110334128521 ============================= 5 Megacity's; Func runs: 10000; result: 0.3230769230769231 25 Megacity's; Func runs: 10000; result: 0.15261538461538465 500 Megacity's; Func runs: 10000; result: 0.09653846153846235 ============================= All score: 2.61389 (29.04%) |
Bitte beachten Sie, dass die Testergebnisse geringfügige Abweichungen voneinander aufweisen und innerhalb des natürlichen Wertebereichs liegen. Dies deutet auf die schwachen Suchfähigkeiten der verwendeten Strategie hin, die sich im Wesentlichen kaum von der Zufallssuche unterscheidet. In diesem Zusammenhang ist es angebracht, die Ergebnisse der Prüfung des Random-Walk-Algorithmus (RW) zu präsentieren. Dieser Algorithmus wurde in früheren Artikeln erwähnt, aber die Ergebnisse seiner Anwendung wurden nicht vorgestellt. Jetzt ist es an der Zeit, es zu tun.
Die Darstellung der Ergebnisse des RW-Algorithmus ist notwendig, um beurteilen zu können, wie viel effizienter die verschiedenen Suchstrategien im Vergleich zur einfachen zufälligen Streuung von Punkten im Raum sind. Unten sehen Sie das durchschnittliche Ergebnis für 100 Testläufe (normalerweise mache ich 10).
RW|Random Walk|50.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.48753502068617777
25 Hilly's; Func runs: 10000; result: 0.3215913699940513
500 Hilly's; Func runs: 10000; result: 0.2578113480890265
=============================
5 Forest's; Func runs: 10000; result: 0.3755402348403822
25 Forest's; Func runs: 10000; result: 0.21943566240362317
500 Forest's; Func runs: 10000; result: 0.15877419882827945
=============================
5 Megacity's; Func runs: 10000; result: 0.27969230769230796
25 Megacity's; Func runs: 10000; result: 0.14916923076923083
500 Megacity's; Func runs: 10000; result: 0.098473846153847
=============================
All score: 2.34802 (26.09%)
Ich werde den Code des RW-Algorithmus zur Verfügung stellen. Es ist ganz einfach. Wie üblich ist die Funktion Moving für die Aktualisierung der Koordinaten jedes Individuums in der Population zuständig. Für jedes Individuum werden Zufallswerte in einem bestimmten Bereich generiert, die dann mit der Funktion SeInDiSp an die Schrittweite angepasst werden.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_RW::Moving () { for (int w = 0; w < popSize; w++) { for (int c = 0; c < coords; c++) { a [w].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [w].c [c] = u.SeInDiSp (a [w].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Die Revisionsfunktion prüft alle Individuen in der Population, um das Individuum mit der besten Fitnessfunktion (fB) zu finden. Wird ein solches Individuum gefunden, werden seine Koordinaten in die globale Bestnote (cB) kopiert.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_RW::Revision () { int ind = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ind = i; } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); } //——————————————————————————————————————————————————————————————————————————————
Wir werden nun einige Änderungen am ursprünglichen BBBC-Algorithmus vornehmen, um seine illusorischen Vorteile bei Problemen mit einem globalen Optimum in der Mitte des zu optimierenden Parameterbereichs zu neutralisieren und um objektive Tests zu ermöglichen. Schauen wir uns die Unterschiede im Code an. Es wurden Änderungen an der Methode „Moving“ vorgenommen:
- Die Berechnung des Massenschwerpunkts wurde entfernt.
- Geänderte Phase des Big Bang:
- Anstelle des Massenschwerpunkts (centerMass) wird die beste Lösung (cB) verwendet
- Verwenden Sie die Gleichung: xnew = cB + r*range/epochNow (“range“ ist jetzt die Differenz zwischen „rangeMax“ und „rangeMin“)
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BBBC::Moving () { epochNow++; // Starting initialization (Big Bang) if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { // Generate random starting dots a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); // Reduction to discrete search grid a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //-------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { //Big Crunch phase - big collapse if (epochNow % bigBangPeriod != 0) { for (int c = 0; c < coords; c++) { // Calculate the size of the search space for the current coordinate double range = rangeMax [c] - rangeMin [c]; // Generate a random number in the range [-1, 1] double r = u.GaussDistribution (0, -1.0, 1.0, 1); // Generate a new point using the equation // xnew = xc + r*(xmax - xmin)/(k) double newPoint = cB [c] + r * range / epochNow; // Constrain within the allowed area and convert to grid a [i].c [c] = u.SeInDiSp (newPoint, rangeMin [c], rangeMax [c], rangeStep [c]); } } // Big Bang phase - big bang else { for (int c = 0; c < coords; c++) { a [i].c [c] = u.GaussDistribution (cB [c], rangeMin [c], rangeMax [c], 8); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } } //——————————————————————————————————————————————————————————————————————————————
Testergebnisse
Ergebnisse des angepassten BBBC-Algorithmus:
BBBC|Big Bang-Big Crunch Algorithm|50.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.6053080737014771
25 Hilly's; Func runs: 10000; result: 0.45249601882946056
500 Hilly's; Func runs: 10000; result: 0.31255376970202864
=============================
5 Forest's; Func runs: 10000; result: 0.5232283922331299
25 Forest's; Func runs: 10000; result: 0.354256711141388
500 Forest's; Func runs: 10000; result: 0.20417356281490023
=============================
5 Megacity's; Func runs: 10000; result: 0.3976923076923077
25 Megacity's; Func runs: 10000; result: 0.19430769230769235
500 Megacity's; Func runs: 10000; result: 0.11286153846153954
=============================
All score: 3.15688 (35.08%)
Die Testergebnisse spiegeln nun objektiv die Fähigkeiten des BBBC-Algorithmus wider. Die Visualisierung zeigt die Bildung der gleichen „Sterne“ wie beim ursprünglichen Algorithmus, aber jetzt wird in wirklich vielversprechenden Bereichen gesucht und nicht nur überwiegend in der Mitte des Suchraums.
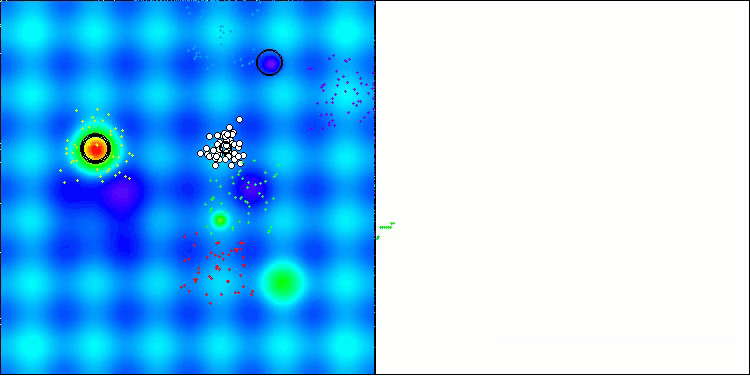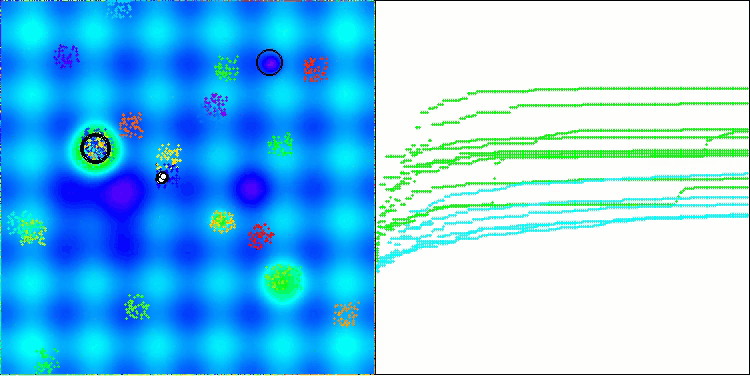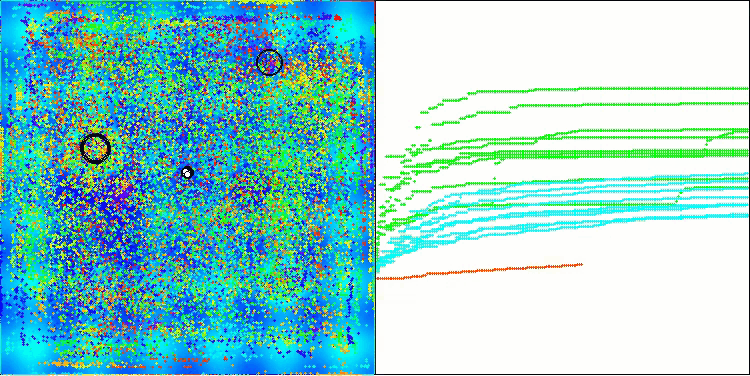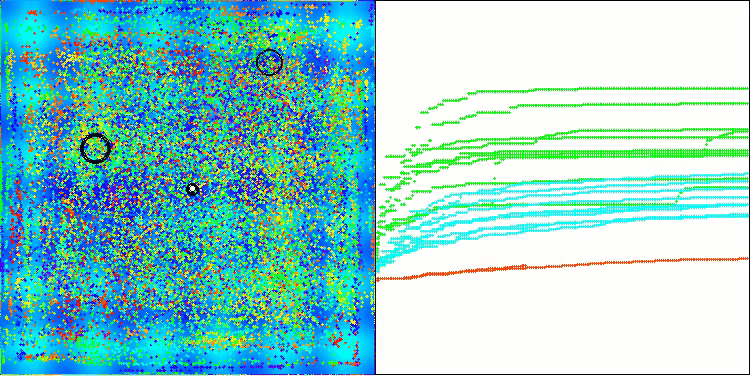
BHAm mit der Testfunktion Hilly
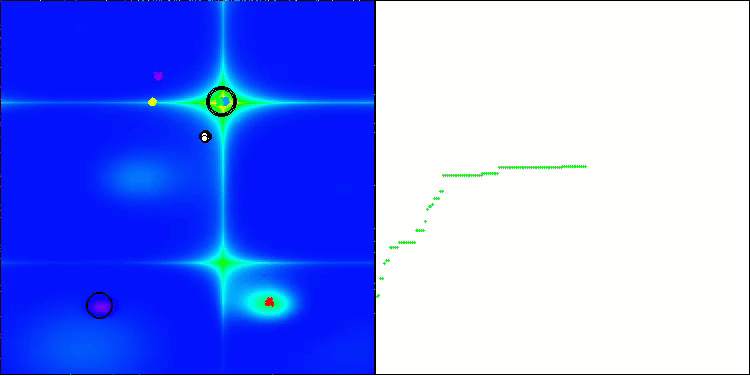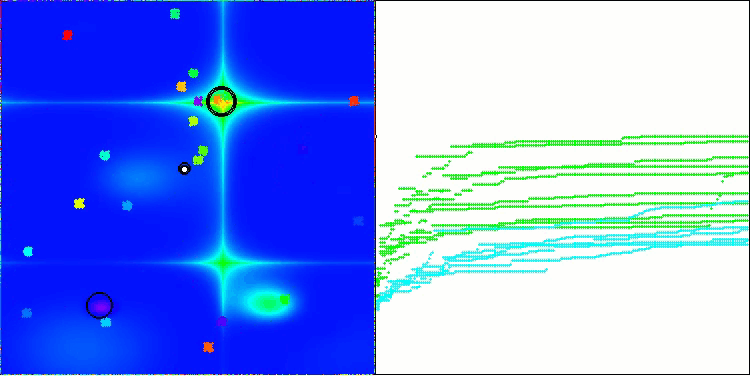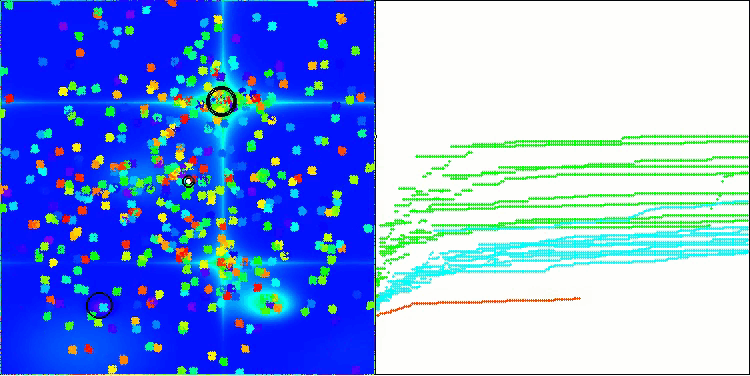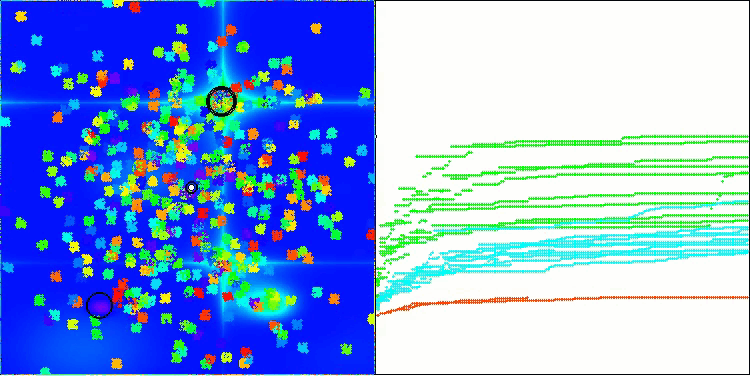
BHAm mit der Testfunktion Forest
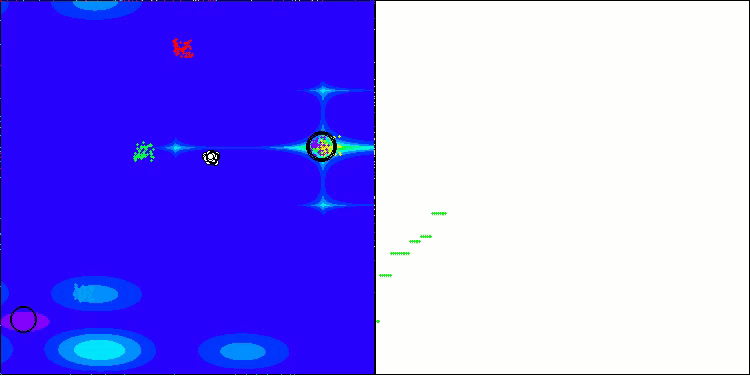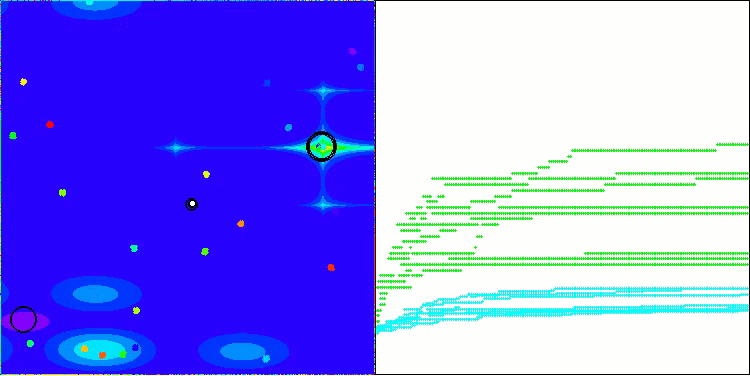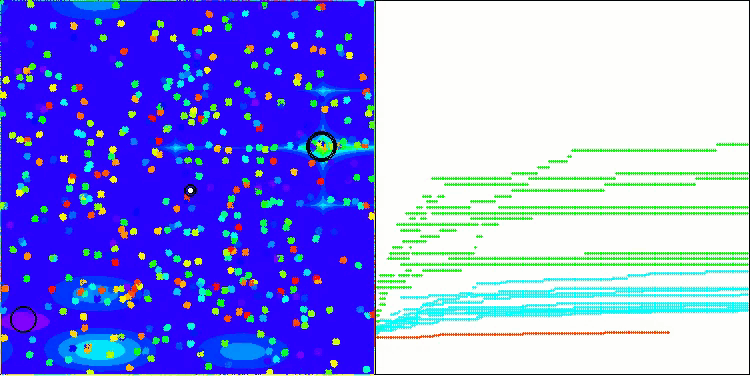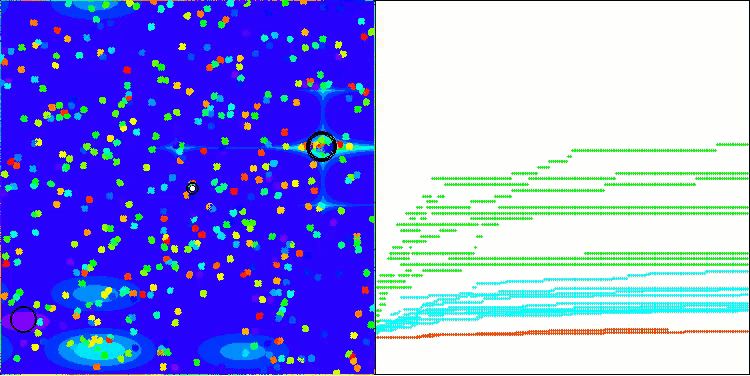
BHAm mit der Testfunktion Megacity
Die überarbeitete BBBC-Version belegte Platz 43 in der Bewertungstabelle. RW wird als Maßstab für die untere Grenze der „Sinnhaftigkeit“ von Suchstrategien angezeigt.
| # | AO | Beschreibung | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | Suche über die gesamte Nachbarschaft | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | Code-Sperr-Algorithmus (joo) | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | AMOm | Optimierung der Tiermigration M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5.987 | 66,52 |
| 4 | (P+O)ES | (P+O) Evolutionsstrategien | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 5 | CTA | Kometenschweif-Algorithmus (joo) | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 6 | SDSm | stochastische Diffusionssuche M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 7 | AAm | Algorithmus für das Bogenschießen M | 0.91744 | 0.70876 | 0.42160 | 2.04780 | 0.92527 | 0.75802 | 0.35328 | 2.03657 | 0.67385 | 0.55200 | 0.23738 | 1.46323 | 5.548 | 61.64 |
| 8 | ESG | Entwicklung sozialer Gruppen (joo) | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 9 | SIA | Simuliertes isotropes Glühen (Joo) | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 10 | ACS | künstliche, kooperative Suche | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 11 | BHAm | Algorithmus für schwarze Löcher M | 0.75236 | 0.76675 | 0.34583 | 1.86493 | 0.93593 | 0.80152 | 0.27177 | 2.00923 | 0.65077 | 0.51646 | 0.15472 | 1.32195 | 5.196 | 57.73 |
| 12 | ASO | Anarchische Gesellschaftsoptimierung | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5.178 | 57,54 |
| 13 | AOSm | Suche nach atomaren Orbitalen M | 0.80232 | 0.70449 | 0.31021 | 1.81702 | 0.85660 | 0.69451 | 0.21996 | 1.77107 | 0.74615 | 0.52862 | 0.14358 | 1.41835 | 5.006 | 55.63 |
| 14 | TSEA | Schildkrötenpanzer-Evolutionsalgorithmus (joo) | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 15 | DE | differentielle Evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 16 | CRO | Optimierung chemischer Reaktionen | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 17 | BSA | Vogelschwarm-Algorithmus | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 18 | HS | Harmoniesuche | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 19 | SSG | Setzen, Säen und Wachsen | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 20 | BCOm | Optimierung mit der bakteriellen Chemotaxis M | 0.75953 | 0.62268 | 0.31483 | 1.69704 | 0.89378 | 0.61339 | 0.22542 | 1.73259 | 0.65385 | 0.42092 | 0.14435 | 1.21912 | 4.649 | 51.65 |
| 21 | ABO | Optimierung des afrikanischen Büffels | 0.83337 | 0.62247 | 0.29964 | 1.75548 | 0.92170 | 0.58618 | 0.19723 | 1.70511 | 0.61000 | 0.43154 | 0.13225 | 1.17378 | 4.634 | 51.49 |
| 22 | (PO)ES | (PO) Evolutionsstrategien | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 23 | TSm | Tabu-Suche M | 0.87795 | 0.61431 | 0.29104 | 1.78330 | 0.92885 | 0.51844 | 0.19054 | 1.63783 | 0.61077 | 0.38215 | 0.12157 | 1.11449 | 4.536 | 50.40 |
| 24 | BSO | Brainstorming-Optimierung | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 25 | WOAm | Wal-Optimierungsalgorithmus M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 26 | AEFA | Algorithmus für künstliche elektrische Felder | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 27 | AEO | Algorithmus zur Optimierung auf der Grundlage künstlicher Ökosysteme | 0.91380 | 0.46713 | 0.26470 | 1.64563 | 0.90223 | 0.43705 | 0.21400 | 1.55327 | 0.66154 | 0.30800 | 0.28563 | 1.25517 | 4.454 | 49.49 |
| 28 | ACOm | Ameisen-Kolonie-Optimierung M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 29 | BFO-GA | Optimierung der bakteriellen Futtersuche — ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 30 | SOA | einfacher Optimierungsalgorithmus | 0.91520 | 0.46976 | 0.27089 | 1.65585 | 0.89675 | 0.37401 | 0.16984 | 1.44060 | 0.69538 | 0.28031 | 0.10852 | 1.08422 | 4.181 | 46.45 |
| 31 | ABHA | Algorithmus für künstliche Bienenstöcke | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 32 | ACMO | Optimierung atmosphärischer Wolkenmodelle | 0.90321 | 0.48546 | 0.30403 | 1.69270 | 0.80268 | 0.37857 | 0.19178 | 1.37303 | 0.62308 | 0.24400 | 0.10795 | 0.97503 | 4.041 | 44.90 |
| 33 | ADAMm | adaptive Momentabschätzung M | 0.88635 | 0.44766 | 0.26613 | 1.60014 | 0.84497 | 0.38493 | 0.16889 | 1.39880 | 0.66154 | 0.27046 | 0.10594 | 1.03794 | 4.037 | 44.85 |
| 34 | ATAm | Algorithmus für künstliche Stämme M | 0.71771 | 0.55304 | 0.25235 | 1.52310 | 0.82491 | 0.55904 | 0.20473 | 1.58867 | 0.44000 | 0.18615 | 0.09411 | 0.72026 | 3.832 | 42.58 |
| 35 | ASHA | Algorithmus für künstliches Duschen | 0.89686 | 0.40433 | 0.25617 | 1.55737 | 0.80360 | 0.35526 | 0.19160 | 1.35046 | 0.47692 | 0.18123 | 0.09774 | 0.75589 | 3.664 | 40.71 |
| 36 | ASBO | Optimierung des adaptiven Sozialverhaltens | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 37 | MEC | Evolutionäre Berechnung des Geistes | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 38 | IWO | Optimierung mit invasiven Unkräutern | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | Evolutionäre | 0.70017 | 3.403 | 37.81 |
| 39 | Micro-AIS | Künstliches Mikro-Immunsystem | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 40 | COAm | Kuckuck-Optimierungsalgorithmus M | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 41 | SDOm | Optimierung der Spiraldynamik M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| 42 | NMm | Nelder-Mead-Verfahren M | 0.73807 | 0.50598 | 0.31342 | 1.55747 | 0.63674 | 0.28302 | 0.08221 | 1.00197 | 0.44667 | 0.18667 | 0.04028 | 0.67362 | 3.233 | 35.92 |
| 43 | BBBC | Algorithmus von Big Bang und Big Crunch | 0,60531 | 0,45250 | 0,31255 | 1,37036 | 0,52323 | 0,35426 | 0,20417 | 1,08166 | 0,39769 | 0,19431 | 0,11286 | 0,70486 | 3,157 | 35,08 |
| 44 | FAm | Firefly-Algorithmus M | 0.58634 | 0.47228 | 0.32276 | 1.38138 | 0.68467 | 0.37439 | 0.10908 | 1.16814 | 0.28667 | 0.16467 | 0.04722 | 0.49855 | 3.048 | 33.87 |
| 45 | GSA | Algorithmus für die Schwerkraftsuche | 0.64757 | 0.49197 | 0.30062 | 1.44016 | 0.53962 | 0.36353 | 0.09945 | 1.00260 | 0.32667 | 0.12200 | 0.01917 | 0.46783 | 2.911 | 32.34 |
| RW | Random Walk | 0.48754 | 0.32159 | 0.25781 | 1.06694 | 0.37554 | 0.21944 | 0.15877 | 0.75375 | 0.27969 | 0.14917 | 0.09847 | 0.52734 | 2.348 | 26.09 | |
Zusammenfassung
Der BBBC-Algorithmus (Big Bang – Big Crunch) ist ein interessanter Ansatz zur globalen Optimierung, der von kosmologischen Prozessen inspiriert ist. Die Testergebnisse zeigen jedoch, dass die behauptete Effizienz übertrieben ist. Es ist wichtig zu beachten, dass der Algorithmus die Suche in der Mitte des Raumes konzentriert, was die Illusion einer hohen Suchkapazität erzeugen kann. Dies deutet nicht auf die herausragenden Fähigkeiten des Algorithmus hin, sondern vielmehr auf die Übereinstimmung der Problembedingungen mit seinen Eigenschaften.
Es ist auch erwähnenswert, dass viele Standard-Testfunktionen, die zur Bewertung von Algorithmen verwendet werden, ein globales Optimum haben, das in der Mitte des Suchraums liegt. Solche Tests sind nicht immer zuverlässig und können irreführend sein, wenn es um die tatsächlichen Suchfähigkeiten von Algorithmen wie BBBC geht, die „Hacking“-Funktionen in ihrer Suchstrategie haben. Daher sollten manchmal weithin bekannte „Wahrheiten“ mit Vorsicht und kritischem Denken behandelt werden.
Die modifizierte Version des BBBC-Algorithmus zeigt jedoch gute Ergebnisse bei hochdimensionalen Problemen, was sein Entwicklungspotenzial unterstreicht. Dies eröffnet neue Möglichkeiten für weitere Forschungen und Verbesserungen, die seine Leistung bei komplexeren und vielfältigeren Optimierungsproblemen verbessern und unsere Wissensbasis mit neuen Techniken zur Suche nach optimalen Lösungen bereichern können.
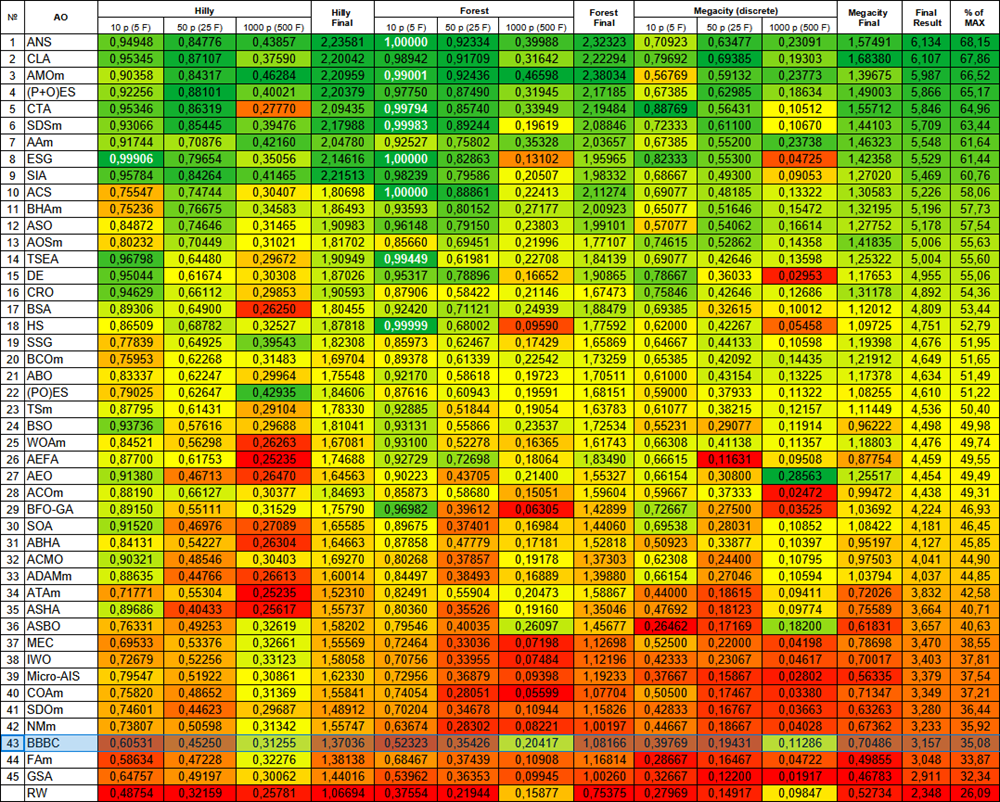
Abbildung 2. Farbliche Abstufung der Algorithmen entsprechend den relevanten Tests Ergebnisse, die größer oder gleich 0,99 sind, werden weiß hervorgehoben
Die Farbabstufung in der Tabelle zeigt deutlich, dass nicht alle Optimierungsalgorithmen effizienter sind als die einfache Zufallssuche (RW), insbesondere bei einigen Problemtypen. Dies wird besonders bei mehrdimensionalen Problemen deutlich, bei denen die Komplexität des Geländes und die Dimensionalität des Suchraums erheblich zunehmen. In solchen Fällen können viele traditionelle Strategien ihre Effizienz verlieren, da sie mit Problemen im Zusammenhang mit lokalen Extremen, dem Fluch der Dimensionalität und anderen Faktoren konfrontiert sind. Das bedeutet jedoch nicht, dass wir die Zufallssuche als primäre Methode befürworten, aber es ist wichtig, sie zu vergleichen, um die Grenzen und Möglichkeiten der verschiedenen Optimierungsstrategien besser zu verstehen.
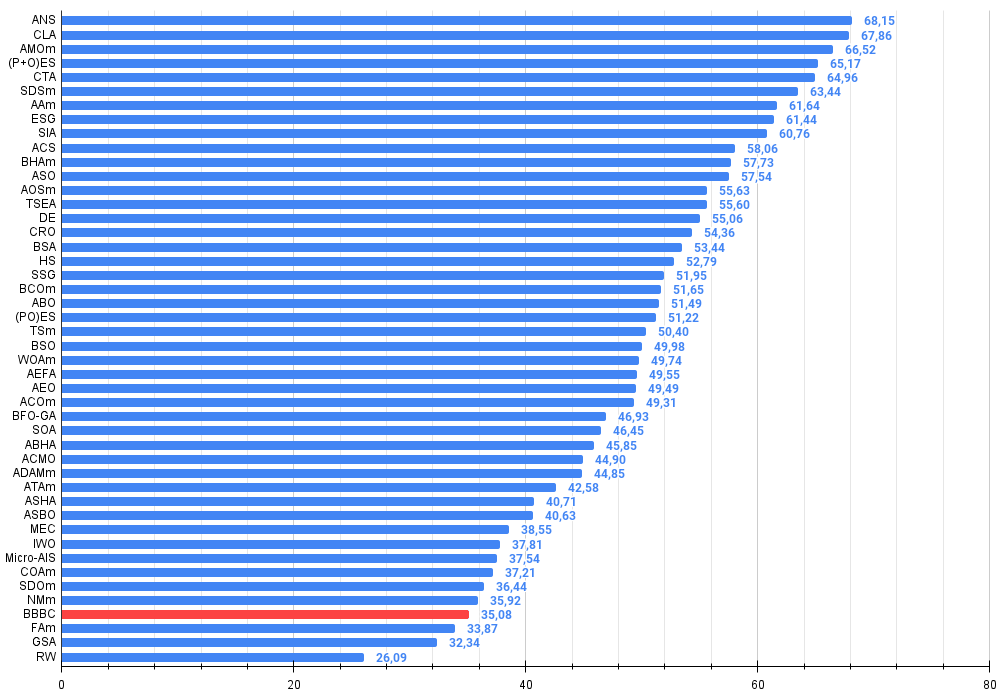
Abbildung 3. Histogramm der Algorithmus-Testergebnisse (Skala von 0 bis 100, je höher, desto besser, wobei 100 das maximal mögliche theoretische Ergebnis ist; im Archiv befindet sich ein Skript zur Berechnung der Bewertungstabelle)
Vor- und Nachteile von BBBC:
Vorteile:
- Der einzige externe Parameter ist die Größe der Population.
- Einfache Umsetzung.
- Sehr schneller EA.
- Funktioniert gut bei groß angelegten Problemen.
Nachteile:
- Große Streuung der Ergebnisse bei kleindimensionalen Problemen.
- Tendenz, bei niedrigdimensionalen Problemen stecken zu bleiben.
Der Artikel wird von einem Archiv mit den aktuellen Versionen der Codes der Algorithmen begleitet. Der Autor des Artikels übernimmt keine Verantwortung für die absolute Richtigkeit der Beschreibung der kanonischen Algorithmen. An vielen von ihnen wurden Änderungen vorgenommen, um die Suchmöglichkeiten zu verbessern. Die in den Artikeln dargelegten Schlussfolgerungen und Urteile beruhen auf den Ergebnissen der Versuche.
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | #C_AO.mqh | Include | Übergeordnete Klasse von Populationsoptimierungsalgorithmen |
| 2 | #C_AO_enum.mqh | Include | Enumeration von Algorithmen zur Populationsoptimierung |
| 3 | TestFunctions.mqh | Include | Bibliothek mit Testfunktionen |
| 4 | TestStandFunctions.mqh | Include | Bibliothek der Testfunktionen |
| 5 | Utilities.mqh | Include | Bibliothek der Hilfsfunktionen |
| 6 | CalculationTestResults.mqh | Include | Skript zur Berechnung der Ergebnisse in der Vergleichstabelle |
| 7 | Testing AOs.mq5 | Skript | Der einheitliche Prüfstand für alle Algorithmen zur Populationsoptimierung |
| 8 | Simple use of population optimization algorithms.mq5 | Skript | Ein einfaches Beispiel für die Verwendung von Algorithmen zur Populationsoptimierung ohne Visualisierung |
| 9 | Test_AO_BBBC.mq5 | Skript | BBBC-Prüfstand |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/16701
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Diskretisierungsmethoden für Preisbewegungen in Python
Diskretisierungsmethoden für Preisbewegungen in Python
 Neuronale Netze im Handel: Modelle mit Wavelet-Transformation und Multitasking-Aufmerksamkeit (letzter Teil)
Neuronale Netze im Handel: Modelle mit Wavelet-Transformation und Multitasking-Aufmerksamkeit (letzter Teil)
 Funktionen zur Aktivierung von Neuronen während des Trainings: Der Schlüssel zur schnellen Konvergenz?
Funktionen zur Aktivierung von Neuronen während des Trainings: Der Schlüssel zur schnellen Konvergenz?
 Neuro-symbolische Systeme im algorithmischen Handel: Kombination von symbolischen Regeln und neuronalen Netzen
Neuro-symbolische Systeme im algorithmischen Handel: Kombination von symbolischen Regeln und neuronalen Netzen
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.