
Алгоритм Большого взрыва и Большого сжатия — BBBC (Big Bang - Big Crunch)
Содержание
Введение
На бескрайних просторах Вселенной, где звезды рождаются и умирают, скрываются тайны, которые человечество стремится разгадать. Метод BBBC (Big Bang-Big Crunch) — это алгоритм глобальной оптимизации, вдохновленный процессами, происходящими в космосе. Давайте разберем эту увлекательную концепцию.
Теория Большого взрыва и сжатия была предложена как альтернативный сценарий конца Вселенной физиками Александром Фридманом и Жоржем Леметром в начале XX века. Они заметили, что уравнения общей теории относительности Эйнштейна допускают как расширение, так и сжатие Вселенной. Фридман математически доказал, что Вселенная не может оставаться статичной и должна либо расширяться, либо сжиматься. Он выделил три возможных сценария ее развития: вечное расширение, расширение с последующим сжатием и колебательный режим.
На протяжении XX века многие ученые развивали идеи объединения Большого взрыва и Большого сжатия в циклическую модель. На сегодняшний день теория Большого сжатия не является основной космологической моделью, так как наблюдения показывают, что Вселенная расширяется с ускорением. Тем не менее, данная концепция представляет собой интересную идею, предполагающую циклический характер эволюции Вселенной. Основные этапы:
- Большой взрыв, когда начальное состояние с высокой плотностью и температурой переходит в стадию быстрого расширения и рассеивания энергии с образованием материи и пространства-времени с хаотическим распределением частиц.
- Большое сжатие, когда гравитационные силы останавливают расширение и начинается обратный процесс сжатия, вся материя стягивается обратно в точку, возвращаясь к состоянию высокой плотности.
- Цикличность выражается в последовательности нового Большого взрыва после Большого сжатия, процесс может повторяться бесконечно, и каждый цикл может иметь разные физические константы.
Алгоритм Big Bang-Big Crunch был предложен в 2006 году учеными Osman K. Erol и Ibrahim Eksin из Стамбульского технического университета (Istanbul Technical University, Turkey).
Реализация алгоритма
Как и в теории Большого взрыва, где Вселенная начинает свое существование с мощного всплеска энергии, так и в методе BBBC мы наблюдаем начальную фазу, полную случайности и разнообразия. В фазе Большого взрыва создается популяция из случайных точек, каждая из которых представляет собой кандидата на решение. Эти точки разбросаны по бескрайнему пространству поиска, готовые к исследованию, но как только хаос находит свое место, начинается фаза Большого сжатия. Точки стремятся к "центру масс", подобно тому, как галактики притягиваются друг к другу через гравитацию. Этот момент — кульминация, когда все усилия объединяются в поисках оптимального решения.
Итак, этапы алгоритма, путь от хаоса к порядку:
1. Фаза Большого взрыва (Big Bang). В этом первом действии создается начальная популяция из N случайных точек. Каждая точка занимает свое место в пространстве, равномерно распределяясь в пределах заданных границ.
2. Фаза Большого сжатия (Big Crunch), переход к вычислению "центра масс" — точки, к которой стремятся все остальные. Используя формулу (рис. 1), находим координаты центра, который станет новым началом для следующих шагов.
3. Генерация новых точек. Вокруг центра масс новые точки начинают свое существование. Они формируются с нормальным распределением, следуя за формулой, которая задает им направление и величину перемещения.
Метод BBBC ищет гармонию между исследованием и уточнением. С каждым новым поколением, разброс точек при генерации уменьшается, что позволяет алгоритму уточнять найденное оптимальное решение.
Как и в космосе, где каждое движение имеет значение, так и в мире оптимизации каждое вычисление приближает нас к нашей цели. Погружаясь в этот метод, мы не только открываем новые горизонты, но и становимся частью великого космического процесса в поисках лучшего решения.
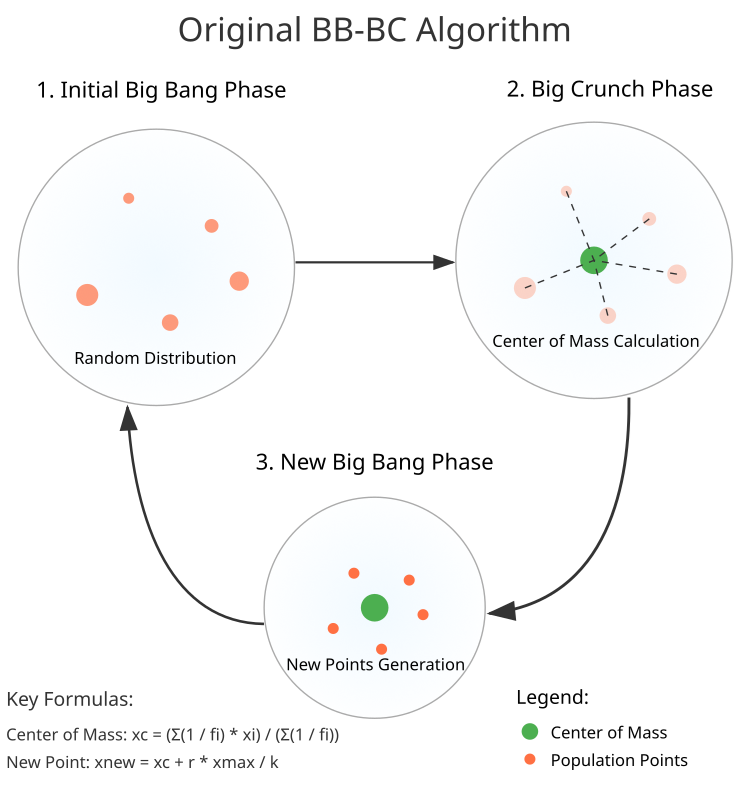
Рисунок 1. Схема работы алгоритма BBBC
Накидаем псевдокод алгоритма BBBC:
Увеличить epochNow
// Инициализация (Большой взрыв)
Если revision == ложь
Для каждого индивида i от 0 до popSize-1
Для каждого координаты c от 0 до coords-1
Новая координата = Генерация случайного числа (rangeMin[c], rangeMax[c])
Установить revision в истину
Вернуться
// Фаза Большого сжатия
Если epochNow % bigBangPeriod != 0
Для каждой координаты c от 0 до coords-1
numerator = 0, denominator = 0
Для каждого индивида i от 0 до popSize-1
приспособленность = Максимум (Абсолютное значение (a [i].f), 1e-10)
вес = 1.0 / приспособленность
numerator += вес * координата точки
denominator += вес
centerMass [c] = (denominator > 1e-10) ? numerator / denominator : cB [c]
Для каждого индивида i от 0 до popSize-1
Для каждой координаты c от 0 до coords-1
r = Генерация нормального случайного числа (0, -1.0, 1.0, 1)
Новая координата = centerMass [c] + r * rangeMax [c] / epochNow
// Фаза Большого взрыва
Иначе
Для каждого индивида i от 0 до popSize-1
Для каждой координаты c от 0 до coords-1
Новая координата = Генерация нормального случайного числа (cB [c], rangeMin [c], rangeMax [c], стандартное отклонение = 8)
Повторять до выполнения критерия останова с фазы Большого сжатия
Переходим к написанию кода. Напишем определение класса C_AO_BBBC, наследника C_AO:
Публичные методы:- Конструктор и деструктор
- SetParams () — установка параметров (размер популяции и периодичность Большого взрыва)
- Init () — инициализация алгоритма с заданными границами поиска
- Moving () — основной метод, реализующий фазы Big Bang и Big Crunch
- Revision () — метод обновления лучшего найденного решения
- epochs — общее количество эпох работы алгоритма
- epochNow — текущая эпоха
- centerMass [] — массив для хранения координат центра масс
Данный класс представляет собой реализацию алгоритма BBBC, где все основные вычисления происходят в методах Moving() и Revision(), а необходимые данные о популяции хранятся в базовом классе C_AO.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_BBBC : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_BBBC () { } C_AO_BBBC () { ao_name = "BBBC"; ao_desc = "Big Bang - Big Crunch Algorithm"; ao_link = "https://www.mql5.com/ru/articles/16701"; popSize = 50; bigBangPeriod = 3; ArrayResize (params, 2); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "bigBangPeriod"; params [1].val = bigBangPeriod; } void SetParams () { popSize = (int)params [0].val; bigBangPeriod = (int)params [1].val; } bool Init (const double &rangeMinP [], // минимальный диапазон поиска const double &rangeMaxP [], // максимальный диапазон поиска const double &rangeStepP [], // шаг поиска const int epochsP = 0); // количество эпох void Moving (); void Revision (); //---------------------------------------------------------------------------- int bigBangPeriod; // периодичность большого взрыва private: //------------------------------------------------------------------- int epochs; // общее число эпох int epochNow; // текущая эпоха double centerMass []; // центр масс }; //——————————————————————————————————————————————————————————————————————————————
Метод "Init" класса C_AO_BBBC:
Метод выполняет инициализацию алгоритма и принимает параметры:
- rangeMinP [] — массив минимальных значений для каждой координаты
- rangeMaxP [] — массив максимальных значений для каждой координаты
- rangeStepP [] — массив шагов дискретизации для каждой координаты
- epochsP — количество эпох работы алгоритма (по умолчанию 0)
Действия метода:
- Вызывает StandardInit () базового класса для инициализации общих параметров
- Устанавливает общее число эпох (epochs) и обнуляет счетчик текущей эпохи (epochNow)
- Выделяет память под массив центра масс (centerMass) размером "coords" (количество координат)
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_BBBC::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { // Инициализация базового класса if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- epochs = epochsP; epochNow = 0; // Выделение памяти для массивов ArrayResize (centerMass, coords); return true; } //——————————————————————————————————————————————————————————————————————————————
Метод "Moving" алгоритма BB-BC состоит из трех основных частей:
1. Начальная инициализация (если revision = false):
- Создает первоначальную популяцию случайных точек
- Приводит их к дискретной сетке поиска
2. Фаза Big Crunch (если epoch не кратен bigBangPeriod):
- Вычисляет центр масс по формуле: xc = (Σ(1/fi)*xi) / (Σ(1/fi))
- Генерирует новые точки вокруг центра масс по формуле: xnew = xc + r * xmax / epoch
- Использует нормальное распределение для случайных чисел
3. Фаза Big Bang (если epoch кратен bigBangPeriod):
- Генерирует новые точки используя нормальное распределение
- Использует лучшее решение как среднее значение
- Использует отклонение = 8 для широкого поиска
Все новые точки ограничиваются заданными границами поиска и приводятся к дискретной сетке.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BBBC::Moving () { epochNow++; // Начальная инициализация (Big Bang) if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { // Генерация случайных начальных позиций a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); // Приведение к дискретной сетке поиска a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- // Фаза Big Crunch - большой коллапс if (epochNow % bigBangPeriod != 0) { for (int c = 0; c < coords; c++) { double numerator = 0; double denominator = 0; for (int i = 0; i < popSize; i++) { // Расчет веса как обратной величины от значения фитнес-функции double fitness = MathMax (MathAbs (a [i].f), 1e-10); double weight = 1.0 / fitness; // Суммирование для вычисления центра масс по формуле // xc = (Σ(1/fi)xi) / (Σ(1/fi)) numerator += weight * a [i].c [c]; denominator += weight; } // Определение координаты центра масс centerMass [c] = denominator > 1e-10 ? numerator / denominator : cB [c]; } for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { double r = u.GaussDistribution (0, -1.0, 1.0, 1); // Генерация новой точки по формуле // xnew = xc + r*xmax/k double newPoint = centerMass [c] + r * rangeMax [c] / epochNow; // Ограничение в пределах допустимой области и приведение к сетке a [i].c [c] = u.SeInDiSp (newPoint, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //---------------------------------------------------------------------------- // Фаза Big Bang - большой взрыв else { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.GaussDistribution (cB [c], rangeMin [c], rangeMax [c], 8); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } } //——————————————————————————————————————————————————————————————————————————————
Метод "Revision" выполняет две основные функции:
Поиск лучшего решения:- Инициализирует индекс лучшего решения (bestInd = -1)
- Перебирает все точки популяции
- Если находит решение лучше текущего:
- Обновляет значение лучшей фитнес-функции (fB)
- Запоминает индекс лучшего решения (bestInd)
- Если найдено лучшее решение (bestInd != -1):
- Копирует все координаты лучшего решения из массива в массив лучшего решения "cB"
- Копирует все координаты лучшего решения из массива в массив лучшего решения "cB"
Этот метод обеспечивает обновление информации о глобально лучшем найденном решении за все время работы алгоритма.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BBBC::Revision () { int bestInd = -1; // Поиск лучшего решения в текущей популяции for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; bestInd = i; } } // Обновление лучшего известного решения if (bestInd != -1) ArrayCopy (cB, a [bestInd].c, 0, 0, WHOLE_ARRAY); } //——————————————————————————————————————————————————————————————————————————————
Авторы алгоритма BBBC утверждают, что он способен конкурировать с известными сильными алгоритмами, такими как генетические алгоритмы (GA), обгоняя их результаты за значительно меньшее количество эпох.
В качестве доказательства они приводят результаты тестов на стандартных и широко используемых синтетических бенчмарках, таких, как сфера (также известная как параболоид или эллипсоид), Ackley и Rastrigin. Давайте взглянем на визуализацию работы алгоритма на двух из этих бенчмарков.
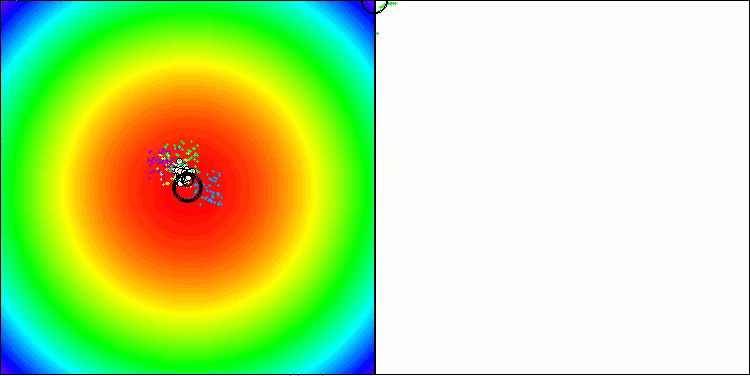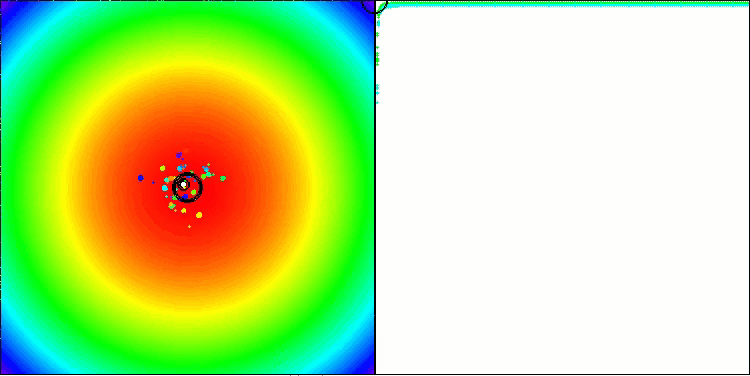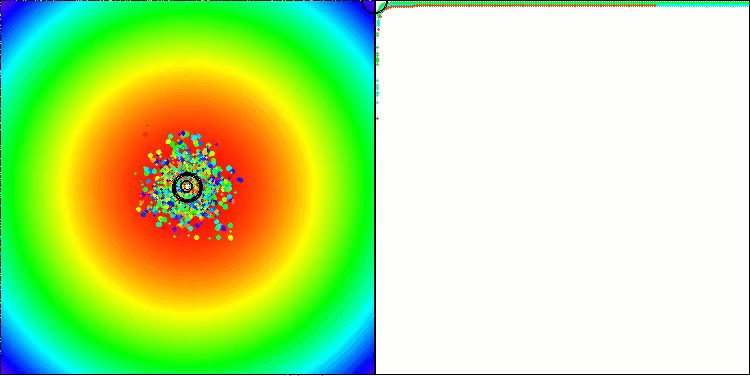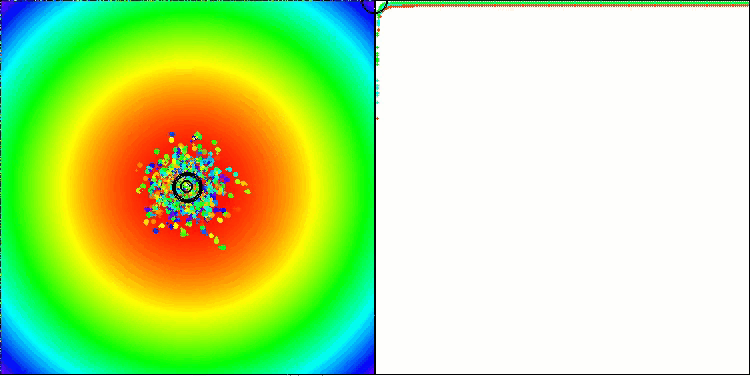
BBBC на тестовой функции Paraboloid
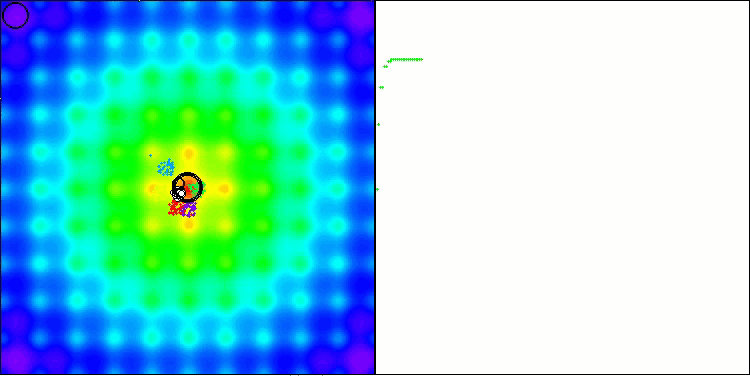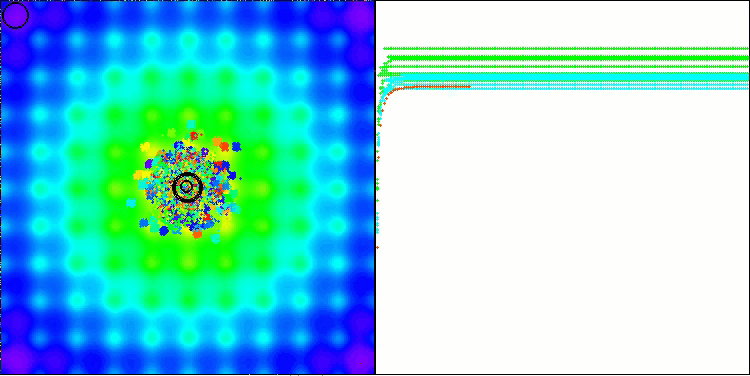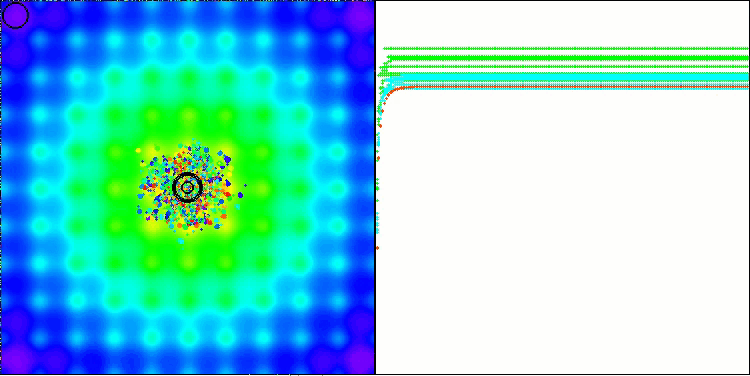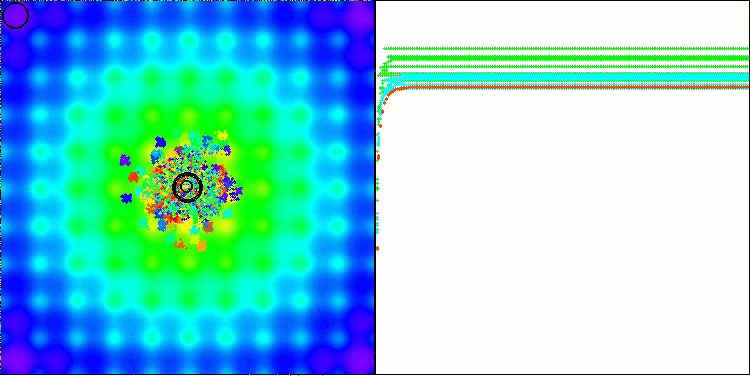
BBBC на тестовой функции Ackley
Действительно, результаты впечатляют. Особенно примечательно, что результаты на больших размерностях (красная линия) мало отличаются от результатов для задач с низкой размерностью (зеленая линия), что свидетельствует о высокой масштабируемости алгоритма. Хотя на функции Ackley точность сходимости не идеальна, результаты всё равно заслуживают внимания.
Теперь давайте рассмотрим результаты работы BBBC на наших, специально разработанных для алгоритмов оптимизации, тестовых функциях.
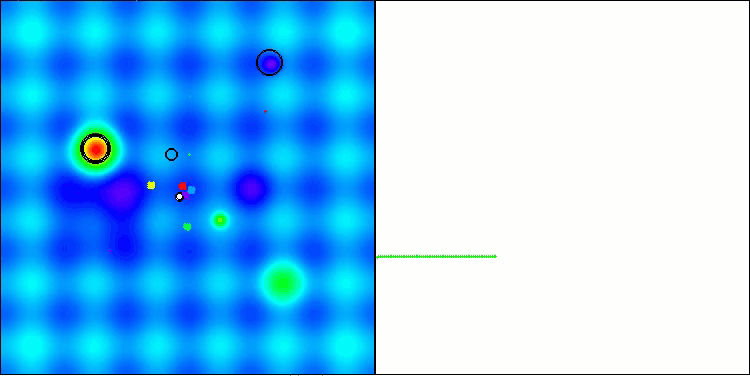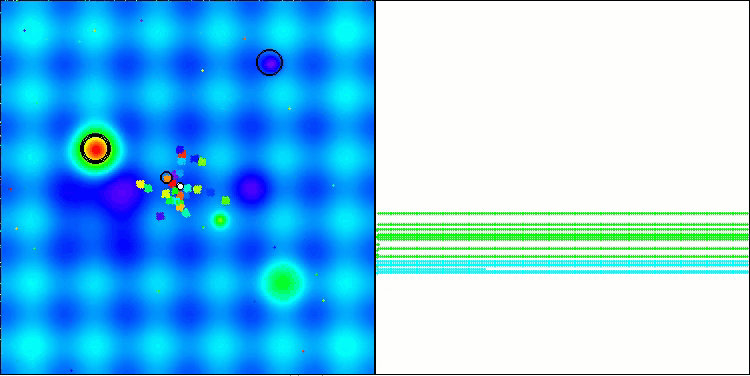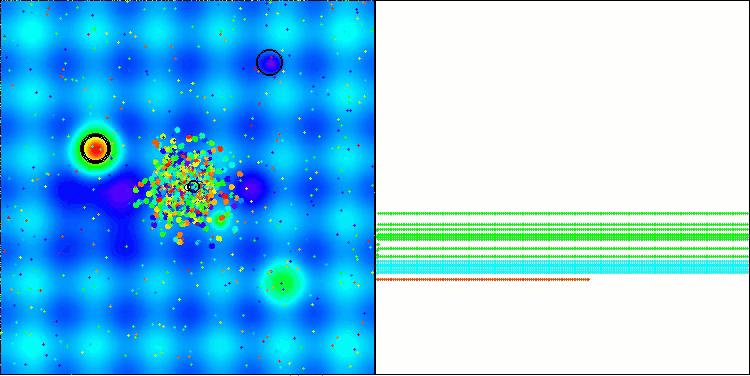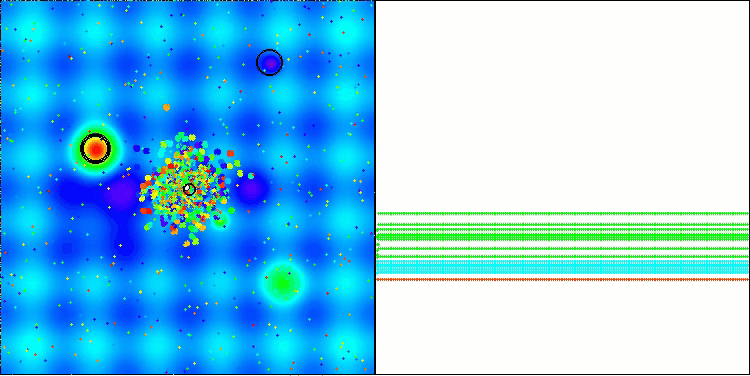
BBBC на тестовой функции Hilly
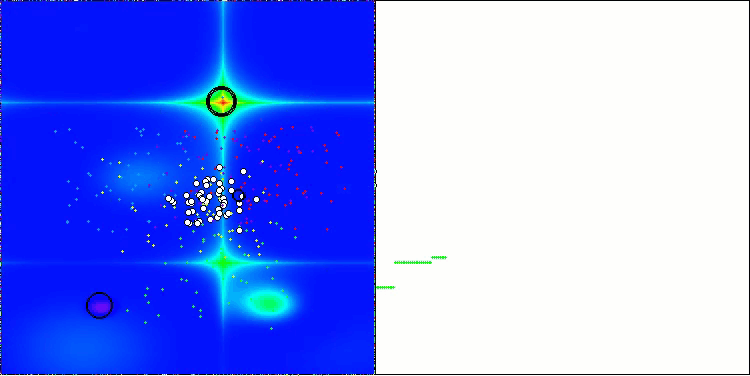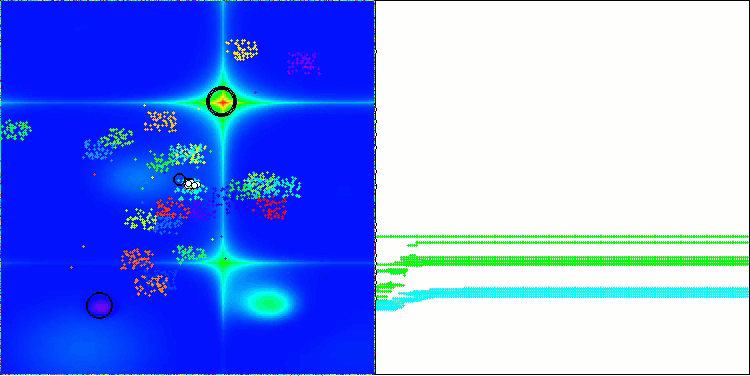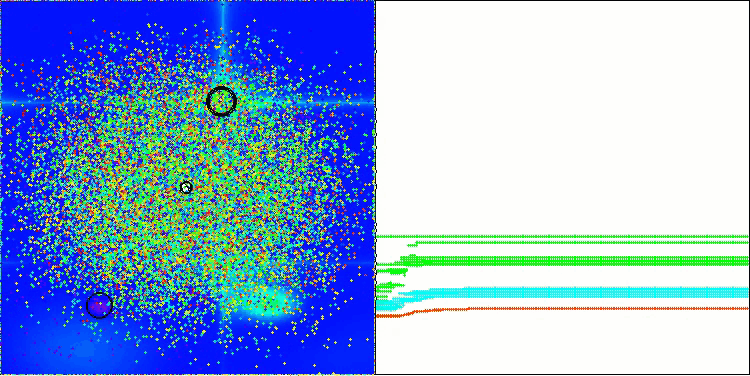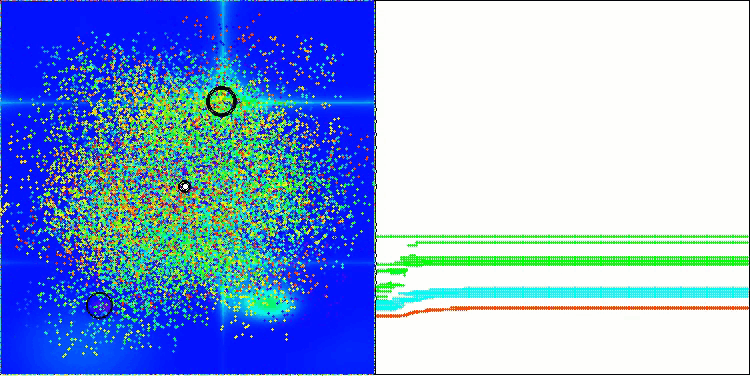
BBBC на тестовой функции Forest
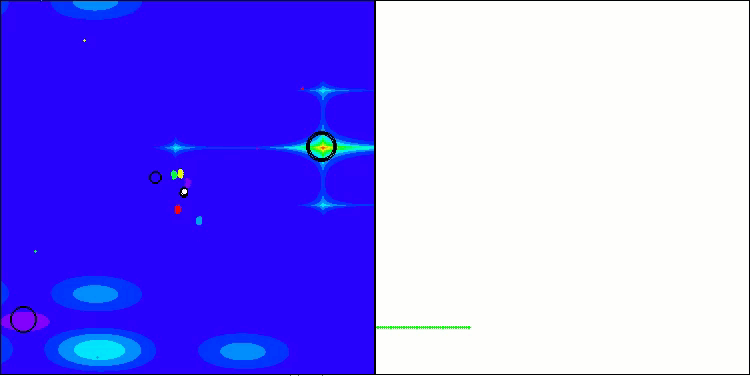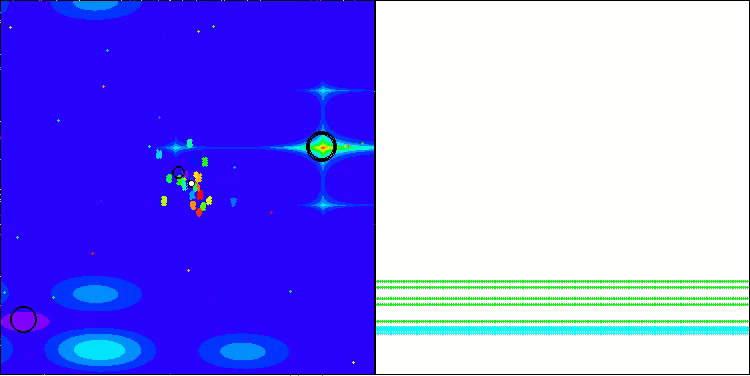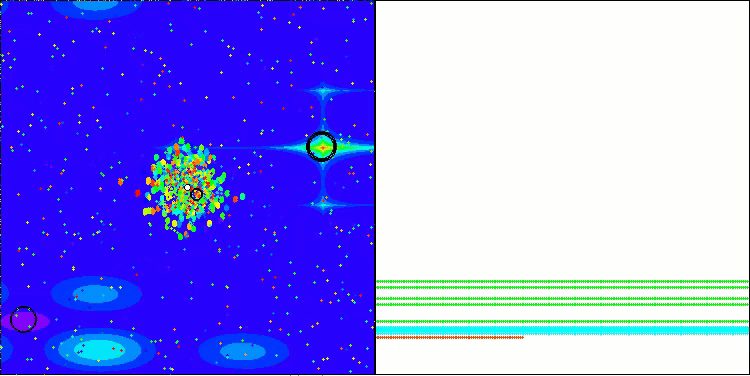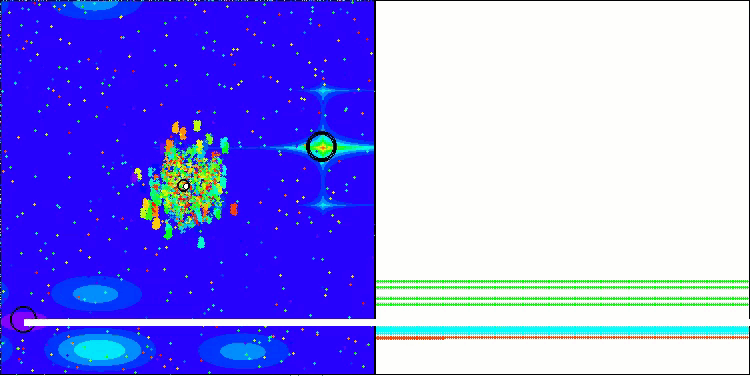
BBBC на тестовой функции Megacity
К сожалению, на наших бенчмарках магия алгоритма перестала работать. В чем же причина? Прежде всего, стоит обратить внимание на то, что, как и в случае с предыдущими функциями, на тестах Hilly, Forest и Megacity популяция алгоритма сосредотачивает свое "внимание" на центральной части пространства поиска. Это наблюдение вызывает определенные вопросы и кажется довольно странным.
Давайте заглянем под капот алгоритма BBBC и рассмотрим его внутренние механизмы. Мы увидим, что при использовании "центра масс", точки, распределенные по пространству, стремятся коллапсировать в середину диапазона функции. Это происходит потому, что центр масс точек оказывается именно в центре, что создает иллюзию эффективности алгоритма. Это совпадение приводит к тому, что алгоритм может успешно находить оптимумы для функций, подобных сфере (с глобальным оптимумом в центре диапазона). Однако на самом деле это не результат выдающихся поисковых способностей алгоритма, а удачное стечение обстоятельств. Например, если бы алгоритм начинал с точки с координатами 0.0, он бы идеально достиг глобального оптимума на первой итерации. Вот и весь секрет.
Следует отметить, что большинство стандартных тестовых функций, широко используемых для оценки различных алгоритмов, имеют глобальный оптимум, расположенный в центре пространства поиска. Такие тесты не всегда могут быть надежными, и для некоторых алгоритмов, таких как BBBC, они могут вводить в заблуждение относительно реальных поисковых возможностей алгоритма.
Чтобы избежать ложноположительных результатов при тестировании, мной были разработаны специальные тестовые функции, которые:
- не симметричны
- имеют глобальный оптимум, расположенный не в центре пространства поиска
- не являются периодическими
- имеют малую долю поверхности, находящейся выше средней линии по высоте.
Теперь давайте обратим внимание на распечатку результатов работы BBBC на тестовых функциях, собранных в таблицу ниже. Это очень важно.
| Большой взрыв на каждой 2-й эпохе | Большой взрыв на каждой 3-й эпохе | Большой взрыв на каждой 10-й эпохе |
|---|---|---|
| BBBC|Big Bang - Big Crunch Algorithm|50.0|2.0| ============================= 5 Hilly's; Func runs: 10000; result: 0.5789409521562645 25 Hilly's; Func runs: 10000; result: 0.36005433010965165 500 Hilly's; Func runs: 10000; result: 0.25650127842145554 ============================= 5 Forest's; Func runs: 10000; result: 0.5232991213500953 25 Forest's; Func runs: 10000; result: 0.293874681679014 500 Forest's; Func runs: 10000; result: 0.18830469994313143 ============================= 5 Megacity's; Func runs: 10000; result: 0.3269230769230769 25 Megacity's; Func runs: 10000; result: 0.15584615384615388 500 Megacity's; Func runs: 10000; result: 0.09743846153846236 ============================= All score: 2.78118 (30.90%) | BBBC|Big Bang - Big Crunch Algorithm|50.0|3.0| ============================= 5 Hilly's; Func runs: 10000; result: 0.5550785088841808 25 Hilly's; Func runs: 10000; result: 0.3605042956384694 500 Hilly's; Func runs: 10000; result: 0.25635343911025843 ============================= 5 Forest's; Func runs: 10000; result: 0.48703749499939086 25 Forest's; Func runs: 10000; result: 0.2897958021406425 500 Forest's; Func runs: 10000; result: 0.1865439156477803 ============================= 5 Megacity's; Func runs: 10000; result: 0.28307692307692306 25 Megacity's; Func runs: 10000; result: 0.15692307692307694 500 Megacity's; Func runs: 10000; result: 0.09701538461538546 ============================= All score: 2.67233 (29.69%) | BBBC|Big Bang - Big Crunch Algorithm|50.0|10.0| ============================= 5 Hilly's; Func runs: 10000; result: 0.4883607839451155 25 Hilly's; Func runs: 10000; result: 0.3344059754605514 500 Hilly's; Func runs: 10000; result: 0.25564528470980497 ============================= 5 Forest's; Func runs: 10000; result: 0.492293124748422 25 Forest's; Func runs: 10000; result: 0.28653857694657936 500 Forest's; Func runs: 10000; result: 0.1844110334128521 ============================= 5 Megacity's; Func runs: 10000; result: 0.3230769230769231 25 Megacity's; Func runs: 10000; result: 0.15261538461538465 500 Megacity's; Func runs: 10000; result: 0.09653846153846235 ============================= All score: 2.61389 (29.04%) |
Обратите внимание, что результаты тестирования показывают незначительные отличия друг от друга и укладываются в естественный разброс значений. Это свидетельствует о слабых поисковых способностях используемой стратегии, которая по сути мало отличается от случайного поиска. В связи с этим, уместно привести результаты тестирования алгоритма случайного блуждания (RW - random walk). Ранее в статьях этот алгоритм упоминался, однако результаты его работы не были представлены. Теперь пришло время это сделать.
Представление результатов алгоритма RW необходимо для того, чтобы оценить, насколько эффективнее различные стратегии поиска по сравнению с простым случайным разбрасыванием точек в пространстве. Ниже приведен усредненный результат по 100 запусков на тестовых функциях (обычно делаем 10).
RW|Random Walk|50.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.48753502068617777
25 Hilly's; Func runs: 10000; result: 0.3215913699940513
500 Hilly's; Func runs: 10000; result: 0.2578113480890265
=============================
5 Forest's; Func runs: 10000; result: 0.3755402348403822
25 Forest's; Func runs: 10000; result: 0.21943566240362317
500 Forest's; Func runs: 10000; result: 0.15877419882827945
=============================
5 Megacity's; Func runs: 10000; result: 0.27969230769230796
25 Megacity's; Func runs: 10000; result: 0.14916923076923083
500 Megacity's; Func runs: 10000; result: 0.098473846153847
=============================
All score: 2.34802 (26.09%)
Приведу код алгоритма RW, он очень простой. Функция "Moving" отвечает, как обычно, за обновление координат каждой особи в популяции. Для каждого индивида она генерирует случайные значения в заданном диапазоне и затем корректирует их с помощью функции "SeInDiSp", чтобы они соответствовали шагу изменения.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_RW::Moving () { for (int w = 0; w < popSize; w++) { for (int c = 0; c < coords; c++) { a [w].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [w].c [c] = u.SeInDiSp (a [w].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Функция "Revision" выполняет проверку всех особей в популяции, чтобы найти индивидуума с наилучшей фитнес-функцией (fB). Если такой индивид найден, его координаты копируются в глобальный лучший результат (cB).
//—————————————————————————————————————————————————————————————————————————————— void C_AO_RW::Revision () { int ind = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ind = i; } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); } //——————————————————————————————————————————————————————————————————————————————
Теперь внесем изменения в оригинальный алгоритм BBBC, чтобы нивелировать его иллюзорные преимущества на задачах с глобальным оптимумом в центре диапазона оптимизируемых параметров и чтобы можно было провести объективные тесты. Рассмотрим отличия в коде, изменения внесены в метод "Moving":
- Удалено вычисление центра масс
- Изменена фаза Big Bang:
- Вместо центра масс (centerMass) используется лучшее решение (cB)
- Использует формулу: xnew = cB + r*range/epochNow ("range" теперь это разница между "rangeMax" и "rangeMin")
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BBBC::Moving () { epochNow++; // Начальная инициализация (Big Bang) if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { // Генерация случайных начальных позиций a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); // Приведение к дискретной сетке поиска a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //-------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { //Фаза Big Crunch - большой коллапс if (epochNow % bigBangPeriod != 0) { for (int c = 0; c < coords; c++) { // Вычисление размера пространства поиска для текущей координаты double range = rangeMax [c] - rangeMin [c]; // Генерация случайного числа в диапазоне [-1, 1] double r = u.GaussDistribution (0, -1.0, 1.0, 1); // Генерация новой точки по формуле // xnew = xc + r*(xmax - xmin)/(k) double newPoint = cB [c] + r * range / epochNow; // Ограничение в пределах допустимой области и приведение к сетке a [i].c [c] = u.SeInDiSp (newPoint, rangeMin [c], rangeMax [c], rangeStep [c]); } } // Фаза Big Bang - большой взрыв else { for (int c = 0; c < coords; c++) { a [i].c [c] = u.GaussDistribution (cB [c], rangeMin [c], rangeMax [c], 8); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } } //——————————————————————————————————————————————————————————————————————————————
Результаты тестов
Результаты работы исправленной версии алгоритма BBBC:
BBBC|Big Bang-Big Crunch Algorithm|50.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.6053080737014771
25 Hilly's; Func runs: 10000; result: 0.45249601882946056
500 Hilly's; Func runs: 10000; result: 0.31255376970202864
=============================
5 Forest's; Func runs: 10000; result: 0.5232283922331299
25 Forest's; Func runs: 10000; result: 0.354256711141388
500 Forest's; Func runs: 10000; result: 0.20417356281490023
=============================
5 Megacity's; Func runs: 10000; result: 0.3976923076923077
25 Megacity's; Func runs: 10000; result: 0.19430769230769235
500 Megacity's; Func runs: 10000; result: 0.11286153846153954
=============================
All score: 3.15688 (35.08%)
Теперь результаты тестирования объективно отражают возможности алгоритма BBBC. На визуализации заметно формирование тех же "звезд", что и у оригинального алгоритма, но теперь происходит поиск в настоящих перспективных областях, а не только преимущественно по центру пространства поиска.
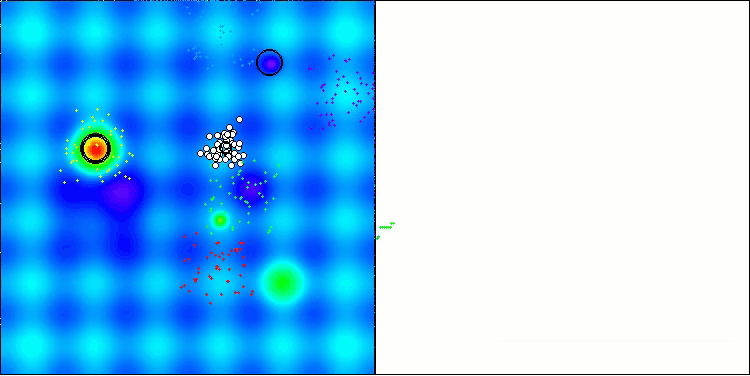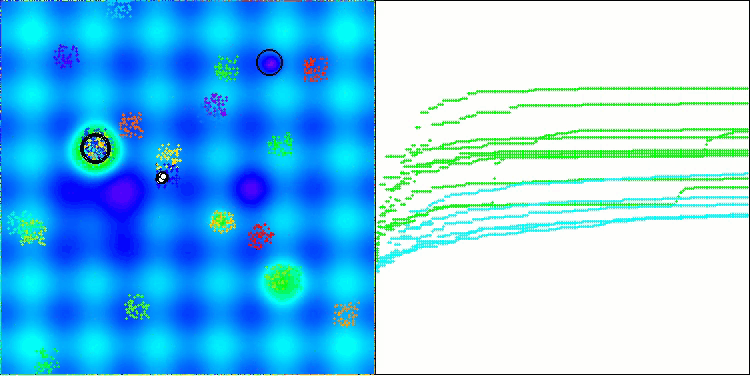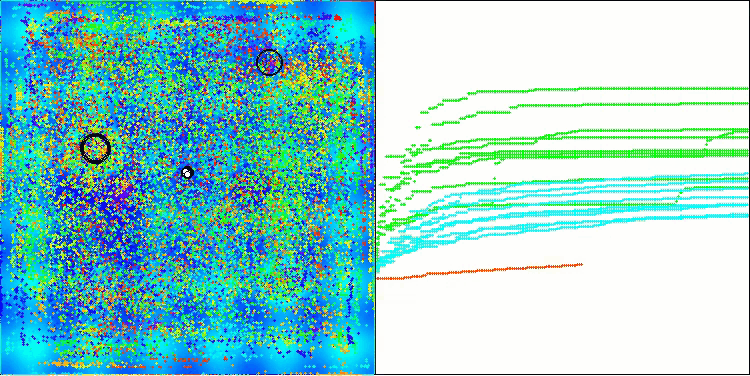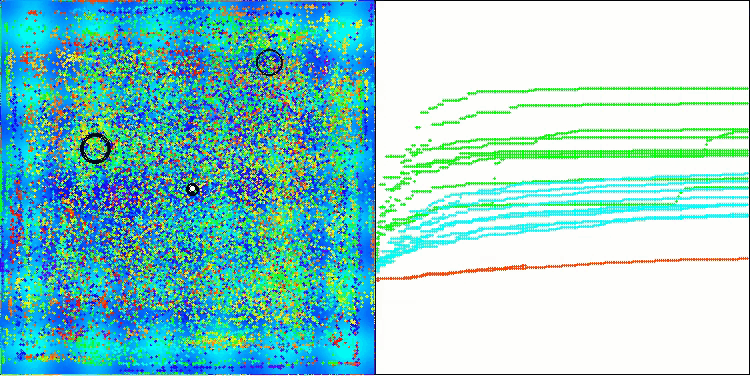
BHAm на тестовой функции Hilly
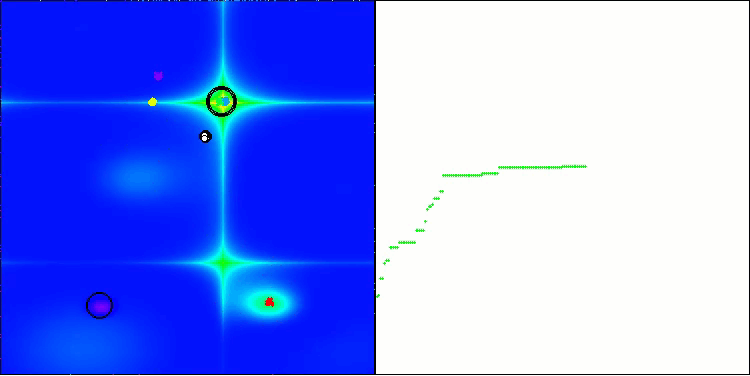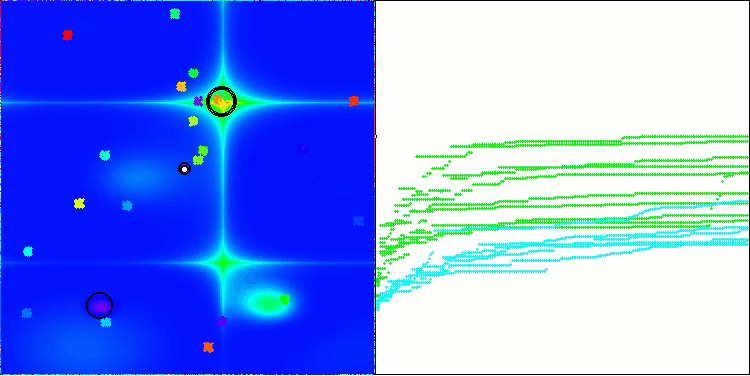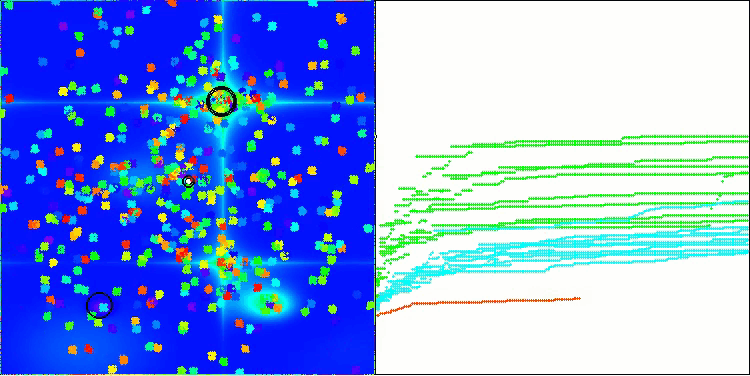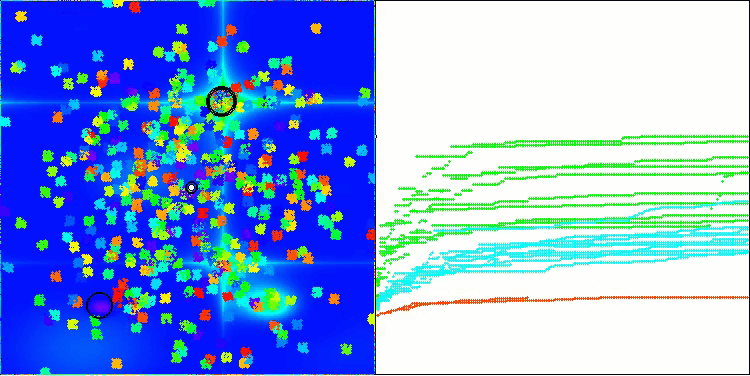
BHAm на тестовой функции Forest
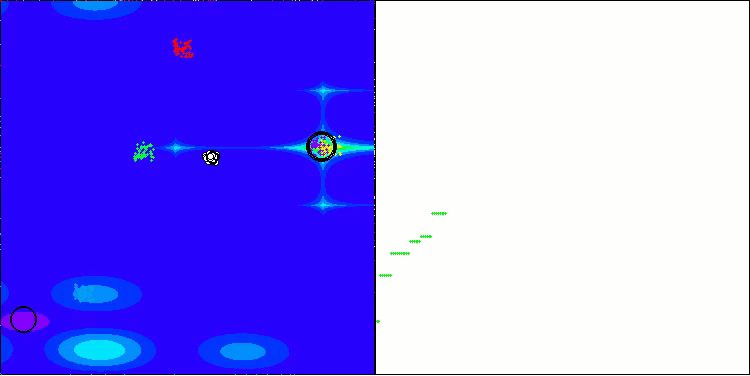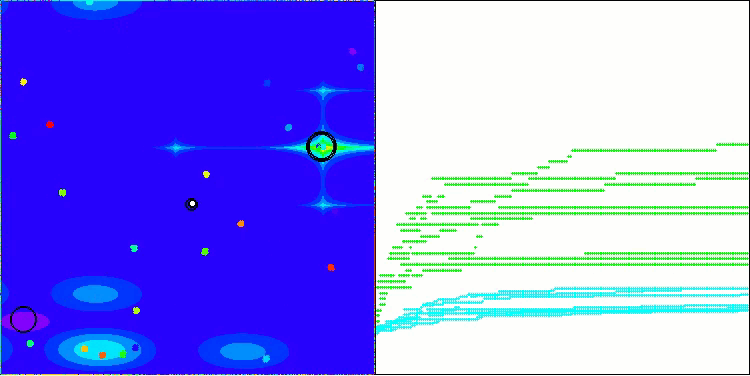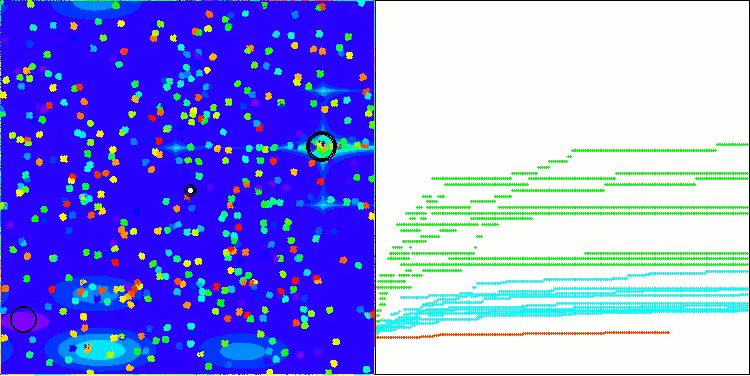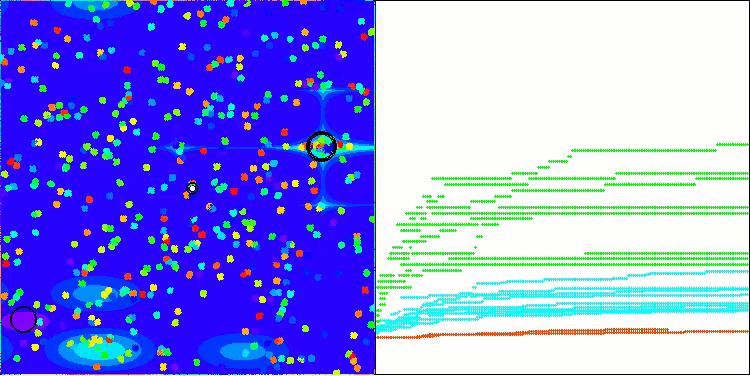
BHAm на тестовой функции Megacity
Исправленный вариант BBBC занял 43-е место в рейтинговой таблице. RW —собранных в таблицу ниже случайный поиск, в рейтинге не участвует и приведен как эталон нижней границы "осмысленности" стратегий поиска.
| № | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration ptimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 7 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 8 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 9 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 10 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 11 | BHAm | black hole algorithm M | 0,75236 | 0,76675 | 0,34583 | 1,86493 | 0,93593 | 0,80152 | 0,27177 | 2,00923 | 0,65077 | 0,51646 | 0,15472 | 1,32195 | 5,196 | 57,73 |
| 12 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 13 | AOSm | atomic orbital search M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| 14 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 15 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 16 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 17 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 18 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 19 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 20 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 21 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 22 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 23 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 24 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 25 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 26 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 27 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 28 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 29 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 30 | SOA | simple optimization algorithm | 0,91520 | 0,46976 | 0,27089 | 1,65585 | 0,89675 | 0,37401 | 0,16984 | 1,44060 | 0,69538 | 0,28031 | 0,10852 | 1,08422 | 4,181 | 46,45 |
| 31 | ABHA | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4,127 | 45,85 |
| 32 | ACMO | atmospheric cloud model optimization | 0,90321 | 0,48546 | 0,30403 | 1,69270 | 0,80268 | 0,37857 | 0,19178 | 1,37303 | 0,62308 | 0,24400 | 0,10795 | 0,97503 | 4,041 | 44,90 |
| 33 | ADAMm | adaptive moment estimation M | 0,88635 | 0,44766 | 0,26613 | 1,60014 | 0,84497 | 0,38493 | 0,16889 | 1,39880 | 0,66154 | 0,27046 | 0,10594 | 1,03794 | 4,037 | 44,85 |
| 34 | ATAm | artificial tribe algorithm M | 0,71771 | 0,55304 | 0,25235 | 1,52310 | 0,82491 | 0,55904 | 0,20473 | 1,58867 | 0,44000 | 0,18615 | 0,09411 | 0,72026 | 3,832 | 42,58 |
| 35 | ASHA | artificial showering algorithm | 0,89686 | 0,40433 | 0,25617 | 1,55737 | 0,80360 | 0,35526 | 0,19160 | 1,35046 | 0,47692 | 0,18123 | 0,09774 | 0,75589 | 3,664 | 40,71 |
| 36 | ASBO | adaptive social behavior optimization | 0,76331 | 0,49253 | 0,32619 | 1,58202 | 0,79546 | 0,40035 | 0,26097 | 1,45677 | 0,26462 | 0,17169 | 0,18200 | 0,61831 | 3,657 | 40,63 |
| 37 | MEC | mind evolutionary computation | 0,69533 | 0,53376 | 0,32661 | 1,55569 | 0,72464 | 0,33036 | 0,07198 | 1,12698 | 0,52500 | 0,22000 | 0,04198 | 0,78698 | 3,470 | 38,55 |
| 38 | IWO | invasive weed optimization | 0,72679 | 0,52256 | 0,33123 | 1,58058 | 0,70756 | 0,33955 | 0,07484 | 1,12196 | 0,42333 | 0,23067 | 0,04617 | 0,70017 | 3,403 | 37,81 |
| 39 | Micro-AIS | micro artificial immune system | 0,79547 | 0,51922 | 0,30861 | 1,62330 | 0,72956 | 0,36879 | 0,09398 | 1,19233 | 0,37667 | 0,15867 | 0,02802 | 0,56335 | 3,379 | 37,54 |
| 40 | COAm | cuckoo optimization algorithm M | 0,75820 | 0,48652 | 0,31369 | 1,55841 | 0,74054 | 0,28051 | 0,05599 | 1,07704 | 0,50500 | 0,17467 | 0,03380 | 0,71347 | 3,349 | 37,21 |
| 41 | SDOm | spiral dynamics optimization M | 0,74601 | 0,44623 | 0,29687 | 1,48912 | 0,70204 | 0,34678 | 0,10944 | 1,15826 | 0,42833 | 0,16767 | 0,03663 | 0,63263 | 3,280 | 36,44 |
| 42 | NMm | Nelder-Mead method M | 0,73807 | 0,50598 | 0,31342 | 1,55747 | 0,63674 | 0,28302 | 0,08221 | 1,00197 | 0,44667 | 0,18667 | 0,04028 | 0,67362 | 3,233 | 35,92 |
| 43 | BBBC | big bang-big crunch algorithm | 0,60531 | 0,45250 | 0,31255 | 1,37036 | 0,52323 | 0,35426 | 0,20417 | 1,08166 | 0,39769 | 0,19431 | 0,11286 | 0,70486 | 3,157 | 35,08 |
| 44 | FAm | firefly algorithm M | 0,58634 | 0,47228 | 0,32276 | 1,38138 | 0,68467 | 0,37439 | 0,10908 | 1,16814 | 0,28667 | 0,16467 | 0,04722 | 0,49855 | 3,048 | 33,87 |
| 45 | GSA | gravitational search algorithm | 0,64757 | 0,49197 | 0,30062 | 1,44016 | 0,53962 | 0,36353 | 0,09945 | 1,00260 | 0,32667 | 0,12200 | 0,01917 | 0,46783 | 2,911 | 32,34 |
| RW | random walk | 0,48754 | 0,32159 | 0,25781 | 1,06694 | 0,37554 | 0,21944 | 0,15877 | 0,75375 | 0,27969 | 0,14917 | 0,09847 | 0,52734 | 2,348 | 26,09 | |
Выводы
Алгоритм BBBC (Big Bang-Big Crunch) представляет собой интересный подход к глобальной оптимизации, вдохновленный космологическими процессами. Однако, результаты тестирования показывают, что его заявленная эффективность преувеличена. Важно отметить, что алгоритм сосредотачивает поиск в центре пространства, что может создавать иллюзию высоких поисковых возможностей. Это не свидетельствует о выдающихся способностях алгоритма, а скорее о совпадении условий задачи с его особенностями.
Следует также упомянуть, что многие стандартные тестовые функции, используемые для оценки алгоритмов, имеют глобальный оптимум, расположенный в центре пространства поиска. Такие тесты не всегда надежны и могут вводить в заблуждение относительно реальных поисковых возможностей алгоритмов, таких как BBBC, которые обладают "хакерскими" особенностями в своей стратегии поиска. Поэтому, порой, к широко известным "истинам" стоит относиться с осторожностью и критическим мышлением.
Тем не менее, доработанный вариант алгоритма BBBC демонстрирует неплохие результаты на задачах высокой размерности, что подчеркивает его потенциал для развития. Это открывает новые возможности для дальнейших исследований и улучшений, которые могут повысить его эффективность в более сложных и разнообразных задачах оптимизации, а также обогатить нашу копилку знаний новыми приемами в поиске оптимальных решений.
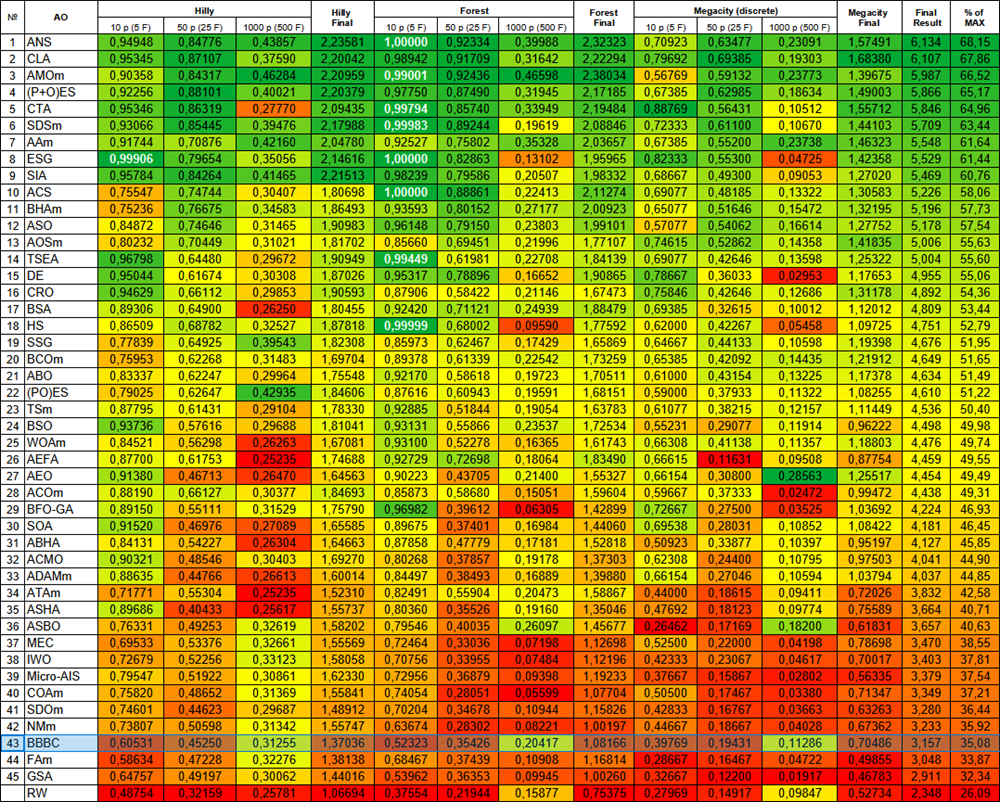
Рисунок 2. Цветовая градация алгоритмов по соответствующим тестам. Белым цветом подсвечены результаты больше или равные 0.99
Цветовая градация в таблице наглядно иллюстрирует, что не все алгоритмы оптимизации оказываются более эффективными по сравнению с простым случайным поиском (RW), особенно на некоторых типах задач. Это особенно ярко проявляется в контексте многомерных задач, где сложность рельефа и размерность пространства поиска значительно увеличиваются. В таких случаях многие традиционные стратегии могут терять свою эффективность, сталкиваясь с проблемами, связанными с локальными экстремумами, проклятием размерности и другими факторами. Однако, это не означает, что мы призываем использовать случайный поиск в качестве основного метода, но важно проводить сравнение с ним, чтобы лучше понять ограничения и возможности различных стратегий оптимизации.
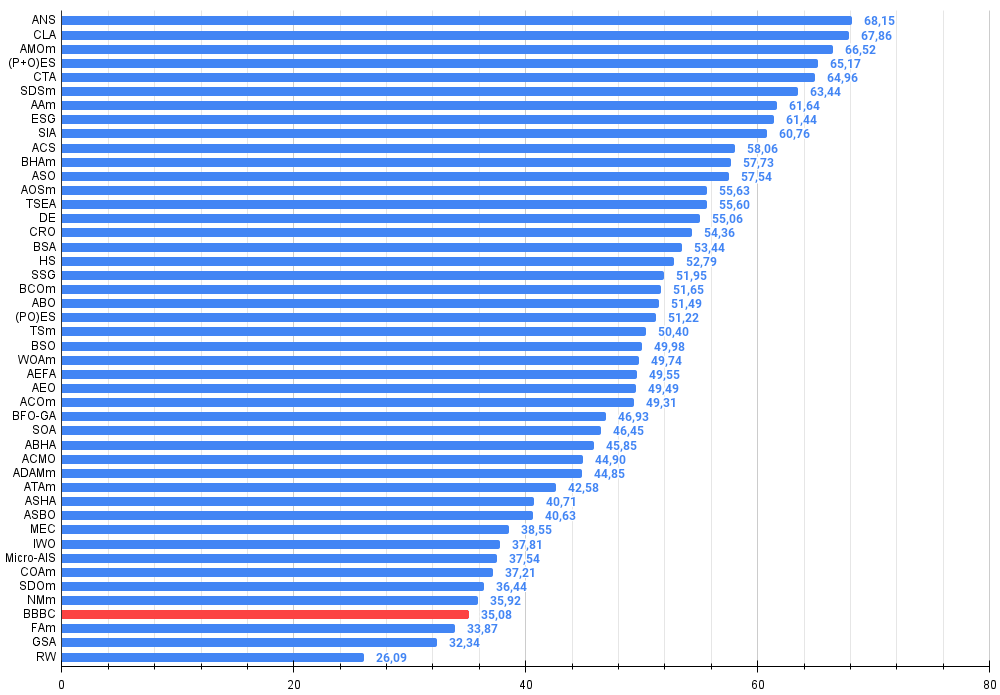
Рисунок 3. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше, где 100 - максимально возможный теоретический результат, в архиве скрипт для расчета рейтинговой таблицы)
Плюсы и минусы исправленной версии алгоритма BBBC:
Плюсы:
- Из внешних параметров только размер популяции.
- Простая реализация.
- Очень быстрый.
- Неплохо работает на задачах больших размерностей.
Минусы:
- Большой разброс результатов на задачах малой размерности.
- Склонность к застреванию на задачах малой размерности.
К статье прикреплён архив с актуальными версиями кодов алгоритмов. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | #C_AO.mqh | Включаемый файл | Родительский класс популяционных алгоритмов оптимизации |
| 2 | #C_AO_enum.mqh | Включаемый файл | Перечисление популяционных алгоритмов оптимизации |
| 3 | TestFunctions.mqh | Включаемый файл | Библиотека тестовых функций |
| 4 | TestStandFunctions.mqh | Включаемый файл | Библиотека функций тестового стенда |
| 5 | Utilities.mqh | Включаемый файл | Библиотека вспомогательных функций |
| 6 | CalculationTestResults.mqh | Включаемый файл | Скрипт для расчета результатов в сравнительную таблицу |
| 7 | Testing AOs.mq5 | Скрипт | Единый испытательный стенд для всех популяционных алгоритмов оптимизации |
| 8 | Simple use of population optimization algorithms.mq5 | Скрипт | Простой пример использования популяционных алгоритмов оптимизации без визуализации |
| 9 | Test_AO_BBBC.mq5 | Скрипт | Испытательный стенд для BBBC |
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Нейросети в трейдинге: Мультимодальный агент, дополненный инструментами (FinAgent)
Нейросети в трейдинге: Мультимодальный агент, дополненный инструментами (FinAgent)
 Индикатор силы и направления тренда на 3D-барах
Индикатор силы и направления тренда на 3D-барах
 Полиномиальные модели в трейдинге
Полиномиальные модели в трейдинге
 Возможности Мастера MQL5, которые вам нужно знать (Часть 27): Скользящие средние и угол атаки
Возможности Мастера MQL5, которые вам нужно знать (Часть 27): Скользящие средние и угол атаки
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования