MetaTrader 5 / 例
English Русский 中文 Español Deutsch Português 한국어 Français Italiano Türkçe
preview
母集団最適化アルゴリズム：ホタルアルゴリズム(FA)

母集団最適化アルゴリズム：ホタルアルゴリズム(FA)

MetaTrader 5 — 例 | 15 2月 2023, 08:58
670 0
Andrey Dik
Andrey Dik

内容

1.はじめに
2.アルゴリズムの説明
3.テスト結果


1.はじめに

自然は常に多くのメタヒューリスティックアルゴリズムにインスピレーションを与えてきました。また、問題解決のために、個々の経験をもとに、指示されることなく解決策を見出すことができました。初期のメタヒューリスティックアルゴリズム創出の主な動機は自然淘汰と適者生存でした。自然界では、動物たちはさまざまな方法でコミュニケーションをとっています。ホタルは点滅する能力を使ってコミュニケーションをとります。ホタルの種類は約2000種あり、それぞれ特殊な発光パターンを持っています。通常、特定のパターンで短く閃光します。光とその強さは、生物発光と呼ばれる生化学的なプロセスの結果となります。このような閃光の主な機能は、交尾のパターンと潜在的な犠牲者を引き寄せることだと考えられています。熱帯地方のホタルの中には、閃光を同期させることができるものがあり、生物の自己組織化の一例を示しています。光の強さは光源からの距離の関数として逆二乗則に従うので、ホタルから出る光が明滅すると、その光が見える範囲で周囲のホタルが反応するのです。

ホタルの行動にヒントを得た集団最適化アルゴリズムには、ホタルアルゴリズムとGSO (Glowworm Swarm Optimization)アルゴリズムという2つのバリエーションがあります。ホタルとGlowworm（ツチボタル）の大きな違いは、後者には翅がないことです。今回は、1つ目のタイプの最適化アルゴリズムについて考えてみます。

2.アルゴリズムの説明

ホタルアルゴリズム(F-algorithm)は、2007年に英国ケンブリッジ大学のX-Sh. Yangによって提案され、すぐに最適化研究者の注目を集めました。ホタルアルゴリズムは、近年、最適化問題の解決に目覚ましい成果を上げている群知能アルゴリズム群の1つです。特にホタルアルゴリズムは、連続離散最適化問題の解法として利用されています。

ホタルアルゴリズムには、実際のホタルの明滅の特徴に基づいた3つのルールがあります。ルールは次のとおりです。

  1. すべてのホタルは、より魅力的で明るい相手に向かっていく。
  2. ホタルの魅力度は明るさに比例し、他のホタルとの距離が離れると、空気が光を吸収するため、明るさが減少する。そのため、明滅している2つのホタルのうち、明るくないほうが明るいほうに寄っていく。より明るい（より魅力的な）相手がいない場合、ホタルはランダムに移動する。
  3. ホタルの明るさや光量は、問題の目的関数の値で決まる。


アルゴリズム開始当初は、すべてのホタルが探索空間全体にランダムに散らばっています。そして、このアルゴリズムは、2つのフェーズに基づいて最適なパーティションを決定します。

  1. 光の強さの変化 - 現在位置のホタルの明るさが適応度の値に反映され、魅力的なホタルに向かって移動する。
  2. ホタルは、隣のホタルの光量を観察して位置を変える。


ここで、ホタル最適化の複雑な仕組みについて、より詳しく掘り下げてみましょう。そのアルゴリズムのエッセンスを図1にわかりやすく示します。

Fas

図1：探索空間におけるホタルの光 - 距離が離れると視認性が低下する

探索原理の主な考え方は、ホタル同士の距離が長くなると視認性が非線形に低下するということです。この非線形関係がなければ、各ホタルは決定論的に明るい光源に向かって移動することになります。ただし、図1にあるように、ホタルの光は環境に吸収されて目立たないため、最も明るい親類を選ぶことはありません。その代わりに、より暗い相手（ただし、その環境では最も明るい相手）を選びます。この特徴は、より小さな群に分割するアルゴリズムの優れた能力を説明するものです。これは、距離による光の吸収の非線形関数によってのみ自然に発生するものです。下の図2には、アルゴリズムのパラメータの1つであるγ（ガンマ）媒体の吸収係数値を変えた場合の、距離に対する視認性の関数が示されています。


視認性

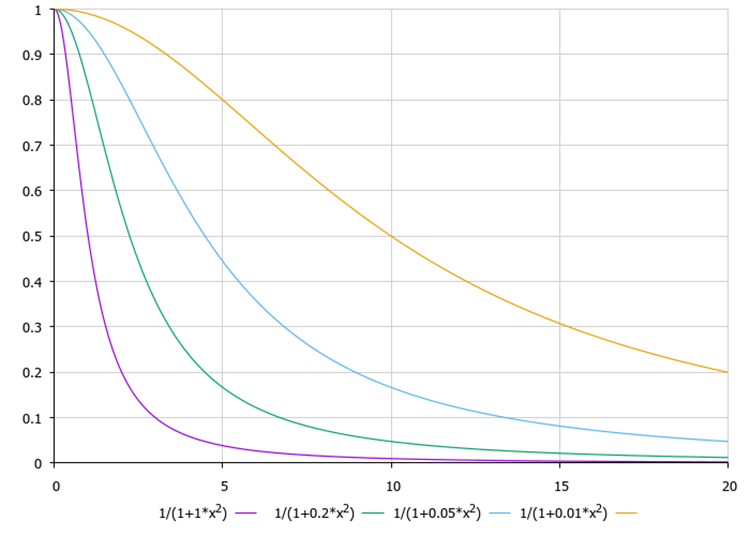
図2：距離f(x)からの媒体の透明度を表す関数（γ透明度係数はそれぞれ1.0, 0.2, 0.05, 0.01）

γが無限大に近づくと環境は不透明になります。γがゼロになると環境は完全に透明になり、各ホタルは探索空間内のどの距離でも相手を見ることができるようになります。γ = 0.0の場合はどうなるのでしょうか。すべてのホタルは、ある最適でない地点に収束する最も明るい相対的な場所に飛ぶことになります。そのため、アルゴリズムは極値から抜け出せず、収束しません。環境が完全に不透明な場合はどうなるのでしょうか。ホタルは、自分より魅力的な個体を見ることはありません。このアルゴリズムの作者が提唱した概念によると、自分より優れた個体がいないことで、ホタルはランダムに動くようになります。アルゴリズムはランダム探索に縮退してしまいます。アルゴリズム分類の評価表では、ランダム検索アルゴリズムは最下位になっています。 

さらにアルゴリズムの解析を掘り下げ、ホタルの動きを表す方程式を考えてみましょう。いわゆる魅力度指数の算出には、視認性対距離の関数が用いられます。

attractiveness = fireflies [k].f / (1.0 + γ * distance * distance);

ここで
attractiveness - 自明
γ - 環境不透明度係数
distance - ホタル間のユークリッド距離
fireflies [k].f - k番目のホタルの光度

この式から、魅力度関数は問題の次元と距離値の限界に直接依存することが明らかです。アルゴリズムの著者は特定の最適化問題に対して透明度係数を選択することを推奨しています。事前にアルゴリズムの挙動がわからない状態でそれをおこなうのは不便で時間もかかるので、0から20の範囲で距離の値を正規化することが必要だと考えています。そのために、他のアルゴリズムで繰り返し使ってきたScale()関数を適用します。魅力度計算前の「距離」の変換は次のようになります。

distance = Scale (distance, 0.0, maxDist, 0.0, 20.0, false);

ここで

maxDist - すべてのホタルの組の中での最大ユークリッド距離

この場合、ホタルの魅力は問題の次元に依存しないので、特定の最適化問題に対してγ係数を選択する必要はありません。魅力関数とは、各ホタルがどのような仲間を選択するかを決めるものです。この選択は厳しく決められています。ホタル同士の魅力の影響で、アルゴリズムの2つ目のパラメータであるβ（ベータ）係数が決まります。対応する反復ごとにホテルの選択があらかじめ決まっている場合、アルゴリズムの探索能力はどのように確保されるのでしょうか。そのために、ランダムなベクトル成分とアルゴリズムの第3パラメータ(α)を導入しています。ホタルの複雑な行動関係は、こんな感じでしょうか。

fireflies [i].c [c] = Xj + β * (Xi - Xj) + α * r * v [c];

ここで
fireflies [i].c [c] - i番目のホタルのc番目の座標
β - ホタル誘引影響係数
α - ホテルを動かすときのランダム要素に影響する係数で、移動目標からのずれを与える
r - 範囲 [-1.0;1.0] の乱数
v[c] - c番目の座標による探索範囲の極限点間の距離を特徴付けるベクトル成分
Хj - 対になったホタルの対応する座標で、移動先となるもの
Xi - 移動が計算されるホタルの対応する座標

さて、いよいよアルゴリズムのコードを記述していきます。比較的シンプルです。もう少し詳しく考えてみましょう。

ホタルは、[] - 座標、f - ホタルの光度（適応度関数）という2つの要素を持つ単純な構造体S_Fireflyで記述されることになります。各ホタルは、対応する繰り返しにおいて、ペアを形成して移動する個体は1つだけなので、次の移動を計算する際に座標を上書きする危険はありません。そのために、以下で考える特殊な構造体を紹介します。
//——————————————————————————————————————————————————————————————————————————————
struct S_Firefly
{
  double c  []; //coordinates
  double f;     //the value of the fitness function
};
//——————————————————————————————————————————————————————————————————————————————

S_Attractiveness構造体は、魅力度と対応するホタルの数をペアとして格納するためのものです。各ホタルは、最も魅力的なホタルの座標に向かって移動するのではなく、パートナーがすでに移動した座標に向かって移動します。著者が説明したアルゴリズムのバージョンとは若干のズレがありますが、この方がうまくいくのです。

//——————————————————————————————————————————————————————————————————————————————
struct S_Attractiveness
{
  double a; //attractiveness
  int    i; //index of the most attractive firefly
};
//——————————————————————————————————————————————————————————————————————————————

ホタルアルゴリズムについては、C_AO_FAクラスを使用して記述しています。ここには3つのpublicメソッドがあり、1つは初期化用のInit()、2つは反復毎に呼び出す必要のあるFlight()とLuminosity()です。Privateヘルパーメソッドとパラメータ定数を保存するためのメンバーがあります。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_FA
{
  //----------------------------------------------------------------------------
  public: S_Firefly fireflies []; //fireflies
  public: double    rangeMax  []; //maximum search range
  public: double    rangeMin  []; //minimum search range
  public: double    rangeStep []; //step search
  public: double    cB        []; //best coordinates
  public: double    fB;           //FF of the best coordinates

  public: void Init (const int    paramsP,  //number of opt. parameters
                     const int    sizeP,    //swarm size
                     const double alphaP,   //alpha, randomness in motion
                     const double betaP,    //beta, effect of attractiveness
                     const double gammaP);  //gamma, transparency of the environment

  public: void Flight ();
  public: void Luminosity ();

  //----------------------------------------------------------------------------
  private: S_Attractiveness att [];
  private: int    swarmSize;
  private: int    params;
  private: double maxDist;
  private: double v [];

  private: double alpha;      //randomness in motion
  private: double beta;       //effect of attractiveness
  private: double gamma;      //transparency of the environment
  private: bool   luminosity;

  private: double SeInDiSp  (double In, double inMin, double inMax, double step);
  private: double RNDfromCI (double min, double max);
  protected: double Scale   (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
};
//——————————————————————————————————————————————————————————————————————————————

Init() publicメソッドは、初期化に使用され、各最適化の開始前に呼び出される必要があります。そのパラメータは、アルゴリズムの上部構造パラメータです。このメソッドは、配列のためのメモリを割り当て、グローバルおよび個々のホタルの光度値をリセットします。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_FA::Init (const int    paramsP, //number of opt. parameters
                    const int    sizeP,   //swarm size
                    const double alphaP,  //alpha, randomness in motion
                    const double betaP,   //beta, effect of attractiveness
                    const double gammaP)  //gamma, transparency of the environment
{
  fB = -DBL_MAX;

  params    = paramsP;
  swarmSize = sizeP;
  alpha     = alphaP;
  beta      = betaP;
  gamma     = gammaP;

  ArrayResize (rangeMax,  params);
  ArrayResize (rangeMin,  params);
  ArrayResize (rangeStep, params);
  ArrayResize (v,         params);
  ArrayResize (att,       swarmSize);

  luminosity = false;

  ArrayResize (fireflies, swarmSize);

  for (int i = 0; i < swarmSize; i++)
  {
    ArrayResize (fireflies [i].c,  params);
    fireflies [i].f = -DBL_MAX;
  }

  ArrayResize (cB, params);
}
//——————————————————————————————————————————————————————————————————————————————

各反復で呼び出される最初のpublicメソッド、Flight()を考えてみましょう。アルゴリズムの主要なロジックはこの方式に集約されているので、より詳細に検討する必要があります。luminosity変数は、アルゴリズムが最初の反復で実行されているか、その後の反復で実行されているかを判断するためのフラグとして機能します。フラグが設定されていない場合は、一様分布に従ってホタルを座標空間内にランダムに分布させる必要があります。この動作に伴い、各座標に変位ベクトルを設定し、直ちにホタル間に存在しうる最大ユークリッド距離を計算します（すでに述べたように、これは環境透明度係数の問題次元への依存を避けるために、ホタル間の距離を正規化するために必要なことです）。これらの操作の後、luminosityフラグを有効にします。

if (!luminosity)
{
  fB = -DBL_MAX;

  //--------------------------------------------------------------------------
  double summCoordinates = 0.0;
  for (int c = 0; c < params; c++)
  {
    v [c] = rangeMax [c] - rangeMin [c];
    summCoordinates += pow (v [c], 2.0);
  }
  maxDist = pow (summCoordinates, 0.5);

  //--------------------------------------------------------------------------
  for (int s = 0; s < swarmSize; s++)
  {
    for (int k = 0; k < params; k++)
    {
      fireflies [s].c  [k] = RNDfromCI (rangeMin [k], rangeMax [k]);
      fireflies [s].c  [k] = SeInDiSp (fireflies [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
    }
  }

  luminosity = true;
}

1回目の反復でランダムに分布したホタルが光り始めた（それに対して適応度関数を計算した）あと、2回目以降の反復から、各ホタルの魅力度を計算することができます。そのためには、考えられるすべてのホタルのペアの間のユークリッド距離を計算する必要があります。これには単に、座標の差の二乗を足して、その和から根を求めます。算出された距離は、魅力度計算式に使用されます。こうして、各ホタルの唯一可能なペアを得ます。すべてのホタルの中で最大輝度を決定します。これは、ペアを見つけることができず、単独で空間を彷徨うことになる最も明るいホタルを決定するために必要なことです。まあ、おそらく、次の反復ではもっと運が良くなるのでしょう。

//measure the distance between all------------------------------------------
for (int i = 0; i < swarmSize; i++)
{
  att [i].a = -DBL_MAX;

  for (int k = 0; k < swarmSize; k++)
  {
    if (i == k) continue;

    summCoordinates = 0.0;
    for (int c = 0; c < params; c++) summCoordinates += pow (fireflies [i].c [c] - fireflies [k].c [c], 2.0);

    distance = pow (summCoordinates, 0.5);
    distance = Scale (distance, 0.0, maxDist, 0.0, 20.0, false);
    attractiveness = fireflies [k].f / (1.0 + gamma * distance * distance);

    if (attractiveness > att [i].a)
    {
      att [i].a = attractiveness;
      att [i].i = k;
    }

    if (fireflies [i].f > maxF) maxF = fireflies [i].f;
  }
}

Flight()メソッドのコードのこの部分は、ホタルの飛行を担当します。光度が他よりも大きい不幸なホタルの場合、計算方法が多少異なります。移動ベクトルに乱数[-1.0;1.0]を乗じたα係数を介して現在位置に加算しています。理論的には、アルゴリズムにおいて、これは最適解追加学習として機能して、さらなる改善を期待できますが、後で見るように、このテクニックは役に立たないことが判明します。現段階では、古典版のアルゴリズムを考察します。

それ以外のホタルではすでにペアが見つかっており、ランダムな要素（先ほども書きました）を加えて、該当するペアに移動する計算となります。

//flight--------------------------------------------------------------------
for (int i = 0; i < swarmSize; i++)
{
  if (fireflies [i].f >= maxF)
  {
    for (int c = 0; c < params; c++)
    {
      r  = RNDfromCI (-1.0, 1.0);
      fireflies [i].c [c] = fireflies [i].c [c] + alpha * r * v [c];
      fireflies [i].c [c] = SeInDiSp (fireflies [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); 
    }
  }
  else
  {
    for (int c = 0; c < params; c++)
    {
      r  = RNDfromCI (-1.0, 1.0);
      Xi = fireflies [i].c [c];
      Xj = fireflies [att [i].i].c [c];
      fireflies [i].c [c] = Xj + beta * (Xi - Xj) + alpha * r * v [c];
      fireflies [i].c [c] = SeInDiSp (fireflies [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}

次は、反復毎に呼び出されるシンプルなpublicメソッドです。ここでは、最適解を更新します。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_FA::Luminosity ()
{
  for (int i = 0; i < swarmSize; i++)
  {
    if (fireflies [i].f > fB)
    {
      fB = fireflies [i].f;
      ArrayCopy (cB, fireflies [i].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

では、テストに移りましょう。テスト関数にアルゴリズムを適用した結果を見てみましょう。

2022.12.16 13:39:00.102    Test_AO_FA (EURUSD,M1)    =============================
2022.12.16 13:39:05.930    Test_AO_FA (EURUSD,M1)    1 Skin's; Func runs 10000 result:4.901742065217812
2022.12.16 13:39:05.930    Test_AO_FA (EURUSD,M1)    Score:0.99603
2022.12.16 13:39:13.579    Test_AO_FA (EURUSD,M1)    20 Skin's; Func runs 10000 result:3.2208359936020665
2022.12.16 13:39:13.579    Test_AO_FA (EURUSD,M1)    Score:0.59468
2022.12.16 13:39:53.607    Test_AO_FA (EURUSD,M1)    500 Skin's; Func runs 10000 result:0.98491319842575
2022.12.16 13:39:53.607    Test_AO_FA (EURUSD,M1)    Score:0.06082
2022.12.16 13:39:53.607    Test_AO_FA (EURUSD,M1)    =============================
2022.12.16 13:39:59.313    Test_AO_FA (EURUSD,M1)    1 Forest's; Func runs 10000 result:1.578196881663454
2022.12.16 13:39:59.313    Test_AO_FA (EURUSD,M1)    Score:0.89271
2022.12.16 13:40:07.274    Test_AO_FA (EURUSD,M1)    20 Forest's; Func runs 10000 result:0.3101994341994826
2022.12.16 13:40:07.274    Test_AO_FA (EURUSD,M1)    Score:0.17546
2022.12.16 13:40:49.159    Test_AO_FA (EURUSD,M1)    500 Forest's; Func runs 10000 result:0.06829102669136165
2022.12.16 13:40:49.159    Test_AO_FA (EURUSD,M1)    Score:0.03863
2022.12.16 13:40:49.159    Test_AO_FA (EURUSD,M1)    =============================
2022.12.16 13:40:54.895    Test_AO_FA (EURUSD,M1)    1 Megacity's; Func runs 10000 result:8.2
2022.12.16 13:40:54.895    Test_AO_FA (EURUSD,M1)    Score:0.68333
2022.12.16 13:41:02.777    Test_AO_FA (EURUSD,M1)    20 Megacity's; Func runs 10000 result:1.5900000000000003
2022.12.16 13:41:02.777    Test_AO_FA (EURUSD,M1)    Score:0.13250
2022.12.16 13:41:43.901    Test_AO_FA (EURUSD,M1)    500 Megacity's; Func runs 10000 result:0.2892
2022.12.16 13:41:43.901    Test_AO_FA (EURUSD,M1)    Score:0.02410
2022.12.16 13:41:43.901    Test_AO_FA (EURUSD,M1)    =============================
2022.12.16 13:41:43.901    Test_AO_FA (EURUSD,M1)    All score for C_AO_FA:0.39980648892951776

その結果は、控えめに言っても印象が悪いものです。このアルゴリズムは、個々のテストにおいて、PSO、FSS、GWOよりもわずかに優れているに過ぎません。しかし、総合評価指標では、ランダム検索アルゴリズムを差し置いて下から2番目の位置にいます。そこで、テストにおける推定指標の算出方法を見直すという発想が生まれました。次の記事では、より便利な評価計算方式に切り替えます。そして、今回の記事では、最終結果のヒストグラムを追加する予定です。個々のアルゴリズム間の性能比を明確に示すことができるようになります。

古典的なホタルアルゴリズムは簡単に実装できますが、多峰性の問題では収束が遅く、極限の罠に陥りやすいという研究結果が出ています。また、現在の反復処理にパラメータ的に依存する係数を欠いています。そこで、この研究の目的の1つは、標準的なホタルアルゴリズムを改良して、その性能を向上させることでした。

アルゴリズムの考え方そのものが非常に独創的で、すべてをそのままにして、その特性を改善しようとしないのは残念なことです。そこで、ランダムな要素をレヴィ飛行に置き換えて、アルゴリズムの修正を試みました。レヴィ飛行はすべてのアルゴリズムの検索能力を向上させることはできません。カッコー検索アルゴリズムを検討した後、この手法で他のアルゴリズムも改良してみましたが、期待通りの結果は得られませんでした。どうやら、これを補完するアルゴリズム内の内部検索戦略と何らかの形で整合性がとれている必要があるようです。この特定の場合には、「レヴィ飛行」を適用することで、アルゴリズムの能力が飛躍的に向上するという顕著な効果が得られました。これについては、テスト結果に関する部分でお話します。

以下は、その変更をおこなったコードの部分です。まず、古典版では、最も輝度の高いホタルが現在位置からランダムな方向に移動します。そして、最適なホタルが最適な大局的位置から移動し、現在位置ではなく、解全体を改善しようとするのです。最適解の座標に、移動ベクトルを考慮したレヴィ飛行分布（尾が重い分布）の乱数を同じα係数で追加します。これによって、本当に近傍を絞り込むことで全体解の座標を向上させることが可能になったのです。

このように、レヴィ飛行のランダム性を調整したとはいえ、他のホタルの挙動も同じ古典的な法則に従うようになりました。これがアルゴリズムに施された修正のすべてです。

//flight--------------------------------------------------------------------
for (int i = 0; i < swarmSize; i++)
{
  if (fireflies [i].f >= maxF)
  {
    for (int c = 0; c < params; c++)
    {
      r1 = RNDfromCI (0.0, 1.0);
      r1 = r1 > 0.5 ? 1.0 : -1.0;
      r2 = RNDfromCI (1.0, 20.0);

      fireflies [i].c [c] = cB [c] + alpha * r1 * pow (r2, -2.0) * v [c];
      fireflies [i].c [c] = SeInDiSp (fireflies [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
  else
  {
    for (int c = 0; c < params; c++)
    {
      r1 = RNDfromCI (0.0, 1.0);
      r1 = r1 > 0.5 ? 1.0 : -1.0;
      r2 = RNDfromCI (1.0, 20.0);

      Xi = fireflies [i].c [c];
      Xj = fireflies [att [i].i].c [c];

      fireflies [i].c [c] = Xj + beta * (Xi - Xj) + alpha * r1 * pow (r2, -2.0) * v [c];
      fireflies [i].c [c] = SeInDiSp (fireflies [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}

図3はレヴィ飛行関数図です。関数式の指数はアルゴリズムの動作にどのような影響を与えるのでしょうか。私の研究によると、次数が高くなると、短いジャンプに比べて長い（尾が重い）ジャンプの数が減り、最適解の近傍で座標を絞り込むアルゴリズムの能力が向上します。長いジャンプが少ないため、極値で行き詰まる確率が高くなります。この効果は離散関数を研究するときに顕著になりますが、滑らかな関数の場合はそれほど顕著にはならありません。逆に指数を小さくすると長いジャンプの回数が増えて、アルゴリズムの探索能力は向上するが収束精度は悪化するので、精度と探索の中間が必要です。その上、最適化問題によって異なることもあります。


リヴィ

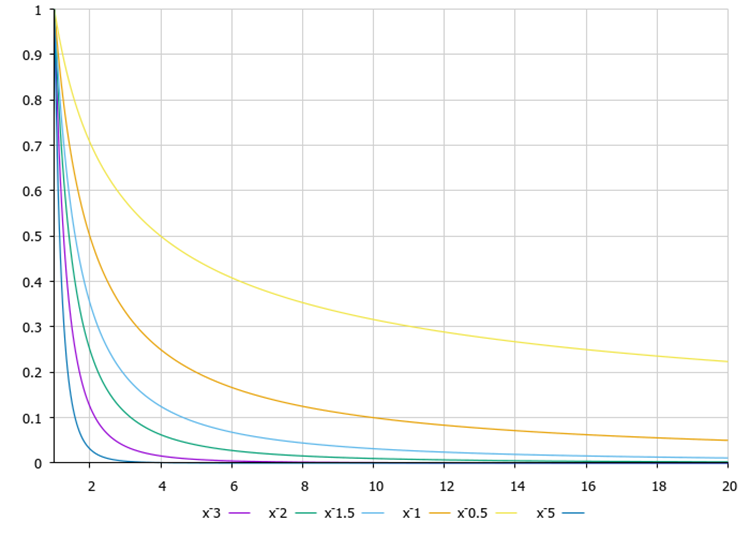
図3：レヴィ飛行関数、度数0.5...3.0 


それでは、修正版のアルゴリズムをテストスタンドで試した結果に移ります。以下では、古典版と比較して、どれだけ性能が向上したかをご覧いただけます。

2022.12.16 13:07:15.925    Test_AO_FAm (EURUSD,M1)    =============================
2022.12.16 13:07:21.544    Test_AO_FAm (EURUSD,M1)    1 Skin's; Func runs 10000 result:4.854437214435259
2022.12.16 13:07:21.544    Test_AO_FAm (EURUSD,M1)    Score:0.98473
2022.12.16 13:07:29.518    Test_AO_FAm (EURUSD,M1)    20 Skin's; Func runs 10000 result:4.588539001298423
2022.12.16 13:07:29.518    Test_AO_FAm (EURUSD,M1)    Score:0.92124
2022.12.16 13:08:12.587    Test_AO_FAm (EURUSD,M1)    500 Skin's; Func runs 10000 result:1.981278990090829
2022.12.16 13:08:12.587    Test_AO_FAm (EURUSD,M1)    Score:0.29872
2022.12.16 13:08:12.587    Test_AO_FAm (EURUSD,M1)    =============================
2022.12.16 13:08:18.336    Test_AO_FAm (EURUSD,M1)    1 Forest's; Func runs 10000 result:1.7665409595127233
2022.12.16 13:08:18.336    Test_AO_FAm (EURUSD,M1)    Score:0.99924
2022.12.16 13:08:26.432    Test_AO_FAm (EURUSD,M1)    20 Forest's; Func runs 10000 result:0.6261364994589462
2022.12.16 13:08:26.432    Test_AO_FAm (EURUSD,M1)    Score:0.35417
2022.12.16 13:09:10.587    Test_AO_FAm (EURUSD,M1)    500 Forest's; Func runs 10000 result:0.14269062630878
2022.12.16 13:09:10.587    Test_AO_FAm (EURUSD,M1)    Score:0.08071
2022.12.16 13:09:10.587    Test_AO_FAm (EURUSD,M1)    =============================
2022.12.16 13:09:16.393    Test_AO_FAm (EURUSD,M1)    1 Megacity's; Func runs 10000 result:10.0
2022.12.16 13:09:16.393    Test_AO_FAm (EURUSD,M1)    Score:0.83333
2022.12.16 13:09:24.373    Test_AO_FAm (EURUSD,M1)    20 Megacity's; Func runs 10000 result:1.7899999999999998
2022.12.16 13:09:24.373    Test_AO_FAm (EURUSD,M1)    Score:0.14917
2022.12.16 13:10:09.298    Test_AO_FAm (EURUSD,M1)    500 Megacity's; Func runs 10000 result:0.5076
2022.12.16 13:10:09.298    Test_AO_FAm (EURUSD,M1)    Score:0.04230
2022.12.16 13:10:09.298    Test_AO_FAm (EURUSD,M1)    =============================
2022.12.16 13:10:09.298    Test_AO_FAm (EURUSD,M1)    All score for C_AO_FAm:0.5181804234713119

ご覧のように、修正したアルゴリズムはより良い結果を示すだけでなく、評価表でトップの座を獲得しています。次節で、その結果を詳しく見ていきましょう。以下は、テストスタンドに設置された修正版アルゴリズムのアニメーションです。

Skin

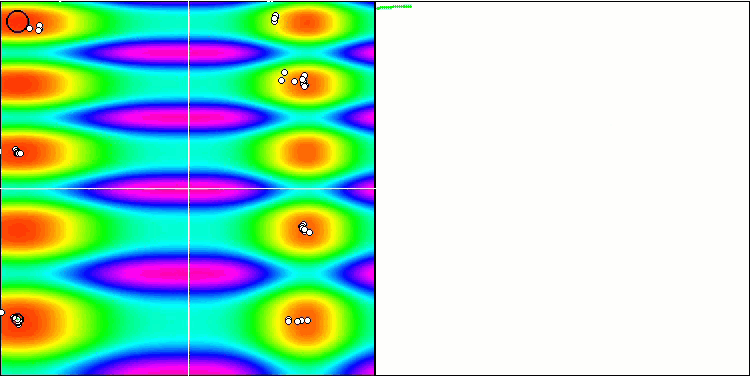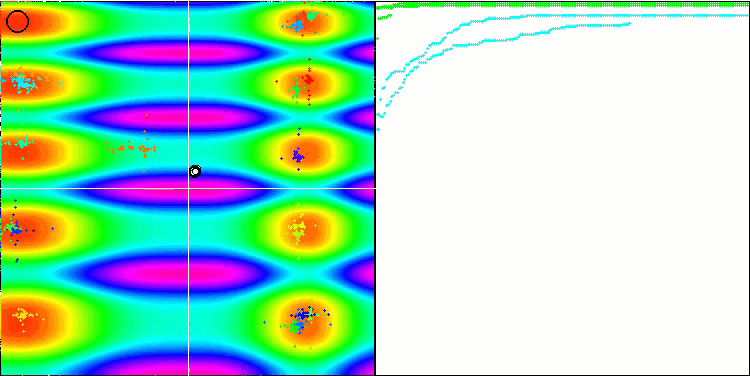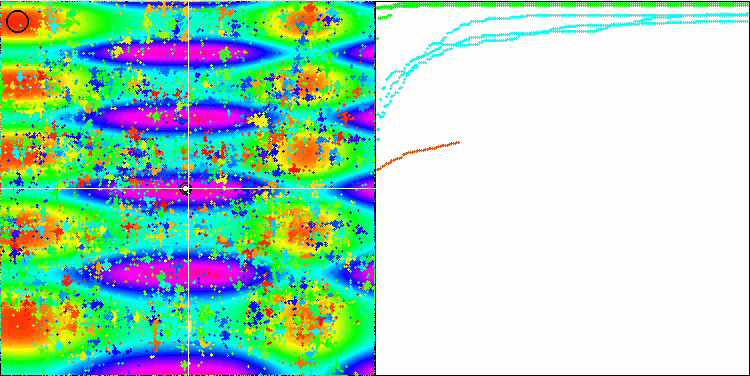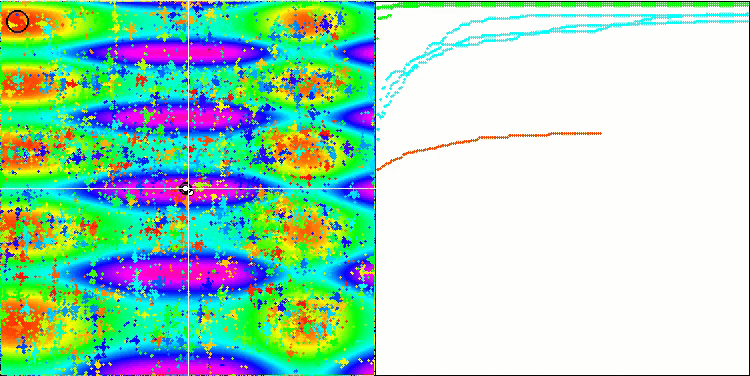
  Skinテスト関数のFAm

Forest

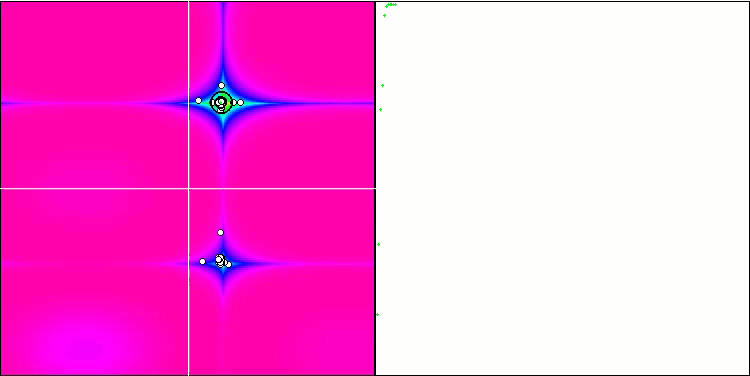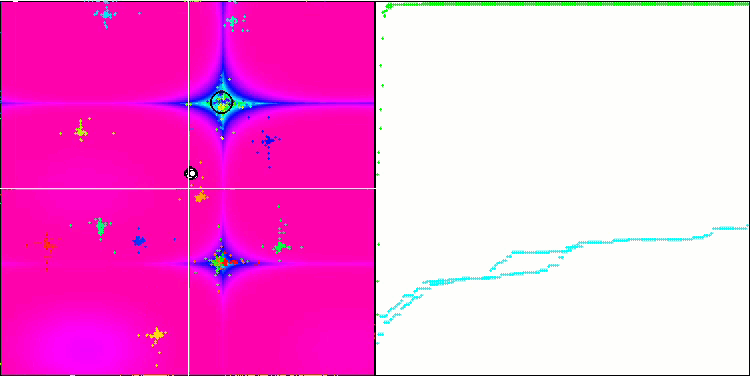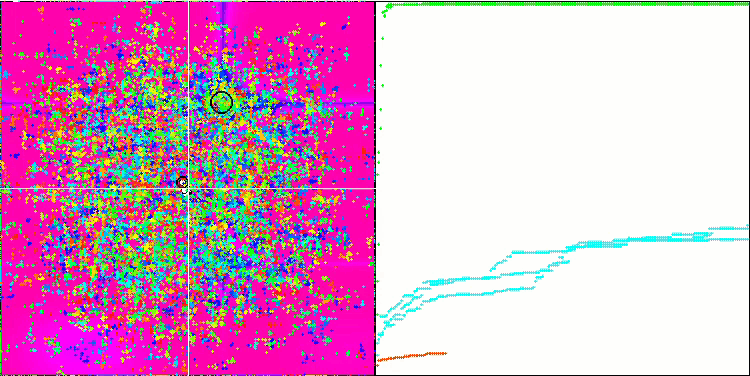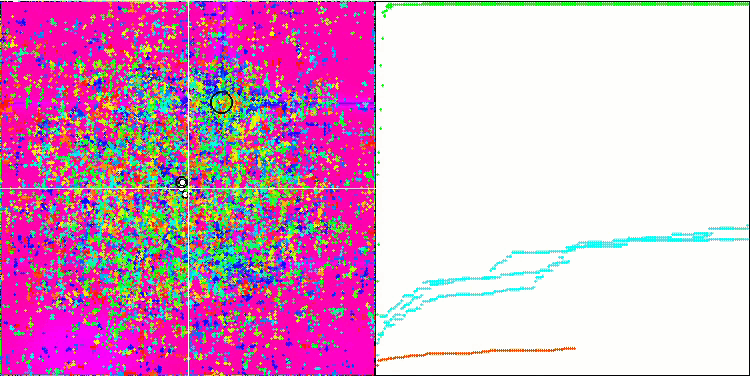
  Forestテスト関数のFAm

Megacity

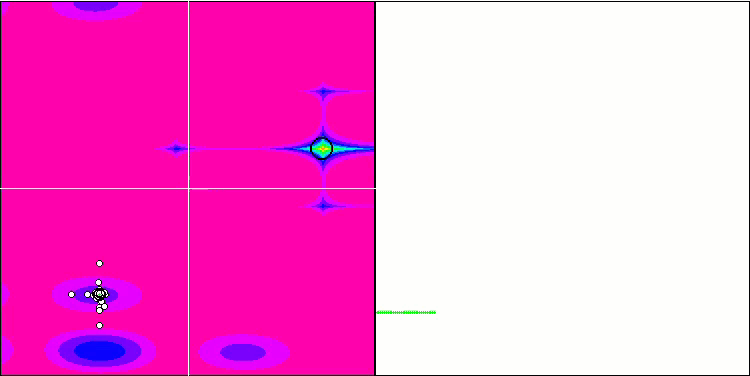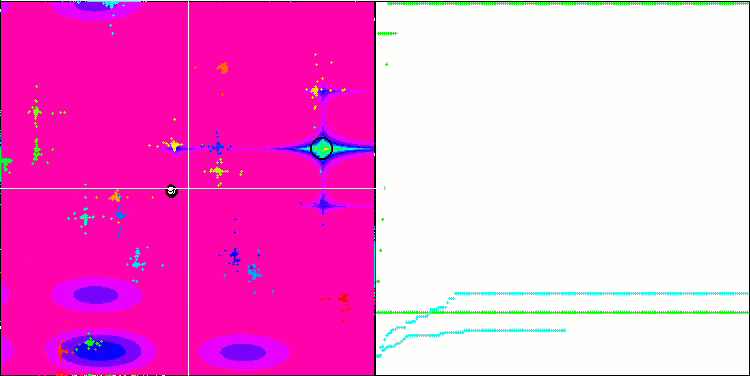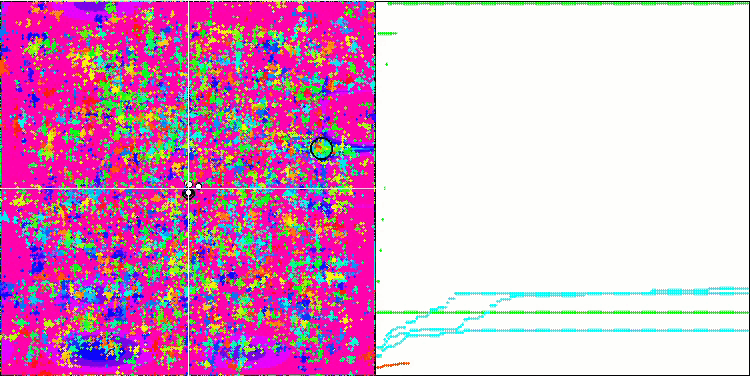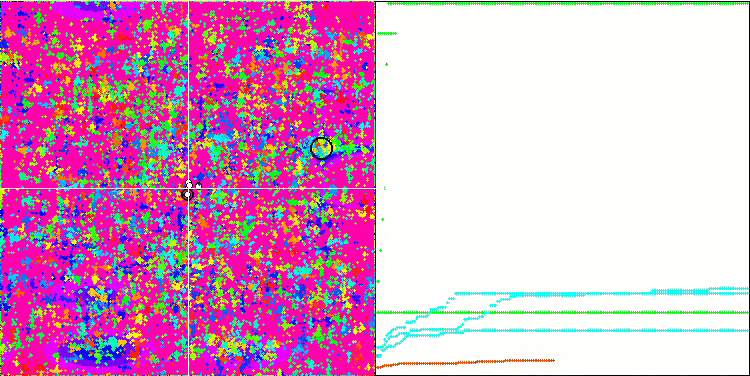
  Megacityテスト関数のFAm


3.テスト結果

修正ホタルアルゴリズム(FAm)は、すべてのテストで優れた性能を発揮しました。一般に、結果はアルゴリズムの設定に依存します。いくつかの設定の場合、2変数の3つの関数すべてで100%の収束が達成されました。アルゴリズムの高いスケーラビリティにより、パラメータが40個と1000個のテストにおいてリーダとなります。βとγのパラメータは強い影響力を持ち、高い収束性と極値への耐性の両方を得ることができます。結果は様々で、一般的にはアルゴリズムの欠点に起因すると考えられます。他の条件がすべて同じであれば、先に検討した中では最強のアルゴリズムと言えるでしょう。機械学習や人工知能の課題、特にニューラルネットワークを学習させる場合など、非常に幅広い用途に推奨することができます。

以下は最終的な評価表です。修正ホタルアルゴリズムがリードしています。残念ながら、古典的なアルゴリズムは、その独創性にもかかわらず、良い結果を得ることができませんでした。チューニングパラメータの選択も成功には至りませんでした。

AO

詳細

Skin

Skin最終

Forest

Forest最終

Megacity (discrete)

Megacity最終

最終結果

2パラメータ（1F）

40パラメータ（20F）

1000パラメータ（500F）

2パラメータ（1F）

40パラメータ（20F）

1000パラメータ（500F）

2パラメータ（1F）

40パラメータ（20F）

1000パラメータ（500F）

FAm

ホタルアルゴリズムM

0.98473

0.92124

0.29872

0.73490

0.99924

0.35417

0.08071

0.47804

0.83333

0.14917

0.04230

0.34160

0.51817889

COAm

カッコウ最適化アルゴリズムM

1.00000

0.85911

0.14316

0.66742

0.99283

0.28787

0.04551

0.44207

1.00000

0.24917

0.03537

0.42818

0.51255778

ACOm

蟻コロニー最適化M

0.98229

0.79108

0.12602

0.63313

1.00000

0.62077

0.11521

0.57866

0.38333

0.44000

0.02377

0.28237

0.49805222

ABCm

人工蜂コロニーM

1.00000

0.63922

0.08076

0.57333

0.99908

0.20112

0.03785

0.41268

1.00000

0.16333

0.02823

0.39719

0.46106556

ABC

人工蜂コロニー

0.99339

0.73381

0.11118

0.61279

0.99934

0.21437

0.04215

0.41862

0.85000

0.16833

0.03130

0.34988

0.46043000

GWO

灰色オオカミオプティマイザ

0.99900

0.48033

0.18924

0.55619

0.83844

0.08755

0.02555

0.31718

1.00000

0.10000

0.02187

0.37396

0.41577556

FSS

魚群検索

0.99391

0.5692

0.11341

0.55884

0.85172

0.12143

0.03223

0.33513

0.91667

0.08583

0.02583

0.34278

0.41224778

PSO

粒子群最適化

0.99627

0.38080

0.05089

0.47599

0.93772

0.14540

0.04856

0.37723

1.00000

0.09333

0.02233

0.37189

0.40836667

FA

ホタルアルゴリズム

0.99603

0.59468

0.06082

0.55051

0.89271

0.17546

0.03863

0.36893

0.68333

0.13250

0.02410

0.27998

0.39980649

RND

ランダム

0.99932

0.44276

0.06827

0.50345

0.83126

0.11524

0.03048

0.32566

0.83333

0.09000

0.02403

0.31579

0.38163222


今回から、テスト時に最も良いアルゴリズムが100点、最も悪いアルゴリズムが1点という条件付きのヒストグラムを公開することにしました。評価表でのアルゴリズムの最終結果のスケールが明確に分かるので、視覚的に最も便利な表示方法だと思います。ここで、ランダムアルゴリズムがリーダーにどれだけ遅れをとっているかを見ることができます。

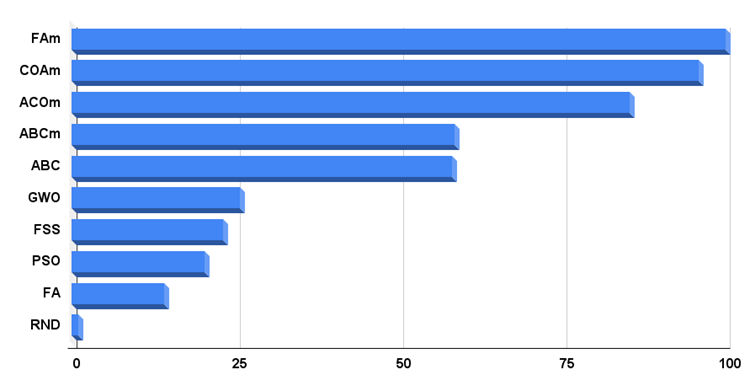評価alt

図4：テストアルゴリズムの最終結果のヒストグラム


覚えていらっしゃるかもしれませんが、メタヒューリスティックアルゴリズムとは、最適化問題を解くための近似的な手法で、その探索エンジンに合理的な仮定によるランダム性の特性を利用し、ランダムに生成した有効解の集合から反復して解空間を調査し利用することで解の質を向上させようとするものです。これらのアルゴリズムは最適であることを保証するものではありませんが、合理的で受け入れ可能な解を与えることがテストされています。また、問題の挙動に大きく影響されないという利点もあり、多くのタスクで活躍することができます。多くの利用可能なアルゴリズムが存在するため、問題の挙動に応じて適切なものを選択して解くことが可能です。

進化的アルゴリズムの登場以来、ヒューリスティックアルゴリズムに関する研究が盛んにおこなわれています。新しいアルゴリズムの実装は、主要な研究分野の1つです。現在、40以上のメタヒューリスティックアルゴリズムが存在します。その多くは、自然界のシナリオをシミュレートして作られたものです。

「賛成」と「反対」は、ホタルアルゴリズムの修正版(FAm)についてです。

賛成：
  • 実装がシンプルで改造が容易
  • 拡張性が高い
  • 収束性が高い（アルゴリズムの設定により異なる可能性）
  • 探索空間の領域を極値付近で別々のグループにクラスタリングする機能

反対：
  • 設定が最適化結果に与える影響が大きい
  • 設定によっては、アルゴリズムが極値から抜け出せなくなる傾向がある

各記事には、過去の記事のアルゴリズムコードを最新版に更新したアーカイブが用意されています。それぞれの新しい記事は、著者の個人的な経験の蓄積であり、結論と判断は、この目的のために開発された特別なテストスタンドでおこなわれた実験に基づいています。



MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/11873

添付されたファイル |
ZIPをダウンロード
8_The_world_of_AO_vFA2.zip (77.04 KB)
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動
ティッカーテープパネルの作成:改良版 ティッカーテープパネルの作成:改良版
ティッカーテープパネルの基本バージョンを復活させるというアイデアはいかがでしょうか。まずおこなうのは、資産のロゴやその他の画像などの画像を追加できるようにパネルを変更して、ユーザーが表示された銘柄をすばやく簡単に識別できるようにすることです。
インディケーター情報の測定 インディケーター情報の測定
機械学習は、ストラテジー開発の手法として注目されています。これまで、収益性と予測精度の最大化が重視される一方で、予測モデル構築のためのデータ処理の重要性はあまり注目されてきませんでした。この記事では、Timothy Masters著の書籍「Testing and Tuning Market Trading Systems」に記載されているように、予測モデル構築に使用するインディケーターの適切性を評価するために、エントロピーの概念を使用することについて考察しています。
ティッカーテープパネルの作成:基本バージョン ティッカーテープパネルの作成:基本バージョン
ここでは、通常取引所の相場表示に使われるプライスティッカーを使った画面を作成する方法を紹介します。複雑な外部プログラミングを使わず、MQL5だけでやってみようと思います。
DoEasy - コントロール（第30部）：ScrollBarコントロールのアニメーション化 DoEasy - コントロール（第30部）：ScrollBarコントロールのアニメーション化
今回は、ScrollBarコントロールの開発の続きと、マウスインタラクション機能の実装を開始します。さらに、マウスの状態フラグやイベントのリストも充実させる予定です。