Algoritmo do Big Bang e do Grande Colapso — BBBC (Big Bang - Big Crunch)
145
0
Conteúdo
Introdução
Nos vastos domínios do Universo, onde nascem e morrem estrelas, escondem-se mistérios que a humanidade busca desvendar. O método BBBC (Big Bang-Big Crunch) é um algoritmo de otimização global inspirado nos processos que ocorrem no cosmos. Vamos entender esse conceito fascinante.
A teoria do Big Bang e do Grande Colapso foi proposta como um cenário alternativo para o fim do Universo pelos físicos Alexander Friedmann e Georges Lemaître no início do século XX. Eles observaram que as equações da teoria da relatividade geral de Einstein permitiam tanto a expansão quanto a contração do Universo. Friedmann demonstrou matematicamente que o Universo não poderia permanecer estático e deveria ou se expandir ou se contrair. Ele identificou três possíveis cenários para sua evolução: expansão eterna, expansão seguida de contração e um modo oscilatório.
Ao longo do século XX, muitos cientistas desenvolveram ideias para unir o Big Bang e o Grande Colapso em um modelo cíclico. Hoje em dia, a teoria do Grande Colapso não é a principal teoria cosmológica, pois as observações indicam que o Universo está se expandindo de forma acelerada. No entanto, essa ideia apresenta um conceito interessante: a evolução cíclica do Universo. Etapas principais:
- O Big Bang, em que um estado inicial de alta densidade e temperatura entra em uma fase de rápida expansão e dispersão de energia, formando matéria e espaço-tempo com uma distribuição caótica de partículas.
- O Grande Colapso, em que as forças gravitacionais interrompem a expansão e inicia-se o processo inverso de contração, com toda a matéria sendo atraída de volta para um ponto, retornando a um estado de alta densidade.
- A ciclicidade se manifesta na sequência de um novo Big Bang após um Grande Colapso, processo que pode se repetir infinitamente e cada ciclo pode apresentar constantes físicas diferentes.
O algoritmo Big Bang-Big Crunch foi proposto em 2006 pelos cientistas Osman K. Erol e Ibrahim Eksin da Universidade Técnica de Istambul (Istanbul Technical University, Turkey).
Implementação do algoritmo
Assim como na teoria do Big Bang, onde o Universo começa sua existência com uma intensa liberação de energia, no método BBBC também observamos uma fase inicial repleta de aleatoriedade e diversidade. Na fase do Big Bang, é criada uma população de pontos aleatórios, cada um representando um candidato à solução. Esses pontos estão espalhados pelo vasto espaço de busca, prontos para a diversificação, mas, assim que o caos encontra seu lugar, tem início a fase do Grande Colapso. Os pontos passam a convergir para o “centro de massa”, assim como as galáxias se atraem por gravidade. Esse momento é o clímax: quando todos os esforços se concentram na busca por uma solução ideal.
Assim, as etapas do algoritmo traçam o caminho do caos à ordem:
1. Fase do Big Bang. Neste primeiro passo, é criada a população inicial com N pontos aleatórios. Cada ponto ocupa sua posição no espaço, distribuído uniformemente dentro dos limites estabelecidos.
2. Fase do Grande Colapso (Big Crunch), a transição para o cálculo do “centro de massa”, isto é, o ponto para o qual todos os demais convergem. Utilizando a fórmula (ver Fig. 1), encontramos as coordenadas do centro, que servirá como nova origem para os próximos passos.
3. Geração de novos pontos. Ao redor do centro de massa, novos pontos começam a ser formados. Eles surgem com distribuição normal, seguindo a fórmula que define sua direção e magnitude de deslocamento.
O método BBBC busca equilíbrio entre diversificação e intensificação. A cada nova geração, a dispersão dos pontos na geração diminui, o que permite ao algoritmo refinar a solução ótima encontrada.
Como no cosmos, onde cada movimento tem importância, no mundo da otimização cada cálculo nos aproxima do objetivo. Ao mergulhar neste método, não apenas desvendamos novos horizontes, mas também nos tornamos parte do grande processo cósmico na busca por uma solução melhor.
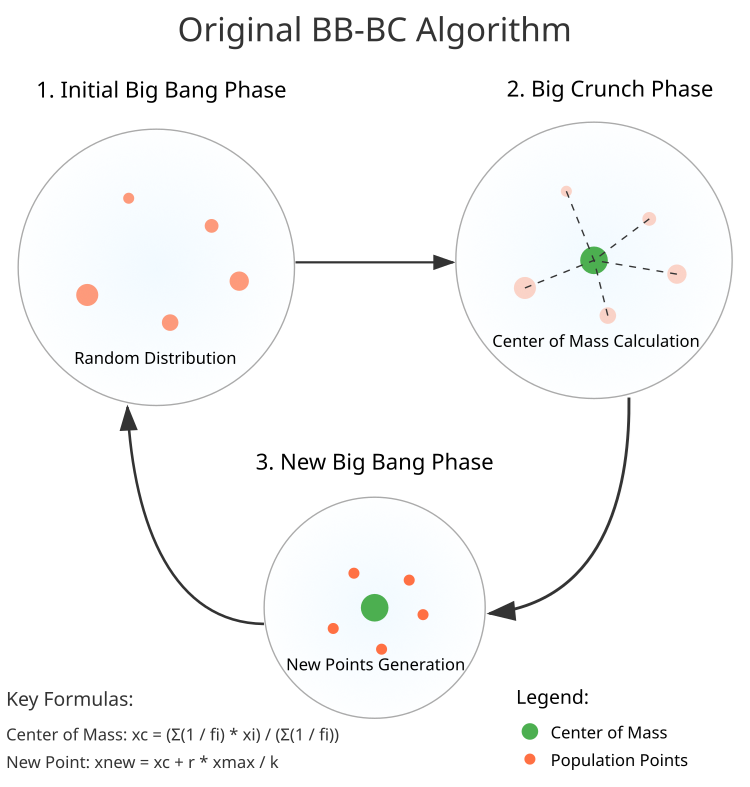
Figura 1. Esquema de funcionamento do algoritmo BBBC
Vamos esboçar o pseudocódigo do algoritmo BBBC:
Incrementar epochNow
// Inicialização (Big Bang)
Se revision == falso
Para cada indivíduo i de 0 até popSize-1
Para cada coordenada c de 0 até coords-1
Nova coordenada = Gerar número aleatório (rangeMin[c], rangeMax[c])
Definir revision como verdadeiro
Retornar
// Fase do Grande Colapso
Se epochNow % bigBangPeriod != 0
Para cada coordenada c de 0 até coords-1
numerador = 0, denominador = 0
Para cada indivíduo i de 0 até popSize-1
adaptabilidade = Máximo (Valor absoluto (a [i].f), 1e-10)
peso = 1.0 / adaptabilidade
numerador += peso * coordenada do ponto
denominador += peso
centerMass [c] = (denominador > 1e-10) ? numerador / denominador : cB [c]
Para cada indivíduo i de 0 até popSize-1
Para cada coordenada c de 0 até coords-1
r = Gerar número aleatório com distribuição normal (0, -1.0, 1.0, 1)
Nova coordenada = centerMass [c] + r * rangeMax [c] / epochNow
// Fase do Big Bang
Caso contrário
Para cada indivíduo i de 0 até popSize-1
Para cada coordenada c de 0 até coords-1
Nova coordenada = Gerar número aleatório com distribuição normal (cB [c], rangeMin [c], rangeMax [c], desvio padrão = 8)
Repetir até que o critério de parada seja atendido, iniciando a partir da fase do Grande Colapso
Vamos agora à implementação do código. Escreveremos a definição da classe C_AO_BBBC, que herda de C_AO:
Métodos públicos:- Construtor e destrutor
- SetParams () — define os parâmetros (tamanho da população e periodicidade do Big Bang)
- Init () — inicializa o algoritmo com os limites de busca fornecidos
- Moving () — método principal que implementa as fases Big Bang e Big Crunch
- Revision () — método de atualização da melhor solução encontrada
- epochs — número total de épocas de execução do algoritmo
- epochNow — época atual
- centerMass [] — array para armazenar as coordenadas do centro de massa
Essa classe representa a implementação do algoritmo BBBC, onde todos os principais cálculos ocorrem nos métodos Moving() e Revision(), enquanto os dados necessários sobre a população são armazenados na classe base C_AO.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_BBBC : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_BBBC () { } C_AO_BBBC () { ao_name = "BBBC"; ao_desc = "Big Bang - Big Crunch Algorithm"; ao_link = "https://www.mql5.com/ru/articles/16701"; popSize = 50; bigBangPeriod = 3; ArrayResize (params, 2); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "bigBangPeriod"; params [1].val = bigBangPeriod; } void SetParams () { popSize = (int)params [0].val; bigBangPeriod = (int)params [1].val; } bool Init (const double &rangeMinP [], // минимальный диапазон поиска const double &rangeMaxP [], // максимальный диапазон поиска const double &rangeStepP [], // шаг поиска const int epochsP = 0); // количество эпох void Moving (); void Revision (); //---------------------------------------------------------------------------- int bigBangPeriod; // периодичность большого взрыва private: //------------------------------------------------------------------- int epochs; // общее число эпох int epochNow; // текущая эпоха double centerMass []; // центр масс }; //——————————————————————————————————————————————————————————————————————————————
Método "Init" da classe C_AO_BBBC:
O método realiza a inicialização do algoritmo e recebe os seguintes parâmetros:
- rangeMinP [] — array com os valores mínimos para cada coordenada
- rangeMaxP [] — array com os valores máximos para cada coordenada
- rangeStepP [] — array com os passos de discretização para cada coordenada
- epochsP — número de épocas de execução do algoritmo (padrão 0)
Ações do método:
- Chama StandardInit () da classe base para configurar os parâmetros gerais
- Define o número total de épocas (epochs) e zera o contador da época atual (epochNow)
- Aloca memória para o array centerMass (centerMass) com tamanho igual ao número de coordenadas (coords)
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_BBBC::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { // Инициализация базового класса if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- epochs = epochsP; epochNow = 0; // Выделение памяти для массивов ArrayResize (centerMass, coords); return true; } //——————————————————————————————————————————————————————————————————————————————
O método "Moving" do algoritmo BB-BC é composto por três partes principais:
1. Inicialização (se revision = false):
- Cria uma população inicial de pontos aleatórios
- Adapta os pontos à grade discreta de busca
2. Fase do Grande Colapso (se a época não for múltipla de bigBangPeriod):
- Calcula o centro de massa com a fórmula: xc = (Σ(1/fi)*xi) / (Σ(1/fi))
- Gera novos pontos ao redor do centro de massa com a fórmula: xnew = xc + r * xmax / epoch
- Utiliza distribuição normal para os números aleatórios
3. Fase do Big Bang (se a época for múltipla de bigBangPeriod):
- Gera novos pontos utilizando distribuição normal
- Utiliza a melhor solução como valor médio
- Utiliza desvio padrão = 8 para realizar uma busca mais ampla
Todos os novos pontos são limitados pelos limites definidos de busca e ajustados à grade discreta.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BBBC::Moving () { epochNow++; // Начальная инициализация (Big Bang) if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { // Генерация случайных начальных позиций a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); // Приведение к дискретной сетке поиска a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- // Фаза Big Crunch - большой коллапс if (epochNow % bigBangPeriod != 0) { for (int c = 0; c < coords; c++) { double numerator = 0; double denominator = 0; for (int i = 0; i < popSize; i++) { // Расчет веса как обратной величины от значения фитнес-функции double fitness = MathMax (MathAbs (a [i].f), 1e-10); double weight = 1.0 / fitness; // Суммирование для вычисления центра масс по формуле // xc = (Σ(1/fi)xi) / (Σ(1/fi)) numerator += weight * a [i].c [c]; denominator += weight; } // Определение координаты центра масс centerMass [c] = denominator > 1e-10 ? numerator / denominator : cB [c]; } for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { double r = u.GaussDistribution (0, -1.0, 1.0, 1); // Генерация новой точки по формуле // xnew = xc + r*xmax/k double newPoint = centerMass [c] + r * rangeMax [c] / epochNow; // Ограничение в пределах допустимой области и приведение к сетке a [i].c [c] = u.SeInDiSp (newPoint, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //---------------------------------------------------------------------------- // Фаза Big Bang - большой взрыв else { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.GaussDistribution (cB [c], rangeMin [c], rangeMax [c], 8); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } } //——————————————————————————————————————————————————————————————————————————————
O método "Revision" executa duas funções principais:
Busca pela melhor solução:- Inicializa o índice da melhor solução (bestInd = -1)
- Percorre todos os pontos da população
- Se encontrar uma solução melhor que a atual:
- Atualiza o valor da melhor função de avaliação (fB)
- Armazena o índice da melhor solução (bestInd)
- Se uma melhor solução for encontrada (bestInd != -1):
- Copia todas as coordenadas da melhor solução do array para o array da solução ótima "cB"
- Copia todas as coordenadas da melhor solução do array para o array da solução ótima "cB"
Esse método garante a atualização das informações sobre a melhor solução global encontrada ao longo de toda a execução do algoritmo.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BBBC::Revision () { int bestInd = -1; // Поиск лучшего решения в текущей популяции for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; bestInd = i; } } // Обновление лучшего известного решения if (bestInd != -1) ArrayCopy (cB, a [bestInd].c, 0, 0, WHOLE_ARRAY); } //——————————————————————————————————————————————————————————————————————————————
Os autores do algoritmo BBBC afirmam que ele é capaz de competir com algoritmos bem estabelecidos, como os algoritmos genéticos (GA), superando seus resultados em um número significativamente menor de épocas.
Como prova, eles apresentam resultados de testes em benchmarks sintéticos padronizados e amplamente utilizados, como a função esfera (também conhecida como parabolóide ou elipsóide), Ackley e Rastrigin. Vamos observar a visualização do desempenho do algoritmo em dois desses benchmarks.
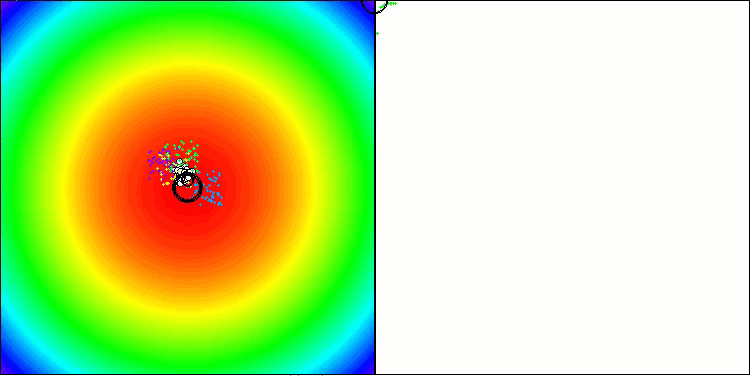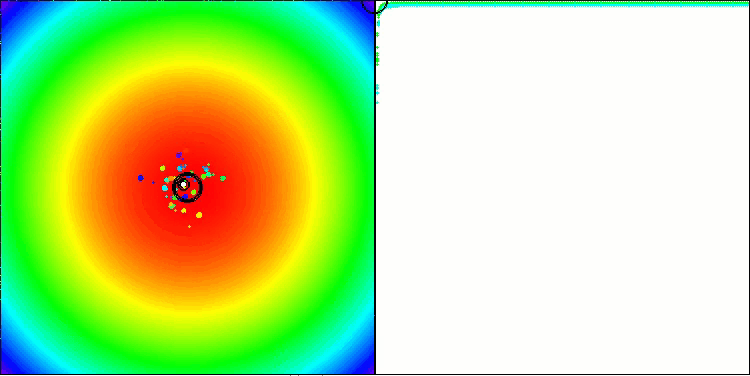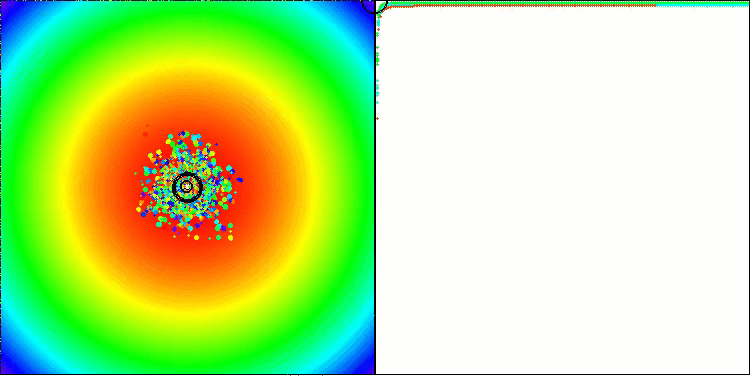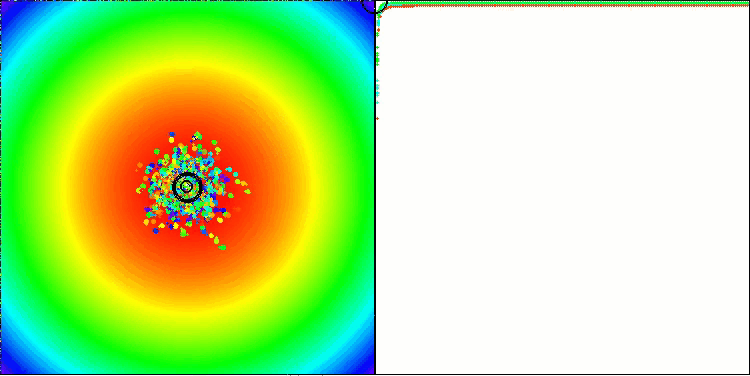
BBBC na função de teste Paraboloide
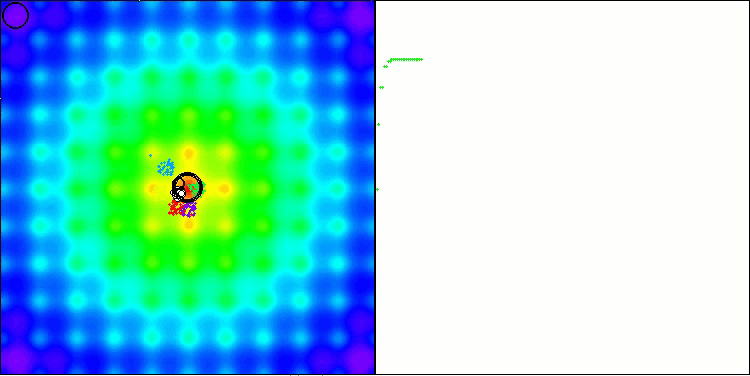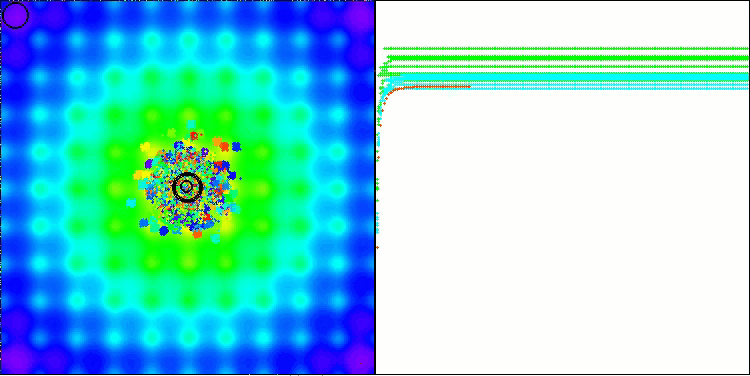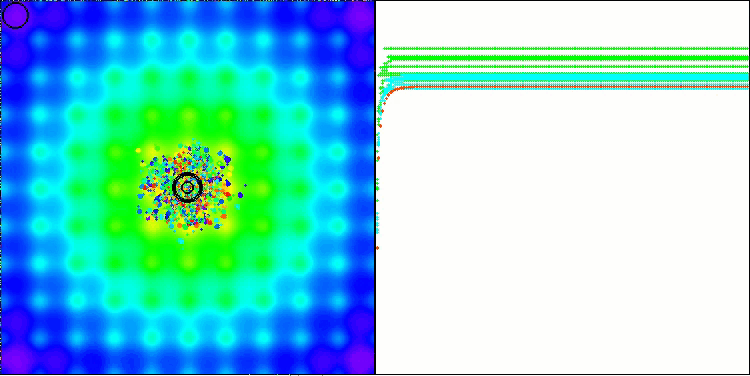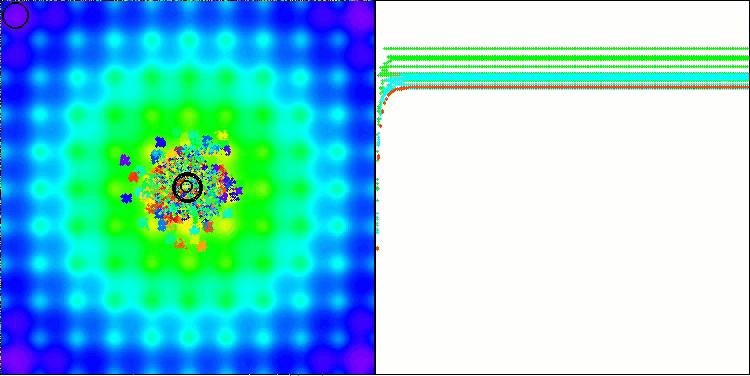
BBBC na função de teste Ackley
De fato, os resultados impressionam. Especialmente notável é o fato de que os resultados em altas dimensionalidades (linha vermelha) diferem pouco dos obtidos para problemas com baixa dimensionalidade (linha verde), o que indica uma alta escalabilidade do algoritmo. Embora na função Ackley a precisão da convergência não seja perfeita, os resultados ainda são dignos de atenção.
Agora vejamos os resultados do BBBC em funções de teste desenvolvidas especificamente para algoritmos de otimização.
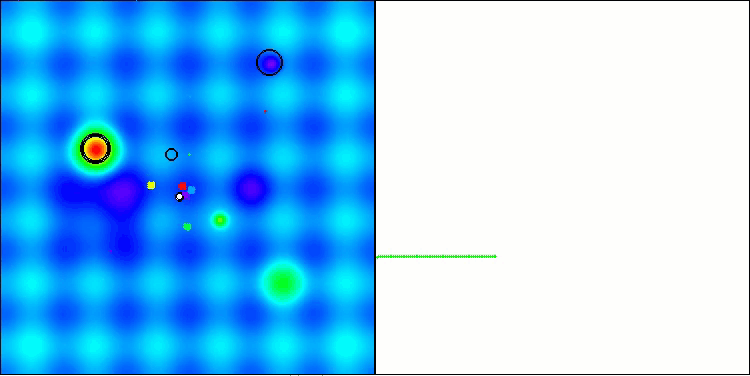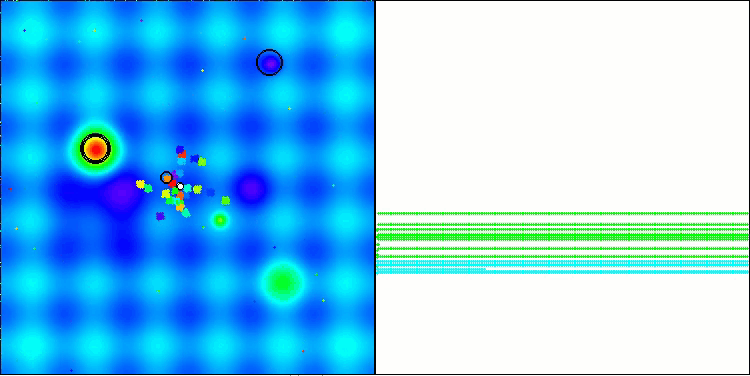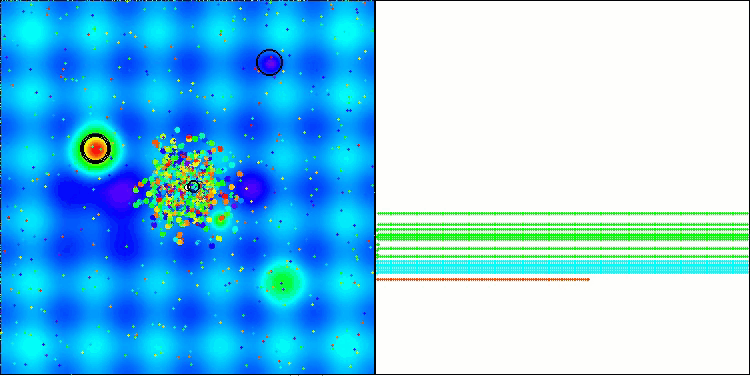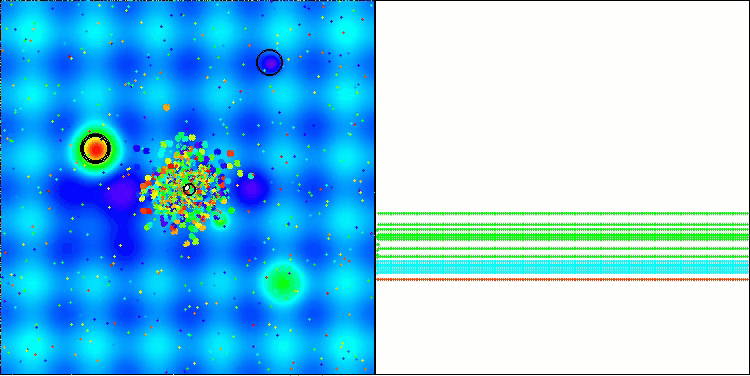
BBBC na função de teste Hilly
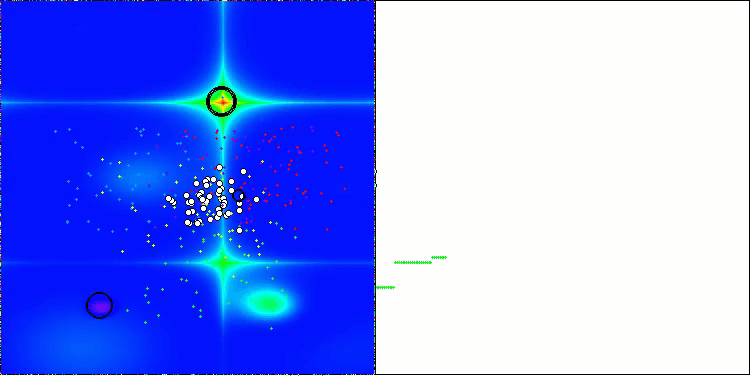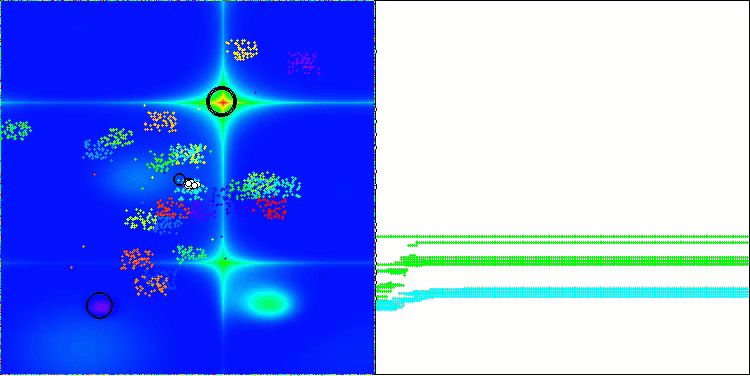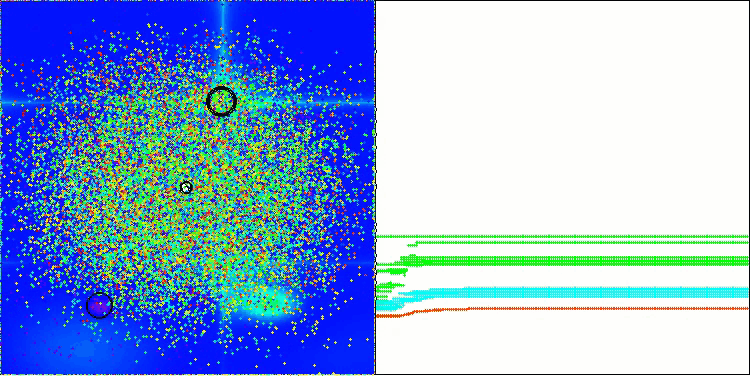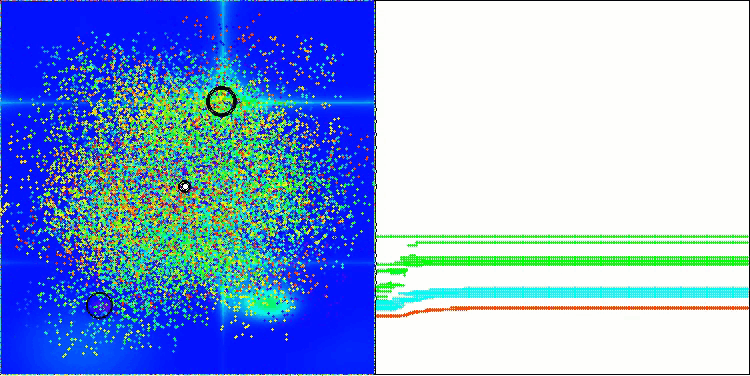
BBBC na função de teste Forest
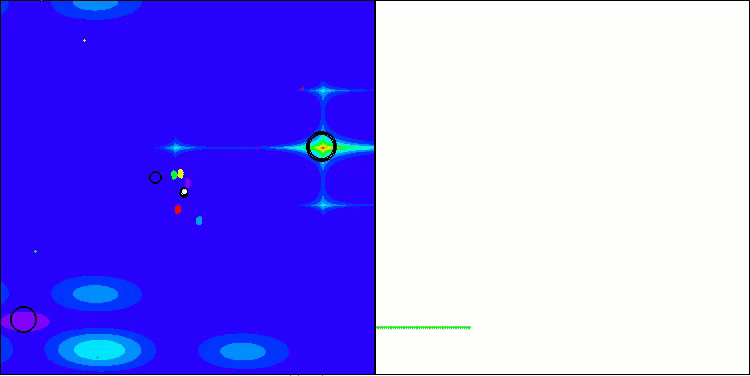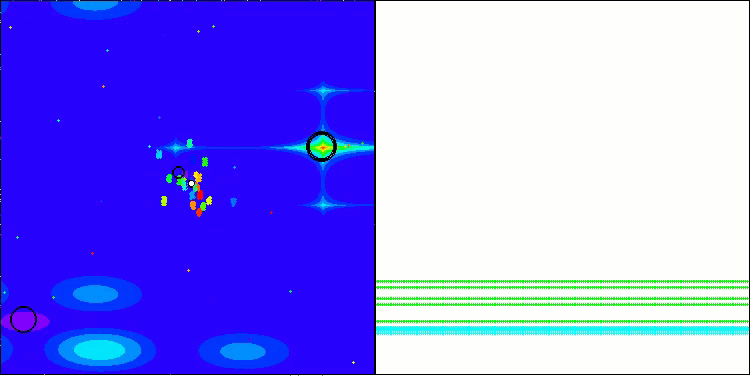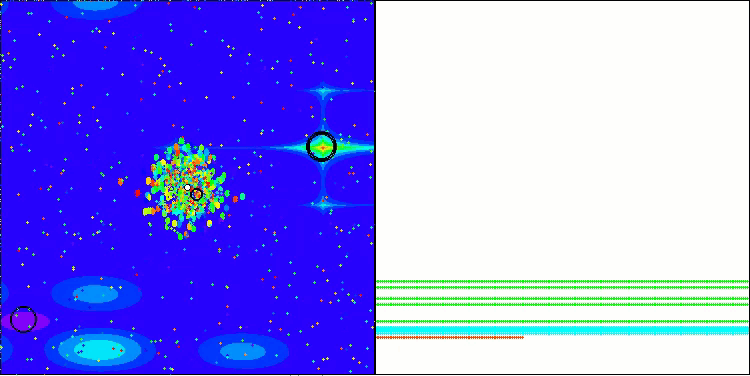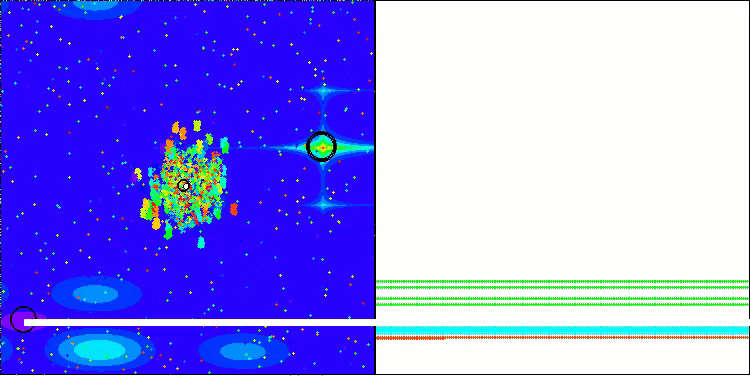
BBBC na função de teste Megacity
Infelizmente, nesses nossos benchmarks, a magia do algoritmo deixou de funcionar. Qual seria a causa disso? Antes de tudo, vale observar que, assim como nas funções anteriores, nos testes Hilly, Forest e Megacity, a população do algoritmo concentra sua “atenção” na região central do espaço de busca. Essa observação levanta certas questões e soa um tanto estranha.
Vamos dar uma olhada por dentro do algoritmo BBBC e examinar seus mecanismos internos. Veremos que, ao utilizar o “centro de massa”, os pontos distribuídos pelo espaço tendem a colapsar para o meio do intervalo da função. Isso acontece porque o centro de massa dos pontos está exatamente no centro, o que cria a ilusão de eficácia do algoritmo. Essa coincidência leva o algoritmo a encontrar com sucesso os ótimos de funções como a esfera (com ótimo global no centro do intervalo). No entanto, isso não resulta de uma capacidade excepcional de busca do algoritmo, mas sim de uma feliz coincidência. Por exemplo, se o algoritmo começasse com um ponto de coordenadas 0.0, ele atingiria perfeitamente o ótimo global já na primeira iteração. Esse é o verdadeiro segredo.
É importante observar que a maioria das funções de teste padrão, amplamente utilizadas para avaliar diferentes algoritmos, possui o ótimo global localizado no centro do espaço de busca. Tais testes nem sempre são confiáveis, e para certos algoritmos, como o BBBC, podem gerar uma impressão equivocada sobre as reais capacidades de busca do método.
Para evitar resultados falsamente positivos durante os testes, desenvolvi funções de teste específicas que:
- não são simétricas
- possuem o ótimo global fora do centro do espaço de busca
- não são periódicas
- apresentam uma pequena proporção da superfície acima da linha média em altura.
Agora vamos observar a saída de resultados do BBBC nas funções de teste, reunida na tabela abaixo. Isso é extremamente relevante.
| Big Bang a cada 2ª época | Big Bang a cada 3ª época | Big Bang a cada 10ª época |
|---|---|---|
| BBBC|Big Bang - Big Crunch Algorithm|50.0|2.0| ============================= 5 Hilly's; Func runs: 10000; result: 0.5789409521562645 25 Hilly's; Func runs: 10000; result: 0.36005433010965165 500 Hilly's; Func runs: 10000; result: 0.25650127842145554 ============================= 5 Forest's; Func runs: 10000; result: 0.5232991213500953 25 Forest's; Func runs: 10000; result: 0.293874681679014 500 Forest's; Func runs: 10000; result: 0.18830469994313143 ============================= 5 Megacity's; Func runs: 10000; result: 0.3269230769230769 25 Megacity's; Func runs: 10000; result: 0.15584615384615388 500 Megacity's; Func runs: 10000; result: 0.09743846153846236 ============================= All score: 2.78118 (30.90%) | BBBC|Big Bang - Big Crunch Algorithm|50.0|3.0| ============================= 5 Hilly's; Func runs: 10000; result: 0.5550785088841808 25 Hilly's; Func runs: 10000; result: 0.3605042956384694 500 Hilly's; Func runs: 10000; result: 0.25635343911025843 ============================= 5 Forest's; Func runs: 10000; result: 0.48703749499939086 25 Forest's; Func runs: 10000; result: 0.2897958021406425 500 Forest's; Func runs: 10000; result: 0.1865439156477803 ============================= 5 Megacity's; Func runs: 10000; result: 0.28307692307692306 25 Megacity's; Func runs: 10000; result: 0.15692307692307694 500 Megacity's; Func runs: 10000; result: 0.09701538461538546 ============================= All score: 2.67233 (29.69%) | BBBC|Big Bang - Big Crunch Algorithm|50.0|10.0| ============================= 5 Hilly's; Func runs: 10000; result: 0.4883607839451155 25 Hilly's; Func runs: 10000; result: 0.3344059754605514 500 Hilly's; Func runs: 10000; result: 0.25564528470980497 ============================= 5 Forest's; Func runs: 10000; result: 0.492293124748422 25 Forest's; Func runs: 10000; result: 0.28653857694657936 500 Forest's; Func runs: 10000; result: 0.1844110334128521 ============================= 5 Megacity's; Func runs: 10000; result: 0.3230769230769231 25 Megacity's; Func runs: 10000; result: 0.15261538461538465 500 Megacity's; Func runs: 10000; result: 0.09653846153846235 ============================= All score: 2.61389 (29.04%) |
Note que os resultados dos testes mostram pequenas diferenças entre si e estão dentro da variação natural dos valores. Isso evidencia a fraca capacidade de busca da estratégia utilizada, que na essência pouco difere de uma busca aleatória. Diante disso, é apropriado apresentar os resultados do algoritmo de caminhada aleatória (RW - random walk). Em artigos anteriores esse algoritmo foi mencionado, mas seus resultados não foram apresentados. Agora chegou o momento de fazê-lo.
Apresentar os resultados do algoritmo RW é fundamental para avaliar o quanto outras estratégias de busca são mais eficazes em comparação com a simples dispersão aleatória de pontos no espaço. Abaixo segue o resultado médio de 100 execuções nas funções de teste (normalmente fazemos 10).
RW|Random Walk|50.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.48753502068617777
25 Hilly's; Func runs: 10000; result: 0.3215913699940513
500 Hilly's; Func runs: 10000; result: 0.2578113480890265
=============================
5 Forest's; Func runs: 10000; result: 0.3755402348403822
25 Forest's; Func runs: 10000; result: 0.21943566240362317
500 Forest's; Func runs: 10000; result: 0.15877419882827945
=============================
5 Megacity's; Func runs: 10000; result: 0.27969230769230796
25 Megacity's; Func runs: 10000; result: 0.14916923076923083
500 Megacity's; Func runs: 10000; result: 0.098473846153847
=============================
All score: 2.34802 (26.09%)
A seguir, mostro o código do algoritmo RW, que é muito simples. A função "Moving" é responsável, como de costume, por atualizar as coordenadas de cada indivíduo da população. Para cada indivíduo, ela gera valores aleatórios dentro do intervalo especificado e depois os ajusta com a função "SeInDiSp" para que respeitem o passo de discretização.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_RW::Moving () { for (int w = 0; w < popSize; w++) { for (int c = 0; c < coords; c++) { a [w].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [w].c [c] = u.SeInDiSp (a [w].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
A função "Revision" realiza a verificação de todos os indivíduos da população para encontrar aquele com a melhor função de avaliação (fB). Se tal indivíduo for encontrado, suas coordenadas são copiadas para o resultado global ótimo (cB).
//—————————————————————————————————————————————————————————————————————————————— void C_AO_RW::Revision () { int ind = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ind = i; } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); } //——————————————————————————————————————————————————————————————————————————————
Agora faremos alterações no algoritmo original BBBC, a fim de neutralizar suas vantagens ilusórias em problemas com o ótimo global localizado no centro do intervalo dos parâmetros otimizáveis e possibilitar testes mais objetivos. Vamos examinar as diferenças no código, com as modificações aplicadas ao método "Moving":
- O cálculo do centro de massa foi removido
- A fase do Big Bang foi modificada:
- Em vez do centro de massa (centerMass), passa-se a utilizar a melhor solução (cB)
- A fórmula utilizada é: xnew = cB + r*range/epochNow (onde "range" é agora a diferença entre "rangeMax" e "rangeMin")
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BBBC::Moving () { epochNow++; // Начальная инициализация (Big Bang) if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { // Генерация случайных начальных позиций a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); // Приведение к дискретной сетке поиска a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //-------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { //Фаза Big Crunch - большой коллапс if (epochNow % bigBangPeriod != 0) { for (int c = 0; c < coords; c++) { // Вычисление размера пространства поиска для текущей координаты double range = rangeMax [c] - rangeMin [c]; // Генерация случайного числа в диапазоне [-1, 1] double r = u.GaussDistribution (0, -1.0, 1.0, 1); // Генерация новой точки по формуле // xnew = xc + r*(xmax - xmin)/(k) double newPoint = cB [c] + r * range / epochNow; // Ограничение в пределах допустимой области и приведение к сетке a [i].c [c] = u.SeInDiSp (newPoint, rangeMin [c], rangeMax [c], rangeStep [c]); } } // Фаза Big Bang - большой взрыв else { for (int c = 0; c < coords; c++) { a [i].c [c] = u.GaussDistribution (cB [c], rangeMin [c], rangeMax [c], 8); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } } //——————————————————————————————————————————————————————————————————————————————
Resultados dos testes
Resultados da versão corrigida do algoritmo BBBC:
BBBC|Big Bang-Big Crunch Algorithm|50.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.6053080737014771
25 Hilly's; Func runs: 10000; result: 0.45249601882946056
500 Hilly's; Func runs: 10000; result: 0.31255376970202864
=============================
5 Forest's; Func runs: 10000; result: 0.5232283922331299
25 Forest's; Func runs: 10000; result: 0.354256711141388
500 Forest's; Func runs: 10000; result: 0.20417356281490023
=============================
5 Megacity's; Func runs: 10000; result: 0.3976923076923077
25 Megacity's; Func runs: 10000; result: 0.19430769230769235
500 Megacity's; Func runs: 10000; result: 0.11286153846153954
=============================
All score: 3.15688 (35.08%)
Agora os resultados dos testes refletem objetivamente as reais capacidades do algoritmo BBBC. Na visualização, nota-se a formação das mesmas “estrelas” que no algoritmo original, mas desta vez a busca ocorre em regiões realmente promissoras, e não apenas predominantemente no centro do espaço de busca.
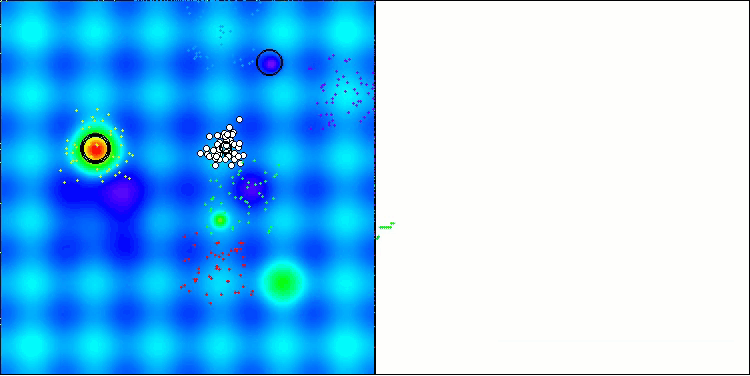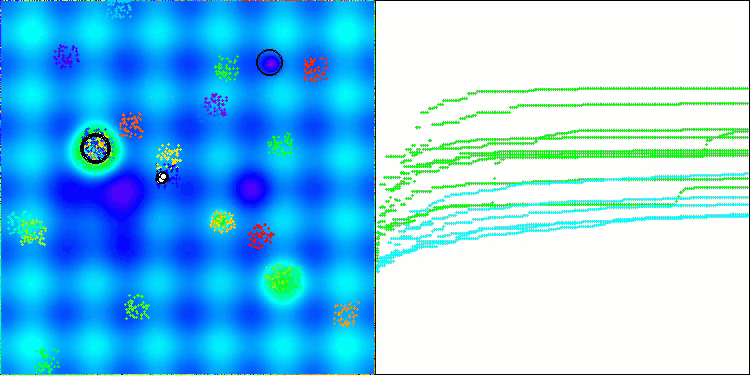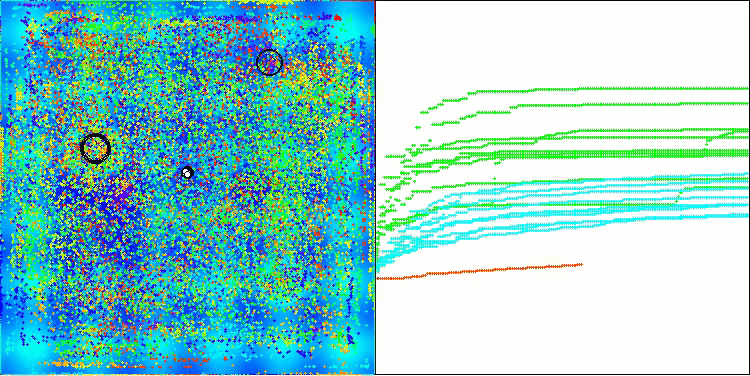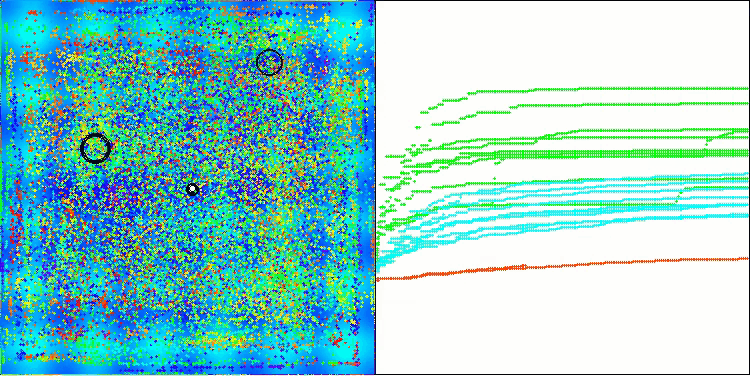
BBBC na função de teste Hilly
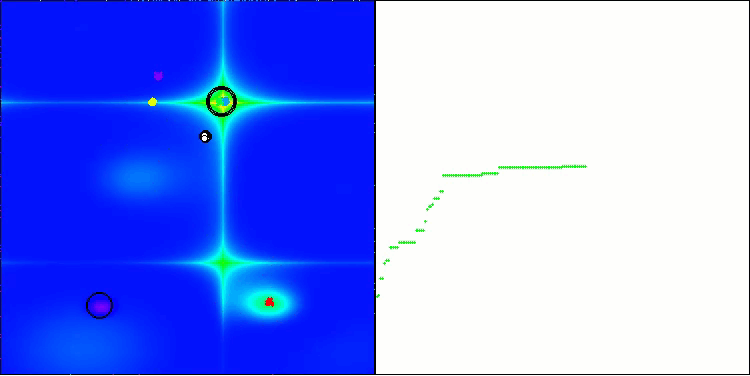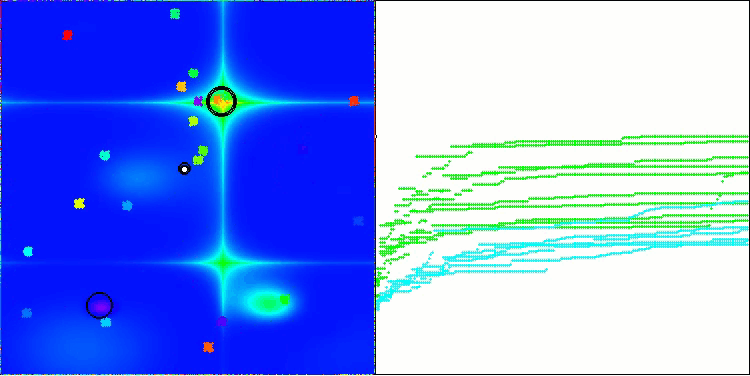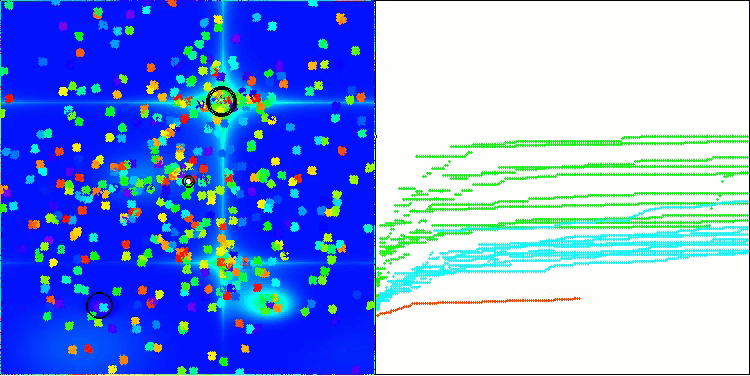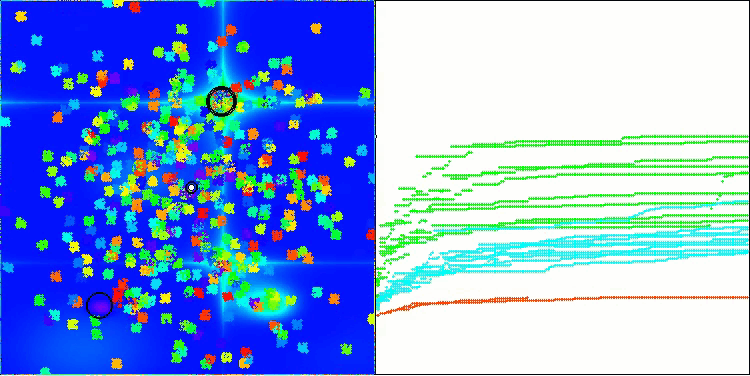
BBBC na função de teste Forest
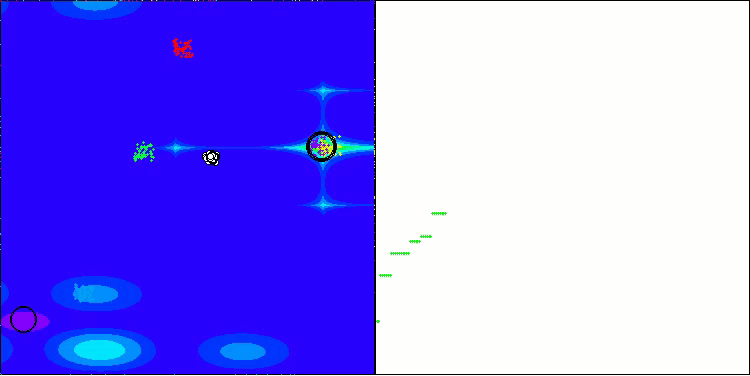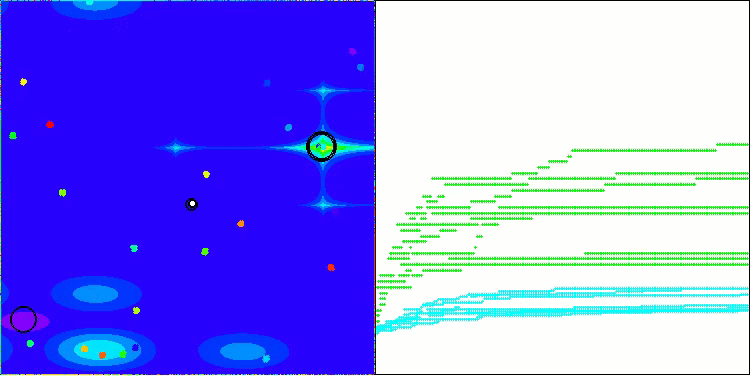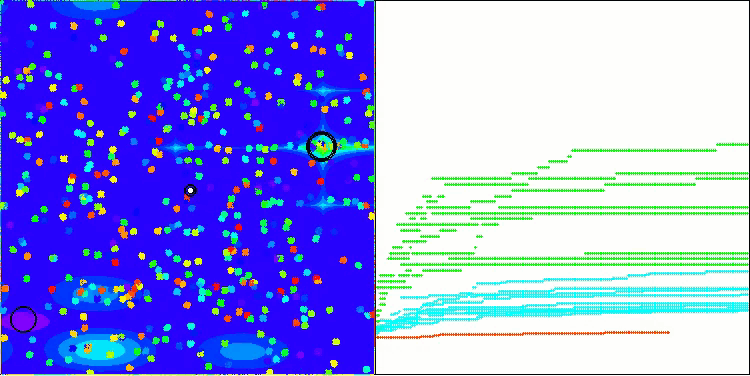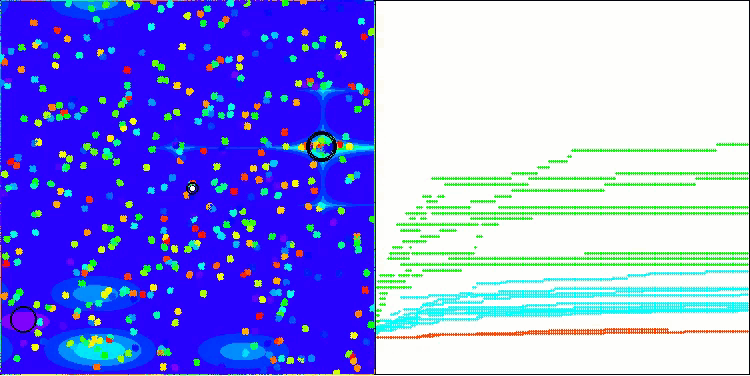
BBBC na função de teste Megacity
A versão corrigida do BBBC ficou na 43ª posição na tabela de classificação. O RW — busca aleatória — não participa do ranking e é apresentado como referência do limite inferior de "sentido" entre as estratégias de busca.
| № | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration ptimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 7 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 8 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 9 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 10 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 11 | BHAm | black hole algorithm M | 0,75236 | 0,76675 | 0,34583 | 1,86493 | 0,93593 | 0,80152 | 0,27177 | 2,00923 | 0,65077 | 0,51646 | 0,15472 | 1,32195 | 5,196 | 57,73 |
| 12 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 13 | AOSm | atomic orbital search M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| 14 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 15 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 16 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 17 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 18 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 19 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 20 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 21 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 22 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 23 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 24 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 25 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 26 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 27 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 28 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 29 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 30 | SOA | simple optimization algorithm | 0,91520 | 0,46976 | 0,27089 | 1,65585 | 0,89675 | 0,37401 | 0,16984 | 1,44060 | 0,69538 | 0,28031 | 0,10852 | 1,08422 | 4,181 | 46,45 |
| 31 | ABHA | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4,127 | 45,85 |
| 32 | ACMO | atmospheric cloud model optimization | 0,90321 | 0,48546 | 0,30403 | 1,69270 | 0,80268 | 0,37857 | 0,19178 | 1,37303 | 0,62308 | 0,24400 | 0,10795 | 0,97503 | 4,041 | 44,90 |
| 33 | ADAMm | adaptive moment estimation M | 0,88635 | 0,44766 | 0,26613 | 1,60014 | 0,84497 | 0,38493 | 0,16889 | 1,39880 | 0,66154 | 0,27046 | 0,10594 | 1,03794 | 4,037 | 44,85 |
| 34 | ATAm | artificial tribe algorithm M | 0,71771 | 0,55304 | 0,25235 | 1,52310 | 0,82491 | 0,55904 | 0,20473 | 1,58867 | 0,44000 | 0,18615 | 0,09411 | 0,72026 | 3,832 | 42,58 |
| 35 | ASHA | artificial showering algorithm | 0,89686 | 0,40433 | 0,25617 | 1,55737 | 0,80360 | 0,35526 | 0,19160 | 1,35046 | 0,47692 | 0,18123 | 0,09774 | 0,75589 | 3,664 | 40,71 |
| 36 | ASBO | adaptive social behavior optimization | 0,76331 | 0,49253 | 0,32619 | 1,58202 | 0,79546 | 0,40035 | 0,26097 | 1,45677 | 0,26462 | 0,17169 | 0,18200 | 0,61831 | 3,657 | 40,63 |
| 37 | MEC | mind evolutionary computation | 0,69533 | 0,53376 | 0,32661 | 1,55569 | 0,72464 | 0,33036 | 0,07198 | 1,12698 | 0,52500 | 0,22000 | 0,04198 | 0,78698 | 3,470 | 38,55 |
| 38 | IWO | invasive weed optimization | 0,72679 | 0,52256 | 0,33123 | 1,58058 | 0,70756 | 0,33955 | 0,07484 | 1,12196 | 0,42333 | 0,23067 | 0,04617 | 0,70017 | 3,403 | 37,81 |
| 39 | Micro-AIS | micro artificial immune system | 0,79547 | 0,51922 | 0,30861 | 1,62330 | 0,72956 | 0,36879 | 0,09398 | 1,19233 | 0,37667 | 0,15867 | 0,02802 | 0,56335 | 3,379 | 37,54 |
| 40 | COAm | cuckoo optimization algorithm M | 0,75820 | 0,48652 | 0,31369 | 1,55841 | 0,74054 | 0,28051 | 0,05599 | 1,07704 | 0,50500 | 0,17467 | 0,03380 | 0,71347 | 3,349 | 37,21 |
| 41 | SDOm | spiral dynamics optimization M | 0,74601 | 0,44623 | 0,29687 | 1,48912 | 0,70204 | 0,34678 | 0,10944 | 1,15826 | 0,42833 | 0,16767 | 0,03663 | 0,63263 | 3,280 | 36,44 |
| 42 | NMm | Nelder-Mead method M | 0,73807 | 0,50598 | 0,31342 | 1,55747 | 0,63674 | 0,28302 | 0,08221 | 1,00197 | 0,44667 | 0,18667 | 0,04028 | 0,67362 | 3,233 | 35,92 |
| 43 | BBBC | big bang-big crunch algorithm | 0,60531 | 0,45250 | 0,31255 | 1,37036 | 0,52323 | 0,35426 | 0,20417 | 1,08166 | 0,39769 | 0,19431 | 0,11286 | 0,70486 | 3,157 | 35,08 |
| 44 | FAm | firefly algorithm M | 0,58634 | 0,47228 | 0,32276 | 1,38138 | 0,68467 | 0,37439 | 0,10908 | 1,16814 | 0,28667 | 0,16467 | 0,04722 | 0,49855 | 3,048 | 33,87 |
| 45 | GSA | gravitational search algorithm | 0,64757 | 0,49197 | 0,30062 | 1,44016 | 0,53962 | 0,36353 | 0,09945 | 1,00260 | 0,32667 | 0,12200 | 0,01917 | 0,46783 | 2,911 | 32,34 |
| RW | random walk | 0,48754 | 0,32159 | 0,25781 | 1,06694 | 0,37554 | 0,21944 | 0,15877 | 0,75375 | 0,27969 | 0,14917 | 0,09847 | 0,52734 | 2,348 | 26,09 | |
Considerações finais
O algoritmo BBBC (Big Bang-Big Crunch) representa uma abordagem interessante para otimização global, inspirada em processos cosmológicos. No entanto, os resultados dos testes demonstram que sua eficácia anunciada é superestimada. É importante destacar que o algoritmo concentra a busca no centro do espaço, o que pode criar a ilusão de grande capacidade de exploração. Isso não é sinal de desempenho excepcional, mas sim uma coincidência entre a estrutura do problema e as particularidades do algoritmo.
Vale também mencionar que muitas funções de teste padrão, usadas na avaliação de algoritmos, possuem o ótimo global no centro do espaço de busca. Esses testes nem sempre são confiáveis e podem levar a conclusões errôneas sobre o verdadeiro potencial de algoritmos como o BBBC, que possuem características "exploratórias forçadas" em sua estratégia. Por isso, é importante encarar certas "verdades conhecidas" com cautela e pensamento crítico.
Mesmo assim, a versão aprimorada do algoritmo BBBC apresenta resultados razoáveis em problemas de alta dimensionalidade, o que destaca seu potencial para desenvolvimento. Isso abre novas possibilidades para futuras pesquisas e aperfeiçoamentos, que podem aumentar sua eficiência em tarefas de otimização mais complexas e variadas, além de enriquecer nosso repertório de técnicas na busca por soluções ótimas.
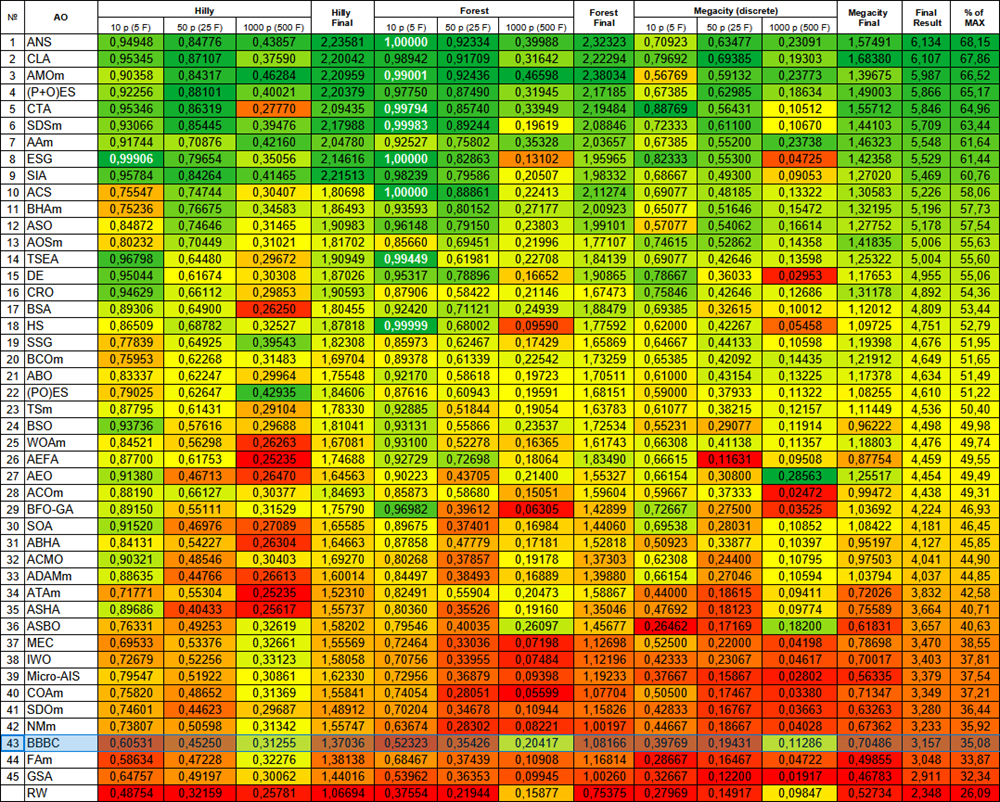
Figura 2. Gradação de cores dos algoritmos nos respectivos testes. A cor branca destaca resultados maiores ou iguais a 0.99
A gradação de cores na tabela ilustra claramente que nem todos os algoritmos de otimização são mais eficazes do que a simples busca aleatória (RW), especialmente em certos tipos de problemas. Isso se manifesta com particular intensidade no contexto de problemas multidimensionais, onde a complexidade do relevo e a dimensionalidade do espaço de busca aumentam consideravelmente. Nessas situações, muitas estratégias tradicionais podem perder sua eficácia ao se depararem com desafios como extremos locais, maldição da dimensionalidade e outros fatores. No entanto, isso não significa que estejamos sugerindo o uso da busca aleatória como método principal, mas sim que é importante utilizá-la como comparação para melhor compreender as limitações e capacidades das diversas estratégias de otimização.
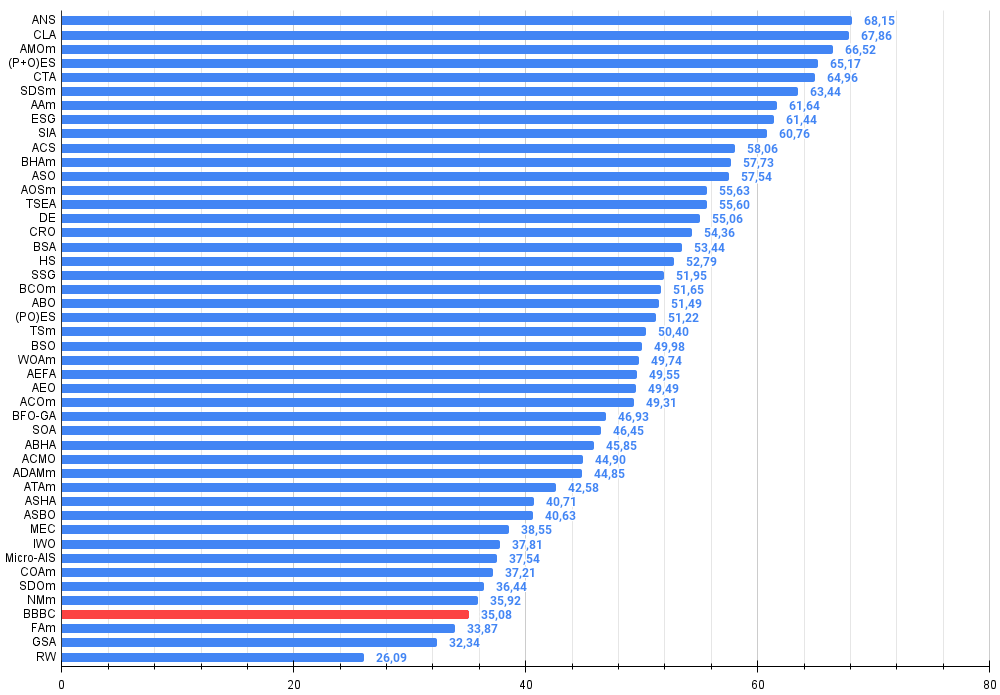
Figura 3. Histograma dos resultados de teste dos algoritmos (em uma escala de 0 a 100, quanto maior, melhor, onde 100 é o resultado teórico máximo possível, no arquivo anexo há um script para cálculo da tabela comparativa)
Pontos positivos e negativos da versão corrigida do algoritmo BBBC:
Pontos positivos:
- O único parâmetro externo é o tamanho da população.
- Implementação simples.
- Muito rápido.
- Apresenta bom desempenho em problemas de alta dimensionalidade.
Pontos negativos:
- Alta variabilidade nos resultados em problemas de baixa dimensionalidade.
- Tendência a ficar preso em problemas de baixa dimensionalidade.
Está anexado ao artigo um arquivo com as versões atualizadas dos códigos dos algoritmos. O autor do artigo não se responsabiliza pela precisão absoluta na descrição dos algoritmos canônicos, pois muitos deles foram modificados para melhorar suas capacidades de busca. As conclusões e interpretações apresentadas nos artigos baseiam-se nos resultados dos experimentos realizados.
Programas utilizados no artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | C_AO.mqh | Arquivo incluído | Classe base dos algoritmos populacionais de otimização |
| 2 | C_AO_enum.mqh | Arquivo incluído | Enumeração dos algoritmos populacionais de otimização |
| 3 | TestFunctions.mqh | Arquivo incluído | Biblioteca de funções de teste |
| 4 | TestStandFunctions.mqh | Arquivo incluído | Biblioteca de funções do ambiente de testes |
| 5 | Utilities.mqh | Arquivo incluído | Biblioteca de funções auxiliares |
| 6 | CalculationTestResults.mqh | Arquivo incluído | Script para calcular os resultados para a tabela comparativa |
| 7 | Testing AOs.mq5 | Script | Ambiente de testes unificado para todos os algoritmos populacionais de otimização |
| 8 | Simple use of population optimization algorithms.mq5 | Script | Exemplo simples de uso dos algoritmos populacionais de otimização sem visualização |
| 9 | Test_AO_BBBC.mq5 | Script | Ambiente de testes para o BBBC |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/16701
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
Técnicas do MQL5 Wizard que você deve conhecer (Parte 38): Bandas de Bollinger
Criando um Expert Advisor Integrado ao Telegram em MQL5 (Parte 6): Adicionando Botões Inline Interativos
Redes neurais em trading: Agente com memória em camadas
Simulação de mercado: Iniciando o SQL no MQL5 (I)
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso