取引におけるニューラルネットワーク：ウェーブレット変換とマルチタスクアテンションを用いたモデル

MetaTrader 5 — トレーディングシステム | YYYY年10月DD日, 09:24

はじめに

資産収益率の予測は、金融分野において広く研究されているテーマです。収益率の予測が困難である理由はいくつかあります。第一に、資産収益率に影響を及ぼす変数が多岐にわたり、さらに大規模でスパースな行列におけるシグナル対雑音比が低いため、従来の計量経済モデルでは有意な情報を抽出することが困難である点が挙げられます。第二に、予測変数と資産収益率との間の機能的関係が明確でなく、それらの間に存在する非線形構造を的確に捉えることが困難であるという課題があります。

近年、ディープラーニング（深層学習）はクオンツ投資の分野で不可欠なツールとなっており、特に金融資産価格の変動を理解する上で基盤となるマルチファクターモデルの高度化に大きく貢献しています。ディープラーニングは、特徴量学習の自動化および金融市場データにおける非線形関係の把握を可能にし、複雑なパターンを効果的に抽出することで、予測精度を向上させます。世界中の研究者が、回帰型ニューラルネットワーク(RNN)や畳み込みニューラルネットワーク(CNN)といったディープニューラルネットワークの株式および先物価格予測への応用可能性を高く評価しています。しかしながら、RNNやCNNが広く活用されている一方で、市場やシグナルの時系列情報をより深く抽出・構築するようなより高度なニューラルアーキテクチャの研究は、まだ十分に進んでいるとは言えません。この点において、ディープラーニングを株式市場分析へさらに発展的に応用するための新たな可能性が開かれています。

本日は、Multitask-Stockformerフレームワーク（論文「Stockformer:A Price-Volume Factor Stock Selection Model Based on Wavelet Transform and Multi-Task Self-Attention Networks」で提案）を紹介します。名称に類似点はありますが、本モデルは先に議論されたStockFormerフレームワークとは無関係であり、共通点は「金融市場で利益を生み出す株式ポートフォリオを構築する」という目的のみです。

Multitask-Stockformerフレームワークは、ウェーブレット変換と自己アテンション(self-attention)機構に基づくマルチタスク型の株式予測モデルを構築するものです。

Multitask-Stockformer アルゴリズム

Multitask-Stockformerフレームワークのアーキテクチャは、フロー分離モジュール、二重周波数時空間エンコーダ、二重周波数デコーダの3つのモジュールに分かれています。まず、履歴資産データ𝒳 ∈ RT1×N×362がフロー分離モジュールに入力されます。この段階では、離散ウェーブレット変換を用いて資産収益テンソルを高周波成分と低周波成分に分解します。一方で、トレンド特徴量や価格出来高比率は変化させずに保持します。これらの成分は、シグナルの最後の次元に沿って連結されます。

低周波成分は長期的なトレンドを表し、高周波成分は短期的な変動や急激なイベントを表現します。これらはそれぞれ𝒳lおよび𝒳h ∈ RT1×N×362と表されます。次に、𝒳hと𝒳lは全結合層を通して線形変換され、RT1×N×Dの次元に写像されます。ここで、T1は分析対象となる履歴データの深さを示します。

続いて、二重周波数時空間エンコーダでは、これら異なる時系列パターンを効果的に表現するための設計がなされています。低周波特徴量は時間的アテンションモジュール（Temporal Attention Module、tatt）に入力され、高周波特徴量は拡張因果畳み込み層（Extended Causal Convolutional Layer、conv）を通じて処理されます。これらの出力は、さらにGraph Attention Network(gat)に入力されます。グラフ構造を利用した相互作用により、本モデルは資産間および時間間の複雑な関係性や依存構造を効果的に捉えることができます。このモジュール内では、空間グラフ(Aspa)および時間グラフ(Atem)が全結合層およびテンソル変換操作を通じて多次元埋め込みρspa, ρtem ∈ RT1×N×Dに変換されます。これらは𝒳l,tattおよび 𝒳h,convと加算やGraph Attention操作を用いて結合され、最終的に𝒳l,gat, 𝒳h,gat ∈ RT1×N×Dが得られます。二重周波数時空間エンコーダはL層で構成され、低周波および高周波の多スケール時空間パターンを効率的に表現することを目的としています。最後に、二重周波数デコーダでは、予測器により𝒴l,f, 𝒴h,f ∈ RT2×N×Dが生成され、これらはフュージョンアテンション(Fusion Attention)による相互作用を通じて統合され、2スケールの時間的パターンを表す潜在表現を得ます。さらに、全結合層（FC1：回帰層、FC2：分類層）を個別に用いることで、マルチタスク出力が生成されます。これには、株式収益率の予測（回帰出力：reg）および株式トレンド予測確率（分類出力：cla）が含まれます。

加えて、低周波成分に対しても回帰値およびトレンド予測確率が導出され、低周波シグナルの学習過程をさらに改善します。

以下に、著者が提供するMultitask-Stockformerフレームワークの可視化図を示します。

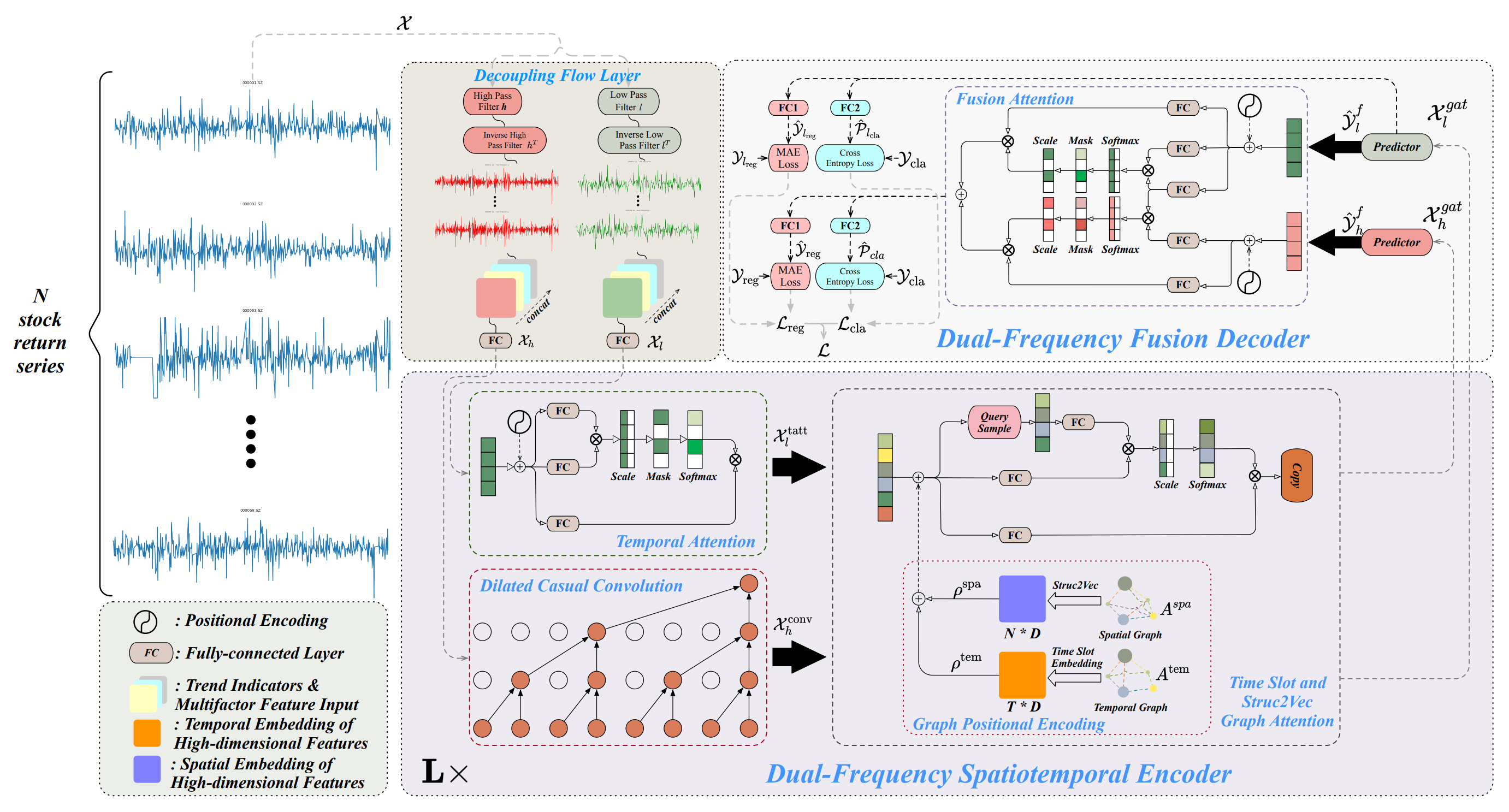
MQL5での実装

上記はMultitask-Stockformerフレームワークの簡潔な説明にすぎません。フレームワークはかなり複雑であるため、個々のアルゴリズムを実装しながら理解を深めるほうが効果的だと考えます。まずは生データのフロー分離モジュールの実装から着手します。

シグナル分解モジュール

解析対象のシグナルを低周波成分と高周波成分に分割するために、本フレームワークの著者は離散ウェーブレット変換(DWT)の利用を提案しています。フーリエ分解と異なり、ウェーブレット変換は周波数成分だけでなくシグナルの局所的な構造も捉えることができるため、シグナルの順序情報が重要となる金融市場の分析には特に有利です。

以前、FEDformerフレームワークを構築した際にも離散ウェーブレット変換を用いましたが、その際は低周波成分のみを抽出していました。今回は高周波成分も必要になりますが、既存の実装を再利用することが可能です。

離散ウェーブレット変換は本質的に、特定のウェーブレットをフィルタとして用いる畳み込み演算に他なりません。したがって、畳み込み層のアルゴリズムを基盤機能として活用できます。ここで重要なのは、本変換においてはパラメータが学習中に変化しない静的（固定）ウェーブレットを使用する点です。したがって、オブジェクトのパラメータに対する最適化（勾配更新等）を無効化する必要があります

以上を踏まえ、離散ウェーブレット変換を用いることで高周波および低周波のシグナル成分を抽出するための新しいオブジェクトCNeuronLegendreWaveletsHLを作成します。

class CNeuronLegendreWaveletsHL :  public CNeuronConvOCL
  {
protected:
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL)   { return true; }

public:
                     CNeuronLegendreWaveletsHL(void) {};
                    ~CNeuronLegendreWaveletsHL(void) {};
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint step, uint units_count, 
                          uint filters, uint variables, 
                          ENUM_OPTIMIZATION optimization_type, uint batch) override;
   //---
   virtual int       Type(void)   const   {  return defNeuronLegendreWaveletsHL;   }
   //---
   virtual uint      GetFilters(void)  const {return (iWindowOut / 2); }
   virtual uint      GetVariables(void)  const {return (iVariables); }
   virtual uint      GetUnits(void)  const {return (Neurons() / (iVariables * iWindowOut)); }
  };

すでに述べたように、離散ウェーブレット変換は、ウェーブレットフィルタを用いた畳み込み演算として定式化できます。この性質により、アルゴリズム構築時には親クラスである畳み込み層クラスの機能をそのまま活用することが可能です。実装上は、初期化メソッドをオーバーライドし、ランダムに生成されるフィルタパラメータをウェーブレットデータに置き換えるだけで十分です。

ただし、使用されるウェーブレットフィルタは静的であり、学習過程において更新されることはありません。そのため、パラメータ最適化メソッドupdateInputWeightsをオーバーライドし、何も処理をおこなわない(no-op)実装に置き換えます。

新しいオブジェクトの初期化はInitメソッドでおこなわれます。通常どおり、このメソッドは外部プログラムから、生成するオブジェクトのアーキテクチャを一意に特定するための定数群を受け取ります。これらには以下のようなパラメータが含まれます。

window：解析ウィンドウのサイズ
step：解析ウィンドウのステップ幅
units_count：1つのシーケンスあたりに実行される畳み込み演算の数
filters：使用するフィルタの数
variables：解析対象となるマルチモーダル時系列内の個々のシーケンス数

bool CNeuronLegendreWaveletsHL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                                     uint window, uint step, uint units_count, 
                                     uint filters, uint variables, 
                                     ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronConvOCL::Init(numOutputs, myIndex, open_cl, window, step, 2 * filters, 
                                  units_count, variables, optimization_type, batch))
      return false;

メソッド本体の内部では、まず受け取ったパラメータを同名の親クラスメソッドへそのまま引き渡します。ただし、このとき注意すべき点として、親メソッドを呼び出す際にフィルタ数を2倍に設定する必要があります。これは、低周波成分および高周波成分の両方を抽出するためのフィルタを生成する必要があるためです。

親メソッドの実行が正常に完了した後、畳み込みパラメータバッファをクリアし、すべての要素をゼロで初期化します。続いて、低周波フィルタと高周波フィルタの間の要素間オフセットを定数として定義します。

   WeightsConv.BufferInit(WeightsConv.Total(), 0);
   const uint shift_hight = (iWindow + 1) * filters;

次に、必要な数のフィルタを生成するための入れ子構造のループシステムを構築します。ここでは、Legendre waveletの再帰的生成を使用し、高次のウェーブレットで順番にフィルタ行列を埋めていきます。

   for(uint i = 0; i < iWindow; i++)
     {
      uint shift = i;
      float k = float(2.0 * i - 1.0) / iWindow;
      for(uint f = 1; f <= filters; f++)
        {
         float value = 0;
         switch(f)
           {
            case 1:
               value = k;
               break;
            case 2:
               value = (3 * k * k - 1) / 2;
               break;
            default:
               value = ((2 * f - 1) * k * WeightsConv.At(shift - (iWindow + 1)) - 
                       (f - 1) * WeightsConv.At(shift - 2 * (iWindow + 1))) / f;
               break;
           }

解析ウィンドウの各要素に対して、フィルタ要素を生成するための内部ループを作成します。そのループ内では、まず対応する低周波フィルタの要素を生成します。

次に、もう一つの入れ子ループを作成し、生成された要素をマルチモーダルシーケンスのすべての独立変数のフィルタに伝搬させます。同時に、対応する低周波フィルタ要素に基づいて形成された高周波フィルタ要素を追加します。

         for(uint v = 0; v < iVariables; v++)
           {
            uint shift_var = 2 * shift_hight * v;
            if(!WeightsConv.Update(shift + shift_var, value))
               return false;
            if(!WeightsConv.Update(shift + shift_var + shift_hight, 
                                    MathPow(-1.0f, float(i))*value))
               return false;
           }

次に、次のフィルタ要素へのオフセットを調整し、ループの次の反復に進みます。

         shift += iWindow + 1;
        }
     }

この初期化メソッドの残りの部分は、これまでに検討したものとは異なります。これまでのところ、オブジェクトの初期化中にOpenCLコードの断片を使用したことはありませんでした。このメソッドはその例外です。ここでは、得られたウェーブレットフィルタを正規化します。

   if(!!OpenCL)
     {
      if(!WeightsConv.BufferWrite())
         return false;
      uint global_work_size[] = {iWindowOut * iVariables};
      uint global_work_offset[] = {0};
      OpenCL.SetArgumentBuffer(def_k_NormilizeWeights, def_k_norm_buffer, WeightsConv.GetIndex());
      OpenCL.SetArgument(def_k_NormilizeWeights, def_k_norm_dimension, (int)iWindow + 1);
      if(!OpenCL.Execute(def_k_NormilizeWeights, 1, global_work_offset, global_work_size))
        {
         string error;
         CLGetInfoString(OpenCL.GetContext(), CL_ERROR_DESCRIPTION, error);
         printf("Error of execution kernel %s Normalize: %s", __FUNCSIG__, error);
         return false;
        }
     }
//---
   return true;
  }

パラメータの正規化が正常に完了した後、メソッドは実行を終了し、呼び出し元のプログラムにBoolean型の結果を返します。

提示したオブジェクトおよびそのすべてのメソッドの完全なコードは、添付資料にて確認可能です。

なお、シグナル分解モジュールの機能は、離散ウェーブレット変換を超えて拡張されていますが、それが核心的な要素であることに変わりはありません。本オブジェクトは、入力が{Bar, Indicator Value}の次元を持つマルチモーダル時系列の二次元テンソルであるモデルで使用する予定です。適切に動作させるためには、離散ウェーブレット変換は入力データの転置を必要とします。これは、オブジェクトにデータを渡す前に外部で行うことが可能です。しかし、私たちの目標は、できるだけ使いやすいオブジェクトを構築することです。したがって、先に作成した離散ウェーブレット変換オブジェクトを親クラスとして使用し、機能を若干拡張したフロー分解モジュールオブジェクト(CNeuronDecouplingFlow)を作成します。

class CNeuronDecouplingFlow   :  public   CNeuronLegendreWaveletsHL
  {
protected:
   CNeuronTransposeOCL  cTranspose;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL);

public:
                     CNeuronDecouplingFlow(void) {};
                    ~CNeuronDecouplingFlow(void) {};
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint step, uint units_count,
                          uint filters, uint variables,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronDecouplingFlow;   }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

新しいオブジェクト内では、データ事前転置層を追加し、Initメソッド内の外部パラメータunits_countを再定義して、よりユーザーフレンドリにします。ここで、units_countは解析対象シーケンスの長さ（バーの数）を表し、variablesは解析対象となるインジケーターの数に対応します。

このアプローチのInitメソッドでの実装を考えてみましょう。メソッド本体では、まず元のシーケンス長、畳み込みウィンドウサイズ、およびステップに基づいて、1つのシーケンスに対する畳み込み演算の回数を再計算します。その後、これらの調整済みパラメータを用いて親クラスのInitメソッドを呼び出します。

bool CNeuronDecouplingFlow::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                 uint window, uint step, uint units_count,
                                 uint filters, uint variables,
                                 ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   uint units_out = (units_count - window + step) / step;
   if(!CNeuronLegendreWaveletsHL::Init(numOutputs, myIndex, open_cl, window, step, units_out, 
                                                filters, variables, optimization_type, batch))
      return false;

親メソッドが正常に実行されたら、データ転置層を初期化します。

   if(!cTranspose.Init(0, 0, OpenCL, units_count, variables, optimization, iBatch))
      return false;
//---
   return true;
  }

メソッドは、呼び出し元のプログラムに論理結果を返すことによって終了します。

フィードフォワードおよびバックプロパゲーションアルゴリズムは簡単です。たとえば、フォワードパスでは、最初に入力データが転置され、結果のテンソルが対応する親クラスメソッドに渡されます。

bool CNeuronDecouplingFlow::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cTranspose.FeedForward(NeuronOCL))
      return false;
   if(!CNeuronLegendreWaveletsHL::feedForward(cTranspose.AsObject()))
      return false;
//---
   return true;
  }

ここでは詳細な検討はおこないません。このオブジェクトとそのすべてのメソッドの完全なコードは添付ファイルに記載されています。

シグナル分解モジュールの出力に関しては、構築された処理フローでは、ニューラル層が2つの別個のテンソルを返すことはできません。そのため、低周波および高周波フィルタの結果は、単一のテンソルとして出力されます。その結果、出力は{Variables, Units, [Low, High], Filtersの四次元テンソルに類似します。異なるデータストリームへの分離は、二重周波数時空間エンコーダでおこなう予定です。

フロー分解モジュールの構築後、次に二重周波数時空間エンコーダの実装に進みます。このエンコーダは、時間的アテンション、拡張因果畳み込み(dilated causal convolution)、Graph Attention Networkを用いた時間スロットの3つの主要コンポーネントで構成されます。

Multitask-Stockformerフレームワークの著者は、低周波成分と高周波成分のために2つの独立したストリームを構築しています。これらのストリームはアーキテクチャ上で異なり、モデルがトレンドと季節性成分を個別に注視できるようにしています。

低周波成分は、長期的かつ低周波のトレンドおよびグローバルなシーケンス関係を捉えるために、時空間アテンションブロックに入力されます。

高周波成分は、ローカルなパターン、高周波の変動、急激なイベントに注目するために、拡張因果畳み込み層で処理されます。

この二重ストリームモデリングアプローチは、複雑な金融シーケンスの予測精度を向上させることが期待されます。

時空間アテンションブロックについては、既存のTransformerベースのエンコーダオブジェクトを活用することが可能です。ただし、拡張因果畳み込みアルゴリズムはカスタム実装が必要です。

拡張因果畳み込み層

フレームワークでは、拡張因果畳み込みを提案しています。これは、定義されたステップで入力値をスキップする1次元畳み込みです。形式的には、シーケンスx ∈ RTとフィルタf ∈ RJに対して、時間ステップtにおける拡張因果畳み込みは次のように定義されます。

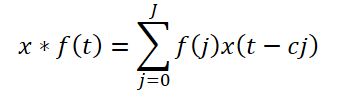
ここでcは膨張係数です。高周波成分の拡張因果畳み込みは次のように表されます。

元の実装では、もう1つのハイパーパラメータとして拡張係数が存在します。この係数は一定であり、依存要素間の距離はシーケンス全体で固定されています。また、元のアルゴリズムでは、この係数は異なるシーケンスに対して一様に適用されます。

本実装では、このアーキテクチャを若干変更します。固定スキップの代わりに、Segment, Shuffle, Stitch (S3)アルゴリズムを導入し、その後に標準の畳み込み層を適用します。

S3により、モデルは入力セグメントの適応的な順列(adaptive permutations)を学習でき、高周波成分内の依存関係をネットワークが発見できるようになります。さらに、複数のS3ブロックを積み重ねることで、複雑な高周波の相互作用を捉える能力が向上します。

このアプローチは、オブジェクトCNeuronDilatedCasualConvに実装します。アルゴリズムは線形であるため、線形アルゴリズム実装の基盤機能およびインターフェースを提供するクラスCNeuronRMATを親オブジェクトとして使用します。新しいオブジェクトの構造を以下に示します。

class CNeuronDilatedCasualConv   :  public CNeuronRMAT
  {
public:
                     CNeuronDilatedCasualConv(void) {};
                    ~CNeuronDilatedCasualConv(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint step, uint dimension,
                          uint units_count, uint variables, uint layers,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronDilatedCasualConv; }
  };

新しいオブジェクトの構造からもわかるように、「正しい」親クラスを選択することで、Initメソッド内でオブジェクトのアーキテクチャを指定するだけで済みます。その他の機能はすべて親クラスのメソッドに実装されており、私たちはそれを継承して利用できます。

Initメソッドでは、外部プログラムから生成するオブジェクトのアーキテクチャを一意に定義する定数群を受け取ります。

window：解析ウィンドウのサイズ
step：解析ウィンドウのステップ幅
dimension：単一シーケンス要素ベクトルの次元
units_count：シーケンス内の要素数
variables：マルチモーダルシーケンスで解析される要素数
layers：畳み込み層の数

これらの変数がどのように使用されるかを理解することが重要です。まず、解析対象の入力データテンソルの次元を思い出してください。前述の通り、シグナル分解モジュールは四次元テンソル{Variables, Units, [Low, High], Filters}を出力します。第三次元に沿って高周波成分と低周波成分を分離すると、単一の値のみが残り、実質的にテンソルは三次元{Variables, Units, Filters}になります。

OpenCLの文脈では、一次元データバッファを扱います。バッファの次元への分解は概念的なものであり、対応する値の順序に従います。

テンソルの次元を理解することで、外部プログラムから受け取ったパラメータと対応させることが可能です。明らかに、variablesは第一次元(Variables)に対応し、units_countは第二次元(Units)に沿ったシーケンス長を指定し、dimensionが最後の次元(Filters)を定義します。これらのパラメータにより、入力データの生テンソル次元が決定されます。

さらに、解析ウィンドウのサイズ(window)およびステップ(step)は、第二次元(Units)の単位で指定されます。たとえば、window = 2 の場合、畳み込みは入力バッファから 2 × dimensionの要素を処理します。

これらを理解した上で、オブジェクトの初期化メソッドのアルゴリズムに戻ることができます。

bool CNeuronDilatedCasualConv::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                    uint window, uint step, uint dimension, uint units_count,
                                    uint variables, uint layers,
                                    ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, 1, optimization_type, batch))
      return false;

通常どおり、メソッド本体内では、まず同名の親クラスメソッドを呼び出します。このメソッド内で、必要なコントロールや継承オブジェクトの初期化がおこなわれます。この時点で、2つの問題に直面します。第一に、親クラスCNeuronRMAT内のオブジェクト構造は、私たちが必要とするものとは大きく異なります。したがって、直接の親クラスからではなく、基底の全結合層からメソッドを呼び出します。ご存じの通り、この全結合層はライブラリ内のすべてのニューラル層を作成する基盤として機能します。

しかし、第二の問題があります。それは、畳み込み中に結果テンソルのサイズが変化することです。現時点では、基底インターフェースのサイズを指定するための最終的な寸法がまだ得られていません。そのため、基底インターフェースは、名目上の単一出力要素で初期化します。

次に、内部オブジェクトへのポインタを格納する動的配列をクリアし、補助変数を準備します。

   cLayers.Clear();
   cLayers.SetOpenCL(OpenCL);
   uint units = units_count;
   CNeuronConvOCL *conv = NULL;
   CNeuronS3 *s3 = NULL;

準備作業が完了した後、次にオブジェクトアーキテクチャの直接的な構築に進みます。そのために、内部層の数と同じ回数の繰り返しを持つループを構築します。

   for(uint i = 0; i < layers; i++)
     {
      s3 = new CNeuronS3();
      if(!s3 ||
         !s3.Init(0, i*2, OpenCL, dimension, dimension*units*variables, optimization, iBatch) ||
         !cLayers.Add(s3))
        {
         if(!!s3)
            delete s3;
         return false;
        }
      s3.SetActivationFunction(None);

ループ内では、まずS3オブジェクトを初期化します。ただし、このオブジェクトは一次元テンソルでのみ動作することに注意が必要です。そのため、シーケンス要素表現ベクトルに「ギャップ」が生じないように、セグメントサイズはこのベクトルの次元の倍数でなければなりません。この場合、両者を等しく設定します。同時に、シーケンス長は、解析対象のすべての変数を考慮したテンソル全体のサイズとして指定します。

オブジェクトの初期化が正常に完了した後、そのポインタを内部オブジェクトへのポインタを格納する動的配列に追加し、活性化関数を無効化します。

次に、畳み込み層の初期化に進みます。新しいオブジェクトの初期化を開始する前に、作成する層に対する畳み込み演算の回数を計算し、この値をローカル変数に保存します。この特定の変数の値は、前のステップで解析対象シーケンスの寸法を指定する際に使用されました。その結果、次のループ反復では、更新されたサイズのS3オブジェクトを作成することになります。

      conv = new CNeuronConvOCL();
      units = MathMax((units - window + step) / step, 1);
      if(!conv ||
         !conv.Init(0, i * 2 + 1, OpenCL, window * dimension, step * dimension, dimension,
                                                   units, variables, optimization, iBatch) ||
         !cLayers.Add(conv))
        {
         if(!!conv)
            delete conv;
         return false;
        }
      conv.SetActivationFunction(GELU);
     }

S3オブジェクトとは異なり、ここで使用する畳み込み層は単変量シーケンス上で動作可能です。これにより、各単位時系列に対して個別に畳み込みをおこなうだけでなく、単変量シーケンスごとに異なるフィルタを適用することができ、その解析を完全に独立させることが可能となります。

畳み込み層の出力では、フレームワークの著者が提案したReLUの代わりに、GELU活性化関数を使用します。

初期化されたオブジェクトのポインタを動的配列に追加し、次のループ反復で続く層を作成します。

オブジェクト内のすべての内部層を正常に初期化した後、再度基底の全結合層の初期化メソッドを呼び出し、ブロック内の最後の内部層のサイズを指定して、正しい外部インターフェースバッファを作成します。

  if(!CNeuronBaseOCL::Init(numOutputs, myIndex, OpenCL, conv.Neurons(), optimization_type, batch))
      return false;

最後に、外部インターフェースバッファへのポインタを、最後の内部層に対応するバッファに置き換えます。

   if(!SetGradient(conv.getGradient(), true) ||
      !SetOutput(conv.getOutput(), true))
      return false;
   SetActivationFunction((ENUM_ACTIVATION)conv.Activation());
//---
   return true;
  }

活性化関数へのポインタをコピーし、操作の論理結果を呼び出し元のプログラムに返して、メソッドの実行を完了します。

ご覧の通り、このブロックアーキテクチャ内では、異なる次元のテンソルで動作する内部オブジェクトを使用しています。最初に、S3層は単変量シーケンスを考慮せず、データバッファ全体の要素を並べ替えます。この場合、単変量シーケンス間での要素の「シャッフル」が完全に可能です。一方で、要素の並べ替えを単変量シーケンスの境界に制限していません。他方で、並べ替えの順序はトレーニングデータセットに基づいて学習されます。モデルが異なる単位シーケンスの要素間の依存関係を特定した場合、これはモデルの性能向上につながる可能性があります。学習結果を観察するのは非常に興味深いでしょう。

記事のボリュームは限界に近づいていますが、作業はここで終わりではありません。次回の記事でこの作業を引き続き展開していきます。

結論

本研究では、Multitask-Stockformerフレームワーク、すなわちウェーブレット変換とマルチタスクSelf-Attentionモジュールを組み合わせた革新的な株式選択モデルを検討しました。ウェーブレット変換の使用により、市場データの時間的および周波数的特徴を特定することが可能となり、Self-Attention機構により解析対象の要因間の複雑な相互作用を正確にモデル化できます。

実践部分では、提案フレームワークの各ブロックをMQL5を用いて独自に実装しました。次回の研究では、今回検討したフレームワークの実装を完成させるとともに、実際の過去データ上で実装手法の有効性を評価する予定です。

参照文献

記事で使用されているプログラム

#	名前	種類	詳細
1	Research.mq5	EA	サンプル収集用EA
2	ResearchRealORL.mq5	EA	Real-ORL法を用いたサンプル収集用EA
3	Study.mq5	EA	モデル訓練EA
4	Test.mq5	EA	モデルテスト用EA
5	Trajectory.mqh	クラスライブラリ	システム状態とモデルアーキテクチャ記述構造
6	NeuroNet.mqh	クラスライブラリ	ニューラルネットワークを作成するためのクラスのライブラリ
7	NeuroNet.cl	コードベース	OpenCLプログラムコードライブラリ

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/16747

添付されたファイル |

ZIPをダウンロード

MQL5.zip (2279.1 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。

この著者による他の記事

最後のコメント | ディスカッションに移動 (1)

Rorschach | 26 12月 2024 において 18:00

グラミアン角差フィールドについて、何か予定されていることはありますか？

3Dバーによるトレンド強度・方向指標

市場マイクロストラクチャの3次元可視化とテンソル分析に基づく、新しい市場トレンド分析のアプローチを検討します。

市場シミュレーション（第2回）：両建て注文(II)

前回の記事とは異なり、今回はエキスパートアドバイザー(EA)を用いて選択オプションをテストしてみます。最終的な解決策ではありませんが、現時点では十分な内容となっています。本記事を通じて、1つの実現可能な解決方法の実装手順を理解できます。

ビッグバンビッグクランチ(BBBC)アルゴリズム

本記事では、ビッグバンビッグクランチ(BBBC)法について紹介します。本手法は2つの主要な段階から構成されます。すなわち、ランダムな点を周期的に生成する段階と、それらを最適解へ圧縮する段階です。本アプローチは探索と精緻化を組み合わせることで、段階的により良好な解を導出し、新たな最適化の可能性を開くことが可能です。

取引におけるニューラルネットワーク：予測符号化を備えたハイブリッド取引フレームワーク（最終回）

予測符号化と強化学習アルゴリズムを組み合わせた金融時系列分析用のハイブリッド取引システム「StockFormer」の検討を引き続きおこないます。本システムは、複雑なパターンや資産間の相互依存関係を捉えることを可能にするDiversified Multi-Head Attention (DMH-Attn)機構を備えた、3つのTransformerブランチに基づいています。前回は、フレームワークの理論的な側面に触れ、DMH-Attn機構を実装しました。今回は、モデルのアーキテクチャと学習について解説します。