取引における多項式モデル

はじめに

取引の効率性は、市場データをどのように分析するかに大きく依存します。その分析手法の一つとして、直交多項式があります。直交多項式は、さまざまな取引関連の課題を解決するために利用できる数学的関数です。

代表的な直交多項式として、ルジャンドル多項式、チェビシェフ多項式、ラゲールの陪多項式、およびエルミート多項式があります。これらの多項式はそれぞれ異なる特性を持ち、目的に応じて多様な問題解決に活用することができます。主な応用例は以下のとおりです。

• 時系列のシミュレーション：直交多項式を用いることで、時系列データをより正確に表現できます。これにより、トレンドやパターンの特定が容易になります。
• 回帰分析：直交多項式を導入することで、モデルの精度を向上させ、解釈性を高めることができます。
• 予測：現在のトレンドが継続した場合の価格変動を予測するために、直交多項式を利用することが可能です。

直交多項式が実際にどのように適用されるかを見てみましょう。

直交多項式とインジケーター

テクニカル分析の本質は、価格変動におけるパターンを特定することにあります。しかし、金融時系列データには通常、これらのパターンを隠してしまうノイズが含まれています。ここでは、直交多項式が市場分析にどのように応用できるかを見ていきます。

基本的な考え方は、直交多項式を用いて複雑なシグナルをより単純なコンポーネントに分解できる、というものです。この分解によって、ノイズを除去し、トレンドを特定しやすくなります。

例として、ルジャンドル多項式を用いて、平滑化インジケーターを作成します。以下に、これらの多項式の一般式および定義域を示します。

ここでは9次までの多項式を使用します。平滑化には十分であり、それ以上の次数を使用すると、ノイズが増加して価格変動の主要なトレンドが見えにくくなる可能性があります。使用する多項式の具体的な式は、以下の表に示しています。

n	ルジャンドル多項式
0	1
1	x
2	(3*x^2-1)/2
3	(5*x^3-3*x)/2
4	(35*x^4-30*x^2+3)/8
5	(63*x^5-70*x^3+15*x)/8
6	(231*x^6-315*x^4+105*x^2-5)/16
7	(429*x^7-693*x^5+315*x^3-35*x)/16
8	(6435*x^8-12012*x^6+6930*x^4-1260*x^2+35)/128
9	(12155*x^9-25740*x^7+18018*x^5-4620*x^3+315*x)/128

まず最初に、価格指数をこれらの多項式の定義域に変換する必要があります。そのために、各インデックスiに対してシフト関数を適用します。

その後、各x[i]の値に対して、関心のあるすべての多項式の値を計算します。たとえば、期間3の2次多項式の値を計算します。

次に、離散性に対する補正を導入する必要があります。1次以上の多項式の値の合計はゼロであるべきです。この条件を満たすために、補正値を計算します。

この補正を用いて、多項式の値を調整します。

ここからが最も興味深い部分です。任意の時系列は、ある重みをもった多項式の和として分解することができます。

重み自体は、次の式で計算できます。

一見すると複雑で少し怖く見えますが、実際には非常にシンプルです。期間Nの0次多項式を考えてみましょう。その値はすべての点で1に等しくなります。そして、その重みは次のようになります。

これは、SMAの式に他なりません。高次多項式の重みは、特別に選ばれた比率を持つ一種のオシレーターに相当します。言い換えれば、直交多項式は、巧妙に計算された追加要素を持つSMAと考えることができます。ルジャンドル多項式はノイズに非常に強く、シグナルの分離や整理の用途で優れた性能を発揮します。たとえば、1次のルジャンドル多項式は次のような形をしています。

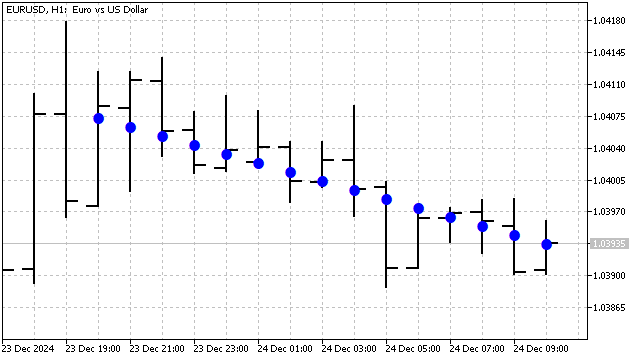
チェビシェフ多項式もルジャンドル多項式と同様に、トレンド検出や平滑化に利用することができます。この多項式には2種類があり、端点での挙動に違いがあります。これらの多項式の主な利点は、価格の急激な変化に対して高い感度を持つ点です。これらの多項式の式は非常にシンプルです。

n	第一種チェビシェフ多項式	第二種チェビシェフ多項式
0	1	1
1	x	2*x
2	2*x^2-1	4*x^2-1
3	4*x^3-3*x	8*x^3-4*x
4	8*x^4-8*x^2+1	16*x^4-12*x^2+1
5	16*x^5-20*x^3+5*x	32*x^5-32*x^3+6*x
6	32*x^6-48*x^4+18*x^2-1	64*x^6-80*x^4+24*x^2-1
7	64*x^7-112*x^5+56*x^3-7*x	128*x^7-192*x^5+80*x^3-8*x
8	128*x^8-256*x^6+160*x^4-32*x^2+1	256*x^8-448*x^6+240*x^4-40*x^2+1
9	256*x^9-576*x^7+432*x^5-120*x^3+9*x	512*x^9-1024*x^7+672*x^5-160*x^3+10*x

以下は、3次チェビシェフ多項式を用いた平滑化の例です。

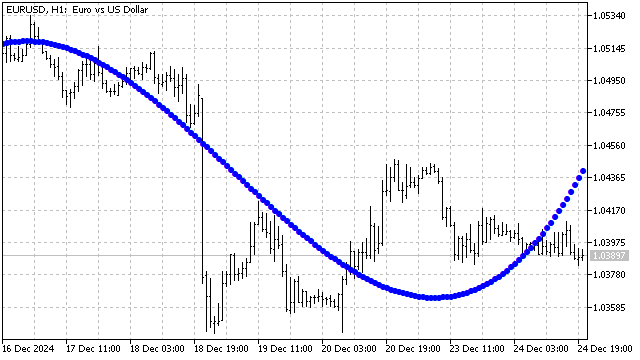
これまで、定義域が±1の多項式を扱ってきましたが、他の定義域を持つ多項式も存在します。 たとえば、ラゲールの陪多項式は、引数がすべて非負の値を取る範囲で定義されています。その方程式は次のようになります。

n	ラゲール多項式
0	1
1	-x+1
2	(x^2-4*x+2)/2
3	(-x^3+9*x^2-18*x+6)/6
4	(x^4-16*x^3+72*x^2-96*x+24)/24
5	(-x^5+25*x^4-200*x^3+600*x^2-600*x+120)/120
6	(x^6-36*x^5+450*x^4-2400*x^3+5400*x^2-4320*x+720)/720
7	(-x^7+49*x^6-882*x^5+7350*x^4-29400*x^3+52920*x^2-35280*x+5040)/5040
8	(x^8-64*x^7+1568*x^6-18816*x^5+117600*x^4-376320*x^3+564480*x^2-322560*x+40320)/40320
9	(-x^9+81*x^8-2592*x^7+42336*x^6-381024*x^5+1905120*x^4-5080320*x^3+6531840*x^2-3265920*x+362880)/362880

そして、その引数に対するシフト関数は次のようになります。

この変換により、ラゲール多項式の挙動は次数だけでなく、期間にも依存するようになります。この多項式は直近の価格変動に対して敏感です。たとえば、5次ラゲール多項式をグラフで表すと、次のような形になります。

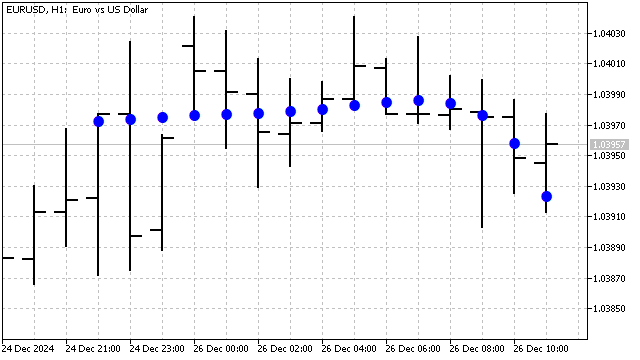
直交性のもう一つの興味深い例が、エルミート多項式です。これらの多項式は、数学や物理学のさまざまな分野で利用されています。エルミート多項式は引数に任意の値を取ることができ、その式は次のようになります。

n	エルミート多項式
0	1
1	x
2	x^2-1
3	x^3-3*x
4	x^4-6*x^2+3
5	x^5-10*x^3+15*x
6	x^6-15*x^4+45*x^2-15
7	x^7-21*x^5+105*x^3-105*x
8	x^8-28*x^6+210*x^4-420*x^2+105
9	x^9-36*x^7+378*x^5-1260*x^3+945*x

シフト関数は、価格の値を中心化します。

その結果、多項式の次数や期間に応じて効率が変わる平滑化フィルタを得ることができました。

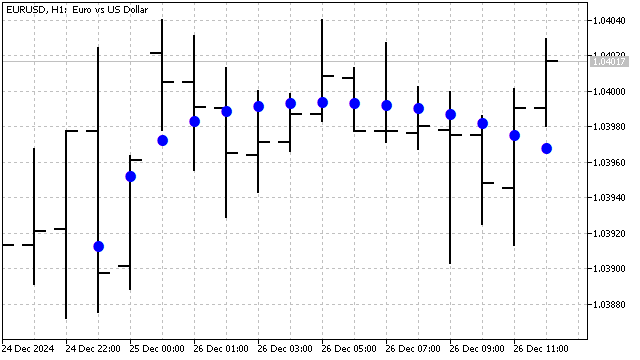
ここまで、基本的な古典的直交多項式を紹介しました。しかし、独自の直交多項式を作成することも十分可能です。たとえば、チェビシェフ多項式とエルミート多項式の利点を組み合わせた多項式は、次の式で表されます。

n	チェビシェフ・エルミート多項式
0	1
1	2*x
2	4*x^2-2
3	8*x^3-12*x
4	16*x^4-48*x^2+12
5	32*x^5-160*x^3+120*x
6	64*x^6-480*x^4+720*x^2-120
7	128*x^7-1344*x^5+3360*x^3-1680*x
8	256*x^8-3584*x^6+13440*x^4-13440*x^2+1680
9	512*x^9-9216*x^7+48384*x^5-80640*x^3+30240*x

この多項式は、2次や3次などの非線形トレンドに敏感です。たとえば、9次チェビシェフ・エルミート多項式をグラフで表すと、次のような形になります。

直交多項式を使用することには、いくつかの利点があります。

• 安定性と無相関性：多項式の直交性により、モデルパラメータの変化に対して安定性が保証されます。各多項式は互いに独立しているため、時系列の各コンポーネントを個別にモデル化し、解析することが可能です。
• 解釈性：各直交多項式は、独自の価格挙動モデルに対応しています。多項式の重み比率により、最も重要なモデルを特定し、それに注目することができます。
• 適応性と効率性：直交多項式は、時系列の特定の値に合わせて調整されます。新しい価格が出現すると重み比率が変化し、これにより多項式モデルは市場の現状に適応します。また、非線形多項式を使用することで、この適応が効率的におこなわれます。

直交多項式の唯一の欠点として、すべての価格を多項式内で処理する点があります。言い換えれば、この多項式を基にしたインジケーターは「描く」ように動きます。しかし、個人的にはこれは欠点ではなく、インジケーターは単に新しいデータが来た際に最適な近似を見つけているだけです。

直交多項式を使用する際にはいくつかの制約もあります。インジケーターの期間は、多項式の次数より大きくする必要があります。実用上、多項式の次数を3次までに制限して問題ありません。このインジケーターは、SMA、線形トレンド、二つの放物線（2次および3次）を組み合わせたもので、かなり複雑な状況でも平滑化が可能です。ただし、インジケーター期間を長くすることで、多項式の次数を増やすこともできます。

それでは、直交多項式を取引に応用した具体例を見ていきましょう。

取引戦略

直交多項式を活用することで、トレーダーはさまざまな取引戦略を作成することができます。たとえば、直交多項式に基づく多項式回帰を用いると、過去の価格変動を分析できるだけでなく、市場の現在の変化に適応できるモデルを作成することも可能です。

例として、平均値からの乖離に基づくいくつかの取引戦略を見てみましょう。

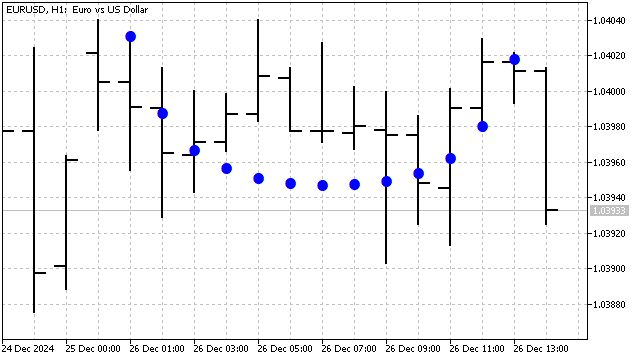
最も単純な戦略を考えます。これは、価格がSMAを横切ったときにポジションを開く戦略です。この移動平均を直交多項式に置き換え、ポジションの開閉ルールは変更しません。

• 価格が多項式を下から上に横切った場合は、買いポジションを開き、売りポジションを閉じる
• 価格が多項式を上から下に横切った場合は、売りポジションを開き、買いポジションを閉じる

シンプルながら、この戦略は十分に効率的です。

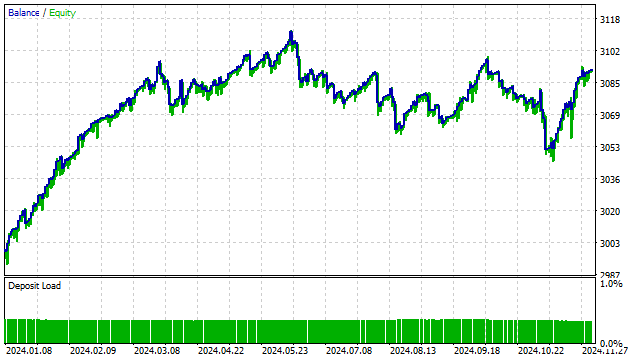
次に、この戦略を少し複雑にして、価格の代わりにある多項式の値を使用してみます。 言い換えれば、2つのSMAの交差戦略のアナログを作成することになります。結果はある程度予想通りで、可能な選択肢の中で、戦略オプティマイザーは直交多項式を選択しました。

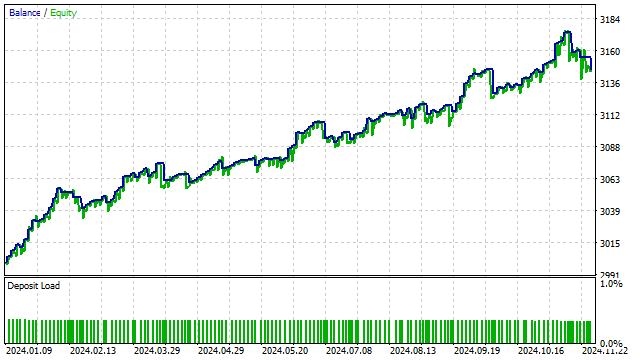
多項式モデルは、より複雑な戦略にも応用できます。戦略が何らかのインジケーターを使用している場合、それを直交多項式に置き換えてみると、戦略の性能を向上させることが可能です。

例として、コモディティチャネルインデックス(CCI)インジケーターを使用します。その典型的な方程式は次のようになります。

このインジケーターに少し変更を加えます。前述の通り、SMAは0次多項式です。SMAの代わりに任意の次数の直交多項式を使用し、この多項式に対する平均絶対偏差を計算します。得られたインジケーターは次の通りです。

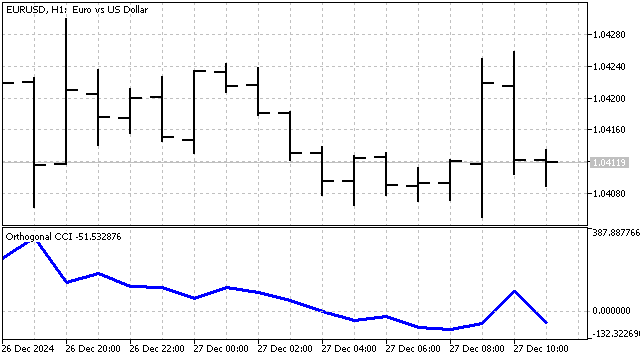
取引戦略は、古典的な戦略に似ています。

• インジケーターが指定レベルを下回り、さらに下降している場合は、買いポジションを開く
• インジケーターが指定レベルを上回り、さらに上昇している場合は、売りポジションを開く
• 逆のシグナルが出たらポジションを閉じる

3次多項式を用いたこの戦略のテスト結果は次の通りです。

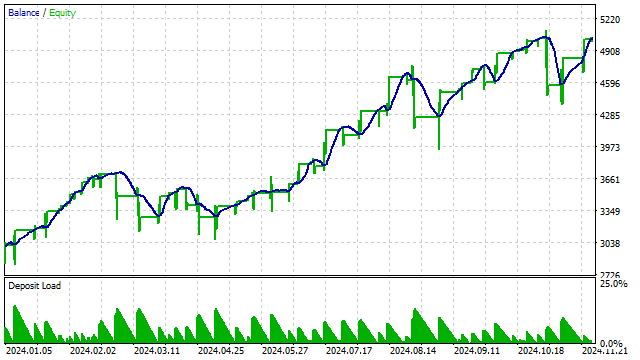
他のインジケーターも直交多項式に基づいて構築可能です。たとえば、RSIの類似インジケーターを作成することができます。その基本的な考え方は簡単で、まず多項式を構築し、その多項式より上にあった価格の数をカウントします。この数に基づき、価格が買われ過ぎか売られ過ぎかを判断します。

このインジケーターを使ってシンプルな戦略を作成します。

• インジケーターが買われ過ぎまたは売られ過ぎのレベルに達したらポジションを開く
• インジケーターが中央にある場合はポジションを閉じる

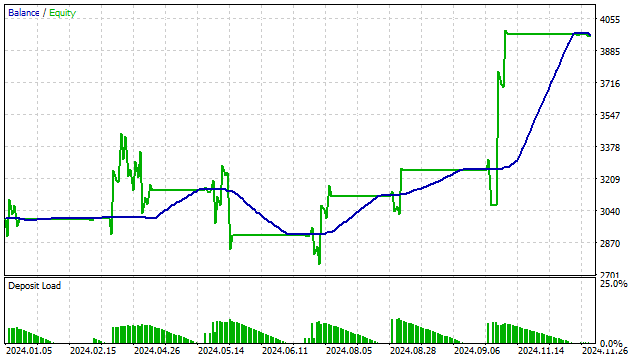
さらに、直交多項式はさまざまな機械学習アルゴリズムに統合することも可能です。多項式関数の柔軟性により、機械学習アルゴリズムはデータ内の複雑な関係を検出できます。 

たとえば、多項式は元データから新しい特徴量を生成するために使用できます。直交多項式は、時系列の異なるコンポーネントを独立して評価することができるため、過学習を減らす効果があります。これにより、学習データの質が向上し、モデルの性能も改善されます。

任意のニューラルネットワークに、多項式の重み比率の値を入力して学習させることができます。この場合、1次の多項式から始め、処理する価格の数をNとした場合はN−1次までの完全な多項式系を構築する必要があります。

結論

直交多項式は、金融時系列を分析するための強力なツールです。これらの多項式を用いることで、多くの利点が得られ、市場の変化を評価することが可能になります。取引戦略に直交多項式を活用することで、戦略の効率を向上させ、取引成果を改善することができます。

この記事を書くにあたり、以下のプログラムを使用しました。

名前	種類	詳細
Orthogonal polynomials	インジケーター	グラフ上で直交多項式をシミュレートする Type：多項式の種類 iPeriod：多項式の期間（2以上） N：多項式の次数（0～9） Shift：インジケーターのシフト
EA Orthogonal polynomials	EA	価格と多項式の交差に基づく取引戦略を実装する
EA Orthogonal polynomials 2	EA	2つの多項式の交差に基づく戦略を実装する
Orthogonal CCI	インジケーター	SMAの代わりに直交多項式を使用可能なCCI
EA Orthogonal CCI	EA	直交多項式版CCIに基づく戦略を実装する
Orthogonal RSI	インジケーター	直交多項式を用いて買われすぎ/売られすぎの状態を判定する
EA Orthogonal RSI	EA	直交多項式版RSIに基づく戦略を実装する