大爆炸-大坍缩（BBBC）算法

MetaTrader 5 — 示例 | 16 九月 2025, 12:40

Andrey Dik

内容

概述

在浩瀚无垠的宇宙中，恒星诞生又消亡，其中隐藏着人类渴望揭示的秘密。大爆炸-大坍缩（BBBC）方法是一种受宇宙空间中发生的过程启发的全局优化算法。让我们一同探索这一引人入胜的概念。

20世纪初，物理学家亚历山大·弗里德曼（Alexander Friedmann）和乔治·勒梅特（Georges Lemaitre）提出了大爆炸-大坍缩理论，作为宇宙终结的另一种可能情景。他们注意到，爱因斯坦的广义相对论方程允许宇宙既膨胀又收缩。弗里德曼通过数学证明，宇宙无法保持静态，必须膨胀或收缩。他确定了宇宙发展的三种可能情景：永恒膨胀、膨胀后收缩以及振荡状态。

20世纪期间，许多科学家提出了将大爆炸和大坍缩结合为一个循环模型的想法。如今，大坍缩理论已不再是主要的宇宙学模型，因为观测表明宇宙正在加速膨胀。然而，这一概念提出了宇宙演化的循环性，是一个有趣的想法。主要阶段：

大爆炸阶段，即初始的高密度高温状态迅速膨胀，能量消散，物质和时空形成，粒子呈混沌分布。
大坍缩阶段，即引力停止膨胀，收缩开始，所有物质被拉回一点，重新回到高密度状态。
循环性体现在大坍缩之后会有新的大爆炸，这一过程可以无限重复，每个周期可能具有不同的物理常数。

大爆炸-大坍缩算法由土耳其伊斯坦布尔技术大学的科学家奥斯曼·K·埃罗尔（Osman K. Erol）和易卜拉欣·埃克辛（Ibrahim Eksin）于2006年提出。

算法实现

正如大爆炸理论中宇宙以强大的能量爆发开始其存在一样，在BBBC方法中，我们观察到一个充满随机性和多样性的初始阶段。在大爆炸阶段，创建了一组随机点。每个点都代表一个候选解。这些点散布在广阔的搜索空间中，等待被探索，但一旦混沌占据主导，大坍缩阶段便开始了。这些点倾向于向“质心”移动，正如星系通过引力相互吸引一样。这一刻是高潮，所有的努力汇聚在一起，寻找最优解。

以下是算法从混沌到有序的各个阶段：

1. 大爆炸阶段。在此第一步中，创建由N个随机点组成的初始种群。每个点在空间中占据自己的位置，在给定边界内均匀分布。

2. 大坍缩阶段。过渡到计算“质心”——所有其他点都努力靠近的点。使用方程（图1）找到质心的坐标，这将成为下一步的新起点。

3. 生成新点。新的点开始在质心周围存在。它们按照正态分布形成，遵循一个赋予它们移动方向和大小的方程。

BBBC方法寻求探索与精炼之间的和谐。随着每一代新点的产生，生成过程中点的分布范围逐渐减小，这使得算法能够优化已找到的最优解。

正如在宇宙空间中，每一次移动都至关重要，在优化世界中，每一次计算都让我们更接近目标。通过深入探索这一方法，我们不仅开辟了新的视野，还成为了寻找更优解这一伟大宇宙过程的一部分。

BBBC

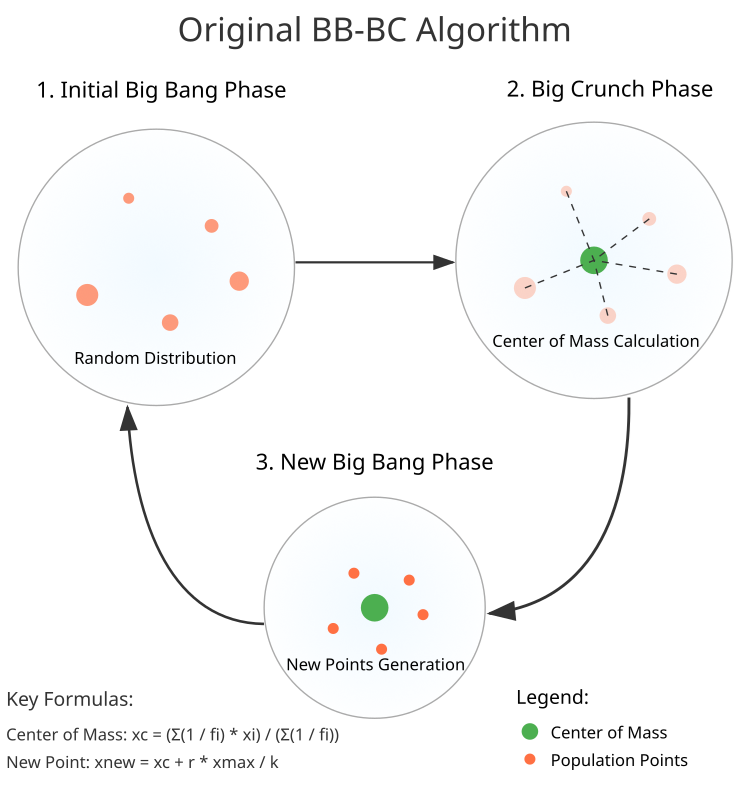
图例1. BBBC算法结构

让我们编写BBBC算法的伪代码：

增加epochNow（当前迭代次数）

// 初始化阶段（大爆炸）
如果revision = false
对于每个个体i（从0到popSize-1）
对于每个坐标c（从0到 coords-1）
新坐标 = 生成随机数（范围：rangeMin[c]到rangeMax[c]）
将 'revision' 设置为 'true' 返回

//大坍缩阶段
如果当前迭代次数epochNow不能被bigBangPeriod整除
对于每个坐标c（从0到coords-1）
分子numerator = 0，分母denominator = 0
对于每个个体i（从0到popSize-1）
适应度fitness取a[i].f绝对值与1e-10二者的最大值
вес = 1.0 / fitness
分子numerator += weight * dot coordinate
分母denominator += weight
如果分母denominator > 1e-10，那么质心centerMass[c] = numerator / denominator；否则直接取当前最优解坐标cB[c]作为质心

对于每个个体i（从0到popSize-1）
对于每个坐标c（从0到 coords-1）
生成一个正态分布随机数r（0, -1.0, 1.0, 1）
新坐标 = centerMass[c] + r * rangeMax[c] / epochNow
//大爆炸阶段
否则
对于每个个体i（从0到popSize-1）
对于每个坐标c（从0到 coords-1）
新坐标 = 生成正态分布随机数（均值为cB[c]，范围在rangeMin[c]到rangeMax[c]之间，标准差为8）

重复上述过程，直到满足大坍缩阶段的停止条件

现在，我们继续编写代码。让我们编写C_AO_BBBC类的定义，它是C_AO的派生类：

公有方法：

构造函数与析构函数
SetParams () — 设置算法参数（种群规模和大爆炸周期）
Init () — 根据给定的搜索边界初始化算法
Moving () — 主方法，实现大爆炸和大坍缩阶段的核心逻辑
Revision () — 更新算法找到的最优解

私有字段：

epochs — 算法运行的总迭代次数
epochNow — 当前迭代次数
centerMass [] — 数组，存储质心的坐标

该类实现了BBBC算法，其核心计算逻辑集中在Moving()和Revision()方法中，种群相关数据存储在基类C_AO中。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_BBBC : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_BBBC () { }
  C_AO_BBBC ()
  {
    ao_name = "BBBC";
    ao_desc = "Big Bang - Big Crunch Algorithm";
    ao_link = "https://www.mql5.com/en/articles/16701";

    popSize       = 50;
    bigBangPeriod = 3;

    ArrayResize (params, 2);
    params [0].name = "popSize";       params [0].val = popSize;
    params [1].name = "bigBangPeriod"; params [1].val = bigBangPeriod;
  }

  void SetParams ()
  {
    popSize       = (int)params [0].val;
    bigBangPeriod = (int)params [1].val;
  }

  bool Init (const double &rangeMinP  [],  // minimum search range
             const double &rangeMaxP  [],  // maximum search range
             const double &rangeStepP [],  // search step
             const int epochsP = 0);       // number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  int bigBangPeriod;       // Big Bang periodicity

  private: //-------------------------------------------------------------------
  int epochs;              // total number of epochs
  int epochNow;            // current epoch
  double centerMass [];    // center of mass
};
//——————————————————————————————————————————————————————————————————————————————

C_AO_BBBC类的Init方法：

该方法用于初始化算法，并接受以下参数：

rangeMinP [] — 每个坐标的最小值数组
rangeMaxP [] — 每个坐标的最大值数组
rangeStepP [] — 每个坐标的离散化步长数组
epochsP — 算法运行的迭代次数（默认值为0）

该方法具体如下：

通过调用基类的StandardInit ()初始化公共参数
设置总迭代次数（epochs）并重置当前迭代计数器（epochNow）
为质心数组（centerMass）分配内存，大小为coords（坐标数量）

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_BBBC::Init (const double &rangeMinP  [],
                      const double &rangeMaxP  [],
                      const double &rangeStepP [],
                      const int epochsP = 0)
{
  // Initialize the base class
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  epochs   = epochsP;
  epochNow = 0;

  // Allocate memory for arrays
  ArrayResize (centerMass, coords);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

BBBC算法中的Moving方法包含以下三个阶段：

1. 开始初始化（当revision = false时执行）：

创建初始随机点种群
将它们映射到离散搜索网格

2. 大坍缩阶段（如果迭代次数不是bigBangPeriod的倍数）：

计算质心：xc = (Σ(1/fi)·xi) / (Σ(1/fi))
围绕质心生成新点：xnew = xc + r · xmax / epoch
随机数采用正态分布

3. 大爆炸阶段（如果迭代次数是bigBangPeriod的倍数）：

以正态分布生成全新点
以当前最优解作为均值
标准差取8，实现大范围搜索

所有新生成的点均受搜索边界限制，并被映射到离散网格。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BBBC::Moving ()
{
  epochNow++;

  // Starting initialization (Big Bang)
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        // Generate random starting dots
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        // Reduction to discrete search grid
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  // Big Crunch phase - big collapse
  if (epochNow % bigBangPeriod != 0)
  {
    for (int c = 0; c < coords; c++)
    {
      double numerator = 0;
      double denominator = 0;

      for (int i = 0; i < popSize; i++)
      {
        // Calculate weight as the inverse of the fitness function value
        double fitness = MathMax (MathAbs (a [i].f), 1e-10);
        double weight = 1.0 / fitness;

        // Summation to calculate the center of mass using the equation
        // xc = (Σ(1/fi)xi) / (Σ(1/fi))
        numerator += weight * a [i].c [c];
        denominator += weight;
      }

      // Determine the coordinates of the center of mass
      centerMass [c] = denominator > 1e-10 ? numerator / denominator : cB [c];
    }

    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        double r = u.GaussDistribution (0, -1.0, 1.0, 1);

        // Generate a new point using the equation
        // xnew = xc + r*xmax/k
        double newPoint = centerMass [c] + r * rangeMax [c] / epochNow;

        // Constrain within the allowed area and convert to grid
        a [i].c [c] = u.SeInDiSp (newPoint, rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
  }
  //----------------------------------------------------------------------------
  // Big Bang phase - big bang
  else
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.GaussDistribution (cB [c], rangeMin [c], rangeMax [c], 8);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Revision方法负责执行以下两大核心功能：

寻找最优解：

初始化最优解索引：bestInd = -1（表示尚未找到有效解）
遍历种群所有个体
如果找到优于当前解的方案：
- 更新最优适应度值（fB）
- 保存最优解的索引（bestInd）

更新最优解：

如果找到更优解（bestInd != -1）：
- 将最优解的所有坐标从种群数组复制到最优解数组cB

该方法在整个算法运行期间持续提供全局最优解的更新信息。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BBBC::Revision ()
{
  int bestInd = -1;

  // Find the best solution in the current population
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      bestInd = i;
    }
  }

  // Update the best known solution
  if (bestInd != -1) ArrayCopy (cB, a [bestInd].c, 0, 0, WHOLE_ARRAY);
}
//——————————————————————————————————————————————————————————————————————————————

BBBC算法的作者声称，该算法能够与著名的强算法（如遗传算法GA）竞争，并且在显著更少的迭代次数内实现更优性能。

作为证据，他们引用了在标准且广泛使用的综合测试函数上的测试结果，例如球面（也称为抛物面或椭球）、Ackley和Rastrigin函数。让我们可视化该算法在两个典型测试函数上的性能表现。

抛物面函数

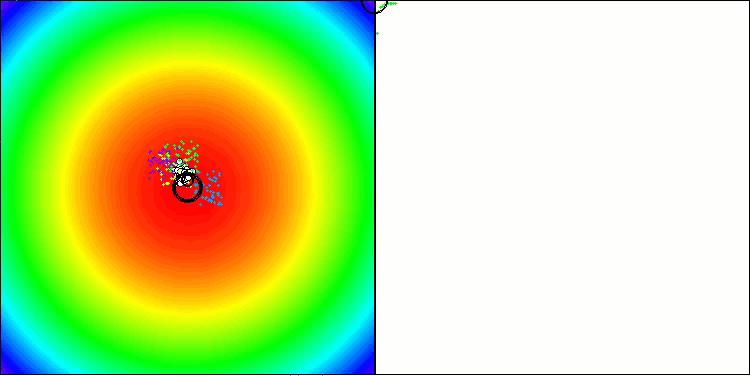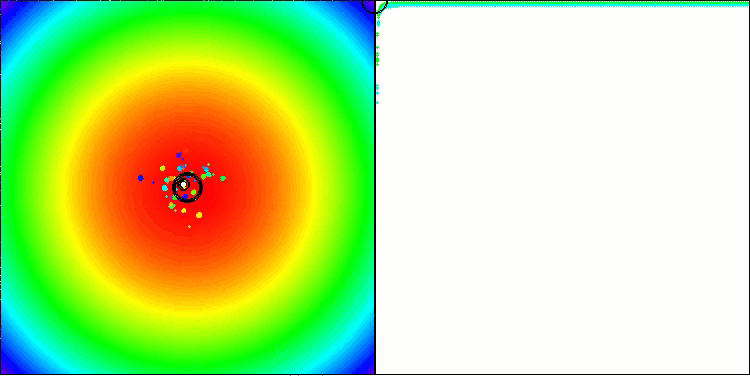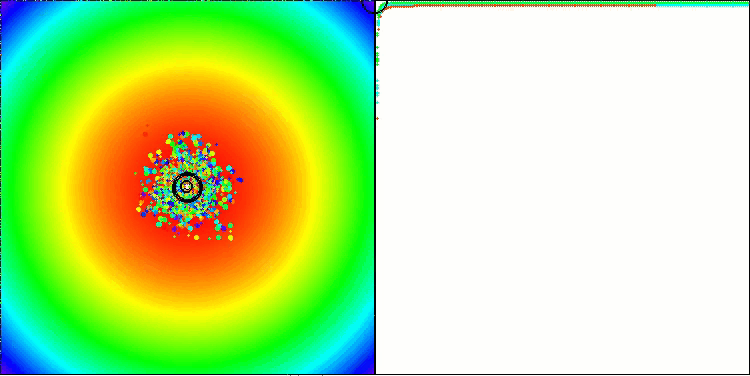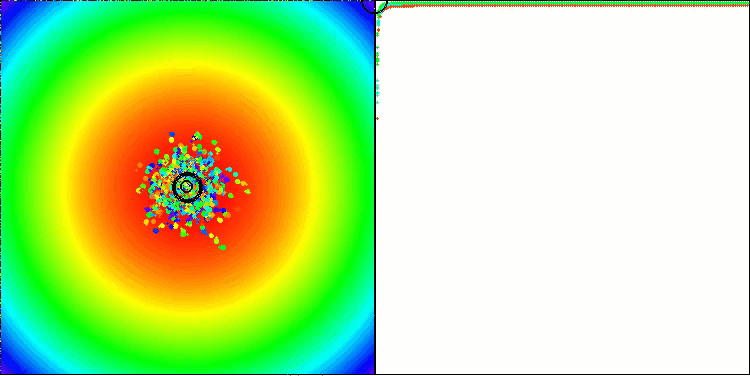
BBBC在抛物面测试函数上

Ackley

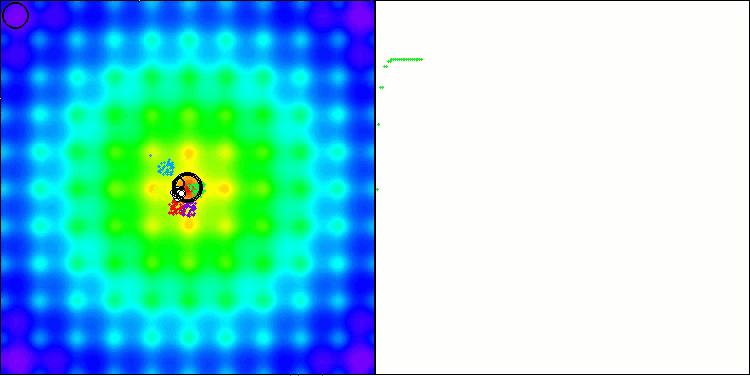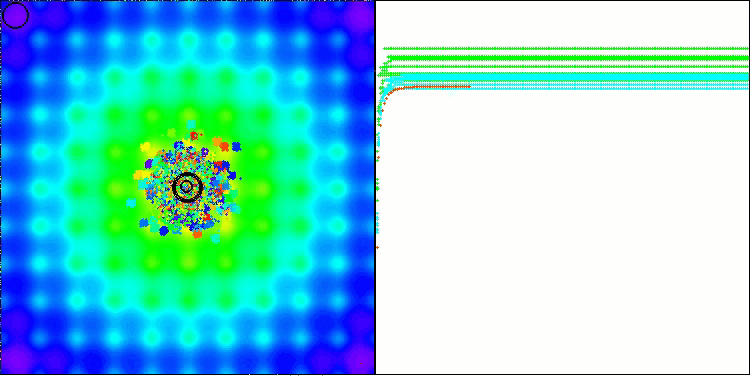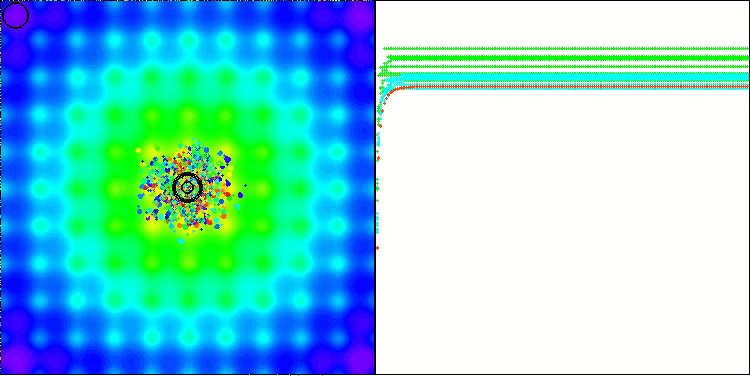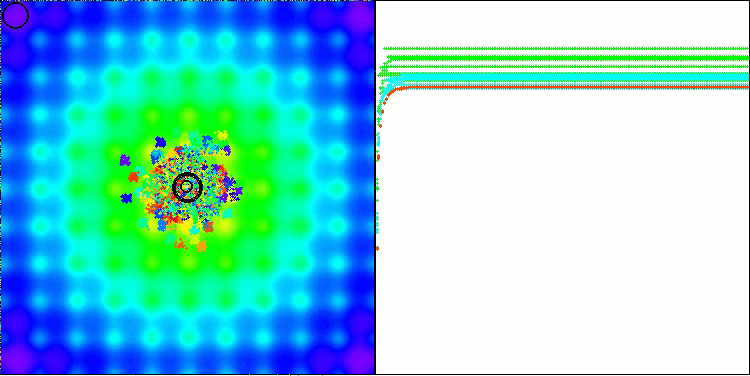
BBBC在Ackley测试函数上

事实上，这些结果令人印象深刻。尤其值得关注的是，高维问题（红线）与低维问题（绿线）的实验结果差异极小，这表明该算法具有极高的可扩展性。尽管算法在Ackley函数上的收敛精度尚未达到理想水平，但其表现仍值得关注。

接下来，让我们看看BBBC算法在专为优化算法设计的测试函数上的实验结果。

Hilly Orig

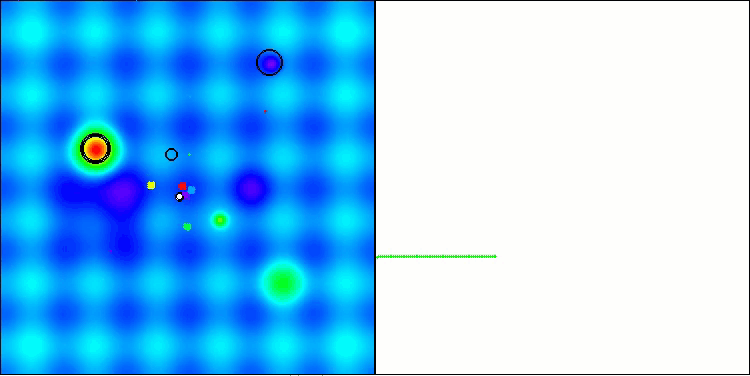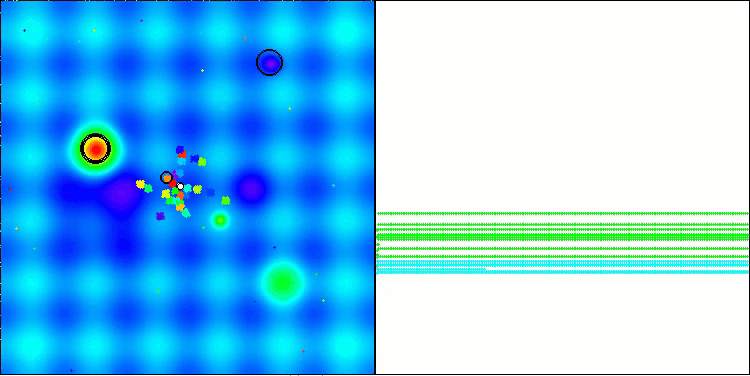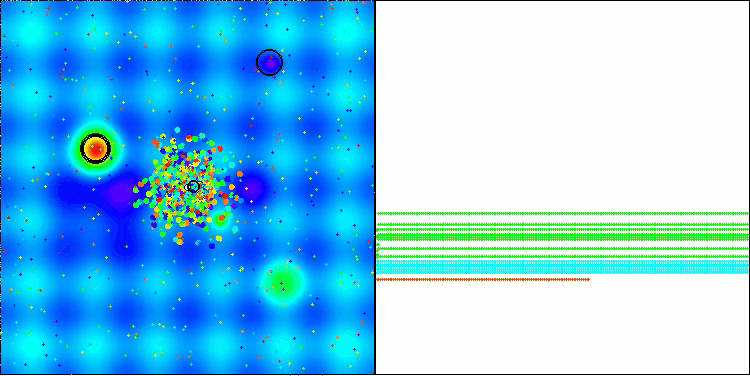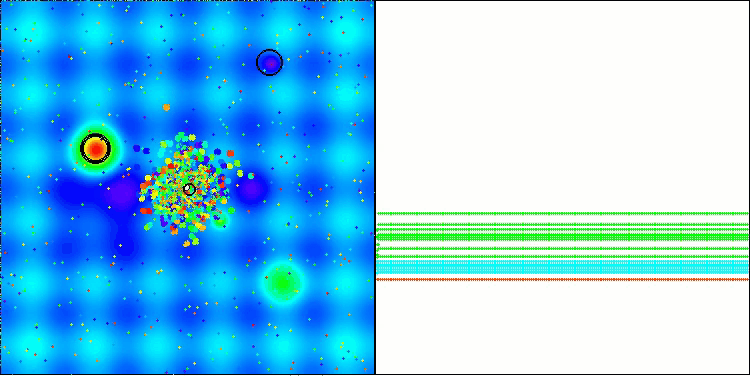
BBBC在Hilly测试函数上

Forest Orig

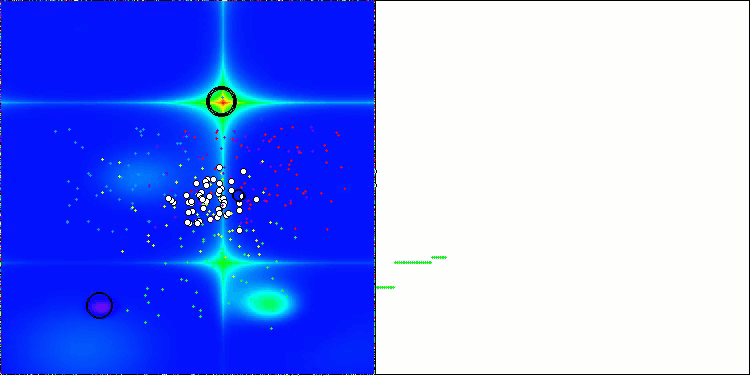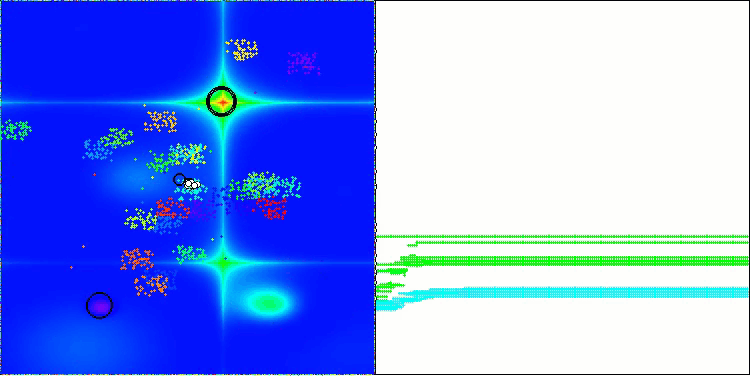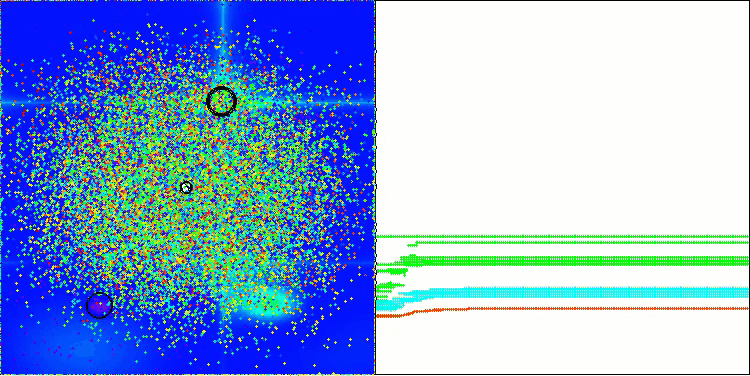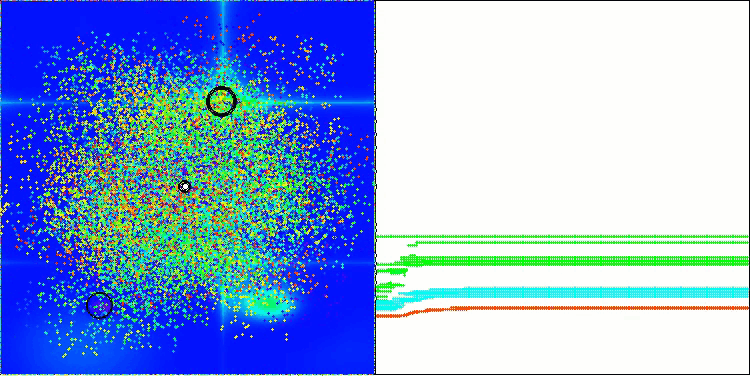
BBBC在Forest测试函数上

Megacity Orig

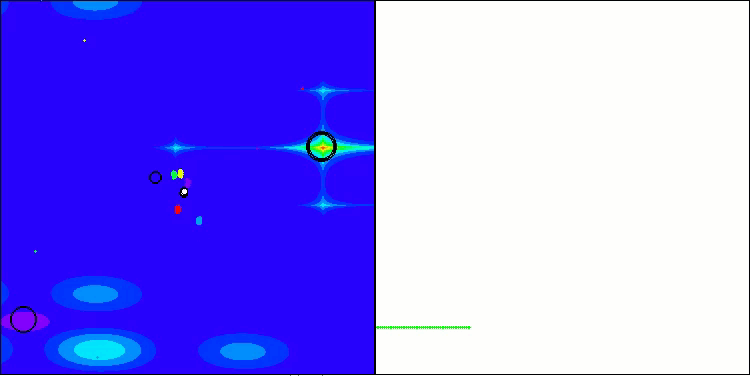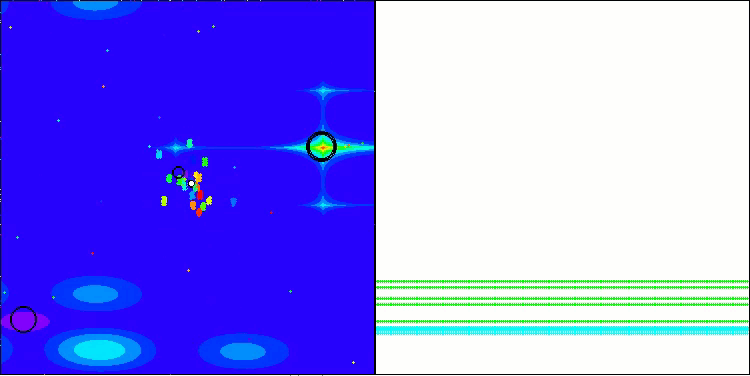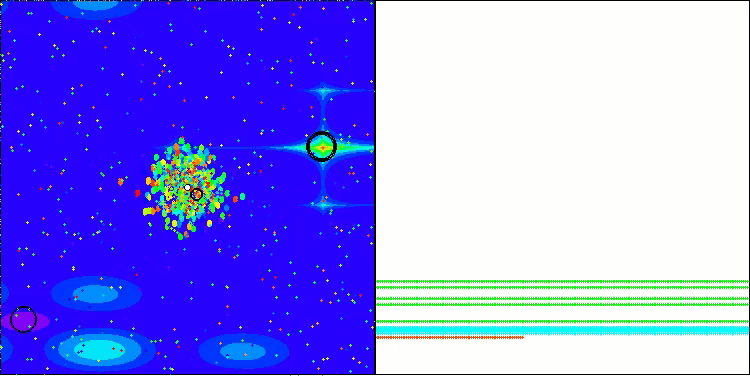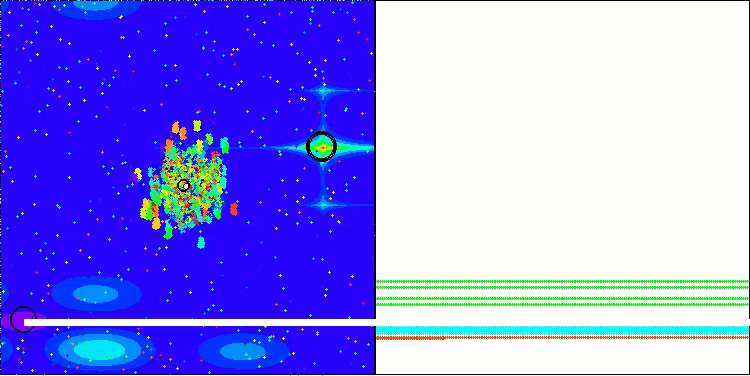
BBBC在Megacity测试函数上

遗憾的是，该算法的“神奇表现”在我们的基准测试中失效了。原因何在？首先，值得注意的是，与之前测试的函数类似，在Hilly、Forest和Megacity测试函数上，算法的种群个体均将“注意力”集中在搜索空间的中心区域。这一现象引发了诸多疑问，且显得颇为反常。

让我们深入剖析BBBC算法的核心机制，探究其运作原理。我们会发现，当采用“质心”策略时，空间中分散的个体点会趋向于聚集到函数定义域的中心位置。这是因为个体点的质心恰好位于中心，从而营造出算法高效的假象。这种巧合使得算法能够成功找到类球面函数（全局最优解位于定义域中心）的最优值。然而，这并非算法搜索能力卓越的体现，而纯属偶然。例如，如果算法初始位置设为坐标0.0，理论上它能在首次迭代时即达到全局最优解。

需要注意的是，大多数用于评估算法性能的标准测试函数，其全局最优解均位于搜索空间的中心。这类测试未必可靠，对于BBBC等算法而言，甚至可能误导对其真实搜索能力的判断。

为避免测试中出现“假阳性”结果，我设计了以下特殊测试函数，其特性包括：

非对称性
全局最优解偏离搜索空间中心
非周期性
函数曲面中位于中线以上的区域占比较小。

这些特性有助于降低偶然触及全局最优解的概率，从而更客观地评估优化算法的效率。

现在，让我们查看BBBC算法在以下表格所列测试函数上的运行结果。这一点至关重要。

每2次迭代触发一次“大爆炸”	每3次迭代触发一次“大爆炸”	每10次迭代触发一次“大爆炸”
BBBC\|Big Bang - Big Crunch Algorithm\|50.0\|2.0\| ============================= 5 Hilly's; Func runs: 10000; result: 0.5789409521562645 25 Hilly's; Func runs: 10000; result: 0.36005433010965165 500 Hilly's; Func runs: 10000; result: 0.25650127842145554 ============================= 5 Forest's; Func runs: 10000; result: 0.5232991213500953 25 Forest's; Func runs: 10000; result: 0.293874681679014 500 Forest's; Func runs: 10000; result: 0.18830469994313143 ============================= 5 Megacity's; Func runs: 10000; result: 0.3269230769230769 25 Megacity's; Func runs: 10000; result: 0.15584615384615388 500 Megacity's; Func runs: 10000; result: 0.09743846153846236 ============================= 总分： 2.78118 (30.90%)	BBBC\|Big Bang - Big Crunch Algorithm\|50.0\|3.0\| ============================= 5 Hilly's; Func runs: 10000; result: 0.5550785088841808 25 Hilly's; Func runs: 10000; result: 0.3605042956384694 500 Hilly's; Func runs: 10000; result: 0.25635343911025843 ============================= 5 Forest's; Func runs: 10000; result: 0.48703749499939086 25 Forest's; Func runs: 10000; result: 0.2897958021406425 500 Forest's; Func runs: 10000; result: 0.1865439156477803 ============================= 5 Megacity's; Func runs: 10000; result: 0.28307692307692306 25 Megacity's; Func runs: 10000; result: 0.15692307692307694 500 Megacity's; Func runs: 10000; result: 0.09701538461538546 ============================= 总分：2.39548 (26.62%)	BBBC\|Big Bang - Big Crunch Algorithm\|50.0\|10.0\| ============================= 5 Hilly's; Func runs: 10000; result: 0.4883607839451155 25 Hilly's; Func runs: 10000; result: 0.3344059754605514 500 Hilly's; Func runs: 10000; result: 0.25564528470980497 ============================= 5 Forest's; Func runs: 10000; result: 0.492293124748422 25 Forest's; Func runs: 10000; result: 0.28653857694657936 500 Forest's; Func runs: 10000; result: 0.1844110334128521 ============================= 5 Megacity's; Func runs: 10000; result: 0.3230769230769231 25 Megacity's; Func runs: 10000; result: 0.15261538461538465 500 Megacity's; Func runs: 10000; result: 0.09653846153846235 ============================= 总分：2.39548 (26.62%)

请注意，测试结果之间差异微小，且均处于正常数值的波动范围内。这表明所采用策略的搜索能力薄弱，本质上与随机搜索无差异。鉴于此，有必要展示随机游走（RW）算法的测试结果。该算法虽在前期文章中提及，但尚未展示过其运行结果。现在正是呈现这一结果的时机。

展示RW算法的结果至关重要，因为这能评估不同搜索策略相较于空间中简单随机散布点的效率提升幅度。以下是在测试函数上运行100次的平均结果（通常我仅运行10次）。

RW|Random Walk|50.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.48753502068617777
25 Hilly's; Func runs: 10000; result: 0.3215913699940513
500 Hilly's; Func runs: 10000; result: 0.2578113480890265
=============================
5 Forest's; Func runs: 10000; result: 0.3755402348403822
25 Forest's; Func runs: 10000; result: 0.21943566240362317
500 Forest's; Func runs: 10000; result: 0.15877419882827945
=============================
5 Megacity's; Func runs: 10000; result: 0.27969230769230796
25 Megacity's; Func runs: 10000; result: 0.14916923076923083
500 Megacity's; Func runs: 10000; result: 0.098473846153847
=============================
总分：2.34802 (26.09%)

我将提供 RW算法的代码。该算法非常简洁。与常规实现类似，Moving函数负责更新种群中每个个体的坐标。针对每个个体，该函数会在给定的范围内生成随机值，随后通过SeInDiSp函数对这些值进行调整，以匹配步长变化。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_RW::Moving ()
{
  for (int w = 0; w < popSize; w++)
  {
    for (int c = 0; c < coords; c++)
    {
      a [w].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
      a [w].c [c] = u.SeInDiSp  (a [w].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Revision函数会遍历种群中的所有个体，寻找适应度函数值最优（fB）的个体。若找到该个体，则将其坐标复制至全局最优解（cB）。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_RW::Revision ()
{
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);
}
//——————————————————————————————————————————————————————————————————————————————

现对原始BBBC算法进行修改，以消除其在参数优化范围中心存在全局最优解的问题上产生的虚假优势，并确保测试的客观性。让我们观察代码差异。对Moving方法进行以下修改：

移除质心计算
修改大爆炸阶段的逻辑：

将参考点从质心（centerMass）替换为全局最优解（cB）
采用新公式生成新解：xnew = cB + r * (rangeMax - rangeMin) / epochNow（其中 "range" 定义为参数范围的上界与下界之差）

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BBBC::Moving ()
{
  epochNow++;

  // Starting initialization (Big Bang)
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        // Generate random starting dots
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        // Reduction to discrete search grid
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
    revision = true;
    return;
  }

  //--------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    //Big Crunch phase - big collapse
    if (epochNow % bigBangPeriod != 0)
    {
      for (int c = 0; c < coords; c++)
      {
        // Calculate the size of the search space for the current coordinate
        double range = rangeMax [c] - rangeMin [c];

        // Generate a random number in the range [-1, 1]
        double r = u.GaussDistribution (0, -1.0, 1.0, 1);

        // Generate a new point using the equation
        // xnew = xc + r*(xmax - xmin)/(k)
        double newPoint = cB [c] + r * range / epochNow;

        // Constrain within the allowed area and convert to grid
        a [i].c [c] = u.SeInDiSp (newPoint, rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
    // Big Bang phase - big bang
    else
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.GaussDistribution (cB [c], rangeMin [c], rangeMax [c], 8);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

测试结果

调整后的BBBC算法的结果：

BBBC|Big Bang-Big Crunch Algorithm|50.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.6053080737014771
25 Hilly's; Func runs: 10000; result: 0.45249601882946056
500 Hilly's; Func runs: 10000; result: 0.31255376970202864
=============================
5 Forest's; Func runs: 10000; result: 0.5232283922331299
25 Forest's; Func runs: 10000; result: 0.354256711141388
500 Forest's; Func runs: 10000; result: 0.20417356281490023
=============================
5 Megacity's; Func runs: 10000; result: 0.3976923076923077
25 Megacity's; Func runs: 10000; result: 0.19430769230769235
500 Megacity's; Func runs: 10000; result: 0.11286153846153954
=============================
总分：3.15688 (35.08%)

如今，测试结果能够客观地反映 BBBC算法的真实性能。可视化结果显示，算法仍会形成与原始版本类似的“星状”解分布模式，但现在的搜索过程聚焦于真正有潜力的区域，而非仅过度集中于搜索空间的中心地带。

Hilly值

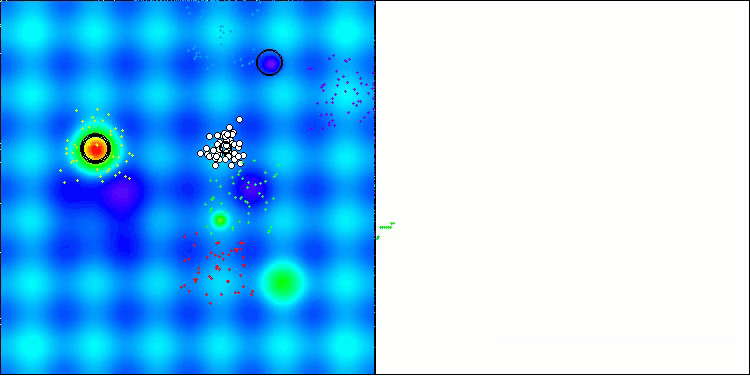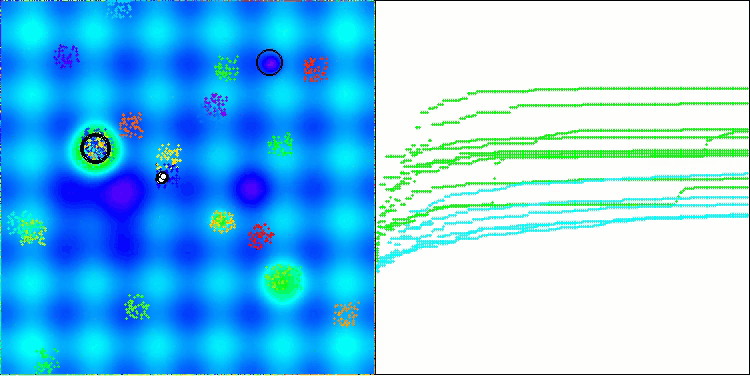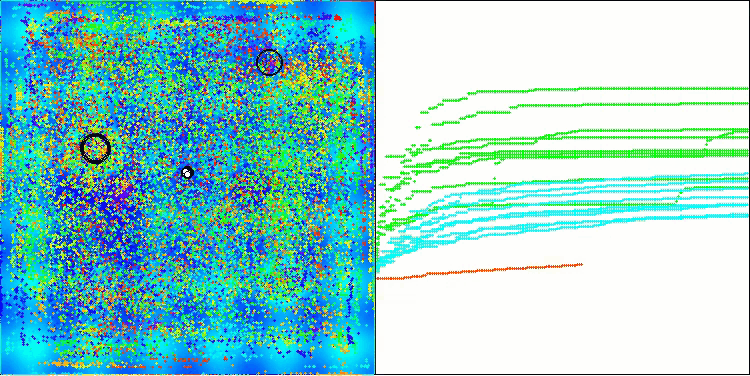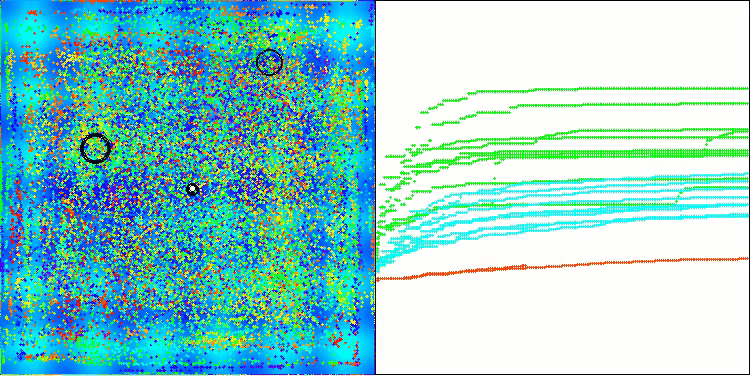
BHAm在Hilly测试函数上

Forest值

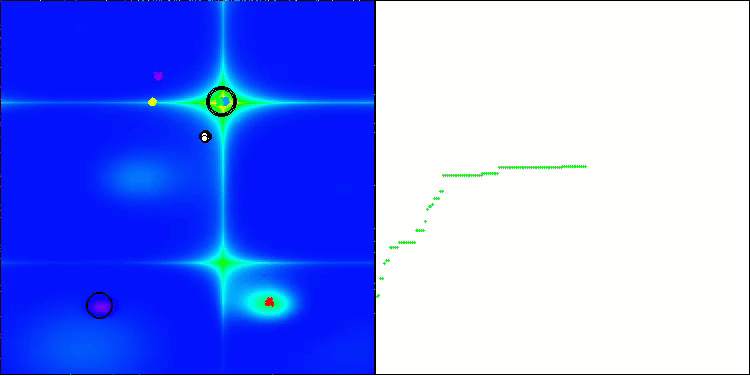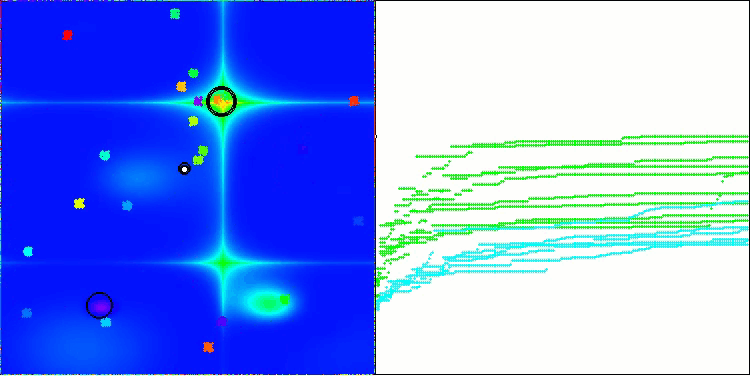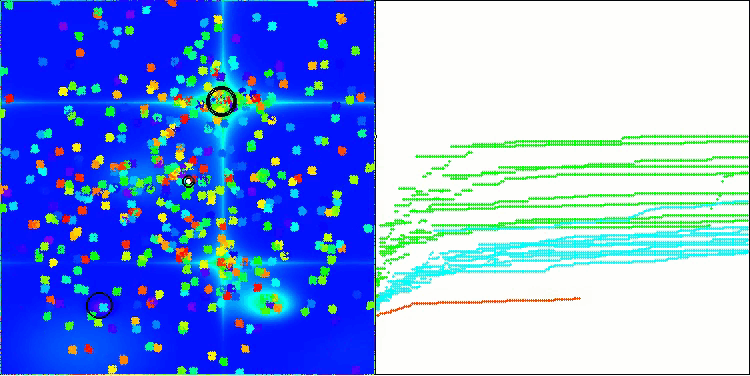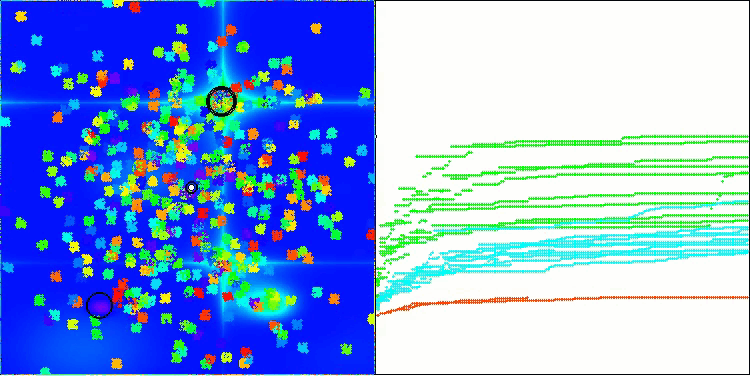
BHAm在Forest测试函数上

Megacity值

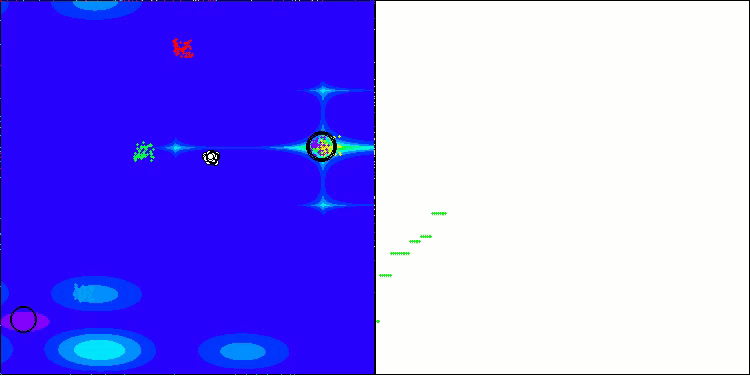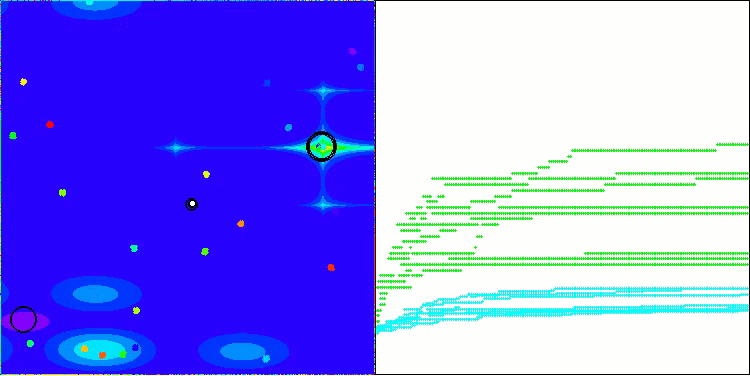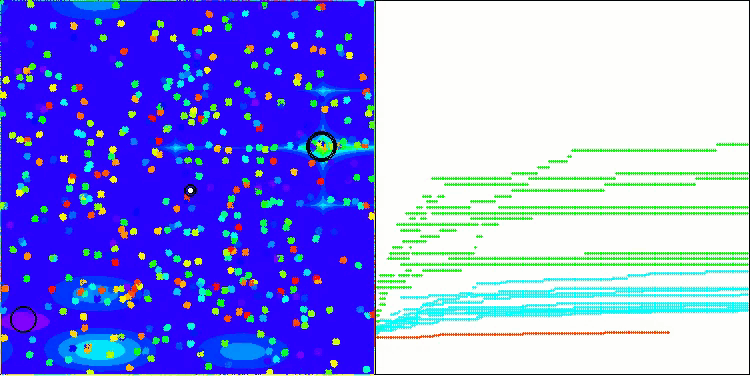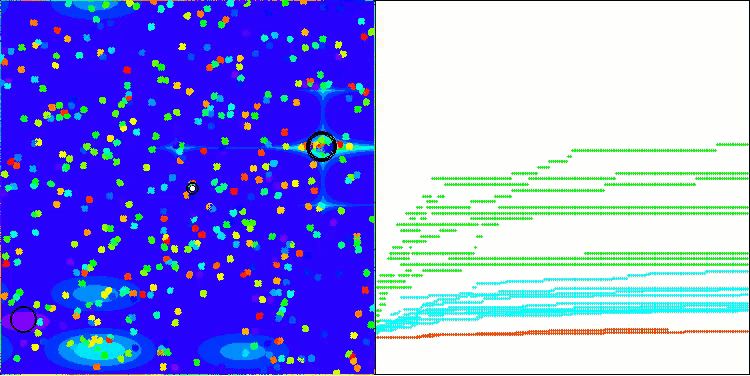
BHAm在Megacity测试函数上

改进后的BBBC算法版本在排名表中位列第43名。随机游走（RW）被设定为搜索策略有效性下限的基准。

#	AO	描述	Hilly值			Hilly最终值	Forest值			Forest最终值	Megacity (离散)			Megacity最终值	最终结果	最大百分比
#	AO	描述	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Hilly最终值	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Forest最终值	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Megacity最终值	最终结果	最大百分比
1	ANS	跨邻域搜索	0.94948	0.84776	0.43857	2.23581	1.00000	0.92334	0.39988	2.32323	0.70923	0.63477	0.23091	1.57491	6.134	68.15
2	CLA	密码锁算法（joo）	0.95345	0.87107	0.37590	2.20042	0.98942	0.91709	0.31642	2.22294	0.79692	0.69385	0.19303	1.68380	6.107	67.86
3	AMOm	动物迁徙优化M	0.90358	0.84317	0.46284	2.20959	0.99001	0.92436	0.46598	2.38034	0.56769	0.59132	0.23773	1.39675	5.987	66.52
4	(P+O)ES	(P+O) 进化策略	0.92256	0.88101	0.40021	2.20379	0.97750	0.87490	0.31945	2.17185	0.67385	0.62985	0.18634	1.49003	5.866	65.17
5	CTA	彗星尾算法（joo）	0.95346	0.86319	0.27770	2.09435	0.99794	0.85740	0.33949	2.19484	0.88769	0.56431	0.10512	1.55712	5.846	64.96
6	SDSm	随机扩散搜索 M	0.93066	0.85445	0.39476	2.17988	0.99983	0.89244	0.19619	2.08846	0.72333	0.61100	0.10670	1.44103	5.709	63.44
7	AAm	射箭算法M	0.91744	0.70876	0.42160	2.04780	0.92527	0.75802	0.35328	2.03657	0.67385	0.55200	0.23738	1.46323	5.548	61.64
8	ESG	社会群体的进化（joo）	0.99906	0.79654	0.35056	2.14616	1.00000	0.82863	0.13102	1.95965	0.82333	0.55300	0.04725	1.42358	5.529	61.44
9	SIA	模拟各向同性退火（joo）	0.95784	0.84264	0.41465	2.21513	0.98239	0.79586	0.20507	1.98332	0.68667	0.49300	0.09053	1.27020	5.469	60.76
10	ACS	人工协同搜索	0.75547	0.74744	0.30407	1.80698	1.00000	0.88861	0.22413	2.11274	0.69077	0.48185	0.13322	1.30583	5.226	58.06
11	BHAm	黑洞算法M	0.75236	0.76675	0.34583	1.86493	0.93593	0.80152	0.27177	2.00923	0.65077	0.51646	0.15472	1.32195	5.196	57.73
12	ASO	无序社会优化	0.84872	0.74646	0.31465	1.90983	0.96148	0.79150	0.23803	1.99101	0.57077	0.54062	0.16614	1.27752	5.178	57.54
13	AOSm	原子轨道搜索M	0.80232	0.70449	0.31021	1.81702	0.85660	0.69451	0.21996	1.77107	0.74615	0.52862	0.14358	1.41835	5.006	55.63
14	TSEA	龟壳演化算法（joo）	0.96798	0.64480	0.29672	1.90949	0.99449	0.61981	0.22708	1.84139	0.69077	0.42646	0.13598	1.25322	5.004	55.60
15	DE	差分进化	0.95044	0.61674	0.30308	1.87026	0.95317	0.78896	0.16652	1.90865	0.78667	0.36033	0.02953	1.17653	4.955	55.06
16	CRO	化学反应优化	0.94629	0.66112	0.29853	1.90593	0.87906	0.58422	0.21146	1.67473	0.75846	0.42646	0.12686	1.31178	4.892	54.36
17	BSA	鸟群算法	0.89306	0.64900	0.26250	1.80455	0.92420	0.71121	0.24939	1.88479	0.69385	0.32615	0.10012	1.12012	4.809	53.44
18	HS	和声搜索	0.86509	0.68782	0.32527	1.87818	0.99999	0.68002	0.09590	1.77592	0.62000	0.42267	0.05458	1.09725	4.751	52.79
19	SSG	树苗播种和生长	0.77839	0.64925	0.39543	1.82308	0.85973	0.62467	0.17429	1.65869	0.64667	0.44133	0.10598	1.19398	4.676	51.95
20	BCOm	细菌趋化性优化算法M	0.75953	0.62268	0.31483	1.69704	0.89378	0.61339	0.22542	1.73259	0.65385	0.42092	0.14435	1.21912	4.649	51.65
21	ABO	非洲水牛优化	0.83337	0.62247	0.29964	1.75548	0.92170	0.58618	0.19723	1.70511	0.61000	0.43154	0.13225	1.17378	4.634	51.49
22	(PO)ES	(PO) 进化策略	0.79025	0.62647	0.42935	1.84606	0.87616	0.60943	0.19591	1.68151	0.59000	0.37933	0.11322	1.08255	4.610	51.22
23	TSm	禁忌搜索M	0.87795	0.61431	0.29104	1.78330	0.92885	0.51844	0.19054	1.63783	0.61077	0.38215	0.12157	1.11449	4.536	50.40
24	BSO	头脑风暴优化	0.93736	0.57616	0.29688	1.81041	0.93131	0.55866	0.23537	1.72534	0.55231	0.29077	0.11914	0.96222	4.498	49.98
25	WOAm	鲸鱼优化算法M	0.84521	0.56298	0.26263	1.67081	0.93100	0.52278	0.16365	1.61743	0.66308	0.41138	0.11357	1.18803	4.476	49.74
26	AEFA	人工电场算法	0.87700	0.61753	0.25235	1.74688	0.92729	0.72698	0.18064	1.83490	0.66615	0.11631	0.09508	0.87754	4.459	49.55
27	AEO	基于人工生态系统的优化算法	0.91380	0.46713	0.26470	1.64563	0.90223	0.43705	0.21400	1.55327	0.66154	0.30800	0.28563	1.25517	4.454	49.49
28	ACOm	蚁群优化 M	0.88190	0.66127	0.30377	1.84693	0.85873	0.58680	0.15051	1.59604	0.59667	0.37333	0.02472	0.99472	4.438	49.31
29	BFO-GA	细菌觅食优化 - ga	0.89150	0.55111	0.31529	1.75790	0.96982	0.39612	0.06305	1.42899	0.72667	0.27500	0.03525	1.03692	4.224	46.93
30	SOA	简单优化算法	0.91520	0.46976	0.27089	1.65585	0.89675	0.37401	0.16984	1.44060	0.69538	0.28031	0.10852	1.08422	4.181	46.45
31	ABHA	人工蜂巢算法	0.84131	0.54227	0.26304	1.64663	0.87858	0.47779	0.17181	1.52818	0.50923	0.33877	0.10397	0.95197	4.127	45.85
32	ACMO	大气云模型优化	0.90321	0.48546	0.30403	1.69270	0.80268	0.37857	0.19178	1.37303	0.62308	0.24400	0.10795	0.97503	4.041	44.90
33	ADAMm	群体自适应矩估计M	0.88635	0.44766	0.26613	1.60014	0.84497	0.38493	0.16889	1.39880	0.66154	0.27046	0.10594	1.03794	4.037	44.85
34	ATAm	人工部落算法M	0.71771	0.55304	0.25235	1.52310	0.82491	0.55904	0.20473	1.58867	0.44000	0.18615	0.09411	0.72026	3.832	42.58
35	ASHA	人工淋浴算法	0.89686	0.40433	0.25617	1.55737	0.80360	0.35526	0.19160	1.35046	0.47692	0.18123	0.09774	0.75589	3.664	40.71
36	ASBO	适应性社会行为优化	0.76331	0.49253	0.32619	1.58202	0.79546	0.40035	0.26097	1.45677	0.26462	0.17169	0.18200	0.61831	3.657	40.63
37	MEC	思维进化计算	0.69533	0.53376	0.32661	1.55569	0.72464	0.33036	0.07198	1.12698	0.52500	0.22000	0.04198	0.78698	3.470	38.55
38	IWO	入侵杂草优化	0.72679	0.52256	0.33123	1.58058	0.70756	0.33955	0.07484	1.12196	0.42333	0.23067	0.04617	0.70017	3.403	37.81
39	Micro-AIS	微型人工免疫系统	0.79547	0.51922	0.30861	1.62330	0.72956	0.36879	0.09398	1.19233	0.37667	0.15867	0.02802	0.56335	3.379	37.54
40	COAm	布谷鸟优化算法 M	0.75820	0.48652	0.31369	1.55841	0.74054	0.28051	0.05599	1.07704	0.50500	0.17467	0.03380	0.71347	3.349	37.21
41	SDOm	螺旋动力学优化 M	0.74601	0.44623	0.29687	1.48912	0.70204	0.34678	0.10944	1.15826	0.42833	0.16767	0.03663	0.63263	3.280	36.44
42	NMm	Nelder-Mead方法 M	0.73807	0.50598	0.31342	1.55747	0.63674	0.28302	0.08221	1.00197	0.44667	0.18667	0.04028	0.67362	3.233	35.92
43	BBBC	大爆炸-大坍缩算法	0,60531	0,45250	0,31255	1,37036	0,52323	0,35426	0,20417	1,08166	0,39769	0,19431	0,11286	0,70486	3,157	35,08
44	FAm	萤火虫算法 M	0.58634	0.47228	0.32276	1.38138	0.68467	0.37439	0.10908	1.16814	0.28667	0.16467	0.04722	0.49855	3.048	33.87
45	GSA	引力搜索算法	0.64757	0.49197	0.30062	1.44016	0.53962	0.36353	0.09945	1.00260	0.32667	0.12200	0.01917	0.46783	2.911	32.34
	RW	随机游走	0.48754	0.32159	0.25781	1.06694	0.37554	0.21944	0.15877	0.75375	0.27969	0.14917	0.09847	0.52734	2.348	26.09

总结

大爆炸-大坍缩（BBBC）算法是一种受宇宙学过程启发的全局优化方法，其设计理念颇具创新性。然而，实验结果表明，该算法宣称的效率存在显著高估。需特别指出的是，BBBC的搜索过程过度集中于搜索空间中心，这种特性可能人为制造出“高效搜索”的假象。这一现象并非反映算法的真实优势，而是源于测试问题特性与算法设计偏好的偶然契合。

此外需强调的是，当前用于算法评估的主流测试函数普遍将全局最优解设置在搜索空间中心。此类测试的可靠性存疑，可能误导对BBBC等算法真实能力的判断——因其搜索策略存在对中心最优的“过度适配”（可视为一种“作弊”特性）。因此，对算法评估领域中某些“公认结论”需保持审慎的态度，避免陷入经验主义。

尽管如此，改进版BBBC算法在高维优化问题中展现出优异性能，表明其仍具备显著的开发潜力。这一发现为算法优化开辟了新方向：通过针对性改进，可提升BBBC在复杂场景下的适应性，同时为全局优化技术提供了新的理论工具与实践方法。

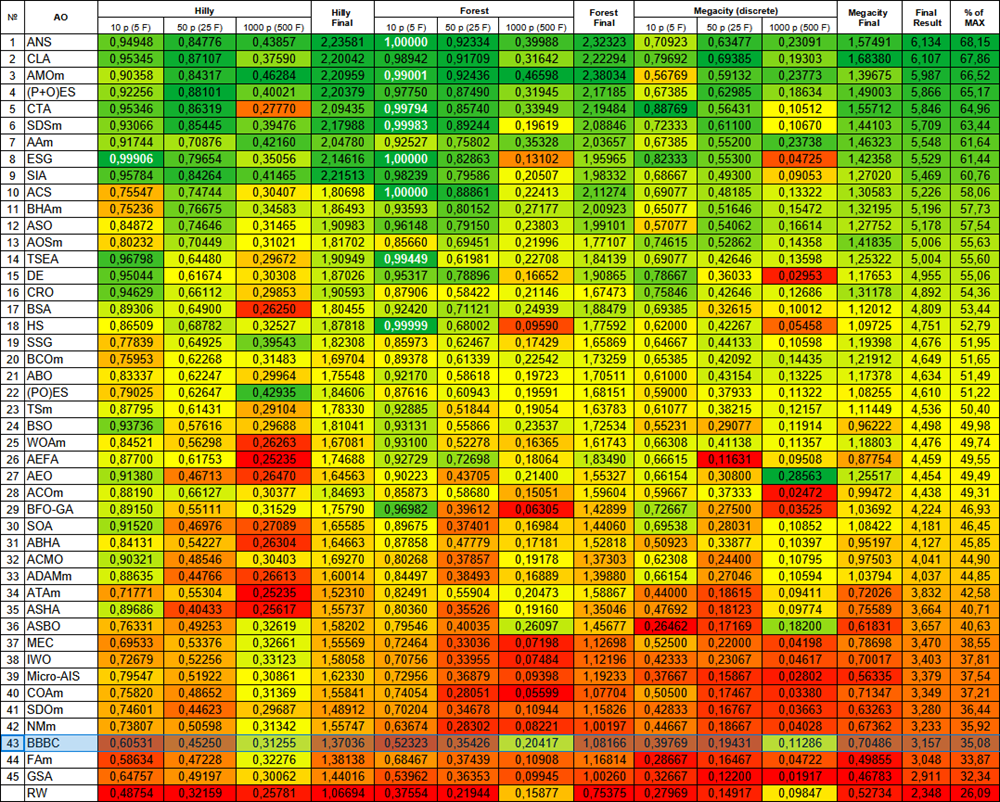
图例2. 根据相关测试，将算法的颜色等级大于或等于0.99的结果以白色突出显示

表格中的颜色渐变直观表明：并非所有优化算法均优于简单随机搜索（RW），尤其是在某些特定的问题类型中。在高维优化问题中，这一情况更为突出——搜索空间的地形复杂度与维度显著增长，导致算法性能急剧分化。在此类场景下，传统优化策略可能因局部极值、维度灾难等问题而失效。然而，需强调的是，我们并非主张将随机搜索作为首选方法，而是通过对比揭示不同优化算法的限制与性能，为算法选择提供理论依据。

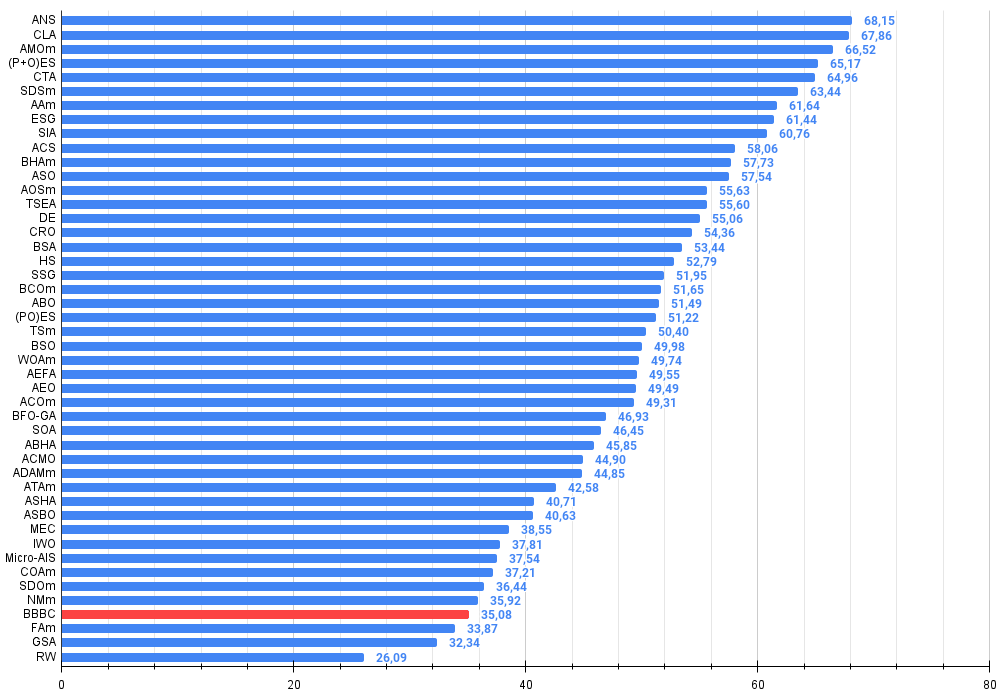
图例3. 算法测试结果的直方图（评分范围为0到100，越高越好，其中100为理论上的最高可能得分，档案中附有计算排名表的脚本）

BBBC的优缺点：

优点：

唯一的外部参数是种群规模。
实现简单。
非常快速的EA。
在大规模问题中表现优异。

缺点：

在低维问题上结果的离散性显著。
在低维问题上易陷入局部最优。

文章附有一个包含当前版本算法代码的归档文件。本文作者对标准算法描述的绝对准确性不承担责任。为提升搜索能力，已经对其中的许多算法进行了修改。文章中表述的结论和论断都是基于实验的结果。

github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5

文中所用的程序

#	名称	类型	描述
1	#C_AO.mqh	库	种群优化算法的基类
2	#C_AO_enum.mqh	库	种群优化算法的枚举说明
3	TestFunctions.mqh	库	测试函数库
4	TestStandFunctions.mqh	库	测试台函数库
5	Utilities.mqh	库	辅助函数库
6	CalculationTestResults.mqh	库	用于计算比较表结果的脚本
7	Testing AOs.mq5	脚本	面向所有种群优化算法的统一测试平台
8	Simple use of population optimization algorithms.mq5	脚本	种群优化算法非可视化简易使用案例
9	Test_AO_BBBC.mq5	脚本	BBBC测试

本文由MetaQuotes Ltd译自俄文
原文地址： https://www.mql5.com/ru/articles/16701

附加的文件 |

下载ZIP

BBBC.zip (151.26 KB)

注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

本文由网站的一位用户撰写，反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责，也不对因使用所述解决方案、策略或建议而产生的任何后果负责。

该作者的其他文章

前往讨论

交易策略

各种交易策略的分类都是任意的，下面这种分类强调从交易的基本概念上分类。

重构经典策略（第十三部分）：最小化均线交叉的滞后性

在我们交易者社区中，均线交叉策略已是广为人知，然而，自该策略诞生以来，其核心思想却几乎一成未变。在本次讨论中，我们将为您呈现对原策略的一项微调，其目的在于最小化该交易策略中存在的滞后性。所有原策略的爱好者们，不妨根据我们今天将要探讨的见解，来重新审视并改进这一策略。通过使用两条周期相同的移动平均线，我们可以在不违背策略基本原则的前提下，显著减少交易策略的滞后。

新手在交易中的10个基本错误

新手在交易中会犯的10个基本错误: 在市场刚开始时交易, 获利时不适当地仓促, 在损失的时候追加投资, 从最好的仓位开始平仓, 翻本心理, 最优越的仓位, 用永远买进的规则进行交易, 在第一天就平掉获利的仓位,当发出建一个相反的仓位警示时平仓, 犹豫。

从基础到中级：数组（四）

在本文中，我们将看看如何做一些与 C、C++ 和 Java 等语言中实现的非常相似的事情。我说的是在函数或过程中传递几乎无限数量的参数。虽然这似乎是一个相当高级的主题，但在我看来，任何理解了前面概念的人都可以很容易地实现这里展示的内容。只要它们真的被正确理解。