Algoritmo do buraco negro — Black Hole Algorithm (BHA)
151
0
Conteúdo
Introdução
O algoritmo do buraco negro (Black Hole Algorithm, BHA) oferece uma abordagem única para o problema de otimização. Criado em 2013 por A. Hatamlou, esse algoritmo se inspira nos objetos mais misteriosos e poderosos do Universo: os buracos negros. Assim como os buracos negros atraem tudo ao seu redor com seu campo gravitacional, o algoritmo busca “atrair” para si as melhores soluções, descartando as menos eficientes.
Imagine um espaço infinito, repleto de soluções, cada uma lutando para sobreviver nesse ambiente hostil. No centro desse caos estão os buracos negros — as soluções com a maior avaliação de qualidade — que possuem força de atração. A cada iteração, o algoritmo do buraco negro decide quais estrelas serão absorvidas pelos buracos negros e quais continuarão sua jornada em busca de condições mais favoráveis.
Com elementos de aleatoriedade, o algoritmo BHA explora regiões desconhecidas, evitando armadilhas de mínimos locais. Isso o torna uma ferramenta poderosa para resolver problemas complexos, desde otimização de funções até problemas combinatórios e até mesmo ajuste de hiperparâmetros em aprendizado de máquina. Neste artigo, vamos examinar detalhadamente o algoritmo do buraco negro, seus princípios de funcionamento, bem como suas vantagens e desvantagens, apresentando um universo onde ciência e arte da otimização se entrelaçam.
Implementação do algoritmo
O algoritmo BHA se baseia na ideia de como as estrelas interagem com o buraco negro para encontrar soluções ótimas dentro de um espaço de busca definido. O processo do algoritmo começa com a inicialização, onde é criada uma população inicial de “estrelas” aleatórias, cada uma representando uma solução potencial para o problema de otimização. Essas estrelas são posicionadas no espaço de busca, limitado por fronteiras superiores e inferiores. Ao longo das iterações do algoritmo, a cada passo, a melhor solução é destacada como o “buraco negro”. As demais estrelas tentam se aproximar do buraco negro usando a seguinte equação:
Xi(t+1) = Xi(t) + rand × (XBH - Xi(t))
onde:
- Xi(t) — posição atual da estrela i
- XBH — posição do buraco negro
- rand — número aleatório entre 0 e 1
Um elemento importante do algoritmo é o horizonte de eventos, que é calculado pela fórmula:
R = fitBH / Σfiti
Estrelas que cruzam esse horizonte são “absorvidas” pelo buraco negro e substituídas por novas estrelas aleatórias. Esse mecanismo mantém a diversidade da população e promove a exploração contínua do espaço.
O algoritmo do buraco negro possui algumas características-chave. Ele tem uma estrutura simples e praticamente não possui parâmetros além do tamanho da população, o que o torna fácil de usar e sem necessidade de ajuste, algo praticamente inexistente em outros algoritmos de otimização.
O algoritmo BHA é semelhante a outros algoritmos populacionais, o que significa que o primeiro passo no processo de otimização é a criação de uma população inicial de soluções aleatórias (estrelas iniciais) e o cálculo da função objetivo para avaliar os valores das soluções. A melhor solução em cada iteração é escolhida como buraco negro, que então começa a atrair outros candidatos a solução ao seu redor, chamados de estrelas. Se os outros candidatos se aproximarem da melhor solução encontrada, eles serão “absorvidos” por ela.
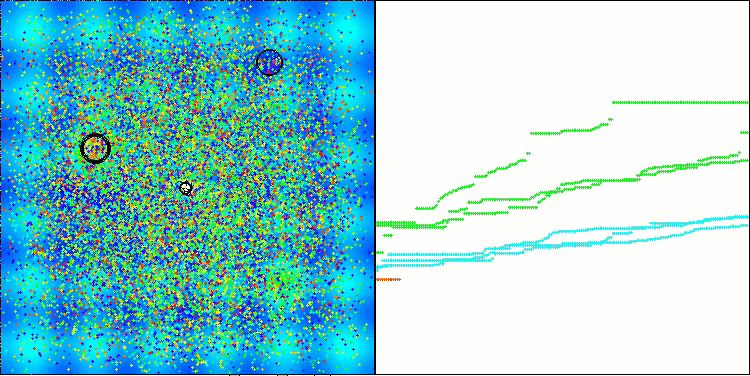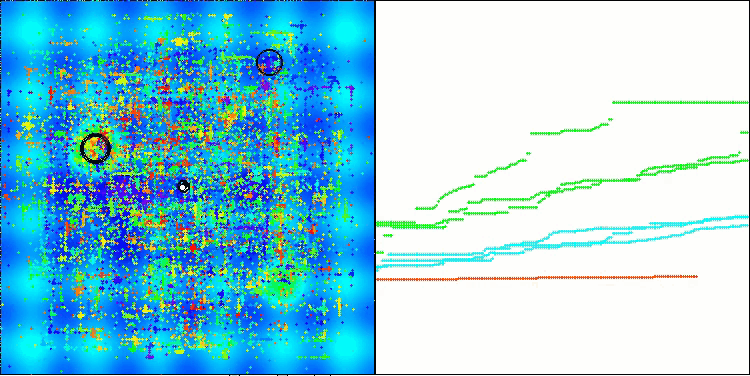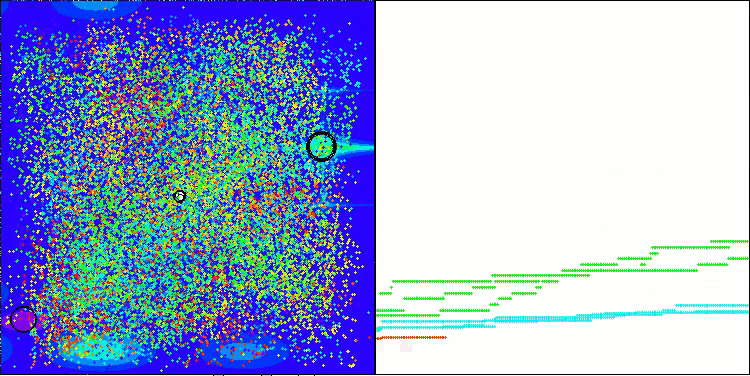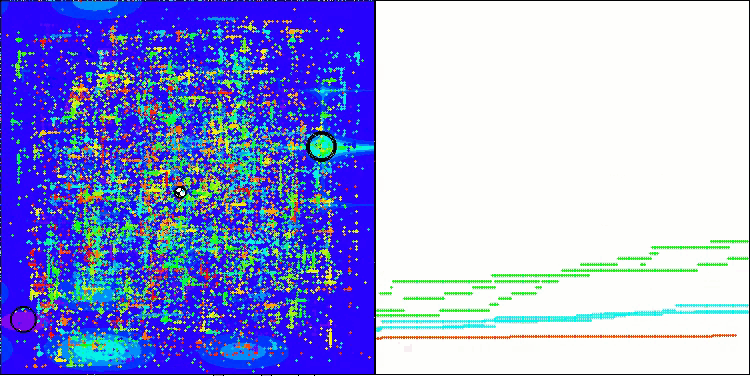
A imagem abaixo mostra uma demonstração da estratégia de busca do algoritmo BHA. Todas as estrelas que estiverem além do horizonte de eventos do buraco negro se moverão em direção ao seu centro, enquanto as estrelas que cruzarem o horizonte serão absorvidas; na prática, a matéria da estrela será teletransportada para outra região do espaço de busca.
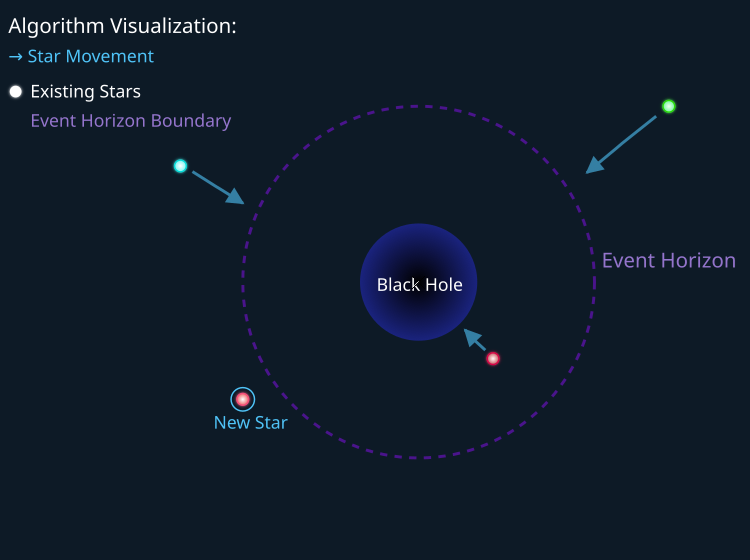
Figura 1. Estratégia de busca BHA. Estrelas verde e azul se movem em direção ao centro do buraco negro, e a estrela vermelha é teletransportada para o ponto "New Star"
Vamos escrever o pseudocódigo do algoritmo Black Hole Algorithm (BHA)
N - número de estrelas (tamanho da população)
tmax - número máximo de iterações
// Inicialização
1. Criar posições iniciais para N estrelas:
Para i = 1 até N:
Xi = LB + rand × (UB - LB)
2. t = 1
// Ciclo principal
3. Enquanto t ≤ tmax:
// Calcular valor da função objetivo para cada estrela
4. Para cada Xi calcular fiti
// Definir o buraco negro
5. Definir XBH como a estrela com o melhor valor de fiti
fitBH = melhor valor de fiti
// Atualizar posições das estrelas
6. Para cada estrela Xi:
Xi(t+1) = Xi(t) + rand × (XBH - Xi(t))
// Calcular o raio do horizonte de eventos
7. R = fitBH / ∑(i=1 até N) fiti
// Verificar absorção das estrelas
8. Para cada estrela Xi:
Se a distância entre Xi e XBH < R:
Gerar nova posição para Xi aleatoriamente
Xi = LB + rand × (UB - LB)
9. t = t + 1
// Retornar a melhor solução encontrada
Retornar XBH
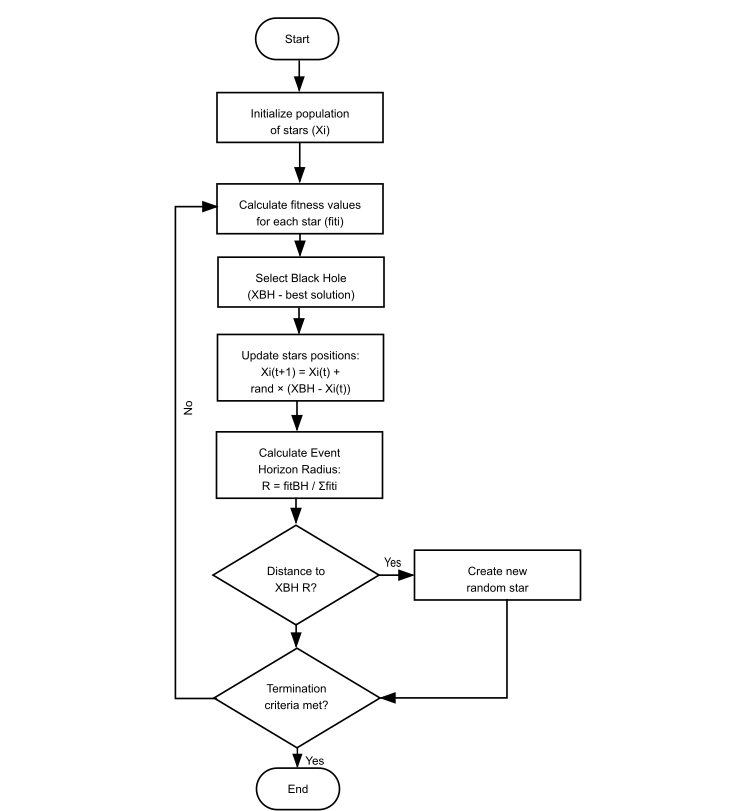
Figura 2. Esquema lógico de funcionamento do algoritmo BHA
Definição da classe C_AO_BHA (Black Hole Algorithm), que herda da classe base C_AO, estrutura da classe:
Construtor e destrutor:
- O construtor inicializa os parâmetros básicos do algoritmo
- SetParams () - define o tamanho da população a partir do array de parâmetros
- Init () - inicializa o espaço de busca com os limites e passo especificados
- Moving () - implementa o movimento das estrelas em direção ao buraco negro
- Revision () - atualiza a melhor solução encontrada (o buraco negro)
- blackHoleIndex - armazena o índice da melhor solução na população
- rangeMinP [] - valores mínimos para cada coordenada
- rangeMaxP [] - valores máximos para cada coordenada
- rangeStepP [] - passo de discretização para cada coordenada
- epochsP - número de iterações do algoritmo
Essa é a estrutura básica para implementar o algoritmo do buraco negro, onde a lógica principal será implementada nos métodos Moving() e Revision().
//—————————————————————————————————————————————————————————————————————————————— class C_AO_BHA : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_BHA () { } C_AO_BHA () { ao_name = "BHA"; ao_desc = "Black Hole Algorithm"; ao_link = "https://www.mql5.com/ru/articles/16655"; popSize = 50; // Размер популяции ArrayResize (params, 1); // Инициализация параметров params [0].name = "popSize"; params [0].val = popSize; } void SetParams () // Метод для установки параметров { popSize = (int)params [0].val; } bool Init (const double &rangeMinP [], // Минимальный диапазон поиска const double &rangeMaxP [], // Максимальный диапазон поиска const double &rangeStepP [], // Шаг поиска const int epochsP = 0); // Количество эпох void Moving (); // Метод перемещения void Revision (); // Метод ревизии private: //------------------------------------------------------------------- int blackHoleIndex; // Индекс черной дыры (лучшего решения) };O método "Init" é simples e sua função é a seguinte:
- Executa a inicialização do algoritmo
- Chama StandardInit para definir os intervalos de busca e o passo
- Define o índice inicial do buraco negro como 0
- Retorna true em caso de sucesso na inicialização, false em caso de erro
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_BHA::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; blackHoleIndex = 0; // Инициализация индекса черной дыры return true; } //——————————————————————————————————————————————————————————————————————————————
O método "Moving" é composto por alguns blocos principais:
a) Inicialização primária (se revision = false):
- Cria a população inicial de estrelas com posições aleatórias
- As posições são geradas dentro do intervalo definido e ajustadas para a grade discreta
- Define o flag "revision" como "true"
b) Algoritmo principal (se revision = true):
- Calcula a soma dos valores da função de aptidão de todas as estrelas
- Calcula o raio do horizonte de eventos: R = fitBH / Σfiti
c) Atualização das posições das estrelas:
- Para cada estrela (exceto o buraco negro):
- Calcula a distância euclidiana até o buraco negro
- Se a distância for menor que o raio do horizonte:
- Cria uma nova estrela aleatória
- Caso contrário:
- Atualiza a posição com a fórmula: Xi(t+1) = Xi(t) + rand × (XBH - Xi(t))
- Ajusta a nova posição aos limites válidos e à grade discreta
Todos os cálculos são realizados respeitando os limites do espaço de busca e o passo de discretização.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BHA::Moving () { // Начальное случайное позиционирование при первом запуске if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { // Генерация случайной позиции в допустимом диапазоне a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); // Приведение к дискретным значениям согласно шагу a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } // Расчет суммы фитнес-значений для радиуса горизонта событий double sumFitness = 0.0; for (int i = 0; i < popSize; i++) { sumFitness += a [i].f; } // Расчет радиуса горизонта событий // R = fitBH / Σfiti double eventHorizonRadius = a [blackHoleIndex].f / sumFitness; // Обновление позиций звезд for (int i = 0; i < popSize; i++) { // Пропускаем черную дыру if (i == blackHoleIndex) continue; // Расчет расстояния до черной дыры double distance = 0.0; for (int c = 0; c < coords; c++) { double diff = a [blackHoleIndex].c [c] - a [i].c [c]; distance += diff * diff; } distance = sqrt (distance); // Проверка пересечения горизонта событий if (distance < eventHorizonRadius) { // Звезда поглощена - создаем новую случайную звезду for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } else { // Обновление позиции звезды по формуле: // Xi(t+1) = Xi(t) + rand × (XBH - Xi(t)) for (int c = 0; c < coords; c++) { double rnd = u.RNDfromCI (0.0, 1.0); double newPosition = a [i].c [c] + rnd * (a [blackHoleIndex].c [c] - a [i].c [c]); // Проверка и коррекция границ newPosition = u.SeInDiSp (newPosition, rangeMin [c], rangeMax [c], rangeStep [c]); a [i].c [c] = newPosition; } } } } //——————————————————————————————————————————————————————————————————————————————
O método "Revision" executa as seguintes funções:
Busca da melhor solução:
- Percorre todas as estrelas da população
- Compara o valor da função de aptidão de cada estrela (a[i].f) com o melhor valor atual (fB)
- Ao encontrar uma solução melhor:
- Atualiza o melhor valor da função de aptidão (fB)
- Armazena o índice do buraco negro (blackHoleIndex)
- Copia as coordenadas da melhor solução para o array "cB"
O objetivo principal do método é rastrear e salvar a melhor solução encontrada (o buraco negro) durante o processo de otimização.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BHA::Revision () { // Поиск лучшего решения (черной дыры) for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; blackHoleIndex = i; ArrayCopy (cB, a [i].c, 0, 0, WHOLE_ARRAY); } } } //——————————————————————————————————————————————————————————————————————————————
Os testes do algoritmo BHA apresentaram os seguintes resultados:
BHA|Black Hole Algorithm|50.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.6833993073000924
25 Hilly's; Func runs: 10000; result: 0.47275633991339616
500 Hilly's; Func runs: 10000; result: 0.2782882943201518
=============================
5 Forest's; Func runs: 10000; result: 0.6821776337288085
25 Forest's; Func runs: 10000; result: 0.3878950941651221
500 Forest's; Func runs: 10000; result: 0.20702263338385946
=============================
5 Megacity's; Func runs: 10000; result: 0.39461538461538465
25 Megacity's; Func runs: 10000; result: 0.20076923076923076
500 Megacity's; Func runs: 10000; result: 0.1076846153846164
=============================
All score: 3.41461 (37.94%)
Os resultados obtidos com o algoritmo ficaram abaixo da média, conforme a tabela. No entanto, uma vantagem evidente desse algoritmo é o fato de ele não possuir parâmetros, exceto o tamanho da população, o que permite considerar os resultados como bastante aceitáveis. Durante sua execução, foi imediatamente perceptível a tendência de estagnação em ótimos locais, causada pela falta de diversidade nas soluções da população. Além disso, para cada estrela é necessário realizar cálculos pesados de distância euclidiana até o buraco negro. Esse fator levou à reflexão sobre possíveis formas de corrigir essas limitações existentes.
No algoritmo original, durante as iterações, as estrelas se movimentam enquanto o buraco negro permanece fixo, embora no espaço todos os corpos, sem exceção, estejam em movimento. Decidi então implementar uma modificação que permitisse ao buraco negro se mover em distâncias definidas por uma distribuição gaussiana em torno de seu centro, além de testar a distribuição por lei de potência. Essa adaptação teve como objetivo melhorar a precisão da convergência sem perder a capacidade de explorar novas regiões do espaço de soluções. No entanto, apesar dessas mudanças, os resultados não apresentaram melhora. Isso pode indicar que a posição estática do buraco negro (especificamente para essa estratégia de busca) é importante para a eficácia do algoritmo, pois garante que as estrelas mantenham o foco nas regiões mais promissoras. Talvez valha a pena considerar outras abordagens ou combinações de métodos para alcançar melhorias mais expressivas nos resultados.
Assim, surgiu a ideia de abandonar o cálculo de distâncias euclidianas e, em vez disso, utilizar o horizonte de eventos do buraco negro como medida probabilística de absorção, em vez de uma absorção real após a travessia do horizonte. Em vez de aplicar o movimento à estrela inteira, essa nova abordagem aplica a probabilidade separadamente a cada coordenada.
Portanto, com base nesses argumentos, foi escrita uma nova versão do método "Moving". As mudanças envolveram a forma de cálculo do horizonte de eventos, que agora realiza a normalização da média da adaptabilidade da população com base na diferença entre a adaptabilidade mínima e máxima da população. Agora, o horizonte de eventos é tratado como uma probabilidade de absorção por coordenada individual das estrelas; caso não haja absorção, realiza-se o deslocamento normal em direção ao centro do monstro galáctico negro utilizando a fórmula original criada pelo autor.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BHAm::Moving () { // Начальное случайное позиционирование при первом запуске if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { // Генерация случайной позиции в допустимом диапазоне a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); // Приведение к дискретным значениям согласно шагу a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- // Расчет среднего значения фитнес-значений для радиуса горизонта событий double aveFit = 0.0; double maxFit = fB; double minFit = a [0].f; for (int i = 0; i < popSize; i++) { aveFit += a [i].f; if (a [i].f < minFit) minFit = a [i].f; } aveFit /= popSize; // Расчет радиуса горизонта событий double eventHorizonRadius = (aveFit - minFit) / (maxFit - minFit); // Обновление позиций звезд for (int i = 0; i < popSize; i++) { // Пропускаем черную дыру if (i == blackHoleIndex) continue; for (int c = 0; c < coords; c++) { if (u.RNDprobab () < eventHorizonRadius * 0.01) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } else { double rnd = u.RNDfromCI (0.0, 1.0); double newPosition = a [i].c [c] + rnd * (a [blackHoleIndex].c [c] - a [i].c [c]); // Проверка и коррекция границ newPosition = u.SeInDiSp (newPosition, rangeMin [c], rangeMax [c], rangeStep [c]); a [i].c [c] = newPosition; } } } } //——————————————————————————————————————————————————————————————————————————————
Vamos analisar as principais diferenças entre as duas versões do algoritmo, começando pelo cálculo do raio do horizonte de eventos. Na primeira versão (BHA), o raio é definido como a razão entre a melhor solução e a soma de todas as soluções, o que faz com que, em populações grandes, o raio se torne muito pequeno e altamente dependente dos valores absolutos da função de aptidão. Na segunda versão (BHAm), o raio é normalizado no intervalo [0,1], permitindo representar a posição relativa da média em relação ao mínimo e máximo, mantendo independência tanto do tamanho da população quanto dos valores absolutos da função de aptidão.
Agora vejamos o mecanismo de absorção das estrelas. Na primeira versão do algoritmo, é verificada a distância euclidiana até o buraco negro e, se ocorrer a absorção, a estrela é completamente substituída por uma nova em uma posição aleatória, o que resulta em mudanças mais bruscas na população. Já a segunda versão utiliza absorção probabilística por coordenada, o que garante modificações mais suaves na população. Aqui, o coeficiente 0.01 reduz a probabilidade de alterações radicais.
Quanto às consequências, a primeira versão apresenta uma exploração mais agressiva do espaço de busca, proporcionando convergência rápida em regiões locais, mas também aumentando o risco de convergência prematura e a perda de áreas promissoras devido à substituição completa das soluções. A segunda versão, ao contrário, propõe uma estratégia de pesquisa mais suave, garantindo melhor equilíbrio entre exploração e intensificação, menor risco de aprisionamento em ótimos locais e uma convergência mais lenta, porém potencialmente mais confiável, além de uma capacidade superior de diversificação da população.
Concluindo, a primeira versão é mais adequada para problemas com ótimos bem definidos, onde é necessária uma convergência rápida e o espaço de busca possui baixa dimensionalidade, enquanto a segunda versão é mais eficaz para problemas complexos e multimodais, nos quais a confiabilidade na busca pelo ótimo global é essencial, além de ser apropriada para problemas de alta dimensionalidade que exigem uma investigação mais detalhada do espaço de busca.
Gostaria também de compartilhar minhas reflexões sobre a visualização do funcionamento dos algoritmos. A visualização oferece uma oportunidade única de compreender mais profundamente os processos internos que ocorrem nos algoritmos, e revelar seus mecanismos ocultos. Com certas configurações, podemos observar como imagens caóticas se transformam gradualmente em padrões estruturados. Esse processo não apenas demonstra os aspectos técnicos do funcionamento do algoritmo, mas também inspira novas ideias e abordagens para sua otimização.
Exemplo de funcionamento do algoritmo BHAm ao gerar a componente aleatória de deslocamento das estrelas no intervalo [0.0;0.1]
É importante destacar que a visualização nos permite não apenas avaliar a eficácia dos algoritmos, mas também identificar padrões que podem não ser evidentes por meio da análise tradicional de dados. Isso promove uma compreensão mais profunda do funcionamento dos algoritmos, e pode inspirar novas soluções e inovações. Dessa forma, a visualização se torna uma ferramenta poderosa que ajuda a unir ciência e criatividade, abrindo novos horizontes para a investigação e o entendimento de processos complexos.
Resultados dos testes
Resultados da execução da versão modificada do algoritmo BHAm:
BHAm|Black Hole Algorithm M|50.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.752359491007831
25 Hilly's; Func runs: 10000; result: 0.7667459889455067
500 Hilly's; Func runs: 10000; result: 0.34582657277589457
=============================
5 Forest's; Func runs: 10000; result: 0.9359337849703726
25 Forest's; Func runs: 10000; result: 0.801524710041611
500 Forest's; Func runs: 10000; result: 0.2717683112397725
=============================
5 Megacity's; Func runs: 10000; result: 0.6507692307692307
25 Megacity's; Func runs: 10000; result: 0.5164615384615385
500 Megacity's; Func runs: 10000; result: 0.154715384615386
=============================
All score: 5.19611 (57.73%)
Os testes demonstram que o algoritmo BHAm apresenta resultados impressionantes, não apenas em comparação com a versão original, mas também de forma geral em relação à tabela. Na visualização, é possível observar que a nova versão com o sufixo "m" realmente superou os problemas característicos da versão original: a tendência ao aprisionamento foi praticamente eliminada, a precisão da convergência foi significativamente melhorada e a dispersão dos resultados foi reduzida. Ao mesmo tempo, foi preservada a "marca registrada" do algoritmo na versão dos autores, ou seja, a formação de aglomerados distintos de estrelas no espaço e sua atração por um determinado atrator no espaço de soluções.
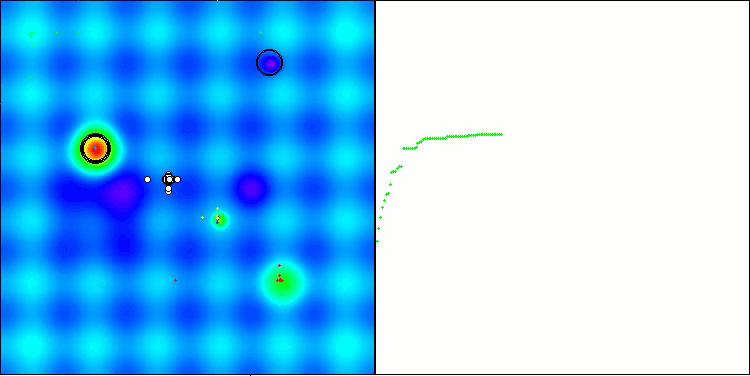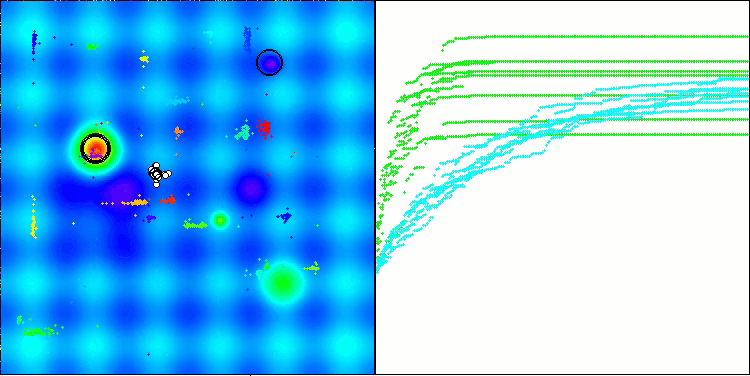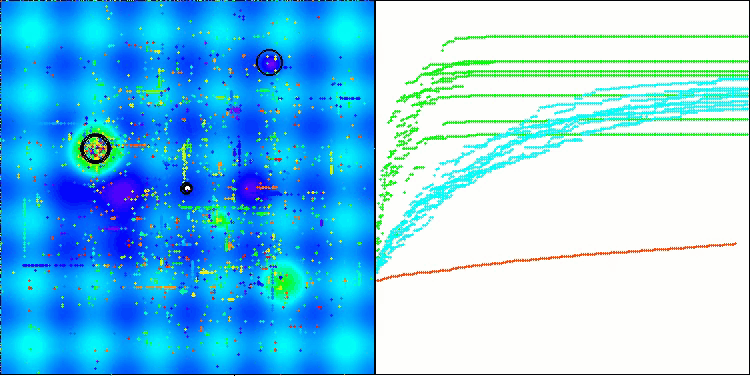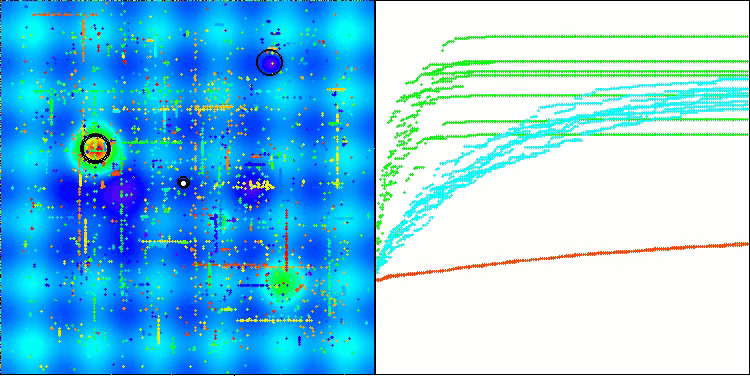
BHAm na função de teste Hilly
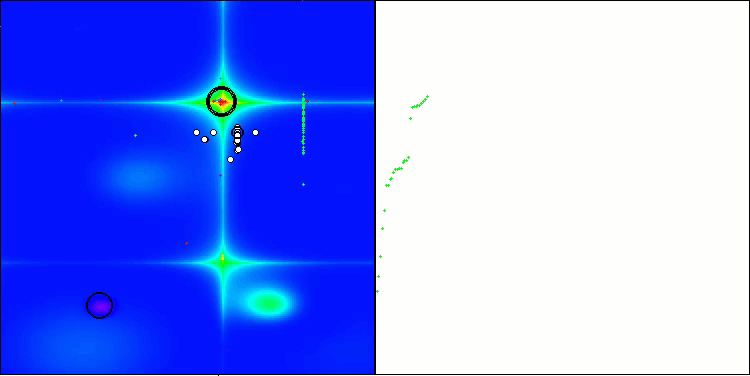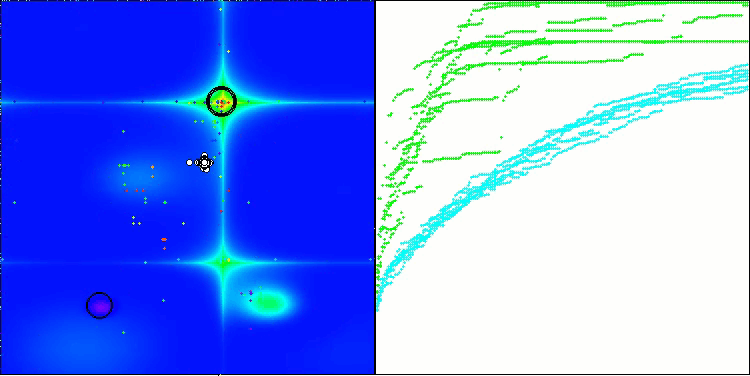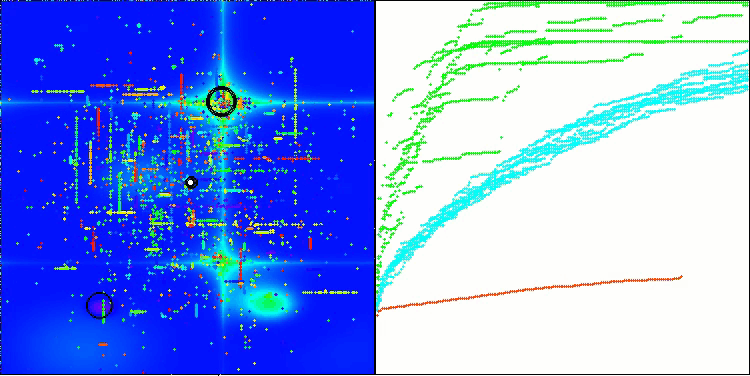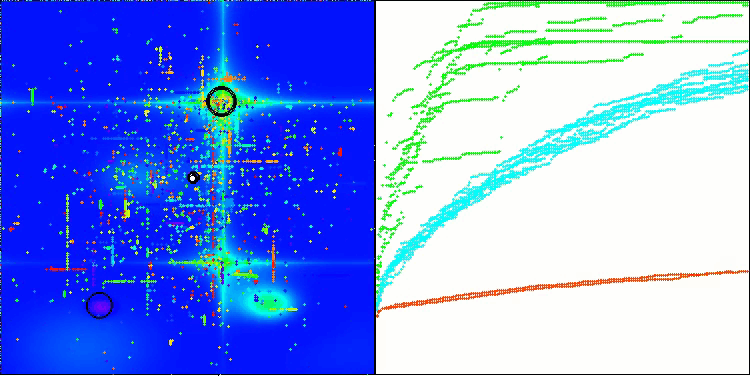
BHAm na função de teste Forest
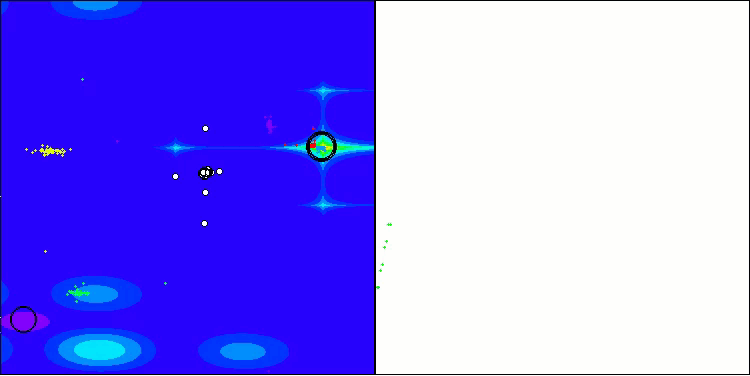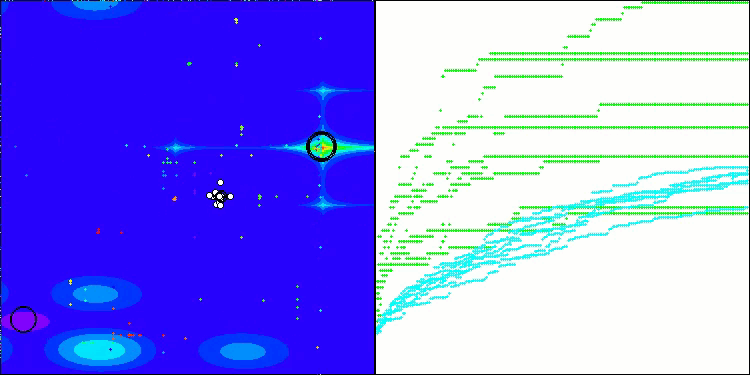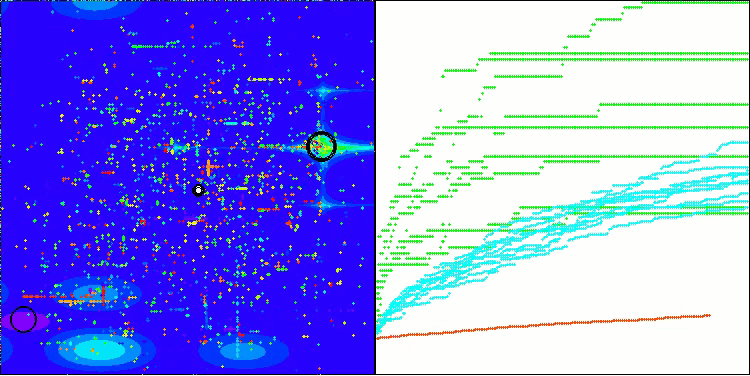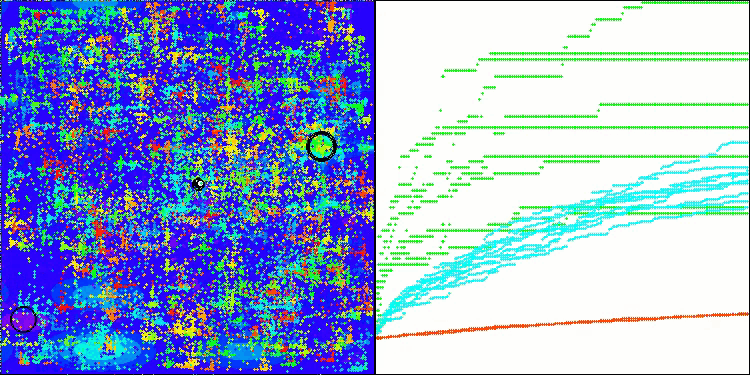
BHAm na função de teste Megacity
Ao final dos testes, o algoritmo BHAm conquistou o honroso 11º lugar, o que é um resultado excelente, considerando a presença de alguns dos algoritmos mais poderosos já conhecidos como concorrentes.
| № | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration ptimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 7 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 8 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 9 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 10 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 11 | BHAm | black hole algorithm M | 0,75236 | 0,76675 | 0,34583 | 1,86493 | 0,93593 | 0,80152 | 0,27177 | 2,00923 | 0,65077 | 0,51646 | 0,15472 | 1,32195 | 5,196 | 57,73 |
| 12 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 13 | AOSm | atomic orbital search M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| 14 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 15 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 16 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 17 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 18 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 19 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 20 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 21 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 22 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 23 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 24 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 25 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 26 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 27 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 28 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 29 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 30 | SOA | simple optimization algorithm | 0,91520 | 0,46976 | 0,27089 | 1,65585 | 0,89675 | 0,37401 | 0,16984 | 1,44060 | 0,69538 | 0,28031 | 0,10852 | 1,08422 | 4,181 | 46,45 |
| 31 | ABHA | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4,127 | 45,85 |
| 32 | ACMO | atmospheric cloud model optimization | 0,90321 | 0,48546 | 0,30403 | 1,69270 | 0,80268 | 0,37857 | 0,19178 | 1,37303 | 0,62308 | 0,24400 | 0,10795 | 0,97503 | 4,041 | 44,90 |
| 33 | ADAMm | adaptive moment estimation M | 0,88635 | 0,44766 | 0,26613 | 1,60014 | 0,84497 | 0,38493 | 0,16889 | 1,39880 | 0,66154 | 0,27046 | 0,10594 | 1,03794 | 4,037 | 44,85 |
| 34 | ATAm | artificial tribe algorithm M | 0,71771 | 0,55304 | 0,25235 | 1,52310 | 0,82491 | 0,55904 | 0,20473 | 1,58867 | 0,44000 | 0,18615 | 0,09411 | 0,72026 | 3,832 | 42,58 |
| 35 | ASHA | artificial showering algorithm | 0,89686 | 0,40433 | 0,25617 | 1,55737 | 0,80360 | 0,35526 | 0,19160 | 1,35046 | 0,47692 | 0,18123 | 0,09774 | 0,75589 | 3,664 | 40,71 |
| 36 | ASBO | adaptive social behavior optimization | 0,76331 | 0,49253 | 0,32619 | 1,58202 | 0,79546 | 0,40035 | 0,26097 | 1,45677 | 0,26462 | 0,17169 | 0,18200 | 0,61831 | 3,657 | 40,63 |
| 37 | MEC | mind evolutionary computation | 0,69533 | 0,53376 | 0,32661 | 1,55569 | 0,72464 | 0,33036 | 0,07198 | 1,12698 | 0,52500 | 0,22000 | 0,04198 | 0,78698 | 3,470 | 38,55 |
| 38 | IWO | invasive weed optimization | 0,72679 | 0,52256 | 0,33123 | 1,58058 | 0,70756 | 0,33955 | 0,07484 | 1,12196 | 0,42333 | 0,23067 | 0,04617 | 0,70017 | 3,403 | 37,81 |
| 39 | Micro-AIS | micro artificial immune system | 0,79547 | 0,51922 | 0,30861 | 1,62330 | 0,72956 | 0,36879 | 0,09398 | 1,19233 | 0,37667 | 0,15867 | 0,02802 | 0,56335 | 3,379 | 37,54 |
| 40 | COAm | cuckoo optimization algorithm M | 0,75820 | 0,48652 | 0,31369 | 1,55841 | 0,74054 | 0,28051 | 0,05599 | 1,07704 | 0,50500 | 0,17467 | 0,03380 | 0,71347 | 3,349 | 37,21 |
| 41 | SDOm | spiral dynamics optimization M | 0,74601 | 0,44623 | 0,29687 | 1,48912 | 0,70204 | 0,34678 | 0,10944 | 1,15826 | 0,42833 | 0,16767 | 0,03663 | 0,63263 | 3,280 | 36,44 |
| 42 | NMm | Nelder-Mead method M | 0,73807 | 0,50598 | 0,31342 | 1,55747 | 0,63674 | 0,28302 | 0,08221 | 1,00197 | 0,44667 | 0,18667 | 0,04028 | 0,67362 | 3,233 | 35,92 |
| 43 | FAm | firefly algorithm M | 0,58634 | 0,47228 | 0,32276 | 1,38138 | 0,68467 | 0,37439 | 0,10908 | 1,16814 | 0,28667 | 0,16467 | 0,04722 | 0,49855 | 3,048 | 33,87 |
| 44 | GSA | gravitational search algorithm | 0,64757 | 0,49197 | 0,30062 | 1,44016 | 0,53962 | 0,36353 | 0,09945 | 1,00260 | 0,32667 | 0,12200 | 0,01917 | 0,46783 | 2,911 | 32,34 |
| 45 | BFO | bacterial foraging optimization | 0,61171 | 0,43270 | 0,31318 | 1,35759 | 0,54410 | 0,21511 | 0,05676 | 0,81597 | 0,42167 | 0,13800 | 0,03195 | 0,59162 | 2,765 | 30,72 |
Considerações finais
O Black Hole Algorithm (BHA) é um exemplo elegante de como leis fundamentais da natureza podem ser transformadas em uma ferramenta eficaz de otimização. A base do algoritmo é uma ideia simples e intuitiva: a atração gravitacional de soluções potenciais em direção à solução central e superior, que atua como o buraco negro. No processo de evolução do algoritmo, observamos um fenômeno fascinante: as soluções-estrelas, ao se moverem em direção ao seu centro galáctico, podem encontrar novos e mais fortes centros de atração — soluções melhores — o que leva a uma mudança dinâmica na estrutura do espaço de busca. Isso demonstra claramente como mecanismos naturais de auto-organização podem ser aplicados de forma eficiente na otimização algorítmica.
A prática revela uma regularidade notável: frequentemente, é justamente a simplificação e a reinterpretação de ideias fundamentais, e não sua complexificação, que conduz a resultados surpreendentemente impressionantes. No mundo da otimização algorítmica, é raro que a complexificação da lógica de busca traga melhorias significativas de desempenho.
Este exemplo ilustra claramente um princípio importante: a autoridade dos criadores de um algoritmo ou a popularidade de um método não devem ser tomadas como garantia definitiva de sua otimização. Qualquer método, mesmo o mais bem-sucedido, pode ser aprimorado tanto em termos de eficiência computacional quanto na qualidade dos resultados obtidos. A versão modificada do algoritmo (BHAm) serve como um excelente exemplo dessa melhoria. Mantendo a simplicidade conceitual do método original e a ausência de parâmetros externos de ajuste, ela demonstra um ganho significativo em desempenho e velocidade de convergência.
Essa experiência nos conduz a uma conclusão fundamental: inovação e experimentação devem ser partes essenciais de qualquer atividade profissional. Seja no desenvolvimento de algoritmos de aprendizado de máquina ou na criação de estratégias de trading, a coragem de explorar novas abordagens e a disposição para reavaliar métodos existentes frequentemente são a chave para alcançar resultados revolucionários.
No fim das contas, o progresso na área de otimização, assim como em qualquer outro campo, é movido não por uma obediência cega às autoridades, mas pela busca constante por soluções novas e mais eficientes, baseadas em uma compreensão profunda dos princípios fundamentais, e na disposição para a experimentação criativa.
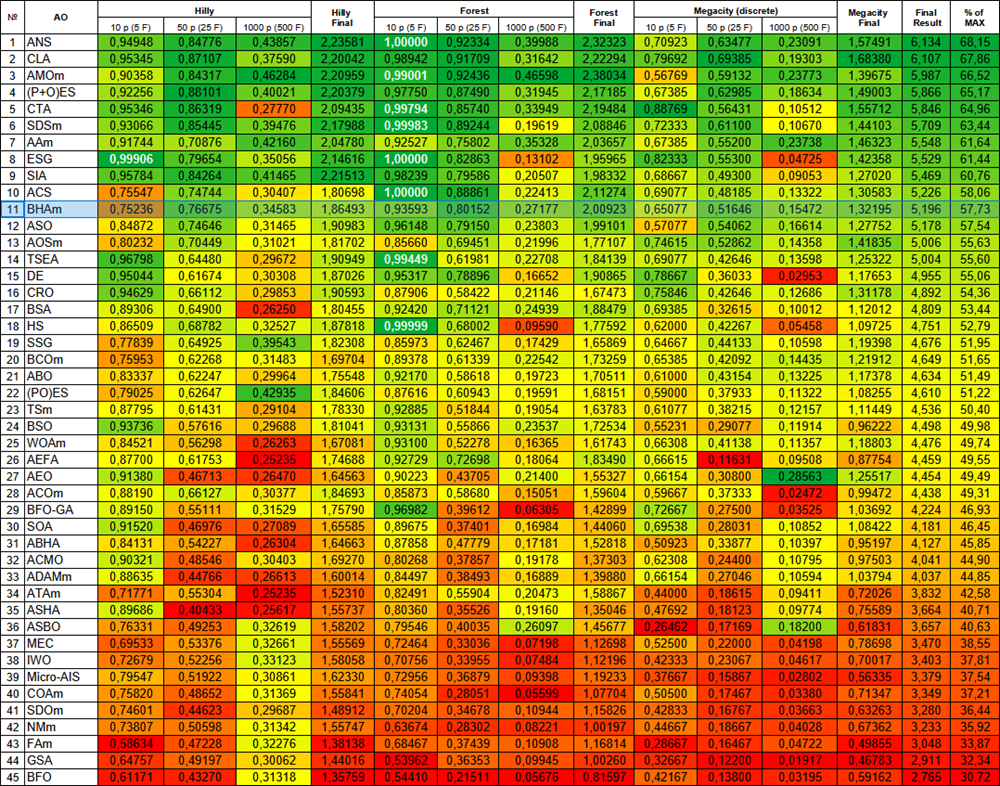
Figura 3. Graduação de cores dos algoritmos conforme os testes correspondentes. A cor branca destaca resultados maiores ou iguais a 0.99
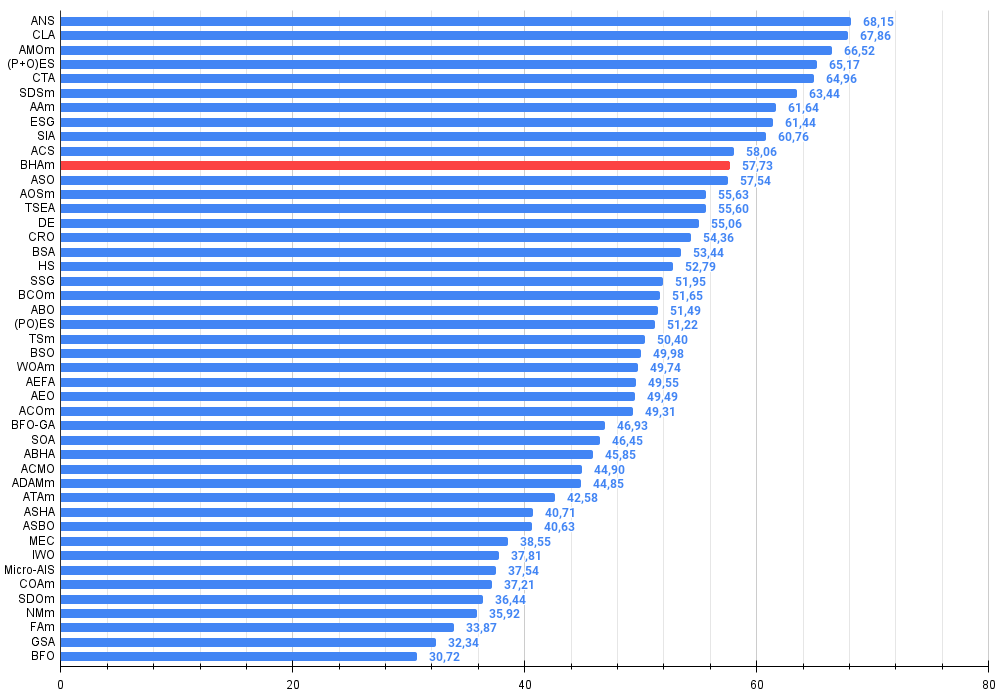
Figura 4. Histograma dos resultados dos testes dos algoritmos (em uma escala de 0 a 100, quanto maior, melhor, onde 100 é o resultado teórico máximo possível, no arquivo está o script para cálculo da tabela de classificação)
Prós e contras do algoritmo BHAm:
Prós:
- O único parâmetro externo é o tamanho da população.
- Implementação simples.
- Muito rápido.
- Funciona bem em problemas de alta dimensionalidade.
Contras:
- Alta variabilidade nos resultados em problemas de baixa dimensionalidade.
- Tendência ao aprisionamento em problemas de baixa dimensionalidade.
Está anexado ao artigo um arquivo com as versões atualizadas dos códigos dos algoritmos. O autor do artigo não se responsabiliza pela precisão absoluta na descrição dos algoritmos canônicos, pois muitos deles foram modificados para melhorar suas capacidades de busca. As conclusões e avaliações apresentadas nos artigos baseiam-se nos resultados dos experimentos realizados.
Programas utilizados no artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | C_AO.mqh | Arquivo incluído | Classe-pai dos algoritmos populacionais de otimização |
| 2 | C_AO_enum.mqh | Arquivo incluído | Enumeração de algoritmos populacionais de otimização |
| 3 | TestFunctions.mqh | Arquivo incluído | Biblioteca de funções de teste |
| 4 | TestStandFunctions.mqh | Arquivo incluído | Biblioteca de funções do ambiente de testes |
| 5 | Utilities.mqh | Arquivo incluído | Biblioteca de funções auxiliares |
| 6 | CalculationTestResults.mqh | Arquivo incluído | Script para cálculo dos resultados na tabela comparativa |
| 7 | Testing AOs.mq5 | Script | Ambiente unificado de testes para todos os algoritmos populacionais de otimização |
| 8 | Simple use of population optimization algorithms.mq5 | Script | Exemplo simples de uso dos algoritmos populacionais de otimização sem visualização |
| 9 | Test_AO_BHAm.mq5 | Script | Ambiente de testes para o BHAm |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/16655
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
Redes neurais em trading: Framework híbrido de negociação com codificação preditiva (Conclusão)
Introdução ao Connexus (Parte 1): Como usar a função WebRequest?
Redes neurais em trading: Modelos com uso de transformação wavelet e atenção multitarefa
Criando um Painel Administrativo de Negociação em MQL5 (Parte II): Aprimorando a Responsividade e Mensagens Rápidas
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso