母集団最適化アルゴリズム：細菌採餌最適化(BFO)

内容

1.はじめに
2.アルゴリズムの説明
3.テスト結果

1.はじめに

細菌採餌最適化（Bacterial Foraging Optimization、BFO）アルゴリズムは、非常に複雑または不可能な数値関数の最大化/最小化問題の近似解を見つけるために使用できる魅力的な最適化手法です。このアルゴリズムは、分散最適化および制御のための大域的最適化アルゴリズムとして広く認識されています。BFOは、大腸菌の社会的採餌行動に触発されています。BFOは、いくつかの適応分野で発生する現実世界の最適化問題を解決する際の有効性について、すでに研究者の注目を集めています。大腸菌の採餌戦略の背後にある生物学は、独自の方法でエミュレートされ、単純な最適化アルゴリズムとして使用されます。

大腸菌やサルモネラ菌などの細菌は、地球上で最も成功している生物の1つです。これらの機敏な細菌は、鞭毛と呼ばれる半硬質の付属物を持ち、それを使ってねじり運動で自分自身を推進します。すべての鞭毛が反時計回りに回転すると、プロペラ効果が生じ、細菌は多かれ少なかれ直線的な方向に移動します。この場合、細菌は遊泳と呼ばれる動きをします。すべての鞭毛は同じ方向に回転します。

鞭毛は、エシェリヒア属大腸菌が回転または遊泳（採餌中に細菌がおこなう2つの主な動作）するのを助けます。鞭毛を時計回りに回転させると、各鞭毛が細胞を押します。鞭毛が異なる方向に回転すると、細菌は回転します。細菌は、好ましい環境ではあまり回転せずに移動しますが、有害な環境では、栄養勾配を見つけるために頻繁に回転します。鞭毛の反時計回りの動きは、細菌が非常に高速で遊泳するのに役立ちます。

上記のアルゴリズムでは、細菌の行動は細菌の走化性と呼ばれるメカニズムによって決定されます。これは、環境内の化学的刺激に対するこれらの微生物の運動反応です。このメカニズムにより、細菌は誘引物質（ほとんどの場合、栄養素）に向かって移動し、忌避物質（細菌にとって潜在的に有害な物質）から離れることができます。誘引物質と忌避物質を検出する受容体は、細菌の極にあります。

細菌のサイズが小さいため、極間の有用物質と有害物質の濃度の違いを捉えることができません。細菌は、移動中の濃度の変化を測定することにより、これらの物質の勾配を決定します。この動きの速度は、毎秒数十細菌の長さに達する可能性があります。たとえば、大腸菌は通常、1秒間にその長さの10～20倍の速度で移動します。

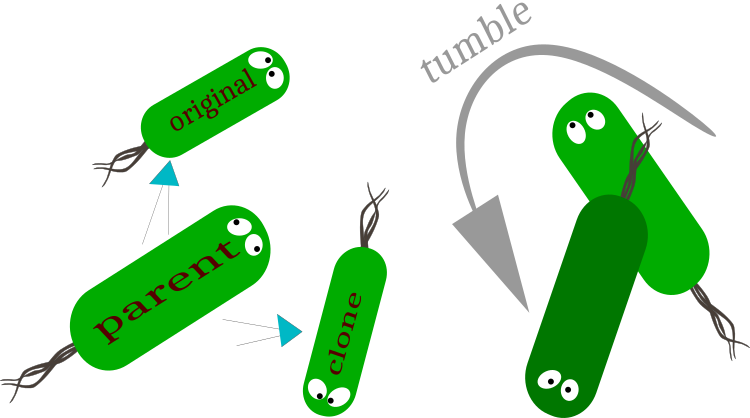
図1：複製：元の細菌(動きベクトルの保存)とクローン細菌(動きベクトルの変更)への分割、
回転：細菌の動きのベクトルの変化

細菌が選んだ移動方向が誘引物質の濃度の増加（忌避物質の濃度の減少）に対応している場合、次の回転までの時間が長くなります。細菌のサイズが小さいため、その動きはブラウン運動の影響を強く受けます。その結果、細菌は平均して、有益な物質に近づき、有害な物質から遠ざかる方向にのみ移動します。

考えられる細菌の動きのメカニズムは唯一のものではありません。一部の細菌は鞭毛を1つ持っています。この場合の細菌の動きのバリアントには、その回転と停止のさまざまなモードがあります。ただし、すべての場合において、細菌が正しい方向に移動すると、そのような移動の期間が長くなります。したがって、一般に、細菌の走化性は、遊泳と回転の複雑な組み合わせとして定義できます。これにより、細菌は高濃度の栄養素の場所にとどまり、許容できない濃度の有害物質を回避できます。

検索エンジンの最適化問題の文脈では、細菌の走化性は、細菌による既知の食物資源の使用を最適化し、潜在的により価値のある新しい領域を探索するためのメカニズムとして解釈することもできます。十分な量の細菌の集団は、複雑な時空間構造を形成することができます。これは、細菌集団における構造形成の効果です。この効果は、走化性と他の多くの理由の両方によって引き起こされる可能性があります。

一部の細菌では、そのような構造の形成は、それらの代謝産物の調節特性によって説明されます。同様の効果は、磁気走性（磁場に対する感受性）、生物対流、負の走性（重力方向に対する微生物の優先的な動き）およびその他の現象に基づいて可能です。原則として、細菌は友好的な環境でより長い距離を移動します。十分な食物を得ると、細菌は長くなり、適切な温度が与えられると、真ん中で壊れて、自身の正確なレプリカに変わります。

この現象は、PassinoがBFOに増殖イベントを導入するのに影響を与えました。環境の急激な変化や攻撃により、走化性プロセスが中断され、細菌群が別の場所に移動する可能性があります。これは、領域内のすべての細菌が死ぬか、細菌のグループが環境の新しい部分に分散するときに、実際の細菌集団での除去と分散イベントを表します。さらに、考えられている走化性と増殖の手順は、一般に、多極値目的関数の大域的最大値を見つけるには不十分です。これは、これらの手順では、細菌が見つけたこの関数の局所的最大値を離れることを許可しないためです。除去と分散の手順は、この欠点を克服するように設計されています。自然淘汰（適者生存）により、適応度の低い細菌は破壊され、適応度の高い細菌は自己増殖します。

2.アルゴリズムの説明

BFOの標準バージョンには、次の主要な手順が含まれます。

1. 細菌コロニーの初期化
2. 走化性
3. 群れ
4. 増殖
5. 粛清と削除

      
1.パラメータを初期化します。
細菌は、いくつかの半固体栄養素の中で複雑で安定した時空間パターンを形成することができ、最初に中心に一緒に置かれた環境で生き残ることができます.。さらに、特定の条件下では、細胞間誘引シグナルを分泌して、クラスター化して互いを保護します。
2.走化性
食物を探す細菌の動きの特徴は、2つの方法で決定できます。つまり、遊泳と回転は共に走化性として知られています。細菌は、正しい方向に動くと「遊泳」する、環境が悪化する方向に動くと「回転」すると言われています。

3.群れ
細菌が最も食物の豊富な場所にたどり着くためには、最適な細菌が、検索期間のある時点まで、他の細菌を引き付けて、目的の場所により早く収束するようにすることが望ましいです。.これをおこなうには、最適な細菌からこの検索期間までの各細菌の相対距離に基づいて、元のコスト関数にペナルティ関数が追加されます。最後に、すべての細菌が決定点に結合されると、このペナルティ関数はゼロになります。群れの効果は、細菌が群れに集まり、高密度の群れで同心円状のパターンで移動することです.。

4.増殖
いくつかの走化性段階を通過した細菌の初期セットは、増殖段階に達します。ここで、細菌の最良のセットは2つのグループに分けられます。より健康な半分は、食物を見つける能力が低いために破壊される細菌の残りの半分に置き換えられます。これにより、進化の過程で細菌の個体数が一定になります。

5.排除と分散
進化の過程で、予期せぬ突然の出来事が発生する可能性があります。これにより、スムーズな進化のプロセスが劇的に変化し、多くの細菌が排除されたり、新しい環境に分散したりします。皮肉なことに、一連の細菌の正常な走化性増殖を妨害する代わりに、この未知のイベントは、より新しい細菌のセットを食物がある場所の近くに配置する可能性があります.広い視野から見ると、排除と分散は長距離にわたる個体群の行動の一部です。これを最適化に適用すると、このような並列検索アルゴリズムでよく見られる停滞を軽減するのに役立ちます。

私のBFOの実装は、標準バージョンとは少し異なります。コードの特定のセクションを検討するときは、これらの変更が必要な理由に加えて、違いについて詳しく説明します。一般に、実装の変更は重要であるとは見なされないため、アルゴリズムの名前に「m」（変更されたバージョン）マーカーを割り当てません。実装された変更により結果が改善されたことにのみ言及します。

次に、実装したアルゴリズムとコードについて考えてみましょう。

アルゴリズムの手順:

1.細菌コロニーの初期化
2.細菌の健康状態（適応）の測定
3.複製？
3.1.はい ->レプリケーションの実行
3.2.いいえ -> p.4
4.古い（寿命に達した）？
4.1.はい ->回転を実行（移動ベクトルを変更）
4.2.いいえ ->p.5
5.正しい方向に進んでいる？
5.1.はい ->同じベクトルで移動を続ける
5.2.いいえ ->回転を実行（移動ベクトルを変更）
6.細菌の健康状態（適応度）を測定する
7.停止基準が満たされるまで、p.3から続行する

アルゴリズムの論理スキームを図1に示します。

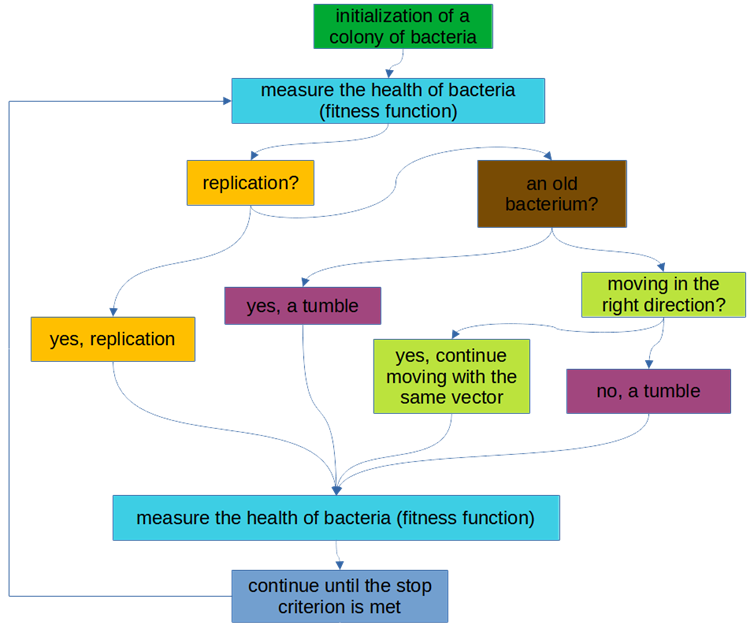
図2：BFOアルゴリズムの論理ブロック図

コードを見てみましょう。

細菌を説明する最良の方法は、座標と動きベクトルの配列を含む構造体です。細菌の現在および以前のヘルス値とライフカウンター。本質的に、ライフカウンターは、寿命に達すると細菌が破壊され、検索空間のランダムな場所に新しい細菌が作成される元のバージョンとは異なり、一方向への連続移動の量を制限するために必要です。ただし、このトピックについては以前の記事で既に触れているため、ランダムな場所に新しいエージェントを作成しても実用的な意味はなく、検索機能が低下するだけです。この場合、最適な解の場所に新しいエージェントを作成するか、現在の場所から移動を続けますが、方向ベクトルを変更することをお勧めします。2番目のオプションは、より良い結果を示しました。

標準バージョンでは、一定の動きベクトルが使用されます。命の数が多いと、これは検索空間内の直線に沿った細菌の移動につながります。この線が極値をうまく通過しない場合、この直線運動のプロセスは無限に発生しますが、ここではカウンターが強制回転の役割を果たし、細菌が生涯にわたって直線運動を回避できるようにします。勾配を持たない領域を持つ関数では、最終的には適合度を改善し始めることができる場所につながります。

//——————————————————————————————————————————————————————————————————————————————
struct S_Bacteria
{
  double c  [];   //coordinates
  double v  [];   //vector
  double f;       //current health
  double fLast;   //previous health
  double lifeCNT; //life counter
};
//——————————————————————————————————————————————————————————————————————————————

BFOアルゴリズムクラスをC_AO_BFOとして宣言しましょう。このクラスには、細菌コロニーの宣言、探索空間の境界、最適解の値、最適解の座標の配列が含まれています。また、アルゴリズムパラメータの定数値を宣言します。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_BFO
{
  //----------------------------------------------------------------------------
  public: S_Bacteria b     []; //bacteria
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: double cB        []; //best coordinates
  public: double fB;           //FF of the best coordinates

  public: void Init (const int    paramsP,         //number of opt. parameters
                     const int    populationSizeP, //population size
                     const double lambdaP,         //lambda
                     const double reproductionP,   //probability of reproduction
                     const int    lifeCounterP);   //life counter

  public: void Swimming   ();
  public: void Evaluation ();

  //----------------------------------------------------------------------------
  private: double NewVector (int paramInd);
  private: S_Bacteria bT []; //bacteria
  private: double v      [];
  private: int    ind    [];
  private: double val    [];
  private: int    populationSize; //population size
  private: int    parameters;     //number of optimized parameters
  private: double lambda;         //lambda
  private: double reproduction;   //probability of reproduction
  private: int    lifeCounter;    //life counter
  private: bool   evaluation;

  private: void   Sorting ();
  private: double SeInDiSp             (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI            (double min, double max);
};
//——————————————————————————————————————————————————————————————————————————————

publicInit()メソッドは、定数変数の初期化、配列サイズの分配、フラグと最適解の値のリセットを目的としています。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BFO::Init (const int    paramsP,         //number of opt. parameters
                     const int    populationSizeP, //population size
                     const double lambdaP,         //lambda
                     const double reproductionP,   //probability of reproduction
                     const int    lifeCounterP)    //life counter
{
  fB = -DBL_MAX;
  evaluation = false;

  parameters      = paramsP;
  populationSize  = populationSizeP;
  lambda          = lambdaP;
  reproduction    = reproductionP;
  lifeCounter     = lifeCounterP;

  ArrayResize (rangeMax,  parameters);
  ArrayResize (rangeMin,  parameters);
  ArrayResize (rangeStep, parameters);
  ArrayResize (v,         parameters);

  ArrayResize (ind,       populationSize);
  ArrayResize (val,       populationSize);

  ArrayResize (b,  populationSize);
  ArrayResize (bT, populationSize);

  for (int i = 0; i < populationSize; i++)
  {
    ArrayResize (b [i].c,  parameters);
    ArrayResize (b [i].v,  parameters);
    b [i].f  = -DBL_MAX;
    b [i].fLast = -DBL_MAX;

    ArrayResize (bT [i].c,  parameters);
    ArrayResize (bT [i].v,  parameters);
  }

  ArrayResize (cB, parameters);
}
//——————————————————————————————————————————————————————————————————————————————

各反復で呼び出す必要がある最初のpublicメソッドのSwimming()（細菌の遊泳）には、アルゴリズムの主要なロジックがすべて含まれています。

void C_AO_BFO::Swimming ()
{}

このメソッドを詳しく考えてみましょう。最初の反復で、評価フラグが「false」に設定されている場合、検索空間全体に細菌を一様分布でランダムに分散させます。この段階では、現在の健康状態（適応度）と以前の健康状態は不明です。DBL_MAX値を対応する変数に割り当てましょう。ランダムに取得された座標が境界を超えていないかを確認し、最適化されたパラメータを変更するステップを適用します。この反復では、NewVector()privateメソッドを使用して、各細菌に個別の変位ベクトルを設定する必要があります（以下で検討）。すべての細菌は、その変化の条件が満たされるまで、同じ個々のベクトルで一様に前方に一直線に遊泳します。

//----------------------------------------------------------------------------
if (!evaluation)
{
  fB = -DBL_MAX;

  for (int s = 0; s < populationSize; s++)
  {
    for (int k = 0; k < parameters; k++)
    {
      b [s].c [k] = RNDfromCI (rangeMin [k], rangeMax [k]);
      b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);

      v [k] = rangeMax [k] - rangeMin [k];

      b [s].v [k] = NewVector (k);

      b [s].f  = -DBL_MAX;
      b [s].fLast = -DBL_MAX;

      b [s].lifeCNT = 0;
    }
  }

  evaluation = true;
}

2回目以降の反復では、寿命に達すると、遊泳、回転、複製、細菌の破壊の操作が実行されます。ロジックの最初の部分は、(パラメータで指定された確率で)増殖の操作です。これは、前の反復で細菌コロニーが健康値の降順で並び替えられたことを意味します。

アルゴリズムでの増殖は重要な機能を実行します。細菌コロニーの「遺伝子プール」を改善することにより、アルゴリズムの収束が加速します。この操作は、細菌を2つの部分に仮想的に分割するものであり、コロニーの最初の、より良い半分だけが分割されます。コロニーの前半は半分になり、元の親バージョンはコロニーの後半に配置されます。親細菌は、そのクローンとは対照的に、同じベクターで動き続けます。クローンはコロニー内のその場所に残り、新しい移動ベクトルが割り当てられます。親とそのクローンは、分割が発生した空間内の点から移動を続けます。

r = RNDfromCI (0.0, 1.0);

//==========================================================================
if (r < reproduction)
{
  int st = populationSize / 2;
  for (int s = 0; s < st; s++)
  {
    //bacterium original--------------------------------------------------
    for (int k = 0; k < parameters; k++)
    {
      b [st + s].v [k] = b [s].v [k];
      b [st + s].c [k] = b [s].c [k] + b [s].v [k];
      b [st + s].c [k] = SeInDiSp (b [st + s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
      b [st + s].fLast = b [s].f;
      b [st + s].lifeCNT++;
    }

    //bacterium clone-------------------------------------------------------
    for (int k = 0; k < parameters; k++)
    {
      b [s].v [k] = NewVector (k);
      b [s].c [k] = b [s].c [k] + b [s].v [k];
      b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
      b [s].fLast = b [s].f;
      b [s].lifeCNT = 0;
    }
  }
}

複製の可能性が実装されていない場合は、細菌が寿命に達したかどうかの確認が実行されます。アルゴリズムの標準バージョンでは、「古い」細菌を破壊し、その代わりに、細菌のリスト内の検索空間内のランダムな場所に新しい細菌を作成する必要があります。一般的なケースでは、増殖と走化性の操作は、多極値適応度関数の最大値を見つけるのに十分ではありません。
これらの手順では、細菌が見つけた極小値を離れることはできません。粛清の手順は、この欠点を克服するように設計されています。ただし、このアルゴリズムや他のアルゴリズムを使用した実験で示されているように、この場合は単純に動きベクトルを変更する方が効率的です。ライフカウンターがリセットされます。カウンターは、一定歩数（ライフ）経過後に移動方向を変えるトリガーです。複製と排除の結果としての細菌の総数は一定のままです。

if (b [s].lifeCNT >= lifeCounter)
{
  for (int k = 0; k < parameters; k++)
  {
    b [s].v [k] = NewVector (k);
    b [s].c [k] = b [s].c [k] + b [s].v [k];
    b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
    b [s].fLast = b [s].f;
    b [s].lifeCNT = 0;
  }
}

寿命が尽きていない場合は、細菌が適応度関数の勾配を改善する方向に動いているかどうかを確認します。つまり、現在の反復と前の反復の2つの健康状態値をチェックします。健康状態が改善した場合、動きベクトルは保持されます。そうでない場合、細菌は回転を実行します（動きベクトルを変更）。

標準バージョンでは、現在の健康状態が以前の健康状態より厳密に「より大きい」ことが確認されますが、私のバージョンでは「より大きいか等しい」が適用されます。研究対象の表面で、適応度関数の勾配がない場合、細菌は1か所で際限なく回転します（健康状態に変化はなく、遊泳に方向がないことを意味します）。この段階で、受信した新しい座標の出力が検索空間の境界を超えているかどうかも確認する必要があります。

else
{
  if (b [s].f >= b [s].fLast)
  {
    for (int k = 0; k < parameters; k++)
    {
      b [s].c [k] = b [s].c [k] + b [s].v [k];
      b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
      b [s].fLast = b [s].f;
      b [s].lifeCNT++;
    }
  }
  else
  {
    for (int k = 0; k < parameters; k++)
    {
      b [s].v [k] = NewVector (k);
      b [s].c [k] = b [s].c [k] + b [s].v [k];
      b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
      b [s].fLast = b [s].f;
      b [s].lifeCNT++;
    }
  }
}

NewVecror()は、動きベクトル（回転）を変更するためのprivateメソッドです。メソッドは座標ごとに適用されます。ここでの考え方は単純です。対応する座標vの検索境界の差に[-1.0;1.0]の範囲の乱数rを掛け、λスケールファクター（アルゴリズムパラメータの1つ）を掛けます。細菌は、寿命が尽きるまで（新しい移動ベクトルを持つ新しい細菌が同じ場所に作成される）、複製中（クローンが新しいベクトルを持つ）、および健康状態の悪化中（新しいより好ましい環境を見つけようとする）、移動ベクトルを変更せずに使用します。 

//——————————————————————————————————————————————————————————————————————————————
double C_AO_BFO::NewVector (int paramInd)
{
  double r = RNDfromCI (-1.0, 1.0);
  return lambda * v [paramInd] * r;
}
//——————————————————————————————————————————————————————————————————————————————

各反復で実行する必要がある2番目のpublic Evaluation()メソッドは、並び替えメソッドを呼び出し、並び替えられたコロニー内の最良の細菌の健康状態を最適な解と比較して、大域的な解の更新を確認します。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BFO::Evaluation ()
{
  Sorting ();

  if (b [0].f > fB)
  {
    fB = b [0].f;
    ArrayCopy (cB, b [0].c, 0, 0, WHOLE_ARRAY);
  }
}
//——————————————————————————————————————————————————————————————————————————————

3.テスト結果

BFOテストスタンドの結果:

2023.01.21 12:52:46.501    Test_AO_BFO (.US500Cash,M1)    C_AO_BFO:50;0.01;0.8;100
2023.01.21 12:52:46.501    Test_AO_BFO (.US500Cash,M1)    =============================
2023.01.21 12:52:48.451    Test_AO_BFO (.US500Cash,M1)    5 Rastrigin's; Func runs 10000 result:72.94540549092933
2023.01.21 12:52:48.451    Test_AO_BFO (.US500Cash,M1)    Score:0.90383
2023.01.21 12:52:51.778    Test_AO_BFO (.US500Cash,M1)    25 Rastrigin's; Func runs 10000 result:54.75744312933767
2023.01.21 12:52:51.778    Test_AO_BFO (.US500Cash,M1)    Score:0.67848
2023.01.21 12:53:21.197    Test_AO_BFO (.US500Cash,M1)    500 Rastrigin's; Func runs 10000 result:40.668487609790404
2023.01.21 12:53:21.197    Test_AO_BFO (.US500Cash,M1)    Score:0.50391
2023.01.21 12:53:21.197    Test_AO_BFO (.US500Cash,M1)    =============================
2023.01.21 12:53:23.211    Test_AO_BFO (.US500Cash,M1)    5 Forest's; Func runs 10000 result:0.8569098398505888
2023.01.21 12:53:23.211    Test_AO_BFO (.US500Cash,M1)    Score:0.48471
2023.01.21 12:53:26.878    Test_AO_BFO (.US500Cash,M1)    25 Forest's; Func runs 10000 result:0.37618151461180294
2023.01.21 12:53:26.878    Test_AO_BFO (.US500Cash,M1)    Score:0.21279
2023.01.21 12:54:22.339    Test_AO_BFO (.US500Cash,M1)    500 Forest's; Func runs 10000 result:0.08748190028975696
2023.01.21 12:54:22.339    Test_AO_BFO (.US500Cash,M1)    Score:0.04948
2023.01.21 12:54:22.339    Test_AO_BFO (.US500Cash,M1)    =============================
2023.01.21 12:54:28.849    Test_AO_BFO (.US500Cash,M1)    5 Megacity's; Func runs 10000 result:4.8
2023.01.21 12:54:28.849    Test_AO_BFO (.US500Cash,M1)    Score:0.40000
2023.01.21 12:54:40.089    Test_AO_BFO (.US500Cash,M1)    25 Megacity's; Func runs 10000 result:2.216
2023.01.21 12:54:40.089    Test_AO_BFO (.US500Cash,M1)    Score:0.18467
2023.01.21 12:55:24.640    Test_AO_BFO (.US500Cash,M1)    500 Megacity's; Func runs 10000 result:0.4232
2023.01.21 12:55:24.640    Test_AO_BFO (.US500Cash,M1)    Score:0.03527

明確な結論を出すのは時期尚早です。最初に、他のテスト参加者との関係で結果を分析する必要があります。

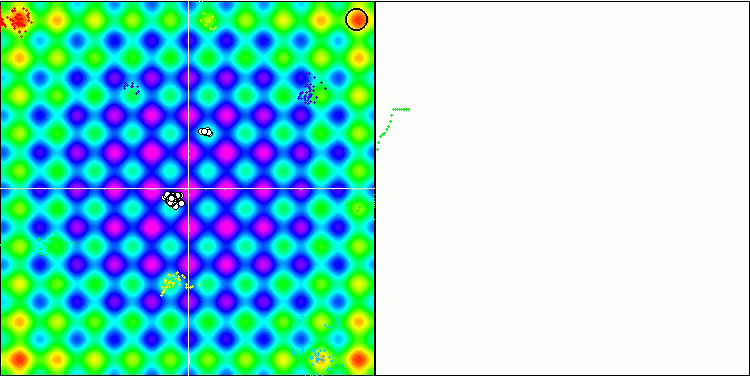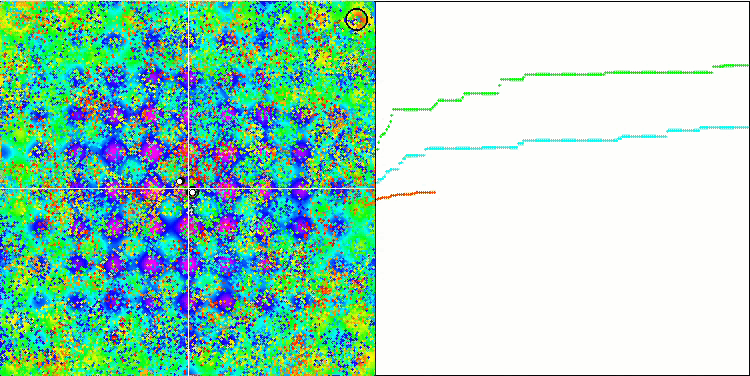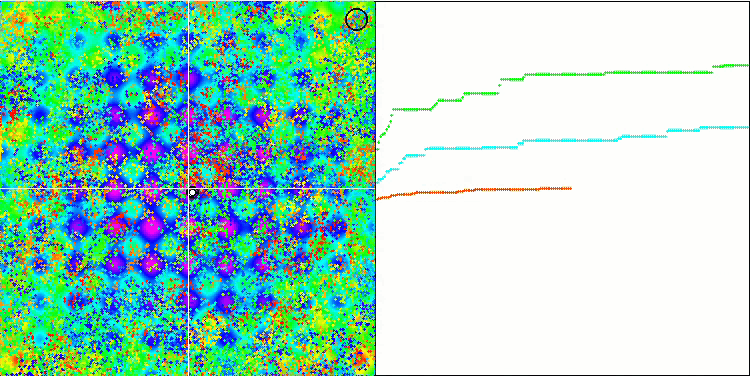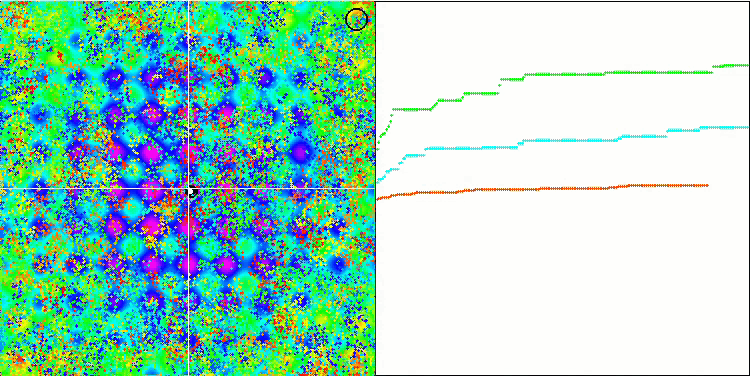
  Rastriginテスト関数のBFO

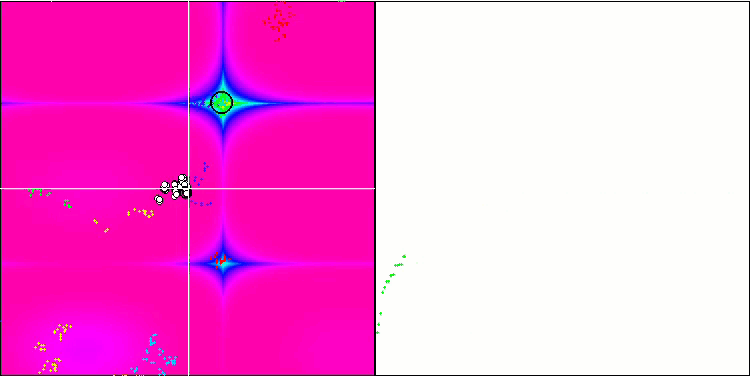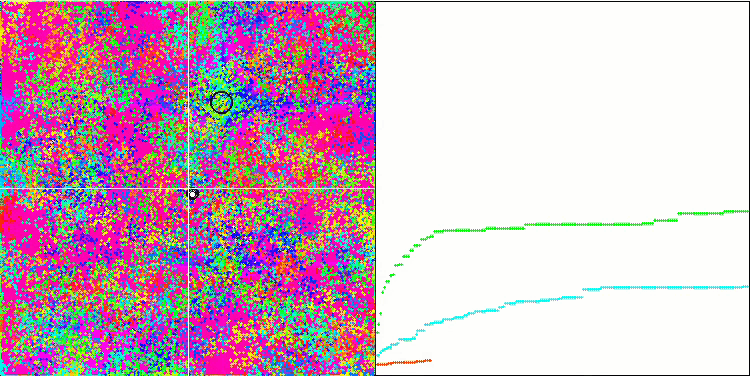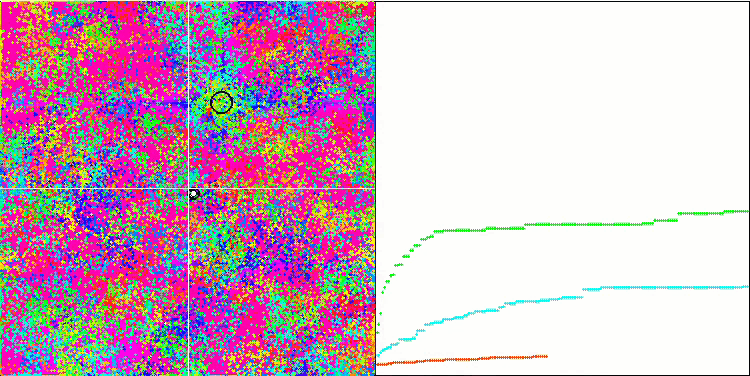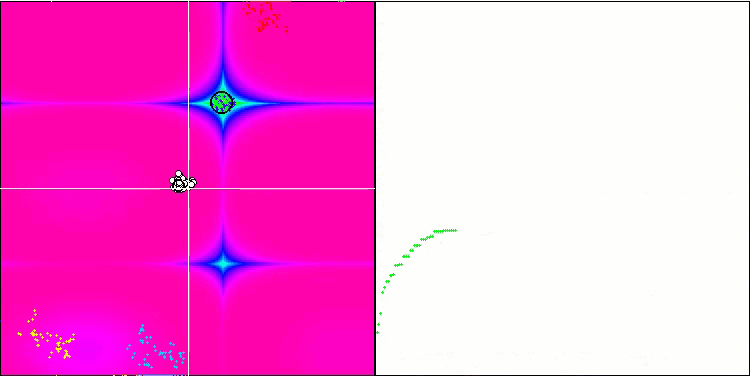
Forestテスト関数のBFO

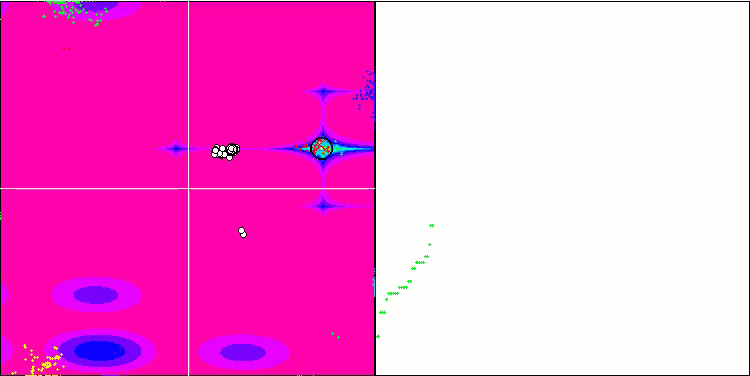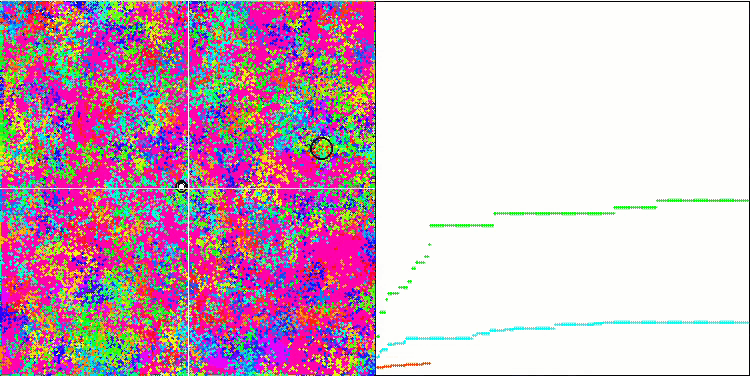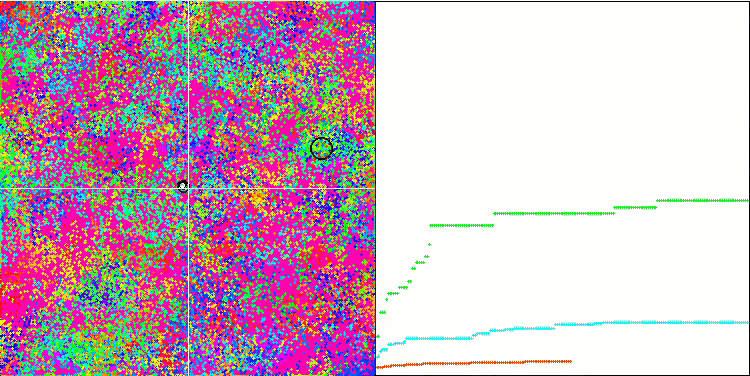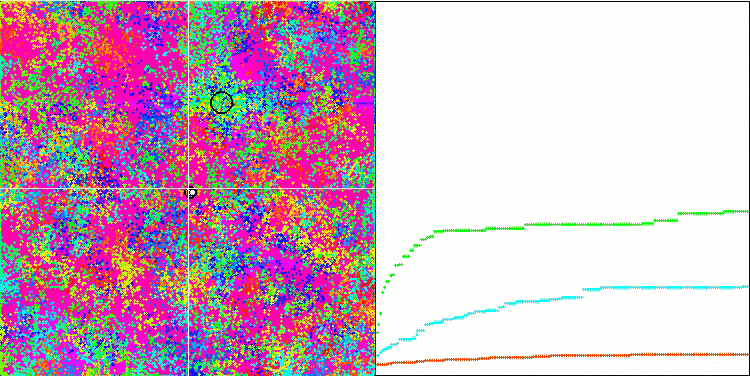
Megacityテスト関数のBFO

テストの視覚化に注目しましょう。アニメーションで、アルゴリズムで「より大きい」記号を「より大きいか等しい」に置き換えるという決定の正しさが確認されました。これにより、細菌はテスト関数の水平セクションで移動し続けることができました。これは、ForestおよびMegacity関数で特に顕著です。細菌は、機能勾配がまったくない場所でも移動しようとします。アルゴリズムにはサブコロニーを形成するための論理的な方法は含まれていませんが、細菌コロニーがいくつかの別個のコロニーに分割され、視覚的に別個の局所極値に分割される能力に注意する必要があります。これは、明確に肯定的な特徴と見なすことができます。一般に、検索空間内の細菌の均一な動きは、どの方向にも急激なジャンプを試みなくても目立ちます。これは、均一な増分運動-走化性によって説明されます。

AO	詳細	Rastrigin			Rastrigin最終	Forest			Forest最終	Megacity(discrete)			Megacity最終	最終結果
		10パラメータ(5F)	50パラメータ(25F)	1000パラメータ（500F）		10パラメータ(5F)	50パラメータ(25F)	1000パラメータ（500F）		10パラメータ(5F)	50パラメータ(25F)	1000パラメータ（500F）
IWO	侵入雑草最適化	1.00000	1.00000	0.33519	2.33519	0.79937	0.46349	0.41071	1.67357	0.75912	0.44903	0.94088	2.14903	100.000
ACOm	蟻コロニー最適化M	0.36118	0.26810	0.17991	0.80919	1.00000	1.00000	1.00000	3.00000	1.00000	1.00000	0.10959	2.10959	95.996
COAm	カッコウ最適化アルゴリズムM	0.96423	0.69756	0.28892	1.95071	0.64504	0.34034	0.21362	1.19900	0.67153	0.34273	0.45422	1.46848	74.204
FAm	ホタルアルゴリズムM	0.62430	0.50653	0.18102	1.31185	0.55408	0.42299	0.64360	1.62067	0.21167	0.28416	1.00000	1.49583	71.024
BA	コウモリアルゴリズム	0.42290	0.95047	1.00000	2.37337	0.17768	0.17477	0.33595	0.68840	0.15329	0.07158	0.46287	0.68774	59.650
ABC	人工蜂コロニー	0.81573	0.48767	0.22588	1.52928	0.58850	0.21455	0.17249	0.97554	0.47444	0.26681	0.35941	1.10066	57.237
BFO	細菌採餌の最適化	0.70129	0.46155	0.11627	1.27911	0.41251	0.26623	0.26695	0.94569	0.42336	0.34491	0.50973	1.27800	55.516
FSS	魚群検索	0.48850	0.37769	0.11006	0.97625	0.07806	0.05013	0.08423	0.21242	0.00000	0.01084	0.18998	0.20082	20.109
PSO	粒子群最適化	0.21339	0.12224	0.05966	0.39529	0.15345	0.10486	0.28099	0.53930	0.08028	0.02385	0.00000	0.10413	14.232
RND	ランダム	0.17559	0.14524	0.07011	0.39094	0.08623	0.04810	0.06094	0.19527	0.00000	0.00000	0.08904	0.08904	8.142
GWO	灰色オオカミオプティマイザ	0.00000	0.00000	0.00000	0.00000	0.00000	0.00000	0.00000	0.00000	0.18977	0.04119	0.01802	0.24898	1.000

テスト結果を分析する時が来ました。BFOは評価表の中央に位置し、現在参加しているアルゴリズムのリストでは総合スコアが55をわずかに上回っています。結果は印象的ではありませんが、悪くもありません。特に、10変数のRastrigin関数で良い結果が得られました。変数が50個と1000個の場合、結果は著しく悪化します。また、アルゴリズムはForest関数ではうまく機能しませんでした。Megacity離散関数の比較的良好な動作は驚くべきことです。なぜなら、アルゴリズムにはそのような関数を処理するためのメカニズムがないからです。さらに、他のアルゴリズムと比較して優れたスケーラビリティがあります（1000 Megacityパラメータでテスト）。

BFOは幅広い可能性を秘めた科学分野です。最適化のパフォーマンスを向上させるためにモデル化できる一般的な細菌採餌および動物採餌の多くの側面があります。BFOアルゴリズムの場合、多くのパラメータがあり、パフォーマンスが向上する可能性があるため、制御パラメータの自動適応が特に重要になる可能性があります。これが追加の実験の理由です。

BFOには、初期化中およびパラメータの選択中の座標の初期値に対する感度の低さ、優れた信頼性、ロジックの単純さ、実装の容易さ、並列化および大域的検索の可能性など、多くの利点があります。したがって、BFOアルゴリズムは、さまざまな最適化問題を解決するために使用されます。ただし、BFOには、収束が遅い、場合によっては局所的な最適値を超えることができない、固定されたステップ長など、多くの欠点もあります。BFOはメタヒューリスティックです。つまり、アルゴリズムの変更を開発するために使用できる単なる概念的なフレームワークです。ここで紹介したBFOのバージョンは、多くの可能性のうちの1つにすぎず、このトピックに関する締めくくりではなく、実験の出発点と見なされるべきです。

アルゴリズムのテスト結果のヒストグラムを以下に示します。

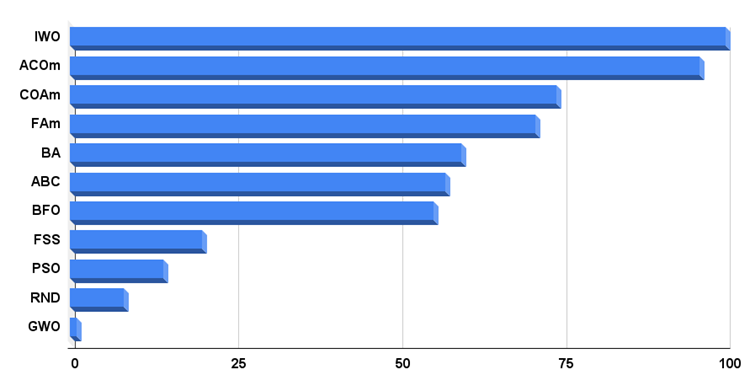
図3：テストアルゴリズムの最終結果のヒストグラム

細菌採餌最適化(BFO)アルゴリズムの特性に関する結論は、次の通りです。

賛成：
1.高速
2.シンプルなロジック
3.低速ではあるが、すべての反復を通じて収束する

反対：
1.収束が遅い
2.極値を終了する方法がない