
Black Hole Algorithmus (BHA)
Inhalt
Einführung
Der Algorithmus Black Hole (BHA, Schwarze Löcher) bietet eine einzigartige Perspektive auf das Optimierungsproblem. Der 2013 von A. Hatamlou entwickelte Algorithmus wurde von den geheimnisvollsten und mächtigsten Objekten des Universums inspiriert: den schwarzen Löchern. So wie schwarze Löcher mit ihrem Gravitationsfeld alles um sich herum anziehen, versucht der Algorithmus, die besten Lösungen an sich zu ziehen und die weniger erfolgreichen abzuschneiden.
Stellen Sie sich einen riesigen Raum vor, der mit vielen Entscheidungen gefüllt ist, die alle darum kämpfen, in dieser rauen Umgebung zu überleben. Im Zentrum dieses Chaos stehen schwarze Löcher – Lösungen mit den höchsten Qualitätsbewertungen, die die Schwerkraft haben. Der Algorithmus für schwarze Löcher entscheidet bei jedem Schritt, welche Sterne von schwarzen Löchern verschluckt werden und welche ihren Weg auf der Suche nach günstigeren Bedingungen fortsetzen werden.
Mit Elementen des Zufalls erkundet der BHA-Algorithmus unerforschte Gebiete und versucht, lokale Minima zu vermeiden. Dies macht sie zu einem leistungsstarken Werkzeug für die Lösung komplexer Probleme, von der Funktionsoptimierung über kombinatorische Probleme bis hin zur Abstimmung von Hyperparametern beim maschinellen Lernen. In diesem Artikel werfen wir einen detaillierten Blick auf den Black-Hole-Algorithmus, seine Funktionsweise sowie seine Vor- und Nachteile und eröffnen damit eine Welt, in der Wissenschaft und Kunst der Optimierung ineinandergreifen.
Implementierung des Algorithmus
Der BHA-Algorithmus nutzt Ideen darüber, wie Sterne mit einem schwarzen Loch interagieren, um optimale Lösungen in einem bestimmten Suchraum zu finden. Der Algorithmus beginnt mit der Initialisierung, bei der eine anfängliche Population von zufälligen „Sternen“ erstellt wird, von denen jeder eine potenzielle Lösung für das Optimierungsproblem darstellt. Diese Sterne befinden sich in einem durch Ober- und Untergrenzen begrenzten Suchraum. Während der Iterationen des Algorithmus wird bei jedem Schritt die beste Lösung ausgewählt, die als „schwarzes Loch“ bezeichnet wird. Die verbleibenden Sterne tendieren dazu, sich dem Schwarzen Loch mit Hilfe der folgenden Gleichung zu nähern:
Xi(t+1) = Xi(t) + rand × (XBH - Xi(t))
wobei:
- Xi(t) – aktuelle Position des Sterns i
- XBH – Position des Schwarzen Lochs
- rand – Zufallszahl von 0 bis 1
Ein wichtiges Element des Algorithmus ist der mithilfe der Gleichung berechnete Ereignishorizont:
R = fitBH / Σfiti
Sterne, die diesen Horizont überschreiten, werden vom Schwarzen Loch „verschluckt“ und durch neue, zufällige Sterne ersetzt. Dieser Mechanismus erhält die Populationsvielfalt und fördert die weitere Erforschung des Weltraums.
Der Black-Hole-Algorithmus hat mehrere wesentliche Merkmale. Es hat eine einfache Struktur und außer der Populationsgröße keine weiteren Parameter, sodass es leicht zu verwenden ist. Er erfordert keine Abstimmung, was bei anderen Optimierungsalgorithmen kaum der Fall ist.
Der BHA-Algorithmus ähnelt anderen populationsbasierten Algorithmen, d. h. der erste Schritt der Optimierung besteht darin, eine Anfangspopulation von Zufallslösungen (Anfangssterne) zu erstellen und eine Zielfunktion zu berechnen, um die Lösungswerte zu schätzen. Die beste Lösung in jeder Iteration wird wie ein schwarzes Loch ausgewählt, das dann beginnt, andere Kandidatenlösungen um sich herum anzuziehen. Sie werden Sterne genannt. Wenn sich andere Lösungsvorschläge der besten Lösung annähern, werden sie von der besten Lösung „absorbiert“.
Die folgende Abbildung zeigt eine Demonstration der Suchstrategie des BHA-Algorithmus in Aktion. Alle Sterne jenseits des Ereignishorizonts des Schwarzen Lochs werden in Richtung seines Zentrums bewegt, und Sterne, die den Horizont überschreiten, werden absorbiert – im Grunde wird die Sternenmaterie in eine neue Region des Suchraums teleportiert.
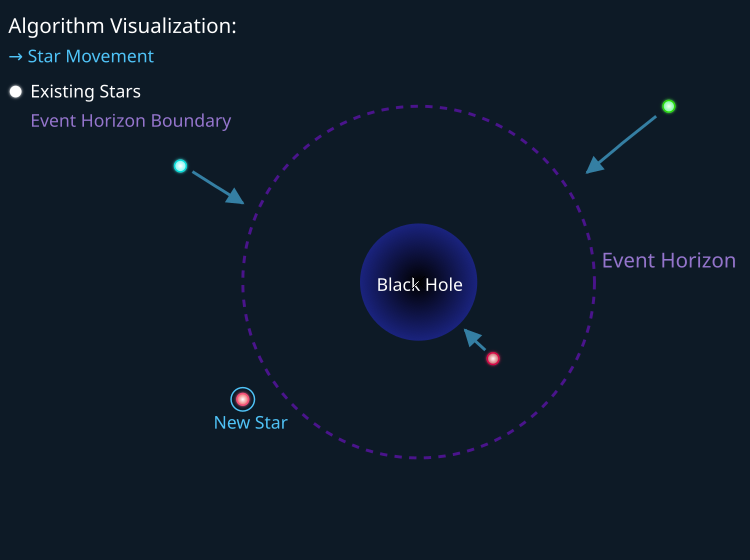
Abbildung 1. BHA-Suchstrategie. Der grüne und der blaue Stern bewegen sich in Richtung des Zentrums des schwarzen Lochs, und der rote Stern teleportiert zum Punkt „New Star“ (neuer Stern).
Schreiben wir einen Pseudocode für den Black-Hole-Algorithmus (BHA)
N – Anzahl der Sterne (Populationsgröße)
tmax – maximale Anzahl von Iterationen
// Initialisierung
1. Erstelle Ausgangspositionen für N Sterne:
Für i = 1 bis N:
Xi = LB + Rand × (UB – LB)
2. t = 1
// Hauptschleife
3. So lange t ≤ tmax:
// Berechnung des Zielfunktionswerts für jeden Stern
4. Für jedes Xi berechne fiti
// Definieren eines schwarzen Lochs
5. Bestimme XBH als den Stern mit dem besten Fiti-Wert
fitBH = bester Fiti-Wert
// Aktualisierung der Sternpositionen
6. Für jeden Stern Xi:
Xi(t+1) = Xi(t) + rand × (XBH - Xi(t))
// Berechnen des Radius‘ des Ereignishorizonts
7. R = fitBH / ∑(i=1 to N) fiti
// Überprüfung der Sternabsorption
8. Für jeden Stern Xi:
Wenn der Abstand zwischen Xi und XBH < R ist:
Erzeuge eine neue Position für Xi nach dem Zufallsprinzip
Xi = LB + Rand × (UB – LB)
9. t = t + 1
// Rückgabe der besten gefundenen Lösung
Rückgabe XBH
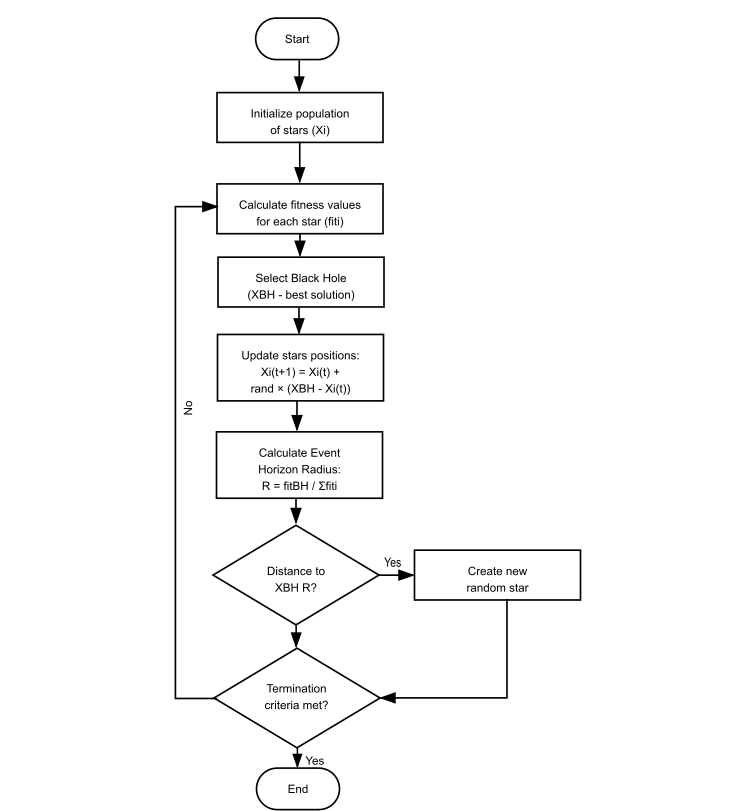
Abbildung 2. Logische Struktur der Funktionsweise des BHA-Algorithmus
Definition der Klasse C_AO_BHA (Black Hole Algorithm), die ein Abkömmling der Basisklasse C_AO ist, Klassenstruktur:
Konstruktor und Destruktor:
- Der Konstruktor initialisiert die grundlegenden Parameter des Algorithmus.
- SetParams () – setzt die Populationsgröße aus dem Parameter-Array
- Init () – initialisiert den Suchraum mit den angegebenen Grenzen und Schritten
- Moving () – implementiert die Bewegung von Sternen in Richtung eines Schwarzen Lochs
- Revision () – aktualisiert die beste gefundene Lösung (schwarzes Loch)
- blackHoleIndex – speichert den Index der besten Lösung in der Population
- rangeMinP [] – Mindestwerte für jede Koordinate
- rangeMaxP [] – Höchstwerte für jede Koordinate
- rangeStepP [] – Diskretisierungsschritt für jede Koordinate
- epochsP – Anzahl der Iterationen des Algorithmus
Dies ist ein Grundgerüst für die Implementierung des Black-Hole-Algorithmus, wobei die Hauptlogik in den Methoden Moving() und Revision() implementiert wird.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_BHA : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_BHA () { } C_AO_BHA () { ao_name = "BHA"; ao_desc = "Black Hole Algorithm"; ao_link = "https://www.mql5.com/en/articles/16655"; popSize = 50; // Population size ArrayResize (params, 1); // Initialize parameters params [0].name = "popSize"; params [0].val = popSize; } void SetParams () // Method for setting parameters { popSize = (int)params [0].val; } bool Init (const double &rangeMinP [], // Minimum search range const double &rangeMaxP [], // Maximum search range const double &rangeStepP [], // Search step const int epochsP = 0); // Number of epochs void Moving (); // Moving method void Revision (); // Revision method private: //------------------------------------------------------------------- int blackHoleIndex; // Black hole index (best solution) };Die Init-Methode ist einfach und hat die folgende Aufgabe:
- Initialisierung des Algorithmus
- Aufruf von StandardInit zum Einstellen von Suchbereichen und Schritten
- Setzen des Anfangsindex des schwarzen Lochs auf 0
- Rückgabe von „true“ bei erfolgreicher Initialisierung, „false“ im Falle eines Fehlers.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_BHA::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; blackHoleIndex = 0; // Initialize black hole index return true; } //——————————————————————————————————————————————————————————————————————————————
Die Methode Moving besteht aus mehreren Hauptblöcken:
a) Primäre Initialisierung (wenn Revision = false):
- Erstellen einer Anfangspopulation von Sternen mit zufälligen Positionen
- Positionen werden in einem bestimmten Bereich erzeugt und auf ein diskretes Raster reduziert
- Revisionsflag auf true setzen
b) Grundlegender Algorithmus (wenn Revision = true):
- Berechnen der Summe der Fitnessfunktionswerte aller Sterne
- Berechnen des Radius‘ des Ereignishorizonts: R = fitBH / Σfiti
c) Aktualisierung der Sternpositionen:
- Für jeden Stern (außer einem schwarzen Loch):
- Berechne den euklidischen Abstand zu einem Schwarzen Loch
- Wenn der Abstand kleiner als der Horizontradius ist:
- Erstelle einen neuen Zufallsstern.
- sonst:
- Aktualisiere die Position anhand der Gleichung: Xi(t+1) = Xi(t) + rand × (XBH - Xi(t))
- Bringe die neue Position in den akzeptablen Bereich und das diskrete Raster.
Alle Berechnungen werden unter Berücksichtigung der Grenzen des Suchraums und des Diskretisierungsschritts durchgeführt.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BHA::Moving () { // Initial random positioning on first run if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { // Generate a random position within the allowed range a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); // Convert to discrete values according to step a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } // Calculate the sum of fitness values for the radius of the event horizon double sumFitness = 0.0; for (int i = 0; i < popSize; i++) { sumFitness += a [i].f; } // Calculate the radius of the event horizon // R = fitBH / Σfiti double eventHorizonRadius = a [blackHoleIndex].f / sumFitness; // Update star positions for (int i = 0; i < popSize; i++) { // Skip the black hole if (i == blackHoleIndex) continue; // Calculate the distance to the black hole double distance = 0.0; for (int c = 0; c < coords; c++) { double diff = a [blackHoleIndex].c [c] - a [i].c [c]; distance += diff * diff; } distance = sqrt (distance); // Check for event horizon crossing if (distance < eventHorizonRadius) { // Star is consumed - create a new random star for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } else { // Update the star position using the equation: // Xi(t+1) = Xi(t) + rand × (XBH - Xi(t)) for (int c = 0; c < coords; c++) { double rnd = u.RNDfromCI (0.0, 1.0); double newPosition = a [i].c [c] + rnd * (a [blackHoleIndex].c [c] - a [i].c [c]); // Check and correct the boundaries newPosition = u.SeInDiSp (newPosition, rangeMin [c], rangeMax [c], rangeStep [c]); a [i].c [c] = newPosition; } } } } //——————————————————————————————————————————————————————————————————————————————
Die Methode Revision erfüllt die folgenden Funktionen:
Finden der besten Lösung:
- Iteriere durch alle Sterne in der Grundgesamtheit
- Vergleiche die Fitnesswerte eines jeden Sterns (a[i].f) mit dem aktuellen Bestwert (fB)
- Wenn die beste Lösung gefunden wurde:
- Aktualisiere den besten Wert der Fitnessfunktion (fB)
- Sichere den Index des schwarzen Lochs (blackHoleIndex)
- Kopiere die Koordinaten der besten Lösung in das Feld cB
Das Hauptziel der Methode ist es, die beste gefundene Lösung (schwarzes Loch) während der Optimierung zu verfolgen und zu speichern.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BHA::Revision () { // Find the best solution (black hole) for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; blackHoleIndex = i; ArrayCopy (cB, a [i].c, 0, 0, WHOLE_ARRAY); } } } //——————————————————————————————————————————————————————————————————————————————
Die Prüfung des BHA-Algorithmus ergab die folgenden Ergebnisse:
BHA|Black Hole Algorithm|50.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.6833993073000924
25 Hilly's; Func runs: 10000; result: 0.47275633991339616
500 Hilly's; Func runs: 10000; result: 0.2782882943201518
=============================
5 Forest's; Func runs: 10000; result: 0.6821776337288085
25 Forest's; Func runs: 10000; result: 0.3878950941651221
500 Forest's; Func runs: 10000; result: 0.20702263338385946
=============================
5 Megacity's; Func runs: 10000; result: 0.39461538461538465
25 Megacity's; Func runs: 10000; result: 0.20076923076923076
500 Megacity's; Func runs: 10000; result: 0.1076846153846164
=============================
All score: 3.41461 (37.94%)
Die Ergebnisse sind unterdurchschnittlich, wie die Tabelle zeigt. Der offensichtliche Vorteil dieses Algorithmus ist jedoch, dass er außer der Populationsgröße keine weiteren Parameter hat, sodass die Ergebnisse als recht zufriedenstellend angesehen werden können. Während des Betriebs fiel mir sofort auf, dass er in lokalen Optima feststeckte, die durch einen Mangel an Vielfalt bei den Populationsentscheidungen verursacht wurden. Außerdem müssen für jeden Stern ressourcenintensive Berechnungen des euklidischen Abstands zum Schwarzen Loch durchgeführt werden. Dieser Umstand veranlasste uns, über Möglichkeiten nachzudenken, wie wir die bestehenden Unzulänglichkeiten beheben können.
Im ursprünglichen Algorithmus bewegen sich bei einer Iteration die Sterne, während das Schwarze Loch an seinem Platz bleibt, obwohl alle Objekte im Raum in Bewegung sind. Ich beschloss, einige Änderungen vorzunehmen und das Schwarze Loch in Abständen zu implementieren, die durch eine Gauß-Verteilung relativ zu seinem Zentrum bestimmt werden, und auch eine Potenzgesetz-Verteilung zu versuchen. Ziel dieser Anpassung war es, die Konvergenzgenauigkeit zu verbessern und gleichzeitig die Fähigkeit zu erhalten, neue Regionen des Lösungsraums zu erkunden. Trotz dieser Änderungen konnten die Ergebnisse jedoch nicht verbessert werden. Dies könnte darauf hindeuten, dass die stabile Position des schwarzen Lochs (speziell für eine bestimmte Suchstrategie) für die Effizienz des Algorithmus wichtig ist, um sicherzustellen, dass sich die Sterne auf die vielversprechendsten Gebiete konzentrieren. Es könnte sich lohnen, andere Ansätze oder Kombinationen von Methoden in Betracht zu ziehen, um bessere Ergebnisse zu erzielen.
So entstand die Idee, von der Berechnung euklidischer Entfernungen abzurücken und stattdessen den Ereignishorizont eines Schwarzen Lochs als Maß für die wahrscheinliche Absorption zu verwenden, anstatt die tatsächliche Durchquerung des Horizonts. Anstatt die Bewegung auf den gesamten Stern anzuwenden, wenden Sie diese Wahrscheinlichkeit separat auf jede Koordinate an.
Auf der Grundlage der obigen Überlegungen werden wir daher eine neue Version der Methode „Moving“ schreiben. Die Änderungen betrafen die Methode zur Berechnung des Ereignishorizonts, bei der der durchschnittliche Fitnesswert für die Population nun auf den Abstand zwischen der minimalen und der maximalen Fitness für die Population normiert wird. Nun ist der Ereignishorizont die Wahrscheinlichkeit der Absorption an den einzelnen Koordinaten der Sterne; wenn die Absorption nicht auftritt, führen wir die übliche Bewegung in Richtung des Zentrums des galaktischen, schwarzen Monsters gemäß der Gleichung des Autors durch.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BHAm::Moving () { // Initial random positioning on first run if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { // Generate a random position within the allowed range a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); // Convert to discrete values according to step a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- // Calculate the average fitness values for the event horizon radius double aveFit = 0.0; double maxFit = fB; double minFit = a [0].f; for (int i = 0; i < popSize; i++) { aveFit += a [i].f; if (a [i].f < minFit) minFit = a [i].f; } aveFit /= popSize; // Calculate the radius of the event horizon double eventHorizonRadius = (aveFit - minFit) / (maxFit - minFit); // Update star positions for (int i = 0; i < popSize; i++) { // Skip the black hole if (i == blackHoleIndex) continue; for (int c = 0; c < coords; c++) { if (u.RNDprobab () < eventHorizonRadius * 0.01) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } else { double rnd = u.RNDfromCI (0.0, 1.0); double newPosition = a [i].c [c] + rnd * (a [blackHoleIndex].c [c] - a [i].c [c]); // Check and correct the boundaries newPosition = u.SeInDiSp (newPosition, rangeMin [c], rangeMax [c], rangeStep [c]); a [i].c [c] = newPosition; } } } } //——————————————————————————————————————————————————————————————————————————————
Analysieren wir die wichtigsten Unterschiede zwischen den beiden Versionen des Algorithmus, beginnend mit der Berechnung von dem Radius des Ereignishorizonts. In der ersten Version (BHA) ist der Radius als das Verhältnis der besten Lösung zur Summe aller Lösungen definiert, was dazu führt, dass der Radius bei einer großen Population sehr klein wird und stark von den absoluten Werten der Fitnessfunktion abhängt. In der zweiten Version (BHAm) ist der Radius im Bereich [0,1] normalisiert, was es ermöglicht, die relative Position des Mittelwerts zwischen dem Minimum und dem Maximum zu zeigen, wobei die Unabhängigkeit von der Populationsgröße und den absoluten Werten der Fitnessfunktion erhalten bleibt.
Schauen wir uns nun den Mechanismus der Sternabsorption an. Die erste Version des Algorithmus prüft den euklidischen Abstand zum Schwarzen Loch, und wenn er absorbiert wird, wird der Stern vollständig durch einen neuen an einem zufälligen Ort ersetzt, was zu dramatischeren Veränderungen in der Population führt. Bei der zweiten Version wird die probabilistische Absorption für jede Koordinate einzeln verwendet, was zu gleichmäßigeren Veränderungen in der Grundgesamtheit führt. Hier verringert das Verhältnis von 0,01 die Wahrscheinlichkeit radikaler Veränderungen.
In Bezug auf die Konsequenzen zeigt die erste Version eine aggressivere Ausnutzung des Suchraums, was zu einer schnellen Konvergenz in lokalen Regionen führt, aber auch das Risiko einer verfrühten Konvergenz erhöht und vielversprechende Regionen aufgrund einer vollständigen Ersetzung von Lösungen verpassen kann. Die zweite Version bietet dagegen eine entspanntere Explorationsstrategie, die ein besseres Gleichgewicht zwischen Exploration und Ausbeutung, ein geringeres Risiko, in lokalen Optima stecken zu bleiben, und eine langsamere, aber potenziell zuverlässigere Konvergenz sowie eine bessere Fähigkeit zur Diversifizierung der Population ermöglicht.
Zusammenfassend lässt sich sagen, dass die erste Version besser für Probleme mit klar definierten Optima geeignet ist, wenn schnelle Konvergenz und kleine Dimensionen des Suchraums erforderlich sind, während die zweite Version effektiver für komplexe, multiextreme Probleme ist, bei denen die Zuverlässigkeit der Suche nach dem globalen Optimum wichtig ist, sowie für hochdimensionale Probleme, die eine gründlichere Erkundung des Suchraums erfordern.
Ich möchte meine Gedanken zur Visualisierung der Arbeit von Algorithmen mit Ihnen teilen. Die Visualisierung bietet eine einzigartige Möglichkeit, ein tieferes Verständnis für die internen Prozesse in Algorithmen zu erlangen und deren verborgene Mechanismen aufzudecken. Mit bestimmten Einstellungen können wir beobachten, wie sich chaotische Bilder allmählich in strukturierte Muster verwandeln. Dieser Prozess demonstriert nicht nur die technischen Aspekte der Funktionsweise des Algorithmus, sondern eröffnet auch neue Ideen und Ansätze für seine Optimierung.
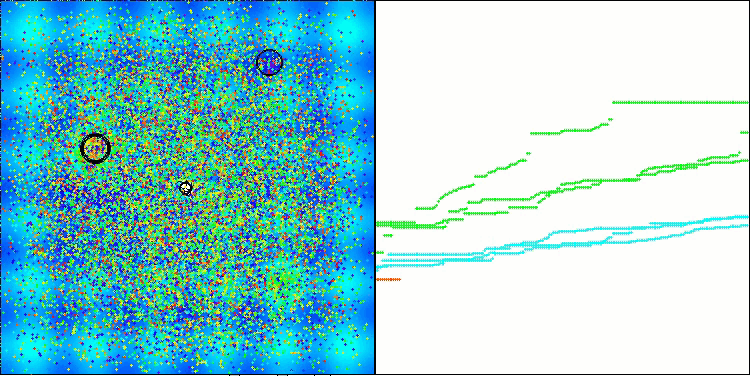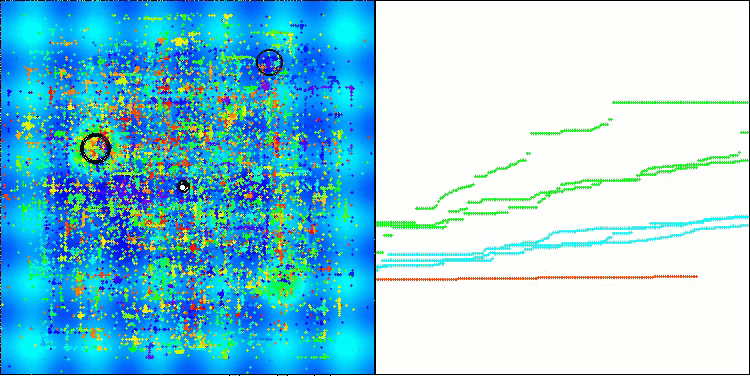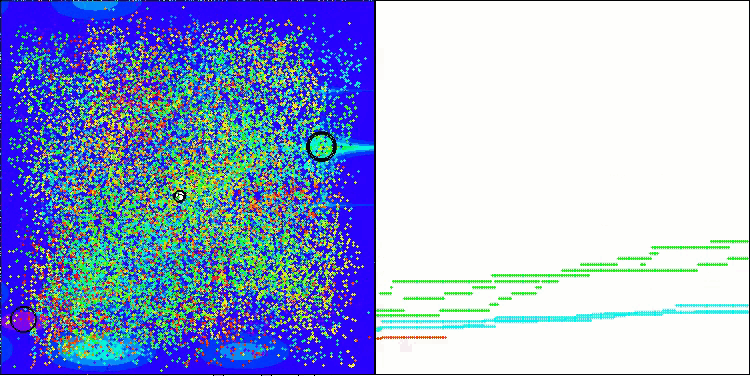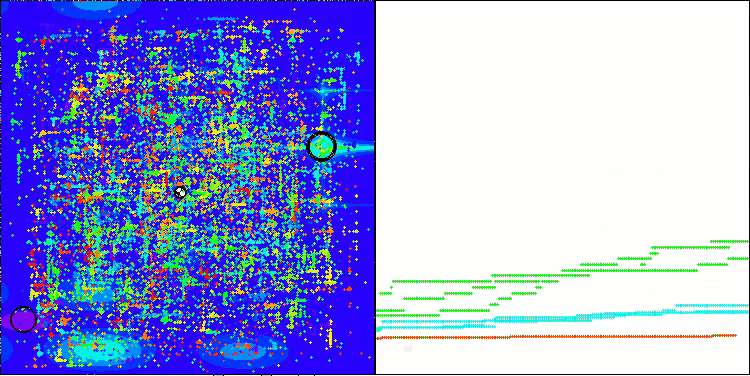
Das Beispiel des BHAm-Algorithmus zur Erzeugung einer zufälligen Komponente der Sternbewegung im Bereich [0,0;0,1]
Es ist wichtig zu erwähnen, dass die Visualisierung es uns nicht nur ermöglicht, die Effizienz von Algorithmen zu bewerten, sondern auch Muster zu erkennen, die bei der herkömmlichen Datenanalyse möglicherweise nicht offensichtlich sind. Dies trägt dazu bei, ein tieferes Verständnis für ihre Arbeit zu entwickeln und kann zu neuen Lösungen und Innovationen inspirieren. So wird die Visualisierung zu einem leistungsstarken Werkzeug, das Wissenschaft und Kreativität miteinander verbindet und neue Horizonte für die Erforschung und das Verständnis komplexer Prozesse eröffnet.
Testergebnisse
Ergebnisse der modifizierten Version des BHAm-Algorithmus:
BHAm|Black Hole Algorithm M|50.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.752359491007831
25 Hilly's; Func runs: 10000; result: 0.7667459889455067
500 Hilly's; Func runs: 10000; result: 0.34582657277589457
=============================
5 Forest's; Func runs: 10000; result: 0.9359337849703726
25 Forest's; Func runs: 10000; result: 0.801524710041611
500 Forest's; Func runs: 10000; result: 0.2717683112397725
=============================
5 Megacity's; Func runs: 10000; result: 0.6507692307692307
25 Megacity's; Func runs: 10000; result: 0.5164615384615385
500 Megacity's; Func runs: 10000; result: 0.154715384615386
=============================
All score: 5.19611 (57.73%)
Aus den Testergebnissen geht hervor, dass der BHAm-Algorithmus nicht nur im Vergleich zur ursprünglichen Version, sondern auch in der Tabelle insgesamt beeindruckende Ergebnisse erzielt. Die Visualisierung zeigt, dass die neue Version mit dem Postfix „m“ tatsächlich frei von den charakteristischen Mängeln des Originals ist: Die Tendenz zum Steckenbleiben ist praktisch eliminiert, die Genauigkeit der Konvergenz ist deutlich erhöht und die Streuung der Ergebnisse ist reduziert. Gleichzeitig bleibt die „Familieneigenschaft“ des ursprünglichen Algorithmus erhalten: die Bildung eigentümlicher Klumpen von Sternen im Raum und die Anziehung zu einem bestimmten Attraktor im Lösungsraum.
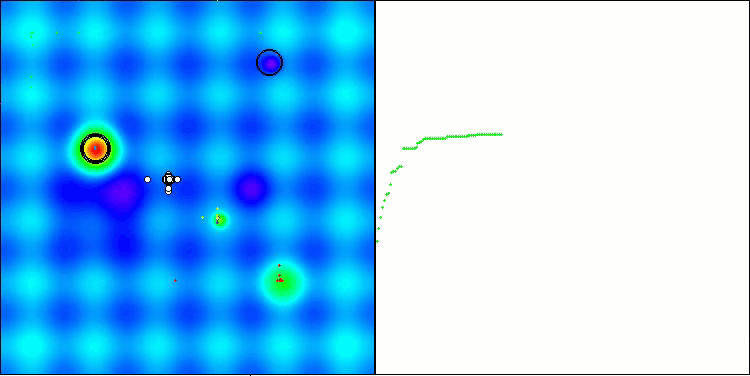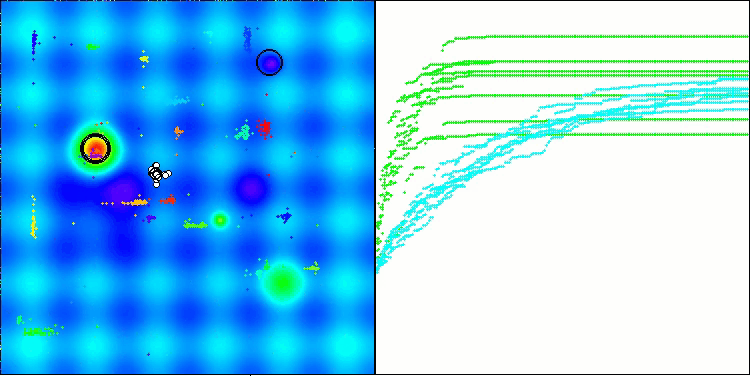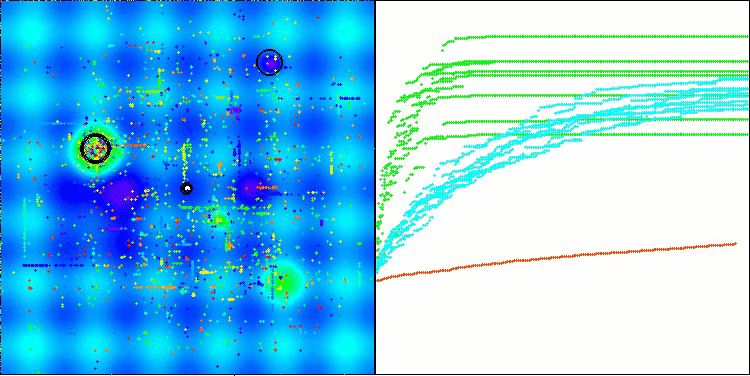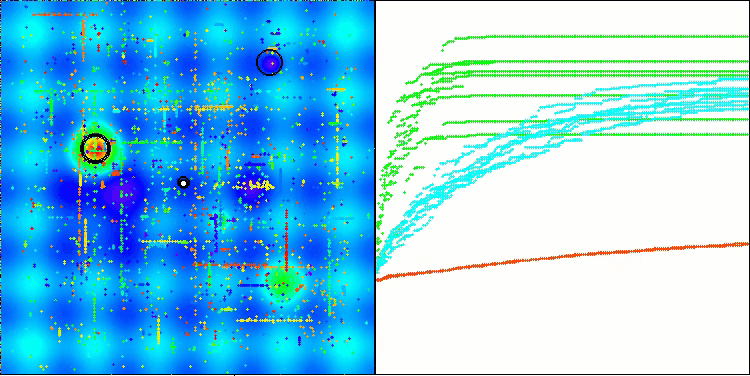
BHAm mit der Testfunktion Hilly
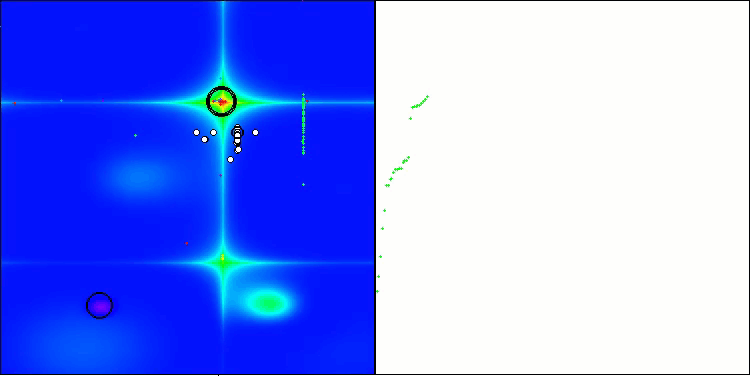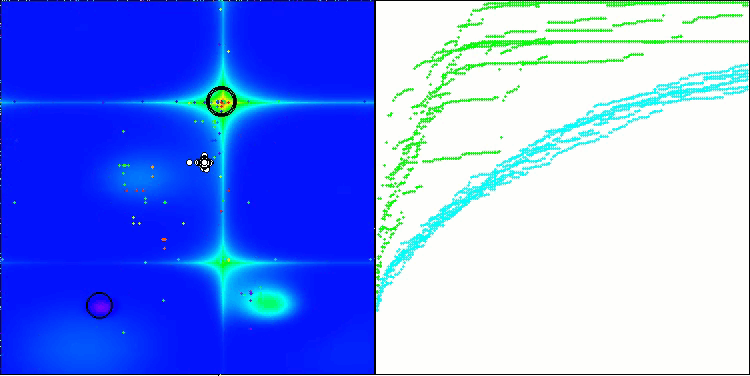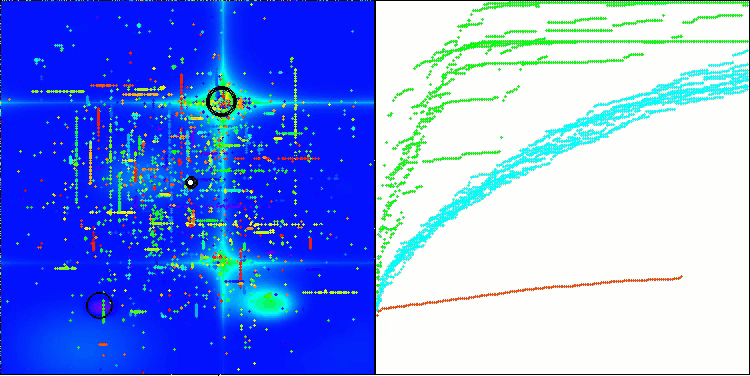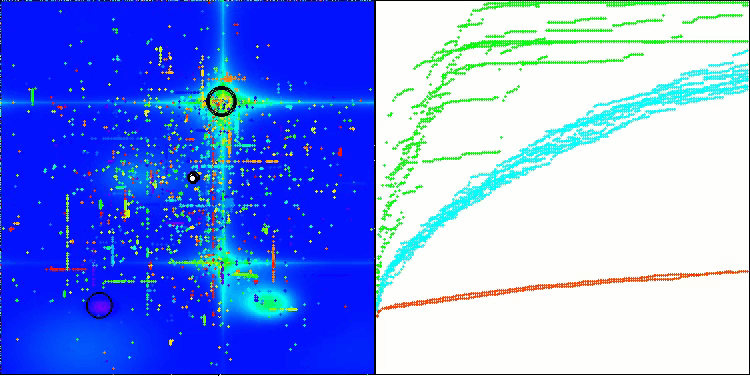
BHAm mit der Testfunktion Forest
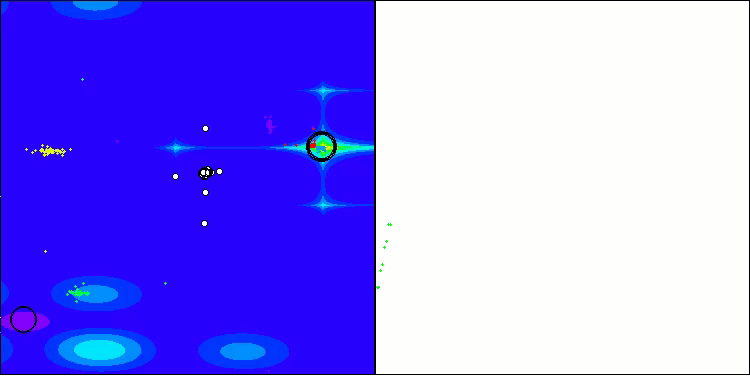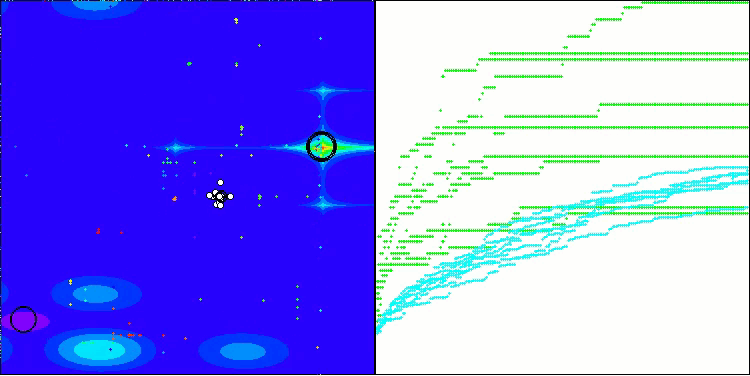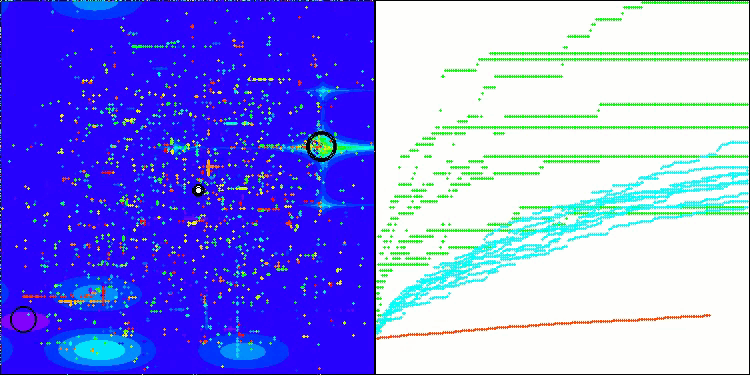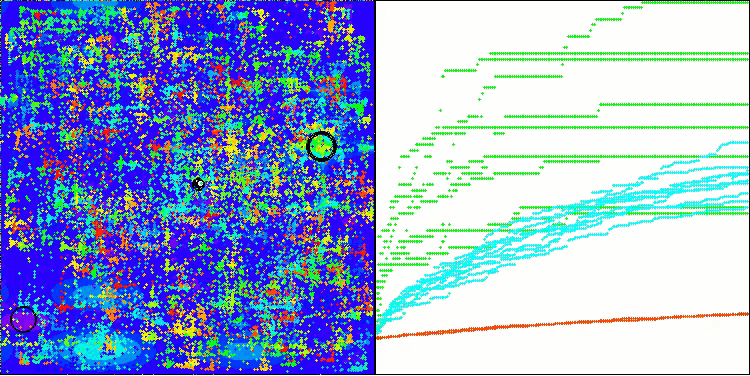
BHAm mit der Testfunktion Megacity
Basierend auf den Testergebnissen belegte der BHAm-Algorithmus den ehrenvollen 11. Platz, was ein sehr gutes Ergebnis ist, wenn man bedenkt, dass die leistungsstärksten bekannten Algorithmen als Konkurrenten vorhanden sind.
| # | AO | Beschreibung | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | Suche über die gesamte Nachbarschaft | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | Code-Sperr-Algorithmus (joo) | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | AMOm | Optimierung der Tiermigration M | 0.90358 | 0.84317 | 0.46284 | 2.20959 | 0.99001 | 0.92436 | 0.46598 | 2.38034 | 0.56769 | 0.59132 | 0.23773 | 1.39675 | 5.987 | 66.52 |
| 4 | (P+O)ES | (P+O) Entwicklungsstrategien | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 5 | CTA | Kometenschweif-Algorithmus (joo) | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 6 | SDSm | stochastische Diffusionssuche M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 7 | AAm | Algorithmus für das Bogenschießen M | 0.91744 | 0.70876 | 0.42160 | 2.04780 | 0.92527 | 0.75802 | 0.35328 | 2.03657 | 0.67385 | 0.55200 | 0.23738 | 1.46323 | 5.548 | 61.64 |
| 8 | ESG | Entwicklung sozialer Gruppen (joo) | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 9 | SIA | Simuliertes isotropes Glühen (Joo) | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 10 | ACS | künstliche, kooperative Suche | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 11 | BHAm | Algorithmus für schwarze Löcher M | 0.75236 | 0.76675 | 0.34583 | 1.86493 | 0.93593 | 0.80152 | 0.27177 | 2.00923 | 0.65077 | 0.51646 | 0.15472 | 1.32195 | 5.196 | 57.73 |
| 12 | ASO | Anarchische Gesellschaftsoptimierung | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5.178 | 57,54 |
| 13 | AOSm | Suche nach atomaren Orbitalen M | 0.80232 | 0.70449 | 0.31021 | 1.81702 | 0.85660 | 0.69451 | 0.21996 | 1.77107 | 0.74615 | 0.52862 | 0.14358 | 1.41835 | 5.006 | 55.63 |
| 14 | TSEA | Schildkrötenpanzer-Evolutionsalgorithmus (joo) | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 15 | DE | differentielle Evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 16 | CRO | Optimierung chemischer Reaktionen | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 17 | BSA | Vogelschwarm-Algorithmus | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 18 | HS | Harmoniesuche | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 19 | SSG | Setzen, Säen und Wachsen | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 20 | BCOm | Optimierung mit der bakteriellen Chemotaxis M | 0.75953 | 0.62268 | 0.31483 | 1.69704 | 0.89378 | 0.61339 | 0.22542 | 1.73259 | 0.65385 | 0.42092 | 0.14435 | 1.21912 | 4.649 | 51.65 |
| 21 | ABO | Optimierung des afrikanischen Büffels | 0.83337 | 0.62247 | 0.29964 | 1.75548 | 0.92170 | 0.58618 | 0.19723 | 1.70511 | 0.61000 | 0.43154 | 0.13225 | 1.17378 | 4.634 | 51.49 |
| 22 | (PO)ES | (PO) Entwicklungsstrategien | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 23 | TSm | Tabu-Suche M | 0.87795 | 0.61431 | 0.29104 | 1.78330 | 0.92885 | 0.51844 | 0.19054 | 1.63783 | 0.61077 | 0.38215 | 0.12157 | 1.11449 | 4.536 | 50.40 |
| 24 | BSO | Brainstorming-Optimierung | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 25 | WOAm | Wal-Optimierungsalgorithmus M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 26 | AEFA | Algorithmus für künstliche elektrische Felder | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 27 | AEO | Algorithmus zur Optimierung auf der Grundlage künstlicher Ökosysteme | 0.91380 | 0.46713 | 0.26470 | 1.64563 | 0.90223 | 0.43705 | 0.21400 | 1.55327 | 0.66154 | 0.30800 | 0.28563 | 1.25517 | 4.454 | 49.49 |
| 28 | ACOm | Ameisen-Kolonie-Optimierung M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 29 | BFO-GA | Optimierung der bakteriellen Futtersuche — ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 30 | SOA | einfacher Optimierungsalgorithmus | 0.91520 | 0.46976 | 0.27089 | 1.65585 | 0.89675 | 0.37401 | 0.16984 | 1.44060 | 0.69538 | 0.28031 | 0.10852 | 1.08422 | 4.181 | 46.45 |
| 31 | ABHA | Algorithmus für künstliche Bienenstöcke | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 32 | ACMO | Optimierung atmosphärischer Wolkenmodelle | 0.90321 | 0.48546 | 0.30403 | 1.69270 | 0.80268 | 0.37857 | 0.19178 | 1.37303 | 0.62308 | 0.24400 | 0.10795 | 0.97503 | 4.041 | 44.90 |
| 33 | ADAMm | adaptive Momentabschätzung M | 0.88635 | 0.44766 | 0.26613 | 1.60014 | 0.84497 | 0.38493 | 0.16889 | 1.39880 | 0.66154 | 0.27046 | 0.10594 | 1.03794 | 4.037 | 44.85 |
| 34 | ATAm | Algorithmus für künstliche Stämme M | 0.71771 | 0.55304 | 0.25235 | 1.52310 | 0.82491 | 0.55904 | 0.20473 | 1.58867 | 0.44000 | 0.18615 | 0.09411 | 0.72026 | 3.832 | 42.58 |
| 35 | ASHA | Algorithmus für künstliches Duschen | 0.89686 | 0.40433 | 0.25617 | 1.55737 | 0.80360 | 0.35526 | 0.19160 | 1.35046 | 0.47692 | 0.18123 | 0.09774 | 0.75589 | 3.664 | 40.71 |
| 36 | ASBO | Optimierung des adaptiven Sozialverhaltens | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 37 | MEC | Evolutionäre Berechnung des Geistes | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 38 | IWO | Optimierung mit invasiven Unkräutern | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 39 | Micro-AIS | Künstliches Mikro-Immunsystem | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 40 | COAm | Kuckuck-Optimierungsalgorithmus M | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 41 | SDOm | Optimierung der Spiraldynamik M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| 42 | NMm | Nelder-Mead-Verfahren M | 0.73807 | 0.50598 | 0.31342 | 1.55747 | 0.63674 | 0.28302 | 0.08221 | 1.00197 | 0.44667 | 0.18667 | 0.04028 | 0.67362 | 3.233 | 35.92 |
| 43 | FAm | Firefly-Algorithmus M | 0.58634 | 0.47228 | 0.32276 | 1.38138 | 0.68467 | 0.37439 | 0.10908 | 1.16814 | 0.28667 | 0.16467 | 0.04722 | 0.49855 | 3.048 | 33.87 |
| 44 | GSA | Algorithmus für die Schwerkraftsuche | 0.64757 | 0.49197 | 0.30062 | 1.44016 | 0.53962 | 0.36353 | 0.09945 | 1.00260 | 0.32667 | 0.12200 | 0.01917 | 0.46783 | 2.911 | 32.34 |
| 45 | BFO | Optimierung der bakteriellen Futtersuche | 0.61171 | 0.43270 | 0.31318 | 1.35759 | 0.54410 | 0.21511 | 0.05676 | 0.81597 | 0.42167 | 0.13800 | 0.03195 | 0.59162 | 2.765 | 30.72 |
Zusammenfassung
Der Algorithmus mit dem Schwarzen Loch (BHA) ist ein elegantes Beispiel dafür, wie fundamentale Naturgesetze in ein effizientes Optimierungswerkzeug umgewandelt werden können. Der Algorithmus basiert auf der einfachen und intuitiven Idee der Anziehungskraft potenzieller Lösungen auf eine zentrale, beste Lösung, die wie ein schwarzes Loch wirkt. Im Laufe der Evolution des Algorithmus beobachten wir ein erstaunliches Phänomen: Sterne-Lösungen, die sich auf ihr galaktisches Zentrum zubewegen, können neue, stärkere Anziehungspunkte entdecken – bessere Lösungen, was zu einer dynamischen Veränderung der Struktur des Suchraums führt. Dies zeigt deutlich, wie natürliche Selbstorganisationsmechanismen in der algorithmischen Optimierung effektiv genutzt werden können.
In der Praxis zeigt sich ein bemerkenswertes Muster: Oft ist es eher die Vereinfachung und das Überdenken grundlegender Ideen als deren Verkomplizierung, die zu unerwartet beeindruckenden Ergebnissen führen. In der Welt der algorithmischen Optimierung gibt es nur selten Situationen, in denen eine Erhöhung der Komplexität der Suchlogik zu einer signifikanten Verbesserung der Leistung führt.
Dieses Beispiel verdeutlicht einen wichtigen Grundsatz: Die Autorität der Erfinder eines Algorithmus oder die Popularität einer Methode sollte nicht als endgültige Garantie für ihre Effizienz angesehen werden. Jede Methode, selbst die erfolgreichste, kann sowohl in Bezug auf die Recheneffizienz als auch auf die Qualität der erzielten Ergebnisse verbessert werden. Die modifizierte Version des Algorithmus (BHAm) ist ein hervorragendes Beispiel für eine solche Verbesserung. Unter Beibehaltung der konzeptionellen Einfachheit der ursprünglichen Methode und der Abwesenheit von externen Abstimmungsparametern weist sie erhebliche Verbesserungen in Bezug auf Leistung und Konvergenzgeschwindigkeit auf.
Diese Erfahrung führt uns zu einer grundlegenden Schlussfolgerung: Innovation und Experimentieren müssen ein fester Bestandteil jeder beruflichen Tätigkeit sein. Ob es um die Entwicklung von Algorithmen für das maschinelle Lernen oder die Erstellung von Handelsstrategien geht, der Mut, neue Wege zu gehen, und die Bereitschaft, bestehende Methoden zu überdenken, sind oft der Schlüssel zu bahnbrechenden Ergebnissen.
Letztendlich wird der Fortschritt in der Optimierung, wie in jedem anderen Bereich auch, nicht durch das blinde Festhalten an Autoritäten vorangetrieben, sondern durch die kontinuierliche Suche nach neuen, effizienteren Lösungen, die auf einem tiefen Verständnis grundlegender Prinzipien und der Bereitschaft zum kreativen Experimentieren basieren.
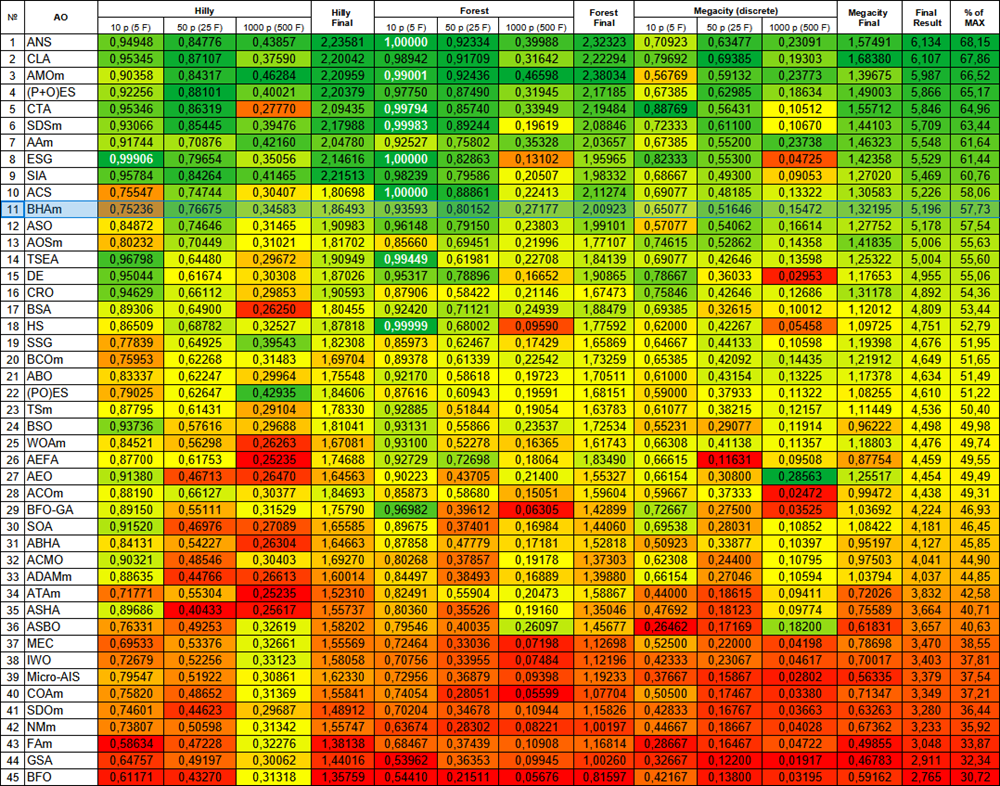
Abbildung 3. Farbliche Abstufung der Algorithmen entsprechend den relevanten Tests Ergebnisse, die größer oder gleich 0,99 sind, werden weiß hervorgehoben
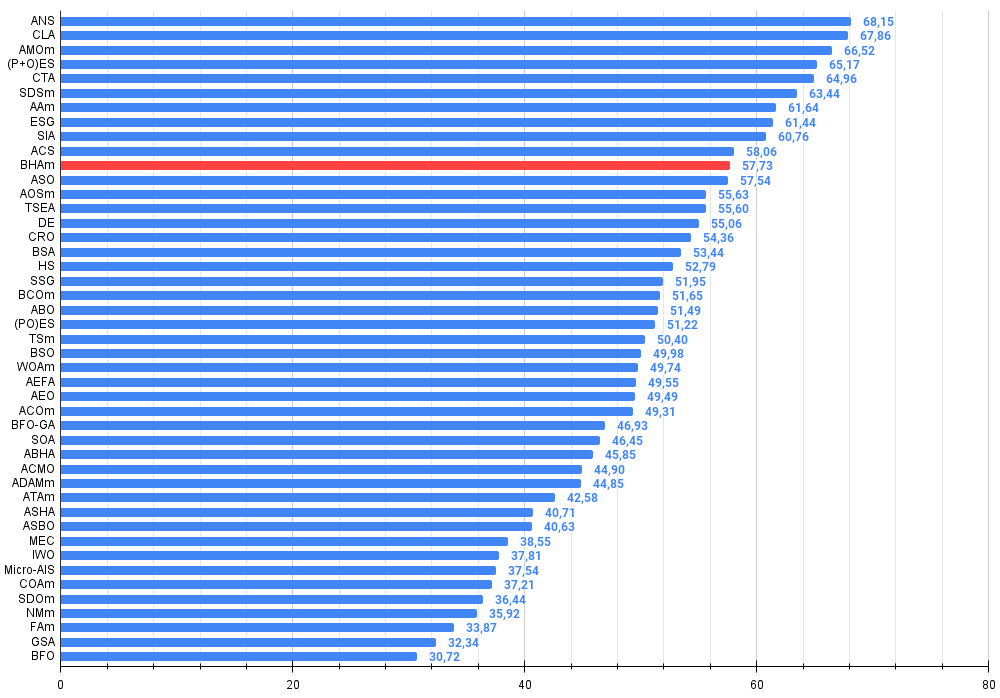
Abbildung 4. Das Histogramm der Algorithmus-Testergebnisse (Skala von 0 bis 100, je höher, desto besser, wobei 100 das maximal mögliche theoretische Ergebnis ist; im Archiv befindet sich ein Skript zur Berechnung der Bewertungstabelle)
Vor- und Nachteile von BHAm:
Vorteile:
- Der einzige externe Parameter ist die Größe der Population.
- Einfache Umsetzung.
- Sehr schneller EA.
- Funktioniert gut bei groß angelegten Problemen.
Nachteile:
- Große Streuung der Ergebnisse bei kleindimensionalen Problemen.
- Tendenz, bei niedrigdimensionalen Problemen stecken zu bleiben.
Der Artikel wird von einem Archiv mit den aktuellen Versionen der Codes der Algorithmen begleitet. Der Autor des Artikels übernimmt keine Verantwortung für die absolute Richtigkeit der Beschreibung der kanonischen Algorithmen. An vielen von ihnen wurden Änderungen vorgenommen, um die Suchmöglichkeiten zu verbessern. Die in den Artikeln dargelegten Schlussfolgerungen und Urteile beruhen auf den Ergebnissen der Versuche.
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | #C_AO.mqh | Include | Übergeordnete Klasse von Populationsoptimierungsalgorithmen |
| 2 | #C_AO_enum.mqh | Include | Enumeration der Algorithmen zur Populationsoptimierung |
| 3 | TestFunctions.mqh | Include | Bibliothek mit Testfunktionen |
| 4 | TestStandFunctions.mqh | Include | Bibliothek der Testfunktionen |
| 5 | Utilities.mqh | Include | Bibliothek der Hilfsfunktionen |
| 6 | CalculationTestResults.mqh | Include | Skript zur Berechnung der Ergebnisse in der Vergleichstabelle |
| 7 | Testing AOs.mq5 | Skript | Der einheitliche Prüfstand für alle Algorithmen zur Populationsoptimierung |
| 8 | Simple use of population optimization algorithms.mq5 | Skript | Ein einfaches Beispiel für die Verwendung von Algorithmen zur Populationsoptimierung ohne Visualisierung |
| 9 | Test_AO_BHAm.mq5 | Skript | BHAm-Prüfstand |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/16655
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Neuronale Netze im Handel: Modelle mit Wavelet-Transformation und Multitasking-Aufmerksamkeit
Neuronale Netze im Handel: Modelle mit Wavelet-Transformation und Multitasking-Aufmerksamkeit
 Quantencomputing und Handel: Ein neuer Ansatz für Preisprognosen
Quantencomputing und Handel: Ein neuer Ansatz für Preisprognosen
 Neuro-symbolische Systeme im algorithmischen Handel: Kombination von symbolischen Regeln und neuronalen Netzen
Neuro-symbolische Systeme im algorithmischen Handel: Kombination von symbolischen Regeln und neuronalen Netzen
 Neuronale Netze im Handel: Ein hybrider Handelsrahmen mit prädiktiver Kodierung (letzter Teil)
Neuronale Netze im Handel: Ein hybrider Handelsrahmen mit prädiktiver Kodierung (letzter Teil)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.