Algoritmo de agujero negro — Black Hole Algorithm (BHA)
48
0
Contenido
Introducción
El algoritmo de agujero negro (BHA) ofrece una perspectiva única del problema de la optimización. Creado en 2013 por A. Hatamlou, este algoritmo se inspira en los objetos más misteriosos y poderosos del universo: los agujeros negros. De la misma forma que los agujeros negros atraen todo lo que les rodea con su campo gravitatorio, el algoritmo tiende a "atraer" hacia sí las mejores soluciones, eliminando las menos acertadas.
Imagine un vasto cosmos lleno de multitud de soluciones, cada una luchando por sobrevivir en este espacio brutal. En el centro de este caos se encuentran los agujeros negros: soluciones con la máxima puntuación de calidad que poseen poder de atracción. El algoritmo de agujero negro decide a cada paso qué estrellas serán engullidas por agujeros negros y cuáles seguirán su camino en busca de condiciones más favorables.
Con elementos de aleatoriedad, el algoritmo BHA explora zonas inexploradas, intentando evitar las trampas de los mínimos locales. Esto la convierte en una potente herramienta para resolver problemas complejos, desde la optimización de funciones a problemas combinatorios e incluso el ajuste de hiperparámetros en aprendizaje automático. En este artículo analizaremos con detalle el algoritmo de agujero negro, sus principios de funcionamiento y sus ventajas e inconvenientes, abriéndole las puertas a un mundo en el que se entrelazan la ciencia y el arte de la optimización.
Implementación del algoritmo
El algoritmo BHA usa las ideas sobre la interacción de las estrellas con los agujeros negros para encontrar soluciones óptimas en un espacio de búsqueda determinado. El proceso del algoritmo comienza con la inicialización, en la que se crea una población inicial de "estrellas" aleatorias, cada una de las cuales representa una solución potencial al problema de optimización. Estas estrellas se ubican en un espacio de búsqueda delimitado por unos límites superior e inferior. Durante las iteraciones del algoritmo, en cada paso se destaca la mejor solución, que se etiqueta como "agujero negro". Las estrellas restantes tienden a acercarse al agujero negro de acuerdo con la siguiente ecuación:
Xi(t+1) = Xi(t) + rand × (XBH - Xi(t))
donde:
- Xi(t) — posición actual de la estrella i
- XBH — posición del agujero negro
- rand — número aleatorio de 0 a 1
Un elemento importante del algoritmo es el horizonte de sucesos, que se calcula usando la fórmula:
R = fitBH / Σfiti
Las estrellas que cruzan dicho horizonte son "absorbidas" por el agujero negro y sustituidas por nuevas estrellas aleatorias. Este mecanismo mantiene la diversidad de la población y fomenta una mayor exploración del espacio.
El algoritmo de agujero negro posee varias características clave. Tiene una estructura sencilla y no tiene ningún parámetro, salvo el tamaño de la población, lo cual facilita su uso y no requiere ningún ajuste, algo casi inaudito en otros algoritmos de optimización.
El algoritmo BHA es similar a otros algoritmos basados en poblaciones, lo que significa que el primer paso en el proceso de optimización consiste en crear una población inicial de soluciones aleatorias (estrellas iniciales) y calcular una función objetivo para estimar los valores de las soluciones. La mejor solución en cada iteración se selecciona como un agujero negro, que entonces empieza a atraer otras soluciones candidatas a su alrededor, llamadas estrellas. Si otras soluciones candidatas se acercan a la mejor solución recibida, serán "absorbidas" por la mejor solución.
La siguiente figura muestra cómo funciona la estrategia de búsqueda del algoritmo BHA. Todas las estrellas más allá del horizonte de sucesos del agujero negro se mueven hacia su centro, mientras que las estrellas que hayan cruzado el horizonte serán absorbidas; en esencia, la materia de la estrella será teletransportada a una nueva región del espacio de búsqueda.
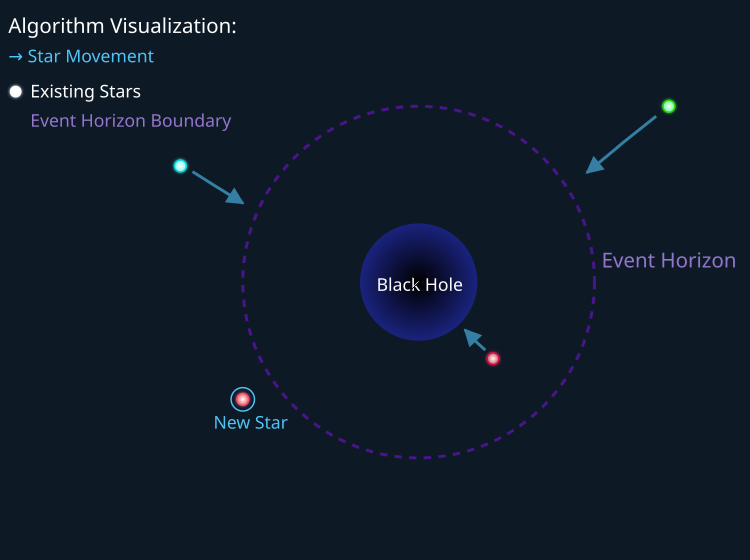
Figura 1. Estrategia de búsqueda del BHA. Las estrellas verde y azul se desplazan hacia el centro de agujero negro, mientras que la estrella roja se teletransporta al punto "New Star"
Vamos a escribir el pseudocódigo del algoritmo de agujero negro (BHA)
N - número de estrellas (tamaño de la población)
tmax - número máximo de iteraciones
// Inicialización
1. Creamos las posiciones iniciales para N estrellas:
Para i = 1 hasta N:
Xi = LB + rand × (UB - LB)
2. t = 1
// Ciclo principal
3. Siempre que t ≤ tmax:
// Calculamos el valor de la función objetivo para cada estrella
4. Para cada Xi calculamos fiti
// Identificamos el agujero negro
5. Identificamos XBH como la estrella con el mejor valor fiti
fitBH = mejor valor fiti
// Actualizamos las posiciones de las estrellas
6. Para cada estrella Xi:
Xi(t+1) = Xi(t) + rand × (XBH - Xi(t))
// Calculamos el radio del horizonte de sucesos
7. R = fitBH / ∑(i=1 hasta N) fiti
// Comprobamos la absorción estelar
8. Para cada estrella Xi:
Si la distancia entre Xi y XBH < R:
Generamos una nueva posición para Xi aleatoriamente
Xi = LB + rand × (UB - LB)
9. t = t + 1
// Retornamos la mejor solución encontrada
Devolvemos XBH
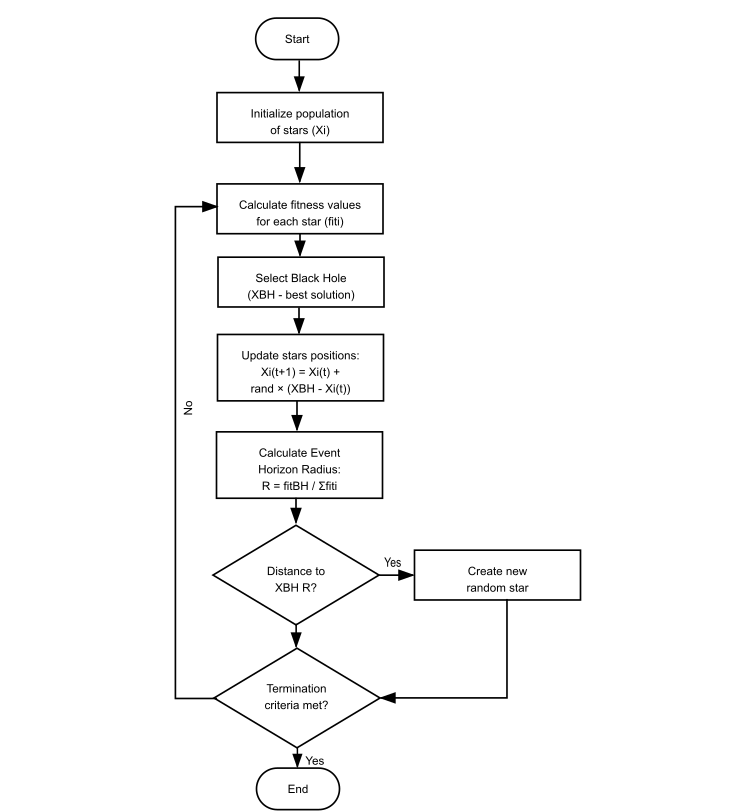
Figura 2. Esquema lógico del funcionamiento del algoritmo BHA
Definición de la clase C_AO_BHA (Black Hole Algorithm), heredera de la clase base C_AO, estructura de la clase:
Constructor y destructor:
- El constructor inicializa los parámetros básicos del algoritmo
- SetParams () - establece el tamaño de la población a partir del array de parámetros
- Init () - inicializa un espacio de búsqueda con los límites y el tamaño de paso especificados.
- Moving () - efectúa el desplazamiento de las estrellas hacia el agujero negro
- Revision () - actualiza la mejor solución (agujero negro) encontrada
- blackHoleIndex - almacena el índice de la mejor solución de la población
- rangeMinP [] - valores mínimos de cada coordenada
- rangeMaxP [] - valores máximos de cada coordenada
- rangeStepP [] - paso de discretización para cada coordenada
- epochsP - número de iteraciones del algoritmo
Este es el marco básico para implementar el algoritmo de agujero negro; la lógica principal se implementará en los métodos Moving() y Revision().
//—————————————————————————————————————————————————————————————————————————————— class C_AO_BHA : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_BHA () { } C_AO_BHA () { ao_name = "BHA"; ao_desc = "Black Hole Algorithm"; ao_link = "https://www.mql5.com/es/articles/16655"; popSize = 50; // Размер популяции ArrayResize (params, 1); // Инициализация параметров params [0].name = "popSize"; params [0].val = popSize; } void SetParams () // Метод для установки параметров { popSize = (int)params [0].val; } bool Init (const double &rangeMinP [], // Минимальный диапазон поиска const double &rangeMaxP [], // Максимальный диапазон поиска const double &rangeStepP [], // Шаг поиска const int epochsP = 0); // Количество эпох void Moving (); // Метод перемещения void Revision (); // Метод ревизии private: //------------------------------------------------------------------- int blackHoleIndex; // Индекс черной дыры (лучшего решения) };El método "Init" es sencillo y su tarea consistirá en lo siguiente:
- Realizará la primera inicialización del algoritmo
- Llamará a StandardInit para establecer los rangos de búsqueda y el paso
- Establecerá el índice inicial de agujero negro en 0
- Retornará true en caso de inicialización correcta, false en caso de error
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_BHA::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; blackHoleIndex = 0; // Инициализация индекса черной дыры return true; } //——————————————————————————————————————————————————————————————————————————————
El métodoMoving consta de varios elementos básicos:
a) Inicialización primaria (si revision = false):
- Creamos una población inicial de estrellas con posiciones aleatorias
- Las posiciones se generarán dentro de un rango especificado y se llevarán a una cuadrícula discreta
- Establecemos la bandera de "revision" en "true"
b) Algoritmo básico (si revision = true):
- Calculamos la suma de los valores de la función de aptitud de todas las estrellas
- Calculamos el radio del horizonte de sucesos: R = fitBH / Σfiti
c) Actualización de las posiciones de las estrellas:
- Para cada estrella (salvo el agujero negro):
- Calculamos la distancia euclidiana al agujero negro
- Si la distancia es inferior al radio del horizonte:
- Creamos una nueva estrella aleatoria
- De lo contrario:
- Actualizamos la posición según la fórmula: Xi(t+1) = Xi(t) + rand × (XBH - Xi(t))
- Llevamos la nueva posición a un rango válido y a una cuadrícula discreta
Todos los cálculos se realizarán según las restricciones del espacio de búsqueda y del paso de discretización.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BHA::Moving () { // Начальное случайное позиционирование при первом запуске if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { // Генерация случайной позиции в допустимом диапазоне a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); // Приведение к дискретным значениям согласно шагу a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } // Расчет суммы фитнес-значений для радиуса горизонта событий double sumFitness = 0.0; for (int i = 0; i < popSize; i++) { sumFitness += a [i].f; } // Расчет радиуса горизонта событий // R = fitBH / Σfiti double eventHorizonRadius = a [blackHoleIndex].f / sumFitness; // Обновление позиций звезд for (int i = 0; i < popSize; i++) { // Пропускаем черную дыру if (i == blackHoleIndex) continue; // Расчет расстояния до черной дыры double distance = 0.0; for (int c = 0; c < coords; c++) { double diff = a [blackHoleIndex].c [c] - a [i].c [c]; distance += diff * diff; } distance = sqrt (distance); // Проверка пересечения горизонта событий if (distance < eventHorizonRadius) { // Звезда поглощена - создаем новую случайную звезду for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } else { // Обновление позиции звезды по формуле: // Xi(t+1) = Xi(t) + rand × (XBH - Xi(t)) for (int c = 0; c < coords; c++) { double rnd = u.RNDfromCI (0.0, 1.0); double newPosition = a [i].c [c] + rnd * (a [blackHoleIndex].c [c] - a [i].c [c]); // Проверка и коррекция границ newPosition = u.SeInDiSp (newPosition, rangeMin [c], rangeMax [c], rangeStep [c]); a [i].c [c] = newPosition; } } } } //——————————————————————————————————————————————————————————————————————————————
En el métodoRevision se realizan las siguientes funciones:
Búsqueda de la mejor solución:
- Iteramos por todas las estrellas de la población
- Comparamos el valor de la función de aptitud de cada estrella (a[i].f) con el mejor valor actual (fB)
- Para encontrar la mejor solución:
- Actualizamos el mejor valor de la función de aptitud (fB)
- Almacenamos el índice de agujero negro (blackHoleIndex)
- Copiamos las coordenadas de la mejor solución en el array "cB".
El objetivo principal del método es monitorear y preservar la mejor solución (agujero negro) encontrada durante el proceso de optimización.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BHA::Revision () { // Поиск лучшего решения (черной дыры) for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; blackHoleIndex = i; ArrayCopy (cB, a [i].c, 0, 0, WHOLE_ARRAY); } } } //——————————————————————————————————————————————————————————————————————————————
Las pruebas del algoritmo BHA muestran los siguientes resultados:
BHA|Black Hole Algorithm|50.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.6833993073000924
25 Hilly's; Func runs: 10000; result: 0.47275633991339616
500 Hilly's; Func runs: 10000; result: 0.2782882943201518
=============================
5 Forest's; Func runs: 10000; result: 0.6821776337288085
25 Forest's; Func runs: 10000; result: 0.3878950941651221
500 Forest's; Func runs: 10000; result: 0.20702263338385946
=============================
5 Megacity's; Func runs: 10000; result: 0.39461538461538465
25 Megacity's; Func runs: 10000; result: 0.20076923076923076
500 Megacity's; Func runs: 10000; result: 0.1076846153846164
=============================
All score: 3.41461 (37.94%)
Según la tabla, los resultados del algoritmo han sido inferiores a la media. Sin embargo, una ventaja obvia de este algoritmo es que no tiene más parámetros que el tamaño de la población, lo cual hace que los resultados sean bastante satisfactorios. En su trabajo, el estancamiento en los óptimos locales resultaba inmediatamente perceptible debido a la falta de diversidad en las soluciones de la población. Además, para cada estrella deben realizarse cálculos de distancia euclidiana hasta el agujero negro que consumen muchos recursos. Este hecho les llevó a reflexionar sobre posibles formas de subsanar las deficiencias existentes.
En el algoritmo original, cuando se produce una iteración, las estrellas se mueven mientras que el agujero negro permanece en su sitio, aunque en el espacio todos los objetos sin excepción estén en movimiento. Así que decidimos hacer una modificación e implementar el desplazamiento del agujero negro a distancias determinadas de acuerdo con una distribución gaussiana relativa a su centro, y también probar una distribución según la ley de potencia. El objetivo de esta adaptación era mejorar la precisión de la convergencia sin perder la capacidad de explorar nuevas regiones del espacio de soluciones. Sin embargo, a pesar de estos cambios, los resultados no mostraron ninguna mejora. Esto puede indicar que la posición estable del agujero negro (específicamente para esta estrategia de búsqueda) resulta importante para la eficiencia del algoritmo, asegurando que las estrellas se centren en las regiones más prometedoras. Puede que merezca la pena considerar otros enfoques o combinaciones de métodos para conseguir mayores mejoras en los resultados.
Así pues, me vino a la cabeza dejar de calcular las distancias euclidianas y utilizar en su lugar el horizonte de sucesos del agujero negro como medida de la absorción probabilística, en lugar del cruce real del horizonte. En lugar de aplicar el movimiento a toda la estrella, aplicamos esta probabilidad por separado a cada coordenada.
Entonces, basándonos en las consideraciones anteriores, vamos a escribir una nueva versión del método "Moving". Hemos introducido cambios en la forma de calcular el horizonte de sucesos: ahora la adaptabilidad media de toda la población se normaliza según la distancia entre la adaptabilidad mínima y máxima de toda la población. Ahora el horizonte de sucesos es la probabilidad de absorción en coordenadas individuales de las estrellas, si la absorción no se ha producido, entonces haremos el movimiento habitual hacia el centro del monstruo negro galáctico según la fórmula del autor.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BHAm::Moving () { // Начальное случайное позиционирование при первом запуске if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { // Генерация случайной позиции в допустимом диапазоне a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); // Приведение к дискретным значениям согласно шагу a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- // Расчет среднего значения фитнес-значений для радиуса горизонта событий double aveFit = 0.0; double maxFit = fB; double minFit = a [0].f; for (int i = 0; i < popSize; i++) { aveFit += a [i].f; if (a [i].f < minFit) minFit = a [i].f; } aveFit /= popSize; // Расчет радиуса горизонта событий double eventHorizonRadius = (aveFit - minFit) / (maxFit - minFit); // Обновление позиций звезд for (int i = 0; i < popSize; i++) { // Пропускаем черную дыру if (i == blackHoleIndex) continue; for (int c = 0; c < coords; c++) { if (u.RNDprobab () < eventHorizonRadius * 0.01) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } else { double rnd = u.RNDfromCI (0.0, 1.0); double newPosition = a [i].c [c] + rnd * (a [blackHoleIndex].c [c] - a [i].c [c]); // Проверка и коррекция границ newPosition = u.SeInDiSp (newPosition, rangeMin [c], rangeMax [c], rangeStep [c]); a [i].c [c] = newPosition; } } } } //——————————————————————————————————————————————————————————————————————————————
Vamos a analizar las principales diferencias entre las dos versiones del algoritmo, empezando por el cálculo del radio del horizonte de sucesos. En la primera versión (BHA), el radio se define como la relación entre la mejor solución y la suma de todas las soluciones, lo cual hace que el radio sea muy pequeño en una población grande y depende en gran medida de los valores absolutos de la función de aptitud. En la segunda versión (BHAm), el radio se normaliza en el intervalo [0,1], lo cual permite mostrar la posición relativa de la media entre el mínimo y el máximo, manteniendo la independencia del tamaño de la población y los valores absolutos de la función de aptitud.
Consideremos ahora el mecanismo de absorción estelar. En la primera versión del algoritmo, se comprueba la distancia euclidiana al agujero negro y, si se absorbe, la estrella será completamente sustituida por una nueva en una ubicación aleatoria, lo cual provocará un cambio más drástico en la población. La segunda versión usa la absorción probabilística para cada coordenada por separado, lo que proporciona cambios más suaves en la población. Aquí, un coeficiente de 0,01 reducirá la probabilidad de un cambio radical.
En términos de consecuencias, la primera versión muestra una explotación más agresiva del espacio de búsqueda, lo que provocá una convergencia rápida en zonas localizadas, pero también aumenta el riesgo de convergencia prematura y puede pasar por alto zonas prometedoras debido a la sustitución completa de soluciones. En cambio, la segunda versión ofrece una estrategia de investigación más suave, que posibilita un mejor equilibrio entre investigación y explotación, un menor riesgo de quedarse atascado en óptimos locales y una convergencia más lenta pero potencialmente más fiable, así como una mayor capacidad para diversificar la población.
En conclusión, la primera versión resultará más adecuada para problemas con óptimos bien definidos cuando se requiere una convergencia rápida y dimensiones reducidas del espacio de búsqueda, mientras que la segunda versión será más eficaz para problemas multiextremos complejos en los que importa la robustez para encontrar el óptimo global, así como para problemas de gran dimensionalidad que requieren una exploración más exhaustiva del espacio de búsqueda.
Me gustaría compartir mis ideas sobre la visualización del funcionamiento de los algoritmos. La visualización ofrece una gran oportunidad para comprender mejor los procesos internos de los algoritmos y desvelar sus mecanismos ocultos. Con determinados ajustes, podemos observar cómo imágenes caóticas se transforman gradualmente en patrones estructurados. Este proceso no solo demuestra los aspectos técnicos del algoritmo, sino que también descubre nuevas ideas y enfoques para optimizarlo.
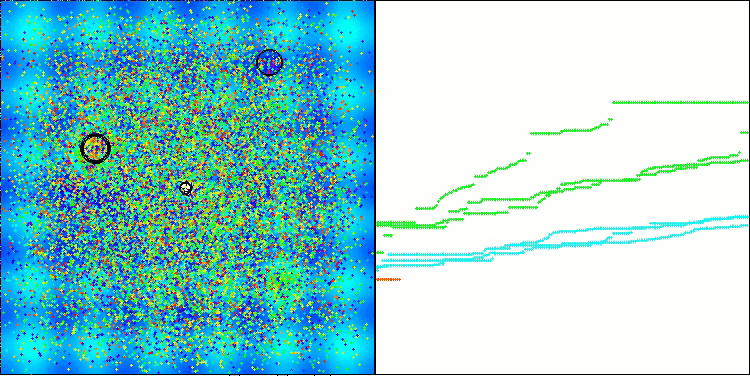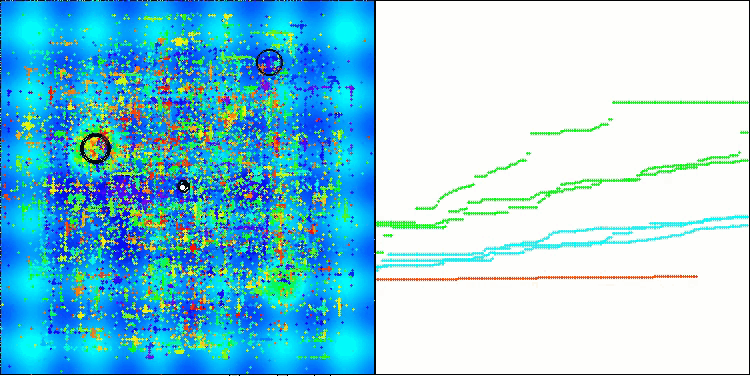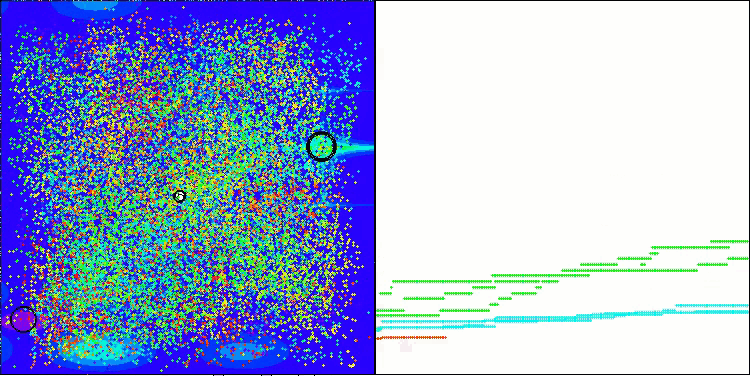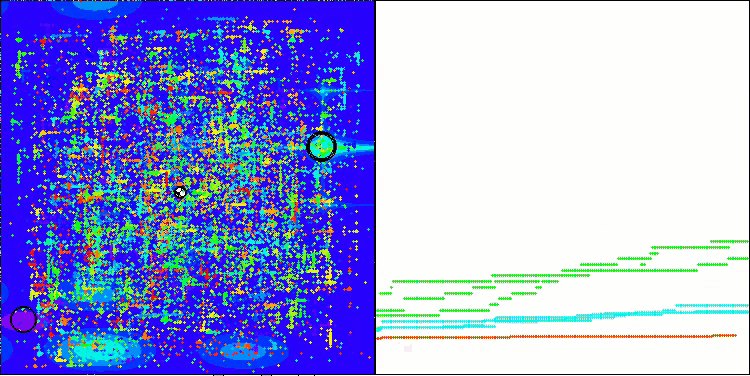
Ejemplo de funcionamiento del algoritmo BHAm generando un componente aleatorio del movimiento estelar en el intervalo [0,0;0,1].
Y lo que es más importante, la visualización no solo nos permite evaluar el rendimiento de los algoritmos, sino también identificar patrones que pueden no resultar obvios en el análisis tradicional de datos. Esto favorece una comprensión más profunda de su funcionamiento y puede inspirar nuevas soluciones e innovación. De esta forma, la visualización se convierte en una poderosa herramienta que ayuda a tender puentes entre ciencia y creatividad, abriendo nuevos horizontes para explorar y comprender procesos complejos.
Resultados de las pruebas
Resultados de la versión modificada del algoritmo BHAm:
BHAm|Black Hole Algorithm M|50.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.752359491007831
25 Hilly's; Func runs: 10000; result: 0.7667459889455067
500 Hilly's; Func runs: 10000; result: 0.34582657277589457
=============================
5 Forest's; Func runs: 10000; result: 0.9359337849703726
25 Forest's; Func runs: 10000; result: 0.801524710041611
500 Forest's; Func runs: 10000; result: 0.2717683112397725
=============================
5 Megacity's; Func runs: 10000; result: 0.6507692307692307
25 Megacity's; Func runs: 10000; result: 0.5164615384615385
500 Megacity's; Func runs: 10000; result: 0.154715384615386
=============================
All score: 5.19611 (57.73%)
Según los resultados de las pruebas, el algoritmo BHAm muestra unos resultados impresionantes, no solo en comparación con la versión original, sino también en la tabla en su conjunto. La visualización muestra que, efectivamente, la nueva versión con el postfijo "m" está libre de los defectos característicos de la original: la tendencia a atascarse queda prácticamente anulada, la precisión de la convergencia mejora notablemente y la dispersión de los resultados se disminuye. Al mismo tiempo, se mantiene el "rasgo familiar" del algoritmo de la versión de los autores, con la formación de peculiares grupos de estrellas en el espacio y la gravitación hacia un determinado atractor en el espacio de soluciones.
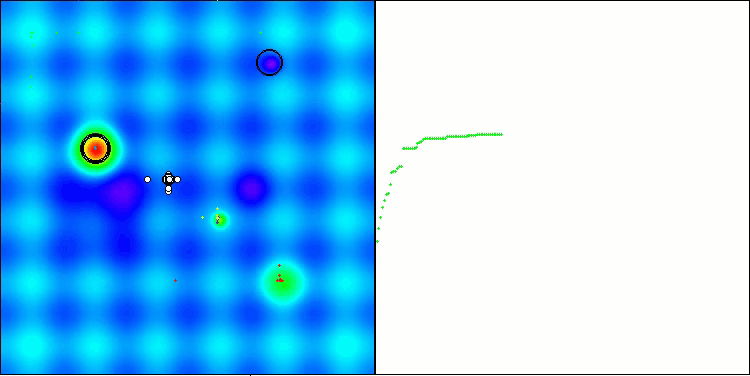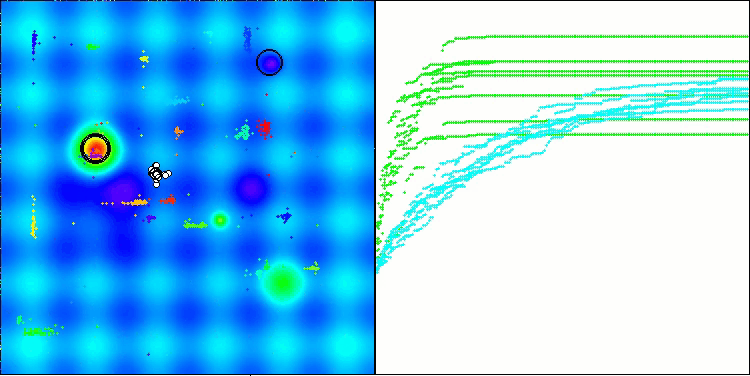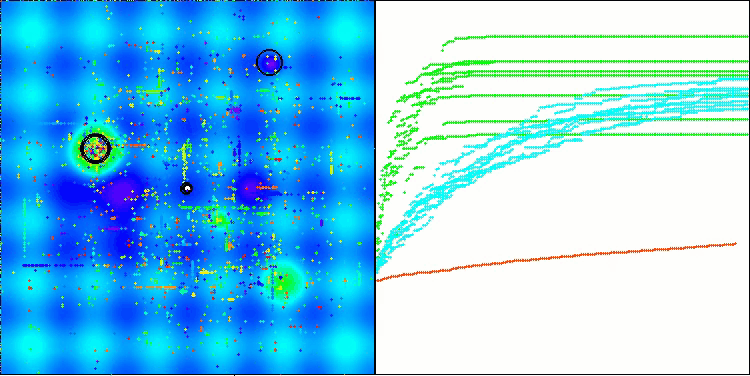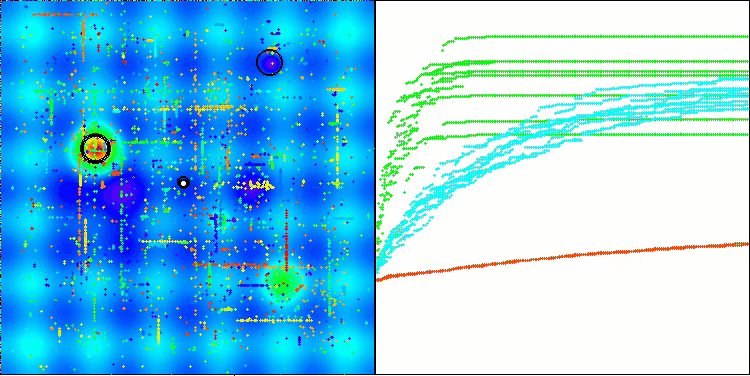
BHAm en la función de prueba Hilly
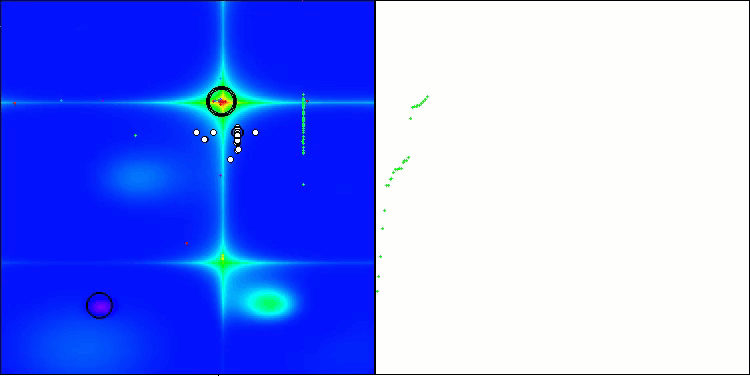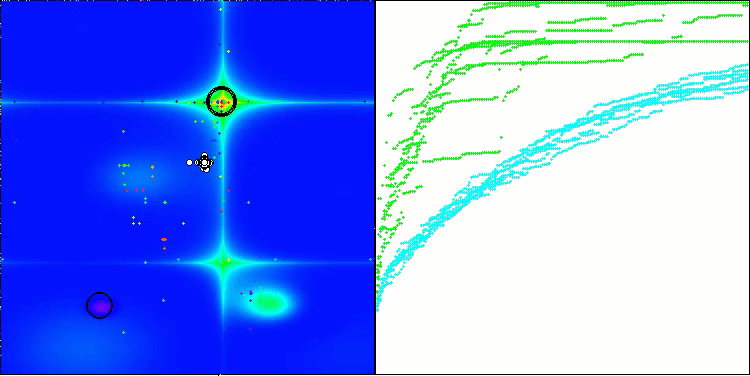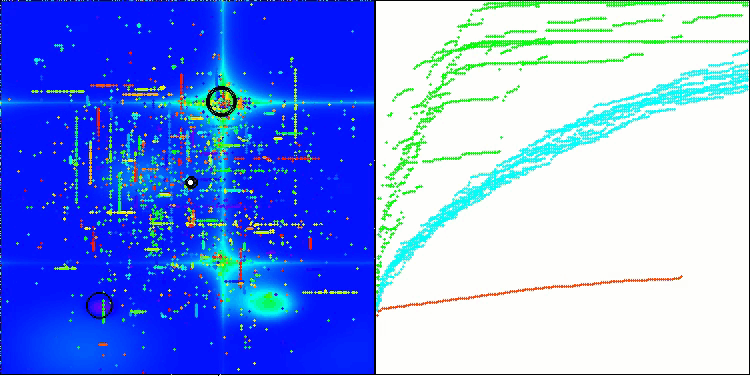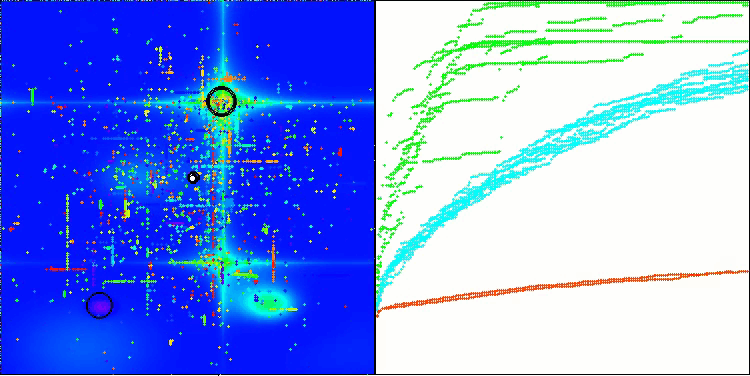
BHAm en la función de prueba Forest
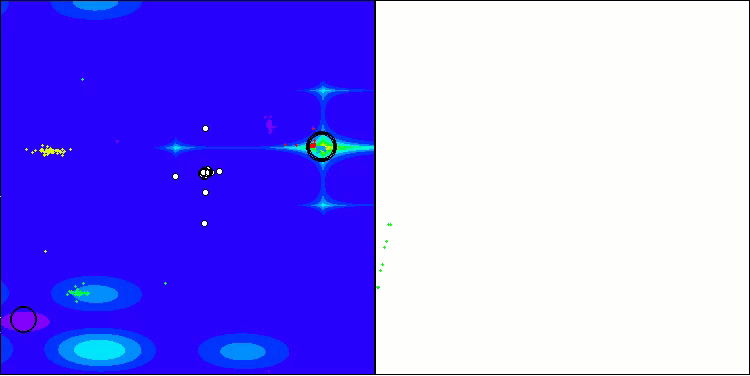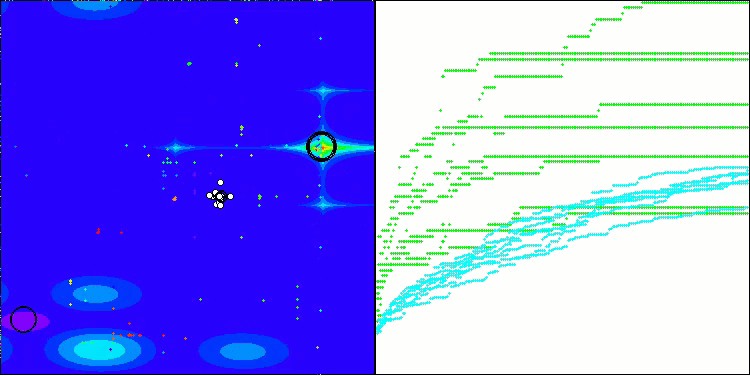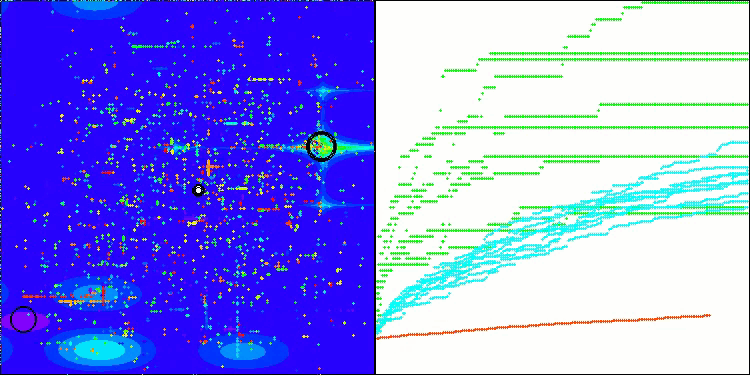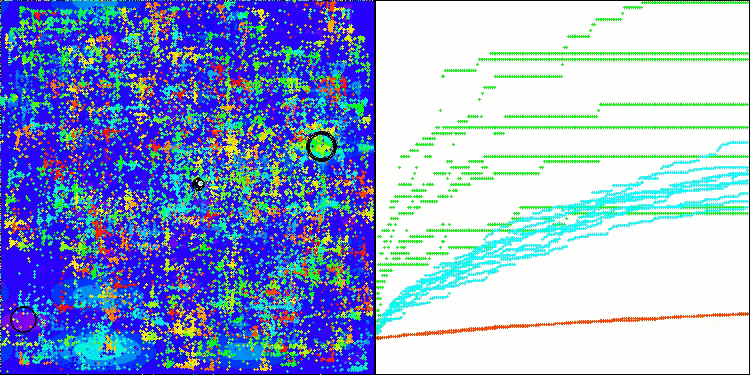
BHAm en la función de prueba Megacity
Según los resultados de las pruebas, el algoritmo BHAm se sitúa en un honorable undécimo puesto; un resultado muy bueno, considerando que compite con conocidos algoritmos más potentes.
| № | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % de MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration optimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 7 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 8 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 9 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 10 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 11 | BHAm | black hole algorithm M | 0,75236 | 0,76675 | 0,34583 | 1,86493 | 0,93593 | 0,80152 | 0,27177 | 2,00923 | 0,65077 | 0,51646 | 0,15472 | 1,32195 | 5,196 | 57,73 |
| 12 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 13 | AOSm | búsqueda de orbitales atómicos M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| 14 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 15 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 16 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 17 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 18 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 19 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 20 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 21 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 22 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 23 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 24 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 25 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 26 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 27 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 28 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 29 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 30 | SOA | simple optimization algorithm | 0.91520 | 0.46976 | 0.27089 | 1,65585 | 0.89675 | 0.37401 | 0.16984 | 1,44060 | 0.69538 | 0.28031 | 0.10852 | 1,08422 | 4.181 | 46,45 |
| 31 | ABH | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4.127 | 45,85 |
| 32 | ACMO | atmospheric cloud model optimization | 0,90321 | 0,48546 | 0,30403 | 1,69270 | 0,80268 | 0,37857 | 0,19178 | 1,37303 | 0,62308 | 0,24400 | 0,10795 | 0,97503 | 4,041 | 44,90 |
| 33 | ADÁN | adaptive moment estimation M | 0.88635 | 0.44766 | 0,26613 | 1.60014 | 0.84497 | 0.38493 | 0.16889 | 1,39880 | 0,66154 | 0.27046 | 0.10594 | 1,03794 | 4.037 | 44.85 |
| 34 | ATAm | artificial tribe algorithm M | 0.71771 | 0.55304 | 0,25235 | 1,52310 | 0.82491 | 0.55904 | 0,20473 | 1,58867 | 0,44000 | 0,18615 | 0.09411 | 0.72026 | 3.832 | 42.58 |
| 35 | ASHA | artificial showering algorithm | 0,89686 | 0,40433 | 0,25617 | 1,55737 | 0,80360 | 0,35526 | 0,19160 | 1,35046 | 0,47692 | 0,18123 | 0,09774 | 0,75589 | 3,664 | 40,71 |
| 36 | ASBO | adaptive social behavior optimization | 0,76331 | 0,49253 | 0,32619 | 1,58202 | 0,79546 | 0,40035 | 0,26097 | 1,45677 | 0,26462 | 0,17169 | 0,18200 | 0,61831 | 3.657 | 40,63 |
| 37 | MEC | mind evolutionary computation | 0,69533 | 0,53376 | 0,32661 | 1,55569 | 0,72464 | 0,33036 | 0,07198 | 1,12698 | 0,52500 | 0,22000 | 0,04198 | 0,78698 | 3,470 | 38,55 |
| 38 | IWO | invasive weed optimization | 0,72679 | 0,52256 | 0,33123 | 1,58058 | 0,70756 | 0,33955 | 0,07484 | 1,12196 | 0,42333 | 0,23067 | 0,04617 | 0,70017 | 3,403 | 37,81 |
| 39 | Micro-AIS | micro artificial immune system | 0,79547 | 0,51922 | 0,30861 | 1,62330 | 0,72956 | 0,36879 | 0,09398 | 1,19233 | 0,37667 | 0,15867 | 0,02802 | 0,56335 | 3,379 | 37,54 |
| 40 | COAm | cuckoo optimization algorithm M | 0,75820 | 0,48652 | 0,31369 | 1,55841 | 0,74054 | 0,28051 | 0,05599 | 1,07704 | 0,50500 | 0,17467 | 0,03380 | 0,71347 | 3,349 | 37,21 |
| 41 | SDOm | spiral dynamics optimization M | 0,74601 | 0,44623 | 0,29687 | 1,48912 | 0,70204 | 0,34678 | 0,10944 | 1,15826 | 0,42833 | 0,16767 | 0,03663 | 0,63263 | 3,280 | 36,44 |
| 42 | NMm | Nelder-Mead method M | 0,73807 | 0,50598 | 0,31342 | 1,55747 | 0,63674 | 0,28302 | 0,08221 | 1,00197 | 0,44667 | 0,18667 | 0,04028 | 0,67362 | 3,233 | 35,92 |
| 43 | FAm | firefly algorithm M | 0,58634 | 0,47228 | 0,32276 | 1,38138 | 0,68467 | 0,37439 | 0,10908 | 1,16814 | 0,28667 | 0,16467 | 0,04722 | 0,49855 | 3,048 | 33,87 |
| 44 | GSA | gravitational search algorithm | 0,64757 | 0,49197 | 0,30062 | 1,44016 | 0,53962 | 0,36353 | 0,09945 | 1,00260 | 0,32667 | 0,12200 | 0,01917 | 0,46783 | 2,911 | 32,34 |
| 45 | BFO | bacterial foraging optimization | 0,61171 | 0,43270 | 0,31318 | 1,35759 | 0,54410 | 0,21511 | 0,05676 | 0,81597 | 0,42167 | 0,13800 | 0,03195 | 0,59162 | 2,765 | 30,72 |
Conclusiones
El algoritmo de agujero negro (BHA) es un ejemplo elegante de cómo las leyes fundamentales de la naturaleza pueden convertirse en una herramienta de optimización eficaz. El algoritmo se basa en la idea simple e intuitiva de la atracción gravitacional de soluciones potenciales hacia una solución central: la mejor, que actúa como un agujero negro. En el proceso de evolución del algoritmo, observamos un fenómeno sorprendente: las estrellas-solución, moviéndose hacia su centro galáctico, pueden descubrir nuevos centros de atracción más poderosos, es decir, mejores soluciones, lo cual provoca un cambio dinámico en la estructura del espacio de búsqueda. Esto demuestra claramente cómo los mecanismos de autoorganización naturales pueden usarse eficazmente en la optimización algorítmica.
La práctica muestra un patrón notable: con frecuencia es la simplificación y el replanteamiento de las ideas básicas, más que su complicación, lo que conduce a resultados inesperadamente impresionantes. En el mundo de la optimización algorítmica, resulta raro encontrar una situación en la que el aumento de la complejidad de la lógica de búsqueda redunde en una mejora significativa del rendimiento.
Este ejemplo ilustra claramente un principio esencial: la autoridad de los creadores de un algoritmo o la popularidad de un método no deben percibirse como una garantía final de su optimalidad. Cualquier método, incluso el más exitoso, puede mejorarse tanto en la eficiencia computacional como en la calidad de los resultados obtenidos. La versión modificada del algoritmo (BHAm) nos sirve como un excelente ejemplo de dicha mejora. Manteniendo la simplicidad conceptual del método original y la ausencia de parámetros de ajuste externos, demuestra mejoras sustanciales en el rendimiento y la velocidad de convergencia.
Esta experiencia nos lleva a una conclusión fundamental: la innovación y la experimentación deben formar parte integral de cualquier actividad profesional. Ya sea desarrollando algoritmos de aprendizaje automático o creando estrategias comerciales, la valentía de explorar nuevos enfoques y la voluntad de repensar los métodos existentes son a menudo la clave para lograr resultados innovadores.
En última instancia, el progreso en la optimización, como en cualquier otro campo, no está impulsado por una obediencia ciega a la autoridad, sino por una búsqueda continua de soluciones nuevas y más efectivas basadas en una comprensión profunda de los principios fundamentales, así como en la voluntad de experimentar creativamente.
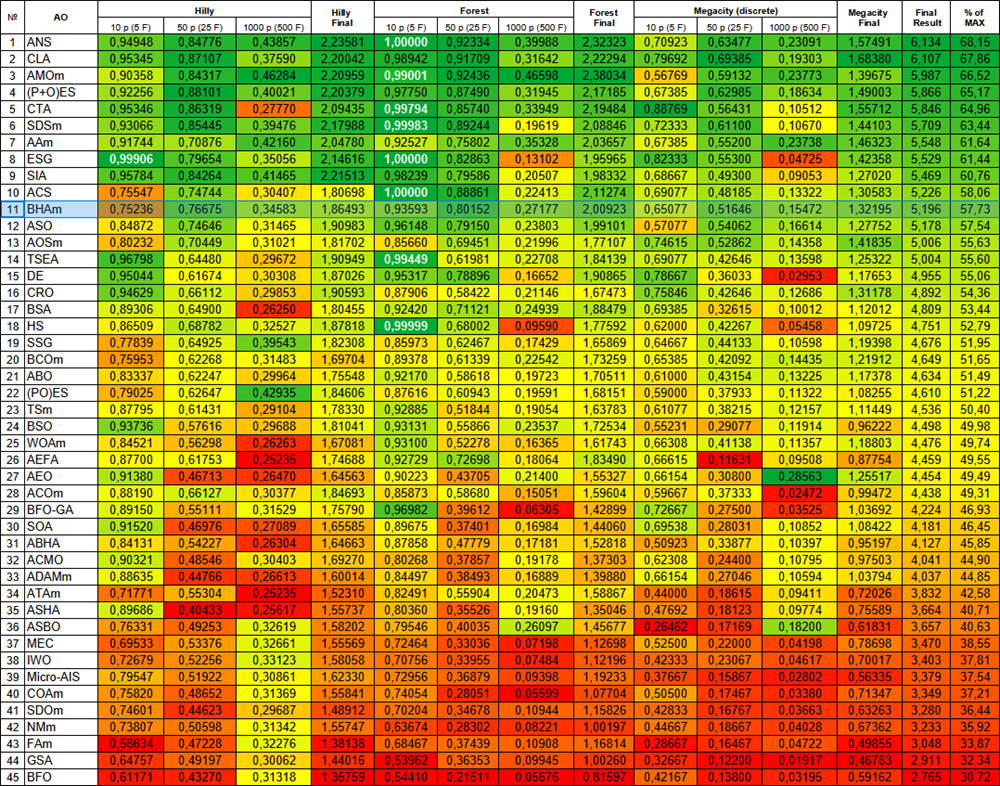
Figura 3. Gradación por colores de los algoritmos según sus respectivas pruebas. Los resultados superiores o iguales a 0.99 se resaltan en blanco.
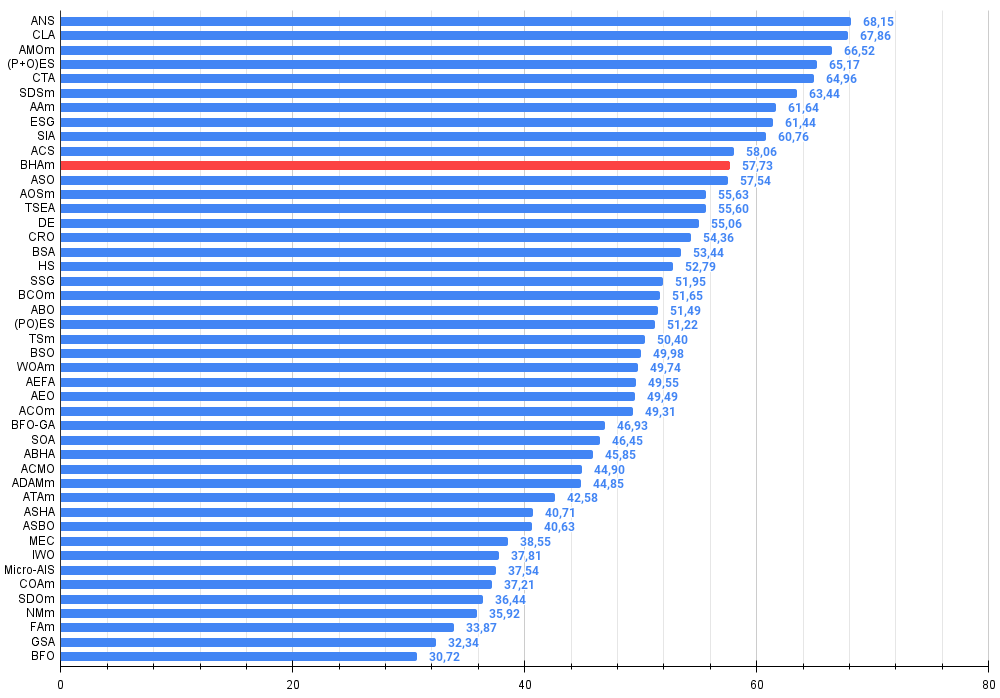
Figura 4. Histograma con los resultados de las pruebas de los algoritmos (en una escala de 0 a 100, cuanto más mejor, donde 100 es el máximo resultado teórico posible, el script para calcular la tabla de puntuación está en el archivo)
Ventajas y desventajas del algoritmo BHAm:
Ventajas:
- El único parámetro externo es el tamaño de la población.
- Implementación sencilla.
- Gran rapidez.
- Funciona bien en problemas de gran escala.
Desventajas:
- Gran dispersión de resultados para problemas de pequeña dimensionalidad.
- Tendencia a estancarse en problemas de baja dimensión.
Adjuntamos al artículo un archivo con las versiones actuales de los códigos de los algoritmos. El autor de este artículo no se responsabiliza de la exactitud absoluta de la descripción de los algoritmos canónicos, muchos de ellos han sido modificados para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos realizados.
Programas usados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | #C_AO.mqh | Archivo de inclusión | Clase padre de algoritmos de optimización basados en la población |
| 2 | #C_AO_enum.mqh | Archivo de inclusión | Enumeración de los algoritmos de optimización basados en la población |
| 3 | TestFunctions.mqh | Archivo de inclusión | Biblioteca de funciones de prueba |
| 4 | TestStandFunctions.mqh | Archivo de inclusión | Biblioteca de funciones del banco de pruebas |
| 5 | Utilities.mqh | Archivo de inclusión | Biblioteca de funciones auxiliares |
| 6 | CalculationTestResults.mqh | Archivo de inclusión | Script para calcular los resultados en una tabla comparativa |
| 7 | Testing AOs.mq5 | Script | Banco de pruebas único para todos los algoritmos de optimización basados en la población |
| 8 | Simple use of population optimization algorithms.mq5 | Script | Ejemplo sencillo de utilización de algoritmos de optimización basados en la población sin visualización |
| 9 | Test_AO_BHAm.mq5 | Script | Banco de pruebas para BHAm |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/16655
Utilizando redes neuronales en MetaTrader
Asesores Expertos Auto-Optimizables con MQL5 y Python (Parte VI): Cómo aprovechar el doble descenso profundo
Particularidades del trabajo con números del tipo double en MQL4
Robot comercial multimodular en Python y MQL5 (Parte I): Creamos la arquitectura básica y los primeros módulos
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso