Алгоритм черной дыры — Black Hole Algorithm (BHA)

MetaTrader 5 — Примеры | 19 декабря 2024, 14:55

636

Andrey Dik

Содержание

Введение

Алгоритм черной дыры (Black Hole Algorithm, BHA) предлагает уникальный взгляд на задачу оптимизации. Созданный в 2013 году А. Хатамлоу, этот алгоритм черпает вдохновение из самых загадочных и мощных объектов во Вселенной — черных дыр. Подобно тому, как черные дыры притягивают все вокруг себя своим гравитационным полем, алгоритм стремится "привлечь" к себе лучшие решения, отсекая менее удачные.

Представьте себе бескрайний космос, заполненный множеством решений, каждое из которых борется за выживание в этом жестоком пространстве. В центре этого хаоса находятся черные дыры — решения с наивысшей качественной оценкой, которые обладают силой притяжения. Алгоритм черной дыры на каждом шаге принимает решения о том, какие звезды будут поглощены черными дырами, а какие продолжат свой путь в поисках более благоприятных условий.

С элементами случайности, алгоритм BHA исследует неизведанные области, стараясь избегать ловушек локальных минимумов. Это делает его мощным инструментом для решения сложных задач, от оптимизации функций до комбинаторных задач и даже настройки гиперпараметров в машинном обучении. В этой статье мы подробно рассмотрим алгоритм черной дыры, его принципы работы, а также его преимущества и недостатки, открывая перед вами мир, где наука и искусство оптимизации переплетаются вместе.

Реализация алгоритма

Алгоритм BHA использует идеи о том, как звезды взаимодействуют с черной дырой, чтобы находить оптимальные решения в заданном пространстве поиска. Процесс работы алгоритма начинается с инициализации, когда создается начальная популяция случайных "звезд", каждая из которых представляет собой потенциальное решение задачи оптимизации. Эти звезды располагаются в пространстве поиска, ограниченном верхними и нижними пределами. В ходе итераций алгоритма, на каждом шаге выделяется лучшее решение, которое обозначается как "черная дыра". Остальные звезды стремятся приблизиться к черной дыре, используя следующее уравнение:

Xi(t+1) = Xi(t) + rand × (XBH - Xi(t))

где:

Xi(t) — текущее положение звезды i
XBH — положение черной дыры
rand —случайное число от 0 до 1

Важным элементом алгоритма является горизонт событий, который вычисляется по формуле:

R = fitBH / Σfiti

Звезды, которые пересекают этот горизонт, "поглощаются" черной дырой и заменяются новыми случайными звездами. Этот механизм поддерживает разнообразие популяции и способствует дальнейшему исследованию пространства.

Алгоритм черной дыры обладает несколькими ключевыми характеристиками. Он имеет простую структуру и вообще не имеет параметров, кроме размера популяции, что делает его простым в использовании и не требующим настройки, что практически не встречается в других алгоритмах оптимизации.

Алгоритм BHA подобен другим популяционным алгоритмам, что означает, что первым шагом в процессе оптимизации является создание начальной популяции случайных решений (начальных звезд) и вычисление целевой функции для оценки значений решений. Лучшее решение в каждой итерации выбирается, как черная дыра, которая затем начинает притягивать другие кандидаты-решения вокруг себя, называемые звездами. Если другие решения-кандидаты приближаются к лучшему полученному решению, они будут "поглощены" лучшим решением.

На рисунке ниже приведена демонстрация работы стратегии поиска алгоритма BHA. Все звезды, находящиеся за горизонтом событий черной дыры, двигаются в сторону ее центра, а звезды, которые пересекли горизонт, будут поглощены, — по сути, материя звезды будет телепортирована в новый участок пространства поиска.

BHA_2

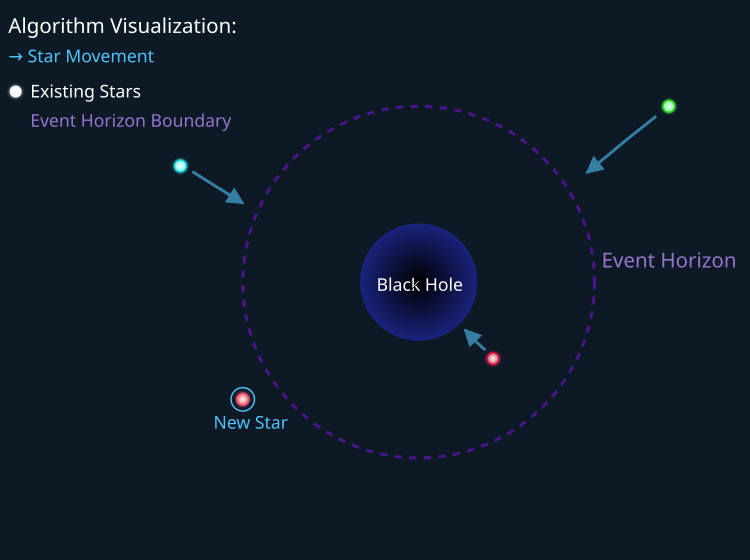
Рисунок 1. Стратегия поиска BHA. Зеленая и синяя звезды двигаются в сторону центра черной дыры, а красная звезда телепортируется в точку "New Star"

Напишем псевдокод алгоритма Black Hole Algorithm (BHA)

// Входные параметры:
N - количество звезд (размер популяции)
tmax - максимальное число итераций

// Инициализация
1. Создать начальные позиции для N звезд:
   Для i = 1 до N:
       Xi = LB + rand × (UB - LB)

2. t = 1

// Основной цикл
3. Пока t ≤ tmax:

    // Вычислить значение целевой функции для каждой звезды
    4. Для каждого Xi вычислить fiti

    // Определить черную дыру
    5. Определить XBH как звезду с наилучшим значением fiti
       fitBH = лучшее значение fiti

    // Обновить позиции звезд
    6. Для каждой звезды Xi:
       Xi(t+1) = Xi(t) + rand × (XBH - Xi(t))

    // Вычислить радиус горизонта событий
    7. R = fitBH / ∑(i=1 до N) fiti

    // Проверить поглощение звезд
    8. Для каждой звезды Xi:
       Если расстояние между Xi и XBH < R:
           Сгенерировать новую позицию для Xi случайным образом
           Xi = LB + rand × (UB - LB)

    9. t = t + 1

// Вернуть лучшее найденное решение
Вернуть XBH

BHA

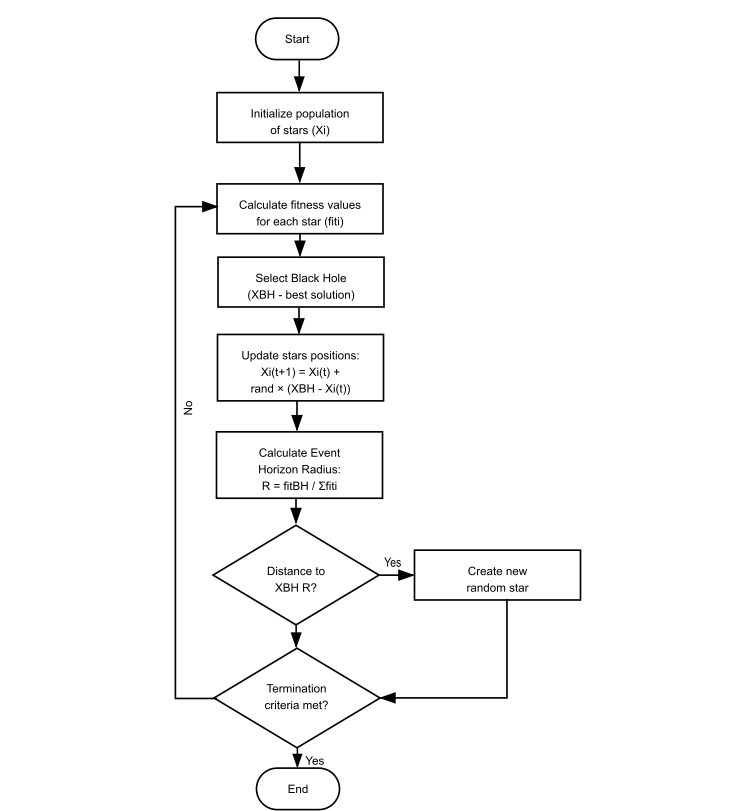
Рисунок 2. Логическая схема работы алгоритма BHA

Определение класса C_AO_BHA (Black Hole Algorithm), который является наследником базового класса C_AO, структура класса:

Конструктор и деструктор:

Конструктор инициализирует базовые параметры алгоритма

Публичные методы:

SetParams () - устанавливает размер популяции из массива параметров
Init () - инициализирует пространство поиска с заданными границами и шагом
Moving () - реализует движение звезд к черной дыре
Revision () - обновляет лучшее найденное решение (черную дыру)

Приватные члены:

blackHoleIndex - хранит индекс лучшего решения в популяции

Параметры оптимизации передаются через массивы:

rangeMinP [] - минимальные значения для каждой координаты
rangeMaxP [] - максимальные значения для каждой координаты
rangeStepP [] - шаг дискретизации для каждой координаты
epochsP - количество итераций алгоритма

Это базовый каркас для реализации алгоритма черной дыры, где основная логика будет реализована в методах Moving() и Revision().

//——————————————————————————————————————————————————————————————————————————————
class C_AO_BHA : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_BHA () { }
  C_AO_BHA ()
  {
    ao_name = "BHA";
    ao_desc = "Black Hole Algorithm";
    ao_link = "https://www.mql5.com/ru/articles/16655";

    popSize = 50;   // Размер популяции

    ArrayResize (params, 1);

    // Инициализация параметров
    params [0].name = "popSize"; params [0].val = popSize;
  }

  void SetParams () // Метод для установки параметров
  {
    popSize = (int)params [0].val;
  }

  bool Init (const double &rangeMinP  [], // Минимальный диапазон поиска
             const double &rangeMaxP  [], // Максимальный диапазон поиска
             const double &rangeStepP [], // Шаг поиска
             const int     epochsP = 0);  // Количество эпох

  void Moving   ();       // Метод перемещения
  void Revision ();       // Метод ревизии

  private: //-------------------------------------------------------------------
  int blackHoleIndex;    // Индекс черной дыры (лучшего решения)
};

Метод "Init" прост и его задача заключается в следующем:

Выполняет начальную инициализацию алгоритма
Вызывает StandardInit для установки диапазонов поиска и шага
Устанавливает начальный индекс черной дыры в 0
Возвращает true при успешной инициализации, false при ошибке

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_BHA::Init (const double &rangeMinP  [],
                     const double &rangeMaxP  [],
                     const double &rangeStepP [],
                     const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  blackHoleIndex = 0; // Инициализация индекса черной дыры
  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Метод "Moving" состоит из нескольких основных блоков:

а) Первичная инициализация (если revision = false):

Создает начальную популяцию звезд со случайными позициями
Позиции генерируются в заданном диапазоне и приводятся к дискретной сетке
Устанавливает флаг "revision" в "true"

б) Основной алгоритм (если revision = true):

Вычисляет сумму значений фитнес-функции всех звезд
Рассчитывает радиус горизонта событий: R = fitBH / Σfiti

в) Обновление позиций звезд:

Для каждой звезды (кроме черной дыры):
1. Вычисляет евклидово расстояние до черной дыры
2. Если расстояние меньше радиуса горизонта:
  - Создает новую случайную звезду
3. Иначе:
  - Обновляет позицию по формуле: Xi(t+1) = Xi(t) + rand × (XBH - Xi(t))
  - Приводит новую позицию к допустимому диапазону и дискретной сетке

Все вычисления производятся с учетом ограничений пространства поиска и шага дискретизации.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BHA::Moving ()
{
  // Начальное случайное позиционирование при первом запуске
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        // Генерация случайной позиции в допустимом диапазоне
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        // Приведение к дискретным значениям согласно шагу
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
    revision = true;
    return;
  }

  // Расчет суммы фитнес-значений для радиуса горизонта событий
  double sumFitness = 0.0;
  for (int i = 0; i < popSize; i++)
  {
    sumFitness += a [i].f;
  }

  // Расчет радиуса горизонта событий
  // R = fitBH / Σfiti
  double eventHorizonRadius = a [blackHoleIndex].f / sumFitness;

  // Обновление позиций звезд
  for (int i = 0; i < popSize; i++)
  {
    // Пропускаем черную дыру
    if (i == blackHoleIndex) continue;

    // Расчет расстояния до черной дыры
    double distance = 0.0;
    for (int c = 0; c < coords; c++)
    {
      double diff = a [blackHoleIndex].c [c] - a [i].c [c];
      distance += diff * diff;
    }
    distance = sqrt (distance);

    // Проверка пересечения горизонта событий
    if (distance < eventHorizonRadius)
    {
      // Звезда поглощена - создаем новую случайную звезду
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
    else
    {
      // Обновление позиции звезды по формуле:
      // Xi(t+1) = Xi(t) + rand × (XBH - Xi(t))
      for (int c = 0; c < coords; c++)
      {
        double rnd = u.RNDfromCI (0.0, 1.0);
        double newPosition = a [i].c [c] + rnd * (a [blackHoleIndex].c [c] - a [i].c [c]);

        // Проверка и коррекция границ
        newPosition = u.SeInDiSp (newPosition, rangeMin [c], rangeMax [c], rangeStep [c]);
        a [i].c [c] = newPosition;
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Метод "Revision" выполняет следующие функции:

Поиск лучшего решения:

Перебирает все звезды популяции
Сравнивает значение фитнес-функции каждой звезды (a [i].f) с текущим лучшим значением (fB)
При нахождении лучшего решения:
- Обновляет лучшее значение фитнес-функции (fB)
- Сохраняет индекс черной дыры (blackHoleIndex)
- Копирует координаты лучшего решения в массив "cB"

Основная цель метода — отслеживание и сохранение лучшего найденного решения (черной дыры) в процессе оптимизации.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BHA::Revision ()
{
  // Поиск лучшего решения (черной дыры)
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      blackHoleIndex = i;
      ArrayCopy (cB, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Тестирование алгоритма BHA показало следующие результаты:

BHA|Black Hole Algorithm|50.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.6833993073000924
25 Hilly's; Func runs: 10000; result: 0.47275633991339616
500 Hilly's; Func runs: 10000; result: 0.2782882943201518
=============================
5 Forest's; Func runs: 10000; result: 0.6821776337288085
25 Forest's; Func runs: 10000; result: 0.3878950941651221
500 Forest's; Func runs: 10000; result: 0.20702263338385946
=============================
5 Megacity's; Func runs: 10000; result: 0.39461538461538465
25 Megacity's; Func runs: 10000; result: 0.20076923076923076
500 Megacity's; Func runs: 10000; result: 0.1076846153846164
=============================
All score: 3.41461 (37.94%)

Результаты работы алгоритма оказались ниже средних, согласно таблице. Однако очевидным достоинством данного алгоритма является то, что он не имеет параметров, кроме размера популяции, что позволяет считать результаты вполне удовлетворительными. При его работе сразу бросилось в глаза застревание в локальных оптимумах, что обусловлено недостатком разнообразия в решениях популяции. Кроме того, для каждой звезды необходимо выполнять ресурсоемкие вычисления евклидова расстояния до черной дыры. Это обстоятельство подтолкнуло к размышлениям о возможных путях исправления существующих недостатков.

В оригинальном алгоритме, когда происходит итерация, звезды перемещаются, в то время как черная дыра остается на месте, хотя в космосе все объекты без исключения находятся в движении. Я решил внести изменения и реализовать перемещение черной дыры на расстояния, определяемые гауссовым распределением относительно ее центра, а также попробовать распределение по степенному закону. Эта адаптация была направлена на улучшение точности сходимости и при этом сохранить способность исследовать новые области пространства решений. Однако, несмотря на эти изменения, результаты не показали улучшения. Это может свидетельствовать о том, что стабильное положение черной дыры (конкретно для данной стратегии поиска) имеет важное значение для эффективности алгоритма, обеспечивая фокусировку звёзд на наиболее перспективных областях. Возможно, стоит рассмотреть другие подходы или комбинации методов, чтобы добиться более значительных улучшений в результатах.

Итак, появилась идея уйти от расчета евклидовых расстояний и вместо этого использовать горизонт событий черной дыры как меру вероятностного поглощения, вместо действительного по факту пересечения горизонта. Вместо применения движения ко всей звезде целиком - применять данную вероятность отдельно к каждой координате.

Тогда, исходя из вышеназванных соображений, напишем новую версию метода "Moving". Изменения коснулись способа расчета горизонта событий, где теперь происходит нормирование среднего значения приспособленности по популяции на расстояние между минимальной и максимальной приспособленностью по популяции. Теперь горизонт событий - вероятность поглощения по отдельным координатам звезд, если поглощения не произошло, то производим обычное перемещение в сторону центра галактического черного монстра по авторской формуле.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BHAm::Moving ()
{
  // Начальное случайное позиционирование при первом запуске
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        // Генерация случайной позиции в допустимом диапазоне
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        // Приведение к дискретным значениям согласно шагу
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  // Расчет среднего значения фитнес-значений для радиуса горизонта событий
  double aveFit = 0.0;
  double maxFit = fB;
  double minFit = a [0].f;

  for (int i = 0; i < popSize; i++)
  {
    aveFit += a [i].f;
    if (a [i].f < minFit) minFit = a [i].f;
  }
  aveFit /= popSize;

  // Расчет радиуса горизонта событий
  double eventHorizonRadius = (aveFit - minFit) / (maxFit - minFit);

  // Обновление позиций звезд
  for (int i = 0; i < popSize; i++)
  {
    // Пропускаем черную дыру
    if (i == blackHoleIndex) continue;

    for (int c = 0; c < coords; c++)
    {
      if (u.RNDprobab () < eventHorizonRadius * 0.01)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
      else
      {
        double rnd = u.RNDfromCI (0.0, 1.0);
        double newPosition = a [i].c [c] + rnd * (a [blackHoleIndex].c [c] - a [i].c [c]);

        // Проверка и коррекция границ
        newPosition = u.SeInDiSp (newPosition, rangeMin [c], rangeMax [c], rangeStep [c]);
        a [i].c [c] = newPosition;
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Давайте проанализируем ключевые различия между двумя версиями алгоритма, начиная с расчета радиуса горизонта событий. В первой версии (BHA) радиус определяется как отношение лучшего решения к сумме всех решений, что приводит к тому, что при большой популяции радиус становится очень маленьким и сильно зависит от абсолютных значений фитнес-функции. Во второй версии (BHAm) радиус нормализован в диапазоне [0,1], что позволяет ему показывать относительное положение среднего значения между минимумом и максимумом, при этом сохраняя независимость от размера популяции и абсолютных значений фитнес-функции.

Теперь рассмотрим механизм поглощения звезд. В первой версии алгоритма проверяется евклидово расстояние до черной дыры, и при поглощении, звезда полностью заменяется новой в случайном месте, что приводит к более резким изменениям в популяции. Вторая версия использует вероятностное поглощение для каждой координаты отдельно, что обеспечивает более плавные изменения в популяции. Здесь коэффициент 0.01 уменьшает вероятность радикальных изменений.

Что касается последствий, первая версия демонстрирует более агрессивную эксплуатацию пространства поиска, что приводит к быстрой сходимости в локальных областях, но также увеличивает риск преждевременной сходимости и может пропустить перспективные области из-за полной замены решений. Вторая версия, напротив, предлагает более мягкую исследовательскую стратегию, обеспечивая лучший баланс между исследованием и эксплуатацией, меньший риск застревания в локальных оптимумах и более медленную, но потенциально более надежную сходимость, а также лучшую способность к диверсификации популяции.

В заключение, первая версия лучше подходит для задач с четко выраженными оптимумами, когда требуется быстрая сходимость и небольшие размерности пространства поиска, в то время как вторая версия более эффективна для сложных многоэкстремальных задач, где важна надежность поиска глобального оптимума, а также для задач большой размерности, требующих более тщательного исследования пространства поиска.

Хотелось бы поделиться своими размышлениями о визуализации работы алгоритмов. Визуализация предоставляет уникальную возможность глубже понять внутренние процессы, происходящие в алгоритмах, и выявить их скрытые механизмы. При определенных настройках мы можем наблюдать, как хаотичные изображения постепенно трансформируются в структурированные узоры. Этот процесс не только демонстрирует технические аспекты работы алгоритма, но и открывает новые идеи и подходы к его оптимизации.

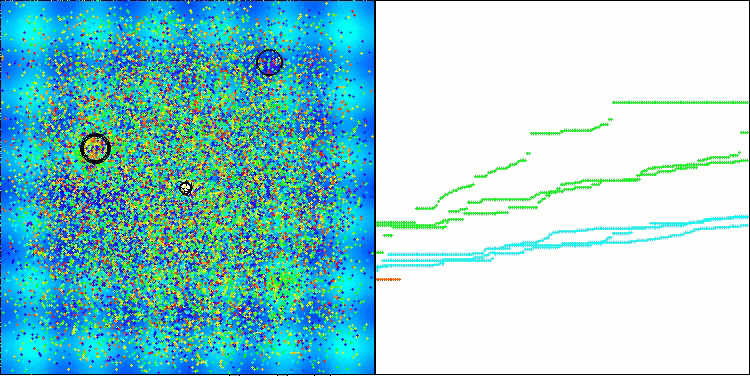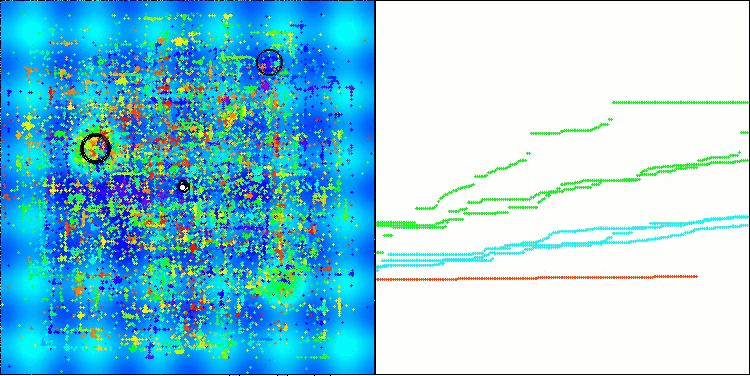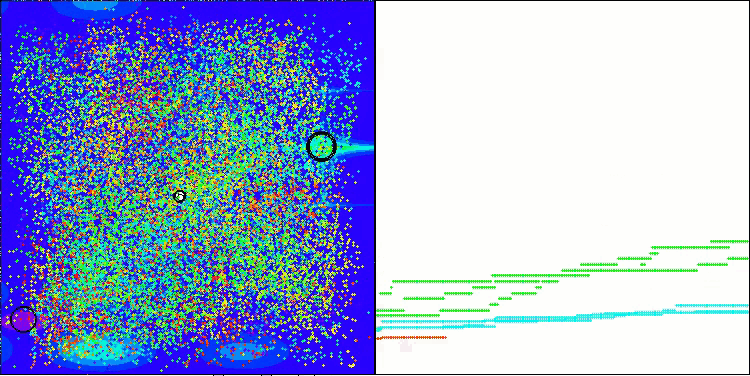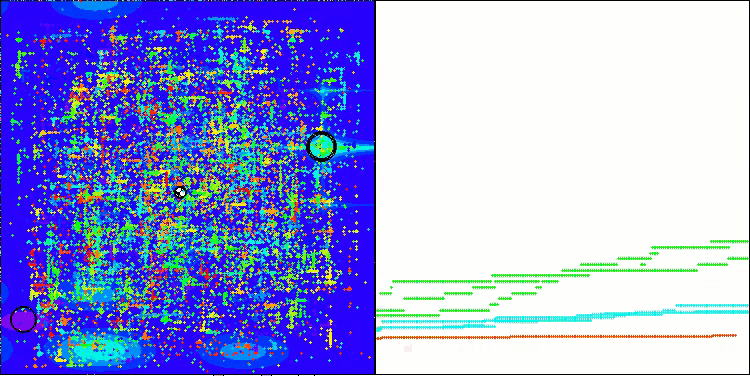
Пример работы алгоритма BHAm при генерации случайной составляющей перемещения звезд в диапазоне [0.0;0.1]

Важно отметить, что визуализация позволяет нам не просто оценивать эффективность алгоритмов, но и выявлять закономерности, которые могут быть неочевидны при традиционном анализе данных. Это способствует более глубокому пониманию их работы и может вдохновить на новые решения и инновации. Таким образом, визуализация становится мощным инструментом, который помогает соединить науку и креативность, открывая новые горизонты для исследования и понимания сложных процессов.

Результаты тестов

Результаты работы модифицированной версии алгоритма BHAm:

BHAm|Black Hole Algorithm M|50.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.752359491007831
25 Hilly's; Func runs: 10000; result: 0.7667459889455067
500 Hilly's; Func runs: 10000; result: 0.34582657277589457
=============================
5 Forest's; Func runs: 10000; result: 0.9359337849703726
25 Forest's; Func runs: 10000; result: 0.801524710041611
500 Forest's; Func runs: 10000; result: 0.2717683112397725
=============================
5 Megacity's; Func runs: 10000; result: 0.6507692307692307
25 Megacity's; Func runs: 10000; result: 0.5164615384615385
500 Megacity's; Func runs: 10000; result: 0.154715384615386
=============================
All score: 5.19611 (57.73%)

По результатам тестирования алгоритм BHAm демонстрирует впечатляющие результаты, не только по сравнению с оригинальной версией, но и в целом по таблице. На визуализации видно, что новая версия с постфиксом "m" действительно избавлена от характерных недостатков оригинала: склонность к застреванию практически сведена на нет, точность сходимости значительно повышена, а разброс результатов уменьшен. При этом сохранена "фамильная черта" алгоритма версии авторов — образование своеобразных сгустков звезд в пространстве и притяжение к определенному аттрактору в пространстве решений.

Hilly

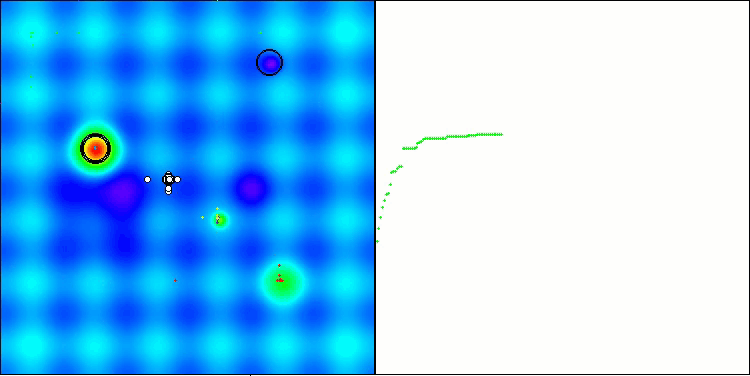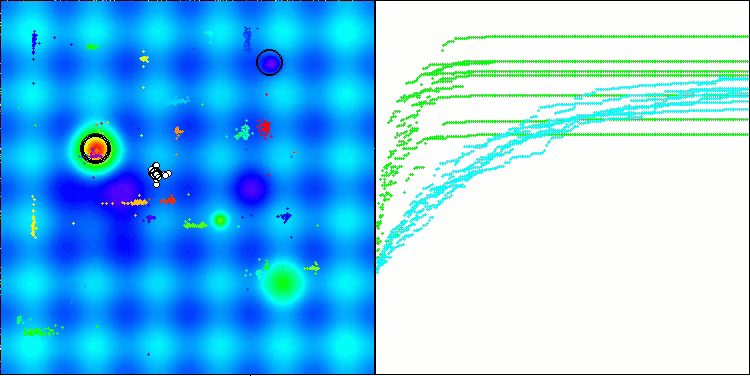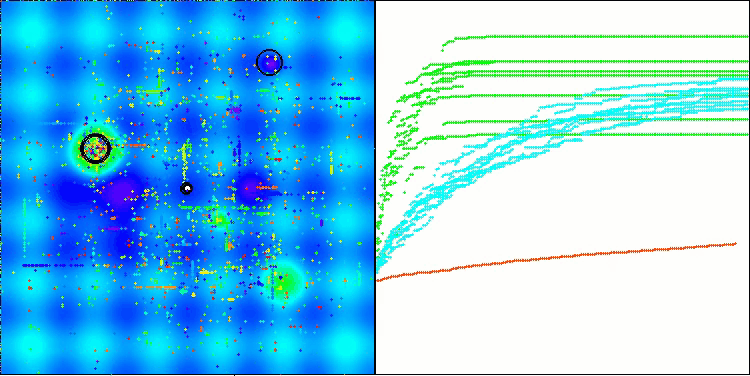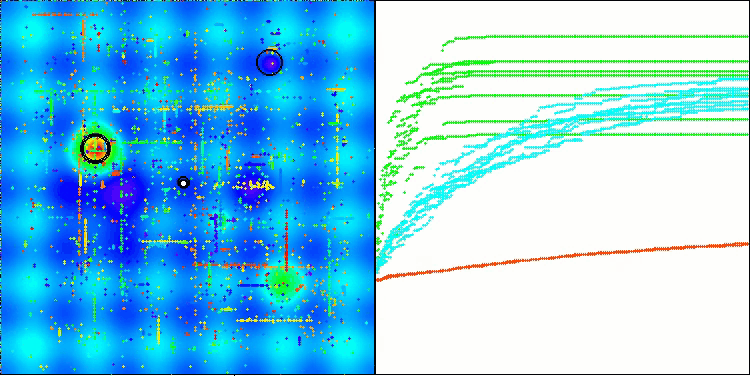
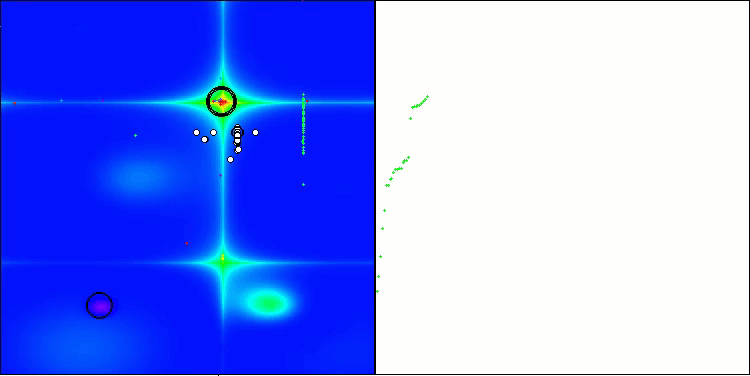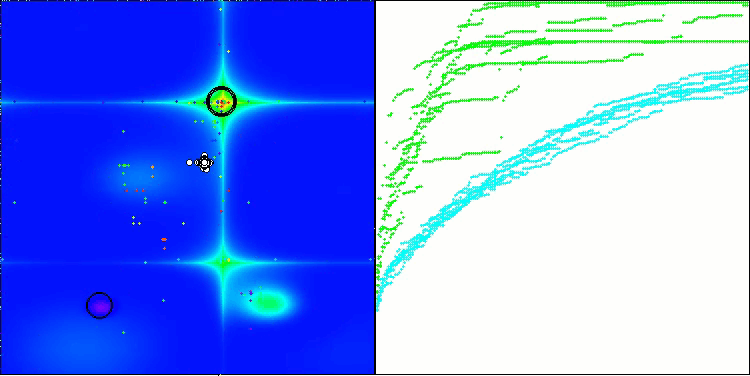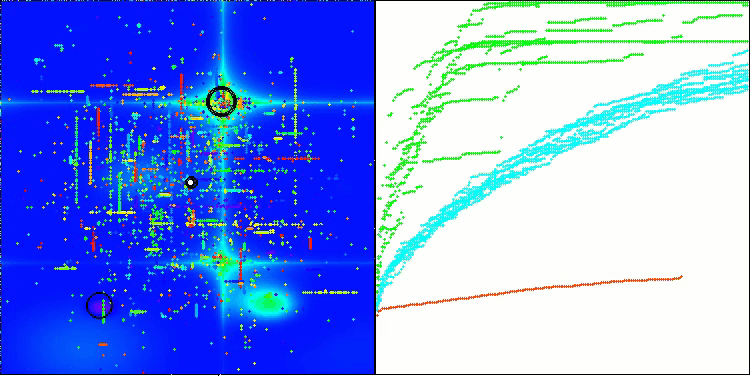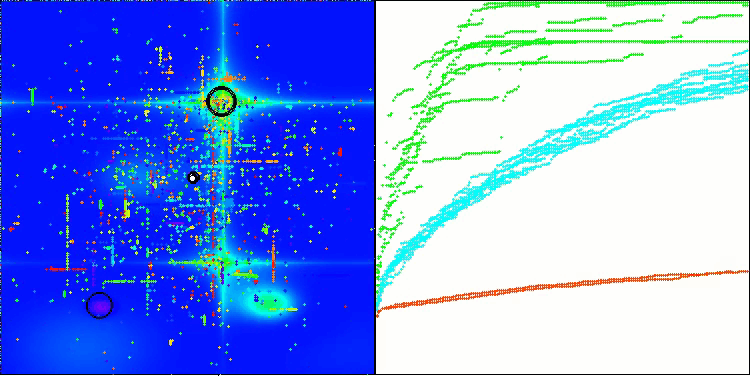
BHAm на тестовой функции Hilly

Forest

BHAm на тестовой функции Forest

Megacity

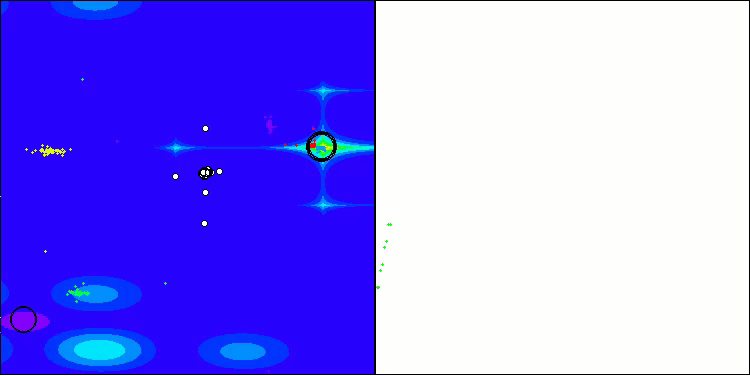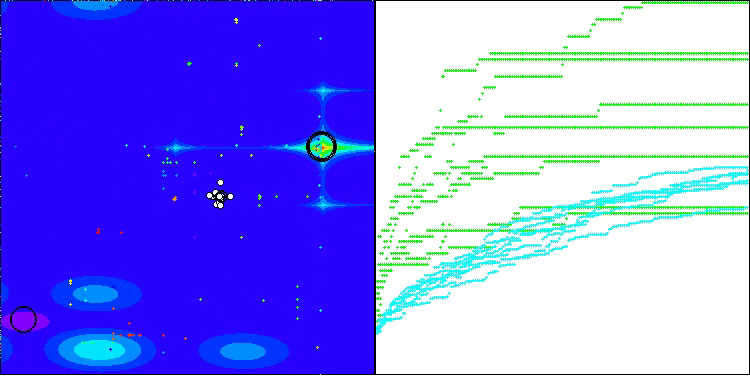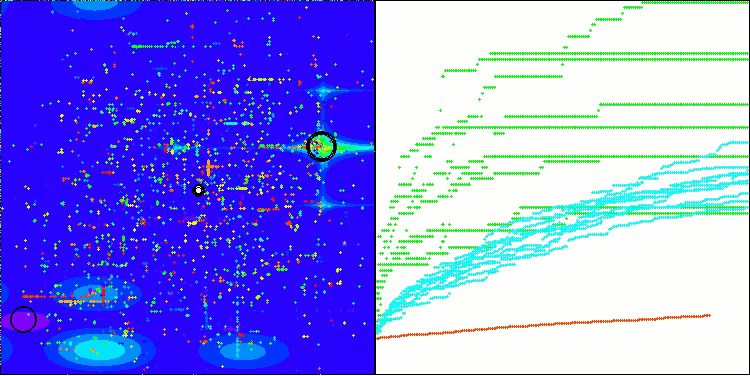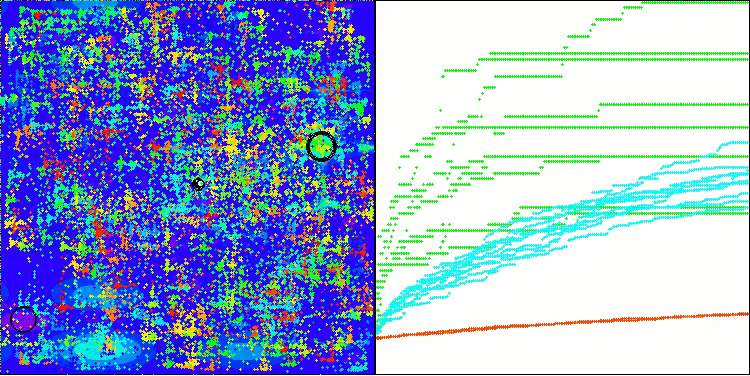
BHAm на тестовой функции Megacity

По итогам тестирования алгоритм BHAm разместился на почетном 11-м месте, это очень хороший результат, учитывая присутствие мощнейших из известных алгоритмов в качестве конкурентов.

№	AO	Description	Hilly			Hilly final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result	% of MAX
№	AO	Description	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Hilly final	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Forest final	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Megacity final	Final result	% of MAX
1	ANS	across neighbourhood search	0,94948	0,84776	0,43857	2,23581	1,00000	0,92334	0,39988	2,32323	0,70923	0,63477	0,23091	1,57491	6,134	68,15
2	CLA	code lock algorithm (joo)	0,95345	0,87107	0,37590	2,20042	0,98942	0,91709	0,31642	2,22294	0,79692	0,69385	0,19303	1,68380	6,107	67,86
3	AMOm	animal migration ptimization M	0,90358	0,84317	0,46284	2,20959	0,99001	0,92436	0,46598	2,38034	0,56769	0,59132	0,23773	1,39675	5,987	66,52
4	(P+O)ES	(P+O) evolution strategies	0,92256	0,88101	0,40021	2,20379	0,97750	0,87490	0,31945	2,17185	0,67385	0,62985	0,18634	1,49003	5,866	65,17
5	CTA	comet tail algorithm (joo)	0,95346	0,86319	0,27770	2,09435	0,99794	0,85740	0,33949	2,19484	0,88769	0,56431	0,10512	1,55712	5,846	64,96
6	SDSm	stochastic diffusion search M	0,93066	0,85445	0,39476	2,17988	0,99983	0,89244	0,19619	2,08846	0,72333	0,61100	0,10670	1,44103	5,709	63,44
7	AAm	archery algorithm M	0,91744	0,70876	0,42160	2,04780	0,92527	0,75802	0,35328	2,03657	0,67385	0,55200	0,23738	1,46323	5,548	61,64
8	ESG	evolution of social groups (joo)	0,99906	0,79654	0,35056	2,14616	1,00000	0,82863	0,13102	1,95965	0,82333	0,55300	0,04725	1,42358	5,529	61,44
9	SIA	simulated isotropic annealing (joo)	0,95784	0,84264	0,41465	2,21513	0,98239	0,79586	0,20507	1,98332	0,68667	0,49300	0,09053	1,27020	5,469	60,76
10	ACS	artificial cooperative search	0,75547	0,74744	0,30407	1,80698	1,00000	0,88861	0,22413	2,11274	0,69077	0,48185	0,13322	1,30583	5,226	58,06
11	BHAm	black hole algorithm M	0,75236	0,76675	0,34583	1,86493	0,93593	0,80152	0,27177	2,00923	0,65077	0,51646	0,15472	1,32195	5,196	57,73
12	ASO	anarchy society optimization	0,84872	0,74646	0,31465	1,90983	0,96148	0,79150	0,23803	1,99101	0,57077	0,54062	0,16614	1,27752	5,178	57,54
13	AOSm	atomic orbital search M	0,80232	0,70449	0,31021	1,81702	0,85660	0,69451	0,21996	1,77107	0,74615	0,52862	0,14358	1,41835	5,006	55,63
14	TSEA	turtle shell evolution algorithm (joo)	0,96798	0,64480	0,29672	1,90949	0,99449	0,61981	0,22708	1,84139	0,69077	0,42646	0,13598	1,25322	5,004	55,60
15	DE	differential evolution	0,95044	0,61674	0,30308	1,87026	0,95317	0,78896	0,16652	1,90865	0,78667	0,36033	0,02953	1,17653	4,955	55,06
16	CRO	chemical reaction optimisation	0,94629	0,66112	0,29853	1,90593	0,87906	0,58422	0,21146	1,67473	0,75846	0,42646	0,12686	1,31178	4,892	54,36
17	BSA	bird swarm algorithm	0,89306	0,64900	0,26250	1,80455	0,92420	0,71121	0,24939	1,88479	0,69385	0,32615	0,10012	1,12012	4,809	53,44
18	HS	harmony search	0,86509	0,68782	0,32527	1,87818	0,99999	0,68002	0,09590	1,77592	0,62000	0,42267	0,05458	1,09725	4,751	52,79
19	SSG	saplings sowing and growing	0,77839	0,64925	0,39543	1,82308	0,85973	0,62467	0,17429	1,65869	0,64667	0,44133	0,10598	1,19398	4,676	51,95
20	BCOm	bacterial chemotaxis optimization M	0,75953	0,62268	0,31483	1,69704	0,89378	0,61339	0,22542	1,73259	0,65385	0,42092	0,14435	1,21912	4,649	51,65
21	ABO	african buffalo optimization	0,83337	0,62247	0,29964	1,75548	0,92170	0,58618	0,19723	1,70511	0,61000	0,43154	0,13225	1,17378	4,634	51,49
22	(PO)ES	(PO) evolution strategies	0,79025	0,62647	0,42935	1,84606	0,87616	0,60943	0,19591	1,68151	0,59000	0,37933	0,11322	1,08255	4,610	51,22
23	TSm	tabu search M	0,87795	0,61431	0,29104	1,78330	0,92885	0,51844	0,19054	1,63783	0,61077	0,38215	0,12157	1,11449	4,536	50,40
24	BSO	brain storm optimization	0,93736	0,57616	0,29688	1,81041	0,93131	0,55866	0,23537	1,72534	0,55231	0,29077	0,11914	0,96222	4,498	49,98
25	WOAm	wale optimization algorithm M	0,84521	0,56298	0,26263	1,67081	0,93100	0,52278	0,16365	1,61743	0,66308	0,41138	0,11357	1,18803	4,476	49,74
26	AEFA	artificial electric field algorithm	0,87700	0,61753	0,25235	1,74688	0,92729	0,72698	0,18064	1,83490	0,66615	0,11631	0,09508	0,87754	4,459	49,55
27	AEO	artificial ecosystem-based optimization algorithm	0,91380	0,46713	0,26470	1,64563	0,90223	0,43705	0,21400	1,55327	0,66154	0,30800	0,28563	1,25517	4,454	49,49
28	ACOm	ant colony optimization M	0,88190	0,66127	0,30377	1,84693	0,85873	0,58680	0,15051	1,59604	0,59667	0,37333	0,02472	0,99472	4,438	49,31
29	BFO-GA	bacterial foraging optimization - ga	0,89150	0,55111	0,31529	1,75790	0,96982	0,39612	0,06305	1,42899	0,72667	0,27500	0,03525	1,03692	4,224	46,93
30	SOA	simple optimization algorithm	0,91520	0,46976	0,27089	1,65585	0,89675	0,37401	0,16984	1,44060	0,69538	0,28031	0,10852	1,08422	4,181	46,45
31	ABHA	artificial bee hive algorithm	0,84131	0,54227	0,26304	1,64663	0,87858	0,47779	0,17181	1,52818	0,50923	0,33877	0,10397	0,95197	4,127	45,85
32	ACMO	atmospheric cloud model optimization	0,90321	0,48546	0,30403	1,69270	0,80268	0,37857	0,19178	1,37303	0,62308	0,24400	0,10795	0,97503	4,041	44,90
33	ADAMm	adaptive moment estimation M	0,88635	0,44766	0,26613	1,60014	0,84497	0,38493	0,16889	1,39880	0,66154	0,27046	0,10594	1,03794	4,037	44,85
34	ATAm	artificial tribe algorithm M	0,71771	0,55304	0,25235	1,52310	0,82491	0,55904	0,20473	1,58867	0,44000	0,18615	0,09411	0,72026	3,832	42,58
35	ASHA	artificial showering algorithm	0,89686	0,40433	0,25617	1,55737	0,80360	0,35526	0,19160	1,35046	0,47692	0,18123	0,09774	0,75589	3,664	40,71
36	ASBO	adaptive social behavior optimization	0,76331	0,49253	0,32619	1,58202	0,79546	0,40035	0,26097	1,45677	0,26462	0,17169	0,18200	0,61831	3,657	40,63
37	MEC	mind evolutionary computation	0,69533	0,53376	0,32661	1,55569	0,72464	0,33036	0,07198	1,12698	0,52500	0,22000	0,04198	0,78698	3,470	38,55
38	IWO	invasive weed optimization	0,72679	0,52256	0,33123	1,58058	0,70756	0,33955	0,07484	1,12196	0,42333	0,23067	0,04617	0,70017	3,403	37,81
39	Micro-AIS	micro artificial immune system	0,79547	0,51922	0,30861	1,62330	0,72956	0,36879	0,09398	1,19233	0,37667	0,15867	0,02802	0,56335	3,379	37,54
40	COAm	cuckoo optimization algorithm M	0,75820	0,48652	0,31369	1,55841	0,74054	0,28051	0,05599	1,07704	0,50500	0,17467	0,03380	0,71347	3,349	37,21
41	SDOm	spiral dynamics optimization M	0,74601	0,44623	0,29687	1,48912	0,70204	0,34678	0,10944	1,15826	0,42833	0,16767	0,03663	0,63263	3,280	36,44
42	NMm	Nelder-Mead method M	0,73807	0,50598	0,31342	1,55747	0,63674	0,28302	0,08221	1,00197	0,44667	0,18667	0,04028	0,67362	3,233	35,92
43	FAm	firefly algorithm M	0,58634	0,47228	0,32276	1,38138	0,68467	0,37439	0,10908	1,16814	0,28667	0,16467	0,04722	0,49855	3,048	33,87
44	GSA	gravitational search algorithm	0,64757	0,49197	0,30062	1,44016	0,53962	0,36353	0,09945	1,00260	0,32667	0,12200	0,01917	0,46783	2,911	32,34
45	BFO	bacterial foraging optimization	0,61171	0,43270	0,31318	1,35759	0,54410	0,21511	0,05676	0,81597	0,42167	0,13800	0,03195	0,59162	2,765	30,72

Выводы

Black Hole Algorithm (BHA) представляет собой элегантный пример того, как фундаментальные законы природы могут быть преобразованы в эффективный инструмент оптимизации. В основе алгоритма лежит простая и интуитивно понятная идея гравитационного притяжения потенциальных решений к центральному, наилучшему решению, выступающему в роли черной дыры. В процессе эволюции алгоритма мы наблюдаем удивительный феномен: звезды-решения, двигаясь к своему галактическому центру, могут обнаруживать новые, более мощные центры притяжения - лучшие решения, что приводит к динамическому изменению структуры поискового пространства. Это наглядно демонстрирует, как природные механизмы самоорганизации могут быть эффективно использованы в алгоритмической оптимизации.

Практика показывает замечательную закономерность: часто именно упрощение и переосмысление базовых идей, а не их усложнение, приводит к неожиданно впечатляющим результатам. В мире алгоритмической оптимизации редко встречается ситуация, когда усложнение логики поиска приводит к значительному улучшению производительности.

Данный пример ярко иллюстрирует важный принцип: авторитет создателей алгоритма или популярность метода не должны восприниматься как окончательная гарантия их оптимальности. Любой метод, даже самый успешный, может быть улучшен как с точки зрения вычислительной эффективности, так и с точки зрения качества получаемых результатов. Модифицированная версия алгоритма (BHAm) служит прекрасным примером такого улучшения. Сохранив концептуальную простоту оригинального метода и отсутствие внешних параметров настройки, она демонстрирует значительное повышение производительности и скорости сходимости.

Этот опыт подводит нас к фундаментальному выводу: инновации и эксперименты должны быть неотъемлемой частью любой профессиональной деятельности. Будь то разработка алгоритмов машинного обучения или создание торговых стратегий, смелость в исследовании новых подходов и готовность переосмыслить существующие методы часто становятся ключом к достижению прорывных результатов.

В конечном счете, прогресс в области оптимизации, как и в любой другой сфере, движим не слепым следованием авторитетам, а непрерывным поиском новых, более эффективных решений, основанных на глубоком понимании фундаментальных принципов и готовности к творческому эксперименту.

Tab

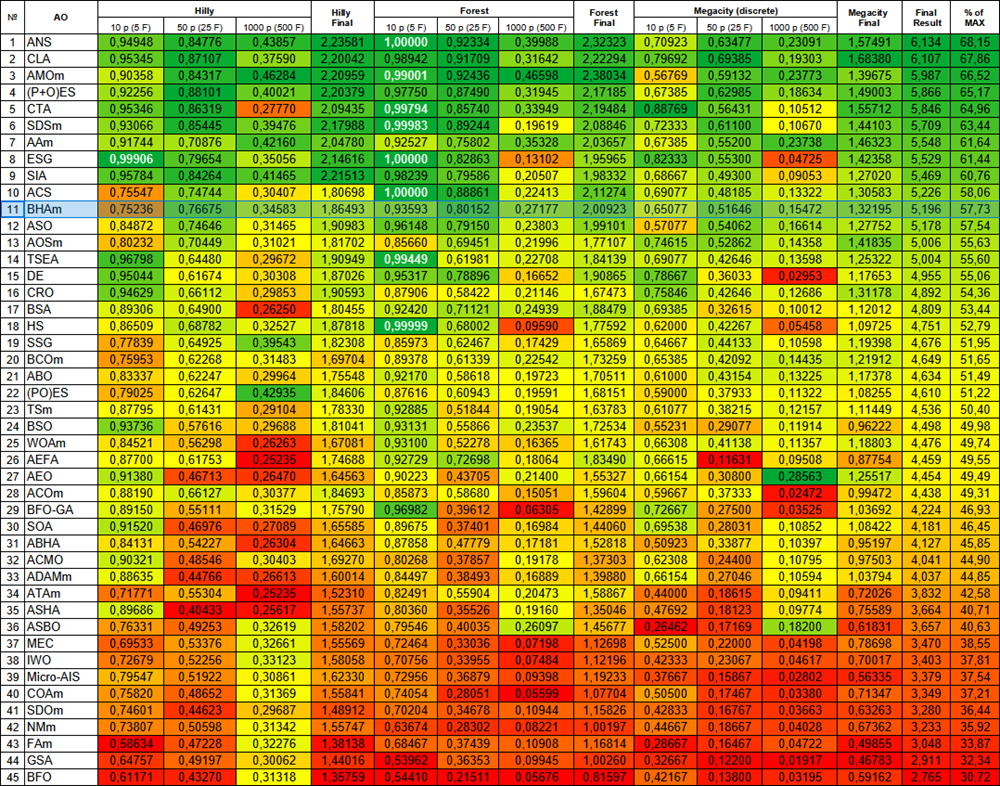
Рисунок 3. Цветовая градация алгоритмов по соответствующим тестам. Белым цветом подсвечены результаты больше или равные 0.99

Chart

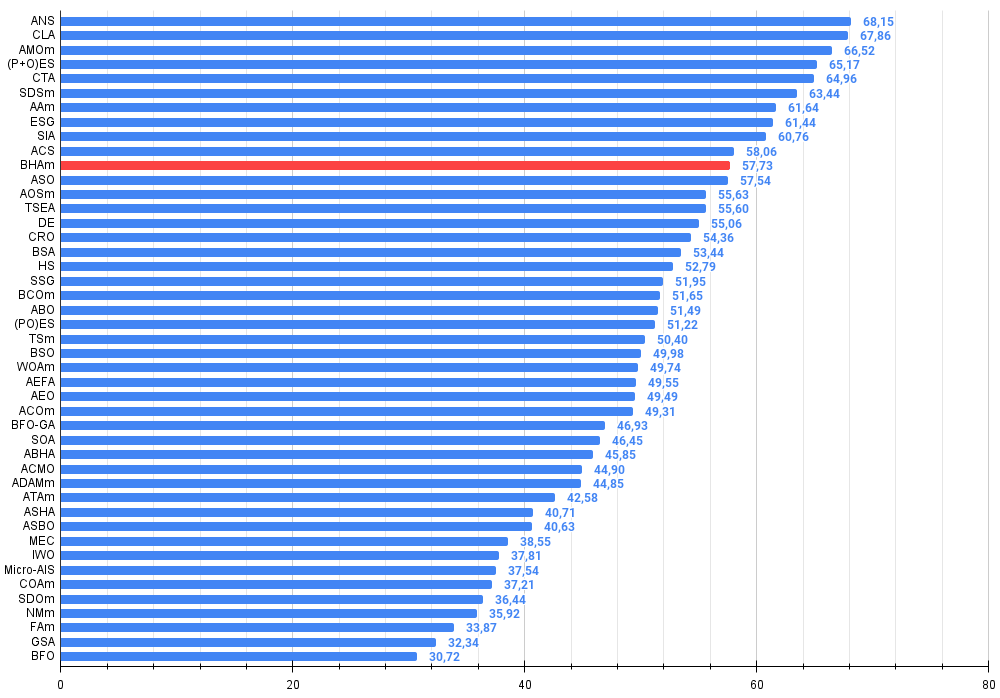
Рисунок 4. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше, где 100 - максимально возможный теоретический результат, в архиве скрипт для расчета рейтинговой таблицы)

Плюсы и минусы алгоритма BHAm:

Плюсы:

Из внешних параметров только размер популяции.
Простая реализация.
Очень быстрый.
Хорошо работает на задачах больших размерностей.

Минусы:

Большой разброс результатов на задачах малой размерности.
Склонность к застреванию на задачах малой размерности.

К статье прикреплён архив с актуальными версиями кодов алгоритмов. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.

github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5

Программы, используемые в статье

#	Имя	Тип	Описание
1	#C_AO.mqh	Включаемый файл	Родительский класс популяционных алгоритмов оптимизации
2	#C_AO_enum.mqh	Включаемый файл	Перечисление популяционных алгоритмов оптимизации
3	TestFunctions.mqh	Включаемый файл	Библиотека тестовых функций
4	TestStandFunctions.mqh	Включаемый файл	Библиотека функций тестового стенда
5	Utilities.mqh	Включаемый файл	Библиотека вспомогательных функций
6	CalculationTestResults.mqh	Включаемый файл	Скрипт для расчета результатов в сравнительную таблицу
7	Testing AOs.mq5	Скрипт	Единый испытательный стенд для всех популяционных алгоритмов оптимизации
8	Simple use of population optimization algorithms.mq5	Скрипт	Простой пример использования популяционных алгоритмов оптимизации без визуализации
9	Test_AO_BHAm.mq5	Скрипт	Испытательный стенд для BHAm

Прикрепленные файлы |

Загрузить ZIP

BHAm.ZIP (145.64 KB)

Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Другие статьи автора

Перейти к обсуждению на форуме трейдеров

Нейросети в трейдинге: Гибридный торговый фреймворк с предиктивным кодированием (Окончание)

Продолжаем рассмотрение гибридной торговой системы StockFormer, которая объединяет предиктивное кодирование и алгоритмы обучения с подкреплением для анализа финансовых временных рядов. Основой системы служат три ветви Transformer с механизмом Diversified Multi-Head Attention (DMH-Attn), позволяющим выявлять сложные паттерны и взаимосвязи между активами. Ранее мы познакомились с теоретическими аспектами фреймворка и реализовали механизмы DMH-Attn, а сегодня поговорим об архитектуре моделей и их обучении.

Многомодульный торговый робот на Python и MQL5 (Часть I): Создание базовой архитектуры и первых модулей

Разрабатываем модульную торговую систему, объединяющую Python для анализа данных с MQL5 для исполнения сделок. Четыре независимых модуля параллельно следят за разными аспектами рынка: объемами, арбитражем, экономикой и рисками, а для анализа используют RandomForest с 400 деревьями. Особый упор сделан на риск-менеджмент, ведь без грамотного управления рисками даже самые продвинутые торговые алгоритмы бесполезны.

Переосмысливаем классические стратегии на языке Python: Пересечения скользящих средних

В этой статье мы пересмотрим классическую стратегию пересечений скользящих средних для оценки ее текущей эффективности. Учитывая, сколько времени прошло с момента ее создания, исследуем потенциальные улучшения, которые ИИ может привнести в эту традиционную торговую стратегию. С помощью методов искусственного интеллекта мы постараемся применить передовые возможнности прогнозирования для потенциальной оптимизации точек входы и выхода из рынка, адаптировать их к меняющимся рыночным условиям и повысить общую эффективность по сравнению с традиционными подходами.

Возможности Мастера MQL5, которые вам нужно знать (Часть 25): Тестирование и торговля на нескольких таймфреймах

Стратегии, основанные на нескольких таймфреймах, по умолчанию не могут быть протестированы в советниках, собранных с помощью Мастера, из-за архитектуры кода MQL5, используемой в классах сборки. Мы рассмотрим способ обхода этого ограничения для стратегий, которые предполагают использование нескольких таймфреймов на примере квадратичной скользящей средней.