MetaTrader 5 / 示例
English Русский Español Deutsch 日本語 Português
preview
黑洞算法（BHA）

黑洞算法（BHA）

MetaTrader 5 — 示例 |
418 0
Andrey Dik
Andrey Dik

内容

  1. 概述
  2. 算法的实现
  3. 测试结果


概述

黑洞算法（BHA）为优化问题提供了独特的视角。该算法由 A. Hatamlou 于 2013 年创建，灵感汲取自宇宙中最神秘、最强大的天体：黑洞。就如同黑洞靠引力场吸引周围的一切，该算法寻求“吸引”最佳解到自己身上，切除不太成功的那些。

想象一个广阔的空间里充满了许多决定，每个都在这个恶劣的环境中挣扎求生。在这种混乱的中心是黑洞 — 重力具有最高质量等级的解。黑洞算法在每一步都会决定哪些星辰将被黑洞吞噬，哪些星辰将寻找更有利的条件来继续它们的行程。

搭配随机性元素，BHA 算法会探索未知领域，尝试避免局部最小陷阱。这令其成为解决复杂问题的强大工具，从函数优化到组合问题，甚至机器学习中的超参数调整。在本文中，我们将详细考察黑洞算法、它如何工作、及其优缺点，打开一个优化科学与艺术交织在一起的世界。


算法的实现

BHA 算法采用的思路，是有关星辰如何与黑洞相互作用，以便在给定的搜索空间中寻找最优解。算法操作从初始化开始，其中创建随机“星辰”的初始群体，每颗星辰代表优化问题的一个潜在解。这些星辰位于由上限和下限限制的搜索空间之中。在算法的迭代期间，每一步都会选择最佳解，其被指定为“黑洞”。其余星辰倾向于遵循以下方程向黑洞靠拢：

Xi(t+1) = Xi(t) + rand × (XBH - Xi(t))

其中：

  • Xi(t) — 索引 i 星辰的当前位置
  • XBH — 黑洞位置
  • rand — 从 0 到 1 的随机数

该算法的一个重要元素是按以下公式计算的事件视界：

R = fitBH / Σfiti

穿过这个视界的星辰被黑洞“吞噬”，并由新的随机星辰所取代。这种机制维护了群体多样性，并促进了对空间的进一步探索。

黑洞算法有几个关键特征。它结构简单，且除了群体大小外，没有任何参数，故易于使用。它不需要调谐，这在其它优化算法中几乎闻所未闻。

BHA 算法与其它基于群体的算法类似，这意味着优化的第一步是按随机解创建一个初始群体（初始星辰），并计算意向函数来估算解的数值。每次迭代中的最佳解都被选出，像是一个黑洞，然后其开始吸引周围的其它候选解。它们被称为星辰。如果其它候选解接近获得的最佳解，它们将被最佳解“吸引”。

下图显示的是 BHA 算法搜索策略的动作演示。黑洞事件视界之外的所有星辰都朝着其中心移动，穿过视界的星辰被吸收 — 本质上，星辰物质将被传送到搜索空间的新区域。

BHA_2

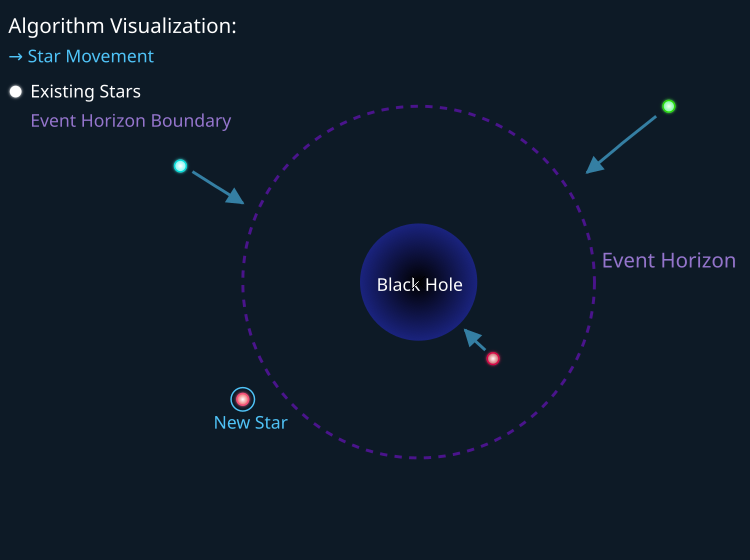
图例 1. BHA 搜索策略。绿色和蓝色的星辰朝向黑洞中心移动，红色的星辰传送到“新星”点。

我们为黑洞算法（BHA）编写一段伪代码

// 输入:
N - 星辰数量（群体大小）
tmax - 最大迭代次数

// 初始化
1. 为 N 颗星辰创建初始位置：
   For i = 1 to N:
       Xi = LB + rand × (UB - LB)

2. t = 1

// 主循环
3. While t ≤ tmax:
    
// 计算每颗星辰的意向函数
    4. For each Xi calculate fiti

// 定义一个黑洞
    5. 判定 XBH 为具有最佳 fiti 值的星辰
       fitBH = best fiti value

// 更新恒星位置
    6. For each Xi star:
       Xi(t+1) = Xi(t) + rand × (XBH - Xi(t))

// 计算事件视界的半径
    7. R = fitBH / ∑(i=1 to N) fiti

// 检查星吸收率
    8. For each Xi star:
       如果 Xi 和 XBH 之间的距离 < R:
           为 Xi 随机生成一个新位置
           Xi = LB + rand × (UB - LB)

    9. t = t + 1

// 返回找到的最佳解
Return XBH

BHA

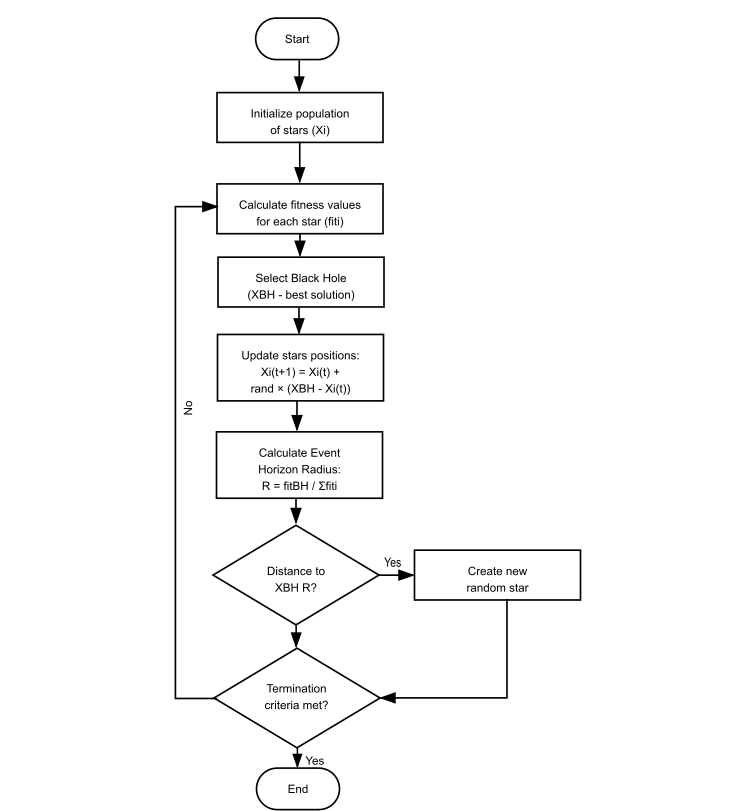
图例 2. BHA 算法运算的逻辑结构

C_AO_BHA（黑洞算法）类的定义，它是 C_AO 基类的后代，类结构：

构造函数和析构函数：

  • 构造函数初始化算法的基本参数。
公开方法：
  • SetParams () - 自参数数组设置群体大小
  • Init () - 按给定的边界和步骤初始化搜索空间
  • Moving () - 实现星辰朝向黑洞的运动
  • Revision () - 更新找到的最佳解（黑洞）
私密成员：
  • blackHoleIndex - 存储群体中最佳解的索引
优化参数通过数组传递：
  • rangeMinP [] - 每个坐标的最小值
  • rangeMaxP [] - 每个坐标的最大值
  • rangeStepP [] - 每个坐标的离散化步骤
  • epochsP - 算法迭代次数

    这是实现黑洞算法的基本框架，其中主要逻辑将在 Moving() 和 Revision() 方法中实现。

    //——————————————————————————————————————————————————————————————————————————————
class C_AO_BHA : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_BHA () { }
  C_AO_BHA ()
  {
    ao_name = "BHA";
    ao_desc = "Black Hole Algorithm";
    ao_link = "https://www.mql5.com/en/articles/16655";

    popSize = 50;   // Population size

    ArrayResize (params, 1);

    // Initialize parameters
    params [0].name = "popSize"; params [0].val = popSize;
  }

  void SetParams () // Method for setting parameters
  {
    popSize = (int)params [0].val;
  }

  bool Init (const double &rangeMinP  [], // Minimum search range
             const double &rangeMaxP  [], // Maximum search range
             const double &rangeStepP [], // Search step
             const int     epochsP = 0);  // Number of epochs

  void Moving   ();       // Moving method
  void Revision ();       // Revision method

  private: //-------------------------------------------------------------------
  int blackHoleIndex;    // Black hole index (best solution)
};
    Init方法很简单，其任务如下：

    • 初始化算法
    • 调用 StandardInit 设置搜索范围和步骤
    • 将黑洞的初始索引设置为 0
    • 初始化成功时返回 “true”，出错时返回 “false”。
    //——————————————————————————————————————————————————————————————————————————————
bool C_AO_BHA::Init (const double &rangeMinP  [],
                     const double &rangeMaxP  [],
                     const double &rangeStepP [],
                     const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  blackHoleIndex = 0; // Initialize black hole index
  return true;
}
//——————————————————————————————————————————————————————————————————————————————

    Moving 方法由若干主要模块组成：

    a）主要初始化（如果 revision = false）：

    • 按随机位置创建星辰的初始群体
    • 在给定范围内生成位置，并降至离散网格
    • 将 revision 标志设置为 true

    b）基本算法（如果 revision = true）：

    • 计算所有星辰的适应度函数值之和
    • 计算事件视界的半径：R = fitBH / Σfiti

    c）更新星辰位置：

    • 对于每颗星辰（黑洞除外）：
      1. 计算到黑洞的欧几里得距离
      2. 如果距离小于视界半径：
        • 创建新的随机星辰
      3. 否则：
        • 遵循以下公式更新位置：Xi(t+1) = Xi(t) + rand × (XBH - Xi(t))
        • 将新位置带入可接受的范围和离散网格

    所有执行的计算都参考搜索空间和离散化步骤的限制。

    //——————————————————————————————————————————————————————————————————————————————
void C_AO_BHA::Moving ()
{
  // Initial random positioning on first run
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        // Generate a random position within the allowed range
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        // Convert to discrete values according to step
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
    revision = true;
    return;
  }

  // Calculate the sum of fitness values for the radius of the event horizon
  double sumFitness = 0.0;
  for (int i = 0; i < popSize; i++)
  {
    sumFitness += a [i].f;
  }

  // Calculate the radius of the event horizon
  // R = fitBH / Σfiti
  double eventHorizonRadius = a [blackHoleIndex].f / sumFitness;

  // Update star positions
  for (int i = 0; i < popSize; i++)
  {
    // Skip the black hole
    if (i == blackHoleIndex) continue;

    // Calculate the distance to the black hole
    double distance = 0.0;
    for (int c = 0; c < coords; c++)
    {
      double diff = a [blackHoleIndex].c [c] - a [i].c [c];
      distance += diff * diff;
    }
    distance = sqrt (distance);

    // Check for event horizon crossing
    if (distance < eventHorizonRadius)
    {
      // Star is consumed - create a new random star
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
    else
    {
      // Update the star position using the equation:
      // Xi(t+1) = Xi(t) + rand × (XBH - Xi(t))
      for (int c = 0; c < coords; c++)
      {
        double rnd = u.RNDfromCI (0.0, 1.0);
        double newPosition = a [i].c [c] + rnd * (a [blackHoleIndex].c [c] - a [i].c [c]);

        // Check and correct the boundaries
        newPosition = u.SeInDiSp (newPosition, rangeMin [c], rangeMax [c], rangeStep [c]);
        a [i].c [c] = newPosition;
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

    Revision 方法执行以下功能：

    查找最佳解：

    • 遍历群体中的所有星辰
    • 将每颗星辰的适应度值 (a[i].f) 与当前最佳值 (fB) 进行比较
    • 在寻找最佳解时：
      • 更新最佳适应度函数值 (fB)
      • 存储黑洞索引（blackHoleIndex）
      • 将最佳解的坐标复制到 cB 数组

      该方法的主要目标是在优化过程中跟踪并保存找到的最佳解（黑洞）。

      //——————————————————————————————————————————————————————————————————————————————
void C_AO_BHA::Revision ()
{
  // Find the best solution (black hole)
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      blackHoleIndex = i;
      ArrayCopy (cB, a [i].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

      测试 BHA 算法显示以下结果：

      BHA|Black Hole Algorithm|50.0|
      =============================
      5 Hilly's; Func runs: 10000; result: 0.6833993073000924
      25 Hilly's; Func runs: 10000; result: 0.47275633991339616
      500 Hilly's; Func runs: 10000; result: 0.2782882943201518
      =============================
      5 Forest's; Func runs: 10000; result: 0.6821776337288085
      25 Forest's; Func runs: 10000; result: 0.3878950941651221
      500 Forest's; Func runs: 10000; result: 0.20702263338385946
      =============================
      5 Megacity's; Func runs: 10000; result: 0.39461538461538465
      25 Megacity's; Func runs: 10000; result: 0.20076923076923076
      500 Megacity's; Func runs: 10000; result: 0.1076846153846164
      =============================
      All score: 3.41461 (37.94%)

      根据表格，结果低于平均水平。然而，该算法的明显优势是它除了群体大小之外没有其它参数，这令我们能够认定结果相当令人满意。在它运行期间，我立即注意到，由于群体决策缺乏多样性，它陷入了局部最优。此外，对于每颗星辰到黑洞的欧几里得距离，都需要进行资源密集型计算。这种境况促使人们反思纠正现有缺陷的可能途径。

      在原版算法中，当迭代发生时，星辰会移动，而黑洞会保持在原位，即便空间中的所有物体其实都在运动。我决定进行一些修改，并实现黑洞按高斯分布相对于其中心的距离移动，并尝试幂律分布。这种适配旨在提升收敛精度，同时保持探索解空间新区域的能力。然而，尽管有这些变化，结果并没有显示出改善。这可能表明黑洞的稳定位置（特别是对于给定的搜索策略）对于算法的效率很重要，确保星辰专注于最有前景的区域。或许值得研究其它方式、或方法的组合，以达成更大的结果改进。

      故此，我们想到的是放弃计算欧几里得距离，而是使用黑洞的事件视界作为概率吸引的量值，而非实际的视界穿越。替代将运动应用于整个星辰，而是将该概率分别应用到每个坐标。

      然后，基于上述研究，我们将编写一个新版本的 Moving 方法。这些变化影响了事件视界的计算方法，其中群体的平均适应度值现在被归一化为群体的最小适应度、和最大适应度之间的距离。现在事件视界是在星辰的各个坐标处被吸引的概率；如果没有发生吸引，那么我们根据作者的方程朝向河系黑怪的中心进行通常的运动。

      //——————————————————————————————————————————————————————————————————————————————
void C_AO_BHAm::Moving ()
{
  // Initial random positioning on first run
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        // Generate a random position within the allowed range
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        // Convert to discrete values according to step
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }
    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  // Calculate the average fitness values for the event horizon radius
  double aveFit = 0.0;
  double maxFit = fB;
  double minFit = a [0].f;

  for (int i = 0; i < popSize; i++)
  {
    aveFit += a [i].f;
    if (a [i].f < minFit) minFit = a [i].f;
  }
  aveFit /= popSize;

  // Calculate the radius of the event horizon
  double eventHorizonRadius = (aveFit - minFit) / (maxFit - minFit);

  // Update star positions
  for (int i = 0; i < popSize; i++)
  {
    // Skip the black hole
    if (i == blackHoleIndex) continue;

    for (int c = 0; c < coords; c++)
    {
      if (u.RNDprobab () < eventHorizonRadius * 0.01)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
      else
      {
        double rnd = u.RNDfromCI (0.0, 1.0);
        double newPosition = a [i].c [c] + rnd * (a [blackHoleIndex].c [c] - a [i].c [c]);

        // Check and correct the boundaries
        newPosition = u.SeInDiSp (newPosition, rangeMin [c], rangeMax [c], rangeStep [c]);
        a [i].c [c] = newPosition;
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

      我们来分析两个算法版本之间的主要区别，从事件视界半径的计算开始。在第一个版本（BHA）中，半径被定义为最佳解与所有解之和的比率，这导致对于大型群体，半径变得非常小，并且强烈依赖于适应度函数的绝对值。在第二个版本（BHAm）中，半径在 [0,1] 范围内归一化，这令它能够展现在最小值和最大值之间的相对平均位置，同时保持与群体大小、和适应度函数的绝对值的独立性。

      现在我们看看星辰吸引的机制。该算法的第一个版本检查到黑洞的欧几里得距离，当它被吸引时，星辰会被随机位置的新恒星完全取代，这导致群体发生更剧烈的变化。第二个版本分别对每个坐标使用概率吸引，从而提供更平滑的群体变化。此处 0.01 的比率降低了发生根本变化的概率。

      就后果而言，第一个版本展现出更积极的利用搜索空间，这导致局部区域的快速收敛，但也增加了过早收敛的风险，并且或许会因完全替换解，而错过有前景的区域。相比之下，第二个版本提供了更宽松的探索策略，在探索和利用之间提供了更好的平衡，陷入局部最优的风险更小，虽慢但更可靠的收敛潜力，以及更好的群体多样化能力。

      总之，第一个版本更适合具有明确定义的最优问题，当需要快速收敛、及搜索空间的维度较小时，而第二个版本更适用于复杂的多极问题，其中搜索全局最优的可靠性很重要，以及需要对搜索空间进行更彻底探索的高维问题。

      我想分享一下我对可视化算法工作的想法。可视化提供了一个独特的机会来更深入地了解算法中发生的内部过程，并揭示其隐藏的机制。按照某些设置，我们能够观察到混沌图像如何逐渐转变为结构化形态。该过程不仅展示了算法操作的技术层面，而且还为优化算法开辟了新思路和方式。

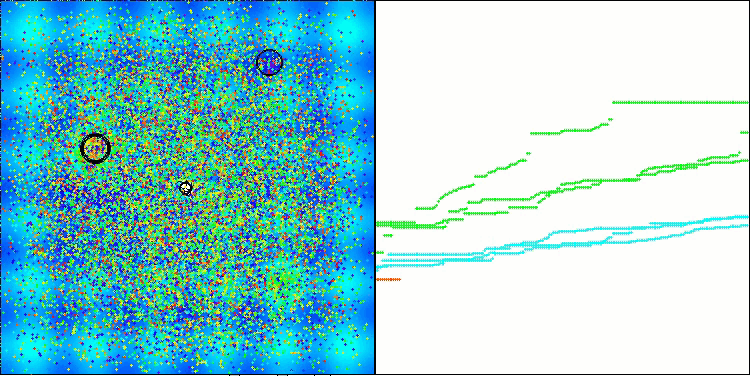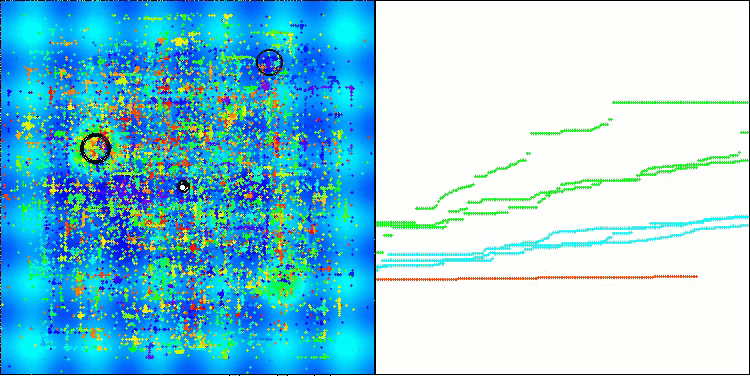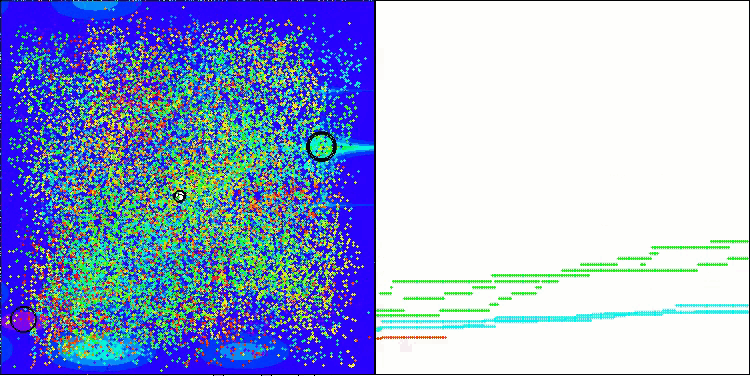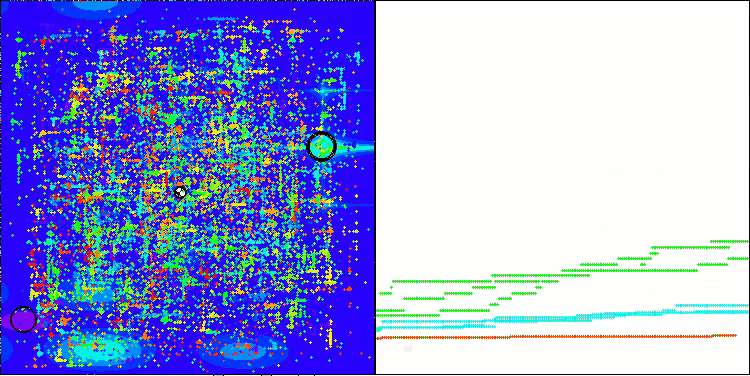
      BHAm算法在 [0.0;0.1] 范围内生成星辰运动随机分量的示例

      重点要注意，可视化不仅令我们能够评估算法的效率，还可识别传统数据分析或许无法观察到的形态。这有助于更深入地理解他们的工作，并能激发新的解决方案和创新。因此，可视化成为一种强大的工具，有助于连结科学和创造力，为探索和理解复杂过程开辟新视野。


      测试结果

      BHAm 算法修改版的结果：

      BHAm|Black Hole Algorithm M|50.0|
      =============================
      5 Hilly's; Func runs: 10000; result: 0.752359491007831
      25 Hilly's; Func runs: 10000; result: 0.7667459889455067
      500 Hilly's; Func runs: 10000; result: 0.34582657277589457
      =============================
      5 Forest's; Func runs: 10000; result: 0.9359337849703726
      25 Forest's; Func runs: 10000; result: 0.801524710041611
      500 Forest's; Func runs: 10000; result: 0.2717683112397725
      =============================
      5 Megacity's; Func runs: 10000; result: 0.6507692307692307
      25 Megacity's; Func runs: 10000; result: 0.5164615384615385
      500 Megacity's; Func runs: 10000; result: 0.154715384615386
      =============================
      All score: 5.19611 (57.73%)

      根据测试结果，BHAm 算法展现出令人印象深刻的结果，不仅与原始版本相比，而且在整个表格中也是如此。可视化表明，带有 “m” 后缀的新版本确实免除了原始版本的特征缺点：几乎消除了卡顿的倾向，收敛的准确性提高可观，结果的分散性降低。同时，保留了原始算法的“家族特征”：在空间中形成奇特的星辰团，并在解空间中对某个吸引物产生吸引力。

      Hilly

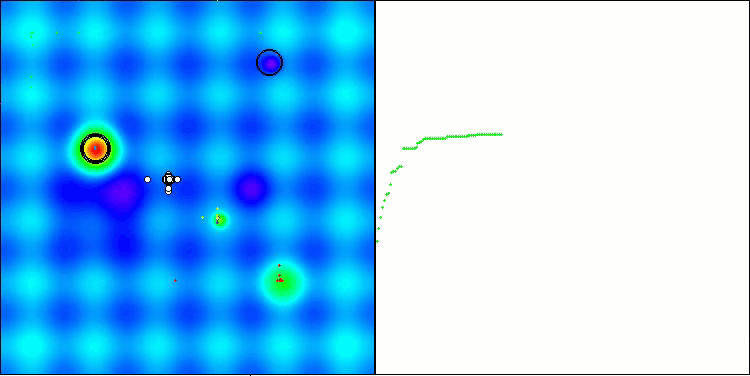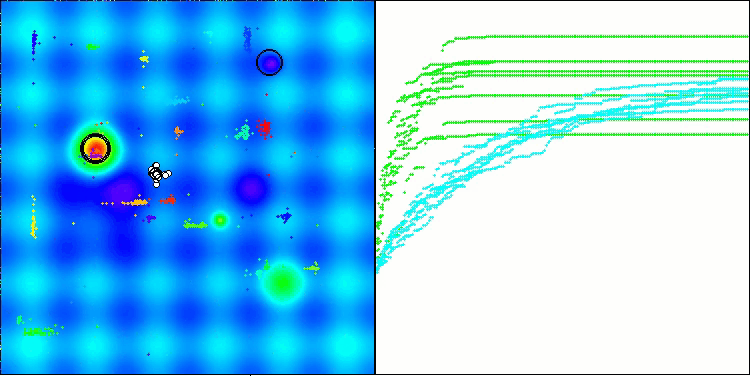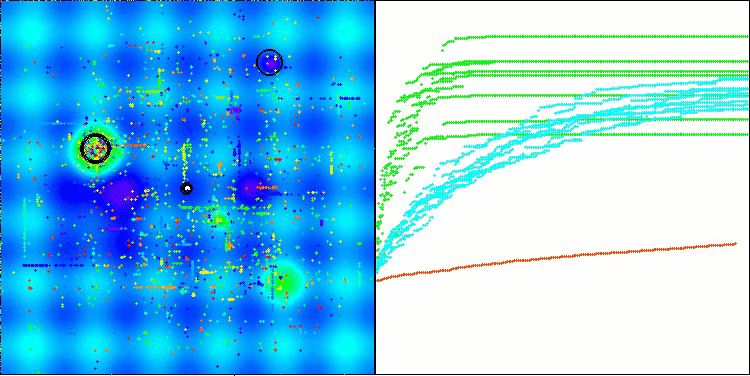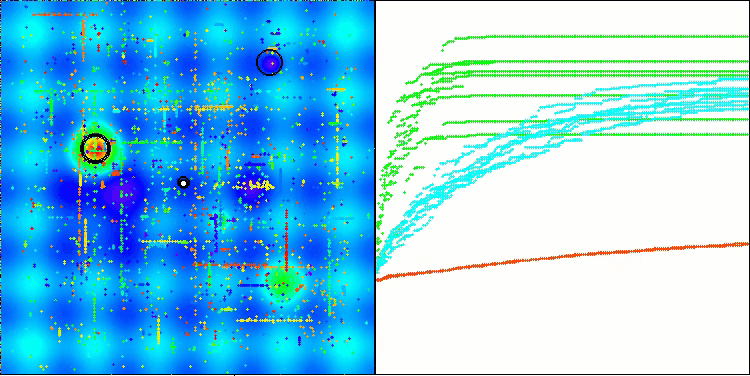
      BHAm 在 Hilly 上的测试

      Forest

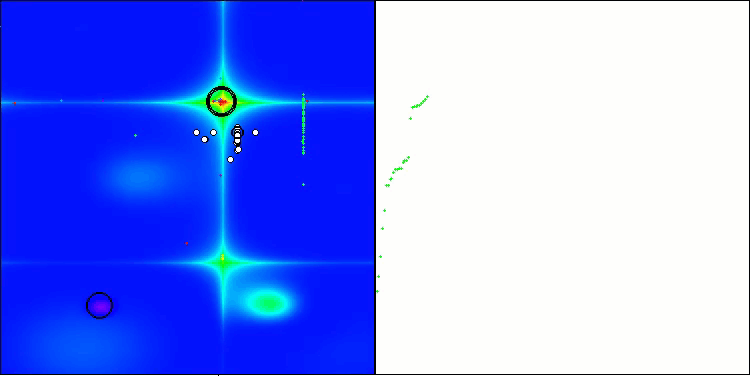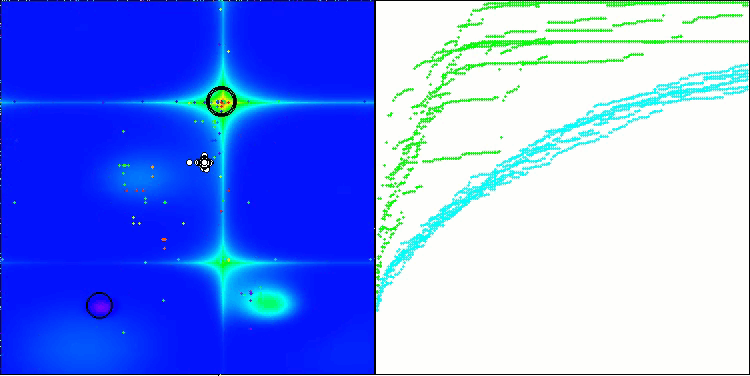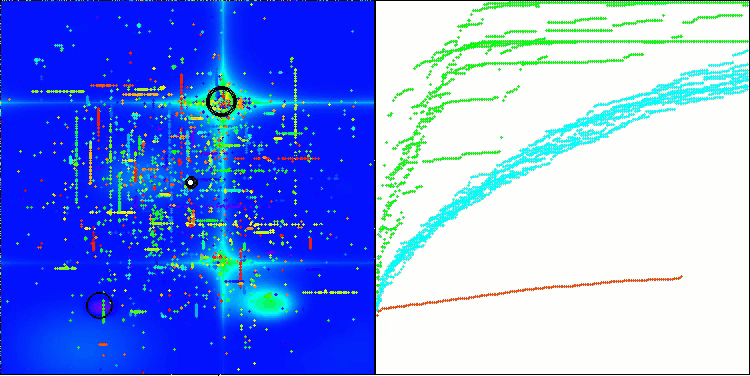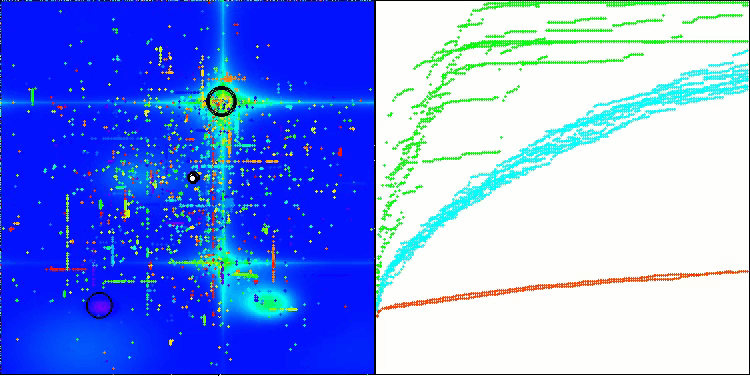
      BHAm 在 Forest 上的测试

      Megacity

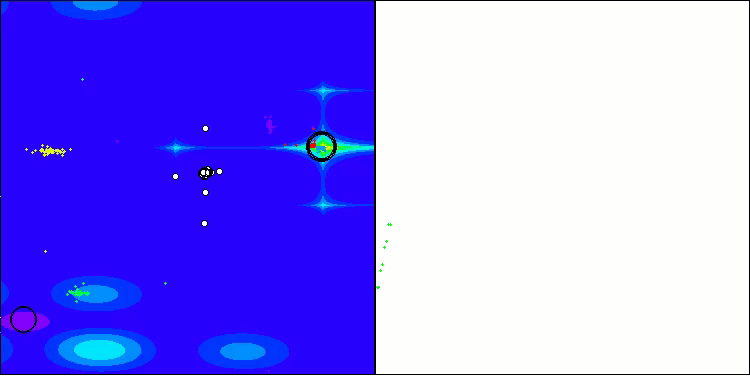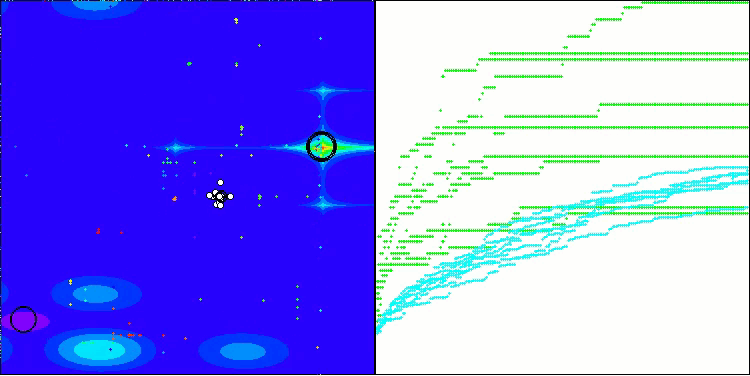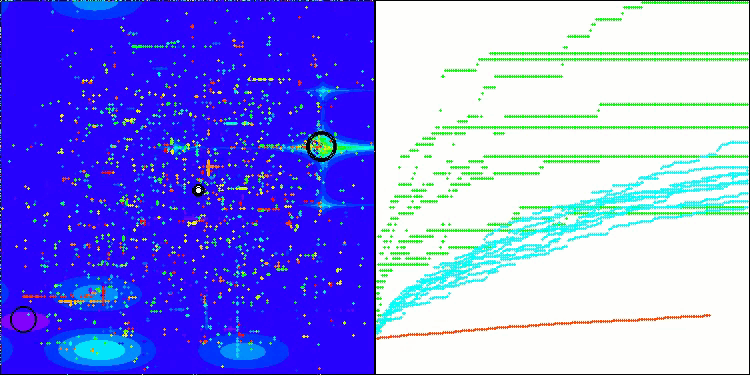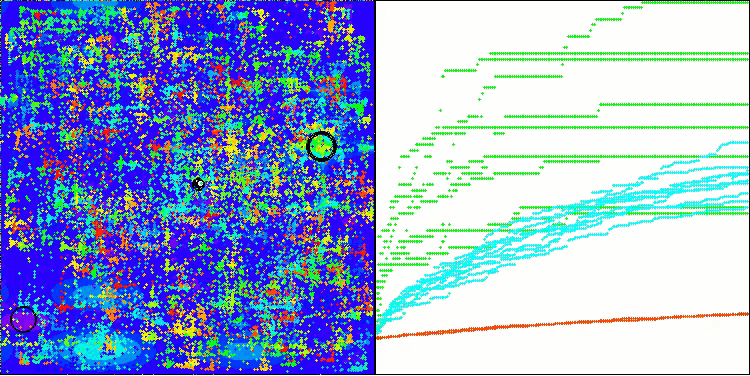
      BHAm 在 Megacity 上的测试

      基于测试结果，BHAm 算法荣获第 11 名，考虑到其竞争对手是已知存在的最强大算法，这是一个非常好的结果。

      # AO 说明 Hilly Hilly 最终 Forest Forest 最终 Megacity (离散) Megacity 最终 最终结果 % of MAX
      10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F)
      1 ANS 跨邻里搜索 0.94948 0.84776 0.43857 2.23581 1.00000 0.92334 0.39988 2.32323 0.70923 0.63477 0.23091 1.57491 6.134 68.15
      2 CLA 代码锁算法（JOO） 0.95345 0.87107 0.37590 2.20042 0.98942 0.91709 0.31642 2.22294 0.79692 0.69385 0.19303 1.68380 6.107 67.86
      3 AMOm 动物迁徙优化 M 0.90358 0.84317 0.46284 2.20959 0.99001 0.92436 0.46598 2.38034 0.56769 0.59132 0.23773 1.39675 5.987 66.52
      4 (P+O)ES （P+O）进化策略 0.92256 0.88101 0.40021 2.20379 0.97750 0.87490 0.31945 2.17185 0.67385 0.62985 0.18634 1.49003 5.866 65.17
      5 CTA 彗尾算法（JOO） 0.95346 0.86319 0.27770 2.09435 0.99794 0.85740 0.33949 2.19484 0.88769 0.56431 0.10512 1.55712 5.846 64.96
      6 SDSm 随机扩散搜索 M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
      7 AAm 射箭算法 M 0.91744 0.70876 0.42160 2.04780 0.92527 0.75802 0.35328 2.03657 0.67385 0.55200 0.23738 1.46323 5.548 61.64
      8 ESG 社群的进化（JOO） 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
      9 SIA 模拟各向同性退火（JOO） 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
      10 ACS 人工合作搜索 0.75547 0.74744 0.30407 1.80698 1.00000 0.88861 0.22413 2.11274 0.69077 0.48185 0.13322 1.30583 5.226 58.06
      11 BHAm 黑洞算法 M 0.75236 0.76675 0.34583 1.86493 0.93593 0.80152 0.27177 2.00923 0.65077 0.51646 0.15472 1.32195 5.196 57.73
      12 ASO 无政府状态社会优化 0.84872 0.74646 0.31465 1.90983 0.96148 0.79150 0.23803 1.99101 0.57077 0.54062 0.16614 1.27752 5.178 57.54
      13 AOSm 原子轨道搜索 M 0.80232 0.70449 0.31021 1.81702 0.85660 0.69451 0.21996 1.77107 0.74615 0.52862 0.14358 1.41835 5.006 55.63
      14 TSEA 龟壳进化算法（JOO） 0.96798 0.64480 0.29672 1.90949 0.99449 0.61981 0.22708 1.84139 0.69077 0.42646 0.13598 1.25322 5.004 55.60
      15 DE 差异进化 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
      16 CRO 化学反应优化 0.94629 0.66112 0.29853 1.90593 0.87906 0.58422 0.21146 1.67473 0.75846 0.42646 0.12686 1.31178 4.892 54.36
      17 BSA 鸟群算法 0.89306 0.64900 0.26250 1.80455 0.92420 0.71121 0.24939 1.88479 0.69385 0.32615 0.10012 1.12012 4.809 53.44
      18 HS 和谐搜索 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
      19 SSG 苗木播种和生长 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
      20 BCOm 细菌趋药性优化 M 0.75953 0.62268 0.31483 1.69704 0.89378 0.61339 0.22542 1.73259 0.65385 0.42092 0.14435 1.21912 4.649 51.65
      21 ABO 非洲水牛优化 0.83337 0.62247 0.29964 1.75548 0.92170 0.58618 0.19723 1.70511 0.61000 0.43154 0.13225 1.17378 4.634 51.49
      22 (PO)ES （PO）进化策略 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
      23 TSm 禁忌搜索 M 0.87795 0.61431 0.29104 1.78330 0.92885 0.51844 0.19054 1.63783 0.61077 0.38215 0.12157 1.11449 4.536 50.40
      24 BSO 头脑风暴优化 0.93736 0.57616 0.29688 1.81041 0.93131 0.55866 0.23537 1.72534 0.55231 0.29077 0.11914 0.96222 4.498 49.98
      25 WOAm 韦尔优化算法 M 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
      26 AEFA 人工电场算法 0.87700 0.61753 0.25235 1.74688 0.92729 0.72698 0.18064 1.83490 0.66615 0.11631 0.09508 0.87754 4.459 49.55
      27 AEO 基于人工生态系统的优化算法 0.91380 0.46713 0.26470 1.64563 0.90223 0.43705 0.21400 1.55327 0.66154 0.30800 0.28563 1.25517 4.454 49.49
      28 ACOm 蚁群优化 M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
      29 BFO-GA 细菌觅食优化 - GA 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
      30 SOA 简单优化算法 0.91520 0.46976 0.27089 1.65585 0.89675 0.37401 0.16984 1.44060 0.69538 0.28031 0.10852 1.08422 4.181 46.45
      31 ABHA 人工蜂巢算法 0.84131 0.54227 0.26304 1.64663 0.87858 0.47779 0.17181 1.52818 0.50923 0.33877 0.10397 0.95197 4.127 45.85
      32 ACMO 大气云层模型优化 0.90321 0.48546 0.30403 1.69270 0.80268 0.37857 0.19178 1.37303 0.62308 0.24400 0.10795 0.97503 4.041 44.90
      33 ADAMm 自适应动量估算 M 0.88635 0.44766 0.26613 1.60014 0.84497 0.38493 0.16889 1.39880 0.66154 0.27046 0.10594 1.03794 4.037 44.85
      34 ATAm 人工部落算法 M 0.71771 0.55304 0.25235 1.52310 0.82491 0.55904 0.20473 1.58867 0.44000 0.18615 0.09411 0.72026 3.832 42.58
      35 ASHA 人工淋浴算法 0.89686 0.40433 0.25617 1.55737 0.80360 0.35526 0.19160 1.35046 0.47692 0.18123 0.09774 0.75589 3.664 40.71
      36 ASBO 自适应社会行为优化 0.76331 0.49253 0.32619 1.58202 0.79546 0.40035 0.26097 1.45677 0.26462 0.17169 0.18200 0.61831 3.657 40.63
      37 MEC 心智进化计算 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
      38 IWO 入侵杂草优化 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
      39 Micro-AIS 微型人工免疫系统 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54
      40 COAm 布谷鸟优化算法 M 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21
      41 SDOm 螺旋动力学优化 M 0.74601 0.44623 0.29687 1.48912 0.70204 0.34678 0.10944 1.15826 0.42833 0.16767 0.03663 0.63263 3.280 36.44
      42 NMm Nelder-Mead 方法 M 0.73807 0.50598 0.31342 1.55747 0.63674 0.28302 0.08221 1.00197 0.44667 0.18667 0.04028 0.67362 3.233 35.92
      43 FAm 萤火虫算法 M 0.58634 0.47228 0.32276 1.38138 0.68467 0.37439 0.10908 1.16814 0.28667 0.16467 0.04722 0.49855 3.048 33.87
      44 GSA 引力搜索算法 0.64757 0.49197 0.30062 1.44016 0.53962 0.36353 0.09945 1.00260 0.32667 0.12200 0.01917 0.46783 2.911 32.34
      45 BFO 细菌觅食优化 0.61171 0.43270 0.31318 1.35759 0.54410 0.21511 0.05676 0.81597 0.42167 0.13800 0.03195 0.59162 2.765 30.72


      总结

      黑洞算法（BHA）是如何将自然基本定律转化为高效优化工具的一个优雅示例。该算法基于简单直观的思路，即潜在解对于充当黑洞的中心最佳解的吸引力。在算法的演化过程中，我们观察到一个惊人的现象：星辰解朝着它们的河系中心移动，可以发现新的、更强大的吸引力中心 -- 更好的解，这导致搜索空间结构的动态变化。这清楚地展示了如何在算法优化中有效地利用自发的自组织机制。

      实践显示出一种非凡的形态：通常是对基本思路的简化和重新思考，而非它们的复杂性，导致了意想不到的令人印象深刻的结果。在算法优化领域，增加搜索逻辑复杂性，却导致性能显著提升的状况很罕见。

      这个示例清晰地说明了一个重要原则：算法创建者的权威、或方法的流行不应被视为其效率的最终保证。任何方法，即使是最成功的方法，都能在计算效率和所获结果的品质方面加以改进。算法的修改版本（BHAm）就是这种改进的一个很好的示例。在保持原版方法概念简单性、和没有外部调谐参数的同时，它在性能和收敛速度方面表现出可观的改进。

      这种经历令我们得出了一个基本结论：创新和实验必须成为任何专业活动不可或缺的一部分。无论是开发机器学习算法，还是制定交易策略，探索新方法的勇气和重新思考现有方法的意愿，往往是取得突破性成果的关键。

      最终，与任何其它领域一样，优化的进步不是盲目遵守权威，而是基于对基本原理的深刻理解，和创造性实验的意愿，不断寻找新的、更有效的解决方案。

      表格

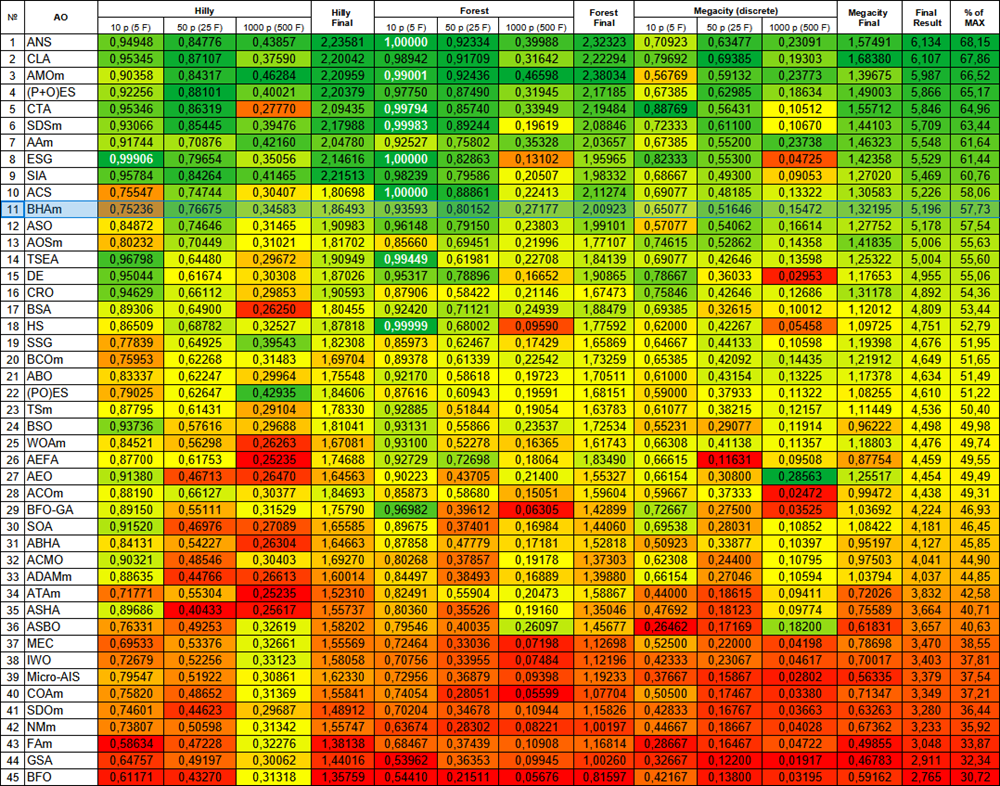
      图例 3. 颜色渐变根据相关算法测试，大于或等于 0.99 的结果以白色高亮显示

      图表

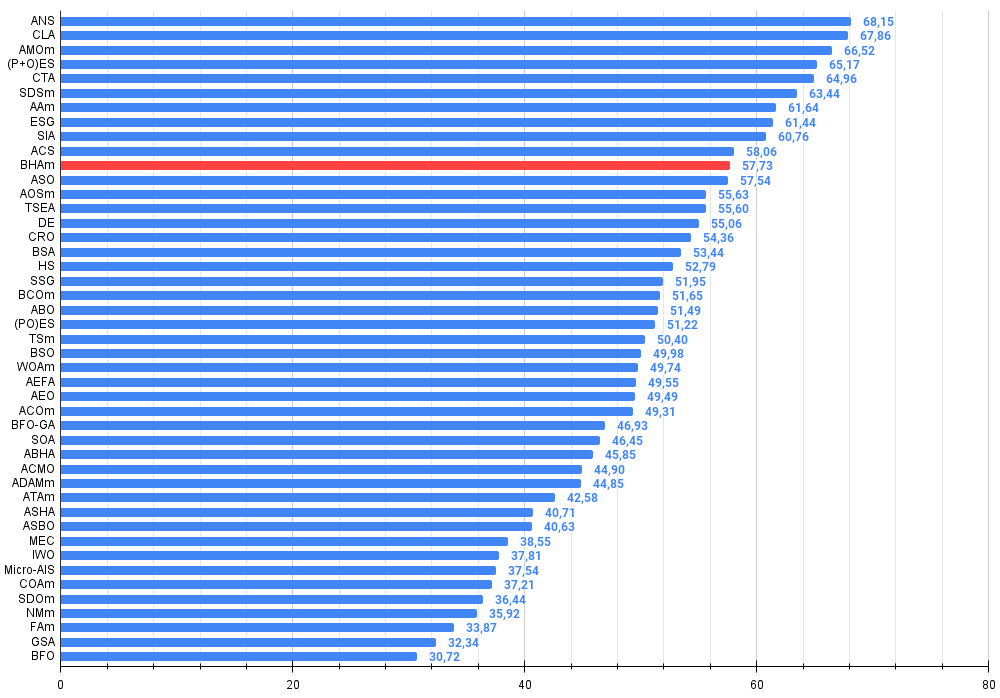
      图例 4. 算法测试结果直方图（从 0 到 100，越高越好，其中 100 是最大可能的理论结果，存档中有一个用于计算评级表的脚本）


      BHAm 的优点和缺点：

      优点：

      1. 唯一的外部参数是群体规模。
      2. 实现简单。
      3. 非常快的 EA。
      4. 适用于大规模问题。

      缺点：

      1. 维都较小问题的结果分散很大。
      2. 有陷入低维问题的倾向。

      本文附有一个存档，其中包含当前版本的算法代码。文章作者不对规范算法描述的绝对准确性负责。其中许多都进行了改动，以便提高搜索能力。文章中提出的结论和判断是基于实验结果。

      文章中用到的程序

      # 名字 类型 说明
      1 #C_AO.mqh
      		 包含
      		 群体优化算法的父类
      2 #C_AO_enum.mqh
      		 包含
      		 群体优化算法的枚举
      3 TestFunctions.mqh
      		 包含
      		 测试函数库
      4
      		 TestStandFunctions.mqh
      		 包含
      		 测试台功能库
      5
      		 Utilities.mqh
      		 包含
      		 辅助函数库
      6
      		 CalculationTestResults.mqh
      		 包含
      		 计算比较表中结果的脚本
      7
      		 Testing AOs.mq5
      		 脚本 所有群体优化算法的统一测试台
      8
      		 Simple use of population optimization algorithms.mq5
      		 脚本
      		未含可视化的群体优化算法的简单示例
      9
      		Test_AO_BHAm.mq5
      		 脚本 BHAm 测试台

      本文由MetaQuotes Ltd译自俄文
      原文地址： https://www.mql5.com/ru/articles/16655

      附加的文件 |
      下载ZIP
      BHAm.zip (147.71 KB)

      注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

      本文由网站的一位用户撰写，反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责，也不对因使用所述解决方案、策略或建议而产生的任何后果负责。

      该作者的其他文章

      前往讨论
      从基础到中级：定义（一） 从基础到中级：定义（一）
      在这篇文章中，我们将做一些许多人会觉得奇怪和完全脱离上下文的事情，但如果使用得当，这将使你的学习更加有趣：我们将能够根据这里显示的内容构建非常有趣的东西。这将使您更好地理解 MQL5 语言的语法。此处提供的材料仅用于教育目的。它不应以任何方式被视为最终应用程序。其目的不是探索所提出的概念。
      循环孤雌生殖算法（CPA） 循环孤雌生殖算法（CPA）
      本文提出了一种新的群体优化算法——循环孤雌生殖算法（CPA），其灵感源自蚜虫独特的生殖策略。该算法融合了两种生殖机制：孤雌生殖（无性繁殖）与有性生殖，并借助蚜虫的群体结构以及群体间的迁徙能力。算法的核心特点包括：在不同生殖策略之间自适应切换和通过“迁飞”机制实现群体间的信息交换。
      精通日志记录（第四部分）：将日志保存到文件 精通日志记录（第四部分）：将日志保存到文件
      在本文中，我将向您讲解基本的文件操作，以及如何配置一个灵活的自定义处理器。我们将更新 CLogifyHandlerFile 类，以将日志直接写入文件。我们将通过在 EURUSD 上模拟一周的策略来进行性能测试，在每个 tick 生成日志，总耗时为 5 分 11 秒。其结果将在未来的文章中进行比较，届时我们将实现一个缓存系统来提升性能。
      开发回放系统（第 76 部分）：新 Chart Trade（三） 开发回放系统（第 76 部分）：新 Chart Trade（三）
      在本文中，我们将看看上一篇文章中缺少的 DispatchMessage 代码是如何工作的。我们还会介绍下一篇文章的主题。因此，在继续下一个主题之前，了解这段代码的工作原理非常重要。此处提供的内容仅用于教育目的。在任何情况下，除了学习和掌握所提出的概念外，都不应出于任何目的使用此应用程序。