MetaTrader 5 / テスター
English Русский 中文 Español Deutsch Português
preview
人工藻類アルゴリズム(AAA)

人工藻類アルゴリズム(AAA)

MetaTrader 5 — テスター | 25 3月 2025, 08:54
82 0
Andrey Dik
Andrey Dik

内容

  1. はじめに
  2. アルゴリズムの実装
  3. テスト結果


はじめに

地球上で最も古い生物のひとつである藻類は、水生生態系において重要な役割を果たしています。藻類は45,000種以上あり、色、形、大きさ、生息地が大きく異なります。藻類は多くの動物種の食事の基礎となるため水生環境に生命を供給し、また光合成によって酸素を生成するため、地球上の生命を維持するために重要です。これらの生物は単細胞であったり多細胞であったりし、しばしばコロニーを形成して一つのユニットとして機能します。

単細胞藻類は有糸分裂によって分裂し、新しい細胞を作り、それが互いにつながってコロニーを形成します。多細胞藻類は、胞子を使って繁殖することができます。胞子は水中に広がり、発芽して新しい生物となり、コロニーも形成します。これらの驚くべき生物は、数学的モデリングと最適化において、生物学的プロセスがいかに革新的な解決策を生み出すために利用できるかを示しています。

2015年にUymaz、Tezel、Yelによって提案された人工藻類アルゴリズム(AAA)は、生物学的自然現象と数学的エレガンスの組み合わせです。このメタヒューリスティック最適化アルゴリズムは、微細藻類の魅惑的な世界からインスピレーションを得ており、そのコロニー習性と適応能力は、アルゴリズム最適化モデル作成の基礎となりました。微細藻類が光源に向かって移動し、環境条件の変化に適応し、光合成を向上させるために有糸分裂によって繁殖する能力にヒントを得て、AAAはこれらのユニークな特性を数学的にモデル化するために開発されました。

このアルゴリズムには、螺旋運動、進化過程、適応過程という3つの重要なプロセスが含まれています。螺旋運動は、養液中の藻類の3次元的な動きをシミュレートし、藻類が成長に最適な条件を見つけることを可能にします。進化過程により、藻類のコロニーは最適な条件下で繁殖し、その発育を促進し、解決策を改善します。適応過程は、あまり成功していないコロニーが最大のコロニーのようになるのを助け、コロニーの生存とさらなる発展を保証します。


アルゴリズムの実装

人工藻類アルゴリズム（AAA）は、藻類の渦巻き運動、適応過程、進化過程などの特性を数学的にモデル化するために開発されました。各藻のコロニーは最適化問題に対する解の候補を表し（コロニー内の各セルは個別の座標）、これらのコロニーが組み合わさって藻の集団を形成します。各コロニーはその大きさによって特徴付けられ、それは提示された解の質を反映します。

進化の過程で、より適した環境条件に到達した藻類のコロニーは、発達し成長することができます。適切な条件を得られないコロニーは発展せず、死滅します。螺旋運動が終わると、藻のコロニーは大きさによってランク付けされます。最大のコロニーからランダムに選ばれたセルは、最小のコロニーから同じセルにコピーされ、進化過程が完了します。

藻類のコロニーは、より良い環境条件を得るために、水中で螺旋運動をおこないます。彼らのエネルギーはコロニーの大きさに比例します。移動中にエネルギーを失うが、より良い環境に到達すれば、失ったエネルギーの半分を回復します。コロニーのエネルギーは栄養分の濃度に正比例するため、エネルギーが多いコロニーほど移動頻度が高くなります。

摩擦力もまた、水中での動きに影響を与える重要な要素です。表面積が小さいコロニーは、摩擦面が小さいため、移動範囲が広くなります。より良い条件を達成したコロニーは、その大きさゆえに摩擦表面積が大きくなるため、コロニーの動きが鈍くなり、発見された解の周辺を探索しやすくなり、局所探索能力が高まります。

適応過程は、螺旋運動中に十分な発達に達していない藻類のコロニーが、最大のコロニーを模倣しようとするときに起こります。飢餓値が最も高いコロニーがこのプロセスを経ます。最適化の開始時、すべてのコロニーのハンガー値はゼロです。螺旋移動の間、より良い解決策を見つけられなかったコロニーの飢餓値は1ずつ増加します。螺旋運動と進化の過程を経て、飢餓値が最も高いコロニーが適応期に入ります。しかし、適応過程はすべての反復でおこなわれるわけではありません。まず、0と1の間のランダムな値が選択されます。この値が適応パラメータより小さい場合、適応が実行されます。

    AAA疑似コードの記述に移りましょう。

    初期化
        エージェントの集団を作る
        各エージェントについて：
            探索空間内のランダムな位置を初期化する
            パラメータ（サイズ、エネルギー、空腹度など）を初期化する

    メインループ
        停止基準に達するまで：
            各エージェントについて：
                移動の実行
                適応度関数を評価する
            
            発見された最善の解決策を更新する
            
            各エージェントについて：
                エネルギーを更新する
                サイズを更新する
                空腹を更新する
            
            進化を遂げる
            適応をおこなう

    移動関数：
        各エージェントについて：
            トーナメント方式で他のエージェントを選ぶ
            各座標について：
                螺旋三角移動方程式を使用してエージェントの位置を更新する
                摩擦比

    EvolutionProcess関数：
        最小サイズのエージェントを探す
        その座標をランダムに選んだエージェントの座標に置き換える

    AdaptationProcess関数：
        最も空腹なエージェントを探す
        一定の確率で：
            最大サイズのエージェントを探す
            空腹なエージェントの座標を更新し、大型エージェントの座標に
            近づける
            空腹なエージェントのパラメータをリセットする

    EnergyCalculation関数：
        コロニーサイズ、栄養濃度、現在の成長率に基づいてエネルギーを
        計算する

    TournamentSelection関数：
        ランダムに2つのエージェントを選ぶ
        最適な適応度関数の値を持つエージェントを返す

    アルゴリズムに使われている方程式を列挙してみましょう。式1～5は、アルゴリズムの基本ロジックの実装に直接関係します。

    1. 集団の初期化：集団 =[[x1_1, x1_2, ..., x1_D],[x2_1, x2_2, ..., x2_D],[xN_1, xN_2, ..., xN_D]]、ここでxj_iはj番目の藻類コロニーのi番目のセル、Dはコロニーの次元、Nは集団のサイズ。

    2. 螺旋運動：x'i_j = xi_j + α * cos (θ) * τ (Xi) * p; y'i_j = yi_j + α * sin (θ) * τ (Xi) * p; z'i_j = zi_j + r * v、ここで(x'i_j, y'i_j, z'i_j)はi番目のコロニーの新しい座標、α,θ∈ [0, 2π],p∈ [-1, 1],r∈ [-1, 1],v∈ [-1, 1], τ(Xi)はi番目のコロニーの摩擦面積

    3. 進化過程：biggest = max (Gi), m = ランダムに選択されたセル,smallest.xm = biggest.xm

    4. 適応：starving = max (Ai);starving.x = starving.x + (biggest.x - starving.x) * rand

    5. 藻類成長のMonodモデル：μt = μtmax * St / (St + Kt)、ここでμtは与えられた時間tにおける藻類の成長速度、μtmaxは最大成長速度、Stは与えられた時間tにおけるコロニーサイズ、Ktは半飽和定数

    6. 摩擦面積：τ(Xi) = 2π * (3√ (3*Gi) / (4π))^2、ここでτ (Xi)はi番目のコロニーの摩擦面積、Giはi番目のコロニーの大きさ

    7. 螺旋移動のためのコロニー選択：トーナメント選択は、移動するコロニーを選択するために用いられます。詳しくは後述します。

    8. 螺旋モーションのためにランダムな次元を選択する：p、r、vは、ランダムに選択された互いに異なる測定指標です。

    9. 螺旋移動のために近隣のコロニーを選択する：Xjはトーナメントで選ばれたコロニーで、Xiのコロニーが移動します。

    10. 全コロニーの初期空腹度すべての iに対してAi=0。

    11. 解決策を改善しなかったコロニーでは空腹度が増加：Ai = Ai + 1、コロニーがより良い解を見つけられなかった場合。

    12. 空腹度が最大のコロニーを選択する：starving = max (Ai)。

    13. 適応確率： rand < Ap、Apは適応パラメータ。

    式6～13は、摩擦面積の計算、移動のためのコロニーの選択、コロニー飢餓の管理、適応確率など、アルゴリズム実装のさらなる詳細を記述しています。

    Monodモデルは、生物系における個体群の成長と挙動を記述するのに非常によく使われます。これは、微生物の増殖速度論を研究したフランスの生化学者、ジャック・モノの業績に基づいています。個体群の成長速度は、基質（栄養素）の濃度に依存します。低濃度の基質では増殖速度は濃度に比例し、高濃度では最大になります。最適化アルゴリズムでは、進化的アルゴリズムにおける集団の成長と適応をモデル化するためにMonodモデルが使用されます。最適化の間、利用可能なリソースに応じて集団パラメータが変化するため、実際の生物学的プロセスをより正確にモデル化することができます。

    コロニー選びのトーナメント選考に注目してください。この方法をアルゴリズムに用いたのは初めてです。この選択法を使った個体群の選択確率の分布をはっきり見るために、スクリプトを書いて結果を出力してみましょう。青くハイライトされたコード部分は、セレクションの際の分配の形成に直接関与しています。

    input int      PopSize = 50;
input int      Count   = 1000000;
input int      BarWidth = 50; // Histogram width in characters

void OnStart()
{
  int pop[];
  ArrayResize(pop, PopSize);

  for(int i = 0; i < PopSize; i++) pop[i] = PopSize - i;

  Print("Original population:");
  ArrayPrint(pop);

  int tur[];
  ArrayResize(tur, PopSize);
  ArrayInitialize(tur, 0);

  int ind1 = 0, ind2 = 0;

  for(int i = 0; i < Count; i++)
  {
    ind1 = MathRand() % PopSize;
    ind2 = MathRand() % PopSize;

    if(pop[ind1] > pop[ind2]) tur[ind1]++;
    else                      tur[ind2]++;
  }

  Print("Probability distribution (in %):");

  double maxPercentage = 0;
  double percentages[];
  ArrayResize(percentages, PopSize);

  for(int i = 0; i < PopSize; i++)
  {
    percentages[i] = (double)tur[i] / Count * 100;
    if(percentages[i] > maxPercentage) maxPercentage = percentages[i];
  }

  for(int i = 0; i < PopSize; i++)
  {
    int barLength = (int)((percentages[i] / maxPercentage) * BarWidth);
    string bar = "";
    for(int j = 0; j < barLength; j++) bar += "|";

    PrintFormat("%2d: %5.2f%% %s", i, percentages[i], bar);
  }
}

    以下は、集団内の各個体の選択確率分布を可視化するスクリプトを実行した結果です。

    元々の集団：
    20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1
    確率分布（単位：%）
     0:  9.76% ||||||||||||||||||||||||||||||||||||||||||||||||||
     1:  9.24% |||||||||||||||||||||||||||||||||||||||||||||||
     2:  8.74% ||||||||||||||||||||||||||||||||||||||||||||
     3:  8.22% ||||||||||||||||||||||||||||||||||||||||||
     4:  7.77% |||||||||||||||||||||||||||||||||||||||
     5:  7.27% |||||||||||||||||||||||||||||||||||||
     6:  6.74% ||||||||||||||||||||||||||||||||||
     7:  6.26% ||||||||||||||||||||||||||||||||
     8:  5.78% |||||||||||||||||||||||||||||
     9:  5.25% ||||||||||||||||||||||||||
    10：  4.75% ||||||||||||||||||||||||
    11：  4.22% |||||||||||||||||||||
    12：  3.73% |||||||||||||||||||
    13：  3.25% ||||||||||||||||
    14：  2.75% ||||||||||||||
    15：  2.25% |||||||||||
    16：  1.75% ||||||||
    17：  1.25% ||||||
    18:  0.77% |||
    19:  0.25% |

    確率分布は直線的に減少し、より高い確率で良い解決策が得られるコロニーが選択されるようになりますが、効率の悪い選択肢も選択される可能性があります。この選択のアプローチは、個体の適応度の絶対値に依存しないため、解の多様性に幅が出ます。

    以前の記事で、選択中に確率分布を変化させる方程式をすでに検討したが、確率の線形および非線形の減少の両方を提供する能力を持ち、計算コストが少なくなります（トーナメント選択では、MathRand()関数の二重呼び出しが必要です）。

    グラフ

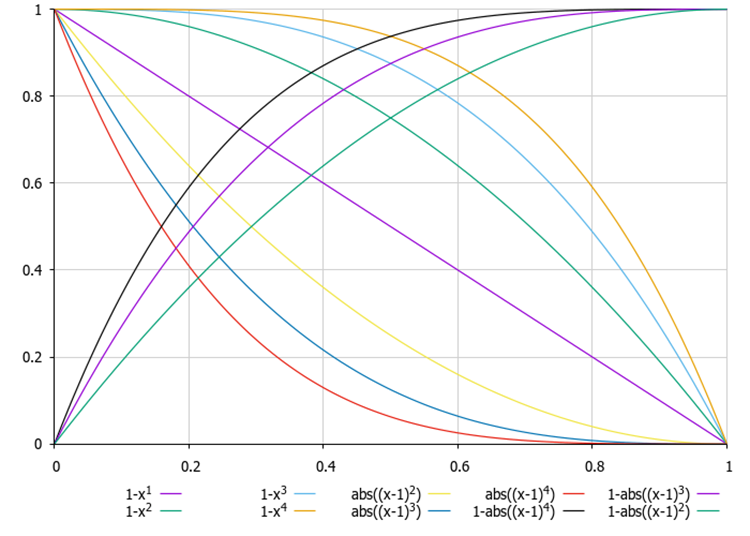
    図1：確率分布の形状を変更するための方程式の例。xは範囲[0.0, 1.0]内の一様分布乱数

    さて、アルゴリズムの複雑さをすべて詳しく説明したので、コードそのものを書き始めることができます。

    アルゴリズムで藻類のコロニー（エージェント）をシミュレートするために使用されるS_AAA_Agent構造を説明しましょう。この構造体には4つのフィールドがある：

    • energy：エージェントのエネルギーレベル
    • hunger：エージェントの空腹度
    • size：エージェントのサイズ（藻の高さと長さ）
    • friction：エージェントの動きに影響する摩擦比

    Init：このメソッドは、構造体メンバをデフォルト値で初期化します。 

    このように、S_AAA_Agent構造体は、基本的な特徴を持つ単純なエージェントモデルです。

    //——————————————————————————————————————————————————————————————————————————————
struct S_AAA_Agent
{
  double energy;
  int    hunger;
  double size;
  double friction;

  void Init ()
  {
    energy   = 1.0;
    hunger   = 0;
    size     = 1.0;
    friction = 0.0;
  }
};
//——————————————————————————————————————————————————————————————————————————————

    C_AO_AAAクラスの定義をC_AO基底クラスから継承して書いてみましょう。これは、基底クラスのすべてのメンバーとメソッドを継承し、それらを拡張またはオーバーライドできることを意味します。

    1. クラスのコンストラクタでは、アルゴリズムに関連するさまざまなパラメータに値が設定され、初期化もおこなわれます。

    • popSize：集団のサイズ
    • adaptationProbability：適応確率
    • energyLoss：エネルギー損失
    • maxGrowthRate：最大成長率
    • halfSaturationConstant：半吸収定数

    これらのパラメータはすべてparams配列に格納されます。

    2. SetParamsメソッドは、params配列からアルゴリズムパラメータの値を更新します。

    3. 以下が使用可能なオプションです。

    • Init ()：初期化メソッドは、パラメータの最小値と最大値、ステップ数、エポック数を配列で受け取ります。
    • Moving ()：エージェントの状態を移動または更新するメソッド
    • Revision ()：状態を見直したり評価したりするメソッド
    • EvolutionProcess ()、AdaptationProcess ()、CalculateEnergy ()、TournamentSelection () ：それぞれ、進化過程、適応過程、トーナメント選択を担当するprivateメソッド

    クラスのフィールド

    • adaptationProbability、energyLoss、maxGrowthRate、halfSaturationConstant： パラメータ値を格納するための変数
    • S_AAA_Agent agent []：エージェントの配列
    • fMin,fMax ：集団の適合値（藻の大きさ）

    C_AO_AAAクラスは、C_AOクラスを継承することで、パラメータやエージェントの状態を便利に管理し、より広いシステムに統合することができる構造です。

    //——————————————————————————————————————————————————————————————————————————————
class C_AO_AAA : public C_AO
{
  public: //--------------------------------------------------------------------

  ~C_AO_AAA () { }

  C_AO_AAA ()
  {
    ao_name = "AAA";
    ao_desc = "Algae Adaptive Algorithm";
    ao_link = "https://www.mql5.com/ja/articles/15565";

    popSize                = 200;
    adaptationProbability  = 0.2;
    energyLoss             = 0.05;
    maxGrowthRate          = 0.1;
    halfSaturationConstant = 1.0;

    ArrayResize (params, 5);

    params [0].name = "popSize";                params [0].val = popSize;
    params [1].name = "adaptationProbability";  params [1].val = adaptationProbability;
    params [2].name = "energyLoss";             params [2].val = energyLoss;
    params [3].name = "maxGrowthRate";          params [3].val = maxGrowthRate;
    params [4].name = "halfSaturationConstant"; params [4].val = halfSaturationConstant;
  }

  void SetParams ()
  {
    popSize                = (int)params [0].val;
    adaptationProbability  = params      [1].val;
    energyLoss             = params      [2].val;
    maxGrowthRate          = params      [3].val;
    halfSaturationConstant = params      [4].val;
  }

  bool Init (const double &rangeMinP  [],
             const double &rangeMaxP  [],
             const double &rangeStepP [],
             const int     epochsP = 0);

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  double adaptationProbability;
  double energyLoss;
  double maxGrowthRate;
  double halfSaturationConstant;

  S_AAA_Agent agent [];

  private: //-------------------------------------------------------------------
  void   EvolutionProcess    ();
  void   AdaptationProcess   ();
  double CalculateEnergy     (int index);
  int    TournamentSelection ();
  double fMin, fMax;
};
//——————————————————————————————————————————————————————————————————————————————

    C_AO_AAAクラスの次のInitメソッドを詳しく見てみましょう。

    • rangeMinP：各パラメータの最小値の配列
    • rangeMaxP：各パラメータの最大値の配列
    • rangeStepP：各パラメータの変更ステップの配列
    • epochsP：エポック数（デフォルト - 0）

    以下がメソッドのフィールドです。

    1. StandardInitメソッドは、渡されたパラメーターで標準的な初期化をおこないます。 

    2. agent配列のサイズをpopSize に変更します。これにより、エージェントを格納するための配列を準備することができます。

    3. 操作中に使用する関数の最小値と最大値を設定します。

    4. ループは各エージェントを通過し、Initメソッドを使って初期化します。

    5. 内側のループは、各エージェントの座標を初期化します。

    • まず、RNDfromCI法を用いて、c座標をrangeMin [c]からrangeMax [c]の範囲でランダムに設定します。
    • 次に、SeInDiSpを使って座標を変更し、値を正規化します。

    すべての操作が成功した場合、このメソッドはtrueを返します。このように、Initメソッドは、与えられた座標の範囲とステップでエージェントの配列を初期化します。標準的な初期化、関数の境界設定、座標値のランダム割り当てが含まれます。

    //——————————————————————————————————————————————————————————————————————————————
bool C_AO_AAA::Init (const double &rangeMinP  [],
                     const double &rangeMaxP  [],
                     const double &rangeStepP [],
                     const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  ArrayResize (agent, popSize);

  fMin = -DBL_MAX;
  fMax =  DBL_MAX;

  for (int i = 0; i < popSize; i++)
  {
    agent [i].Init ();

    for (int c = 0; c < coords; c++)
    {
      a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
      a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

    C_AO_AAAクラスのMovingメソッドのコードを考えてみましょう。一般的な構造と機能：

    1. revision変数がfalseの場合、それはtrueに設定され、関数は終了します。つまり、Movingメソッドの基本ロジックは最初の反復では実行されません。

    2. ループは全てのpopSize集団要素を通過します。

    3. トーナメントの選択はTournamentSelection関数でおこなわれ、エージェント（藻）のインデックスを返します。

    4. 内側のループは、各座標（coords変数で指定された空間の次元）を繰り返し処理します。

    5. u.RNDfromCI法を用いて、αとβ（角度）とρ （-1から1の範囲の値）の3つのランダム値を生成します。

    6. variant値（0から2まで変化する）に応じて、a [i].c [c]座標が更新されます。

    • variantが0の場合、α角の余弦が使われます。
    • variantが1の場合、β角の正弦が使われます。
    • variantが2の場合、ρ値が使われます。

    variant変数を使うことで、多次元空間における藻の3次元的な螺旋運動をシミュレートすることができます。座標の更新は、agent[i].frictionとして指定された摩擦を考慮します。

    7. a[i].c[c]座標は、u.SeInDiSp関数を使用して制限され、所定の範囲内で所定のステップで値が設定されます。

    Moving関数は、エージェントの現在の状態と他のエージェントの状態に基づいて、エージェントの座標をランダムに変化させる処理を実行します。摩擦とランダムな値を使うことで、探索空間におけるエージェントの行動をシミュレートするダイナミクスを作り出すことができます。このコードには、有効な座標値を維持するために重要な、指定された範囲を超えないようにするメカニズムが含まれています。

    //——————————————————————————————————————————————————————————————————————————————
void C_AO_AAA::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    int variant = 0;

    int j = TournamentSelection ();

    for (int c = 0; c < coords; c++)
    {
      double α = u.RNDfromCI (0.0, 2 * M_PI);
      double β = u.RNDfromCI (0.0, 2 * M_PI);
      double ρ = u.RNDfromCI (-1.0, 1.0);

      if (variant == 0) a [i].c [c] += (a [j].c [c] - a [i].c [c]) * agent [i].friction * MathCos (α);
      if (variant == 1) a [i].c [c] += (a [j].c [c] - a [i].c [c]) * agent [i].friction * MathSin (β);
      if (variant == 2) a [i].c [c] += (a [j].c [c] - a [i].c [c]) * agent [i].friction * ρ;

      variant++;

      if (variant > 2) variant = 0;

      a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

    Movingメソッドの後、C_AO_AAAクラスのRevisionメソッドに移ります。このメソッドは、エージェントの特性と相互作用に基づいて、集団内のエージェントの状態を更新する役割を担います。一般的な構造：

    1. ind変数は-1で初期化されます。これは、最高の関数値を持つエージェントのインデックスを格納するために使用されます。

    2. ループはpopSize集団内のすべてのエージェントを通過します。ループ内：a [i].f関数値が現在のfB最大値を超えた場合、 

    • fBの最大値が更新されます。
    • 最良の値を持つエージェントのインデックスがind変数に格納されます。
    • agent [i].sizeエージェントサイズは、a [i].f適性関数値に従って更新されます。
    • 現在のエージェントの適応度関数の最小値fMinと最大値fMaxが更新されます。

    3. 最大適合値fを持つエージェントが見つかった場合、その座標はArrayCopy関数を使ってcB配列にコピーされます。

    4. エネルギーやその他のエージェントパラメータを更新する：

    • そのエネルギーはCalculateEnergy関数を使って計算されます。
    • 摩擦が計算され、fMinと fMaxで正規化されます。
    • エージェントのエネルギーはenergyLoss分減少します。
    • 新しいエネルギーが現在のエネルギーより大きければ、エネルギーは損失の半分だけ増加し、エージェントの空腹はリセットされます。そうでなければ、空腹の度合いは増します。
    • エージェントの現在のサイズと満腹度に基づいて成長係数が計算され、エージェントのサイズが更新されます。

    5. プロセスの呼び出し：関数の最後で、EvolutionProcessメソッドとAdaptationProcessメソッドが呼び出されます。メソッドは、エージェントの現在の状態に基づいて、エージェントをさらに進化させ、適応させる役割を担っています。

    一般的に、Revision関数は、エージェントの特性と相互作用に基づいて、集団内のエージェントの状態を更新する役割を担っています。分析だけでなく、更新や追加プロセスの呼び出しも含まれており、個体群動態をモデル化することができます。

    //——————————————————————————————————————————————————————————————————————————————
void C_AO_AAA::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;

      ind = i;
    }

    agent [i].size = a [i].f;

    if (a [i].f < fMin) fMin = a [i].f;
    if (a [i].f > fMax) fMax = a [i].f;
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    agent [i].energy   = CalculateEnergy (i);

    agent [i].friction = u.Scale (a [i].f, fMin, fMax, 0.1, 1.0, false);

    agent [i].energy -= energyLoss;

    double newEnergy = CalculateEnergy (i);

    if (newEnergy > agent [i].energy)
    {
      agent [i].energy += energyLoss / 2;
      agent [i].hunger = 0;
    }
    else
    {
      agent [i].hunger++;
    }

    double growthRate = maxGrowthRate * agent [i].size / (agent [i].size + halfSaturationConstant);

    agent [i].size *= (1 + growthRate);
  }

  //----------------------------------------------------------------------------
  EvolutionProcess  ();
  AdaptationProcess ();
}
//——————————————————————————————————————————————————————————————————————————————

    EvolutionProcess ()関数について説明しましょう。集団内のエージェントの進化を担っています。この関数の主な目的は、最も適応度の低いエージェント（最も低い藻）を見つけ、その座標を、より適応度の高いランダムなエージェント（より高い藻）の座標に置き換えることです。

    1. 最も適さないエージェントを見つける

    • 変数smallestIndexが初期化されます。最も不適当なエージェントのインデックスが保存されます。初期値は0です。
    • ループはすべてのエージェントを通過し（最初のエージェントから始まる）、その適合を比較します。現在のエージェントの適合が、smallestIndexインデックスを持つエージェントの適合より小さい場合、smallestIndexが更新されます。

    2. 座標をコピーする：

    • ランダムエージェントインデックスを格納するためのm変数が初期化されます。
    • ループは0からcoordsまでのすべての座標を繰り返し処理します。
    • ループの中で、u.RNDminusOne (popSize)メソッドが呼ばれます。0からpopSize 1 までの範囲でm個のランダムインデックスを生成します。
    • その後、smallestIndexインデックスの最も不適合なエージェントの座標は、mインデックスのランダムなエージェントの座標に置き換えられます。

    EvolutionProcess関数は、集団の中で最も適応度の低いエージェントがランダムなエージェントの座標を受け取るという単純な進化メカニズムを実装しています。この操作は適応メカニズムの一部であり、エージェントは他のエージェントからより成功した座標を選択することで、その特性を向上させることができます。一般的には、アルゴリズムの組み合わせ機能を実行します。

    //——————————————————————————————————————————————————————————————————————————————
void C_AO_AAA::EvolutionProcess ()
{
  int smallestIndex = 0;

  for (int i = 1; i < popSize; i++)
  {
    if (agent [i].size < agent [smallestIndex].size) smallestIndex = i;
  }

  int m = 0;

  for (int c = 0; c < coords; c++)
  {
    m = u.RNDminusOne (popSize);

    a [smallestIndex].c [c] = a [m].c [c];
  }
}
//——————————————————————————————————————————————————————————————————————————————

    AdaptationProcess ()関数のコードを詳しく見てみましょう。これは、集団内のエージェントの空腹度とサイズに基づく適応を担当します。この関数の主な目的は、ある適応確率の条件が満たされた場合、最も空腹度の高いエージェントの座標を変更することです。

    1. 最も空腹度の高いエージェント（藻類）を探す：

    • 空腹度の高いエージェントのインデックスを格納するstarvingIndex変数が初期化されます。初期値は0です。
    • ループはすべてのエージェントを（最初のエージェントから）繰り返し、空腹度を比較します。現在のエージェントの空腹度が、starvingIndexのインデックスを持つエージェントの空腹度より大きい場合、starvingIndexが更新されます。

    2. 適応確率のチェック

    • 乱数（確率）を生成するu.RNDprobab ()メソッドが使用されます。この数値が与えられた適応確率(adaptationProbability)より小さい場合、以下のコードブロックが実行されます。

    3. 最高の藻を見つける - エージェント：

    • 最初のステップと同様に、ここでは集団の中で最も高いエージェントの指数を求める。初期状態では、biggestIndexは0に設定されています。
    • ループはすべてのエージェントを通過し、現在のエージェントの方が高ければBiggestIndexをを更新します。

    4. 座標の適応：

    • ループはすべての座標を反復します。
    • starvingIndexのインデックスを持つエージェントの座標は、最も高いエージェントと最も空腹度の高いエージェントの座標の差として計算された値にランダムな確率を掛けた値を加えることによって更新されます。
    • このメソッドは、指定された範囲（rangeMin、rangeMax、rangeStep）内で座標をチェックし、調整します。

    5. エージェントのステータス更新

    • エージェントのサイズは、配列aの適合値fによって更新されます。
    • hungerレベルは0に設定され、エージェントは満腹であることを意味します。
    • エージェントのenergyは1.0に設定されています。これが最大値です。

    AdaptationProcess関数は、確率条件が満たされた場合、最も空腹度の高いエージェントが、最も高いエージェントから座標を借りて、その座標を向上させることができる適応メカニズムを実装しています。これは自然選択を模倣したシステムの一部であり、エージェントは生存の可能性を高めるために環境に適応します。

    //——————————————————————————————————————————————————————————————————————————————
void C_AO_AAA::AdaptationProcess ()
{
  int starvingIndex = 0;

  for (int i = 1; i < popSize; i++) if (agent [i].hunger > agent [starvingIndex].hunger) starvingIndex = i;
  
  if (u.RNDprobab () < adaptationProbability)
  {
    int biggestIndex = 0;

    for (int i = 1; i < popSize; i++) if (agent [i].size > agent [biggestIndex].size) biggestIndex = i;

    for (int j = 0; j < coords; j++)
    {
      a [starvingIndex].c [j] += (a [biggestIndex].c [j] - a [starvingIndex].c [j]) * u.RNDprobab ();

      a [starvingIndex].c [j] = u.SeInDiSp (a [starvingIndex].c [j], rangeMin [j], rangeMax [j], rangeStep [j]);
    }

    agent [starvingIndex].size   = a [starvingIndex].f;
    agent [starvingIndex].hunger = 0;
    agent [starvingIndex].energy = 1.0;
  }
}
//——————————————————————————————————————————————————————————————————————————————

    次に、CalculateEnergy関数のコードです。これは、コロニーの大きさ、エネルギーレベル、栄養濃度などの特徴に基づいて、与えられたエージェントのエネルギーを計算するように設計されています。この関数は、アルゴリズムの他の部分で使用されるエネルギー値を返します。

    1. 変数の初期化

    • colony_size ：indexを使用して藻の高さを取得します。
    • max_growth_rate：最大成長率
    • half_saturation_constant ：飽和定数の半分

    2. 適応度関数の正規化：栄養濃度の正規化値が計算されます。fMaxとfMinの間の範囲に対する、（a配列からの）fとfMinの最小値との差の比率として計算されます。1e-10を加えることで、ゼロ除算を防ぐことができます。

    3. 現在の成長率を得る：current_growth_rate - エージェントのエネルギーの現在値を得る。

    4. 成長率(growth_rate)の計算：最大成長率、正規化栄養濃度、現在の成長率に基づいて計算。この式は飽和効果を考慮しており、現在の成長率が上昇するにつれて成長率は低下します。

    5. エネルギー計算：energyは、growth_rateといくつかのエネルギー損失(energyLoss）の差として計算されます。この値は、ロスを考慮した後のエージェントが受け取るエネルギー量を示しています。

    6. 計算されたエネルギーが負の場合、0に設定されます。これにより、負のエネルギー値を防ぐことができます。

    7. この関数は、計算されたエネルギー値を返します。

    CalculateEnergy関数は、エージェントがその成長速度、コロニーサイズ、および栄養濃度に基づいてエネルギーを獲得するプロセスをモデル化します。また、シミュレーションにおけるエージェントの現実的な挙動を保証するために、エネルギー損失も考慮されています。 

    //——————————————————————————————————————————————————————————————————————————————
double C_AO_AAA::CalculateEnergy (int index)
{
  double colony_size              = agent [index].size;
  double max_growth_rate          = maxGrowthRate;
  double half_saturation_constant = halfSaturationConstant;

  // Use the normalized value of the fitness function
  double nutrient_concentration = (a [index].f - fMin) / (fMax - fMin + 1e-10);

  double current_growth_rate = agent [index].energy;

  double growth_rate = max_growth_rate * nutrient_concentration / (half_saturation_constant + current_growth_rate) * colony_size;

  double energy = growth_rate - energyLoss;

  if (energy < 0) energy = 0;

  return energy;
}
//——————————————————————————————————————————————————————————————————————————————

    最後の方法は、トーナメント選出メカニズムを導入することです。TournamentSelectionメソッドは、適応度関数の値に基づいて、集団から2つの候補のうちの1つを選択します。これは、最高の適合値を持つ候補のインデックスを返します。トーナメントのセレクションはセレクションを提供します。集団内のエージェント間の確率分布についてはすでに述べました。

    //——————————————————————————————————————————————————————————————————————————————
int C_AO_AAA::TournamentSelection ()
{
  int candidate1 = u.RNDminusOne (popSize);
  int candidate2 = u.RNDminusOne (popSize);

  return (a [candidate1].f > a [candidate2].f) ? candidate1 : candidate2;
}
//——————————————————————————————————————————————————————————————————————————————


    テスト結果

    AAAテストスタンドの結果：

    AAA|Algae Adaptive Algorithm|200.0|0.2|0.05|0.1|0.1|
    =============================
    5 Hilly's; Func runs:10000; result:0.5000717048088521
    25 Hilly's; Func runs:10000; result:0.3203956013467087
    500 Hilly's; Func runs:10000; result:0.25525273777603685
    =============================
    5 Forest's; Func runs:10000; result:0.37021025883379577
    25 Forest's; Func runs:10000; result:0.2228350161785575
    500 Forest's; Func runs:10000; result:0.16784823154308887
    =============================
    5 Megacity's; Func runs:10000; result:0.2784615384615384
    25 Megacity's; Func runs:10000; result:0.14800000000000005
    500 Megacity's; Func runs:10000; result:0.097553846153847
    =============================
    All score:2.36063 (26.23%)

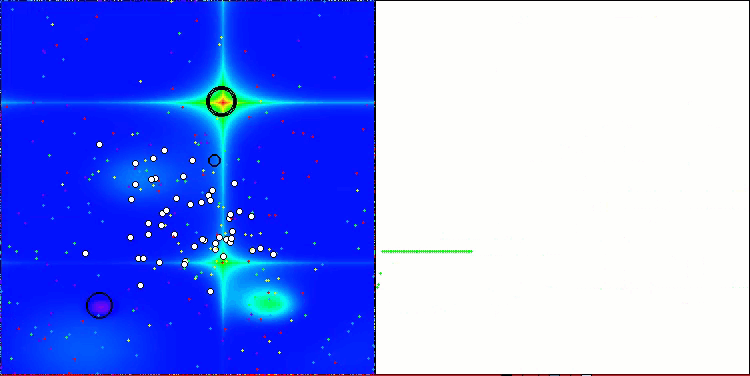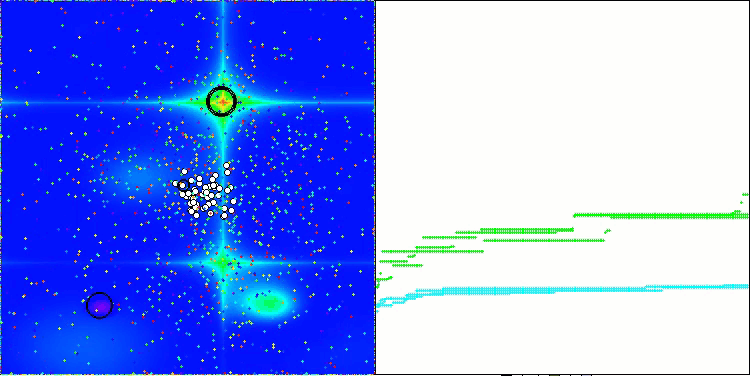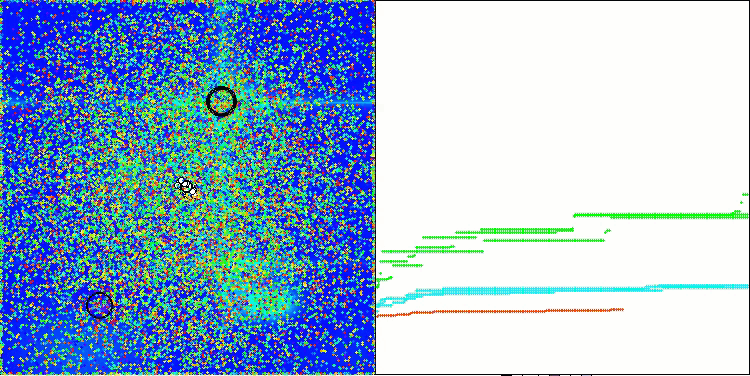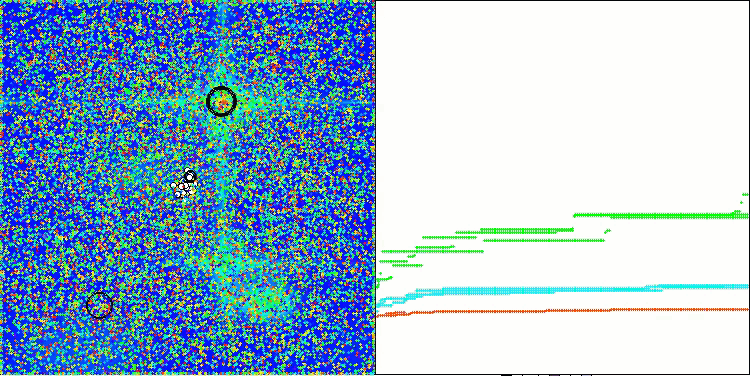
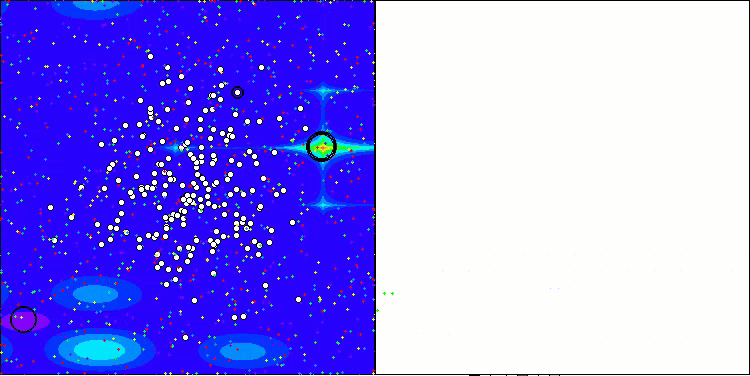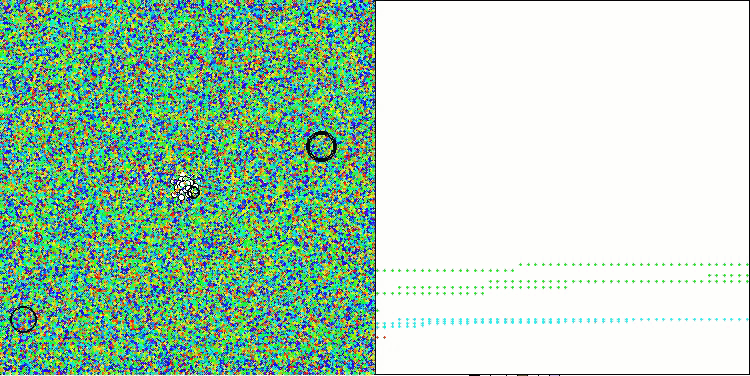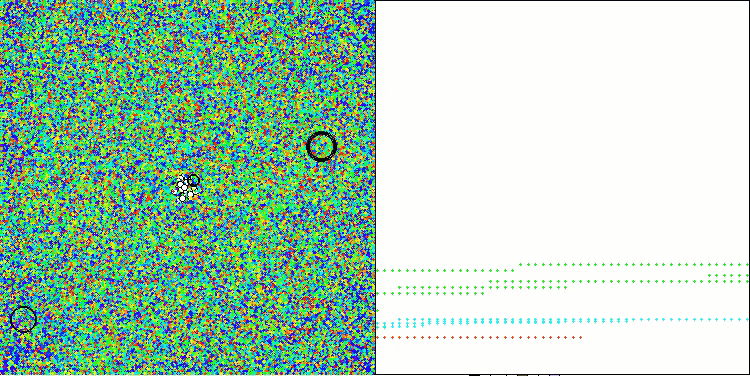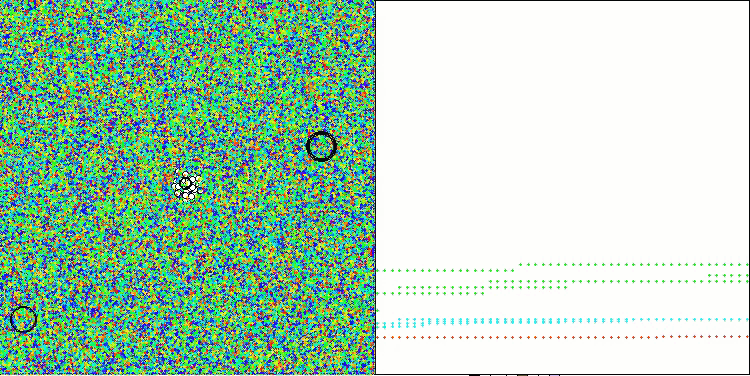
    出力とアルゴリズム動作の視覚化の両方が弱い収束を示しており、これはテスト結果によって確認されました。残念ながら、高い結果を期待していた私の期待は裏切られました。アルゴリズムの複雑な探索戦略を考慮すると、大域的最適解を弱く局所化するため、その非効率性の理由を特定するのは難しいですが、これらの欠点にもかかわらず、このアルゴリズムにはまだ利点があります。

    Hilly

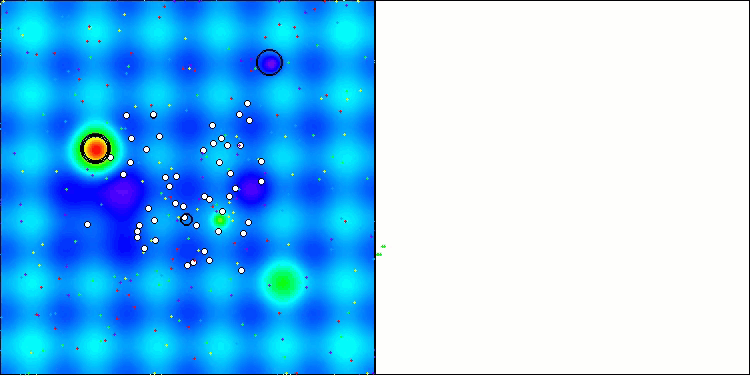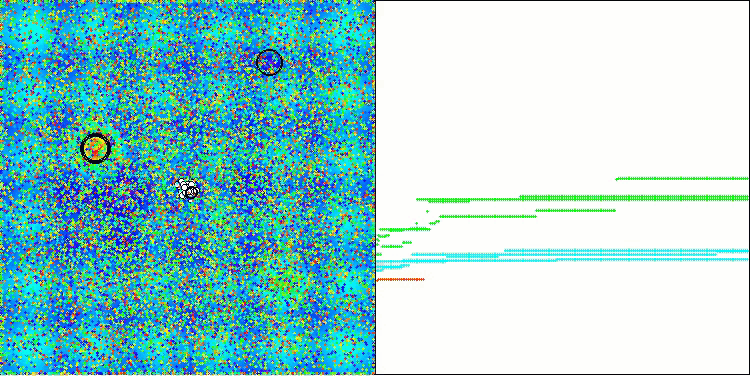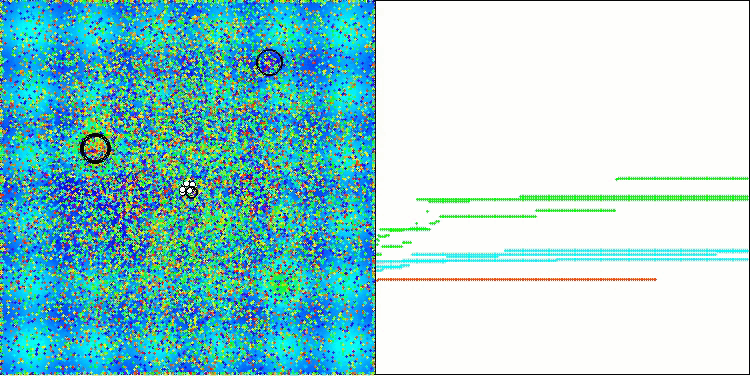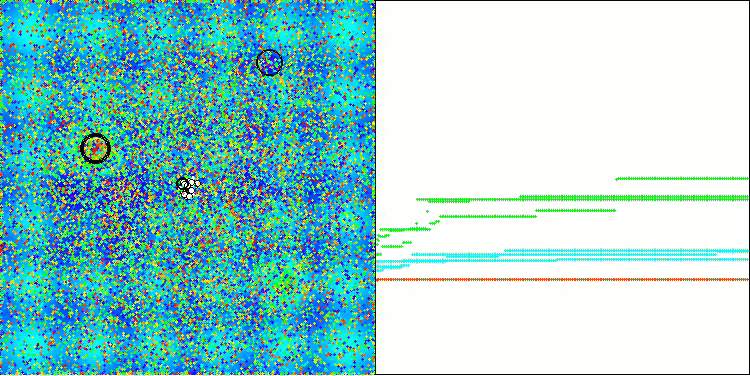
    Hillyテスト関数のAAA

    Forest

    Forestテスト関数のAAA

    Megacity

    Megacityテスト関数のAAA

    テスト結果に基づき、このアルゴリズムは評価表で36位にランクされました。

    # AO 詳細 Hilly Hilly最終 Forest Forest最終 Megacity（離散） Megacity最終 最終結果 MAXの%
    10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F)
    1 ANS across neighbourhood search 0.94948 0.84776 0.43857 2.23581 1.00000 0.92334 0.39988 2.32323 0.70923 0.63477 0.23091 1.57491 6.134 68.15
    2 CLA コードロックアルゴリズム 0.95345 0.87107 0.37590 2.20042 0.98942 0.91709 0.31642 2.22294 0.79692 0.69385 0.19303 1.68380 6.107 67.86
    3 AMOm 動物移動最適化 M 0.90358 0.84317 0.46284 2.20959 0.99001 0.92436 0.46598 2.38034 0.56769 0.59132 0.23773 1.39675 5.987 66.52
    4 (P+O)ES (P+O）進化戦略 0.92256 0.88101 0.40021 2.20379 0.97750 0.87490 0.31945 2.17185 0.67385 0.62985 0.18634 1.49003 5.866 65.17
    5 CTA 彗尾アルゴリズム 0.95346 0.86319 0.27770 2.09435 0.99794 0.85740 0.33949 2.19484 0.88769 0.56431 0.10512 1.55712 5.846 64.96
    6 SDSm 確率的拡散探索M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
    7 ESG 社会母集団の進化 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
    8 SIA 等方的焼きなまし 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
    9 ACS 人工協調探索 0.75547 0.74744 0.30407 1.80698 1.00000 0.88861 0.22413 2.11274 0.69077 0.48185 0.13322 1.30583 5.226 58.06
    10 ASO 無政府社会最適化 0.84872 0.74646 0.31465 1.90983 0.96148 0.79150 0.23803 1.99101 0.57077 0.54062 0.16614 1.27752 5.178 57.54
    11 TSEA 亀甲進化アルゴリズム 0.96798 0.64480 0.29672 1.90949 0.99449 0.61981 0.22708 1.84139 0.69077 0.42646 0.13598 1.25322 5.004 55.60
    12 DE 差分進化 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
    13 CRO 化学反応の最適化 0.94629 0.66112 0.29853 1.90593 0.87906 0.58422 0.21146 1.67473 0.75846 0.42646 0.12686 1.31178 4.892 54.36
    14 BSA 鳥群アルゴリズム 0.89306 0.64900 0.26250 1.80455 0.92420 0.71121 0.24939 1.88479 0.69385 0.32615 0.10012 1.12012 4.809 53.44
    15 HS ハーモニー検索 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
    16 SSG 苗木の播種と育成 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
    17 (PO)ES (PO)進化戦略 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
    18 BSO ブレインストーム最適化 0.93736 0.57616 0.29688 1.81041 0.93131 0.55866 0.23537 1.72534 0.55231 0.29077 0.11914 0.96222 4.498 49.98
    19 WOAm クジラ最適化アルゴリズム M 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
    20 AEFA 人工電界アルゴリズム 0.87700 0.61753 0.25235 1.74688 0.92729 0.72698 0.18064 1.83490 0.66615 0.11631 0.09508 0.87754 4.459 49.55
    21 ACOm 蟻コロニー最適化M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
    22 BFO-GA 細菌採食の最適化：Ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
    23 ABHA 人工蜂の巣アルゴリズム 0.84131 0.54227 0.26304 1.64663 0.87858 0.47779 0.17181 1.52818 0.50923 0.33877 0.10397 0.95197 4.127 45.85
    24 ASBO 適応型社会行動最適化(ASBO) 0.76331 0.49253 0.32619 1.58202 0.79546 0.40035 0.26097 1.45677 0.26462 0.17169 0.18200 0.61831 3.657 40.63
    25 MEC Mind Evolutionary Computation 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
    26 IWO 侵入雑草最適化 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
    27 Micro-AIS 微小人工免疫系 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54
    28 COAm カッコウ最適化アルゴリズムM 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21
    29 SDOm 螺旋ダイナミクス最適化M 0.74601 0.44623 0.29687 1.48912 0.70204 0.34678 0.10944 1.15826 0.42833 0.16767 0.03663 0.63263 3.280 36.44
    30 NMm ネルダー=ミード法M 0.73807 0.50598 0.31342 1.55747 0.63674 0.28302 0.08221 1.00197 0.44667 0.18667 0.04028 0.67362 3.233 35.92
    31 FAm ホタルアルゴリズムM 0.58634 0.47228 0.32276 1.38138 0.68467 0.37439 0.10908 1.16814 0.28667 0.16467 0.04722 0.49855 3.048 33.87
    32 GSA 重力探索法 0.64757 0.49197 0.30062 1.44016 0.53962 0.36353 0.09945 1.00260 0.32667 0.12200 0.01917 0.46783 2.911 32.34
    33 BFO 細菌採餌最適化 0.61171 0.43270 0.31318 1.35759 0.54410 0.21511 0.05676 0.81597 0.42167 0.13800 0.03195 0.59162 2.765 30.72
    34 ABC 人工蜂コロニー 0.63377 0.42402 0.30892 1.36671 0.55103 0.21874 0.05623 0.82600 0.34000 0.14200 0.03102 0.51302 2.706 30.06
    35 BA コウモリアルゴリズム 0.59761 0.45911 0.35242 1.40915 0.40321 0.19313 0.07175 0.66810 0.21000 0.10100 0.03517 0.34617 2.423 26.93
    36 AAA 藻類適応アルゴリズム 0.50007 0.32040 0.25525 1.07572 0.37021 0.22284 0.16785 0.76089 0.27846 0.14800 0.09755 0.52402 2.361 26.23
    37 SA 焼きなまし 0.55787 0.42177 0.31549 1.29513 0.34998 0.15259 0.05023 0.55280 0.31167 0.10033 0.02883 0.44083 2.289 25.43
    38 IWDm intelligent water drops M 0.54501 0.37897 0.30124 1.22522 0.46104 0.14704 0.04369 0.65177 0.25833 0.09700 0.02308 0.37842 2.255 25.06
    39 PSO 粒子群最適化 0.59726 0.36923 0.29928 1.26577 0.37237 0.16324 0.07010 0.60572 0.25667 0.08000 0.02157 0.35823 2.230 24.77
    40 ボイド ボイドアルゴリズム 0.43340 0.30581 0.25425 0.99346 0.35718 0.20160 0.15708 0.71586 0.27846 0.14277 0.09834 0.51957 2.229 24.77
    41 MA モンキーアルゴリズム 0.59107 0.42681 0.31816 1.33604 0.31138 0.14069 0.06612 0.51819 0.22833 0.08567 0.02790 0.34190 2.196 24.40
    42 SFL Shuffled Frog-Leaping 0.53925 0.35816 0.29809 1.19551 0.37141 0.11427 0.04051 0.52618 0.27167 0.08667 0.02402 0.38235 2.104 23.38
    43 FSS 魚群検索 0.55669 0.39992 0.31172 1.26833 0.31009 0.11889 0.04569 0.47467 0.21167 0.07633 0.02488 0.31288 2.056 22.84
    44 RND ランダム 0.52033 0.36068 0.30133 1.18234 0.31335 0.11787 0.04354 0.47476 0.25333 0.07933 0.02382 0.35648 2.014 22.37
    45 GWO 灰色オオカミオプティマイザ 0.59169 0.36561 0.29595 1.25326 0.24499 0.09047 0.03612 0.37158 0.27667 0.08567 0.02170 0.38403 2.009 22.32



    まとめ

    出力は収束度が低いことを示しています。アルゴリズムの機能には少々がっかりしました。複数の方法と複雑なステップ ロジックを使用しているにもかかわらず、結果的に表で最下位になってしまいました。おそらく、使用される方法の量が必ずしも品質を保証するわけではないので、使用される方法にもっと注意を払い、理解する価値があるでしょう。読者の皆さんも自由に試してみてください。もしアルゴリズムがより良い結果を示したら、ぜひ共有してください。記事に対するコメントを楽しみにしています。

    アルゴリズムの良い点としては、最も近い競合アルゴリズムと比較して、1000個の変数を持つForest関数とMegacity関数で良い結果が得られたことが挙げられます。これは、「鋭い」極値を持つ問題や離散的な問題に対するスケーラビリティという点で、アルゴリズムの可能性を示しています。

    タブ

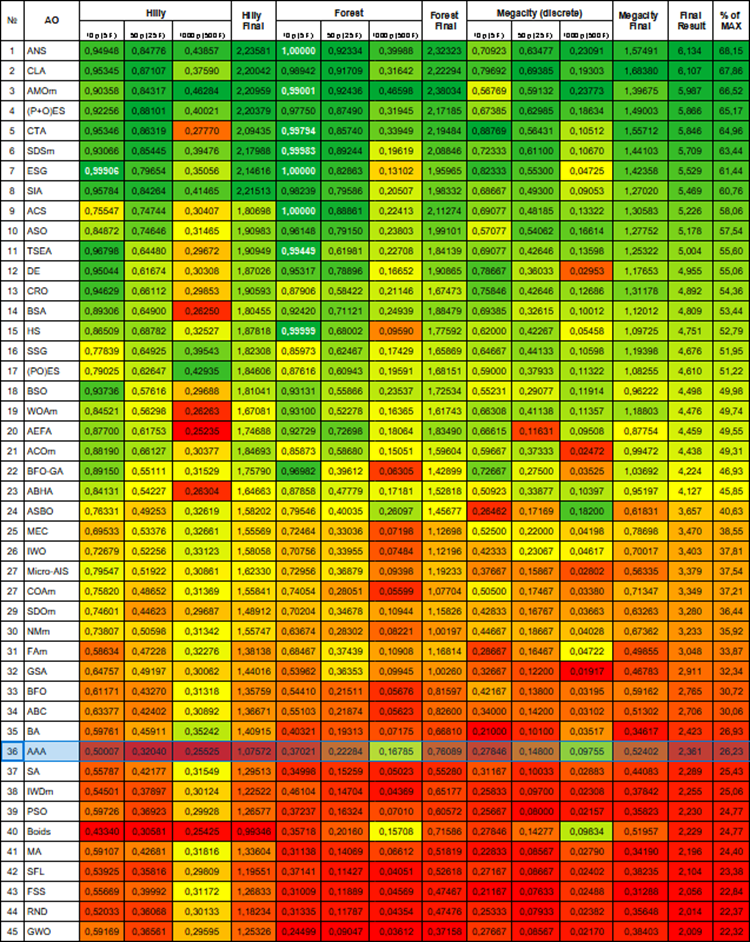
    図1：関連テストによるアルゴリズムのカラーグラデーション 0.99以上の結果は白で強調表示される

    チャート

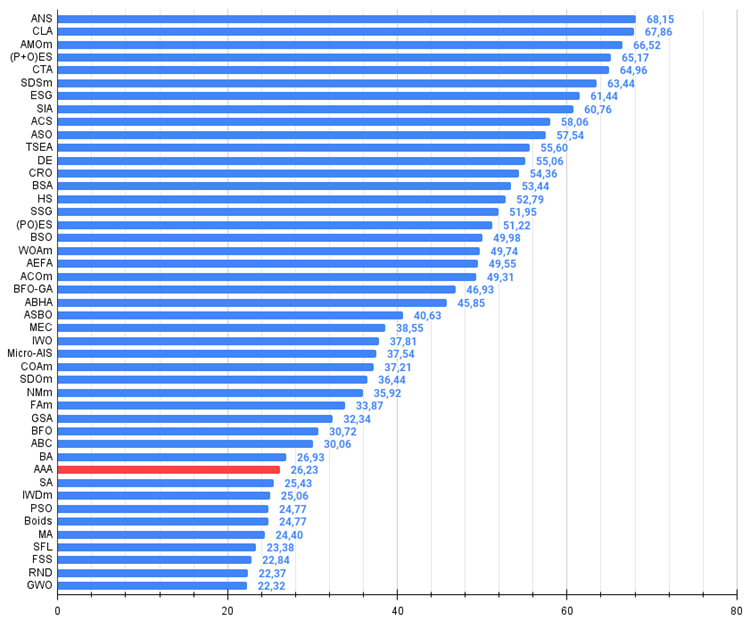
    図2：アルゴリズムのテスト結果のヒストグラム（0から100までのスケールで、多ければ多いほど良い、

    ここで、100は理論的に可能な最大の結果であり、アーカイブにはレーティングテーブルを計算するスクリプトが含まれている)

    AAAの長所と短所

    長所

    1. 有望なアイデアと革新的なアプローチ

    短所

    1. パラメータの数が多い（設定が非常に難しい）
    2. 収束が弱い
    3. デバッグが難しい

    この記事には、最新版のアルゴリズムコードを含むアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。

    MetaQuotes Ltdによってロシア語から翻訳されました。
    元の記事: https://www.mql5.com/ru/articles/15565

    添付されたファイル |
    ZIPをダウンロード
    AAA.zip (31.11 KB)
    警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

    この著者による他の記事

    ディスカッションに移動
    取引におけるニューラルネットワーク：状態空間モデル 取引におけるニューラルネットワーク：状態空間モデル
    これまでにレビューしたモデルの多くは、Transformerアーキテクチャに基づいています。ただし、長いシーケンスを処理する場合には非効率的になる可能性があります。この記事では、状態空間モデルに基づく時系列予測の別の方向性について説明します。
    ウィリアム・ギャンの手法（第2回）：ギャンスクエアインジケーターの作成 ウィリアム・ギャンの手法（第2回）：ギャンスクエアインジケーターの作成
    ギャンのSquare of 9に基づいて、時間と価格を2乗したインジケーターを作成します。コードを準備し、プラットフォームで異なる時間間隔でインジケーターをテストします。
    リプレイシステムの開発（第60回）：サービスの再生(I) リプレイシステムの開発（第60回）：サービスの再生(I)
    これまで長い間インジケーターだけに取り組んできましたが、今度はサービスを再び稼働させて、提供されたデータに基づいてチャートがどのように構築されるかを確認するときが来ました。しかし、すべてがそれほど単純ではないので、先に何が待ち受けているのかを理解するために注意深くならなければなりません。
    無政府社会最適化(ASO)アルゴリズム 無政府社会最適化(ASO)アルゴリズム
    この記事では、無政府社会最適化(ASO)アルゴリズムに触れ、無政府社会（中央集権的な権力や様々な種類のヒエラルキーから解放された社会的相互作用の異常なシステム）の参加者の非合理的で冒険的な行動に基づくアルゴリズムが、解空間を探索し、局所最適の罠を回避できることを議論します。本稿では、連続問題にも離散問題にも適用可能な統一的なASO構造を提示します。